Abstract
Urbanization necessitates Low Impact Development (LID) practices for sustainable development, but existing studies lack analysis about the comprehensive effect and optimal allocation of LID combination practices. To address this gap, this study conducted an in-depth analysis of the runoff control effects of individual and combined LID practices and pollutants under varying retrofit proportions, utilizing the Storm Water Management Model (SWMM). Four evaluation metrics were employed for parameter calibration and validation assessment to ensure the accuracy of the SWMM. The Response Surface Methodology (RSM) was then employed to optimize the retrofit proportions of LID practices due to its high efficiency and statistical rigor. The results showed that, under the same retrofit ratio, bio-retention (BC) has a better runoff reduction rate and pollutant removal rate. For example, when the retrofit proportion is 100%, the runoff pollutant removal rates of BC in Parcel 1 and Parcel 2 are 29.6% and 32.9%, respectively. To achieve a 70% runoff control rate, the optimal retrofit proportions for Parcel 1 were 67.5% for green roofs (GR), 92.2% for permeable pavements (PP), 88.9% for bio-retention cells (BC), and 50% for low-elevation greenbelts (LEG); these correspond to the proportions for Parcel 2 that were 65.1%, 68.1%, 82.0%, and 50%, respectively. In conclusion, this study provides scientific and technical support for urban planners and policymakers in urban rainwater management, especially in similar regions.
1. Introduction
Urbanization is one of the most significant global trends of the 21st century, profoundly changing surface cover and land use patterns, which in turn have far-reaching effects on the urban hydrological cycle [1]. The expansion of impervious surfaces in urban areas leads to a dramatic increase in rainfall runoff volume and accelerated flow rates, overwhelming traditional drainage systems. This results in waterlogging, the pollution of water bodies, and ecological degradation [1]. Low Impact Development (LID) is a design strategy aimed at managing and reducing the environmental impact of urban development by simulating natural hydrological processes [2]. LID not only effectively manages rainwater, reduces flood risks, improves water quality, but also enhances the ecological resilience of cities, making it crucial for urban planning and rainwater management [3]. LID practices have been developed to mitigate the effects of urbanization on the hydrological cycle by emulating natural hydrological processes [4]. Recent LID practices include source control techniques such as rain gardens, permeable pavements, and green roofs, which are effective in controlling rainfall runoff, reducing peak flows, and enhancing water quality by dispersing and delaying the flow of rainfall runoff [5,6]. However, the successful implementation of LID practices is a challenging endeavor, and their efficacy is contingent upon a variety of factors, including the type of practice, scale, layout, and integration with the urban drainage systems [7].
Current research demonstrates that the implementation of LID practices can significantly reduce urban rainfall runoff, lower peak flows, and improve water quality [8]. Su et al. [9] studied a university in Xi’an by setting up a LID facility program, and their results showed that the LID facilities improved the runoff control rate. In the study by Fei et al. [10], 75% of the total suspended solids (TSS) were removed through the proper use of LID. Kim and Kim [11] highlighted the effectiveness of multiple LID practices in reducing runoff and peak flows across varying return periods. Furthermore, the combination and layout of different LID practices significantly affects their effectiveness. Optimal design must account for local climatic conditions, land use characteristics, and the specifics of the urban drainage system [12]. The study conducted by Di Natale et al. [4] discovered that bio-retention cells, permeable pavements, and green roofs are effective in reducing stormwater runoff during the summer months and are equally effective in other seasons, when seasonal and regional factors are taken into account. He et al. [13] investigated the effects of installing LID facilities in cold-climate cities, finding that peak runoff reductions exceeded 40%, following the implementation of various LID practices. The study demonstrated that both non-series and series connections, as well as the strategic placement of LIDs, offer a diverse range of benefits in terms of their combination and layout. Notably, combining LID practices often leads to superior results compared to standalone non-series LID practices. A combination of LID facilities such as vegetated swales, rain barrels, and sunken green spaces are effective in reducing peak flows [14], and a combination of bio-retention and permeable paving systems may prove advantageous in dealing with worsening weather patterns [10]. Zhao et al. [15] proposed a LID approach to vertical construction, combining roof gardens, permeable pavers, and rain barrels to enhance total drainage and runoff control. Although extensive research exists on the design and configuration of LID facility combinations, studies examining the synergies among various LID facilities remain scarce.
Current hydrological studies on LID primarily focus on optimizing LID facility ratios, optimizing LID facility combinations, and evaluating benefits under multi-objective conditions. In the context of optimizing LID facilities, one of the most effective approaches in the current research is combining hydrological models with multi-objective algorithms [16]. Common hydrological models include SWMM, InfoWorks ICM, Hydrus-1D, and MIKE SHE, among others [17,18,19,20,21,22,23,24]. Each model has distinct characteristics and is suited to specific conditions. The choice of an appropriate hydrological model typically depends on the study’s purpose, available data, and geographical area. Multi-objective algorithms are used to simultaneously optimize multiple conflicting objectives. These algorithms generate multiple solutions, helping decision makers balance various optimization objectives. In stormwater management, the commonly used algorithms are Non-dominated Sorting Genetic Algorithm (NSGA) [25], Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO) [26], Simulated Annealing (SA) [27], Response Surface Methodology (RSM), and so on. Currently, the Non-dominated Sorting Genetic Algorithm II (NSGA-II) is widely used in multi-objective optimization. However, NSGA-II calculates dominance relations and the number of dominated solutions, which increases computational complexity. Additionally, when constrained optimization problems arise, NSGA-II may face difficulties in handling them [28]. PSO is prone to becoming stuck in local optima when dealing with problems that have multiple local extrema. It may fail to find the global optimum and is highly sensitive to parameters. If the parameters are not set properly, the algorithm can converge too slowly, prematurely, or fail to converge to the global optimum [29]. When dealing with multiple objectives, existing algorithms often exhibit inefficiencies, and few studies have explored the combination of RSM methods with the optimization of LID practices. RSM is a statistical technique that is employed to investigate the interplay between multiple independent variables and one or more response variables. By leveraging RSM, researchers can identify the optimal solution in complex multivariate systems, thereby enhancing efficiency and effectiveness. RSM possesses the capability to systematically collect and analyze data through statistical models, a capability that enables it to outperform other algorithms in addressing complex problems [30].
In summary, the optimization and synergistic effects of LID practices in response to urbanization challenges is a research direction that warrants further exploration. Therefore, in this study, the software park plot in the eastern part of the core area of the Smart City in the Tianhe District, Guangzhou City, is selected as the study area. There are software technology companies and government service centers in this area, making it vulnerable to floods. In May 2020, the tunnel near the area was flooded, causing casualties and economic losses. The research objectives of this paper are as follows: (1) to calibrate and validate the accuracy of the SWMM based on the on-site monitoring data; (2) to estimate the effect of single LID practices and combined LID practices; (3) to employ RSM to determine the optimal retrofit ratio for each LID practice in the combination scheme. The innovation of this study lies in its focus on not only the individual effects of LID practices, but also on the synergistic effects of different practice combinations and their integrated application at specific regional scales. This research aims to provide a scientific and systematic foundation, along with technical support, for urban rainwater management. Additionally, it seeks to promote sustainable urban development and to offer feasible rainwater management strategies for similar urban environments.
2. Materials and Methods
This research first describes the study area, then evaluates and validates the parameters of the SWMM, which include modular units such as the hydrological-hydraulic module, the water quality module, and the uncertain parameter module. Subsequently, LID practices were implemented in Parcel 1 and Parcel 2, and the effects of both non-series and series LID practices were evaluated. Finally, series LID practices were optimized using RSM to derive the optimal implementation ratio of LID practices. Figure 1 shows the flowchart to better elucidate the article’s research methodology.
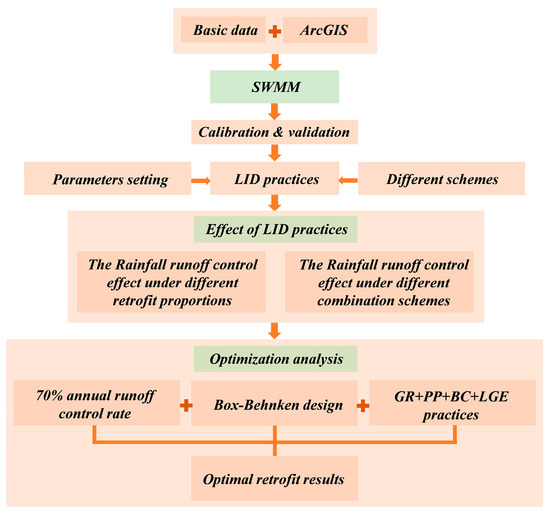
Figure 1.
Frame flowchart of this research.
2.1. Study Area
Guangzhou is situated within the subtropical monsoon climate zone, where short-term and intense rainfall events are frequent, leading to urban flooding issues. As a large city in the subtropical region, its geographical location, climatic conditions, urbanization process, and hydrological characteristics make it vulnerable to floods. Therefore, the flood vulnerability characteristics of Guangzhou can represent other cities with rapid urbanization that are located in coastal or estuarine areas to a certain extent. A typical study area was selected in Guangzhou Tianhe Smart City, covering 17.21 ha. This area serves as one of the pilot sites for sponge city construction in Guangzhou. Based on the layout of the rainfall drainage systems, ground elevations, and slopes, the study area was divided into two drainage sub-areas as follows: the first sub-area covers 11.57 ha and the second sub-area covers 5.64 ha, as depicted in Figure 2a. The impervious surfaces in the study area primarily include roofs, green spaces, permeable paving, roads, and impervious plazas, as shown in Figure 2b. In addition, the proportion of land use types in the study area is as shown in Table S1. The impervious surfaces in the study area primarily include roofs, green spaces, permeable paving, roads, and impervious plazas, as shown in Figure 2b. The study area contains 38 stormwater pipe sections, with a total length of 1632 m. All pipes are concrete circular pipes, with diameters ranging from 0.5 m to 0.8 m and an average slope of 0.0123.
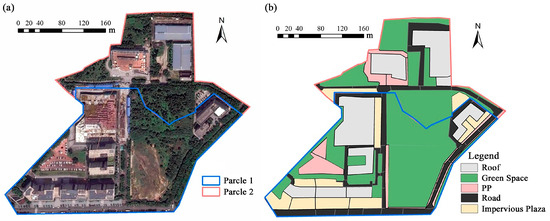
Figure 2.
Study area information: (a) study area parcel delineation; (b) type of subsurface in the study.
2.2. On-Site Monitoring of Rainfall Runoff
To gain insights into the rainfall runoff volume and water quality within the study area, and to provide essential data for determining model parameters, the on-site monitoring of rainfall runoff from various underlying surfaces was conducted. The monitored surfaces included roofs, roads, green spaces, and permeable pavements (PP), as shown in Figure 3. The rainfall runoff monitoring instruments primarily consisted of a tipping bucket rain gauge and a Doppler ultrasonic flow meter. The tipping bucket rain gauge, installed on a rooftop near the research area, had a measurement accuracy of 0.2 mm. The Doppler ultrasonic flow meter, installed at the rainwater discharge outlet, provided a liquid level accuracy of 1% of full scale (FS) and a flow velocity accuracy of 2% FS. The sampling scheme for rainfall runoff and water quality monitoring was as follows: Sampling began at the onset of flow, with one sample collected every 5 min at the outlet of the flow meter. During periods of reduced runoff, the sampling interval was extended as needed until flow ceased. The primary pollutant indicator for runoff and water quality monitoring was SS (suspended solids), measured using a BSA224S electronic balance with an accuracy of one part per ten thousand (ppt), in accordance with the GB/T 11901-1989 Weight Method [31]. Due to the challenges of manual sampling for water quality monitoring, final samples were collected during specific rainfall events, including 3 and 23 July 2018, and 6 March 2019.
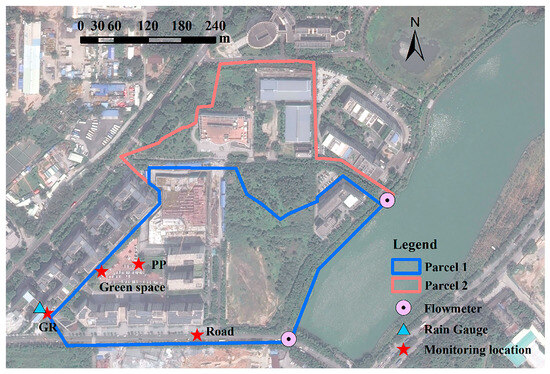
Figure 3.
Rain gauge and flow meter installation locations and sampling locations for each underlayment.
2.3. SWMM Construction
The SWMM (Storm Water Management Model) is a dynamic hydrological and hydraulic simulation model developed by the United States Environmental Protection Agency (EPA) [32]. And it is widely utilized for planning, analyzing, and designing urban drainage systems, particularly with the incorporation of LID practices modules in SWMM V5.1. These modules enable the simulation and analysis of the effects of LID practices on runoff and water quality within the research area [33]. SWMM is a modular model system, which is mainly composed of the runoff module, transport module, extended transport module, storage/processing module, low impact development module, etc. [13] These modules cooperate with each other to realize the comprehensive simulation of the urban drainage system. Using basic data on drainage networks, topography, land use, and remote sensing images, along with ArcGIS 10.8 for data processing, the SWMM for the study area was developed. Subcatchments were delineated based on land use types and surface conditions, with each sub-drainage area representing a single surface condition. The study area was divided into two parcels as follows: Parcel 1, which includes 29 rainwater inspection wells, 29 rainwater pipes, 1 rainwater discharge outlet, and 66 subcatchments; and Parcel 2, which includes 9 rainwater inspection wells, 9 rainwater pipes, 1 rainwater discharge outlet, and 25 subcatchments. The SWMM for the study area is shown in Figure S1.
The modules in the model that require input parameters primarily include the hydrological hydraulic module and the water quality module. For the hydrological hydraulic module, deterministic parameters such as pipe length, slope, and elevation at the pipe bottom are derived from actual collected pipe network data. Similarly, deterministic parameters for subcatchments, including the area, impermeability rate, and slope, are directly calculated using the collected basic data. While the calculation principle for the characteristic width typically involves dividing the drainage area by flow length, this study uses the area square root method to calculate the characteristic width due to challenges in determining flow length during actual operations [34]. The area square root method more accurately reflects actual hydrological processes by considering the geometric features and topographic complexity of the sub-basin. This method enhances the simulation of rainfall runoff distribution and transport, thereby enhancing the model’s accuracy [34]. Additionally, it provides a more precise description of the sub-basin’s hydrological response, enabling more accurate predictions of flood peaks during extreme flood events. Uncertain parameters requiring calibration primarily include the Manning coefficient for permeable areas, the Manning coefficient for impermeable areas, and the depression storage depth. In terms of urban runoff pollutant control indicators, this study uses SS as the pollutant control indicator and calibrates relevant parameters for the following four land use types: roofs, roads, green spaces, and permeable pavements. In the context of urban runoff, SS often correlates with other indicators of pollution [35].
2.4. Calibration and Validation of Model Parameters
2.4.1. Evaluation Indicators
The model parameters were carefully adjusted and verified using the field monitoring data to ensure accuracy. Various evaluation metrics such as the Nash-Sutcliffe efficiency (NSE) [36], relative error coefficient (Re), coefficient of determination (R2), and peak flow relative error coefficient (EPR) were employed for parameter calibration and validation assessment. By combining multiple metrics, we can comprehensively evaluate the performance of the model and avoid the limitations of using a single indicator. Equations (1) to (4) provide the formulas for calculating NSE, Re, R2, and EPR, allowing for a comprehensive analysis of the model’s performance based on these key indicators.
Here, represents the simulation duration; represents the measured flow rate at time; represents the simulated flow rate at time; represents the average measured flow rate over the simulation duration; represents the average simulated flow rate over the simulation duration; represents the peak measured flow rate, m3/s; and represents the peak simulated flow rate, m3/s. Due to the high uncertainty in pollutant concentrations, the calibration and validation of water quality parameters are evaluated using NSE and R2. The calculation formulas for these metrics are the same as those in Equations (1) and (3), except that in these formulas, the flow rate is replaced with pollutant concentration. According to the previous study [37,38], when NSE > 0.5, the model accuracy is satisfactory; when Re ≤ 10%, the model performance is excellent; when 10% ≤ Re ≤ 20%, the model performance is good; when R2 ≥ 0.8, the simulation effect is high-accuracy; and when 20% < EPR ≤ 30%, the simulation accuracy is acceptable.
2.4.2. Hydrological and Hydraulic Parameters
Based on the land use types, surface conditions, and pipe materials of the subcatchment, the initial values for uncertain hydrological and hydraulic parameters were determined by referencing the SWMM user manual [39] and the relevant local research findings [40]. The calibration of these hydrological and hydraulic parameters was subsequently conducted using the following four rainfall events: 27 May 2018, 24 July 2018, 22 July 2019, and 2 September 2020. The dry periods preceding these events were 10 days, 0.5 days, 2 days, and 0.75 days, respectively. The trial-and-error method was used to adjust the hydrological and hydraulic parameters, ensuring that the NSE value of the model simulation results for both parcels during calibration exceeded 0.8 [37,38], while keeping the absolute value of Re within a range of ±20%. Some researchers have shown that an NSE greater than 0.7 indicates a relatively accurate SWMM [41,42]. Following parameter adjustment, the simulated flow values for both parcels during typical rainfall events are presented in Figure 4 and Figure 5. The water hydrological parameters for the two parcels were validated separately using four additional rainfall events, with the calibration and validation results presented in Table S2. The water hydrological parameters for the study area model are displayed in Table S3. From Table S2, it is evident that during both the calibration and validation periods, the NSE values for the water hydrological parameters of the two parcels in the study area all exceeded 0.81, with the absolute value of Re being less than 20%, R2 being greater than 0.83, and EPR less than 23.2%.
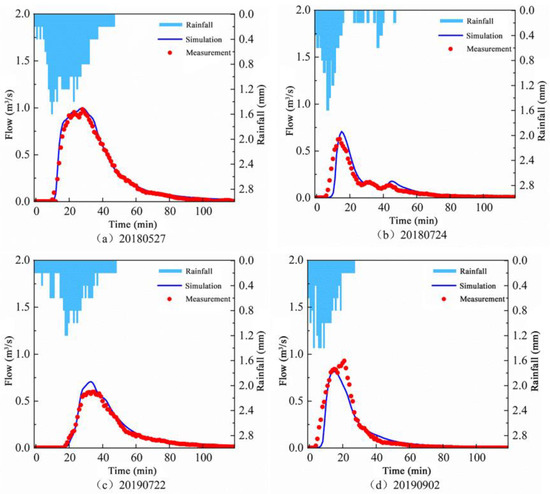
Figure 4.
Comparison of the simulated flow value and the measure flow value in Parcel 1. (a) 20180527, (b) 20180724, (c) 20190722, (d) 20190902.
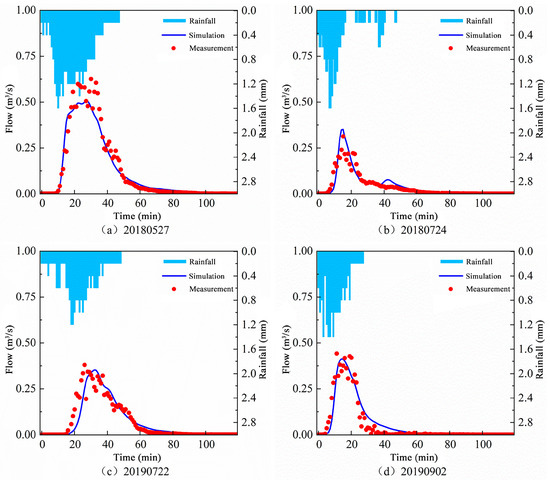
Figure 5.
Comparison of the simulated flow value and the measure flow value in Parcel 2. (a) 20180527, (b) 20180724, (c) 20190722, (d) 20190902.
2.4.3. Water Quality Parameters
The water quality data obtained from sampling and analyzing roofs, roads, green spaces, and permeable pavements as the underlying surfaces were subsequently employed for the calibration and validation of the water quality parameters, with SS serving as the indicator of runoff pollutants. However, there was missing water quality data for roofs during the 20180703 event, and insufficient samples for green spaces and permeable pavements during the 20190306 event. Therefore, calibration was performed using the 20180723 rainfall event data, while validation was conducted using the 20180703 event data for permeable pavements, green spaces, and roads. The roof water quality parameters were validated using data from the 20190306 event. The evaluation results of the model calibration and validation are presented in Table 1, and the obtained water quality parameters are shown in Table 2. The results in both tables indicate that the calibrated model can be used for further simulation analysis. Since no water quality sampling was conducted for the impervious plaza, its parameters could not be calibrated. However, because permeable pavements function similarly to impervious plazas in this study, their water quality parameters were assumed to be identical.

Table 1.
The evaluation results of model calibration and validation.

Table 2.
The obtained water quality parameters.
2.5. Implementation of LID
A variety of LID setting schemes can be developed by integrating different setting ratios and series connections for each LID practice. Consequently, a quantitative assessment of these diverse LID practice combination schemes provides a crucial foundation for investigating regional sponge city construction and LID retrofit. The selection of a suitable combination of LID practices must align with the specific needs of the study region, and LID practices should be implemented in designated areas that are suited for modification.
2.5.1. Suitable Areas for LID Practices
When choosing LID practices, it is essential to assess the actual conditions of the study area and determine the suitability of these practices to logically define the types and scales of the LID implementations. Depending on whether solar panels or machines have been installed on existing roofs, we select the more open roofs to be further improved as green roofs in order to reduce the impact of the retrofit. Similarly, to reduce construction impact and difficulty, non-main roads—particularly those within the district—will be paved beforehand; for the green space with a large catchment area, we will consider ways to transform it into a bio-retention pond.
Based on the actual conditions of the research area, suitable renovation areas and their underlying surface types were determined, as shown in Figure 6a. Pitched roofs and tin roofs (without load-bearing capacity) are not considered for renovation. Regarding road load-bearing capacity, only the internal permeable paved roads are considered for renovation, while the main road is excluded. Renovation is limited to areas that are clearly designated as parks and green belts within the neighborhood, with green spaces intended for future residential construction excluded from the scope. This includes converting roofs into green roofs, renovating damaged permeable pavements, impermeable plazas, and internal roads within residential areas into permeable pavements, as well as transforming some green spaces into low-elevation greenbelts and others into infiltration basins. Renovation areas for various LID practices are illustrated in Figure 6b, with the corresponding areas and their respective proportions detailed in Table S4.
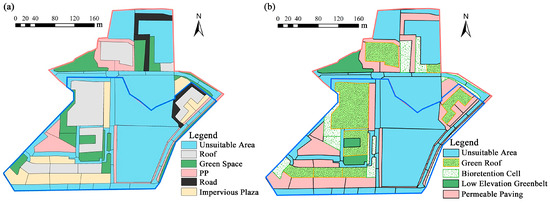
Figure 6.
Site status and suitable areas for LID practices. (a) Underlying surface types of suitable renovation areas; (b) LID practices in renovation areas.
2.5.2. Selection and Setting of LID Practices Parameters
Building on the author’s previous research (LID practice tests [43,44], monitoring [45], and simulation results of individual LID practices [46]), the essential parameters of each LID practice—such as surface retention depth, bank storage, soil layer thickness, and saturated hydraulic conductivity—are determined. Additional parameters are established according to the suggested range in the SWMM user manual [39] and the relevant codes [47,48]. In this study, drainage of the drainage layer is not considered for the bio-retention cell and permeable pavement. Table 3 presents the relevant parameter values for the four LID procedures employed in this investigation.

Table 3.
Parameters of LID practices in the SWMM.
2.6. Response Surface Methodology
Currently, the optimization of LID practice layouts has become a hot topic in the research field, with the core challenge being how to efficiently obtain the optimal Pareto solution set. Traditional intelligent optimization algorithms often rely on extensive computational and iterative processes. In response, this study proposes a novel and practical layout optimization strategy using Response Surface Methodology (RSM) to optimize the retrofit proportion scheme of LID combination practices. RSM, as an effective tool that combines comprehensive experimental design and mathematical statistics, focuses on establishing a functional relationship model between input parameters and complex model output. Through regression analysis, it reveals the optimal levels of various factors, enabling the prediction and optimization of target response values without the need for extensive experimentation. This method has shown significant advantages in fields such as chemical engineering, environmental science, and pharmaceuticals. Abdulgader et al. [49] effectively utilized it to identify the ideal combination of experimental design parameters to achieve the desired target response.
In this study, we selected the annual runoff control rate of two parcels within the study area as the key response indicators and systematically explored the optimal retrofit proportion scheme for LID combination practices using RSM. Through carefully designed experiments and data analysis, our aim is to uncover the impact patterns of different LID practice configuration ratios on annual runoff control effectiveness, ultimately determining the retrofit proportion scheme that achieves the optimal annual runoff control rates. The polynomial regression model equation is shown in Equation (5).
where is the output response value; , ,..., represent the enter variable value; and and represent the coefficients of quadratic term and interactive term, respectively.
In 1960, George E. P. Box and Donald Behnken introduced the Box–Behnken design, an experimental design methodology that is primarily used in RSM [50]. Particularly in experimental designs that involve three or more independent variables, it is utilized to mathematically model the relationship between one or more response variables and multiple independent variables. This design approach is based on the concept of response surface design, which explores the interaction effects between variables and the effects on response variables by setting specific factor levels. After determining the factors to be optimized and their levels, the experimental matrix is generated according to the Box–Behnken design and the experimental response values are recorded. The Box–Behnken design is currently widely used in fields such as industry, drug development, environmental protection, and biotechnology. However, its application in multi-objective optimization in the field of LID remains relatively underexplored. Therefore, the Box–Behnken design method was selected to determine the simulation schemes in this study.
Cross-Validation of the RSM Model
Leave-One-Out Cross-Validation (LOOCV) is a rigorous evaluation method that operates by iteratively excluding individual instances as test sets while training on all the remaining data. This process exhaustively cycles through the entire dataset, making it particularly effective for assessing model robustness in small-scale datasets [51,52]. Based on the combination of LID practices calculated by RSM, the coefficient of determination (R2), mean squared error (MSE), root mean squared error (RMSE), and mean absolute error (MAE) were employed to assess the robustness of the RSM results. The equations are as follows (Equations (6)–(8)):
where is the number of combination schemes, is the actual value, and is the predicted value. According to previous studies [53,54,55,56], when R2 approaches 1 and the values of MSE, RMSE, and MAE are close to 0, this indicates that the model exhibits excellent robustness.
3. Results and Discussion
3.1. The Rainfall Runoff Control Effect Under Different Retrofit Proportions
3.1.1. The Runoff Reduction Effect
Based on the buildable area, the retrofit proportion of each LID practice was set between 0% and 100%. The retrofit proportion of 0% means that the study area has not been transformed by LID practices. The selected rainfall data consist of a design rainfall with a 2-year return period, a rainfall coefficient of 0.4, and a duration of 1 h. The design rainfall was calculated using the Guangzhou rainfall intensity formula and the Chicago rainfall pattern. [57]. The total external drainage volume of the study area was used as the baseline, and then, the runoff volume reduction rate for two parcels under varying proportions of LID practices was calculated based on the model simulation results. The results are shown in Figure 7. As illustrated in Figure 7, as the retrofit proportion of LID practices increases, the runoff volume reduction rate for both parcels increases across all LID practices. This result aligns with the study conclusions of Abdulgader et al. [49].
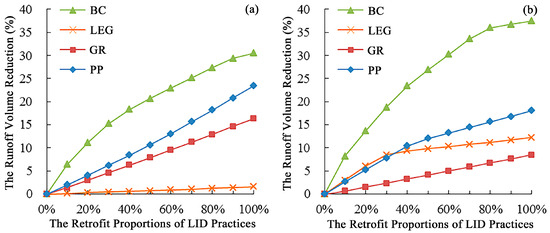
Figure 7.
Runoff volume reduction under different retrofit proportions: (a) Parcel 1; (b) Parcel 2.
In Parcel 1, for the same retrofit proportion, the bio-retention cell exhibits the highest runoff volume reduction rate, followed by permeable pavement and green roofs, while the low-elevation greenbelt shows the lowest rate. When the retrofit proportion is 100%, the runoff volume reduction rates of BC, LRG, GR, and PP are 30.5%, 1.6%, 16.3%, and 23.4%, respectively. In Parcel 1, the bio-retention cell significantly reduces the runoff volume, owing to its robust infiltration and filtering capabilities, with the reduction rate increasing as the LID area expands. Permeable pavement and green roofs show similar reduction rates, with permeable pavement performing slightly better. The low-elevation greenbelt exhibits a lower reduction rate due to its smaller size and limited capacity to capture additional runoff. As the proportion of LID retrofit increases, the reduction rate of the bio-retention cell grows more slowly, while the reduction rates for permeable pavement, low-elevation greenbelt, and green roofs continue to rise.
In Parcel 2, different characteristics are observed. The bio-retention cell has the highest reduction rate due to its large area and high runoff collection capacity, particularly at a 100% retrofit proportion, where it reaches 37.5%. The permeable pavement and green roofs exhibit lower runoff volume reduction rates compared to Parcel 1 due to their smaller areas. The low-elevation greenbelt shows an increased reduction rate because of its ability to collect runoff from nearby areas. The runoff volume reduction rates for different LID practices fluctuate depending on the extent of LID transformation as follows: the bio-retention cell experiences moderate growth from 80% to 100%; permeable pavement and the low-elevation greenbelt show slow growth after reaching a certain proportion; and green roofs exhibit a linear growth rate. In summary, the area, layout, and collection capacity all influence the effectiveness of LID practices.
3.1.2. The Runoff Pollutant Load Removal Effect
To calculate the retrofit proportions of two parcels in the study area under various LID practices, the current pollutant load (using SS as the representative pollutant) of the outflow runoff was considered, as illustrated in Figure 8. The pollutant load removal rates of the two parcels were determined based on the model simulation results.
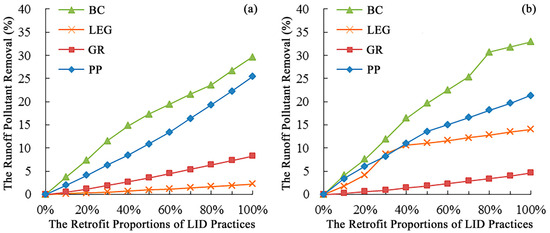
Figure 8.
Runoff pollutant reduction under different retrofit proportions: (a) Parcel 1; (b) Parcel 2.
For Parcel 1, under the same retrofit proportions, bio-retention cells exhibit the highest runoff pollutant load removal rate, followed by permeable pavement and green roofs; meanwhile, low-elevation greenbelts show the lowest rate. Another study also shows that bio-retention cells are the most effective in reducing runoff pollutants [58]. When the retrofit proportion is 100%, the runoff pollutant removal rates of BC, LRG, GR, and PP are 29.6%, 2.2%, 8.2%, and 25.4%, respectively. In Parcel 1, the impact of the LID methods on the removal rate of runoff contaminants parallels their influence on the reduction rate of the runoff volume. The reason for this lies in the SWMM’s water quality simulation for LID practices, which does not directly alter the pollutants’ concentrations within runoff, but rather controls pollution loads by reducing runoff volumes. As a result, there is a close correlation between runoff pollution load removal and volume reduction. However, due to the varying concentrations of pollutants reduced by each LID practice, it is evident that the removal rate of the runoff pollution load does not directly correlate to the volume reduction rates. This is exemplified by the fact that green roofs demonstrate lower pollutant load removal rates compared to their corresponding volume reduction rates.
In the reconstruction of LID practices on Parcel 2, it was observed that the retrofit proportion has a similar impact on both the removal rate of the runoff pollutant load and the reduction rate of runoff volume, with a strong correlation between the two. At a consistent retrofit proportion, the bio-retention cell demonstrates the greatest capacity for removing runoff pollutant load, followed by permeable pavement and low-elevation greenbelts, while green roofs have a relatively weaker removal capacity. When the retrofit proportion is 100%, the runoff pollutant removal rates of BC, LRG, GR, and PP are 32.9%, 14.0%, 4.6%, and 21.3%, respectively. According to the data shown in Figure 8b, within the retrofit proportion range from 0% to 35%, the removal rate of runoff pollutant load for low-elevation greenbelts exhibits a rapid upward trend, reaching a turning point at a 35% retrofit proportion, after which it gradually approaches stable growth.
3.2. The Rainfall Runoff Control Effect Under Different Combination Schemes
3.2.1. Runoff Reduction Effect
LID practices can manage runoff from upstream sub-catchment areas individually or be combined with other LID practices. Numerous studies have demonstrated that combining various LID strategies can enhance runoff management efficacy [9,10,59,60]. The types of LID practices are diverse, and the combination schemes among them are even more complex and varied. Based on the series connection mode of LID practices, this study formulated the following three combination schemes: Scheme 1, where LID practices operate independently with no series connection; Scheme 2, where green roofs are used in series only with bio-retention cells; and Scheme 3, where green roofs are used in series with both bio-retention cells and a low-elevation greenbelt in close proximity. Using the total external discharge volume of the study area as a benchmark and a 100% retrofit ratio for LID practices, simulations were conducted to analyze and calculate the runoff reduction rates for different LID practice combination schemes in the two parcels. The results are presented in Table S5. The results show that for Parcel 1, the order of runoff reduction rates for different LID practice combination schemes during return periods from 0.5a to 2a are as follows: Scheme 3 = Scheme 2 > Scheme 1; while for a return period of 5a, it is Scheme 3 > Scheme 2 > Scheme 1. For a return period of 5a, the order is as follows: Scheme 3 > Scheme 2 > Scheme 1. The data reveal that, in Parcel 1, the runoff reduction rate of Scheme 3 is either comparable to or exceeds that of Scheme 2 and surpasses Scheme 1. As the return period shortens, the runoff reduction capabilities of Schemes 2 and 1 gradually converge. The analysis reveals that the series connection of LID practices enhances the treatment of runoff generated by green roofs, resulting in higher runoff reduction rates for the series connection schemes compared to the non-series connection scheme. This finding is consistent with the conclusions of other studies [61,62]. Furthermore, Scheme 3, which represents a more dispersed series connection of LID practices than Scheme 2, demonstrates superior runoff reduction capabilities during high return periods. For Parcel 2, the runoff reduction rates for different combination schemes during return periods from 0.5a to 5a are in the following order: Scheme 3 = Scheme 2 > Scheme 1, mirroring the results for Parcel 1. This suggests that the runoff reduction capabilities of Schemes 2 and 3 are comparable across both parcels. Additionally, as the return period increases, the runoff reduction rate decreases for all schemes.
3.2.2. The Runoff Pollutant Load Removal Effect
Using the benchmark of the existing external discharge runoff pollution load in the study area, with SS (suspended solids) as the representative pollutant, the runoff pollutant load removal rates for the two parcels under different LID (low-impact development) practice combinations were calculated based on model simulation results, as shown in Table S6. According to Table S6, for Parcel 1, the ranking of runoff pollutant load removal rates for different combination schemes during return periods from 0.5a to 2a is as follows: Scheme 3 = Scheme 2 > Scheme 1. For a return period of 5a, the order is the following: Scheme 3 > Scheme 2 > Scheme 1. These findings indicate that, in Parcel 1, Scheme 3 demonstrates a runoff pollutant load removal rate that is equal to or greater than that of Scheme 2, and superior to that of Scheme 1. As the return period decreases, the runoff pollutant load removal capabilities of Schemes 1 and 2 gradually converge. For Parcel 2, the ranking of runoff pollutant load removal rates for different combination schemes during return periods from 0.5a to 5a remains consistent as follows: Scheme 3 = Scheme 2 > Scheme 1. The similar results across both parcels suggest the comparable runoff pollutant reduction capabilities of Schemes 2 and 3. These outcomes demonstrate that the runoff pollutant load removal rates and runoff volume reduction rates for the two parcels follow similar patterns under different combination schemes. This further illustrates the positive correlation between pollutant load removal and runoff volume reduction in the SWMM simulations. This correlation is rooted in the principles underlying the water quality simulation calculations for LID practices in the SWMM. Gao, et al. [61] demonstrated a strong correlation between the trend of runoff management rates and sediment reduction.
3.3. Optimization Analysis of LID Combination Practices Retrofit Proportion Schemes
3.3.1. Scheme Design and Fitting of Regression Equations
The design factors included the retrofit proportions of green roofs, permeable pavements, bio-retention cells, and low-elevation greenbelts. For each factor, the levels were set to 50%, 75%, and 100%. The simulation outcome (response value) was the annual total runoff control rate. Model simulations for each scheme were conducted using the SWMM, with rainfall data from the monitored rainfall in the study area during 2019. Based on the Box–Behnken design, a total of 29 runs were generated by setting five central points for each parcel. The annual total runoff control rates of these 29 runs for the two parcels were analyzed and presented in Table S7.
Based on the annual runoff volume control rate results of the two parcels under various design schemes, a second-order standard response surface function was employed to conduct a regression equation analysis. The fitted regression equations, which depict the functional relationships between the annual runoff volume control rate and the retrofit proportions of different LID practices for the two parcels, are presented in Equations (9) and (10), respectively.
In the equations, represents the annual runoff volume control rate (%) for Parcel 1, while represents the annual runoff volume control rate (%) for Parcel 2. Additionally, denotes the retrofit proportion (%) of green roofs, represents the retrofit proportion (%) of permeable pavements, indicates the retrofit proportion (%) of bio-retention cells, and signifies the retrofit proportion (%) of low-elevation greenbelts.
To examine the significance and reliability of the regression equation, variance analysis and error statistical analysis were conducted on the fitted regression equation, with the results presented in Table 4. A larger F-value and a smaller p-value indicate a more significant model with better fitting accuracy. As evident from Table 4, the F of the fitted regression models are all greater than 225, and the p is much less than 0.05, suggesting that the adopted second-order standard response surface function is significant and has high fitting accuracy. Furthermore, the error statistical analysis of the regression equation reveals that both R2 and adjusted R2 are greater than 0.999, indicating an excellent correlation with the fitted model. CV is much lower than 1%, demonstrating high credibility and precision, while the precision value exceeds 4, further confirming the robustness of the regression equation. In conclusion, the fitted regression equations are highly significant and reliable, making the established multivariate quadratic model suitable for optimizing the proportion of combined LID practices.

Table 4.
Variance analysis and error statistical analysis of the fitted regression equation.
3.3.2. Validation of the RSM Model
The results of 29 experimental runs of RSM (as shown in Table S7) were statistically confirmed using LOOCV for the model’s robustness, and Table 5 presents the validation results. The RSM model demonstrated robust performance, with R2 values of 0.99953 and 0.99954, MSE values of 0.00551, RMSE values of 0.07427 and 0.07192, and MAE values of 0.04137 and 0.04483. The results indicate that the RSM model demonstrates high predictive accuracy and robustness. Based on the combined results of the LID practices provided by the RSM, 29 datasets were used for the LOOCV. Tables S8 and S9 present detailed information on the actual and predicted values of the RSM model.

Table 5.
Robustness analysis of the RSM model.
3.3.3. Variance and Outlier Analysis
In the ANOVA table (Tables S10 and S11), p-values less than 0.0500 indicate the model terms are significant. Values less than 0.1000 indicate the model terms are significant. The results of the analysis of variance indicate that the interaction between GR and BC (A × B) has a significant effect on the response value (p < 0.0001). In the Residuals and Influence Diagnostic Statistics table (Tables S12 and S13), observations with a Cook’s distance greater than 1 are considered to have strong influence, and values of studentized residuals with an absolute value greater than 3 are considered outliers. As can be seen from the table, all data points fall outside the range of the outliers, indicating no outliers occur.
3.3.4. Optimization Results of the Retrofit Ratio Scheme for LID Combination Practices
In line with the ‘Guangzhou Sponge City Special Plan (2016–2030)’, which mandates that the annual runoff total control rate for Guangzhou should not be lower than 70%, this study sets an optimization target of achieving a 70% annual total runoff control rate. Therefore, the optimization conditions for the LID combination practices are established to attain this 70% runoff control rate with the minimum retrofit ratio. The optimal results are summarized in Table 6. As shown in Table 6, to achieve the 70% target for the annual runoff total control rate in Parcel 1, permeable pavements require a significant retrofit ratio (92.2%), followed by bio-retention cells (88.9%). The low-elevation greenbelt, on the other hand, requires the smallest retrofit ratio (50%). This indicates that permeable pavements and bio-retention cells have a greater impact on runoff control in Parcel 1. In Parcel 2, to meet the target, the retrofit ratio for bio-retention cells is the highest (82.0%). Overall, to reach the 70% annual runoff control target, the required LID retrofit ratio in Parcel 1 is higher than in Parcel 2, with the overall retrofit ratio for the study area falling between the two. Thus, the use of RSM facilitates the determination of the optimal retrofit ratios for LID combination practices in each parcel and for the study area to achieve the desired runoff control targets.

Table 6.
Optimal results of the retrofit ratio scheme for LID combination practices.
3.3.5. Current Limitations and Future Prospects
The effective implementation of LID practices can provide environmental, social, and economic benefits. It efficiently manages pollution and runoff from rainfall, recharges groundwater, and improves the living environment. This study achieves the goal of limiting annual runoff by at least 70% through LID transformation in suitable construction zones. Additionally, we simulated the synergistic effects between different LID practices, offering a novel approach for future low-impact development research by establishing these effects in both series and parallel configurations. Furthermore, the RSM provides the advantages of low cost and high efficiency, presenting a promising alternative for future researchers to consider when applying the algorithm.
However, at the same time, this study does have some limitations. The optimization objectives of the study are limited to the annual total runoff control rate and single pollutant removal efficiency, without considering other important environmental and social economic indicators, such as cost-effectiveness and ecological impact. This may limit the practical applicability of the optimization scheme, as urban planning and decision making typically require a more holistic approach that integrates multiple objectives. Future research will address these gaps by incorporating multi-objective optimization criteria, including cost–benefit analysis, pollutant removal efficiency for various contaminants, and ecological impact, to ensure the comprehensiveness and sustainability of the optimization scheme in real-world applications. Furthermore, the RSM was employed to optimize the retrofit ratio of LID practices, while the Box–Behnken design mitigates extreme factor levels, improving practical applicability but potentially reducing efficiency in analyzing higher-order interactions [63]. Moving forward, future studies will explore the interrelationships between variables and incorporate both local and global optimization methods to achieve more robust and comprehensive outcomes.
In addition, climate change must be considered a significant factor. As climate change intensifies, extreme weather events are expected to occur more frequently, with droughts and floods, in particular, having a considerable impact on natural ecosystems [64,65,66]. For cities in the subtropical monsoon zone, such as Guangzhou, global climate change will lead to the more uneven spatial and temporal distribution of precipitation, thereby increasing the risk of flooding. In the context of climate change, the synergistic effect of combining multiple LID facilities enhances resilience to extreme rainfall and helps mitigate the risks of flooding. However, this does not mean that LID practices will always function efficiently, as these facilities are also vulnerable to the effects of climate change. It has been found that climate change has a greater impact on the short-term performance of LID practices than on their long-term performance [67]. Specifically, short-term heavy rainfall can impose greater runoff regulation pressures, preventing LID practices from fully utilizing their flood peak reduction and rainwater retention functions, thereby increasing the risk of urban flooding. An increase in rainfall intensity can also lead to changes in the runoff coefficients of LID facilities, thereby affecting their effectiveness in infiltrating, retaining, and purifying rainwater. Therefore, the following points should be considered in future research on LID to address the impact of climate change: (1) Conduct a climate risk assessment to enable the more targeted implementation of LID facilities; (2) Adjust and optimize the parameters of various LID practices to enhance their storage capacity for extreme precipitation; (3) Regularly maintain and manage LID practices to ensure their proper functioning.
4. Conclusions
This study developed the SWMM, utilizing fundamental data regarding the drainage network, topography, land use type, and remote sensing imagery of the area under investigation. The relevant parameters were determined and validated using field-monitored water quantity and quality data. Subsequently, based on the specific conditions of the study area, suitable locations for implementing LID practices were identified, and key parameters—such as structural specifications and infiltration coefficients—were established in line with previous research and applicable standards. The study then analyzed the impact of varying LID retrofit proportions on runoff quantity and quality control. The effectiveness of different LID practice combination schemes on runoff control, water quality, and total annual runoff was evaluated. Finally, an optimization analysis of the retrofit proportions for LID combinations was conducted using the Response Surface Methodology (RSM). The main findings are as follows:
- As the proportion of retrofitted LID practices increases, the runoff volume reduction rate and the runoff pollutant load removal rate for each LID practice increase for both parcels. In Parcel 1, at the same retrofit percentage, bio-retention cells have the highest runoff volume reduction and runoff pollutant load removal rates, followed by permeable pavements and green roofs, with the lowest being the low-elevation greenbelt. In Parcel 2, bio-retention cells also lead in runoff volume reduction and pollutant load removal rates, followed by permeable pavements and low-elevation greenbelts, while green roofs show the least impact.
- In Parcel 1, the runoff volume reduction rate and the runoff pollutant load removal rate for Scheme 3 (series connection) are greater than or equal to those of Scheme 2, outperforming the non-series scheme. Both the runoff volume reduction and pollutant load removal rates for Schemes 2 and 3 gradually decrease as the return period increases. In Parcel 2, the runoff volume reduction and pollutant load removal rates for Schemes 2 and 3 are essentially identical and outperform the non-series Scheme 1. The effects on runoff and pollutant control are similar to those observed in Parcel 1.
- The RSM analysis yielded the fitted regression equations correlating the overall yearly runoff control rate with the retrofit proportion of each LID practice for the two parcels and the study region. The optimal retrofit proportions for each parcel and the study area were identified to achieve the target for total annual runoff control. For instance, to reach the 70% total annual runoff control rate in Parcel 1, the optimal retrofit proportions for green roofs, permeable pavements, bio-retention cells, and low-elevation greenbelts are 67.5%, 92.2%, 88.9%, and 50%, respectively. For Parcel 2, the corresponding retrofit proportions are 65.1%, 68.1%, 82.0%, and 50%.
This research also provides scientific data to support urban planners and policymakers. Based on the data from LID practices, urban planners can more effectively allocate resources, such as prioritizing the application of LID facilities in areas with high flood vulnerability, thereby improving urban flood control and drainage capacity. Furthermore, future research will incorporate climate change as a critical factor in the analysis, while considering additional optimization objectives to achieve more comprehensive results.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su17052015/s1, Figure S1. SWMM generalization of the study area. Table S1. The proportion of land use types in the study area. Table S2. The calibration and validation evaluation results of the water hydrological parameters. Table S3. The water hydrological parameters of the study area model. Table S4. Suitable area for each LID practice and its proportion of the area. Table S5. Runoff reduction rates under different LID practices combination schemes for two parcels. Table S6. Runoff pollutant load removal rates under different combinations of LID practices. Table S7. Simulation schemes and results of RSM. Table S8. Robustness analysis of RSM model in Parcel 1. Table S9. Robustness analysis of RSM model in Parcel 2. Table S10. Variance analysis results of runoff reduction rate in Parcel 1. Table S11. Variance analysis results of runoff reduction rate in Parcel 1. Table S12. Residuals and Influence Diagnostic Statistics in Parcel 1. Table S13. Residuals and Influence Diagnostic Statistics in Parcel 2.
Author Contributions
Data analysis, Writing—Reviewing and Editing, and Funding acquisition, Y.M. (Yepeng Mai); Writing—original draft and Formal analysis, X.M.; Writing—original draft and Investigation, F.C.; Investigation and Conceptualization, Y.M. (Yelin Mai); Methodology, G.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Guangdong Basic and Applied Basic Research Foundation (2023A1515010754) and the Start-up Scientific Research Foundation from Hainan University (KYQD (ZR) 23131).
Institutional Review Board Statement
This study does not involve humans or animals.
Informed Consent Statement
This study does not involve humans.
Data Availability Statement
Data will be made available upon request.
Acknowledgments
We would also like to sincerely extend our thanks and acknowledgement to the reviewers who provided editorial suggestions and comments.
Conflicts of Interest
Author Yelin Mai was employed by Hainan Hualong Tongguling Tourism Holding Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LID | Low Impact Development |
| SWMM | Storm Water Management Model |
| RSM | Response Surface Methodology |
| NSGA | Non-dominated Sorting Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| ACO | Ant Colony Optimization |
| SA | Simulated Annealing |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| FS | Full Scale |
| TSS | Total Suspended Solids |
| SS | Suspended Solids |
| NSE | Nash-Sutcliffe efficiency |
| PP | Permeable Pavements |
| GR | Green Roofs |
| BC | Bio-retention Cells |
| LEG | Low-elevation Greenbelt |
| TN | Total Nitrogen |
| TP | Total Phosphorus |
References
- Le Floch, N.; Pons, V.; Abdalla, E.M.H.; Alfredsen, K. Catchment scale effects of low impact development implementation scenarios at different urbanization densities. J. Hydrol. 2022, 612, 128178. [Google Scholar] [CrossRef]
- Boongaling, C.G.K.; Sevilla-Nastor, J.B.; Espaldon, M.V.O.; Sanchez, P.A.J.; Villanueva-Peyraube, J.D.; Jago-on, K.A.B. Assessment of low impact development (LID) strategies under different land uses in an urban sub-catchment in the Philippines. J. Environ. Manag. 2024, 369, 122328. [Google Scholar] [CrossRef]
- Liao, Z.L.; Zhang, G.Q.; Wu, Z.H.; He, Y.; Chen, H. Combined sewer overflow control with LID based on SWMM: An example in Shanghai, China. Water Sci. Technol. 2015, 71, 1136–1142. [Google Scholar] [CrossRef]
- Di Natale, C.M.; Tamm, O.; Koivusalo, H. Climate change adaptation using low impact development for stormwater management in a Nordic catchment. Boreal Environ. Res. 2023, 28, 243–258. [Google Scholar]
- Kaykhosravi, S.; Khan, U.T.; Jadidi, M.A. A simplified geospatial model to rank LID solutions for urban runoff management. Sci. Total Environ. 2022, 831, 154937. [Google Scholar] [CrossRef]
- Shannak, S.d. Assessment of Low-Impact development for managing aquatic ecosystem. Ecol. Indic. 2021, 132, 108235. [Google Scholar] [CrossRef]
- Ashofteh, P.-S.; Dougaheh, M.P. Ranking the optimal combination of low-impact urban development systems under climate change with the TODIM multi-criteria decision-making method. J. Clean. Prod. 2024, 434, 140108. [Google Scholar] [CrossRef]
- Nazari, A.; Roozbahani, A.; Shahdany, S.M.H. Integrated SUSTAIN-SWMM-MCDM Approach for Optimal Selection of LID Practices in Urban Stormwater Systems. Water Resour. Manag. 2023, 37, 3769–3793. [Google Scholar] [CrossRef]
- Su, J.H.; Li, J.K.; Gao, X.J.; Yao, Y.T.; Jiang, C.B. Comprehensive analysis of waterlogging control and carbon emission reduction for optimal LID layout: A case study in campus. Environ. Sci. Pollut. Res. 2022, 29, 87802–87816. [Google Scholar] [CrossRef]
- Fei, Y.; Rene, E.R.; Shang, Q.; Singh, R.P. Comprehensive effect evaluation of LID facilities implemented in sponge campuses: A case study. Ecol. Indic. 2023, 155, 110912. [Google Scholar] [CrossRef]
- Kim, H.; Kim, G. An Effectiveness Study on the Use of Different Types of LID for Water Cycle Recovery in a Small Catchment. Land 2021, 10, 1055. [Google Scholar] [CrossRef]
- Mehri, M.; Shahdany, S.M.H.; Javadi, S.; Movahedinia, M.; Berndtsson, R. Block-scale use of bioretention cells to restore the urban water balance: A case study in Tehran metropolis. J. Hydrol.-Reg. Stud. 2024, 51, 101621. [Google Scholar] [CrossRef]
- He, L.; Li, S.; Cui, C.H.; Yang, S.S.; Ding, J.; Wang, G.Y.; Bai, S.W.; Zhao, L.; Cao, G.L.; Ren, N.Q. Runoff control simulation and comprehensive benefit evaluation of low-impact development strategies in a typical cold climate area. Environ. Res. 2022, 206, 112630. [Google Scholar] [CrossRef]
- Rong, G.W.; Hu, L.Y.; Wang, X.; Jiang, H.L.; Gan, D.N.; Li, S.S. Simulation and evaluation of low-impact development practices in university construction: A case study of Anhui University of Science and Technology. J. Clean. Prod. 2021, 294, 126232. [Google Scholar] [CrossRef]
- Zhou, Q.; Feng, J.; Feng, W.E. How does flow connection path and vertical spatial layout of LIDs affect urban runoff? A new LID construction method based on refined landuse and hydrologic characterization. J. Hydrol. 2023, 623, 129809. [Google Scholar] [CrossRef]
- Zhang, X.; Jia, H. Low impact development planning through a comprehensive optimization framework: Current gaps and future perspectives. Resour. Conserv. Recycl. 2023, 190, 106861. [Google Scholar] [CrossRef]
- Behrouz, M.S.; Sample, D.J.; Yazdi, M.N. Robustness of storm water management model parameter sets for dry and wet hydroclimatic conditions. J. Clean. Prod. 2023, 411, 137328. [Google Scholar] [CrossRef]
- Chen, Y.; Hou, H.; Li, Y.; Wang, L.; Fan, J.; Wang, B.; Hu, T. Urban Inundation under Different Rainstorm Scenarios in Lin′an City, China. Int. J. Environ. Res. Public Health 2022, 19, 7210. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Sim, H.; Hong, S.; Geem, Z.W.; Aksoy, H.; Hong, Y.; Yoon, J. Comparative Evaluation of Evapotranspiration and Optimization Schemes for Green Roof Runoff Simulations Using HYDRUS-1D. Water 2024, 16, 2835. [Google Scholar] [CrossRef]
- Lagos, M.S.; Munoz, J.F.; Suarez, F.I.; Fuenzalida, M.J.; Yanez-Morroni, G.; Sanzana, P. Investigating the effects of channelization in the Silala River: A review of the implementation of a coupled MIKE-11 and MIKE-SHE modeling system. Wiley Interdiscip. Rev.-Water 2024, 11, e1673. [Google Scholar] [CrossRef]
- Stafford, M.J.; Hollaender, H.M.; Dow, K. Estimating groundwater recharge in the assiniboine delta aquifer using HYDRUS-1D. Agric. Water Manag. 2022, 267, 107514. [Google Scholar] [CrossRef]
- Wang, B.; Li, S.; Ge, Y. Numerical Simulation of the Lower and Middle Reaches of the Yarkant River (China) Using MIKE SHE. Water 2023, 15, 2492. [Google Scholar] [CrossRef]
- Wei, H.; Wu, H.; Zhang, L.; Liu, J. Urban flooding simulation and flood risk assessment based on the InfoWorks ICM model: A case study of the urban inland rivers in Zhengzhou, China. Water Sci. Technol. 2024, 90, 1338–1358. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.; Liu, Z.; Liu, D.; Huang, Q.; Xia, J. Coupling a Distributed Time Variant Gain Model into a Storm Water Management Model to Simulate Runoffs in a Sponge City. Sustainability 2023, 15, 3804. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, C.; Xu, T.; Jia, H.; Zhang, X.; Chen, Z.; Yin, D. Integrating socioecological indexes in multiobjective intelligent optimization of green-grey coupled infrastructures. Resour. Conserv. Recycl. 2021, 174, 105801. [Google Scholar] [CrossRef]
- Hou, J.; Hou, B.; Sun, S. Spatial Optimization of Low-Impact Development Facilities Based on a p-Median Model and an Ant Colony Optimization. J. Hydrol. Eng. 2019, 24. [Google Scholar] [CrossRef]
- She, L.; Wei, M.; You, X.-y. Multi-objective layout optimization for sponge city by annealing algorithm and its environmental benefits analysis. Sustain. Cities Soc. 2021, 66, 102706. [Google Scholar] [CrossRef]
- Kidanu, R.A.; Cunha, M.; Salomons, E.; Ostfeld, A. Improving Multi-Objective Optimization Methods of Water Distribution Networks. Water 2023, 15, 2561. [Google Scholar] [CrossRef]
- van Zyl, J.-P.; Engelbrecht, A.P. Set-Based Particle Swarm Optimisation: A Review. Mathematics 2023, 11, 2980. [Google Scholar] [CrossRef]
- Szpisjak-Gulyas, N.; Al-Tayawi, A.N.; Horvath, Z.H.; Laszlo, Z.; Kertesz, S.; Hodur, C. Methods for experimental design, central composite design and the Box-Behnken design, to optimise operational parameters: A review. Acta Aliment. 2023, 52, 521–537. [Google Scholar] [CrossRef]
- GB/T 11901-1989; Water Quality. Determination of Suspended Substance. Gravimetric Method. Chinese Standard: Beijing, China, 1989.
- Zhuang, Q.; Li, M.; Lu, Z. Assessing runoff control of low impact development in Hong Kong’s dense community with reliable SWMM setup and calibration. J. Environ. Manag. 2023, 345, 118599. [Google Scholar] [CrossRef]
- Kong, Z.; Shao, Z.; Shen, Y.; Zhang, X.; Chen, M.; Yuan, Y.; Li, G.; Wei, Y.; Hu, X.; Huang, Y.; et al. Comprehensive evaluation of stormwater pollutants characteristics, purification process and environmental impact after low impact development practices. J. Clean. Prod. 2021, 278, 123509. [Google Scholar] [CrossRef]
- Zhou, Y.; Yu, M.; Chen, Y. Estimation of Sub-catchment Width in SWMM. China Water Wastewater 2014, 30, 61–64. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development. Technical Guidelines for Sponge City Construction—Construction of Rainwater System for Low-Impact Development (Trial); Ministry of Housing and Urban-Rural Development: Beijing, China, 2014. [Google Scholar]
- Gong, Y.; Li, X.; Zhai, D.; Yin, D.; Song, R.; Li, J.; Fang, X.; Yuan, D. Influence of Rainfall, Model Parameters and Routing Methods on Stormwater Modelling. Water Resour. Manag. 2018, 32, 735–750. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.1; United States Environmental Protection Agency: Washington, DC, USA, 2015; Volume 353. [Google Scholar]
- Ren, X.; Tang, W. Application of Capture Ratio of Total Annual Runoff Volume in Spongy City. China Water Wastewater 2015, 31, 105–109. [Google Scholar] [CrossRef]
- Li, Y.; Huang, J.J.; Hu, M.; Yang, H.; Tanaka, K. Design of low impact development in the urban context considering hydrological performance and life-cycle cost. J. Flood Risk Manag. 2020, 13, e12625. [Google Scholar] [CrossRef]
- Masseroni, D.; Cislaghi, A.; Camici, S.; Massari, C.; Brocca, L. A reliable rainfall-runoff model for flood forecasting: Review and application to a semi-urbanized watershed at high flood risk in Italy. Hydrol. Res. 2017, 48, 726–740. [Google Scholar] [CrossRef]
- Mai, Y.; Huang, G. Hydrology and rainfall runoff pollutant removal performance of biochar-amended bioretention facilities based on field-scale experiments in lateritic red soil regions. Sci. Total Environ. 2021, 761, 143252. [Google Scholar] [CrossRef] [PubMed]
- Mai, Y.; Zhang, M.; Chen, W.; Chen, X.; Huang, G.; Li, D. Experimental study on the effects of LID measures on the control of rainfall runoff. Urban Water J. 2018, 15, 827–836. [Google Scholar] [CrossRef]
- Mai, Y.; Zhao, X.; Huang, G. Temporal and spatial variability of water quality in an urban wetland and the effects of season and rainfall: A case study in the Daguan Wetland, China. Environ. Monit. Assess. 2022, 194, 347. [Google Scholar] [CrossRef]
- Mai, Y.; Huang, G.; Xie, H.; Zeng, B.; Ma, X. Study on rainwater runoff control effect of LID measures based on Hydrus-1D. J. Hydraul. Eng. 2022, 53, 811–822. [Google Scholar] [CrossRef]
- DB440100/T 114-2007; Code for Construction and Acceptance of Urban Greening. Guangzhou Municipal Forestry and Landscaping Bureau: Guangzhou, China, 2007.
- CJJ/T 188-2012; Technical Specification for Pavement of Water Permeable Brick. China Architecture & Building Press: Beijing, China, 2012.
- Abdulgader, M.; Yu, J.; Zinatizadeh, A.A.; Williams, P.; Rahimi, Z. Process analysis and optimization of single stage flexible fibre biofilm reactor treating milk processing industrial wastewater using response surface methodology (RSM). Chem. Eng. Res. Des. 2019, 149, 169–181. [Google Scholar] [CrossRef]
- Box, G.E.P.; Behnken, D.W. Some New Three Level Designs for the Study of Quantitative Variables. Technometrics 1960, 2, 455–475. [Google Scholar] [CrossRef]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Üncü, Y.A.; Danışman, T.; Özdoğan, H. Predicting (n,3n) nuclear reaction cross-sections using XGBoost and Leave-One-Out Cross-Validation. Appl. Radiat. Isot. 2025, 219, 111714. [Google Scholar] [CrossRef] [PubMed]
- Robinson, T.P.; Metternicht, G. Testing the performance of spatial interpolation techniques for mapping soil properties. Comput. Electron. Agric. 2006, 50, 97–108. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Garosi, Y.; Ayoubi, S.; Nussbaum, M.; Sheklabadi, M. Effects of different sources and spatial resolutions of environmental covariates on predicting soil organic carbon using machine learning in a semi-arid region of Iran. Geoderma Reg. 2022, 29, e00513. [Google Scholar] [CrossRef]
- Araz, O.U.; Kemiklioglu, E.; Gurboga, B. Modeling of the lyotropic cholesteric liquid crystal based toxic gas sensor using adaptive neuro-fuzzy inference systems. Expert Syst. Appl. 2024, 240, 122326. [Google Scholar] [CrossRef]
- Li, J.; Deng, C.; Li, H.; Ma, M.; Li, Y. Hydrological Environmental Responses of LID and Approach for Rainfall Pattern Selection in Precipitation Data-Lacked Region. Water Resour. Manag. 2018, 32, 3271–3284. [Google Scholar] [CrossRef]
- Rong, Q.; Liu, Q.; Yue, W.; Xu, C.; Su, M. Optimal design of low impact development at a community scale considering urban non-point source pollution management under uncertainty. J. Clean. Prod. 2024, 434, 139934. [Google Scholar] [CrossRef]
- Yang, W.; Brueggemann, K.; Seguya, K.D.; Ahmed, E.; Kaeseberg, T.; Dai, H.; Hua, P.; Zhang, J.; Krebs, P. Measuring performance of low impact development practices for the surface runoff management. Environ. Sci. Ecotechnol. 2020, 1, 100010. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Zhang, T.; Li, J.; Zhang, L.; Feng, P. Numerical simulation study of urban hydrological effects under low impact development with a physical experimental basis. J. Hydrol. 2023, 618, 129191. [Google Scholar] [CrossRef]
- Gao, J.; Li, J.; Li, Y.; Xia, J.; Lv, P. A Distribution Optimization Method of Typical LID Facilities for Sponge City Construction. Ecohydrol. Hydrobiol. 2021, 21, 13–22. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, H.; Liu, H.; Zhou, B. The Application of Low Impact Development Facility Chain on Storm Rainfall Control: A Case Study in Shenzhen, China. Water 2021, 13, 3375. [Google Scholar] [CrossRef]
- Narukulla, S.; Bogadi, S.; Tallapaneni, V.; Sanapalli, B.K.R.; Sanju, S.; Khan, A.A.; Malik, A.; Barai, H.R.; Mondal, T.K.; Karri, V.V.S.R.; et al. Comparative study between the Full Factorial, Box-Behnken, and Central Composite Designs in the optimization of metronidazole immediate release tablet. Microchem. J. 2024, 207, 111875. [Google Scholar] [CrossRef]
- Suresh, A.; Pekkat, S.; Subbiah, S. Quantifying the efficacy of Low Impact Developments (LIDs) for flood reduction in micro-urban watersheds incorporating climate change. Sustain. Cities Soc. 2023, 95, 104601. [Google Scholar] [CrossRef]
- Zamani, M.G.; Saniei, K.; Nematollahi, B.; Zahmatkesh, Z.; Poor, M.M.; Nikoo, M.R. Developing sustainable strategies by LID optimization in response to annual climate change impacts. J. Clean. Prod. 2023, 416, 137931. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, W.; Feng, Q.; Zeng, J. Multi-objective optimization of the spatial layout of green infrastructures with cost-effectiveness analysis under climate change scenarios. Sci. Total Environ. 2024, 948, 174851. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, J.; Krebs, P. Low impact development practices mitigate urban flooding and non-point pollution under climate change. J. Clean. Prod. 2022, 347, 131320. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).