Machine Learning to Forecast Airborne Parietaria Pollen in the North-West of the Iberian Peninsula
Abstract
1. Introduction
2. Materials and Methods
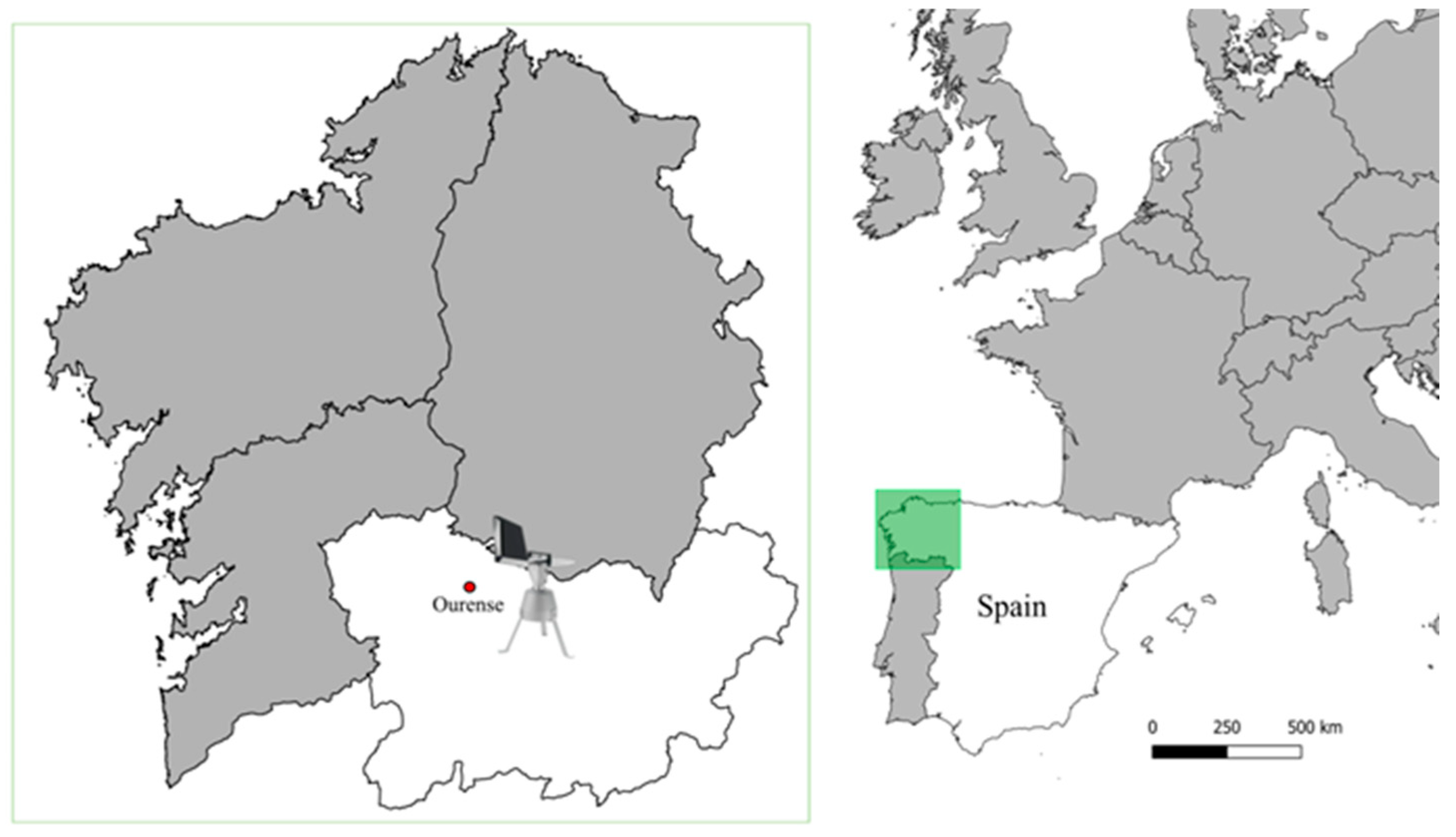
2.1. Location, Study Area, and Climatic Characterization of the Study Area
2.2. Pollen Study and Meteorological Variables
2.3. Machine Learning Model Development
2.3.1. Procedure Carried Out
2.3.2. Random Forest
2.3.3. Support Vector Machine
2.3.4. Artificial Neural Network
2.4. Data Processing and Statistical Analysis
2.5. Computer Resources and Software Used for Modelling Parietaria Pollen
3. Results
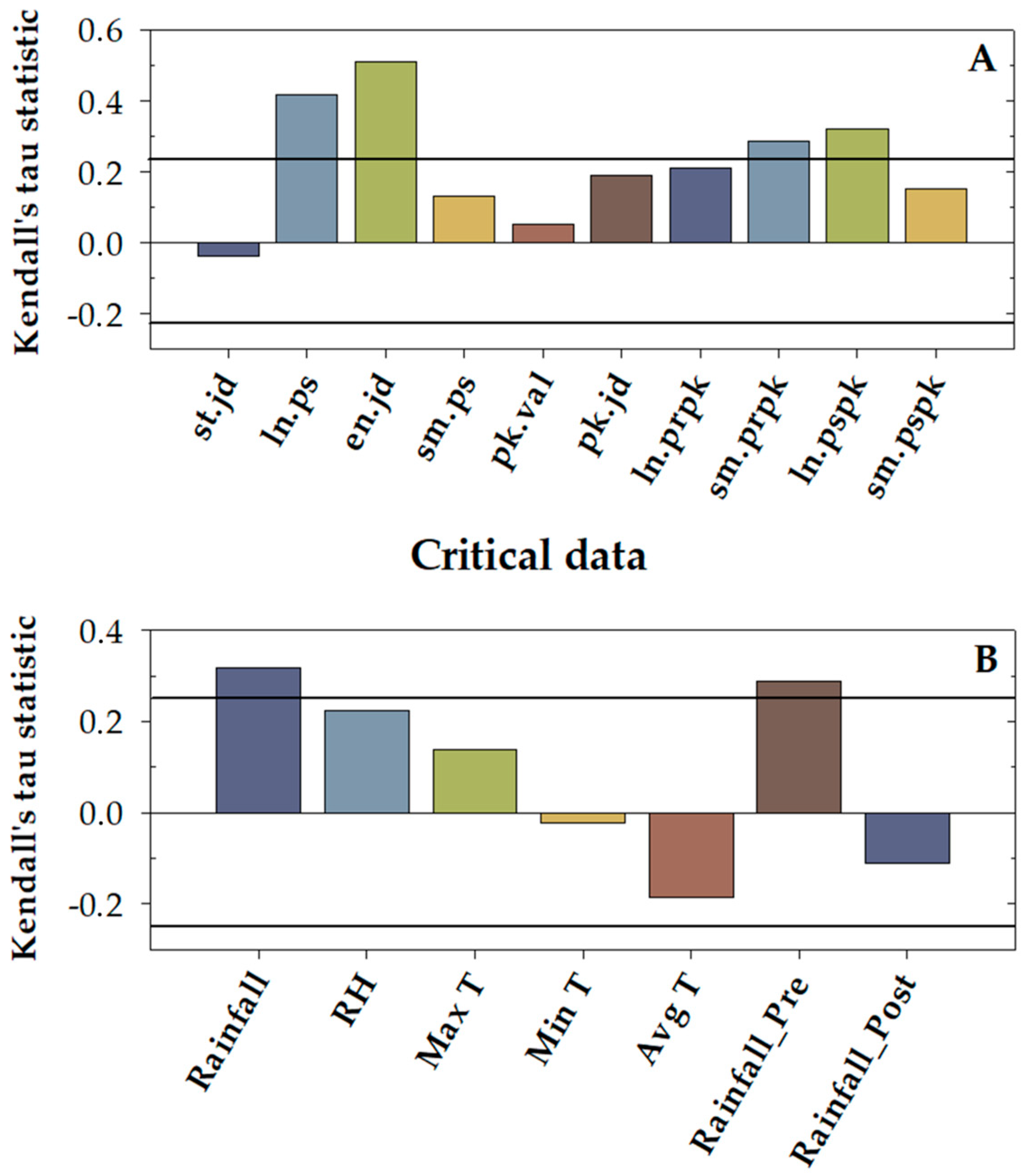
3.1. Parietaria Main Pollen Season Trends and Meteorological Trends
3.2. Prediction One Day Ahead
3.3. Prediction Two Days Ahead
3.4. Prediction Three Days Ahead
4. Discussion
- Study the possibility of increasing the number of input variables, not only by using variables different from those used in the present research, but also variables that include a time scale and backwards, as could have been seen in the paper carried out by Voukantsis et al. (2010) [94];
- The authors understand that increasing the number of years in the database would be a positive fact, but it would be interesting to study the variation in the number years in the training, validation, and consultation groups to see how this modification could alter the results obtained;
- Likewise, it would also be advisable to study a variation in the hyperparameters analyzed in this research, not only by increasing their ranges, but also by analyzing a different step series and even incorporating new hyperparameters;
- Another interesting point to consider when improving prediction models would be to explore techniques such as the stacking or blending models. This procedure could allow for the taking advantage of the strengths of each base model when creating a combined model, allowing for improved prediction performance;
- Finally, it would be interesting to develop a pollen neural network aimed at predicting the pollen concentration, not at a specific point, but rather in an extensive region, to see how geographic location and altitude could modify the performance of the developed models.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| end.jd | End of the MPS |
| ln.prpk | Length of the pre-peak period |
| ln.ps | Length of the pollen season |
| ln.pspk | Length of the post-peak period |
| MPS | Main Pollen Season |
| pk.jd | Pollen peak day |
| pk.val | Pollen peak |
| sm.prpk | Pollen integral of the pre-peak period |
| sm.ps | Pollen integral |
| sm.pspk | Pollen integral of the post-peak period |
| SPIn | Seasonal Pollen Integral |
| st.jd | Onset of the MPS |
| SDGs | Sustainable Development Goals |
| ANN | Artificial neural network |
| ANNL | Artificial neural network with logarithmic scale |
| ANNR | Artificial neural network with range normalization and linear scale |
| ANNR-L | Artificial neural network with range normalization and logarithmic scale |
| ANNZ | Artificial neural network with Z transformation and linear scale |
| ANNZ-L | Artificial neural network with Z transformation and logarithmic scale |
| DTs | Decision trees |
| RF | Random forest |
| RFR | Random forest with range normalization |
| RFZ | Random forest with Z normalization |
| SVM | Support vector machine with linear scale |
| SVML | Support vector machine with logarithmic scale |
| SVMR | Support vector machine with range normalization and linear scale |
| SVMR-L | Support vector machine with range normalization and logarithmic scale |
| SVMZ | Support vector machine with Z transformation and linear scale |
| SVMZ-L | Support vector machine with Z transformation and logarithmic scale |
| MAE | Mean absolute error |
| r | Correlation coefficient |
| RMSE | Root mean square error |
References
- Hornick, T.; Richter, A.; Harpole, W.S.; Bastl, M.; Bohlmann, S.; Bonn, A.; Bumberger, J.; Dietrich, P.; Gemeinholzer, B.; Grote, R.; et al. An Integrative Environmental Pollen Diversity Assessment and Its Importance for the Sustainable Development Goals. Plants People Planet 2022, 4, 110–121. [Google Scholar] [CrossRef]
- Morton, S.; Pencheon, D.; Squires, N. Sustainable Development Goals (SDGs), and Their Implementation: A National Global Framework for Health, Development and Equity Needs a Systems Approach at Every Level. Br. Med. Bull. 2017, 124, 81–90. [Google Scholar] [CrossRef] [PubMed]
- Blaiss, M.S. Allergic Rhinitis: Direct and Indirect Costs. Allergy Asthma Proc. 2010, 31, 375–380. [Google Scholar] [CrossRef] [PubMed]
- Katelaris, C.H.; Sacks, R.; Theron, P.N. Allergic Rhinoconjunctivitis in the Australian Population: Burden of Disease and Attitudes to Intranasal Corticosteroid Treatment. Am. J. Rhinol. Allergy 2013, 27, 506–509. [Google Scholar] [CrossRef]
- Dwarakanath, D.; Milic, A.; Beggs, P.J.; Wraith, D.; Davies, J.M. A Global Survey Addressing Sustainability of Pollen Monitoring. World Allergy Organ. J. 2024, 17, 100997. [Google Scholar] [CrossRef]
- Pereira, C.; Cadahía, O.L.A. MESA REDONDA: POLINOSIS III Polinosis Por Parietaria. Alergol. Inmunol. Clin. 2003, 18, 61–85. [Google Scholar]
- Crimi, P.; Macrina, G.; Folli, C.; Bertoluzzo, L.; Brichetto, L.; Caviglia, I.; Fiorina, A. Correlation between Meteorological Conditions and Parietaria Pollen Concentration in Alassio, North-West Italy. Int. J. Biometeorol. 2004, 49, 13–17. [Google Scholar] [CrossRef]
- De Linares, C.; Alcázar, P.; Valle, A.M.; Díaz de la Guardia, C.; Galán, C. Parietaria Major Allergens vs Pollen in the Air We Breathe. Environ. Res. 2019, 176, 108514. [Google Scholar] [CrossRef]
- Del Trigo, M.M.; Rodríguez, M.V.J.; González, D.F.; Galán, C. Atlas Aeropalinológico de España; Secretariado de publicaciones de la Universidad de Leon: Leon, Spain, 2008; pp. 145–155. [Google Scholar]
- Guardia, R.; Belmonte, J. Phenology and Pollen Production of Parietaria judaica L. in Catalonia (NE Spain). Grana 2004, 43, 57–64. [Google Scholar] [CrossRef]
- Jato, V.; Fernández, I.I.; Aira, M.J. Atlas de Polen Alergógeno: Datos Aerobiologicos de Galicia (1993–1999). In Consellería de Medio Ambiente; Xunta de Galicia: Santiago de Compostela, Spain, 2001; ISBN 84-453-3058-6. [Google Scholar]
- Masullo, M.; Mariotta, S.; Torrelli, L.; Graziani, E.; Anticoli, S.; Mannino, F. Respiratory Allergy to Parietaria Pollen in 348 Subjects. Allergol. Immunopathol. 1996, 24, 3–6. [Google Scholar]
- Hájková, L.; Možný, M.; Bartošová, L.; Dížková, P.; Žalud, Z. A Prediction of the Beginning of the Flowering of the Common Hazel in the Czech Republic. Aerobiologia 2023, 39, 21–35. [Google Scholar] [CrossRef]
- Iglesias-Otero, M.A.; Astray, G.; Vara, A.; Galvez, J.F.; Mejuto, J.C.; Rodriguez-Rajo, F.J. Forecasting Olea Airborne Pollen Concentration by Means of Artificial Intelligence. Fresenius Environ. Bull. 2015, 24, 4574–4580. [Google Scholar]
- Galán, C.; Cariñanos, P.; Alcázar, P.; Domínguez, E. Manual de Calidad y Gestión de La Red Española de Aerobiología; Servicio de Publicaciones de la Universidad de Córdoba: Córdoba, Spain, 2007; ISBN 9788469063545. [Google Scholar]
- Fischer, B.; Hartwich, C. Flora Ibérica. Plantas Vasculares de La Península Ibérica e Islas Baleares. Hagers Handb. Pharm. Prax. 2012, 49, 563. [Google Scholar] [CrossRef]
- Li, C.; Polling, M.; Cao, L.; Gravendeel, B.; Verbeek, F.J. Analysis of Automatic Image Classification Methods for Urticaceae Pollen Classification. Neurocomputing 2023, 522, 181–193. [Google Scholar] [CrossRef]
- Zhong, J.; Xiao, R.; Wang, P.; Yang, X.; Lu, Z.; Zheng, J.; Jiang, H.; Rao, X.; Luo, S.; Huang, F. Identifying Influence Factors and Thresholds of the next Day’s Pollen Concentration in Different Seasons Using Interpretable Machine Learning. Sci. Total Environ. 2024, 935, 173430. [Google Scholar] [CrossRef]
- Bastl, M.; Bastl, K.; Karatzas, K.; Aleksic, M.; Zetter, R.; Berger, U. The Evaluation of Pollen Concentrations with Statistical and Computational Methods on Rooftop and on Ground Level in Vienna—How to Include Daily Crowd-Sourced Symptom Data. World Allergy Organ. J. 2019, 12, 100036. [Google Scholar] [CrossRef]
- Ritenberga, O.; Sofiev, M.; Siljamo, P.; Saarto, A.; Dahl, A.; Ekebom, A.; Sauliene, I.; Shalaboda, V.; Severova, E.; Hoebeke, L.; et al. A Statistical Model for Predicting the Inter-Annual Variability of Birch Pollen Abundance in Northern and North-Eastern Europe. Sci. Total Environ. 2018, 615, 228–239. [Google Scholar] [CrossRef] [PubMed]
- Khwarahm, N.R.; Dash, J.; Skjøth, C.A.; Newnham, R.M.; Adams-Groom, B.; Head, K.; Caulton, E.; Atkinson, P.M. Mapping the Birch and Grass Pollen Seasons in the UK Using Satellite Sensor Time-Series. Sci. Total Environ. 2017, 578, 586–600. [Google Scholar] [CrossRef]
- García-Mozo, H.; Yaezel, L.; Oteros, J.; Galán, C. Statistical Approach to the Analysis of Olive Long-Term Pollen Season Trends in Southern Spain. Sci. Total Environ. 2014, 473–474, 103–109. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Rajo, F.J.; Valencia-Barrera, R.M.; Vega-Maray, A.M.; Suárez, F.J.; Fernández-González, D.; Jato, V. Prediction of Airborne Alnus Pollen Concentration by Using ARIMA Models. Ann. Agric. Environ. Med. 2006, 13, 25–32. [Google Scholar]
- Muzalyova, A.; Brunner, J.O.; Traidl-Hoffmann, C.; Damialis, A. Forecasting Betula and Poaceae Airborne Pollen Concentrations on a 3-Hourly Resolution in Augsburg, Germany: Toward Automatically Generated, Real-Time Predictions. Aerobiologia 2021, 37, 425–446. [Google Scholar] [CrossRef]
- Mills, S.A.; Maya-Manzano, J.M.; Tummon, F.; MacKenzie, A.R.; Pope, F.D. Machine Learning Methods for Low-Cost Pollen Monitoring–Model Optimisation and Interpretability. Sci. Total Environ. 2023, 903, 165853. [Google Scholar] [CrossRef] [PubMed]
- Lo, F.; Bitz, C.M.; Hess, J.J. Development of a Random Forest Model for Forecasting Allergenic Pollen in North America. Sci. Total Environ. 2021, 773, 145590. [Google Scholar] [CrossRef]
- Martínez Cortizas, A.; Pérez Alberti, A. Atlas Climático de Galicia; Xunta de Galicia: Santiago de Compostela, Spain, 1999; ISBN 8445326112. [Google Scholar]
- Rodríguez Guitián, M.A.; Ramil-Rego, P. Clasificaciones Climáticas Aplicadas a Galicia: Revisión Desde Una Perspectiva Biogeográfica. Recur. Rurais 2018, 1, 31–53. [Google Scholar] [CrossRef]
- Agencia Estatal Meteorolia. AEMet Guía Resumida Del Clima En España (1981–2010); Agencia Estatal Meteorolia: Madrid, Spain, 2012; pp. 1–110. [Google Scholar]
- Hirst, J.M. An Automatic Volumetric Spore Trap. Ann. Appl. Biol. 1952, 39, 257–265. [Google Scholar] [CrossRef]
- Galán, C.; Ariatti, A.; Bonini, M.; Clot, B.; Crouzy, B.; Dahl, A.; Fernandez-González, D.; Frenguelli, G.; Gehrig, R.; Isard, S.; et al. Recommended Terminology for Aerobiological Studies. Aerobiologia 2017, 33, 293–295. [Google Scholar] [CrossRef]
- Andersen, T.B. A Model to Predict the Beginning of the Pollen Season. Grana 1991, 30, 269–275. [Google Scholar] [CrossRef]
- Vergni, L.; Todisco, F. A Random Forest Machine Learning Approach for the Identification and Quantification of Erosive Events. Water 2023, 15, 2225. [Google Scholar] [CrossRef]
- Breda, L.S.; de Melo Nascimento, J.E.; Alves, V.; de Alencar Arnaut de Toledo, V.; de Lima, V.A.; Felsner, M.L. Green and Fast Prediction of Crude Protein Contents in Bee Pollen Based on Digital Images Combined with Random Forest Algorithm. Food Res. Int. 2024, 179, 113958. [Google Scholar] [CrossRef] [PubMed]
- Babenko, V.; Nastenko, I.; Pavlov, V.; Horodetska, O.; Dykan, I.; Tarasiuk, B.; Lazoryshinets, V. Classification of Pathologies on Medical Images Using the Algorithm of Random Forest of Optimal-Complexity Trees. Cybern. Syst. Anal. 2023, 59, 346–358. [Google Scholar] [CrossRef]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Machado, G.; Mendoza, M.R.; Corbellini, L.G. What Variables Are Important in Predicting Bovine Viral Diarrhea Virus? A Random Forest Approach. Vet. Res. 2015, 46, 85. [Google Scholar] [CrossRef] [PubMed]
- Keshtegar, B.; Heddam, S.; Sebbar, A.; Zhu, S.-P.; Trung, N.-T. SVR-RSM: A Hybrid Heuristic Method for Modeling Monthly Pan Evaporation. Environ. Sci. Pollut. Res. 2019, 26, 35807–35826. [Google Scholar] [CrossRef] [PubMed]
- Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hossain, M.E.; Khan, A.; Moni, M.A.; Uddin, S. Use of Electronic Health Data for Disease Prediction: A Comprehensive Literature Review. IEEE/ACM Trans. Comput. Biol. Bioinforma. 2021, 18, 745–758. [Google Scholar] [CrossRef] [PubMed]
- Lovatti, B.P.O.; Nascimento, M.H.C.; Neto, Á.C.; Castro, E.V.R.; Filgueiras, P.R. Use of Random Forest in the Identification of Important Variables. Microchem. J. 2019, 145, 1129–1134. [Google Scholar] [CrossRef]
- Kang, B.; Seok, C.; Lee, J. Prediction of Molecular Electronic Transitions Using Random Forests. J. Chem. Inf. Model. 2020, 60, 5984–5994. [Google Scholar] [CrossRef]
- Fang, Z.; Yu, X.; Zeng, Q. Random Forest Algorithm-Based Accurate Prediction of Chemical Toxicity to Tetrahymena Pyriformis. Toxicology 2022, 480, 153325. [Google Scholar] [CrossRef]
- Lam, K.-L.; Cheng, W.-Y.; Su, Y.; Li, X.; Wu, X.; Wong, K.-H.; Kwan, H.-S.; Cheung, P.C.-K. Use of Random Forest Analysis to Quantify the Importance of the Structural Characteristics of Beta-Glucans for Prebiotic Development. Food Hydrocoll. 2020, 108, 106001. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X.; Zhang, Z.; Han, Q.; Deng, H.; Jiang, Y.; Tang, C.; Yang, L. Support Vector Machine Deep Mining of Electronic Medical Records to Predict the Prognosis of Severe Acute Myocardial Infarction. Front. Physiol. 2022, 13, 991990. [Google Scholar] [CrossRef] [PubMed]
- Bisgin, H.; Bera, T.; Ding, H.; Semey, H.G.; Wu, L.; Liu, Z.; Barnes, A.E.; Langley, D.A.; Pava-Ripoll, M.; Vyas, H.J.; et al. Comparing SVM and ANN Based Machine Learning Methods for Species Identification of Food Contaminating Beetles. Sci. Rep. 2018, 8, 6532. [Google Scholar] [CrossRef]
- Battineni, G.; Chintalapudi, N.; Amenta, F. Machine Learning in Medicine: Performance Calculation of Dementia Prediction by Support Vector Machines (SVM). Inform. Med. Unlocked 2019, 16, 100200. [Google Scholar] [CrossRef]
- Wang, J.; Tian, G.; Tao, Y.; Lu, C. Prediction of Chongqing’s Grain Output Based on Support Vector Machine. Front. Sustain. Food Syst. 2023, 7, 1015016. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, X.; Fang, Z.; Yu, X. Support Vector Machine-Based Global Classification Model of the Toxicity of Organic Compounds to Vibrio Fischeri. Molecules 2023, 28, 2703. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 17 October 2022).
- Muravyev, N.V.; Luciano, G.; Ornaghi, H.L.; Svoboda, R.; Vyazovkin, S. Artificial Neural Networks for Pyrolysis, Thermal Analysis, and Thermokinetic Studies: The Status Quo. Molecules 2021, 26, 3727. [Google Scholar] [CrossRef]
- An, J.; Qin, F.; Zhang, J.; Ren, Z. Explore Artificial Neural Networks for Solving Complex Hydrocarbon Chemistry in Turbulent Reactive Flows. Fundam. Res. 2022, 2, 595–603. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.R.; Chaudhury, S. Texture Analysis for Rice Grain Classification Using Wavelet Decomposition and Back Propagation Neural Network; Dawn, S., Balas, V.E., Esposito, A., Gope, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 55–65. [Google Scholar]
- Przybył, K.; Gawałek, J.; Koszela, K. Application of Artificial Neural Network for the Quality-Based Classification of Spray-Dried Rhubarb Juice Powders. J. Food Sci. Technol. 2023, 60, 809–819. [Google Scholar] [CrossRef] [PubMed]
- Rojo, J.; Picornell, A.; Oteros, J. AeRobiology: The Computational Tool for Biological Data in the Air. Methods Ecol. Evol. 2019, 10, 1371–1376. [Google Scholar] [CrossRef]
- RStudio Team. RStudio: Integrated Development Environment for R; RStudio Team: Boston, MA, USA, 2021. [Google Scholar]
- Wang, W.; Lu, Y. Analysis of the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) in Assessing Rounding Model. IOP Conf. Ser. Mater. Sci. Eng. 2018, 324, 012049. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A.G. The Correlation Coefficient: An Overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Forrest, J.R.K. Plant–Pollinator Interactions and Phenological Change: What Can We Learn about Climate Impacts from Experiments and Observations? Oikos 2015, 124, 4–13. [Google Scholar] [CrossRef]
- Díaz, S.; Settele, J.; Brondízio, E.S.; Ngo, H.T.; Guèze, M.; Agard, J.; Arneth, A.; Balvanera, P.; Brauman, K.A.; Butchart, S.H.M.; et al. IPBES Summary for Policymakers of the Global Assessment Report on Biodiversity and Ecosystem Services; Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services: Bonn, Germany. [CrossRef]
- Linneberg, A.; Dam Petersen, K.; Hahn-Pedersen, J.; Hammerby, E.; Serup-Hansen, N.; Boxall, N. Burden of Allergic Respiratory Disease: A Systematic Review. Clin. Mol. Allergy 2016, 14, 12. [Google Scholar] [CrossRef]
- Zuberbier, T.; Lötvall, J.; Simoens, S.; Subramanian, S.V.; Church, M.K. Economic Burden of Inadequate Management of Allergic Diseases in the European Union: A GA2LEN Review. Allergy 2014, 69, 1275–1279. [Google Scholar] [CrossRef]
- Eisenman, T.S.; Jariwala, S.P.; Lovasi, G.S. Urban Trees and Asthma: A Call for Epidemiological Research. Lancet Respir. Med. 2019, 7, e19–e20. [Google Scholar] [CrossRef] [PubMed]
- Treudler, R.; Zeynalova, S.; Kirsten, T.; Engel, C.; Loeffler, M.; Simon, J.-C. Living in the City Centre Is Associated with Type 1 Sensitization to Outdoor Allergens in Leipzig, Germany. Clin. Respir. J. 2018, 12, 2686–2688. [Google Scholar] [CrossRef]
- Ziska, L.H.; Makra, L.; Harry, S.K.; Bruffaerts, N.; Hendrickx, M.; Coates, F.; Saarto, A.; Thibaudon, M.; Oliver, G.; Damialis, A.; et al. Temperature-Related Changes in Airborne Allergenic Pollen Abundance and Seasonality across the Northern Hemisphere: A Retrospective Data Analysis. Lancet Planet. Heal. 2019, 3, e124–e131. [Google Scholar] [CrossRef] [PubMed]
- Tseng, Y.-T.; Kawashima, S.; Kobayashi, S.; Takeuchi, S.; Nakamura, K. Algorithm for Forecasting the Total Amount of Airborne Birch Pollen from Meteorological Conditions of Previous Years. Agric. For. Meteorol. 2018, 249, 35–43. [Google Scholar] [CrossRef]
- Bruffaerts, N.; De Smedt, T.; Delcloo, A.; Simons, K.; Hoebeke, L.; Verstraeten, C.; Van Nieuwenhuyse, A.; Packeu, A.; Hendrickx, M. Comparative Long-Term Trend Analysis of Daily Weather Conditions with Daily Pollen Concentrations in Brussels, Belgium. Int. J. Biometeorol. 2018, 62, 483–491. [Google Scholar] [CrossRef]
- Khwarahm, N.; Dash, J.; Atkinson, P.M.; Newnham, R.M.; Skjøth, C.A.; Adams-Groom, B.; Caulton, E.; Head, K. Exploring the Spatio-Temporal Relationship between Two Key Aeroallergens and Meteorological Variables in the United Kingdom. Int. J. Biometeorol. 2014, 58, 529–545. [Google Scholar] [CrossRef]
- Alcázar, P.; Galán, C.; Torres, C.; Domínguez-Vilches, E. Detection of Airborne Allergen (Pla a 1) in Relation to Platanus Pollen in Córdoba, South Spain. Ann. Agric. Environ. Med. 2015, 22, 96–101. [Google Scholar] [CrossRef] [PubMed]
- Plaza, M.P.; Alcázar, P.; Hernández-Ceballos, M.A.; Galán, C. Mismatch in Aeroallergens and Airborne Grass Pollen Concentrations. Atmos. Environ. 2016, 144, 361–369. [Google Scholar] [CrossRef]
- Ruiz-Mata, R.; Trigo, M.M.; Recio, M.; de Gálvez-Montañez, E.; Picornell, A. Comparative Aerobiological Study between Two Stations Located at Different Points in a Coastal City in Southern Spain. Aerobiologia 2023, 39, 195–212. [Google Scholar] [CrossRef]
- Sánchez Mesa, J.A.; Galán, C.; Hervás, C. The Use of Discriminant Analysis and Neural Networks to Forecast the Severity of the Poaceae Pollen Season in a Region with a Typical Mediterranean Climate. Int. J. Biometeorol. 2005, 49, 355–362. [Google Scholar] [CrossRef]
- Reyes, E.S.; de la Cruz, D.R.; Sánchez, J.S. First Fungal Spore Calendar of the Middle-West of the Iberian Peninsula. Aerobiologia 2016, 32, 529–539. [Google Scholar] [CrossRef]
- Mardones, P.; Ripoll, E.; Rojas, I.; González, M.C.; Montealegre, C.; Pizarro, D.; Córdova, A.; Torres, M.; Aguilera-Insunza, R.; Yepes-Nuñez, J.J.; et al. Parietaria Pollen a New Aeroallergen in the City of Valparaiso, Chile. Aeroboilogia 2013, 29, 449–454. [Google Scholar] [CrossRef]
- Valencia, J.A.; Astray, G.; Fernández-González, M.; Aira, M.J.; Rodríguez-Rajo, F.J. Assessment of Neural Networks and Time Series Analysis to Forecast Airborne Parietaria Pollen Presence in the Atlantic Coastal Regions. Int. J. Biometeorol. 2019, 63, 735–745. [Google Scholar] [CrossRef] [PubMed]
- Vega-Maray, A.M.; Fernández-González, D.; Valencia-Barrera, R.; Polo, F.; Seoane-Camba, J.A.; Suárez-Cervera, M. Lipid Transfer Proteins in Parietaria judaica L. Pollen Grains: Immunocytochemical Localization and Function. Eur. J. Cell Biol. 2004, 83, 493–497. [Google Scholar] [CrossRef] [PubMed]
- Thompson, K.; Grime, J.P.; Mason, G. Seed Germination in Response to Diurnal Fluctuations of Temperature. Nature 1977, 267, 147–149. [Google Scholar] [CrossRef]
- Jato, V.; Rodríguez-Rajo, F.J.; González-Parrado, Z.; Elvira-Rendueles, B.; Moreno-Grau, S.; Vega-Maray, A.; Fernández-González, D.; Asturias, J.A.; Suárez-Cervera, M. Detection of Airborne Par j 1 and Par j 2 Allergens in Relation to Urticaceae Pollen Counts in Different Bioclimatic Areas. Ann. Allergy Asthma Immunol. 2010, 105, 50–56. [Google Scholar] [CrossRef] [PubMed]
- Cheddadi, R.; Guiot, J.; Jolly, D. The Mediterranean Vegetation: What If the Atmospheric CO2 Increased? Landsc. Ecol. 2001, 16, 667–675. [Google Scholar] [CrossRef]
- Fotiou, C.; Damialis, A.; Krigas, N.; Halley, J.M.; Vokou, D. Parietaria judaica Flowering Phenology, Pollen Production, Viability and Atmospheric Circulation, and Expansive Ability in the Urban Environment: Impacts of Environmental Factors. Int. J. Biometeorol. 2011, 55, 35–50. [Google Scholar] [CrossRef] [PubMed]
- Damialis, A.; Halley, J.M.; Gioulekas, D.; Vokou, D. Long-Term Trends in Atmospheric Pollen Levels in the City of Thessaloniki, Greece. Atmos. Environ. 2007, 41, 7011–7021. [Google Scholar] [CrossRef]
- D’Amato, G.; Ruffilli, A.; Sacerdoti, G.; Bonini, S. Parietaria Pollinosis: A Review. Allergy 1992, 47, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Charpin, H.; Davies, R.; Nolard, N.; Spieksma, F.; Stix, E. Concentration Urbaine Des Spores Dans Ies Pays de La Communauté Économique Européenne: Ies Urticacées. Rev. Fr. Allergol. 1977, 17, 181–187. [Google Scholar]
- Bousquet, J.; Hewitt, B.; Guérin, B.; Dhivert, H.; Michel, F.-B. Allergy in the Mediterranean Area II: Cross-Allergenicity among Urticaceae Pollens (Parietaria and Urtica). Clin. Exp. Allergy 1986, 16, 57–64. [Google Scholar] [CrossRef]
- Quevedo Coury, V. Influencia de La Precipitación En La Polinización de Artemisia: Repercusión En La Salud Pública; Universidad Autónoma de Barcelona: Barcelona, Spain, 2015. [Google Scholar]
- Recio, M.; Rodríguez-Rajo, F.J.; Jato, M.V.; Trigo, M.M.; Cabezudo, B. The Effect of Recent Climatic Trends on Urticaceae Pollination in Two Bioclimatically Different Areas in the Iberian Peninsula: Malaga and Vigo. Clim. Change 2009, 97, 215–228. [Google Scholar] [CrossRef]
- Alcázar, P.; Stach, A.; Nowak, M.; Galán, C. Comparison of Airborne Herb Pollen Types in Córdoba (Southwestern Spain) and Poznan (Western Poland). Aerobiologia 2009, 25, 55–63. [Google Scholar] [CrossRef]
- Howard, L.E.; Levetin, E. Ambrosia Pollen in Tulsa, Oklahoma: Aerobiology, Trends, and Forecasting Model Development. Ann. Allergy Asthma Immunol. 2014, 113, 641–646. [Google Scholar] [CrossRef] [PubMed]
- Zewdie, G.K.; Liu, X.; Wu, D.; Lary, D.J.; Levetin, E. Applying Machine Learning to Forecast Daily Ambrosia Pollen Using Environmental and NEXRAD Parameters. Environ. Monit. Assess. 2019, 191, 261. [Google Scholar] [CrossRef]
- Cordero, J.M.; Rojo, J.; Gutiérrez-Bustillo, A.M.; Narros, A.; Borge, R. Predicting the Olea Pollen Concentration with a Machine Learning Algorithm Ensemble. Int. J. Biometeorol. 2021, 65, 541–554. [Google Scholar] [CrossRef]
- Vovk, T.; Kryza, M.; Tomczyk, S.; Malkiewicz, M.; Lipiński, P.; Werner, M. Prediction of Airborne Allergenic Pollen Concentrations with Machine Learning. In Proceedings of the EGU General Assembly 2024, Vienna, Austria, 14–19 April 2024. [Google Scholar]
- Voukantsis, D.; Niska, H.; Karatzas, K.; Riga, M.; Damialis, A.; Vokou, D. Forecasting Daily Pollen Concentrations Using Data-Driven Modeling Methods in Thessaloniki, Greece. Atmos. Environ. 2010, 44, 5101–5111. [Google Scholar] [CrossRef]
- Čorić, R.; Matijević, D.; Marković, D. PollenNet-a Deep Learning Approach to Predicting Airborne Pollen Concentrations. Croat. Oper. Res. Rev. 2023, 14, 1–13. [Google Scholar] [CrossRef]
- Polling, M.; Li, C.; Cao, L.; Verbeek, F.; de Weger, L.A.; Belmonte, J.; De Linares, C.; Willemse, J.; de Boer, H.; Gravendeel, B. Neural Networks for Increased Accuracy of Allergenic Pollen Monitoring. Sci. Rep. 2021, 11, 11357. [Google Scholar] [CrossRef] [PubMed]



| Start MPS | End MPS | Length MPS | SPIn | Pollen Peak | Pollen Peak Date | |
|---|---|---|---|---|---|---|
| 1999 | 23-Jan | 13-Sep | 234 | 306 | 21 | 14-Jun |
| 2000 | 6-Feb | 8-Sep | 216 | 264 | 13 | 17-Jul |
| 2001 | 4-Feb | 15-Oct | 254 | 188 | 11 | 29-Jul |
| 2002 | 24-Apr | 28-Oct | 188 | 662 | 27 | 14-Jun |
| 2003 | 12-Mar | 1-Dec | 265 | 375 | 19 | 12-Jun |
| 2004 | 15-Feb | 25-Sep | 224 | 227 | 14 | 14-Jun |
| 2005 | 19-May | 4-Oct | 139 | 320 | 17 | 6-Jul |
| 2006 | 5-Apr | 7-Nov | 217 | 1384 | 39 | 29-Jun |
| 2007 | 20-Apr | 19-Oct | 183 | 2406 | 70 | 5-Jul |
| 2008 | 10-Mar | 23-Oct | 228 | 2626 | 117 | 9-Jun |
| 2009 | 17-Mar | 15-Oct | 213 | 1779 | 66 | 18-Jun |
| 2010 | 23-Mar | 13-Oct | 205 | 1870 | 71 | 23-Jun |
| 2011 | 22-Mar | 15-Nov | 239 | 1692 | 53 | 24-Jun |
| 2012 | 10-Mar | 23-Nov | 259 | 2354 | 69 | 24-Jun |
| 2013 | 16-Mar | 25-Oct | 224 | 2811 | 78 | 26-Jun |
| 2014 | 16-Mar | 9-Nov | 239 | 2726 | 75 | 14-Jun |
| 2015 | 20-Mar | 17-Dec | 273 | 1788 | 50 | 18-Jun |
| 2016 | 1-Apr | 23-Nov | 237 | 3380 | 124 | 20-Jun |
| 2017 | 2-Mar | 14-Nov | 258 | 2581 | 96 | 11-Jun |
| 2018 | 19-Mar | 24-Nov | 251 | 3104 | 91 | 23-Jun |
| 2019 | 21-Feb | 1-Nov | 254 | 1606 | 49 | 3-Jul |
| 2020 | 10-Feb | 24-Oct | 258 | 1963 | 64 | 23-Jun |
| 2021 | 2-Mar | 15-Nov | 259 | 1583 | 58 | 15-Jul |
| 2022 | 1-Mar | 17-Dec | 292 | >2094 | 70 | 11-Jul |
| Mean. | 12-Mar | 31-Oct | 234 | 1670 | 57 | 25-Jun |
| Max. | 19-May | 17-Dec | 292 | 3380 | 124 | 29-Jul |
| Min. | 23-Jan | 8-Sep | 139 | 188 | 11 | 9-Jun |
| SD | 26.64 | 26.43 | 33.14 | 1004.41 | 32.26 | 12.91 |
| RSD (%) | 0.07 | 0.07 | 14.18 | 60.13 | 56.84 | 0.04 |
| Training | Validation | Testing | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | r | RMSE | MAE | r | RMSE | MAE | r | |
| One day ahead prediction | |||||||||
| RF | 2.15 | 0.80 | 0.969 | 6.25 | 3.23 | 0.878 | 5.84 | 3.01 | 0.845 |
| SVMR-L | 4.56 | 1.82 | 0.845 | 6.12 | 3.31 | 0.885 | 5.72 | 3.20 | 0.851 |
| ANNR-L | 4.58 | 2.08 | 0.842 | 5.92 | 3.18 | 0.887 | 5.55 | 2.97 | 0.859 |
| Two days ahead prediction | |||||||||
| RFR | 2.58 | 1.10 | 0.956 | 7.57 | 3.81 | 0.814 | 7.17 | 3.59 | 0.754 |
| SVML | 5.00 | 2.01 | 0.810 | 7.51 | 3.67 | 0.821 | 7.12 | 3.49 | 0.760 |
| ANN | 5.14 | 2.29 | 0.795 | 7.34 | 3.73 | 0.825 | 6.79 | 3.49 | 0.781 |
| Three days ahead prediction | |||||||||
| RF | 2.91 | 1.20 | 0.946 | 8.39 | 4.14 | 0.763 | 7.66 | 3.83 | 0.713 |
| SVM/SVML | 5.45 | 2.17 | 0.773 | 8.43 | 4.06 | 0.774 | 7.59 | 3.77 | 0.727 |
| ANN | 5.40 | 2.47 | 0.771 | 8.10 | 4.08 | 0.781 | 7.32 | 3.64 | 0.741 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Astray, G.; Amigo Fernández, R.; Fernández-González, M.; Dias-Lorenzo, D.A.; Guada, G.; Rodríguez-Rajo, F.J. Machine Learning to Forecast Airborne Parietaria Pollen in the North-West of the Iberian Peninsula. Sustainability 2025, 17, 1528. https://doi.org/10.3390/su17041528
Astray G, Amigo Fernández R, Fernández-González M, Dias-Lorenzo DA, Guada G, Rodríguez-Rajo FJ. Machine Learning to Forecast Airborne Parietaria Pollen in the North-West of the Iberian Peninsula. Sustainability. 2025; 17(4):1528. https://doi.org/10.3390/su17041528
Chicago/Turabian StyleAstray, Gonzalo, Rubén Amigo Fernández, María Fernández-González, Duarte A. Dias-Lorenzo, Guillermo Guada, and Francisco Javier Rodríguez-Rajo. 2025. "Machine Learning to Forecast Airborne Parietaria Pollen in the North-West of the Iberian Peninsula" Sustainability 17, no. 4: 1528. https://doi.org/10.3390/su17041528
APA StyleAstray, G., Amigo Fernández, R., Fernández-González, M., Dias-Lorenzo, D. A., Guada, G., & Rodríguez-Rajo, F. J. (2025). Machine Learning to Forecast Airborne Parietaria Pollen in the North-West of the Iberian Peninsula. Sustainability, 17(4), 1528. https://doi.org/10.3390/su17041528








