Abstract
This research provides a thorough examination of the industrial sector’s forecasting of renewable energy consumption, utilizing sophisticated machine learning techniques to enhance the accuracy and reliability of the predictions. LASSO regression, random forest (RF), Support Vector Regression (SVR), eXtreme Gradient Boosting (XGBoost 2.1.3), LightGBM, and multilayer perceptron (MLP) were all selected due to their ability to effectively handle large datasets. Our primary goal was to demonstrate the utility of the Energy Uncertainty Index (EUI) within commonly accepted models to ensure replicability and relevance to a broad audience. The integration of the EUI as an independent variable is a critical innovation of this research, as it addresses the challenges presented by fluctuations in energy markets. A more nuanced comprehension of consumption trends in the presence of uncertainty is achieved through this inclusion. We evaluate the performance of these models in the context of renewable energy consumption forecasting, identifying their strengths and limitations. The results indicate that the prognostic potential of the models is considerably improved by the inclusion of the EUI, providing valuable insights for energy policymakers, investors, and industry stakeholders. These advancements emphasize the role of machine learning in achieving efficient resource allocation, guiding infrastructure development, minimizing risks, and supporting the global transition toward renewable energy and sustainability.
1. Introduction
Forecasting energy consumption is essential for efficient energy management and policymaking, supporting both immediate operational choices and long-term strategic planning. Precise projections empower energy producers, distributors, and legislators to enhance resource allocation, devise infrastructure investments, mitigate the environmental effect of energy use, and guarantee a reliable energy supply [1]. Global energy consumption is projected to increase by 25% by 2040, necessitating accurate and dependable forecasting due to the growing incorporation of renewable energy sources into the energy mix.
The importance of energy forecasting has been extensively recorded in the literature [2,3,4,5]. Precise forecasts are essential to equilibrate supply and demand, thereby averting overproduction or energy deficits. For nations transitioning to renewable energy, forecasting is particularly difficult owing to the fluctuation of sources such as wind and solar power. Energy demand forecasting has extensively utilized conventional econometric models such as autoregressive integrated moving average (ARIMA) (Wang et al. [6]). Nonetheless, these models find it challenging to encapsulate the non-linear and intricate patterns characteristic of contemporary energy data, especially when renewable energy sources are included [5,7,8,9]. The reliance of solar and wind energy production on variable weather conditions creates significant fluctuation and uncertainty in supply predictions [10]. Consequently, modern data analytics and machine learning (ML) methodologies have become vital instruments for improving prediction precision and dependability [11].
External influences, like economic cycles, policy alterations, and technology advancements, impact energy consumption, hence complicating forecasting models [12,13,14,15]. The COVID-19 pandemic highlighted the vulnerability of energy consumption to unforeseen macroeconomic disturbances, resulting in significant divergences from anticipated trends across all sectors. Such interruptions underscore the need for resilient forecasting models that can adjust to swiftly evolving circumstances.
Due to the constraints of conventional forecasting approaches, machine learning (ML) and deep learning (DL) techniques have garnered heightened interest [16,17]. These methodologies are proficient in managing non-linear, high-dimensional, and multi-seasonal energy datasets. In contrast to traditional models, machine learning and deep learning algorithms may autonomously discern intricate relationships within the data, facilitating enhanced flexibility to changes in consumption patterns. Recent studies have shown the effectiveness of machine learning in energy forecasting across multiple sectors. Shapi et al. [18] examined energy usage in smart buildings using support vector machines, artificial neural networks, and k-nearest neighbors, highlighting the necessity for model adaptation. Elhabyb et al. [19] utilized machine learning methodologies, including LSTM and random forest, to enhance real-time energy efficiency in educational edifices. Talwariya et al. [5] introduced neural network models for forecasting renewable energy output and consumption, focusing on the unpredictability of solar and wind resources. Likewise, Qureshi et al. [20] employed LSTM models in building management systems to attain precise electricity estimates. Ensemble approaches, including random forests and gradient boosting, have demonstrated enhanced prediction accuracy by compensating for the deficiencies of individual models [21].
Deep learning models, especially Long Short-Term Memory (LSTM) networks, have demonstrated significant efficacy in energy forecasting [22]. The integration of LSTMs with external variables such as meteorological data or economic indicators has enhanced forecasting accuracy, particularly in the realm of renewable energy [21]. Research has employed Convolutional Neural Networks (CNNs) to model geographical and temporal dependencies, demonstrating their capacity to forecast energy consumption based on distributed variables such as temperature and humidity fluctuations [23].
The pursuit of sustainability has become a critical global objective, aiming to balance economic development, environmental health, and social equity. Sustainable energy practices, in particular, are central to addressing climate change and reducing the ecological footprint of industrial activities. Accurate energy forecasting contributes significantly to this endeavor by enabling efficient resource management, minimizing waste, and fostering the transition toward renewable energy sources. This alignment with sustainability not only supports global climate commitments such as the Paris Agreement but also strengthens energy security and resilience against market volatility.
Moreover, integrating sustainability into energy systems encourages innovations in technology, policies, and business models, facilitating long-term socio-economic benefits. Machine learning-driven forecasting models play a pivotal role in this transformation, offering precise insights into consumption trends and aiding in the design of proactive energy strategies. By addressing uncertainties and enhancing efficiency, these models contribute to a sustainable energy future that prioritizes environmental preservation, economic stability, and societal well-being.
This work enhances the energy forecasting literature by concentrating on renewable energy consumption predictions for the industrial sector through the application of sophisticated machine learning methods. Building on the predictive power of energy-related uncertainty indexes (EUIs) for financial market volatility [10], our work extends this concept to the energy sector by incorporating EUIs into machine learning models for forecasting renewable energy consumption. This integration highlights the broader applicability of EUI as significant predictor, offering insights for both economic stability and sustainable energy management. The utilized models are random forest (RF), Support Vector Regression (SVR), eXtreme Gradient Boosting (XGBoost), LASSO regression, Light Gradient-Boosting Machine (LightGBM), and multilayer perceptron (MLP). Although these models exhibit strong predictive accuracy, their utilization in renewable energy forecasting incorporating uncertainty factors is yet little investigated. Our primary goal was to demonstrate the utility of the EUI within commonly accepted models to ensure replicability and relevance to a broad audience. To this end, this study assesses the advantages and disadvantages of different models, providing a thorough comparison to improve the forecasting of renewable energy use.
The research also includes the Energy Uncertainty Index (EUI) as a predictive variable. This study highlights the impact of energy-related uncertainty on consumption patterns, in contrast to previous research that mostly concentrated on economic, weather-related, or policy-driven aspects. Ref. [24] has identified the EUI as a key element in understanding the influence of energy market volatility on economic indicators, encompassing cryptocurrencies and commodities such as gold. Research by Işık et al. [25] and Xu et al. [26] underscores the impact of energy price volatility on consumption and investment behaviors. Incorporating the EUI into forecasting models offers an innovative method for addressing uncertainty and enhances model resilience in unstable markets. Specifically, the incorporation of the Energy Uncertainty Index (EUI) addresses a critical gap in the energy forecasting literature, particularly in the context of renewable energy consumption. Traditional forecasting models often struggle to encapsulate the complexities of market volatility and the uncertainties inherent in renewable energy sources, such as solar and wind, which are heavily influenced by unpredictable external factors like weather conditions and economic disruptions. The EUI serves as a key predictive variable by quantifying these uncertainties and their potential impacts on energy consumption patterns. Furthermore, this approach aligns with sustainability goals, as it supports the efficient management of energy resources and aids in the strategic planning necessary for transitioning to renewable energy systems. The inclusion of the EUI not only enriches the predictive accuracy of energy models but also provides actionable insights for policymakers and industry stakeholders in navigating volatile energy markets and fostering a sustainable energy future. Overall, this study advances the energy forecasting literature by emphasizing the role of machine learning techniques in enhancing the sustainability of energy systems. Through a focus on renewable energy consumption in the industrial sector, the research assesses the effectiveness of various ML models, including their ability to incorporate uncertainty factors through the Energy Uncertainty Index (EUI).
The subsequent sections of the paper are organized as follows: Section 2 delineates the process, encompassing data sources and assessment measures. Section 3 delineates the results of one-step and multi-step out-of-sample projections. Section 4 closes by emphasizing the ramifications for energy policy and market risk management, aimed at facilitating the renewable energy transition and guaranteeing energy security.
2. Materials and Methods
In this study, we employ several machine learning algorithms to forecast one-step-ahead out-of-sample renewable energy consumption using the Energy Uncertainty Index (EUI) as an independent variable. The models used include random forest (RF), Support Vector Regression (SVR), eXtreme Gradient Boosting (XGBoost), Least Absolute Shrinkage and Selection Operator (LASSO), Light Gradient-Boosting Machine (LightGBM), and multilayer perceptron (MLP). A brief description of each algorithm, along with relevant mathematical formulations, is provided below.
2.1. Machine Learning Models
2.1.1. Random Forest (RF)
Random forest is an ensemble learning method used for both classification and regression tasks [27]. It functions by constructing multiple decision trees during training and outputting the average prediction for regression tasks.
The procedure can be described as follows: Given a training set , where represents the feature vector and the target variable, RF constructs decision trees. The final prediction for an unseen instance is the average of the predictions from all trees:
where is the prediction of the -th tree.
RF effectively reduces overfitting by averaging out noise in the training data, thus providing robust predictions.
2.1.2. Support Vector Regression (SVR)
Support Vector Regression (SVR) is an extension of the support vector machine (SVM) used for regression [28]. Specifically, the procedure can be described as follows: it seeks to find a function that deviates from the true output by a value no greater than for all training data points while keeping the model complexity as low as possible.
The objective of SVR is to minimize the following loss function:
where represents the regularization term to prevent overfitting, is the regularization parameter, and defines the margin within which no penalty is assigned to errors. Specifically, it only penalizes predictions that fall outside the specified margin from the target value. The width of this margin, or tube, is controlled by the parameter, allowing the model to adjust for varying levels of error tolerance. Various loss functions, such as linear or quadratic, can be selected based on the specific requirements of the prediction task.
2.1.3. eXtreme Gradient Boosting (XGBoost)
XGBoost, a robust machine learning algorithm within the tree-based ensemble family, is an optimized implementation of the gradient-boosting framework as outlined by [29]. The model initiates with a base prediction and iteratively adds decision trees that are trained on the residuals from prior predictions, sequentially reducing errors to achieve improved predictive accuracy. Each new tree is fit to the errors of previous trees, refining the model’s performance at every stage. To control model complexity and prevent overfitting, XGBoost incorporates regularization, a convex loss function, and a penalty term. This combination enables XGBoost to balance predictive accuracy with model generalization, making it highly suitable for applications requiring precision and computational efficiency.
2.1.4. Least Absolute Shrinkage and Selection Operator (LASSO)
LASSO is a linear regression method that performs both variable selection and regularization to improve the prediction accuracy [30]. LASSO minimizes the sum of squared residuals, subject to the sum of the absolute values of the coefficients being less than a constant.
The LASSO optimization problem is expressed as:
where is a regularization parameter that controls the trade-off between fitting the data well and keeping the model simple.
2.1.5. Light Gradient-Boosting Machine (LightGBM)
LightGBM is an advanced boosting algorithm designed to enhance the traditional gradient-boosting framework by employing a leaf-wise growth strategy, which allows it to reduce loss more efficiently at each iteration compared to level-wise approaches [31]. This leaf-wise method, combined with automatic feature selection, optimizes both computational efficiency and model accuracy, making LightGBM particularly effective for large datasets and high-dimensional problems.
2.1.6. Multilayer Perceptron (MLP)
Multilayer perceptron (MLP) is a type of artificial neural network composed of an input layer, one or more hidden layers, and an output layer [32]. Each neuron in an MLP applies a weighted sum of inputs, followed by a non-linear activation function. The forward pass for a neuron in layer is represented by:
where denotes the weight matrix, is the input from the previous layer, and is the bias term. Activation functions, such as ReLU or sigmoid, are applied to introduce non-linearity. MLP is trained using backpropagation, optimizing weights through gradient descent to minimize prediction error.
2.2. Model Evaluation
In the forecasting literature, a variety of metrics have been employed to assess the predictive performance of regression models [33,34]. In this study, we use three commonly adopted evaluation criteria: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE).
The Mean Absolute Error (MAE) measures the average magnitude of prediction errors, without considering their direction, and computes the average of the absolute differences between the actual and predicted values. It is given by:
stands for the predicted values and stands for the actual values.
Similarly, the Root Mean Square Error (RMSE), often employed in forecasting and regression analysis, provides the standard deviation of the prediction errors. It validates the experimental models and is calculated as:
The Mean Absolute Percentage Error (MAPE) is a popular metric that expresses prediction accuracy as a percentage by comparing the absolute difference between the actual and predicted values relative to the actual values. It is defined as:
2.3. Model Training
This section elucidates the procedures involved in training and testing machine learning models to forecast renewable energy consumption. The methods include the implementation of rolling-window cross-validation for performance assessment and model training. These components are critical for generating accurate predictions and ensuring reliable models. The methodology is detailed below, with specific explanations of the rolling-window cross-validation process and procedures employed to document results.
Rolling-Window Cross-Validation
To evaluate the generalizability of models in the context of time-series data, rolling-window cross-validation was employed, as recommended by Hyndman and Athanasopoulos [35]. This approach systematically validates the model by repeatedly splitting the dataset into training and validation sets based on temporal order. Various rolling-window lengths were explored, including 6, 12, 18, and 24 months, to ensure a robust assessment of temporal patterns and model adaptability. This method ensures that temporal dependencies in the data are respected, thereby reducing bias and improving the reliability of predictions.
The evaluation process involved training the model on an initial segment of the data (80% of the data used for train set) and then testing it on subsequent segments (20% of the data used for test set) in a rolling manner. This procedure was repeated for each rolling-window length to derive a comprehensive understanding of the model’s performance across different time horizons. The average performance metrics obtained through this process provide a robust estimate of the model’s predictive accuracy.
Default settings were employed for specific hyperparameters for simplicity and to establish a baseline for model evaluation (Table 1). For the random forest model, parameters included 500 trees and 2 variables per split. Similarly, XGBoost retained default settings, such as a learning rate of 0.2, maximum tree depth of 2, and 150 boosting rounds. Support Vector Regression (SVR) utilized its default cost parameter and radial basis function kernel, while LASSO regression relied on the default regularization setting. LightGBM used a learning rate of 0.1 and 100 boosting rounds, while the multilayer perceptron (MLP) model employed two hidden layers with 10 and 5 neurons, a learning rate of 0.1, and a maximum of 100 iterations (Table 1). These default settings facilitated a standardized comparison of model performance while acknowledging the potential for future hyperparameter optimization to enhance results further.

Table 1.
Hyperparameters for the machine learning models.
2.4. Data
The dataset for this study comprises two key components: the Energy Uncertainty Index (EUI), spanning from January 2001 to September 2022 with monthly frequency (https://www.policyuncertainty.com/energy_uncertainty.html, accessed on 26 October 2024), and monthly data on renewable energy consumption, sourced from the U.S. Energy Information Administration. The analysis specifically utilizes the Renewable Energy Consumption Index, representing total renewable energy consumption by the industrial sector, measured in trillion Btu. To enhance statistical stability and ensure comparability, logarithmic differencing was applied to both variables (it is implicitly assumed that each variable’s time series is stationary. Formal unit root tests strongly reject the null hypothesis of non-stationarity for all series).
Table 2 summarizes the descriptive statistics for the transformed variables. The logarithm of renewable energy consumption exhibits a relatively symmetric distribution, as shown by a median of 5.261 closely aligning with the mean of 5.191. The slight left skewness (−0.5035) and kurtosis value of 1.8862, which is below 3, indicate a distribution with flatter peaks and lighter tails compared to a normal distribution. However, the Jarque–Bera test (χ2 = 24.516, p < 0.0001) rejects the assumption of normality, highlighting deviations from the normal distribution. Despite this, the data reveal low variability and overall stability, requiring consideration of these deviations in subsequent modeling.

Table 2.
Descriptive statistics for each variable.
Similarly, the logarithmic transformation of the Energy Uncertainty Index reveals a left-skewed distribution with heavier tails, as indicated by skewness and kurtosis metrics (Figure 1). The high standard deviation suggests significant variability in the EUI data. The Jarque–Bera test (p < 0.05) confirms non-normality, which further emphasizes the complexity of the EUI variable. Figure 2 illustrates a cross-correlation plot between EUI and renewable energy consumption, revealing significant negative correlations at multiple lags, especially near lag 0 and positive lags. This indicates that heightened energy uncertainty corresponds with reduced renewable energy consumption in the industrial sector over time. The lack of significant positive correlations across the lags supports the inclusion of the EUI as a critical predictor in modeling renewable energy consumption, further motivating its relevance to forecasting efforts.
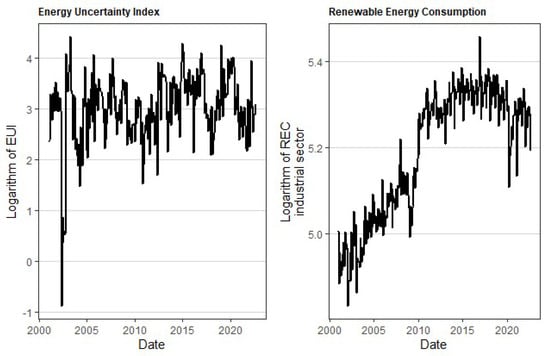
Figure 1.
This figure presents the logarithm of each variable using monthly data for the period from January 2001 to September 2022 for the Energy Uncertainty Index, as well as renewable energy consumption focusing on the Industrial Sector Index.
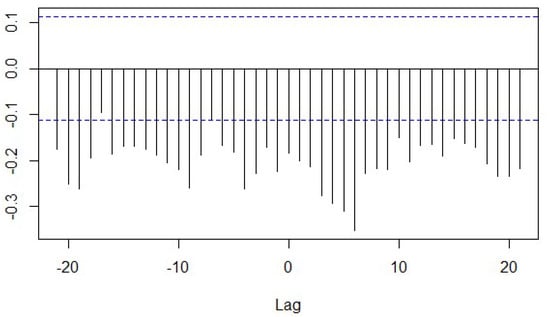
Figure 2.
This plot depicts the cross-correlation results for the pair of variables considered in the analysis, namely, the Energy Uncertainty Index and Renewable Energy Uncertainty Index on monthly basis from January 2001 to September 2022.
3. Results
Next, we present the results of a one-step-ahead out-of-sample forecasting exercise for renewable energy consumption on a monthly basis, which includes the Energy Uncertainty Index in the forecasting models. Random forest (RF), Support Vector Regression (SVR), eXtreme Gradient Boosting (XGBoost), LASSO regression, LightGBM, and multilayer perceptron (MLP) are the machine learning models that are specifically being considered. In this analysis, we have implemented the rolling-window cross-validation method for time series [35]. We have evaluated various rolling-window lengths, including 6, 12, 18, and 24 months. Additionally, we optimized each model’s hyperparameters; however, we ultimately implemented default values to streamline the process. We assign the default values of 500 and two to the number of trees and variables considered at each division in the random forest model. In the same vein, the XGBoost model implemented default settings for critical parameters such as the learning rate, maximal tree depth, and number of boosting cycles, which were set to 0.2, 2, and 150, respectively. For Support Vector Regression (SVR), we maintained the default configurations of the cost parameter and the radial basis function kernel parameter. In the LASSO regression case, we also maintained the regularization parameter at its default value. We utilized LightGBM’s default parameters for the learning rate, number of leaves, and boosting rounds, and configured the multilayer perceptron (MLP) model with default values for the number of hidden layers, neurons, and learning rate. In this study, the use of default values establishes a baseline for evaluating the efficacy of the model despite the potential for hyperparameter tuning to enhance model performance. The R programming language was employed to implement the project.
The results of the forecasting performance of each of the machine learning models considered across the error metrics MAE, RMSE, and MAPE are presented in Table 3. The Model Confidence Set (MCS) approach, which was devised by Hansen et al. [36], is also employed to identify the set of models with statistically superior performance. The MCS procedure enables the comparison of multiple models by eliminating those that are notably less accurate one by one, based on the null hypothesis that all models are equally accurate. This enables us to draw statistically significant conclusions regarding the performance of the model in multiple comparisons. Ref. [36] provides an exhaustive overview of the MCS procedure.

Table 3.
Estimation results for the renewable energy consumption for the industrial sector (forecasting horizon h = 1).
Table 3 offers a comprehensive assessment of the forecasting capabilities of six models: random forest (RF), eXtreme Gradient Boosting (XGB), Support Vector Regression (SVR), LASSO regression, LightGBM, and multilayer perceptron (MLP). The results are also presented for a variety of rolling intervals, including 6, 12, 18, and 24 months. These metrics are instrumental in evaluating the precision of each model in predicting renewable energy consumption for the industrial sector, thereby offering valuable insights into the applicability of each method.
LightGBM consistently outperforms all other models, as evidenced by the results, demonstrating extraordinary efficacy across all rolling windows. It accomplishes a Mean Absolute Error (MAE) of 0.03604, a Root Mean Square Error (RMSE) of 0.04586, and a Mean Absolute Percentage Error (MAPE) of 1.14589 within the 6-month window presented in Table 3, Panel A. It is closely followed by XGBoost, which exhibits robust results, particularly in the areas of RMSE and MAPE. It obtains an MAPE of 1.44260 and an RMSE of 0.05421 within the 6-month window. However, Support Vector Regression (SVR) and LASSO regression exhibit distinct capabilities. In the 6-month rolling-window length, SVR attains an MAE value of 0.04228 and an RMSE of 0.05502. In the same vein, LASSO regression displays an RMSE of 0.05413 and an MAE of 0.04222. Nevertheless, LASSO’s linear assumptions limit its ability to simulate the intricate dynamics that are inherent in renewable energy consumption data. In comparison to the boosting methods, the multilayer perceptron (MLP) model exhibits a marginally inferior performance, with an RMSE of 0.05509. Although MLP is capable of effectively capturing non-linear relationships, its relatively higher MAE error rates indicate that additional hyperparameter tailoring may be required to achieve a more accurate fit.
Finally, random forest (RF) consistently demonstrates the highest errors across all metrics, with an MAE of 0.04162, an RMSE of 0.05748, and an MAPE of 1.99008 in the 6-month window. RF’s performance in this time-series forecasting context is significantly inferior to that of the gradient-boosting models, despite its widespread use in regression tasks. Although its ensemble nature is effective in other applications, it seems to have difficulty conveying intricate temporal dependencies. Nevertheless, the metric ratings of the methodologies under investigation exhibit minimal variation. Furthermore, the findings suggest that specific methodologies may be more suitable for distinct rolling-window lengths, contingent upon the error metric that is considered.
The industrial sector is significantly impacted by the findings of this analysis, particularly in the context of renewable energy consumption forecasting. The significance of employing sophisticated gradient-boosting techniques for time-series forecasting tasks, particularly in intricate domains like energy consumption, is underscored by the exceptional performance of LightGBM and XGBoost. These models are more adept at managing complexity and changes associated with renewable-energy-use data due to their ability to manage non-linear relationships, feature selection, and reducing residual errors. This implies that industries seeking to optimize energy consumption and improve sustainability should contemplate the implementation of such sophisticated models to achieve more precise and dependable forecasting. The limitations of relying on simplified, linear approaches for such tasks are further emphasized by the relatively poor performance of traditional models such as random forest and LASSO regression. These models may provide computational efficiency and simplicity of interpretation; however, they exhibit slightly inferior performance when applied to more complex, non-linear time-series data.
4. Discussion and Conclusions
The comparative analysis of forecasting models for renewable energy consumption in the industrial sector has yielded substantial insights into the efficacy of various machine learning algorithms. LightGBM consistently demonstrated superior performance across all rolling windows and assessment criteria, including MAE, RMSE, and MAPE. Its prediction accuracy underscores its capacity to manage intricate time-series data effectively, providing a strong and dependable solution for predicting energy use. This indicates that LightGBM is particularly adept at handling tasks characterized by significant fluctuation and dynamic patterns in energy use, positioning it as a valuable option for industrial applications aimed at maximizing energy resources.
XGBoost exhibited robust performance, particularly with RMSE and MAPE. Nonetheless, its efficacy, especially in long-term predictions, suggests that it might gain from further improvement relative to LightGBM. Support Vector Regression (SVR) and multilayer perceptron (MLP) models exhibit good performance but were inadequate in addressing the complexities of renewable energy consumption data. The non-linear capabilities of MLP, although promising, led to somewhat elevated error rates, indicating the necessity for more architectural optimization to enhance performance.
The conventional models, including random forest and LASSO regression, demonstrated less robustness, especially with extended rolling windows. Although random forest is recognized for its efficacy in general regression tasks, its inability to capture temporal connections renders it less appropriate for forecasting energy usage. LASSO regression, while consistent in performance, exhibits limits owing to its linear character, which constrains its capacity to represent the non-linear connections present in the data. These findings underscore the necessity for more advanced models when addressing intricate time-series data such as energy use. Nonetheless, we saw slight variations in metric scores among the evaluated approaches. Moreover, when evaluating a certain error metric, certain approaches may be better suited for varying rolling-window lengths.
This work underscores the importance of employing sophisticated machine learning models, namely gradient-boosting techniques such as LightGBM and XGBoost, for predicting renewable energy consumption in the industrial sector. These models provide substantial enhancements in predictive accuracy and stability compared to conventional methods, making them extremely beneficial for enterprises aiming to optimize energy use and save expenses. The reliable performance of LightGBM over various timeframes makes it a crucial instrument for energy management, facilitating better informed decision-making upon its implementation.
From a sustainability perspective, this study contributes to global efforts to enhance energy efficiency and reduce environmental impacts. By improving the precision of renewable energy forecasts, enterprises can better align their energy strategies with sustainable practices, thus contributing to the global transition toward low-carbon energy systems. Accurate forecasting mitigates the risks of overproduction and underutilization, promoting the efficient use of resources and supporting long-term environmental goals.
Future research should investigate hybrid models that integrate the advantages of several methods to enhance forecasting efficacy in the energy sector. Specifically, hybrid approaches that combine ensemble machine learning techniques with traditional econometric models (e.g., ARIMA or Hetereogeneous Autoregressive Model for Realized Volatility/HAR-RV) to produce forecasts leverage the robustness of econometric models in time-series trends and the flexibility of machine learning to capture non-linear patterns, thereby improving the forecasting of renewable energy consumption under uncertainty. Additionally, the integration of external variables such as economic indicators, jumps in the price process detected with traditional econometric approaches and/or with the use of unsupervised anomaly detection machine learning algorithms, weather patterns, and technological innovations into existing models may further improve accuracy and resilience. These advancements could pave the way for more robust, adaptable, and sustainable energy systems tailored to the complexities of industrial energy consumption.
Funding
This research received external funding. This work has received funding from the European Union’s Horizon Europe research and innovation programme under grant agreement No. 101178789 (EVOSST). Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union. Neither the European Union nor the granting authority can be held responsible for them.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
This work has received funding from the European Union’s Horizon Europe research and innovation programme under grant agreement No. 101178789 (EVOSST). Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union. Neither the European Union nor the granting authority can be held responsible for them.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alqaralleh, H.S.; Al-Saraireh, A.; Canepa, A. Energy market risk management under uncertainty: A VAR based on wavelet approach. Int. J. Energy Econ. Policy 2021, 11, 130–137. [Google Scholar] [CrossRef]
- Abisoye, B.O.; Sun, Y.; Zenghui, W. A survey of artificial intelligence methods for renewable energy forecasting: Methodologies and insights. Renew. Energy Focus 2024, 48, 100529. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, H.; Yan, B. A review on renewable energy and electricity requirement forecasting models for smart grid and buildings. Sustain. Cities Soc. 2020, 55, 102052. [Google Scholar] [CrossRef]
- Eddaoudi, Z.; Aarab, Z.; Boudmen, K.; Elghazi, A.; Rahmani, M.D. A Brief Review of Energy Consumption Forecasting Using Machine Learning Models. Procedia Comput. Sci. 2024, 236, 33–40. [Google Scholar] [CrossRef]
- Talwariya, A.; Singh, P.; Jobanputra, J.H.; Kolhe, M.L. Machine learning based renewable energy generation and energy consumption forecasting. Energy Sources Part A Recovery Util. Environ. Eff. 2023, 45, 3266–3278. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Srinivasan, D.; Wang, Z. Wind Power Curve Modeling and Wind Power Forecasting With Inconsistent Data. IEEE Trans. Sustain. Energy 2019, 10, 16–25. [Google Scholar] [CrossRef]
- Agrawal, H.; Talwariya, A.; Gill, A.; Singh, A.; Alyami, H.; Alosaimi, W.; Ortega-Mansilla, A. A Fuzzy-Genetic-Based Integration of Renewable Energy Sources and E-Vehicles. Energies 2022, 15, 3300. [Google Scholar] [CrossRef]
- Mathew, M.S.; Kolhe, M.L. Performance Modelling of Renewable Energy Systems Using kNN Algorithm for Smart Grid Applications. In Proceedings of the 7th International Conference on Smart and Sustainable Technologies (SpliTech), Bol, Croatia, 5–8 July 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Singh, P.; Talwariya, A.; Kolhe, M. Demand Response Management in the Presence of Renewable Energy Sources using Stackelberg Game Theory. IOP Conf. Ser. Mater. Sci. Eng. 2019, 605, 12004. [Google Scholar] [CrossRef]
- Salisu, A.A.; Ogbonna, A.E.; Gupta, R.; Bouri, E. Energy-related uncertainty and international stock market volatility. Q. Rev. Econ. Financ. 2024, 95, 280–293. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Bloch, H.; Rafiq, S.; Salim, R. Economic growth with coal, oil and renewable energy consumption in China: Prospects for fuel substitution. Econ. Model. 2015, 44, 104–115. [Google Scholar] [CrossRef]
- Cai, Y.; Wu, Y. Time-varying interactions between geopolitical risks and renewable energy consumption. Int. Rev. Econ. Financ. 2021, 74, 116–137. [Google Scholar] [CrossRef]
- Rajaguru, G.; Khan, S.U. Causality between Energy Consumption and Economic Growth in the Presence of Growth Volatility: Multi-Country Evidence. J. Risk Financ. Manag. 2021, 14, 471. [Google Scholar] [CrossRef]
- Salim, R.A.; Shafiei, S. Urbanization and renewable and non-renewable energy consumption in OECD countries: An empirical analysis. Econ. Model. 2014, 38, 581–591. [Google Scholar] [CrossRef]
- Mystakidis, A.; Koukaras, P.; Tsalikidis, N.; Ioannidis, D.; Tjortjis, C. Energy Forecasting: A Comprehensive Review of Techniques and Technologies. Energies 2024, 17, 1662. [Google Scholar] [CrossRef]
- Wazirali, R.; Yaghoubi, E.; Abujazar, M.S.S.; Ahmad, R.; Vakili, A.H. State-of-the-art review on energy and load forecasting in microgrids using artificial neural networks, machine learning, and deep learning techniques. Electr. Power Syst. Res. 2023, 225, 109792. [Google Scholar] [CrossRef]
- Shapi, M.K.M.; Ramli, N.A.; Awalin, L.J. Energy consumption prediction by using machine learning for smart building: Case study in Malaysia. Dev. Built Environ. 2021, 5, 100037. [Google Scholar] [CrossRef]
- Elhabyb, K.; Baina, A.; Bellafkih, M.; Deifalla, A.F. Machine Learning Algorithms for Predicting Energy Consumption in Educational Buildings. Int. J. Energy Res. 2024, 2024, 6812425. [Google Scholar] [CrossRef]
- Qureshi, M.; Arbab, M.A.; Rehman, S.U. Deep learning-based forecasting of electricity consumption. Sci. Rep. 2024, 14, 6489. [Google Scholar] [CrossRef]
- Zhen, H.; Niu, D.; Yu, M.; Wang, K.; Liang, Y.; Xu, X. A Hybrid Deep Learning Model and Comparison for Wind Power Forecasting Considering Temporal-Spatial Feature Extraction. Sustainability 2020, 12, 9490. [Google Scholar] [CrossRef]
- Casolaro, A.; Capone, V.; Iannuzzo, G.; Camastra, F. Deep Learning for Time Series Forecasting: Advances and Open Problems. Information 2023, 14, 598. [Google Scholar] [CrossRef]
- Mustaqeem Ishaq, M.; Kwon, S. Short-Term Energy Forecasting Framework Using an Ensemble Deep Learning Approach. IEEE Access 2021, 9, 94262–94271. [Google Scholar] [CrossRef]
- Wang, J.-N.; Vigne, S.A.; Liu, H.-C.; Hsu, Y.-T. Divergent jump characteristics in brown and green cryptocurrencies: The role of energy-related uncertainty. Energy Econ. 2024, 138, 107847. [Google Scholar] [CrossRef]
- Işık, C.; Kuziboev, B.; Ongan, S.; Saidmamatov, O.; Mirkhoshimova, M.; Rajabov, A. The volatility of global energy uncertainty: Renewable alternatives. Energy 2024, 297, 131250. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y.; Chen, J.; Lin, H.; Yu, P. Evaluating the Predictive Power of the Energy-Related Uncertainty Index on Bitcoin Volatility. Eur. Acad. J. II China 2024, 1, 1. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149–3157. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Botchkarev, A. A new typology design of performance metrics to measure errors in machine learning regression algorithms. Interdiscip. J. Inf. Knowl. Manag. 2019, 14, 045–076. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Clayton, Australia, 2018; Available online: https://otexts.org/fpp2/ (accessed on 25 October 2024).
- Hansen, P.R.; Lunde, A.; Nason, J.M. The Model Confidence Set. Econometrica 2011, 79, 453–497. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).