Investigation of Coral Reefs for Coastal Protection: Hydrodynamic Insights and Sustainable Flow Energy Reduction

Abstract

Coral reefs are integral components of tropical coastal marine ecosystems that have considerable capacity to mitigate extreme flows and marine floods caused by storms and tsunamis. However, limited studies on coral reef efficacy in reducing such flows, coupled with variable roughness coefficient characteristics, hinder their broader utilization in sustainable engineering applications for societal benefit. In this study, we conducted comprehensive experimental investigations to examine flow–coral interactions and the flow energy reduction capabilities of coral reefs. Three-dimensional-printed coral reefs were used to simulate actual coral reefs, providing a scalable and environmentally responsible approach for studying nature-based coastal protection systems. Flow characteristics within the coral reef were investigated through flow depth and velocity measurements taken at the front of, over, and behind the reef. Analysis was performed considering nondimensional parameters, i.e., the Froude number (Fr), the depth effect (DE; ratio of flow depth to coral height), and the size effect (SE; ratio of coral length to coral height), to assess the flow energy reduction under different coral combinations and flow conditions. Spatial variations in flow depth over the reef showed that fast and shallow flows exhibited a reduction gradient toward the back of the reef. The findings revealed a substantial reduction in flow depth and velocity, reaching up to 27.5% and 25%, respectively, at the back boundary of the coral. Two-layered velocity analyses showed that the velocity over the top of corals could be six times higher than that through the coral reef structure for deep flows. Manning’s roughness coefficient varied considerably from 0.03 to 0.26. Overall, this study contributes to sustainable coastal engineering by demonstrating how bio-inspired coral reef structures can be applied to reduce flow energy and enhance coastal resilience in an environmentally adaptive manner.

1. Introduction

In recent years, the role of coral reefs in mitigating shoreline erosion and marine flooding has gained considerable attention from the scientific and engineering communities [1,2]. Coral reefs act as natural barriers, dissipating wave energy and reducing the impact of tsunamis and extreme weather events such as storm surges. This role is particularly important in tropical coastal regions, where dense populations and rich ecosystems coexist, making these areas especially susceptible to climate-related threats such as sea-level rise, storm surges, and coastal erosion [1]. Structurally, coral reefs exhibit remarkable morphological complexity—from millimeter-scale branches to extensive reef flats—which significantly influence flow dynamics [3].

The hydrodynamic interaction between flowing water and coral structures results in changes to flow velocity, turbulence intensity, and energy dissipation [4]. Numerous studies, both numerical and experimental, have shown that coral reefs can reduce incoming wave and current energy by up to 97% [5]. These reductions are attributed to processes such as flow deflection, bottom friction, flow stagnation, and turbulence induced by reef geometry. Key parameters controlling energy dissipation include reef width, water depth, surface roughness, and coral morphology [6,7]. Despite these insights, important knowledge gaps remain. Many numerical studies depend on simplified geometric assumptions that fail to capture the intricacies of coral topography. Similarly, roughness parameters are often estimated using constant Manning’s coefficients, which do not fully reflect spatial and temporal variations in coral structure or hydrodynamic conditions [8,9]. Measuring reef roughness is particularly challenging due to the dynamic nature of coral growth, biological deposition, and flow-induced changes [10]. Furthermore, few studies provide experimental validation under controlled conditions using morphologically representative coral analogs [11]. Most field-based studies are limited by unpredictable natural variability and lack reproducibility [12], while many lab-based studies use oversimplified models that ignore the physical complexity of coral formations [13].

In this context, three-dimensional (3D) printing has emerged as a powerful tool for replicating real-world reef geometries. Advances in additive manufacturing now allow researchers to fabricate coral analogs with high morphological fidelity and customized roughness properties [14,15]. These synthetic reefs can be used in large-scale flume experiments to simulate a wide range of hydraulic conditions while maintaining strict control over flow parameters. However, there remains a lack of comprehensive studies that utilize 3D-printed models to examine the effects of reef size, coral roughness, and nondimensional flow characteristics—such as the Froude number and depth effect—on flow attenuation.

This study aims to address these gaps by investigating the hydrodynamic behavior of steady flows over 3D-printed Acropora coral models in a controlled flume environment. The coral models replicate realistic morphological features of naturally occurring branching corals and are designed to maintain geometric similarity with field specimens as shown in Figure 1. Flow depth and velocity are measured at the front, over, and behind the reef under varying flow conditions. The analysis incorporates nondimensional parameters including the Froude number (Fr), depth effect (DE), and size effect (SE), which help in generalizing the results across a range of reef geometries and hydraulic scenarios.

In addition to quantifying flow depth and velocity reductions, the study calculates hydrodynamically dependent Manning’s roughness coefficient across the reef structure. This approach provides practical insights for engineers and modelers who seek to incorporate coral reef effects into hydrodynamic simulations. The combination of accurate physical modeling and parameterized analysis enhances our understanding of how coral structures dissipate flow energy and offers a validated framework for using coral-based interventions in coastal protection.

Ultimately, this research supports the development of bio-inspired coastal infrastructure that leverages natural processes for climate resilience. By addressing existing knowledge gaps in coral roughness characterization and flow interaction, the study contributes valuable experimental data and methodological insights to the growing field of nature-based solutions in sustainable engineering.

To guide readers through the paper, Section 2 describes the experimental setup and methodology, Section 3 presents the results and analysis, Section 4 discusses the implications and comparisons with previous studies, and Section 5 concludes with key findings and recommendations for future work.

2. Materials and Methods

2.1. Modeling Coral Structure: Depth Ratio and Porosity

To ensure geometric similarity between the experimental model and natural reef conditions, it is important to compare the height of real coral structures relative to ocean water depth with the height of the 3D-printed coral model relative to the flume flow depth. To attain geometric similarity, the model coral reefs were scaled based on field measurements of real Acropora species reported in existing literature. Ensuring the proportionate relationships between the model and the prototype was necessary to properly generalize the experimental results to natural conditions. The height of the model corals was set within the range of 0.05 to 0.1 m, consistent with height variations in Acropora species reported in previous field studies. To accomplish this, staghorn Acropora species were selected as a reference to calculate similarity ratios, as shown in Table 1.

The experiment is based on branch-type Acropora corals, which are a prominent type of reef-building coral. They are well-known for their branching and plate-like structures and are considered keystone species in coral reef ecosystems [16]. This study maintained geometric similarity between the natural reef (prototype) and the experimental model by matching both the porosity and the ratio of coral height to water depth. The model’s height was precisely determined based on the maximum and minimum flow depths within the flume and was scaled using field data reported in previous studies. This approach ensured that the suggested coral height ranged between 0.05 and 0.1 m, effectively replicating real corals in the sea. The chosen coral height was evaluated using a ratio, denoted as R, which signifies the proportion of the actual coral height to the actual sea depth, as elaborated in Table 1.

Table 1. Parameters of actual species: establishing a relation with the flume model for the assessment of sea depth and coral height.

Acropora Species	Sea Depth (m)	Coral Height (m)	Sea Depth Reference	Coral Height Reference	Ratio (Coral Height/Water Depth) (R)
Acropora pharaonis Site 7	4	2	[17]	[18]	0.5
Acropora pharaonis Site 27	7	2	[17]	[19]	0.29
Acropora pharaonis Site 26	5	2	[17]	[19]	0.4
Acropora cervicornis	0–5	2	[20]	[21]	0.4–0.8
Acropora muricata	5	1	[22]	[23]	0.2
Acropora prolifera	7	0.02	[24]	[25]	0.00286

Table 1. Parameters of actual species: establishing a relation with the flume model for the assessment of sea depth and coral height.

Acropora Species	Sea Depth (m)	Coral Height (m)	Sea Depth Reference	Coral Height Reference	Ratio (Coral Height/Water Depth) (R)
Acropora pharaonis Site 7	4	2	[17]	[18]	0.5
Acropora pharaonis Site 27	7	2	[17]	[19]	0.29
Acropora pharaonis Site 26	5	2	[17]	[19]	0.4
Acropora cervicornis	0–5	2	[20]	[21]	0.4–0.8
Acropora muricata	5	1	[22]	[23]	0.2
Acropora prolifera	7	0.02	[24]	[25]	0.00286

The coral height and sea depth data used for model design were derived from field studies conducted in the Red Sea and Arabian Gulf regions, where Acropora species such as A. pharaonis and A. muricata are common [17,18,19,20,21,22,23,24,25]. These datasets provided representative geometric parameters for branching corals typically found in tropical and subtropical reef systems. Accordingly, the present model design and findings are most applicable to shallow-water Acropora-dominated reefs in arid and semi-arid coastal regions, such as those in the Arabian Gulf and adjacent waters, where similar coral morphologies and hydrodynamic conditions prevail.

Natural Acropora corals have highly porous skeletal structures, offering advantages to both the corals and the ecosystem [26]. Porosity levels typically range from 40% to 90% [26,27,28,29] and are influenced by factors such as species, age, and environmental conditions. The bulk volume of the 3D-printed coral model was determined by wrapping the model in plastic film to exclude water infiltration, submerging the model, and collecting the water displaced. This procedure was repeated without the plastic film to measure the volume of coral. Porosity was calculated by dividing the difference between the displaced water volume with plastic and without plastic by the total volume. This method follows a standard volume-displacement approach adapted for highly porous 3D-printed structures, where the model is first sealed to obtain the bulk (coral + void) volume and then re-submerged unsealed to measure only the solid volume.

To validate the representativeness of the model porosity, values from several Acropora species were considered. Reported porosity ranges include approximately 54–81% for Acropora palmata, 51–75% for Acropora cervicornis, and 62–88% for Acropora hyacinthus, with mean values near 65–75%. The model porosity of ~71%, therefore, falls well within the natural variability observed in real coral skeletons, confirming its physical plausibility. Although this technique is less precise than imaging-based methods such as micro-CT, it provides a simple and effective experimental approach for assessing porosity in scaled hydraulic models.

The model porosity of ~71% was within the range of real coral porosity, indicating that the modelling method effectively simulates natural coral reef environments.

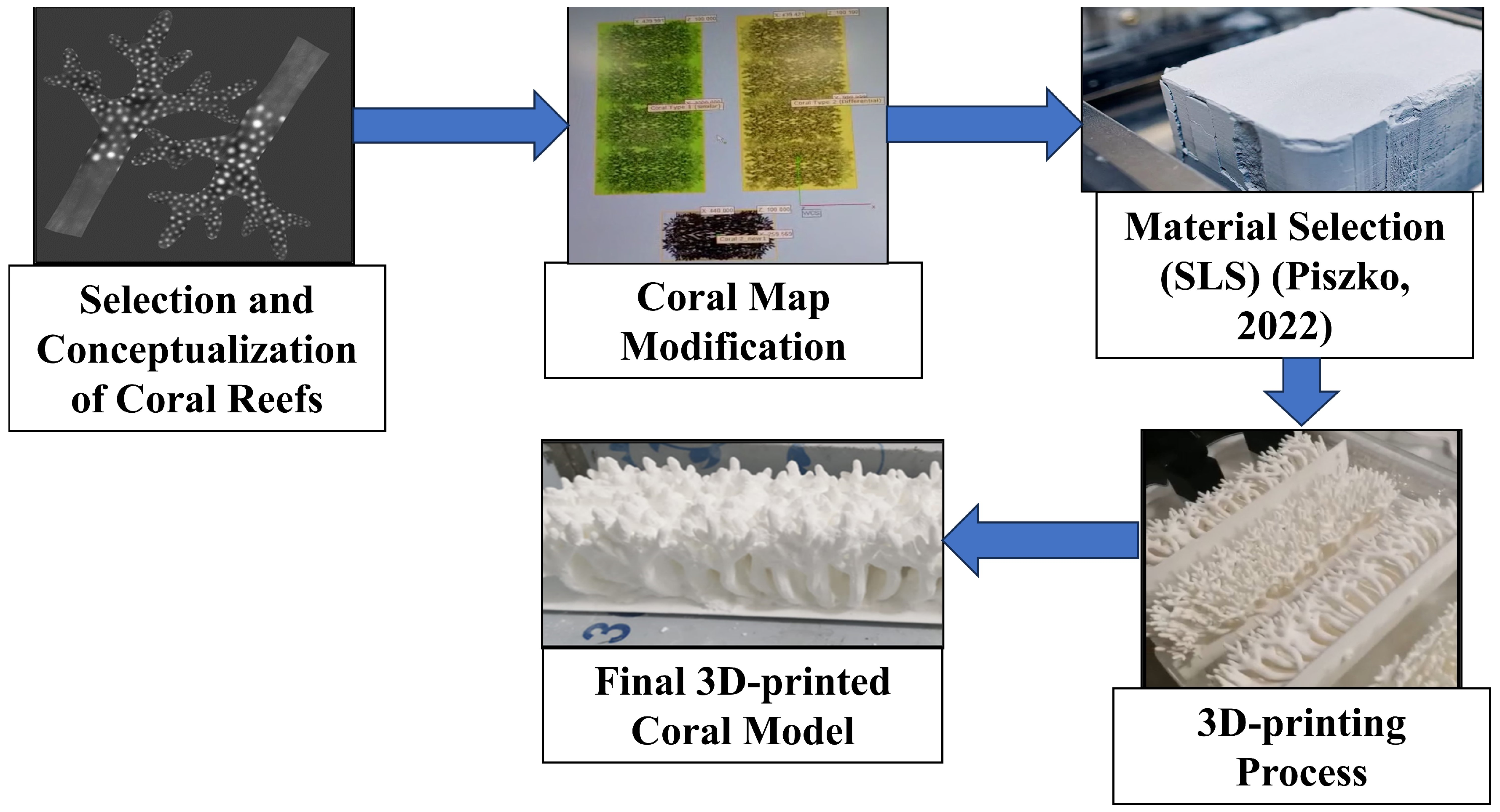
2.2. 3D-Printed Coral Reefs

This study used 3D-printed coral models and controlled flow conditions in a flume environment. The aim was to examine the relationship between continuous flow and the structures of coral reefs to analyze flow velocity, depth, and turbulence intensity. This enables the evaluation of the capacity of coral reefs to reduce flow energy. Coral reef models were built using 3D-printing technology to ensure representative morphometry and roughness. The accuracy of 3D-printed coral models depends on several variables, including printing technology, material quality, design correctness, and postprocessing [30]. It allows building complex reef structures that are impractical to build using traditional methods.

A digital model of the coral reef, referred to as a 3D coral map, was created using computer-aided design software as the initial step in the 3D-printing process. The type of corals used, Acropora Staghorn corals, served as the main basis for our model maps. Coral maps were modified using a 3D-printing modeling program called Materialise Magics to simulate the force on the reef that determines the strength of the materials for 3D printing. After receiving the digital model, 3D printers were utilized to create the coral reef layer by layer [31]. The selective laser sintering method was used for 3D printing to produce the best mechanical properties and the greatest strength and stiffness, with the highest level of resolution, as shown in Figure 2.

The corals were constructed as uniform, identical strips to enable experimentation, i.e., tests on various reef lengths. Each strip was 0.1 m in length, 0.45 m in width, and 0.1 m in height. Six strips in total, adding up to 0.6 m in length, were utilized in the experiment. Each coral strip had a mass of 0.848 kg and a volume of 0.0129 m³, yielding a mass density of roughly 940 kg/m³. The strips were arranged sequentially across the width of the flume in such a way that mass and volume were distributed symmetrically over the cross-section. This uniform distribution was necessary to ensure flow conditions in all parts were the same and eliminated any undesirable hydrodynamic effects during the experiment due to the non-uniform distribution of coral strips. The selection of the coral strip length (0.1 m) was entirely determined by the size limitations of the laboratory flume. Rather than focusing on dimensional features, the study was designed based on nondimensional similarity parameters between the prototype and the model, specifically the Froude number (Fr), depth effect (DE), and size effect (SE), to maintain dynamic consistency. This modular configuration allowed systematic variation in reef width (SE = 1–6) to assess the influence of reef size under controlled conditions. Test cases were also repeated to verify measurement consistency, and negligible variations were observed across repeated runs, confirming the reliability of the experimental data. While the uniform arrangement of coral strips may not fully replicate the natural irregularity of coral reef distributions, this controlled configuration was deliberately chosen to isolate hydrodynamic effects under repeatable laboratory conditions, as shown in Figure 3. Uniform placement minimizes variability due to random coral positioning, enabling a clearer understanding of fundamental flow–structure interactions and roughness effects. The results therefore provide baseline hydrodynamic relationships that can later be extended to more complex, spatially heterogeneous reef geometries through numerical or scaled physical modeling. In practical terms, these findings are applicable to the design and parameterization of engineered or restored reef systems where modular or regular reef elements are deployed for coastal protection purposes. These strips were all attached with an adhesive to an acrylic sheet to ensure that they were firmly secured with the support. The support was fixed to the flume using fiberglass that was fastened by nuts and bolts to maintain a stable coral structure in the flume. The support was carefully removed from the flume after an experiment for a particular case (for instance, experiments for the first strip) was completed. The next strip was then placed with adhesive and left in place for a day to ensure that the strip would not move under any favorable or unfavorable conditions, such as a high flow rate. The rest of the strips followed this same process.

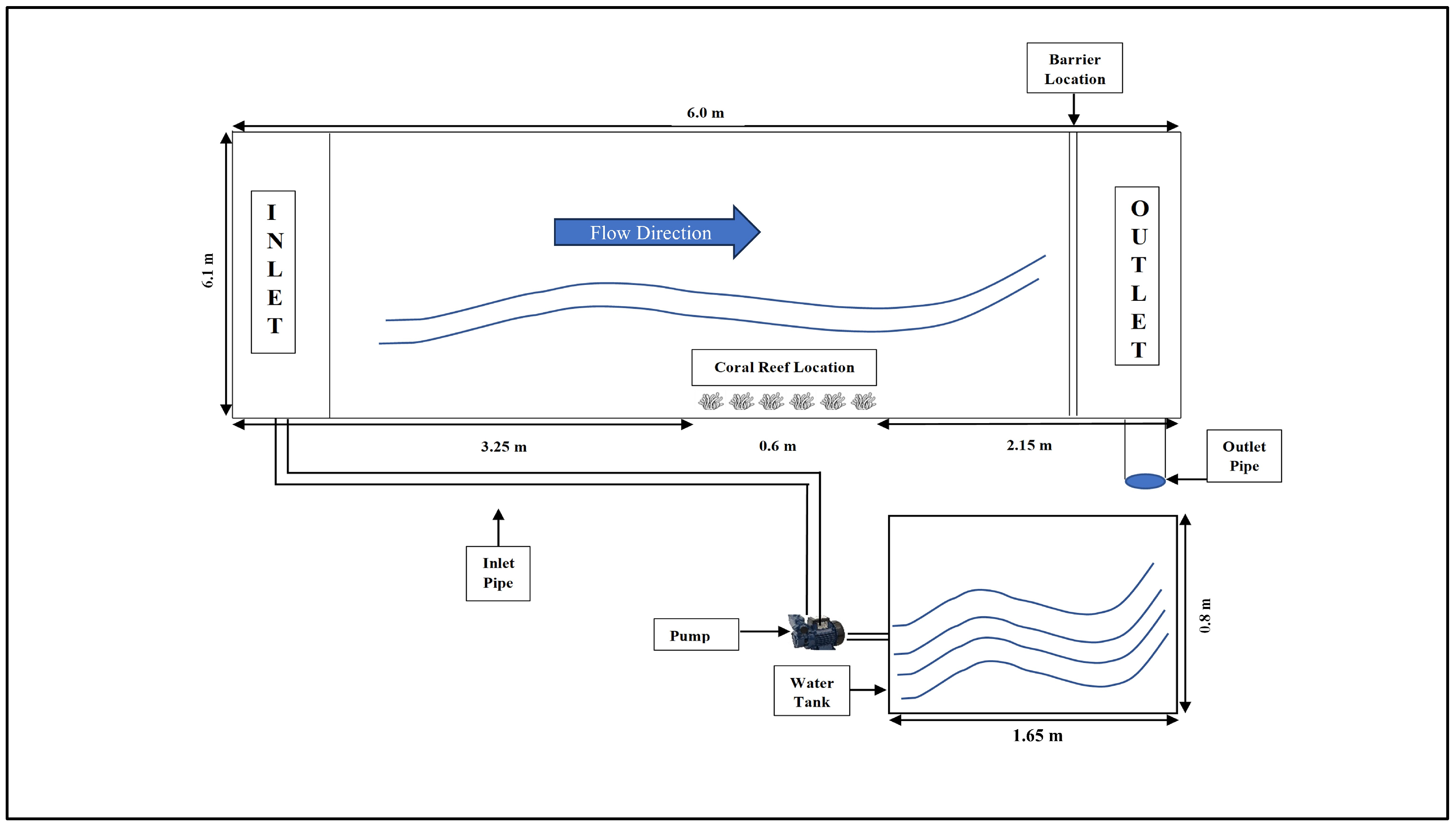
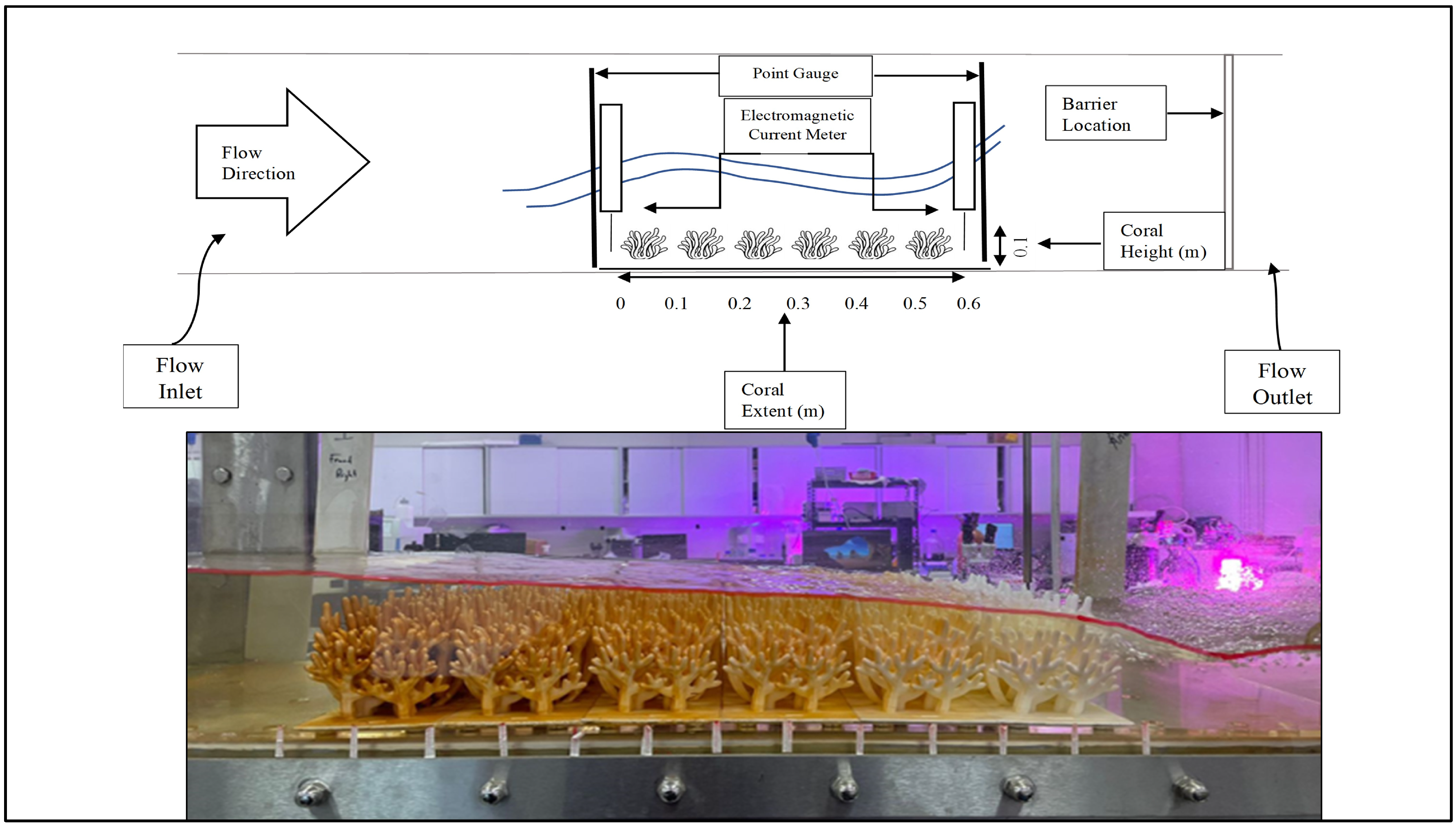
2.3. Experimental Setup

The experiments were conducted in the water lab at United Arab Emirates University. Steady flow was generated in a wide flume (6 m in length, 0.45 m in width, and 0.5 m in depth), as illustrated in Figure 4. While natural coral reefs are influenced by oscillatory wave motion and tidal currents, this study focused on long-period wave events such as tsunamis and major storm surges, where the overtopping flow across reefs behaves as quasi-steady and unidirectional for a significant duration. This approach allows for isolating the mean hydrodynamic behavior and quantifying the flow resistance caused by coral roughness under conditions representative of these extreme events. The trials were carried out in a flume tank specifically built to replicate a range of flow characteristics commonly observed in coastal regions where coral reefs are located. The flume configuration consists of the flow velocity, which is adjusted to replicate various energy situations, ranging from tranquil seas to surges caused by storms, often falling within the range of 0.2 to 1.5 m per second. Grid structures are used to simulate natural turbulence levels found in reef ecosystems. The tests were intended to imitate the dynamic conditions that coral reefs confront in their natural surroundings by altering these factors. This allowed for a realistic assessment of the coral reefs’ ability to reduce flow energy. The study involved performing experiments to comprehend the hydrodynamical characteristics through and on top of the coral reefs. To this end, we used an electromagnetic current meter (ECM) manufactured by JFE Advantech Co., Ltd., from Nishinomiya, Japan and point gauges to measure flow velocity and depth at the front of, back of, and over the coral reefs, which enabled the calculation of flow energy reduction and Manning’s roughness coefficient of the coral reef under various coral properties and flow conditions. Being able to capture instantaneous velocity measurements, the current meters had an accuracy of ±0.5 cm/s and a measurement range of ±250 cm/s in the x- and y-axes. They played a pivotal role in assessing the flow velocity in this experiment. They operated on the principle of electromagnetic induction, enabling them to precisely calculate water velocity as it passed by the reef model [32].

The material that is well-suited for correctly reproducing the complex architecture of coral reefs in our 3D-printed models was used. This material also offers the necessary strength and durability required for hydrodynamic testing. The selected material was a high-performance photopolymer resin, renowned for its capacity to create intricate details and strong mechanical characteristics. To ensure the fidelity of the 3D-printed models to real coral structures, meticulous attention was paid to the scale and resolution of the printing process. The 3D printing process was carried out via a high-precision Selective Laser Sintering (SLS) printer (Formlabs Inc., Somerville, MA, USA), which enables the creation of intricate shapes with exceptional mechanical characteristics and surface quality. An assessment was conducted to analyze the mechanical characteristics of the 3D-printed corals and compare them with those of the original coral samples. The objective was to verify if the printed models accurately replicated the behavior of real corals when subjected to flow conditions. The digital models utilized for 3D printing were derived from meticulous scans and measurements of actual Acropora corals, guaranteeing precise replication of essential morphological characteristics. The flow tests demonstrated that the 3D-printed models exhibited comparable turbulence patterns and wake dynamics to those observed in real coral reefs. This was confirmed by conducting physical flow tank experiments and Computational Fluid Dynamics (CFD) simulations. The trials demonstrated substantial decreases in both flow velocity and depth across the coral models, aligning with the anticipated characteristics of actual coral reefs. This confirms that the 3D-printing process reliably replicated the geometric and hydrodynamic behavior of real coral colonies, validating the printed models for experimental use.

ECMs were regularly calibrated under controlled conditions to ensure data reliability, involving systematic vertical sensor submersion and zero-point adjustment for velocity stability, primarily in the x-axis direction, which aligned with the study’s focus. Data were collected at a frequency of 20 Hz within a 60-s range. To verify repeatability, several test cases were conducted more than once, and consistent readings of velocity and depth were obtained across repeated trials. The overall measurement uncertainty was minimized through careful calibration of instruments and stable flow control during each experiment. Spatially, measurements involved a 0.1-m separation between coral strips, and they progressed upward at intervals of 0.02 m for deeper flows. This ensured the acquisition of the flow characteristics in a two-dimensional vertical plane in the center line of the coral reef, as shown in Figure 5. However, due to the limitations of sensors stemming from the high density of coral reefs, measuring velocities within the corals was limited. The point gauge was used to measure the flow depth. It consisted of a vertical staff that bore a mark indicating the flow depth. Point gauge readings were routinely confirmed through scale readings; as the steady flow was considered when conducting the tests, temporal fluctuations were minimal, as depicted in Figure 5. The flow structure over the coral reef was all altered by changing the water depth in the wide flume using a barrier fixed downstream of the flume. The related factors, namely flow depth, flow velocity, and coral reef length, were systematically accounted for while developing the test cases.

Velocity and depth were measured along the central axis of the flume at the front, middle, and back of each coral strip. The inlet included a flow straightener to ensure uniform inflow, while a tailgate at the outlet controlled depth and subsidized backflow. Measurements were taken well upstream of the outlet (midway of the flume), and the last coral strip was placed greater than 1.0 m to avoid recirculation effects. Variations in flow depth, velocity, and coral submergence were incorporated into the analysis through nondimensional parameters such as the Froude number and depth effect. The flume setup, though simplified, provided a controlled environment suitable for isolating key hydrodynamic processes relevant to real coral reef conditions.

2.4. Nondimensional Numbers of the Flow–Coral Interaction and Test Cases

Coral hydrodynamical studies use variables to explain the flow qualities and flow change both through and on top of the coral reef to understand the flow–coral interaction [33]. Several typical variables in reef hydrodynamics include (a) coral reef width, (b) coral reef length, (c) coral porosity, (d) water density, (e) flow depth, and (f) flow velocity. For the current study experiment, the altering parameters were coral reef length, flow depth, and flow velocity. Here, the flow potential, the combination of flow depth and velocity, can be related to the Froude number (F_r). It is expressed as

$$F_r=V/\surd \left(gD\right)$$

(1)

where F_r is the Froude number, V is the depth-averaged flow velocity across the flume, g is the gravitational acceleration, and D is the hydraulic depth of the channel, which is the flow depth in the flume in this study. Higher F_r represents shallow and fast flows, while lower F_r represents deep and slower flows. In control tests (experiments without corals), a steady and uniform flow regime was typically maintained. It encompassed the entire subcritical flow area, and F_r varied from 1.05 (shallow fast flow) to 0.06 (deep slow flow) in this study. The F_r was calculated without the effect of corals in the analysis. One crucial metric is the relation between flow depth and coral height [34]. The ratio of the average water or flow depth to the average height of the coral structure within a certain area is known as the depth effect, which is widely used for analyzing flow structure interaction. The determination of the depth effect is achieved using the following equation:

$$DE= {\displaystyle \frac{h}{H}}$$

(2)

where DE is the depth effect, h is the flow depth without coral reefs, and H is the coral height. DE varied from 0.42 (shallow water corals) to 2.38 (deep water corals) in this study, as shown in

Table 2. Test cases with and without corals (control). F_r and DE were calculated without the effect of the coral reef.

	Coral Reef Length (m)	Froude Number (Fr)	Depth Effect (DE) $\frac{\mathit{h}}{\mathit{H}}$	Size Effect (SE) $\frac{\mathit{L}}{\mathit{H}}$
No strip (Control)	-	1.05	-	-
	-	0.3	-	-
	-	0.14	-	-
	-	0.08	-	-
	-	0.06	-	-
Strip 1	0.1	1.05	0.4	1
	0.1	0.3	0.84	1
	0.1	0.14	1.35	1
	0.1	0.08	1.88	1
	0.1	0.06	2.38	1
Strip 2	0.2	1.05	0.4	2
	0.2	0.3	0.84	2
	0.2	0.14	1.35	2
	0.2	0.08	1.88	2
	0.2	0.06	2.38	2
Strip 3	0.3	1.05	0.4	3
	0.3	0.3	0.84	3
	0.3	0.14	1.35	3
	0.3	0.08	1.88	3
	0.3	0.06	2.38	3
Strip 4	0.4	1.05	0.4	4
	0.4	0.3	0.84	4
	0.4	0.14	1.35	4
	0.4	0.08	1.88	4
	0.4	0.06	2.38	4
Strip 5	0.5	1.05	0.4	5
	0.5	0.3	0.84	5
	0.5	0.14	1.35	5
	0.5	0.08	1.88	5
	0.5	0.06	2.38	5
Strip 6	0.6	1.05	0.4	6
	0.6	0.3	0.84	6
	0.6	0.14	1.35	6
	0.6	0.08	1.88	6
	0.6	0.06	2.38	6

.

The coral height-to-length ratio is determined as the size effect (SE) [35]. Coral colonies with a high length-to-height ratio typically have a more complex and irregular structure, with multiple branching or finger-like projections that enhance the surface area for water movement [36]. This can lead to more turbulence and water mixing. Calculation of SE is performed using the following equation:

$$SE= {\displaystyle \frac{L}{H}}$$

(3)

where L is the coral length (measured parallel to the flow) and H is the coral height. SE varied from 1 (narrow corals) to 6 (wider corals) in this study, as shown in Table 2.

The test cases were divided into two parts, a) experiments without the coral reef (control experiments) and b) experiments with the coral reef, as shown in Table 2. Control experiments were conducted to isolate influential factors, ensuring a focused study on the variable of interest. In this experiment, we conducted control experiments to assess the effect of coral reefs on reducing flow energy. We identified test cases using the nondimensional parameters F_r, DE, and SE. Six identical coral reef strips, five different flow conditions, and five controls generated 35 test cases.

2.5. Roughness Estimation

Calculating depth-averaged velocity is crucial for roughness analysis, as the coral structure considerably changes the horizontal flow velocity over depth. For each test case, the velocity measurements above the reef over a specific depth were performed independently at a vertical interval of 0.02 m and averaged to obtain the depth-averaged velocity. Manning’s roughness coefficient has been widely used in civil engineering hydraulics research to model surface roughness. Because our main objective was to investigate the roughness characteristics of corals under varying hydrodynamic conditions, Manning’s roughness coefficient was calculated with the measured data. The higher the Manning’s roughness coefficient, the greater the flow resistance [37]. In general, Manning’s roughness coefficient is assumed to depend on the surface texture but not on flow characteristics [38]. However, this may not be true for cases with higher roughness heights, such as corals. Past studies used a constant roughness coefficient despite varying flow-wise and coral-wise parameters [39]. In this study, the sensitivity of the coefficient to F_r, size, and depth effects was analyzed. Consequently, the key factors controlling the coefficient were understood. The study was primarily able to determine the relative importance of each parameter and how they interact to affect the coefficient by examining the sensitivity of Manning’s roughness coefficient to these parameters. In coral reef hydrodynamics, the coefficient represents the frictional resistance of water flowing over the coral surface, which is primarily a function of surface roughness. Therefore, the expression of n given by Manning’s equation is

$$n={\displaystyle \frac{1}{V}}{R}^{{\displaystyle \frac{2}{3}}}{S}^{{\displaystyle \frac{1}{2}}}$$

(4)

where V is the flow velocity, R is the hydraulic radius, S is the energy head loss gradient, and n is the Manning’s roughness coefficient.

The spatial variation in n was calculated from the reef front to the end by zoning the reef length. The hydraulic radius was calculated in the middle of the zone using the average flow depth between the front and end of the zone, as elaborated in Figure 6. The width of the reef was kept at a constant value of 0.45 m. The hydraulic radius was determined by

$$R={\displaystyle \frac{Bh}{B+2h}}$$

(5)

where R is the hydraulic radius, B is the width of the reef, and h is the average flow depth at the mid-zone.

The head loss across each reef zone was determined using the difference in total head between the front and back of the zone, as expressed in Figure 6. Therefore, the head loss gradient is calculated using the following equation:

$$Energy (head) Loss Gradient= {\displaystyle \frac{H_b-H_f}{L}}$$

(6)

where H_f is the total head at the front of the zone, H_b is the total head at the back of the zone, and L is the length of the zone (0.1 m).

3. Results

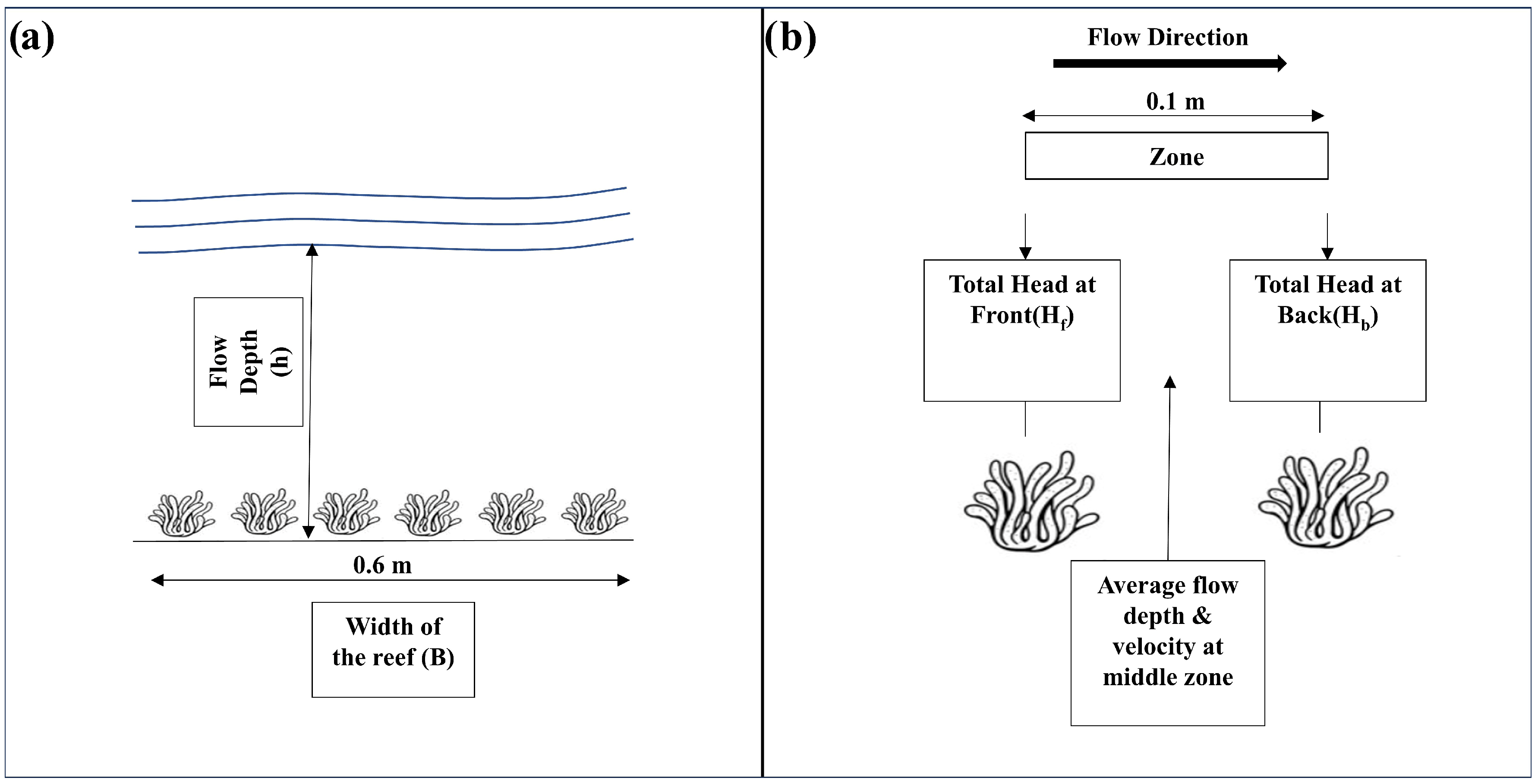
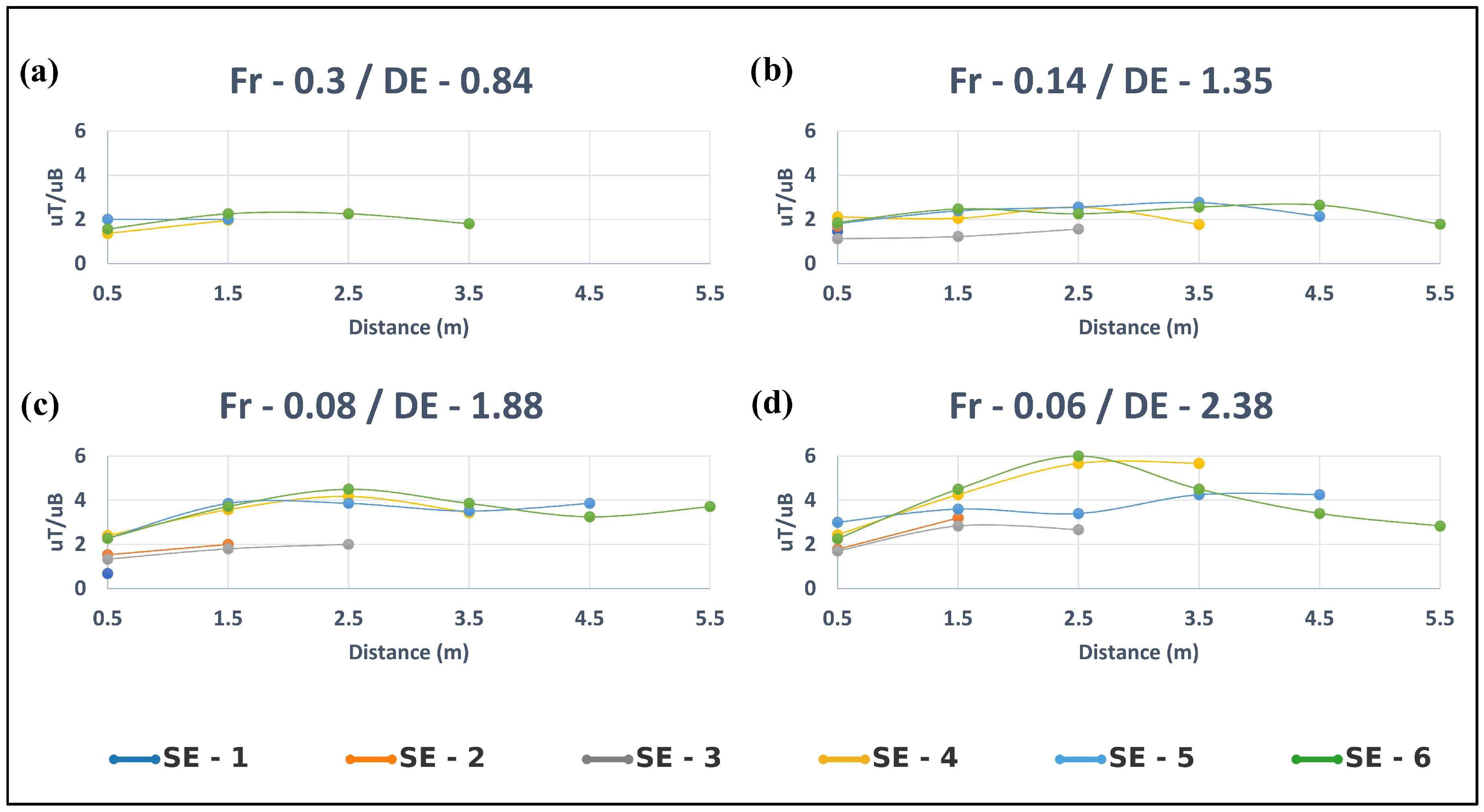
3.1. Spatial Variation in Flow Depth over the Reef

The spatial flow depth variation in coral reef environments results from various factors, such as reef topography, flow dynamics, and the coral ecosystem [40]. This analysis emphasized the interaction between coral reefs and the flow structure. A coral span of narrow coral (0.1 m) and wide coral (0.6 m), i.e., SE-1 and SE-6, was employed to assess spatial flow depth variations across various F_r and depth effect scenarios as elaborated in Figure 7. Here, the noncoral depth (control results) case was used to compare the spatial flow depth variation over the reef. F_r–1.05/DE–0.4 for SE-1 showed higher flow depth in front of the coral compared to the noncoral cases, which is due to the reflection of the coral with the depth reduction that was only seen toward the reef end (Figure 7a). F_r–0.3/DE–0.84 (Figure 7b) unveiled a relation where the coral presence considerably decreased the flow depth at 0.07 m from the start of the reef. F_r–0.14/DE–1.35, F_r–0.08/DE–1.88, and F_r–0.06/DE–2.38 (Figure 7c–e) showed relatively consistent flow depth reductions across the study area, with marginal differences between coral and noncoral conditions. For SE-6, at F_r–1.05/DE–0.4, the flow depth in the presence of corals was higher than that of the noncoral case near the reef’s leading edge, indicating flow obstruction and localized backwater effects caused by the coral structure (Figure 7f), and the flow depth gradually returned to the same level as the noncoral case toward the end of the reef, indicating that the coral did not cause any net reduction in flow depth along its length for this condition. For F_r–0.14/DE–1.35, the flow depth for coral and noncoral cases was the same at the beginning of the reef, and it gradually decreased depending on the coral case (Figure 7h). F_r–0.08/DE–1.88 and F_r–0.06/DE–2.38 (Figure 7i,j) showed relatively consistent flow depth reductions for SE-6 with marginal differences between coral and noncoral conditions.

After observing the comparative analysis of flow depth variations with and without the presence of coral reefs, it can be observed that there was no gradient for control cases in both the SE cases, as there was no energy dissipation or blockage. Comparing SE-1 and SE-6, for shallow and fast flows (Figure 7a,f), the gradient of flow depth with the coral case was higher for SE-6 compared to SE-1 toward the end of the reef. This indicates that an increase in coral size could reflect the flow considerably. The high gradient was due to higher energy dissipation and blocking effects. Approaching the slow deep flows for both SE-1 and SE-6 (Figure 7e,j) showed that there was no gradient for cases with corals compared to noncoral cases. This shows that SE-1 and SE-6 had similar spatial variations in flow depth. Overall, this analysis indicates that both narrow and wide coral reefs under shallow, fast-flow conditions caused notable changes in the flow profile over the reef, whereas these effects were minimal under deeper, slower flows. This also emphasizes that the roughness effect (analyzed later) of corals was greater when they were in a shallower flow (F_r > 0.2, DE < 1).

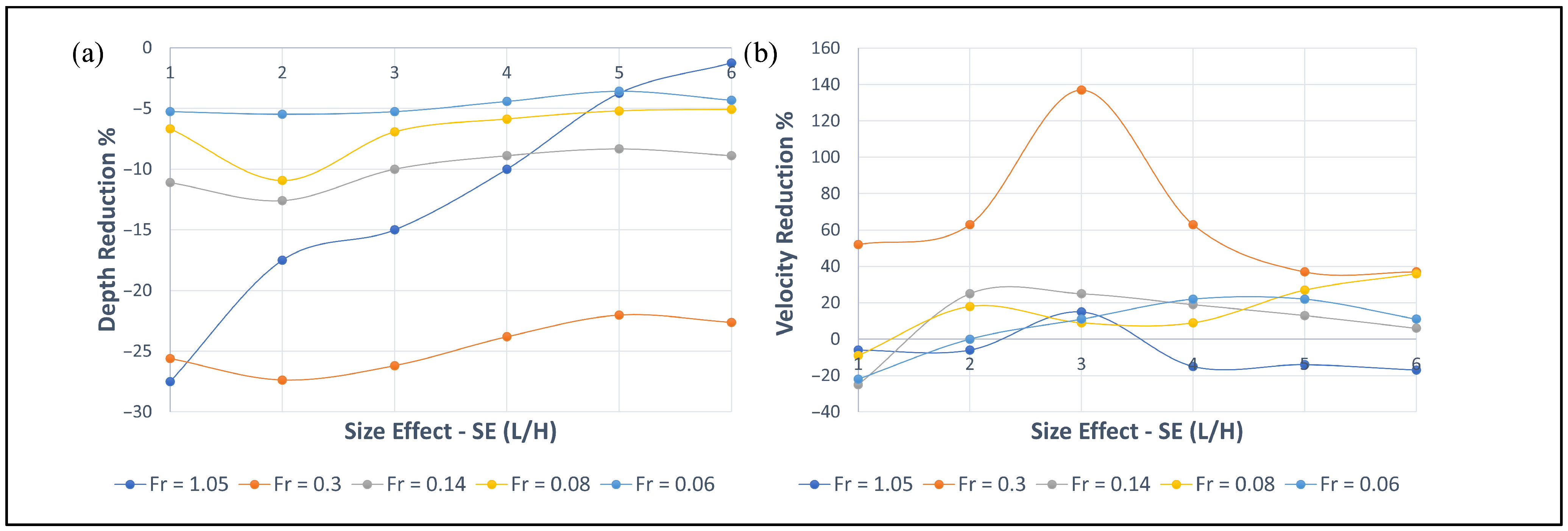
3.2. Flow Depth and Velocity Reduction Behind the Reef

Figure 8 shows the flow depth and flow velocity reductions behind the reef compared to cases without the reef. The reductions are indicated in negative numbers; higher negative values represent the greatest reduction. The percentage of the reduction is calculated using depth and velocity differences in cases with and without corals divided by depth and velocity in cases without corals. F_r–1.05 had the highest depth reduction percentage of −27.5% at SE-1, and the depth increased (depth reduction percentage decreased) to −1.25% for SE-6, which was the least among all cases. Velocity reduction for F_r–1.05 was also evident at −8% for SE-1. As it approached SE-3, there was a gradual velocity increment of ~18%. From SE onward, the reduction percentage decreased to −20%. This indicates a greater reduction at the reef end for the cases of SE-6 for F_r–1.05. For flow with F_r ranging between 0.3 and 0.08, there was a gradual increase in the depth reduction for SE-2 and then the depth reduction steadily decreased. In the case of F_r–0.3, only the velocity increment was noticed for all SE cases, with its value peaking up to 135% at SE-3. This local velocity increase at F_r–0.3 can be attributed to flow acceleration over partially submerged coral tops and wake reattachment effects, where reduced depth and flow constriction caused localized increases in mean velocity despite overall energy loss. This behavior suggests a transitional regime between subcritical and near-critical conditions and will be further investigated in future work using higher-resolution flow measurements. For F_r–0.14 to F_r–0.06, velocity reductions were only valid for SE-1, with other Ses showing velocity increments instead. The general trend showed that the flow depth reduction rate decreased as F_r decreased. However, this is not the case for the flow velocity reduction rate. F_r–0.06 and F_r–0.14 had the highest reduction; on the contrary, F_r–0.3 had a velocity increase at SE-1. It can also be observed that for all F_r cases except for F_r–1.05, the velocity increase occurred throughout all SE except for a decrease (narrow to wider coral) (Figure 8a,b).

For a given SE (SE-1), it was observed that the depth reduction rate increased for shallower and faster flows (increased F_r). This indicates that the fast flow and the narrowest coral length had the biggest flow depth reduction behind the reef. For the rest of the SE cases, the case remained the same. The only notable contrary exception was for the shallow and fast flow (F_r–1.05) at the widest coral (SE-6), where it had a lower depth reduction rate compared to the other cases. At SE-1, velocity reduction for F_r–0.14 and F_r–0.06 had a high reduction of ~25%, while F_r–1.05 and F_r–0.08 had similar velocity reduction rates of ~10%. Approaching SE-3, depth reduction was higher for F_r–0.3 compared to F_r–1.05. However, there was a velocity increment for all the F_r cases. In terms of SE, the pattern observed in the velocity reduction graph showed that there was a reduction for the low SE (narrow corals); as SE increased (wider corals), we noticed the velocity gradually increase.

The conservation of mass principle in fluid dynamics asserts that the mass of a fluid remains constant within a closed system as time progresses. The study identified a distinct interrelationship among crucial flow parameters, such as flow depth, velocity, and flow rate. The findings illustrated the profound influence that alterations in a single parameter can have on the other variables, thus emphasizing the intricate dynamics of fluid movement surrounding coral reef formations. Moreover, the correlation between the speed of flow and the volume of flow was determined by the cross-sectional area of the flow. If the cross-sectional area is constant, an increase in velocity can lead to higher flow rates, whilst a drop in velocity can result in lower flow rates.

A coral reef can decrease the depth of flow downstream of the reef [41]. This is brought on by several elements, such as the shape and size of the reef. In addition to altering flow depth, the velocity variations across the reef influence nutrient transport and mass exchange within the water column [42]. According to modeling and field observations, the flow depth can be greatly reduced behind coral reefs, with some studies indicating decreases of up to 70% compared to open-water circumstances [43]. However, these previous studies were based on oscillatory wave-driven conditions, which differ from the steady unidirectional flow regime used in this experiment. Therefore, the reduction values are not directly comparable, though the general trend remains consistent. Our study showed that depth reductions can be up to 27.5%, which is considerably less than the 70% value reported in previous studies, because of the size of the reef model used and the limited flow conditions in this research. This study also showed notable velocity reductions, given the limited size and pattern of the corals. Generally, flow velocity reduces as it passes behind a reef’s edge [44]. Reef size and porosity, as well as flow speed, direction, and depth, are only a few variables that affect how much the flow velocity is reduced behind the reef [45]. The study showed that the flow velocity reduction behind the reef was more prominent for narrow corals (up to 25%). This study primarily revealed that shallow and narrow coral reefs decreased the flow depth more than the flow velocity. On the contrary, shallow and wide coral reefs decreased flow velocity more than flow depth behind the reef subjected to fast flow inundations.

3.3. Two-Layered Flow Analysis

Submerged corals exhibit a two-layer flow regime [46]. A distinct flow separation can be observed above and through the corals [47]. The upper flow layer above the coral is influenced by top surface roughness. In contrast, the lower flow layer is controlled by the blockage and pore structure of the coral. This causes a nonlinear flow velocity distribution over the depth. The analysis examined four F_r cases, except for the one with the highest F_r of 1.05, as the flow depth is below the reef height. A single velocity measurement through the corals was possible due to the highly porous nature of the reef bottom. The ratio of the two-layered flow was determined using the following equation:

$$Two layered flow ratio= {\displaystyle \frac{Depth Averaged velocity above the corals \left(u_T\right)}{Flow velocity through the corals \left(u_B\right)}}$$

(7)

For flow with F_r–0.3/DE–0.84 (Figure 9a), SE-1 had twice the difference in top and bottom velocity compared to SE-4 at 0.5 m from the start of the reef. For F_r–0.08/DE–1.88 (Figure 9c), SE-3 had a velocity difference two times less than SE-4, SE-5, and SE-6 at 2.5 m from the start of the coral. F_r–0.06/DE–2.38 (Figure 9d) showed that SE-6 had velocity differences between the regions above and through the corals that were up to six times higher compared to SE-3 in the mid-regions. This explains that there was a notable difference between top-layer velocity and velocity through the corals in deeper flow. In general, as the depth increased (increased DE), the ratio between velocity over the coral and velocity through the coral increased. On the contrary, based on the effect of distances on the two-layered flow, the ratio was highest in the mid-regions of the reef, most notably in F_r–0.08/DE–1.88 and F_r–0.06/DE–2.38 (Figure 9c,d). This can be explained by the fact that a velocity increase occurred, as was seen in the velocity reduction analysis. Based on all the graphs, it was also evident that two-layered flows were more highly significant in wider coral sizes (high SE) compared to narrow ones (low SE). It must also be noted that for some cases, such as F_r–0.3/DE–0.84 (Figure 9a), the ratio for SE-1 could not be calculated due to the absence of top-layer flow. Regarding F_r, shallower fast flows had a lower two-layer flow ratio compared to deeper flows. A common observation was that, for all the cases, velocity over the coral was greater than velocity through the corals.

The analysis reveals that, for subcritical flow conditions, the velocity over the reef could be two to three times greater than that through the reef. Overlooking this effect may result in the inappropriateness of actual coral flow velocities and inaccurate predictions of coral responses to varying flow conditions.

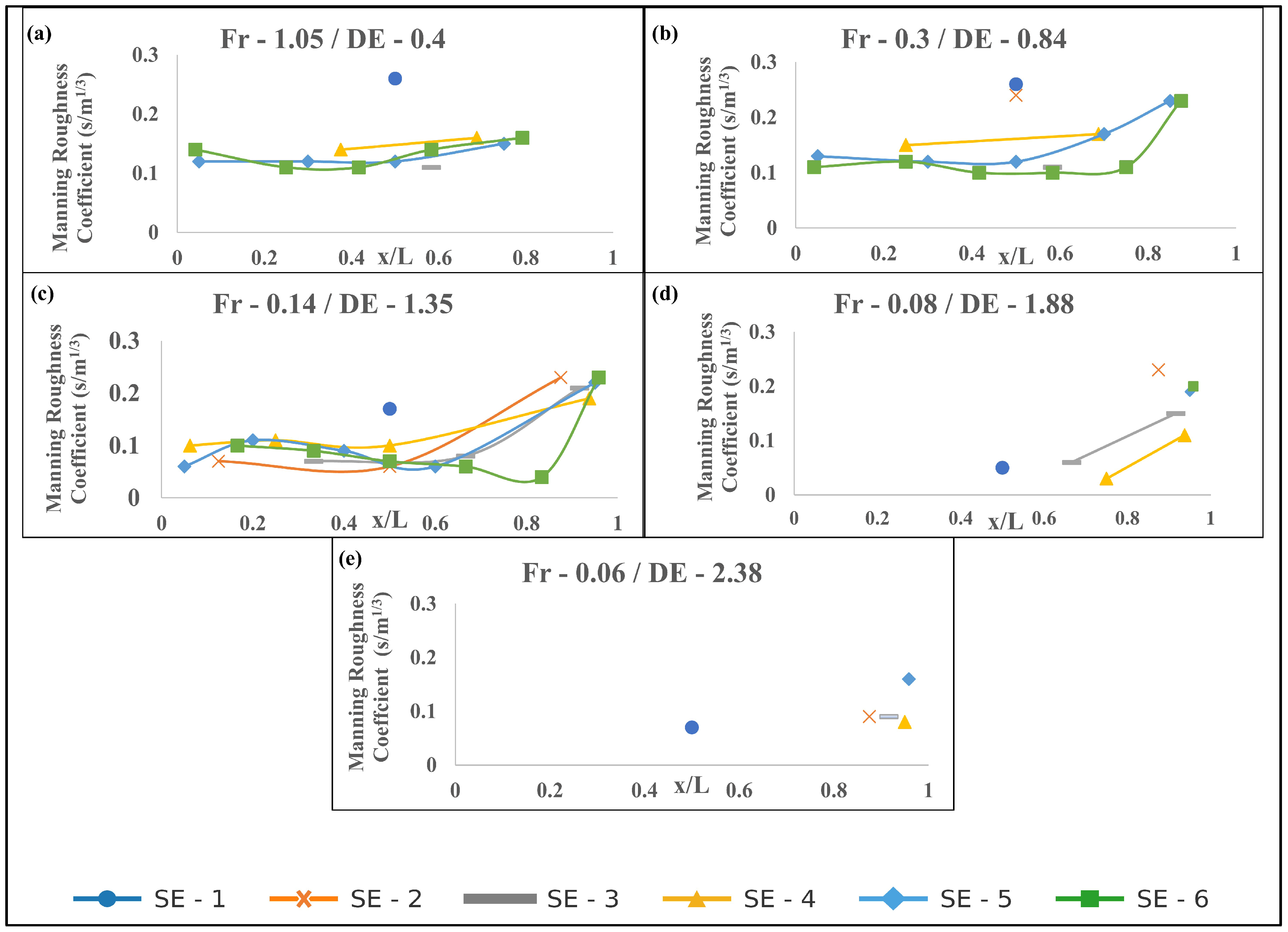
3.4. Coral Roughness Coefficient

Figure 10 shows the change in n over the reef for different flow conditions. For all the cases involved in this analysis, Manning’s coefficient n ranged from 0.03 to 0.26. Flow with F_r–1.05/DE–0.4 showed the roughness coefficient values ranging from 0.1 to 0.15 throughout the reef for all SE except for SE-1, which had the highest coefficient value of 0.26 (Figure 10a). This explains that fast and shallow flows with narrow reefs provide high resistance to the flow. For F_r–0.3/DE–0.84, it was seen that lower SE had greater coefficients, specifically in the middle of the reef. However, as SE increased, the roughness coefficient value decreased, specifically at the start and middle of the coral zone. This indicates that flow energy dissipation was reduced in cases of wide corals (Figure 10b). Only SE-5 and SE-6 had high roughness coefficients toward x/L–0.9 (end of the zone). For F_r–0.14/DE–1.35, the roughness coefficient values were low at the start of the zone for all coral cases. It gradually varied spatially with high n values at the leeward end for all SE except for SE-1 (Figure 10c). One notable observation was for the case of F_r–0.14/DE–1.35 (Figure 10c), where the value went down to 0.03 at x/L–0.8 and then spiked up to 0.25, showing properties of higher resistance at the end of the coral reef. For F_r–0.08/DE–1.88, interestingly, the coefficient value reduced SE-1 down to 0.05 at x/L–0.5 (middle of the reef), contradicting the previous cases of flow (Figure 10d). For F_r–0.06/DE–2.38, all SE had coefficients ranging from 0.08 to 0.16 (Figure 10e). Here, the limited values of the roughness coefficient for deep and slow flows could be explained by the fact that the energy gradient was positive, i.e., no energy reduction.

4. Discussion

4.1. Contribution to Sustainable Coastal Engineering

This study provides vital data to the field of coastal engineering by clarifying the relationship between flow and coral and quantifying the ability of coral reefs to reduce flow energy. This highlights the potential benefits of incorporating coral reef structures into coastal protection designs, such as breakwaters or hybrid engineering systems, to help reduce the impact of strong water flows on vulnerable shorelines. The results offered valuable insights into the hydrodynamic interactions between coral structures and water flows. The results indicated that coral reefs have a substantial impact on the depth and speed of water flow, therefore validating their ability to reduce hydrodynamic forces.

4.2. Flow Behavior and Depth Variation

More precisely, in situations where the Froude number is high and the depth is low, there was a noticeable initial rise in the depth of the flow near the front of the reef, followed by a continuous decrease in the slope towards the downwind side. Moreover, the measurement of flow in two layers demonstrated a notable disparity in velocities above and within the coral structures, highlighting the intricate nature of flow dynamics surrounding corals. The disparity in Manning’s roughness coefficient across various flow conditions underscores the significance of incorporating coral morphology and flow variables into hydrodynamic models. The findings from the study demonstrated that coral reefs have a substantial impact on reducing both the depth and velocity of water flow. The reductions seen can reach up to 27.5% for flow depth and 25% for flow velocity.

Our velocity reduction findings align with recent experimental work on flow–structure interactions under steady conditions. Zhao et al. [48] conducted flume experiments on cubic artificial reefs with multiscale cavities at Re = 11,236 using Particle Tracking Velocimetry, demonstrating that structural porosity significantly influences velocity stratification with distinct flow layers above and within porous structures. Their findings that increased porosity extends recirculation length and creates low-velocity zones support our measured depth and velocity reductions of 27.5% and 25%, respectively. Ben Natan et al. [49] investigated water flow around breakwater structures using plaster clod-card methods, showing that structural sheltering creates complex flow patterns including vortex formation in sheltered zones. These studies reinforce that structural complexity—whether in coral reefs, 3D-printed models, or artificial structures—is a key parameter governing flow attenuation in marine environments.

4.3. Contextualizing with Previous Research

This study also examines previous research to place the findings of the current study within the wider context of the existing literature. It emphasizes the similarities and differences between previous studies and offers a balanced perspective regarding how the current study’s conclusions align with the broader scientific discussion. Ferrario et al. [5] showed that coral reefs can decrease energy in the flow by as much as 97%, highlighting their efficacy as natural barriers. The significant dissipation of energy is mainly caused by the intricate structure and uneven surface of coral reefs, which disturb the flow patterns and intensify turbulence [50]. Cano et al. [9] obtained roughness and friction parameters using physical and field surveys. These data were then used to develop numerical models that were calibrated and validated. The study also discusses the strengths and limitations of the different modeling approaches applied in the test cases. It also emphasizes the importance of studying physical processes and analyzing reef hydrodynamics to assist effective ecosystem-based management.

4.4. Spatial Variation and Velocity Layers

The current study also found that there is a gradual decrease in the depth of flow along the length of the coral reef, with the most noticeable decreases occurring towards the end of the reef. The spatial variation mentioned corresponds to the findings of Rogers et al. [44], who observed that the gradient effect observed can be attributed to the slow reduction in flow energy as water interacts with the intricate structure of the coral reef. The dual-layer velocity analyses revealed that the velocity above corals can reach up to six times the velocity within the coral reef for deep flows. The differential flow pattern highlights how coral form plays a crucial role in regulating hydrodynamic behavior.

4.5. Influence of Coral Structure and Flow Parameters

According to Monismith et al. [45], the frictional impacts of coral reefs are greatly influenced by their structural characteristics, including their height, density, and branching complexity. These characteristics augment the unevenness of the reef surface, resulting in heightened dissipation of energy and diminished flow velocities. The study’s analysis of nondimensional characteristics, including the Froude number, depth effect, and size effect, offers a thorough comprehension of how various flow conditions and coral topologies impact energy dissipation. In a study related to circulation and flow regime over reefs, Lowe et al. highlighted the importance of the Froude number in shaping reef flows [6]. Our findings regarding the influence of coral depth and size on energy dissipation are conceptually similar to the trends reported by Hearn [41]; however, Hearn’s work focused on oscillatory wave-driven flows, whereas the present study is based on steady unidirectional flow conditions. Therefore, while the general pattern of increased dissipation with larger and deeper reefs is consistent, the mechanisms differ due to the contrasting flow regimes.

4.6. Implications for Modeling and Reef Management

The range of Manning’s roughness coefficient, which spans from 0.03 to 0.26, indicates the wide array of structural properties exhibited by the coral models employed in our tests. In a recent study, Pomeroy et al. [47] presented a methodology that allows the estimation of the flow inside existing numerical models, such as a wall-type function, without the requirement of explicitly representing the physical structure of the benthos in these models at regional scales, strengthening our study. They represented a significant advancement in comprehending the various mechanisms by which environmental factors, including heat, nutrients, and sometimes living organisms, are transported throughout reef systems. It also has implications for predicting the future changes in coastal areas next to reefs, specifically in terms of sediment supply and loss. Furthermore, it contributes to the development of precise and measurable strategies for restoring reefs.

Building on these modeling advances, recent data-driven methods also offer new opportunities. Studies such as [48] show how experimental datasets like ours could be used in machine-learning frameworks to predict flow behavior and energy dissipation. Integrating clustering or neural-network approaches could enhance understanding of nonlinear coral–flow interactions and complement traditional hydrodynamic models.

The results of this study have important consequences for policies aimed at protecting coastal areas. The research quantifies how coral reefs can reduce flow energy and supports the adoption of bio-inspired engineering solutions to improve coastal resilience where there is a lack of coral reef habitats. Integrating 3D-printed coral structures with coastal defense systems offers a sustainable and efficient method for reducing the effects of severe weather occurrences. Marino et al. [51] highlighted the capacity of nature-based solutions to mitigate coastal flood hazards and advocate for ecosystem-based management techniques.

It is important to note that this study was conducted under steady flow conditions using scaled, idealized 3D-printed coral models. The absence of oscillatory wave forcing, biological growth, and sediment transport limits the direct extrapolation of these results to natural reef systems. However, the controlled setup provides fundamental insights into flow resistance and energy dissipation processes that can inform the design of coral-mimicking coastal protection systems. Future studies incorporating wave-driven and larger-scale flume tests would help bridge this gap and validate the applicability of these findings under more realistic marine conditions.

5. Conclusions

Experimental studies were conducted to investigate the water flow hydrodynamics over coral reefs when they are subjected to steady flows. The study provided comprehensive experimental insights into the hydrodynamic interactions between coral reefs and water flows, emphasizing their capacity to mitigate flow energy. Through the use of three-dimensional-printed coral reefs, we were able to closely emulate the physical characteristics of actual coral reefs and analyze their effect on flow depth and velocity. Nondimensional parameters such as F_r, SE, and DE were used to develop the test cases and analyze the results. The study reported the spatial variation in the water surface over the reef, reduction at the reef end (velocity and depth-wise), an understanding of the two-layer flow, and Manning’s roughness coefficient calculation for corals under several flow conditions. The results were summarized as follows:

• Analysis of the spatial flow depth variation for narrow and wide corals showed that in shallower and fast flows (high F_r and low DE), the depth initially increased at the reef front (due to reflection) but gradually decreased toward the leeward end. For deeper slow flows (low F_r and high DE), the reduction observed in the coral case compared to the case without corals was less significant but remained constant throughout the reef for narrower and wider corals. It was also observed that the water surface gradient was higher for wider corals compared to narrower corals for fast and shallow flows at the reef end.
• Shallower fast flow (greater F_r) led to higher flow depth reduction, with consistent reduction magnitudes except for F_r–1.05, where depth reduction decreased over wider corals (higher SE). Velocity reductions for narrow and wide corals were more notable for shallow and fast flows (F_r–1.05). In other flow cases of F_r = 0.3, 0.14, 0.08, and 0.06, velocity increments occurred over wider corals (increasing SE), which is due to the two-layered velocity effect.
• The two-layered flow analysis revealed that the flow velocity above the coral was considerably greater than the flow through the coral. The difference in velocity over and through the corals for deep and slow flows (lower F_r and higher DE) was six times.

The Manning’s roughness coefficient ranged from 0.03 to 0.26. The roughness coefficient was typically more prominent in fast and shallow flows throughout the reef. The values increased as it approached the end of the reef in all flow cases (shallow to deep). It is important to note that this study was conducted at a laboratory scale, which introduces scaling limitations when extrapolating to natural reef systems. Furthermore, only one coral morphology (Acropora) was tested, and flow conditions were limited to steady subcritical regimes without wave-induced or unsteady flow components. These constraints should be considered when interpreting the findings.

To address these limitations, future research should extend this work to long-period wave events such as tsunamis and major storm surges, where the flow overtopping coral reefs can behave as quasi-steady and unidirectional. Large-scale flume experiments are recommended to reduce scaling effects and better represent natural reef environments. Including varied coral morphologies, such as branching, massive, and plate-like forms, as well as corals with structural gaps and internal porosity, would help capture a broader range of hydrodynamic behaviors. Further studies should also focus on detailed flow structure analysis, including two-layer flow interaction, turbulence, and momentum transfer. Advancing hydraulically and spatially dependent roughness characterization will strengthen the reliability of coral-based flow resistance estimation. Field-based validation of laboratory results is also recommended to verify scaling relationships and improve model transferability to real coastal systems. These steps will enhance the practical application of coral-inspired and nature-based coastal protection strategies.