Spatial Interdependence, Spillover Effects and Moderating Mechanisms of the Digital Economy on Carbon Productivity: Empirical Analysis Based on Spatial Econometric Models
Abstract
1. Introduction
2. Literature Review
2.1. The Concept and Measurement of Carbon Productivity
2.2. The Impact of Digital Economy on Low-Carbon Development
3. Theoretical Analysis and Research Hypotheses
3.1. The Spatial Impact of Digital Economy Development on Carbon Productivity
3.2. The Moderating Effect of Industrial Structure Transformation and Upgrading
4. Models, Variables, and Data
4.1. Exploratory Spatial Data Analysis (ESDA)
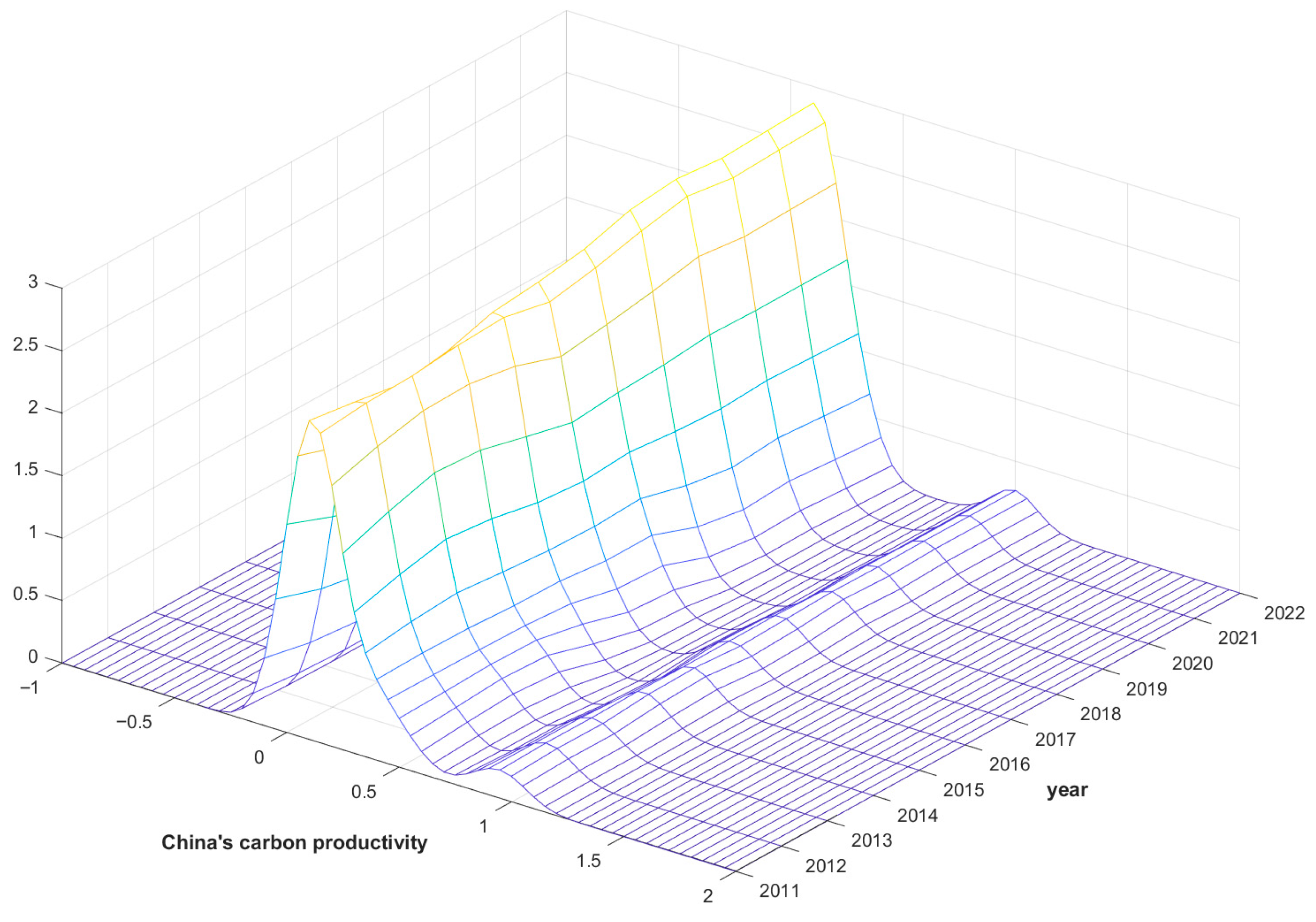
4.1.1. Kernel Density Estimation
4.1.2. Spatial Markov Matrix Approach
4.1.3. Global Spatial Autocorrelation Analysis
4.2. Spatial Regression Model
4.3. Variable Settings and Data Sources
4.3.1. Dependent Variable
4.3.2. Explanatory Variable
4.3.3. Moderating Variable
4.3.4. Control Variables
5. Empirical Results Analysis
5.1. Data Sources, Descriptive Statistics and Correlation Analysis
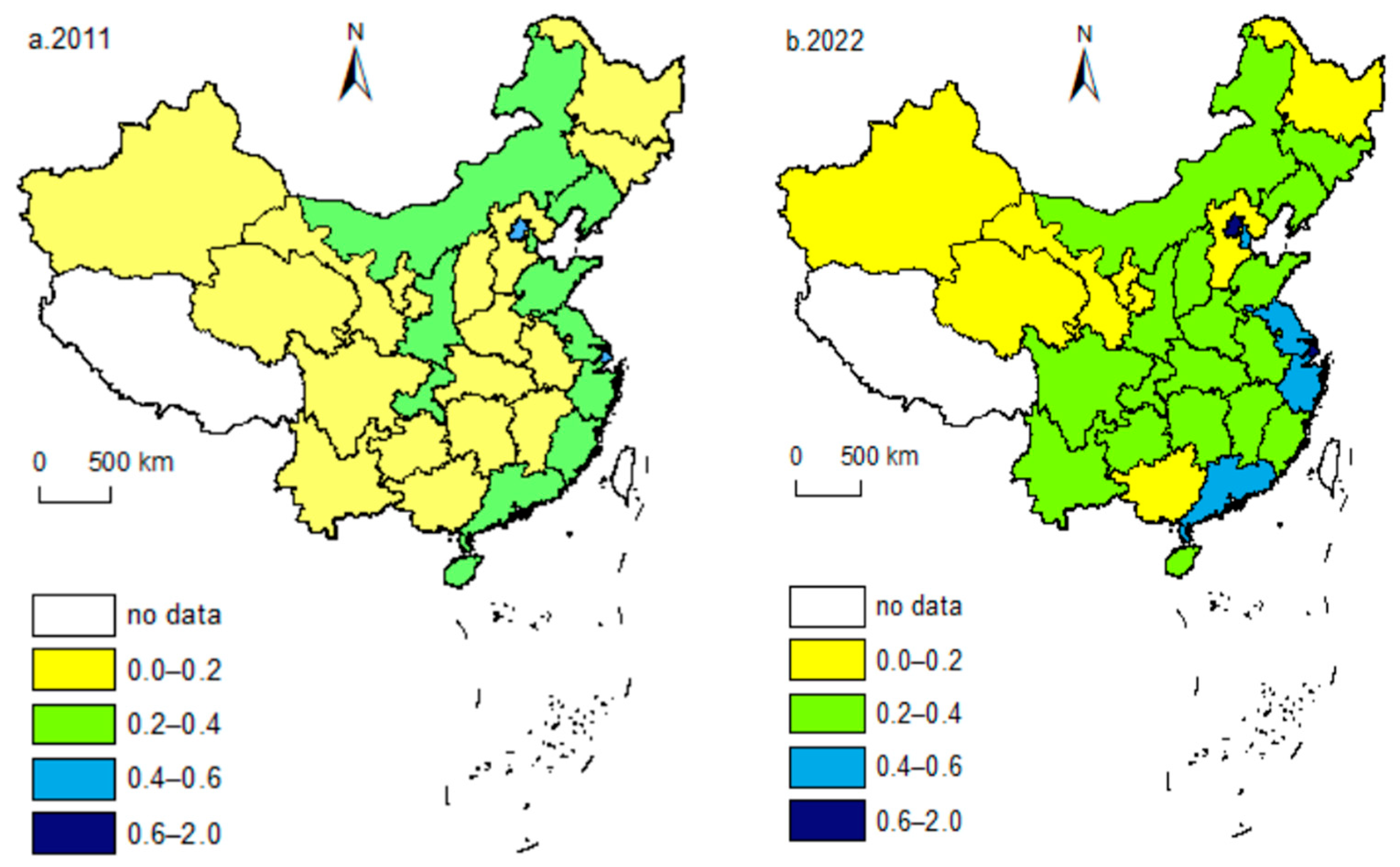
5.2. Spatiotemporal Trends Analysis
5.3. Markov Transition Trend Prediction
5.4. Spatial Econometric Analysis
5.4.1. Spatial Agglomeration Effects Analysis
5.4.2. Spatial Regression Model Specification
5.4.3. Empirical Analysis of the Spatial Regression Models
5.4.4. Analysis of Spatial Spillover Effects
5.4.5. Analysis of Spatial Heterogeneity
5.4.6. Robustness Tests
Analysis Through Alternatives to the Spatial Weight Matrix
Replacing the Explanatory Variable
| Variable | Adjacency Matrix | Distance Matrix | Geoeconomic Weight Matrix | Variable Replacement |
|---|---|---|---|---|
| DED | −0.0897 *** (0.0098) | −0.0793 *** (0.0102) | −0.0773 *** (0.0115) | 0.5275 ** (0.2058) |
| DED2 | 0.0071 *** (0.0004) | 0.0069 *** (0.0005) | 0.0066 *** (0.0006) | −0.6608 *** (0.2149) |
| W*DED | 0.1095 *** (0.0212) | 0.0984 *** (0.0230) | 0.0309 (0.0290) | −1.6413 * (0.9351) |
| W*DED2 | −0.0021 * (0.0011) | −0.0026 ** (0.0010) | −0.0000 (0.0014) | 0.5335 (0.9350) |
| Controlled Variable | YES | YES | YES | YES |
| R2 | 0.8096 | 0.6198 | 0.7820 | 0.3413 |
| Log-likelihood | 794.2891 | 800.7231 | 739.7103 | 691.2335 |
5.4.7. Analysis of the Moderating Mechanism
6. Conclusions and Recommendations
6.1. Conclusions and Discussion
6.2. Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Global Energy Review 2025. Available online: https://www.iea.org/reports/global-energy-review-2025 (accessed on 1 August 2025).
- World Meteorological Organization. The State of the Global Climate 2024. Available online: https://library.wmo.int/records/item/69455-state-of-the-global-climate-2024 (accessed on 30 October 2025).
- United Nations. The Sustainable Development Goals Report 2024. Available online: https://unstats.un.org/sdgs/report/2024/The-Sustainable-Development-Goals-Report-2024.pdf (accessed on 30 October 2025).
- China’s Pivot from Energy Consumption to Carbon Emissions Controls: Impact on Companies. Available online: https://www.china-briefing.com/news/china-carbon-emissions-reduction-dual-control-explained (accessed on 16 August 2025).
- Su, J.; Su, K.; Wang, S. Does the digital economy promote industrial structural upgrading?—A test of mediating effects based on heterogeneous technological innovation. Sustainability 2021, 13, 10105. [Google Scholar] [CrossRef]
- Tan, L.; Yang, Z.; Irfan, M.; Ding, C.J.; Hu, M.; Hu, J. Toward low-carbon sustainable development: Exploring the impact of digital economy development and industrial restructuring. Bus. Strategy Environ. 2024, 33, 2159–2172. [Google Scholar] [CrossRef]
- Li, R.; Rao, J.; Wan, L. The digital economy, enterprise digital transformation, and enterprise innovation. Manag. Decis. Econ. 2022, 43, 2875–2886. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Yang, J. Digital economy, green dual innovation and carbon emissions. Sustainability 2024, 16, 7291. [Google Scholar] [CrossRef]
- Yan, X.; Deng, Y.; Peng, L.; Jiang, Z. Study on the impact of digital economy development on carbon emission intensity of urban agglomerations and its mechanism. Environ. Sci. Pollut. Res. 2023, 30, 33142–33159. [Google Scholar] [CrossRef]
- Chen, W. Digital economy development, corporate social responsibility and low-carbon innovation. Corp. Soc. Responsib. Environ. Manag. 2023, 30, 1664–1679. [Google Scholar] [CrossRef]
- Sorrell, S. Jevons’ Paradox revisited: The evidence for backfire from improved energy efficiency. Energy Policy 2009, 37, 1456–1469. [Google Scholar] [CrossRef]
- Jevons, W.S.; Flux, A.W. The Coal Question: An Inquiry Concerning the Progress of the Nation and the Probable Exhaustion of Our Coal-mines; Macmillan and Company: London, UK, 1865. [Google Scholar]
- Kaya, Y.; Yokobori, K. Environment, Energy, and Economy: Strategies for Sustainability; United Nations University Press: Tokyo, Japan, 1997; Volume 4. [Google Scholar]
- McKinsey Global Institute. The Carbon Productivity Challenge: Curbing Climate Change and Sustaining Economic Growth; McKinsey Global Institute: San Francisco, CA, USA, 2008. [Google Scholar]
- Du, K.; Li, J. Towards a green world: How do green technology innovations affect total-factor carbon productivity. Energy Policy 2019, 131, 240–250. [Google Scholar] [CrossRef]
- Li, W.; Wang, W.; Wang, Y.; Ali, M. Historical growth in total factor carbon productivity of the Chinese industry—A comprehensive analysis. J. Clean. Prod. 2018, 170, 471–485. [Google Scholar] [CrossRef]
- Bai, C.; Du, K.; Yu, Y.; Feng, C. Understanding the trend of total factor carbon productivity in the world: Insights from convergence analysis. Energy Econ. 2019, 81, 698–708. [Google Scholar] [CrossRef]
- Malmquist, S. Index numbers and indifference surfaces. Trab. De Estadística 1953, 4, 209–242. [Google Scholar] [CrossRef]
- Wei, F.; Yuan, C.; Song, J.; Peng, F.; Han, L. Carbon productivity: Reexamining the quality of economic growth in China with fixed-sum CO2 emission constraint. Energy Econ. 2025, 144, 108363. [Google Scholar] [CrossRef]
- Aigner, D.; Lovell, C.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Fan, L.-W.; You, J.; Zhou, P. How does technological progress promote carbon productivity? Evidence from Chinese manufacturing industries. J. Environ. Manag. 2021, 277, 111325. [Google Scholar] [CrossRef]
- Li, Z.; Pang, C. Does digital economy contribute to regional carbon productivity? Evidence of China. Math. Probl. Eng. 2022, 2022, 6815133. [Google Scholar] [CrossRef]
- Shen, N.; Peng, H.; Wang, Q. Spatial dependence, agglomeration externalities and the convergence of carbon productivity. Socio-Econ. Plan. Sci. 2021, 78, 101060. [Google Scholar] [CrossRef]
- Zhao, X.; Dong, Y.; Gong, X. The digital economy and carbon productivity: Evidence at China’s city level. Sustainability 2022, 14, 10642. [Google Scholar] [CrossRef]
- Liu, B.; Ding, C.J.; Hu, J.; Su, Y.; Qin, C. Carbon trading and regional carbon productivity. J. Clean. Prod. 2023, 420, 138395. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Yan, B.; Zhang, H. The impact of new infrastructure development on urban total factor carbon productivity-empirical evidence based on Chinese cities. Front. Environ. Sci. 2024, 12, 1432534. [Google Scholar] [CrossRef]
- Li, S.; Ma, Y. Whether Scientific and Technological Innovation Can Promote Carbon Productivity: An Empirical Analysis Based on Spatial Durbin Model and Threshold Effect Model. Pol. J. Environ. Stud. 2025, 34, 3637–3655. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Song, M.; Shen, Z. Industrial structure upgrading, technological innovation and comprehensive utilisation of solid waste. Technol. Anal. Strateg. Manag. 2024, 36, 3637–3652. [Google Scholar] [CrossRef]
- Shi, Z.; Loh, L.; Wu, H.; Han, D. Smarter and cleaner: How does energy digitalization affect carbon productivity? Energy Strategy Rev. 2024, 52, 101347. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, S. Digital economy and carbon neutrality: Exploring the pathways and implications for China’s sustainable development. J. Knowl. Econ. 2024, 15, 20390–20407. [Google Scholar] [CrossRef]
- Xie, J.; Xiao, Z. Spatiotemporal patterns and carbon emissions of shared-electric-bike trips in Chicago. J. Geovisualization Spat. Anal. 2024, 8, 13. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, G.; Wu, X.; Shen, C. Digital economy, technological progress, and carbon emissions in Chinese provinces. Sci. Rep. 2024, 14, 23001. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Zhang, X.; Zheng, W. On green credits and carbon productivity in China. Environ. Sci. Pollut. Res. 2022, 29, 44308–44323. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Liu, C. Carbon productivity: A case study in the Australian construction industry. J. Clean. Prod. 2016, 112, 2354–2362. [Google Scholar] [CrossRef]
- Geldres-Weiss, V.V.; Guerrero-Stuardo, P.E.; Marinova, S.; Ortiz-Cea, V.; Reveco, R. Firm-level carbon productivity, home country environmental performance, and firm performance in the exporting meat industry. Sustainability 2025, 17, 5381. [Google Scholar] [CrossRef]
- Meng, M.; Niu, D. Three-dimensional decomposition models for carbon productivity. Energy 2012, 46, 179–187. [Google Scholar] [CrossRef]
- Guo, J.; Wang, H. Study on carbon emission reduction effect of institutional openness in China. Sci. Rep. 2023, 13, 254. [Google Scholar] [CrossRef]
- Weili, L.; Khan, H.; Khan, I.; Han, L. The impact of information and communication technology, financial development, and energy consumption on carbon dioxide emission: Evidence from the Belt and Road countries. Environ. Sci. Pollut. Res. 2022, 29, 27703–27718. [Google Scholar] [CrossRef]
- Pan, W.; Xie, T.; Wang, Z.; Ma, L. Digital economy: An innovation driver for total factor productivity. J. Bus. Res. 2022, 139, 303–311. [Google Scholar] [CrossRef]
- Moyer, J.D.; Hughes, B.B. ICTs: Do they contribute to increased carbon emissions? Technol. Forecast. Soc. Change 2012, 79, 919–931. [Google Scholar] [CrossRef]
- Han, D.; Ding, Y.; Shi, Z.; He, Y. The impact of digital economy on total factor carbon productivity: The threshold effect of technology accumulation. Environ. Sci. Pollut. Res. 2022, 29, 55691–55706. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhou, H.; Chen, J.; Fan, Z. An empirical analysis of the impact of digital economy on manufacturing green and low-carbon transformation under the dual-carbon background in China. Int. J. Environ. Res. Public Health 2022, 19, 13192. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Bai, G.; Shen, Z.; Xia, L. Digital economy and its spatial effect on green productivity gains in manufacturing: Evidence from China. J. Clean. Prod. 2022, 378, 134539. [Google Scholar] [CrossRef]
- Zhang, X.; Yao, S.; Zheng, W.; Fang, J. On industrial agglomeration and industrial carbon productivity—Impact mechanism and nonlinear relationship. Energy 2023, 283, 129047. [Google Scholar] [CrossRef]
- Feng, Y.; Wu, H. How does industrial structure transformation affect carbon emissions in China: The moderating effect of financial development. Environ. Sci. Pollut. Res. 2022, 29, 13466–13477. [Google Scholar] [CrossRef]
- Li, Z.; Shao, S.; Shi, X.; Sun, Y.; Zhang, X. Structural transformation of manufacturing, natural resource dependence, and carbon emissions reduction: Evidence of a threshold effect from China. J. Clean. Prod. 2019, 206, 920–927. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, Y.; Wang, J.; Jiang, J. The impact of the urban digital economy on China’s carbon intensity: Spatial spillover and mediating effect. Resour. Conserv. Recycl. 2023, 189, 106762. [Google Scholar] [CrossRef]
- Sun, H.; Chen, T.; Wang, C.N. Spatial impact of digital finance on carbon productivity. Geosci. Front. 2024, 15, 101674. [Google Scholar] [CrossRef]
- Bivand, R.S. Exploratory spatial data analysis. In Handbook of Applied Spatial Analysis: Software Tools, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2009; pp. 219–254. [Google Scholar]
- Guillain, R.; Le Gallo, J. Agglomeration and dispersion of economic activities in and around Paris: An exploratory spatial data analysis. Environ. Plan. B Plan. Des. 2010, 37, 961–981. [Google Scholar] [CrossRef]
- Gramacki, A. Nonparametric Kernel Density Estimation and Its Computational Aspects; Springer: Berlin/Heidelberg, Germany, 2018; Volume 37. [Google Scholar]
- Du, Q.; Deng, Y.; Zhou, J.; Wu, J.; Pang, Q. Spatial spillover effect of carbon emission efficiency in the construction industry of China. Environ. Sci. Pollut. Res. 2022, 29, 2466–2479. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, S.; Cao, F. The Impact of Rural Digital Economy Development on Agricultural Carbon Emission Efficiency: A Study of the N-Shaped Relationship. Agriculture 2025, 15, 1583. [Google Scholar] [CrossRef]
- Zhao, S.; Peng, D.; Wen, H.; Wu, Y. Nonlinear and spatial spillover effects of the digital economy on green total factor energy efficiency: Evidence from 281 cities in China. Environ. Sci. Pollut. Res. 2023, 30, 81896–81916. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Liu, G.; Wang, J. The Impact of Digital Economy on Total Factor Carbon Productivity: Empirical Analysis Based on Spatial and Mediating Effects. Pol. J. Environ. Stud. 2023, 32, 3809–3823. [Google Scholar] [CrossRef] [PubMed]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Liu, Z.; Xin, L. Has China’s Belt and Road Initiative promoted its green total factor productivity?—Evidence from primary provinces along the route. Energy Policy 2019, 129, 360–369. [Google Scholar] [CrossRef]
- Bolte, A.-M.; Kistemann, T.; Dehbi, Y.; Kötter, T. (Un)just Distribution of Visible Green Spaces? A Socio-Economic Window View Analysis on Residential Buildings: The City of Cologne as Case Study. J. Geovisualization Spat. Anal. 2025, 9, 17. [Google Scholar] [CrossRef]
- Luo, K.; Liu, Y.; Chen, P.-F.; Zeng, M. Assessing the impact of digital economy on green development efficiency in the Yangtze River Economic Belt. Energy Econ. 2022, 112, 106127. [Google Scholar] [CrossRef]
- Xu, Y.; Li, T. Measuring digital economy in China. Natl. Account. Rev. 2022, 4, 251–272. [Google Scholar] [CrossRef]
- Du, C.; Wang, C. Digitization and carbon emissions: How does the development of China’s digital economy affect carbon intensity? Environ. Sci. Pollut. Res. 2024, 31, 26895–26915. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.; Ding, Q.; Zhao, W.; Hou, N.; Liu, W. The digital economy, industrial structure upgrading, and carbon emission intensity—Empirical evidence from China’s provinces. Energy Strategy Rev. 2023, 50, 101218. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, C.-N.; Wang, Z.-S.; Rebai, N.-E.H.; Lai, X.-M. The Role of Industrial Structure Upgrading in Moderating the Impact of Environmental Regulation on Air Pollution: Evidence from China. Atmosphere 2023, 14, 1537. [Google Scholar] [CrossRef]
- Shao, C.; Dong, H.; Gao, Y. New quality productivity and industrial structure in China: The moderating effect of environmental regulation. Sustainability 2024, 16, 6796. [Google Scholar] [CrossRef]
- Ausloos, M.; Miśkiewicz, J. Entropy correlation distance method applied to study correlations between the gross domestic product of rich countries. Int. J. Bifurc. Chaos 2010, 20, 381–389. [Google Scholar] [CrossRef]
- Cai, Z. Upgrading of industrial structure in China’s economic growth and the belt and road initiative. In The Belt and Road: Industrial and Spatial Coordinated Development; Springer: Berlin/Heidelberg, Germany, 2022; pp. 85–135. [Google Scholar]
- Sánchez-Bayón, A. Digital transition and readjustment on EU tourism industry. Stud. Bus. Econ. 2023, 18, 275–297. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Li, H.; Zhong, K. Digital economy development, industrial structure upgrading and green total factor productivity: Empirical evidence from China’s cities. Int. J. Environ. Res. Public Health 2022, 19, 2414. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y. An analysis of the influence and mechanisms of the digital economy on the disparities in urban total factor productivity. Technol. Econ. Dev. Econ. 2025, 31, 1–28. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, Z.; Shen, P.; Zhang, L.; Ni, T. Efficiency evaluation and influencing factors of green innovation in Chinese resource-based cities: Based on SBM-undesirable and spatial durbin model. Int. J. Environ. Res. Public Health 2022, 19, 13772. [Google Scholar] [CrossRef]
- Li, C.; Zhou, W. Can digital economy development contribute to urban carbon emission reduction?—Empirical evidence from China. J. Environ. Manag. 2024, 357, 120680. [Google Scholar] [CrossRef]
- LeSage, J. Introduction to Spatial Econometrics; Chapman &Hall/CRC: New York, NY, USA, 2009; p. 340. [Google Scholar]
- Jebli, M.B.; Youssef, S.B. The environmental Kuznets curve, economic growth, renewable and non-renewable energy, and trade in Tunisia. Renew. Sustain. Energy Rev. 2015, 47, 173–185. [Google Scholar] [CrossRef]
- The Paper Guangdong Information Platform. The Fifth Institute of Electronics of the Ministry of Industry and Information Technology Released the “China Digital Economy Development Index Report (2024). Available online: https://m.thepaper.cn/newsDetail_forward_28907157 (accessed on 1 August 2025).
- Dong, F.; Hu, M.; Gao, Y.; Liu, Y.; Zhu, J.; Pan, Y. How does digital economy affect carbon emissions? Evidence from global 60 countries. Sci. Total Environ. 2022, 852, 158401. [Google Scholar] [CrossRef] [PubMed]
- Yi, M.; Liu, Y.; Sheng, M.S.; Wen, L. Effects of digital economy on carbon emission reduction: New evidence from China. Energy Policy 2022, 171, 113271. [Google Scholar] [CrossRef]
| Fundamentals | Primary Indicators | Secondary Indicators | Unit | Weight Coefficient |
|---|---|---|---|---|
| Digital Infrastructure | Internet infrastructure construction | Mobile Telephone Penetration Rate | subscriptions per 100 inhabitants | 1.80% |
| Optical Fiber Cable Density | fiber-km/104 km2 | 7.21% | ||
| Base Station Density | units/km2 | 8.13% | ||
| Internet Broadband Access Port Density | ports/km2 | 9.42% | ||
| Industry Integration | Digital industrialization | per Capita Software Revenue | CNY/capita | 10.67% |
| The proportion of employed persons in the ICT industry to total urban employment. | % | 5.97% | ||
| per Capita Telecom Service Volume | CNY/capita | 6.46% | ||
| Digital Inclusive Finance Index | / | 1.52% | ||
| Industrial digitization | Enterprises with websites per 100 establishments | Websites/100 est. | 0.46% | |
| Percentage of Enterprises with E-commerce Transactions | % | 1.70% | ||
| E-commerce sales | 100 million yuan | 7.10% | ||
| Number of Internet domain names | 10 thousand units | 7.60% | ||
| Innovation Capacity | Innovation input | Intramural Expenditure on R&D | 10 thousand yuan | 5.93% |
| Full-Time Equivalent (FTE) Personnel in R&D | person-year | 5.61% | ||
| Innovation output | Valid Invention Patents of Above-Scale Industrial Enterprises | item | 10.00% | |
| Total Transaction Value of Technology Contracts | 10 thousand yuan | 10.36% |
| Variable Name (Unit) | Notation | Mean | Median | SD | Min | Max |
|---|---|---|---|---|---|---|
| Total Factor Carbon Productivity | TFCP | 0.285 | 0.232 | 0.184 | 0.130 | 1.243 |
| Digital Economy Development Index | DED | 0.173 | 0.112 | 0.169 | 0.0180 | 0.737 |
| Industrial Structure Rationalization | ISR | 0.161 | 0.145 | 0.104 | 0.00600 | 0.498 |
| Industrial Structure Advancement | ISA | 1.266 | 1.112 | 0.722 | 0.518 | 5.297 |
| Urbanization Level | URB | 0.600 | 0.587 | 0.122 | 0.350 | 0.938 |
| Labor Force Quality | LAB | 0.021 | 0.020 | 0.006 | 0.008 | 0.044 |
| Economic Development Level | ECO | 10.872 | 10.835 | 0.461 | 9.682 | 12.161 |
| Level of Openness | OPEN | 0.272 | 0.146 | 0.281 | 0.00800 | 1.464 |
| Energy Structure | ES | 0.371 | 0.382 | 0.149 | 0.00600 | 0.687 |
| Variable | TFCP | DED | ECO | OPEN | URB | ES | LAB | ISR |
|---|---|---|---|---|---|---|---|---|
| DED | 0.773 *** | |||||||
| ECO | 0.755 *** | 0.856 *** | ||||||
| OPEN | 0.664 *** | 0.454 *** | 0.582 *** | |||||
| URB | 0.766 *** | 0.746 *** | 0.866 *** | 0.662 *** | ||||
| ES | −0.632 *** | −0.720 *** | −0.661 *** | −0.552 *** | −0.616 *** | |||
| LAB | 0.322 *** | 0.432 *** | 0.532 *** | 0.317 *** | 0.608 *** | −0.274 *** | ||
| ISR | −0.540 *** | −0.609 *** | −0.698 *** | −0.578 *** | −0.648 *** | 0.577 *** | −0.389 *** | |
| ISA | 0.737 *** | 0.762 *** | 0.525 *** | 0.359 *** | 0.548 *** | −0.642 *** | 0.321 *** | −0.476 *** |
| t/t + 1 | Low | Medium-Low | Medium-High | High |
|---|---|---|---|---|
| Low | 0.8372 | 0.1512 | 0.0116 | 0 |
| Medium-Low | 0.0824 | 0.7529 | 0.1529 | 0.0118 |
| Medium-High | 0 | 0.0250 | 0.9000 | 0.0750 |
| High | 0 | 0 | 0 | 1 |
| Neighboring Level | t/t + 1 | Low | Medium-Low | Medium-High | High |
|---|---|---|---|---|---|
| Low | Low | 0.9375 | 0.0625 | 0 | 0 |
| Medium-Low | 0.0769 | 0.9231 | 0 | 0 | |
| Medium-High | 0 | 0 | 1 | 0 | |
| High | 0 | 0 | 0 | 1 | |
| Neighboring level | t/t + 1 | Low | Medium-Low | Medium-High | High |
| Medium-Low | Low | 0.8235 | 0.1569 | 0.0303 | 0 |
| Medium-Low | 0.0303 | 0.7179 | 0.1795 | 0.0256 | |
| Medium-High | 0 | 0.0417 | 0.9167 | 0.0417 | |
| High | 0 | 0 | 0 | 1 | |
| Neighboring level | t/t + 1 | Low | Medium-Low | Medium-High | High |
| Medium-High | Low | 0.6667 | 0.3333 | 0 | 0 |
| Medium-Low | 0.0938 | 0.0938 | 0.1875 | 0 | |
| Medium-High | 0 | 0.0294 | 0.9412 | 0.0294 | |
| High | 0 | 0 | 0 | 1 | |
| Neighboring level | t/t + 1 | Low | Medium-Low | Medium-High | High |
| High | Low | 1 | 0 | 0 | 0 |
| Medium-Low | 0 | 1 | 0 | 0 | |
| Medium-High | 0 | 0 | 0.8182 | 0.1818 | |
| High | 0 | 0 | 0 | 1 |
| Year. | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | 5.098 | 5.099 | 5.297 | 5.213 | 5.182 | 5.236 | 5.107 | 5.010 | 4.693 | 4.931 | 4.881 | 4.833 |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Moran’s I | 0.201 | 0.201 | 0.211 | 0.205 | 0.198 | 0.198 | 0.190 | 0.180 | 0.165 | 0.176 | 0.173 | 0.170 |
| Variable | (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|---|
| SDM | SAR | SEM | Direct Effects | Indirect Effects | Total Effects | ||
| Main | Wx | ||||||
| DED | −0.0790 *** (0.0107) | −0.0852 (0.0598) | −0.0709 *** (0.0105) | −0.0710 *** (0.0105) | −0.0773 *** (0.0110) | −0.0425 (0.0447) | −0.1199 *** (0.0454) |
| DED2 | 0.0071 *** (0.0006) | 0.0118 *** (0.0029) | 0.0059 *** (0.0005) | 0.0062 *** (0.0005) | 0.0069 *** (0.0006) | 0.0070 *** (0.0023) | 0.0138 *** (0.0024) |
| URB | −0.0929 ** (0.1518) | 0.2113 * (0.1094) | −0.4955 *** (0.1397) | −0.5056 *** (0.1339) | −0.01344 (0.1522) | 0.16043 * (0.8458) | 0.14699 * (0.8446) |
| LAB | −0.3367 ** (0.1687) | 1.0659 (0.9831) | −0.5329 *** (0.1735) | −0.49661 *** (0.1729) | −0.3719 ** (0.1681) | 0.4169 (0.7647) | 0.0450 (0.7548) |
| ECO | 0.1558 *** (0.0349) | 0.0833 (0.1695) | 0.1876 *** (0.0340) | 0.1908 *** (0.0329) | 0.1551 *** (0.0344) | 0.0246 (0.1358) | 0.1798 * (0.1299) |
| OPEN | −0.0808 ** (0.0346) | −0.2123 (0.1743) | −0.0763 ** (0.0352) | −0.0776 ** (0.0340) | −0.0763 ** (0.0350) | −0.1417 (0.1285) | −0.2179 * (0.1225) |
| ES | −0.0898 * (0.0528) | −0.2500 (0.2273) | −0.0484 (0.0513) | −0.0546 (0.0504) | −0.0836 (0.0540) | −0.1537 (0.1726) | −0.2373 (0.1774) |
| R2 | −0.0790 *** (0.0107) | −0.0852 (0.0598) | −0.0709 *** (0.0105) | −0.0710 *** (0.0105) | −0.0773 *** (0.0110) | −0.0425 (0.0447) | −0.1199 *** (0.0454) |
| Log- likelihood | 755.4764 | 736.7537 | 738.6103 | ||||
| Variable | Baseline Regression | East | Central | West | First Tire | Second Tire | Third Tire |
|---|---|---|---|---|---|---|---|
| DED | −0.0790 *** (0.0107) | −0.1265 *** (0.0157) | −0.0508 ** (0.0238) | 0.0253 ** (0.0100) | −0.0994 *** (0.0164) | −0.0137 (0.0221) | −0.0147 (0.0128) |
| DED2 | 0.0071 *** (0.0006) | 0.0075 *** (0.0007) | 0.0110 ** (0.0048) | 0.0000 (0.0009) | 0.0078 *** (0.0007) | 0.0024 (0.0021) | 0.0030 ** (0.0013) |
| W*DED | −0.0724 (0.0566) | −0.1335 * (0.0807) | 0.2159 ** (0.0916) | 0.0640 (0.0564) | −0.2789 *** (0.0790) | 0.0838 (0.0801) | −0.0633 (0.0503) |
| W*DED2 | 0.0110 *** (0.0028) | 0.0160 *** (0.0031) | −0.0294 * (0.0154) | 0.0089 (0.0057) | 0.0173 *** (0.0026) | 0.0041 (0.0075) | 0.0066 (0.0053) |
| Controlled Variable | YES | YES | YES | YES | YES | YES | YES |
| R2 | 0.5922 | 0.5973 | 0.6017 | 0.6644 | 0.7729 | 0.6819 | 0.4055 |
| Log-likelihood | 755.4764 | 283.8762 | 281.0313 | 461.7946 | 254.0304 | 409.2298 | 337.0064 |
| Variable | (1) | (2) | (3) | |||
|---|---|---|---|---|---|---|
| Main | Wx | Main | Wx | Main | Wx | |
| DED | −0.0780 *** (0.0107) | −0.0785 (0.0615) | −0.0916 *** (0.0157) | −0.0024 (0.0824) | −0.0988 *** (0.0154) | 0.0790 (0.0867) |
| DED2 | 0.0070 *** (0.0006) | 0.0108 *** (0.0029) | 0.0050 *** (0.0012) | 0.0033 (0.0058) | 0.0063 *** (0.0012) | −0.0050 (0.0064) |
| DED*ISR | 0.1674 *** (0.0569) | 0.6293 ** (0.2809) | 0.1689 *** (0.0542) | −0.0138 (0.2841) | ||
| DED2*ISR | −0.0214 ** (0.0087) | −0.0981 ** (0.0470) | −0.0188 ** (0.0081) | −0.0379 (0.0453) | ||
| ISR | 0.1131 (0.1003) | −0.6572 (0.4861) | 0.0523 (0.0976) | 0.4443 (0.4917) | ||
| DED*ISA | 0.0238 *** (0.0051) | 0.0081 (0.0327) | 0.0200 *** (0.0051) | −0.0316 (0.0337) | ||
| DED2*ISA | −0.0008 *** (0.0003) | 0.0001 (0.0019) | −0.0008 *** (0.0003) | 0.0029 (0.0020) | ||
| ISA | −0.0515 ** (0.0234) | 0.1616 (0.1094) | −0.0148 (0.0244) | 0.1613 (0.1132) | ||
| Controlled Variable | YES | YES | YES | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Shi, J.; Wang, Q.; Shi, C.; Ausloos, M. Spatial Interdependence, Spillover Effects and Moderating Mechanisms of the Digital Economy on Carbon Productivity: Empirical Analysis Based on Spatial Econometric Models. Sustainability 2025, 17, 10593. https://doi.org/10.3390/su172310593
Lin S, Shi J, Wang Q, Shi C, Ausloos M. Spatial Interdependence, Spillover Effects and Moderating Mechanisms of the Digital Economy on Carbon Productivity: Empirical Analysis Based on Spatial Econometric Models. Sustainability. 2025; 17(23):10593. https://doi.org/10.3390/su172310593
Chicago/Turabian StyleLin, Shoufu, Jiajing Shi, Qian Wang, Chenyong Shi, and Marcel Ausloos. 2025. "Spatial Interdependence, Spillover Effects and Moderating Mechanisms of the Digital Economy on Carbon Productivity: Empirical Analysis Based on Spatial Econometric Models" Sustainability 17, no. 23: 10593. https://doi.org/10.3390/su172310593
APA StyleLin, S., Shi, J., Wang, Q., Shi, C., & Ausloos, M. (2025). Spatial Interdependence, Spillover Effects and Moderating Mechanisms of the Digital Economy on Carbon Productivity: Empirical Analysis Based on Spatial Econometric Models. Sustainability, 17(23), 10593. https://doi.org/10.3390/su172310593


_Li.png)





