Exploring Traffic Paradoxes: A Study of Roundabout Corridors and Their Effects on Network Dynamics
Abstract
1. Introduction
2. Theoretical Background
2.1. The Graph Theory
2.2. Traffic Paradoxes
- Pigou-Knight-Downs Paradox [14,15]: adding a faster or higher-capacity route can unintentionally increase travel times. When drivers prioritize the quickest route, the new capacity may attract excess traffic, leading to congestion. This paradox underscores the need for network-wide considerations, particularly in roundabout corridors where isolated improvements may disrupt overall performance;
- Downs-Thomson Paradox [16,17,18]: Road capacity improvements without corresponding public transport enhancements can reduce system efficiency. As private car travel becomes more attractive, public transport ridership declines, potentially increasing road congestion. This paradox is especially critical in urban roundabout corridors, where balancing road and public transport efficiency is vital;
- Beckmann’s Paradox [19,20]: optimizing traffic flow on individual links can worsen overall network performance. Local improvements, such as capacity expansion or route prioritization, may disrupt global traffic dynamics. For roundabout corridors, this highlights the importance of avoiding isolated optimization and considering the entire network;
- Induced Demand Paradox [21]: expanding road capacity often attracts additional traffic, negating congestion reductions. This phenomenon demonstrates the limitations of capacity expansion as a stand-alone solution. In roundabout corridors, this paradox reinforces the need of demand management strategies;
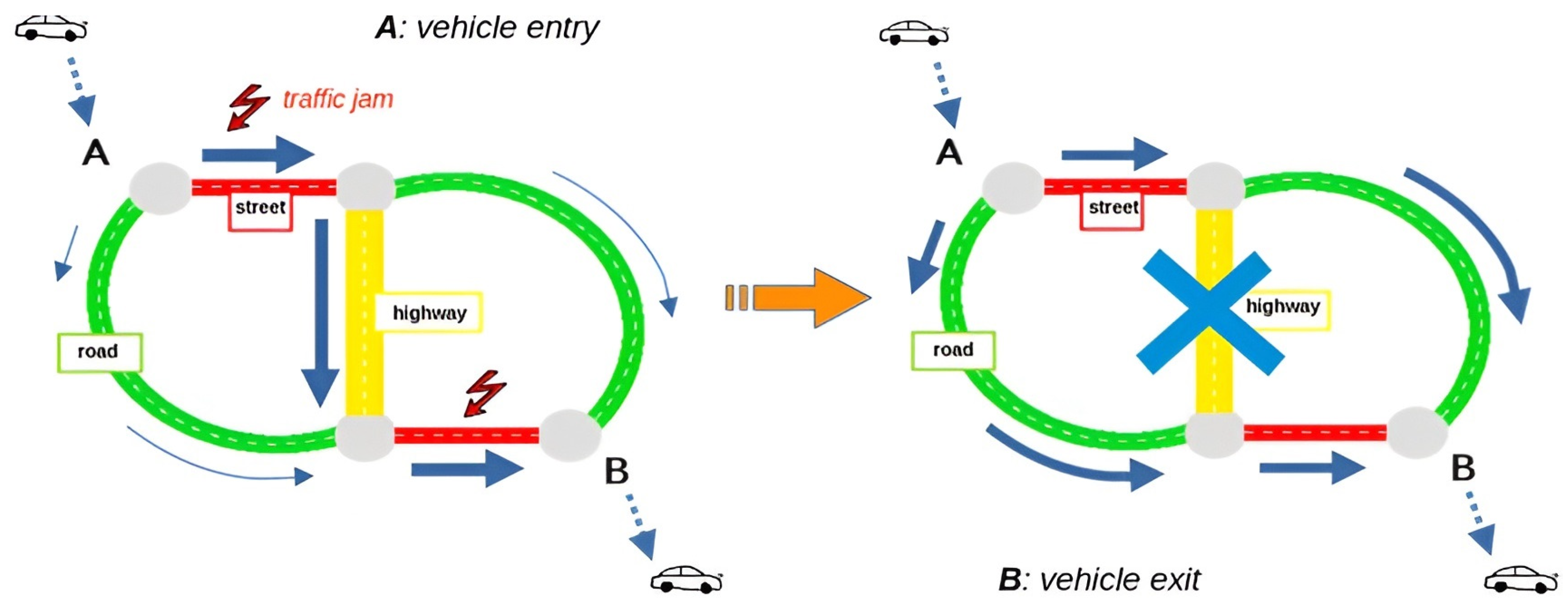
2.3. The Braess Paradox
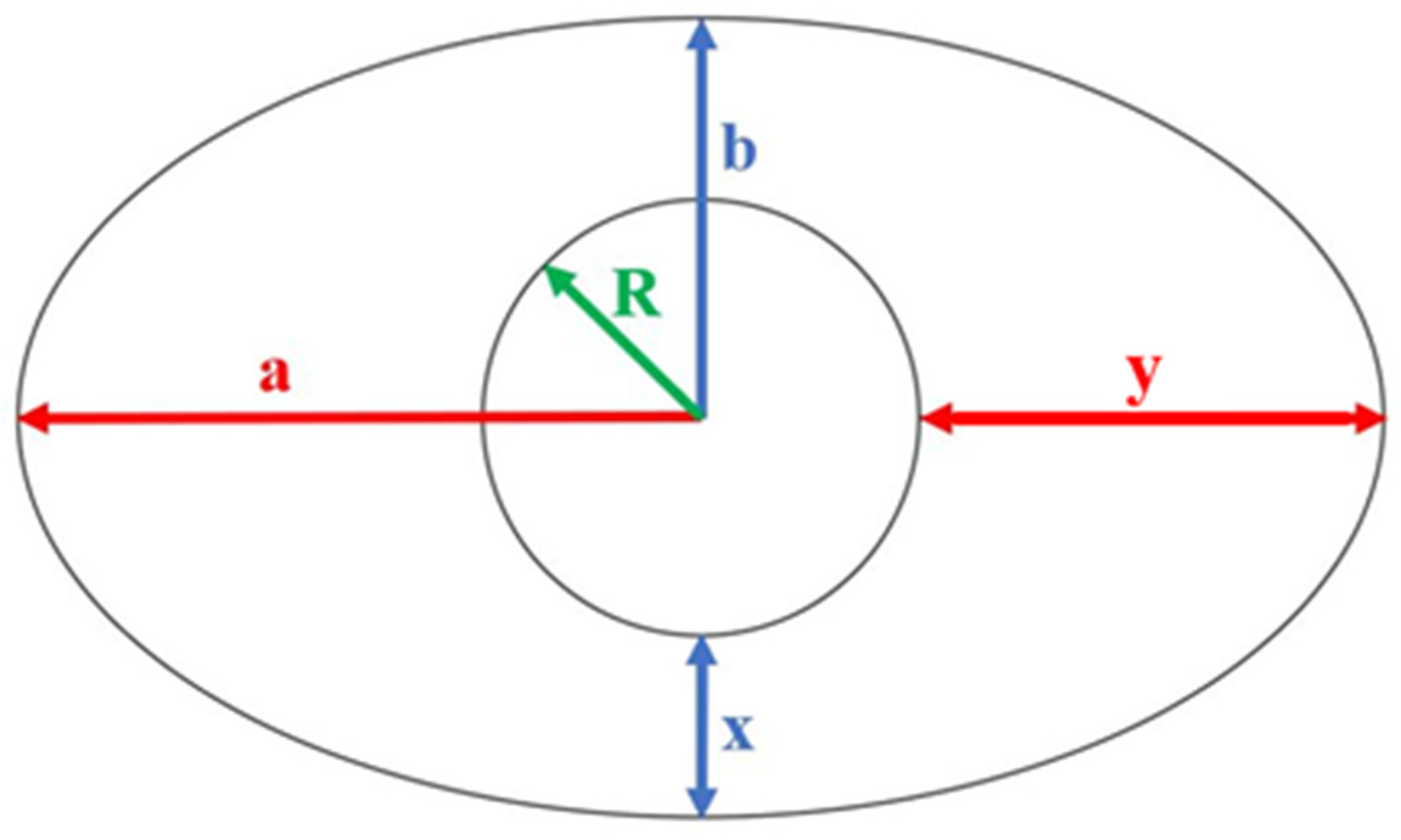
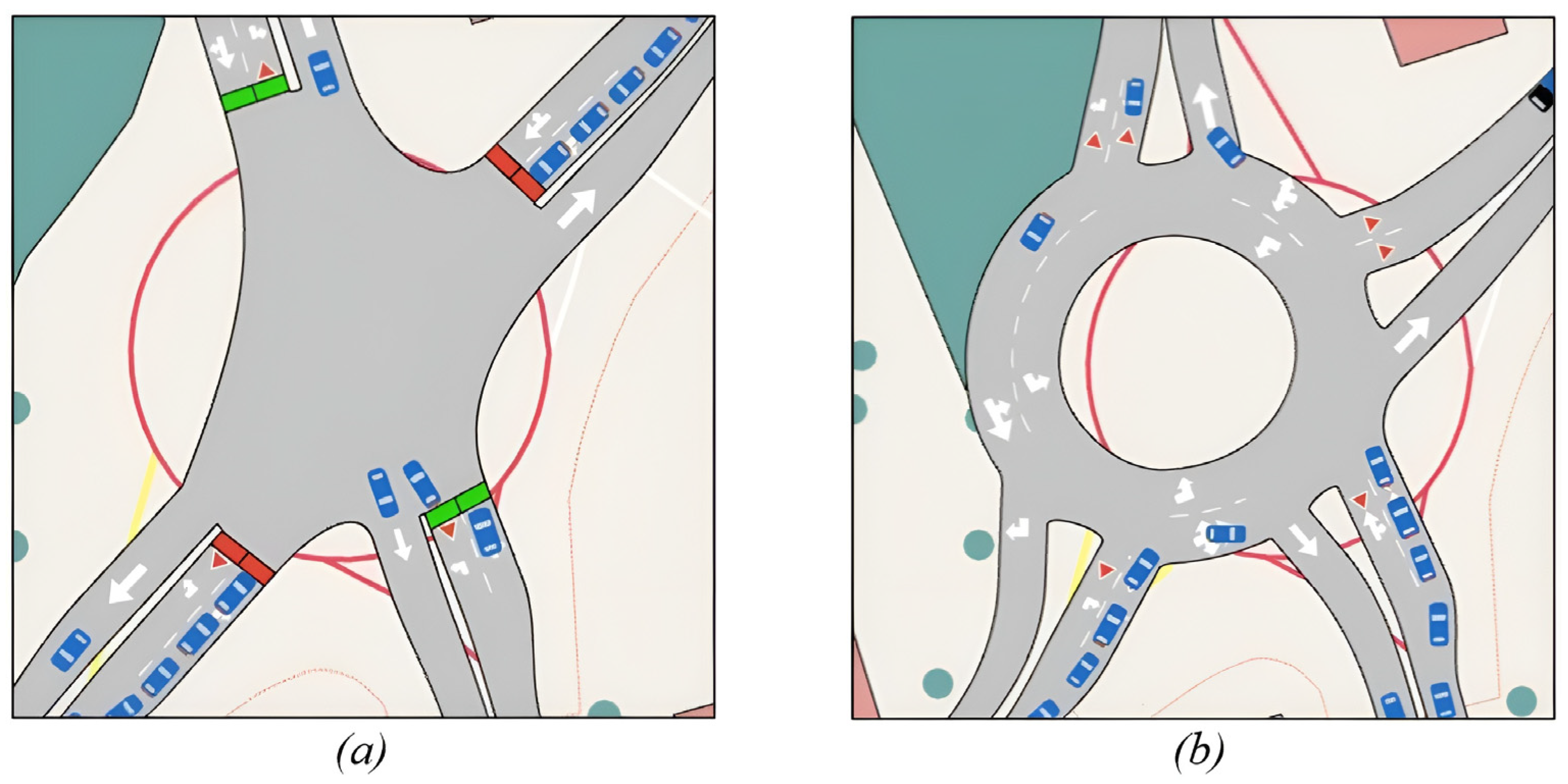
2.4. The Roundabout Corridors Theory
- The corridor must have from three to six roundabouts;
- Branches must be two or four lanes, mainly suburban;
- Roundabouts must have one or two lanes in the ring;
- The speed limit must be between 25 mph (~40 km/h) and 50 mph (~80 km/h);
- The total length must be between 0.5 miles (~800 m) and 4.5 miles (~7200 m);
- The distance between two consecutive roundabouts must be between 650 feet (~200 m) and 6465 feet (~1970 m);
- The characteristics of the lateral arrangements may vary (e.g., the presence or absence of sidewalks, pedestrian crossings, cycle paths, rest areas).
3. Materials and Methods
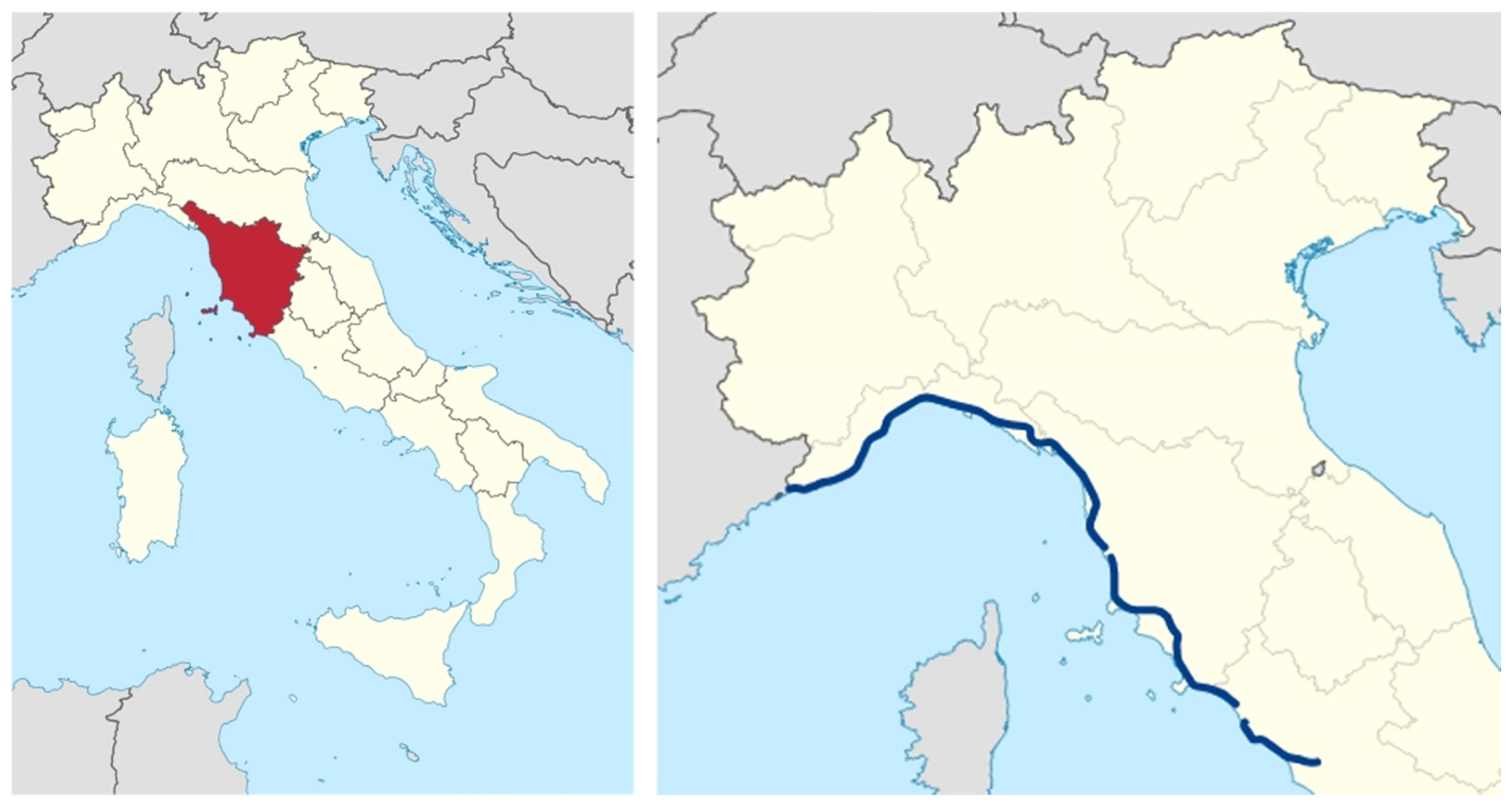
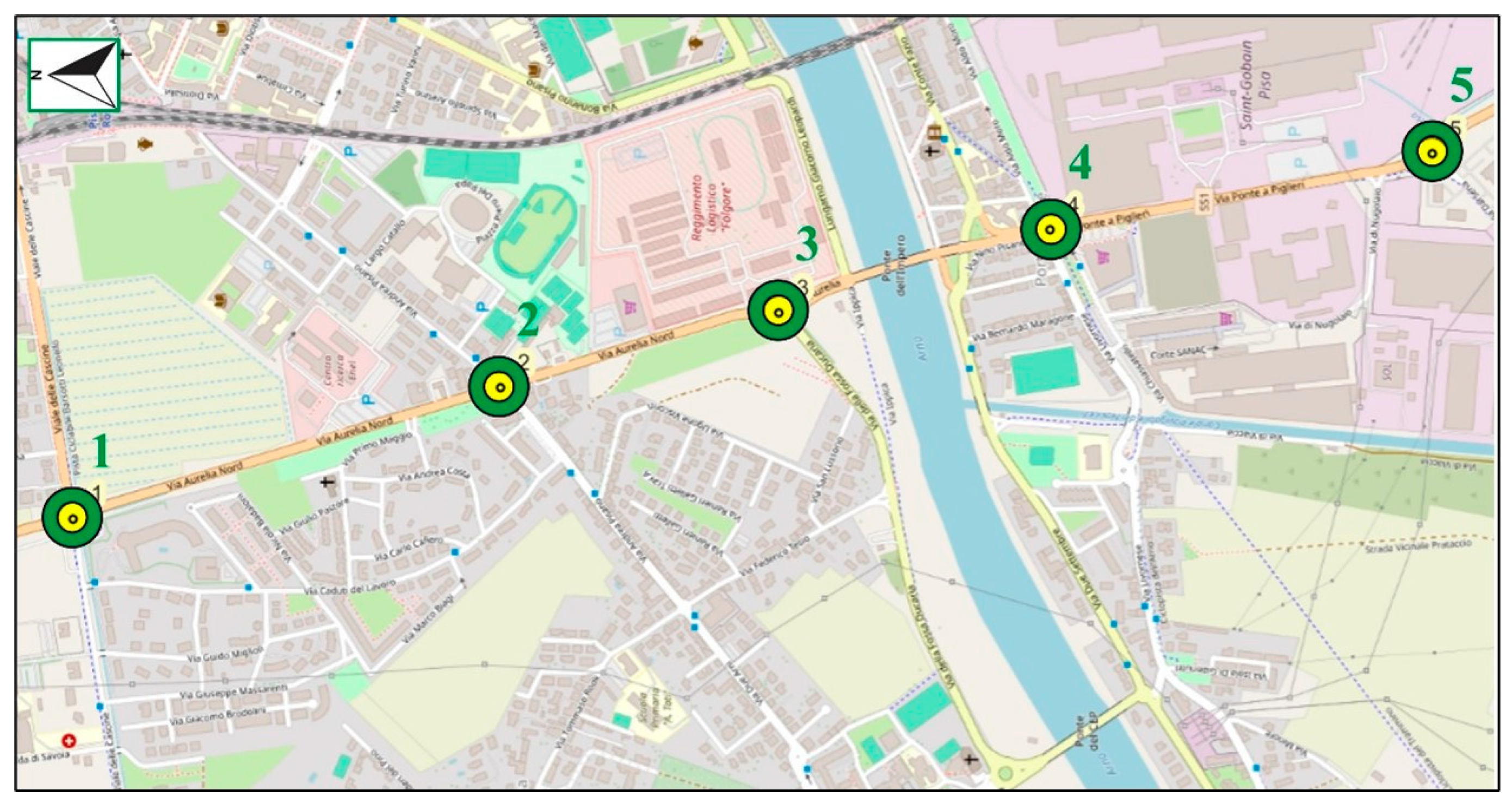
3.1. Characteristics of the Pisa Roundabout Corridor
- Intersection number 1: Via Aurelia Nord—Via delle Cascine (Figure 4);
- Intersection number 2: Via Aurelia Nord—Via Andrea Pisano (Figure 5);
- Intersection number 3: Via Aurelia Nord—Via della Fossa Ducaria (Figure 6);
- Intersection number 4: Via Aurelia Nord—Via Livornese (Figure 7);
- Intersection number 5: Via Aurelia Nord—Via Darsena (Figure 8).
3.2. Tools and Software Used
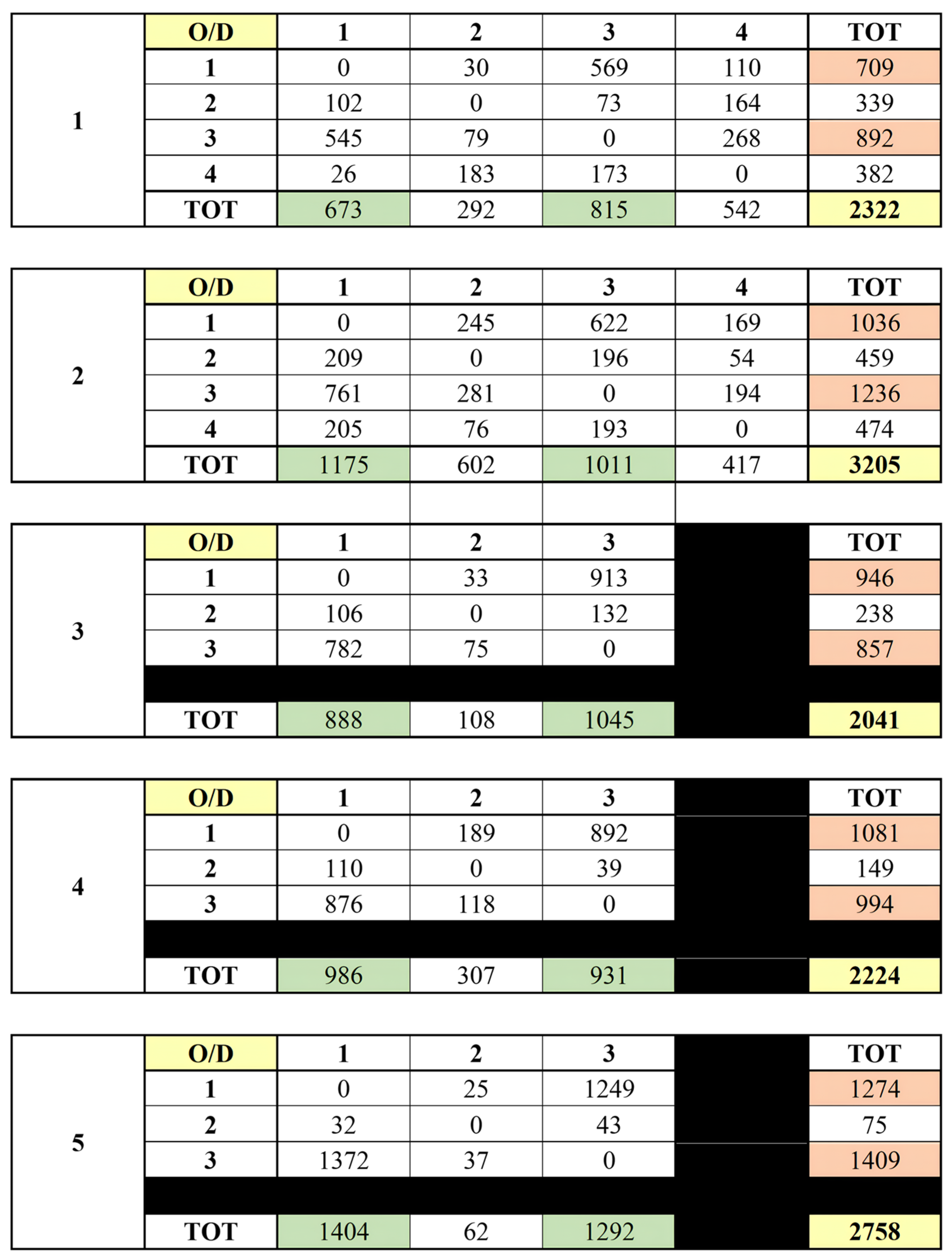
3.3. Data Collection and Processing
- Simulation Step = 0.80 s;
- Reaction Time at Stop = 1.20 s;
- Reaction Time at Traffic Light = 1.60
4. Results and Discussion
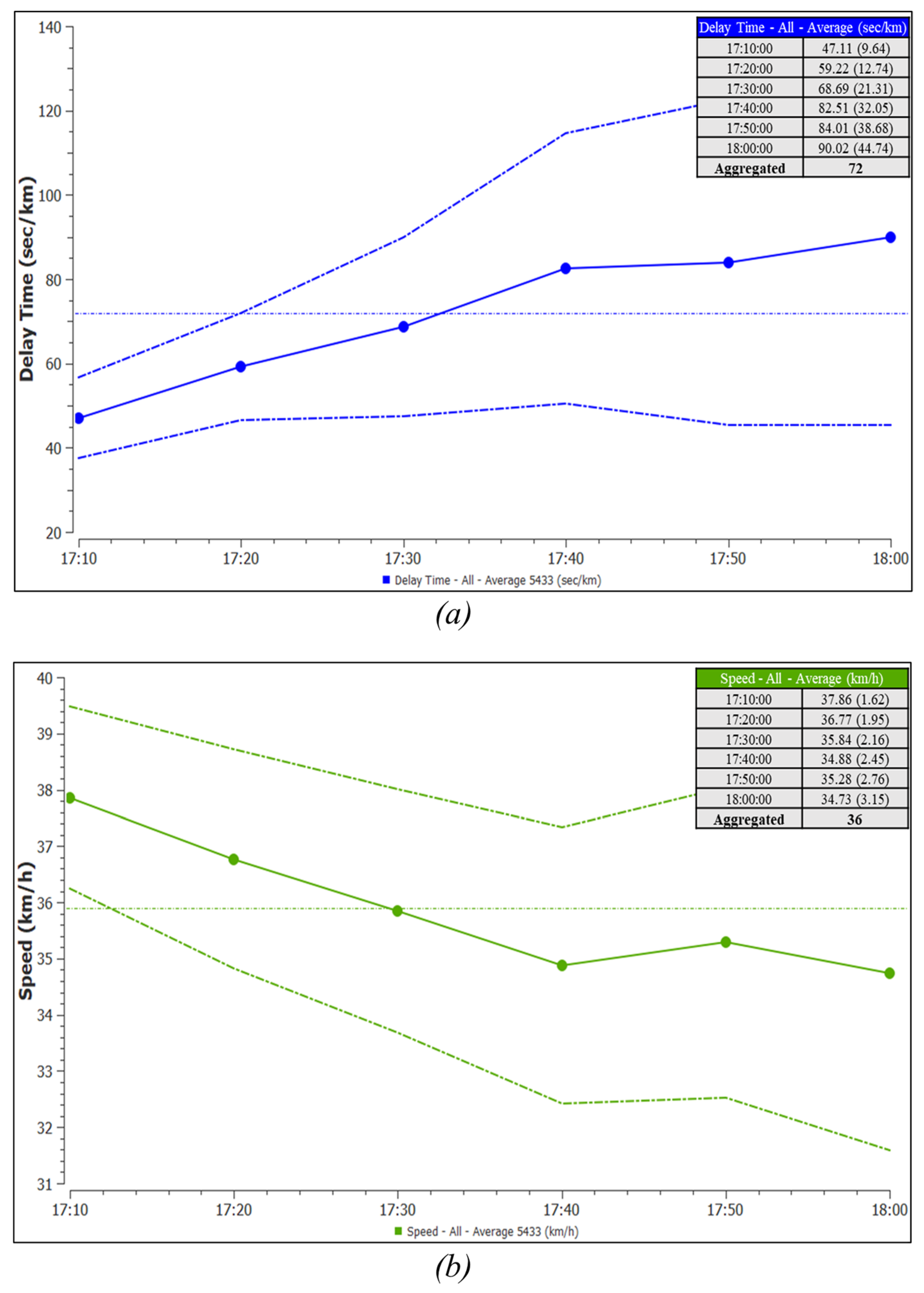
4.1. Performance Comparison Between Configurations
4.2. Introduction of the Novel Performance Index CRC
4.3. Identification of Paradoxical Effects
- Braess Paradox: The transformation of the corridor into a roundabout corridor introduced new paths and altered the distribution of traffic flows, but instead of improving travel times, it resulted in higher delays for certain movements.
- Pigou-Knight-Downs Paradox: The increased capacity at roundabout intersections may have unintentionally attracted additional traffic, raising congestion and reducing expected benefits.
- Induced Demand Paradox: The infrastructural upgrade may have encouraged higher traffic volumes, leading to congestion levels that offset the anticipated efficiency gains.
- Beckmann’s Paradox: The focus on optimizing individual intersections rather than the entire system contributed to inefficiencies in the overall traffic flow.
4.4. Discussion of Findings
5. Conclusions
Study Limitations and Future Research Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bugg, H.D.; Hummer, J.E.; Schroeder, B.J. Methodology to Compute Travel Time of a Roundabout Corridor. Transp. Res. Rec. J. Transp. Res. Board 2015, 2483, 20–29. [Google Scholar] [CrossRef]
- Fernandes, P.; Fontes, T.; Pereira, S.R.; Rouphail, N.M.; Coelho, M.C. Multicriteria Assessment of Crosswalk Location in Urban Roundabout Corridors. Transp. Res. Rec. J. Transp. Res. Board 2015, 2517, 37–47. [Google Scholar] [CrossRef]
- Fernandes, P.; Guarnaccia, C.; Teixeira, J.; Sousa, A.; Coelho, M.C. Multi-Criteria Assessment of Crosswalk Location on a Corridor with Roundabouts: Incorporating a Noise Related Criterion. Transp. Res. Procedia 2017, 27, 460–467. [Google Scholar] [CrossRef]
- Fernandes, P.; Salamati, K.; Rouphail, N.M.; Coelho, M.C. The effect of a roundabout corridor’s design on selecting the optimal crosswalk location: A multi-objective impact analysis. Int. J. Sustain. Transp. 2016, 11, 206–220. [Google Scholar] [CrossRef]
- Fernandes, P.; Rouphail, N.M.; Coelho, M.C. Turboroundabouts Along Corridors: Analysis of Operational and Environmental Impacts. Transp. Res. Rec. J. Transp. Res. Board 2017, 2627, 45–56. [Google Scholar] [CrossRef]
- Bagloee, S.; Ceder, A.; Tavana, M.; Bozic, C. A heuristic methodology to tackle the Braess Paradox detecting problem tailored for real road networks. Transp. A Transp. Sci. 2014, 10, 437–456. [Google Scholar] [CrossRef]
- Braess, D. Über ein Paradoxon aus der Verkehrsplanung. Unternehmensforschung Oper. Res. 1968, 12, 258–268. [Google Scholar] [CrossRef]
- Pas, E.I.; Principio, S.L. Braess’ paradox: Some new insights. Transp. Res. Part B Methodol. 1997, 31, 265–276. [Google Scholar] [CrossRef]
- Nagurney, A.; Ladimer, S.N. The Braess Paradox. Int. Encycl. Transp. 2021, 601–607. [Google Scholar] [CrossRef]
- Nikolova, N.D.; Armenski, I.S.; Tenekedjieva, L.T.K.; Mednikarov, B. Domains and Solutions of the Braess Paradox. J. Appl. Comput. Sci. Methods 2011, 3, 17–43. Available online: https://bibliotekanauki.pl/articles/108705 (accessed on 30 April 2025).
- Sousa, A.A.; Chaves, A.; Farias, G.A.; Peeters, F.M. Braess paradox at the mesoscopic scale. Phys. Rev. B 2013, 88, 245417. [Google Scholar] [CrossRef]
- Zverovich, V.; Avineri, E. Braess’ Paradox in a Generalised Traffic Network. J. Adv. Transp. 2015, 49, 114–138. [Google Scholar] [CrossRef]
- Coletta, T.; Philippe, J. Linear Stability and the Braess Paradox in Coupled Oscillators Networks and Electric Power Grids. Phys. Rev. E 2016, 93, 032222. [Google Scholar] [CrossRef] [PubMed]
- Morgan, J.; Orzen, H.; Sefton, M. Network architecture and traffic flows: Experiments on the Pigou–Knight–Downs and Braess Paradoxes. Games Econ. Behav. 2009, 66, 348–372. [Google Scholar] [CrossRef]
- Ding, C.; Song, S. Traffic Paradoxes and Economic Solutions. J. Urban Manag. 2012, 1, 63–76. [Google Scholar] [CrossRef]
- Dechenaux, E.; Mago, S.D.; Razzolini, L. Traffic congestion: An experimental study of the Downs-Thomson paradox. Exp. Econ. 2014, 17, 461–487. [Google Scholar] [CrossRef]
- Afimeimounga, H.; Solomon, W.; Ziedins, I. The Downs-Thomson Paradox: Existence, Uniqueness and Stability of User Equilibria. Queueing Syst. 2005, 49, 321–334. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, H.; Liu, W. The Downs–Thomson Paradox with responsive transit service. Transp. Res. Part A Policy Pract. 2014, 70, 244–263. [Google Scholar] [CrossRef]
- Boyce, D.E.; Mahmassani, H.S.; Nagurney, A. A Retrospective on Beckmann, McGuire and Winsten’s Studies in the Economics of Transportation. In Papers in Regional Science; Wiley: Hoboken, NJ, USA, 2005; Volume 84, pp. 85–103. [Google Scholar] [CrossRef]
- Boyce, D.E. Beckmann’s transportation network equilibrium model: Its history and relationship to the Kuhn–Tucker conditions. Econ. Transp. 2013, 2, 47–52. [Google Scholar] [CrossRef]
- Hymel, K. If you build it, they will drive: Measuring induced demand for vehicle travel in urban areas. Transp. Policy 2019, 76, 57–66. [Google Scholar] [CrossRef]
- Grinberg, D. An introduction to graph theory. arXiv 2023, arXiv:2308.04512. [Google Scholar] [CrossRef]
- Gowda, D.V.; Shashidhara, K.S.; Ramesha, M.; Sridhara, S.B.; Manoj Kumar, S.B. Recent Advances in Graph Theory and its Applications. Adv. Math. Sci. J. 2021, 10, 1407–1412. [Google Scholar] [CrossRef]
- Cirilovic, J.; Vajdic, N.; Mladenovic, G.; Queiroz, C. Developing Cost Estimation Models for Road Rehabilitation and Reconstruction: Case Study of Projects in Europe and Central Asia. J. Constr. Eng. Manag. 2014, 140, 04013065. [Google Scholar] [CrossRef]
- Liu, T.; Meidani, H. End-to-end heterogeneous graph neural networks for traffic assignment. Transp. Res. Part C Emerg. Technol. 2024, 165, 104695. [Google Scholar] [CrossRef]
- Razemon, O. Quand les voitures s’évaporent. Le Monde, 23 August 2016. Available online: https://www.lemonde.fr/blog/transports/2016/08/23/voitures-evaporees/ (accessed on 30 April 2025).
- Rapoport, A.; Kugler, T.; Dugar, S.; Gisches, E.J. Choice of routes in congested traffic networks: Experimental tests of the Braess Paradox. Games Econ. Behav. 2009, 65, 538–571. [Google Scholar] [CrossRef]
- Bazzan, A.L.C.; Klügl, F. Case studies on the Braess Paradox: Simulating route recommendation and learning in abstract and microscopic models. Transp. Res. Part C Emerg. Technol. 2005, 13, 299–319. [Google Scholar] [CrossRef]
- Wardrop, J. Some Theoretical Aspects of Road Traffic Research. Proc. Inst. Civ. Eng. Part II 1952, 1, 325–378. [Google Scholar] [CrossRef]
- Correa, J.R.; Stier-Moses, N.E. Wardrop Equilibria. In Wiley Encyclopedia of Operations Research and Management Science; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Aashtiani, H.Z.; Poorzahedy, H.; Nourinejad, M. Wardrop’s first principle: Extension for capacitated networks. Sci. Iran. 2021, 28, 175–191. [Google Scholar] [CrossRef]
- Kuang, Z.; Mazalov, V.V.; Tang, X.; Zheng, J. Transportation network with externalities. J. Comput. Appl. Math. 2021, 382, 113091. [Google Scholar] [CrossRef]
- Wang, A.; Tang, Y.; Mohamand, Y.T.; Xu, P. Modifying link capacity to avoid Braess Paradox considering elastic demand. Phys. A Stat. Mech. Its Appl. 2022, 605, 127951. [Google Scholar] [CrossRef]
- Monks, K.M. Braess’ Paradox in City Planning: An Application of Multivariable Optimization. Calculus. 2019. Available online: https://digitalcommons.ursinus.edu (accessed on 30 April 2025).
- Steinberg, R.; Zangwill, W.I. The Prevalence of Braess’ Paradox. Transp. Sci. 1983, 17, 301–318. [Google Scholar] [CrossRef]
- Alperovich, G. An Economic Interpretation of Braess’ Paradox. Int. J. Transp. Econ. 1997, 24, 145–155. Available online: http://www.jstor.org/stable/42747285 (accessed on 30 April 2025).
- Eriksson, K.; Eliasson, J. The Chicken Braess Paradox. Math. Mag. 2019, 92, 213–221. [Google Scholar] [CrossRef]
- Passacantando, M.; Gnecco, G.; Hadas, Y.; Sanguineti, M. Braess’ paradox: A cooperative game-theoretic point of view. Networks 2021, 78, 264–283. [Google Scholar] [CrossRef]
- Schäfer, B.; Pesch, T.; Manik, D.; Gollenstede, J.; Lin, G.; Beck, H.P.; Witthaut, D.; Timme, M. Understanding Braess’ Paradox in power grids. Nat. Commun. 2022, 13, 5396. [Google Scholar] [CrossRef]
- Lepore, D.M.; Barratt, C.; Schwartz, P.M. Computational Models of Chemical Systems Inspired by Braess’ Paradox. J. Math. Chem. 2011, 49, 356–370. [Google Scholar] [CrossRef]
- Pala, M.G.; Baltazar, S.; Liu, P.; Sellier, H.; Hackens, B.; Martins, F.; Bayot, V.; Wallart, X.; Desplanque, L.; Huant, S. Transport Inefficiency in Branched-Out Mesoscopic Networks: An Analog of the Braess Paradox. Phys. Rev. Lett. 2012, 108, 076802. [Google Scholar] [CrossRef]
- Bittihn, S.; Schadschneider, A. The Effect of Modern Traffic Information on Braess’ Paradox. Phys. A Stat. Mech. Appl. 2021, 571, 125829. [Google Scholar] [CrossRef]
- Zhuang, D.; Huang, Y.; Jayawardana, V.; Zhao, J.; Suo, D.; Wu, C. The Braess’s Paradox in Dynamic Traffic. In Proceedings of the 25th IEEE International Conference on Intelligent Transportation Systems (ITSC) 2022, Macau, China, 8–12 October 2022. [Google Scholar] [CrossRef]
- Amini, A.; Ameli, M.; Winzenrieth, B.; Busch, F.; Bogenberger, K.; Leclercq, L. A Braess Paradox Exploitation Framework for Optimal Traffic Banning Strategy. In Proceedings of the Transportation Research Board 101st Annual Meeting 2022, Washington, DC, USA, 9–13 January 2022; Available online: https://hal.science/hal-03680834 (accessed on 30 April 2025).
- Bagloee, S.A.; Cederc, A.A.; Sarvi, M.; Asadi, M. Is it time to go for no-car zone policies? Braess Paradox Detection. Transp. Res. Part A 2019, 121, 251–264. [Google Scholar] [CrossRef]
- Zhao, C. Dynamic Traffic Network Model and Time-Dependent Braess’ Paradox. In Discrete Dynamics in Nature and Society; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Ciardo, L. The Braess’ Paradox for Pendent Twins. In Linear Algebra and its Applications; Elsevier: Amsterdam, The Netherlands, 2020; Volume 590, pp. 304–316. [Google Scholar] [CrossRef]
- Chen, X.; Diao, Z.; Hu, X. Network Characterizations for Excluding Braess’s Paradox. Theory Comput. Syst. 2016, 59, 747–780. [Google Scholar] [CrossRef]
- Acemoglu, D.; Makhdoumi, A.; Malekian, A.; Ozdaglar, A. Informational Braess’ Paradox: The Effect of Information on Traffic Congestion. Oper. Res. 2018, 66, 893–917. [Google Scholar] [CrossRef]
- Raza, S.; Al-Kaisy, A.; Washburn, S. Investigation of Roundabouts Influence Areas Along Rural and Suburban Corridors. Adv. Transp. Stud. 2022, 58, 21–38. Available online: https://www.atsinternationaljournal.com/2022-issues/investigation-of-roundabout-influence-areas-along-rural-and-suburban-corridors/ (accessed on 30 April 2025).
- National Cooperative Highway Research Program (NCHRP). Report 772: Evaluating the Performance of Corridors with Roundabouts; Transportation Research Board: Washington, DC, USA, 2014. [Google Scholar] [CrossRef]
- Brocchini, L.; Pratelli, A.; Josselin, D.; Losa, M. A Microsimulation-Based Methodology for Evaluating Efficiency and Safety in Roundabout Corridors: Case Studies of Pisa (Italy) and Avignon (France). Infrastructures 2025, 10, 186. [Google Scholar] [CrossRef]
- Pratelli, A.; Souleyrette, R.R.; Brocchini, L. Two-Geometry Roundabouts: Design Principles. Transp. Res. Procedia 2022, 64, 299–307. [Google Scholar] [CrossRef]
- Pratelli, A.; Brocchini, L. Two-Geometry Roundabouts: Estimation of Capacity. Transp. Res. Procedia 2022, 64, 232–239. [Google Scholar] [CrossRef]
- Campo, A.; D’Autilia, R. Simulation tools to compare and optimize mobility plans. In Proceedings of the 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS) 2017, Naples, Italy, 26–28 June 2017. [Google Scholar] [CrossRef]
- Mahut, M.; Florian, M.; Tremblay, N.; Campbell, M.; Patman, D.; Krnic McDaniel, Z. Calibration and Application of a Simulation-Based Dynamic Traffic Assignment Model. Transportation Res. Rec. J. Transp. Res. Board 2004, 1876, 101–111. [Google Scholar] [CrossRef]
- Theil, H. Applied Economic Forecasting; North-Holland Publishing Company: Amsterdam, The Netherlands, 1966. [Google Scholar]
- Tratar, L.F.; Strmčnik, E. Forecasting methods in engineering. IOP Conf. Ser. Mater. Sci. Eng. 2019, 657, 012027. [Google Scholar] [CrossRef]
- Feldman, O. The GEH Measure and Quality of the Highway Assignment Models. Association for European Transport and Contributors. 2012. Available online: https://trid.trb.org/view/1324899 (accessed on 30 April 2025).
- Xiao-Yun, L.; Lee, J.; Chen, D.; Bared, J.; Dailey, D.J.; Shladover, S.E. Freeway Micro-Simulation Calibration: Case Study Using Aimsun and VISSIM with Detailed Field Data. In Proceedings of the 93rd TRB Annual Meeting, Washington, DC, USA, 12–16 January 2014; Available online: https://www.academia.edu/25092992/Freeway_Micro_simulation_Calibration_Case_Study_Using_Aimsun_and_VISSIM_with_Detailed_Field_Data (accessed on 30 April 2025).
- National Academies of Sciences, Engineering, and Medicine. Highway Capacity Manual, 6th ed.; The National Academies Press: Washington, DC, USA, 2016; Available online: https://nap.nationalacademies.org/catalog/24798/highway-capacity-manual (accessed on 30 April 2025).
- National Academies of Sciences, Engineering, and Medicine. Highway Capacity Manual, 7th ed.; The National Academies Press: Washington, DC, USA, 2022; Available online: https://nap.nationalacademies.org/catalog/26432/highway-capacity-manual (accessed on 30 April 2025).
- National Cooperative Highway Research Program (NCHRP). Report 672: Roundabouts: An Informational Guide—Second Edition; Transportation Research Board: Washington, DC, USA, 2010. [Google Scholar] [CrossRef]
- Guerrieri, M.; Khanmohamadi, M. COM-Roundabout: The first smart commutable and self-regulating roundabout for HDVs and CAVs. Int. J. Transp. Sci. Technol. 2025, in press. [Google Scholar] [CrossRef]
- Boulagouas, W.; Catalina, O.C.A.; Mariscal, M.A.; Herrera, S.; García-Herrero, S. Effects of mobile phone-related distraction on driving performance at roundabouts: Eye movements tracking perspective. Heliyon 2024, 10, e29456. [Google Scholar] [CrossRef]
- Shatnawi, A.; Drine, A.; Al-Zinati, M.; Althebyan, Q. Simulation Study of Speed Control at Congested Arms of Roundabouts. In Proceedings of the 22nd International Arab Conference on Information Technology (ACIT), Muscat, Oman, 21–23 December 2021. [Google Scholar] [CrossRef]
- Lebacque, J.P.; Haj-Salem, H. Ramp Metering, Speed Management and Braess-like Paradoxes. In Proceedings of the TRISTAN V: The Fifth Triennial Symposium on Transportation Analysis, Le Gosier, Guadeloupe, France, 13–18 June 2004; Available online: https://tristanconference.org/system/tristan-v/website/pdf/abstract_00153.pdf (accessed on 30 April 2025).
- Akçelik, R. Roundabout Metering Signals: Capacity, Performance and Timing. Procedia Soc. Behav. Sci. 2011, 16, 686–696. [Google Scholar] [CrossRef]
- Trubia, S.; Curto, S.; Barberi, S.; Severino, A.; Arena, F.; Pau, G. Analysis and Evaluation of Ramp Metering: From Historical Evolution to the Application of New Algorithms and Engineering Principles. Sustainability 2021, 13, 850. [Google Scholar] [CrossRef]
- Brocchini, L.; Pratelli, A. Exploring the Potential Application of Ramp Metering Systems to Improve the Performances of Roundabout Corridors. In Proceedings of the ITFT 2024: International Conference on Intelligent Transport Systems, Helsinki, Finland, 19–21 October 2024; Springer: Cham, Switzerland, 2025; pp. 260–270. [Google Scholar] [CrossRef]






| Node | Type | Diameter [m] | Ring Width [m] | N° of Legs | Entry Lane Configuration |
|---|---|---|---|---|---|
| 1 | Conventional Roundabout | 38 | 9 | 4 | 2 per arm (6–7 m) |
| 2 | Conventional Roundabout | 40 | 9.5 | 4 | 2 per arm (6–7 m) |
| 3 | Conventional Roundabout | 40 | 9.5 | 3 | 2 per arm (7 m) |
| 4 | Two-Geometry Roundabout | 44 × 36 | 9–10 | 3 | 2 per arm (6.5–7.5 m) |
| 5 | Conventional Roundabout | 37 | 9 | 3 | 2 per arm (7 m) |
| Entry | Simulated Flow [veh/h] | Observed Flow [veh/h] | GEH |
|---|---|---|---|
| E1 R1 | 706 | 709 | 0.11 |
| E1 R2 | 972 | 1036 | 2.02 |
| E1 R3 | 837 | 946 | 3.65 |
| E1 R4 | 983 | 1081 | 3.05 |
| E1 R5 | 1070 | 1274 | 5.96 |
| E3 R1 | 669 | 892 | 7.98 |
| E3 R2 | 799 | 1236 | 13.70 |
| E3 R3 | 759 | 857 | 3.45 |
| E3 R4 | 844 | 994 | 4.95 |
| E3 R5 | 1286 | 1409 | 3.35 |
| Indices | |||
| R | 0.830 | 0.8–1 | yes |
| U | 0.096 | <0.1 | yes |
| Average GEH | 4.822 | <5 | yes |
| Intersection 1 | Intersection 2 | Intersection 3 | Intersection 4 | Intersection 5 | |
|---|---|---|---|---|---|
| delay current state branch 1 [s] | 2.25 | 0.84 | 0.26 | 0.58 | 0.31 |
| delay previous state branch 1 [s] | 3.82 | 3.14 | 3.58 | 297 | 1.83 |
| Q branch 1 [veh/h] | 709 | 1036 | 946 | 1081 | 1274 |
| delay current state branch 3 [s] | 2.48 | 9.93 | 4.93 | 7.72 | 1.56 |
| delay previous state branch 3 [s] | 4.26 | 4.58 | 3.68 | 4.20 | 1.92 |
| Q branch 3 [veh/h] | 892 | 1236 | 857 | 994 | 1409 |
| CRC | 0.59 | 1.47 | 0.68 | 1.12 | 0.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brocchini, L.; Pratelli, A.; Josselin, D. Exploring Traffic Paradoxes: A Study of Roundabout Corridors and Their Effects on Network Dynamics. Sustainability 2025, 17, 10290. https://doi.org/10.3390/su172210290
Brocchini L, Pratelli A, Josselin D. Exploring Traffic Paradoxes: A Study of Roundabout Corridors and Their Effects on Network Dynamics. Sustainability. 2025; 17(22):10290. https://doi.org/10.3390/su172210290
Chicago/Turabian StyleBrocchini, Lorenzo, Antonio Pratelli, and Didier Josselin. 2025. "Exploring Traffic Paradoxes: A Study of Roundabout Corridors and Their Effects on Network Dynamics" Sustainability 17, no. 22: 10290. https://doi.org/10.3390/su172210290
APA StyleBrocchini, L., Pratelli, A., & Josselin, D. (2025). Exploring Traffic Paradoxes: A Study of Roundabout Corridors and Their Effects on Network Dynamics. Sustainability, 17(22), 10290. https://doi.org/10.3390/su172210290






