Dynamic Pricing for Wireless Charging Lane Management Based on Deep Reinforcement Learning
Abstract
1. Introduction
2. Related Work
3. Problem Statement
- In the lane-changing zone (see Figure 1), each EV can choose one lane. Its lane choice mainly depends on three factors: the current SOC, the observed travel speeds on each lane, and the charging price.
- Once an EV enters the GPL or WCL, lane changing behavior is restricted unless its SOC drops below the minimum or exceeds the maximum threshold. All EVs obey this rule, which is enforced by the advanced ITS.
- EVs entering the WCL must charge their battery until their SOC reaches its maximum SOC level.
- The charging price is modeled as a discrete variable and can be changed at regular intervals, e.g., every three minutes.
- EVs receive charging-price information via the ITS with onboard communication support.
- The WCL-equipped traffic system is publicly funded and operated, with the primary goal of maximizing social welfare, that is, minimizing total congestion and maximizing EV energy uptake, rather than profit. Hence, the revenue is not considered.
- Traffic demand and downstream traffic conditions within the control horizon are assumed to be predictable by the system with the support of ITS.
4. Method
4.1. Agent-Based Model (ABM)
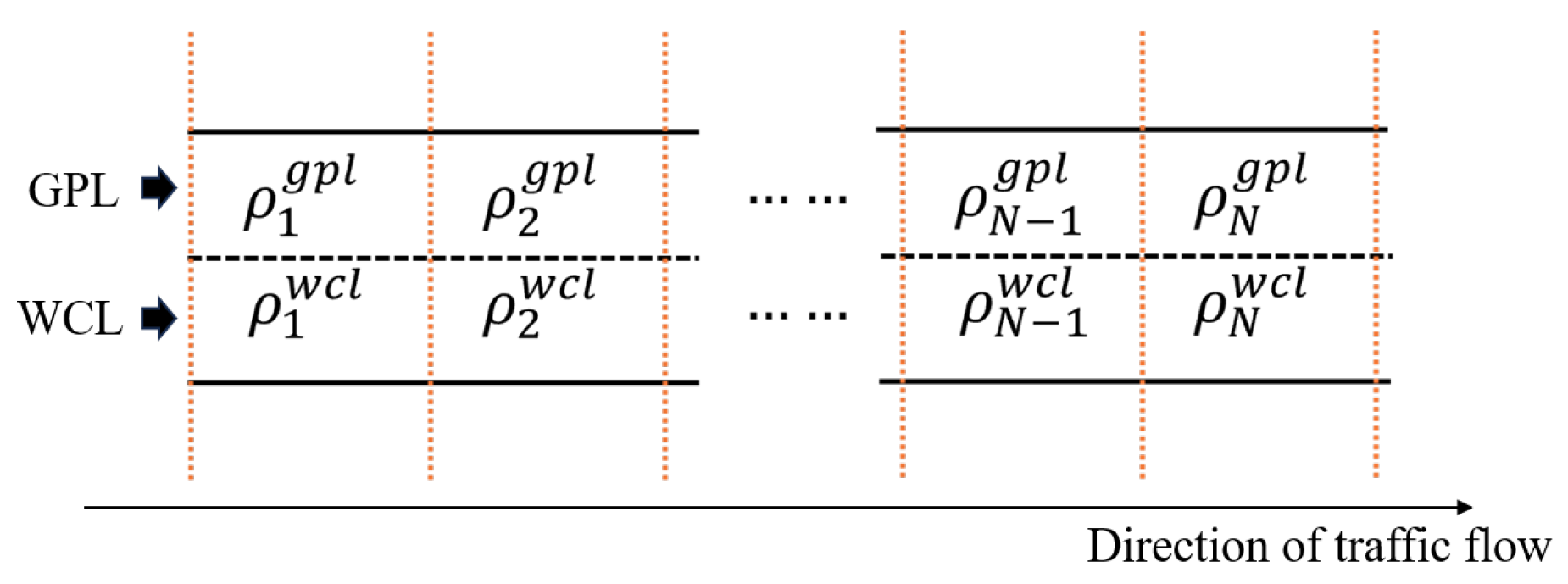
4.1.1. Global Variables
- Speed limit on GPL (): This denotes the maximum speed at which an EV is permitted to travel on the GPL. In our model, it is defined as a constant. Its unit is km/h.
- Speed limit on WCL (): This denotes the maximum speed at which an EV is permitted to travel on the WCL. Generally, is set slightly lower than to allow EVs more time to charge [15].
- Charging power (e): This denotes the power available at the WCLs, assumed to be constant over time and uniform along the lane, measured in kilowatts (kW).
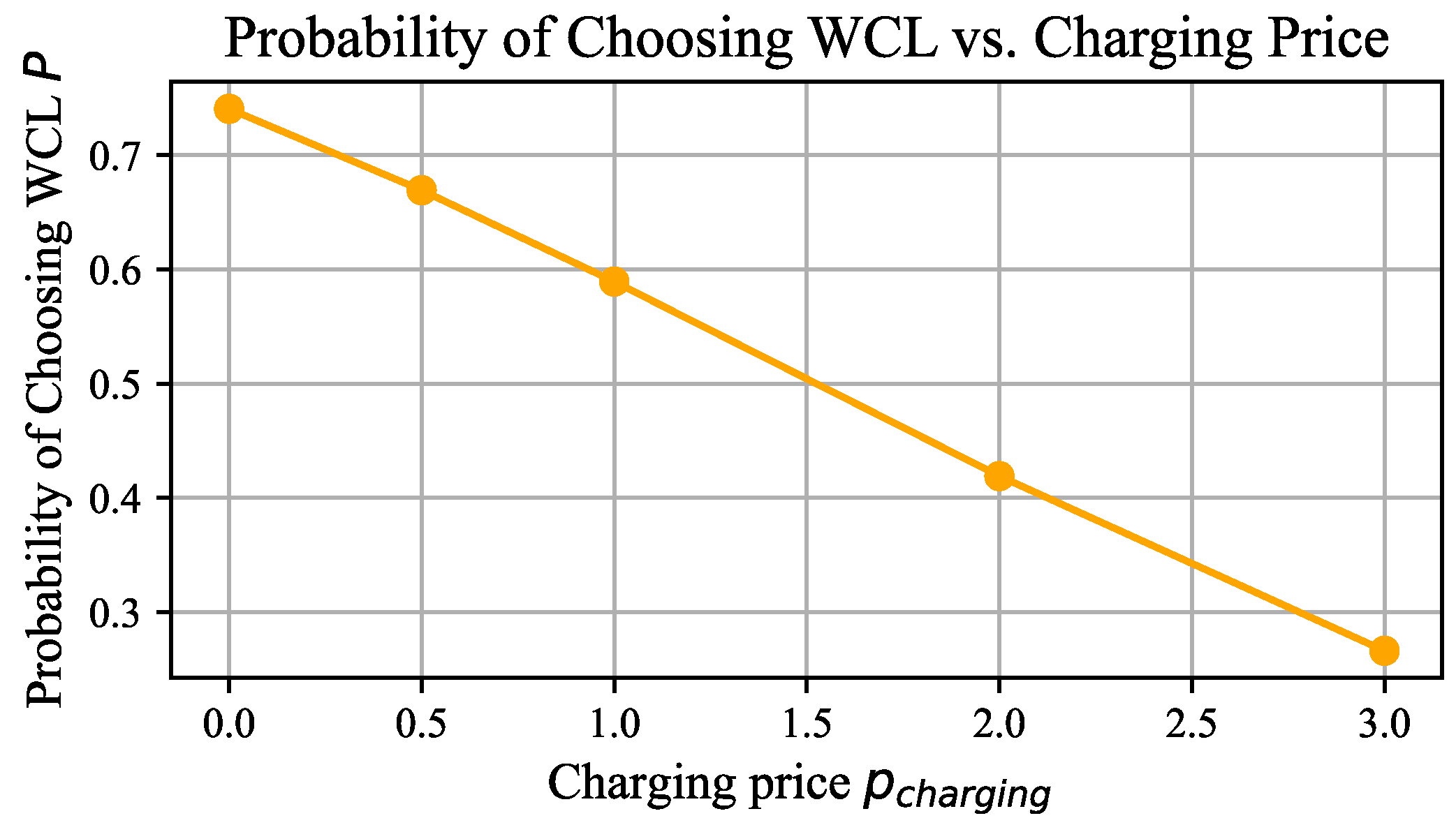
- Charging price (p): This refers to the cost of charging per kilowatt–hour on the WCL, communicated in real-time to all EVs to facilitate informed lane choices. We assume that p is a discrete variable, priced at USD/kWh.
- Total throughput (): This denotes the cumulative number of vehicles that pass a specific point, such as the entrance of the road, within a given time interval, measured in vehicles per hour (veh/h).
- Total energy (): This denotes the total energy delivered to vehicles via the WCL, calculated as the sum of the energy received by each vehicle, measured in kilowatt–hours (kWh).
4.1.2. EV Attributes
- Maximum travel speed (): This attribute specifies the upper limit of an EV’s speed, normalized to the range . In our model, its value is defined as a constant, which is generally bigger than and .
- Current travel speed (): This attribute describes the instantaneous speed of the EV. Its value is constrained within a normalized range of 0 (stationary) to 1 (maximum travel speed).
- Observed travel speed (,): This attribute captures the speed of EVs within a lane as observed by an individual EV. It is quantified as the average speed of EVs along a specified observable distance (e.g., 100 m) ahead of the observing EV. In this model, we assume it to be the average speed of vehicles across the entire lane, which is disseminated to all vehicles in real time through advanced vehicle communication systems. Its value is normalized to the range .
- Acceleration (): This attribute describes the change of an EV’s speed within one time interval. In our model, their values are defined as constants.
- SOC (): The SOC is a crucial attribute for operations and management on WCLs, indicating the current energy level of the EV’s battery. The value is constrained within a normalized range of 0 (completely depleted) to 1 (fully charged).
- Minimum SOC level (): This threshold represents the critical SOC below which an EV risks imminent power depletion, potentially leading to operational failure and reduced battery lifespan. In our model, an EV is allowed to change to the WCL whenever its SOC level drops below this point.
- Maximum SOC level (): This threshold signifies the optimal SOC at which an EV’s battery is considered fully charged without exceeding the manufacturer’s recommended limits to prevent overcharging. In our model, an EV is allowed to change to the GPL whenever its SOC level exceeds this point.
- Location (): The EV’s location in the context of the NetLogo model is captured by a two-dimensional coordinate , where represents the longitudinal axis along the road while denotes the lateral position across lanes.
- Target location (): This attribute is denoted as the y axis value of the target location of an EV (corresponding to the target lane). In our double-lane system, the GPL and the WCL can be expressed as and , respectively.
- Lateral speed (): This attribute signifies the speed at which an EV executes a lane-changing behavior. In our model, this parameter is defined as a constant.
4.1.3. Exogenous Input
4.1.4. Scale
4.1.5. Lane-Choice Model
4.1.6. EV Driving Behavior
4.2. NetLogo
4.3. Deep Q-Learning Algorithm
4.3.1. Background
Notation
- x—state; a—action; r—reward; —policy; —discount factor.
- —action-value function; —optimal action-value function.
- —network parameters; —loss function with weights .
4.3.2. State
4.3.3. Action
4.3.4. Reward
4.3.5. Q-Network
4.3.6. Training
| Algorithm 1 Deep Q-learning with experience replay |
| Require: : discount factor, : learning rate, : exploration rate |
| Require: C: memory capacity for experience replay, M: minibatch size |
|
4.4. The CART Algorithm
Training
- 1.
- Data generation: Utilizing an Agent-Based Model (ABM), we generate a dataset , where comprises the feature vector. Here, represents the state, specifically only including the immediate future traffic demand, distinct from the states used in DQL. The action a is also included in X. The corresponding consists of the rewards for each charging price p, illustrating the reward’s dependency on the price.
- 2.
- Decision tree training: We apply the CART algorithm to map the relationship between X and Y (as defined in (26)), thereby modeling how different charging prices influence the rewards. The purity of each node is measured using the MSE.
- 3.
- Optimal price implementation: The price yielding the highest reward is selected and implemented in the system, optimizing the charging strategy within the defined parameters.
| Algorithm 2 Modified CART |
|
5. Numerical Experiments
5.1. Parameter Settings for the Lane-Choice Model
5.2. Simulation for Sample Scenarios
5.3. Parameter Settings for the Deep Q-Learning Algorithm
5.4. Parameter Settings for the CART Algorithm
5.5. Simulation of Real Traffic Scenarios
6. Results and Discussions
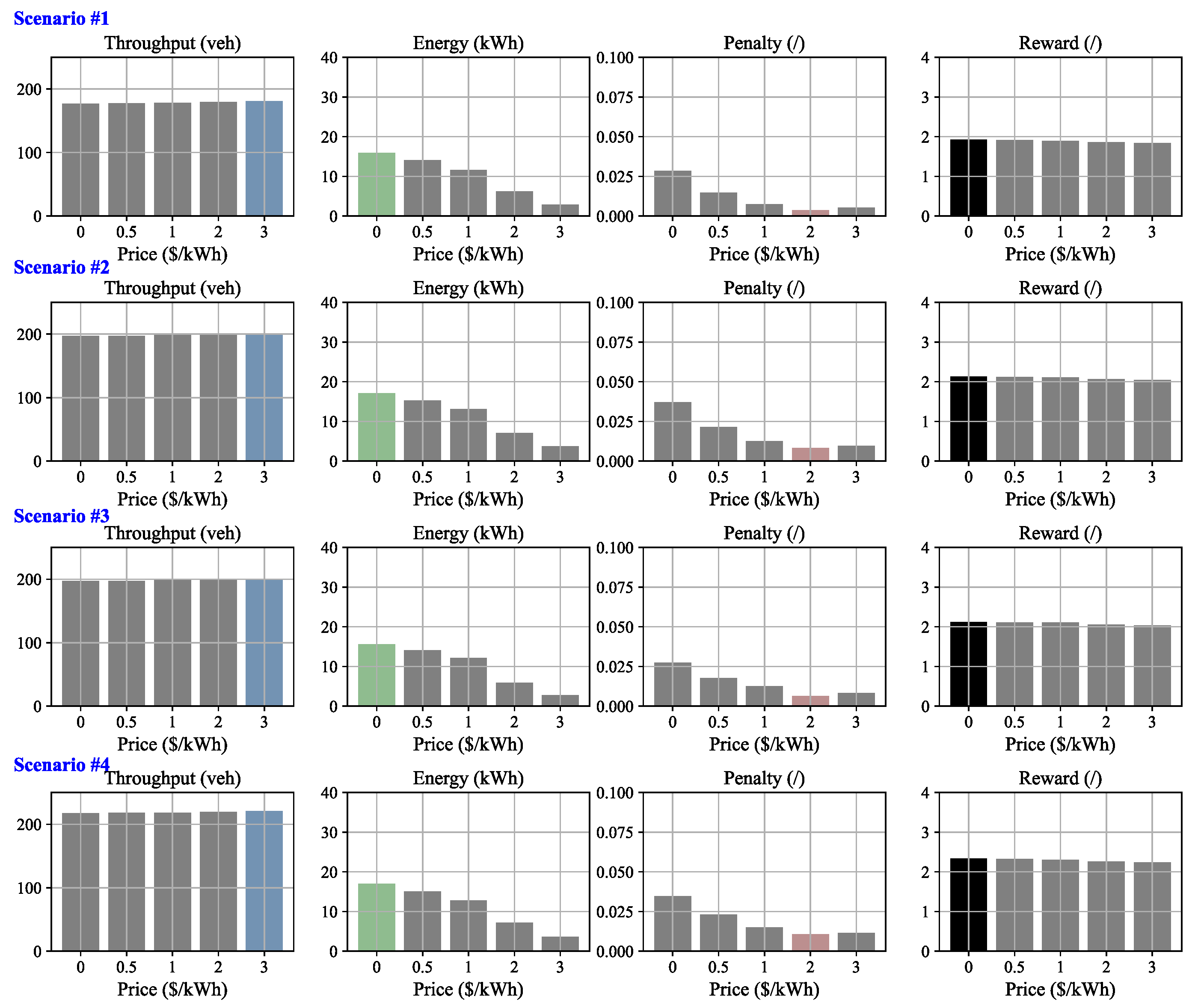
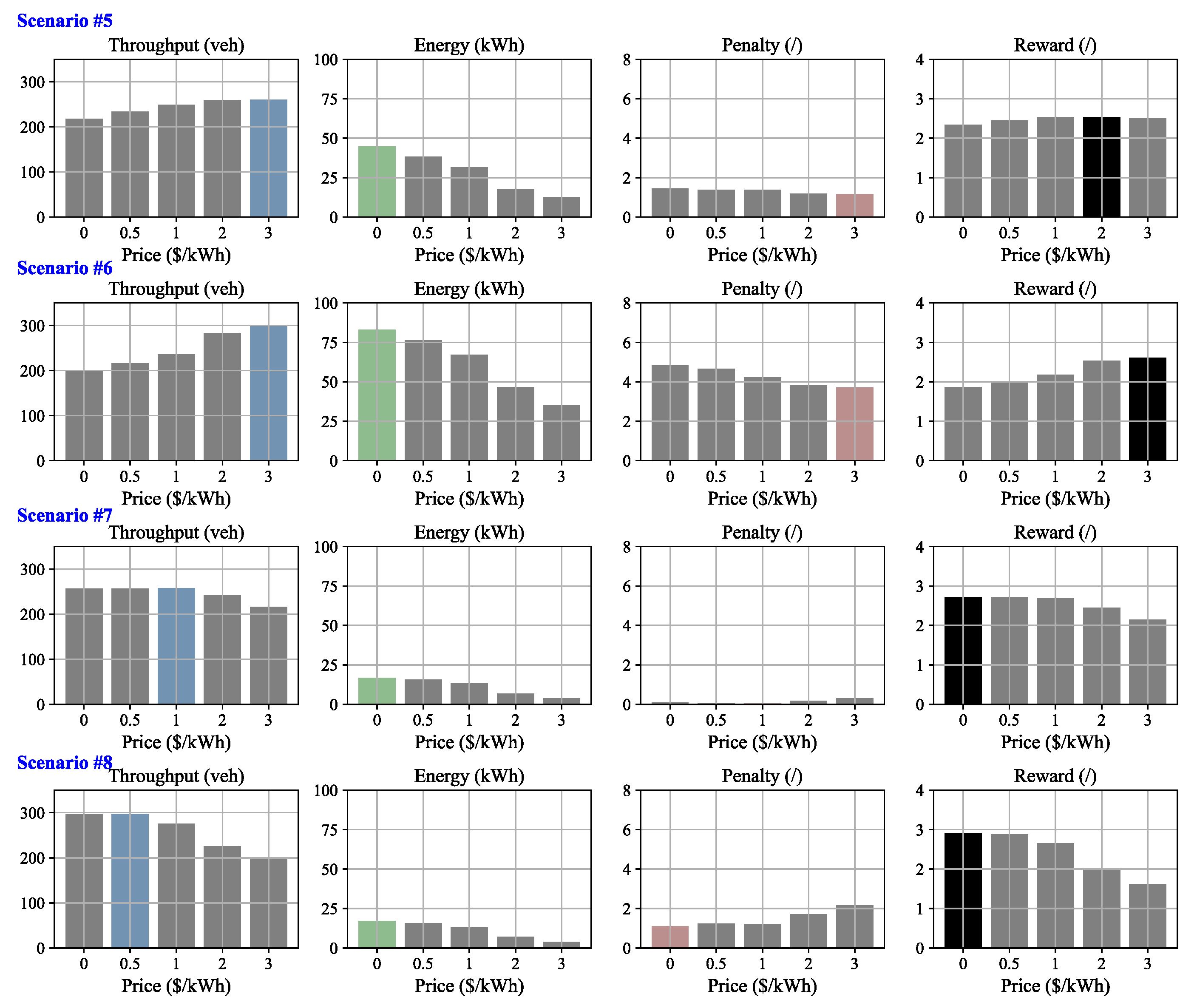
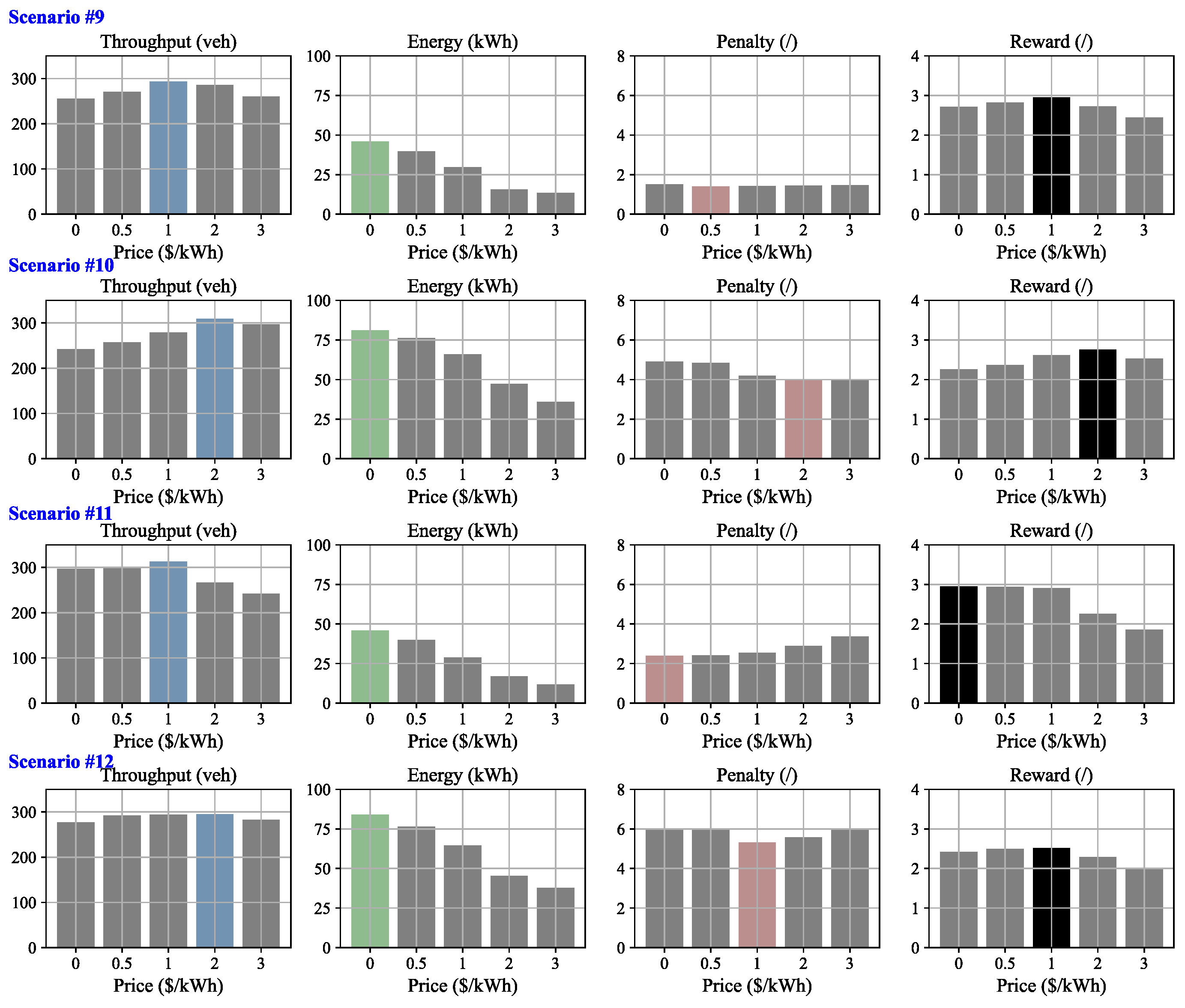
6.1. Results for Sample Scenarios
6.2. Learning Performance of the Decision Tree Algorithm
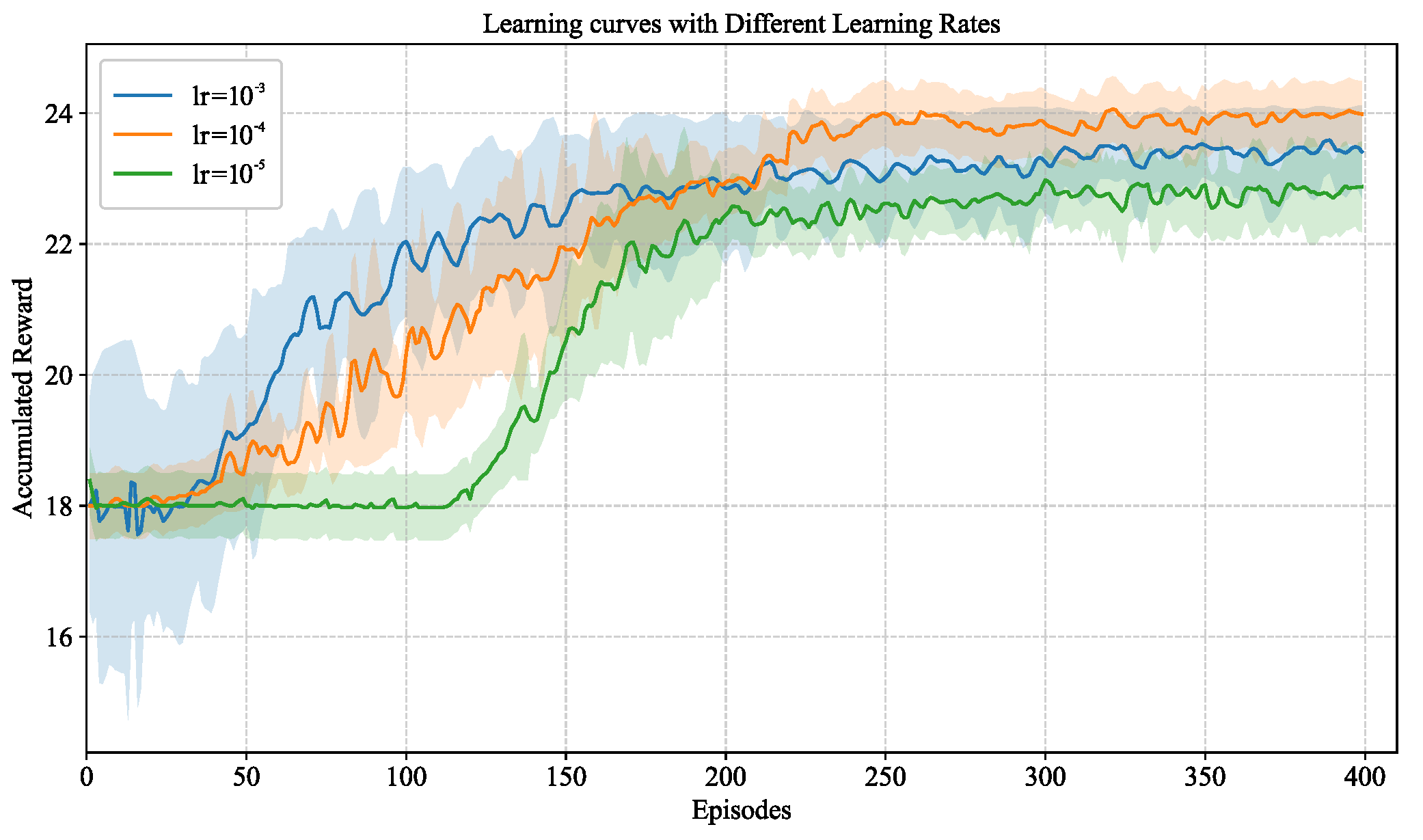
6.3. Learning Performance of Deep Q-Learning
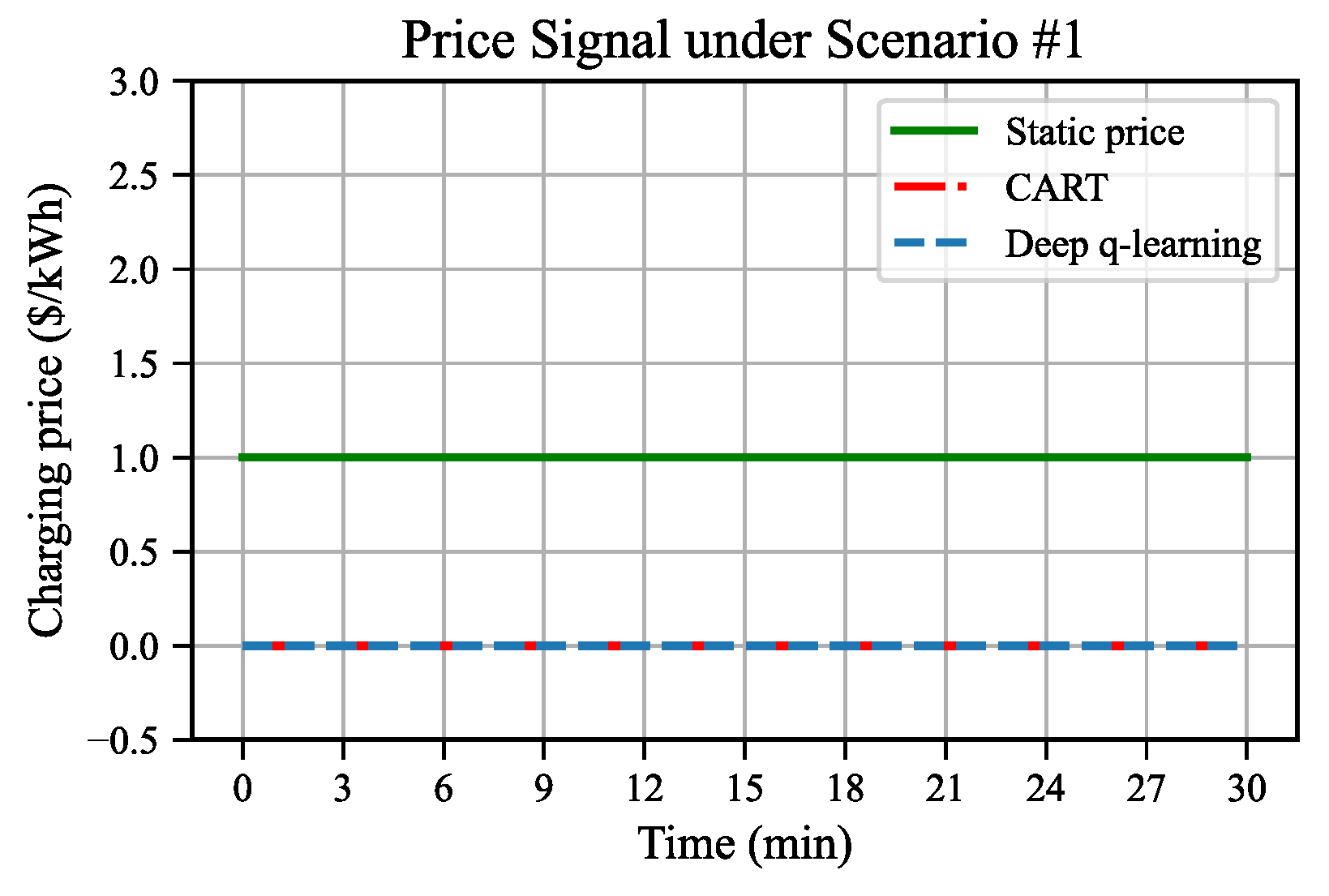
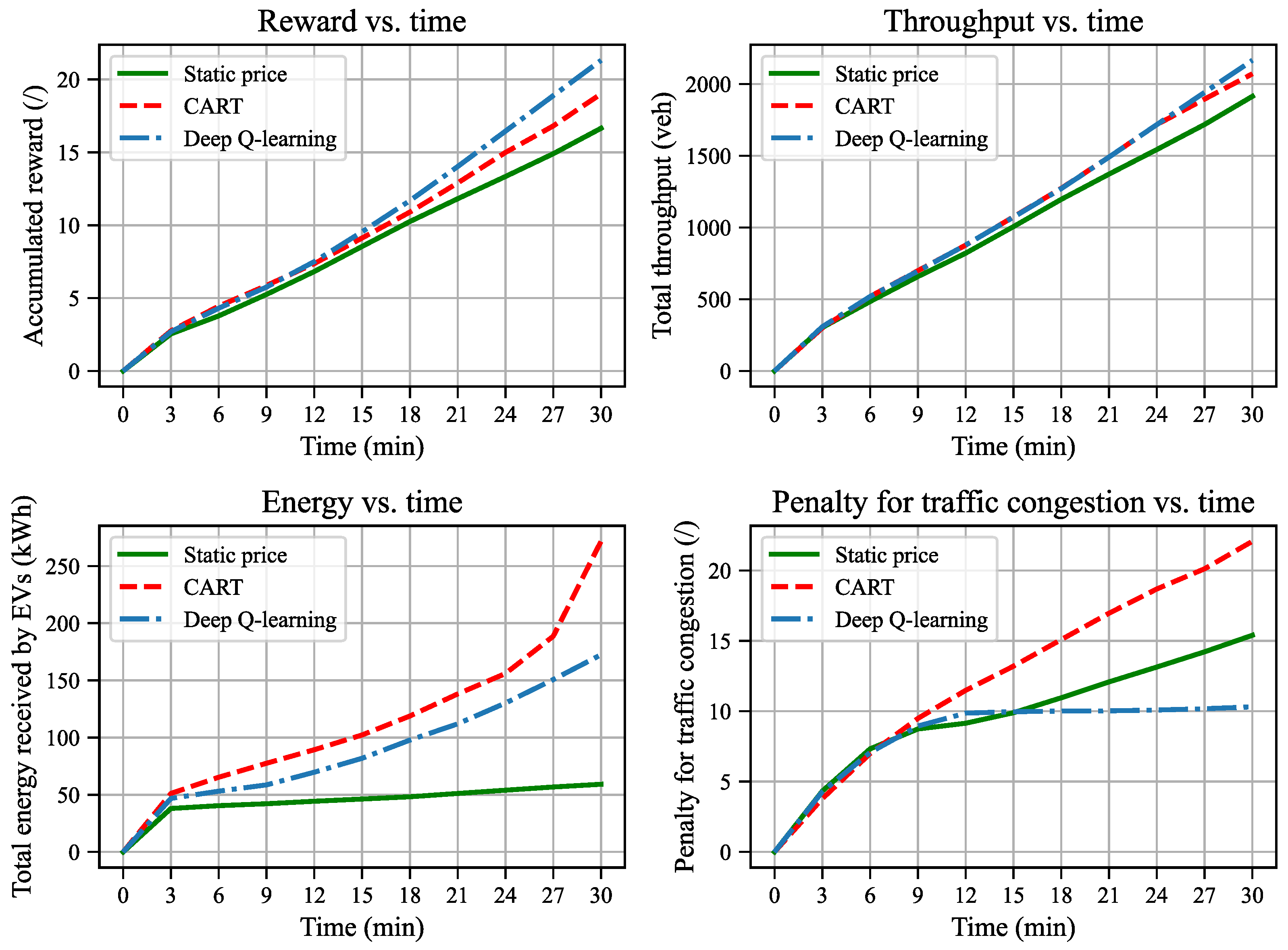
6.4. Results Under Real Traffic Scenarios
6.5. Model Validation and Calibration
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tan, Z.; Liu, F.; Chan, H.K.; Gao, H.O. Transportation systems management considering dynamic wireless charging electric vehicles: Review and prospects. Transp. Res. Part E Logist. Transp. Rev. 2022, 163, 102761. [Google Scholar] [CrossRef]
- Miller, J.M.; Jones, P.T.; Li, J.M.; Onar, O.C. ORNL experience and challenges facing dynamic wireless power charging of EV’s. IEEE Circuits Syst. Mag. 2015, 15, 40–53. [Google Scholar] [CrossRef]
- Lee, M.S.; Jang, Y.J. Charging infrastructure allocation for wireless charging transportation system. In Proceedings of the Eleventh International Conference on Management Science and Engineering Management 11, Changchun, China, 17–19 August 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1630–1644. [Google Scholar]
- Chen, Z.; He, F.; Yin, Y. Optimal deployment of charging lanes for electric vehicles in transportation networks. Transp. Res. Part B Methodol. 2016, 91, 344–365. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, W.; Yin, Y. Deployment of stationary and dynamic charging infrastructure for electric vehicles along traffic corridors. Transp. Res. Part C Emerg. Technol. 2017, 77, 462–477. [Google Scholar] [CrossRef]
- Alwesabi, Y.; Wang, Y.; Avalos, R.; Liu, Z. Electric bus scheduling under single depot dynamic wireless charging infrastructure planning. Energy 2020, 213, 118855. [Google Scholar] [CrossRef]
- Ngo, H.; Kumar, A.; Mishra, S. Optimal positioning of dynamic wireless charging infrastructure in a road network for battery electric vehicles. Transp. Res. Part D Transp. Environ. 2020, 85, 102393. [Google Scholar] [CrossRef]
- Mubarak, M.; Üster, H.; Abdelghany, K. Strategic network design and analysis for in-motion wireless charging of electric vehicles. Transp. Res. Part E Logist. Transp. Rev. 2021, 145, 102159. [Google Scholar] [CrossRef]
- Liu, H.; Zou, Y.; Chen, Y.; Long, J. Optimal locations and electricity prices for dynamic wireless charging links of electric vehicles for sustainable transportation. Transp. Res. Part E Logist. Transp. Rev. 2021, 145, 102174. [Google Scholar] [CrossRef]
- Alwesabi, Y.; Liu, Z.; Kwon, S.; Wang, Y. A novel integration of scheduling and dynamic wireless charging planning models of battery electric buses. Energy 2021, 230, 120806. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Bock, S.; Boysen, N.; Briskorn, D. Optimizing the electrification of roads with charge-while-drive technology. Eur. J. Oper. Res. 2022, 299, 1111–1127. [Google Scholar] [CrossRef]
- Deflorio, F.P.; Castello, L.; Pinna, I.; Guglielmi, P. “Charge while driving” for electric vehicles: Road traffic modeling and energy assessment. J. Mod. Power Syst. Clean Energy 2015, 3, 277–288. [Google Scholar] [CrossRef]
- Deflorio, F.; Pinna, I.; Castello, L. Dynamic charging systems for electric vehicles: Simulation for the daily energy estimation on motorways. IET Intell. Transp. Syst. 2016, 10, 557–563. [Google Scholar] [CrossRef]
- García-Vázquez, C.A.; Llorens-Iborra, F.; Fernández-Ramírez, L.M.; Sánchez-Sainz, H.; Jurado, F. Comparative study of dynamic wireless charging of electric vehicles in motorway, highway and urban stretches. Energy 2017, 137, 42–57. [Google Scholar] [CrossRef]
- He, J.; Huang, H.J.; Yang, H.; Tang, T.Q. An electric vehicle driving behavior model in the traffic system with a wireless charging lane. Phys. A Stat. Mech. Its Appl. 2017, 481, 119–126. [Google Scholar] [CrossRef]
- He, J.; Yang, H.; Huang, H.J.; Tang, T.Q. Impacts of wireless charging lanes on travel time and energy consumption in a two-lane road system. Phys. A Stat. Mech. Appl. 2018, 500, 1–10. [Google Scholar] [CrossRef]
- Jansuwan, S.; Liu, Z.; Song, Z.; Chen, A. An evaluation framework of automated electric transportation system. Transp. Res. Part E Logist. Transp. Rev. 2021, 148, 102265. [Google Scholar] [CrossRef]
- Liu, F.; Tan, Z.; Chan, H.K.; Zheng, L. Ramp Metering Control on Wireless Charging Lanes Considering Optimal Traffic and Charging Efficiencies. IEEE Trans. Intell. Transp. Syst. 2024, 25, 11590–11601. [Google Scholar] [CrossRef]
- Liu, F.; Tan, Z.; Chan, H.K.; Zheng, L. Model-based variable speed limit control on wireless charging lanes: Formulation and algorithm. Transp. Res. Part E Logist. Transp. Rev. 2025. [Google Scholar] [CrossRef]
- Zhang, Y.; Hong, Y.; Tan, Z. Design of Coordinated EV Traffic Control Strategies for Expressway System with Wireless Charging Lanes. World Electr. Veh. J. 2025, 16, 496. [Google Scholar] [CrossRef]
- He, F.; Yin, Y.; Zhou, J. Integrated pricing of roads and electricity enabled by wireless power transfer. Transp. Res. Part C Emerg. Technol. 2013, 34, 1–15. [Google Scholar] [CrossRef]
- Wang, T.; Yang, B.; Chen, C. Double-layer game based wireless charging scheduling for electric vehicles. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Esfahani, H.N.; Liu, Z.; Song, Z. Optimal pricing for bidirectional wireless charging lanes in coupled transportation and power networks. Transp. Res. Part C Emerg. Technol. 2022, 135, 103419. [Google Scholar] [CrossRef]
- Lei, X.; Li, L.; Li, G.; Wang, G. Review of multilane traffic flow theory and application. J. Chang. Univ. (Nat. Sci. Ed.) 2020, 40, 78–90. [Google Scholar]
- Jiang, J.; Ren, Y.; Guan, Y.; Eben Li, S.; Yin, Y.; Yu, D.; Jin, X. Integrated decision and control at multi-lane intersections with mixed traffic flow. J. Phys. Conf. Ser. 2022, 2234, 012015. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, W.; Yin, G.; Liu, H.; Qiu, C. Cooperative on-ramp merging control of connected and automated vehicles: Distributed multi-agent deep reinforcement learning approach. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 402–408. [Google Scholar]
- Bouktif, S.; Cheniki, A.; Ouni, A.; El-Sayed, H. Deep reinforcement learning for traffic signal control with consistent state and reward design approach. Knowl.-Based Syst. 2023, 267, 110440. [Google Scholar] [CrossRef]
- Li, D.; Lasenby, J. Imagination-Augmented Reinforcement Learning Framework for Variable Speed Limit Control. IEEE Trans. Intell. Transp. Syst. 2024, 25, 1384–1393. [Google Scholar] [CrossRef]
- Chen, S.; Wang, M.; Song, W.; Yang, Y.; Fu, M. Multi-agent reinforcement learning-based decision making for twin-vehicles cooperative driving in stochastic dynamic highway environments. IEEE Trans. Veh. Technol. 2023, 72, 12615–12627. [Google Scholar] [CrossRef]
- Jiang, K.; Lu, Y.; Su, R. Safe Reinforcement Learning for Connected and Automated Vehicle Platooning. In Proceedings of the 2024 IEEE 7th International Conference on Industrial Cyber-Physical Systems (ICPS), St. Louis, MO, USA, 12–15 May 2024; pp. 1–6. [Google Scholar]
- Pandey, V.; Wang, E.; Boyles, S.D. Deep reinforcement learning algorithm for dynamic pricing of express lanes with multiple access locations. Transp. Res. Part C Emerg. Technol. 2020, 119, 102715. [Google Scholar] [CrossRef]
- Abdalrahman, A.; Zhuang, W. Dynamic pricing for differentiated PEV charging services using deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1415–1427. [Google Scholar] [CrossRef]
- Cui, L.; Wang, Q.; Qu, H.; Wang, M.; Wu, Y.; Ge, L. Dynamic pricing for fast charging stations with deep reinforcement learning. Appl. Energy 2023, 346, 121334. [Google Scholar] [CrossRef]
- Wilensky, U.; Payette, N. NetLogo Traffic 2 Lanes Model; Center for Connected Learning and Computer-Based Modeling, Northwestern University: Evanston, IL, USA, 1998; Available online: http://ccl.northwestern.edu/netlogo/models/Traffic2Lanes (accessed on 15 March 2025).
- Triastanto, A.N.D.; Utama, N.P. Model Study of Traffic Congestion Impacted by Incidents. In Proceedings of the 2019 International Conference of Advanced Informatics: Concepts, Theory and Applications (ICAICTA), Yogyakarta, Indonesia, 20–21 September 2019; pp. 1–6. [Google Scholar]
- Mitrovic, N.; Dakic, I.; Stevanovic, A. Combined alternate-direction lane assignment and reservation-based intersection control. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1779–1789. [Google Scholar] [CrossRef]
- Jaxa-Rozen, M.; Kwakkel, J.H. Pynetlogo: Linking netlogo with python. J. Artif. Soc. Soc. Simul. 2018, 21, 4. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, L.; Chen, Z.; Xie, H. A Queuing Model for Mixed Traffic Flows on Highways considering Fluctuations in Traffic Demand. J. Adv. Transp. 2022, 2022, 4625690. [Google Scholar] [CrossRef]
- Medhi, J. Stochastic Models in Queueing Theory; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Hu, L.; Dong, J.; Lin, Z. Modeling charging behavior of battery electric vehicle drivers: A cumulative prospect theory based approach. Transp. Res. Part C Emerg. Technol. 2019, 102, 474–489. [Google Scholar] [CrossRef]
- McFadden, D. Conditional Logit Analysis of Qualitative Choice Behavior; Frontiers in Econometrics: New York, NY, USA, 1972. [Google Scholar]
- Train, K.E. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Lou, Y.; Yin, Y.; Laval, J.A. Optimal dynamic pricing strategies for high-occupancy/toll lanes. Transp. Res. Part C Emerg. Technol. 2011, 19, 64–74. [Google Scholar] [CrossRef]
- Tan, Z.; Gao, H.O. Hybrid model predictive control based dynamic pricing of managed lanes with multiple accesses. Transp. Res. Part B Methodol. 2018, 112, 113–131. [Google Scholar] [CrossRef]
- Li, C.; Dong, X.; Cipcigan, L.M.; Haddad, M.A.; Sun, M.; Liang, J.; Ming, W. Economic viability of dynamic wireless charging technology for private EVs. IEEE Trans. Transp. Electrif. 2022, 9, 1845–1856. [Google Scholar] [CrossRef]
- Ge, Y.; MacKenzie, D. Charging behavior modeling of battery electric vehicle drivers on long-distance trips. Transp. Res. Part D Transp. Environ. 2022, 113, 103490. [Google Scholar] [CrossRef]
- Zhou, S.; Qiu, Y.; Zou, F.; He, D.; Yu, P.; Du, J.; Luo, X.; Wang, C.; Wu, Z.; Gu, W. Dynamic EV charging pricing methodology for facilitating renewable energy with consideration of highway traffic flow. IEEE Access 2019, 8, 13161–13178. [Google Scholar] [CrossRef]
- Galvin, R. Energy consumption effects of speed and acceleration in electric vehicles: Laboratory case studies and implications for drivers and policymakers. Transp. Res. Part D Transp. Environ. 2017, 53, 234–248. [Google Scholar] [CrossRef]
- Wilensky, U. NetLogo; Center for Connected Learning and Computer-Based Modeling, Northwestern University: Evanston, IL, USA, 1999. [Google Scholar]
- Railsback, S.F.; Grimm, V. Agent-Based and Individual-Based Modeling: A Practical Introduction; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Mostafizi, A.; Koll, C.; Wang, H. A decentralized and coordinated routing algorithm for connected and autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11505–11517. [Google Scholar] [CrossRef]
- Kponyo, J.; Nwizege, K.; Opare, K.; Ahmed, A.; Hamdoun, H.; Akazua, L.; Alshehri, S.; Frank, H. A distributed intelligent traffic system using ant colony optimization: A NetLogo modeling approach. In Proceedings of the 2016 International Conference on Systems Informatics, Modelling and Simulation (SIMS), Riga, Latvia, 1–3 June 2016; pp. 11–17. [Google Scholar]
- Wang, L.; Yang, M.; Li, Y.; Hou, Y. A model of lane-changing intention induced by deceleration frequency in an automatic driving environment. Phys. A Stat. Mech. Appl. 2022, 604, 127905. [Google Scholar] [CrossRef]
- Nguyen, J.; Powers, S.T.; Urquhart, N.; Farrenkopf, T.; Guckert, M. An overview of agent-based traffic simulators. Transp. Res. Interdiscip. Perspect. 2021, 12, 100486. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Ha, D.; Schmidhuber, J. Recurrent world models facilitate policy evolution. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Rummery, G.A.; Niranjan, M. On-Line Q-Learning Using Connectionist Systems; Department of Engineering, University of Cambridge: Cambridge, UK, 1994; Volume 37. [Google Scholar]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Adv. Neural Inf. Process. Syst. 1999, 12. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Ukkusuri, S.V. Accounting for dynamic speed limit control in a stochastic traffic environment: A reinforcement learning approach. Transp. Res. Part C Emerg. Technol. 2014, 41, 30–47. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Xu, C.; Duan, H.; Wang, W. Reinforcement learning-based variable speed limit control strategy to reduce traffic congestion at freeway recurrent bottlenecks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3204–3217. [Google Scholar] [CrossRef]
- Müller, E.R.; Carlson, R.C.; Kraus, W.; Papageorgiou, M. Microsimulation analysis of practical aspects of traffic control with variable speed limits. IEEE Trans. Intell. Transp. Syst. 2015, 16, 512–523. [Google Scholar] [CrossRef]
- Wen, Y.; MacKenzie, D.; Keith, D.R. Modeling the charging choices of battery electric vehicle drivers by using stated preference data. Transp. Res. Rec. 2016, 2572, 47–55. [Google Scholar] [CrossRef]
- Tympakianaki, A.; Spiliopoulou, A.; Kouvelas, A.; Papamichail, I.; Papageorgiou, M.; Wang, Y. Real-time merging traffic control for throughput maximization at motorway work zones. Transp. Res. Part C Emerg. Technol. 2014, 44, 242–252. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Y.; Zhang, J.; Ran, B. Integrated traffic control for freeway recurrent bottleneck based on deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15522–15535. [Google Scholar] [CrossRef]
- Aslani, M.; Mesgari, M.S.; Wiering, M. Adaptive traffic signal control with actor-critic methods in a real-world traffic network with different traffic disruption events. Transp. Res. Part C Emerg. Technol. 2017, 85, 732–752. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Cole Statistics/Probability Series; Wadsworth & Brooks; Chapman and Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: Oxfordshire, UK, 2017. [Google Scholar]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Bock, S.; Weis, M. A proof of local convergence for the adam optimizer. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Shi, Y.; Wang, Z.; LaClair, T.J.; Wang, C.; Shao, Y.; Yuan, J. A novel deep reinforcement learning approach to traffic signal control with connected vehicles. Appl. Sci. 2023, 13, 2750. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D.; Nguyen, C.T.; Yuen, K.F.; Wang, X. “Freedom–enslavement” paradox in consumers’ adoption of smart transportation: A comparative analysis of three technologies. Transp. Policy 2025, 164, 206–216. [Google Scholar] [CrossRef]
- Owais, M. Deep Learning for Integrated Origin–Destination Estimation and Traffic Sensor Location Problems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6501–6513. [Google Scholar] [CrossRef]
- Owais, M.; Moussa, G.S. Global sensitivity analysis for studying hot-mix asphalt dynamic modulus parameters. Constr. Build. Mater. 2024, 413, 134775. [Google Scholar] [CrossRef]
- Jin, J.; Zhu, X.; Wu, B.; Zhang, J.; Wang, Y. A dynamic and deadline-oriented road pricing mechanism for urban traffic management. Tsinghua Sci. Technol. 2021, 27, 91–102. [Google Scholar] [CrossRef]






| Notations | Definitions | Units | Type 1 |
|---|---|---|---|
| Global variables/parameters | |||
| N | Number of road segments | / | New |
| Length of the multi-lane system | / | New | |
| Charging power on the WCL | kW | New | |
| p | Charging price on the WCL | USD/kWh | New |
| Speed limit on GPL | km/h | New | |
| Speed limit on WCL | km/h | New | |
| Total throughput | veh | New | |
| Total energy | kWh | New | |
| EV attributes | |||
| Energy consumption of the i-th EV | kW | New | |
| Maximum travel speed the i-th EV | km/h | Old | |
| Current travel speed of the i-th EV | km/h | Old | |
| Observed travel speed on the GPL by the i-th EV | km/h | New | |
| Observed travel speed on the WCL by the i-th EV | km/h | New | |
| Acceleration the i-th EV | m/s2 | Old | |
| SOC of the i-th EV | percent | New | |
| Minimum SOC level of the i-th EV | percent | New | |
| Maximum SOC level of the i-th EV | percent | New | |
| The mean value of initial SOC of incoming EVs | percent | New | |
| The standard deviation of initial SOC of incoming EVs | percent | New | |
| Location of the i-th EV | km | New | |
| Target lane of the i-th EV | / | New | |
| Lateral speed of the i-th EV | km/h | Old |
| Hyper-Parameters | Values |
|---|---|
| Learning rate | 0.0001 |
| Discount factor 1 | 0.99 |
| Initial exploration rate 1 | 1 |
| Final exploration rate 1 | 0.01 |
| Batch size | 32 |
| Number of hidden layers | 2 |
| Size of a hidden layer | 64 |
| Gradient descent optimizer | Adam [73] |
| Memory capacity | 10,000 |
| Parameters | Values |
| 15 | |
| p | {0.5, 1, 1.5, 3, 5} |
| 1 | 22 |
| 1 | 20 |
| 100 | |
| 1 | 3 |
| 1 | −4.5 |
| 20 | |
| 80 | |
| 1 | |
| 150 | |
| 0.01 | |
| 0.01 | |
| −0.2 |
| No. of Scenarios | Traffic State | 1 (veh) | 2 (veh) | 3 (veh/min) |
|---|---|---|---|---|
| #1 | Free-flow | 100 | 100 | 60 |
| #2 | 100 | 200 | 60 | |
| #3 | 200 | 100 | 60 | |
| #4 | 200 | 200 | 60 | |
| #5 | Congested (medium) | 200 | 400 | 60 |
| #6 | 200 | 600 | 60 | |
| #7 | 400 | 200 | 60 | |
| #8 | 600 | 200 | 60 | |
| #9 | Congested (heavy) | 400 | 400 | 60 |
| #10 | 400 | 600 | 60 | |
| #11 | 600 | 400 | 60 | |
| #12 | 600 | 600 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Tan, Z.; Chan, H.K. Dynamic Pricing for Wireless Charging Lane Management Based on Deep Reinforcement Learning. Sustainability 2025, 17, 9831. https://doi.org/10.3390/su17219831
Liu F, Tan Z, Chan HK. Dynamic Pricing for Wireless Charging Lane Management Based on Deep Reinforcement Learning. Sustainability. 2025; 17(21):9831. https://doi.org/10.3390/su17219831
Chicago/Turabian StyleLiu, Fan, Zhen Tan, and Hing Kai Chan. 2025. "Dynamic Pricing for Wireless Charging Lane Management Based on Deep Reinforcement Learning" Sustainability 17, no. 21: 9831. https://doi.org/10.3390/su17219831
APA StyleLiu, F., Tan, Z., & Chan, H. K. (2025). Dynamic Pricing for Wireless Charging Lane Management Based on Deep Reinforcement Learning. Sustainability, 17(21), 9831. https://doi.org/10.3390/su17219831






