Research on a Short-Term Electric Load Forecasting Model Based on Improved BWO-Optimized Dilated BiGRU
Abstract
1. Introduction
2. Materials and Methods
2.1. Feature Engineering
2.2. Beluga Whale Optimization
2.2.1. Population Initialization
2.2.2. Exploration Phase
2.2.3. Exploitation Phase
2.2.4. Whale Fall Phase
2.3. Improved Beluga Whale Optimization
2.3.1. Tanh-Sobol Population Initialization
- Define the population dimension as , the upper bound of the search space as , the lower bound as , and let represent the search domain.
- First, call the function to generate a Sobol sequence and assign it to the variable , where is defined as
- To retain the spatial uniformity and low discrepancy properties of the Sobol sequence while introducing greater randomness, this paper applies the Matoušek–Affine–Owen scrambling method to the original Sobol sequence. The corresponding formula is shown below. This method ensures that the generated population exhibits different point distribution characteristics in each run, making it particularly suitable for optimization algorithms that require multiple independent initializations.
- To address the issue that traditional Sobol sequence initialization methods exhibit excessive regularity and insufficient randomness, this paper proposes an improved method based on nonlinear function perturbation. The formula is defined as follows:
- 5.
- To ensure that the perturbed population points remain within the interval [0, 1] after applying the disturbance, boundary correction is applied, as defined by the following formula:
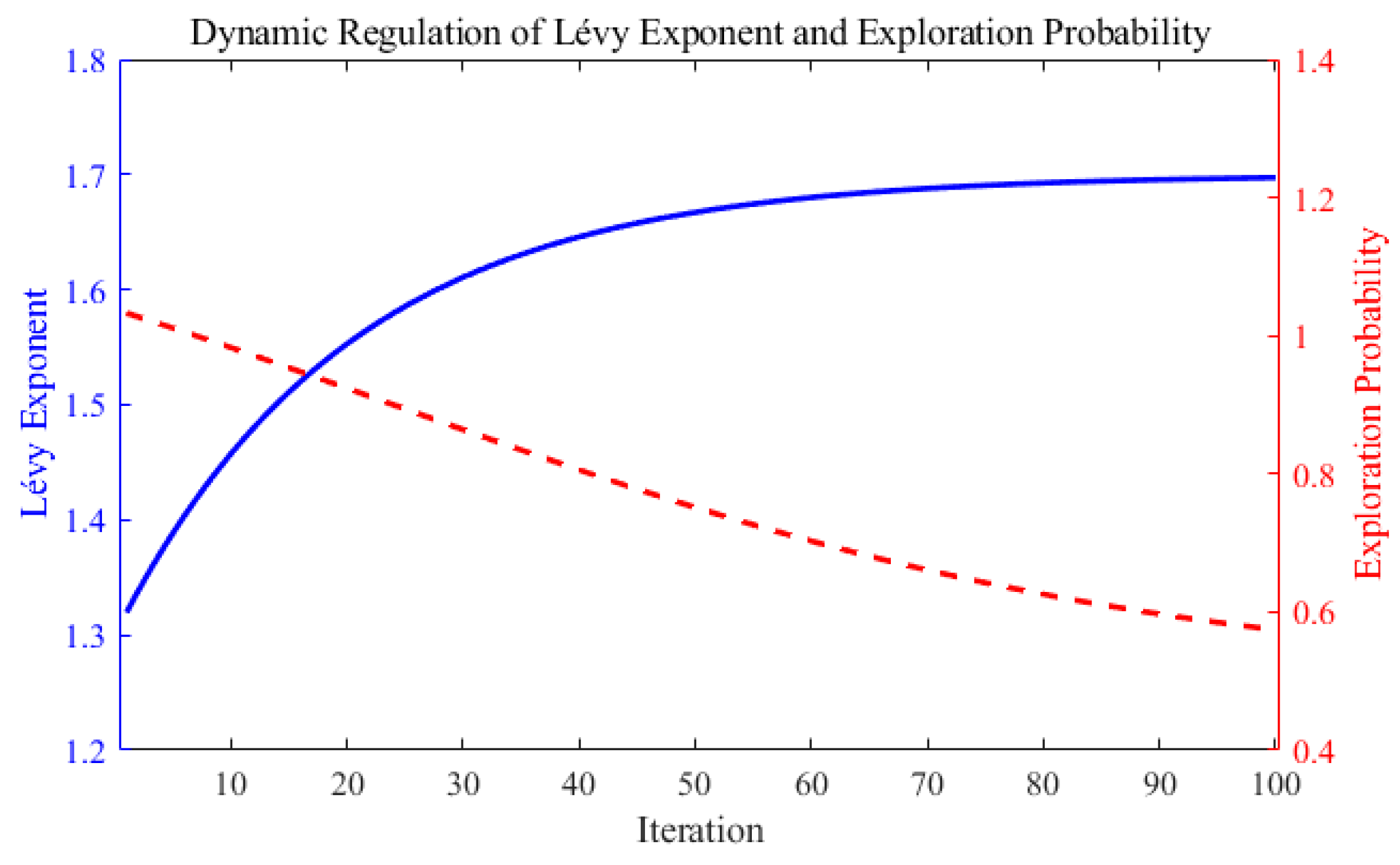
2.3.2. Dynamic Lévy Flight Mechanism
- When approaches 1.7, the generated step sizes become more stable, resulting in smaller solution updates. This is more favorable for fine-grained local search and exploitation, making it suitable for the convergence phase of the optimization algorithm.
- When decreases to around 1.3, the step size exhibits more pronounced non-Gaussian jumps, which helps individuals escape local optima in the early stages of the search process.
2.3.3. Improved Whale Fall Step Strategy
2.3.4. Coordinated Regulation Advantages of Exploration Strategy and Lévy Index
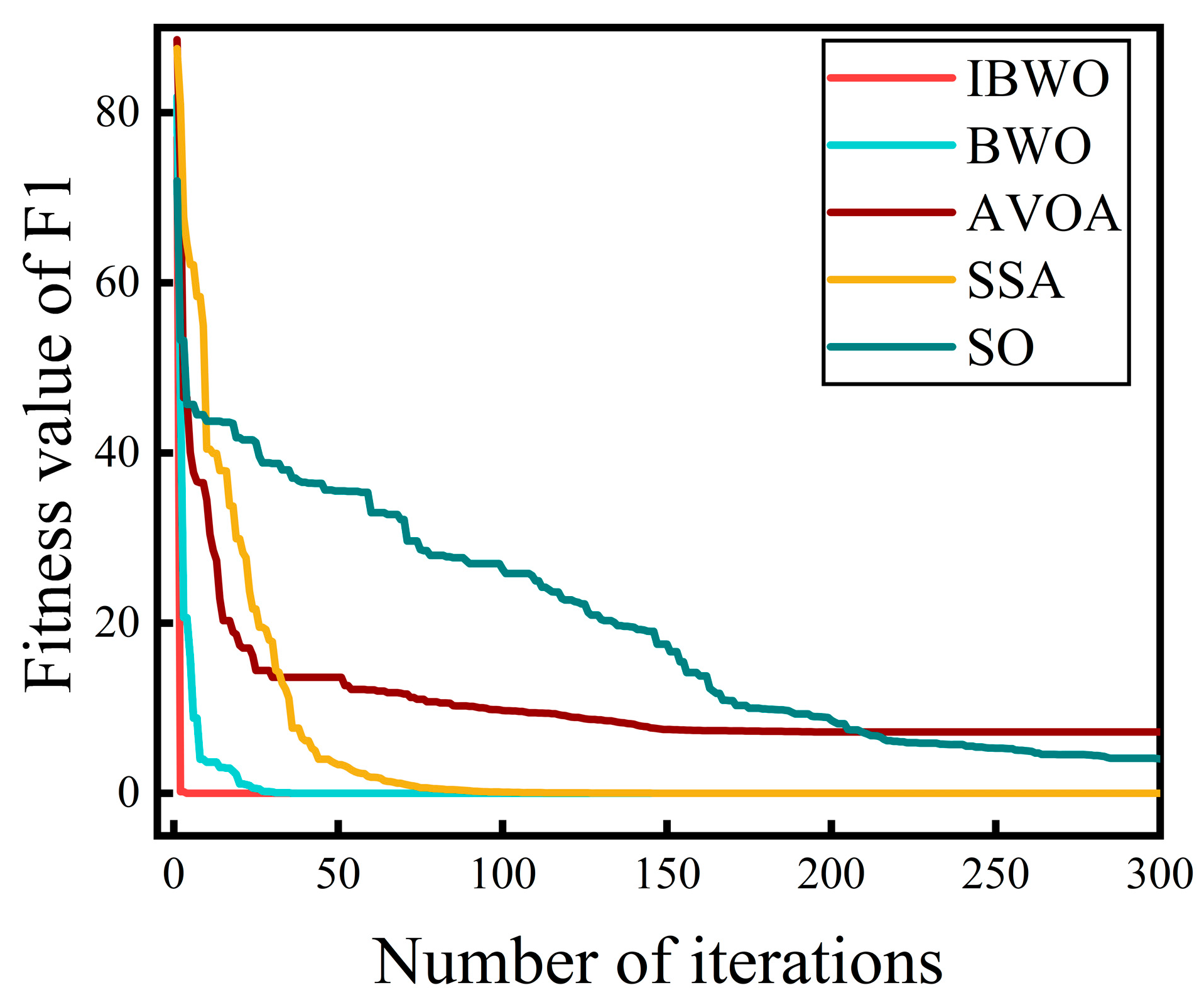
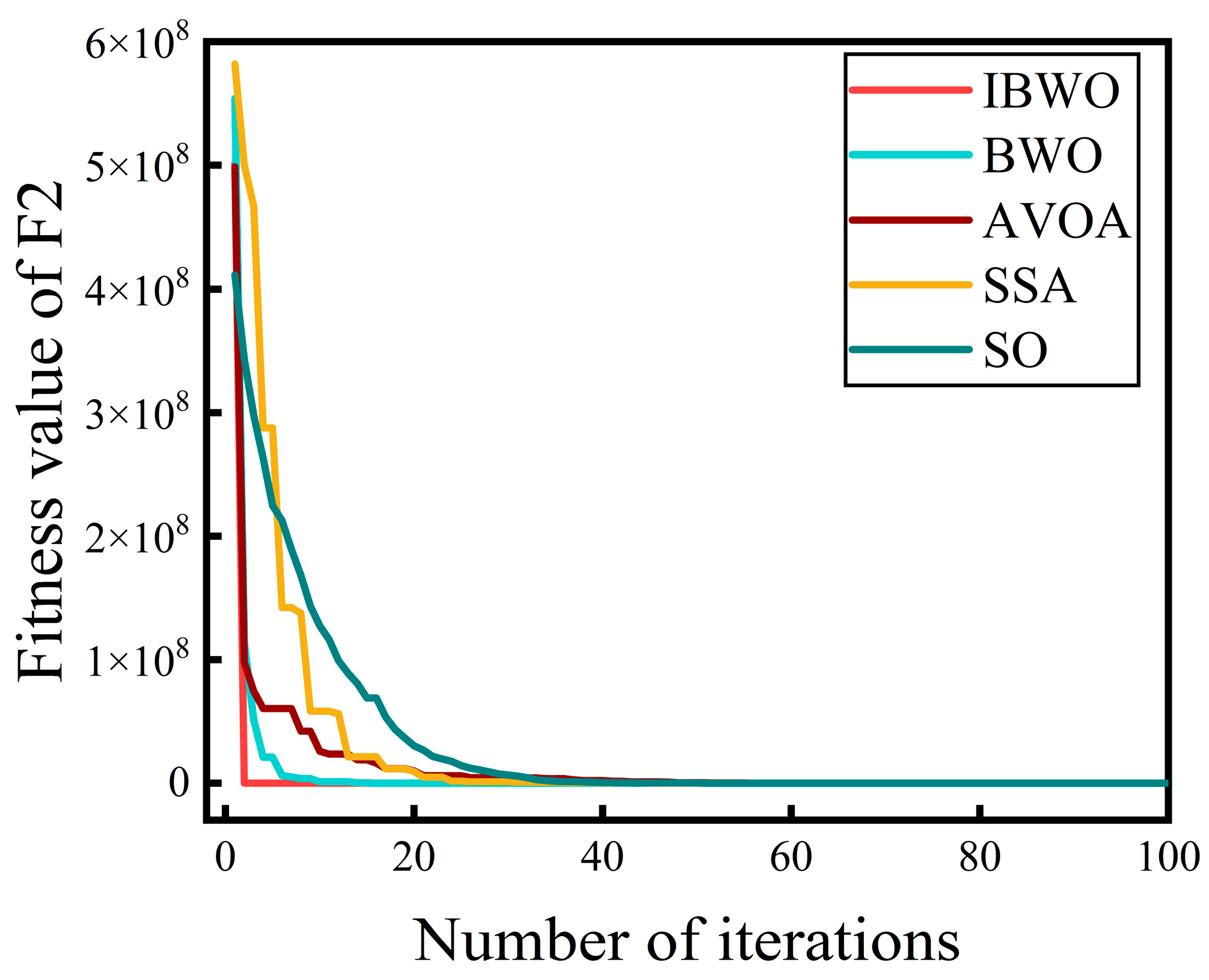
2.3.5. Testing the Improved IBWO Algorithm

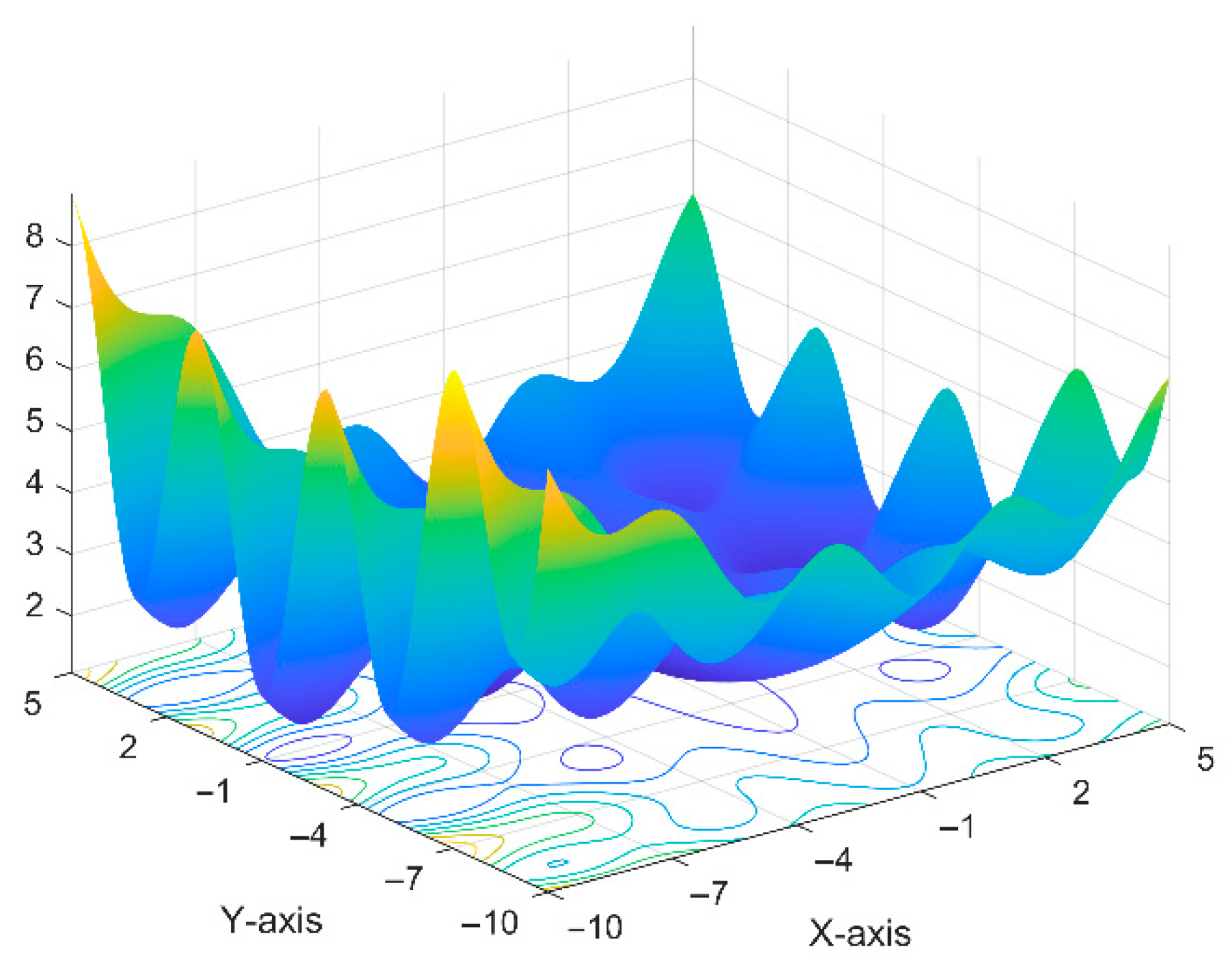
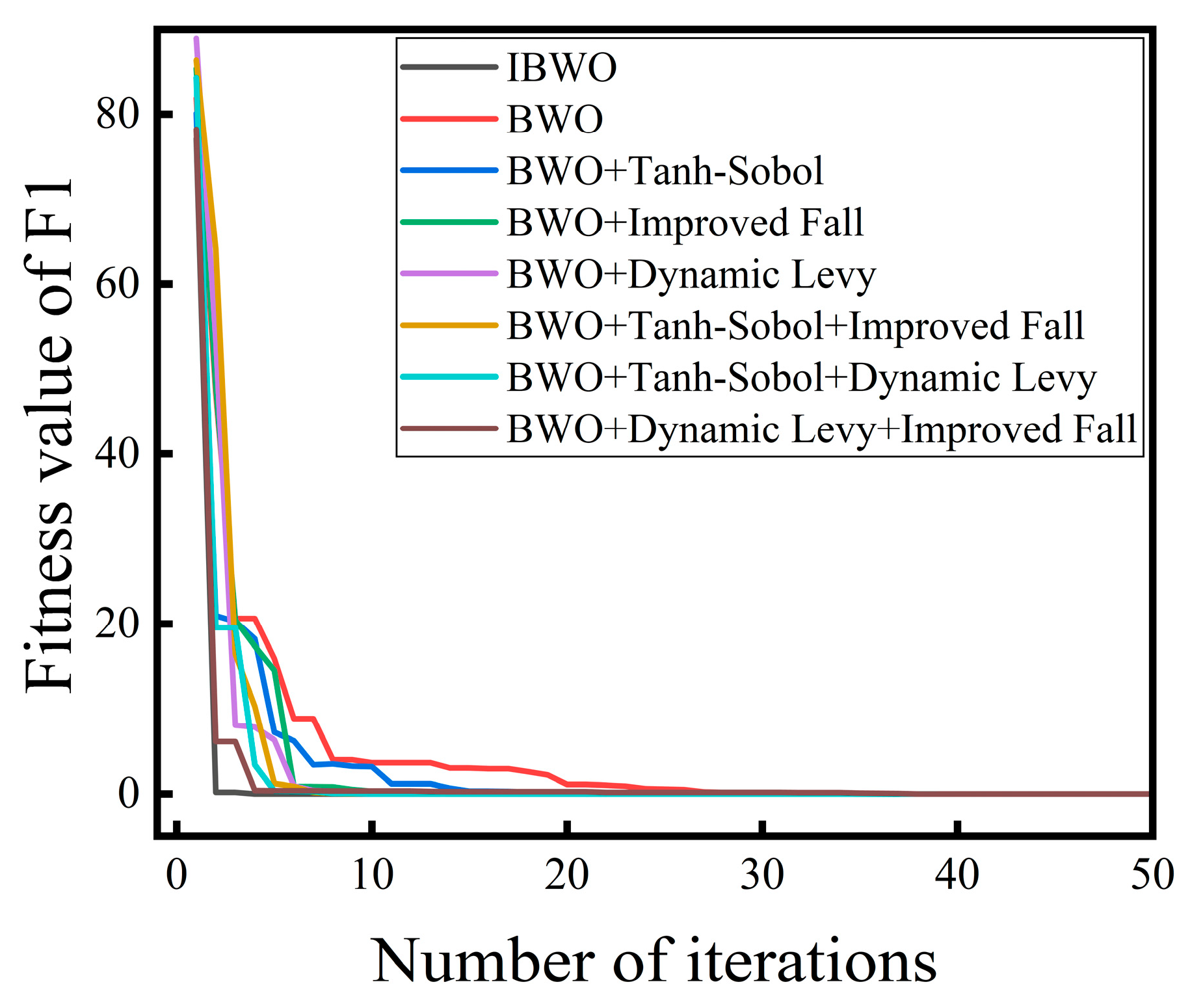
2.3.6. Ablation Study of IBWO Algorithm
2.4. Dilated BiGRU
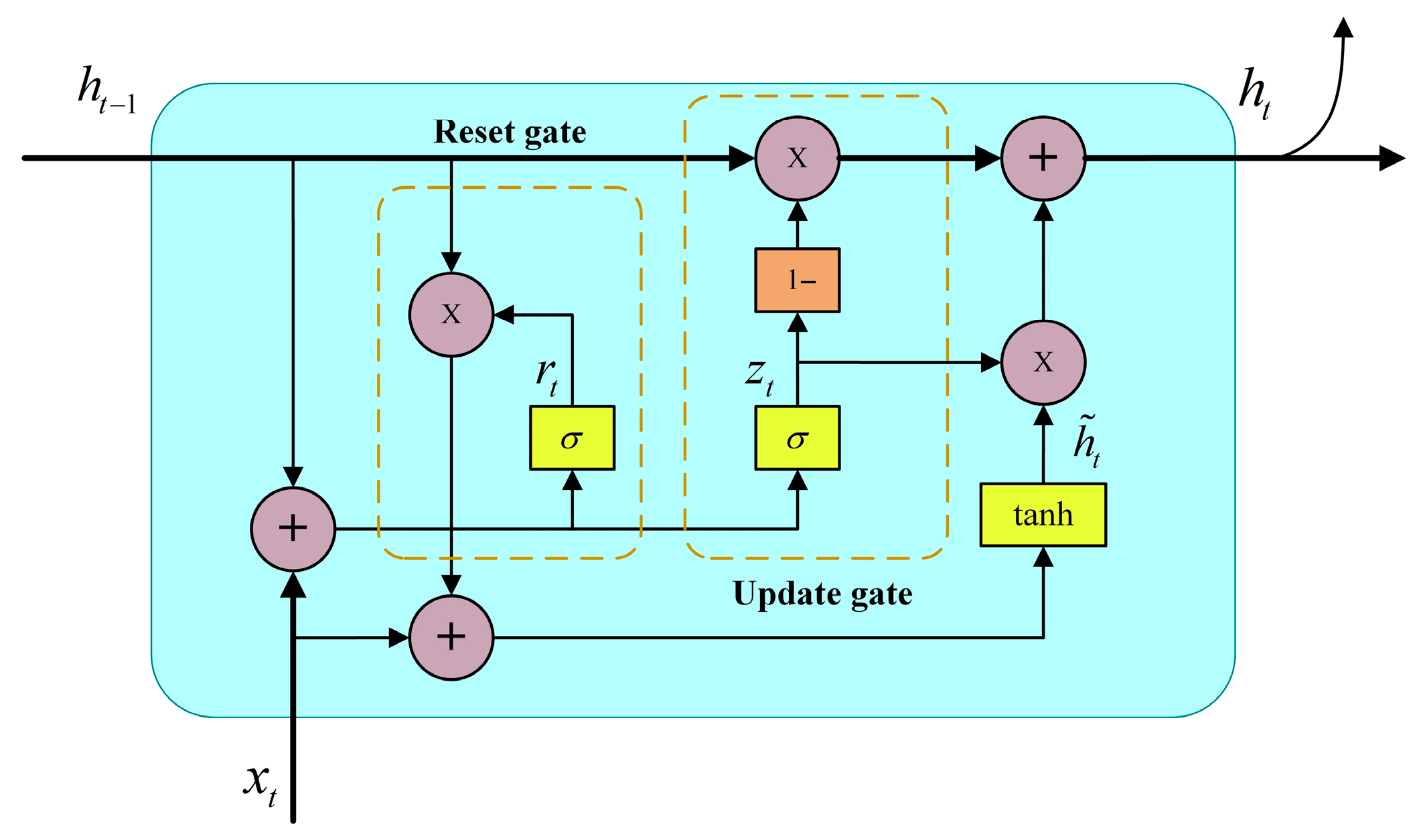
2.4.1. GRU
- Computation of the Update Gate: The update gate determines how much of the previous hidden state should be retained in the current time step. Its output ranges between 0 and 1; a larger value indicates more past information is preserved, while a smaller value suggests greater reliance on the current input. The computation is formulated as follows:where and are the weight matrix and bias vector, respectively; is the hidden state from the previous time step; is the current input; and denotes the Sigmoid activation function.
- Computation of the Reset Gate: The reset gate determines the extent to which the previous hidden state should be forgotten. When the reset gate outputs a value close to 0, the network tends to “forget” the information from the previous time step and relies solely on the current input. Conversely, an output close to 1 leads to more retention of the previous hidden state. The formula is as follows:where and are the weight matrix and bias vector of the reset gate.
- Computation of the Candidate Hidden State: The GRU uses the reset gate to control the extent to which the previous hidden state contributes to the current candidate hidden state. The candidate hidden state is computed aswhere represents the element-wise combination of the previous hidden state and the reset gate , which controls the degree of influence from past information. and denote the parameter matrix and bias vector, respectively.
- Update of the Hidden State: The update gate is used to compute the current hidden state as follows:where represents the preserved historical information, while corresponds to the newly introduced information. This formula determines that the current hidden state retains part of the previous time step’s information while incorporating new information derived from the current input.
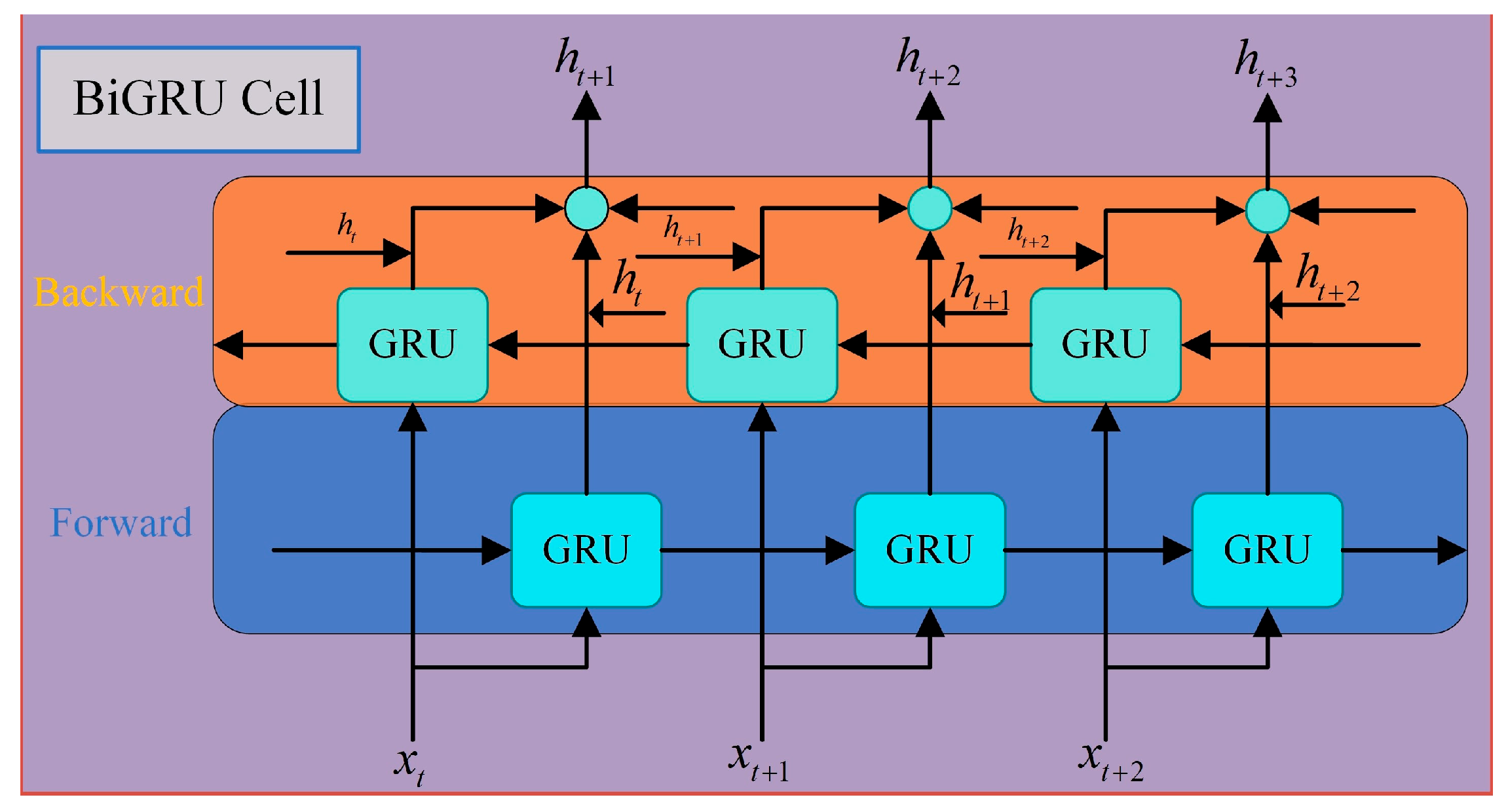
2.4.2. BiGRU
- The forward GRU processes the input sequence , producing the forward hidden state sequence .
- The backward GRU processes the reversed sequence , yielding the backward hidden state sequence .
2.4.3. Dilated-BiGRU
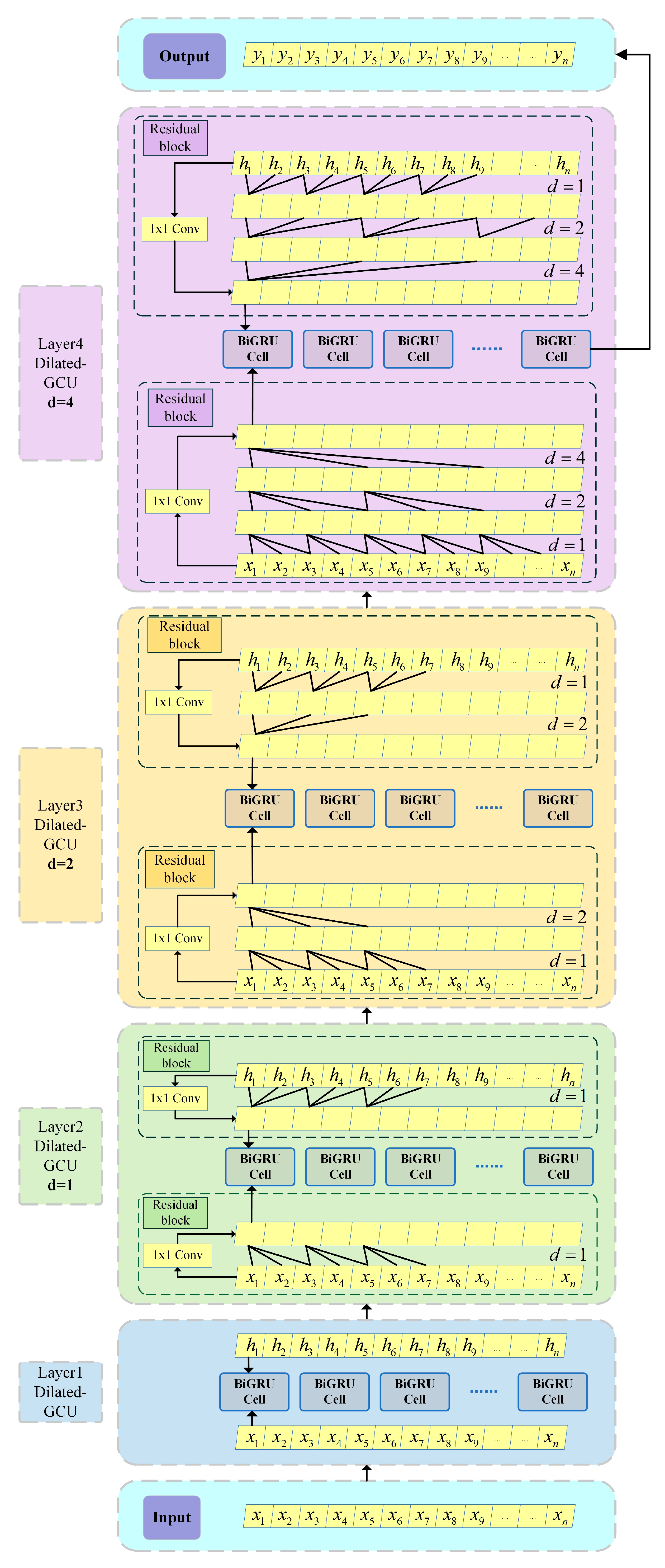
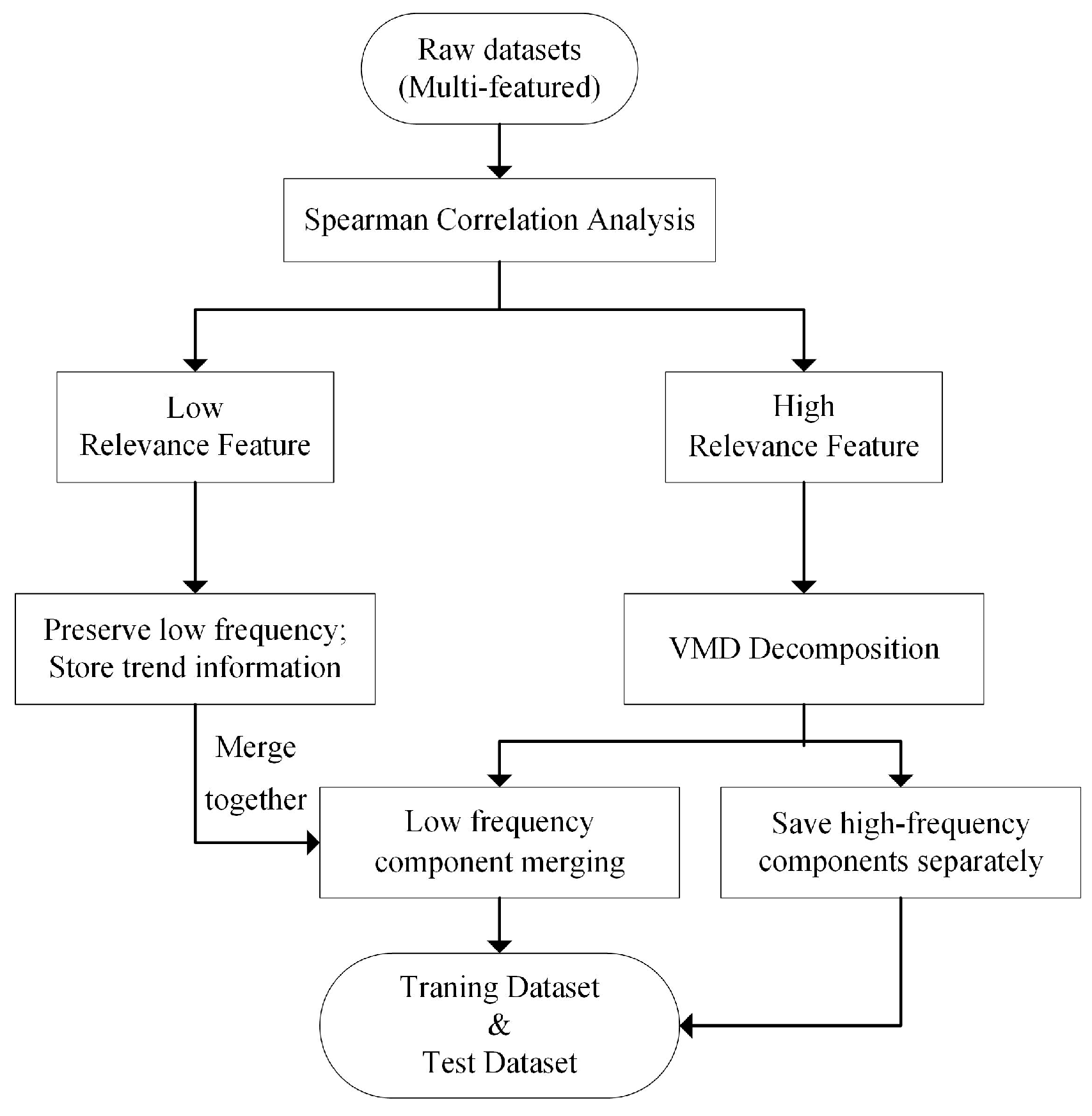
2.5. Model Construction: Steps and Architecture
- Perform Spearman correlation analysis on the high-dimensional raw dataset to evaluate the correlation strength between each feature and the load target.
- For features with low correlation, low-frequency trend components are retained to enhance model training and improve forecasting accuracy.
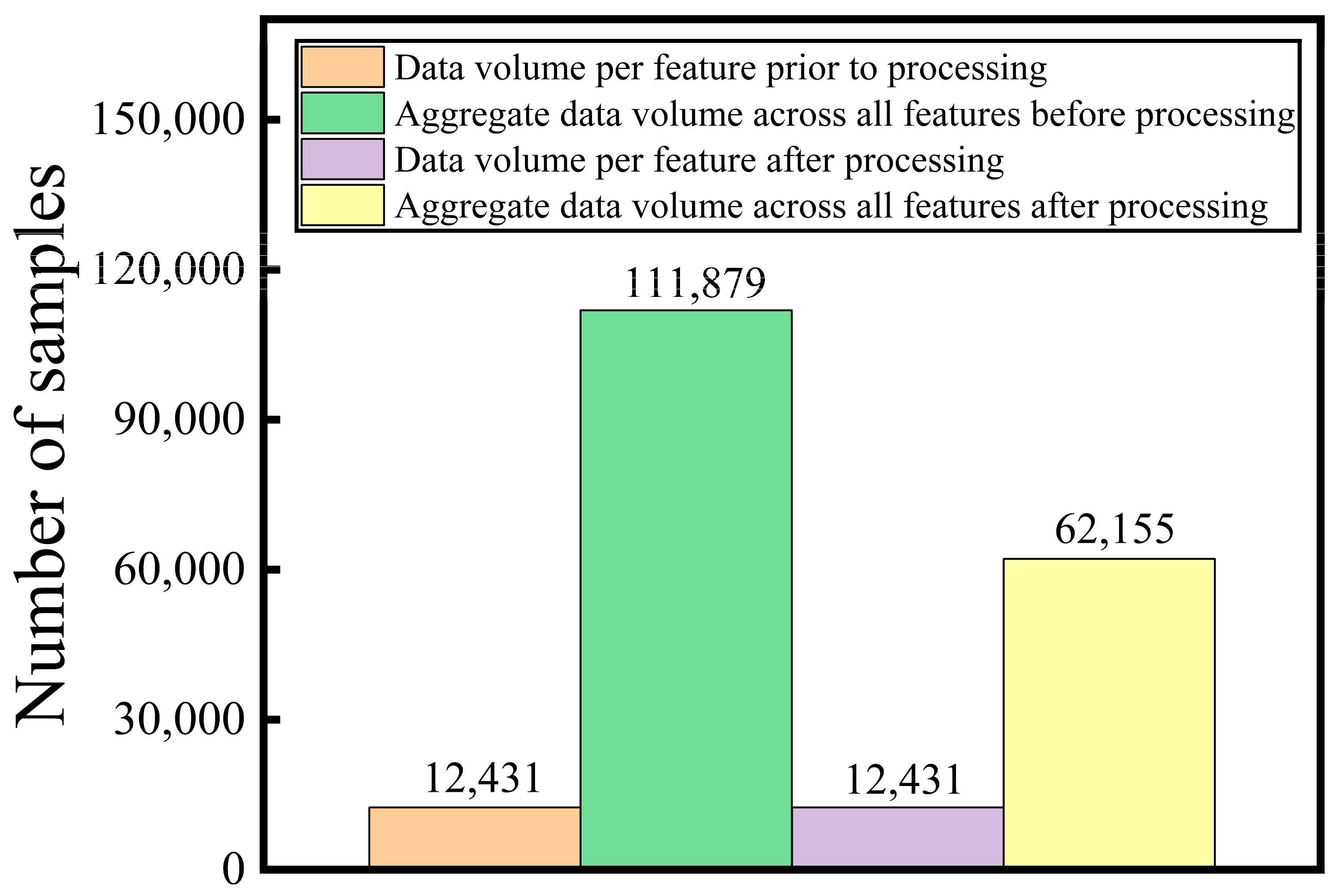
- For features with high correlation, secondary modal decomposition is applied to generate refined training data. After VMD, the low-frequency components are fused with the outputs from step 2 to form the low-frequency portion of the new dataset; the high-frequency components are stored separately to serve as the high-frequency data of the new dataset.
- The data processed through feature engineering is split in a 70%:30% ratio to form the training set and testing set for the model.
- The Beluga Whale Optimization algorithm is enhanced as described in the earlier Section 2.3, resulting in the improved version named IBWO.
- The number of hidden units, batch size, and learning rate are selected as the optimization targets.
- The optimal solution set obtained through IBWO is fed into the forecasting model to complete hyperparameter optimization, thereby improving predictive accuracy.
- The forecasting model is constructed based on the method introduced in the earlier Section 2.4.
- The optimal hyperparameter set obtained in Part (b) is applied to the appropriate positions in the model.
- The model is trained using the training set from Part (a).
- The model’s prediction performance is evaluated using the testing set from Part (a).
3. Results
3.1. Performance Evaluation Metrics
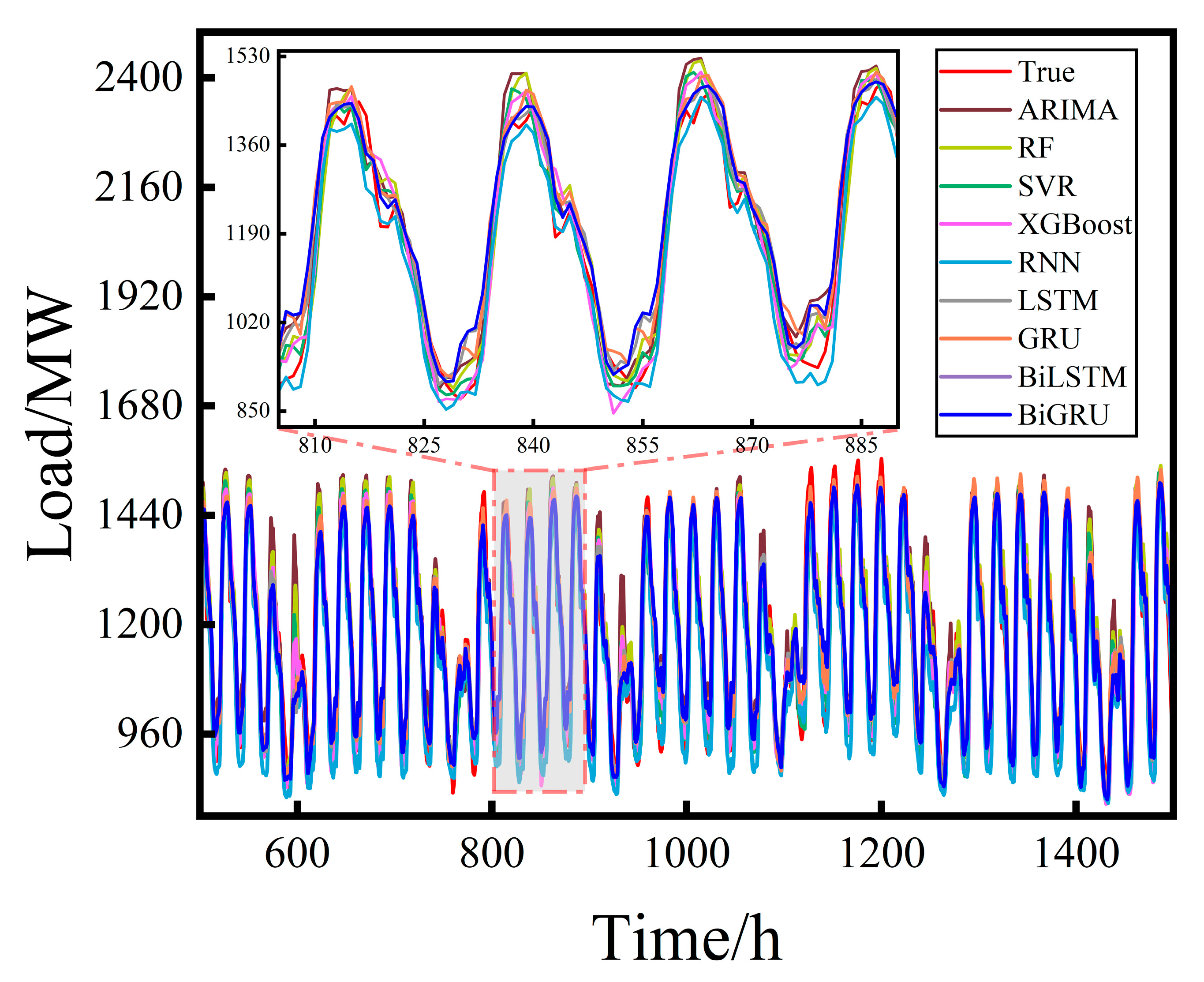
3.2. Baseline Prediction Models
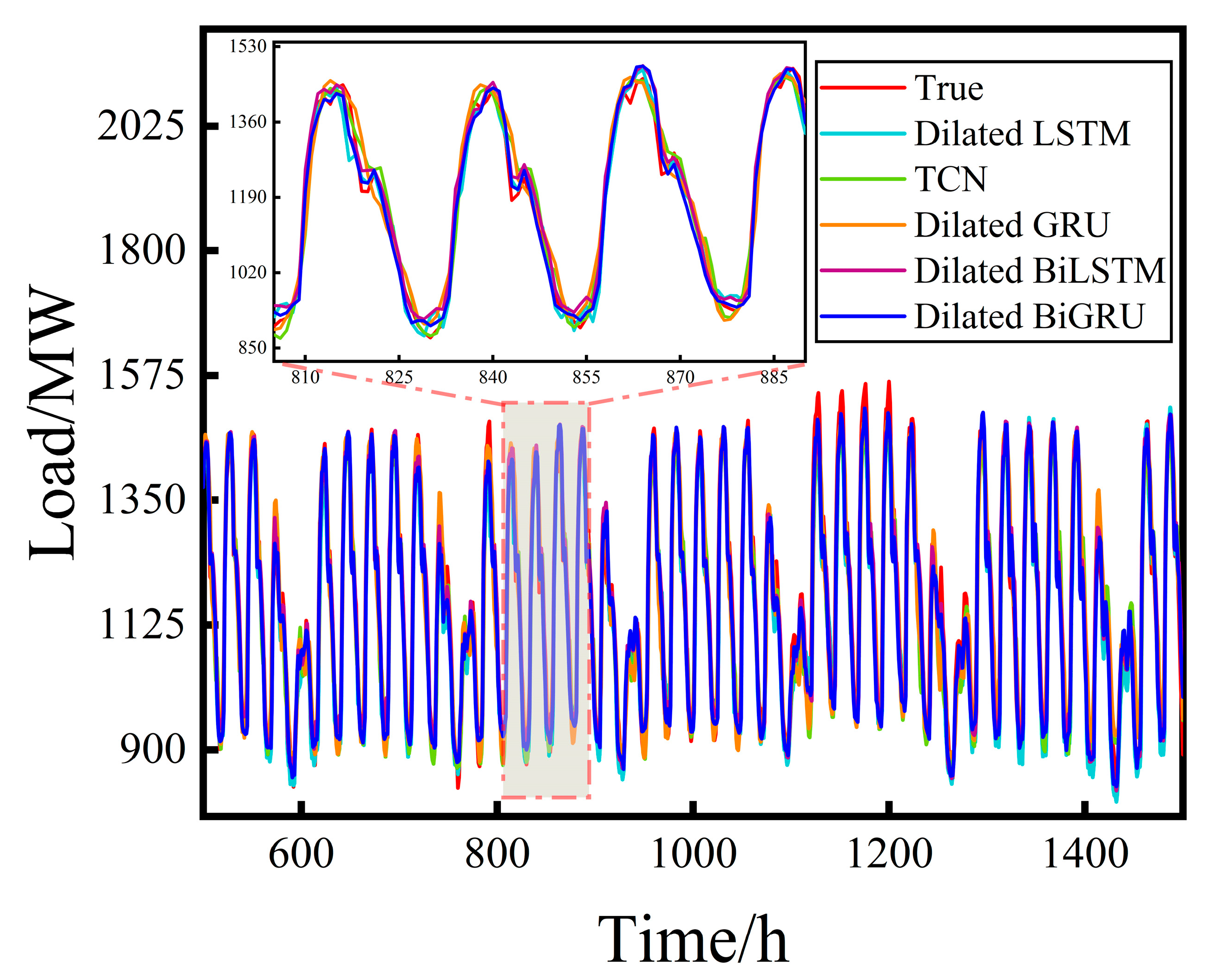
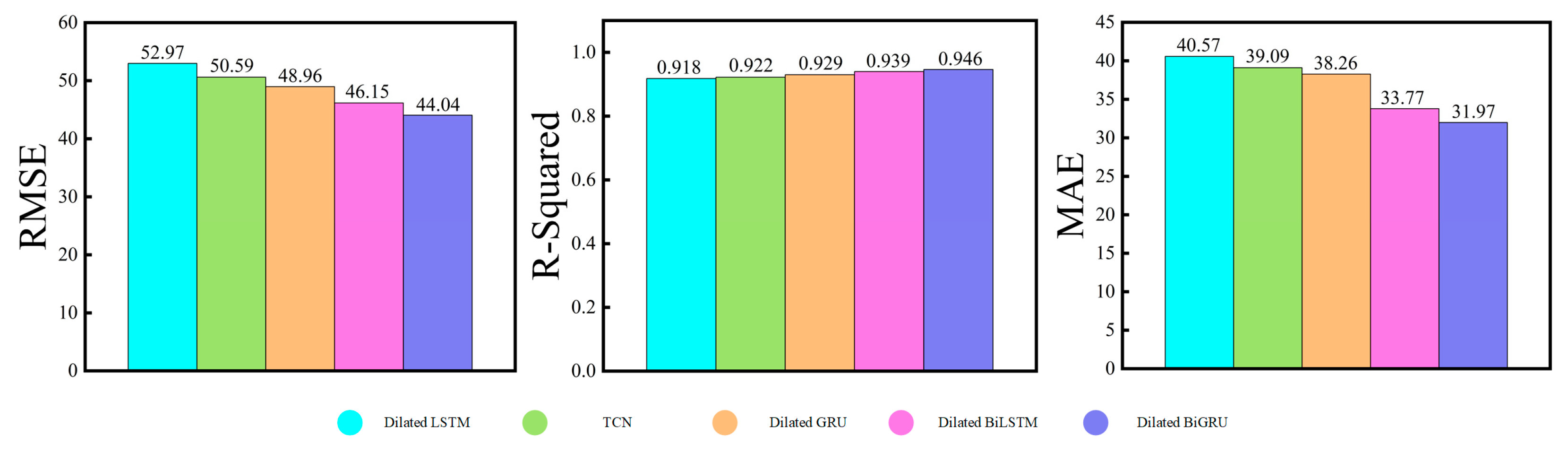
3.3. Validation Experiments for Dilated BiGRU
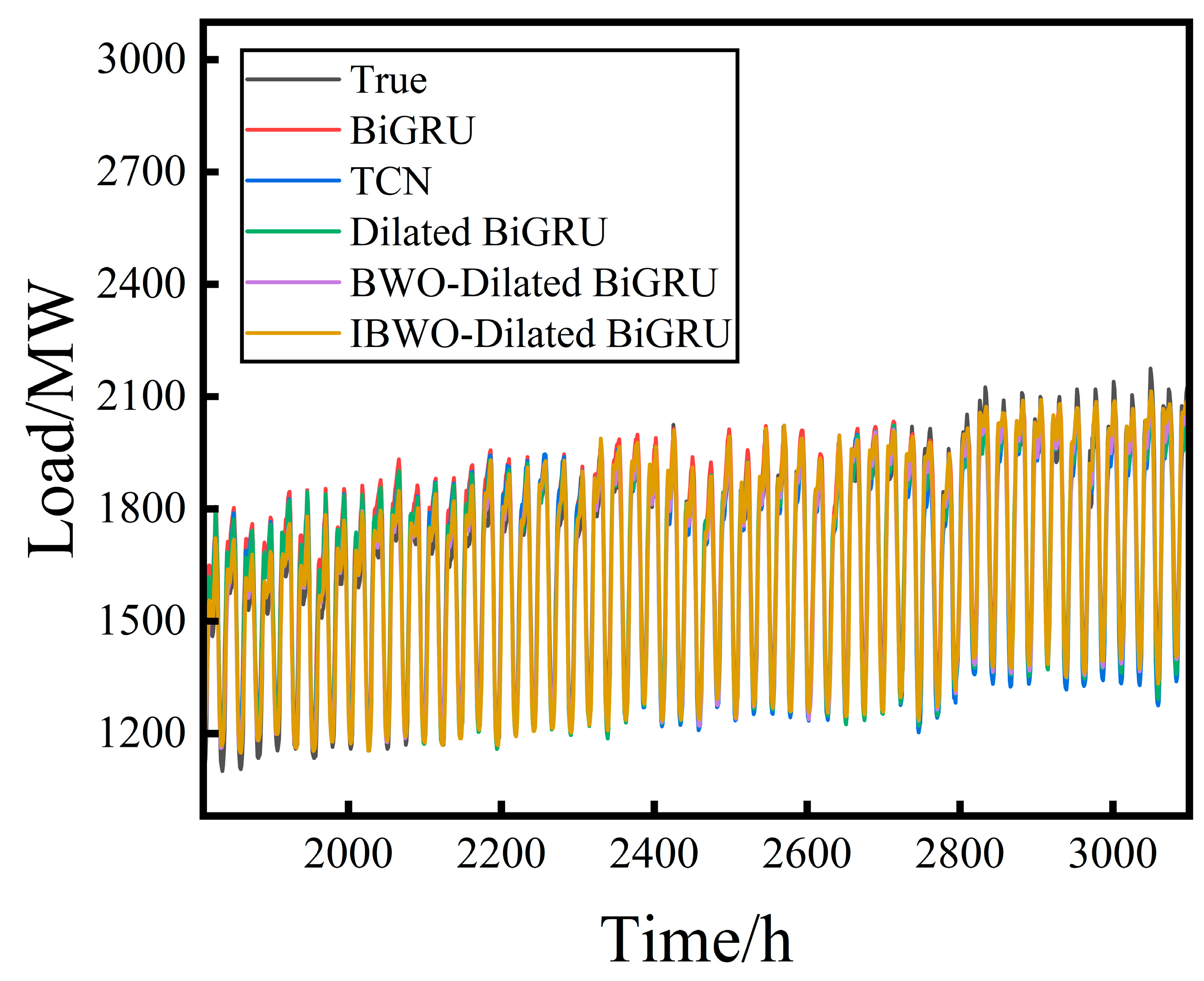
- Dilated BiGRU exhibits the best performance: Its fitting curve closely matches the actual values, particularly in regions with sharp load fluctuations. It responds more smoothly and accurately, demonstrating superior trend-tracking capability and forecasting precision. Compared with it, Dilated-BiLSTM shows larger deviations in detailed regions and lacks stability. Dilated-GRU and Dilated-LSTM suffer from delayed responses and amplified errors during periods of abrupt change. Although the TCN model performs well in tracking the global trend, it lags behind Dilated BiGRU in terms of responsiveness and fitting accuracy at local turning points.
- The Dilated module enhances overall model fitting performance: As shown in the figure, all models embedded with the Dilated mechanism produce smoother forecasting curves in areas of significant load variation. These curves are closer to the actual values compared to their original counterparts, revealing stronger fitting characteristics. This validates the advantages of the Dilated module in capturing long-term dependencies and mitigating short-term disturbances.
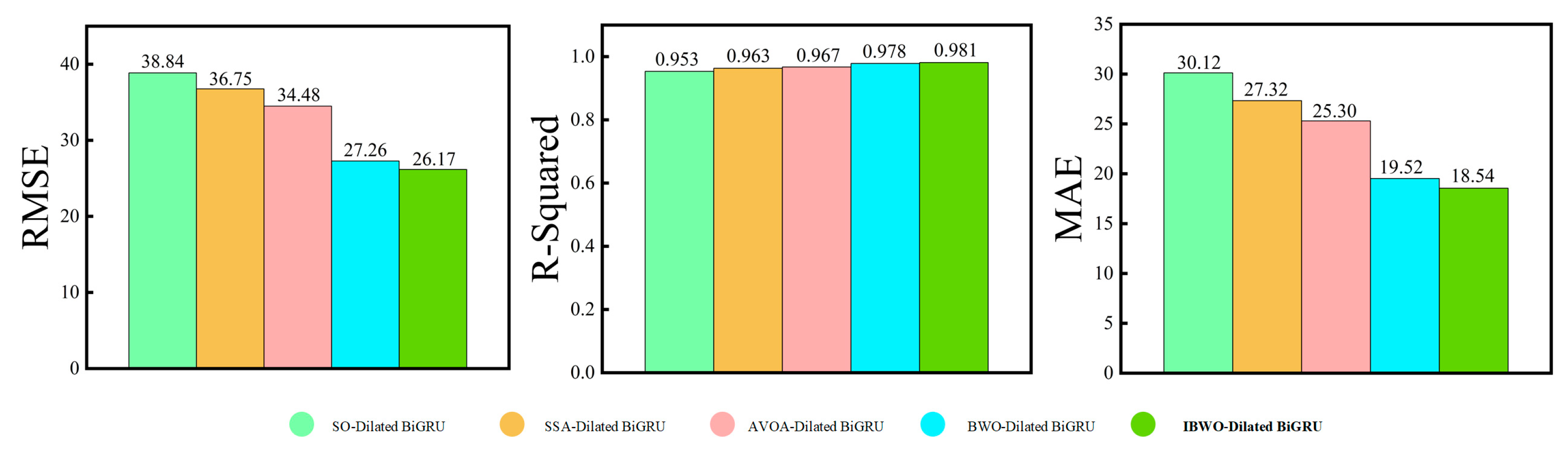
3.4. Validation Experiments for Optimization Algorithm Performance
3.5. Robustness Experiment
3.6. Comparative Analysis of Prediction Accuracy and Resource Usage
4. Conclusions
- Valuable predictive information may reside in data segments previously discarded as redundant. This study utilizes time–frequency analysis methods such as VMD and CEEMDAN to explore the latent structure within such data, thereby preserving informative components and enriching the dataset. This approach significantly improves prediction accuracy.
- BiGRU exhibits clear advantages in modeling local dynamics in time series. Building upon this, the incorporation of a dilated module effectively expands the receptive field without increasing model complexity. This enhances the model’s ability to capture long-range temporal relationships and improves overall prediction performance.
- The proposed IBWO algorithm introduces multi-level enhancements to the original BWO framework by incorporating tanh-Sobol initialization to improve population diversity, dynamic Lévy flight to strengthen the ability to escape local optima, and a whale-fall-based step-size strategy guided by exploration probability to balance global exploration and local exploitation. The algorithm demonstrates excellent optimization performance and strong application potential on standard benchmark functions.
- By integrating feature engineering, model structure refinement, and parameter adjustment strategies, the IBWO-Dilated BiGRU model achieved an RMSE of 26.1706, an R2 of 0.9812, and an MAE of 18.5462 in load forecasting experiments—representing improvements of 26.1455, 0.068, and 21.3323, respectively, over the baseline BiGRU model. These results highlight the effectiveness of the proposed method in enhancing both prediction accuracy and stability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rahmani-Sane, G.; Azad, S.; Ameli, M.T.; Haghani, S. The Applications of Artificial Intelligence and Digital Twin in Power Systems: An In-Depth Review. IEEE Access 2025, 13, 108573–108608. [Google Scholar] [CrossRef]
- Akhtar, S.; Shahzad, S.; Zaheer, A.; Ullah, H.S.; Kilic, H.; Gono, R.; Jasiński, M.; Leonowicz, Z. Short-term load forecasting models: A review of challenges, progress, and the road ahead. Energies 2023, 16, 4060. [Google Scholar] [CrossRef]
- Andriopoulos, N.; Magklaras, A.; Birbas, A.; Papalexopoulos, A.; Valouxis, C.; Daskalaki, S.; Birbas, M.; Housos, E.; Papaioannou, G.P. Short term electric load forecasting based on data transformation and statistical machine learning. Appl. Sci. 2020, 11, 158. [Google Scholar] [CrossRef]
- Singh, A.K.; Khatoon, S.; Muazzam, M.; Chaturvedi, D.K. Load forecasting techniques and methodologies: A review. In Proceedings of the 2012 2nd International Conference on Power, Control and Embedded Systems, Allahabad, India, 17–19 December 2012; pp. 1–10. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Dudek, G. Short-term load forecasting using random forests. In Proceedings of the Intelligent Systems’ 2014: Proceedings of the 7th IEEE International Conference Intelligent Systems IS’2014, Warsaw, Poland, 24–26 September 2014; Volume 2: Tools, Architectures, Systems, Applications. pp. 821–828. [Google Scholar] [CrossRef]
- Magalhães, B.; Bento, P.; Pombo, J.; Calado, M.; Mariano, S. Short-Term Load Forecasting Based on Optimized Random Forest and Optimal Feature Selection. Energies 2024, 17, 1926. [Google Scholar] [CrossRef]
- Fan, G.-F.; Peng, L.-L.; Hong, W.-C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Chen, B.; Lin, R.; Zou, H. A short term load periodic prediction model based on GBDT. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 1402–1406. [Google Scholar] [CrossRef]
- Abbasi, R.A.; Javaid, N.; Ghuman, M.N.J.; Khan, Z.A.; Ur Rehman, S.; Amanullah. Short term load forecasting using XGBoost. In Proceedings of the Web, Artificial Intelligence and Network Applications: Proceedings of the Workshops of the 33rd International Conference on Advanced Information Networking and Applications (WAINA-2019) 33; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1120–1131. [Google Scholar] [CrossRef]
- Azeem, A.; Ismail, I.; Jameel, S.M.; Harindran, V.R. Electrical load forecasting models for different generation modalities: A review. IEEE Access 2021, 9, 142239–142263. [Google Scholar] [CrossRef]
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical load forecasting models: A critical systematic review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Fernández, S.; Schmidhuber, J. Bidirectional LSTM networks for improved phoneme classification and recognition. In Proceedings of the International Conference on Artificial Neural Networks, Kaunas, Lithuania, 9–12 September 2005; pp. 799–804. [Google Scholar] [CrossRef]
- Bohara, B.; Fernandez, R.I.; Gollapudi, V.; Li, X. Short-term aggregated residential load forecasting using BiLSTM and CNN-BiLSTM. In Proceedings of the 2022 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT), Sakheer, Bahrain, 20–21 November 2022; pp. 37–43. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, G.; Huang, X.; Huang, S.; Wu, M. Probabilistic load forecasting based on quantile regression parallel CNN and BiGRU networks. Appl. Intell. 2024, 54, 7439–7460. [Google Scholar] [CrossRef]
- Ageng, D.; Huang, C.-Y.; Cheng, R.-G. A short-term household load forecasting framework using LSTM and data preparation. IEEE Access 2021, 9, 167911–167919. [Google Scholar] [CrossRef]
- Sun, Q.; Cai, H. Short-term power load prediction based on VMD-SG-LSTM. IEEE Access 2022, 10, 102396–102405. [Google Scholar] [CrossRef]
- Zang, H.; Xu, R.; Cheng, L.; Ding, T.; Liu, L.; Wei, Z.; Sun, G. Residential load forecasting based on LSTM fusing self-attention mechanism with pooling. Energy 2021, 229, 120682. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Qazi, A.B.; Khan, I.; Usman, M.; Khan, F.A.; Wadud, Z. A hybrid approach for energy consumption forecasting with a new feature engineering and optimization framework in smart grid. IEEE Access 2020, 8, 96210–96226. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
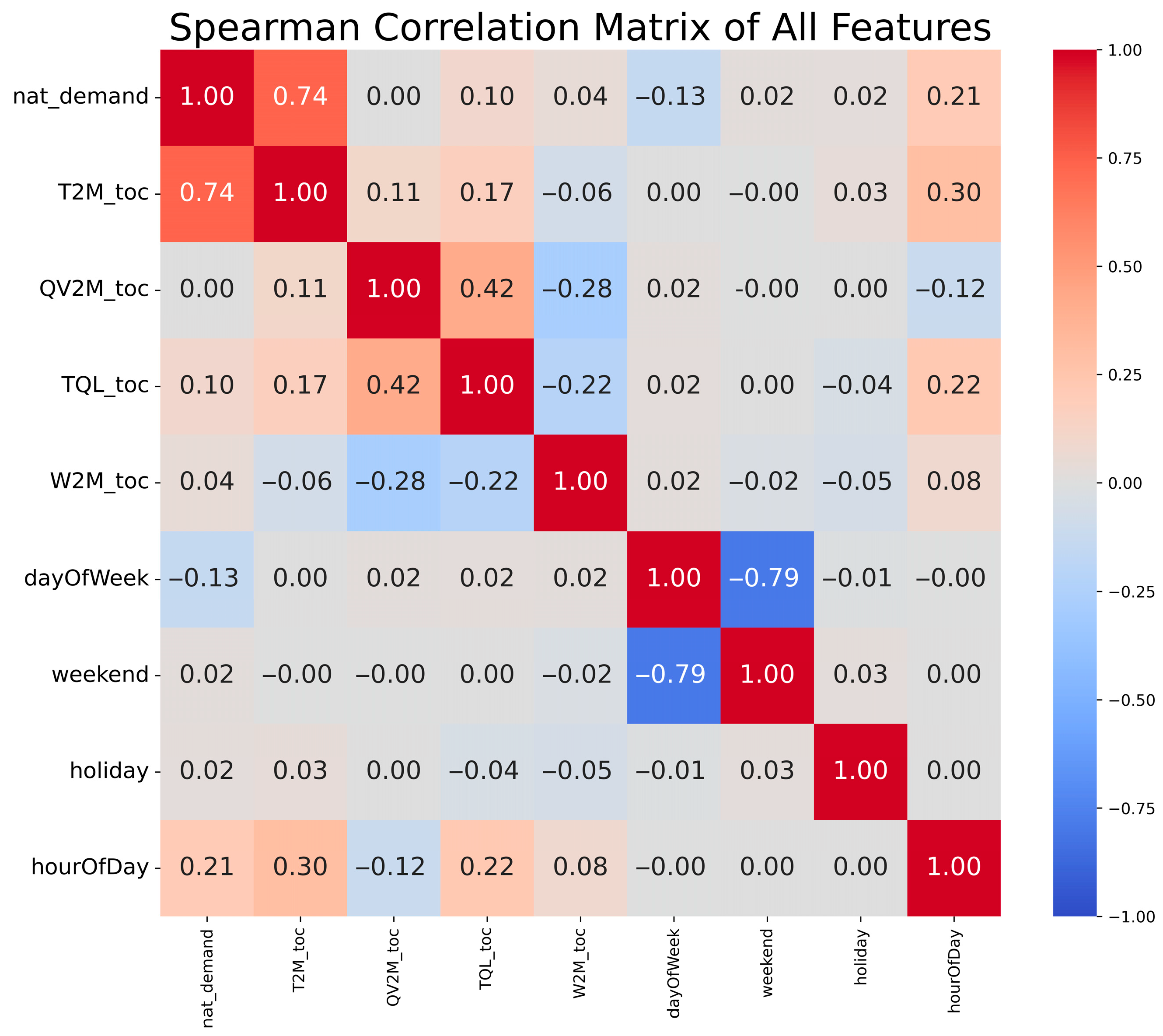









| Column Name | Description |
|---|---|
| nat_demand | National electricity load |
| T2M_toc | Temperature at 2 m in Tocumen, Panama City |
| QV2M_toc | Relative humidity at 2 m in Tocumen, Panama City |
| TQL_toc | Liquid precipitation in Tocumen, Panama City |
| W2M_toc | Wind Speed at 2 m in Tocumen, Panama City |
| dayOfWeek | Day of the week, starting on Saturdays |
| weekend | Weekend binary indicator |
| holiday | Holiday binary indicator |
| hourOfDay | Hour of the day |
| Column Name | Description | Sample Count |
|---|---|---|
| nat_demand | National electricity load | 12,431 |
| nat_high | High-frequency component of nat_demand extracted via VMD | 12,431 |
| T2M_high | High-frequency component of temperature (T2M_toc) extracted via VMD | 12,431 |
| hour_high | High-frequency component of time (hourOfDay) extracted via VMD | 12,431 |
| low | Combined result of all low-frequency components | 12,431 |
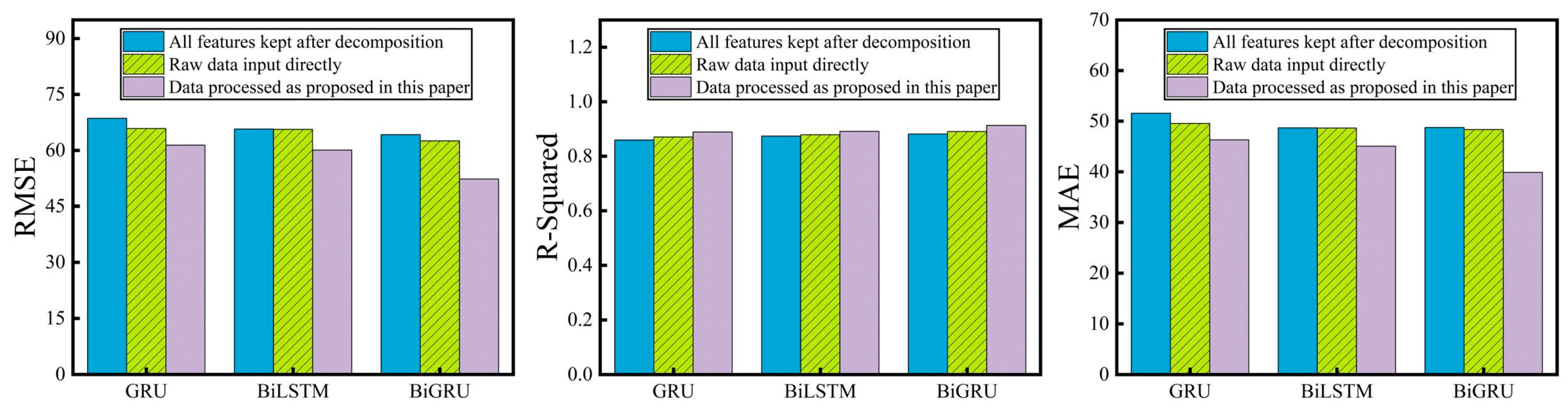
| All Features Kept After Decomposition | Raw Data Input Directly | Data Processed as Proposed in This Paper | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE |
| GRU | 68.5934 | 0.8597 | 51.5732 | 65.8601 | 0.8705 | 49.5442 | 61.3893 | 0.8888 | 46.3095 |
| BiLSTM | 65.7128 | 0.8738 | 48.6737 | 65.6279 | 0.8786 | 48.6312 | 60.0619 | 0.8912 | 45.0527 |
| BiGRU | 64.2005 | 0.8817 | 48.7456 | 62.5517 | 0.8904 | 48.3497 | 52.3161 | 0.9132 | 39.8785 |
| IBWO | BWO | AVOA | SSA | SO | |
|---|---|---|---|---|---|
| Optimum value | 0.0000 | 0.0000 | 7.2146 | 0.0007 | 4.0316 |
| Average value | 0.2582 | 0.8342 | 10.6977 | 4.7188 | 19.2316 |
| Standard deviation | 4.4499 | 5.8163 | 8.3188 | 13.5542 | 13.7100 |
| IBWO | BWO | AVOA | SSA | SO | |
|---|---|---|---|---|---|
| Optimum value | 4.64 × 10−24 | 1.18 × 10−5 | 0.6306 | 3.71 × 10−2 | 4.4151 |
| Average value | 1.67 × 106 | 2.61 × 106 | 4.28 × 106 | 9.77 × 106 | 1.07 × 107 |
| Standard deviation | 2.89 × 107 | 3.27 × 107 | 3.06 × 107 | 5.83 × 107 | 4.71 × 107 |
| IBWO | Original BWO | BWO+ Tanh-Sobol | BWO+ Improved Fall | BWO+ Dynamic Levy | BWO+ Tanh-Sobol+ Improved Fall | BWO+ Tanh-Sobol+ Dynamic Levy | BWO+ Dynamic Levy+ Improved Fall | |
|---|---|---|---|---|---|---|---|---|
| Optimum value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Average value | 0.2582 | 0.8342 | 0.5758 | 0.6298 | 0.5550 | 0.5982 | 0.4264 | 0.3301 |
| Standard deviation | 4.4499 | 5.8163 | 5.0560 | 5.8947 | 6.0157 | 6.2886 | 5.1161 | 4.5394 |
| Model | RMSE | R2 | MAE |
|---|---|---|---|
| ARIMA | 77.1089 | 0.8272 | 59.6386 |
| RF | 74.0867 | 0.8453 | 57.1238 |
| SVR | 71.1453 | 0.8590 | 52.6656 |
| RNN | 69.7217 | 0.8613 | 54.5778 |
| XGBoost | 69.3699 | 0.8636 | 52.9690 |
| LSTM | 63.2030 | 0.8748 | 46.4893 |
| GRU | 61.3893 | 0.8888 | 46.3095 |
| BiLSTM | 60.0619 | 0.8912 | 45.0527 |
| BiGRU | 52.3161 | 0.9132 | 39.8785 |
| Model | RMSE | R2 | MAE |
|---|---|---|---|
| Dilated LSTM | 52.9719 | 0.9180 | 40.5714 |
| TCN | 50.5941 | 0.9222 | 39.0946 |
| Dilated GRU | 48.9688 | 0.9297 | 38.2667 |
| Dilated BiLSTM | 46.1517 | 0.9399 | 33.7720 |
| Dilated BiGRU | 44.0456 | 0.9464 | 31.9781 |
| Model | RMSE | R2 | MAE |
|---|---|---|---|
| SO-Dilated BiGRU | 38.8469 | 0.9535 | 30.1231 |
| SSA-Dilated BiGRU | 36.7520 | 0.9632 | 27.3250 |
| AVOA-Dilated BiGRU | 34.4826 | 0.9671 | 25.3018 |
| BWO-Dilated BiGRU | 27.2682 | 0.9784 | 19.5211 |
| IBWO-Dilated BiGRU | 26.1706 | 0.9812 | 18.5462 |
| Model | RMSE | R2 | MAE |
|---|---|---|---|
| BiGRU | 82.5158 | 0.8954 | 68.2491 |
| TCN | 76.0564 | 0.9035 | 64.4329 |
| Dilated BiGRU | 60.8832 | 0.9424 | 50.0802 |
| BWO-Dilated BiGRU | 46.3615 | 0.9661 | 36.8688 |
| IBWO-Dilated BiGRU | 38.8091 | 0.9783 | 31.0496 |
| Model | RMSE | R2 | MAE | Time | Memory Usage |
|---|---|---|---|---|---|
| ARIMA | 77.1089 | 0.8272 | 59.6386 | 314.2 | 207.1 |
| RF | 74.0867 | 0.8453 | 57.1238 | 377.1 | 214.5 |
| SVR | 71.1453 | 0.8590 | 52.6656 | 410.7 | 226.8 |
| RNN | 69.7217 | 0.8613 | 54.5778 | 450.6 | 230.4 |
| XGBoost | 69.3699 | 0.8636 | 52.9690 | 540.3 | 291.7 |
| LSTM | 63.2030 | 0.8748 | 46.4893 | 513.6 | 240.1 |
| GRU | 61.3893 | 0.8888 | 46.3095 | 498.7 | 233.8 |
| BiLSTM | 60.0619 | 0.8912 | 45.0527 | 554.9 | 251.1 |
| BiGRU | 52.3161 | 0.9132 | 39.8785 | 521.7 | 247.6 |
| TCN | 50.5941 | 0.9222 | 39.0946 | 566.8 | 307.4 |
| Dilated BiGRU | 44.0456 | 0.9464 | 31.9781 | 589.1 | 266.3 |
| BWO-Dilated BiGRU | 27.2682 | 0.9784 | 19.5211 | 852.7 | 279.4 |
| IBWO-Dilated BiGRU | 26.1706 | 0.9812 | 18.5462 | 873.5 | 286.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Han, H.; Ma, J. Research on a Short-Term Electric Load Forecasting Model Based on Improved BWO-Optimized Dilated BiGRU. Sustainability 2025, 17, 9746. https://doi.org/10.3390/su17219746
Peng Z, Han H, Ma J. Research on a Short-Term Electric Load Forecasting Model Based on Improved BWO-Optimized Dilated BiGRU. Sustainability. 2025; 17(21):9746. https://doi.org/10.3390/su17219746
Chicago/Turabian StylePeng, Ziang, Haotong Han, and Jun Ma. 2025. "Research on a Short-Term Electric Load Forecasting Model Based on Improved BWO-Optimized Dilated BiGRU" Sustainability 17, no. 21: 9746. https://doi.org/10.3390/su17219746
APA StylePeng, Z., Han, H., & Ma, J. (2025). Research on a Short-Term Electric Load Forecasting Model Based on Improved BWO-Optimized Dilated BiGRU. Sustainability, 17(21), 9746. https://doi.org/10.3390/su17219746







