Upgrading Sustainability in Clean Energy: Optimization for Proton Exchange Membrane Fuel Cells Using Heterogeneous Comprehensive Learning Bald Eagle Search Algorithm
Abstract
1. Introduction
Literature Survey
- A novel optimization framework (HCLBES) is introduced, leveraging heterogeneous learning and comprehensive learning strategies to enhance search capabilities.
- The proposed HCLBES is applied for accurate parameter estimation of the different PEMFC model, which serves as a benchmark in the literature.
- Comparative analysis with state-of-the-art algorithms is presented to demonstrate the novelty of the proposed HCLBES superiority in terms of accuracy, convergence speed, and computational efficiency.
- Validation is carried out across multiple PEMFC stack ratings to confirm the robustness and versatility of the proposed method.
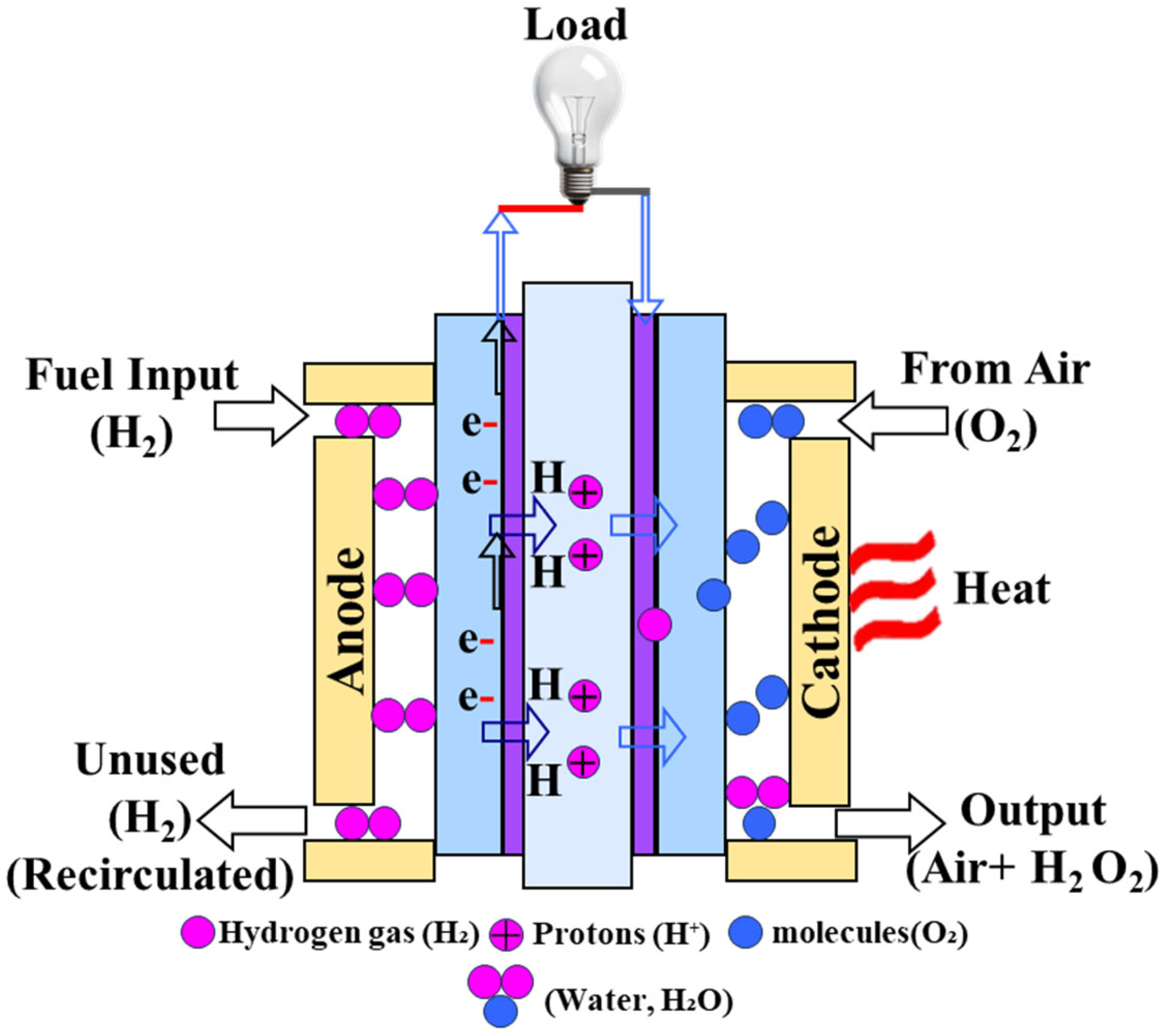
2. Mathematical Model of PEMFC
3. Bald Eagle Search (BES) Optimization Algorithm
- Selection stage (defining the search space): The eagle selects an appropriate search space based on its prior movements, as expressed by:
- 2.
- Search stage (Spiral Flight to Explore the Space): It explores the space using a spiral flight pattern to locate the best dive position.
- 3.
- Swooping stage (Diving Toward the Optimal Solution): The eagle executes a final descent toward the prey while others in the population also move toward the optimal position:
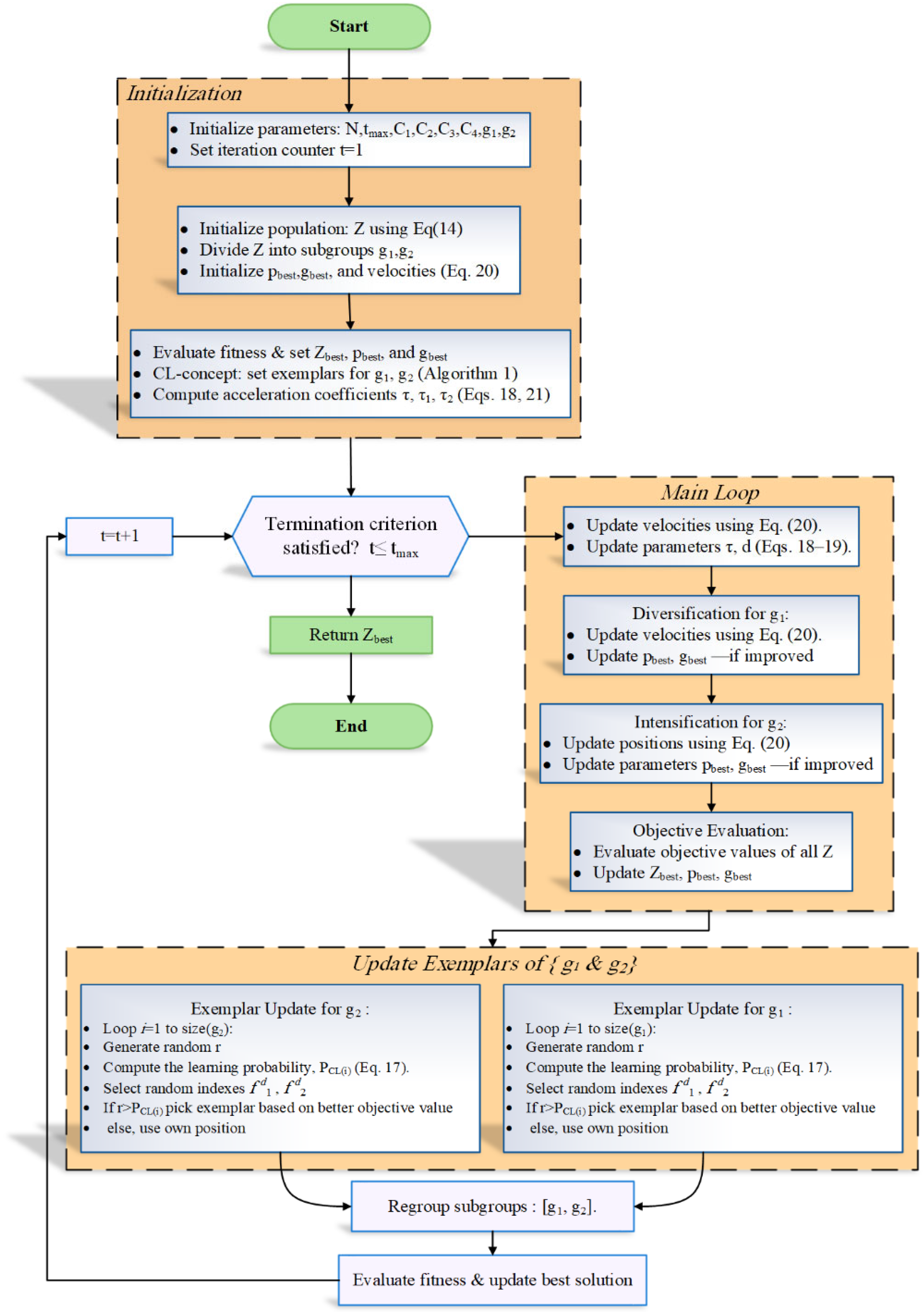
4. The Proposed HCLBES Optimization Algorithm
4.1. Heterogeneous Comprehensive Learning
| Algorithm 1. Steps of Comprehensive Learning Strategy. |
|
|
|
|
|
|
4.2. Heterogeneous Comprehensive Learning Bald Eagle Search (HCLBES) Algorithm
| Algorithm 2. Pseudo code of the HCLBES. |
|
5. Formulation of the Optimization Model
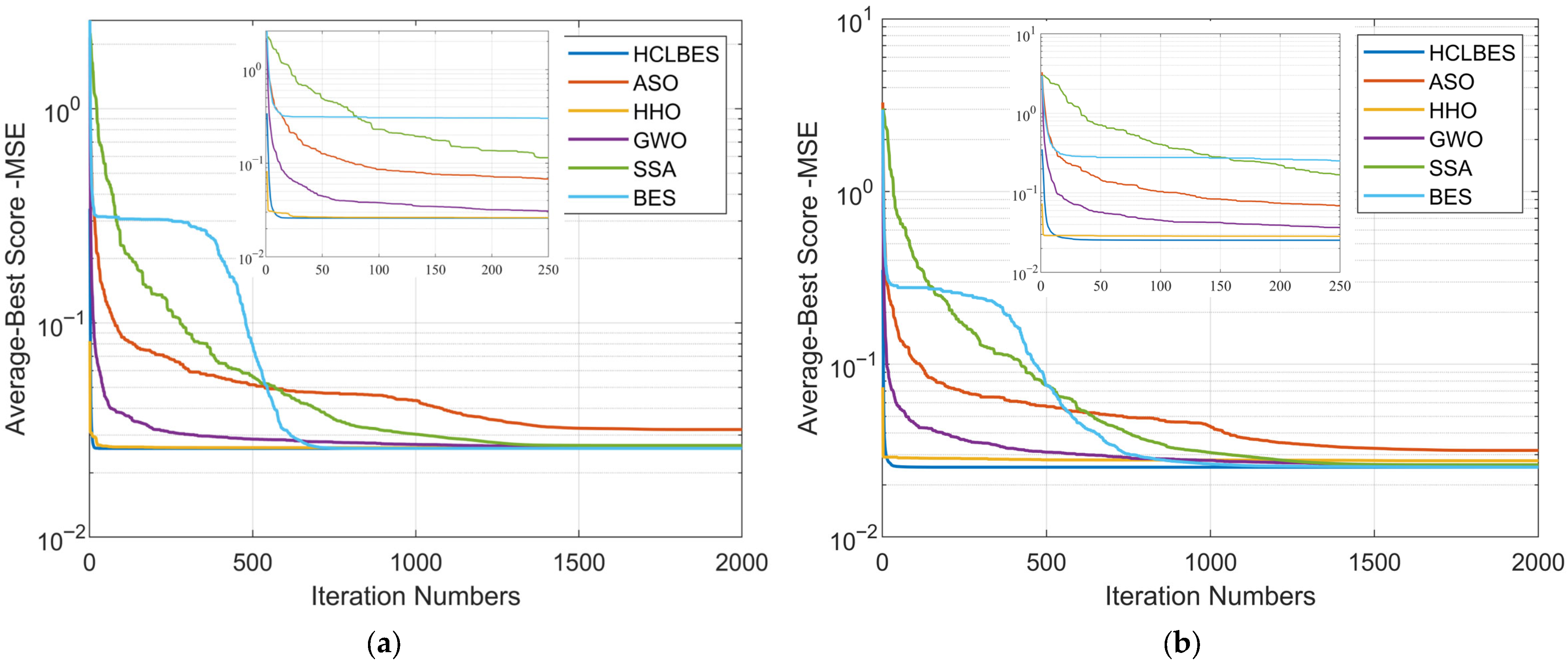
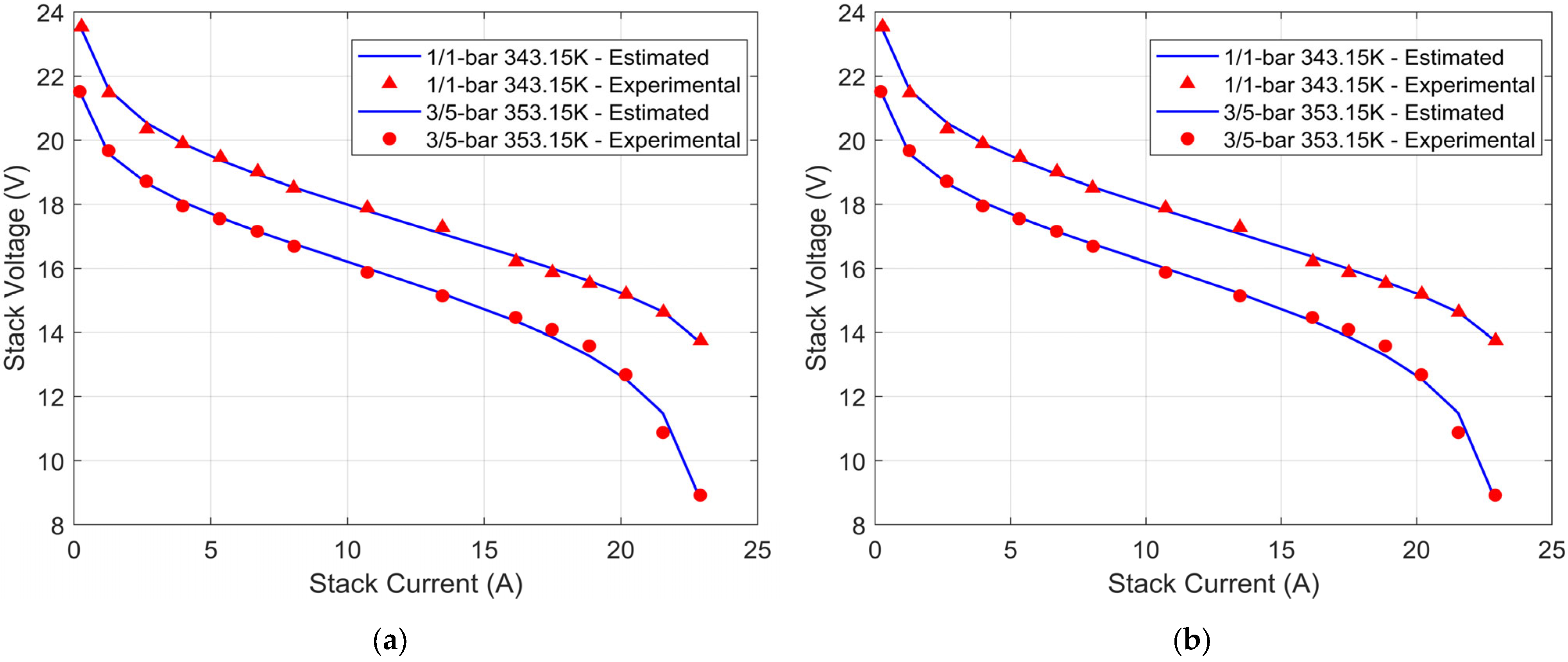
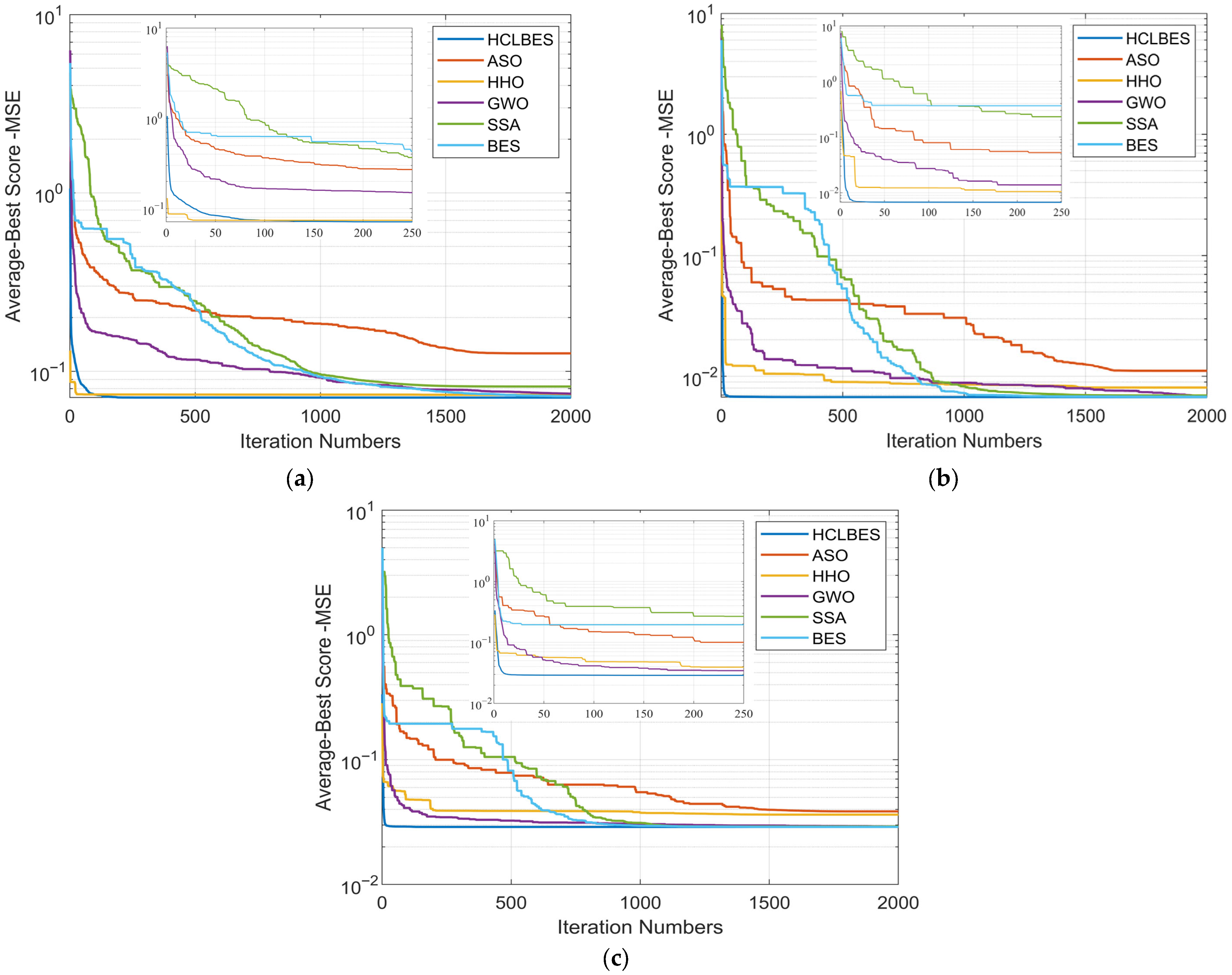
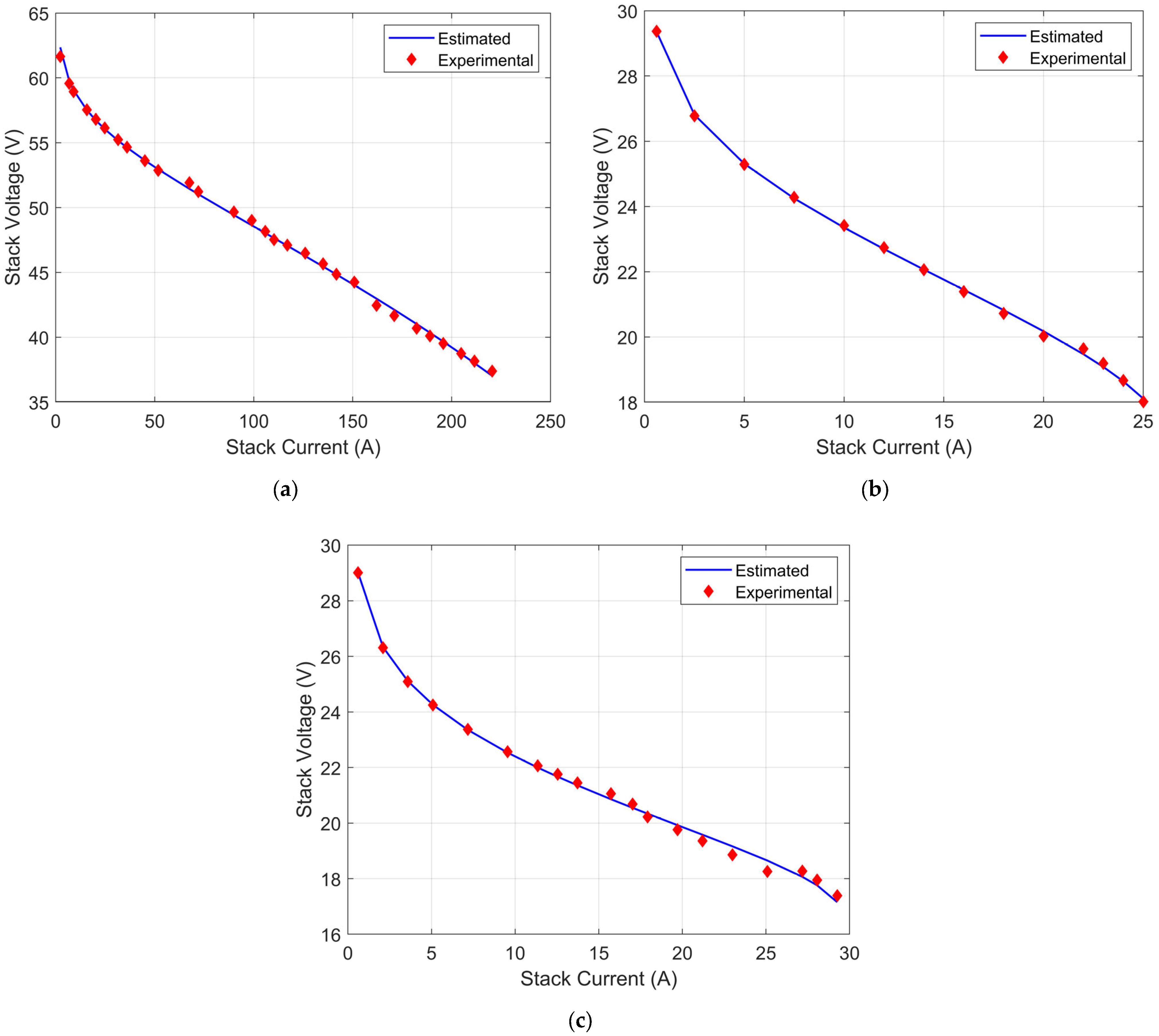
6. Simulation-Based Analysis and Results
6.1. Parameter Identification for PEMFC 250 W Stack-Models
6.2. Parameter Identification for PEMFC 500 W Stack-Models
6.3. Computational Time Analysis
7. Discussion
8. Conclusions
- Statistical analyses under various temperature and pressure conditions show that HCLBES regularly obtained lower error rates than conventional methods.
- Simulations were conducted on several PEMFC models to evaluate the performance of the proposed HCLBES algorithm.
- The current voltage curves predicted by HCLBES algorithm showed excellent agreement with the experimental data, with an average error below 2% and a low RMSE value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Active cell area | |
| Transfer coefficient—(dimensionless) | |
| A constant related to concentration voltage drop | |
| Oxygen concentration | |
| Reference voltage | |
| Reversible thermodynamic potential (Nernst-voltage) | |
| Electrons—(elementary charge) | |
| Faraday’s constant with numerical value 96486 | |
| Hydrogen gas | |
| Water | |
| Protons | |
| Fuel cell current | |
| Exchange current density | |
| Maximum current density | |
| Membrane thickness | |
| Number of search agents | |
| Number of series-connected cells | |
| Oxygen gas | |
| Partial pressure of hydrogen | |
| Partial pressure of oxygen | |
| Universal gas constant | |
| Random coefficient | |
| Membrane resistivity | |
| Contact resistance to electron conduction | |
| Cell temperature in Kelvin | |
| Number of iterations | |
| Activation voltage drops | |
| Concentration voltage drops | |
| Terminal voltage of a PEMFC | |
| Ohmic voltage drop | |
| Overall voltage of a PEMFC stack | |
| Population of solutions | |
| Optimal search position | |
| Current position of the eagle in the search space at iteration t | |
| Updated position after selection, search, or swooping stage | |
| Mean position from the previous search | |
| Number of electrons transferred | |
| Empirical coefficients for the activation overpotentials | |
| Reversible (thermodynamic) voltage | |
| Activation losses | |
| Ohmic losses | |
| Concentration losses | |
| Membrane water content ratio— | |
| Location update parameter |
References
- Rashid, F.L.; Al-Obaidi, M.A.; Hussein, A.K.; Akkurt, N.; Ali, B.; Younis, O. Floating Solar Stills and Floating Solar-Driven Membranes: Recent Advances and Overview of Designs, Performance and Modern Combinations. Sol. Energy 2022, 247, 355–372. [Google Scholar] [CrossRef]
- Priya, K.; Sathishkumar, K.; Rajasekar, N. A Comprehensive Review on Parameter Estimation Techniques for Proton Exchange Membrane Fuel Cell Modelling. Renew. Sustain. Energy Rev. 2018, 93, 121–144. [Google Scholar] [CrossRef]
- Mirzapour, F.; Lakzaei, M.; Varamini, G.; Teimourian, M.; Ghadimi, N. A New Prediction Model of Battery and Wind-Solar Output in Hybrid Power System. J. Ambient Intell. Humaniz. Comput. 2019, 10, 77–87. [Google Scholar] [CrossRef]
- Gong, W.; Yan, X.; Hu, C.; Wang, L.; Gao, L. Fast and Accurate Parameter Extraction for Different Types of Fuel Cells with Decomposition and Nature-Inspired Optimization Method. Energy Convers. Manag. 2018, 174, 913–921. [Google Scholar] [CrossRef]
- Liu, B.; Chen, H.; Zhang, T.; Pei, P. A Vehicular Proton Exchange Membrane Fuel Cell System Co-Simulation Modeling Method Based on the Stack Internal Distribution Parameters Monitoring. Energy Convers. Manag. 2019, 197, 111898. [Google Scholar] [CrossRef]
- Bankupalli, P.T.; Ghosh, S.; Kumar, L.; Samanta, S.; Dixit, T.V. A Non-Iterative Approach for Maximum Power Extraction from PEM Fuel Cell Using Resistance Estimation. Energy Convers. Manag. 2019, 187, 565–577. [Google Scholar] [CrossRef]
- Stepančič, M.; Juričić, Ð.; Boškoski, P. Fault Detection of Fuel Cell Systems Based on Statistical Assessment of Impedance Data. Energy Convers. Manag. 2019, 195, 76–85. [Google Scholar] [CrossRef]
- Su, C.; Xu, Z.; Wang, X.; Li, B. Research on the Co-Evolution Mechanism of Electricity Market Entities Enabled by Shared Energy Storage: A Tripartite Game Perspective Incorporating Dynamic Incentives/Penalties and Stochastic Disturbances. Systems 2025, 13, 817. [Google Scholar] [CrossRef]
- Yang, S.; Chellali, R.; Lu, X.; Li, L.; Bo, C. Modeling and Optimization for Proton Exchange Membrane Fuel Cell Stack Using Aging and Challenging P Systems Based Optimization Algorithm. Energy 2016, 109, 569–577. [Google Scholar] [CrossRef]
- Ettihir, K.; Boulon, L.; Becherif, M.; Agbossou, K.; Ramadan, H.S. Online Identification of Semi-Empirical Model Parameters for PEMFCs. Int. J. Hydrogen Energy 2014, 39, 21165–21176. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Baumert, R.M.; Mann, R.F.; Peppley, B.A.; Roberge, P.R.; Harris, T.J. Performance Modeling of the Ballard Mark IV Solid Polymer Electrolyte Fuel Cell: II. Empirical Model Development. J. Electrochem. Soc. 1995, 142, 9–15. [Google Scholar] [CrossRef]
- Saadi, A.; Becherif, M.; Aboubou, A.; Ayad, M.Y. Comparison of Proton Exchange Membrane Fuel Cell Static Models. Renew. Energy 2013, 56, 64–71. [Google Scholar] [CrossRef]
- Kandidayeni, M.; Macias, A.; Khalatbarisoltani, A.; Boulon, L.; Kelouwani, S. Benchmark of Proton Exchange Membrane Fuel Cell Parameters Extraction with Metaheuristic Optimization Algorithms. Energy 2019, 183, 912–925. [Google Scholar] [CrossRef]
- Priya, K.; Sudhakar Babu, T.; Balasubramanian, K.; Sathish Kumar, K.; Rajasekar, N. A Novel Approach for Fuel Cell Parameter Estimation Using Simple Genetic Algorithm. Sustain. Energy Technol. Assess. 2015, 12, 46–52. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, N. An Adaptive RNA Genetic Algorithm for Modeling of Proton Exchange Membrane Fuel Cells. Int. J. Hydrogen Energy 2013, 38, 219–228. [Google Scholar] [CrossRef]
- Mo, Z.J.; Zhu, X.J.; Wei, L.Y.; Cao, G.Y. Parameter Optimization for a PEMFC Model with a Hybrid Genetic Algorithm. Int. J. Energy Res. 2006, 30, 585–597. [Google Scholar] [CrossRef]
- Ohenoja, M.; Leiviskä, K. Validation of Genetic Algorithm Results in a Fuel Cell Model. Int. J. Hydrogen Energy 2010, 35, 12618–12625. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. A New Artificial Bee Swarm Algorithm for Optimization of Proton Exchange Membrane Fuel Cell Model Parameters. J. Zhejiang Univ. Sci. C 2011, 12, 638–646. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Artificial Immune System-Based Parameter Extraction of Proton Exchange Membrane Fuel Cell. Int. J. Electr. Power Energy Syst. 2011, 33, 933–938. [Google Scholar] [CrossRef]
- Al-Hotmani, O.M.A.; Al-Obaidi, M.A.; Li, J.P.; John, Y.M.; Patel, R.; Mujtaba, I.M. A Multi-Objective Optimisation Framework for MED-TVC Seawater Desalination Process Based on Particle Swarm Optimisation. Desalination 2022, 525, 115504. [Google Scholar] [CrossRef]
- Al-Obaidi, M.; Li, J.-P.; Alsadaie, S.; Kara-Zaïtri, C.; Mujtaba, I. Modelling and Optimisation of a Multistage Reverse Osmosis Processes with Permeate Reprocessing and Recycling for the Removal of N-Nitrosodimethylamine from Wastewater Using Species Conserving Genetic Algorithms. Chem. Eng. J. 2018, 37, 735–760. [Google Scholar] [CrossRef]
- Fathy, A.; Babu, T.S.; Abdelkareem, M.A.; Rezk, H.; Yousri, D. Recent Approach Based Heterogeneous Comprehensive Learning Archimedes Optimization Algorithm for Identifying the Optimal Parameters of Different Fuel Cells. Energy 2022, 248, 123587. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, N.; Yang, S. Hybrid Artificial Bee Colony Algorithm for Parameter Estimation of Proton Exchange Membrane Fuel Cell. Int. J. Hydrogen Energy 2013, 38, 5796–5806. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Multi-Verse Optimizer for Identifying the Optimal Parameters of PEMFC Model. Energy 2018, 143, 634–644. [Google Scholar] [CrossRef]
- Ayyarao, T.S.L.V.; Polumahanthi, N.; Khan, B. An Accurate Parameter Estimation of PEM Fuel Cell Using War Strategy Optimization. Energy 2024, 290, 130235. [Google Scholar] [CrossRef]
- Rao, Y.; Shao, Z.; Ahangarnejad, A.H.; Gholamalizadeh, E.; Sobhani, B. Shark Smell Optimizer Applied to Identify the Optimal Parameters of the Proton Exchange Membrane Fuel Cell Model. Energy Convers. Manag. 2019, 182, 1–8. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Elhoseny, M.; Chakrabortty, R.K.; Ryan, M.J. An Efficient Heap-Based Optimization Algorithm for Parameters Identification of Proton Exchange Membrane Fuel Cells Model: Analysis and Case Studies. Int. J. Hydrogen Energy 2021, 46, 11908–11925. [Google Scholar] [CrossRef]
- Li, J.; Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Zhang, Z. Accurate, Efficient and Reliable Parameter Extraction of PEM Fuel Cells Using Shuffled Multi-Simplexes Search Algorithm. Energy Convers. Manag. 2020, 206, 112501. [Google Scholar] [CrossRef]
- Rezk, H.; Wilberforce, T.; Olabi, A.G.; Ghoniem, R.M.; Sayed, E.T.; Ali Abdelkareem, M. Optimal Parameter Identification of a PEM Fuel Cell Using Recent Optimization Algorithms. Energies 2023, 16, 5246. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Wang, Z. Parameter Estimation of Proton Exchange Membrane Fuel Cells Using Eagle Strategy Based on JAYA Algorithm and Nelder-Mead Simplex Method. Energy 2019, 173, 457–467. [Google Scholar] [CrossRef]
- Gong, W.; Yan, X.; Liu, X.; Cai, Z. Parameter Extraction of Different Fuel Cell Models with Transferred Adaptive Differential Evolution. Energy 2015, 86, 139–151. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, N.; Bi, Y.; Srinivasan, D. Parameter Identification of PEMFC Model Based on Hybrid Adaptive Differential Evolution Algorithm. Energy 2015, 90, 1334–1341. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. A Grouping-Based Global Harmony Search Algorithm for Modeling of Proton Exchange Membrane Fuel Cell. Int. J. Hydrogen Energy 2011, 36, 5047–5053. [Google Scholar] [CrossRef]
- El-Fergany, A.A. Electrical Characterisation of Proton Exchange Membrane Fuel Cells Stack Using Grasshopper Optimizer. IET Renew. Power Gener. 2018, 12, 9–17. [Google Scholar] [CrossRef]
- Niu, Q.; Zhang, L.; Li, K. A Biogeography-Based Optimization Algorithm with Mutation Strategies for Model Parameter Estimation of Solar and Fuel Cells. Energy Convers. Manag. 2014, 86, 1173–1185. [Google Scholar] [CrossRef]
- Turgut, O.E.; Coban, M.T. Optimal Proton Exchange Membrane Fuel Cell Modelling Based on Hybrid Teaching Learning Based Optimization—Differential Evolution Algorithm. Ain Shams Eng. J. 2016, 7, 347–360. [Google Scholar] [CrossRef]
- Agwa, A.M.; El-Fergany, A.A.; Sarhan, G.M. Steady-State Modeling of Fuel Cells Based on Atom Search Optimizer. Energies 2019, 12, 1884. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, N. Cuckoo Search Algorithm with Explosion Operator for Modeling Proton Exchange Membrane Fuel Cells. Int. J. Hydrogen Energy 2019, 44, 3075–3087. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- El-Fergany, A.A. Extracting Optimal Parameters of PEM Fuel Cells Using Salp Swarm Optimizer. Renew. Energy 2018, 119, 641–648. [Google Scholar] [CrossRef]
- Priya, K.; Rajasekar, N. Application of Flower Pollination Algorithm for Enhanced Proton Exchange Membrane Fuel Cell Modelling. Int. J. Hydrogen Energy 2019, 44, 18438–18449. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M.; Agwa, A.M. Semi-Empirical PEM Fuel Cells Model Using Whale Optimization Algorithm. Energy Convers. Manag. 2019, 201, 112197. [Google Scholar] [CrossRef]
- Shehab, M.; Mashal, I.; Momani, Z.; Shambour, M.K.Y.; AL-Badareen, A.; Al-Dabet, S.; Bataina, N.; Alsoud, A.R.; Abualigah, L. Harris Hawks Optimization Algorithm: Variants and Applications. Arch. Comput. Methods Eng. 2022, 29, 5579–5603. [Google Scholar] [CrossRef]
- Rezk, H.; Olabi, A.G.; Ferahtia, S.; Sayed, E.T. Accurate Parameter Estimation Methodology Applied to Model Proton Exchange Membrane Fuel Cell. Energy 2022, 255, 124454. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S. A New Heuristic Optimization Algorithm for Modeling of Proton Exchange Membrane Fuel Cell: Bird Mating Optimizer. Arch. Thermodyn. 2012, 33, 23–40. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Fathy, A.; Elaziz, M.A.; Alharbi, A.G. A Novel Approach Based on Hybrid Vortex Search Algorithm and Differential Evolution for Identifying the Optimal Parameters of PEM Fuel Cell. Renew. Energy 2020, 146, 1833–1845. [Google Scholar] [CrossRef]
- Guo, C.; Lu, J.; Tian, Z.; Guo, W.; Darvishan, A. Optimization of Critical Parameters of PEM Fuel Cell Using TLBO-DE Based on Elman Neural Network. Energy Convers. Manag. 2019, 183, 149–158. [Google Scholar] [CrossRef]
- Fawzi, M.; El-Fergany, A.A.; Hasanien, H.M. Effective Methodology Based on Neural Network Optimizer for Extracting Model Parameters of PEM Fuel Cells. Int. J. Energy Res. 2019, 43, 8136–8147. [Google Scholar] [CrossRef]
- Kandidayeni, M.; Macias, A.; Amamou, A.A.; Boulon, L.; Kelouwani, S.; Chaoui, H. Overview and Benchmark Analysis of Fuel Cell Parameters Estimation for Energy Management Purposes. J. Power Sources 2018, 380, 92–104. [Google Scholar] [CrossRef]
- Rathod, A.A.; Sharma, P.; Choudhary, A.; Raju, S.; Subramanian, B. An Efficient Framework for Proton Exchange Membrane Fuel Cell Parameter Estimation Using Numerous MH Algorithms. Renew. Sustain. Energy Rev. 2025, 216, 115603. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Baumert, R.M.; Mann, R.F.; Peppley, B.A.; Roberge, P.R.; Rodrigues, A. Parametric Modelling of the Performance of a 5-KW Proton-Exchange Membrane Fuel Cell Stack. J. Power Sources 1994, 49, 349–356. [Google Scholar] [CrossRef]
- Squadrito, G.; Maggio, G.; Passalacqua, E.; Lufrano, F.; Patti, A. Empirical Equation for Polymer Electrolyte Fuel Cell (PEFC) Behaviour. J. Appl. Electrochem. 1999, 29, 1449–1455. [Google Scholar] [CrossRef]
- Rowe, A.; Li, X. Mathematical Modeling of Proton Exchange Membrane Fuel Cells. J. Power Sources 2001, 102, 82–96. [Google Scholar] [CrossRef]
- Alsattar, H.A.; Zaidan, A.A.; Zaidan, B.B. Novel Meta-Heuristic Bald Eagle Search Optimisation Algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Niu, Q.; Zhang, H.; Li, K. An Improved TLBO with Elite Strategy for Parameters Identification of PEM Fuel Cell and Solar Cell Models. Int. J. Hydrogen Energy 2014, 39, 3837–3854. [Google Scholar] [CrossRef]
- Yadav, P.; Kumar, R.; Panda, S.K.; Chang, C.S. An Intelligent Tuned Harmony Search Algorithm for Optimisation. Inf. Sci. 2012, 196, 47–72. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive Learning Particle Swarm Optimizer for Global Optimization of Multimodal Functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]


| Ref. | Algorithm | Studied Fuel Cell-Model | Comparison Study | Objective Function | |||||
|---|---|---|---|---|---|---|---|---|---|
| Modular–1 | Modular–2 | Modular–3 | Modular–4 | ||||||
| [15] | ARNA-GA | Modular 1: PEMFC 250 W | SGA, HGA, Real-GA [17] | † | † | † | SSE | 1000 | 50 |
| [23] | HABC | Modular 2: PEMFC stack | Real-GA, H-GA, S-GA [23] | † | † | † | SSE | 2000 | – |
| [14] | S-GA | Modular 3: PEM 250 W | BIPOA, PSO, SGA, HGA [14], Real-GA [17], AIS [19] | † | † | † | SSE | 100–500 | 20–30 |
| [24] | MVO | Modular 1: PEMFC 250 W | HGA, SGA [16], HADE [32], Real-GA [17], and HABC [23] | † | † | † | SSE | 2000 | 50 |
| [26] | Shark Smell | Modular 1: PEMFC250 W | TLBO-DE [45], ARNA-GA [23], Real-GA, MPSO, and QPSO [26], Sa-DE, HIS, and STLBO [56] | † | † | † | SSE | 500 | 100 |
| [30] | JAYA | Modular 1: PEMFC 250 W | GOA, GWO, SSO, MVO, JAYA, and, JAYA−NM [30] | † | † | † | SSE | 5000 | 30 |
| [28] | SMS | Modular 1: BCS 500 W Modular 2: NedStackPS6 Modular 3: Harizon500 W Modular 4: PEMFCs250 W | FOA, SFLA, and ICA [49], VSA [47], SSO [26], NNA [24], VSDE, SP-UCI, and ISCE [28], DEM, GWO, SSO [40] | SP−UCI, SCE−UA, ISCE [28], VSDE, VSA [47], NNA [45], FOA, ICA [13], SSO [40], GA, GHO [34] | SP−UCI, SCE−UA, and ISCE [28], SFLA [13] | SP−UCI, SCE−UA, and ISCE [28], JAYA−NM, MVO, GWO, JAYA [30] | SSE | 5000 | – |
| [47] | VSDE | Modular 1: BCS 500 W Modular 2: NedStackPS6 Modular 3: SR-12 PEM 500 W Modular 4: PEMFCs250 W | SSO [40], SSO [26] | GHO [34] SSO [40] | GWO [47], SSO [26] | STLBO, and TLBO [56], ITHS [57], HABC [23], MVO [24], Real GA [17] | SSE | 500 | 50 |
| [27] | IHBO | Modular 1: BCS 500 W Modular 2: NedStackPS6 Modular 3: H-12 stack Modular 4: SR-12 500 W | WOA [42], FPA [41], HBO, ISA, MFO, MRFO, EO, AEO, TSA, and STSA [27], SSA [40] | WOA [42], FPA [41], HBO, ISA, MFO, MRFO, EO, AEO, TSA, and STSA [27], SSA [40] | WOA [42], FPA [41], HBO, ISA. MFO, MRFO, EO, AEO, TSA, and STSA [27], SSA [40] | WOA [42], FPA [41], HBO, ISA, MFO, MRFO, EO, AEO, TSA, STSA [27], SSA [40] | SSE | 5000 | – |
| [22] | HLCAOA | Modular 1: BCS500 W Modular 2: NedStackPS6 Modular 3: SR-12 500 W Modular 4: PEMFC 250 W | VSDE, VSA [47] | VSDE, VSA [47] | VSDE, VSA [47] | VSDE, VSA, and ABC[47], MVO [22], HABC [24], ITHS [57], STLBO.TLBO [56], Real-GA [17] | MSE | 2000 | 100 |
| [29] | BES | Modular1: Avista SR-12 | ALO, BES, COOT, EO, HBO [29] | † | † | † | SSE | – | – |
| [25] | WSO | Modular 1: BCS500 W Modular 2: NedStackPS6 Modular 3: Harizon250 W Modular 4: Horizon500 W | SFLA, FOA, and ICA [13], NNA [25], HHO [43], GWO [46], Shark-Smell [26] | BES [44], IBHO [27], AEFA, IAEO, STSA, NNA, and EO [13], SFLA, FOA, and ICA [13], SSO [40], GOA [34], VSDE and VSA [47] | † | ISCE [42], GWO [46], SFLA [13], HHO [43] | SSE | 1000 | 50 |
| Parameters | PEMFC-250 W Stack-Model | PEMFC-500 W Stack-Model | ||
|---|---|---|---|---|
| Horizon 250 W | Nedstack PS6 | BCS 500 W | Horizon 500 W | |
| 24 | 65 | 32 | 36 | |
| 27 | 240 | 64 | 52 | |
| 0.86 | 1.4 | 0.469 | 0.025 | |
| 127 | 178 | 178 | 0.51923 | |
| 1.0–3.0 | 0.5–5 | 1 | 1 | |
| 1.0–5.0 | 0.5–5 | 0.2075 | 0.55 | |
| 343.15–353.15 | 343 | 333 | 333 | |
| 1.0 | 1.0 | 1.0 | 1 | |
| 1.0 | 1.0 | 1.0 | 1 | |
| Fuel Cell | Ranges | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 250 W-stack | Range-1 | Upper bound | −0.944 | 5 Ɛ−3 | 7.8 Ɛ−5 | −1.88 Ɛ−5 | 23 | 8 Ɛ−4 | 0.5 |
| Lower bound | −0.952 | 1 Ɛ−3 | 7.4 Ɛ−5 | −1.98 Ɛ−5 | 14 | 1 Ɛ−4 | 0.016 | ||
| 500 W-stack | Range-2 | Upper bound | −0.8532 | 33,487 Ɛ−3 | 9.80 Ɛ−5 | −9.54 Ɛ−5 | 23 | 8 Ɛ−4 | 0.5 |
| Lower bound | −1.19969 | 33,487 Ɛ−3 | 3.60 Ɛ−5 | −26 Ɛ−4 | 13 | 1 Ɛ−4 | 0.0136 | ||
| Algorithm | MSE | MAE | RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Range-1 | Proposed HCLBES | −9.48 Ɛ−1 | 2.89 Ɛ−3 | 7.60 Ɛ−5 | −1.37 Ɛ−4 | 1.40 Ɛ1 | 1.60 Ɛ−2 | 7.84 Ɛ−4 | 1.10 Ɛ−2 | 8.69 Ɛ−2 | 1.05 Ɛ−1 |
| ASO | −9.48 Ɛ−1 | 2.89 Ɛ−3 | 7.59 Ɛ−5 | −1.43 Ɛ−4 | 1.75 Ɛ1 | 2.27 Ɛ−2 | 5.86 Ɛ−4 | 1.90 Ɛ−2 | 1.16 Ɛ−1 | 1.37 Ɛ−1 | |
| HHO | −9.52 Ɛ−1 | 2.88 Ɛ−3 | 7.40 Ɛ−5 | −1.38 Ɛ−4 | 1.40 Ɛ1 | 1.61 Ɛ−2 | 6.89 Ɛ−4 | 1.11 Ɛ−2 | 8.69 Ɛ−2 | 1.05 Ɛ−1 | |
| GWO | −9.48 Ɛ−1 | 2.89 Ɛ−3 | 7.58 Ɛ−5 | −1.37 Ɛ−4 | 1.40 Ɛ1 | 1.60 Ɛ−2 | 7.62 Ɛ−4 | 1.11 Ɛ−2 | 8.68 Ɛ−2 | 1.05 Ɛ−1 | |
| SSA | −9.48 Ɛ−1 | 2.89 Ɛ−3 | 7.57 Ɛ−5 | −1.40 Ɛ−4 | 1.40 Ɛ1 | 1.66 Ɛ−2 | 5.18 Ɛ−4 | 1.15 Ɛ−2 | 8.85 Ɛ−2 | 1.07 Ɛ−1 | |
| BES | −9.48 Ɛ−1 | 2.90 Ɛ−3 | 7.60 Ɛ−5 | −1.37 Ɛ−4 | 1.40 Ɛ1 | 1.60 Ɛ−2 | 7.84 Ɛ−4 | 1.10 Ɛ−2 | 8.69 Ɛ−2 | 1.05 Ɛ−1 | |
| VSDE [46] | −9.47 Ɛ−1 | 2.90 Ɛ−3 | 7.63 Ɛ−5 | −1.37 Ɛ−4 | 1.40 Ɛ1 | 1.60 Ɛ−2 | 7.84 Ɛ−4 | 1.10 Ɛ−2 | 8.69 Ɛ−2 | 1.05 Ɛ−1 | |
| ABC [46] | −9.49 Ɛ−1 | 2.89 Ɛ−3 | 7.55 Ɛ−5 | −1.37 Ɛ−4 | 1.40 Ɛ1 | 1.60 Ɛ−2 | 7.84 Ɛ−4 | 1.10 Ɛ−2 | 8.69 Ɛ−2 | 1.05 Ɛ−1 | |
| HABC [21] | −9.49 Ɛ−1 | 2.89 Ɛ−3 | 7.56 Ɛ−5 | −1.37 Ɛ−4 | 1.40 Ɛ1 | 1.60 Ɛ−2 | 7.84 Ɛ−4 | 1.10 Ɛ−2 | 8.69 Ɛ−2 | 1.05 Ɛ−1 | |
| ITHS [32] | −9.45 Ɛ−1 | 2.87 Ɛ−3 | 7.54 Ɛ−5 | −1.32 Ɛ−4 | 1.75 Ɛ1 | 2.53 Ɛ−2 | 6.66 Ɛ−4 | 4.83 Ɛ−2 | 1.34 Ɛ−1 | 1.73 Ɛ−1 | |
| MVO [22] | −9.48 Ɛ−1 | 2.90 Ɛ−3 | 7.62 Ɛ−5 | −1.39 Ɛ−4 | 1.40 Ɛ1 | 1.63 Ɛ−2 | 6.03 Ɛ−4 | 1.13 Ɛ−2 | 8.76 Ɛ−2 | 1.06 Ɛ−1 | |
| STLBO [55] | −9.48 Ɛ−1 | 2.90 Ɛ−3 | 7.62 Ɛ−5 | −1.37 Ɛ−4 | 1.40 Ɛ1 | 1.60 Ɛ−2 | 7.84 Ɛ−4 | 1.10 Ɛ−2 | 8.69 Ɛ−2 | 1.05 Ɛ−1 | |
| TLBO [55] | −9.46 Ɛ−1 | 2.87 Ɛ−3 | 7.47 Ɛ−5 | −1.37 Ɛ−4 | 1.40 Ɛ1 | 1.60 Ɛ−2 | 7.84 Ɛ−4 | 1.10 Ɛ−2 | 8.69 Ɛ−2 | 1.05 Ɛ−1 | |
| VSA [46] | −9.47 Ɛ−1 | 2.95 Ɛ−3 | 7.64 Ɛ−5 | −1.55 Ɛ−4 | 1.40 Ɛ1 | 2.47 Ɛ−2 | 5.15 Ɛ−4 | 7.27 Ɛ−1 | 2.79 Ɛ−2 | 3.69 Ɛ−1 | |
| HCLAOA [20] | −9.48 Ɛ−1 | 2.91 Ɛ−3 | 7.59 Ɛ−5 | −1.20 Ɛ−4 | 1.99 Ɛ1 | 4.76 Ɛ−2 | 5.19 Ɛ−4 | 5.93 Ɛ−1 | 3.85 Ɛ−1 | 5.39 Ɛ−1 | |
| Range-2 | Proposed HCLBES | −1.03 | 3.02 Ɛ−3 | 6.69 Ɛ−5 | −1.37 Ɛ−4 | 1.21 Ɛ1 | 1.36 Ɛ−2 | 1.00 Ɛ−4 | 4.09 Ɛ−2 | 1.41 Ɛ−1 | 2.02 Ɛ−1 |
| ASO | −1.01 | 2.99 Ɛ−3 | 7.08 Ɛ−5 | −1.42 Ɛ−4 | 1.70 Ɛ1 | 2.16 Ɛ−2 | 5.78 Ɛ−4 | 4.46 Ɛ−2 | 1.51 Ɛ−1 | 2.07 Ɛ−1 | |
| HHO | −1.03 | 2.65 Ɛ−3 | 3.87 Ɛ−5 | −1.32 Ɛ−4 | 1.24 Ɛ1 | 1.36 Ɛ−2 | 5.37 Ɛ−4 | 4.12 Ɛ−2 | 1.41 Ɛ−1 | 2.03 Ɛ−1 | |
| GWO | −1.05 | 3.04 Ɛ−3 | 6.42 Ɛ−5 | −1.36 Ɛ−4 | 1.24 Ɛ1 | 1.37 Ɛ−2 | 3.42 Ɛ−4 | 4.11 Ɛ−2 | 1.41 Ɛ−1 | 2.03 Ɛ−1 | |
| SSA | −1.02 | 2.88 Ɛ−3 | 5.99 Ɛ−5 | −1.36 Ɛ−4 | 1.27 Ɛ1 | 1.39 Ɛ−2 | 4.48 Ɛ−4 | 4.21 Ɛ−2 | 1.46 Ɛ−1 | 2.05 Ɛ−1 | |
| BES | −1.02 | 2.99 Ɛ−3 | 6.71 Ɛ−5 | −1.36 Ɛ−4 | 1.22 Ɛ1 | 1.36 Ɛ−2 | 1.68 Ɛ−4 | 4.09 Ɛ−2 | 1.41 Ɛ−1 | 2.02 Ɛ−1 | |
| VSDE [46] | −1.06 | 3.23 Ɛ−3 | 7.78 Ɛ−5 | −1.37 Ɛ−4 | 1.20 Ɛ1 | 1.36 Ɛ−2 | 1.02 Ɛ−4 | 4.09 Ɛ−2 | 1.41 Ɛ−1 | 2.02 Ɛ−1 | |
| ABC [46] | −1.00 | 3.02 Ɛ−3 | 7.41 Ɛ−5 | −1.37 Ɛ−4 | 1.24 Ɛ1 | 1.38 Ɛ−2 | 2.55 Ɛ−4 | 4.09 Ɛ−2 | 1.41 Ɛ−1 | 2.02 Ɛ−1 | |
| HABC [21] | −1.11 | 3.06 Ɛ−3 | 5.32 Ɛ−5 | −1.36 Ɛ−4 | 1.22 Ɛ1 | 1.37 Ɛ−2 | 1.61 Ɛ−4 | 4.09 Ɛ−2 | 1.41 Ɛ−1 | 2.02 Ɛ−1 | |
| ITHS [32] | −9.62 Ɛ−1 | 2.93 Ɛ−3 | 7.66 Ɛ−5 | −1.33 Ɛ−4 | 1.68 Ɛ1 | 2.33 Ɛ−2 | 5.66 Ɛ−4 | 4.88 Ɛ−2 | 1.66 Ɛ−1 | 2.12 Ɛ−1 | |
| MVO [22] | −1.04 | 2.97 Ɛ−3 | 6.24 Ɛ−5 | −1.36 Ɛ−4 | 1.25 Ɛ1 | 1.36 Ɛ−2 | 3.95 Ɛ−4 | 4.20 Ɛ−2 | 1.45 Ɛ−1 | 2.05 Ɛ−1 | |
| STLBO [55] | −1.06 | 3.05 Ɛ−3 | 6.24 Ɛ−5 | −1.37 Ɛ−4 | 1.21 Ɛ1 | 1.36 Ɛ−2 | 1.00 Ɛ−4 | 4.09 Ɛ−2 | 1.41 Ɛ−1 | 2.02 Ɛ−1 | |
| TLBO [55] | −8.71 Ɛ−1 | 2.21 Ɛ−3 | 3.98 Ɛ−5 | −1.37 Ɛ−4 | 1.21 Ɛ1 | 1.36 Ɛ−2 | 1.00 Ɛ−4 | 4.09 Ɛ−2 | 1.41 Ɛ−1 | 2.02 Ɛ−1 | |
| VSA [46] | −8.57 Ɛ−1 | 2.65 Ɛ−3 | 7.49 Ɛ−5 | −9.73 Ɛ−5 | 1.00 Ɛ1 | 2.45 Ɛ−2 | 3.96 Ɛ−4 | 1.10 | 4.94 Ɛ−1 | 6.02 Ɛ−1 | |
| HCLAOA [20] | −1.02 | 3.02 Ɛ−3 | 6.14 Ɛ−5 | −1.64 Ɛ−4 | 2.05 Ɛ1 | 4.89 Ɛ−2 | 4.61 Ɛ−4 | 3.20 Ɛ−1 | 3.16 Ɛ−1 | 3.79 Ɛ−1 |
| Algorithm | MSE | MAE | RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Range-1 | Proposed HCLBES | −9.48 Ɛ−1 | 2.81 Ɛ−3 | 7.63 Ɛ−5 | −1.21 Ɛ−4 | 2.30 Ɛ+1 | 6.25 Ɛ−2 | 1.00 Ɛ−4 | 1.00 Ɛ−2 | 8.17 Ɛ−2 | 1.00 Ɛ−1 |
| ASO | −9.48 Ɛ−1 | 2.81 Ɛ−3 | 7.59 Ɛ−5 | −1.16 Ɛ−4 | 1.98 Ɛ+1 | 6.02 Ɛ−2 | 1.17 Ɛ−4 | 1.78 Ɛ−2 | 1.18 Ɛ−1 | 1.38 Ɛ−1 | |
| HHO | −9.44 Ɛ−1 | 2.78 Ɛ−3 | 7.52 Ɛ−5 | −1.20 Ɛ−4 | 2.28 Ɛ+1 | 6.22 Ɛ−2 | 1.38 Ɛ−4 | 1.11 Ɛ−2 | 8.53 Ɛ−2 | 1.03 Ɛ−1 | |
| GWO | −9.48 Ɛ−1 | 2.80 Ɛ−3 | 7.58 Ɛ−5 | −1.20 Ɛ−4 | 2.30 Ɛ+1 | 6.22 Ɛ−2 | 1.78 Ɛ−4 | 1.02 Ɛ−2 | 8.14 Ɛ−2 | 1.01 Ɛ−1 | |
| SSA | −9.48 Ɛ−1 | 2.81 Ɛ−3 | 7.63 Ɛ−5 | −1.18 Ɛ−4 | 2.30 Ɛ+1 | 6.13 Ɛ−2 | 4.29 Ɛ−4 | 1.04 Ɛ−2 | 8.19 Ɛ−2 | 1.02 Ɛ−1 | |
| BES | −9.48 Ɛ−1 | 2.81 Ɛ−3 | 7.60 Ɛ−5 | −1.21 Ɛ−4 | 2.30 Ɛ+1 | 6.25 Ɛ−2 | 1.00 Ɛ−4 | 1.01 Ɛ−2 | 8.16 Ɛ−2 | 1.00 Ɛ−1 | |
| VSDE [46] | −9.49 Ɛ−1 | 2.81 Ɛ−3 | 7.61 Ɛ−5 | −1.21 Ɛ−4 | 2.30 Ɛ+1 | 6.25 Ɛ−2 | 1.00 Ɛ−4 | 1.00 Ɛ−2 | 8.19 Ɛ−2 | 1.00 Ɛ−1 | |
| ABC [46] | −9.47 Ɛ−1 | 2.82 Ɛ−3 | 7.68 Ɛ−5 | −1.21 Ɛ−4 | 2.30 Ɛ+1 | 6.25 Ɛ−2 | 1.00 Ɛ−4 | 1.03 Ɛ−2 | 8.13 Ɛ−2 | 1.01 Ɛ−1 | |
| HABC [21] | −9.48 Ɛ−1 | 2.81 Ɛ−3 | 7.63 Ɛ−5 | −1.21 Ɛ−4 | 2.30 Ɛ+1 | 6.25 Ɛ−2 | 1.00 Ɛ−4 | 1.02 Ɛ−2 | 8.20 Ɛ−2 | 1.00 Ɛ−1 | |
| ITHS [32] | −9.45 Ɛ−1 | 2.79 Ɛ−3 | 7.55 Ɛ−5 | −1.11 Ɛ−4 | 2.20 Ɛ+1 | 6.18 Ɛ−2 | 4.69 Ɛ−4 | 4.16 Ɛ−2 | 1.43 Ɛ−1 | 1.81 Ɛ−1 | |
| MVO [22] | −9.49 Ɛ−1 | 2.81 Ɛ−3 | 7.61 Ɛ−5 | −1.18 Ɛ−4 | 2.30 Ɛ+1 | 6.15 Ɛ−2 | 3.86 Ɛ−4 | 1.02 Ɛ−2 | 8.15 Ɛ−2 | 1.01 Ɛ−1 | |
| STLBO [55] | −9.49 Ɛ−1 | 2.81 Ɛ−3 | 7.61 Ɛ−5 | −1.21 Ɛ−4 | 2.30 Ɛ+1 | 6.25 Ɛ−2 | 1.00 Ɛ−4 | 1.00 Ɛ−2 | 8.17 Ɛ−2 | 1.00 Ɛ−1 | |
| TLBO [55] | −9.47 Ɛ−1 | 2.79 Ɛ−3 | 7.55 Ɛ−5 | −1.21 Ɛ−4 | 2.30 Ɛ+1 | 6.25 Ɛ−2 | 1.00 Ɛ−4 | 1.00 Ɛ−2 | 8.17 Ɛ−2 | 1.00 Ɛ−1 | |
| VSA [46] | −9.46 Ɛ−1 | 2.86 Ɛ−3 | 7.59 Ɛ−5 | −1.68 Ɛ−4 | 1.40 Ɛ+1 | 2.80 Ɛ−2 | 3.83 Ɛ−4 | 1.05 | 3.98 Ɛ−1 | 4.58 Ɛ−1 | |
| HCLAOA [20] | −9.48 Ɛ−1 | 2.84 Ɛ−3 | 7.63 Ɛ−5 | −1.03 Ɛ−4 | 2.10 Ɛ+1 | 7.35 Ɛ−2 | 4.63 Ɛ−4 | 1.47 | 6.12 Ɛ−1 | 8.01 Ɛ−1 | |
| Range-2 | Proposed HCLBES | −1.02 | 2.97 Ɛ−3 | 7.21 Ɛ−5 | −1.22 Ɛ−4 | 2.40 Ɛ+1 | 6.31 Ɛ−2 | 1.00 Ɛ−4 | 4.07 Ɛ−2 | 1.40 Ɛ−1 | 2.02 Ɛ−1 |
| ASO | −1.02 | 2.91 Ɛ−3 | 6.83 Ɛ−5 | −1.17 Ɛ−4 | 1.98 Ɛ+1 | 5.79 Ɛ−2 | 2.77 Ɛ−4 | 4.56 Ɛ−2 | 1.45 Ɛ−1 | 2.13 Ɛ−1 | |
| HHO | −1.06 | 3.35 Ɛ−3 | 9.18 Ɛ−5 | −1.16 Ɛ−4 | 2.29 Ɛ+1 | 6.04 Ɛ−2 | 5.83 Ɛ−4 | 4.42 Ɛ−2 | 1.47 Ɛ−1 | 2.08 Ɛ−1 | |
| GWO | −1.05 | 2.79 Ɛ−3 | 5.46 Ɛ−5 | −1.21 Ɛ−4 | 2.40 Ɛ+1 | 6.26 Ɛ−2 | 2.20 Ɛ−4 | 4.10 Ɛ−2 | 1.40 Ɛ−1 | 2.02 Ɛ−1 | |
| SSA | −1.04 | 2.93 Ɛ−3 | 6.57 Ɛ−5 | −1.18 Ɛ−4 | 2.35 Ɛ+1 | 6.14 Ɛ−2 | 4.70 Ɛ−4 | 4.20 Ɛ−2 | 1.45 Ɛ−1 | 2.05 Ɛ−1 | |
| BES | −1.01 | 2.86 Ɛ−3 | 6.73 Ɛ−5 | −1.22 Ɛ−4 | 2.40 Ɛ+1 | 6.31 Ɛ−2 | 1.01 Ɛ−4 | 4.07 Ɛ−2 | 1.40 Ɛ−1 | 2.02 Ɛ−1 | |
| VSDE [46] | −1.09 | 3.30 Ɛ−3 | 8.11 Ɛ−5 | −1.22 Ɛ−4 | 2.40 Ɛ+1 | 6.31 Ɛ−2 | 1.00 Ɛ−4 | 4.07 Ɛ−2 | 1.40 Ɛ−1 | 2.02 Ɛ−1 | |
| ABC [46] | −1.05 | 2.91 Ɛ−3 | 6.10 Ɛ−5 | −1.22 Ɛ−4 | 2.40 Ɛ+1 | 6.31 Ɛ−2 | 1.00 Ɛ−4 | 4.07 Ɛ−2 | 1.40 Ɛ−1 | 2.02 Ɛ−1 | |
| HABC [21] | −1.06 | 2.95 Ɛ−3 | 6.24 Ɛ−5 | −1.22 Ɛ−4 | 2.40 Ɛ+1 | 6.31 Ɛ−2 | 1.03 Ɛ−4 | 4.07 Ɛ−2 | 1.40 Ɛ−1 | 2.02 Ɛ−1 | |
| ITHS [32] | −9.51 Ɛ−1 | 2.82 Ɛ−3 | 7.66 Ɛ−5 | −1.14 Ɛ−4 | 2.20 Ɛ+1 | 6.14 Ɛ−2 | 4.66 Ɛ−4 | 5.55 Ɛ−2 | 1.58 Ɛ−1 | 2.09 Ɛ−1 | |
| MVO [22] | −1.03 | 2.87 Ɛ−3 | 6.40 Ɛ−5 | −1.19 Ɛ−4 | 2.38 Ɛ+1 | 6.20 Ɛ−2 | 3.68 Ɛ−4 | 4.16 Ɛ−2 | 1.43 Ɛ−1 | 2.04 Ɛ−1 | |
| STLBO [55] | −1.00 | 2.92 Ɛ−3 | 7.20 Ɛ−5 | −1.22 Ɛ−4 | 2.40 Ɛ+1 | 6.31 Ɛ−2 | 1.00 Ɛ−4 | 4.07 Ɛ−2 | 1.40 Ɛ−1 | 2.02 Ɛ−1 | |
| TLBO [55] | −8.70 Ɛ−1 | 2.22 Ɛ−3 | 5.06 Ɛ−5 | −1.22 Ɛ−4 | 2.40 Ɛ+1 | 6.31 Ɛ−2 | 1.00 Ɛ−4 | 4.07 Ɛ−2 | 1.40 Ɛ−1 | 2.02 Ɛ−1 | |
| VSA [46] | −8.58 Ɛ−1 | 2.60 Ɛ−3 | 7.73 Ɛ−5 | −1.15 Ɛ−4 | 1.00 Ɛ+1 | 2.90 Ɛ−2 | 4.49 Ɛ−4 | 8.41 Ɛ−2 | 3.41 Ɛ−1 | 4.46 Ɛ−1 | |
| HCLAOA [20] | −1.04 | 3.07 Ɛ−3 | 6.81 Ɛ−5 | −1.52 Ɛ−4 | 2.30 Ɛ+1 | 6.78 Ɛ−2 | 3.75 Ɛ−4 | 5.05 Ɛ−2 | 4.59 Ɛ−1 | 5.42 Ɛ−1 |
| Algorithm | Best | Worst | Aver | Median | Var | Std | |
|---|---|---|---|---|---|---|---|
| Range-1 | Proposed HCLBES | 1.10 Ɛ−2 | 1.10 Ɛ−2 | 1.10 Ɛ−2 | 1.10 Ɛ−2 | 1.43 Ɛ−29 | 3.77 Ɛ−15 |
| ASO | 1.14 Ɛ−2 | 2.61 Ɛ−2 | 1.90 Ɛ−2 | 1.93 Ɛ−2 | 1.45 Ɛ−5 | 3.80 Ɛ−3 | |
| HHO | 1.10 Ɛ−2 | 1.15 Ɛ−2 | 1.11 Ɛ−2 | 1.10 Ɛ−2 | 2.92 Ɛ−8 | 1.71 Ɛ−4 | |
| GWO | 1.10 Ɛ−2 | 1.19 Ɛ−2 | 1.11 Ɛ−2 | 1.10 Ɛ−2 | 2.72 Ɛ−8 | 1.65 Ɛ−4 | |
| SSA | 1.10 Ɛ−2 | 1.29 Ɛ−2 | 1.15 Ɛ−2 | 1.15 Ɛ−2 | 2.53 Ɛ−7 | 5.03 Ɛ−4 | |
| BES | 1.10 Ɛ−2 | 1.10 Ɛ−2 | 1.10 Ɛ−2 | 1.10 Ɛ−2 | 5.68 Ɛ−17 | 7.54 Ɛ−9 | |
| Range-2 | Proposed HCLBES | 1.00 Ɛ−2 | 1.01 Ɛ−2 | 1.00 Ɛ−2 | 1.00 Ɛ−2 | 1.23 Ɛ−10 | 1.11 Ɛ−5 |
| ASO | 1.10 Ɛ−2 | 2.70 Ɛ−2 | 1.78 Ɛ−2 | 1.78 Ɛ−2 | 2.32 Ɛ−5 | 4.82 Ɛ−3 | |
| HHO | 1.03 Ɛ−2 | 1.75 Ɛ−2 | 1.11 Ɛ−2 | 1.03 Ɛ−2 | 3.08 Ɛ−6 | 1.76 Ɛ−3 | |
| GWO | 1.00 Ɛ−2 | 1.06 Ɛ−2 | 1.02 Ɛ−2 | 1.01 Ɛ−2 | 2.23 Ɛ−8 | 1.49 Ɛ−4 | |
| SSA | 1.00 Ɛ−2 | 1.37 Ɛ−2 | 1.04 Ɛ−2 | 1.03 Ɛ−2 | 4.28 Ɛ−7 | 6.54 Ɛ−4 | |
| BES | 1.00 Ɛ−2 | 1.04 Ɛ−2 | 1.01 Ɛ−2 | 1.00 Ɛ−2 | 9.51 Ɛ−9 | 9.75 Ɛ−5 |
| Algorithm | Best | Worst | Aver | Median | Var | Std | |
|---|---|---|---|---|---|---|---|
| Range-1 | Proposed HCLBES | 4.09 Ɛ−2 | 4.09 Ɛ−2 | 4.09 Ɛ−2 | 4.09 Ɛ−2 | 8.09 Ɛ−30 | 2.84 E Ɛ−15 |
| ASO | 4.13 Ɛ−2 | 5.45 Ɛ−2 | 4.46 Ɛ−2 | 4.37 Ɛ−2 | 9.47 Ɛ−6 | 3.08 Ɛ−3 | |
| HHO | 4.09 Ɛ−2 | 4.23 Ɛ−2 | 4.12 Ɛ−2 | 4.10 Ɛ−2 | 1.56 Ɛ−7 | 3.95 Ɛ−4 | |
| GWO | 4.09 Ɛ−2 | 4.18 Ɛ−2 | 4.11 Ɛ−2 | 4.11 Ɛ−2 | 6.60 Ɛ−8 | 2.57 Ɛ−4 | |
| SSA | 4.10 Ɛ−2 | 4.29 Ɛ−2 | 4.21 Ɛ−2 | 4.20 Ɛ−2 | 3.17 Ɛ−7 | 5.63 Ɛ−4 | |
| BES | 4.09 Ɛ−2 | 4.09 Ɛ−2 | 4.09 Ɛ−2 | 4.09 Ɛ−2 | 2.38 Ɛ−16 | 1.54 Ɛ−8 | |
| Range-2 | Proposed HCLBES | 4.0 Ɛ−2 | 4.07 Ɛ−2 | 4.07 Ɛ−2 | 4.07 Ɛ−2 | 1.84 Ɛ−22 | 1.36 Ɛ−11 |
| ASO | 4.20 Ɛ−2 | 5.62 Ɛ−2 | 4.56 Ɛ−2 | 4.48 Ɛ−2 | 1.05 Ɛ−5 | 3.24 Ɛ−3 | |
| HHO | 4.20 Ɛ−2 | 6.57 Ɛ−2 | 4.42 Ɛ−2 | 4.20 Ɛ−2 | 2.66 Ɛ−5 | 5.16 Ɛ−3 | |
| GWO | 4.07 Ɛ−2 | 4.24 Ɛ−2 | 4.10 Ɛ−2 | 4.08 Ɛ−2 | 2.19 Ɛ−7 | 4.68 Ɛ−4 | |
| SSA | 4.09 Ɛ−2 | 4.33 Ɛ−2 | 4.20 Ɛ−2 | 4.20 Ɛ−2 | 2.95 Ɛ−7 | 5.43 Ɛ−4 | |
| BES | 4.07 Ɛ−2 | 4.07 Ɛ−2 | 4.07 Ɛ−2 | 4.07 Ɛ−2 | 1.85 Ɛ−10 | 1.36 Ɛ−5 |
| Algorithm | MSE | MAE | RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NedStack PS6—Model | Proposed HCLBES | −1.08 | 3.54 Ɛ−3 | 7.06 Ɛ−5 | −9.54 Ɛ−5 | 1.26 Ɛ+1 | 1.36 Ɛ−2 | 1.00 Ɛ−4 | 7.12 Ɛ−2 | 2.05 Ɛ−1 | 2.67 Ɛ−1 |
| ASO | −1.04 | 3.43 Ɛ−3 | 7.11 Ɛ−5 | −9.54 Ɛ−5 | 1.72 Ɛ+1 | 1.68 Ɛ−1 | 2.41 Ɛ−4 | 1.26 Ɛ−1 | 3.10 Ɛ−1 | 4.02 Ɛ−1 | |
| HHO | −8.53 Ɛ−1 | 2.61 Ɛ−3 | 5.07 Ɛ−5 | −9.54 Ɛ−5 | 1.29 Ɛ+1 | 3.95 Ɛ−2 | 1.06 Ɛ−4 | 7.38 Ɛ−2 | 2.07 Ɛ−1 | 2.71 Ɛ−1 | |
| GWO | −1.03 | 3.31 Ɛ−3 | 6.36 Ɛ−5 | −9.54 Ɛ−5 | 1.30 Ɛ+1 | 5.43 Ɛ−2 | 1.05 Ɛ−4 | 7.49 Ɛ−2 | 2.09 Ɛ−1 | 2.73 Ɛ−1 | |
| SSA | −1.03 | 3.22 Ɛ−3 | 5.71 Ɛ−5 | −9.54 Ɛ−5 | 1.37 Ɛ+1 | 1.15 Ɛ−1 | 1.04 Ɛ−4 | 8.21 Ɛ−2 | 2.19 Ɛ−1 | 2.94 Ɛ−1 | |
| BES | −1.00 | 3.24 Ɛ−3 | 6.46 Ɛ−5 | −9.54 Ɛ−5 | 1.27 Ɛ+1 | 1.81 Ɛ−2 | 1.04 Ɛ−4 | 7.23 Ɛ−2 | 2.06 Ɛ−1 | 2.68 Ɛ−1 | |
| WSO [23] | −8.62 Ɛ−1 | 3.05 Ɛ−3 | 8.07 Ɛ−5 | −9.54 Ɛ−5 | 1.26 Ɛ+1 | 1.36 Ɛ−2 | 1.00 Ɛ−4 | 7.12 Ɛ−2 | 2.05 Ɛ−1 | 2.67 Ɛ−1 | |
| MVO [22] | −1.01 | 3.20 Ɛ−3 | 6.10 Ɛ−5 | −9.54 Ɛ−5 | 1.39 Ɛ+1 | 1.38 Ɛ−1 | 1.00 Ɛ−4 | 8.33 Ɛ−2 | 2.19 Ɛ−1 | 2.90 Ɛ−1 | |
| VSDE [46] | −1.09 | 3.68 Ɛ−3 | 7.86 Ɛ−5 | −9.54 Ɛ−5 | 1.26 Ɛ+1 | 1.40 Ɛ−2 | 1.00 Ɛ−4 | 7.13 Ɛ−2 | 2.05 Ɛ−1 | 2.67 Ɛ−1 | |
| HBO [25] | −1.06 | 3.54 Ɛ−3 | 7.50 Ɛ−5 | −9.54 Ɛ−5 | 1.2 Ɛ+1 | 1.36 Ɛ−2 | 1.01 Ɛ−4 | 7.13 Ɛ−2 | 2.05 Ɛ−1 | 2.67 Ɛ−1 | |
| ALO [24] | −8.53 Ɛ−1 | 2.41 Ɛ−3 | 3.65 Ɛ−5 | −9.54 Ɛ−5 | 1.29 Ɛ+1 | 4.47 Ɛ−2 | 1.00 Ɛ−4 | 7.42 Ɛ−2 | 2.06 Ɛ−1 | 2.72 Ɛ−1 | |
| HCLAOA [20] | −1.02 | 3.42 Ɛ−3 | 6.35 Ɛ−5 | −1.30 Ɛ−4 | 1.97 Ɛ+1 | 1.74 Ɛ−1 | 2.67 Ɛ−4 | 1.03 | 6.04 Ɛ−1 | 8.64 Ɛ−1 | |
| Horizon 500—Model | Proposed HCLBES | −1.03 | 3.22 Ɛ−3 | 6.85 Ɛ−5 | −1.90 Ɛ−4 | 2.17 Ɛ+1 | 1.36 Ɛ−2 | 8.00 Ɛ−4 | 2.89 Ɛ−2 | 1.33 Ɛ−1 | 1.70 Ɛ−1 |
| ASO | −1.02 | 3.18 Ɛ−3 | 6.70 Ɛ−5 | −1.92 Ɛ−4 | 1.95 Ɛ+1 | 1.70 Ɛ−2 | 1.61 Ɛ−4 | 3.86 Ɛ−2 | 1.41 Ɛ−1 | 1.95 Ɛ−1 | |
| HHO | −1.20 | 3.49 Ɛ−3 | 5.44 Ɛ−5 | −1.83 Ɛ−4 | 1.52 Ɛ+1 | 1.38 Ɛ−2 | 1.38 Ɛ−4 | 3.63 Ɛ−2 | 1.36 Ɛ−1 | 1.80 Ɛ−1 | |
| GWO | −1.02 | 3.09 Ɛ−3 | 6.16 Ɛ−5 | −1.91 Ɛ−4 | 1.95 Ɛ+1 | 1.36 Ɛ−2 | 5.21 Ɛ−4 | 2.92 Ɛ−2 | 1.31 Ɛ−1 | 1.71 Ɛ−1 | |
| SSA | −1.01 | 3.23 Ɛ−3 | 7.29 Ɛ−5 | −1.91 Ɛ−4 | 1.93 Ɛ+1 | 1.36 Ɛ−2 | 5.15 Ɛ−4 | 2.92 Ɛ−2 | 1.32 Ɛ−1 | 1.71 Ɛ−1 | |
| BES | −1.03 | 3.17 Ɛ−3 | 6.61 Ɛ−5 | −1.90 Ɛ−4 | 2.15 Ɛ+1 | 1.36 Ɛ−2 | 7.96 Ɛ−4 | 2.90 Ɛ−2 | 1.32 Ɛ−1 | 1.70 E−1 | |
| WSO [23] | −9.10 Ɛ−1 | 3.31 Ɛ−3 | 9.78 Ɛ−5 | −1.90 Ɛ−4 | 2.17 Ɛ+1 | 1.36 Ɛ−2 | 8.00 Ɛ−4 | 2.89 Ɛ−2 | 1.33 Ɛ−1 | 1.70 Ɛ−1 | |
| MVO [22] | −9.51 Ɛ−1 | 2.91 Ɛ−3 | 6.43 Ɛ−5 | −1.90 Ɛ−4 | 1.91 Ɛ+1 | 1.36 Ɛ−2 | 5.05 Ɛ−4 | 2.92 Ɛ−2 | 1.32 Ɛ−1 | 1.71 Ɛ−1 | |
| VSDE [46] | −1.04 | 3.28 Ɛ−3 | 7.03 Ɛ−5 | −1.90 Ɛ−4 | 2.15 Ɛ+1 | 1.36 Ɛ−2 | 7.89 Ɛ−4 | 2.90 Ɛ−2 | 1.33 Ɛ−1 | 1.70 Ɛ−1 | |
| HBO [25] | −1.12 | 3.60 Ɛ−3 | 7.60 Ɛ−5 | −1.90 Ɛ−4 | 2.17 Ɛ+1 | 1.36 Ɛ−2 | 8.00 Ɛ−4 | 2.89 Ɛ−2 | 1.33 Ɛ−1 | 1.70 Ɛ−1 | |
| ALO [24] | −9.24 Ɛ−1 | 2.76 Ɛ−3 | 5.94 Ɛ−5 | −1.91 Ɛ−4 | 1.76 Ɛ+1 | 1.36 Ɛ−2 | 2.67 Ɛ−4 | 2.94 Ɛ−2 | 1.33 Ɛ−1 | 1.72 Ɛ−1 | |
| HCLAOA [20] | −1.05 | 3.14 Ɛ−3 | 6.09 Ɛ−5 | −1.45 Ɛ−4 | 2.01 Ɛ+1 | 4.41 Ɛ−2 | 4.79 Ɛ−4 | 8.88 Ɛ−1 | 6.10 Ɛ−1 | 7.47 Ɛ−1 | |
| BCS 500 W—Model | Proposed HCLBES | −1.03 | 2.97 Ɛ−3 | 7.71 Ɛ−5 | −1.31 Ɛ−4 | 2.25 Ɛ+1 | 2.17 Ɛ−2 | 8.00 Ɛ−4 | 6.74 Ɛ−3 | 6.57 Ɛ−2 | 8.21 Ɛ−2 |
| ASO | −9.90 Ɛ−1 | 2.65 Ɛ−3 | 6.24 Ɛ−5 | −1.27 Ɛ−4 | 1.84 Ɛ+1 | 2.30 Ɛ−2 | 1.28 Ɛ−4 | 1.11 Ɛ−2 | 8.07 Ɛ−2 | 9.66 Ɛ−2 | |
| HHO | −1.12 | 3.07 Ɛ−3 | 6.36 Ɛ−5 | −1.28 Ɛ−4 | 1.76 Ɛ+1 | 2.00 Ɛ−2 | 1.75 Ɛ−4 | 8.08 Ɛ−3 | 6.97 Ɛ−2 | 8.54 Ɛ−2 | |
| GWO | −1.02 | 2.77 Ɛ−3 | 6.49 Ɛ−5 | −1.33 Ɛ−4 | 2.01 Ɛ+1 | 2.20 Ɛ−2 | 3.21 Ɛ−4 | 6.85 Ɛ−3 | 6.53 Ɛ−2 | 8.27 Ɛ−2 | |
| SSA | −1.03 | 2.73 Ɛ−3 | 5.80 Ɛ−5 | −1.30 Ɛ−4 | 1.93 Ɛ+1 | 2.01 Ɛ−2 | 4.22 Ɛ−4 | 6.93 Ɛ−3 | 6.64 Ɛ−2 | 8.33 Ɛ−2 | |
| BES | −9.93 Ɛ−1 | 2.95 Ɛ−3 | 8.31 Ɛ−5 | −1.32 Ɛ−4 | 2.16 Ɛ+1 | 2.17 Ɛ−2 | 6.65 Ɛ−4 | 6.78 Ɛ−3 | 6.58 Ɛ−2 | 8.22 Ɛ−2 | |
| WSO [23] | −1.01 | 2.42 Ɛ−3 | 4.15 Ɛ−5 | −1.31 Ɛ−4 | 2.25 Ɛ+1 | 2.18 Ɛ−2 | 8.00 Ɛ−4 | 6.74 Ɛ−3 | 6.57 Ɛ−2 | 8.21 Ɛ−2 | |
| MVO [22] | −1.02 | 2.87 Ɛ−3 | 7.08 Ɛ−5 | −1.31 Ɛ−4 | 1.96 Ɛ+1 | 2.04 Ɛ−2 | 3.98 Ɛ−4 | 6.95 Ɛ−3 | 6.90 Ɛ−2 | 8.70 Ɛ−2 | |
| VSDE [46] | −1.08 | 3.03 Ɛ−3 | 6.91 Ɛ−5 | −1.31 Ɛ−4 | 2.15 Ɛ+1 | 2.16 Ɛ−2 | 6.57 Ɛ−4 | 6.81 Ɛ−3 | 6.60 Ɛ−2 | 8.24 Ɛ−2 | |
| HBO [25] | −1.11 | 3.38 Ɛ−3 | 8.86 Ɛ−5 | −1.32 Ɛ−4 | 2.24 Ɛ+1 | 2.20 Ɛ−2 | 7.52 Ɛ−4 | 6.77 Ɛ−3 | 6.57 Ɛ−2 | 8.22 Ɛ−2 | |
| ALO [24] | −9.90 Ɛ−1 | 2.51 Ɛ−3 | 5.16 Ɛ−5 | −1.31 Ɛ−4 | 1.88 Ɛ+1 | 2.03 Ɛ−2 | 2.91 Ɛ−4 | 6.84 Ɛ−3 | 6.62 Ɛ−2 | 8.28 Ɛ−2 | |
| HCLAOA [20] | −1.04 | 2.96 Ɛ−3 | 6.29 Ɛ−5 | −1.50 Ɛ−4 | 2.21 Ɛ+1 | 4.81 Ɛ−2 | 5.08 Ɛ−4 | 1.42 | 7.89 Ɛ−1 | 9.11 Ɛ−1 |
| Algorithm | Best | Worst | Aver | Median | Var | Std | |
|---|---|---|---|---|---|---|---|
| NedStack PS6—Model | Proposed HCLBES | 7.12 Ɛ−2 | 7.13 Ɛ−2 | 7.12 Ɛ−2 | 7.12 Ɛ−2 | 2.96 Ɛ−10 | 1.72 Ɛ−5 |
| ASO | 8.30 Ɛ−2 | 1.87 Ɛ−1 | 1.26 Ɛ−1 | 1.27 Ɛ−1 | 7.58 Ɛ−4 | 2.75 Ɛ−2 | |
| HHO | 7.17 Ɛ−2 | 8.69 Ɛ−2 | 7.38 Ɛ−2 | 7.28 Ɛ−2 | 1.26 Ɛ−5 | 3.54 Ɛ−3 | |
| GWO | 7.13 Ɛ−2 | 8.29 Ɛ−2 | 7.49 Ɛ−2 | 7.36 Ɛ−2 | 1.49 Ɛ−5 | 3.85 Ɛ−3 | |
| SSA | 7.12 Ɛ−2 | 1.12 Ɛ−1 | 8.21 Ɛ−2 | 7.60 Ɛ−2 | 1.43 Ɛ−4 | 1.20 Ɛ−2 | |
| BES | 7.12 Ɛ−2 | 7.81 Ɛ−2 | 7.23 Ɛ−2 | 7.21 Ɛ−2 | 1.99 Ɛ−6 | 1.41 Ɛ−3 | |
| Horizon 500—Model | Proposed HCLBES | 2.89 Ɛ−2 | 2.89 Ɛ−2 | 2.89 Ɛ−2 | 2.89 Ɛ−2 | 5.33 Ɛ−19 | 7.30 Ɛ−10 |
| ASO | 3.14 Ɛ−2 | 4.84 Ɛ−2 | 3.86 Ɛ−2 | 3.84 Ɛ−2 | 2.39 Ɛ−5 | 4.89 Ɛ−3 | |
| HHO | 2.98 Ɛ−2 | 8.83 Ɛ−2 | 3.63 Ɛ−2 | 3.03 Ɛ−2 | 3.35 Ɛ−4 | 1.83 Ɛ−2 | |
| GWO | 2.90 Ɛ−2 | 2.95 Ɛ−2 | 2.92 Ɛ−2 | 2.90 Ɛ−2 | 5.91 Ɛ−8 | 2.43 Ɛ−4 | |
| SSA | 2.90 Ɛ−2 | 2.95 Ɛ−2 | 2.92 Ɛ−2 | 2.91 Ɛ−2 | 4.24 Ɛ−8 | 2.06 Ɛ−4 | |
| BES | 2.89 Ɛ−2 | 2.90 Ɛ−2 | 2.90 Ɛ−2 | 2.89 Ɛ−2 | 3.45 Ɛ−10 | 1.86 Ɛ−5 | |
| BCS 500 W—Model | Proposed HCLBES | 6.74 Ɛ−3 | 6.74 Ɛ−3 | 6.74 Ɛ−3 | 6.74 Ɛ−3 | 4.90 Ɛ−13 | 7.00 Ɛ−7 |
| ASO | 6.83 Ɛ−3 | 2.10 Ɛ−2 | 1.11 Ɛ−2 | 9.78 Ɛ−3 | 2.29 Ɛ−5 | 4.78 Ɛ−3 | |
| HHO | 6.88 Ɛ−3 | 1.63 Ɛ−2 | 8.08 Ɛ−3 | 6.91 Ɛ−3 | 8.63 Ɛ−6 | 2.94 Ɛ−3 | |
| GWO | 6.77 Ɛ−3 | 7.11 Ɛ−3 | 6.85 Ɛ−3 | 6.81 Ɛ−3 | 1.07 Ɛ−8 | 1.04 Ɛ−4 | |
| SSA | 6.77 Ɛ−3 | 7.26 Ɛ−3 | 6.93 Ɛ−3 | 6.90 Ɛ−3 | 2.59 Ɛ−8 | 1.61 Ɛ−4 | |
| BES | 6.75 Ɛ−3 | 6.82 Ɛ−3 | 6.78 Ɛ−3 | 6.77 Ɛ−3 | 5.63 Ɛ−10 | 2.37 Ɛ−5 |
| Algorithm | PEMFC 250 W | PEMFC 5000 W | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1/1-Bar 343.15 K | 3/5-Bar 343.15 K | NedStack PS6 | BSC500 W | Horizon 500 W | |||||||||||
| Aver | Std | Aver | Std | Aver | Std | Aver | Std | Aver | Std | ||||||
| Proposed HCLBES | 46.45 | 26.44 | 1 | 38.49 | 21.91 | 1 | 60.33 | 34.95 | 1 | 14.61 | 7.83 | 1 | 17.10 | 9.24 | 1 |
| ASO | 8.68 | 0.91 | 16 | 7.18 | 0.32 | 29 | 8.76 | 0.57 | 28 | 7.50 | 0.20 | 3 | 9.31 | 1.20 | 1 |
| HHO | 5.76 | 0.25 | 14 | 4.86 | 0.04 | 7 | 6.06 | 0.25 | 1 | 5.56 | 0.04 | 6 | 6.60 | 0.81 | 2 |
| GWO | 2.25 | 0.18 | 19 | 1.85 | 0.04 | 11 | 2.39 | 0.31 | 3 | 2.09 | 0.03 | 4 | 2.32 | 0.10 | 9 |
| SSA | 3.34 | 0.32 | 9 | 2.39 | 0.08 | 11 | 2.80 | 0.04 | 14 | 2.64 | 0.05 | 3 | 2.90 | 0.17 | 4 |
| BES | 3.70 | 0.20 | 10 | 2.48 | 0.04 | 22 | 2.98 | 0.07 | 6 | 2.79 | 0.12 | 8 | 3.13 | 0.17 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, A.K.; Hussain, A.N.; Al-Obaidi, M.A.; Al-Anssari, S. Upgrading Sustainability in Clean Energy: Optimization for Proton Exchange Membrane Fuel Cells Using Heterogeneous Comprehensive Learning Bald Eagle Search Algorithm. Sustainability 2025, 17, 9729. https://doi.org/10.3390/su17219729
Ali AK, Hussain AN, Al-Obaidi MA, Al-Anssari S. Upgrading Sustainability in Clean Energy: Optimization for Proton Exchange Membrane Fuel Cells Using Heterogeneous Comprehensive Learning Bald Eagle Search Algorithm. Sustainability. 2025; 17(21):9729. https://doi.org/10.3390/su17219729
Chicago/Turabian StyleAli, Ahmed K., Ali Nasser Hussain, Mudhar A. Al-Obaidi, and Sarmad Al-Anssari. 2025. "Upgrading Sustainability in Clean Energy: Optimization for Proton Exchange Membrane Fuel Cells Using Heterogeneous Comprehensive Learning Bald Eagle Search Algorithm" Sustainability 17, no. 21: 9729. https://doi.org/10.3390/su17219729
APA StyleAli, A. K., Hussain, A. N., Al-Obaidi, M. A., & Al-Anssari, S. (2025). Upgrading Sustainability in Clean Energy: Optimization for Proton Exchange Membrane Fuel Cells Using Heterogeneous Comprehensive Learning Bald Eagle Search Algorithm. Sustainability, 17(21), 9729. https://doi.org/10.3390/su17219729








