Incentives for Sustainable Governance in Blockchain-Based Organizations ^†

Abstract

This study analyzes how blockchain technology can be interpreted through an economic perspective, viewing network nodes as rational agents whose strategic behavior affects the efficiency and sustainability of decentralized systems. Using a multi-player non-cooperative game with complete but imperfect information, we model validators’ decisions in voting-based consensus mechanisms and compare alternative incentive configurations through simulation results. The analysis shows how variations in reward schemes influence validators’ behavior and consensus reliability. Extending the framework to Decentralized Autonomous Organizations (DAOs), the study explores how blockchain-based incentives can enhance participation, accountability, and decentralized governance. The findings highlight that incentive design plays a decisive role in aligning individual motivations with collective goals, ensuring both network integrity and long-term sustainability. Overall, this study connects economic theory with blockchain governance, extending its relevance to business and organizational contexts beyond cryptocurrencies.

1. Introduction

Blockchain technology has drawn increasing interest from both computer scientists and economists recently, initially because of its role in supporting cryptocurrencies, such as Bitcoin [1], the most well-known example of a blockchain-based decentralized cryptocurrency. It is now widely recognized, however, as a general-purpose technology [2] with potential applications far beyond monetary systems. Blockchain solutions are being adopted in diverse sectors, including supply chain management, healthcare, digital identity, finance, education, environmental governance, and both private and public administration, where their decentralized structure enhances transparency, security, and efficiency [3].

In supply chain logistics, blockchain technology offers the advantages of reducing supply chain fraud and enhancing traceability because it ensures transparent records and accountability [4]. In the healthcare domain, blockchain enables the safe and efficient sharing of medical records and safeguards the confidentiality of health data [5]. Similarly, blockchain-enabled digital identity systems offer decentralized and resilient platforms for verifying individual identities, thereby lowering the risk of identity theft and strengthening personal control over one’s private data [6]. In these settings, blockchain adoption not only fosters transparency and curtails opportunistic behavior but also supports greater economic and environmental sustainability. For instance, in supply chains, blockchain-enabled traceability can help minimize waste, streamline logistics operations, and improve energy efficiency, directly contributing to lower emissions and reduced overall coordination costs.

Participation in blockchain networks relies on incentive mechanisms. In cryptocurrency-based blockchains, such incentives usually take the form of cryptocurrency rewards. In non-cryptocurrency applications, participation is encouraged by rewards or digital assets. For instance, in supply chains that leverage blockchain technology, participants are rewarded with tokens for providing precise and timely data inputs. This practice underpins the overall efficiency and trustworthiness of the supply chain [7]. These incentive structures not only safeguard the system’s integrity but also promote cooperative behavior among stakeholders. At the same time, incentive design must consider long-term economic and environmental sustainability, favoring consensus protocols, such as Proof-of-Stake or hybrid variants, that limit energy consumption while ensuring efficiency and fairness.

This study aims to integrate key blockchain features into an economic framework. An economic perspective can complement the extensive body of research developed within computer science and provide valuable insights into decision-making and the management of incentive problems. Such interdisciplinary integration is particularly important in applications where opportunistic behavior may emerge. From an economic standpoint, blockchain nodes are viewed as agents with their own preferences and incentives, capable of free-riding. In economic terms, a free-rider is someone who benefits from public goods without bearing any of the associated costs. If not properly addressed, free-riding undermines not only the integrity of decentralized systems but also their economic sustainability, as it increases overall their maintenance costs. From an environmental perspective, inefficiencies in participation mechanisms may amplify energy waste and reduce the comparative advantage of blockchain solutions over centralized alternatives.

Blockchain technology has revolutionized various industries by introducing decentralized systems that enhance transparency, security, and efficiency [8]. Previous research has extensively analyzed incentive mechanisms within blockchain networks, focusing on how they influence participant behavior and network performance. These analyses often employ game theory to model strategic interactions among network participants, considering both economic incentives and the ethical and legal challenges that arise in decentralized systems. The present study contributes to this body of literature by analyzing different reward mechanisms designed to align the incentives of self-interested agents seeking to maximize their utility functions. The contribution is primarily analytical, supported by formal mathematical proofs and validated through simulation results. Compared to existing research [9], this study extends the evaluation of incentive compatibility constraints by explicitly considering the intrinsic satisfaction deriving from adherence to or sabotage of organizational stability, beyond simple extrinsic rewards.

Furthermore, by extending the concept of incentive compatibility to organizational frameworks structured as DAOs, this study investigates how incentive mechanisms can support decentralized governance systems, while considering economic implications and legal constraints. This extension is essential for understanding how authority can be decentralized in organizations, reflecting the distributed nature of blockchain technology itself. The analysis illustrates how reward structures and blockchain-based organizational models can be designed to ensure economic efficiency, reduce energy costs, and enhance organizational resilience.

Overall, this study seeks to understand how economic incentives can foster forms of decentralized governance that are both efficient and sustainable. The research question is formulated as follows: How can incentive design promote sustainable governance in decentralized organizations?

This study is a revised and expanded version of a paper entitled “Incentive Compatibility in Consensus Protocols and DAOs: A Game-Theoretic Approach,” which was presented at the 6th Distributed Ledger Technology Workshop (DLT2024), Turin (Italy) [10]. In this extended version, the incentive compatibility issue within non-cryptocurrency blockchain is explored in its implications for Decentralized Autonomous Organizations (DAOs). DAOs are explored not only as a technological innovation but as a novel approach to economic organization and governance. While the technical aspects of DAOs and vulnerabilities, like the Reentrancy Attack, have been thoroughly explored in the IT literature, there is a noticeable gap in the analysis of their economic and legal implications.

The remainder of this study is organized as follows: Section 2 presents and discusses case studies on free-riding within blockchain technology. Section 3 reviews the economic literature on blockchain technologies. Section 4 analyzes the incentive compatibility of two alternative reward schemes for voting-based consensus mechanisms. Section 5 examines governance challenges within DAOs and their role in the blockchain ecosystem. Section 6 concludes with our key findings and policy implications.

2. Free-Riding and the Blockchain: Some Case Studies

Free-riding is a well-established topic in the literature on public economics [11] and can be analyzed through a game-theoretic lens. In a simplified two-player economy, the socially optimal Pareto outcome diverges from the Nash equilibrium because each participant has an incentive to under-contribute.

In decentralized blockchain environments, the coordination of multiple autonomous agents creates similar opportunities for free-riding. Without a central authority to monitor and enforce compliance, participants may strategically withhold information or misreport transactions. These vulnerabilities are particularly significant in applications, such as supply chain management, public record-keeping, and collective decision-making. In blockchain-enabled supply chains, participants may underreport transactions or distort information to gain an advantage while still benefiting from the shared infrastructure. In decentralized finance (DeFi), free-riding can emerge through collusion or strategic inaction, reducing accountability. Similarly, in blockchain-based identity, certification, or procurement systems, actors may submit false or redundant verification requests, undermining trust and efficiency. In the absence of the direct oversight characteristic of centralized systems, such practices can erode the integrity and trust that are fundamental to blockchain operations. Free-riding also generates inefficiencies and raises operating costs, potentially making blockchain networks economically unsustainable unless effective incentive mechanisms are in place [12]. Simulations confirm that the level of honest participation in a blockchain system is critically dependent on the design of the incentives and highlight the fragility of the cooperative balance required to sustain blockchain networks [13].

Economics addresses problem-solving and decision-making through an emphasis on agent behavior, dynamic interactions, and systemic interdependencies. By contrast, computer science focuses on system architecture, algorithmic optimization, and information processing, typically dealing with well-defined and logically structured problems to ensure technical efficiency and precision. Bridging these two perspectives is crucial for designing blockchain solutions that combine technical robustness with long-term economic viability. Computer science typically models agents in dichotomous terms, as “honest” or “malicious” and shows that protocols remain reliable as long as the proportion of malicious participants remains below a defined threshold [14].

The 2016 attack on the Decentralized Autonomous Organization (DAO) serves as a significant illustration of blockchain’s ethical and security challenges. Exploiting a flaw in the code of the DAO, a hacker diverted 3.6 million Ether (approximately 50 million U.S. dollars) into a personal account. The DAO represented an early experiment in blockchain-based governance, designed to democratize fundraising for participants. This incident exposed critical vulnerabilities in such platforms and triggered a contentious debate on the principle of blockchain immutability. As a consequence, a network hard fork was implemented with the creation of Ethereum Classic, leading to a fundamental reassessment of the roles of hard and soft forks in blockchain governance [15].

The incident escalated when the attacker published an open letter to the Ethereum and DAO communities arguing that exploiting a systemic flaw was legal and threatening legal action against any effort to recover the funds. These actions highlighted the challenges of translating ethical norms into purely technical safeguards. Ultimately, the community abandoned the soft fork due to these newly discovered vulnerabilities and adopted a hard fork instead. The resulting split into Ethereum (ETH) and Ethereum Classic (ETC) not only resolved the immediate crisis but also stimulated a wider debate about censorship resistance and the principle of blockchain immutability [16].

The breadth of the economic questions raised by blockchain becomes particularly evident in contexts of asymmetric information. Several studies underscore the considerable room for investigation and theoretical development that remains within this emerging area of research [17]. Moreover, several studies highlight the divergence between assumptions made by computer science and economic theories concerning individual behavior [18]. Game-theoretic approaches typically assume fully rational agents, while traditional computer-science frameworks distinguish between processes that follow the prescribed protocol and Byzantine processes that deviate from it, thereby offering a more nuanced, yet still rule-based, view of behavior [18].

An illustrative case of behavioral complexity is Dogecoin, a cryptocurrency created in 2013 as a parody. Defying the rational predictions posited by game theory, Dogecoin has nevertheless achieved substantial popularity and market capitalization despite its satirical origins [19]. From an economic standpoint, the presence of cryptocurrencies like Dogecoin underscores the influence of psychological and social factors on market valuation. This example demonstrates that economic analysis of blockchain phenomena cannot disregard human behavioral dynamics, which add further complexity to the relationship between information technology and economics in this emerging field.

Recognizing this complexity, the following section reviews how previous research has addressed the interplay among incentives, behavior, and governance in blockchain systems from both economic and computer-science perspectives.

3. Overview of Previous Work

Numerous authors have explored the effect of an economic perspective on blockchain technology [20], but their discussion has mainly focused on the cryptocurrency field. Non-cryptocurrency blockchains differ substantially in the design of their monetary incentives and are frequently implemented as permissioned systems, since fully public blockchains can be unsuitable for corporate or administrative use [21]. This divergence raises important questions about how incentive structures developed for cryptocurrencies can be adapted to alternative settings.

In blockchain ecosystems, incentive structures are pivotal in encouraging miners to engage in validation activities, thereby ensuring the ongoing operation and stability of the network. Although such mechanisms have proven effective in cryptocurrency contexts, adapting them to non-cryptocurrency applications presents a considerable challenge. Insufficient or poorly aligned incentives can therefore hinder the broader adoption of blockchain technology.

The concept of incentive compatibility, which ensures that no participant finds it advantageous to break the rules [22], is particularly relevant in this context. Within the blockchain context, incentive mechanisms are designed to ensure that the consensus protocol motivates validators to act honestly and cooperatively, complying with established rules and supporting the network’s security and stability. Such incentives can include crypto rewards and penalties, as well as reputational incentives, including trust-based ratings or sanctions for deviations from expected behavior. The incentive-compatible mechanisms that operate successfully in cryptocurrency blockchains, however, are not easily transferable to non-cryptocurrency applications [9]. This requirement is particularly evident in blockchain applications that employ voting-based consensus algorithms. The existing research on this topic remains limited and predominantly focuses on designing incentive mechanisms for cryptocurrency systems that rely on proof-based consensus models [9].

It is, therefore, crucial to recognize that analyses of incentive compatibility developed for Proof-of-Work (PoW) systems cannot be directly applied to Practical Byzantine Fault Tolerance (PBFT)-based blockchains, given the fundamental differences between proof-based and voting-based consensus mechanisms. Overcoming this divide is vital for effectively integrating blockchain technology into non-cryptocurrency applications. The effectiveness of any consensus mechanism ultimately depends on the strategic behavior of the participating entities [23].

Voting-based consensus is also used in some permissionless cryptocurrency blockchains, where the large number of unidentified nodes allows for probabilistic consensus. Within this setting, rapid probabilistic consensus protocols [24,25] can lower communication costs without incurring PoW energy costs [26]. Nevertheless, to preserve network consistency and security, nodes must adhere strictly to protocol rules. The inclusion of the term “Byzantine” reflects the recognition that some nodes may act maliciously or fail to comply with the protocol. This concept is derived from the well-known Byzantine Generals Problem [27], a theoretical framework that describes the coordination problem that arises when erroneous information or malicious behavior occurs. To ensure the security and integrity of the system, a consensus algorithm is needed to prevent such malicious behavior.

Identity management and voting further illustrate these challenges [28]. Secure blockchain-based voting frameworks combine immutable identity records with cryptographic methods, such as zero-knowledge proofs and homomorphic encryption, to guarantee both voter anonymity and ballot integrity [29,30]. Digital identities are stored on-chain and governed by smart contracts that specify the creation and update rules, including possible verification by trusted authorities [31]. The voting process is regulated through smart contracts, and cryptography ensures the anonymity of votes. Smart contracts regulate the addition of new identities to the registry through a majority rule [32]. New identities are added through majority approval or other anti-Sybil mechanisms [33].

Approaches to malicious behavior differ markedly among disciplines. Computer science generally classifies nodes as either honest or faulty and analyzes protocols that remain secure as long as the percentage of faulty nodes stays below a critical threshold. Economics, by contrast, focuses on agents’ utility functions and equilibrium strategies, yielding a richer account of strategic behavior. Game theory can be indispensable in addressing the self-interested nature of participants by suggesting how the incentive design may efficiently persuade participants to behave proactively [34]. Designing blockchain incentives through a game-theoretic lens is essential for motivating rational, self-interested participants and improving network performance [35]. While game theory has proven effective in many blockchain studies, its application to PBFT is limited.

The existing studies on PBFT incentive compatibility illustrate both the progress in the field and the persistent gaps. For example, the SmartCast framework [36] introduces an off-chain incentive mechanism to address such issues, yet its effectiveness diminishes in public peer-to-peer environments, as illustrated by certain Internet of Things (IoT) applications [37]. Solidus [38] proposes a PoW-based PBFT algorithm that improves incentive compatibility but remains tied to PoW proposer selection, restricting its relevance to cryptocurrency contexts. Similarly, Wei et al. (2020) present a game-theoretic approach that concentrates on business-model incentives but offers only limited insight into the operational complexities of sustaining blockchain networks [39]. In parallel, researchers have enhanced PBFT consensus with reputation-based techniques [40,41]. While these methods improve validator selection efficiency, they do not directly resolve the fundamental incentive-compatibility problems of PBFT-based blockchains.

Taken together, these contributions underscore both the theoretical and practical importance of incentive design for non-cryptocurrency blockchains. They also reveal significant research gaps, particularly the need for integrated frameworks that reconcile consensus efficiency with robust incentive compatibility in PBFT-based architecture.

4. Reward Schemes for Vote-Based Consensus Blockchains

The broadcast process is a core element of blockchain technology. This implies the emergence of potential asymmetric information, as nodes possess private information about the content of each message they receive. The message may take a binary form, such as the retrieve/attack signal described in the Byzantine problem [27].

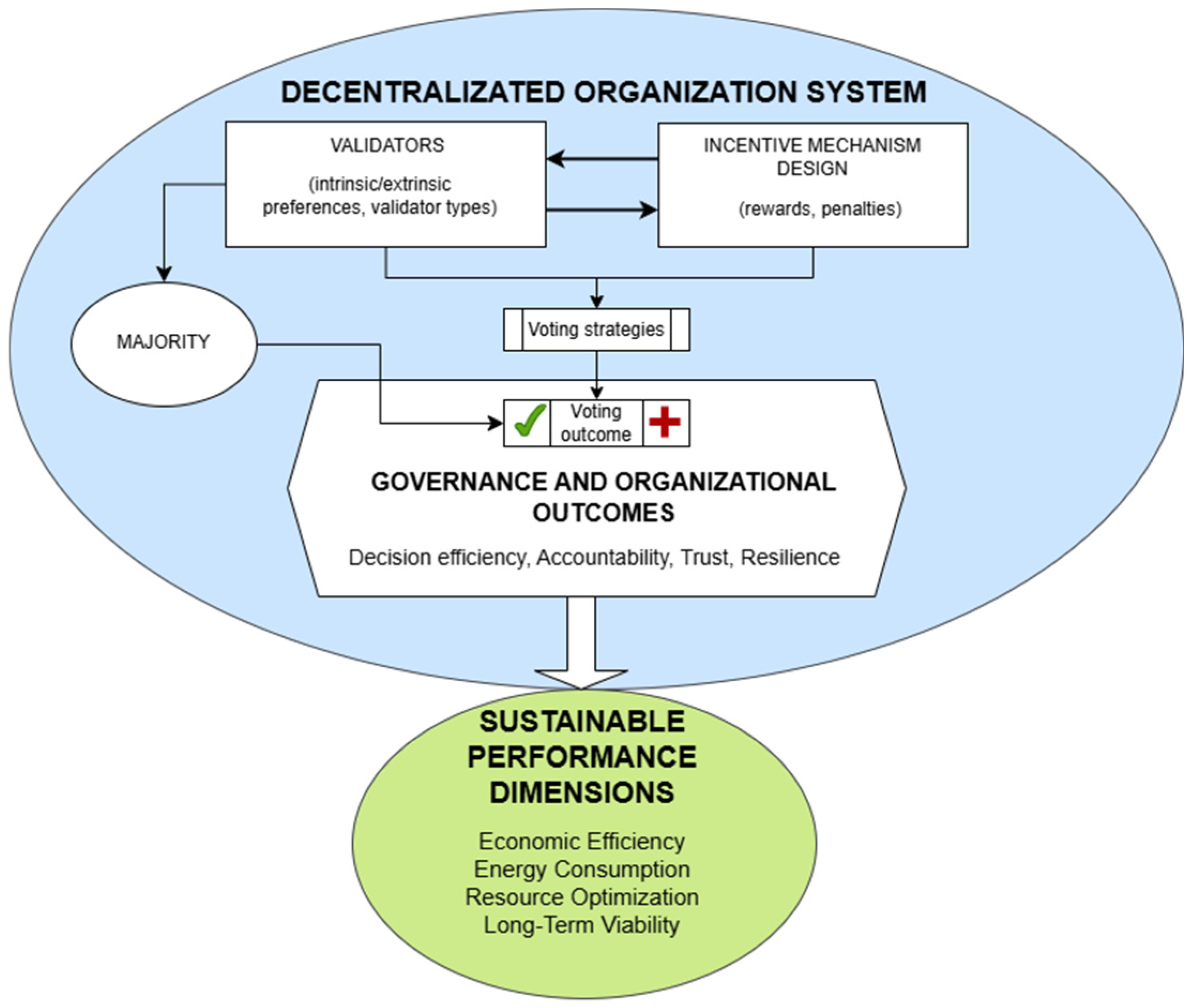
When coming to a non-crypto blockchain, the binary choice may be a true/false alternative. Consider the use of non-cryptocurrency blockchains for certifying competencies, property rights, or other individual characteristics. Agents acting as faulty or malicious nodes may obtain private gains by certifying false information. Consequently, the malicious agent may be externally incentivized to certify features that are not true and to broadcast messages that differ from the ones received. This is an opportunist behavior, adopted by a self-interested validator. In contrast, the honest node always broadcasts the message received. In what follows, it will be assumed that honest and malicious nodes (agents) have different utility functions. Different incentive compatibility constraints and the dominant strategies (when they exist) for each type of agent will be consequently derived. The objective is to show how an optimal reward scheme can be designed. This could be a prominent feature to ensure a reliable application of blockchain technologies for commercial, institutional, and industrial uses.

4.1. Theoretical Model

The base model considers a blockchain with n = 3k + 1 validators. The PBFT protocol assumes that a block is accepted if at least 2k + 1 validators agree on its acceptance. Each validator i agrees upon the block acceptance through a v_i vote (i = 1, …, n), which can take two values:

$$v_i=\left\{ \begin{array}{c}1 agreement\\ 0 rejection\end{array}\right.$$

(1)

The block is accepted if ${\sum }_{i=1}^n{v}_i>{\displaystyle \frac{2}{3}}n$. The block is rejected if ${\sum }_{i=1}^n{v}_i\le {\displaystyle \frac{2}{3}}n$.

This scenario is a simple representation of a PBFT protocol, where validators receive a block proposal message M = (x, y), where x is the content and y is the result of the voting process on the message. In detail:

$$x=\left\{\begin{array}{c}1 if the message is true\\ 0 if the message is false\end{array}\right.$$

(2)

$$y=\left\{\begin{array}{c}1 if the message is approved\\ 0 if the message is not approved\end{array}\right.$$

(3)

In the blockchain validation process, validators may receive a positive reward (w_i > 0).

The following behavioral hypotheses will be adopted:

H1. 

Validators can read the message and comprehend whether it is either valid or invalid.

H2. 

Honest validators gain increasing utility from the acceptance of valid blocks and the rejection of false blocks (with the same satisfaction gain). Faulty validators gain increasing utility from the acceptance of invalid blocks and the rejection of valid blocks (with the same satisfaction gain).

H3. 

Both types of validators have increasing utility in positive w_i.

The utility functions of the faulty (F) and honest (H) agents, as $U_{H,F}=f(M, w_i)$ can be accordingly described in their functional forms.

$${{U\prime }_H}_M={\displaystyle \frac{\partial U_H}{\partial M}}\left\{\begin{array}{ccc}>0 if M& =& \left\{\begin{array}{c}\left(\mathrm{1,1}\right) a true message is approved\\ \left(\mathrm{0,0}\right) a false message is not approved\end{array}\right.\\ & =& 0 otherwise\end{array}\right.$$

(4)

$${U\prime }_{F_M}={\displaystyle \frac{\partial U_F}{\partial M}}\left\{\begin{array}{ccc}>0 if M& =& \left\{\begin{array}{c}\left(\mathrm{1,0}\right) a true message is not approved\\ \left(\mathrm{0,1}\right) a false message is approved\end{array}\right.\\ & =& 0 otherwise\end{array}\right.$$

(5)

Accordingly, honest validators gain increasing utility both from the acceptance of valid blocks and from the rejection of false ones. This represents the intrinsic satisfaction derived from contributing to the proper functioning of the blockchain or the involvement in community [41]. Faulty validators, by contrast, aim to accept invalid blocks and reject valid ones (H2); their intrinsic satisfaction is thus associated with the attempt to disrupt the system. In both cases, utility also increases with the extrinsic reward (H3).

$${U\prime }_{H_w}={\displaystyle \frac{\partial U_H}{\partial w}}>0$$

(6)

$${U\prime }_{F_w}={\displaystyle \frac{\partial U_F}{\partial w}}>0$$

(7)

To simplify the notations without losing generality, let a = ${{U\prime }_H}_M/{U\prime }_{H_w}$ denote the ratio between intrinsic and extrinsic marginal satisfaction for honest nodes, and let b = ${{U\prime }_F}_M/{U\prime }_{F_w}$ represent the corresponding ratio for faulty nodes.

Based on these behavioral assumptions, the analysis will compare two remuneration schemes to verify the final payoffs for both types of validators. The two schemes can be summarized as follows:

Scheme A. If the vote is v_i = 1 and the block is accepted, the validator receives a positive w_i. If the vote is v_i = 0, no reward is provided.

Scheme B. If the vote is v_i = 1 and the block is accepted, the validator receives a positive w_i. If the vote is v_i = 0, and the block is rejected, the validator receives a positive w_i.

The difference between the two schemes lies in the treatment of rejection votes, which becomes critical in aligning individual incentives with collective objectives. By comparing payoffs (see

Table A1. Final payoffs—Scheme A—honest nodes.

Strategies	Messages
	M = (1, 1)	M = (1, 0)	M = (0, 0)	M = (0, 1)
vi = 1	$(a+1){U\prime }_{H_w}$		$a{U\prime }_{H_w}$	${U\prime }_{H_w}$
vi = 0	$a{U\prime }_{H_w}$		$a{U\prime }_{H_w}$

,

Table A2. Final payoffs—Scheme A—faulty nodes.

Strategies	Messages
	M = (1, 1)	M = (1, 0)	M = (0, 0)	M = (0, 1)
vi = 1	${U\prime }_{F_w}$	${bU\prime }_{F_w}$		$(b+1){U\prime }_{F_w}$
vi = 0		${bU\prime }_{F_w}$		${bU\prime }_{F_w}$

,

Table A3. Final payoffs—Scheme B—honest nodes.

Strategies	Messages
	M = (1, 1)	M = (1, 0)	M = (0, 0)	M = (0, 1)
vi = 1	$(a+1){U\prime }_{H_w}$		$a{U\prime }_{H_w}$	${U\prime }_{H_w}$
vi = 0	$a{U\prime }_{H_w}$	${U\prime }_{H_w}$	$(a+1){U\prime }_{H_w}$

and

Table A4. Final payoffs—Scheme B—faulty nodes.

Strategies	Messages
	M = (1, 1)	M = (1, 0)	M = (0, 0)	M = (0, 1)
vi = 1	${U\prime }_{F_w}$	${bU\prime }_{F_w}$		$(b+1){U\prime }_{F_w}$
vi = 0		$(b+1){U\prime }_{F_w}$	${U\prime }_{F_w}$	${bU\prime }_{F_w}$

in the Appendix A), it emerges that, in Scheme A, the agreement vote (v_i = 1) is a dominant strategy for both honest and faulty nodes since only validators who agree on the block are rewarded. In Scheme B, no dominant strategy emerges for either type of node.

Nevertheless, payoffs depend on the voting outcome. Validators make their choices based on whether the message content is valid or invalid, without knowing if it will ultimately be accepted. The final payoffs must be expressed as expected value, conditional on the probability of block acceptance or rejection.

To compute the expected results y^e, we assume expectations follow on the PBFT distribution between honest and faulty nodes. Recalling that the PBFT protocol assumes that 2k + 1 validators are honest, the probability of block acceptance/rejection follows Equations (8) and (9).

$$\pi \left(\mathrm{1,1}\right)=\pi \left(\mathrm{0,0}\right)={\displaystyle \frac{2}{3}}n+1$$

(8)

$$\pi \left(\mathrm{1,0}\right)=\pi \left(\mathrm{0,1}\right)={\displaystyle \frac{1}{3}}n-1$$

(9)

Using these probabilities, the expected payoffs for the honest (EV_H) and faulty (EV_F) nodes in Scheme A can be computed (see Equations (A1)–(A4) in the Appendix A).

By comparing the expected payoffs, it emerges that, for honest validators, v_i = 1 is a dominant strategy when facing valid blocks. Conversely, for false blocks, v_i = 0 becomes dominant only if $a>{\displaystyle \frac{1}{3}}n$. In this framework, rejection of false blocks depends on the validator’s preference for honest behavior and on the network size. The balance between intrinsic and extrinsic satisfaction is crucial in determining dominant strategies.

For faulty nodes, v_i = 1 is a dominant strategy for false blocks, while, for valid block they vote v_i = 0 if $b>{\displaystyle \frac{2}{3}}n+2$. Hence, even malicious behavior is influenced by the relative strength of intrinsic versus extrinsic satisfaction.

The expected payoffs for Scheme B are displayed in Equations (A5)–(A8) in the Appendix A. This scheme awards both positive votes for accepted blocks and negative votes for rejected blocks. For honest nodes, v_i = 1 is a dominant strategy with valid blocks and v_i = 0 with false ones. Faulty nodes vote 0 for a valid block if $a>{\displaystyle \frac{1}{3}}n+3$ and v_i = 1 for false block if the same condition holds.

The honest validator is incentivized to behave correctly, as they will agree on the valid blocks and reject the false ones. On the other hand, the faulty nodes will be incentivized to behave maliciously only if their motivation is strong enough: that is, if $b>{\displaystyle \frac{1}{3}}n+3$.

Schemes A and B are compared in

Table 1. Dominant strategies in Schemes A and B.

	True Blocks	False Blocks
	Scheme A
Honest nodes	V = 1	V = 0 if $a>{\displaystyle \frac{1}{3}}n$
Faulty nodes	V = 0 if $b>{\displaystyle \frac{2}{3}}n+2$	V = 1
	Scheme B
Honest nodes	V = 1	V = 0
Faulty nodes	V = 0 if $b>{\displaystyle \frac{1}{3}}n+3$	V = 1 if $b>{\displaystyle \frac{1}{3}}n+3$

, where the dominant strategies for each type of validator are displayed. Scheme B offers stronger incentives and is incentive-compatible for honest nodes, who have as dominant strategies both to accept valid blocks and reject false blocks. Scheme A is less reliable as it depends heavily on the intrinsic motivation of honest validators. At the same time, faulty nodes have a conditional dominant strategy under Scheme B for false blocks, which does not occur under Scheme A. The inclusion of extrinsic rewards in Scheme B reinforces the blockchain resistance to dishonest validation behavior.

4.2. Simulation Results

To assess the effectiveness of the proposed incentive schemes, some simulations were conducted under two main scenarios, defined by the relative weights of the coefficients a and b, and across four blockchain network sizes (n = 12, 120, 1200, and 12,000).

In the first scenario, the validators derive stronger intrinsic satisfaction from adhering to their individual objectives than from the extrinsic reward (labeled ‘Strong intrinsic satisfaction’ in

Table 2. Simulation results with two thirds honest nodes.

	Scheme A				Scheme B
	True block approvals
	N = 12	N = 120	N = 1200	N = 12,000	N = 12	N = 120	N = 1200	N = 12,000
Strong Intrinsic Satisfaction	✓	✓	✓	✓	✓	✓	✓	✓
Votes (%)	75	67.5	66.75	66.67	75	67.5	66.75	66.67
Weak Intrinsic Satisfaction	✓	✓	✓	✓	✓	✓	✓	✓
Votes (%)	100	100	100	100	100	100	100	100
	False block approvals
Strong Intrinsic Satisfaction	✕	✕	✕	✕	✕	✕	✕	✕
Votes (%)	25	32.5	33.25	33.32	25	32.5	33.25	33.32
Weak Intrinsic Satisfaction	✓	✓	✓	✓	✕	✕	✕	✕
Votes (%)	100	100	100	100	25	32.5	33.25	33.32

and

Table 3. Simulation results with one-half-plus-one honest nodes.

	Scheme A				Scheme B
	True block approvals
	n = 12	n = 120	n = 1200	n = 12,000	n = 12	n = 120	n = 1200	n = 12,000
Strong Intrinsic Satisfaction	✓	✓	✓	✓	✓	✓	✓	✓
Votes (%)	75	67.5	66.75	66.67	58.33	50.83	50.08	50.01
Weak Intrinsic Satisfaction	✓	✓	✓	✓	✓	✓	✓	✓
Votes (%)	100	100	100	100	100	100	100	100
	False blocks approvals
Strong Intrinsic Satisfaction	✕	✕	✕	✕	✕	✕	✕	✕
Votes (%)	25	32.5	33.25	33.32	41.66	49.16	49.91	49.99
Weak Intrinsic Satisfaction	✓	✓	✓	✓	✕	✕	✕	✕
Votes (%)	100	100	100	100	41.66	49.16	49.91	49.99

). The second scenario assumes the opposite condition, where extrinsic satisfaction dominates (‘Weak intrinsic satisfaction’ in Table 2 and Table 3).

Additionally, two different voter compositions were tested. Table 2 presents results assuming that two thirds of nodes are honest; Table 3 considers a simple majority (one half plus one) of honest voters. For each configuration, the percentage of approval votes was recorded both for true and false blocks.

Comparing the results of Scheme A and Scheme B, both schemes clearly perform robustly when approving true blocks. When false blocks are proposed, however, Scheme A tends to approve them, whereas Scheme B consistently rejects them.

These outcomes highlight the greater robustness and reliability of Scheme B, particularly in maintaining consensus integrity against dishonest behaviors and suggest that the design of the reward mechanism plays a decisive role in sustaining the integrity and efficiency of decentralized systems. By ensuring that honest behavior is both individually rational and collectively beneficial, Scheme B provides a more sustainable equilibrium between autonomy and accountability within blockchain-based organizations. Moreover, the observed stability of the results across different network dimensions implies scalability, making the incentive structure potentially applicable to both small and large decentralized organizations, such as DAOs.

5. Incentives and Governance Challenges in Decentralized Autonomous Organizations

This section examines how blockchain-based incentive mechanisms can strengthen Decentralized Autonomous Organizations (DAOs) and, more broadly, decentralized governance. Building on the previous analysis of incentive compatibility, it considers DAOs not only as technological innovations but also as new forms of economic organization.

DAOs are blockchain-driven organizations that allow participants to coordinate and govern themselves through self-executing smart contracts, with decision-making distributed across the network [42]. The study of decentralized organizational models has a long history in organizational theory, with significant discussions emerging as early as the mid-20th century [43,44]. The rise in peer-to-peer economies underscores the need for adaptive organizational models that mirror the dynamics of complex systems, where collective output exceeds the sum of individual members’ contributions [45]. The discussion on DAOs has evolved over time, from early applications in multi-agent systems and IoT networks [46] to contemporary blockchain-based implementations. Some scholars even view Bitcoin as the first DAO [47].

Vitalik Buterin, in the Ethereum white paper, described a DAO as a “virtual entity” that allows members or shareholders to manage funds and governance purely through blockchain-based systems [48]. This approach aims to replicate the operational and governance frameworks of traditional companies or nonprofits but with enforcement achieved through cryptography rather than legal institutions [49].

Ethereum played a pivotal role in the DAO ecosystem, notably with The DAO in 2016 [50], a venture-capital project that attracted significant attention despite its failure, which was primarily due to a vulnerability known as the Reentrancy Attack, which occurs when an attacker drains funds from a target contract by recursively calling its withdrawal function before the initial execution is complete. This oversight allows the attacker to repeatedly invoke the withdrawal function, effectively draining the contract’s funds. In the case of the DAO, the attacker exploited this vulnerability to siphon approximately 3.6 million Ether, valued at around 50 million U.S. dollars at the time [51]. The vulnerability lies in the victim’s contract failing to update the balance of the malicious actor before transferring the funds, allowing the attacker to re-enter the withdrawal process and drain more Ether than the number to which they were entitled [52].

This incident highlights a critical oversight in the development and auditing processes of smart contracts. Despite this significant setback, the DAO’s experiment paved the way for the development of other DAOs, such as MolochDAO and MetaCartel. It led to the creation of platforms that support DAOs, such as Aragon and DAOstack. Colony is a blockchain-based DAO for labor-managed firms [53]. These DAOs have inspired related models, such as the Decentralized Collaborative Organization (DCO), which emphasizes collaboration among participants [54].

DAOs are recognized for enabling online coordination and self-management and maintaining governance that is independent of any central authority [54,55]. Although the academic study of DAOs is still in its early stages, a growing body of research focuses on blockchain’s role in new business models, such as decentralized exchanges [56] and prediction markets [57]. DAOs offer flexibility, enabling the creation of diverse entities, from crowdfunding platforms to fully automated companies and decision-making systems.

Governance within DAOs has become a key area of research. Some studies have examined how blockchain and smart contracts can facilitate new decentralized governance models [58,59]. Questions surrounding accountability and regulatory challenges remain significant obstacles, however [50,60,61,62]. While DAOs are seen as tools for economic and political decentralization [63], questions persist regarding autonomy, human oversight, and legal recognition [64,65]. The question of DAO legal personhood is especially challenging, since autonomous smart contracts lack the identifiable actors required for legal liability.

Aligning individual incentives with collective objectives remains a fundamental challenge for DAOs. Traditional command structures often fail to adapt to the decentralized nature of DAOs, whereas blockchain-based smart contracts can formalize governance rules and maintain transparent, immutable records of participation. By incentivizing participation through blockchain-based rewards, organizations can foster decentralized governance structures that combine autonomy with accountability. The extension of blockchain-based incentive models to DAOs represents a significant opportunity for businesses to decentralize authority and to scale efficiently without sacrificing individual autonomy, without the bottlenecks of resource constraints or centralized decision-making. Additionally, this decentralized approach reduces the risks associated with central points of failure, enhancing an organization’s overall resilience and adaptability.

As summarized in Figure 1, sustainable governance in blockchain-based organizations emerges from the interaction among validator preferences, incentive mechanisms, and consensus outcomes. This integrated framework emphasizes that the design of reward structures has cascading effects on organizational performance and the broader sustainability of the system.

The interaction depicted in Figure 1 reveals how economic incentives translate into governance outcomes within decentralized systems. By influencing validator behavior, reward structures determine whether a DAO achieves sustainable coordination or degenerates into opportunistic dynamics. In this sense, incentive design acts as an institutional substitute for traditional hierarchies, providing order and predictability in otherwise self-organizing systems. This perspective highlights that the sustainability of DAOs ultimately rests on the alignment of economic rationality with collective governance goals.

6. Conclusions

The objective of this study was to show that applications of blockchain technology enable a more accurate evaluation of the individual behaviors of agents participating in the network. Viewing nodes as economic actors enables a more precise understanding of how incentive mechanisms and consensus protocols shape behavior. At the same time, the deployment of blockchain technologies must also be assessed in terms of their long-term economic viability and environmental sustainability. The design of incentive mechanisms and consensus protocols must not only align with agents’ strategic behavior but also ensure that the system operates with acceptable energy consumption and resource efficiency.

Using a game-theoretic approach, this study analyzed typical challenges of voting-based consensus mechanisms by comparing two alternative reward schemes to show how mechanism design influences adherence to protocol rules. Furthermore, the incentive compatibility problem of voting-based consensus mechanisms was compared with some case studies specifically concerning DAOs. These organizations represent a significant opportunity for businesses and communities to decentralize authority, enhance member engagement, and ensure operational efficiency through structured and equitable reward systems. By implementing smart contracts and blockchain-based incentives, DAOs can overcome traditional organizational challenges related to accountability and scalability.

Future research should further investigate how DAOs and other decentralized governance models can integrate sustainability criteria directly into their design. Embedding energy efficiency, fair resource allocation, and long-term resilience into smart contracts and incentive schemes will be key to ensuring that decentralized systems contribute positively to both economic development and environmental stewardship.

The limitations of the present study lie in its inherently static framework. A dynamic perspective would provide a more realistic representation of cooperative behavior. In repeated games, the “grim trigger strategy” serves as a mechanism to encourage cooperation among players [66,67]. The dynamic perspective is crucial not only to reinforce cooperative behavior [68] but also for sustainability: inefficient consensus models that encourage short-term opportunistic behavior or consume excessive computational resources may undermine both the economic and ecological feasibility of blockchain adoption. Incorporating adaptive, reputation-based mechanisms reduces wasted effort and energy while reinforcing cooperative dynamics. Further research could also clarify how a more nuanced classification of agent behaviors could enrich the analysis. Moreover, the present work focuses on conceptual and simulation-based analysis, but a quantitative assessment of energy efficiency or economic cost metrics remains an open area for future investigation, pending the availability of robust empirical data.

In conclusion, this study highlights the pivotal role of incentive mechanisms in shaping participant behavior and ensuring network integrity of blockchain networks. By applying game theory, we demonstrated how strategic interactions within these networks can be optimized to promote cooperation and discourage malicious activities. Ethical and legal considerations remain central to the broader adoption of blockchain technologies. Overall, the findings suggest that blockchain and DAOs hold significant potential to transform economic and governance structures by balancing autonomy with accountability and leveraging transparency and security to achieve sustainable and resilient organizational models. The ongoing research and development in this field will be central to addressing the remaining challenges and fully realizing the potential of decentralized organizations.