Abstract
Social housing in tropical regions faces critical thermal comfort challenges that will intensify under future climate change, yet current design practices lack systematic frameworks for evaluating long-term performance across multiple climate scenarios. This study assesses the thermal performance of social housing in southeastern Mexico using energy simulation, supervised machine learning, and global sensitivity analysis. Two housing typologies (single-story and two-story) were modeled across four cities (Mérida, Campeche, Cancún, and Tuxtla Gutiérrez) under climate change scenarios (RCP 2.6, 4.5, and 8.5) for 2050 and 2100. Various machine learning models were trained to predict comfort temperature and cooling degree days. Regression Trees demonstrated superior performance, with R2 values exceeding 0.98 for both thermal comfort indicators, achieving RMSE values of 0.0095 °C for comfort temperature and 0.2613 °C for cooling degree days. Global sensitivity analysis using the PAWN method revealed that ambient temperature was the most influential variable, accounting for 45–49% of the total sensitivity, followed by solar radiation (17–22%) and relative humidity (10–12%), while building-specific parameters had modest impacts (0.6–3.8%). Geographic variations were significant, with Mérida and Campeche showing higher cooling demands than Cancún and Tuxtla Gutiérrez. Future climate projections indicate substantial increases in cooling requirements by 2100, with CDD values expected to increase by approximately 40–50% under the RCP 8.5 scenario compared to current conditions. This research presents a computational framework for assessing thermal comfort in social housing, providing evidence-based insights for climate-adaptive building strategies in tropical regions.
1. Introduction
The global imperative to address climate change has intensified focus on building sector decarbonization, which accounts for approximately 40% of global energy consumption and 36% of CO2 emissions worldwide [1]. As the world grapples with rising temperatures and increasingly extreme weather events, the built environment faces unprecedented challenges in maintaining occupant comfort while minimizing energy consumption [2]. The Intergovernmental Panel on Climate Change (IPCC) has emphasized that building sector transformation is crucial for achieving global climate targets, particularly in developing countries, where rapid urbanization and growing middle-class populations are driving substantial increases in cooling demand [3]. In tropical and subtropical regions, where over 3 billion people currently reside, the challenge is particularly acute as rising temperatures and humidity levels are pushing traditional building designs beyond their thermal comfort limits [4]. The intersection of climate change effects, urban heat island phenomena, and socioeconomic inequalities has generated an urgent need for innovative strategies in building design and performance evaluation, particularly within the social housing sector, where at-risk communities are disproportionately affected [5]. Advanced computational tools, including machine learning and sensitivity analysis, offer promising pathways for developing climate-resilient building solutions that can adapt to both current and future environmental conditions while remaining economically viable for large-scale implementation [6].
1.1. Thermal Comfort Challenges in Tropical Climates and Social Housing
Thermal comfort is a critical component in the design and construction of homes, significantly influencing the well-being, health, and productivity of occupants. It encompasses the subjective experience of a satisfactory thermal environment, which is essential for maintaining a healthy and productive living space. The integration of thermal comfort into building design not only enhances occupant satisfaction but also contributes to energy efficiency and sustainability [7]. Globally, the search for solutions that optimize indoor environmental conditions has intensified in recent decades, driven by growing concerns about climate change and energy efficiency [8]. Furthermore, organizations such as the International Organization for Standardization (ISO) and the American Society of Heating, Refrigerating, and Air-Conditioning Engineers (ASHRAE) have established standards and regulations to assess and improve thermal comfort in buildings [9]. These efforts reflect the importance placed on this aspect in contemporary architecture and sustainable development policies. In Mexico, these international standards underscore the urgent need to strengthen public policies for social housing construction, particularly in establishing mandatory thermal performance requirements and energy efficiency standards that address the specific climatic challenges of tropical regions.
In Mexico, the challenge of achieving thermal comfort takes on nuanced aspects due to the country’s diverse climatic conditions. Strategies that work in temperate or cold regions are not always applicable in areas with hot and humid climates, which has led to the need to develop approaches adapted to each regional context [10]. Specifically, the Mexican southeast, particularly the Yucatan Peninsula and the state of Chiapas, is characterized by a tropical climate with high temperatures and humidity throughout the year [11,12]. In these regions, the design of housing that provides adequate thermal comfort without relying excessively on artificial air conditioning systems have become a crucial challenge, especially in the social housing sector. The consumption of electrical energy for thermal comfort is becoming increasingly important, as users in warm areas consume up to twice as much electricity as those in temperate climates. This difference reflects the impact of the climate on the demand for thermal comfort and the need for efficient solutions [13]. The tropical climate of southeastern Mexico presents unique challenges for thermal comfort, with ambient temperatures frequently exceeding 35 °C and relative humidity levels above 80% for extended periods [14]. These conditions create a complex thermal environment where traditional passive cooling strategies may prove insufficient, particularly in low-income housing where mechanical cooling systems are economically unfeasible [15].
Within a home, it is essential to maintain uniform conditions to ensure thermal comfort and prevent discomfort, such as asymmetric thermal radiation, which occurs when the body is exposed to surfaces with different temperatures. This phenomenon can be minimized by implementing efficient thermal insulation in walls and, especially, in ceilings [16]. The roof, being the element most exposed to direct solar radiation, plays a crucial role in regulating the home’s thermal balance. The lack of adequate insulation contributes to an increase in internal temperature, which in turn leads to higher energy consumption [17].
The thermal comfort challenges described above are further compounded by uncertainties in future climate conditions and the need to evaluate numerous design alternatives across different geographical contexts. Traditional building simulation approaches, while accurate for individual case studies, become computationally prohibitive when assessing multiple housing typologies, construction systems, and climate scenarios simultaneously. This complexity necessitates the adoption of advanced computational methodologies that can efficiently process large datasets, identify critical design parameters, and provide rapid predictions across diverse conditions [18]. In this context, machine learning and global sensitivity analysis have emerged as powerful tools for building performance assessment, offering the capability to extract meaningful patterns from extensive simulation data and quantify the relative importance of multiple influencing factors.
1.2. Machine Learning and Sensitivity Analysis in Building Performance Assessment
Given the multifaceted thermal comfort challenges in tropical climates and the imperative to develop climate-resilient housing solutions, advanced computational tools have become essential for comprehensive building performance assessment. In recent years, Artificial Intelligence (AI) tools, particularly supervised Machine Learning (ML) models, have gained prominence in various research fields, from geosciences to building science, including the study of thermal comfort in buildings [19,20]. These predictive models have been successfully applied to assess the effectiveness of different insulation materials, housing designs, and regional climate conditions. The popularity of these techniques in the field of thermal comfort is due to their ability to process large amounts of data, identify complex patterns, and provide accurate predictions, allowing for the more efficient optimization of building design and energy management compared to traditional methods. For instance, several studies have utilized artificial intelligence models to predict indoor comfort [21], thermal and comfort parameters [22], building energy consumption [23], and HVAC system performance [24], among other applications.
Machine learning algorithms have demonstrated particular effectiveness in building performance applications due to their ability to capture nonlinear relationships between multiple variables simultaneously, a capability that traditional analytical models struggle to achieve [25]. Recent advances in ensemble methods and deep learning architectures have further enhanced prediction accuracy for complex thermal phenomena [26,27,28]. In addition to machine learning (ML) models, Global Sensitivity Analysis (GSA) has emerged as a powerful tool in the field of thermal comfort and building energy performance. GSA methods offer valuable insights into how various input parameters impact the output of complex systems, enabling researchers and designers to identify the most critical factors influencing thermal comfort and energy efficiency [29]. The integration of GSA with machine learning represents a significant methodological advancement, enabling the quantification of parameter importance while preserving the predictive power of ML models. This combination enables decision-makers to prioritize design interventions based on their relative impact on thermal performance. Therefore, the author’s pursuit of this research stems from the possibilities offered by hybridizing thermal comfort using sophisticated computing technologies. A selection of studies that have incorporated this framework is presented in Table 1.

Table 1.
Comparison of machine learning studies for thermal comfort and building energy performance.
As reported in Table 1, various research efforts have tackled thermal comfort and building envelope characteristics across different climates. However, there is a growing need to consider future climate scenarios, particularly in regions highly vulnerable to climate change. The Representative Concentration Pathways (RCPs) developed by the IPCC provide crucial projections for future climate conditions, essential for long-term building design [36]. Additionally, machine learning and sensitivity analysis serve as alternatives to traditional models, enabling improved adaptation to specific climatic conditions [37]. Despite these advances, significant gaps remain in the application of integrated computational frameworks that combine high-fidelity building simulation, machine learning prediction, and global sensitivity analysis for climate-adaptive building design, particularly in tropical developing regions where social housing represents a critical infrastructure challenge.
Social housing units often prioritize cost and tenure security, relegating thermal efficiency to a secondary concern [38]. These standardized models are frequently adapted from other regions without considering local climatic conditions, forcing residents to rely on mechanical cooling systems [39]. This study evaluates the thermal performance of social housing in southeastern Mexico, creating ML models to forecast comfort temperature and cooling degree days, key indicators of thermal comfort and energy demand.
1.3. Research Gaps and Scientific Contributions
The comprehensive literature review reveals that existing thermal comfort research in tropical climates shows critical limitations in addressing future climate impacts and multi-scenario building performance assessment. Current studies predominantly focus on present-day climatic conditions or employ simplified climate change projections, failing to adequately integrate systematic Representative Concentration Pathway (RCP) scenarios for long-term building design evaluation. Most machine learning applications in thermal comfort assessment lack comprehensive integration of future climate projections as direct input variables, limiting their utility for climate-adaptive building design. There is a notable absence of computational frameworks that simultaneously evaluate multiple building configurations (typologies, construction systems, locations) across systematically varied climate change pathways within integrated predictive models. Additionally, existing research does not adequately address the systematic quantification of parameter importance across multiple RCP scenarios using global sensitivity analysis methods specifically designed for climate-resilient building design.
The novelty of this research lies in its integration of advanced computational techniques with systematic climate change scenario assessments for evaluating social housing performance under future climatic conditions. By developing a comprehensive machine learning framework based on energy simulation data from social housing prototypes across four capital cities representing different climatic zones in southeastern Mexico, Mérida (Yucatán), Campeche (Campeche), Cancún (Quintana Roo), and Tuxtla Gutiérrez (Chiapas), this study addresses a critical regional challenge affecting millions of inhabitants under both current and projected climate conditions. As state capitals and primary economic hubs, these cities experience the highest demand for social housing, with thousands of low-income housing units constructed annually. The scale of this challenge is considerable, as inadequate thermal performance in social housing affects individual household comfort, energy costs, and contributes to broader issues of energy poverty, public health, and regional sustainability in southeastern Mexico [40].
In this study, we contribute to the existing body of literature by introducing a comprehensive computational framework that systematically integrates climate change projections with building performance assessment. The scientific and methodological contributions of this work, which constitute the novelty of this study, are outlined as follows:
- This study presents a machine learning framework specifically designed for thermal comfort prediction under systematic RCP climate scenarios (2.6, 4.5, and 8.5 for 2050 and 2100), enabling direct assessment of social housing thermal performance across multiple future climate pathways in tropical hot-humid regions.
- A multi-scenario computational approach is developed that simultaneously evaluates building performance across four distinct climatic locations, two housing typologies, and two construction systems (with and without roof insulation), creating a comprehensive parametric assessment framework for climate-adaptive design.
- This work represents the first systematic application of the PAWN global sensitivity analysis method to quantify the relative importance of climatic variables versus building design parameters across multiple RCP scenarios, enabling evidence-based prioritization of climate adaptation strategies.
- The research introduces an innovative database structure comprising seven distinct climate scenarios (current + six future RCP projections) as direct input variables in machine learning models, representing the most comprehensive climate-integrated dataset for thermal comfort analysis in Mexican social housing.
- The study establishes a highly accurate predictive framework (R2 > 0.98 for both comfort temperature and cooling degree days) that enables rapid assessment of thermal comfort under future climate conditions, thereby eliminating the need for individual building simulations across multiple climate scenarios.
This research addresses a critical knowledge gap in climate-adaptive building design for tropical developing regions, providing evidence-based insights for building codes, policy development, and design guidelines that account for both current and future climate conditions. The computational framework developed herein offers a scalable methodology that can be adapted to other tropical regions facing similar challenges in social housing thermal performance under climate change.
2. Computational Methodology
The methodology used in this research work is depicted in Figure 1, along with the phases in which it was divided.
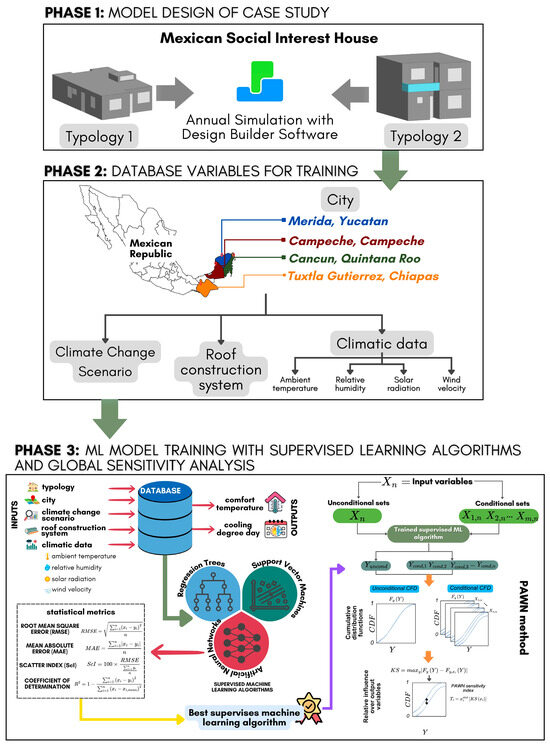
Figure 1.
Schematic diagram corresponding to the computational methodology implemented in this study.
The phases described in Figure 1 are explained below.
2.1. Phase 1: Model Design of Case Study
The initial phase of this study focused on developing comprehensive computational models for two distinct social housing typologies prevalent in Mexico [40]. These models were based on specifications derived from residential developments in Yucatán’s capital city, reflecting real-world housing conditions. To ensure accurate energy and environmental analysis, the Design Builder software v7.3.0.029, a powerful tool for simulating building performance, was utilized. This study focused on two housing typologies that represent common social housing configurations. The first typology is a single-story house covering 70 m2, while the second is a two-story structure with 50 m2 per floor. The single-story model incorporates two bedrooms, a bathroom, and a versatile common area that combines kitchen, living, and dining spaces. In contrast, the two-story model expands vertically, adding two more bathrooms, a dedicated study room, and staircase access on the upper level. Figure 2 provides a visual representation of the 3D models and floor plans for both housing typologies, illustrating the spatial arrangement and structural design of these social housing units.
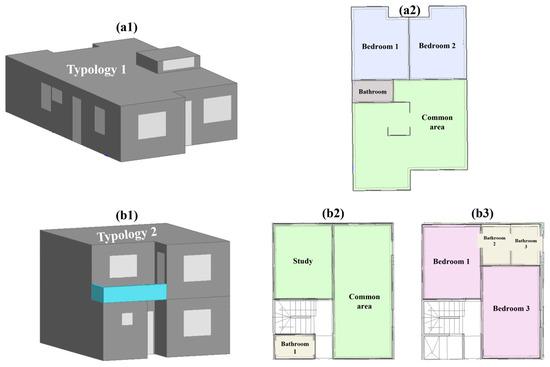
Figure 2.
Model designs of both typologies used in this study: (a1) Isometric view of typology 1, (a2) Top view of typology 1, (b1) Isometric view of typology 2, (b2) First-floor plan of typology 2, and (b3) Second-floor plan of typology 2. These representations serve as schematic illustrations of the architectural configuration and spatial distribution of each housing typology.
On the other hand, the computational models were designed considering various detailed construction specifications. The roof system, a critical component for thermal regulation, consists of multiple layers: 2.5 cm of waterproofing, 2.5 cm of mortar, 10 cm of concrete, and 2.5 cm of plaster. To enhance thermal performance, an 8 cm thick layer of expanded polystyrene insulation was integrated into the roof structure as a passive cooling measure. Every aspect of the building envelope was carefully considered, including wall construction, window specifications, and floor materials. These elements were defined in the model with precise thermal properties, conductivity, specific heat, density, and thermal resistance to ensure that the simulations accurately reflect real-world thermal behavior. The modeling approach was designed with foresight, allowing for the evaluation of thermal performance not only under current climate conditions but also under projected scenarios for 2050 and 2100. This forward-thinking methodology enables the assessment of the long-term sustainability and climate adaptability of these housing designs, providing valuable insights for future-proof social housing development.
It should be noted that the computational models were configured to evaluate the passive thermal performance of the building envelope under free-running conditions (without mechanical heating or cooling systems). This modeling approach deliberately excludes occupancy schedules, internal heat gains from occupants and equipment, and variable infiltration rates to isolate the thermal response of the building envelope to external climatic conditions and variations in construction systems. This methodological decision enables a focused assessment of how building typology, geographical location, roof insulation, and climatic variables influence thermal comfort indicators across multiple climate change scenarios, providing a baseline evaluation of the envelope’s intrinsic thermal behavior.
2.2. Phase 2: Database Variables for Training
The second phase of this study focused on creating a comprehensive database for training the machine learning models. This phase involved several key aspects that collectively formed the input parameters for our simulations and subsequent analysis.
- City
The study centered on four major cities in the Yucatan Peninsula region: Mérida, Campeche, Cancun, and Tuxtla Gutiérrez. These locations were strategically chosen to represent the diverse climatic conditions within the peninsula, offering a robust dataset for analysis. The Yucatan Peninsula was selected as the focal point due to its unique tropical climate and the growing challenges it faces in terms of thermal comfort and energy efficiency in residential buildings.
- Climate Change Scenario
To account for future climate variability, the study incorporated seven distinct scenarios based on Representative Concentration Pathways (RCPs). These included a reference scenario for 2024, three 2050 scenarios (RCP 2.6, RCP 4.5, and RCP 8.5), and three 2100 scenarios (RCP 2.6, RCP 4.5, and RCP 8.5).
RCPs are greenhouse gas concentration trajectories adopted by the Intergovernmental Panel on Climate Change (IPCC). They provide plausible future climate scenarios based on various levels of emissions, land-use changes, and other factors [41]. The inclusion of these scenarios enables a comprehensive assessment of how social housing might perform under various future climate conditions, thereby enhancing the long-term relevance of our findings.
- Roof construction system
The study examined two construction typologies: a reference design reflecting current building practices and an enhanced design incorporating thermal insulation as a passive cooling strategy. Figure 3 illustrates the constructive profiles of these systems, highlighting the differences in material layering and thermal properties, while Table 2 presents the thermophysical properties of the materials used in both typologies, providing crucial data for thermal performance simulations. To enhance thermal performance, an 8 cm thick layer of expanded polystyrene insulation was integrated into the roof structure as a passive cooling measure. This solution was adopted from previous laboratory research [40] that identified it as the most feasible and cost-effective passive cooling strategy for social housing in tropical climates, considering the economic constraints typical of these developments.

Figure 3.
Layers of the roof construction system: (a) reference roof, (b) insulated roof.

Table 2.
Thermo-physical properties of the roof construction system implemented [42,43].
- Climatic Data
All climatic data for current and future scenarios were obtained from Meteonorm v8.0.2 software [44], a comprehensive meteorological database that provides validated climate data for locations worldwide. Future climate scenarios (RCP 2.6, 4.5, and 8.5 for years 2050 and 2100) were generated using Meteonorm’s climate change projection module, which incorporates IPCC climate models to produce synthetic weather files. The weather data were extracted in EnergyPlus Weather (EPW) format, containing Typical Meteorological Year (TMY) type data with hourly temporal resolution for all required climatic variables: ambient temperature (°C), relative humidity (%), global horizontal solar radiation (W/m2), and wind velocity (m/s). These four key climatic variables were considered essential for accurately modeling the thermal behavior of buildings and assessing comfort levels across each of the studied cities.
To visually represent the complex interplay of variables in this study, Figure 3 presents a decision tree diagram illustrating all possible combinations of parameters considered in our simulations. Based on the combination of the parameters described above, a comprehensive dataset was generated for training the machine learning models. In total, 112 energy simulations were performed, resulting from the combination of the two housing typologies, the four selected cities, the seven climate scenarios, and the two construction systems (with and without thermal insulation). For each of these combinations, daily average data was collected over a full year of simulation, resulting in 365 records per combination, for a total of 40,880 records in the database [44]. This data structure enables the capture of seasonal variability in climatic conditions (ambient temperature, relative humidity, solar radiation, and wind speed) and their impact on the thermal performance of dwellings, thereby providing a solid basis for training and validating predictive models.
2.3. Phase 3: ML Model Training with Supervised Learning Algorithms and Global Sensitivity Analysis
The third phase of this research focuses on developing supervised machine-learning models and conducting global sensitivity analysis. This phase encompasses several key aspects, which are described below.
- Output Variables
The Design Builder software v7.3.0.029 provides the outdoor operating temperature (Toutdoor) of the dwelling as part of its energy simulation results. However, to determine thermal comfort, it is necessary to calculate the comfort temperature (Tcomf) using the adaptive thermal comfort model established by ASHRAE Standard 55 [45,46]. The adaptive model is specifically designed for naturally ventilated buildings where occupants can adapt to their thermal environment through behavioral adjustments (e.g., opening windows, adjusting clothing, changing activity levels). This approach is particularly suitable for social housing in tropical climates, where mechanical cooling systems are often absent or underutilized due to economic constraints, and residents primarily rely on passive strategies. The adaptive model has been extensively validated across diverse climatic conditions and provides a more accurate representation of actual thermal comfort in free-running buildings compared to static models, such as PMV-PPD [47]. The comfort temperature is calculated using Equation (1) [48].
This comfort temperature represents one of the primary output variables for our machine-learning model. Although Design Builder cannot directly estimate the adaptive comfort temperature, the development of an ML model allows it to be predicted directly from the input variables, thus avoiding intermediate calculations.
On the other hand, the second variable considered is the Cooling Degree Day (CDD), an annual indicator of the energy demand for cooling. This parameter is calculated as the daily difference between the operating temperature and the comfort temperature, as indicated by Equation (2) [49].
For our machine learning framework, we calculate the mean daily CDD () which represents the arithmetic average of daily CDD values over the entire year, as shown in Equation (3):
It is important to clarify that this metric differs from the conventional annual CDD used in building energy consumption calculations, which represents the cumulative sum of daily values () over the year. The mean daily CDD provides a normalized indicator of average cooling demand per day, which is particularly suitable for our machine learning approach, where the models are trained on daily observations and need to establish relationships between daily climatic conditions and thermal performance. This metric facilitates direct comparison across different climate scenarios, geographical locations, and housing configurations by eliminating the influence of the number of days in the calculation period.
- Database preparation
Once the input variables (typology, city, RCP scenario, roof construction system, and climatic data) and output variables (comfort temperature and cooling degree day) were established, the complete database was built for training the models.
- Coding of categorical variables
Categorical variables, such as housing typology, city, RCP scenario, and roof construction system, were numerically coded for processing in the machine learning (ML) algorithms, as shown in Figure 4. This coding transforms the qualitative data into numerical values that the computational models can interpret.
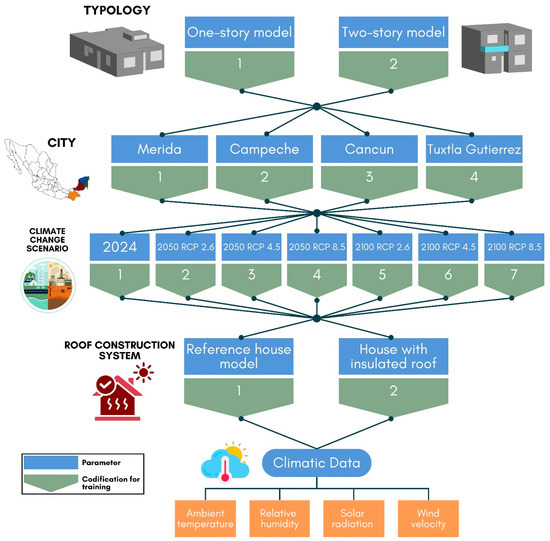
Figure 4.
Tree diagram of the different parameters implemented in this research study.
- Normalization of data
To ensure efficient training of the models, the numerical variables were normalized using Equation (4) [50].
This normalization process is crucial in preventing variables with different magnitudes from having a disproportionate impact on the model’s training, thereby enhancing its convergence and precision [51].
- Supervised ML algorithm training
With the prepared, encoded, and normalized database in place, it proceeded to train various supervised learning algorithms. This phase was developed in the MATLAB R2021b programming environment, specifically using its Regression Learner tool due to its robust capacity to work with various algorithms and optimize hyperparameters [52]. Hence, three main supervised learning algorithms were selected: Regression Trees (RT) [53], Support Vector Machines (SVM) [54], and Artificial Neural Networks (ANN) [55]. The Regression Learner tool enabled the systematic exploration of different hyperparameter combinations for each algorithm, aiming to identify the optimal configuration for our specific case. To ensure the robustness and generalization of the models, a k-fold cross-validation procedure was implemented, dividing the data into subsets for training and validation [56]. This methodology is fundamental in avoiding overfitting and ensuring that the developed models are applicable to new data.
Table 3 presents the implemented algorithms along with the hyperparameter ranges explored during the optimization process.

Table 3.
Supervised ML algorithms and hyperparameter tuning used in this study.
The selection of Regression Trees, Support Vector Machines, and Artificial Neural Networks was based on their demonstrated effectiveness in building energy and thermal comfort applications. Comparative studies have shown that these three algorithms consistently deliver robust performance for predicting building thermal behavior and energy consumption [57,58]. Regression Trees offer high interpretability and effectively capture nonlinear relationships and threshold effects in thermal performance [59]. Support Vector Machines excel at finding optimal decision boundaries in high-dimensional spaces and have demonstrated superior accuracy in building energy prediction tasks [60]. Artificial Neural Networks offer powerful nonlinear approximation capabilities and have demonstrated excellent performance in predicting thermal comfort across diverse climatic conditions [55]. These three algorithms represent distinct modeling paradigms: tree-based, kernel-based, and neural network-based approaches, enabling comprehensive evaluation of different learning strategies for our multi-scenario framework.
- Statistical metrics for model evaluation
The evaluation of model performance was based on three complementary statistical metrics: the Root Mean Square Error (RMSE), which quantifies the average error between the model’s predictions and the actual values, providing a measure of the model’s overall error. The Mean Absolute Error (MAE) represents the average of the absolute differences between predicted and observed values. It is a straightforward metric that indicates, on average, how much the predictions deviate from the actual data, regardless of the direction of the error. MAE is particularly useful for understanding the typical magnitude of prediction errors in a more interpretable and less sensitive manner to outliers compared to RMSE. Furthermore, the Scatter Index (ScI) measures the relative dispersion of prediction errors concerning the magnitude of the observed values, offers a perspective on the consistency of the model, and finally, the coefficient of determination (R2) that evaluates the proportion of variance in the dependent variable that is predictable from the independent variables, providing a measure of the predictive accuracy of the model. The calculus of RMSE, ScI, and R2 can be determined by Equations (5)–(8), respectively.
where xi denotes the real value, xi,mean represents the actual value’s average, yi is the predicted value, and n indicates the total data.
- Global Sensitivity Analysis with the PAWN method
To identify the relative influence of input parameters, a Global Sensitivity Analysis (GSA) was conducted using the PAWN method. The PAWN method was over variance-based approaches. PAWN is a distribution-based method that analyzes Cumulative Distribution Functions rather than relying solely on variance decomposition, making it more robust for outputs with non-normal or multimodal distributions [61,62]. Critically, PAWN achieves stable sensitivity estimates with significantly smaller sample sizes, often requiring 5–10 times fewer model evaluations to reach convergence [63], which was essential given our framework’s computational complexity. This density-based approach utilizes cumulative distribution functions and the Kolmogorov–Smirnov statistical test to quantify the influence of parameters on model outputs. The PAWN method effectively handles nonlinear relationships, is computationally efficient, and can simultaneously analyze multiple output variables with different statistical distributions [61].
The PAWN implementation generates unconditional and conditional sample groups, comparing conditional CDFs against unconditional CDFs using the Kolmogorov–Smirnov statistical test to quantify parameter influence [64]. The method effectively handles nonlinear relationships, provides computational efficiency, and yields robust results with relatively small sample sizes while simultaneously analyzing multiple output variables [65]. The PAWN method was applied to the best-performing Regression Trees model to evaluate the influence of building typology, geographical location, climate change scenarios, roof construction systems, and climatic variables on thermal comfort outcomes. The resulting sensitivity indices provide valuable insights for prioritizing design interventions and policy measures to improve thermal comfort in social housing under current and future climate conditions.
3. Results and Discussion
The following section presents the key findings of this research regarding thermal comfort in social housing units across southeastern Mexico.
3.1. Comfort Temperature and Cooling Degree Day
Figure 5 presents a heat map corresponding to the comfort temperature of the typology and the roof construction system for the four cities studied.
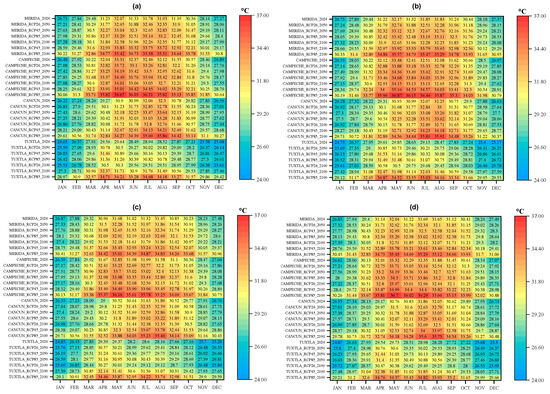
Figure 5.
Heat maps of comfort temperature (°C) for different climate scenarios in the four studied cities: (a) typology 1 housing with reference roof, (b) typology 2 housing with reference roof, (c) typology 1 housing with insulated roof, and (d) typology 2 housing with insulated roof.
Figure 5 presents heat maps corresponding to the monthly comfort temperature (Tcomf) for the different configurations analyzed. These maps enable the visualization of temporal and spatial variations in comfort temperature, revealing distinct seasonal patterns and differences among the studied cities.
All four heat maps show a clear seasonal variation in comfort temperature, with maximum values during the warmest months (April to September) and minimum values during the cooler months (November to February). This trend is consistent across all cities and climate scenarios analyzed, although with different magnitudes depending on geographical location.
The results demonstrate a clear progression in thermal severity across climate scenarios, with RCP 8.5 2100 representing the most extreme conditions, as expected from Representative Concentration Pathway projections [66]. Campeche presents the highest comfort temperature values, reaching up to 36.87 °C in May for the RCP 8.5 scenario of 2100 in typology 2 with reference roof (Figure 5b). Mérida follows with comfort temperatures reaching up to 35.57 °C in the same scenario and month. The consistently higher comfort temperatures in Campeche compared to other cities reflect its specific climatic characteristics. Campeche experiences a tropical savanna climate with elevated ambient temperatures and significantly reduced coastal wind speeds compared to Cancún, which benefits from stronger and more consistent Caribbean maritime breezes that provide natural cooling effects. While both coastal cities receive similar levels of solar radiation, Campeche’s position on the Gulf of Mexico results in less maritime temperature moderation and weaker cooling breezes than Cancún. Tuxtla Gutiérrez, despite its tropical setting, is situated at a higher elevation (approximately 522 m above sea level) in an inland valley, resulting in more moderate temperatures. Since comfort temperature is calculated from outdoor operating temperature, these climatic differences directly explain the geographic variations observed in the heat maps.
Based on the climatic data obtained from Meteonorm v8.0.2, the four studied cities experience high solar radiation levels typical of tropical climates, with average daily values ranging from approximately 5.5 to 6.5 kWh/m2 during the peak months (April-September). The thermal performance results reflect the complex interplay of heat gains through different building envelope components under free-running conditions. Given the roof’s direct exposure to solar radiation and its surface area, solar heat gains through the roof constitute the primary thermal load in both typologies. The monthly heat maps presented in Figure 5 implicitly capture these cumulative heat gains, as the outdoor operating temperatures used to calculate comfort temperatures result from the building’s overall thermal balance, including solar gains, conduction through the envelope, and convective exchanges. The implementation of roof insulation (8 cm EPS) specifically targets the reduction in solar heat gains through this critical component, as evidenced by the slightly lower comfort temperatures observed in Figure 5c,d compared to reference configurations (Figure 5a,b).
When comparing typologies 1 and 2 (Figure 5a,b and Figure 5c,d, respectively), it is observed that the two-story housing (typology 2) presents slightly higher comfort temperatures than the single-story housing (typology 1) in most scenarios. This difference can be attributed to the greater surface area exposure to solar radiation in the two-story housing, resulting in higher thermal gains. The effect of thermal insulation on the roof can be appreciated by comparing Figure 5a,c (typology 1) or Figure 5b,d (typology 2). Houses with insulated roofs show slightly lower comfort temperatures than the reference ones, although this reduction varies according to the city and month of the year. For example, in Mérida, the implementation of thermal insulation reduces the comfort temperature by up to 0.5 °C during the warmest months in typology 1, while the effect is less pronounced in typology 2.
Future climate scenarios show a logical progression of increasing thermal stress, with RCP 8.5 for 2100 demonstrating the most severe conditions across all cities, consistent with IPCC projections that identify this pathway as representing the highest greenhouse gas concentrations and most extreme warming scenarios [67]. The temperature escalation follows the expected hierarchy: current conditions (2024) < RCP 2.6 scenarios < RCP 4.5 scenarios < RCP 8.5 scenarios, with 2100 projections showing more severe impacts than 2050 for each respective pathway. Tuxtla Gutiérrez experiences the greatest proportional increase in comfort temperature between the current scenario (2024) and the most extreme future scenario (RCP 8.5 2100), suggesting a greater vulnerability of this region to climate change.
The chromatic analysis of the heat maps reveals critical zones (red and orange colors) where comfort temperatures exceed 32 °C. The most extensive critical areas appear under the RCP 8.5 2100 scenarios, mainly concentrated in the months from April to September for the most severe climate projections. These critical zones are more extensive in Campeche and Mérida than in Cancún and Tuxtla Gutiérrez, indicating the need for more intensive adaptation strategies in these cities.
On the other hand, the analysis of Cooling Degree Day (CDD) values across different climate change scenarios reveals significant patterns in the thermal performance of social housing units in southeastern Mexico. Figure 6 illustrates the mean daily CDD values for both housing typologies across the four studied cities under various climate change scenarios, with and without the implementation of roof insulation.
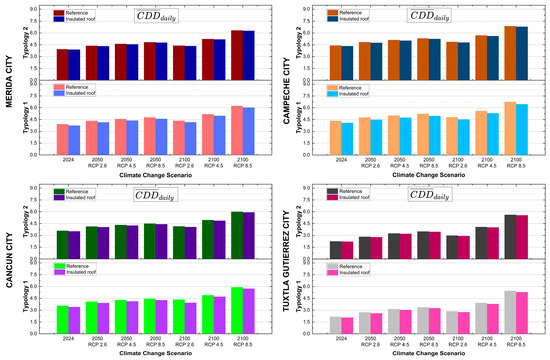
Figure 6.
Mean daily CDD values for each climate change scenario for the four study cities.
A progressive increase in CDD values is observed across all cities as climate change scenarios advance from 2024 toward more extreme projections for 2100, with a logical progression following RCP pathways: RCP 2.6 < RCP 4.5 < RCP 8.5. This trend is particularly pronounced under the RCP 8.5 scenario, which represents the most severe warming trajectory. This trend indicates a growing cooling demand over time, with CDD values peaking in the 2100 RCP 8.5 scenario across all locations, suggesting substantially higher cooling requirements by the end of the century. For instance, in Mérida, CDD values for Typology 2 increased from approximately 4.0 in 2024 to approximately 6.0 in the 2100 RCP 8.5 scenario, representing a significant rise in cooling demand.
Geographic variations in CDD values are pronounced, with Mérida and Campeche consistently showing higher cooling demands compared to Cancún and Tuxtla Gutiérrez. Mérida exhibits the highest CDD values across most scenarios for both typologies, reaching approximately 6.0 for Typology 2 under the 2100 RCP 8.5 scenario, followed closely by Campeche, with values ranging from approximately 5.5 to 6.0 under the same conditions. This pattern reflects the distinct climatic characteristics of these regions, with Mérida and Campeche experiencing more intense hot and humid conditions typical of the Yucatan Peninsula. In contrast, Tuxtla Gutiérrez consistently shows lower CDD values (ranging from approximately 2.0 to 5.5), suggesting somewhat less severe cooling requirements despite also experiencing significant increases in future scenarios.
The proportional increase in CDD values is particularly pronounced in Tuxtla Gutiérrez, which experiences the greatest relative growth between current conditions and extreme future scenarios despite having lower absolute CDD values than coastal cities. This pattern reflects Tuxtla Gutiérrez’s inland valley location, which currently benefits from more moderate temperatures but exhibits greater temperature variability and sensitivity to climate change projections. In contrast, Cancún’s Caribbean maritime climate provides stronger temperature buffering through ocean thermal inertia and consistent sea breezes, resulting in more gradual increases in CDD despite higher baseline cooling demands. The differential response to climate change across cities underscores the importance of location-specific adaptation strategies, with inland cities like Tuxtla Gutiérrez requiring particular attention as they transition from moderate to high cooling demand zones.
On the other hand, the comparison between housing typologies reveals that Typology 2 (the two-story model) generally exhibits higher CDD values than Typology 1 (the single-story model) across all cities and scenarios. In Mérida, for example, Typology 2 shows CDD values approximately 0.5–1.0 higher than Typology 1 across all scenarios. This difference suggests that the vertical expansion of housing units results in increased cooling demands, likely due to factors such as greater surface area exposure to solar radiation and more complex heat transfer dynamics in multi-level structures.
When comparing reference houses with insulated roof models, the data reveal a slight but consistent reduction in CDD values with the implementation of insulation. The effectiveness of roof insulation consistently shows modest benefits across all locations and scenarios, with reductions typically ranging from 0.1 to 0.3 CDD units. However, these reductions appear relatively modest (generally less than 0.5 CDD), suggesting that roof insulation alone, while beneficial, has a limited impact on reducing overall cooling demands, particularly in more extreme climate change scenarios.
The results also reveal interesting temporal patterns in the effectiveness of roof insulation. The relative benefit of insulation remains consistent across different periods and RCP scenarios, indicating that while absolute cooling demands increase with climate change, the proportional benefit of this passive cooling strategy remains stable. This finding suggests that roof insulation remains a valuable intervention, even under future climate conditions, although its absolute impact may be insufficient to address increased cooling needs fully.
These findings underscore the need for developing comprehensive adaptation strategies for social housing in southeastern Mexico that extend beyond single interventions, such as roof insulation. While insulation provides some thermal performance improvement, the significant increase in CDD values across all future scenarios indicates that more robust passive cooling approaches and possibly supplementary active systems may be necessary to adequately address the growing cooling demands in this region, particularly as climate change accelerates.
3.2. Supervised Machine Learning Models
The development of machine learning models represents a fundamental shift from traditional building simulation approaches, enabling the creation of a comprehensive predictive framework that encapsulates the collective knowledge derived from extensive energy simulations. Rather than relying on individual software-based analyses for specific scenarios, the ML approach enables the development of a global function that can simultaneously predict thermal comfort indicators across diverse conditions. The primary objective of this section is to establish predictive models derived from the complete dataset, which encompasses all combinations of building typologies, geographical locations, climate change scenarios (RCP pathways), and construction systems. Three supervised learning algorithms were systematically evaluated to develop this unified predictive capability: Regression Trees (RT), Support Vector Machines (SVM), and Artificial Neural Networks (ANN). For the RT algorithm, optimal hyperparameters included a minimum leaf size of 13 for comfort temperature prediction and 1 for cooling degree day (CDD). For the SVM algorithm, the optimal parameters for Tcomf were a Gaussian Kernel function with a Kernel scale of 724.9, a box constraint of 939.8, and an epsilon value of 0.1137. For CDD, the optimal Kernel function was Cubic, with a Kernel scale of 1, a box constraint of 0.23649, and an epsilon value of 0.0369. The optimal ANN architecture for predicting comfort temperature consisted of one hidden layer with 285 neurons, using a sigmoid activation function and a regularization strength of 0.00065194. In contrast, the CDD prediction required a more complex ANN structure with two hidden layers (64 neurons in the first layer and 2 neurons in the second), also using a sigmoid activation function, but with a substantially lower regularization strength of 1.97 × 10−9.
Figure 7 illustrates the comparative performance of these models through various diagnostic plots for the comfort temperature results.
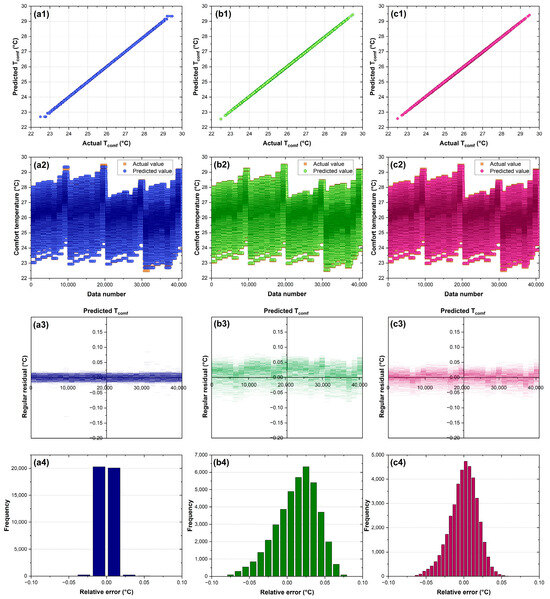
Figure 7.
Performance evaluation of supervised machine learning models for comfort temperature prediction: (a1–a4) Regression Trees, (b1–b4) Support Vector Machine, and (c1–c4) Artificial Neural Network. The rows display (1) the correlation between predicted and actual values, (2) a time series comparison between actual and predicted comfort temperatures, (3) regular residual plots, and (4) histograms of error distributions. Overall, these plots collectively illustrate the superior predictive accuracy and minimal residual error of the Regression Trees model compared to the SVM and ANN alternatives.
The scatter plots in the top row (Figure 7(a1–c1)) demonstrate the correlation between predicted and actual comfort temperature values for each algorithm. All three models show strong linear relationships, indicating high predictive accuracy, with data points closely aligned along the diagonal line of perfect prediction. This visual assessment is supported by the subsequent rows of diagnostic plots that provide deeper insights into model performance.
The time series comparison plots Figure 7(a2–c2) display the predicted values alongside actual comfort temperatures across the entire dataset. These plots reveal how well each model captures the temporal variations in comfort temperature. While all models track the actual values effectively, subtle differences in their predictive behavior can be observed, particularly during rapid fluctuations in temperature.
The regular residual plots (Figure 7(a3–c3)) show the difference between predicted and actual values, which helps identify any systematic prediction errors. The RT model Figure 7(a3) exhibits notably compact residuals clustered tightly around zero with minimal spread, indicating highly consistent predictions. The SVM model Figure 7(b3) and ANN model Figure 7(c3) exhibit slightly wider residual distributions, though still within acceptable ranges (±0.10 °C), indicating good model fit but with marginally greater prediction variability than RT.
The error distribution histograms (Figure 7(a4–c4)) further quantify the models’ prediction accuracy. The RT model Figure 7(a4) exhibits a distinctive narrow bimodal error distribution centered around zero, which is characteristic of tree-based algorithms and reflects the model’s hierarchical decision-making structure. This bimodal pattern indicates that the RT model has effectively identified and learned two primary predictive pathways within the dataset, likely corresponding to distinct thermal performance regimes: one pathway for scenarios with lower thermal stress, and another for scenarios with higher thermal stress. The fact that both error peaks are tightly clustered within ±0.02 °C demonstrates that the model maintains a good accuracy across both pathways, confirming its ability to capture the complex, nonlinear relationships between input parameters and thermal comfort outcomes. In contrast, the SVM Figure 7(b4) and ANN Figure 7(c4) models display more typical bell-shaped error distributions, suggesting normally distributed prediction errors with a slightly broader spread than the RT model.
On the other hand, Figure 8 shows the comparative performance plots for the cooling degree day results.
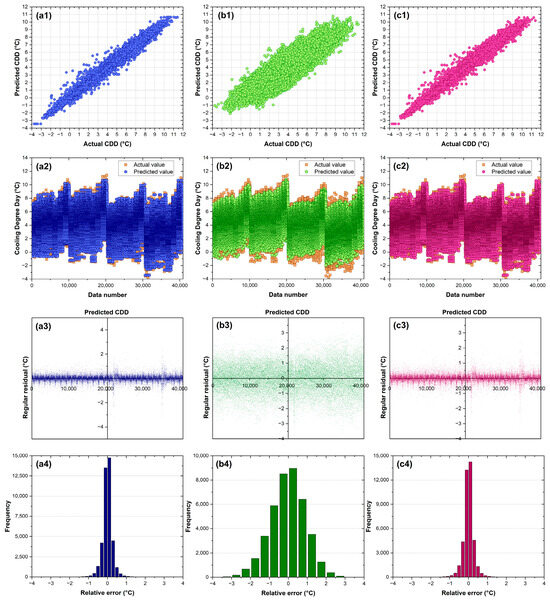
Figure 8.
Performance evaluation of supervised machine learning models for Cooling Degree Day prediction: (a1–a4) Regression Trees, (b1–b4) Support Vector Machine, and (c1–c4) Artificial Neural Network. The rows display (1) the correlation between predicted and actual values, (2) a time series comparison between actual and predicted CDD values, (3) regular residual plots, and (4) histograms of the error distribution. Overall, these plots together demonstrate the superior predictive accuracy and tighter residual distribution of the Regression Trees model compared to the SVM and ANN models.
In the top scatter plots (Figure 8(a1–c1)), the correlation between predicted and actual values for each model is displayed. The Regression Trees model (column a) exhibits a tighter correlation, with points clustered closer to the diagonal line of perfect prediction, compared to the SVM (column b) and ANN (column c) models.
The time series plots (Figure 8(a2–c2)) illustrate how each model captures variations in CDD across the dataset. All three models follow the general trend of the actual values, but the RT model appears to have better point-by-point matching with actual values, particularly at the extremes of the distribution.
In the regular residual plots (Figure 8(a3–c3)), a significant difference between the models is evident. The residuals of the RT model Figure 8(a3) are more densely concentrated around zero and exhibit less dispersion, whereas the SVM model Figure 8(b3) presents a much wider distribution of residuals, indicating greater variability in its predictions. The ANN model Figure 8(c3) exhibits intermediate behavior, with more controlled residuals than the SVM but less precision than the RT.
The error distribution histograms (Figure 8(a4–c4)) confirm these observations. The RT model Figure 8(a4) presents a narrow distribution concentrated around zero, indicating high precision. The SVM model Figure 8(b4) exhibits a wider and flatter distribution, whereas the ANN Figure 8(c4) has a relatively narrow but less concentrated distribution compared to the RT.
This visual assessment suggests that the Regression Trees model provides more accurate and consistent predictions for CDD values, making it the preferred option for applications requiring reliable estimates of cooling demand in social housing under different climate scenarios.
Finally, Table 4 presents the statistical values of each previously presented metric.

Table 4.
Results of the statistical metrics of the three supervised machine learning algorithms.
As reported in Table 4, the results demonstrate the superior performance of the Regression Trees model for both output variables.
For comfort temperature prediction, the Regression Trees algorithm achieved exceptional accuracy with the lowest RMSE (0.0095 °C) and MAE (0.0075 °C) values among all models. Its Scatter Index of just 0.036% and an R2 value of 0.9999 further confirm its outstanding predictive capability. While the Artificial Neural Networks model also performed very well with an RMSE of 0.0183 °C and R2 of 0.9997, it did not match the precision of the Regression Trees model. The Support Vector Machine showed the least favorable performance for this variable, with an RMSE of 0.0302 °C and higher error metrics across all categories.
The performance differences between algorithms are even more pronounced for Cooling Degree Day predictions. The Regression Trees model again demonstrated superior performance with an RMSE of 0.2613 °C and an R2 value of 0.9845. The Artificial Neural Networks model followed closely with similar metrics (RMSE of 0.2767 °C and R2 of 0.9826). However, the Support Vector Machine model showed significantly poorer performance for CDD prediction, with an RMSE of 0.9211 °C and a considerably lower R2 value of 0.8074. The high Scatter Index of 20.7% for the SVM model indicates substantial relative dispersion in its predictions, making it less reliable for practical applications in thermal comfort assessment.
The superior performance of Regression Trees over Support Vector Machines and Artificial Neural Networks can be attributed to the specific characteristics of our dataset and modeling framework. RT algorithms naturally capture threshold effects and discrete decision boundaries that characterize thermal comfort phenomena, where specific climatic conditions trigger distinct comfort responses. The dataset structure, combining categorical variables with continuous climatic parameters, particularly favors the recursive partitioning mechanism of RT. While all three algorithms are well-established methods for thermal prediction, the encoded categorical variables (typologies: 1–2, cities: 1–4, scenarios: 1–7) create natural splitting points that RT exploits more efficiently through its tree-based structure. SVM and ANN, designed primarily for continuous feature spaces, achieved good performance but were less effective in leveraging these categorical distinctions within our specific dataset configuration. Additionally, RT models demonstrated greater stability during hyperparameter optimization and produced more consistent predictions across the diverse climate scenarios and building configurations analyzed.
These results align with the visual assessment provided in Figure 7 and Figure 8, confirming that the Regression Trees algorithm provides the most accurate and reliable predictions for both comfort temperature and cooling degree day values. The superior performance of tree-based models in this application can be attributed to their ability to effectively capture nonlinear relationships between variables and their robustness when handling normalized data. Particularly, the categorical variables that were encoded numerically (such as typologies coded as 1–2, cities as 1–4, and climate scenarios as 1–7) resulted in similar value ranges after normalization, which facilitated the training process for the models, especially for the Regression Trees algorithm that inherently works well with discretized data.
Based on these comprehensive evaluation results, the Regression Trees model was selected for subsequent analyses, including the global sensitivity analysis, to determine the relative influence of different input parameters on thermal comfort outcomes in social housing units across southeastern Mexico.
3.3. Global Sensitivity Analysis Using the PAWN Method
The established Regression Trees model offers an opportunity to explore the comprehensive knowledge gained from extensive simulations and systematically identify the variables that most significantly impact thermal comfort indicators. This machine learning-based approach enables efficient sensitivity analysis across the entire parameter space, allowing for quantification of the relative importance of location, building characteristics, climate scenarios, and environmental factors. The PAWN method was employed to analyze this predictive framework and determine the contribution of each input variable to the model outputs. The results of the GSA performed using the PAWN method are presented below. Figure 9 reports the sensitivity index obtained for the model outputs and their corresponding inputs.
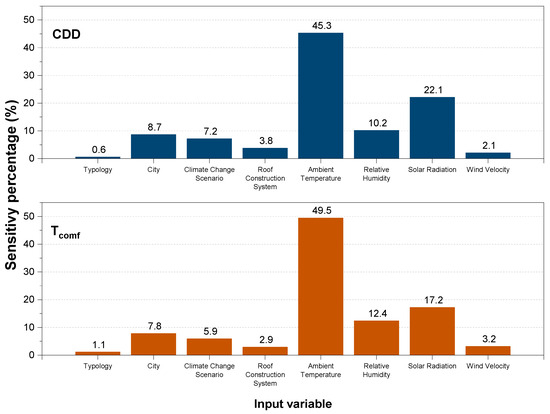
Figure 9.
Sensitivity analysis results obtained with the PAWN method using the Regression Tree algorithm.
The sensitivity analysis reveals significant differences in how input variables influence each output parameter. For both cooling degree days (CDD) and comfort temperature (Tcomf), ambient temperature emerges as the dominant factor, accounting for 45.3% and 49.5% of the sensitivity index, respectively. This substantial influence aligns with expectations since ambient temperature directly affects the building’s thermal behavior and occupant comfort.
Solar radiation represents the second most influential parameter, contributing 22.1% to CDD and 17.2% to Tcomf. The stronger effect on CDD can be attributed to solar radiation’s direct impact on cooling loads, as increased solar gains translate to higher cooling demands. For comfort temperature, while still significant, the influence of solar radiation is moderated by the building’s thermal mass and other factors that buffer immediate temperature changes.
Relative humidity shows a consistent influence across both output variables (10.2% for CDD and 12.4% for Tcomf), highlighting its importance in thermal comfort perception. The slightly higher impact on Tcomf reflects the direct role of humidity in physiological comfort mechanisms, as it affects the evaporative cooling potential of human skin.
City and climate change parameters contribute moderately to both outputs, with sensitivity indices ranging from 5.9% to 8.7%. These parameters encompass broader climatic conditions that influence the building’s thermal response over extended periods. The city parameter captures location-specific climate characteristics, while the climate change scenario reflects projected future conditions.
Building-related parameters, such as roof construction system and typology, demonstrated relatively lower sensitivity indices (0.6% to 3.8%). It suggests that while architectural decisions remain important for sustainable building design, their impact is overshadowed by climate variables in this analysis. The roof construction system shows a slightly higher influence (3.8% for CDD and 2.9% for Tcomf) compared to the typology, indicating that the roof’s thermal properties play a more significant role in the thermal behavior of the analyzed building models.
Wind velocity has a limited influence on both output variables (2.1% for CDD and 3.2% for Tcomf), indicating that, in the studied context, natural ventilation effects have a lesser impact on thermal conditions compared to other environmental factors.
The dominance of ambient temperature (45–49%) over solar radiation (17–22%) in the sensitivity analysis warrants clarification, as solar radiation is typically considered the primary heat source in tropical climates. This ranking reflects the comprehensive nature of ambient temperature in the adaptive comfort model, which captures the cumulative effect of multiple interacting factors, including absorbed solar radiation by surfaces, convective heat exchange, urban heat island effects, and atmospheric conditions. Since comfort temperature is calculated directly from outdoor operating temperature, ambient temperature inherently incorporates the thermal consequences of solar radiation, along with other climatic factors, making it a more comprehensive predictor of thermal comfort outcomes. Solar radiation’s independent contribution (17–22%) represents its direct influence beyond what is already captured through ambient temperature. The relatively low sensitivity to wind velocity (2.1–3.2%) reflects the free-running, naturally ventilated conditions modeled in this study, where wind effects on indoor comfort are limited compared to mechanically conditioned or mixed-mode buildings, where ventilation strategies would play a more significant role.
These findings are consistent with previous research in the field. A similar sensitivity hierarchy was observed by Cetina-Quiñones et al. (2023) [31] in their analysis of adaptive thermal comfort for social housing in the Dominican Republic, where outdoor temperature and radiant temperature demonstrated the highest influence on comfort predictions, followed by humidity-related parameters, while building-specific factors showed comparatively lower sensitivity indices. This consistency across different geographic contexts reinforces the importance of prioritizing climate-responsive strategies in sustainable building design.
The dominance of ambient temperature and solar radiation highlights the critical importance of implementing appropriate shading strategies, selecting materials with suitable thermal properties, and considering orientation to minimize solar gains. While designers have limited control over environmental parameters, understanding their relative influence allows for more effective prioritization of passive design strategies to enhance comfort and reduce cooling energy requirements.
The moderate influence of city and climate change scenario parameters underscores the importance of location-specific design approaches and future-proofing buildings against projected climate changes. Although building typology and roof construction show lower sensitivity indices, they represent actionable design variables that can be optimized, especially when considered collectively with other architectural strategies.
4. Conclusions
This study assessed the thermal performance of social housing in southeastern Mexico by integrating energy simulation, supervised machine learning, and global sensitivity analysis under current and future climate scenarios. Two housing typologies were modeled across four cities under RCP 2.6, 4.5, and 8.5 scenarios for 2050 and 2100, generating a comprehensive dataset for machine learning analysis. The Regression Trees algorithm demonstrated superior predictive accuracy, with R2 values exceeding 0.98 for both comfort temperature (RMSE = 0.0095 °C) and cooling degree days (RMSE = 0.2613 °C), significantly outperforming Support Vector Machines and Artificial Neural Networks. This computational framework enables the rapid assessment of thermal performance across multiple climate scenarios, eliminating the need for individual building simulations for each configuration.
Global sensitivity analysis using the PAWN method revealed that ambient temperature emerges as the most influential variable, accounting for 45–49% of total sensitivity, followed by solar radiation (17–22%) and relative humidity (10–12%), while building-specific parameters, including typology and roof construction, showed modest impacts ranging from 0.6 to 3.8%. These findings suggest that climatic variables overwhelmingly determine thermal performance in tropical social housing contexts, indicating that adaptation strategies should prioritize climate-responsive design over incremental modifications to the building envelope alone. Geographic variations were pronounced, with Mérida and Campeche consistently exhibiting higher cooling demands than Cancún and Tuxtla Gutiérrez across all scenarios analyzed.
Future climate projections indicate substantial increases in cooling requirements by 2100, with CDD values expected to increase by approximately 40–50% under the RCP 8.5 scenario compared to current conditions. This increase is particularly pronounced in Tuxtla Gutiérrez, which experiences the greatest proportional growth despite lower absolute CDD values, reflecting its inland valley location and heightened sensitivity to climate change compared to maritime-moderated coastal cities. The implementation of 8 cm EPS roof insulation provided consistent but modest thermal performance improvements, with CDD reductions typically ranging from 0.1 to 0.3 units, suggesting that passive cooling strategies alone are insufficient to counteract the projected increases in cooling demands under severe climate change scenarios.
This research presents a replicable computational framework for assessing thermal comfort in social housing under climate change, providing evidence-based insights for climate-adaptive building strategies in tropical regions. The methodology’s scalability and the integration of systematic RCP scenarios with machine learning represent significant advances for future-oriented building design in vulnerable regions.
Author Contributions
Conceptualization, D.R., K.A.T., J.G. and A.B.; Data curation, D.R., K.A.T., J.G. and A.J.C.-Q.; Formal analysis, D.R., K.A.T. and J.G.; Funding acquisition, A.B.; Investigation, D.R., K.A.T. and J.G.; Methodology, D.R., K.A.T., J.G. and A.J.C.-Q.; Project administration, C.A., M.S. and A.B.; Resources, A.B.; Software, D.R., K.A.T., J.G. and A.J.C.-Q.; Supervision, C.A., M.S. and A.B.; Validation, D.R., K.A.T., J.G. and A.J.C.-Q.; Visualization, D.R., K.A.T. and J.G.; Writing—original draft, D.R., K.A.T., J.G. and A.J.C.-Q.; Writing—review and editing, D.R., K.A.T., J.G. and A.J.C.-Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request since they are part of a broader research project and will be used in future publications.
Acknowledgments
The authors Diana Romero, Karla A. Torres, and Joanny Gonzalez are grateful for the financial support from SECIHTI (Secretaría de Ciencia, Humanidades, Tecnología e Innovación) for their graduate studies in the Maestría en Ingeniería, opción Energías Renovables at Facultad de Ingeniería, Universidad Autónoma de Yucatán with CVU: 1171844 (Diana Romero), 1294942 (Karla A. Torres), 1310008 (Joanny Gonzalez). The authors thank Claudia Eréndira Vázquez Torres and José Gabriel Hernández Pérez, at the Facultad de Ingeniería, Universidad Autónoma de Yucatán, for the support and information provided during the realization of this research. Additionally, during the preparation of this manuscript, the authors used Grammarly (https://www.grammarly.com/) to verify grammatical accuracy and QuillBot for text paraphrasing to enhance readability and avoid redundancy. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CDD | Cooling Degree Day |
| COMF | Comfort |
| GSA | Global Sensitivity Analysis |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| RCP | Representative Concentration Pathway |
| RMSE | Root Mean Square Error |
| ScI | Scatter Index |
References
- Abam, F.I.; Nwachukwu, C.O.; Emodi, N.V.; Okereke, C.; Diemuodeke, O.E.; Owolabi, A.B.; Owebor, K.; Suh, D.; Huh, J.-S. A Systematic Literature Review on the Decarbonisation of the Building Sector—A Case for Nigeria. Front. Energy Res. 2023, 11, 1253825. [Google Scholar] [CrossRef]
- Jankovic, L. Designing Resilience of the Built Environment to Extreme Weather Events. Sustainability 2018, 10, 141. [Google Scholar] [CrossRef]
- Limmeechokchai, B.; Kongphunphin, C.; Winyuchakrit, P.; Pita, P.; Misila, P. Climate Change 2022 Mitigation of Climate Change: Urban System. Int. J. Build. Urban Inter. Landsc. Technol. 2024, 22, 21–22. [Google Scholar] [CrossRef]
- Babalola, O.; Ugah, U.U.K.; Ekeh, E. Tropical Building Sustainability and the Energy Regulations. Preptint 2024. [Google Scholar] [CrossRef]
- Gonçalves, E.L.S.; Braga, J.L.; de Oliveira Sampaio, A.; dos Santos Batista, V.; da Rocha Menezes, L.J.; Eli, L.G.; Barata, M.S.; Neto, R.d.S.V.; Zemero, B.R. Multiscale Modeling to Optimize Thermal Performance Design for Urban Social Housing: A Case Study. Appl. Therm. Eng. 2024, 236, 121379. [Google Scholar] [CrossRef]
- Ding, Z.; Li, J.; Wang, Z.; Xiong, Z. Multi-Objective Optimization of Building Envelope Retrofits Considering Future Climate Scenarios: An Integrated Approach Using Machine Learning and Climate Models. Romero 2024, 16, 8217. [Google Scholar] [CrossRef]
- Assymkhan, N.; Kartbaev, A.Z. THERMAL COMFORT PREDICTION USING SVM AND RANDOM FOREST MODEL. Вестник КазУТБ 2024, 4, 36–49. [Google Scholar] [CrossRef]
- Jain, H. Critical Insights into Thermal Comfort Optimization and Heat Resilience in Indoor Spaces. City Built Environ. 2024, 2, 14. [Google Scholar] [CrossRef]
- Sadeghi, M.; Chen, D.; Wright, A. A Critical Review of Overheating Risk Assessment Criteria in International and National Regulations—Gaps and Suggestions for Improvements. Energies 2024, 17, 6354. [Google Scholar] [CrossRef]
- Guzmán Hernández, I.A. Estrategias de Diseño Bioclimático Para Una Vivienda Popular En Clima Cálido-Húmedo de México: Protección Solar, Ventilación y Técnicas de Deshumidificación. Ph.D. Thesis, Universitat Politécnica de Catalunya, Barcelona, Spain, 2023. [Google Scholar]
- Andrade-Velázquez, M.; Medrano-Pérez, O.R.; Montero-Martínez, M.J.; Alcudia-Aguilar, A. Regional Climate Change in Southeast Mexico-Yucatan Peninsula, Central America and the Caribbean. Appl. Sci. 2021, 11, 8284. [Google Scholar] [CrossRef]
- INEGI Climatologia. Available online: https://www.inegi.org.mx/temas/climatologia/ (accessed on 8 March 2025).
- CONUEE. Clasificación de Climas y Su Aplicación a La Norma Para La Envolvente de Viviendas: Notas Para Discusión; CONUEE: Ciudad de México, Mexico, 2020. [Google Scholar]
- Rincón-Martínez, J.C.; García-Gómez, C.; González-Trevizo, M.E. Estimación Del Rango de Confort Higrotérmico Para Exteriores En Dos Bioclimas Extremos de México. Ing. Investig. Tecnol. 2022, 23, 14. [Google Scholar] [CrossRef]
- Adaji, M.U. Thermal Comfort in a Hot-Humid Climate Through Passive Cooling in Low-Income Residential Buildings in Abuja, Nigeria; University of Kent (United Kingdom): Canterbury, UK, 2017; ISBN 9798790680748. [Google Scholar]
- Dowou, K.; Nougbléga, Y.; Toka, K.A.; Amou, K.A. Numerical Study of Integrating Thermal Insulation Local Bio-Sourced Materials into Walls and Roofs for Thermal Comfort Improvement in Buildings in a Tropical Climate. Constr. Mater. 2025, 5, 4. [Google Scholar] [CrossRef]
- Aidi, M.; Harnane, Y.; Bordja, L. Thermal Performance and Energy Efficiency of Bio-Sourced Insulated Roofs. Stud. Eng. Exact Sci. 2024, 5, e8239. [Google Scholar] [CrossRef]
- Cunha, L.F.; Barbosa, J.A.d.S.; Sampaio, A.d.O.; Gonçalves, E.L.S.; Menezes, L.; Barata, M.S.; Zemero, B.R. Impacts of Local and Global Climate Change on the Thermal Performance of Social Interest Housing in Hot and Humid Climates. Available SSRN 4719210 2024. [Google Scholar] [CrossRef]
- Luo, K.; Zong, Z.; Yin, X.; Zuo, Y.; Fu, Y.; Zhan, W. Shale Pore Pressure Seismic Prediction Based on the Hydrogen Generation and Compaction-Based Rock-Physics Model and Bayesian Hamiltonian Monte Carlo Inversion Method. Geophysics 2025, 90, M15–M30. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Zhuang, M.; Zhan, W.; Liu, N.; Liu, Q.H. An Efficient Thin Layer Equivalent Technique of SETD Method for Thermo-Mechanical Multi-Physics Analysis of Electronic Devices. Int. J. Heat Mass Transf. 2022, 192, 122816. [Google Scholar] [CrossRef]
- Arnesano, M. Development and Application of EEG Signal Pattern Analysis and Artificial Neural Network for Indoor Comfort Measurement. In Proceedings of the 2024 IEEE International Workshop on Metrology for Living Environment (MetroLivEnv), Chania, Greece, 12–14 June 2024; IEEE: Chania, Greece, 2024; pp. 11–15. [Google Scholar]
- Dogan, A.; Kayaci, N.; Bacak, A. Machine Learning-Based Predictive Model for Temperature and Comfort Parameters in Indoor Enviroment Using Experimantal Data. Appl. Therm. Eng. 2025, 259, 124852. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Sulaimon, I.; Sunmola, F.; Ajayi, S. Building Energy Consumption Prediction for Residential Buildings Using Deep Learning and Other Machine Learning Techniques. J. Build. Eng. 2022, 45, 103406. [Google Scholar] [CrossRef]
- Esrafilian-Najafabadi, M.; Haghighat, F. Impact of Occupancy Prediction Models on Building HVAC Control System Performance: Application of Machine Learning Techniques. Energy Build. 2022, 257, 111808. [Google Scholar] [CrossRef]
- Rožman, M.; Kišić, A.; Oreški, D. Comparative Analysis of Nonlinear Models Developed Using Machine Learning Algorithms. WSEAS Trans. Inf. Sci. Appl. 2024, 21, 303–307. [Google Scholar] [CrossRef]
- Bist, A.S.; Rawat, B.; Joshi, Y.; Aini, Q.; Santoso, N.P.L.; Kusumawardhani, D.A.R. Harnessing Deep Learning for Accurate Climate Change Predictions. In Proceedings of the 2024 3rd International Conference on Creative Communication and Innovative Technology (ICCIT), Tangerang, Indonesia, 7–8 August 2024; pp. 1–6. [Google Scholar]
- Rane, N.; Choudhary, S.P.; Rane, J. Ensemble Deep Learning and Machine Learning: Applications, Opportunities, Challenges, and Future Directions. Stud. Med. Heal. Sci. 2024, 1, 18–41. [Google Scholar]
- Zhu, C.; Shen, X.; Zhu, G.; |Li, B. Prediction of Thermal Conductance of Complex Networks with Deep Learning. Chin. Phys. Lett. 2023, 40, 124402. [Google Scholar] [CrossRef]
- Mazo, G. A New Paradigm for Global Sensitivity Analysis. arXiv 2024, arXiv:2409.06271. [Google Scholar] [CrossRef]
- Alsharif, R.; Arashpour, M.; Golafshani, E.M.; Hosseini, M.R.; Chang, V.; Zhou, J. Machine Learning-Based Analysis of Occupant-Centric Aspects: Critical Elements in the Energy Consumption of Residential Buildings. J. Build. Eng. 2022, 46, 103846. [Google Scholar] [CrossRef]
- Cetina-Quiñones, A.J.; Bassam, A.; Quintal-Palomo, R.E.; Pérez-Fargallo, A. Surrogate Model of Adaptive Thermal Comfort of a Social Housing in the Dominican Republic Micro-Climates: A Predictive Approach toward Sustainable Buildings. Energy Sources Part A Recover. Util. Environ. Eff. 2023, 46, 804–819. [Google Scholar] [CrossRef]
- Boutahri, Y.; Tilioua, A. Machine Learning-Based Predictive Model for Thermal Comfort and Energy Optimization in Smart Buildings. Results Eng. 2024, 22, 102148. [Google Scholar] [CrossRef]
- Karimi, A.; Mohajerani, M.; Alinasab, N.; Akhlaghinezhad, F. Integrating Machine Learning and Genetic Algorithms to Optimize Building Energy and Thermal Efficiency Under Historical and Future Climate Scenarios. Sustainability 2024, 16, 9324. [Google Scholar] [CrossRef]
- Karyono, K.; Abdullah, B.M.; Cotgrave, A.; Bras, A.; Cullen, J. Field Studies of the Artificial Intelligence Model for Defining Indoor Thermal Comfort to Acknowledge the Adaptive Aspect. Eng. Appl. Artif. Intell. 2024, 133, 108381. [Google Scholar] [CrossRef]
- Hussien, A.; Maksoud, A.; Al-Dahhan, A.; Abdeen, A.; Baker, T. Machine Learning Model for Predicting Long-Term Energy Consumption in Buildings. Discov. Internet Things 2025, 5, 18. [Google Scholar] [CrossRef]
- Burgos, E.M. Incorporating Climate Projections into Infrastructure Planning and Design; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2024. [Google Scholar] [CrossRef]
- Lucay, F.A. Accelerating Global Sensitivity Analysis via Supervised Machine Learning Tools: Case Studies for Mineral Processing Models. Minerals 2022, 12, 750. [Google Scholar] [CrossRef]
- Sánchez, J.F.P.; Fernández, P.M.E. Propuestas de Mejora Para Incrementar La Calidad Del Hábitat En Viviendas de Interés Social En México: Caso de Estudio Las Dunas. Master’s Thesis, Universidad de Sevilla, Sevilla, Spain, 2021. [Google Scholar]
- Alrasheed, M.; Mourshed, M. Domestic Overheating Risks and Mitigation Strategies: The State-of-the-Art and Directions for Future Research. Indoor Built Environ. 2023, 32, 1057–1077. [Google Scholar] [CrossRef]
- Hernández, G.; Cetina-Quiñones, A.J.; Bassam, A.; Carrillo, J.G. Passive Strategies towards Energy Efficient Social Housing: A Parametric Case Study and Decision-Making Framework in the Mexican Tropical Climate. J. Build. Eng. 2024, 82, 108282. [Google Scholar] [CrossRef]
- Gurney, K.R.; Kılkış, Ş.; Seto, K.C.; Lwasa, S.; Moran, D.; Riahi, K.; Keller, M.; Rayner, P.; Luqman, M. Greenhouse Gas Emissions from Global Cities under SSP/RCP Scenarios, 1990 to 2100. Glob. Environ. Change 2022, 73, 102478. [Google Scholar] [CrossRef]
- Vázquez-Torres, C.E.; Beizaee, A.; Bienvenido-Huertas, D. The Impact of Human Occupancy in Thermal Performance of a Historic Religious Building in Sub-Humid Temperate Climate. Energy Build. 2022, 259, 111912. [Google Scholar] [CrossRef]
- Cengel, Y. Heat and Mass Transfer: Fundamentals and Applications; McGraw-Hill Higher Education: Columbus, OH, USA, 2014; ISBN 0077654765. [Google Scholar]
- Meteonorm Meteonorm: World Irradiation Data. Available online: https://meteonorm.com/en/ (accessed on 6 June 2025).
- Simmonds, P. Using ASHRAE Standard 55 Adaptive Comfort Method for Practical Applications. In Proceedings of the REHVA 14th HVAC World Congress, Rotterdam, The Netherlands, 22–25 May 2022; pp. 1–8. [Google Scholar]
- ANSI/ASHRAE, 55; Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air-Conditioning Engineers: Peachtree Corners, GA, USA, 1992.
- De Dear, R.J.; Brager, G.S. Thermal Comfort in Naturally Ventilated Buildings: Revisions to ASHRAE Standard 55. Energy Build. 2002, 34, 549–561. [Google Scholar] [CrossRef]
- Pérez-Fargallo, A.; Pulido-Arcas, J.A.; Rubio-Bellido, C.; Trebilcock, M.; Piderit, B.; Attia, S. Development of a New Adaptive Comfort Model for Low Income Housing in the Central-South of Chile. Energy Build. 2018, 178, 94–106. [Google Scholar] [CrossRef]
- Castaño-Rosa, R.; Barrella, R.; Sánchez-Guevara, C.; Barbosa, R.; Kyprianou, I.; Paschalidou, E.; Thomaidis, N.S.; Dokupilova, D.; Gouveia, J.P.; Kádár, J.; et al. Cooling Degree Models and Future Energy Demand in the Residential Sector. A Seven-Country Case Study. Sustainability 2021, 13, 2987. [Google Scholar] [CrossRef]
- Tran, T.N.; Lam, B.M.; Nguyen, A.T.; Le, Q.B. Load Forecasting with Support Vector Regression: Influence of Data Normalization on Grid Search Algorithm. Int. J. Electr. Comput. Eng. 2022, 12, 3410–3420. [Google Scholar] [CrossRef]
- Huang, L.; Qin, J.; Zhou, Y.; Zhu, F.; Liu, L.; Shao, L. Normalization Techniques in Training Dnns: Methodology, Analysis and Application. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10173–10196. [Google Scholar] [CrossRef]
- Hrehova, S.; Husár, J. Selected Application Tools for Creating Models in the Matlab Environment. In Proceedings of the International Conference on Future Access Enablers of Ubiquitous and Intelligent Infrastructures, Virtual, 4 May 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 181–192. [Google Scholar]
- Jiang, Y. Personalized Thermal Comfort Model with Decision Tree. Intell. Control Autom. 2019, 10, 168–177. [Google Scholar] [CrossRef]
- Zhou, X.; Xu, L.; Zhang, J.; Niu, B.; Luo, M.; Zhou, G.; Zhang, X. Data-Driven Thermal Comfort Model via Support Vector Machine Algorithms: Insights from ASHRAE RP-884 Database. Energy Build. 2020, 211, 109795. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Q. Artificial Neural Network Models Using Thermal Sensations and Occupants’ Behavior for Predicting Thermal Comfort. Energy Build. 2018, 174, 587–602. [Google Scholar] [CrossRef]
- Seraj, A.; Mohammadi-Khanaposhtani, M.; Daneshfar, R.; Naseri, M.; Esmaeili, M.; Baghban, A.; Habibzadeh, S.; Eslamian, S. Cross-Validation. In Handbook of Hydroinformatics; Elsevier: Amsterdam, The Netherlands, 2023; pp. 89–105. [Google Scholar]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Trees vs Neurons: Comparison between Random Forest and ANN for High-Resolution Prediction of Building Energy Consumption. Energy Build. 2017, 147, 77–89. [Google Scholar] [CrossRef]
- Walker, S.; Khan, W.; Katic, K.; Maassen, W.; Zeiler, W. Accuracy of Different Machine Learning Algorithms and Added-Value of Predicting Aggregated-Level Energy Performance of Commercial Buildings. Energy Build. 2020, 209, 109705. [Google Scholar] [CrossRef]
- Shi, P.; Shi, R.; Zhang, L. Regression Tree-Based Predictive Control with Variable Separation for Airport Terminal HVAC Optimization. Build. Serv. Eng. Res. Technol. 2025. [Google Scholar] [CrossRef]
- Zileska Pancovska, V.; Petrusheva, S.; Sekovska, B. Prediction of Energy Consumption in Buildings Using Support Vector Machine. Teh. Vjesn. 2021, 28, 649–656. [Google Scholar]
- Pianosi, F.; Wagener, T. A Simple and Efficient Method for Global Sensitivity Analysis Based Oncumulative Distribution Functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. Distribution-Based Sensitivity Analysis from a Generic Input-Output Sample. Environ. Model. Softw. 2018, 108, 197–207. [Google Scholar] [CrossRef]
- Zadeh, F.K.; Nossent, J.; Sarrazin, F.; Pianosi, F.; Van Griensven, A.; Wagener, T.; Bauwens, W. Comparison of Variance-Based and Moment-Independent Global Sensitivity Analysis Approaches by Application to the SWAT Model. Environ. Model. Softw. 2017, 91, 210–222. [Google Scholar] [CrossRef]
- Berger, V.W.; Zhou, Y. Kolmogorov–Smirnov Test: Overview. Wiley Statsref Stat. Ref. Online 2014. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Rajasekar, E. Application of a Probabilistic LHS-PAWN Approach to Assess Building Cooling Energy Demand Uncertainties. In Proceedings of the Building Simulation, Chambery, France, 25–28 August 2013; Springer: Amsterdam, The Netherlands, 2022; Volume 15, pp. 373–387. [Google Scholar]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; ISBN 9291691437. [Google Scholar]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.L.T.; Lamarque, J.-F.; Matsumoto, K.; Montzka, S.A.; Raper, S.C.B.; Riahi, K. The RCP Greenhouse Gas Concentrations and Their Extensions from 1765 to 2300. Clim. Change 2011, 109, 213–241. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).