Modelling the Cyclical Variability of Nitrogen Dioxide in Urban Areas of Poland, 2001–2021
Abstract
1. Introduction
2. Materials and Methods
- Gaussian: for ,
- Polynomial: for ,
- Rational: for ,
- Sum of sines: for ,
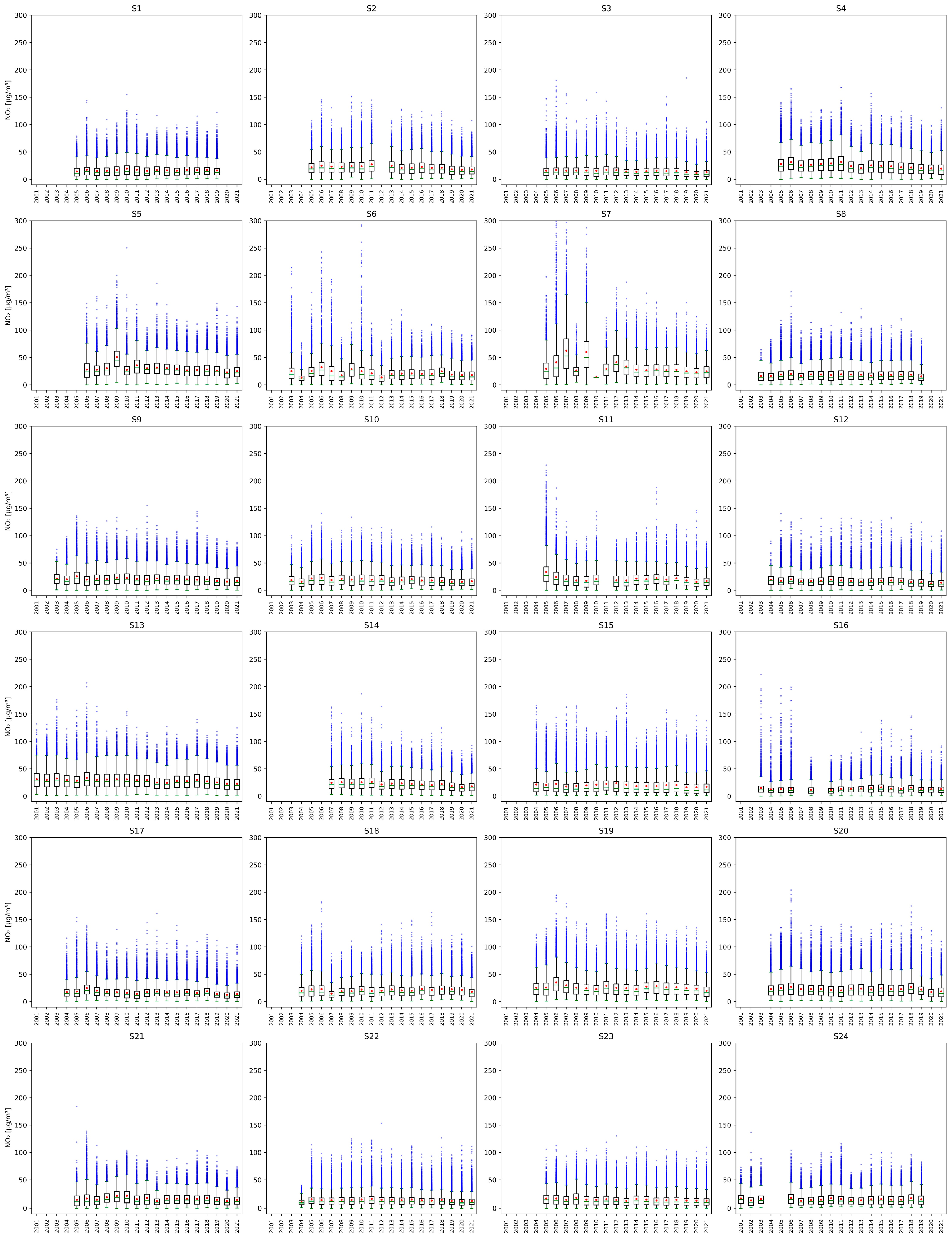
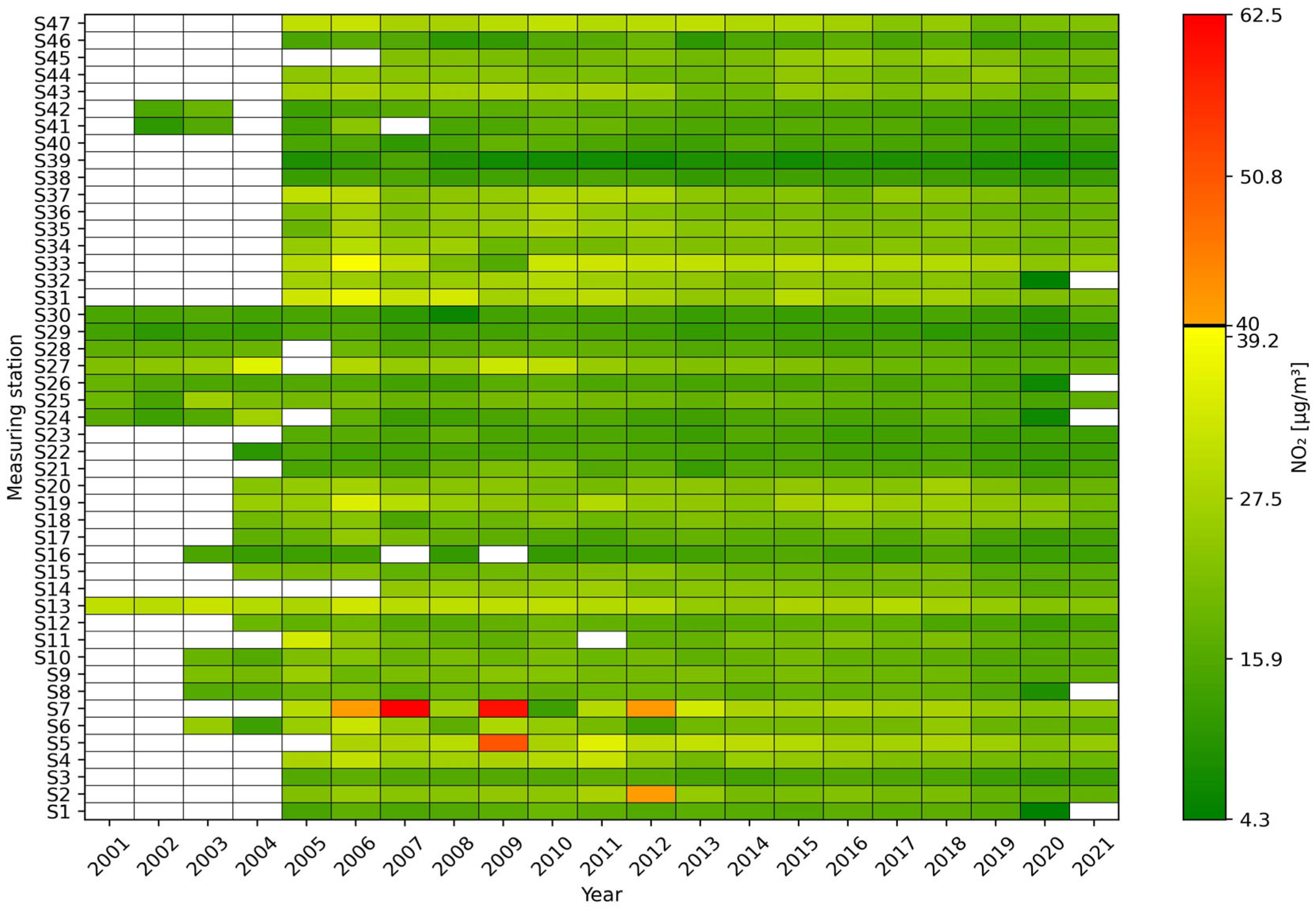
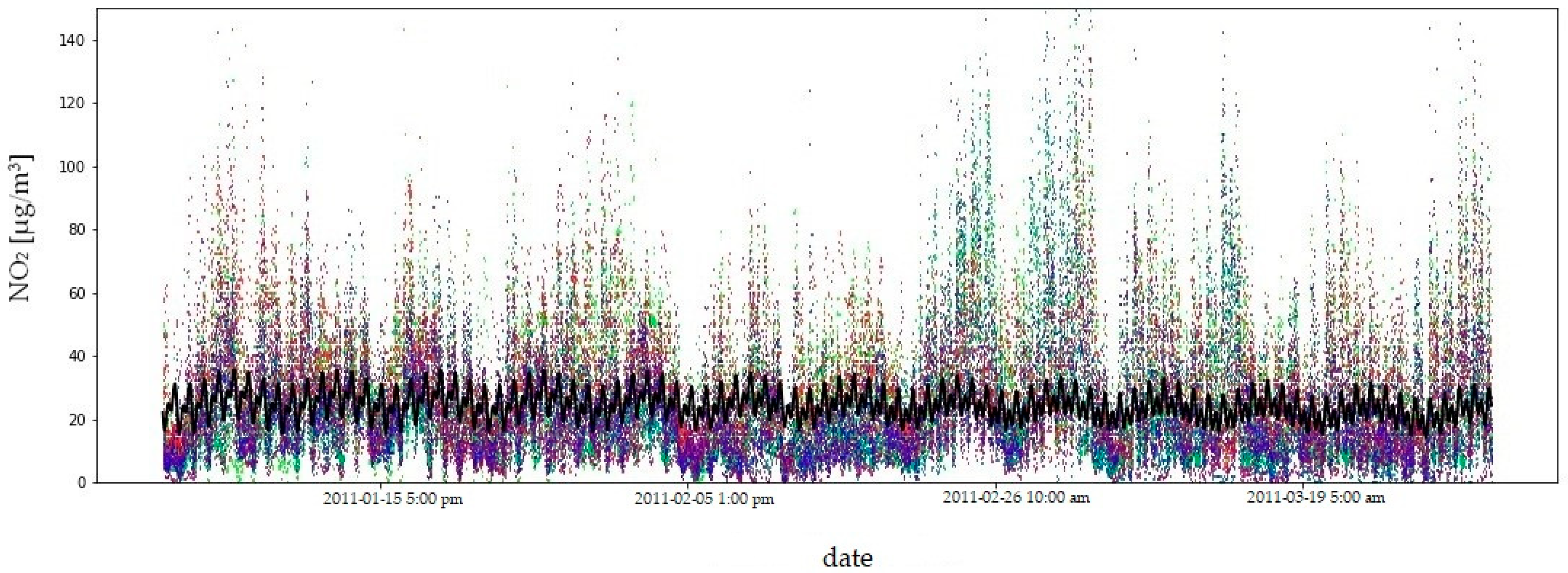
3. Results
- If is (much) greater than the length of the range , then the property for is used. In this case, behaves similarly to a linear expression dependent on the variable x. can be assumed, and in this case, an almost linear trend is obtained for the data with a directional coefficient and a shift
- If is (much) smaller than the length of the range , describes the ‘sinusoidal’ cyclical nature of the changes in the measured feature during the measurement period. In this case, the interval determines the range of variation of the measured feature in one full period of length , and is an offset.
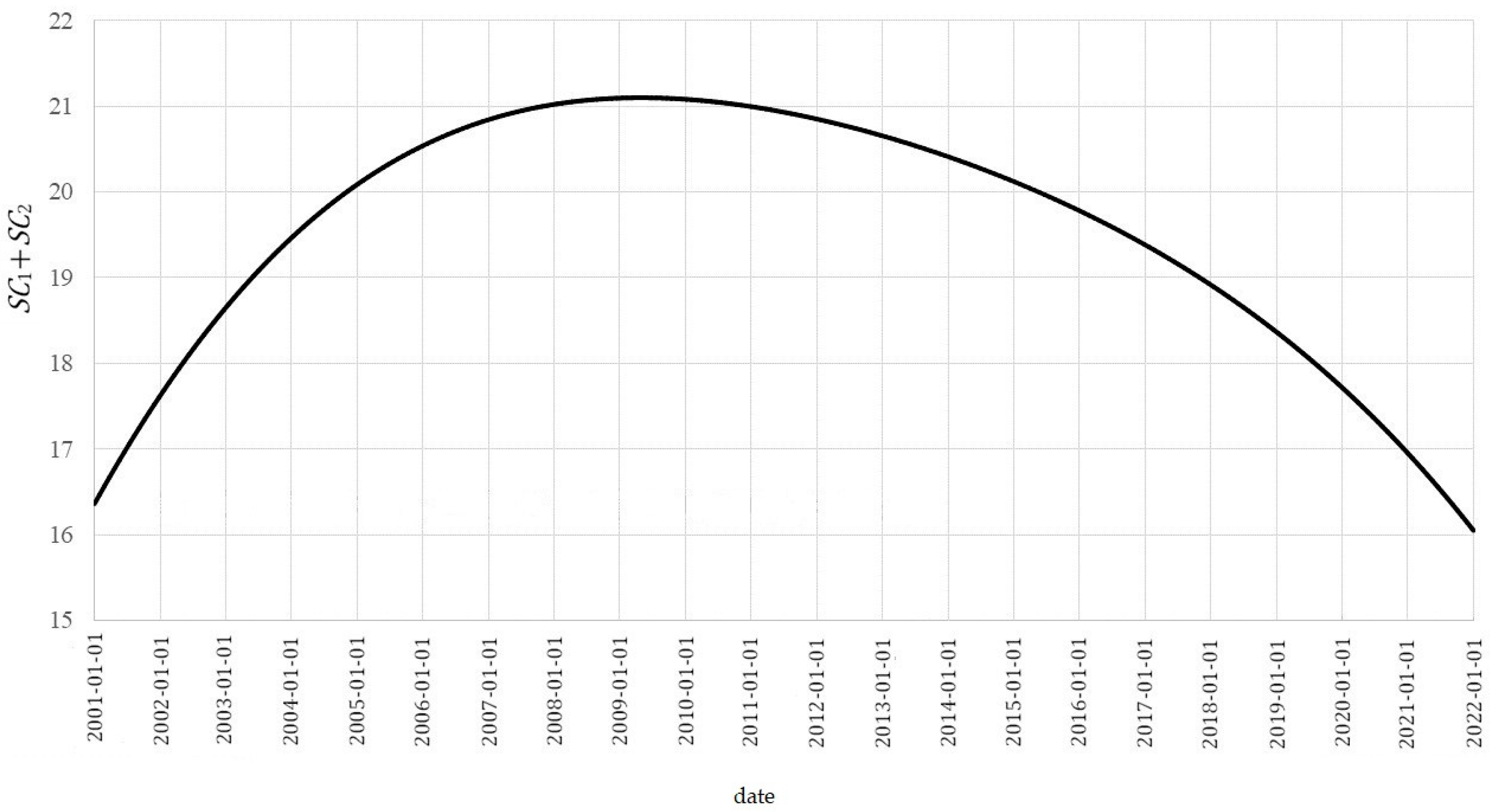
- General trend for the data (Figure 3):
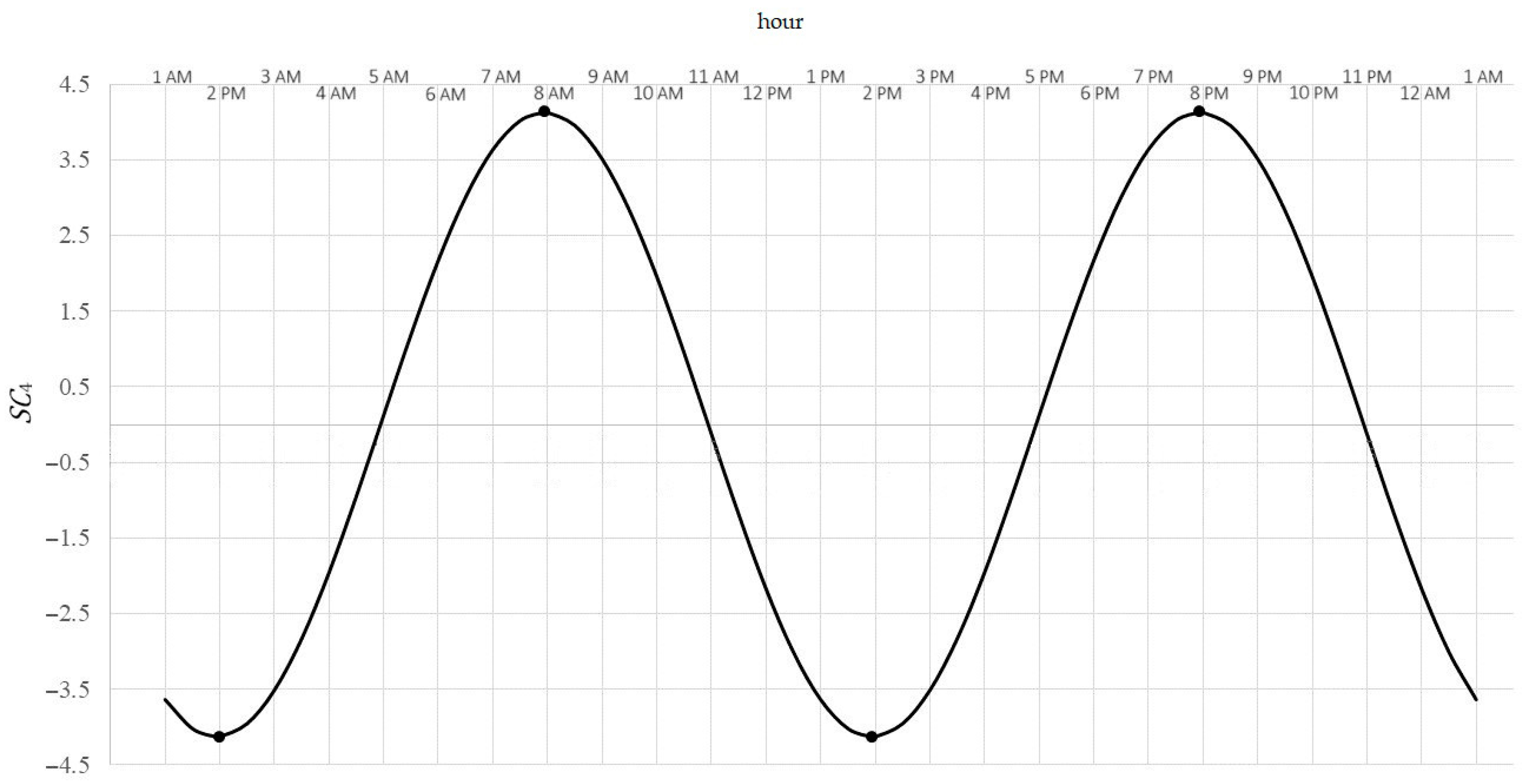
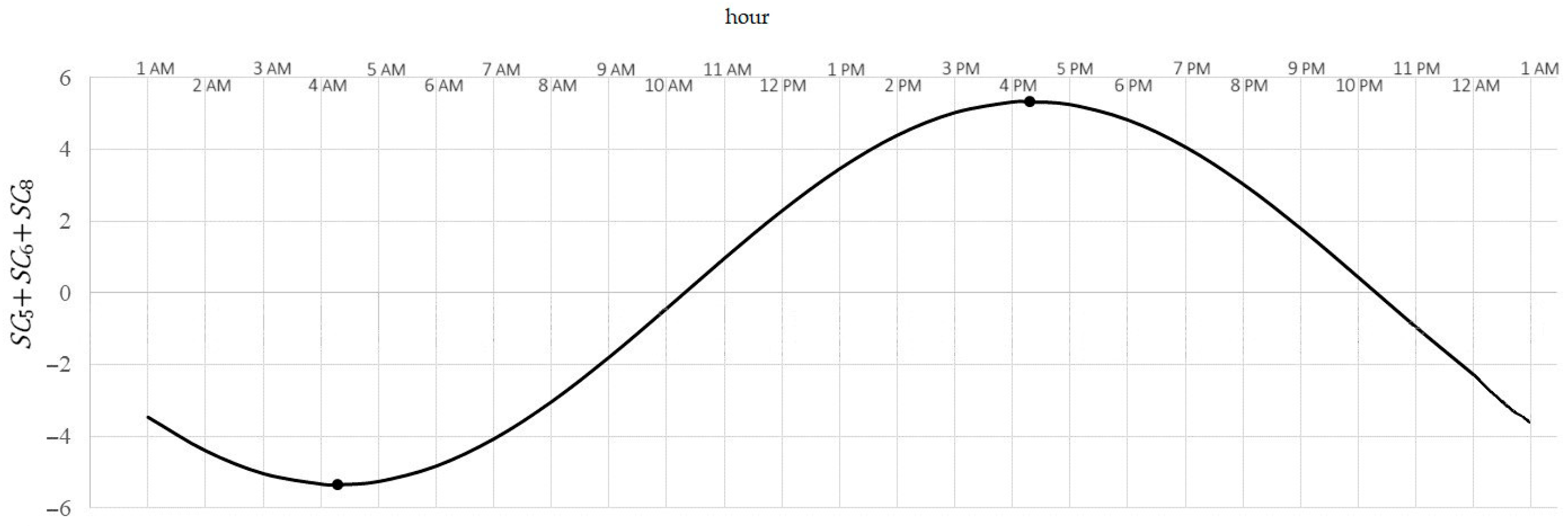
- 12-h variability (Figure 4):
- 24-h variability (Figure 5):
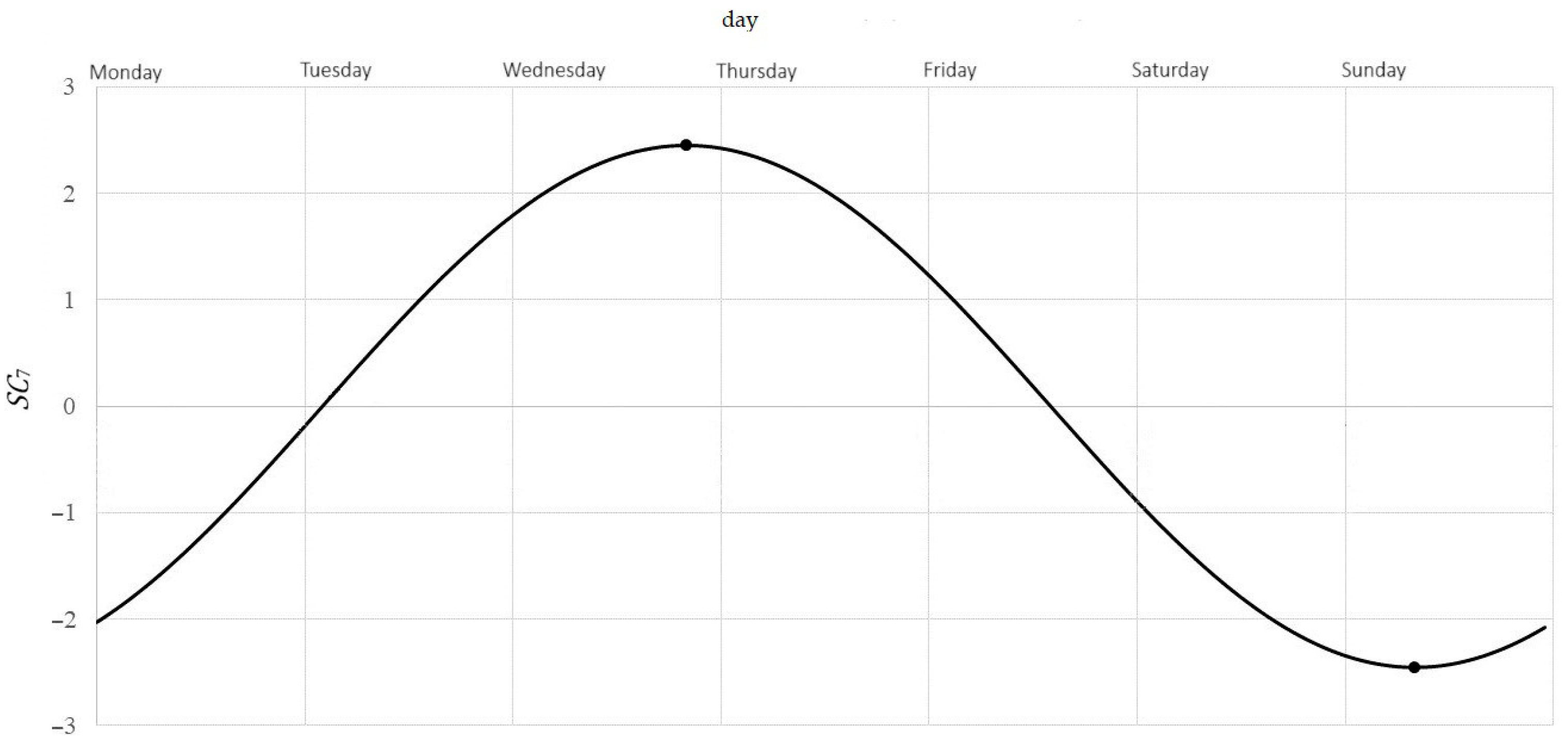
- Weekly variability (Figure 6):
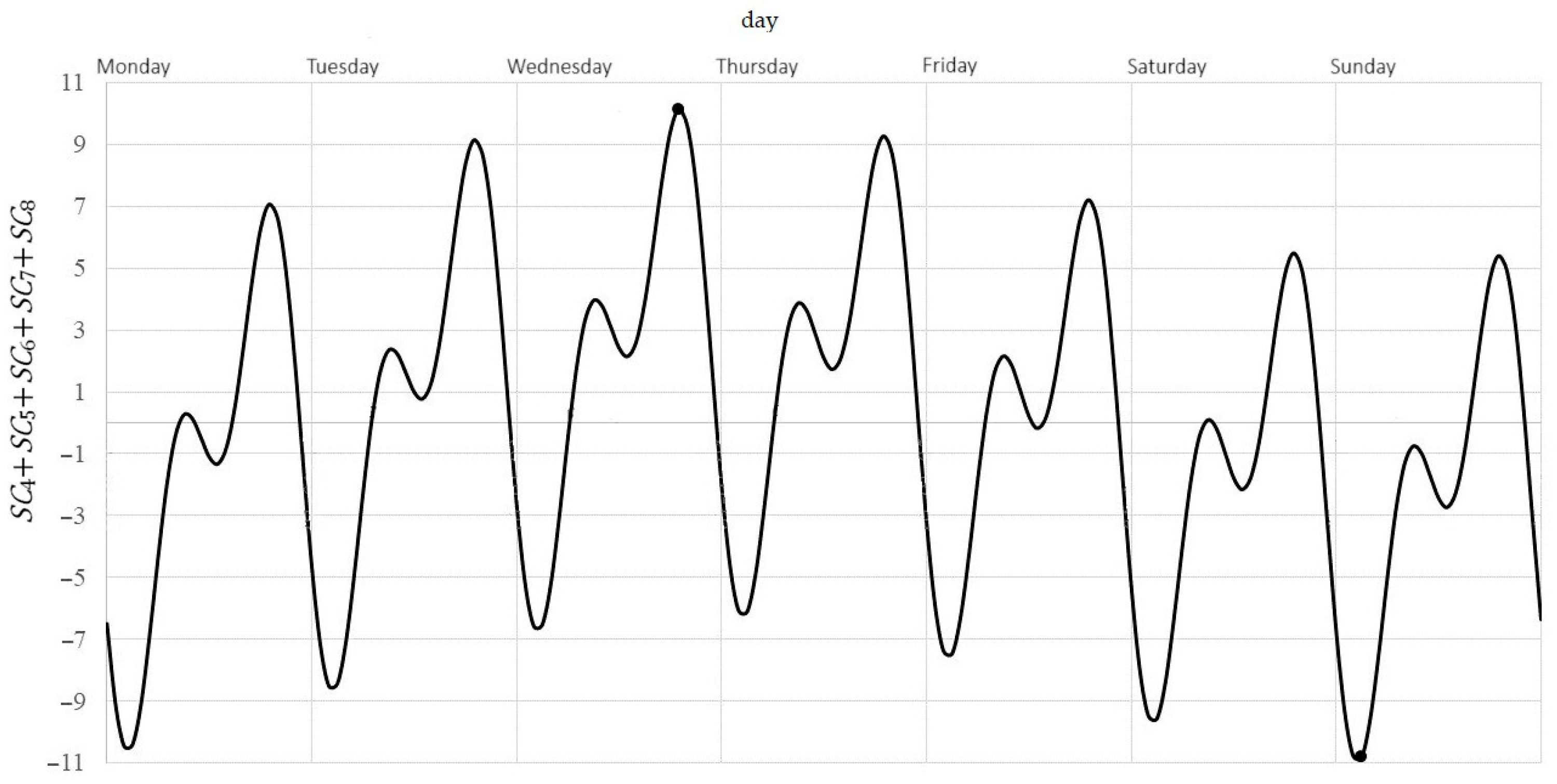
- Total weekly variability (Figure 7):
- Annual variability (Figure 8):
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Bourdrel, T.; Bind, M.-A.; Bejot, Y.; Morel, O.; Argacha, J.-F. Cardiovascular effects of air pollution. Arch. Cardiovasc. Dis. 2017, 110, 634–642. [Google Scholar] [CrossRef] [PubMed]
- Goshua, A.; Akdis, C.A.; Nadeau, K.C. World Health Organization global air quality guideline recommendations: Executive summary. Allergy 2022, 77, 1955–1960. [Google Scholar] [CrossRef]
- Guarnieri, M.; Balmes, J.R. Outdoor air pollution and asthma. Lancet 2014, 383, 1581–1592. [Google Scholar] [CrossRef]
- Jiang, X.-Q.; Mei, X.-D.; Feng, D. Air pollution and chronic airway diseases: What should people know and do? J. Thorac. Dis. 2016, 8, E31–E40. [Google Scholar]
- Manisalidis, I.; Stavropoulou, E.; Stavropoulos, A.; Bezirtzoglou, E. Environmental and health impacts of air pollution: A review. Front. Public Health 2020, 8, 505570. [Google Scholar] [CrossRef]
- Mo, Z.; Fu, Q.; Lyu, D.; Zhang, L.; Qin, Z.; Tang, Q.; Yin, H.; Xu, P.; Wu, L.; Wang, X.; et al. Impacts of air pollution on dry eye disease among residents in Hangzhou, China: A case-crossover study. Environ. Pollut. 2019, 246, 183–189. [Google Scholar] [CrossRef] [PubMed]
- Gawełko, J.; Cierpiał-Wolan, M.; Bwanakare, S.; Czarnota, M. Association between Air Pollution and Squamous Cell Lung Cancer in South-Eastern Poland. Int. J. Environ. Res. Public Health 2022, 19, 11598. [Google Scholar] [CrossRef] [PubMed]
- Emberson, L.D.; Pleijel, H.; Ainsworth, E.A.; den Berg, M.; Ren, W.; Osborne, S.; Mills, G.; Pandey, D.; Dentener, F.; Büker, P.; et al. Ozone effects on crops and consideration in crop models. Eur. J. Agron. 2018, 100, 19–34. [Google Scholar] [CrossRef]
- Saxena, V. Water Quality, Air Pollution, and Climate Change: Investigating the Environmental Impacts of Industrialization and Urbanization. Water Air Soil Pollut. 2025, 236, 73. [Google Scholar] [CrossRef]
- Treder, M. Smog—A threat to health safety in Poland. Rocz. Bezpieczeństwa Międzynarodowego 2017, 11, 190–204. [Google Scholar]
- Lasne, J.; Lostier, A.; Salameh, T.; Athanasopoulou, E.; Karagiannis, D.; Kakouri, A.; Vassaux, S.; Lesueur, D.; Romanias, M.N. NOx emissions by real-world fresh and old asphalt mixtures: Impact of temperaturę, relative humidity, and UV-irradiation. Urban Clim. 2023, 49, 101457. [Google Scholar] [CrossRef]
- United Nations, Department of Economic and Social Affairs, Population Division. World Urbanization Prospects: The 2018 Revision. Available online: https://www.un.org/development/desa/pd/content/publications (accessed on 12 August 2021).
- The Ella Roberta Fundation. Available online: https://www.ellaroberta.org/about-ella (accessed on 6 October 2024).
- Health Impacts of Air Pollution in Europe. 2022. Available online: https://www.eea.europa.eu/publications/air-quality-in-europe-2022/health-impacts-of-air-pollution (accessed on 25 November 2023).
- Pope, C.A.; Dockery, D.W. Health Effects of Fine Particulate Air Pollution: Lines that Connect. J. Air Waste Manag. Assoc. 2006, 56, 709–742. [Google Scholar] [CrossRef]
- Kampa, M.; Castanas, E. Human health effects of air pollution. Environ. Pollut. 2008, 151, 362–367. [Google Scholar] [CrossRef]
- Brook, R.D.; Rajagopalan, S.; Brook, J.R.; Bhatnagar, A.; Diez-Roux, A.V.; Holguin, F.; Hong, Y.; Luepker, R.V.; Mittleman, M.A.; Peters, A.; et al. Particulate matter air pollution and cardiovascular disease an update to the scientific statement from the American Heart Association. Circulation 2010, 121, 2331–2378. [Google Scholar] [CrossRef]
- Künzli, N.; Perez, L.; Rapp, R. Air Quality and Health; European Respiratory Society: Lausanne, Switzerland, 2010; Available online: https://www.ersnet.org/wp-content/uploads/2021/03/Air-Quality-and-Health-2010.pdf (accessed on 17 December 2024).
- Kelly, F.J.; Fussell, J.C. Air pollution and airway disease. Clin. Exp. Allergy 2011, 41, 1059–1071. [Google Scholar] [CrossRef] [PubMed]
- Genc, S.; Zadeoglulari, Z.; Fuss, S.H.; Genc, K. The adverse effects of air pollution on the nervous system. J. Toxicol. 2012, 2012, 782462. [Google Scholar] [CrossRef]
- Ding, L.; Zhu, D.; Peng, D. Meta-analysis of the relationship between particular matter (PM(10) and PM(2.5)) and asthma hospital admissions in children. Chin. J. Pediatr. 2015, 53, 129–135. [Google Scholar]
- Yamazaki, S.; Shima, M.; Yoda, Y.; Oka, K.; Kurosaka, F.; Shimizu, S. Exposure to air pollution and meteorological factors associated with children’s primary care visit at night due to asthma attack: Case-crossover design for 3-tear pooled patients. BMJ Open. 2015, 5, e005736. [Google Scholar] [CrossRef]
- Clifford, A.; Lang, L.; Chen, R.; Anstey, K.J.; Seaton, A. Exposure to air pollution and cognitive functioning across the life course—A systematic literature review. Environ. Res. 2016, 147, 383–398. [Google Scholar] [CrossRef] [PubMed]
- Krzyżanowski, M. Wpływ zanieczyszczenia powietrza pyłami na układ krążenia i oddychania. Lek. Wojsk. 2016, 1, 17–22. [Google Scholar]
- Wojdat, M.; Stańczyk, A.; Gielerak, G. Zanieczyszczenia powietrza a choroby układu sercowo-naczyniowego—Niedoceniany problem. Lek. Wojsk. 2016, 1, 10–16. [Google Scholar]
- Compa, M.F.; Baumbach, C.; Kaczmarek-Majer, K.; Buczyłowska, D.; Gradys, G.; Skotak, K.; Degórska, A.; Bratkowski, J.; Wierzba-Łukaszyk, M.; Mysak, Y.; et al. Air Pollution and Attention in Polish Schoolchildren with and without ADHD. Sci. Total Environ. 2023, 892, 164759. [Google Scholar] [CrossRef]
- Thurston, G.D.; Kipen, H.; Annesi-Maesano, I.; Balmes, J.; Brook, R.D.; Cromar, K.; De Matteis, S.; Forastiere, F.; Forsberg, B.; Frampton, M.W.; et al. A joint ERA/ATS policy statement: What constitutes an adverse health effect of air pollution? An analytical framework. Eur. Respir. J. 2017, 49, 1600419. [Google Scholar] [CrossRef]
- First, M.W. HEPA filters. J. Am. Biol. Saf. Assoc. 1998, 3, 33–42. [Google Scholar] [CrossRef]
- Liao, J.; Ye, W.; Pillarisetti, A.; Clasen, T.F. Modeling the Impact of Indoor Air Folter on Air Pollution Exposure Reduction and Associated Mortality in Urban Household. Int. J. Environ. Res. Public Health 2019, 16, 1391. [Google Scholar] [CrossRef] [PubMed]
- Dreisbach, R.H.; Robertson, W. Vademecum Zatruć: Zapobieganie, Rozpoznawanie I Postępowanie; PZWL: Warszawa, Poland, 1995. [Google Scholar]
- Eum, K.; Honda, T.J.; Wang, B.; Kazemiparkouhi, F.; Manjourides, J.; Pun, V.C.; Suh, H. Long-term nitrogen dioxide exposure and cause-specific mortality in the U.S. Medicare Population. Environ. Res. 2022, 207, 112154. [Google Scholar] [CrossRef]
- Krzyżanowski, M. Wpływ Zanieczyszczenia Powietrza Atmosferycznego Dwutlenkiem Azotu na Zdrowie. 2023. Available online: https://healpolska.pl/wp-content/uploads/2023/06/NO2_a_zdrowie20230629_PL.pdf (accessed on 12 June 2023).
- Bărbulescu, A.; Hosen, K. Cement Industry Pollution and Its Impact on the Environment and Population Health: A Review. Toxics 2025, 13, 587. [Google Scholar] [CrossRef]
- Křůmal, K.; Mikuška, P.; Horák, J.; Hopan, F.; Kuboňová, L. Influence of boiler output and type on gaseous and particulate emissions from the combustion of coal for residential heating. Chemosphere 2021, 278, 130402. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yao, Z.; Zheng, X.; Subramaniam, L.; Butterbach-Bahl, K. A synthesis of nitric emissions across global fertilized croplands from crop-specific emission factors. Glob. Change Biol. 2022, 28, 4395–4408. [Google Scholar] [CrossRef]
- Air Quality in Europe 2022. Sources and Emissions of Air Pollutants in Europe. Available online: https://www.eea.europa.eu/publications/air-quality-in-europe-2022/sources-and-emissions-of-air (accessed on 17 September 2023).
- A Technical Summary of Euro 6/VI Vehicle Emission Standards. Available online: https://theicct.org/sites/default/files/publications/ICCT_Euro6-VI_briefing_jun2016.pdf (accessed on 11 January 2024).
- Average Age of the EU Vehicle Fleet, by Country—ACEA—European Automobile Manufacturers’ Association. Available online: https://www.acea.auto/figure/average-age-of-eu-vehicle-fleet-by-country/ (accessed on 29 September 2024).
- Available online: https://trueinitiative.org/insights/new-true-analysis-shows-imported-used-light-duty-vehicles-in-warsaw-emit-two-to-three-times-as-much-pollution-as-domestic-vehicles?tag=Brussels/ (accessed on 25 May 2024).
- Bernard, Y.; Tietge, U.; Pniewska, I. Remote Sensing of Motor Vehicle Emissions in Krakow. 2020. Available online: https://theicct.org/wp-content/uploads/2021/06/Remote-sensing-Krakow-sept2020-1.pdf (accessed on 25 May 2024).
- Centralna Ewidencja Pojazdów i Kierowców. Available online: https://www.gov.pl/web/cepik (accessed on 3 March 2024).
- Bank Danych Lokalnych. Available online: https://bdl.stat.gov.pl/bdl/dane/podgrup/temat (accessed on 11 March 2024).
- Regulation (EU) 2023/851 of the European Parliament and of the Council of 19 April 2023 amending Regulation (EU) 2019/631 as regards strengthening the CO2 emission performance standards for new passenger cars and new light commercial vehicles in line with the Union’s increased climate ambition (OJ L 110, 25.4.2023, pp. 5–20). Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32023R0851 (accessed on 11 March 2024).
- Directive 2008/50/EC of the European Parliament and of the Council of 21 May 2008 on Ambient Air Quality and Cleaner Air for Europe. Available online: https://www.eumonitor.eu/9353000/1/j9vvik7m1c3gyxp/vhvvygrp44xc (accessed on 3 March 2024).
- Ustawa z Dnia 27 Kwietnia 2001, r. Prawo Ochrony Środowiska. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=wdu20010620627 (accessed on 4 December 2023).
- Rozporządzenie Ministra Środowiska z Dnia 24 Sierpnia 2012 r. w Sprawie Poziomów Niektórych Substancji w Powietrzu. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20120001031 (accessed on 4 December 2023).
- Available online: https://www.who.int/news-room/feature-stories/detail/what-are-the-who-air-quality-guidelines (accessed on 4 December 2023).
- Wielgosiński, G.; Czerwińska, J.; Niemiecińska, O.; Cichowicz, R. Smog episodes in the Lodz agglomeration in the years 2014–17. In Proceedings of the E3S Web of Conferences, Zakopane, Poland, 18–21 October 2018; Volume 28, p. 01039. [Google Scholar] [CrossRef]
- Sówka, I.; Chlebowska-Styś, A.; Pachurka, Ł.; Rogula-Kozłowska, W.; Mathews, B. Analysis of particular matter concentration variability and origin in selected urban areas in Poland. Sustainability 2019, 11, 5735. [Google Scholar] [CrossRef]
- GIOŚ. Available online: https://powietrze.gios.gov.pl/pjp/maps/measuringstation (accessed on 4 October 2023).
- Standard PN-EN 14211:2013-02; Atmospheric Air—Standard Method for Measuring the Concentration of Nitrogen Dioxide and Nitrogen Oxide Using Chemiluminescence. Polski Komitet Normalizacyjny: Warszawa, Poland, 2013.
- GIOŚ. Available online: https://powietrze.gios.gov.pl/pjp/archives (accessed on 4 October 2023).
- Ignaciuk, S.; Wawrzosek, J.; Zarajczyk, J.; Choszcz, D. Periodisity of changes in nitrogen oxides concentrations in the urban environment, Part 2. Nitrogen dioxide concentration. Przemysł Chem. 2019, 98, 1927–1929. [Google Scholar]


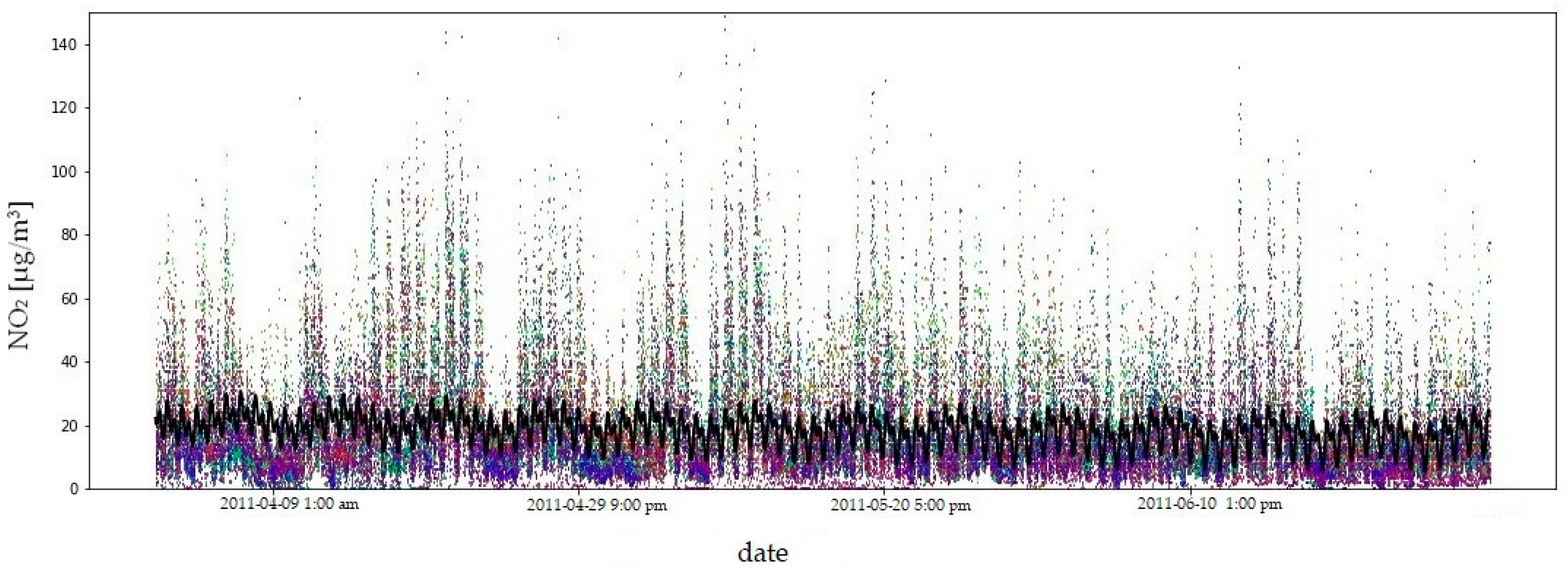
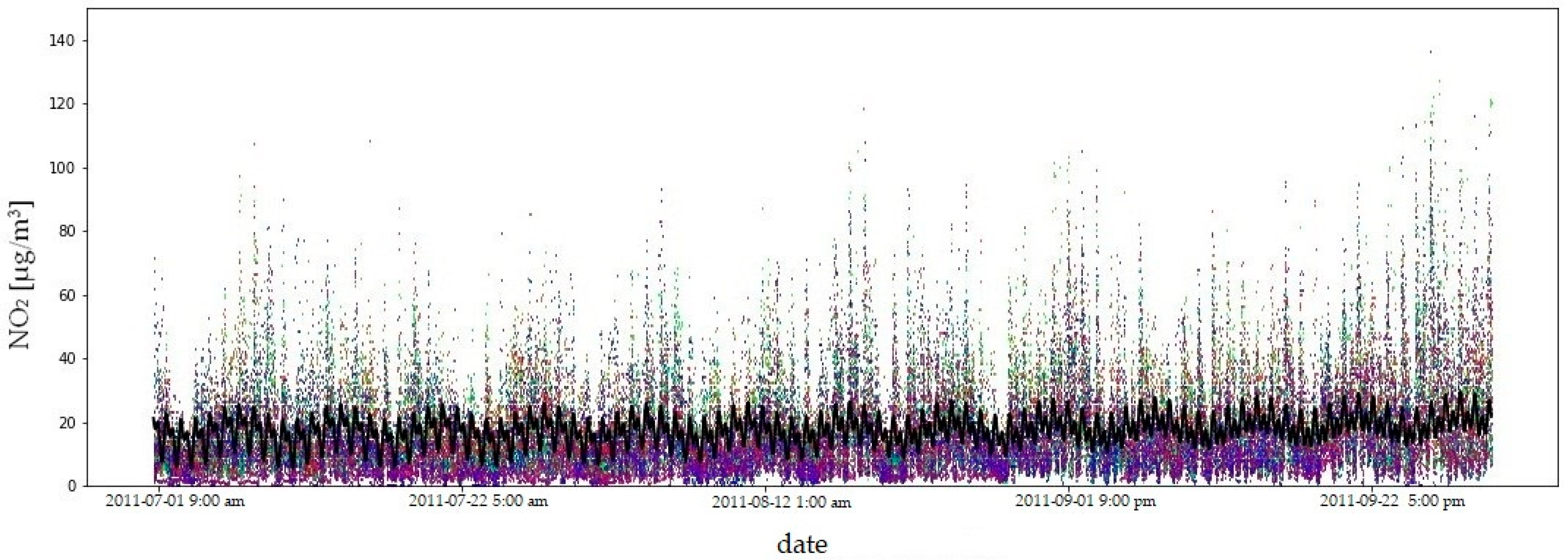
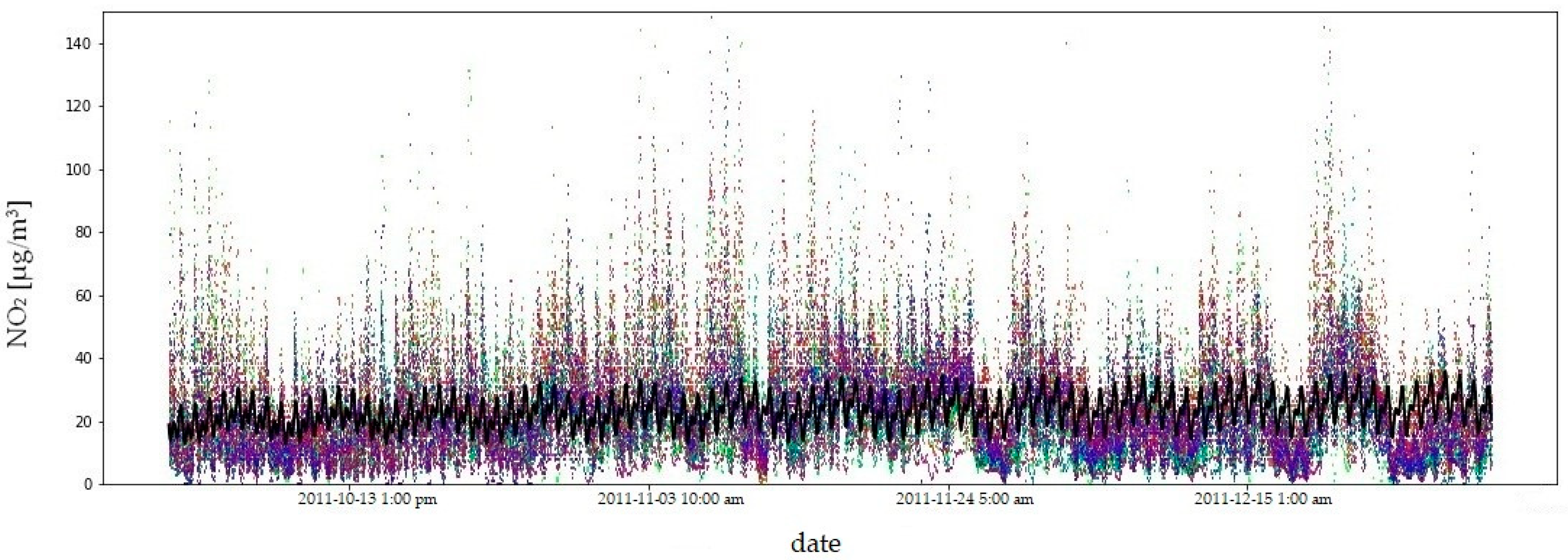
| Symbol | Internationale Code | City/Town | WGS84 φ N | WGS84 λ E |
|---|---|---|---|---|
| S1 | PL0187A | Dzierżoniów | 50.732817 | 16.648050 |
| S2 | PL0190A | Legnica | 51.204503 | 16.180513 |
| S3 | PL0192A | Wałbrzych | 50.768729 | 16.269677 |
| S4 | PL0194A | Wrocław | 51.129378 | 17.029250 |
| S5 | PL0252A | Bydgoszcz | 53.121774 | 17.987883 |
| S6 | PL0064A | Bydgoszcz | 53.134088 | 17.995712 |
| S7 | PL0205A | Włocławek | 52.658467 | 19.059314 |
| S8 | PL0096A | Łódź | 51.758050 | 19.529786 |
| S9 | PL0104A | Pabianice | 51.667981 | 19.368683 |
| S10 | PL0115A | Zgierz | 51.856692 | 19.421231 |
| S11 | PL0209A | Gorzów Wielkopolski | 52.738214 | 15.228667 |
| S12 | PL0213A | Zielona Góra | 51.939783 | 15.518861 |
| S13 | PL0039A | Kraków | 50.069308 | 20.053492 |
| S14 | PL0273A | Skawina | 49.971047 | 19.830422 |
| S15 | PL0126A | Zakopane | 49.293564 | 19.960083 |
| S16 | PL0398A | Płock | 52.556279 | 19.687672 |
| S17 | PL0136A | Płock | 52.550938 | 19.709791 |
| S18 | PL0138A | Radom | 51.399084 | 21.147474 |
| S19 | PL0143A | Warszawa | 52.290864 | 21.042458 |
| S20 | PL0141A | Warszawa | 52.160772 | 21.033819 |
| S21 | PL0218A | Kędzierzyn-Koźle | 50.349608 | 18.236575 |
| S22 | PL0148A | Białystok | 53.126689 | 23.155869 |
| S23 | PL0151A | Łomża | 53.181394 | 22.054381 |
| S24 | PL0046A | Gdańsk | 54.367778 | 18.701111 |
| S25 | PL0052A | Gdańsk | 54.380279 | 18.620274 |
| S26 | PL0049A | Gdańsk | 54.328336 | 18.557781 |
| S27 | PL0045A | Gdańsk | 54.353336 | 18.635283 |
| S28 | PL0047A | Gdańsk | 54.400833 | 18.657497 |
| S29 | PL0048A | Gdynia | 54.560836 | 18.493331 |
| S30 | PL0050A | Sopot | 54.431667 | 18.579722 |
| S31 | PL0237A | Dąbrowa Górnicza | 50.329111 | 19.231222 |
| S32 | PL0238A | Gliwice | 50.279481 | 18.655736 |
| S33 | PL0008A | Katowice | 50.264611 | 18.975028 |
| S34 | PL0239A | Rybnik | 50.111181 | 18.516139 |
| S35 | PL0240A | Tychy | 50.099903 | 18.990236 |
| S36 | PL0241A | Wodzisław Śląski | 50.007629 | 18.455548 |
| S37 | PL0242A | Zabrze | 50.316500 | 18.772375 |
| S38 | PL0295A | Elbląg | 54.167847 | 19.410942 |
| S39 | PL0312A | Gołdap | 54.305908 | 22.307681 |
| S40 | PL0175A | Olsztyn | 53.789233 | 20.486075 |
| S41 | PL0031A | Konin | 52.225633 | 18.269036 |
| S42 | PL0468A | Piła | 53.154408 | 16.759572 |
| S43 | PL0245A | Poznań | 52.420319 | 16.877289 |
| S44 | PL0244A | Poznań | 52.398175 | 16.959519 |
| S45 | PL0298A | Koszalin | 54.193986 | 16.172544 |
| S46 | PL0248A | Szczecin | 53.380975 | 14.663347 |
| S47 | PL0249A | Szczecin | 53.432169 | 14.553900 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ignaciuk, S.; Domagała, D.; Szczepanik, M. Modelling the Cyclical Variability of Nitrogen Dioxide in Urban Areas of Poland, 2001–2021. Sustainability 2025, 17, 9456. https://doi.org/10.3390/su17219456
Ignaciuk S, Domagała D, Szczepanik M. Modelling the Cyclical Variability of Nitrogen Dioxide in Urban Areas of Poland, 2001–2021. Sustainability. 2025; 17(21):9456. https://doi.org/10.3390/su17219456
Chicago/Turabian StyleIgnaciuk, Szymon, Dorota Domagała, and Małgorzata Szczepanik. 2025. "Modelling the Cyclical Variability of Nitrogen Dioxide in Urban Areas of Poland, 2001–2021" Sustainability 17, no. 21: 9456. https://doi.org/10.3390/su17219456
APA StyleIgnaciuk, S., Domagała, D., & Szczepanik, M. (2025). Modelling the Cyclical Variability of Nitrogen Dioxide in Urban Areas of Poland, 2001–2021. Sustainability, 17(21), 9456. https://doi.org/10.3390/su17219456






