Abstract
The earthquakes that impacted Kahramanmaraş on 6 February 2023, caused multidimensional destruction across the southeastern provinces of Türkiye and incurred severe business losses. This study provides a comparative assessment of four heavily affected provinces (Adıyaman, Hatay, Kahramanmaraş, and Malatya) in terms of business losses. Eleven criteria, grouped as human and operational losses (HOL) and commercial and economic losses (CEL), were considered in the evaluation. For the first time, the Ranking Comparison (RANCOM) method was integrated into the Modified Kemeny Median Ranks Accordance (KEMIRA-M) framework to determine the weights of the criteria and ensure consistency in the ranking process. The findings indicate that Hatay suffered the highest level of losses, followed by Adıyaman, Kahramanmaraş, and Malatya, respectively. This study fills a gap in the disaster economics literature by emphasizing workforce and business continuity dimensions, an area where business losses have received relatively less attention. The results highlight that post-disaster recovery policies should not be limited to physical reconstruction but should also emphasize human capital, supply chain resilience, and sustainability-focused recovery strategies.
1. Introduction
The earthquakes centered in Kahramanmaraş on 6 February 2023, directly impacted eleven provinces in southeastern Türkiye, creating one of the most devastating disasters in the history of the Republic. More than 50,000 people lost their lives, hundreds of thousands were injured, and millions were left homeless [1]. The economic consequences were severe: these provinces, which represented approximately 9.3% of Türkiye’s 2023 GDP, experienced major disruptions that caused a significant national economic contraction [2,3].
Business losses from the earthquake varied by province, demonstrating the connection between local economies and the impacts of disasters. The earthquake severely disrupted industry, business, and agriculture in Hatay, Kahramanmaraş, Malatya, and Adıyaman, causing losses exceeding 40% in Hatay and 35% in Kahramanmaraş [4]. In contrast, Gaziantep’s stronger and more diverse industry enabled a faster recovery, limiting losses by approximately 20%. These differences demonstrate that post-disaster economic impacts depend not only on devastation but also on economic diversity, infrastructure, and sustainability.
In this context, sustainability should be addressed through economic (sectoral diversity, circular economy), social (migration management, resilience), environmental (waste management, green restructuring), and institutional (crisis management, transparent governance, insurance) dimensions. Developing sustainable strategies in the provinces experiencing the greatest business losses is critical for both short-term recovery and long-term resilience [5].
The extent of post-earthquake business losses varies significantly across provinces. These differences are shaped by each province’s production structure, the diversity of sectors employed, industrial and commercial density, population size, and pre-disaster economic resilience [2,4]. In provinces with high industrial and commercial activity, damage to production facilities triggered a chain reaction that affected not only local employment but also national supply chains [6]. On the other hand, business losses were more pronounced in provinces with a higher prevalence of agriculture and small-scale businesses [5].
A comparative ranking of provinces based on business losses is crucial for understanding the regional economic impacts of the disaster, providing a scientific basis for resource allocation, and guiding reconstruction efforts. In the existing literature, analysis of post-disaster economic losses is generally conducted through direct assessment of physical damage, infrastructure destruction, and macroeconomic indicators [1,3]. However, studies focusing on labor losses are relatively rare. There is a significant gap in the literature regarding comprehensive studies providing comparative rankings at the provincial level using multi-criteria methods.
Labor and business losses disrupt economic activities, leading to a decline in social welfare, lower household income levels, and accelerated migration [2,4]. Therefore, analyzing business losses provides a comprehensive perspective on the long-term socioeconomic impacts of disasters. International research, particularly studies conducted after the 2010 Haiti earthquake, the 2011 Japan Tōhoku earthquake, and the 2015 Nepal earthquake, has emphasized that labor losses are one of the most critical and long-lasting consequences of disasters [7,8,9]. However, such analyses have mostly been conducted at the macroeconomic level, with limited comparative studies at the micro level, i.e., the local or provincial level. In Turkey, existing reports have generally focused on damage assessment, infrastructure losses, or residential demolitions; a comprehensive and methodological evaluation of the spatial distribution of labor force losses has mainly been lacking. Therefore, this study has the potential to contribute to both national and international research.
Multi-criteria decision-making (MCDM) methods are quantitative analytical tools used to evaluate and prioritize different alternatives based on specific criteria. These methods are commonly used in supply chain management [10], green supplier selection [11], location selection [12], healthcare planning [13], and engineering [14]. MCDM approaches are powerful tools that allow decision-makers to rank alternatives while considering criteria weights, especially in situations involving multi-dimensional uncertainty. In this respect, the methods used in the current study are also applicable to assessment problems, such as ranking the provinces according to their job loss levels.
This study aims to fill this gap and comparatively examines the provinces affected by the 6 February 2023, earthquakes in terms of business losses. In the study, the ranking of provinces was carried out within the framework of MCDM approaches. The Kemeny Median Ranks Accordance (KEMIRA-M) approach was utilized to rank the provinces according to business losses, and the Ranking Comparison (RANCOM) method was applied for criteria weighting. The integration of these two methods makes it possible to determine the criteria weights more reliably and to rank the provinces more objectively based on business losses.
The KEMIRA-M method is a MCDM method introduced by Krylovas et al. in 2016 [15]. Since the technique was introduced, there have been attempts to develop various aspects of this method by many researchers. One of the most essential advantages of the KEMIRA-M method over other MCDM methods is that the number of criteria is not limited. In the classical KEMIRA-M method, the criteria are first divided into two groups and named. In their most general form, groupings are divided into and groups, and these groups can also be named according to their subject matter. Then, the decision-makers/experts are asked to rank the criteria within their groups. According to the Kemeny Median Rank Accordance method, the median decision-maker is determined for each group. The decision-maker’s criteria ranking is determined as the median priority components (MPC) for that group. The weights of the criteria in each group are determined according to the MPC ranking. The ranking of the criteria defined by MPC also reveals the relationship between the criteria weights. In the literature, researchers have suggested determining criteria weights using different methods.
In this study, the use of the RANCOM method for determining criteria weights is recommended. Using the RANCOM method, criteria weights can be easily determined based on the existing MPC ranking, and consistency can then be tested with the Triad Consistency Check. Thus, the consistency of the criteria rankings obtained from MPC, as in the AHP method, is also checked.
In this respect, the study makes three fundamental contributions to the literature:
- It provides a methodological contribution through the integration of the RANCOM and KEMIRA-M methods, resulting in a multi-dimensional and more reliable ranking of business losses.
- The study provides a comparative analysis at the provincial level, which is missing in the literature, and considers different criteria simultaneously.
- The findings provide concrete data for designing post-disaster reconstruction and regional development policies in a more just, balanced, and prioritized manner.
Finally, the article is structured as follows: The literature review is given in Section 2. In Section 3, after defining the dataset used in this study, the proposed approach based on the integration of RANCOM with KEMIRA-M is explained in detail. Section 4 presents the analysis findings and the ranking of provinces based on business losses, and Section 5 presents the results of the study. In Section 6, the discussions and the future directions of the study are summarized.
2. Literature Review
The Kemeny Median Indicator Ranks Accordance (KEMIRA) method was introduced first in 2014 by Krylovas et al. In the MCDM problem addressed with this method, the idea of examining the criteria by dividing them into two different groups emerged. In this method, after the median decision-makers are determined for both criteria groups using the Kemeny Median method, the criteria weights are determined. The rankings of alternatives are obtained through optimization based on minimizing the weighted normalized squared values. This proposed approach is used to select the security personnel [16]. In the same year, Dadelo et al. proposed two optimization algorithms for the KEMIRA method based on heuristic reselection and random points generation methods of interval points [17]. Two years later, the Modified Kemeny Median Rank Accordance (KEMIRA-M) method was first introduced by Krylovas et al. in 2016 [15] and applied to a location selection problem. The only difference between the KEMIRA and KEMIRA-M methods is the optimization procedure. The optimization procedure in the KEMIRA method is based on the sum of the squared differences in the weighted normalized vector elements. In contrast, the KEMIRA-M method is based on the sum of absolute differences [15,16].
After the introduction of the KEMIRA-M method, many researchers have included studies on its applications in various fields. For example, the KEMIRA-M method was used in the evaluation of forklift alternatives [18]; in the ranking of construction sites according to risk levels in terms of occupational health and safety [19]; in the selection of a sawmill machine for the lumber business [20]; in the ranking of shopping malls according to universal design criteria [21]; in the warehouse location selection problem for the electric distribution company [22]; in the personal drone selection problem [23]; in the ergonomic risk assessment problems [24,25]; in project prioritization in healthcare industry [26]; in the prioritization of risks in the thrombolysis catheter production process [27]; in risk assessment of health sector [28]; and in the determination of the risk levels of construction sites [29].
In the KEMIRA-M method, the criteria rankings of the median decision-makers are called median priority components (MPCs). The weights of the criteria are determined by considering this ranking. In the literature, researchers have proposed many methods for determining the criteria weights of the KEMIRA-M method. In a 2019 study, Toktaş and Can proposed using the stochastic Analytic Hierarchy Process (AHP) method to determine the weights of criteria based on the MPC ranking [16]. In another study, Toktaş and Can conducted a risk assessment using the KEMIRA-M method, employing the Decision-Making Trial and Evaluation Laboratory (DEMATEL) method for criteria weighting [30]. Ay et al. used the Rank Sum (RS), Rank Exponent (RE), and Rank Reciprocal (RR) methods, which consider the MPC ranking, to determine the criteria weights [31]. Soltanifar and Artega presented a novel method that combines Multiple Attribute Decision-Making (MADM), the Best-Worst Method (BWM), Data Envelopment Analysis (DEA), and the KEMIRA method. DEA is employed to obtain the optimal weights of criteria [32]. In 2025, Toktaş and Can suggested using the Factor Relationships (FARE) method for the criteria weighting procedure [33]. As a result, it has been observed that the elimination of subjectivity in the weights of the criteria in the KEMIRA-M method and the determination of the weights of the criteria by considering the MPC ranking are still interesting topics for researchers.
This study proposes the utilization of the RANCOM approach to derive the weights of criteria after the acquisition of MPC rankings. Więckowski et al. introduced the RANCOM method in 2023 [34]. RANCOM is a subjective weighting method that uses expert criteria rankings to figure out the weights of the criteria. The ranking results of the criteria, obtained from the MPC ranking in this study, are directly converted into inputs for the formulation of a weight vector. Więckowski et al. showed that when five or more criteria are considered in the RANCOM method, more reliable and reproducible results are obtained compared to the AHP method [34].
The RANCOM approach, which was developed in 2023, has rapidly gained utility across various domains. The study focused on uncertainty, error tolerance, and their derivatives, including fuzzy, polytopic fuzzy, and gray, to demonstrate the method’s adaptability and effectiveness. Więckowski et al. introduced the fuzzy RANCOM method for modeling uncertainty using the triangular fuzzy numbers and compared it with the fuzzy AHP method [35]. Bitarafan et al. developed the fuzzy bilateral RANCOM method to evaluate both the weight and interrelationships of criteria for the assessment of earthquake resilience in urban areas [36]. RANCOM has become an indispensable tool in MCDM applications, especially in logistics, urban planning, and location selection for offshore wind power station and housing [37,38,39,40].
The literature includes studies where the RANCOM method is integrated with many MCDM methods: Więckowski et al. addressed the electric car selection problem with a proposed method that combines RANCOM and the Expected Solution Point Stable Preference Ordering Toward Ideal Solution (ESP-SPOTIS) methods [41]. While Mishra et al. used the Method based on the Removal Effects of Criteria (MEREC) and RANCOM methods for criteria weighting, they also prioritized energy storage technology with their newly proposed Simple Weighted Sum product (WISP) method [42]. Sustainable human resource management of manufacturing firms in India was evaluated using the combined Single-Valued Neutrosophic–Distance Measure (SVN-DM)–RANCOM–Alternative Ranking Order Method Accounting for two-step Normalization (AROMAN) methods [43].
There is no existing research in the literature that uses both the RANCOM approach and the KEMIRA-M method together. By using the RANCOM method, the weights of the criteria can be easily determined using the MPC ranking obtained in the KEMIRA-M method, and the consistency of the criteria rankings can also be checked. In the next section, the proposed RANCOM-KEMIRA-M methodology is explained in detail.
3. Materials and Methods
3.1. Methodological Framework
This study advances the KEMIRA-M methodology by using the RANCOM method for determining criterion weights. The proposed approach shows significant differences from methods commonly used in the literature, such as AHP, TOPSIS, and DEMATEL, both structurally and in terms of application. These differences can be explained as follows:
When considering these methods in terms of the number of decision-makers, the AHP method can be used only to a limited extent because the consistency ratio deteriorates rapidly in situations with many decision-makers [44]. The TOPSIS method was primarily developed for single-decision-maker problems [45]. The DEMATEL approach, however, has limited applicability in group decision-making processes because it focuses on examining the causal relationships between criteria [46]. In contrast, the RANCOM-KEMIRA-M model achieves group consensus by combining rankings from multiple decision-makers using the principle of median rank.
In AHP, criteria weights are entirely based on subjective pairwise comparisons [44]. In the TOPSIS method, weights are determined using other MCDM methods [45]. In the DEMATEL method, the weights are derived from the cause-and-effect relationships between the criteria [46]. In the proposed approach, the weights are obtained from comparative rankings determined by the decision-makers (RANCOM). This approach generates multiple valid weight combinations corresponding to different degrees of importance while maintaining consistency among decision-makers.
AHP uses criterion weights to generate a final ranking based on relative priority scores. TOPSIS ranks alternatives based on their distance from the ideal solution. The DEMATEL method analyzes the inter-criteria effects but does not directly produce an alternative ranking. In contrast, the RANCOM–KEMIRA-M model obtains the final ranking that best reflects the consensus of decision-makers through the median ranking optimization of KEMIRA-M.
The AHP method is highly sensitive to consistency ratios, and even small inconsistencies can change the outcome. Because the TOPSIS method is dependent on the normalization process, it has moderate robustness, while DEMATEL has limited stability in terms of repeatability. The RANCOM-KEMIRA-M models, on the other hand, exhibit a high degree of robustness because they consider different combinations of criteria weights and are based on decision-maker consensus.
The AHP and TOPSIS methods are the most widely used techniques in the literature and have low levels of innovation. DEMATEL is a specific-purpose method designed particularly for analyzing criterion dependence. In contrast, RANCOM–KEMIRA-M, with dynamic weight generation based on ranking comparison, was applied for the first time in the context of inter-provincial comparison of post-disaster job losses. Therefore, the method not only offers an analytical framework but also a new decision support framework focused on sustainability.
The proposed methodology consists of three stages: In the first stage, the criteria are divided into two groups and obtained their priorities. Then, the criteria weights are computed by RANCOM method in the second stage. The rankings of the alternatives are obtained in the last stage. The steps of the proposed approach are given in Figure 1.
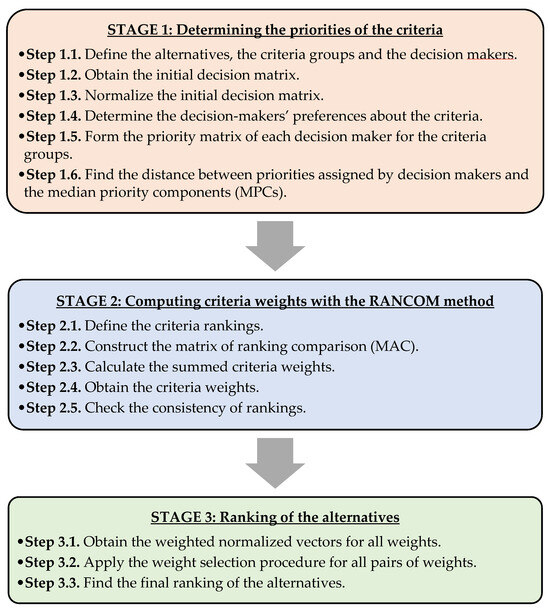
Figure 1.
The steps of the proposed approach.
All application steps are explained in general and in detail so that researchers and practitioners can easily apply this proposed method to MCDM problems.
3.2. Stage 1: Determining the Priorities of the Criteria
Step 1.1: Define the alternatives, the criteria groups, and the decision-makers.
Since the alternatives are ranked according to the criteria with the help of the decision-makers’ opinions, the alternatives, the criteria groups, and the decision-makers are determined in the first step. In the proposed approach, the criteria are divided into two groups: the first criteria set and the second criteria set . Decision-makers evaluate both criteria groups (). Alternatives are denoted as .
Step 1.2: Obtain the initial decision matrix.
The initial decision matrix is formed as in Equation (1).
In Equation (1), is the value of the th alternative for the th criterion, and is the value of the th alternative for the th criterion, .
Step 1.3: Normalize the initial decision matrix.
First, the “cost-type” criteria should be turned into “benefit-type” by and . Then, Equations (2) and (3) are used for the normalization procedure.
In Equations (2) and (3), and show the minimum values of the criteria. and are the maximum values of the criteria.
Step 1.4: Determine the decision-makers’ preferences about the criteria.
The decision-makers rank the criteria in each group. The criterion having the smallest rank means that this criterion is the most important one according to the decision-maker.
Step 1.5: Form the priority matrix of each decision-maker for the criteria groups.
is the priority matrix of the th decision-maker for the first criteria group. The elements of are given in Equation (4).
Similarly, is the priority matrix of the th decision-maker for the second criteria group.
Step 1.6: Find the distance between the priorities assigned by the decision-makers and the median priority components.
The priority distances of the th decision-maker for the first criteria group are computed as in Equation (5).
The priority ranking of the decision-maker providing in Equation (6) is defined as median priority components (MPC) for the first criteria group .
Similarly, all procedures are repeated for the second criteria group .
3.3. Stage 2: Computing the Criteria Weights with the RANCOM Method
Step 2.1: Define the criteria rankings.
According to the KEMIRA-M method, the MPCs found in Stage 1 determine the priority rankings of the criteria and the relations between the criteria weights. In the KEMIRA-M method, the relational operator between the criteria weights is . In this case, the criteria weights are less than or may be equal. As a result, it introduces two relational operators: or . Thus, assuming there are criteria in group and criteria in group in the KEMIRA-M method, different weight combinations will be obtained for group and for group . The resulting ranking combinations of criteria for each group are evaluated in pairs (a total of combinations) in the weight determination procedure of KEMIRA-M.
Step 2.2: Construct the matrix of ranking comparison (MAC).
In this step, the MAC of the first criteria group is obtained for each possible weight combination. The elements of the MAC are denoted by and determined by Equation (7).
Similarly, the elements of MAC for the second criteria group are obtained for each possible weight combination.
Step 2.3: Calculate the summed criteria weights .
After obtaining the MAC, the summed criteria weights () are calculated using Equation (8).
In the same way, the summed criteria weights are determined.
Step 2.4: Obtain the criteria weights.
In this step, the values are divided by the total summed criteria weights. Therefore, the final criteria weights for group are obtained as in Equation (9).
Similarly, the final criteria weights for Y group () are calculated using .
Step 2.5: Check the consistency of rankings.
In the traditional KEMIRA-M method, it is essential to obtain the criteria weights satisfying the MPCs. In this study, the RANCOM method is recommended to calculate the criteria weights for the KEMIRA-M method. The most important reason for selecting the RANCOM method is the consistency checking of the weights. The consistency checking of the weights is based on the relationships between the elements of the MAC. Three criteria () are selected and called triads. The total number of triads () are calculated in Equation (10), where shows the total number of the criteria.
According to the MAC, the relationships between the criteria are checked using Table 1.

Table 1.
The combinations of the consistent, the unknown, the weak, and the strong triads.
The first row of Table 1 can be interpreted as follows: if and , then . That is, if and , then . Then, the given operational relationship is consistent. Another example from Table 1: if and , then . Then, the given operational relationship is weak inconsistent. If and , then it is not possible to have the operational relationship . All possible triads are inspected, and the consistency coefficient () is calculated by Equation (11).
In Equation (11), and denote the total number of the inconsistent, the weak inconsistent, and the strong inconsistent triads, respectively. The RANCOM method’s lead article provides evidence that using the triad consistency check is a robust approach [34].
3.4. Stage 3: Ranking of the Alternatives
Step 3.1: Obtain the weighted normalized vectors for all weight combinations.
In this step, the normalized initial decision matrix is multiplied by the obtained weights as in Equations (12) and (13) for groups and , respectively.
In Equations (12) and (13), and are the normalized initial decision matrices calculated in Step 1.3. Dimensions of are , and dimensions of are . is the th weight combination vector for group and is the th weight combination vector for group. The elements of these vectors are calculated using Equation (9).
Step 3.2: Apply the weight selection procedure for all pairs of weights.
In this step, the final weight combination for and groups is obtained using Equations (14) and (15).
In Equation (14), the sum of the differences in the weighted normalized vector elements is calculated. Then, the weighted normalized vectors satisfying Equation (15) are used to obtain the final rankings of the alternatives in the next step.
Step 3.3: Find the final rankings of alternatives.
The final ranking of the alternatives is obtained by ordering the elements of the vector given in Equation (16).
The alternative corresponding to the element of the vector calculated in Equation (16) with the maximum value is the most important alternative. Note that if the number of weight combinations to be used in the decision problem is large, algorithms developed in MATLAB R2025a or a programming language such as Python 3.13.9 can be used to find the weight combination that satisfies the equation in Equation (15).
4. Application of the Proposed Approach
4.1. Data Description
The proposed modified KEMIRA-M method was used to rank the provinces most affected by the 7.7 and 7.6 magnitude earthquakes that occurred in Türkiye on 6 February 2023, in terms of business losses. In 2024, the Adhoc Research Company conducted research for the International Labor Organization (ILO). The “Enterprises Survey in Post-Disaster Setting” study was initiated to assess the status of enterprises and their recovery initiatives in earthquake-affected regions, as well as to analyze the economic repercussions on the labor market. The findings were reported in March 2024 [47]. Regional disparities resulted in varying degrees of impact on cities from the earthquake. The ILO-funded study covers five provinces affected by the earthquake. Data used in the analysis of business losses were obtained from responses from businesses in Hatay, Kahramanmaraş, Adıyaman, and Malatya, excluding Gaziantep, where the scope of reconstruction was significantly limited. This study includes data from 579 firms in the specified provinces for the assessment of the earthquake’s impact. Studied data came from the answers of 130 firms from Hatay, 134 firms from Kahramanmaraş, 139 firms from Adıyaman, and 176 firms from Malatya. The distribution of participating firms by province is given in Figure 2.
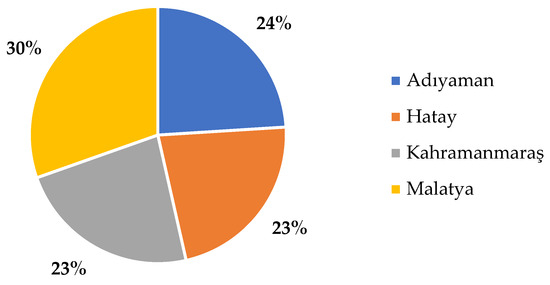
Figure 2.
Distribution of participating firms by province [47].
Many businesses were destroyed by the earthquake, and significant job losses occurred across various sectors. Figure 3 shows the distribution of sectors experiencing business losses due to the earthquake. The service sector accounts for the largest share of job losses (72.6%), followed by the construction and real estate sector (7.9%) and the manufacturing and utilities sector (6.4%).
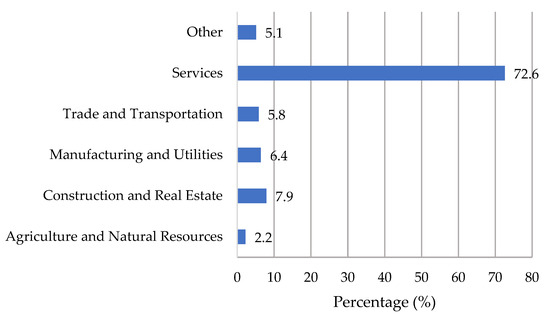
Figure 3.
Distribution of participating firms by sector [47].
This study aims to rank the four provinces impacted by the earthquake based on company loss rates. In assessing the provinces’ conditions regarding business losses post-earthquake, eleven factors were evaluated from the report. The dataset used to create the initial decision matrix was taken from the analysis results tables in the report “ILO Enterprises Survey in Post-Disaster Setting (2023)” [47] (p. 42, Table 33).
The application steps of the proposed approach are as follows:
4.2. Application of Stage 1: Determining the Priorities of the Criteria
Step 1.1: Define the alternatives, the criteria groups, and the decision-makers.
In the case study, four provinces affected by the earthquake are alternatives: Adıyaman (), Hatay (), Kahramanmaraş (), and Malatya (). These provinces are evaluated by eleven criteria derived from a study conducted for the ILO in 2024 [47]. The first criteria group (human and operational losses) consists of 5 criteria and the second criteria group (commercial and economic losses) consists of 6 criteria set . The definitions and the notations of the criteria are depicted in Figure 4.
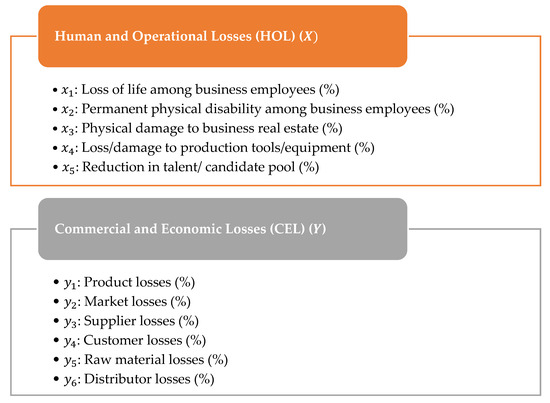
Figure 4.
The definitions and the notations of the criteria.
Three different decision-makers who experienced the earthquakes were chosen to represent different perspectives: an employer (company owner/manager) (), an employee (), and a government representative (). The employer () is a person who directly experienced the earthquake, whose 32-year-old medium-sized food business is unusable, and who has lost a large portion of their employees. The employee () is a person directly affected by the earthquake, who has lost family members, lost their income, and has limited alternative opportunities. The government representative () is a person appointed to oversee public interests in the earthquake zone, promote economic recovery, and develop social assistance and employment policies.
Step 1.2: Obtain the initial decision matrix.
The initial decision matrix is given in Table A1. All the criteria show the percentage of losses. For example, is the percentage of reduction in talent/candidate pool () for Hatay ( in Table A1.
The graphical representation of the initial decision matrix for HOL group and the CEL group by provinces are depicted in Figure 5 and Figure 6, respectively. In Figure 5, Hatay has the highest losses in all criteria, especially (loss of life among business employes) and (permanent disability) criteria. Particularly, Adıyaman has high rates in and criteria, indicating a high level of losses in production, equipment, and labor. Kahramanmaraş has lower rates across all criteria, while Malatya generally exhibits moderate losses. This distribution reflects the different economic structures among the provinces and the diversity of how they are affected by the earthquake. Figure 6 shows the percentage values for the six criteria in the CEL group by province. Overall, Hatay represents the province with the highest rates for many criteria (especially , and representing the highest trade and supply chain losses. Adıyaman and Kahramanmaraş show a similar trend, exhibiting moderate-to-high losses, while Malatya, with relatively lower rates across all criteria, represents the province with the most limited economic impact. Particularly, customer () and market losses () are prominent in all four provinces, revealing the impact of the earthquake on regional trade networks.
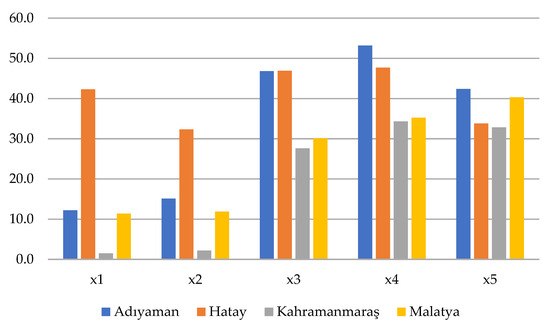
Figure 5.
The percentages of losses for HOL by province.
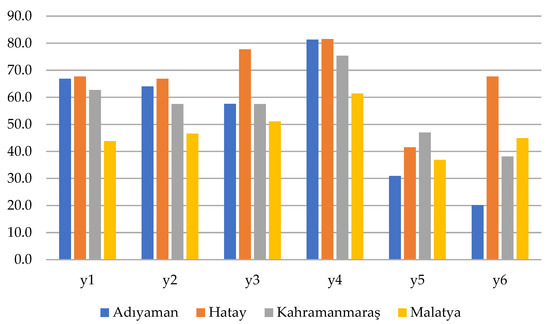
Figure 6.
The percentages of losses for CEL by province.
Step 1.3: Normalize the initial decision matrix.
In the case study, since all criteria show the losses, all of them are turned into benefit-type by taking the inverse. The normalized initial decision matrices for HOL and CEL ( and ), calculated using Equations (2) and (3), are depicted in Table A2. All criteria used in the study are based on percentage loss rates. Therefore, the assumption is that each criterion defined in the 0 and 100 range is positive and directly comparable. This increases the reliability of normalization in datasets where there are no negative values, and all criteria are expressed on the same scale.
Step 1.4: Determine the decision-makers’ preferences about the criteria.
In this step, the criteria in each group are ranked by the decision-makers. If a decision-maker ranks a criterion as 1, this criterion is the most important one among others in the group. In this study, three decision-makers are determined to reflect the different perspectives: an employer (company owner/manager) (), an employee (), and a government representative (). The ranking preferences of the decision-makers are given in Table A3.
To statistically assess the level of agreement between the decision-makers’ rankings in Table A3, Kendall’s Coefficient of Concordance () was calculated separately for the HOL and CEL criteria groups. According to the results of Kendall’s analysis for the HOL and CEL groups, the levels of agreement among decision-makers differ. For the HOL group, Kendall’s indicates a high level of agreement among the three decision-makers. This finding suggests that decision-makers prioritize similar issues regarding human and operational losses (e.g., loss of life, physical damage, equipment loss). In contrast, for the CEL group, Kendall’s indicates a moderate level of agreement among decision-makers. The result indicates that stakeholders’ perspectives differed somewhat in the assessment of commercial and economic losses (e.g., market, customer, and supplier losses), but their overall ranking trends were similar. The finding of in both analyses indicates that there was no full statistical consensus among the decision-makers, but the observed agreement was far from randomness and was reliable.
The radar charts of the ranking of decision-makers’ preferences for HOL and CEL are given in Figure 7 and Figure 8, respectively.
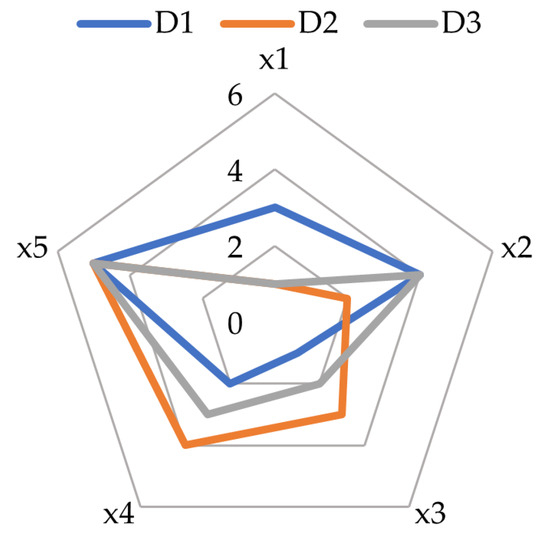
Figure 7.
The radar chart of the ranking of decision-makers’ preferences for HOL.
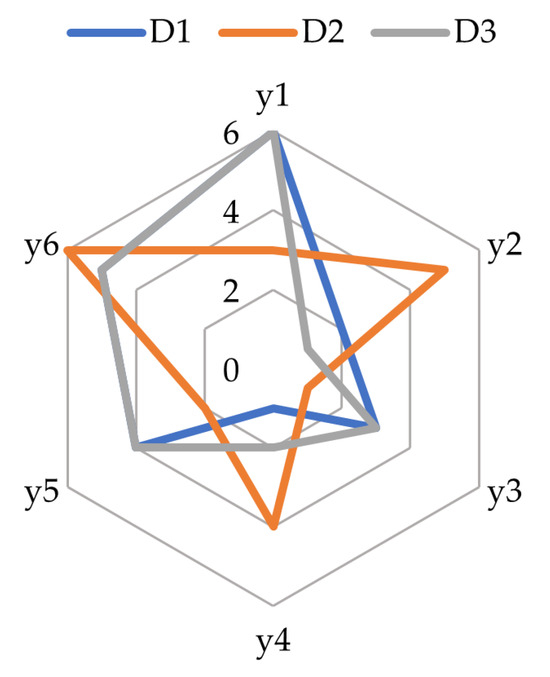
Figure 8.
The radar chart of the ranking of decision-makers’ preferences for CEL.
In prioritizing the criteria in the HOL group in Figure 7, prioritized infrastructure and operational continuity, as the sustainability of the business was critical. In ’s assessment, life safety and health were the most important considerations, so these criteria were ranked highest. prioritized both the protection of human life and the maintenance of economic stability.
When evaluating the criteria in the CEL group in Figure 8, for , customer loss is one of the biggest risks directly affecting the company’s future. While product losses can cause short-term losses, market loss and supplier issues can also hinder long-term growth, so they were not considered as critical as other factors. For , production continuity is crucial. Supplier and raw material losses directly impact their business. Product losses also threaten job security. While customer and market losses pose long-term risks, they are not a priority for employees. For , maintaining large-scale economic stability is the most important concern. Market losses can affect overall economic stability and growth. Customer losses can weaken the economy by reducing consumption. Supplier and raw material losses are important because they can disrupt the production chain. Distribution and product losses are relatively lower priority criteria for .
Step 1.5: Form the priority matrix of each decision-maker for the criteria groups.
The priority matrices of decision-makers for each criteria group are obtained using Equation (4). shows the priority matrix of the first decision-maker in Equation (17) as an example.
Since the priority ranking of the criteria HOL for the first decision-maker is , the element at row 2, column 5 of the matrix is equal to 1 in Equation (17). It is denoted by and means that the second criterion is more important than the fifth criterion (or the ranking of the second criterion is less than that of the fifth criterion). Similarly, the priority matrices of CEL are obtained .
Step 1.6: Find the distance between the priorities assigned by the decision-makers and the median priority components (MPCs).
The priority distances of the decision-makers are calculated as and for HOL using Equation (5). In Equation (18), the priority distance of the first decision-maker is calculated as an example.
Equation (18) calculates the total absolute difference between the priority matrix elements of the first decision-maker and the priority matrix values of the other decision-makers. The value that minimizes the sum of the absolute differences is the median. Therefore, the decision-maker closest to everyone’s views is designated as the median decision-maker, and his or her criteria ranking is adopted as the MPC for the group of interest in the continuation of the decision problem. given in Equation (6) is the minimum value obtained for the third decision-maker. Therefore, the MPC of HOL is which is the priority ranking of the third decision-maker. The criteria weights of HOL must satisfy the MPC; that is, the weights of the criteria of HOL must satisfy . Similarly, the priority distances of the decision-makers for CEL are obtained as and . The minimum value of the priority distances for CEL is . Therefore, the MPC of CEL is which is the priority ranking of the first decision-maker. Thus, the weights of the criteria of CEL must satisfy the following condition: .
4.3. Application of Stage 2: Computing the Criteria Weights with the RANCOM Method
Step 2.1: Define the criteria rankings.
According to the KEMIRA-M method, the MPCs found in Stage 1 determine the priority rankings of the criteria and the relations between the criteria weights. Since the relational operator between the criteria in MPC is , the relational operators between the criteria can be more important than () or identical to (). Therefore, the relational operators between the weights of the corresponding criteria will also be greater than (>) or equal to (=).
Since there are five criteria in HOL, there are four relational operators between the weights of the criteria. Then, there are possible weight combinations for HOL (). Similarly, there are six criteria in CEL, so there are possible weight combinations for CEL (). As a result, there are pairs of the criteria groups combinations obtained for the KEMIRA-M’s weight selection procedure, which will be explained in the second step of the third stage. All possible weight combinations can be seen in Table A4 and Table A5.
Step 2.2: Construct the matrix of ranking comparison (MAC).
The MACs of HOL and CEL are obtained for each possible weight combination using Equation (7). The MAC for the priority rankings of the criteria (corresponding to the weight combination ) is given in Table 2 as an example.

Table 2.
The MAC, and values for .
Another MAC example for the priority rankings of the criteria (corresponding to the weight combination ) is given in Table 3.

Table 3.
The MAC, and values for .
Step 2.3: Calculate the summed criteria weights .
After calculating the MACs for HOL and CEL, the row sums are obtained to have the summed criteria weights using Equation (8). Example calculations for HOL and CEL are depicted in Table 2 and Table 3, respectively.
Step 2.4: Obtain the criteria weights.
In this step, all final criteria weights for both groups using values are calculated by Equation (9). Again, example calculations can be seen in Table 2 and Table 3.
Step 2.5: Check the consistency of rankings.
In the case study, there are 15 weight combinations for HOL and 32 weight combinations for CEL. Since there are five criteria in HOL, the number of triads is . For each criteria weight combination, 10 triads are evaluated according to Table 1. Then, each criteria combination is checked for consistency using Equation (11). All the weight combinations are consistent, as seen in Table A4 and Table A5. The reason all weight combinations are consistent is that the third decision-maker for HOL and the first decision-maker for CEL, who determine the MPCs, made consistent prioritizations.
4.4. Application of Stage 3: Ranking of the Alternatives
Step 3.1: Obtain the weighted normalized vectors for all weight combinations.
The weighted normalized vectors of HOL and CEL are calculated using Equations (12) and (13) and depicted in Table A6 and Table A7, respectively.
Step 3.2: Apply the weight selection procedure for all pairs of weights.
The sum of the differences in the weighted normalized vector elements for each weight combination is calculated using Equation (14). Table A8 shows the sum of the differences in the weighted normalized vector elements for 512 pairs of the weight combination. The shaded cell indicates the minimum value for the sum of differences in the weighted normalized vector elements satisfying Equation (15). Thus, the vectors and will be used to rank the alternatives in the next step. Note that MS Excel was used for calculations when evaluating 512 combinations.
Step 3.3 Find the final rankings of alternatives.
The elements of the vectors and are used to obtain the final rankings of the provinces using Equation (16). The final rankings of the provinces are given in Table 4. As a result, in terms of business losses caused by the earthquake, Malatya was the least affected province, while Hatay was the most affected province.

Table 4.
Final ranking of the provinces from those with the least losses to those with the most losses.
4.5. Sensitivity Analysis
When performing alternative ranking with the KEMIRA-M method, numerous criteria can be considered. It allows decision-makers to evaluate the criteria, which are divided into two groups, internally. Thus, it stands out among other MCDM methods, considering that criteria can be consistently evaluated in each criteria group.
In contrast, the weakest point of the KEMIRA-M method is how to determine the criteria weights based on the ranking of MPCs obtained at the end of Stage 1. According to the MPC, the criteria weights must be determined consistently, and their sum must be 1. Selecting the appropriate combinations from an infinite number of criteria weights remains a hot topic among researchers. In this study, the use of the RANCOM method facilitated obtaining consistent criteria weights that sum to 1. Subsequently, the most suitable criterion weight pair is selected using KEMIRA-M’s criteria selection procedure, and the final alternative ranking is obtained.
In the study conducted to test the robustness of the proposed method, the ranking of the criteria weights obtained for each group using the KEMIRA-M method’s criterion selection procedure was taken into account. The criteria weights used in the final ranking, corresponding to the rankings tested using the Triad consistency check, are as follows: and . These rankings are provided in the and columns of Table A9 and Table A10, respectively. Since and are of equal importance in the HOL group, they are calculated as . That is, the rankings of criteria having the same importance are shared with each other equally. The others are , and . The rankings of criteria for the CEL group were also obtained similarly in Table A10.
In this analysis, the following three different objective criteria weighting methods were used, in accordance with the rankings determined here: The Rank Sum (RS) method, The Rank Reciprocal (RR) method, and The Rank Exponent (RE) method [48].
In the RS method, the rankings of the criteria are first converted into criteria loads using the formula Then, the normalization procedure is applied to obtain the criteria weights: The values are divided by the sum of all loads. The RR weights are obtained from the normalization of values, where In the RE method, the first values are calculated using and then values are normalized. All of the calculated values and the criteria weights for HOL and CEL are depicted in Table A9 and Table A10, respectively.
In Figure 9, the weights obtained for the five criteria are compared for HOL. When examining how each method prioritizes the criteria, some consistent trends and differences are observed: and have the same and high importance levels. Therefore, this criterion carries the highest weight in all methods. The values among the RANCOM, RS, and RR methods are quite close (between 0.30 and 0.32), but the RE method weighted this criterion slightly higher than the others (0.37). When examining the weights determined for criterion , it is observed that the weight obtained by the RE method is the lowest (0.07), while there are small differences between the RANCOM, RS, and RR methods (0.12 and 0.13). While criterion has the same weight for the RANCOM and RS methods (0.20), the RR and RE methods are close to each other but have a lower weight (0.16 and 0.17). For , especially in the RE and RANCOM methods, the criterion weight falls below 5%.
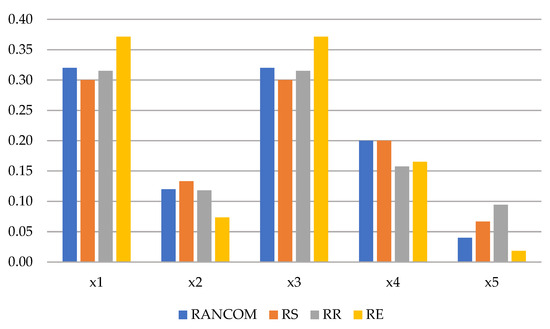
Figure 9.
The comparison of the criteria weights for HOL.
The graphical comparison of the criteria weights for CEL is shown in Figure 10. According to Figure 10, since , , and are the same and have the lowest level of importance, their criteria weights are the same. While consistency was observed among the RANCOM, RS, and RR methods, the lowest criterion weight was found using the RE method. Similarly, and also have the highest and same criteria weights. Although the RANCOM, RS, and RR methods yielded similar weights, the weight of this criterion was high with the RE method. The RANCOM and RS methods yielded the same weight values (0.19) for , which is close to the weight found by the RE method (0.18). In the RR method, the lowest weight value was obtained.
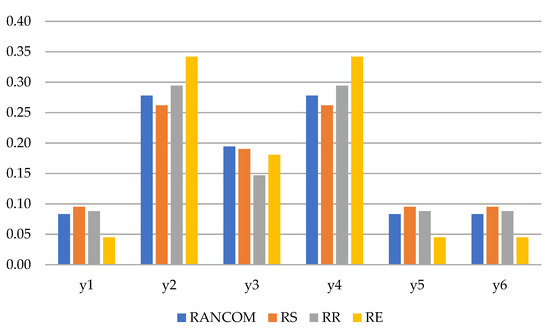
Figure 10.
Comparison of the weights of criteria for CEL.
As a result, the RANCOM method generally produced results quite consistent with the RS and RR methods, thus demonstrating that the method is robust in terms of consistency and reliability.
For the criterion weights of each method, weighted normalized vectors were calculated using Equations (12) and (13). Then, using these weighted vectors, the final rankings of the provinces were obtained using the weighted sum scores in Equation (16). The weighted sum scores () and the rankings of provinces for each method are given in Table 5.

Table 5.
The weighted sum scores (s) and the rankings of provinces for each method.
Table 5 shows how the final rankings of the provinces change under four different methods (RANCOM, RS, RR, and RE). Based on the operational relationship between the criteria based on RANCOM-KEMIRA-M, sensitivity analysis was performed to test the stability of the ranking results and the robustness of the model, depending on the method used.
In all the methods, Malatya (A4) ranked first, while Hatay (A2) ranked last. Kahramanmaraş (A3) came in second in every method, while Adıyaman (A1) came in third. Therefore, all the methods produced the same ranking order. This result indicates that the model has a high degree of consistency and that differences related to the method do not change the relative positions of the provinces. The fact that Malatya and Kahramanmaraş are at the top of the list indicates that labor force losses in these provinces are relatively low and economic activities can recover more quickly. Hatay consistently ranking last indicates that sustainable recovery policies should be particularly directed toward social employment support, supply chain repair, and infrastructure strengthening in this province.
When examining the score differences, the difference between Malatya and Kahramanmaraş is quite small, indicating that these two provinces have similar rates of job losses. The fact that Hatay scored the lowest by a wide margin in all methods confirms that it is the most vulnerable province in terms of both human and economic losses.
All four methods (RANCOM, RS, RR, RE) produced the same ranking result. This situation indicates that the KEMIRA-M model is not very sensitive to parametric changes, meaning the decision outputs are stable. Since the deviation between the highest and lowest scores (e.g., 1.3493–1.4423 for Malatya) is small, it can be said that weight changes did not affect the ranking. This finding supports the robustness of the integrated RANCOM–KEMIRA–M approach used in the study against decision-making inconsistencies.
Sensitivity analysis confirmed the robustness of the integrated RANCOM–KEMIRA-M approach. The identical ranking order across all four methods demonstrates that the final prioritization is stable and not significantly affected by methodological variations, which strengthens the reliability of the proposed model in post-disaster sustainability assessments. The results are reliable and suitable for policy development.
5. Results
The two major earthquakes that occurred on 6 February 2023, centered in Kahramanmaraş and followed one after another, caused multi-dimensional destruction in Turkey’s southern and southeastern provinces. These earthquakes, recorded as one of the most devastating disasters in the history of the Republic in terms of their magnitude and impact, were not limited to physical damage and loss of life; they also deeply shook the region’s economic, social, and demographic structure. The destruction or long-term inactivity of many firms in the agricultural, industrial, and service sectors has had both direct and indirect effects on businesses. In this context, business losses stand out as an essential indicator in measuring the socioeconomic impacts of the disaster.
In this study, the four alternative provinces most affected by the February 6th earthquake (Adıyaman (), Hatay (), Kahramanmaraş (), and Malatya ()) were ranked based on their business losses. Provinces have been ranked by considering eleven different criteria. The KEMIRA-M method was selected for the study, as it is a method that facilitates the evaluation of eleven criteria by decision-makers and optimizes the weights of the selected criteria. According to the KEMIRA-M method, the criteria showing business losses are divided into two groups: Human and operational losses (HOL) () group includes losses that directly harm employees and operational processes. Commercial and Economic Losses (CEL) () group includes losses related to the company’s financial situation and business relationships.
There are five criteria in the HOL group and six criteria in the CEL group. First, decision-makers are asked to rank the criteria within each criteria group. In this study, the opinions of three different decision-makers representing different perspectives were utilized: an employer (, an employee and a government representative .
After obtaining the prioritization matrices, for HOL and for CEL were determined as the median decision-makers. The decision-makers’ MPC rankings for HOL and CEL were obtained as and , respectively. For HOL, the percentage of life among business employees () emerged as the most important criterion, followed by the percentage of physical damage to business real estate () in second place, and the percentage of reduction in talent/candidate pool () in last place. For CEL, the percentage of customer losses () emerged as the most important criterion, followed by the percentage of market losses () in second place and the percentage of product losses () in last place.
The relationship operator between the criteria rankings being () indicates the superiority () or equality () of the criteria. The different operational relationship operators between the criteria also lead to different prioritized criteria arrangements. These rankings also determine the relationships between the criteria weights. At this stage, it is recommended to use the RANCOM method to determine the criteria weights. This proposal, which was not included in any previous KEMIRA-M studies, allows for the easy determination of criteria weights based on the priority ranking of the criteria (MPC), as well as checking the consistency of the criteria rankings.
After calculations were performed for a total of criteria pairs across 16 different rankings for HOL and 32 for CEL, the final rankings of the provinces were obtained using the KEMIRA-M optimization procedure. Accordingly, the ranking from the province with the least loss to the province with the most loss is as follows: Malatya (), Kahramanmaraş (), Adıyaman (), and Hatay ().
At the end, a sensitivity analysis was conducted to show the robustness of the proposed approach. The sensitivity analysis validated the resilience of the combined RANCOM–KEMIRA-M methodology. The consistent ranking across all four techniques indicates that the final prioritized is stable and less influenced by methodological differences, hence enhancing the trustworthiness of the proposed model in post-disaster sustainability evaluations. The findings are dependable and appropriate for policy formulation.
6. Discussion
In this study, four provinces affected by the 6 February 2023, earthquake were ranked according to business losses using the integrated RANCOM and KEMIRA-M methods. The results of the study can be discussed as follows:
When the prioritization of criteria in the HOL group and the final rankings of the provinces are examined together, the following conclusions can be drawn: According to the ranking of the median decision-maker in the HOL group, the employee loss rate () was the most important criterion. This result shows that the earthquake has seriously affected not only physical but also human life. When examining the initial decision matrix provided in Table 2, Hatay recorded the highest employee loss rate () at 42.3%, which explains why Hatay ranked last as the city with the most business losses. On the other hand, the fact that the initial decision matrix shows low values for employee loss rate () at 1.5% and market losses rate () at 2.2% in Kahramanmaraş indicates that business losses are relatively limited. This situation supports Kahramanmaraş emerging as the province with the least business losses in the final ranking of provinces.
When the prioritization of criteria in the CEL group and the final ranking of provinces are examined together, the following conclusions can be drawn: According to the ranking of the median decision-maker in the CEL group, the prominence of the customer loss rate () and market loss rate () criteria in the CEL group indicates the demand-side effects of the earthquake. Among the listed provinces, Hatay ranks last with an 81.5% customer loss rate and a 77.7% supplier loss rate. Since the rates of product loss (43.8%) and market loss (46.6%) in Malatya are lower than in other provinces, it is more advantageous than Hatay and Adıyaman in the final ranking.
In the final ranking of the KEMIRA-M method, Malatya () came out on top with the least proportional loss, followed by Kahramanmaraş (), Adıyaman (), and Hatay (). This ranking shows that Hatay is in the most unfavorable position due to both high human losses ( and ) and high commercial losses (, and ). Despite the high rates of physical damage () in Malatya, the low business losses and relatively lower economic losses explain the province’s advantage in the ranking.
Integrating the RANCOM method to the KEMIRA-M method made it easy to weight the criteria according to their priority ranking, and by checking the consistency of the criteria rankings, it increased the robustness of the KEMIRA-M method. This approach offers an innovative contribution by directly including business losses (e.g., loss of life, disability, shrinking talent pool) in the ranking of provinces affected by the earthquake.
According to the findings of the study, which were obtained after the earthquake, it shows that not only infrastructure but also human capital and the chain of business relationships need to be protected after the earthquake. Developing sustainable recovery strategies specific to each province is essential. While social sustainability, such as migration management and employment support, should be prioritized for Hatay and Adıyaman, economic sustainability policies, such as SME support and the rebuilding of markets and customers, should be prioritized for Malatya and Kahramanmaraş.
The findings suggest that a comprehensive evaluation of business losses is essential for sustainable recovery strategies following the earthquake. In areas with high human losses, social resilience becomes a key policy focus; in provinces with high commercial losses, economic diversity and supply chain management are prioritized.
By examining the rankings of the provinces, it was seen that the results of this study were consistent with the results of the studies in the literature: Hatay has emerged as the province most affected by the earthquake. The main reasons for this are that the province has a production infrastructure concentrated in the industrial, commercial, and logistics sectors, and it is located directly on a fault line. The majority of businesses in Hatay operate in the manufacturing, transportation, and service sectors. This finding aligns with the results stated in [49], which indicate that labor loss and production disruption in Hatay are above the national average. Additionally, in the securities analysis conducted by Güneş et al., the significant decline in the performance of the construction, cement, and real estate sectors after the earthquake confirms Hatay’s economic vulnerability [50].
Adıyaman ranked second. The majority of businesses this year are small and medium-sized enterprises (SMEs) with limited financial reserves. In the study by Yanardağ et al., it was also stated that the recovery took a long time, and labor losses became permanent because businesses in Adıyaman had weak capital structures [51].
Although Kahramanmaraş has a strong industrial infrastructure, it ranked third. This situation is related to the textile sector’s ability to regain its production capacity quickly. The TEPAV (2023) report highlights that regional recovery occurred relatively faster in Kahramanmaraş due to its industrial clustering and supply chain resilience [52].
Malatya, on the other hand, ranked last on the list as the least affected province. The province’s economic structure, which is primarily in the agriculture, food processing, and service sectors, has limited the economic impact of physical destruction due to the limited presence of capital-intensive industrial activities. This result is consistent with the findings in the OECD (2023) report, which states that economic recovery is more balanced in provinces with low capital-intensive sectors [53].
The findings of the study are consistent with previous research in the literature. Yanardağ et al., Dündar, and Özsalman stated that Hatay and Adıyaman stood out in terms of economic losses, while the recovery process was faster in Kahramanmaraş and Malatya [49,51,54]. Similarly, OECD (2023) and TEPAV (2023) reports also emphasize that regional resilience is a key determinant in the rebuilding process [52,53].
These results show that sustainable recovery policies should be determined based on provincial differences. Priority should be given to rebuilding infrastructure and production capacity in Hatay and Adıyaman. On the other hand, the policies should be developed for Kahramanmaraş and Malatya, considering prioritizing sectoral diversity, encouraging innovation, and protecting local employment.
In conclusion, the provincial rankings obtained through this study not only reflect business loss rates but also provide important indicators for guiding regional resilience, economic sustainability, and post-disaster development policies.
The future directions of the study can be summarized as follows: The proposed approach can be implemented in different fields, including risk assessment tools, production, or healthcare. The criteria rankings of the decision-makers can be transformed into fuzzy numbers to model uncertainty. The existing framework offers a static multi-criteria evaluation of business losses; however, subsequent research could improve the model by incorporating dynamic monitoring and early-warning systems. Time-series data (e.g., production, energy consumption, or social media metrics) could facilitate predictive modeling and disaster resilience assessment, drawing from methodologies employed in rock mechanics [55,56].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| KEMIRA-M | Modified Kemeny Median Ranks Accordance |
| RANCOM | Ranking Comparison |
| HOL | Human and Operational Losses |
| CEL | Commercial and Economic Losses |
| MPC | Median Priority Components |
| AHP | Analytic Hierarchy Process |
| DEMATEL | Decision-Making Trial and Evaluation Laboratory |
| RS | Rank Sum |
| RE | Rank Exponent |
| RR | Rank Reciprocal |
| MADM | Multi Attribute Decision-Making |
| BWM | Best-Worst Method |
| DEA | Data Envelopment Analysis |
| ESP-SPOTIS | Expected Solution Point Stable Preference Ordering Toward Ideal Solution |
| MEREC | Method based on the Removal Effects of Criteria |
| WISP | Simple Weighted Sum Product |
| SVN-DM | Single—Valued Neutrosophic—Distance Measure |
| AROMAN | Alternative Ranking Order Method Accounting for two-step Normalization |
| MAC | Matrix of Comparison |
Appendix A

Table A1.
The initial decision matrix.
Table A1.
The initial decision matrix.
| ) | ) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Adıyaman | 12.2 | 15.1 | 46.8 | 53.2 | 42.4 | 66.9 | 64.0 | 57.6 | 81.3 | 30.9 | 20.1 |
| Hatay | 42.3 | 32.3 | 46.9 | 47.7 | 33.8 | 67.7 | 66.9 | 77.7 | 81.5 | 41.5 | 67.7 |
| Kahramanmaraş | 1.5 | 2.2 | 27.6 | 34.3 | 32.8 | 62.7 | 57.5 | 57.5 | 75.4 | 47.0 | 38.1 |
| Malatya | 11.4 | 11.9 | 30.1 | 35.2 | 40.3 | 43.8 | 46.6 | 51.1 | 61.4 | 36.9 | 44.9 |
Source: International Labor Organization (ILO), 2024 [47].

Table A2.
The normalized initial decision matrix.
Table A2.
The normalized initial decision matrix.
| ) | ) | ||||||||||
| Adıyaman | 0.09 | 0.08 | 0.00 | 0.00 | 0.00 | 0.02 | 0.10 | 0.67 | 0.01 | 1.00 | 1.00 |
| Hatay | 0.00 | 0.00 | 0.00 | 0.21 | 0.87 | 0.00 | 0.00 | 0.00 | 0.00 | 0.25 | 0.00 |
| Kahramanmaraş | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.15 | 0.38 | 0.67 | 0.25 | 0.00 | 0.33 |
| Malatya | 0.10 | 0.13 | 0.80 | 0.93 | 0.18 | 1.00 | 1.00 | 1.00 | 1.00 | 0.53 | 0.21 |

Table A3.
The criteria ranking preferences of the decision-maker.
Table A3.
The criteria ranking preferences of the decision-maker.
| HOL | CEL | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 1 | 2 | 5 | 6 | 2 | 3 | 1 | 4 | 5 | |
| 1 | 2 | 3 | 4 | 5 | 3 | 5 | 1 | 4 | 2 | 6 | |
| 1 | 4 | 2 | 3 | 5 | 6 | 1 | 3 | 2 | 4 | 5 | |

Table A4.
Obtained the criteria weights of HOL and their consistency ratios.
Table A4.
Obtained the criteria weights of HOL and their consistency ratios.
| Weight Combinations | Consistency (%) | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.360 | 0.120 | 0.280 | 0.200 | 0.040 | 100 | |
| 2 | 0.360 | 0.080 | 0.280 | 0.200 | 0.080 | 100 | |
| 3 | 0.360 | 0.160 | 0.280 | 0.160 | 0.040 | 100 | |
| 4 | 0.360 | 0.120 | 0.280 | 0.120 | 0.120 | 100 | |
| 5 | 0.360 | 0.120 | 0.240 | 0.240 | 0.040 | 100 | |
| 6 | 0.360 | 0.080 | 0.240 | 0.240 | 0.080 | 100 | |
| 7 | 0.360 | 0.200 | 0.200 | 0.200 | 0.040 | 100 | |
| 8 | 0.360 | 0.160 | 0.160 | 0.160 | 0.160 | 100 | |
| 9 | 0.320 | 0.120 | 0.320 | 0.200 | 0.040 | 100 | |
| 10 | 0.320 | 0.080 | 0.320 | 0.200 | 0.080 | 100 | |
| 11 | 0.320 | 0.160 | 0.320 | 0.160 | 0.040 | 100 | |
| 12 | 0.320 | 0.120 | 0.320 | 0.120 | 0.120 | 100 | |
| 13 | 0.280 | 0.120 | 0.280 | 0.280 | 0.040 | 100 | |
| 14 | 0.280 | 0.080 | 0.280 | 0.280 | 0.080 | 100 | |
| 15 | 0.240 | 0.240 | 0.240 | 0.240 | 0.040 | 100 | |
| 16 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 100 | |

Table A5.
Obtained criteria weights of CEL and their consistency ratios.
Table A5.
Obtained criteria weights of CEL and their consistency ratios.
| Weight Combinations | Consistency (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.028 | 0.250 | 0.194 | 0.306 | 0.139 | 0.083 | 100 | |
| 2 | 0.061 | 0.273 | 0.121 | 0.333 | 0.152 | 0.061 | 100 | |
| 3 | 0.028 | 0.250 | 0.194 | 0.306 | 0.111 | 0.111 | 100 | |
| 4 | 0.083 | 0.250 | 0.194 | 0.306 | 0.083 | 0.083 | 100 | |
| 5 | 0.028 | 0.250 | 0.167 | 0.306 | 0.167 | 0.083 | 100 | |
| 6 | 0.056 | 0.250 | 0.167 | 0.306 | 0.167 | 0.056 | 100 | |
| 7 | 0.028 | 0.250 | 0.139 | 0.306 | 0.139 | 0.139 | 100 | |
| 8 | 0.111 | 0.250 | 0.111 | 0.306 | 0.111 | 0.111 | 100 | |
| 9 | 0.028 | 0.222 | 0.222 | 0.306 | 0.139 | 0.083 | 100 | |
| 10 | 0.056 | 0.222 | 0.222 | 0.306 | 0.139 | 0.056 | 100 | |
| 11 | 0.028 | 0.222 | 0.222 | 0.306 | 0.111 | 0.111 | 100 | |
| 12 | 0.083 | 0.222 | 0.222 | 0.306 | 0.083 | 0.083 | 100 | |
| 13 | 0.028 | 0.194 | 0.194 | 0.306 | 0.194 | 0.083 | 100 | |
| 14 | 0.056 | 0.194 | 0.194 | 0.306 | 0.194 | 0.056 | 100 | |
| 15 | 0.028 | 0.167 | 0.167 | 0.306 | 0.167 | 0.167 | 100 | |
| 16 | 0.139 | 0.139 | 0.139 | 0.306 | 0.139 | 0.139 | 100 | |
| 17 | 0.028 | 0.278 | 0.194 | 0.278 | 0.139 | 0.083 | 100 | |
| 18 | 0.056 | 0.278 | 0.194 | 0.278 | 0.139 | 0.056 | 100 | |
| 19 | 0.028 | 0.278 | 0.194 | 0.278 | 0.111 | 0.111 | 100 | |
| 20 | 0.083 | 0.278 | 0.194 | 0.278 | 0.083 | 0.083 | 100 | |
| 21 | 0.028 | 0.278 | 0.167 | 0.278 | 0.167 | 0.083 | 100 | |
| 22 | 0.056 | 0.278 | 0.167 | 0.278 | 0.167 | 0.056 | 100 | |
| 23 | 0.028 | 0.278 | 0.139 | 0.278 | 0.139 | 0.139 | 100 | |
| 24 | 0.111 | 0.278 | 0.111 | 0.278 | 0.111 | 0.111 | 100 | |
| 25 | 0.028 | 0.250 | 0.250 | 0.250 | 0.139 | 0.083 | 100 | |
| 26 | 0.056 | 0.250 | 0.250 | 0.250 | 0.139 | 0.056 | 100 | |
| 27 | 0.028 | 0.250 | 0.250 | 0.250 | 0.111 | 0.111 | 100 | |
| 28 | 0.083 | 0.250 | 0.250 | 0.250 | 0.083 | 0.083 | 100 | |
| 29 | 0.028 | 0.222 | 0.222 | 0.222 | 0.222 | 0.083 | 100 | |
| 30 | 0.056 | 0.222 | 0.222 | 0.222 | 0.222 | 0.056 | 100 | |
| 31 | 0.028 | 0.194 | 0.194 | 0.194 | 0.194 | 0.194 | 100 | |
| 32 | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 | 100 | |

Table A6.
The weighted normalized vectors of HOL.
Table A6.
The weighted normalized vectors of HOL.
| Adıyaman | 0.04 | 0.04 | 0.05 | 0.04 | 0.04 | 0.03 | 0.04 | 0.04 | |
| Hatay | 0.08 | 0.11 | 0.07 | 0.13 | 0.09 | 0.13 | 0.08 | 0.22 | |
| Kahramanmaraş | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Malatya | 0.47 | 0.47 | 0.44 | 0.41 | 0.53 | 0.54 | 0.48 | 0.43 |

Table A7.
The weighted normalized vectors of CEL.
Table A7.
The weighted normalized vectors of CEL.
| Adıyaman | 0.38 | 0.33 | 0.38 | 0.33 | 0.48 | 0.45 | 0.54 | 0.47 | |
| Hatay | 0.04 | 0.04 | 0.03 | 0.02 | 0.06 | 0.06 | 0.05 | 0.04 | |
| Kahramanmaraş | 0.33 | 0.30 | 0.34 | 0.34 | 0.32 | 0.31 | 0.32 | 0.30 | |
| Malatya | 0.87 | 0.88 | 0.86 | 0.89 | 0.83 | 0.85 | 0.75 | 0.79 |

Table A8.
The sum of the differences in the weighted normalized vector elements.
Table A8.
The sum of the differences in the weighted normalized vector elements.
| 1.4488 | 1.4382 | 1.4372 | 1.4260 | 1.4929 | 1.4856 | |||
| 1.4848 | 1.4742 | 1.4732 | 1.4620 | 1.5289 | 1.5216 | |||
| 1.4692 | 1.4586 | 1.4577 | 1.4464 | 1.5133 | 1.5060 | |||
| 1.5616 | 1.5510 | 1.5500 | 1.5388 | 1.6057 | 1.5984 | |||
| 1.4521 | 1.4415 | 1.4405 | 1.4293 | 1.4962 | 1.4889 | |||
| 1.4881 | 1.4775 | 1.4765 | 1.4653 | 1.5322 | 1.5249 | |||
| 1.4962 | 1.4857 | 1.4847 | 1.4734 | 1.5403 | 1.5330 | |||
| 1.6483 | 1.6378 | 1.6368 | 1.6255 | 1.6924 | 1.6851 | |||
| 1.4244 | 1.4138 | 1.4128 | 1.4015 | 1.4685 | 1.4612 | |||
| 1.4604 | 1.4498 | 1.4488 | 1.4375 | 1.5045 | 1.4972 | |||
| 1.4448 | 1.4342 | 1.4332 | 1.4219 | 1.4889 | 1.4816 | |||
| 1.5372 | 1.5266 | 1.5256 | 1.5143 | 1.5813 | 1.5740 | |||
| 1.4065 | 1.3960 | 1.3950 | 1.3837 | 1.4507 | 1.4433 | |||
| 1.4425 | 1.4320 | 1.4310 | 1.4197 | 1.4866 | 1.4793 | |||
| 1.4499 | 1.4394 | 1.4384 | 1.4271 | 1.4940 | 1.4867 | |||
| 1.6373 | 1.6267 | 1.6257 | 1.6144 | 1.6814 | 1.6741 |

Table A9.
The calculated values of RANCOM, RS, RR and RE methods and the criteria weights for HOL.
Table A9.
The calculated values of RANCOM, RS, RR and RE methods and the criteria weights for HOL.
| 0.32 | 1.50 | 4.50 | 0.30 | 0.67 | 0.31 | 20.25 | 0.37 | |
| 0.12 | 4.00 | 2.00 | 0.13 | 0.25 | 0.12 | 4.00 | 0.07 | |
| 0.32 | 1.50 | 4.50 | 0.30 | 0.67 | 0.31 | 20.25 | 0.37 | |
| 0.20 | 3.00 | 3.00 | 0.20 | 0.33 | 0.16 | 9.00 | 0.17 | |
| 0.04 | 5.00 | 1.00 | 0.07 | 0.20 | 0.09 | 1.00 | 0.02 | |
| Total | 1.00 | 15.00 | 15.00 | 1.00 | 2.12 | 1.00 | 54.50 | 1.00 |

Table A10.
The calculated values of RANCOM, RS, RR and RE methods and the criteria weights for CEL.
Table A10.
The calculated values of RANCOM, RS, RR and RE methods and the criteria weights for CEL.
| 0.08 | 5.00 | 2.00 | 0.10 | 0.20 | 0.09 | 4.00 | 0.05 | |
| 0.28 | 1.50 | 5.50 | 0.26 | 0.67 | 0.29 | 30.25 | 0.34 | |
| 0.19 | 3.00 | 4.00 | 0.19 | 0.33 | 0.15 | 16.00 | 0.18 | |
| 0.28 | 1.50 | 5.50 | 0.26 | 0.67 | 0.29 | 30.25 | 0.34 | |
| 0.08 | 5.00 | 2.00 | 0.10 | 0.20 | 0.09 | 4.00 | 0.05 | |
| 0.08 | 5.00 | 2.00 | 0.10 | 0.20 | 0.09 | 4.00 | 0.05 | |
| Total | 1.00 | 21.00 | 21.00 | 1.00 | 2.27 | 1.00 | 88.50 | 1.00 |
References
- Disaster and Emergency Management Authority (AFAD). 6 Şubat 2023 Pazarcık-Elbistan (Kahramanmaraş) Mw: 7.7 Alan Sismoloji ve Saha Gözlemleri Raporu; AFAD: Ankara, Turkey, 2023. Available online: https://deprem.afad.gov.tr/assets/pdf/Kahramanmara%C5%9F%20Depremi%20%20Raporu_02.06.2023.pdf (accessed on 13 September 2025).
- Türkiye İstatistik Kurumu (TÜİK), İşgücü İstatistikleri. 2023. Available online: https://data.tuik.gov.tr/Bulten/Index?p=Isgucu-Istatistikleri-2023-53521 (accessed on 13 September 2025).
- World Bank. Global Rapid Post-Disaster Damage Estimation (GRADE) Report: February 6, 2023 Kahramanmaraş Earthquakes—Türkiye (Report No: P178843; World Bank: Washington, DC, USA, 2023; Available online: https://documents1.worldbank.org/curated/en/099022723021250141/pdf/P1788430aeb62f08009b2302bd4074030fb.pdf (accessed on 13 September 2025).
- Türkiye Odalar ve Borsalar Birliği (TOBB). 2023 Ekonomik Rapor; Türkiye Odalar ve Borsalar Birliği (TOBB): Ankara, Turkey, 2023; Available online: https://tobb.org.tr/Documents/yayinlar/2024/80ER.pdf (accessed on 13 September 2025).
- United Nations Development Programme (UNDP). Türkiye Earthquake Flash Appeal; UNDP: New York, NY, USA, 2023; Available online: https://www.undp.org/sites/g/files/zskgke326/files/2023-02/UNDP%20T%C3%BCrkiye%20Earthquake%20Flash%20Appeal%20ENG.pdf (accessed on 13 September 2025).
- World Bank. Türkiye Earthquake Recovery and Reconstruction Project (Project Appraisal Document, Report No: BOSIB0be8dfe3b0e40b4d704983cde266fa); World Bank: Washington, DC, USA, 2023; Available online: https://documents1.worldbank.org/curated/en/099061423141522303/pdf/BOSIB0be8dfe3b0e40b4d704983cde266fa.pdf (accessed on 13 September 2025).
- DesRoches, R.; Comerio, M.; Eberhard, M.; Mooney, W.; Rix, G.J. Overview of the 2010 Haiti earthquake. Earthq. Spectra 2011, 27 (Suppl. S1), 1–21. [Google Scholar] [CrossRef]
- Kajitani, Y.; Chang, S.E.; Tatano, H. Economic impacts of the 2011 Tohoku-Oki earthquake and tsunami. Earthq. Spectra 2013, 29 (Suppl. S1), 457–478. [Google Scholar] [CrossRef]
- Lallemant, D.; Soden, R.; Rubinyi, S.; Loos, S.; Barns, K.; Bhattacharjee, G. Post-disaster damage assessments as catalysts for recovery: A look at assessments conducted in the wake of the 2015 Gorkha, Nepal, earthquake. Earthq. Spectra 2017, 33 (Suppl. S1), 435–451. [Google Scholar] [CrossRef]
- Paul, A.; Shukla, N.; Paul, S.K.; Trianni, A. Sustainable supply chain management and multi-criteria decision-making methods: A systematic review. Sustainability 2021, 13, 7104. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Goswami, S.S. Green supplier selection using MCDM: A comprehensive review of recent studies. Spectr. Eng. Manag. Sci. 2021, 2, 1–16. [Google Scholar] [CrossRef]
- Ayyildiz, E.; Erdogan, M. Literature analysis of the location selection studies related to the waste facilities within MCDM approaches. Environ. Sci. Pollut. Res. 2024, 32, 19574–19595. [Google Scholar] [CrossRef]
- Khan, I.; Pintelon, L.; Martin, H. The application of multicriteria decision analysis methods in health care: A literature review. Med. Decis. Mak. 2022, 42, 262–274. [Google Scholar] [CrossRef]
- Štilić, A.; Puška, A. Integrating multi-criteria decision-making methods with sustainable engineering: A comprehensive review of current practices. Eng 2023, 4, 1536–1549. [Google Scholar] [CrossRef]
- Krylovas, A.; Zavadskas, E.K.; Kosareva, N. Multiple criteria decision-making KEMIRA-M method for solution of location alternatives. Econ. Res.-Ekon. Istraživanja 2016, 29, 50–65. [Google Scholar] [CrossRef]
- Krylovas, A.; Zavadskas, E.K.; Kosareva, N.; Dadelo, S. New KEMIRA method for determining criteria priority and weights in solving MCDM problem. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 1119–1133. [Google Scholar] [CrossRef]
- Dadelo, S.; Krylovas, A.; Kosareva, N.; Zavadskas, E.K.; Dadeliene, R. Algorithm of maximizing the set of common solutions for several MCDM problems and it’s application for security personnel scheduling. Int. J. Comput. Commun. Control. 2014, 9, 151–159. [Google Scholar] [CrossRef]
- Sarıçalı, G.; Kundakcı, N. Forklift alternatiflerinin KEMIRA-M yöntemi ile değerlendirilmesi. Optim. Ekon. Ve Yönetim Bilim. Derg. 2017, 4, 35–53. [Google Scholar] [CrossRef][Green Version]
- Toktaş, P.; Can, G.F. Şantiyelerin İş Sağliği Ve Güvenliği Açisindan Risk Düzeylerine Göre Kemira-M Yöntemi İle Siralanmasi. Ergonomi 2018, 1, 123–136. [Google Scholar] [CrossRef]
- Sarıçalı, G.; Kundakcı, N. Bütünleşik KEMIRA-M ve Copras Yöntemi ile Mermer İşletmesi için Katrak Makinesi Seçimi. Kafkas Univ. Fac. Econ. Adm. Sci. J. 2019, 10, 1028–1061. [Google Scholar] [CrossRef][Green Version]
- Toktaş, P.; Can, G.F. Stochastic KEMIRA-M approach with consistent weightings. Int. J. Inf. Technol. Decis. Mak. 2019, 18, 793–831. [Google Scholar] [CrossRef]
- Kış, Ö.; Can, G.F.; Toktaş, P. Warehouse location selection for an electricity distribution company by KEMIRA-M method. Pamukkale Üniv. Mühendis. Bilim. Derg. 2020, 26, 227–240. [Google Scholar] [CrossRef]
- Arslan, N.; Delice, E.K. KEMIRA-M yöntemi ile kişisel kullanıcılar için dron seçimi: Bir uygulama. Endüstri Mühendisliği 2020, 31, 159–179. [Google Scholar] [CrossRef]
- Delice, E.K.; Can, G.F. A new approach for ergonomic risk assessment integrating KEMIRA, best–worst and MCDM methods. Soft Comput. 2020, 24, 15093–15110. [Google Scholar] [CrossRef]
- Can, G.F.; Toktaş, P. An advanced stochastic risk assessment approach proposal based on KEMIRA-M, QFD and Fine–Kinney hybridization. Int. J. Inf. Technol. Decis. Mak. 2021, 20, 431–468. [Google Scholar] [CrossRef]
- Pakdil, F.; Toktaş, P.; Can, G.F. Six sigma project prioritization and selection: A multi-criteria decision making approach in healthcare industry. Int. J. Lean Six Sigma 2021, 12, 553–578. [Google Scholar] [CrossRef]
- Tutuş, A.C.; Can, G.F.; Çökeliler, D. Tromboliz kateter üretim sürecindeki risklerin KEMIRA-M yöntemi ile önceliklendirilmesi. Avrupa Bilim Ve Teknol. Derg. 2021, 25, 763–773. [Google Scholar] [CrossRef]
- Arslan, N.; Delice, E.K. HTEA tabanlı KEMIRA-M yöntemi ile sağlık sektöründe risk değerlendirme. Avrupa Bilim Ve Teknol. Derg. 2021, 28, 853–862. [Google Scholar] [CrossRef]
- Berk, A.B.; Can, G.F. Evaluation of Risk Levels of an Engineering Company’s Constructions in Terms of Occupational Health and Safety. J. Optim. Decis. Mak. 2022, 1, 1–18. Available online: https://dergipark.org.tr/en/pub/jodm/issue/76301/1257543 (accessed on 22 October 2025).
- Toktaş, P.; Can, G.F. A three-stage holistic risk assessment approach proposal based on KEMIRA-M and DEMATEL integration. Knowl. Inf. Syst. 2023, 65, 1735–1768. [Google Scholar] [CrossRef]
- Ay, S.; Can, G.F.; Toktaş, P. A Novel Multi-Criteria Decision-Making Approach proposal based on KEMIRA-M with four criteria groups. Int. J. Inf. Technol. Decis. Mak. 2023, 22, 991–1032. [Google Scholar] [CrossRef]
- Soltanifar, M.; Santos-Artega, F.J. Hybrid DEA-BWM-KEMIRA approach for multiple attribute decision-making: A weighted analysis perspective: M. Soltanifar, FJ Santos-Arteaga. Soft Comput. 2024, 28, 12061–12079. [Google Scholar] [CrossRef]
- Toktaş, P.; Can, G.F. An advanced KEMIRA-M method proposal based on FARE method to perform ergonomic risk evaluation in a dishwasher assembly line. Pamukkale Üniv. Mühendis. Bilim. Derg. 2025, 31, 49931. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Shekhovtsov, A.; Sałabun, W. RANCOM: A novel approach to identifying criteria relevance based on inaccuracy expert judgments. Eng. Appl. Artif. Intell. 2023, 122, 106114. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Sałabun, W. Fuzzy RANCOM: A novel approach for modeling uncertainty in decision-making processes. Inf. Sci. 2025, 694, 121716. [Google Scholar] [CrossRef]
- Bitarafan, M.; Hosseini, K.A.; Hashemkhani Zolfani, S.; Ziari, K. Evaluating earthquake resilience in urban areas: A novel fuzzy RANCOM approach: M. Bitarafan et al. In Environment, Development and Sustainability; Springer: Berlin/Heidelberg, Germany, 2025; pp. 1–38. [Google Scholar] [CrossRef]
- Reyes-Norambuena, P.; Martinez-Torres, J.; Nemati, A.; Hashemkhani Zolfani, S.; Antucheviciene, J. Towards sustainable urban futures: Integrating a novel grey multi-criteria decision making model for optimal pedestrian walkway site selection. Sustainability 2024, 16, 4437. [Google Scholar] [CrossRef]
- Korucuk, S.; Aytekin, A. A field study examining barriers to logistics 4.0 using polytopic fuzzy RANCOM. J. Process Manag. New Technol. 2024, 12, 90–100. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Cavallaro, F.; Alrasheedi, A.F. Location selection for offshore wind power station using interval-valued intuitionistic fuzzy distance measure-RANCOM-WISP method. Sci. Rep. 2024, 14, 4706. [Google Scholar] [CrossRef] [PubMed]
- Więckowski, J.; Wątróbski, J.; Sałabun, W. Inaccuracies in expert judgment: Comparative analysis of RANCOM and AHP methods in housing location selection problem. IEEE Access 2024, 12, 142083–142100. [Google Scholar] [CrossRef]
- Więckowski, J.; Wątróbski, J.; Shkurina, A.; Sałabun, W. Adaptive multi-criteria decision making for electric vehicles: A hybrid approach based on RANCOM and ESP-SPOTIS. Artif. Intell. Rev. 2024, 57, 270. [Google Scholar] [CrossRef]
- Mishra, A.R.; Pamucar, D.; Rani, P.; Hezam, I.M. Single-Valued Neutrosophic Distance Measure-Based MEREC-RANCOM-WISP for Solving Sustainable Energy Storage Technology Problem. Cogn. Comput. 2025, 17, 87. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Alrasheedi, A.F.; Alshamrani, A.M.; Dwivedi, R. New distance measure-based RANCOM-AROMAN approach for evaluating sustainable human resource management factors in the manufacturing firms. Oper. Res. 2025, 25, 41. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer-Verlag: Berlin, Germany, 1981. [Google Scholar] [CrossRef]
- Gabus, A.; Fontela, E. Perceptions of the World Problematic: Communication Procedure, Communicating with Those Bearing Collective Responsibility (DEMATEL Report); Battelle Geneva Research Centre: Geneva, Switzerland, 1973. [Google Scholar]
- International Labour Organization (ILO). Enterprises Survey in a Post-Disaster Setting; International Labour Organization (ILO): Geneva, Switzerland, 2024; Available online: https://www.ilo.org/publications/enterprises-survey-post-disaster-setting (accessed on 13 September 2025).
- Yusop, Z.B.; Ahmed, K.; Shirazi, S.M.; Zardari, N.H. Weighting Methods and Their Effects on Multi-Criteria Decision Making Model Outcomes in Water Resources Management; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Dündar, H.Ç. 6 Şubat Kahramanmaraş Depremlerinin İş Dünyasına Etkileri. Anadolu Yönetim Derg. 2023, 2, 261–280. Available online: https://dergipark.org.tr/tr/download/article-file/3253924 (accessed on 13 October 2025).
- Güneş, G.Ş.; Güneş, T.; Güneş, S. The Impact of 2023 Kahramanmaraş Earthquakes on Real Estate Related Sectors: An Event Study Analysis. KAU IIBF Derg. 2023, 14, 789–811. [Google Scholar] [CrossRef]
- Yanardağ, R.; Toper, F.; Yağar, F. 6 Şubat 2023 Kahramanmaraş Merkezli Depremlerin Psikososyal ve Ekonomik Etkilerinin Analizi. Sosyoekonomi Derg. 2025, 33, 45–68. Available online: https://dergipark.org.tr/tr/pub/sosyoekonomi/issue/89774/1498911 (accessed on 13 October 2025).
- TEPAV; Aydın Özüdoğru, B. The Impact of and Policies for the 2023 Kahramanmaraş Earthquake; The Economic Policy Research Foundation of Türkiye: Ankara, Turkey, 2023; Available online: https://tepav.s3.eu-west-1.amazonaws.com/upload/files/1682309440-3.The_Impact_of_and_Policies_for_the_2023_Kahramanmaras_Earthquake.pdf (accessed on 13 October 2025).
- Paterson, A.; Matsumoto, T.; Özgüzel, C.; Visser, S.; Özçelik, E.; Kendir, C.; Wheeler, C. OECD Regional Development Papers. In The Territorial Impact of the Earthquakes in Türkiye—Policy Note; OECD Publishing: Paris, France, 2023; Available online: https://www.oecd.org/content/dam/oecd/en/publications/reports/2023/06/the-territorial-impact-of-the-earthquakes-in-turkiye_3e1731ee/bb5c07e6-en.pdf (accessed on 13 October 2025).
- Özsalman, E. 6 Şubat 2023 Kahramanmaraş Depremlerinin Dış Ticaret Üzerindeki Etkileri. Aydın İktisat Fakültesi Derg. 2024, 9, 65–82. Available online: https://dergipark.org.tr/tr/pub/ayd/issue/83271/1411837 (accessed on 13 October 2025).
- Niu, Y.; Zhou, X.P. Forecast of time-of-instability in rocks under complex stress conditions using spatial precursory AE response rate. Int. J. Rock Mech. Min. Sci. 2021, 147, 104908. [Google Scholar] [CrossRef]
- Kong, D.; Saroglou, C.; Wu, F.; Sha, P.; Li, B. Development and application of UAV-SfM photogrammetry for quantitative characterization of rock mass discontinuities. Int. J. Rock Mech. Min. Sci. 2021, 141, 104729. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).