Virtual Inertia of Electric Vehicle Fast Charging Stations with Dual Droop Control and Augmented Frequency Support
Abstract
1. Introduction
- Single droop control-G2V mode: In this mode, the charging current references are reduced in proportion to their individual ratings when there is a frequency dip.
- Single droop control-V2G mode: In this mode, the operation changes from G2V to V2G and power is fed to the grid from the batteries.
- Dual droop control mode: In this mode, the inertia support is provided by utilizing the energy from the DC link capacitors and by reducing the charging current references.
- Grid-forming mode: In this mode, both the VSCs act analogous to a VSG and behave like a voltage source.
- Augmented Frequency Support mode (AFS): In this mode, the energy from the DC link capacitors is utilized to provide frequency support whereas the batteries are in idle state.
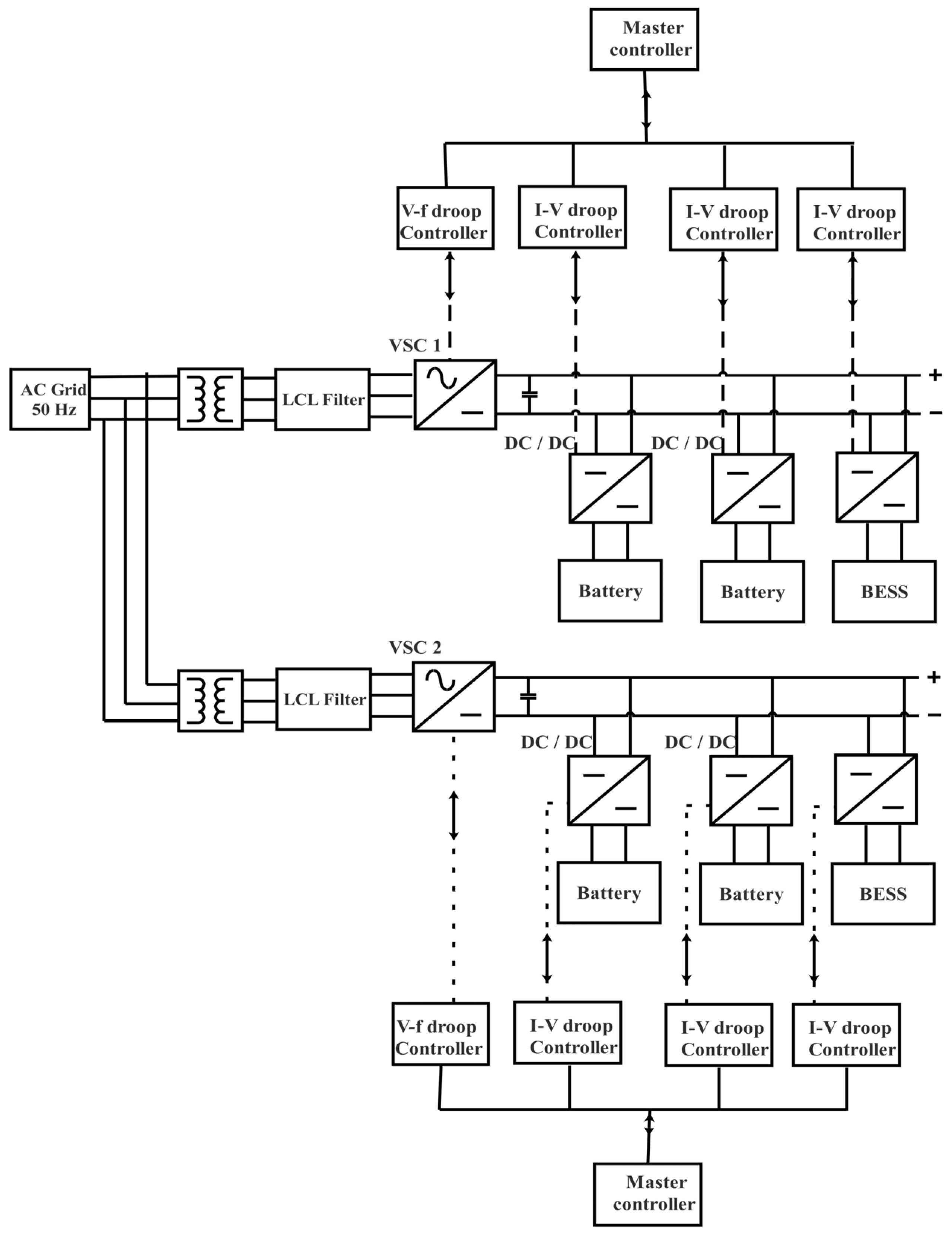
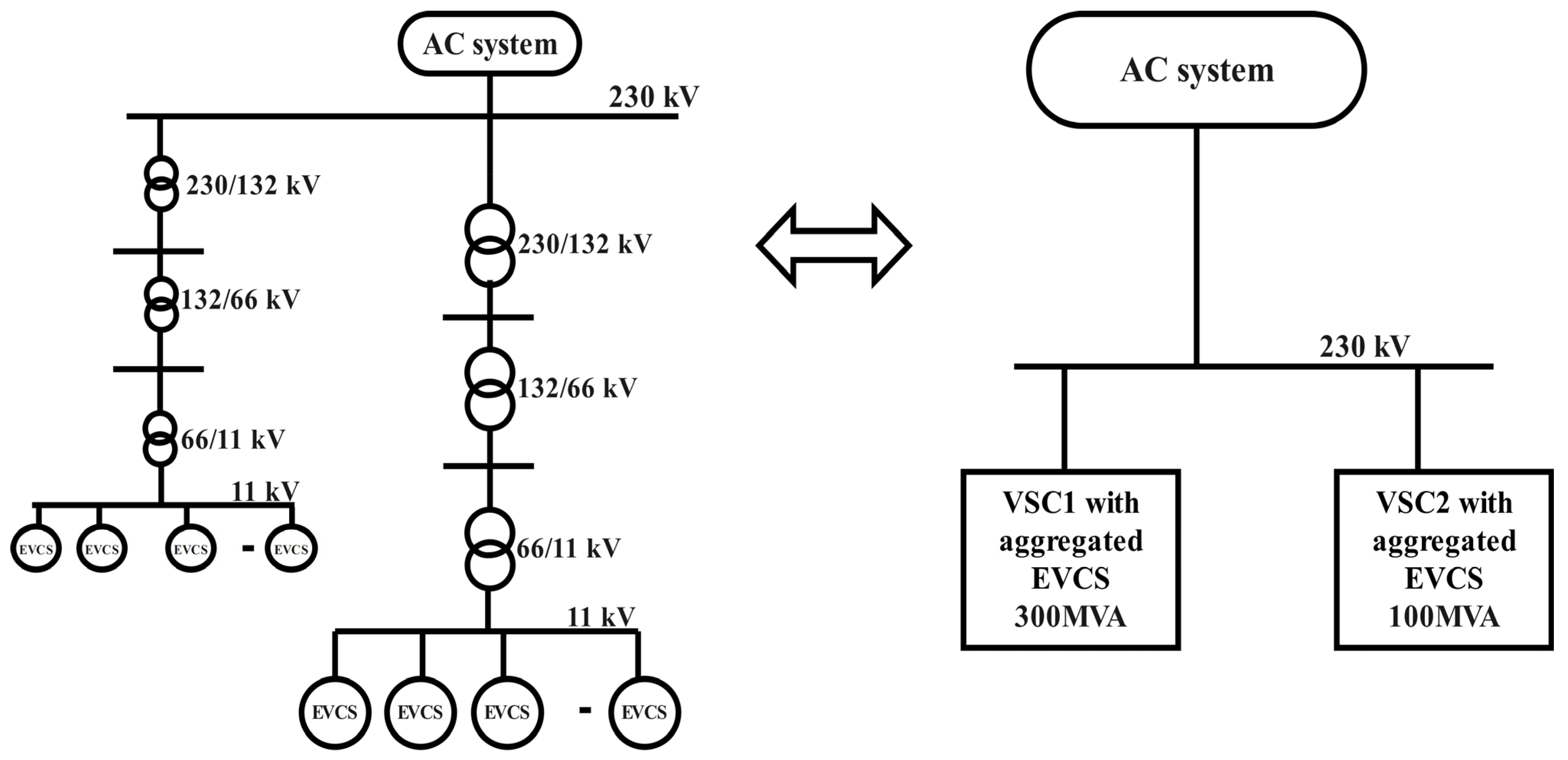
2. Electric Vehicle Fast Charging System (EVFCS) Architecture
3. Control of Electric Vehicle Fast Charging System
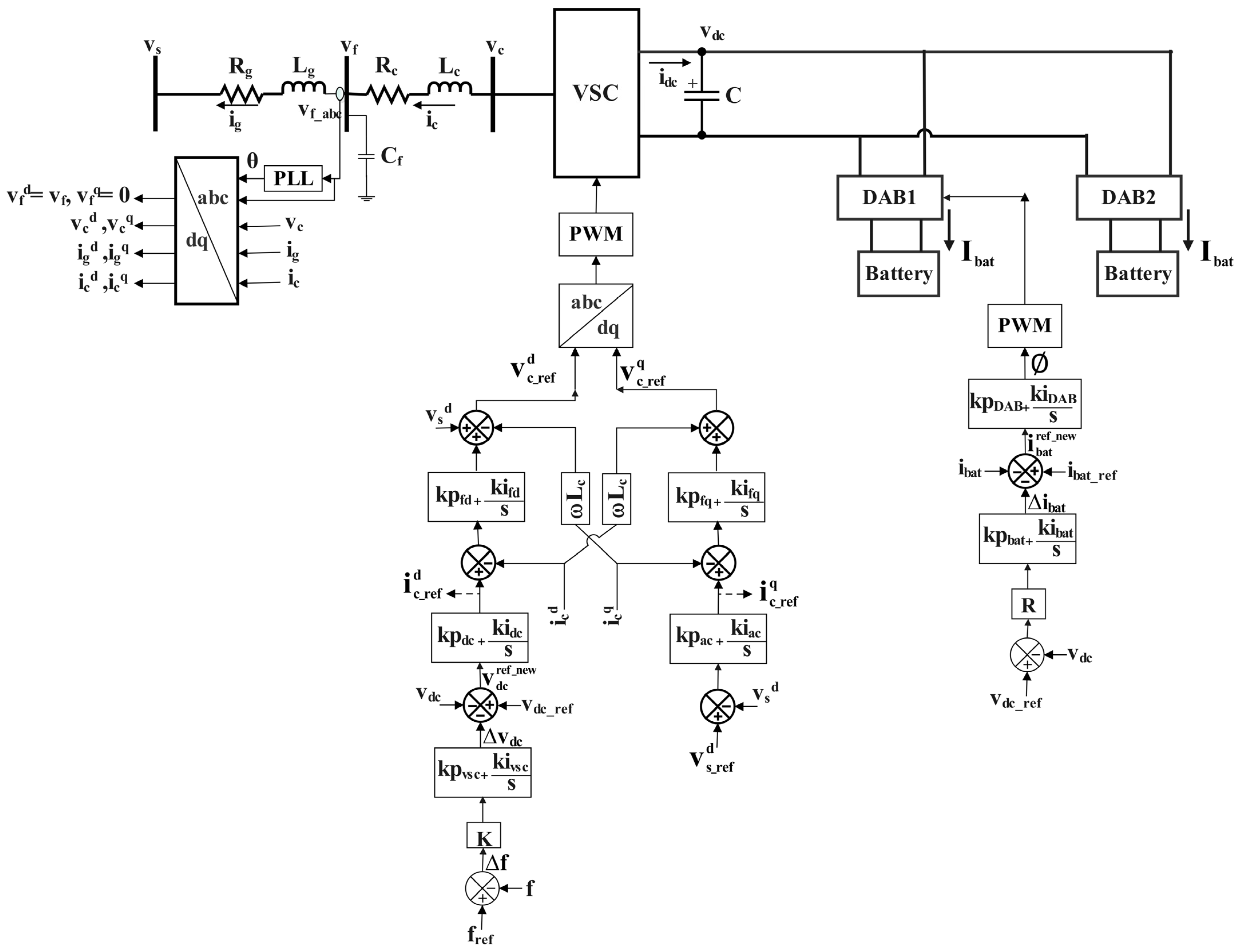
3.1. Control of Grid Tied VSC
3.2. Modeling of Grid Tied VSC
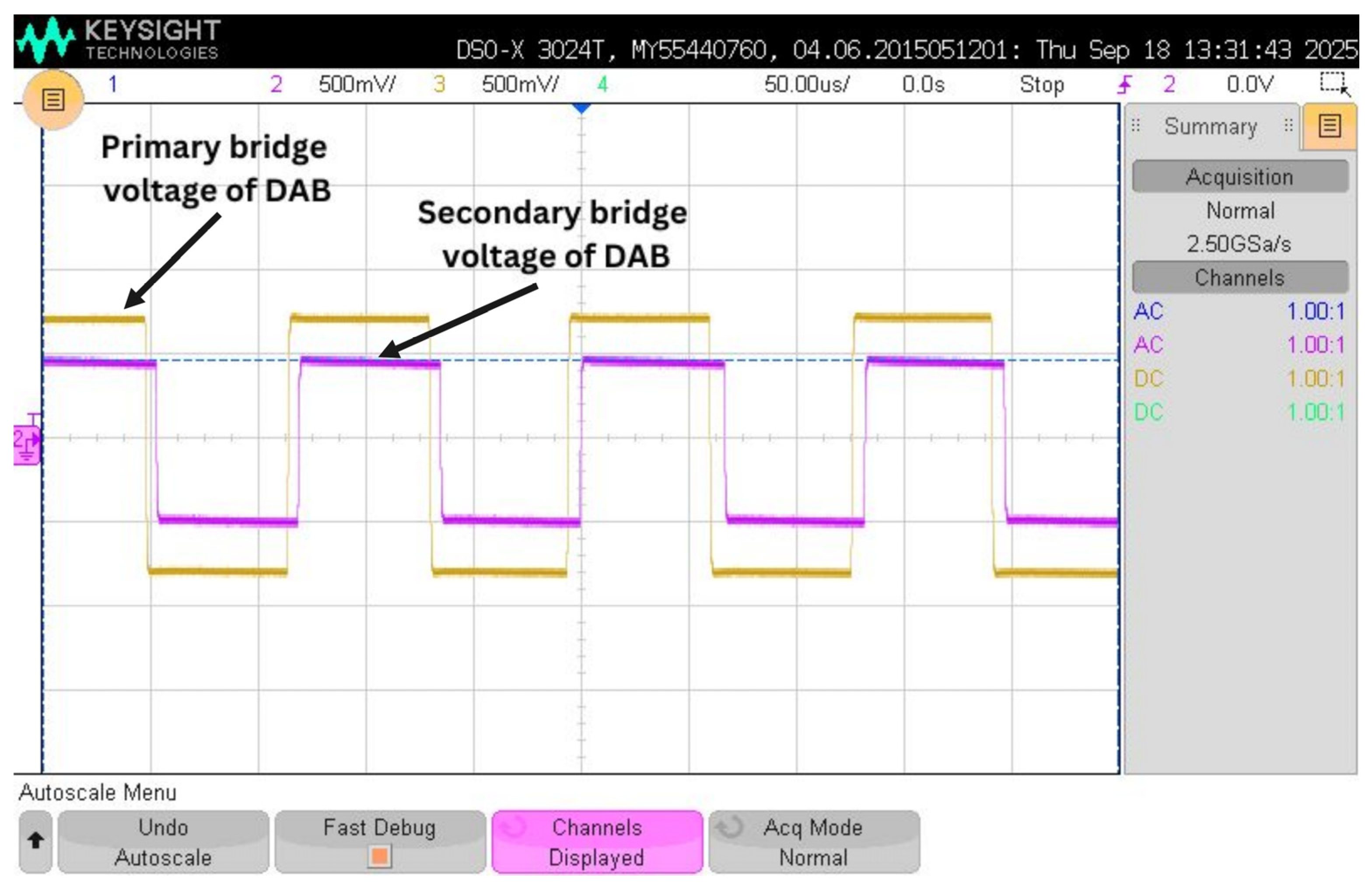
3.3. Control of Dual Active Bridge Converter
- Vbat is the battery voltage
- n is the transformer turns ratio
- L is the leakage inductance of the transformer
- is the phase shift between the two H-bridges of the DAB converter
- is the switching frequency
4. Inertia Control Strategy
- Single droop control-G2V mode
- Single droop control-V2G mode
- Dual droop Control Mode
- Grid-forming mode
- Augmented Frequency Support Mode
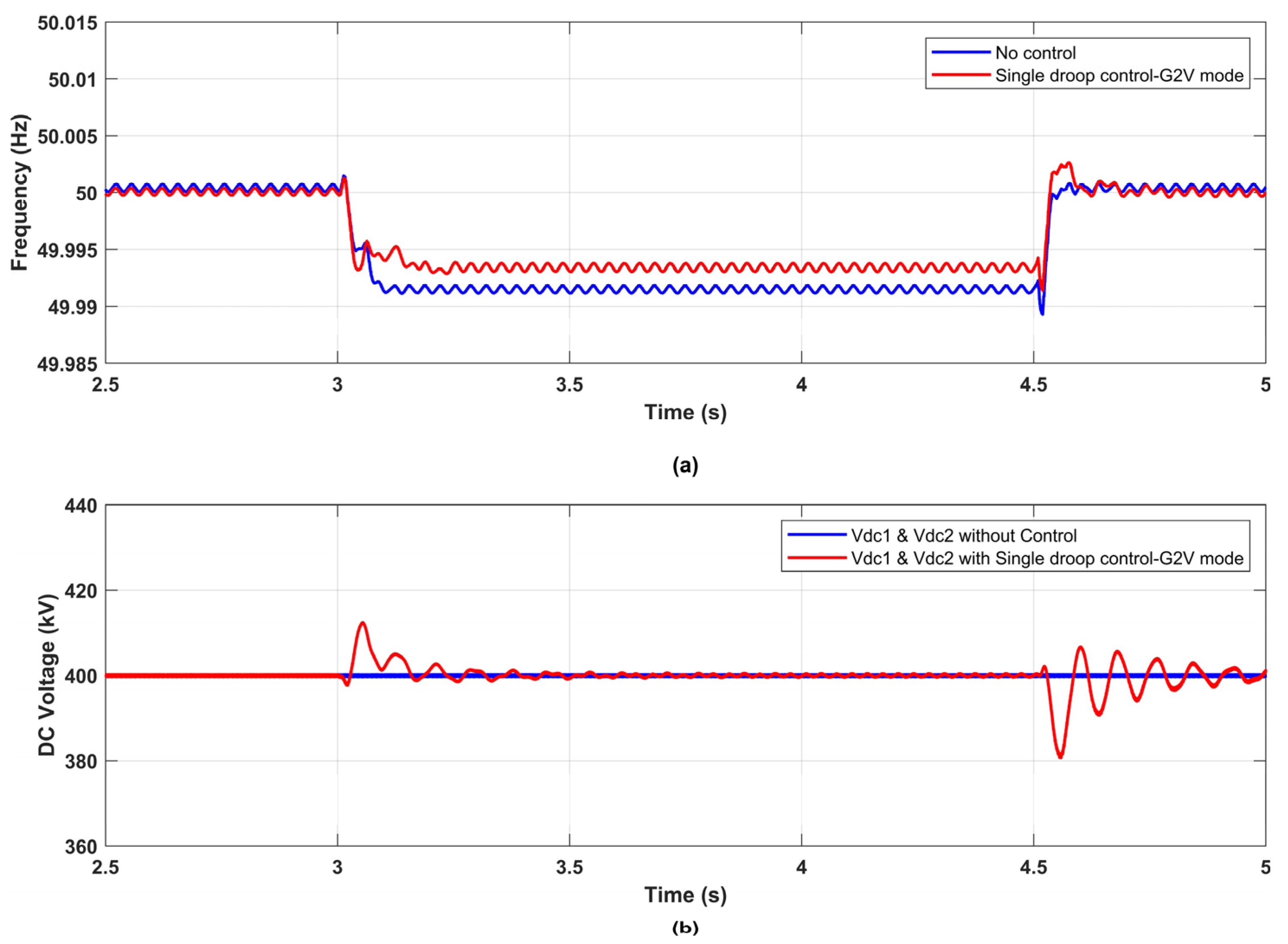
4.1. Single Droop Control-G2V Mode
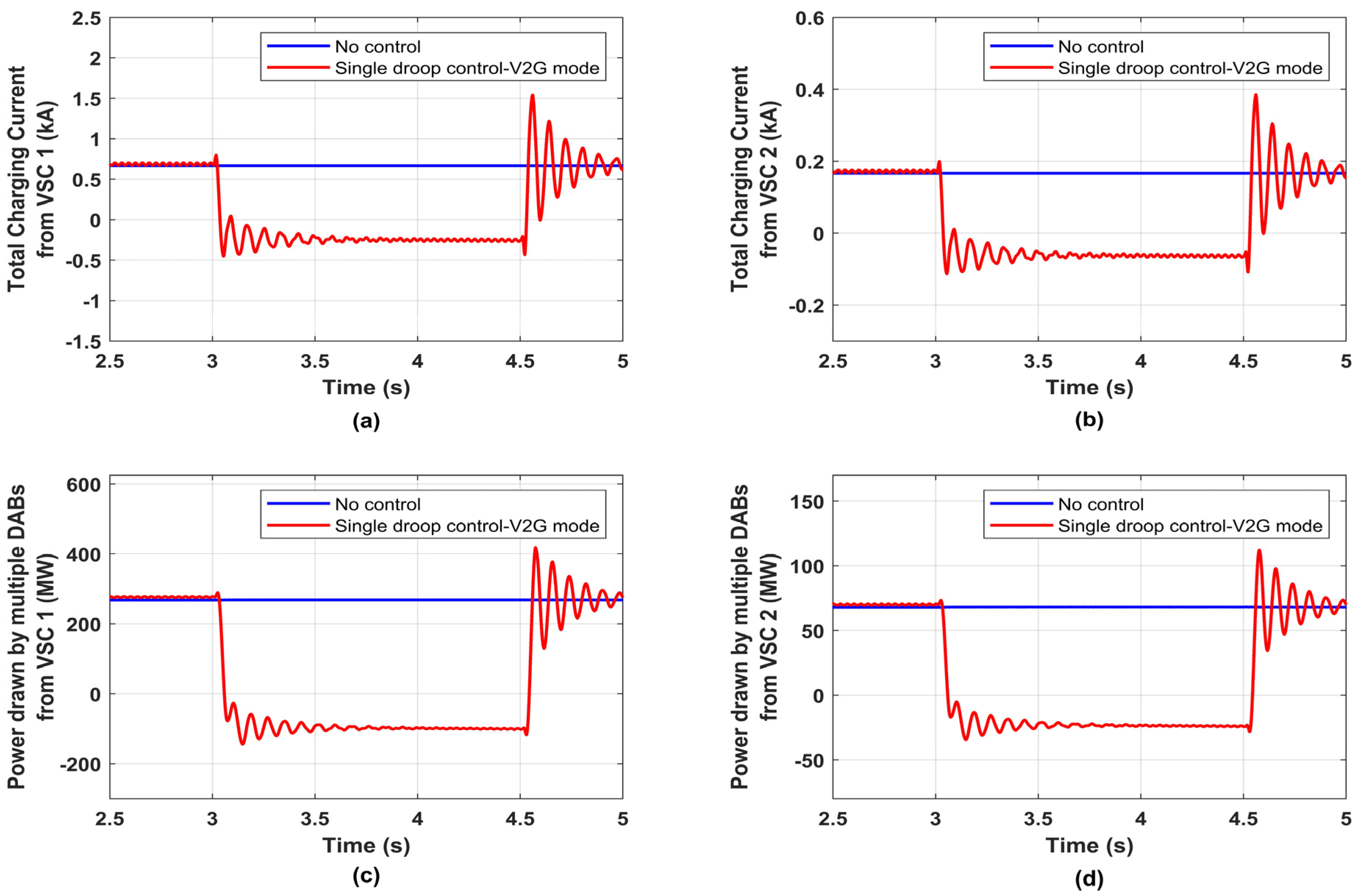
4.2. Single Droop Control-V2G Mode
4.3. Dual Droop Control
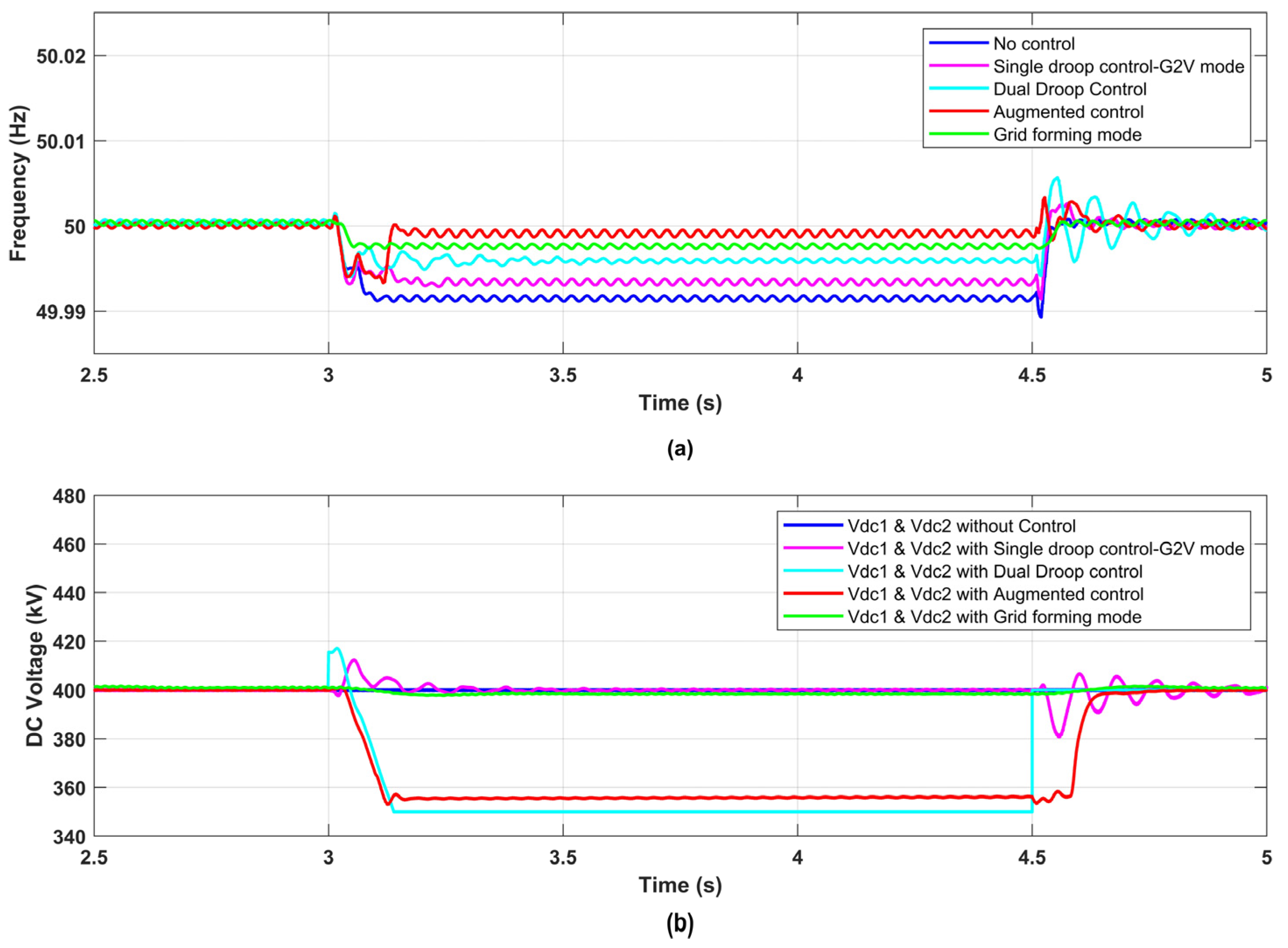
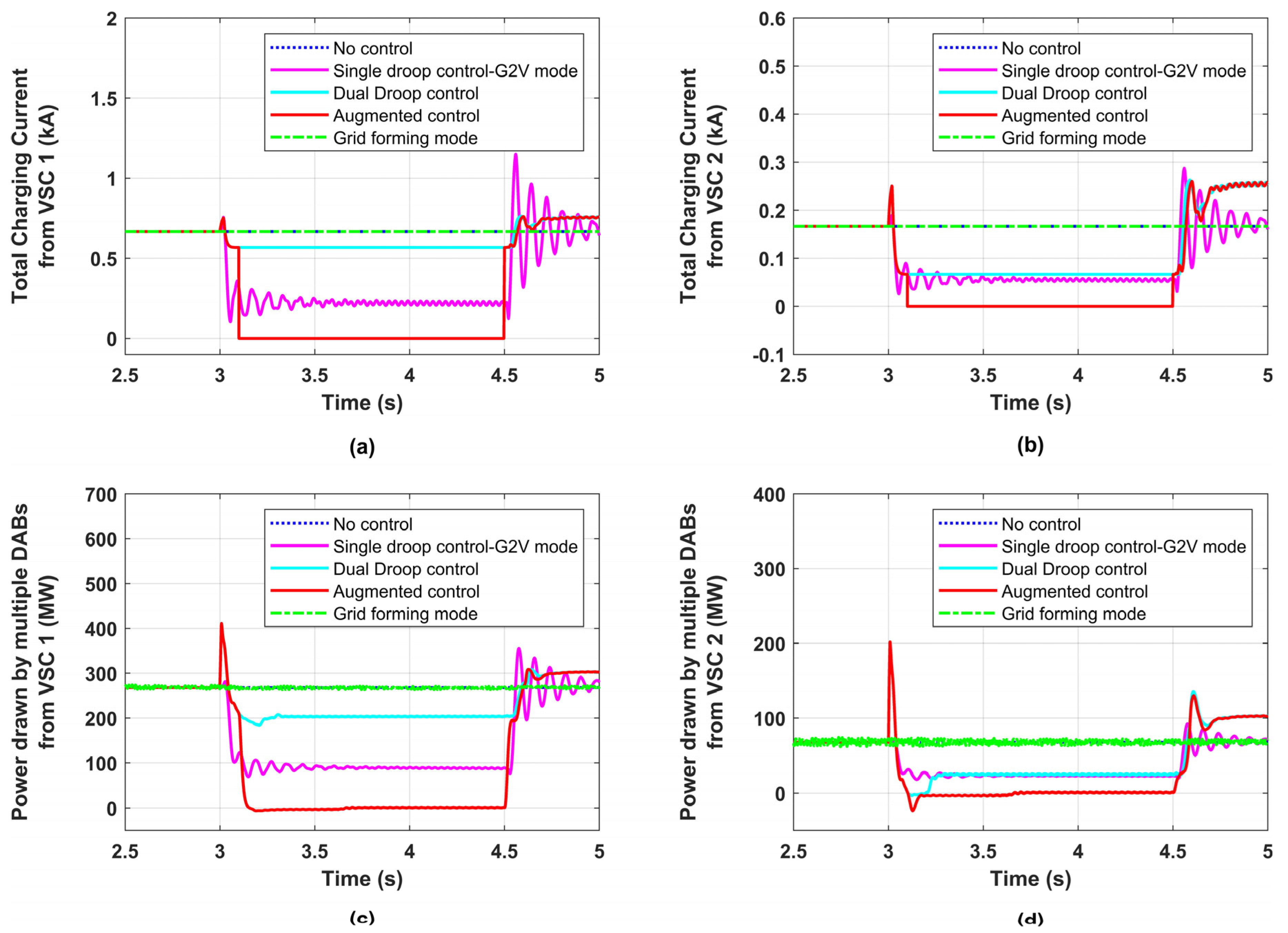
4.4. Grid-Forming Mode
- f0 is the nominal frequency
- P is the measure power at the given time instant
- P0 is the Active power reference
- m is the droop coefficient
- m is the sensitivity factor relating to frequency and active power. If m increases, the change in frequency increases for a given change in power.
4.5. Augmented Frequency Support
- In this mode
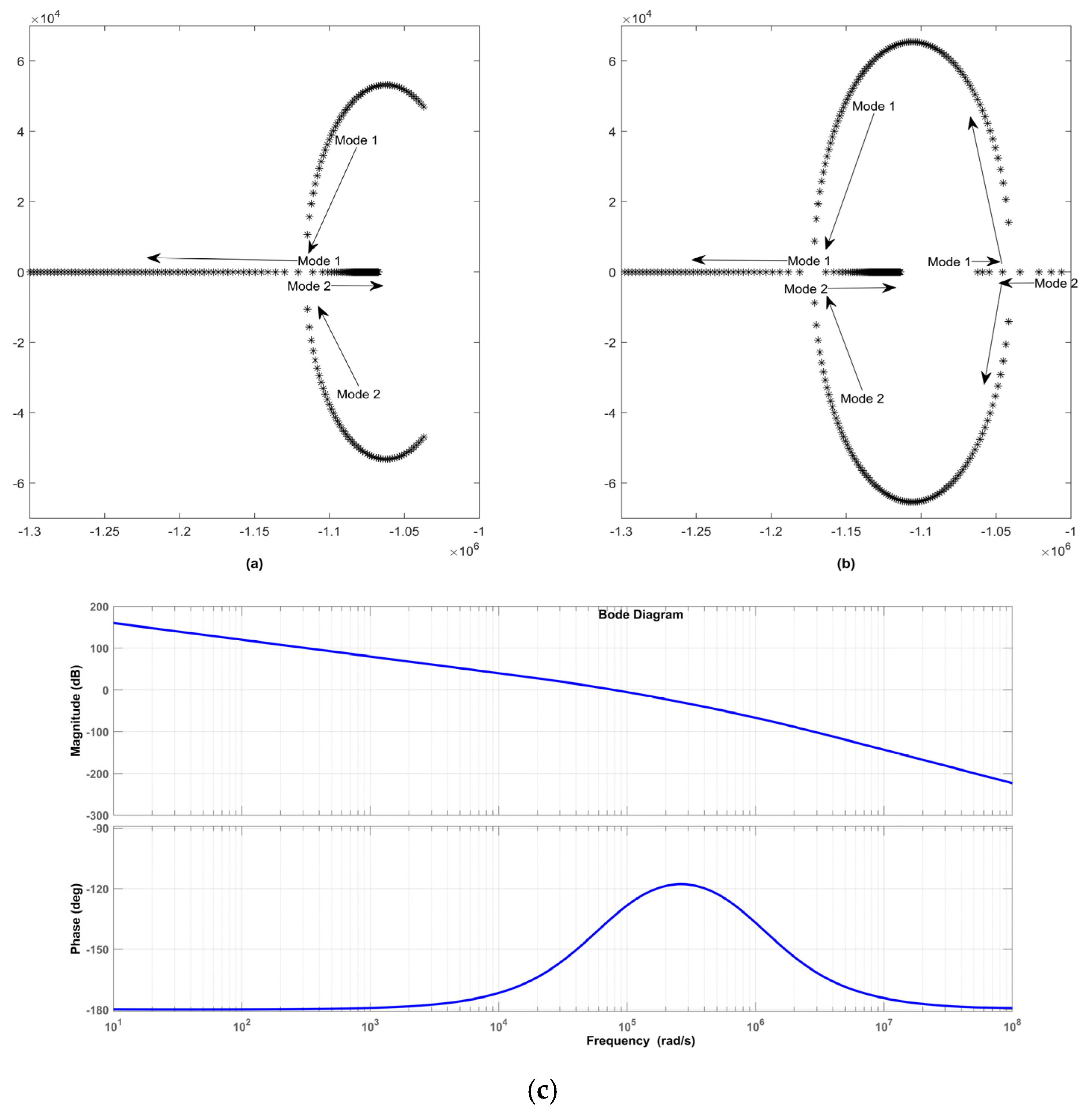
5. Results and Discussion
5.1. Single Droop Control
5.1.1. G2V Mode
5.1.2. V2G Mode
5.2. Grid-Forming Mode
5.3. Augmented Frequency Support
5.4. Real-Time Digital Simulation of AFS
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DAB | Dual Active Bridge |
| IBR | Inverter-Based Resource |
| EVFCS | Electric Vehicle Fast Charging System |
| VSC | Voltage Source Converter |
| PI | Proportional Integral |
| AFS | Augmented Frequency Support |
| ESS | Energy Storage Systems |
| EV | Electric Vehicle |
| G2V | Grid to Vehicle |
| V2G | Vehicle to Grid |
| ZVS | Zero Voltage Switching |
| SPS | Single Phase Shift |
| PFC | Power Factor Correction |
| SST | Solid State Transformer |
| ROCOF | Rate of Change of Frequency |
| SG | Synchronous Generator |
References
- Castro, L.M.; Acha, E. On the Provision of Frequency Regulation in Low Inertia AC Grids Using HVDC Systems. IEEE Trans. Smart Grid 2016, 7, 2680–2690. [Google Scholar] [CrossRef]
- Bevrani, H.; Ghosh, A.; Ledwich, G. Renewable energy sources and frequency regulation: Survey and new perspectives. IET 2010, 4, 438–457. [Google Scholar] [CrossRef]
- Dreidy, M.; Mokhlis, H.; Mekhilef, S. Inertia response and frequency control techniques for renewable energy sources: A review. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Bevrani, H.; Golpira, H.; Messina, A.R.; Hatziargyriou, N.; Milano, F.; Ise, T. Power system frequency control: An updated review of current solutions and new challenges. Electr. Power Syst. Res. 2021, 194, 107114. [Google Scholar] [CrossRef]
- Akram, U.; Nadarajah, M.; Shah, R.; Milano, F. A review on rapid responsive energy storage technologies for frequency regulation in modern power systems. Renew. Sustain. Energy Rev. 2020, 120, 109626. [Google Scholar] [CrossRef]
- Hussain, M.T.; Sulaiman, N.B.; Hussain, M.S.; Jabir, M. Optimal management strategies to solve issues of grid having electric vehicles (EV): A review. J. Energy Storage 2021, 33, 102114. [Google Scholar] [CrossRef]
- Tomic, J.; Kempton, W. Using fleets of electric-drive vehicles for grid support. J. Power Sources 2007, 168, 459–468. [Google Scholar] [CrossRef]
- Negri, S.; Tironi, E.; Danna, D.S. Integrated control strategy for islanded operation in smart grids: Virtual inertia and ancillary services. IEEE Trans. Ind. Appl. 2019, 55, 2401–2411. [Google Scholar] [CrossRef]
- Jafari, H.; Moghaddami, M.; Olowu, T.O.; Sarwat, A.I.; Mahmoudi, M. Virtual inertia-based multipower level controller for inductive electric vehicle charging systems. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 7369–7382. [Google Scholar] [CrossRef]
- Sockeel, N.; Gafford, J.; Papari, B.; Mazzola, M. Virtual inertia emulator-based model predictive control for grid frequency regulation considering high penetration of inverter-based energy storage system. IEEE Trans. Sustain. Energy 2020, 11, 2932–2939. [Google Scholar] [CrossRef]
- Lu, D.; Hu, D.; Wang, J.; Wei, W.; Zhang, X. A Data-Driven Vehicle Speed Prediction Transfer Learning Method with Improved Adaptability Across Working Conditions for Intelligent Fuel Cell Vehicle. IEEE Trans. Intell. Transp. Syst. 2025, 26, 10881–10891. [Google Scholar] [CrossRef]
- Heo, J.; Chang, S. Optimal planning for electric vehicle fast charging stations placements in a city scale using an advantage actor-critic deep reinforcement learning and geospatial analysis. Sustain. Cities Soc. 2024, 113, 105567. [Google Scholar] [CrossRef]
- Jamroen, C.; Dechanupapritta, S. Coordinated control of battery energy storage system and plug-in electric vehicles for frequency regulation in smart grid. In Proceedings of the 2019 IEEE PES GTD Grand International Conference and Exposition Asia (GTD Asia), Bangkok, Thailand, 19–23 March 2019; p. 286291. [Google Scholar] [CrossRef]
- Zhu, X.; Xia, M.; Chiang, H.-D. Coordinated sectional droop charging control for EV aggregator enhancing frequency stability of microgrid with high penetration of renewable energy sources. Appl. Energy 2018, 210, 936943. [Google Scholar] [CrossRef]
- Kheraluwala, M.N.; Gascoigne, R.W.; Divan, D.M.; Baumann, E.D. Performance characterization of a high-power dual active bridge DC-to-DC converter. IEEE Trans. Ind. Appl. 1992, 28, 1294–1301. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, X.; Zhang, D.; Liu, Y. Rapid Power Compensation-Based Frequency Response Strategy for Low-Inertia Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4500–4513. [Google Scholar] [CrossRef]
- Peng, Q.; Yang, Y.; Liu, T.; Blaabjerg, F. Coordination of virtual inertia control and frequency damping in PV systems for optimal frequency support. CPSS Trans. Power Electron. Appl. 2020, 5, 305–316. [Google Scholar] [CrossRef]
- Ke, S.; Yang, J.; Lu, Z.; Fan, P.; Peng, X.; Chen, L.; Qian, B.; Zhang, F. Consistency Collaboration Control Strategy Based on Adaptive Virtual Inertia in Multiple Charging Stations. IEEE Trans. Energy Convers. 2024, 39, 896–913. [Google Scholar] [CrossRef]
- Kaur, K.; Kumar, N.; Singh, M. Coordinated Power Control of Electric Vehicles for Grid Frequency Support: MILP-Based Hierarchical Control Design. IEEE Trans. Smart Grid 2019, 10, 3364–3373. [Google Scholar] [CrossRef]
- Ghatuari, I.; Kumar, N.S. A Coordinated Control Strategy of Electric Vehicles for Frequency Control in Modern Power Grids. IEEE Access 2025, 1. [Google Scholar] [CrossRef]
- Bernal-Sancho, M.; Rocca, R.; Fernández-Aznar, G.; Comech, M.P.; Galán-Hernández, N. Grid Impact of Frequency Regulation Provided by V2Gs Aggregated at HV, MV, and LV Level. IEEE Access 2023, 11, 76768–76780. [Google Scholar] [CrossRef]
- Jie, B.; Baba, J.; Kumada, A. Contribution to V2G System Frequency Regulation by Charging/Discharging Control of Aggregated EV Group. IEEE Trans. Ind. Appl. 2024, 60, 1129–1140. [Google Scholar] [CrossRef]
- Zheng, L.; Marellapudi, A.; Chowdhury, V.R.; Bilakanti, N.; Kandula, R.P.; Saeedifard, M.; Grijalva, S.; Divan, D. Solid-State Transformer and Hybrid Transformer with Integrated Energy Storage in Active Distribution Grids: Technical and Economic Comparison, Dispatch, and Control. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3771–3787. [Google Scholar] [CrossRef]
- Paucara, J.D.; Peña, J.C.U.; Rosas, D.S.Y. HESS Management for Virtual Inertia, Frequency, and Voltage Support Through Off-Board EV Bidirectional Chargers. IEEE Open J. Ind. Electron. Soc. 2024, 5, 376–385. [Google Scholar] [CrossRef]
- Kazemtarghi, A.; Dey, S.; Mallik, A. Optimal Utilization of Bidirectional EVs for Grid Frequency Support in Power Systems. IEEE Trans. Power Deliv. 2023, 38, 998–1010. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of the Impact of Vehicle-to-Grid Technologies on Distribution Systems and Utility Interfaces. IEEE Trans. Power Electron. 2013, 28, 5673–5689. [Google Scholar] [CrossRef]
- Sharida, A.; Bayindir, A.B.; Bayhan, S.; Abu-Rub, H. Hierarchical Control of DC Coupled Fast EV Charging Station. IEEE Trans. Power Electron. 2025, 40, 11690–11700. [Google Scholar] [CrossRef]
- Lin, G.; Liu, J.; Rehtanz, C.; Li, C.; Li, Y.; Wang, P. Inertia Droop Control and Stability Mechanism Analysis of Energy Storage Systems for DC-Busbar Electric Vehicle Charging Station. IEEE Trans. Transp. Electrif. 2023, 9, 266–282. [Google Scholar] [CrossRef]
- Rana, R.; Singh, M.; Mishra, S. Design of Modified Droop Controller for Frequency Support in Microgrid Using Fleet of Electric Vehicles. IEEE Trans. Power Syst. 2017, 32, 3627–3636. [Google Scholar] [CrossRef]
- Anbuselvi, S.V.; Devi, R.P.K.; Brinda, R. Coordinated Control of EV Charging stations for Grid Frequency Support. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; pp. 1–6. [Google Scholar] [CrossRef]





| Case | Scheme | Mode of Operation of Front-End VSC/MMC and Governing Equations | Mode of Operation of Front-End DAB and Governing Equations |
|---|---|---|---|
| 1 | Single droop control (G2V mode/V2G mode) | Vdc tracking without reference modulation | |
| 2 | Dual droop support | Vdc tracking with reference modulation with droop | Individual battery currents are modulated based on droop. Droop based on individual DAB converter ratings |
| 3 | Grid-forming mode | Pac tracking (P-f) droop characteristics share real power proportionally to frequency deviation, thereby stabilizing the system frequency. | None of the DC-side references are changed. Same steady-state operating condition prevails |
| 4 | Augmented Frequency Support | Pdc tracking Grid tied VSC’s feeding Charging stations share power proportionally based on droop coefficients. | Charging station ESS and EV’s opting to participate in frequency support act as distributed slack converters to maintain VC bus voltage on VSC side. In this mode wherein = |
| Parameter | Specification |
|---|---|
| System Frequency | 50 Hz |
| Grid Voltage | 420 kV |
| Real Power Generation | 350 MW |
| VSC 1 Power Rating | 400 MVA |
| VSC 2 Power Rating | 100 MVA |
| DC Bus Voltage | 400 kV |
| LCL filter parameters | Lg = 252 mH, Rg = 2.31 ohm, Lc = 72.4 mH, Rc = 0, Cf = 5 uF |
| Gain parameters of VSC controller | |
| DC Voltage controller | Kp = 0.05, Ti = 1.1 |
| AC voltage controller | Kp = 10, Ti = 0.0012 |
| Inner current controllers | Kp = 60, Ti = 0.0002 |
| Droop, K1 | 0.8 |
| Droop, K2 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thangavel Sampathkumar, N.; Shanmugam Velu, A.; Rajasekaran, B.; Raguru Pandu, K.D. Virtual Inertia of Electric Vehicle Fast Charging Stations with Dual Droop Control and Augmented Frequency Support. Sustainability 2025, 17, 8997. https://doi.org/10.3390/su17208997
Thangavel Sampathkumar N, Shanmugam Velu A, Rajasekaran B, Raguru Pandu KD. Virtual Inertia of Electric Vehicle Fast Charging Stations with Dual Droop Control and Augmented Frequency Support. Sustainability. 2025; 17(20):8997. https://doi.org/10.3390/su17208997
Chicago/Turabian StyleThangavel Sampathkumar, Nargunadevi, Anbuselvi Shanmugam Velu, Brinda Rajasekaran, and Kumudini Devi Raguru Pandu. 2025. "Virtual Inertia of Electric Vehicle Fast Charging Stations with Dual Droop Control and Augmented Frequency Support" Sustainability 17, no. 20: 8997. https://doi.org/10.3390/su17208997
APA StyleThangavel Sampathkumar, N., Shanmugam Velu, A., Rajasekaran, B., & Raguru Pandu, K. D. (2025). Virtual Inertia of Electric Vehicle Fast Charging Stations with Dual Droop Control and Augmented Frequency Support. Sustainability, 17(20), 8997. https://doi.org/10.3390/su17208997






