City-Level Critical Thresholds for Road Freight Decarbonization: Evidence from EVT Modeling Under Economic Fluctuation

Abstract

The rapid growth of road freight has increased urban carbon emissions, but decarbonization in this sector remains slow compared to other areas. This study examines city-level road freight decarbonization, focusing on extreme values, with the goal of establishing a quantitative reference indicator for tailored policies. Using data from 342 Chinese cities, we applied K-means clustering and Extreme Value Theory (EVT) to estimate the extreme levels of freight vehicles decarbonization (FVDEL) under various economic scenarios. Results show notable differences among city types. High-Tech and Light Industry Cities (Type I) display a more substantial decarbonization potential, with a key threshold around 1.27%. Surpassing this level indicates higher readiness for zero-emission road freight, while Heavy Industry-Manufacturing Cities (Type II) tend to behave more predictably during economic ups and downs because of their close ties between industry and freight activities. The study also finds that purchase subsidies tend to have diminishing returns, whereas operational incentives like electricity price discounts and road access advantages are more effective in maintaining adoption. By proposing EVT-based thresholds as practical benchmarks, this research connects statistical modeling with policy implementation. The proposed reference indicator offers useful guidance for assessing urban decarbonization capacity and developing customized strategies to promote zero-emission freight systems.

1. Introduction

Urban decarbonization pathways typically refer to a city’s plan or scenario for lowering greenhouse gas emissions to reach carbon neutrality. This includes the technological changes, policy actions, and sector-specific strategies needed to meet reduction targets. Creating clear decarbonization pathways is essential for planning and monitoring emission cuts, as it offers governments, businesses, and researchers a common framework to communicate and compare different cities’ goals and progress [1]. Typically, these pathways are categorized into major emitting sectors, including energy supply, buildings, transportation, and waste management, which collectively generate the majority of urban emissions and are under the control of local governments to reduce [2].

Within this broader framework, the road freight sector is a significant and challenging component, where decarbonization has lagged behind overall progress [3]. Between 2000 and 2022, road freight CO₂ emissions rose by 55%, making up 5% of global energy-related CO₂ emissions [4]. In many regions, the transport sector’s share of total greenhouse gas emissions has increased rather than decreased. For example, in France, the share grew from 22.9% in 1990 to 34% in 2023, making it the fastest-growing sector [3]. Meanwhile, national decarbonization strategies often include specific timelines for phasing out fossil-fuel passenger cars (e.g., 2030 or 2035), while heavy-duty trucks are generally delayed until around 2040 [5]. For instance, the UK government promised to phase out diesel trucks under 26 tons by 2035 and ban all new diesel trucks by 2040, while the European Union has also committed to nearly eliminating new diesel trucks by 2040 [6].

The delay in decarbonizing road freight comes from three main challenges. First, technological barriers still exist: battery-electric trucks face issues with driving range, charging time, and payload capacity, making them unsuitable for long-distance, high-volume freight [7]; hydrogen fuel cell trucks are still in early testing stages, with hydrogen production and refueling infrastructure far from sufficient, and high life-cycle costs [8]. Second, economic hurdles remain: the total cost of ownership (TCO) of electric trucks is still higher than that of diesel trucks [9], while “range anxiety” and limited charging spots further raise perceived costs [10]. Studies show these intangible costs can increase user expenses by nearly 27%, reducing the competitiveness of zero-emission trucks [7]. Third, institutional and coordination issues also slow the transition. For example, power grids need to be planned to handle the high-power charging needs of electric trucks, but coordination between transportation and electricity sectors is often lacking [11]; meanwhile, subsidy policies are gradually ending [12]. Overall, decarbonizing road freight faces both “hard challenges” (technological and cost barriers) and “soft challenges” (institutional and market factors), making it one of the toughest sectors to decarbonize.

Against this backdrop, the prevailing academic view proposes a phased strategy: slowing the growth of freight emissions in the short term, waiting for technological breakthroughs in the medium term, and focusing on eliminating residual emissions in the long term. However, a key but underexplored question remains: can a specific critical threshold be identified to differentiate cities’ freight emission control efforts at this stage? Specifically, tailored strategies could be developed for cities above or below this threshold to speed up road freight decarbonization without hindering urban economic growth. This question is essential for three reasons. First, the freight market is highly competitive with long vehicle replacement cycles [3], meaning the current emission structure will lock in trajectories for years to come, especially during economic fluctuations [13]. Second, cities vary significantly in financial structure and sustainability stages, making differentiated pathways essential. Third, precise thresholds can help guide policies to accelerate the turning point of freight decarbonization through economic and institutional measures, leading to longer-term sustainability outcomes [14].

Previous research has proposed freight decarbonization thresholds at the aggregate level, with total cost of ownership (TCO) being the most critical. Once TCO for electric trucks approaches parity with diesel, coupled with stricter regulations, zero-emission trucks rapidly gain market share [15]. Hunter et al. (2021) estimated the TCO of conventional, hybrid, and zero-emission technologies in the U.S., finding that electric trucks could compete in single-shift operations before 2050, while FCEVs could become competitive in multi-shift heavy-duty scenarios by 2050 [16]. Fuel costs, tolls, and subsidies are key economic indicators [14]. Since the TCO for electric trucks remains generally higher than for diesel trucks, many policymakers are working to speed up decarbonization through operating incentives—such as road pricing/access charges, purchase subsidies, and priority access policies—to lower the use-phase costs and vehicle price premium for zero-emission freight. For example, a recent study of Guangdong Province quantifies that policies including purchase subsidies, road toll reductions, expressway/toll exemptions, and road access privileges significantly move forward the year in which electric trucks reach TCO parity with diesel counterparts under various use cases [17]. Another study shows that changes in road toll fees and providing right-of-way priority can meaningfully reduce the cost gap between zero-emission and conventional commercial vehicles in China [18]. Zhao et al. (2024) emphasized that policy mixes have varying effectiveness depending on a city’s sales volume, income level, and population density [19]. Cao & Chong (2025) highlighted the need for tailored decarbonization pathways in resource-based cities [20]. However, these studies have not yet established a unified, city-level reference indicator applicable across different urban contexts, nor have they clearly compared operating incentives vs. vehicle price premiums in extreme decarbonization thresholds.

This study addresses that gap by proposing a city-level reference indicator for road-freight decarbonization. Specifically, we aim to: (1) combine empirical evidence with theoretical reasoning to categorize cities and identify distinct types (Type I and Type II) that vary in industrial structure and freight profiles; (2) use extreme value theory (EVT) to develop a policy-oriented benchmark for road-freight decarbonization; and (3) turn these findings into staged, type-specific policy recommendations, providing a clear analytical basis for future targeted interventions.

Furthermore, different countries can estimate the relevant city-level reference indicators using the ideas outlined in this article and data from specific cities, thereby offering targeted policy advice for each nation. Importantly, the reference indicator is not purely theoretical; it is grounded in EVT estimates within the methodology, employed in the results to identify critical thresholds for various city types, and serves as the direct basis for subsequent tailored policy recommendations.

2. Methodology

2.1. Research Framework

The primary objective of this study is to examine how the decarbonization levels of extreme freight vehicles at the city level fluctuate in response to economic changes, particularly during economic shocks or recessions. The methodology is organized into four interconnected stages to address this goal.

City Classification: Recognizing that different city types have unique freight decarbonization pathways, we classify cities using the K-means clustering method based on their industrial emissions characteristics. Decarbonization and Economic Level.

Measurement: The decarbonization levels of freight vehicles and city economic development indicators (GRP) are quantified to explore their relationships and provide a basis for further analysis.

Identification of Influencing Factors: The Optimal Parameters-based Geographical Detector (OPGD) is used to identify key factors affecting urban decarbonization levels. This method accounts for spatial heterogeneity and nonlinear relationships, helping to reduce the multicollinearity issues common in urban data.

Extreme Value Prediction: The Generalized Extreme Value (GEV) model forecasts cities’ extreme road decarbonization potentials under different economic scenarios, offering insights into the economic thresholds needed to achieve zero-emission freight.

The research hypothesis suggests that for cities of the same type, their extreme road decarbonization potentials relative to GDP are similar, just like Wu et al.’s research [21]. The study models cities’ decarbonization extremes and lays the foundation for constructing a quantitative reference indicator.

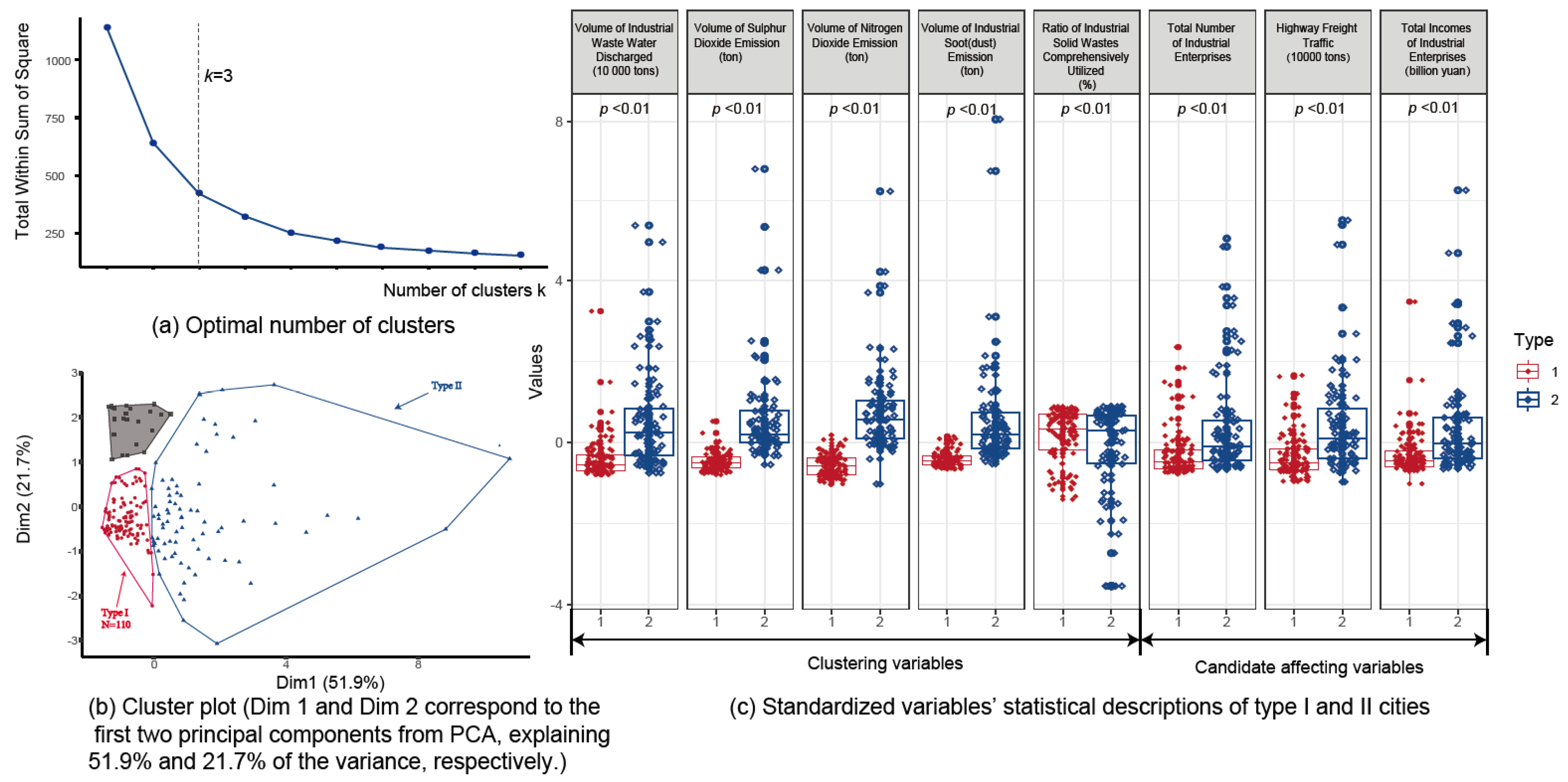
2.2. City Classification Based on Industrial Emission Characteristics

Cities vary greatly in industrial structure, emissions intensity, and economic makeup, resulting in different potentials and pathways for decarbonization [22]. This study uses the K-means clustering method to analyze and forecast road decarbonization extremes and classify cities based on their industrial emission characteristics.

The K-means clustering algorithm divides cities into separate groups by minimizing intra-cluster variance (SSE). The best number of clusters (k) is identified by finding the “elbow” point, where the decrease in SSE slows considerably. The clustering formula is described as follows [23]:

$$\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\sum _{i=1}^k \sum _{x\in S_i} \parallel x-{\mu }_i{\parallel }^2$$

(1)

where $x$ represents the vector of city industrial emission features, ${\mu }_i$ represents the centroid of cluster $S_i$, and $k$ is the number of clusters.

This classification allows for targeted examination of how various urban industrial settings influence road decarbonization potential and their responsiveness to economic changes, directly supporting this study’s goals and clarifying subsequent analysis.

2.3. Measurement of Urban Road Decarbonization and Economic Development Levels

Accurately measuring cities’ decarbonization and economic development levels is crucial for understanding how the potential for urban road freight decarbonization changes in response to economic fluctuations. This study quantifies freight vehicles decarbonization levels using the weighted average emission reduction rates of various truck types registered annually within each city.

The Freight Vehicle Decarbonization Level (FVDL) refers to the decarbonization level achievable based on the type of truck and its decarbonization rate, calculated under the current ownership of these vehicles, in accordance with similar indicators defined in the literature [21]. FVDL does not account for the decarbonization level at the city level, but rather the decarbonization condition when these freight transportation vehicles are owned. Specifically, the freight vehicle decarbonization level (FVDL) is calculated as:

$$F={\displaystyle \frac{\sum _{i=1}^n{P}_i\times Q_i}{\sum _{i=1}^n{P}_i}}$$

(2)

where $F$ represents the city’s freight vehicles decarbonization levels, $P_i$ denotes the annual purchase quantity of truck type $i$, and $Q_i$ indicates the emission reduction rate of truck type $i$.

Table 1. Emissions Reduction Percentage.

Truck Type	Emissions Reduction Rate (%)	Reference
Diesel truck	0	-
Gasoline truck	0	-
Electric truck	100	-
Hydrogen fuel cell truck	33	[24]
Gas-fueled truck	12	[25]
Hybrid power truck	6	[26]
Trucks using intelligent connected technology	15.1	[27]

presents truck types and their corresponding emission reduction percentages, referencing studies on vehicle emissions and technological impacts.

Gross Regional Product (GRP) indicates cities’ economic development level. The economic level of each city is expressed as:

$$D=\ln \left(\mathrm{GRP}\right)$$

(3)

where D shows the city’s development level, using 100 million yuan as the unit.

This measurement framework effectively captures the relationship between cities’ economic status and road decarbonization capacities, providing a quantitative basis for further analysis of decarbonization potential under economic fluctuation scenarios.

2.4. Extreme Value Modeling (EVM)

Since cities with similar economic levels often have different capacities for freight decarbonization, understanding these differences, especially at extreme ends, requires specialized statistical methods. Extreme Value Theory provides a robust framework for analyzing and forecasting these extreme cases, surpassing the limitations of traditional linear regressions or standard machine learning techniques, which typically restrict predictions to observed data ranges [28].

This study used EVT to examine the extreme potential of extreme levels of freight vehicle decarbonization (FVDEL) under various economic conditions. The reason for selecting EVT was that it can nonlinearly predict and forecast extreme outcomes, quantify the likelihood and extent of extreme levels, evaluate the resilience or maximum capacity of cities under stress scenarios, and effectively capture situations such as major economic recessions or booms and their influence on freight emissions [28,29], thereby providing a more powerful, resilient, and forward-looking foundation for urban freight policy development.

The process of modeling extreme values involves three main steps.

(1) Transformation of the Dependent Variable

The original decarbonization rate FVDEL lies between 0 and 1. Values close to 1 indicate near-complete decarbonization, which can make statistical estimation difficult because these values cluster together. To spread them out and make patterns easier to detect, we transform FVDEL using:

Y = −ln(1 − FVDEL)

(4)

This transformation extends beyond low values, making differences in top-performing cities more pronounced.

(2) Extreme Value Sampling (Block Maxima Approach)

The Block Maxima (BM) sampling method is used to ensure the validity of extreme value data. The BM method divides the dataset into fixed intervals and selects the minimum or maximum value within each interval as the extreme observation [28]. Choosing appropriate intervals requires balancing data use and independence; therefore, an autocorrelation function (ACF) test is conducted to confirm extreme values’ independence, ensuring there is no autocorrelation at the selected intervals.

(3) Generalized Extreme Value (GEV) Distribution Fitting

According to EVT, the sampled extreme values from independent and identically distributed datasets converge asymptotically to a generalized extreme value (GEV) distribution [30]. The probability density function of the GEV distribution is given as follows:

$$G\left(z;\mu ,\sigma ,\xi \right)=\mathrm{e}\mathrm{x}\mathrm{p}\left\{-{\left[1+\xi \left({\displaystyle \frac{z-\mu }{\sigma }}\right)\right]}^{-1/\xi }\right\}, 1+\xi \left({\displaystyle \frac{z-\mu }{\sigma }}\right)>0$$

(5)

where $\mu$, $\sigma$, and $\xi$ denote the location, scale, and shape parameters, respectively. The shape parameter $\xi$ characterizes the tail behavior of the extreme value distribution, influencing predictive reliability and model applicability [28].

(4) Incorporation of Influencing Factors as Covariates

Key influences identified by the OPGD model are added as covariates into the GEV model to improve predictive accuracy and better understand the factors driving extreme decarbonization levels. Specifically, covariates are used to model the location parameter $\mu$ and scale parameter $\sigma$, while the shape parameter $\xi$ usually remains fixed to ensure model stability [28,31]. The covariate-based GEV model is defined as follows:

Location parameter model:

$$\mu \left(T\right)={\alpha }_0+{\alpha }_{1}T$$

(6)

Scale parameter model:

$$\sigma \left(T\right)={\beta }_0+{\beta }_{1}T$$

(7)

where $T$ represents selected covariates, ${\alpha }_0,{\alpha }_1,{\beta }_0,{\beta }_1$ are parameters to be estimated. Positive values of covariate coefficients indicate positive effects on urban road decarbonization potential.

(5) Predicting Return Levels

From the fitted GEV model, we can estimate return levels, such as:

FVDELmax(p) = 1 − exp(−q_p)

(8)

where q_p is the predicted p-th quantile of the transformed variable Y. For example, p = 0.95 is a conservative estimate of the maximum achievable decarbonization rate; p = 0.99 is an optimistic upper bound.

These values serve as targets for benchmarking and help identify which cities are performing close to their potential.

The predicted return levels provide the quantitative basis for identifying a city’s maximum feasible FVDEL under different economic scenarios. We establish the reference indicator as a critical threshold by comparing these return levels with observed decarbonization performance. This threshold links the methodological results to the study’s central aim of differentiating policy recommendations for cities above and below the benchmark.

2.5. Data Sources and Processing

This study uses cross-sectional data for 342 prefecture-level Chinese cities. The sample exhibits high diversity in economic scale, industrial composition, and freight demand, lending the analysis a degree of generalizability beyond the national context. Economically, the data span low-, middle-, and high-income urban economies; industrially, they cover both technology-intensive and heavy-manufacturing profiles; and in freight, they include a wide range of shipment intensities and modal mixes. This breadth helps ensure that the clustering and EVT results remain informative across different city types [32,33].

The primary dataset used in this research comprises truck registration data from 342 Chinese cities, encompassing various truck types and their corresponding annual purchase volumes. This data was obtained from reputable commercial data trading platforms specializing in vehicle registration records, offering detailed insights into the market share of alternative fuel trucks and trucks equipped with intelligent connected technologies.

City-level socio-economic and industrial data, including Gross Regional Product (GRP), highway freight traffic, industrial enterprises, and total industrial incomes, were obtained from the China Urban Statistical Yearbook [34].

2.6. Reference Indicator Construction and Application

Building on the EVT results, this study develops a city-level reference indicator to identify the critical threshold for freight decarbonization. The indicator is generated by aligning the extreme modeled FVDEL values with the previously identified city clusters. Cities that surpass the threshold are considered to have a higher capacity for promoting zero-emission road freight, while those below the threshold face structural or economic barriers that require tailored support. This reference indicator is then used in the results to categorize city types and develop differentiated policy recommendations in the discussion.

3. Results

3.1. Clustering Results and Statistics Description

We selected a set of indicators to reflect industrial emissions, environmental quality, economic size, freight intensity, and industrial structure. Specifically, three types of industrial air pollutants—particulate matter, SO₂, and NO_x emissions—were included to represent industrial emission characteristics. Annual mean PM2.5 concentration was used as an environmental proxy reflecting cumulative emission impacts. Gross regional product (GRP, current prices) and highway freight traffic captured economic scale and freight intensity. Finally, the shares of the primary, secondary, and tertiary sectors in GRP were included to reflect differences in industrial structure. Descriptive statistics of these variables are reported in

Table 2. Descriptive Statistics of Clustering Indicators.

Variable	Definition	Max	Min	Mean	Std. Dev.
Industrial PM Emissions (tons)	Total industrial particulate matter emissions	61,528.00	171	8076.85	7566.61
Industrial SO2 Emissions (tons)	Total industrial sulfur dioxide emissions	41,856.00	427	6636.93	5260.61
Industrial NOx Emissions (tons)	Total industrial nitrogen oxide emissions	125,050.00	391	12,584.84	12,426.55
Annual Mean PM2.5 Concentration	Annual average fine particulate matter concentration (µg/m3)	62	15	35.5	11.18
Gross Regional Product (100 million yuan, current prices)	Regional GDP at current prices	38,701.00	206	4256.67	5460.69
Highway Freight Traffic (10,000 tons)	Total highway freight volume	51,258.00	602	12,843.24	9860.27
Primary Industry Share (%)	Primary industry share of GRP	48.7	0.09	11.36	8.54
Secondary Industry Share (%)	Secondary industry share of GRP	57.17	11.3	39.15	8.72
Tertiary Industry Share (%)	Tertiary industry share of GRP	83.87	35.02	49.49	7.17

.

The SSE values at different k values are shown in Figure 1a, indicating that k = 3 is the most suitable choice. Figure 1b then presents our clustering results, with the number of cities in each of the three types being 110, 78, and 23, respectively. In the subsequent EVT modeling analysis, at least 30 extreme value observations are required [28], and the data volume for the third type of cities (N = 23) is insufficient. Therefore, they are not included in the remaining research. Notably, this does not mean that research on the third type of cities has no value; it is not considered in this case. More data can be added in future studies for further exploration. Figure 1c presents the statistical description of each variable for the first and second types of cities. An independent sample Student’s t-test was used to confirm the significant differences between these two groups.

The clustering results show that lower industrial emissions and higher waste utilization rates characterize the first group of cities. This suggests that type I cities likely have more environmentally friendly industrial businesses and stricter environmental regulations. As a result, we categorize them as high-tech light industrial cities. In contrast, type II cities host more industrial enterprises, handle higher freight volumes, and have greater income levels. They are considered to have more polluting industries and more lenient ecological policies, leading us to classify them as heavy industrial manufacturing cities.

3.2. Modeling Results

3.2.1. Correlation

The correlation between different variables was first analyzed to determine the factors affecting the building of the extreme value models. The results are shown in

Table 3. The Results of Factor Detector and Pearson Correlation.

Types	Variables	Road Decarbonization Level	Total Number of Industrial Enterprises	Highway Freight Traffic (10,000 Tons)	Total Incomes of Industrial Enterprises (Billion Yuan)	GRP (100 Million Yuan)
I	Road decarbonization level
	Total Number of Industrial Enterprises	−0.09
	Highway Freight Traffic (10,000 tons)	−0.29 **	0.45 **
	Total Incomes of Industrial Enterprises (billion yuan)	−0.32 **	0.68 **	0.53 **
	GRP (100 million yuan)	−0.41 **	0.61 **	0.53 **	0.95 **
II	Road decarbonization level
	Total Number of Industrial Enterprises	0.15
	Highway Freight Traffic (10,000 tons)	0.26 *	0.42 **
	Total Incomes of Industrial Enterprises (billion yuan)	0.21	0.62 **	0.43 **
	GRP (100 million yuan)	0.56 **	0.65 **	0.56 **	0.85 **

**: p < 0.01, *: p < 0.05.

.

The GRP has a significant impact on the decarbonization levels of freight vehicles and exhibits the highest correlation values in both the OPGD model and the correlation analysis. It supported our research on the relationship between cities’ GRP and road decarbonization level.

In high-tech and light industry cities, both analyses show that highway freight traffic and total incomes of industrial enterprises are closely linked to freight vehicle decarbonization levels. However, there is a strong correlation between these two variables. Therefore, we select highway freight traffic as a covariate in the EVT model for heavy industry-manufacturing cities. In heavy industry-manufacturing cities, highway freight traffic has a significant but weak correlation with freight vehicle decarbonization levels. As a result, we do not include covariates in the EVT model for heavy industry-manufacturing cities.

3.2.2. Independence and Distributional Diagnostics

To ensure that the assumptions of extreme value theory are not violated, we performed diagnostic tests on the block maxima (BM) samples. First, we applied the Wald–Wolfowitz runs test to the FVDL series, sorted by lnGDP, within each city type. The null hypothesis is that the sequence is random, i.e., approximately independent. The results (Table S1) show that for both Type I and Type II cities, the null could not be rejected (p > 0.7), suggesting no systematic departure from independence.

Second, we examined whether FVDL values follow the same marginal distribution across city types. Both the Kolmogorov–Smirnov test and the Mann–Whitney U test fail to reject the null of equal distributions (Table S2), indicating no statistically significant differences in the overall distributional form between the two groups.

These findings suggest that the block maxima samples can be treated as approximately independent and identically distributed (i.i.d.) within each city type, thereby meeting the regularity conditions required for EVT-based inference.

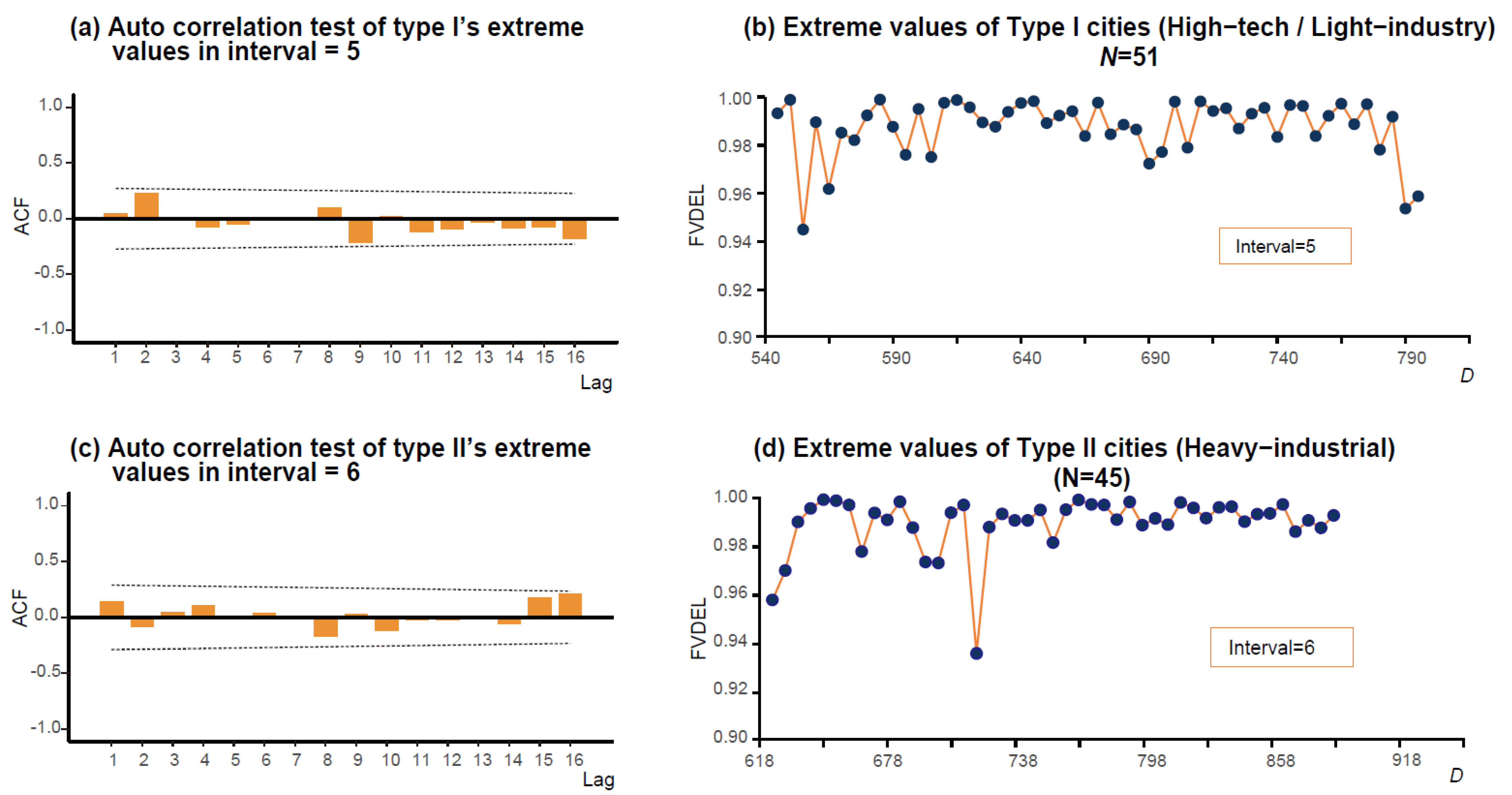
3.2.3. Extreme Value Sampling

Determining the sampling interval is the first step in EVT modeling. A larger interval may lead to lower data utilization, but a smaller interval could cause autocorrelation among extreme data. Therefore, we used a relatively small interval with an autocorrelation function (ACF) autocorrelation test to ensure the independence of extreme data. An ACF value higher than 1 indicates the presence of autocorrelation. Additionally, minimum values were selected for sampling to assess the development potential of low-carbon cities. The results of the extreme value sampling are shown in Figure 2.

Figure 2a shows the ACF test results for High-Tech and Light Industry Cities, indicating no autocorrelation among extreme values when the interval is 5. The sample size (N = 55) also satisfies the extreme value model requirement, which calls for more than 30 extreme values. Figure 2b suggests that the extreme values for High-Tech and Light Industry Cities fluctuate significantly at the ends of the GRP values but are generally stationary sequences. Figure 2c supported the interval selection of Heavy Industry-Manufacturing Cities, and according to Figure 2d, the extreme values of Heavy Industry-Manufacturing Cities are also generally stationary.

3.2.4. GEV Distribution Fitting Using the BM Approach

Three parameters are estimated in the BM approach: (a) the locational parameter μ determines the GEV distribution’s location. (b) The shape parameter ξ mainly reflects the GEV distribution’s tail behavior. (c) The scale parameter σ indicates the distribution’s shape convexity.

The estimation results for High-Tech, Light Industry Cities, and Heavy Industry-Manufacturing Cities are shown in

Table 4. The GEV Estimation Results of High-Tech and Light Industry Cities and Heavy Industry-Manufacturing Cities (Not Considering Covariates).

Classical GEV Model	Types	Estimators and Standard Errors
		$\widehat{\mathit{\mu }}$	$\widehat{\mathit{\sigma }}$	$\widehat{\mathit{\xi }}$
Model 1	I	0.48 (±0.09)	0.53 (±0.09)	0.55 (±0.21)
Model 2	II	0.42 (±0.08)	0.43 (±0.07)	0.49 (±0.17)

.

• Model’s validity: these two models’ validity is verified, as each shape parameter ξ is higher than −0.5, showing that the models’ maximum likelihood estimators are regular in the sense of having the usual asymptotic properties.
• Model’s distribution: It has been shown in Figure 3a that Heavy Industry-Manufacturing Cities has a more concentrated distribution of extreme values, and High-Tech and Light Industry Cities has a higher extreme distribution probability after FVDEL is greater than 1.27%. This implies that under the research data of this article, when the FVDL of a city exceeds 1.27, the changes in the freight decarbonization potential of the two types of cities will differ. This implies that under the research data of this article, when the FVDL of a city exceeds 1.27, the changes in the freight decarbonization potential of the two types of cities will differ. Figure 3a also shows that Heavy-Industrial Manufacturing Cities tend to be more concentrated near the center, while High-Tech/Light Industry Cities have a thicker upper tail. To highlight the difference in the tails,

  Table 5. RDEL Thresholds by Quantile and City Type.

  Quantile	Type I (High-Tech/Light-Industry)	Type II (Heavy-Industrial)
  90%	2.84	2.19
  95%	4.45	3.3
  99%	11.61	7.9

  reports FVDEL thresholds at key quantiles: Type I = 2.84 (90%), 4.45 (95%), 11.61 (99%); Type II = 2.19 (90%), 3.30 (95%), 7.90 (99%). Moving from the 90th to the 99th percentile, the Type I threshold increases by about 4.09 times (from 2.84 to 11.61), while Type II increases by roughly 3.61 times (from 2.19 to 7.90); the gap between them expands from 0.65 at 90% to 3.71 at 99%. This indicates that the extreme decarbonization potential is systematically higher in Type I cities, and the difference becomes more pronounced at higher quantiles—something that mean-based models would overlook.

• Model’s prediction under economic scenarios (boom vs. recession): Figure 3b (regression curves with 95% CIs) shows an upward shift in predicted extreme FVDL with higher $\mathrm{l}\mathrm{n}GDP$ for both city types (boom-like conditions), with a visibly steeper rise for Type I—consistent with its larger scale parameter ${\sigma }_I=0.53$ vs. ${\sigma }_{II}=0.43$. In recession-like ranges of $\mathrm{l}\mathrm{n}GDP$, predicted extremes decline more for Type II, reflecting tighter coupling between industrial output and freight activity. Taken together, the quantile thresholds (Table 5) and the $\mathrm{l}\mathrm{n}GDP$ curves indicate that (i) macro upswings amplify tail potential in both types but more strongly in Type I; and (ii) downturns compress extremes more in Type II, consistent with business-cycle sensitivity.
• Extrapolation accuracy and sources of prediction error: Comparing EVT-based predictions with observed outcomes, systematic deviations align with contextual conditions. Heavy-industrial cities with coal-intensive power mixes, slower charging-infrastructure roll-out, or fragmented logistics governance tend to underperform the EVT benchmark in booms (negative prediction errors). By contrast, high-tech/light industry cities with stronger institutional capacity (e.g., plate-auction/lottery priority for zero-emission trucks) and active “vehicle–battery separation” pilots often meet or exceed predictions (positive errors). These differences indicate that integrating energy mix, policy enforcement, and infrastructure readiness as conditioning variables in future extensions would further align EVT-based thresholds with realized city outcomes.

3.2.5. BM Models Using the Highway Freight Traffic as a Covariate

The model estimation results of High-Tech and Light Industry Cities with a covariate (the highway freight traffic) are shown in

Table 6. The GEV Estimation Results of High-Tech and Light Industry Cities (Considering Covariates).

Covariate Model	Estimators and Standard Errors
	$\widehat{\mathit{\mu }}$		$\widehat{\mathit{\sigma }}$		$\widehat{\mathit{\xi }}$
	α0	α1	β0	β1
Model 3: μ(T) = α0 + α1T	0.29 (±0.08)	0.2 (±0.02)	0.47 (±0.08)		0.60 (±0.20)
Model 4: σ(T) = β0 + β1T	0.47 (±0.09)		0.51 (±0.09)	0.02 (±0.01)	0.52 (±0.20)

. In Model 3, the highway freight traffic was added to estimate the locational parameter. In Model 4, the highway freight traffic was added to estimate the position parameters. The shape parameter is often not used to construct the covariate model because of its more significant impact on the BM model.

• Model’s validity: Models 3 and 4 are proven valid as their shape parameters ξ are higher than −0.5.
• Covariates’ influence: The highway freight traffic positively influences models’ locational and scale parameters, as its coefficients are positive in models 3 and 4 (α₁ = 0.2, β₁ = 0.02). A larger locational parameter will push the probability density curve to the right. Thus, the distribution probability of cities with a higher low-carbon degree is greater. A larger scale parameter will result in a flatter density curve, increasing the distribution of higher low-carbon cities. Hence, highway freight traffic positively influences the distribution of low-carbon goods in cities.

3.3. Predictive Accuracy and Comparative Analyses

Three common indicators, the root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE) are used to measure predictive accuracy, with a lower value indicating higher prediction accuracy. Moreover, the Akaike Information Criterion (AIC) and deviance statistic are used to decide the final covariate-adding BM model. The model with the lower AIC is better. And the deviance statistic is defined for non-stationary extremum model selection, which can be shown as:

$$D{S}_{a-b}=2\left\{l_a(M_a)-l_b(M_b)\right\}$$

(9)

where l_a(M_a) and l_b(M_b) are the maximized log-likelihoods of model a and model b. Larger DS suggests model a is preferred to model b, as model a explains substantially more of the variation in the data. The results are shown in

Table 7. Predictive Accuracy and Comparative Analyses.

Estimated Interval	High-Tech and Light Industry Cities				Heavy Industry-Manufacturing Cities
	Extreme D’s Upper Limit	$\left|\mathit{F}-\widehat{\mathit{F}}\right|$			Extreme D’s Upper Limit	$\left|\mathit{F}-\widehat{\mathit{F}}\right|$
		Model 1	Model 3	Model 4		Model 2
10	5.95	2.62	2.72	2.72	6.84	0.78
15	6.2	1.77	1.9	1.96	7.14	0.44
20	6.45	1.04	1.14	1.3	7.44	3.57
25	6.7	0.39	0.43	0.7	7.74	3.06
30	6.95	0.21	0.28	0.11	8.04	2.62
35	7.2	0.75	0.79	0.31	8.34	2.22
40	7.45	1.26	1.62	1.06	8.64	1.86
45	7.7	1.74	2.29	1.48	8.94	1.20
RMSE		1.43	1.62	1.45		2.23
MAPE		23%	26%	22%		35%
MAE		1.22	1.40	1.21		1.97
AIC		132.09	134.06	126.13		96.32
Maximized log-likelihood value		63.05	59.06	63.03		45.16
DS		DS13 = 3.99	DS34 = 3.97	DS41 = −0.02		DS12 = 17.89

. It shows that:

• Predictive accuracy: For the classical BM model, High-Tech and Light Industry Cities (Model 1) shows higher predictive accuracy than Heavy Industry-Manufacturing Cities (Model 3), with lower values in RMSE, MAPE, and MAE. The deviance statistic of Type II also indicates its weaker explanatory power regarding data variation. For covariate-adding BM models, Model 4 suggests the best accuracy but only has a slight difference from the classical BM model (Model 1).
• Comparative analyses: Model 4 is the most suitable choice in High-Tech and Light Industry Cities, as it has the lowest AIC value (126.13) and its DS value is very close to the highest (DS₁₃ = 3.99, DS₃₄ = 3.97).

Based on the EVT results, we identify a quantitative reference indicator that serves as the critical threshold for road freight decarbonization. Specifically, High-Tech and Light Industry Cities have a 1.27% higher possibility of experiencing FVDEL, and this can be used as a benchmark to distinguish cities with greater potential for decarbonization. Cities operating above this threshold are more likely to achieve zero-emission road freight amid economic growth scenarios, whereas those below the threshold need targeted interventions to address structural or economic barriers. This reference indicator thus creates a clear and practical connection between the modeling results and subsequent tailored policy recommendations.

4. Discussion

The findings of this study offer new insights into how cities can advance toward zero-emission road freight under varying economic and industrial conditions. One of the most notable results is that High-Tech and Light Industry Cities show significantly higher levels of road decarbonization, with a critical threshold around 1.27%. This figure serves as a reference point that distinguishes cities with enough structural readiness from those still facing major barriers. Similar thresholds have been found in studies of zero-emission truck competitiveness, which indicate that once energy costs and infrastructure reach certain levels, adoption speeds up rapidly [15,35]. In fact, research on economic–environmental decoupling suggests that service-oriented cities with stronger innovation capabilities are much more likely to achieve reductions while maintaining growth [36]. Conversely, cities dominated by labor-intensive manufacturing often encounter efficiency constraints that limit their ability to cross such thresholds [32]. Our interpretation is that high-tech/light industry cities, with their advanced economic structures and stronger institutional capacity, provide fertile ground for the application of new technologies. Their lower industrial inertia allows them to respond more flexibly to incentive measures, which gives them higher extreme decarbonization potential and makes them more sensitive to covariates such as freight volume. For policymakers, given their high potential and responsiveness, the focus should be on accelerating the transition. Strengthening operational-phase incentives, combined with China’s unique license-plate auction/lottery system, could grant zero-emission trucks priority registration rights. We further recommend promoting the “vehicle–battery separation” business model, which is currently a policy priority in China’s commercial-vehicle sector and can effectively ease both high purchase costs and range-anxiety concerns.

Equally noteworthy is the performance of heavy-industrial manufacturing cities. They display higher predictive accuracy during both economic downturns and booms, reflecting the tight coupling between industrial output and freight demand. Prior studies have shown that emissions in energy-intensive regions respond sharply to economic cycles, frequently shifting between weak decoupling and re-coupling [9,33]. Our findings support this pattern: freight emissions increase with economic growth and fall in a predictable manner during recessions. However, this contrasts with machine-learning studies, which often achieve high accuracy under average conditions but perform less well in simulating extreme cases [37]. The difference may stem from EVT’s explicit focus on tail behavior, under which heavy-industrial manufacturing cities exhibit more consistent patterns. For policymakers, given these cities’ cyclical vulnerability and structural coupling, policies must aim to stabilize and reduce transition risks. Counter-cyclical fleet-renewal programs—such as phasing out outdated capacity and consolidating logistics resources—can reduce freight-demand intensity at its source. Leveraging China’s strong digital infrastructure, unified city-level freight-dispatch platforms can be established to optimize routing, raise vehicle utilization, and thus lower emissions per unit of freight moved.

Policy measures also need to be differentiated by city type. For high-tech/light industry cities, two approaches are particularly important: reducing the operating costs of zero-emission freight and promoting large-scale technology adoption. During the pilot phase, a “city freight database” should be launched and interdepartmental working groups established. In the full roll-out phase, auditing procedures should be formalized and a “corporate credit-linking mechanism” created. In the evaluation and optimization phase, third-party evaluators should be engaged, with policy implementation data disclosed to the public for social oversight. For heavy-industrial manufacturing cities, boom periods call for “freight quota management” and mandatory “off-peak delivery orders,” while recessions should trigger “diesel truck retirement subsidies” and the launch of “freight-infrastructure upgrading programs.” In the pilot phase, an “economic–freight linkage monitoring model” should be established with defined trigger thresholds. In the full roll-out phase, cross-departmental data interfaces should be integrated. In the evaluation and optimization phase, policies should clarify the scope of tax use and the mechanisms for transparent allocation.

Another contribution of this study is in turning EVT outputs into practical policy tools. Extreme value theory has long been used for natural hazards and environmental risks [28,31], but its use in transport decarbonization is still uncommon. Another contribution of this study is in translating EVT outputs into practical policy tools. Extreme value theory has long been applied to natural hazards and environmental risks [26,28], but its application to transport decarbonization remains uncommon. Traditional machine-learning methods and linear regressions mainly focus on central tendencies, aiming to explain or predict average levels of decarbonization under historical conditions, and their predictive scope is constrained by the distribution of observed data. In contrast, EVT focuses on tail behavior. Its key advantage lies in quantifying rare but policy-relevant extreme events without requiring strong assumptions about the underlying data distribution. By applying EVT, we are able to estimate cities’ extreme levels of freight-vehicle decarbonization, thereby uncovering the maximum attainable levels rather than simply modeling mean outcomes, as conventional approaches do.

By viewing EVT return levels as critical thresholds, this study shows how statistical forecasts can directly guide urban policy.

Additionally, the study shows that the marginal impact of purchase subsidies decreases compared to operating-phase incentives. Recent empirical research supports this idea, indicating that electricity price discounts, road access privileges, and other continuous incentives are more effective than one-time subsidies in encouraging adoption [12,19]. However, some analyses argue that large purchase subsidies can provide a short-term boost to market entry [9]. This apparent contradiction arises because subsidies may help lower initial barriers but do little to alter the long-term economics of fleet operation.

Our analysis indicates that operational costs—such as energy prices, vehicle utilization, and charging convenience—primarily shape freight companies’ decisions. Consequently, operating incentives (e.g., road pricing/access policies, as well as use-phase cost relief) function as a more durable lever than one-off purchase subsidies. This mechanism is consistent with the descriptive patterns observed in the extreme-value results. Once a city’s FVDL surpasses the EVT-based reference zone, tail outcomes become more sensitive to use-phase frictions than to upfront price adjustments.

Finally, the robustness of our EVT modeling enhances the credibility of these findings. Independence tests verified the suitability of our extreme value samples, and the stability of the shape parameter provided additional confidence [28]. Including highway freight traffic as a covariate improved model performance based on AIC and deviance statistics, demonstrating that EVT can be adapted to incorporate relevant urban features. Compared to machine learning models that excel at predicting average outcomes, EVT offers a unique advantage in capturing rare but policy-relevant tail behaviors. For policymakers, this suggests that both approaches should be used in conjunction: machine learning to monitor routine patterns and EVT to stress-test resilience during shocks.

While our EVT-based analysis provides useful insights into the statistical properties of extreme decarbonization levels, we acknowledge that certain contextual determinants—such as the energy mix, regional policy frameworks, and infrastructure readiness—are not explicitly incorporated in the present model. These factors can strongly influence the feasibility and pace of freight decarbonization across cities. For example, cities with a coal-intensive power mix may experience smaller effective emission reductions from electric trucks than those with a greener energy portfolio. Similarly, differences in local subsidies, regulatory enforcement, and charging or logistics infrastructure can shape the realized outcomes of policy interventions.

To mitigate oversimplification, our clustering approach partially captures heterogeneity in industrial structure and freight intensity, which are correlated with energy demand and policy capacity. Nevertheless, future work should explicitly integrate variables on electricity carbon intensity, regional policy regimes, and infrastructure indices into the modeling framework. This extension would allow the EVT-based benchmark to be interpreted not only as a statistical threshold but also as one conditioned on critical contextual enablers of decarbonization.

Of course, this study is not without limitations. The cross-sectional nature of the data restricts our ability to test the stability of the 1.27% threshold over time, and panel data would be valuable to verify whether such thresholds persist or shift across cycles. Additional variables such as energy prices, trade exposure, or road-use policies could also provide further insight, especially in explaining Heavy Industry-Manufacturing Cities’ sensitivity to extremes. Moreover, while our analysis points to potential spatial spillovers through industrial and logistics networks, further work using spatial econometric models is needed to capture these dynamics more directly. Addressing these gaps could deepen our understanding of how critical thresholds function across city types, regions, and over time, providing stronger foundations for sustainable freight policies.

5. Conclusions

This study aimed to examine how FVDEL varies across different city types under economic fluctuation conditions to identify a quantitative reference indicator that can help shape targeted policies. Using EVT modeling, we found that High-Tech and Light Industry Cities have significantly higher decarbonization potential, with a critical threshold around 1.27%. In contrast, Heavy Industry-Manufacturing Cities are more predictable during boom and recession scenarios, reflecting their strong link between industrial activity and freight emissions. Together, these findings reveal the heterogeneity of urban decarbonization capacities and highlight the importance of employing extreme value approaches to identify policy-relevant thresholds.

The significance of this research lies in transforming complex modeling outputs into a practical benchmark for policy. By establishing 1.27% as a reference point, the study offers a clear and actionable method for identifying cities with stronger capabilities versus those needing targeted support. Innovations include applying EVT to urban freight decarbonization, explicitly focusing on extreme conditions rather than average trends; demonstrating how EVT-derived thresholds can link statistical modeling to real-world decision-making; and showing that the impact of purchase subsidies decreases, while incentives during the operational phase become more important in encouraging adoption. These contributions expand both the methodological toolkit and the policy discussion around achieving zero-emission road freight.

Nevertheless, this study has limitations. Because the analysis relies on cross-sectional data, the key threshold derived here is a fixed value over time. In reality, however, such a threshold may vary across cities and fluctuate with other contextual factors. Future research should therefore use panel data to track changes in the threshold over different years, allowing the development of a more broadly applicable and policy-relevant reference indicator.

Additionally, the benchmark could undergo out-of-sample validation, longitudinal testing, or case-based examination to strengthen empirical support. Finally, adding panel data to the dataset would also enable further exploration of the third city type, making the analysis more comprehensive and thorough. The spatial spillovers of freight and industrial networks remain an open question, requiring the use of more advanced spatial econometric methods.

Addressing these issues will not only improve the accuracy of threshold estimates but also enhance our understanding of how critical benchmarks function across different temporal and spatial contexts, thereby strengthening their role in guiding sustainable freight transitions.