Adaptive Thermal Comfort in the Different Buildings of Temperate Climates—Comparison Between High-Latitude Europe and Mountainous Himalayas in India
Abstract
1. Introduction
2. Review of the Literature
3. Research Gaps and Objectives of the Study
- To compare and analyze the adaptive thermal comfort responses of occupants in NV buildings across two distinct temperate oceanic climatic regions, separated by high latitudes (European) and high altitudes (Himalayan), identifying key differences and similarities to inform sustainable and energy-efficient building designs.
- To evaluate the thermal comfort ranges and adaptive behaviors of building occupants in European and Indian temperate climates;
- To assess the impact of environmental variables, such as air temperature and relative humidity on indoor thermal comfort in different building types;
- To identify limitations in existing datasets and propose recommendations for future research to improve the reliability of thermal comfort models under varying climatic conditions and the applicability of the adaptive thermal comfort model in the different locations.
4. Methodology
4.1. Analyzed Datasets
4.2. Assumptions and Calculated Comfort Indicators
4.3. Statistical Analysis
5. Results
5.1. Outdoor Environmental Conditions
5.2. Indoor Environmental Condition
5.3. Clothing Insulation, Icl
- (i).
- Complex Adaptive Behavior: Adaptive thermal comfort involves multiple factors, including physiological, behavioral and psychological adaptation. Clothing adjustment is just one of these mechanisms, and its influence may vary depending on cultural norms, building design or on occupants’ preference.
- (ii).
- Uniform clothing norms: Dress code in specific environments, like classrooms or offices, limit the variability of clothing insulation, thereby reducing the correlation with temperature.
- (iii).
- Insulation and Energy Efficiency: Compared to the buildings in India, those in Europe could have better insulation and heating systems, which minimize the temperature fluctuation of the indoor environment. This reduces the necessity for frequent clothing adjustments, and thereby weakening the correlation.
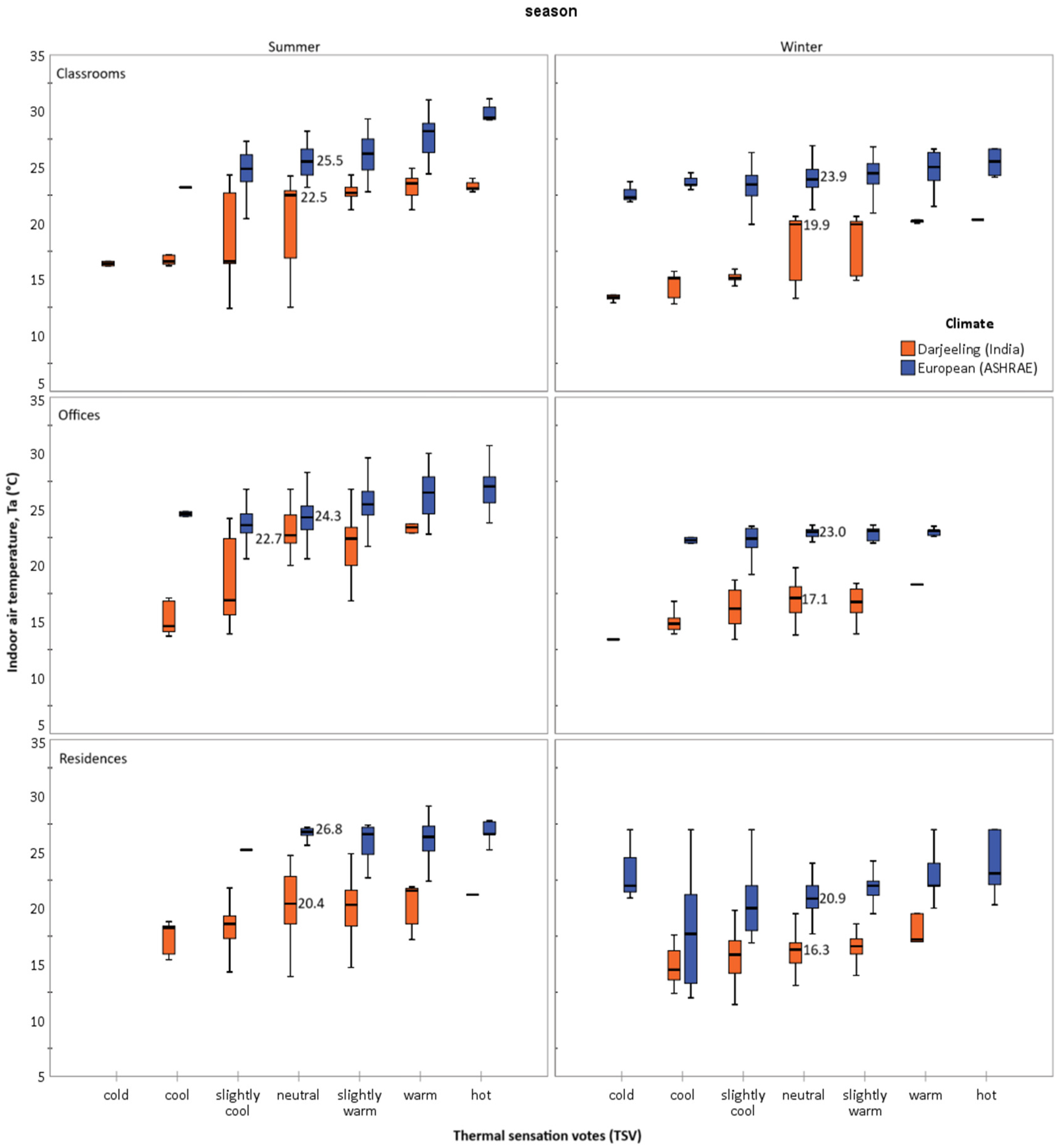
5.4. Thermal Sensation Votes (TSVs)
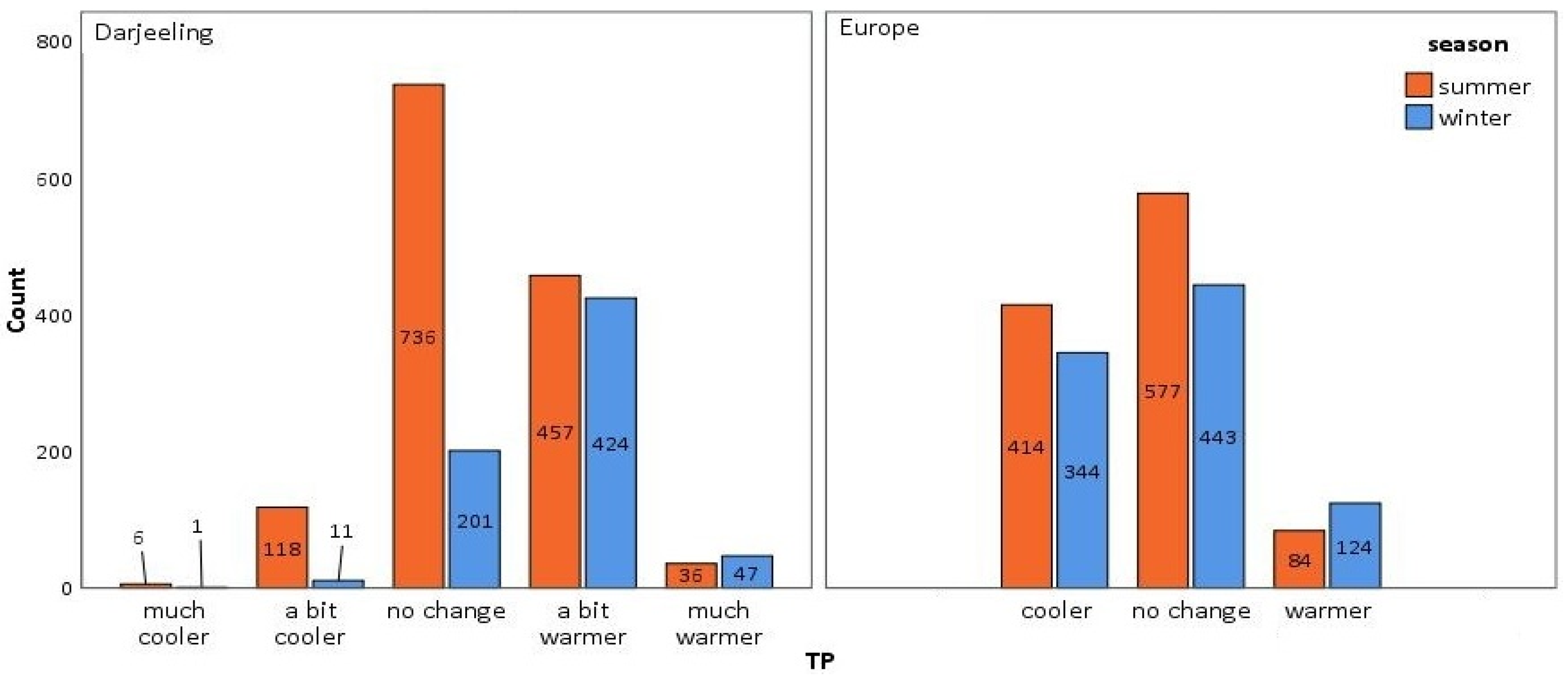
5.5. Thermal Preference (TPV)
5.6. Standard Effective Temperature (SET)
5.7. Predicted Mean Vote–Predicted Percentage of Dissatisfaction (PMV–PPD)
5.8. Thermal Sensation Votes (TSVs) Versus Predicted Mean Vote (PMV)
5.9. Indoor Comfort Assessment
5.10. The Thermal Neutrality (Comfort)
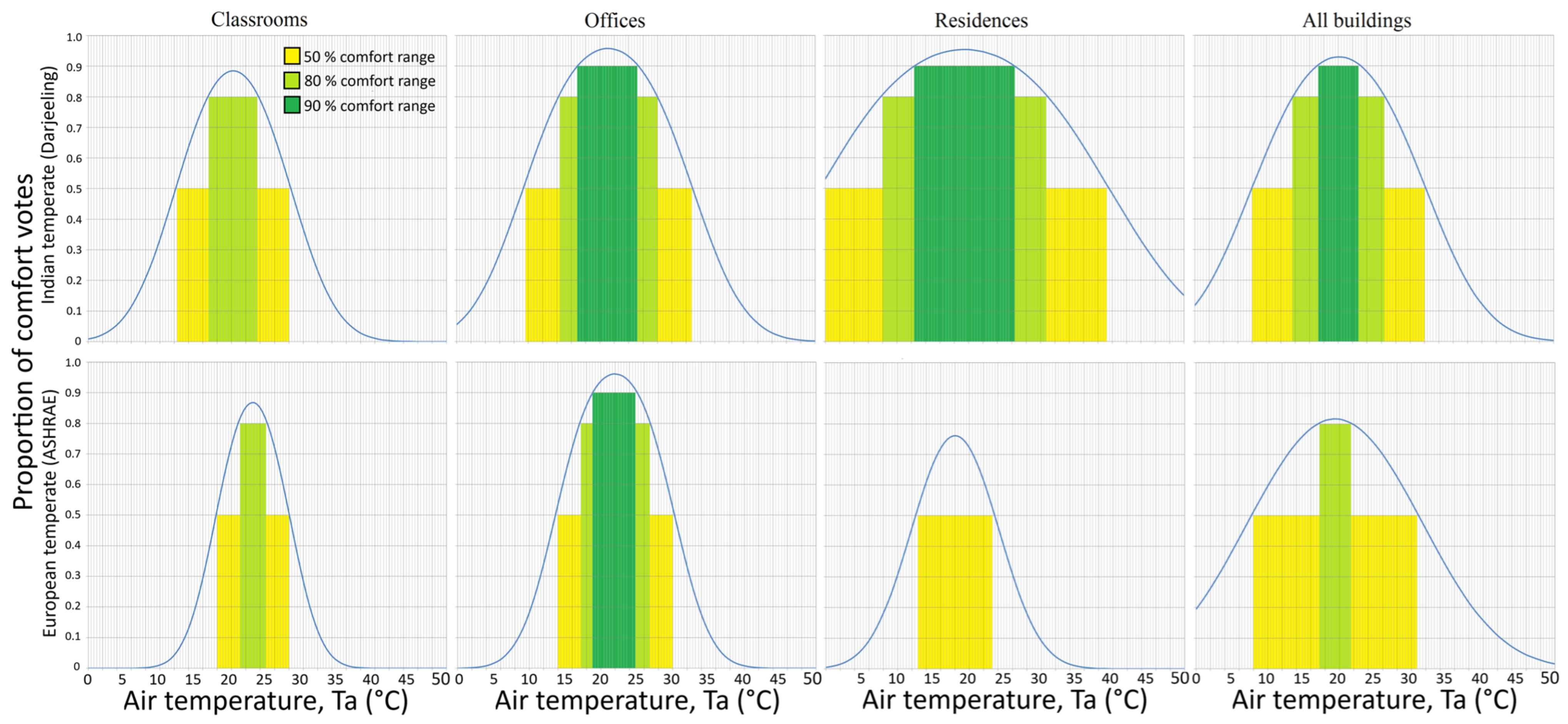
5.11. The Comfort Range
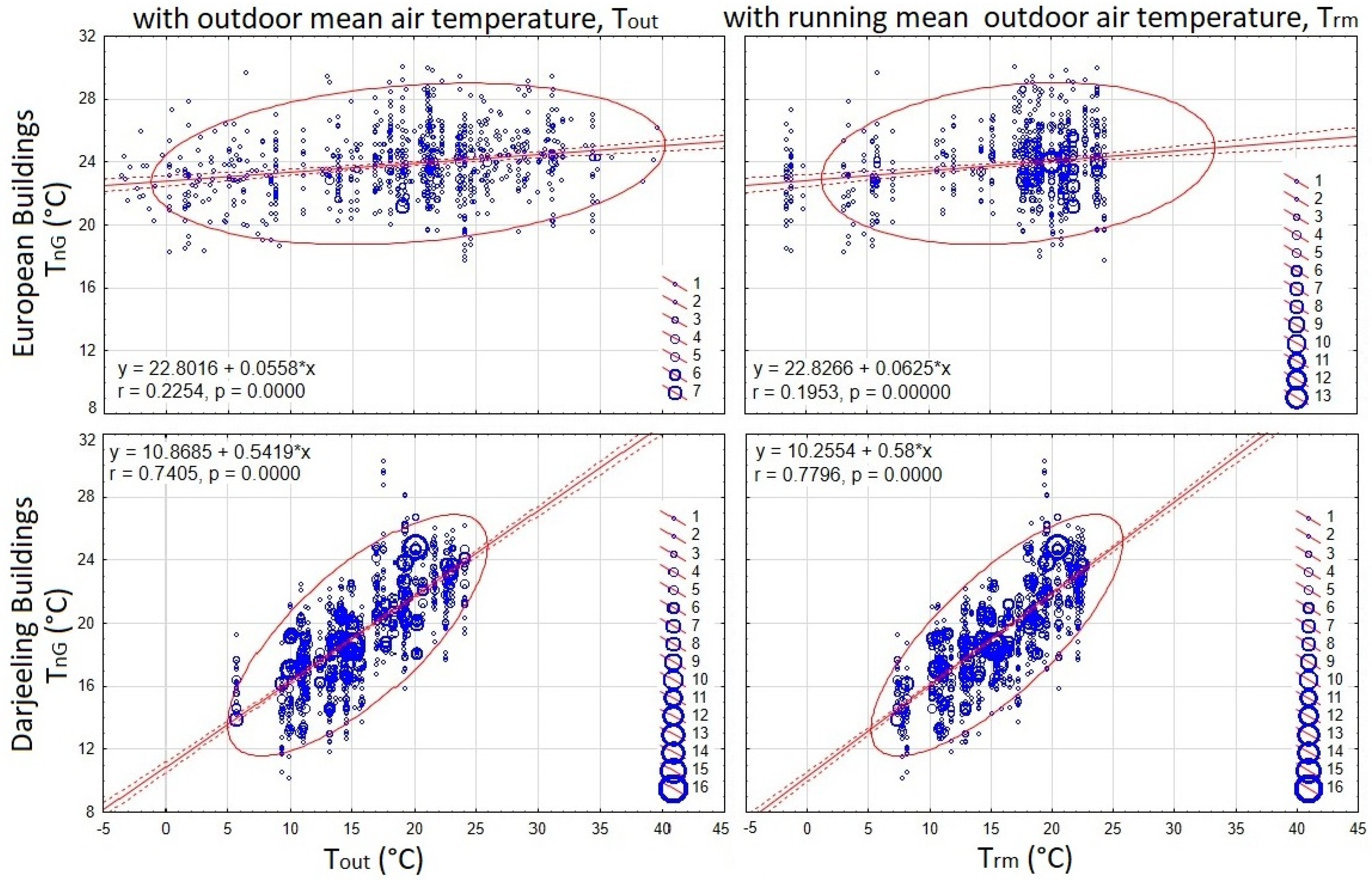
5.12. Variation in Comfort Temperature with Outdoor Condition
6. Discussion
7. Conclusions
- The comfort temperature ranges varied significantly between the two regions. European buildings exhibited narrower comfort ranges due to likely inclusion of superior insulation and energy-efficient designs, while Darjeeling buildings showed broader comfort ranges, reflecting higher occupant adaptability to fluctuating indoor conditions, e.g., the 80% comfort range for classrooms in Europe was narrower (21.2~24.8 °C) than that in Darjeeling (16.0~21.6 °C), indicating greater reliance on adaptive strategies in the latter.
- Further, European buildings maintained more stable indoor conditions, which reduces reliance on adaptive behaviors like clothing adjustment, while Darjeeling buildings were more influenced by outdoor variations. These differences could be explained by a generally higher insulation level and by more energy-efficient designs of European buildings.
- Cultural and environmental factors influence adaptive behaviors. For instance, clothing insulation (Icl) was a more prominent adaptive measure in Darjeeling buildings, while strict dress codes in educational institutions limited this adaptation in classrooms.
- Comfort temperature showed significant variations between climates and seasons. The comfort range derived from probit lines showed wider ranges and lower comfort temperatures for Darjeeling buildings compared to that in European buildings.
- The adaptive model of thermal comfort revealed a stronger positive correlation between comfort temperature and the outdoor conditions. Darjeeling buildings exhibited a stronger coupling of indoor and outdoor environmental conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bureau of Energy Efficiency. Energy Conservation Building Code; Bureau of Energy Efficiency, Government of India: New Delhi, India, 2007.
- ASHRAE. ANSI/ASHRAE Standard 55—Thermal Environmental Conditions for Human Occupancy. 2023. Available online: https://www.ashrae.org/technical-resources/bookstore/standard-55-thermal-environmental-conditions-for-human-occupancy (accessed on 28 October 2024).
- Thapa, S. Revisiting thermal comfort in the cold climate of Darjeeling, India—Effect of assumptions in comfort scales. Build. Environ. 2021, 203, 108095. [Google Scholar] [CrossRef]
- Fanger, P.O. Thermal Comfort, Analysis and Applications in Environmental Engineering; McGraw Hill: New York, NY, USA, 1972. [Google Scholar]
- ISO 7730:2005; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. International Organization for Standardization: Geneva, Switzerland, 2005.
- Nicol, J.F.; Humphreys, M.A. Adaptive thermal comfort and sustainable standards for buildings. Energy Build. 2002, 34, 563–572. [Google Scholar] [CrossRef]
- McCartney, K.J.; Nicol, J.F. Developing an adaptive control algorithm for Europe: Results of the SCATs project. Energy Build. 2002, 34, 623–635. [Google Scholar] [CrossRef]
- Nicol, J.F. Adaptive thermal comfort standards in the hot-humid tropics. Energy Build. 2004, 36, 620–637. [Google Scholar] [CrossRef]
- de Dear, R.J.; Brager, G.S. Thermal comfort in naturally ventilated buildings: Revisions to ASHRAE 55. Energy Build. 2002, 34, 549–561. [Google Scholar] [CrossRef]
- Shen, C.; Yu, N. Study of thermal comfort in free-running buildings based on Adaptive Predicted Mean Vote. In Proceedings of the 2010 International Conference on E-Product E-Service and E-Entertainment, Henan, China, 7–9 November 2010. [Google Scholar]
- Ning, H.; Wang, Z.; Zhang, X.; Ji, Y. Adaptive thermal comfort in university dormitories in the severe cold area of China. Build. Environ. 2016, 99, 161–169. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ramgopal, M. An adaptive thermal comfort model for the tropical climatic regions of India (Koppen climate type A). Build. Environ. 2015, 85, 134–143. [Google Scholar] [CrossRef]
- Veronika, F.; Cheung, T.; Zhang, H.; de Dear, R.; Parkinson, T.; Arens, E.; Chun, C.; Schiavon, S.; Luo, M.; Brager, G.; et al. Development of the ASHRAE Global Thermal Comfort Database II. Build. Environ. 2018, 142, 502–512. [Google Scholar]
- Yang, Z.; Zhang, W.; Qin, M.; Liu, H. Comparative study of indoor thermal environment and human thermal comfort in residential buildings among cities. towns and rural areas in arid regions of China. Energy Build. 2022, 273, 112373. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; He, Y.; Luo, M.; Li, Z.; Hong, T.; Lin, B. Revisiting individual and group differences in thermal comfort based on ASHRAE database. Energy Build. 2020, 219, 110017. [Google Scholar] [CrossRef]
- Lai, D.; Liu, J.; Wu, Z.; Pei, J.; Qi, Y.; Zhang, H.; Yoshino, H. Thermal comfort diversity in Chinese urban residential buildings across various climates. Energy Build. 2021, 231, 110632. [Google Scholar] [CrossRef]
- Romero, P.; Valero-Amaro, V.; Isidoro, R.; Miranda, M.T. Analysis of determining factors in the thermal comfort of university students. A comparative study between Spain and Portugal. Energy Build. 2024, 308, 114022. [Google Scholar] [CrossRef]
- Cao, B.; Luo, M.; Li, M.; Zhu, Y. Too cold or too warm? A winter thermal comfort study in different climate zones in China. Energy Build. 2016, 133, 469–477. [Google Scholar] [CrossRef]
- Chen, L.; Kantor, N.; Nikolopoulou, M. Meta-analysis of outdoor thermal comfort surveys in different European cities using the RUROS database: The role of background climate and gender. Energy Build. 2022, 256, 111757. [Google Scholar] [CrossRef]
- Zhang, N.; Cao, B.; Wang, Z.; Zhu, Y.; Lin, B. A comparison of winter indoor thermal environment and thermal comfort between regions in Europe, North America and Asia. Build. Environ. 2017, 117, 208–217. [Google Scholar] [CrossRef]
- Jeong, B.; Kim, J.; Chen, D.; de Dear, R. Comparison of residential thermal comfort in two different climates in Australia. Build. Environ. 2022, 211, 108706. [Google Scholar] [CrossRef]
- Yang, L.; Wang, F.; Zhao, S.; Gao, S.; Yan, H.; Sun, Z.; Lian, Z.; Duanmu, L.; Zhang, Y.; Zhou, X.; et al. Comparative analysis of indoor thermal environment characteristics and occupants’ adaptability: Insights from ASHRAE RP-884 and the Chinese thermal comfort database. Energy Build. 2024, 309, 114033. [Google Scholar] [CrossRef]
- Pistore, L.; Varin, C.; Pasut, W. Development of climate-based thermal comfort ranges from existing data: Analysis of Smart Controls and thermal comfort (SCATs) database. Energy Build. 2023, 298, 113509. [Google Scholar] [CrossRef]
- Williamson, T.; Daniel, L. A new adaptive thermal comfort model for homes in temperate climates of Australia. Energy Build. 2020, 210, 109728. [Google Scholar] [CrossRef]
- Jebaei, H.A.; Aryal, A. Quantifying the impact of personal comfort systems on thermal satisfaction and energy consumption in office buildings under different U.S. climates. Energy Build. 2022, 274, 112448. [Google Scholar] [CrossRef]
- Thapa, S.; Indraganti, M. Evaluation of thermal comfort in two neighboring climatic zones in Eastern India—An adaptive approach. Energy Build. 2020, 213, 109767. [Google Scholar] [CrossRef]
- Singh, M.K.; Ooka, R.; Rijal, H.B.; Kumar, S.; de Dear, R. Adaptive thermal comfort in the offices of three climates of North-East India. J. Build. Eng. 2023, 75, 106843. [Google Scholar] [CrossRef]
- Kumar, S. Subject’s thermal adaptation in different built environments: An analysis of updated metadata-base of thermal comfort data in India. J. Build. Eng. 2022, 46, 103844. [Google Scholar] [CrossRef]
- Kaushal, A.A.; Anand, P.; Aithal, B.H.; Sen, J. Thermal comfort in Indian naturally ventilated buildings: A comprehensive review. Energy Build. 2024, 306, 113923. [Google Scholar] [CrossRef]
- Sharma, A.; Kumar, A.; Kulkarni, K.S. Thermal comfort studies for the naturally ventilated built environments in Indian subcontinent: A review. J. Build. Eng. 2021, 44, 103242. [Google Scholar] [CrossRef]
- Halawa, E.; van Hoof, J. The adaptive approach to thermal comfort: A critical overview. Energy Build. 2012, 51, 101–110. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Koppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. Available online: www.hydrol-earth-syst-sci.net/11/1633/2007/ (accessed on 28 October 2024). [CrossRef]
- Ahmed, K.; Carlier, M.; Feldmann, C.; Kurnitski, J. A new method for Contrasting Energy Performance and Near-Zero Energy Building Requirements in Different Climates and Countries. Energies 2018, 11, 1344. [Google Scholar] [CrossRef]
- Bureau of Indian Standard (BIS). National Building Code of India; Bureau of Indian Standard: New Delhi, India, 2017.
- Thapa, S.; Bansal, A.K.; Panda, G.K.; Indraganti, M. Adaptive thermal comfort in the different buildings of Darjeeling Hills in eastern India—Effect of difference in elevation. Energy Build. 2018, 173, 649–677. [Google Scholar] [CrossRef]
- Thapa, S. Thermal Comfort Dataset—Darjeeling, 2015, Version 2; Mendeley Data. 2018. Available online: https://data.mendeley.com/datasets/55rddfmfsz/2 (accessed on 28 October 2024).
- Humphreys, M. A simple theoretical derivation of thermal comfort conditions. J. Inst. Heat. Vent. Eng. 1970, 33, 95–98. [Google Scholar]
- Humphreys, M.A.; Nicol, J.F. The validity of ISO-PMV for predicting comfort votes in every day thermal environment. Energy Build. 2002, 34, 667–684. [Google Scholar] [CrossRef]
- Gagge, A.P.; Nishi, Y.; Gonzalez, R.R. Standard Effective Temperature—A single temperature index of temperature sensation and thermal discomfort. In Thermal Comfort and Moderate Heat Stress: Proceedings of the CIB Commission W45 (Human Requirements) Symposium Held at the Building Research Station 13–15 September 1972; Her Majesty’s Stationery Office: London, UK, 1973; pp. 229–250. [Google Scholar]
- Gagge, A.P.; Fobelets, A.P.; Berglund, L.G. A Standard Predictive Index of Human Response to the Thermal Environment. ASHRAE Trans. 1986, 92, 709–731. [Google Scholar]
- Ji, W.; Zhu, Y.; Du, H.; Cao, B.; Lian, Z.; Geng, Y.; Liu, S.; Xiong, J.; Yang, C. Interpretation of standard effective temperature (SET) and explorations on its modification and development. Build. Environ. 2022, 210, 108714. [Google Scholar] [CrossRef]
- Tartarini, F.; Schiavon, S.; Cheung, T.; Hoyt, T. CBE Thermal Comfort Tool: Online tool for thermal comfort calculations and visualizations. SoftwareX 2020, 12, 100563. Available online: https://www.sciencedirect.com/science/article/pii/S2352711020302454?via%3Dihub (accessed on 28 October 2024). [CrossRef]
- Rijal, H.B.; Humphreys, M.A.; Nicol, J.F. Towards an adaptive model for thermal comfort in Japanese offices. Build. Res. Inf. 2017, 45, 717–729. [Google Scholar] [CrossRef]
- Finney, D.J. Probit Analysis: A Statistical Treatment of the Sigmoid Response Curve; Cambridge University Press: Cambridge, UK, 1971; pp. 1–331. [Google Scholar]
- Nicol, J.F.; Humphreys, M.A. A stochastic approach to thermal comfort—Occupant Behavior and energy use in buildings. ASHRAE Trans. 2004, 110, 554–568. [Google Scholar]
- Thapa, S.; Bansal, A.K.; Panda, G.K. Adaptive thermal comfort in the residential buildings of north east India—An effect of difference in elevation. Build. Simul. 2018, 11, 245–267. [Google Scholar] [CrossRef]
- Singh, M.K.; Ooka, R.; Rijal, H.B.; Takasu, M. Adaptive thermal comfort in the offices of North-East India in autumn season. Build. Environ. 2017, 124, 14–30. [Google Scholar] [CrossRef]
- Humphreys, M.A.; Nicol, J.F.; Roaf, S. Adaptive Thermal Comfort: Foundations and Analysis, 1st ed.; Routledge: London, UK, 2015; Volume 2, pp. 259–269. [Google Scholar]
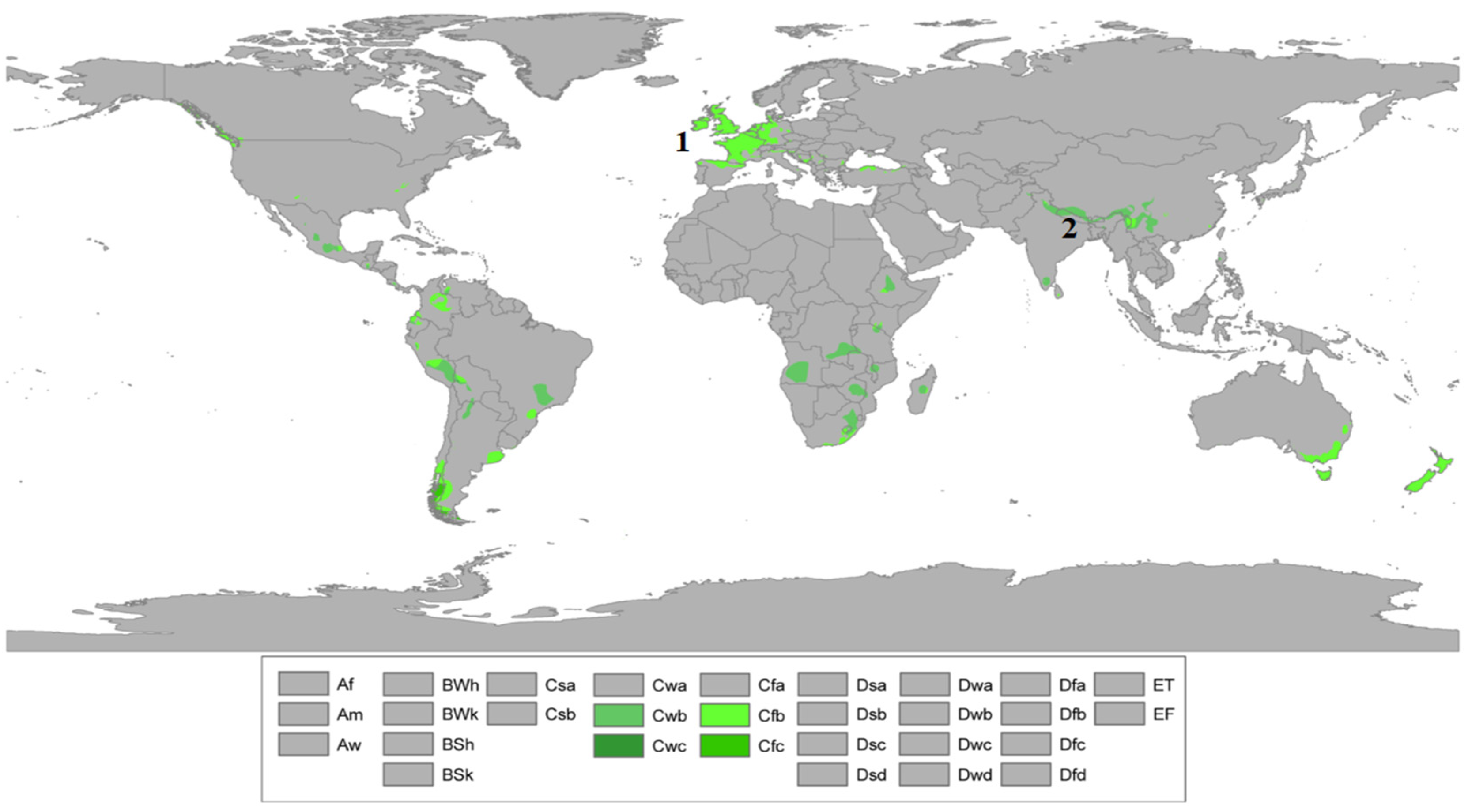
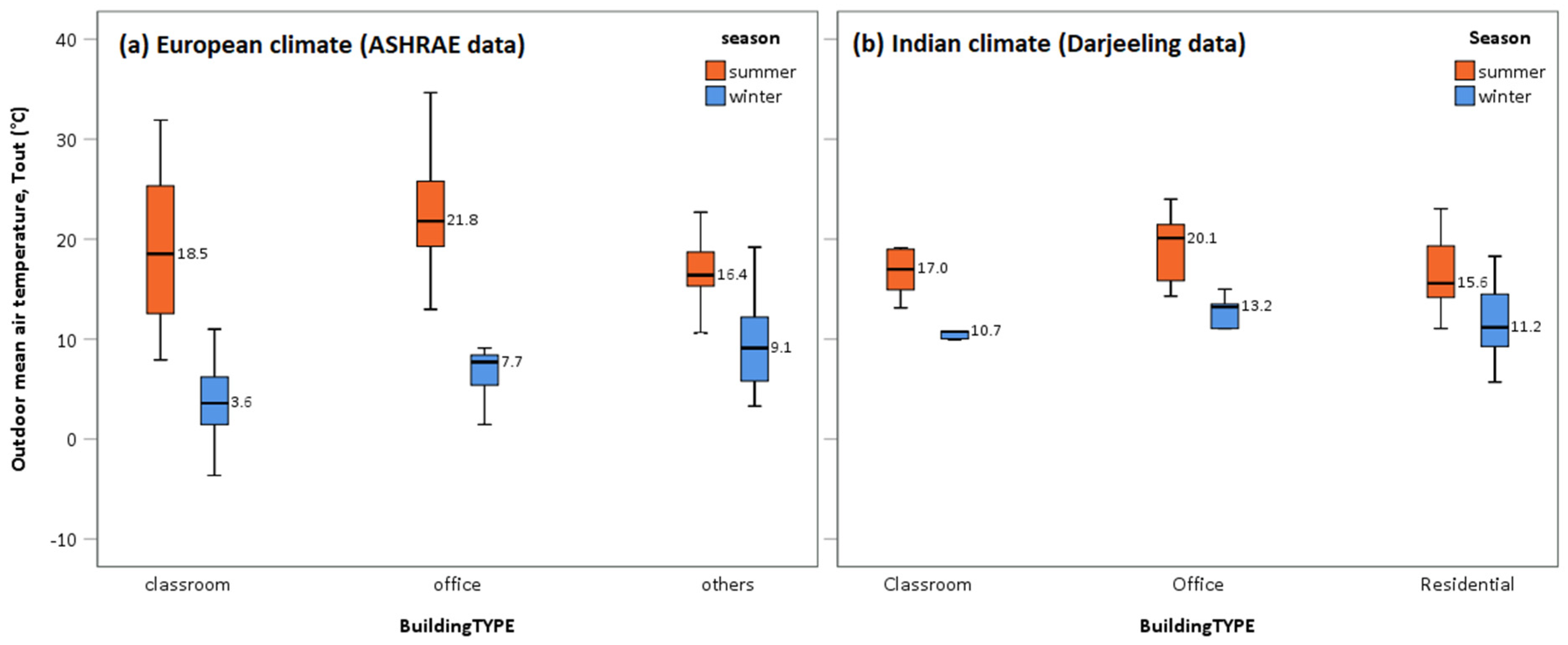

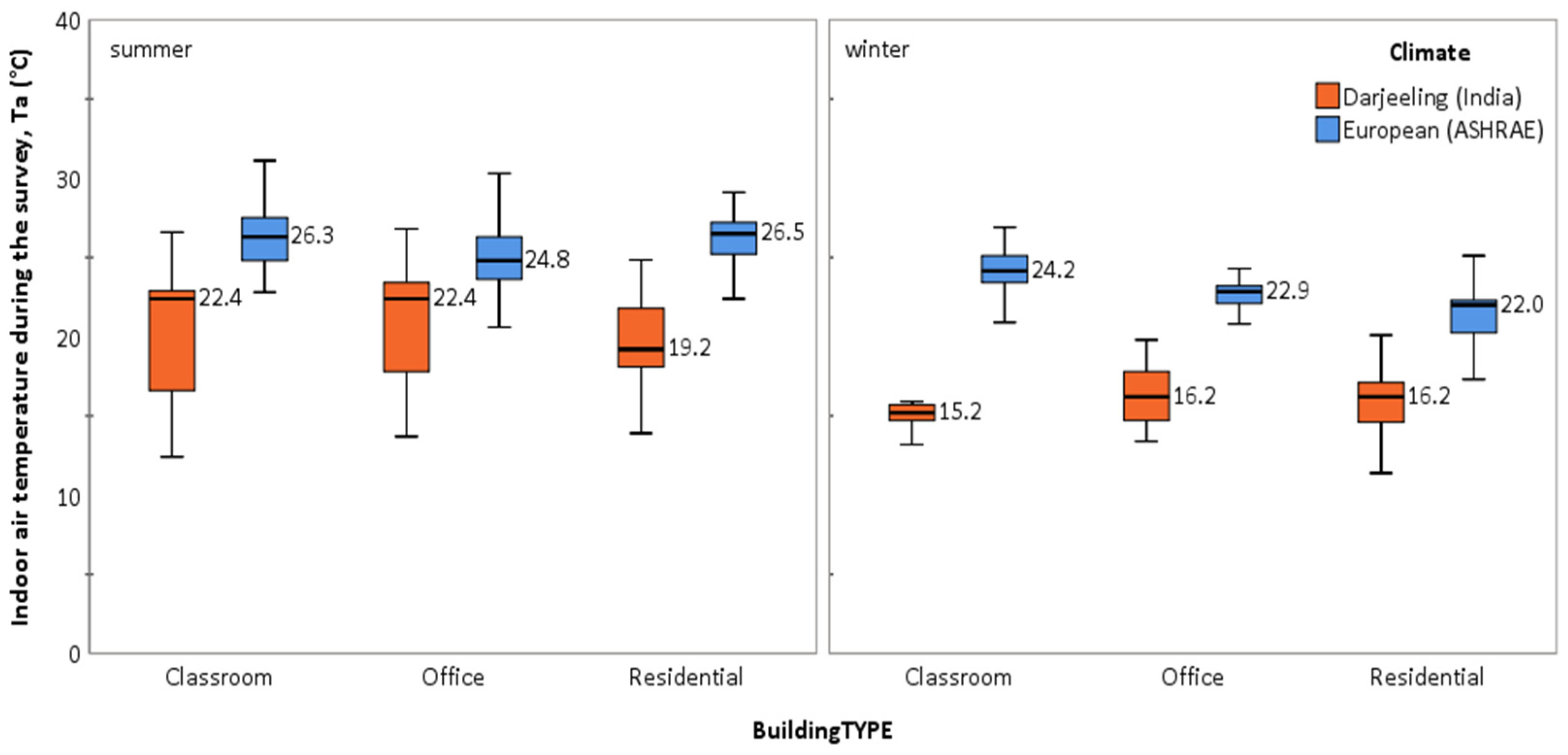

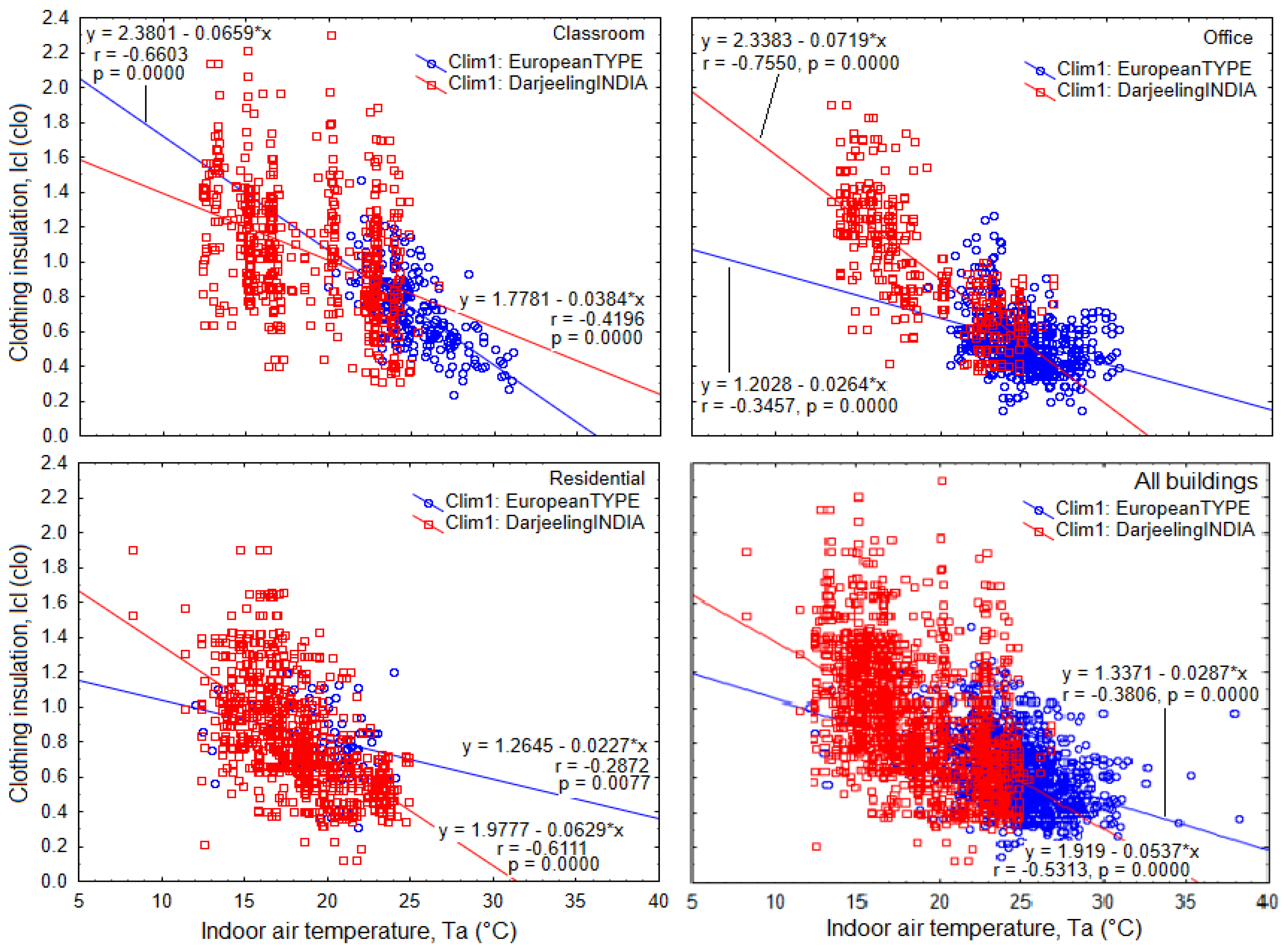





| Location | Building_id | Building_type | Location | Latitude (° N) | Longitude (° E) | Elevation (m Above Mean Sea Level) | Sample Size | Mean Tout (°C) | Mean RH (%) |
|---|---|---|---|---|---|---|---|---|---|
| Europe (ASHRAE db-II) | 557 | Office | Karlsruhe | 49.00 | 8.43 | 118 | 421 | 22.6 | 64.4 |
| 621 | MFH | Bratislava | 48.15 | 17.11 | 140 | 74 | NA | NA | |
| 622 | MFH | Bratislava | 48.15 | 17.11 | 140 | 94 | NA | NA | |
| 629 | Office | Karlsruhe | 49.01 | 8.40 | 118 | 132 | 25.8 | 64.2 | |
| 632 | Office | Stuttgart | 48.78 | 9.18 | 245 | 105 | 20.8 | 66.7 | |
| 652 | Cl | Elsinore | 56.03 | 12.59 | 395 | 170 | NA | NA | |
| 704 | MFH | Bratislava | 48.15 | 17.11 | 140 | 289 | NA | NA | |
| 727 | MFH | Liege | 50.63 | 5.57 | 70 | 85 | NA | NA | |
| 740 | Cl | Lyon | 45.76 | 4.84 | 237 | 109 | 18.8 | 70.1 | |
| 742 | Office | Lyon | 45.76 | 4.84 | 237 | 15 | 22.1 | 57.1 | |
| 744 | Cl | Lyon | 45.76 | 4.84 | 237 | 112 | 4.7 | 77.7 | |
| 746 | Office | Lyon | 45.76 | 4.84 | 237 | 46 | 7.4 | 85.0 | |
| Total | 1652 | 19.5 | 67.5 | ||||||
| India (Darjeeling database) | K1420 | MFH | Kurseong | 26.88 | 88.27 | 1420 | 489 | 18.4 | 74.5 |
| M1650 | Office | Mirik | 26.88 | 88.18 | 1640 | 444 | 17.3 | 71.8 | |
| S1950 | Cl | Sonada | 26.95 | 88.28 | 1950 | 577 | 14.5 | 73.4 | |
| T2565 | MFH | Tiger Hills | 26.99 | 88.28 | 2565 | 528 | 12.2 | 75.1 | |
| Total | 2038 | 15.5 | 71.6 | ||||||
| Building TYPE | Season | Gender | European Temperate (ASHRAE) | Indian Temperate (Darjeeling) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean (clo) | S.D. (clo) | Min (clo) | Max (clo) | N | Mean (clo) | S.D. (clo) | Min (clo) | Max (clo) | N | |||
| classroom | Summer | Female | 0.59 | 0.20 | 0.24 | 1.07 | 47 | 0.93 | 0.34 | 0.37 | 1.98 | 170 |
| Male | 0.61 | 0.16 | 0.32 | 1.19 | 62 | 1.01 | 0.32 | 0.32 | 1.90 | 212 | ||
| Total | 0.60 | 0.18 | 0.24 | 1.19 | 109 | 0.98 | 0.33 | 0.32 | 1.98 | 382 | ||
| Winter | Female | 0.88 | 0.18 | 0.56 | 1.47 | 43 | 1.18 | 0.33 | 0.58 | 2.31 | 90 | |
| Male | 0.81 | 0.17 | 0.45 | 1.25 | 69 | 1.28 | 0.32 | 0.64 | 2.22 | 105 | ||
| Total | 0.84 | 0.18 | 0.45 | 1.47 | 112 | 1.24 | 0.33 | 0.51 | 2.31 | 195 | ||
| Total | Female | 0.73 | 0.24 | 0.24 | 1.47 | 90 | 1.02 | 0.36 | 0.37 | 2.31 | 260 | |
| Male | 0.72 | 0.20 | 0.32 | 1.25 | 131 | 1.10 | 0.34 | 0.32 | 2.22 | 317 | ||
| Total | 0.72 | 0.22 | 0.24 | 1.47 | 221 | 1.07 | 0.35 | 0.32 | 2.31 | 577 | ||
| office | Summer | Female | 0.56 | 0.11 | 0.28 | 0.97 | 192 | 0.95 | 0.26 | 0.47 | 1.88 | 127 |
| Male | 0.56 | 0.09 | 0.37 | 0.84 | 232 | 0.79 | 0.28 | 0.41 | 1.71 | 158 | ||
| NA | 0.45 | 0.13 | 0.15 | 0.82 | 230 | NA | NA | NA | NA | NA | ||
| Total | 0.52 | 0.12 | 0.15 | 0.97 | 654 | 0.86 | 0.29 | 0.41 | 1.88 | 285 | ||
| Winter | Female | 0.82 | 0.15 | 0.55 | 1.24 | 30 | 1.26 | 0.27 | 0.61 | 1.76 | 71 | |
| Male | 1.03 | 0.11 | 0.86 | 1.27 | 16 | 1.24 | 0.30 | 0.73 | 1.95 | 88 | ||
| Total | 0.90 | 0.17 | 0.55 | 1.27 | 46 | 1.25 | 0.29 | 0.61 | 1.95 | 159 | ||
| Total | Female | 0.60 | 0.15 | 0.28 | 1.24 | 222 | 1.06 | 0.30 | 0.47 | 1.88 | 198 | |
| Male | 0.59 | 0.15 | 0.37 | 1.27 | 248 | 0.95 | 0.36 | 0.41 | 1.95 | 246 | ||
| NA | 0.45 | 0.13 | 0.15 | 0.82 | 230 | NA | NA | NA | NA | NA | ||
| Total | 0.55 | 0.16 | 0.15 | 1.27 | 700 | 1.00 | 0.34 | 0.41 | 1.95 | 444 | ||
| Residential | Summer | Female | NA | NA | NA | NA | NA | 0.71 | 0.20 | 0.19 | 2.36 | 240 |
| Male | NA | NA | NA | NA | NA | 0.84 | 0.31 | 0.17 | 2.72 | 446 | ||
| Total | NA | NA | NA | NA | NA | 0.79 | 0.28 | 0.17 | 2.72 | 686 | ||
| Winter | Female | 0.82 | 0.22 | 0.37 | 1.20 | 35 | 1.01 | 0.19 | 0.51 | 1.66 | 120 | |
| Male | 0.82 | 0.20 | 0.31 | 1.19 | 50 | 1.16 | 0.35 | 0.21 | 2.27 | 210 | ||
| Total | 0.82 | 0.20 | 0.31 | 1.20 | 85 | 1.10 | 0.31 | 0.21 | 2.27 | 330 | ||
| Total | Female | 0.82 | 0.22 | 0.37 | 1.20 | 35 | 0.81 | 0.24 | 0.19 | 2.36 | 360 | |
| Male | 0.82 | 0.20 | 0.31 | 1.19 | 50 | 0.94 | 0.35 | 0.21 | 2.27 | 656 | ||
| Total | 0.82 | 0.20 | 0.31 | 1.20 | 85 | 0.90 | 0.32 | 0.17 | 2.36 | 1016 | ||
| All Buildings | Summer | Female | 0.57 | 0.14 | 0.24 | 1.07 | 239 | 0.84 | 0.29 | 0.19 | 2.36 | 537 |
| Male | 0.57 | 0.11 | 0.32 | 1.19 | 294 | 0.87 | 0.32 | 0.17 | 2.72 | 816 | ||
| NA | 0.45 | 0.13 | 0.15 | 0.82 | 230 | NA | NA | NA | NA | NA | ||
| Total | 0.53 | 0.13 | 0.15 | 1.19 | 763 | 0.86 | 0.31 | 0.17 | 2.72 | 1353 | ||
| Winter | Female | 0.84 | 0.19 | 0.37 | 1.47 | 108 | 1.13 | 0.28 | 0.51 | 2.31 | 281 | |
| Male | 0.84 | 0.19 | 0.31 | 1.27 | 135 | 1.21 | 0.33 | 0.21 | 2.27 | 403 | ||
| Total | 0.84 | 0.19 | 0.31 | 1.47 | 243 | 1.18 | 0.32 | 0.21 | 2.31 | 684 | ||
| Total | Female | 0.65 | 0.20 | 0.24 | 1.47 | 347 | 0.94 | 0.32 | 0.17 | 2.36 | 818 | |
| Male | 0.65 | 0.19 | 0.31 | 1.27 | 429 | 0.99 | 0.36 | 0.17 | 2.72 | 1219 | ||
| NA | 0.45 | 0.13 | 0.15 | 0.82 | 230 | NA | NA | NA | NA | NA | ||
| Total | 0.61 | 0.20 | 0.15 | 1.47 | 1006 | 0.97 | 0.34 | 0.17 | 2.72 | 2037 | ||
| Building TYPE | Statistics | European Buildings | Darjeeling Buildings | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TSV | PMV | TSV | PMV | ||||||||||
| S | W | Y | S | W | Y | S | W | Y | S | W | Y | ||
| Office | Mean | 0.56 | −0.02 | 0.52 | −0.13 | 0.34 | −0.10 | −0.10 | −0.75 | −0.33 | −0.49 | −1.12 | −0.72 |
| s.d. | 0.89 | 1.04 | 0.91 | 0.74 | 0.41 | 0.74 | 0.82 | 0.89 | 0.90 | 0.64 | 0.51 | 0.67 | |
| Min | −2.0 | −2.0 | −2.0 | −3.12 | −0.51 | −3.12 | −2.0 | −3.0 | −3.0 | −2.93 | −2.77 | −2.93 | |
| Max | 3.0 | 2.0 | 3.0 | 1.81 | 1.32 | 1.81 | 2.0 | 2.0 | 2.0 | 0.76 | 0.13 | 0.76 | |
| N | 670 | 46 | 716 | 666 | 46 | 712 | 285 | 159 | 444 | 285 | 159 | 444 | |
| Classrooms | Mean | 0.86 | 0.42 | 0.54 | −0.07 | 0.22 | 0.14 | −0.09 | −0.79 | −0.33 | −0.50 | −1.19 | −0.73 |
| s.d. | 1.10 | 1.09 | 1.11 | 0.41 | 0.51 | 0.50 | 1.26 | 1.33 | 1.32 | 0.93 | 0.78 | 0.94 | |
| Min | −2.0 | −3.0 | −3.0 | −1.12 | −1.19 | −1.19 | −3.0 | −3.0 | −3.0 | −3.79 | −3.40 | −3.79 | |
| Max | 2.0 | 2.0 | 2.0 | 0.76 | 1.97 | 1.97 | 2.0 | 2.0 | 2.0 | 1.19 | 1.04 | 1.19 | |
| N | 109 | 280 | 389 | 109 | 279 | 388 | 382 | 195 | 577 | 382 | 195 | 577 | |
| Residential Buildings | Mean | 1.66 | 0.88 | 0.98 | NA | NA | NA | −0.11 | −0.32 | −0.18 | −1.05 | −1.38 | −1.16 |
| s.d. | 0.83 | 1.18 | 1.17 | NA | NA | NA | 0.82 | 0.96 | 0.87 | 0.65 | 0.68 | 0.68 | |
| Min | −1.0 | −3.0 | −3.0 | NA | NA | NA | −2.0 | −2.0 | −2.0 | −3.93 | −4.37 | −4.37 | |
| Max | 2.0 | 2.0 | 2.0 | NA | NA | NA | 2.0 | 2.0 | 3.0 | 0.54 | 0.27 | 0.54 | |
| N | 74 | 468 | 542 | NA | NA | NA | 687 | 330 | 1017 | 687 | 330 | 1017 | |
| All Buildings | Mean | 0.69 | 0.66 | 0.68 | −0.12 | 0.24 | −0.01 | −0.11 | −0.55 | −0.26 | −0.78 | −1.26 | −0.94 |
| s.d. | 0.963 | 1.18 | 1.07 | 0.71 | 0.50 | 0.67 | 0.96 | 1.09 | 1.03 | 0.79 | 0.68 | 0.79 | |
| Min | −2.0 | −3.0 | −3.0 | −3.12 | −1.19 | −3.12 | −3.0 | −3.0 | −3.0 | −3.93 | −4.37 | −4.37 | |
| Max | 2.0 | 2.0 | 2.0 | 1.81 | 1.97 | 1.97 | 2.0 | 2.0 | 2.0 | 1.19 | 1.04 | 1.19 | |
| N | 853 | 794 | 1647 | 775 | 325 | 1100 | 1354 | 684 | 2038 | 1354 | 684 | 2038 | |
| Building TYPE | Statistics | European Buildings (ASHRAE) | Darjeeling Buildings (India) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <Cool | <sl. Cool | <Neutral | <sl. Warm | <Warm | <Hot | <Cool | <sl. Cool | <Neutral | <sl. Warm | <Warm | <Hot | ||
| Office | Coefficient, Ta | 0.249 | 0.172 | ||||||||||
| Estimate | 3.39 | 4.57 | 6.38 | 7.54 | 8.14 | −0.04 | 1.59 | 3.21 | 4.43 | 5.66 | |||
| p-value | Not sig. | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.936 | 0.000 | 0.000 | 0.000 | 0.000 | Not sig. | |
| Median | 13.6 | 18.3 | 25.6 | 30.3 | 32.7 | −0.2 | 9.3 | 18.7 | 25.8 | 32.9 | |||
| SD | 4.02 | 5.82 | |||||||||||
| Classrooms | Coefficient, Ta | 0.294 | 0.196 | ||||||||||
| Estimate | 4.59 | 5.23 | 6.11 | 7.23 | 8.25 | 9.54 | 1.85 | 2.38 | 3.59 | 4.39 | 5.54 | 6.49 | |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Median | 15.6 | 17.8 | 20.8 | 24.6 | 28.1 | 32.5 | 9.5 | 12.2 | 18.4 | 22.4 | 28.3 | 33.2 | |
| SD | 3.41 | 5.11 | |||||||||||
| Residential | Coefficient, Ta | 0.209 | 0.099 | ||||||||||
| Estimate | 1.76 | 2.58 | 3.20 | 4.17 | 4.94 | 6.60 | −0.08 | 1.55 | 2.62 | 3.92 | 5.01 | ||
| p-value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | Not sig. | 0.722 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Median | 8.4 | 12.4 | 15.3 | 19.9 | 23.7 | 31.6 | −0.8 | 15.6 | 26.5 | 39.6 | 50.5 | ||
| SD | 4.79 | 10.09 | |||||||||||
| All | Coefficient, Ta | 0.113 | 0.149 | ||||||||||
| Estimate | 0.14 | 0.86 | 1.51 | 2.68 | 3.52 | 4.55 | 0.49 | 1.19 | 2.61 | 3.63 | 4.81 | 5.77 | |
| p-value | 0.564 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Median | 1.2 | 7.6 | 13.3 | 23.7 | 31.1 | 40.2 | 3.3 | 7.9 | 17.5 | 24.3 | 32.2 | 38.6 | |
| SD | 8.84 | 6.69 | |||||||||||
| Building TYPE | Parameter | European Temperate (ASHRAE) Climate | Indian Temperate (Darjeeling) Climate | ||
|---|---|---|---|---|---|
| Summer | Winter | Summer | Winter | ||
| Office | Regression | TSV = 0.18Ta − 3.91 | TSV = 0.35Ta − 8.02 | TSV = 0.10Ta − 2.31 | TSV = 0.18Ta − 3.72 |
| R | 0.40 | 0.28 | 0.42 | 0.33 | |
| p-value | p < 0.001 | p = 0.055 | p < 0.001 | p < 0.0001 | |
| Tn (°C) | 22.0 | 22.9 | 22.0 | 20.4 | |
| Mean TnG (°C) | 24.0 | 22.7 | 21.3 | 17.8 | |
| N | 670 | 46 | 285 | 159 | |
| Range (°C) | 17.8~30.1 | 18.6~26.5 | 13.8~26.8 | 11.9~21.8 | |
| Classrooms | Regression | TSV = 0.31Ta − 7.45 | TSV = 0.28Ta − 6.34 | TSV = 0.18Ta − 3.82 | TSV = 0.37Ta − 6.71 |
| R | 0.61 | 0.37 | 0.53 | 0.67 | |
| p-value | p < 0.001 | p < 0.001 | p < 0.001 | p < 0.001 | |
| Tn (°C) | 23.7 | 22.5 | 20.8 | 18.0 | |
| Mean TnG (°C) | 24.7 | 23.3 | 20.5 | 17.5 | |
| N | 109 | 280 | 382 | 195 | |
| Range (°C) | 20.4~29.3 | 17.5~29.7 | 12.5~30.3 | 12.9~22.5 | |
| Residential | Regression | TSV = 0.003Ta − 1.58 | TSV = 0.24Ta − 4.41 | TSV = 0.08Ta − 1.64 | TSV = 0.13Ta − 2.33 |
| R | 0.006 | 0.44 | 0.25 | 0.24 | |
| p-value | Not significant | p < 0.001 | p < 0.001 | p < 0.0001 | |
| Tn (°C) | * (extraneous value) | 18.4 | 21.1 | 18.4 | |
| Mean TnG (°C) | 22.8 | 20.0 | 19.9 | 16.5 | |
| N | 74 | 468 | 687 | 330 | |
| Range (°C) | 18.4~28.1 | 14.3~33.0 | 12.7~26.7 | 10.2~21.8 | |
| All Buildings | Regression | TSV = 0.20Ta − 4.5 | TSV = 0.129Ta − 2.25 | TSV = 0.12Ta − 2.55 | TSV = 0.24Ta − 4.32 |
| R | 0.44 | 0.26 | 0.39 | 0.42 | |
| p-value | p < 0.001 | p < 0.001 | p < 0.001 | p < 0.001 | |
| Tn (°C) | 22.5 | 17.4 | 21.0 | 18.3 | |
| Mean TnG (°C) | 24.0 | 21.3 | 20.3 | 17.1 | |
| N | 853 | 794 | 1354 | 684 | |
| Range (°C) | 17.8~30.1 | 14.3~33.0 | 12.5~30.3 | 10.2~22.5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thapa, S.; Pernigotto, G. Adaptive Thermal Comfort in the Different Buildings of Temperate Climates—Comparison Between High-Latitude Europe and Mountainous Himalayas in India. Sustainability 2025, 17, 404. https://doi.org/10.3390/su17020404
Thapa S, Pernigotto G. Adaptive Thermal Comfort in the Different Buildings of Temperate Climates—Comparison Between High-Latitude Europe and Mountainous Himalayas in India. Sustainability. 2025; 17(2):404. https://doi.org/10.3390/su17020404
Chicago/Turabian StyleThapa, Samar, and Giovanni Pernigotto. 2025. "Adaptive Thermal Comfort in the Different Buildings of Temperate Climates—Comparison Between High-Latitude Europe and Mountainous Himalayas in India" Sustainability 17, no. 2: 404. https://doi.org/10.3390/su17020404
APA StyleThapa, S., & Pernigotto, G. (2025). Adaptive Thermal Comfort in the Different Buildings of Temperate Climates—Comparison Between High-Latitude Europe and Mountainous Himalayas in India. Sustainability, 17(2), 404. https://doi.org/10.3390/su17020404









