Enhancing Corporate Transparency: AI-Based Detection of Financial Misstatements in Korean Firms Using NearMiss Sampling and Explainable Models
Abstract
1. Introduction
2. Literature Review
2.1. Foundations and Classical Approaches
2.2. Machine Learning and Recent Advances
2.3. Research Gap and Contribution
3. Methodology
3.1. Logistic Regression
3.2. Decision Tree
3.3. Random Forest
3.4. Gradient Boosting Algorithm
3.5. XGBoost Algorithm
3.6. CatBoost Algorithm
3.7. AdaBoost Algorithm
3.8. Explainable AI Techniques: SHAP and PFI
3.9. Nearmiss Undersampling
4. Data
5. Results and Discussion
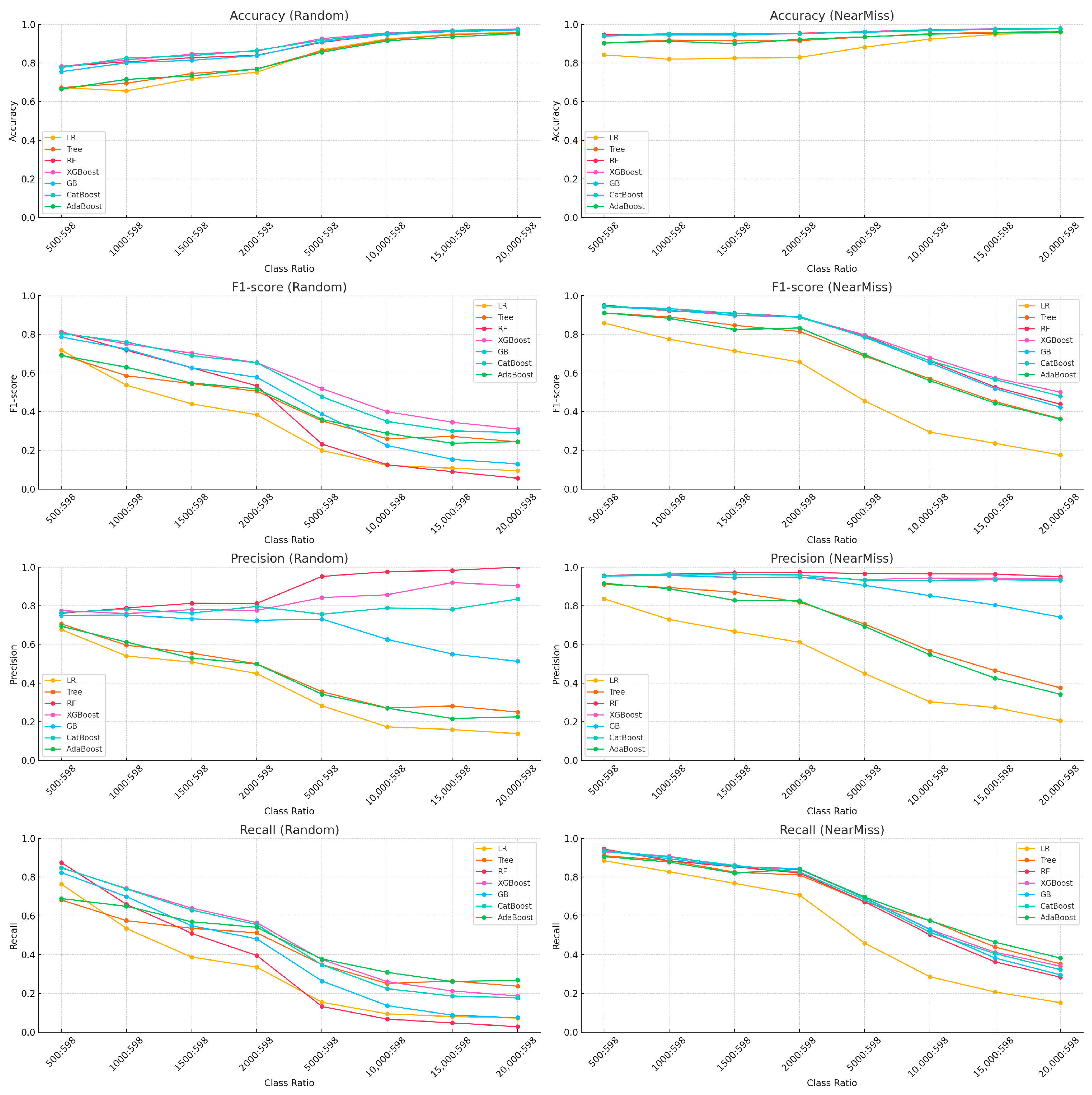
5.1. Effects of Undersampling and Class Imbalance on Model Performance
5.1.1. Experimental Design and Performance Metrics
5.1.2. Empirical Results and Interpretation
5.2. Understanding Variable Influence Through XAI: Linear vs. Random Forest
5.2.1. Experimental Design for Interpretability Analysis
5.2.2. Empirical Results and Feature Importance Interpretation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable Name | Description |
|---|---|
| RDTOT | R&D Expenditures—Consolidated |
| RDTOT_NCS | R&D Expenditures |
| RDCAP | R&D Assets—Consolidated |
| RDCAP_NCS | R&D Assets |
| RDEXP | R&D Expenses—Consolidated |
| RDEXP_NCS | R&D Expenses |
| CLS | Ownership of Largest Shareholders—Common Stocks |
| PLS | Ownership of Largest Shareholders—Preferred Stocks |
| INVENTORY | Inventory |
| SHTLOAN | Short-term Loans Receivable |
| RECEIVABLES | Trade Receivables |
| SHTCONTAT | Short-term Contract Assets |
| SHTCO2AT | Short-term Emission Rights |
| CASH | Cash and Cash Equivalents |
| TA | Tangible Assets |
| PPE | Property, Plant and Equipment |
| INTANGIBLES | Intangible Assets |
| GOODWILL | Goodwill |
| RDASSET | Development costs recorded as intangible assets |
| IP | Industrial Property Rights |
| LTFININS | Long-term Financial Instruments |
| LTAFVPL | FVTPL Financial Assets |
| LTFVOCI | FVOCI Financial Assets |
| LTACSEC | Held-to-Maturity Securities |
| LTACFIN | Amortized Cost Financial Assets |
| LTLOAN | Long-term Loans Receivable |
| DEFTAXASSET | Deferred Tax Assets |
| LTCONTAT | Long-term Contract Assets |
| LTCO2AT | Long-term Emission Rights |
| SHTBOND | Short-term Bond Payable |
| SHTBORROWINGS | Short-term Borrowings |
| CURLTDEBT | Current portion of long-term borrowings |
| CURFINDEBT | Current Financial Liabilities |
| SHTLEASE | Short-term Lease Liabilities |
| SALESPAYABLE | Trade Payables |
| DBCURDT | Current Portion of Defined Benefit Liabilities |
| TAXPAYABLE | Current Tax Payable |
| SHTCO2DT | Short-term Emission Liabilities |
| LTBOND | Long-term Bond Payable |
| LTBORROWINGS | Long-term Borrowings |
| LTLEASE | Long-term Lease Liabilities |
| DBLT | Non-current Defined Benefit Liabilities |
| LTTAXPAYABLE | Long-term Income Tax Payable |
| LTCO2DT | Long-term Emission Liabilities |
| COMSTOCK | Common Stock Capital |
| PRESTOCK | Preferred Stock Capital |
| AOCI | Accumulated Other Comprehensive Income |
| RETEARNING | Retained Earnings |
| SALES | Sales Revenue |
| COGS | Cost of Sales |
| EMPEXPS | Personnel Expenses |
| DEPEXPS | Depreciation Expense |
| AMTEXPS | Amortization of Intangible Assets |
| RDEXPS | R&D Expenses |
| ADVEXPS | Advertising Expenses |
| SELLEXPS | Selling Expenses |
| RENTEXPS | Rental Expenses |
| LEASEEXPS | Lease Expenses |
| OI | Income (Loss) from Operations |
| INTEXPS | Interest Expense |
| TAXEXPENSE | Income Tax Expense |
| CTNDOI | Net Profit (Loss) from Continuing Operations |
| DISCTNDOI | Net Profit (Loss) from Discontinued Operations |
| NI | Net Income (Loss) |
| OCI | Other Comprehensive Income |
| CEPS_B | Basic EPS from Continuing Operations |
| EPS_B | Basic Earnings per Share |
| CEPS_D | Diluted EPS from Continuing Operations |
| EPS_D | Diluted Earnings per Share |
| EXPSTOT | Expense Classified by Nature |
| EXPSMAT | Change in Finished Goods and Work-in-Progress |
| EXPSSVC | Capitalized Services Rendered |
| EXPSRAW | Raw Materials and Supplies Used |
| EXPSGOOD | Sales of Goods |
| EXPSCOGSOTH | Other Costs |
| EXPSEMP | Employee Benefits Expense |
| EXPSDEP | Depreciation, Amortization and Impairment Losses |
| EXPSTAX | Taxes and Public Charges |
| EXPSBAD | Bad Debt Expense |
| EXPSLOGI | Logistic Expenses |
| EXPSPROMO | Advertising and Sales Promotion Expenses |
| EXPSRENT | Rental and Lease Expenses |
| EXPSRND | Ordinary R&D Expenses |
| EXPSOTH | Other Expenses |
| OCF | Cash Flows from Operating Activities |
| TA_DEC | Decrease in Tangible Assets |
| PPE_DEC | Decrease in Property, Plant and Equipment |
| TA_INC | Increase in Tangible Assets |
| PPE_INC | Increase in Property, Plant and Equipment |
| RDASSET_INC | Increase in Development Costs |
| CASHTAX | Income Taxes Paid |
| BOND_INC | Increase in Bonds Payable |
| LTBOND_INC | Increase in Long-term Bonds |
| BORROWINGS_INC | Increase in Borrowings |
| BOND_DEC | Decrease in Bonds Payable |
| LTBOND_DEC | Decrease in Long-term Bonds |
| BORROWINGS_DEC | Decrease in Borrowings |
| DIVOUT | Dividends Paid |
| AR (Target variable) | Detected Financial Misstatements |
References
- Dyck, A.; Morse, A.; Zingales, L. How pervasive is corporate fraud? Rev. Account. Stud. 2024, 29, 736–769. [Google Scholar] [CrossRef]
- Lokanan, M.; Sharma, S. The use of machine learning algorithms to predict financial statement fraud. Br. Account. Rev. 2024, 56, 101441, reprinted in Br. Account. Rev. 2025, 57, 101222. [Google Scholar] [CrossRef]
- Beasley, M.S. An empirical analysis of the relation between the board of director composition and financial statement fraud. Account. Rev. 1996, 71, 443–465. [Google Scholar]
- Bell, T.B.; Carcello, J.V. A decision aid for assessing the likelihood of fraudulent financial reporting. Audit. J. Pract. Theory 2000, 19, 169–184. [Google Scholar] [CrossRef]
- Hogan, C.E.; Rezaee, Z.; Riley, R.A.; Velury, U.K. Financial statement fraud: Insights from the academic literature. Audit. J. Pract. Theory 2008, 27, 231–252. [Google Scholar] [CrossRef]
- Trompeter, G.M.; Carpenter, T.D.; Desai, N.; Jones, K.L.; Riley, R.A. A synthesis of fraud-related research. Audit. J. Pract. Theory 2013, 32 (Suppl. S1), 287–321. [Google Scholar] [CrossRef]
- Ruhnke, K.; Schmidt, M. Misstatements in financial statements: The relationship between inherent and control risk factors and audit adjustments. Audit. J. Pract. Theory 2014, 33, 247–269. [Google Scholar] [CrossRef]
- Yu, S.J.; Rha, J.S. Research trends in accounting fraud using network analysis. Sustainability 2021, 13, 5579. [Google Scholar] [CrossRef]
- Ramos Montesdeoca, M.; Sanchez Medina, A.J.; Blazquez Santana, F. Research topics in accounting fraud in the 21st century: A state of the art. Sustainability 2019, 11, 1570. [Google Scholar] [CrossRef]
- Healy, P.M. The effect of bonus schemes on accounting decisions. J. Account. Econ. 1985, 7, 85–107. [Google Scholar] [CrossRef]
- Jones, J.J. Earnings management during import relief investigations. J. Account. Res. 1991, 29, 193–228. [Google Scholar] [CrossRef]
- Dechow, P.M.; Sloan, R.G.; Sweeney, A.P. Detecting earnings management. Account. Rev. 1995, 70, 193–225. [Google Scholar]
- Beneish, M.D. The detection of earnings manipulation. Financ. Anal. J. 1999, 55, 24–36. [Google Scholar] [CrossRef]
- Dechow, P.M.; Ge, W.; Larson, C.R.; Sloan, R.G. Predicting material accounting misstatements. Contemp. Account. Res. 2011, 28, 17–82. [Google Scholar] [CrossRef]
- Spathis, C.T. Detecting false financial statements using published data: Some evidence from Greece. Manag. Audit. J. 2002, 17, 179–191. [Google Scholar] [CrossRef]
- Qin, R. Identification of accounting fraud based on support vector machine and logistic regression model. Complexity 2021, 2021, 5597060. [Google Scholar] [CrossRef]
- Ramzan, S.; Lokanan, M. The application of machine learning to study fraud in the accounting literature. J. Account. Lit. 2024, 47, 570–596. [Google Scholar] [CrossRef]
- Cecchini, M.; Aytug, H.; Koehler, G.J.; Pathak, P. Detecting management fraud in public companies. Manag. Sci. 2010, 56, 1146–1160. [Google Scholar] [CrossRef]
- Perols, J. Financial statement fraud detection: An analysis of statistical and machine learning algorithms. Audit. J. Pract. Theory 2011, 30, 19–50. [Google Scholar] [CrossRef]
- Alden, M.E.; Ciconte, W.A.; Steiger, J. Detection of financial statement fraud using evolutionary algorithms. J. Emerg. Technol. Account. 2012, 9, 71–94. [Google Scholar] [CrossRef]
- Chen, S.; Goo, Y.J.J.; Shen, Z.D. A hybrid approach of stepwise regression, logistic regression, support vector machine, and decision tree for forecasting fraudulent financial statements. Sci. World J. 2014, 2014, 968712. [Google Scholar] [CrossRef]
- Bai, B.; Yen, J.; Yang, X. False financial statements: Characteristics of China’s listed companies and CART detecting approach. Int. J. Inf. Technol. Decis. Mak. 2008, 7, 339–359. [Google Scholar] [CrossRef]
- Bertomeu, J.; Taylor, D.J.; Xue, Y. Using machine learning to detect misstatements. Rev. Account. Stud. 2021, 26, 468–519. [Google Scholar] [CrossRef]
- Liu, C.; Chan, Y.; Kazmi, S.H.A.; Fu, H. Financial fraud detection model: Based on random forest. Int. J. Econ. Financ. 2015, 7, 178. [Google Scholar] [CrossRef]
- Liou, F.M. Fraudulent financial reporting detection and business failure prediction models: A comparison. Manag. Audit. J. 2008, 23, 650–662. [Google Scholar] [CrossRef]
- Beneish, M.D.; Vorst, P. The cost of fraud prediction errors. Account. Rev. 2022, 97, 91–121. [Google Scholar] [CrossRef]
- Van Vlasselaer, V.; Bravo, C.; Caelen, O.; Eliassi-Rad, T.; Akoglu, L.; Snoeck, M.; Baesens, B. APATE: A novel approach for automated credit card transaction fraud detection using network-based extensions. Decis. Support Syst. 2015, 75, 38–48. [Google Scholar] [CrossRef]
- Kim, Y.J.; Park, H.J.; Lee, J.H. Detecting financial misstatements with fraud intention using multi-class cost-sensitive learning. Expert Syst. Appl. 2016, 62, 32–43. [Google Scholar] [CrossRef]
- Bao, Y.; Ke, B.; Li, B.; Yu, Y. Detecting accounting fraud in publicly traded U.S. firms using a machine learning approach. J. Account. Res. 2020, 58, 199–235. [Google Scholar] [CrossRef]
- Na, H.J.; Jung, T. An explorative study to detect accounting fraud using a machine learning approach. Korean Account. Rev. 2022, 47, 177–205. (In Korean) [Google Scholar] [CrossRef]
- An, B.; Suh, Y. Identifying financial statement fraud with decision rules obtained from Modified Random Forest. Data Technol. Appl. 2020, 54, 235–255. [Google Scholar] [CrossRef]
- Mani, I.; Zhang, I. kNN approach to unbalanced data distributions: A case study involving information extraction. In Proceedings of the Workshop on Learning from Imbalanced Datasets, Washington, DC, USA, 21 August 2003; ICML: San Diego, CA, USA; Volume 126, pp. 1–7. [Google Scholar]
- Mqadi, N.M.; Naicker, N.; Adeliyi, T. Solving misclassification of the credit card imbalance problem using near miss. Math. Probl. Eng. 2021, 2021, 7194728. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, M.; Liu, G.; Xie, Y.; Liu, S.; Guo, C. NUS: Noisy-sample-removed undersampling scheme for imbalanced classification and application to credit card fraud detection. IEEE Trans. Comput. Soc. Syst. 2023, 11, 1793–1804. [Google Scholar] [CrossRef]
- Lin, K.; Gao, Y. Model interpretability of financial fraud detection by group SHAP. Expert Syst. Appl. 2022, 210, 118354. [Google Scholar] [CrossRef]
- Zhang, C.A.; Cho, S.; Vasarhelyi, M. Explainable artificial intelligence (XAI) in auditing. Int. J. Account. Inf. Syst. 2022, 46, 100572. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ali, A.A.; Khedr, A.M.; El-Bannany, M.; Kanakkayil, S. A powerful predicting model for financial statement fraud based on optimized XGBoost ensemble learning technique. Appl. Sci. 2023, 13, 2272. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Brooklyn, NY, USA, 2018; Volume 31. [Google Scholar]
- Nguyen, N.; Duong, T.; Chau, T.; Nguyen, V.H.; Trinh, T.; Tran, D.; Ho, T. A proposed model for card fraud detection based on Catboost and deep neural network. IEEE Access 2022, 10, 96852–96861. [Google Scholar] [CrossRef]
- Chen, Y.; Han, X. CatBoost for fraud detection in financial transactions. In Proceedings of the 2021 IEEE International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 15–17 January 2021; pp. 176–179. [Google Scholar]
- Theodorakopoulos, L.; Theodoropoulou, A.; Tsimakis, A.; Halkiopoulos, C. Big data-driven distributed machine learning for scalable credit card fraud detection using PySpark, XGBoost, and CatBoost. Electronics 2025, 14, 1754. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Dutta, I. Data Mining Techniques to Identify Financial Restatements. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2018. [Google Scholar]
- Shapley, L.S. Stochastic games. Proc. Natl. Acad. Sci. USA 1953, 39, 1095–1100. [Google Scholar] [CrossRef]
- Goyal, S. Handling class-imbalance with KNN (neighbourhood) under-sampling for software defect prediction. Artif. Intell. Rev. 2022, 55, 2023–2064. [Google Scholar] [CrossRef]
- Du, X. Optimized convolutional neural network for intelligent financial statement anomaly detection. J. Comput. Technol. Softw. 2024, 3. [Google Scholar]
- Nemati, Z.; Mohammadi, A.; Bayat, A.; Mirzaei, A. Predicting fraud in financial statements using supervised methods: An analytical comparison. Int. J. Nonlinear Anal. Appl. 2024, 15, 259–272. [Google Scholar]
- Tang, Y.; Liu, Z. A distributed knowledge distillation framework for financial fraud detection based on transformer. IEEE Access 2024, 12, 62899–62911. [Google Scholar] [CrossRef]
| Year | Number of Observations (A) | Number of Misstatements (B) | Misstatement Rate (B/A) |
|---|---|---|---|
| 2009 | 1651 | 42 | 2.54% |
| 2010 | 1653 | 59 | 3.57% |
| 2011 | 1688 | 55 | 3.26% |
| 2012 | 1694 | 65 | 3.84% |
| 2013 | 1714 | 60 | 3.50% |
| 2014 | 1759 | 68 | 3.87% |
| 2015 | 1844 | 69 | 3.74% |
| 2016 | 1895 | 62 | 3.27% |
| 2017 | 1967 | 47 | 2.39% |
| 2018 | 2037 | 37 | 1.82% |
| 2019 | 2115 | 23 | 1.09% |
| 2020 | 2179 | 7 | 0.32% |
| 2021 | 2254 | 3 | 0.13% |
| 2022 | 2304 | 1 | 0.04% |
| 2023 | 2380 | 0 | 0.00% |
| Total | 29,134 | 598 | 2.05% |
| Class Ratio | Algorithm | Random Sampling | NearMiss | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A | F | P | R | A | F | P | R | ||
| 500:598 | LR | 0.673 | 0.718 | 0.677 | 0.764 | 0.842 | 0.859 | 0.836 | 0.885 |
| Tree | 0.672 | 0.694 | 0.706 | 0.682 | 0.903 | 0.911 | 0.911 | 0.911 | |
| RF | 0.782 | 0.814 | 0.761 | 0.876 | 0.947 | 0.951 | 0.956 | 0.946 | |
| XGBoost | 0.783 | 0.810 | 0.775 | 0.848 | 0.939 | 0.943 | 0.955 | 0.931 | |
| GB | 0.755 | 0.786 | 0.750 | 0.824 | 0.940 | 0.944 | 0.954 | 0.935 | |
| CatBoost | 0.776 | 0.805 | 0.765 | 0.849 | 0.942 | 0.946 | 0.954 | 0.938 | |
| AdaBoost | 0.665 | 0.691 | 0.694 | 0.689 | 0.903 | 0.911 | 0.916 | 0.906 | |
| 600:598 | LR | 0.648 | 0.674 | 0.626 | 0.731 | 0.841 | 0.847 | 0.818 | 0.878 |
| Tree | 0.656 | 0.656 | 0.655 | 0.657 | 0.905 | 0.904 | 0.907 | 0.901 | |
| RF | 0.783 | 0.788 | 0.768 | 0.809 | 0.949 | 0.948 | 0.964 | 0.933 | |
| XGBoost | 0.779 | 0.784 | 0.764 | 0.806 | 0.936 | 0.935 | 0.944 | 0.926 | |
| GB | 0.768 | 0.773 | 0.756 | 0.791 | 0.942 | 0.940 | 0.960 | 0.921 | |
| CatBoost | 0.794 | 0.801 | 0.772 | 0.833 | 0.946 | 0.945 | 0.963 | 0.926 | |
| AdaBoost | 0.668 | 0.674 | 0.661 | 0.687 | 0.917 | 0.917 | 0.924 | 0.910 | |
| 1000 :598 | LR | 0.655 | 0.537 | 0.540 | 0.535 | 0.820 | 0.775 | 0.729 | 0.828 |
| Tree | 0.695 | 0.586 | 0.596 | 0.575 | 0.918 | 0.890 | 0.894 | 0.886 | |
| RF | 0.806 | 0.718 | 0.788 | 0.659 | 0.944 | 0.922 | 0.964 | 0.885 | |
| XGBoost | 0.815 | 0.750 | 0.759 | 0.741 | 0.952 | 0.934 | 0.961 | 0.908 | |
| GB | 0.801 | 0.724 | 0.752 | 0.699 | 0.946 | 0.925 | 0.957 | 0.895 | |
| CatBoost | 0.825 | 0.760 | 0.782 | 0.739 | 0.951 | 0.933 | 0.964 | 0.903 | |
| AdaBoost | 0.715 | 0.630 | 0.612 | 0.649 | 0.913 | 0.883 | 0.888 | 0.878 | |
| 1500: 598 | LR | 0.718 | 0.440 | 0.508 | 0.388 | 0.825 | 0.714 | 0.667 | 0.768 |
| Tree | 0.745 | 0.545 | 0.555 | 0.535 | 0.915 | 0.847 | 0.870 | 0.826 | |
| RF | 0.827 | 0.627 | 0.813 | 0.510 | 0.951 | 0.909 | 0.971 | 0.853 | |
| XGBoost | 0.846 | 0.703 | 0.780 | 0.640 | 0.945 | 0.898 | 0.946 | 0.855 | |
| GB | 0.814 | 0.627 | 0.732 | 0.548 | 0.945 | 0.898 | 0.946 | 0.855 | |
| CatBoost | 0.838 | 0.690 | 0.762 | 0.630 | 0.951 | 0.909 | 0.963 | 0.861 | |
| AdaBoost | 0.733 | 0.548 | 0.529 | 0.569 | 0.900 | 0.825 | 0.828 | 0.821 | |
| Class Ratio | Algorithm | Random Sampling | NearMiss | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A | F | P | R | A | F | P | R | ||
| 2000 :598 | LR | 0.752 | 0.384 | 0.449 | 0.336 | 0.829 | 0.656 | 0.611 | 0.707 |
| Tree | 0.769 | 0.506 | 0.499 | 0.513 | 0.915 | 0.815 | 0.819 | 0.811 | |
| RF | 0.840 | 0.533 | 0.812 | 0.396 | 0.954 | 0.891 | 0.974 | 0.821 | |
| XGBoost | 0.862 | 0.653 | 0.776 | 0.564 | 0.952 | 0.890 | 0.947 | 0.839 | |
| GB | 0.838 | 0.578 | 0.724 | 0.482 | 0.953 | 0.893 | 0.949 | 0.843 | |
| CatBoost | 0.865 | 0.653 | 0.796 | 0.554 | 0.952 | 0.888 | 0.959 | 0.826 | |
| AdaBoost | 0.769 | 0.518 | 0.498 | 0.540 | 0.922 | 0.833 | 0.825 | 0.841 | |
| 5000 :598 | LR | 0.868 | 0.199 | 0.282 | 0.154 | 0.882 | 0.455 | 0.449 | 0.460 |
| Tree | 0.863 | 0.352 | 0.355 | 0.349 | 0.935 | 0.687 | 0.705 | 0.671 | |
| RF | 0.907 | 0.232 | 0.952 | 0.132 | 0.962 | 0.793 | 0.966 | 0.672 | |
| XGBoost | 0.926 | 0.519 | 0.842 | 0.375 | 0.962 | 0.797 | 0.935 | 0.694 | |
| GB | 0.911 | 0.388 | 0.731 | 0.264 | 0.959 | 0.785 | 0.906 | 0.692 | |
| CatBoost | 0.918 | 0.477 | 0.756 | 0.348 | 0.961 | 0.789 | 0.932 | 0.684 | |
| AdaBoost | 0.856 | 0.359 | 0.342 | 0.378 | 0.935 | 0.695 | 0.693 | 0.697 | |
| 10,000 :598 | LR | 0.924 | 0.122 | 0.173 | 0.094 | 0.923 | 0.294 | 0.303 | 0.286 |
| Tree | 0.920 | 0.260 | 0.271 | 0.251 | 0.951 | 0.570 | 0.566 | 0.575 | |
| RF | 0.947 | 0.125 | 0.976 | 0.067 | 0.971 | 0.662 | 0.965 | 0.503 | |
| XGBoost | 0.956 | 0.400 | 0.857 | 0.261 | 0.972 | 0.679 | 0.943 | 0.530 | |
| GB | 0.947 | 0.225 | 0.626 | 0.137 | 0.968 | 0.652 | 0.852 | 0.528 | |
| CatBoost | 0.953 | 0.349 | 0.788 | 0.224 | 0.970 | 0.663 | 0.931 | 0.515 | |
| AdaBoost | 0.914 | 0.288 | 0.270 | 0.309 | 0.949 | 0.560 | 0.546 | 0.574 | |
| 15,000: 598 | LR | 0.949 | 0.107 | 0.159 | 0.080 | 0.948 | 0.236 | 0.273 | 0.207 |
| Tree | 0.946 | 0.272 | 0.281 | 0.264 | 0.959 | 0.452 | 0.464 | 0.440 | |
| RF | 0.963 | 0.089 | 0.983 | 0.047 | 0.975 | 0.527 | 0.964 | 0.363 | |
| XGBoost | 0.969 | 0.345 | 0.920 | 0.212 | 0.977 | 0.574 | 0.943 | 0.413 | |
| GB | 0.963 | 0.153 | 0.550 | 0.087 | 0.973 | 0.519 | 0.804 | 0.383 | |
| CatBoost | 0.967 | 0.300 | 0.782 | 0.186 | 0.976 | 0.566 | 0.935 | 0.406 | |
| AdaBoost | 0.935 | 0.236 | 0.256 | 0.261 | 0.955 | 0.444 | 0.425 | 0.465 | |
| 20,000: 598 | LR | 0.960 | 0.095 | 0.138 | 0.072 | 0.958 | 0.175 | 0.205 | 0.152 |
| Tree | 0.957 | 0.243 | 0.250 | 0.237 | 0.964 | 0.363 | 0.375 | 0.353 | |
| RF | 0.972 | 0.055 | 1.000 | 0.028 | 0.979 | 0.438 | 0.950 | 0.284 | |
| XGBoost | 0.976 | 0.310 | 0.903 | 0.187 | 0.980 | 0.501 | 0.940 | 0.341 | |
| GB | 0.971 | 0.129 | 0.512 | 0.074 | 0.977 | 0.423 | 0.741 | 0.296 | |
| CatBoost | 0.975 | 0.292 | 0.835 | 0.177 | 0.980 | 0.480 | 0.932 | 0.323 | |
| AdaBoost | 0.952 | 0.245 | 0.225 | 0.269 | 0.961 | 0.361 | 0.342 | 0.383 | |
| Logistic Regression Model | ||||
|---|---|---|---|---|
| Rank | PFI | SHAP | ||
| 1 | EXPSOTH | 0.214572 | COGS | 224.9572806 |
| 2 | RDTOT_NCS | 0.191985 | SALES | 167.3553631 |
| 3 | EXPSRAW | 0.178871 | DIVOUT | 40.59469412 |
| 4 | RDTOT | 0.176138 | EXPSTOT | 33.7529652 |
| 5 | SALES | 0.175956 | BORROWINGS_INC | 24.81593337 |
| 6 | INTEXPS | 0.149727 | INTEXPS | 24.10728485 |
| 7 | EXPSEMP | 0.14408 | EMPEXPS | 23.05113003 |
| 8 | EXPSTOT | 0.106557 | EXPSLOGI | 21.50173439 |
| 9 | RDEXP_NCS | 0.0981785 | LTBOND | 21.43660984 |
| 10 | BORROWINGS_INC | 0.0928962 | TA | 21.18560568 |
| 11 | DIVOUT | 0.084153 | BORROWINGS_DEC | 17.88946911 |
| 12 | EXPSCOGSOTH | 0.0797814 | OI | 15.73371231 |
| 13 | COGS | 0.0741348 | SALESPAYABLE | 15.68294781 |
| 14 | SALESPAYABLE | 0.0661202 | CURFINDEBT | 11.3551659 |
| 15 | TA | 0.0637523 | AOCI | 11.04812898 |
| 16 | TAXEXPENSE | 0.0628415 | EXPSOTH | 10.93668593 |
| 17 | LTBOND | 0.0599271 | TAXEXPENSE | 10.39631399 |
| 18 | EXPSGOOD | 0.0571949 | LTFININS | 9.931261421 |
| 19 | CTNDOI | 0.0562842 | INVENTORY | 8.750782913 |
| 20 | RDEXP | 0.0539162 | DEFTAXASSET | 8.591080109 |
| 21 | RETEARNING | 0.0522769 | EXPSRAW | 8.571741124 |
| 22 | OI | 0.0486339 | SELLEXPS | 8.103085643 |
| 23 | NI | 0.045173 | EXPSRENT | 7.989591611 |
| 24 | EXPSDEP | 0.0440801 | CASH | 7.521913646 |
| 25 | BORROWINGS_DEC | 0.0437158 | OCI | 7.228263512 |
| Random Forest Model | ||||
|---|---|---|---|---|
| Rank | PFI | SHAP | ||
| 1 | INTEXPS | 0.0229508 | INTEXPS | 0.199420242 |
| 2 | COMSTOCK | 0.00491803 | SALES | 0.079550986 |
| 3 | EXPSGOOD | 0.00255009 | EXPSTOT | 0.055302776 |
| 4 | RETEARNING | 0.00200364 | COMSTOCK | 0.036331639 |
| 5 | CLS | 0.00182149 | CLS | 0.027605796 |
| 6 | SHTLOAN | 0.00163934 | RDTOT | 0.01647187 |
| 7 | RECEIVABLES | 0.00145719 | LTBOND | 0.006915916 |
| 8 | INVENTORY | 0.00145719 | BOND_INC | 0.006796722 |
| 9 | AMTEXPS | 0.00127505 | LTBOND_INC | 0.006556615 |
| 10 | EXPSOTH | 0.00127505 | RDEXP | 0.005646649 |
| 11 | NI | 0.00127505 | NI | 0.005459114 |
| 12 | RENTEXPS | 0.0010929 | EXPSOTH | 0.005421135 |
| 13 | SALESPAYABLE | 0.0010929 | RETEARNING | 0.005313095 |
| 14 | TA_DEC | 0.0010929 | SHTBOND | 0.005244374 |
| 15 | CASH | 0.000910747 | SALESPAYABLE | 0.004962876 |
| 16 | PPE | 0.000910747 | BORROWINGS_DEC | 0.004868177 |
| 17 | DEFTAXASSET | 0.000910747 | CASH | 0.004706878 |
| 18 | RDEXPS | 0.000910747 | DIVOUT | 0.004585846 |
| 19 | DISCTNDOI | 0.000910747 | EMPEXPS | 0.004481484 |
| 20 | TA_INC | 0.000910747 | TA_INC | 0.004139376 |
| 21 | OCI | 0.000728597 | TA | 0.003939147 |
| 22 | EXPSBAD | 0.000728597 | EXPSLOGI | 0.003838548 |
| 23 | EPS_B | 0.000728597 | OI | 0.003732307 |
| 24 | OI | 0.000546448 | DEFTAXASSET | 0.003614583 |
| 25 | BORROWINGS_DEC | 0.000546448 | LTBORROWINGS | 0.003327861 |
| Logistic Regression Model | ||||
|---|---|---|---|---|
| Rank | PFI | SHAP | ||
| 1 | SALES | 0.282304 | COGS | 61.53445135 |
| 2 | EXPSOTH | 0.234558 | SALES | 45.59872648 |
| 3 | RDTOT | 0.2202 | EXPSLOGI | 25.53142992 |
| 4 | EXPSRAW | 0.197329 | BORROWINGS_INC | 19.68857208 |
| 5 | RDTOT_NCS | 0.174958 | DIVOUT | 17.69124581 |
| 6 | EXPSEMP | 0.153255 | OI | 14.14559552 |
| 7 | INTEXPS | 0.143072 | EMPEXPS | 12.70261301 |
| 8 | BORROWINGS_INC | 0.107179 | INTEXPS | 12.1180114 |
| 9 | DIVOUT | 0.0943239 | EXPSTOT | 9.989317447 |
| 10 | EXPSTOT | 0.0864775 | LTBOND | 8.602903724 |
| 11 | SALESPAYABLE | 0.0809683 | LTFININS | 7.631990299 |
| 12 | EXPSCOGSOTH | 0.0801336 | TA | 7.398501825 |
| 13 | TA | 0.0776294 | EXPSOTH | 6.496375107 |
| 14 | RECEIVABLES | 0.0742905 | SALESPAYABLE | 6.446622027 |
| 15 | RDEXP_NCS | 0.0729549 | TAXEXPENSE | 6.040313269 |
| 16 | COGS | 0.0716194 | INVENTORY | 5.892306269 |
| 17 | RDEXP | 0.0687813 | TAXPAYABLE | 5.211915496 |
| 18 | TAXEXPENSE | 0.0647746 | PPE | 4.601470208 |
| 19 | EXPSGOOD | 0.0604341 | RECEIVABLES | 4.512144215 |
| 20 | LTBOND | 0.0590985 | RDTOT | 3.650243276 |
| 21 | OI | 0.0587646 | RETEARNING | 3.568175264 |
| 22 | RETEARNING | 0.0552588 | EXPSRENT | 3.497344791 |
| 23 | DEFTAXASSET | 0.0520868 | COMSTOCK | 3.370334989 |
| 24 | EXPSLOGI | 0.0504174 | RDEXPS | 3.344085502 |
| 25 | SHTLOAN | 0.0398998 | BORROWINGS_DEC | 3.066701029 |
| Random Forest Model | ||||
|---|---|---|---|---|
| Rank | PFI | SHAP | ||
| 1 | INTEXPS | 0.0247078 | INTEXPS | 0.217342819 |
| 2 | COMSTOCK | 0.00467446 | SALES | 0.065933972 |
| 3 | INVENTORY | 0.00283806 | EXPSTOT | 0.042612209 |
| 4 | RDTOT | 0.00217028 | COMSTOCK | 0.039590058 |
| 5 | AMTEXPS | 0.00217028 | CLS | 0.024625831 |
| 6 | EXPSGOOD | 0.00217028 | RDTOT | 0.01095623 |
| 7 | EXPSOTH | 0.00200334 | EXPSOTH | 0.01047819 |
| 8 | CLS | 0.00166945 | EMPEXPS | 0.010419105 |
| 9 | RECEIVABLES | 0.0015025 | CASH | 0.007371457 |
| 10 | CASH | 0.0015025 | RETEARNING | 0.007330844 |
| 11 | PPE | 0.00133556 | TA_INC | 0.006274468 |
| 12 | RETEARNING | 0.00133556 | SHTLOAN | 0.006131024 |
| 13 | TA | 0.00116861 | TA_DEC | 0.00598646 |
| 14 | SALESPAYABLE | 0.00116861 | LTBOND_INC | 0.005816972 |
| 15 | TA_INC | 0.00116861 | SALESPAYABLE | 0.005810318 |
| 16 | SHTLOAN | 0.00100167 | TA | 0.005521536 |
| 17 | EXPSTOT | 0.00100167 | NI | 0.00517267 |
| 18 | RDEXP_NCS | 0.000834725 | SHTBOND | 0.005113623 |
| 19 | SHTBORROWINGS | 0.000834725 | BOND_INC | 0.004639136 |
| 20 | COGS | 0.000834725 | DIVOUT | 0.004391363 |
| 21 | DISCTNDOI | 0.000834725 | BORROWINGS_DEC | 0.004366225 |
| 22 | EPS_B | 0.000834725 | INTANGIBLES | 0.004243866 |
| 23 | EXPSBAD | 0.000834725 | RDEXPS | 0.003807693 |
| 24 | TA_DEC | 0.000834725 | LTBORROWINGS | 0.003581214 |
| 25 | RDTOT_NCS | 0.00066778 | RDTOT_NCS | 0.00348957 |
| Class Ratio | Algorithm | NearMiss | |||
|---|---|---|---|---|---|
| A | F | P | R | ||
| 500:598 | Logistic regression | 0.849 | 0.868 | 0.827 | 0.913 |
| Random Forest | 0.934 | 0.947 | 0.951 | 0.943 | |
| 600:598 | Logistic regression | 0.834 | 0.841 | 0.804 | 0.883 |
| Random Forest | 0.945 | 0.944 | 0.957 | 0.931 | |
| 1000:598 | Logistic regression | 0.806 | 0.762 | 0.704 | 0.831 |
| Random Forest | 0.947 | 0.926 | 0.966 | 0.890 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, W.; Kim, S. Enhancing Corporate Transparency: AI-Based Detection of Financial Misstatements in Korean Firms Using NearMiss Sampling and Explainable Models. Sustainability 2025, 17, 8933. https://doi.org/10.3390/su17198933
Kim W, Kim S. Enhancing Corporate Transparency: AI-Based Detection of Financial Misstatements in Korean Firms Using NearMiss Sampling and Explainable Models. Sustainability. 2025; 17(19):8933. https://doi.org/10.3390/su17198933
Chicago/Turabian StyleKim, Woosung, and Sooin Kim. 2025. "Enhancing Corporate Transparency: AI-Based Detection of Financial Misstatements in Korean Firms Using NearMiss Sampling and Explainable Models" Sustainability 17, no. 19: 8933. https://doi.org/10.3390/su17198933
APA StyleKim, W., & Kim, S. (2025). Enhancing Corporate Transparency: AI-Based Detection of Financial Misstatements in Korean Firms Using NearMiss Sampling and Explainable Models. Sustainability, 17(19), 8933. https://doi.org/10.3390/su17198933






