Network Equilibrium Analysis of Dual-Channel Environmental Hotel Supply Chains with M&A Using Variational Inequalities

Abstract

This paper develops a dual-channel environmental hotel supply chain equilibrium model to investigate the impact of mergers and acquisitions (M&A), decision makers’ altruistic preferences, and consumers’ low-carbon preferences under demand uncertainty. The model incorporates hotels, online travel agency (OTA) platforms, and demand markets and captures interactions under both the merchant and agency models. Variational inequalities are employed to describe interdependent decision-making behaviors, and the projection gradient algorithm is used to obtain equilibrium solutions. The numerical analysis reveals that sustainability factors directly affect the profitability of both hotels and OTAs. Under the agency model, higher commission rates reduce hotel profits while significantly increasing OTA gains. When comparing the merchant and agency models without M&A, the merchant model yields higher hotel profits, whereas the agency model favors OTAs. Furthermore, when M&A is combined with altruistic preferences, the utility of hotels and OTAs under the agency model reaches the highest level, while M&A offers limited advantages for OTAs. Overall, the findings highlight that sustainability factors, altruistic preferences, and M&A jointly interact with merchant and agency governance structures to shape profitability and utility. These results provide theoretical insights and managerial implications for developing resilient, cooperative, and low-carbon hotel supply chains under demand uncertainty.

1. Introduction

Sustainability has become a critical issue in the hospitality industry, particularly in the hotel sector, under the pressures of climate change, carbon reduction policies, and the United Nations’ Sustainable Development Goals (SDGs). These forces drive hotels to adapt toward low-carbon operations and align with sustainable tourism practices to meet the rising expectations of consumers. However, hotels continue to face demand uncertainty arising from seasonal fluctuations, shifts in consumer preferences, and behavioral factors, which may lead to capacity mismatches in the form of either excess rooms or shortages. This complexity is further heightened by the growing role of Online Travel Agencies (OTAs), such as Expedia and Booking.com, which, while expanding market reach and access to customers, also impose high commission fees and reduce hotels’ control over pricing.

Several recent works have examined hotel-OTA cooperation strategy. Jolene [1] investigates how participation in OTAs influences hotel revenue and channel distribution strategies, highlighting both opportunities and challenges in commission and channel mix. Ma [2] analyzes the Agent vs. Merchant selling formats between hotels and OTAs using a differential game model, offering insights about how bargaining power and format choice shape profitability. Atanasova and Ivanov [3] empirically study interactions between hotels and OTAs in urban Bulgaria, showing that OTA share, number of OTAs, and digital tools significantly affect distribution performance.

These challenges add layers of complexity to hotel supply chain management, making the formulation of appropriate strategies essential. Beyond economic strategies such as mergers and acquisitions (M&A) which are employed to integrate resources and enhance efficiency, resilience under volatile market conditions and risk mitigation can also be achieved through behavioral factors, particularly altruism, which fosters trust, sustains business relationships, and reduces overall risks. Behavioral economics research [4] has shown that when players in a system exhibit altruistic behavior, the system becomes more efficient and generates greater total benefits compared to the selfish benchmark.

This study seeks to bridge the identified research gap by developing a network equilibrium model for an environmentally conscious dual-channel hotel supply chain under demand uncertainty. The model integrates M&A structures, OTA platforms, and consumer sustainability preferences expressed through altruistic behaviors. Variational inequality theory is applied to capture interdependent decision-making processes, and the projection extragradient method is employed to compute equilibrium solutions.

Within this framework, four central research questions are investigated. First, how do M&A structures influence supply chain equilibrium under demand uncertainty? Second, what is the impact of commission rates in the agency model on the profitability of hotels and OTA platforms? Third, what roles do consumer low-carbon preferences and altruistic behaviors play in shaping decision-making outcomes? Finally, how do the agency and merchant OTA models differ in their effects on profitability and utility, thereby revealing the governance mechanisms that drive performance in dual-channel hotel supply chains?

This paper’s remaining sections are organized as follows. Section 2 reviews the related literature on demand uncertainty, low-carbon preferences, and supply chain networks. Section 3 presents the problem statement, introduces the relevant notation, and outlines the model assumptions, while Section 4 formulates the supply chain model with dual channels under the merchant and agency structures, develops the corresponding variational inequality, analyzes decision behavior and equilibrium, and establishes the existence and uniqueness of solutions. Section 5 reports numerical results, Section 6 outlines the managerial implications, offering practical insights for hotel managers, OTA platforms, and policymakers, Section 7 discusses the results, and Section 8 concludes the paper by summarizing the main findings, highlighting limitations, and suggesting directions for future research.

2. Literature Review

The literature review synthesizes prior studies and highlights the gaps that motivate the proposed model.

2.1. Demand Uncertainty

Demand uncertainty is a fundamental characteristic of the hospitality industry and directly shapes supply chain decision-making, which involves not only strategic considerations of profit maximization but also behavioral factors such as preferences and reciprocity. Suh [5] notes that the trust inherent in altruism helps maintain reputational capital in business relationships, while Bassi et al. [6] incorporate altruistic preferences into a principal–agent setting and show that when agents are altruistic, overall efficiency and benefits exceed the selfish benchmark. Demand uncertainty typically arises when service supply does not match market demand, producing excess capacity or shortages [7,8]. Earlier supply chain research under uncertainty proposed heuristics for agile environments [9], multi-period equilibrium models with static and dynamic loss aversion [10], and competitive equilibrium with cost and demand uncertainty [11].

Recent work in tourism and operations extends these insights. Erol et al. [12] analyzes supply chain resilience in tourism and hospitality under fluctuating demand, identifying drivers and inhibitors of adaptive capacity; An et al. [13] show how outsourcing and IT adoption mitigate risk in tourism supply chains facing volatile demand; and Guo et al. [14] reviews inventory strategies that enhance resilience to demand shocks. Complementary studies indicate that demand uncertainty moderates the relationship between supply chain risk and organizational performance [15].

These studies collectively point to the importance of cooperation mechanisms under uncertainty. In hospitality, horizontal altruism cooperation among hotels via cross-selling, shared customer bases, or post-M&A integration can redistribute risk, expand effective market demand, and stabilize profitability. While altruism has been modeled in dual-channel hotel supply chains under uncertainty [16], explicit integration of demand uncertainty with horizontal altruistic behaviors in a hospitality equilibrium framework remains limited.

2.2. Low-Carbon Preferences

Low-carbon preferences have increasingly shaped supply chain strategies, particularly in tourism and hospitality industries where consumer perception, environmental awareness, and sustainability are decisive factors. Early studies in the hospitality sector, such as Wang et al. [17], highlighted the identification of key sustainability dimensions and indicators as a strategic approach to guide the development of effective hotel business models. Sari and Suslu [18] further developed a model to assess green efficiency in hotel supply chains, helping to identify areas for improvement and enhance operational performance.

From a modeling perspective, Wan et al. [16] examined the interplay between altruistic preferences and low-carbon consumer demand in dual-channel hotel supply chains under uncertainty, applying variational inequalities to achieve optimal decision-making. Similarly, Valderrama et al. [19] proposed a supply chain network model aimed at reducing carbon emissions in the mining sector, while Cheng et al. [20] analyzed cooperation structures in assembly supply chains, deriving optimal decisions alongside carbon reduction strategies. In tourism contexts, Gössling [21] underscored that reducing the carbon footprint of travel and hospitality services is not only an ecological necessity but also a strategic imperative for long-term competitiveness.

Recent advances have extended this discussion into dual-channel and service-oriented supply chains. Wang et al. [4] examined altruistic fairness in supply chain decision-making, illustrating how behavioral preferences interact with economic outcomes. Fan et al. [22] further demonstrated the hotel industry must transition to green hotels to mitigate energy consumption, waste, and pollution, thereby generating both economic and social benefits. In particular, consumers’ low-carbon preferences serve as a critical driving force, encouraging hotel operators to adopt low-carbon strategies and move toward sustainable operations.

2.3. Supply Chain Network

The notion of variational inequality (VI) has been widely used to create equilibrium models for supply chain networks. From the early 2000s until now, the main methods for solving these Variational Inequality Models (VIMs) have been the Projection Method (PM), Modified Projection Method (MPM), and Euler Algorithm (EA).

Nagurney et al. [23] developed a variational inequality framework for supply chain networks incorporating electronic commerce, which they solved using the MPM. Dong et al. [24] proposed a Supply Chain Network Equilibrium Model (SCNEM) that incorporated stochastic demand and solved it using the MPM. In a related study, Nagurney et al. [25], introduced a multi-tier SCNEM that emphasized profit maximization and risk minimization in decision-making. Hsueh and Chang [26] explored the relationship between manufacturer coordination, corporate social responsibility, and the profitability of a three-tier supply chain involving manufacturers, distributors, and retailers. Their approach employed a hybrid solution algorithm that merged the diagonalization method with a user-equilibrium traffic assignment. Over the past decade, research has advanced to cover more specialized areas of supply chains through variational inequality modeling. Liu and Nagurney [27] analyzed financial risk using a VI framework and solved it with the MPM. Zhou et al. [10] contributed a multi-period supply chain VI model that incorporated time-varying loss-averse preferences. Liu and Wang [11] addressed risk hedging via futures contracts with a VI equilibrium approach, while Zhang et al. [28] formulated and solved a dual-channel SCNEM using MPM.

Recently, scholars have examined topics such as sustainability, uncertainty, global supply chain outsourcing, and competitive dynamics among supply chains. Chen et al. [29] applied a VI equilibrium approach to the automotive supply chain, incorporating uncertain payment delays. Korpeoglu et al. [30] explored supply chain competition by modeling the influence of supplier and retailer decisions on wholesale prices. He et al. [31] analyzed a dual-channel supply chain consisting of a manufacturer and a retailer, examining two periods to determine the optimal pricing strategy.

Additionally, Wan et al. [16] developed a dual-channel environmental hotel supply chain equilibrium model under demand uncertainty, integrating altruistic and low-carbon preferences, and solved it using an improved gradient algorithm. They examined decision-making under the merchant and agency models in dual-channel hotel supply chains (Figure 1). In the agency model, OTAs charge a commission while hotels control pricing and allocation; in the merchant model, OTAs purchase rooms at wholesale prices, set retail rates, and assume inventory risk. These differences shift pricing power, risk, and profitability between hotels and OTAs [32].

The hotel business is currently very competitive and changing quickly. Market expansion, risk diversification, and access to new resources and technology, including green advances, are all made possible through industry mergers and acquisitions (M&A). According to Real Capital Analytics (RCA) data from 2009–2019, global hotel M&A transactions grew from USD 20 billion to USD 70 billion, with major deals such as Marriott’s USD 13.6 billion acquisition of Starwood and Pebblebrook’s USD 5.2 billion acquisition of LaSalle. While M&A research exists in management and supply chain contexts [33,34] studies specifically addressing hotel industry M&A remain limited despite its unique capital-intensive and brand-driven characteristics.

By analyzing sustainability, low-carbon preferences, altruistic behaviors, and governance mechanisms under demand uncertainty, the body of extant literature has substantially improved our understanding of hotel supply chains. The integration of these aspects with mergers and acquisitions (M&A) under a single analytical framework has received little attention, despite the fact that previous studies offer insightful information about customer preferences, commission structures, and strategic collaboration between hotels and OTAs. This disparity highlights the need for more studies that integrate behavioral preferences, structural dynamics, and environmental sustainability to more fully explain equilibrium results in dual-channel hotel supply chains.

3. Problem Statement and Formulation

3.1. Problem Statement

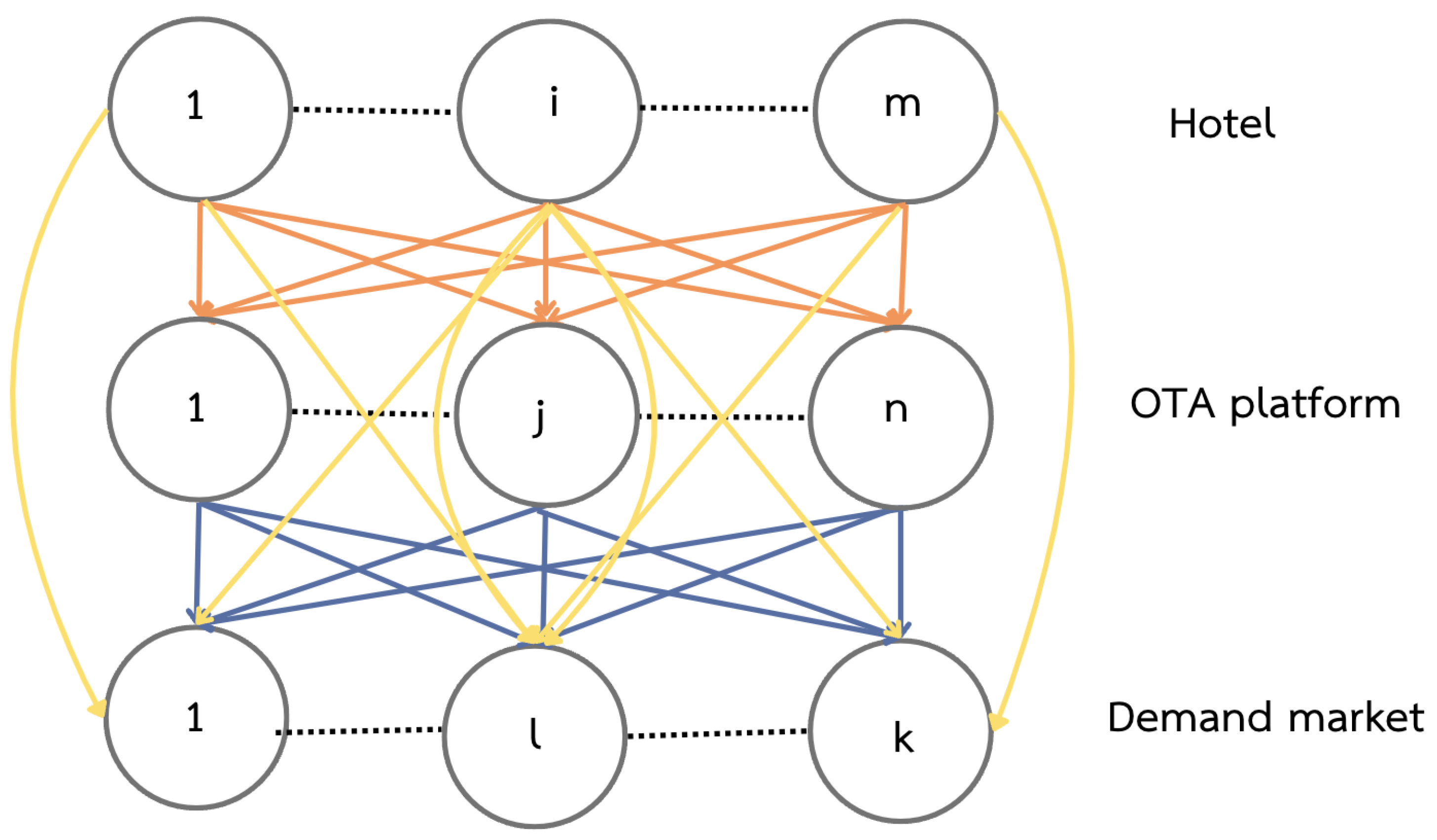
The dual-channel hotel supply chain network used in this study, as illustrated in Figure 2, integrates both direct sales and OTA-mediated channels while incorporating strategic mergers and acquisitions (M&A). In this structure, hotels may sell Travel Service Packages (TS&P) to OTA platforms, which subsequently distribute Environmental Travel Service & Packages (ETS&P) to the demand market at a retail price. At the same time, hotels may bypass intermediaries by selling ETS &P directly to the demand market, creating a competitive dual-channel environment.

The network also incorporates vertical integration through M&A, wherein merged hotels acquire other hotels to expand market share and enhance operational efficiency. This strategic interaction between channel selection and M&A activities introduces complex decision-making dynamics, influenced by pricing strategies, demand uncertainty, and environmental considerations.

Given that OTA–hotel cooperation typically follows either the agency model or the merchant model, each with distinct implications for pricing control, inventory ownership, and revenue sharing, understanding these differences is essential for analyzing equilibrium outcomes in this study.

3.2. Model Assumptions

The following are the main hypotheses of the supply chain with dual channel in relation to M&A and carbon reduction:

Hypothesis 1.

Carbon Emissions and Their Impact on Hotel Costs.

The implementation of carbon emission reduction measures by hotels can be classified into the following two scenarios:

• Case 1: No Carbon Emission Reduction Measures
  In this case, the hotel does not implement any emission reduction strategies. The carbon emissions from the production or service processes remain at the base level, denoted as $e_0$. The cost function of the hotel, without any emission reduction effort, is represented by $f_{i0}\left(q_i\right)$, which reflects the baseline cost structure associated with carbon-intensive operations.
• Case 2: Implementation of Carbon Emission Reduction Measures
  In this scenario, the hotel engages in efforts to reduce emissions, thereby lowering the total emission level to e, where $e_0>e>0$. The emission reduction level is defined by the parameter $\phi$, calculated as follows:

  $$\phi ={\displaystyle \frac{e_0-e}{e_0}}=1-{\displaystyle \frac{e}{e_0}},$$

  where $0<\phi \le 1$. The cost function of the hotel that incorporates the carbon emission reduction is adjusted accordingly:

  $$f_i\left(q_i\right)={\phi }^{-h}{f}_{i0}\left(q_i\right),$$

  where $h>0$ is the sensitivity coefficient, reflecting how significantly the reduction level $\phi$ affects the cost. A higher value of h implies a greater impact of emission reduction on the hotel’s cost. This hypothesis aligns with the concept proposed by [35].

Hypothesis 2.

Consumers’ Preference for Environmentally Products.

Customers exhibit a preference for hotels that offer environmentally friendly tourism products and services (ETP&S). In general, these customers are prepared to pay more for goods or services that support environmental sustainability. This relationship can be captured through a demand function, expressed as follows:

$$d_l\left({\rho }_l\right)=d-{\phi }^g{\rho }_l,$$

(1)

where d denotes for the basic market demand and g for the degree of customer preference for low-carbon products. As g increases, the term ${\phi }^g$ becomes smaller, thus reducing the negative impact of price ${\rho }_l$ on the demand $d_l$. This formulation is consistent with the findings of Fan et al. [36], which emphasize that greater consumer preference for environmental sustainability enhances market demand for green products and services.

Hypothesis 3.

Transaction Costs in the OTA Platform.

When hotel i conducts business with OTA platform j, transaction costs will be incurred [24,36]. These transaction costs can be represented by a cost function $c_{ij}\left(q_{ij}^{\mathrm{OTA}}\right)$. Similarly, in the case where hotel i engages in transactions with market l, the transaction cost is given by the function $c_{il}\left(q_{il}^H\right)$. Furthermore, when OTA platform j transacts with market l, the associated transaction cost is expressed as $c_{jl}\left(q_{jl}^{\mathrm{OTA}}\right)$. It is assumed that $f_i\left(q_i\right)$, $c_{ij}\left(q_{ij}^{\mathrm{OTA}}\right)$, and $c_{il}\left(q_{il}^H\right)$ are quadratic continuously differentiable convex functions.

Hypothesis 4.

Hotel Business Mergers.

Hotel mergers within a supply chain can generate synergies that benefit both demand and cost structures. Specifically, revenue synergy arises when merged hotels leverage shared customer data and cross-selling strategies, A profit-sharing rate of $r\%$ is assumed, to expand market reach. The resulting demand after the merger can be represented as follows:

$$d_{jl}^{\mathrm{OTA}}={\gamma }_j·d_l\left({\rho }_l\right),d_{il}^H={\gamma }_i·d_l\left({\rho }_l\right),$$

(2)

where ${\gamma }_j,{\gamma }_i>1$. Here, ${\gamma }_j$ and ${\gamma }_i$ reflect the demand amplification due to synergy effects.

Meanwhile, cost synergy is achieved through reduced OTA commission fees when multiple hotels use the same platform. This relationship is given by the following:

$${\alpha }_j={\alpha }_0-{\varphi }_j·N_j,$$

(3)

where ${\alpha }_0$ is the base fee when there is only one hotel, $N_j$ is the number of hotels under M&A which use the same platform on OTA, and ${\varphi }_j$ captures the rate at which decreases with each additional hotel. These synergy effects are consistent with insights from Deloitte [37]. Such effects are well documented in hospitality management literature, where empirical studies (e.g., [34,38]) demonstrate that resource sharing and organizational consolidation frequently lead to enhanced efficiency and improved competitive positioning in hotel markets.

Hypothesis 5.

Mergers and acquisition.

• Merging Hotel: In this study, a Merging Hotel refers to a hotel that has acquired another hotel (Acquired Hotel) through a merger or acquisition process. Although the Acquired Hotel may continue its operations independently, the Merging Hotel benefits from the combined synergy and receives a portion of the Acquired Hotel’s profit due to ownership rights.
• Acquired Hotel: An Acquired Hotel is a hotel that has been taken over by a Merging Hotel but continues to operate under its original management. It contributes to the synergy generated from the merger while sharing a portion of its profit with the Merging Hotel as part of the acquisition agreement.

4. Model Building

The network equilibrium of the hotel supply chain with dual-channel is examined in this section using the merchant model and agency model with M&A in the basic case, demand uncertainty, and altruistic preferences cases.

4.1. Basic Dual-Channel Supply Chain Model

In the basic setting, each decision maker in the hotel supply chain with a dual channel seeks to maximize profit from its objective function subject to demand and capacity constraints.

4.1.1. The Merchant Model with M&A

In the merchant model with mergers and acquisitions (M&A), OTA platforms act as resellers: they purchase hotel room inventory at wholesale prices and sell it to consumers at retail prices. Following M&A activities among hotels, wholesale prices may decrease due to enhanced bargaining power, cost synergies, and economies of scale. These dynamics affect how profits are distributed between hotels and OTAs, as well as how demand markets respond to adjusted prices. To capture these interactions, the model is structured into three interconnected components: (i) hotels, (ii) OTA platforms, and (iii) demand markets.

• Hotels: Each hotel maximizes profit from both direct sales and OTA channels, accounting for operating and transaction costs as well as possible M&A structures (e.g., profit-sharing and synergies). The hotel i distributes room inventory to OTA platform j through wholesale pricing ${\omega }_{ij}$. These wholesale prices incorporate per-hotel discounts ${\varphi }_{ij}$, which increase with the number of hotels $N_{ij}$ partnering with OTA j, reflecting enhanced bargaining power and cost synergies. The generic profit function of hotel i can be expressed as follows:

  $$\begin{array}{cc}\hfill max{\pi }_i^{\mathrm{merging}}(q,Q^1,Q^2)=& \sum _{l=1}^k{q}_{il}^H{\rho }_{il}^H+\sum _{j=1}^n\sum _{l=1}^k{q}_{ij}^{OTA}\left({\omega }_{ij}^{OTA}+{\varphi }_{ij}·N_{ij}\right)-f_i\left(q\right)\hfill \\ \hfill & -\sum _{l=1}^k{c}_{il}\left(q_{il}^H\right)-\sum _{j=1}^n{c}_{ij}\left(q_{ij}^{OTA}\right)+r_i\sum _{M=1}^s{\pi }_M^{\mathrm{acquired}}\hfill \\ \hfill & -C_i(q^{\mathrm{merging}},q^{\mathrm{acquired}}),\hfill \end{array}$$

  (4)

  $$\begin{array}{cc}\hfill max{\pi }_i^{\mathrm{acquired}}(q,Q^1,Q^2)=& \left(1-r_i\right)(\sum _{l=1}^k{q}_{il}^H{\rho }_{il}^H+\sum _{j=1}^n\sum _{l=1}^k{q}_{ij}^{OTA}\left({\omega }_{ij}^{OTA}+{\varphi }_{ij}·N_{ij}\right)-f_i\left(q\right)\hfill \\ \hfill & -\sum _{l=1}^k{c}_{il}\left(q_{il}^H\right)-\sum _{j=1}^n{c}_{ij}\left(q_{ij}^{OTA}\right)),\hfill \end{array}$$

  (5)

  $$\begin{array}{cc}\hfill max{\pi }_i^{\text{non-M\&A}}(q,Q^1,Q^2)=& \sum _{l=1}^k{q}_{il}^H{\rho }_{il}^H+\sum _{j=1}^n\sum _{l=1}^k{q}_{ij}^{OTA}{\omega }_{ij}^{OTA}-f_i\left(q\right)\hfill \\ \hfill & -\sum _{l=1}^k{c}_{il}\left(q_{il}^H\right)-\sum _{j=1}^n{c}_{ij}\left(q_{ij}^{OTA}\right).\hfill \end{array}$$

  (6)
• OTA platforms: The OTA acts as a reseller, purchasing hotel room inventory at wholesale prices and reselling it to consumers at retail prices. Mergers and acquisitions among hotels enhance the OTA’s bargaining power and generate cost synergies, which reduce wholesale prices by a discount term as ${\varphi }_{ij}{N}_{ij}$ where ${\varphi }_{ij}$ is the per-hotel discount rate, and $N_{ij}$ is the number of hotels associated with OTA j. As illustrated in Figure 2, the OTA’s profit function can then be written as follows:

  $$\begin{array}{cc}\hfill max{\pi }_j^{OTA}(Q^1,Q^3)=& \sum _{l=1}^k{q}_{jl}^{OTA}{\rho }_{jl}^{OTA}-\sum _{i=1}^s{q}_{ij}^{OTA}\left({\omega }_{ij}^{OTA}+{\varphi }_{ij}{N}_{ij}\right)-\sum _{i=s+1}^m{q}_{ij}^{OTA}{\omega }_{ij}^{OTA}\hfill \\ \hfill & -c_j(Q^1,Q^3),\hfill \end{array}$$

  (7)
• Demand market: A demand market l reaches equilibrium when the total supply of services provided by hotels and OTA platforms equals the demand of that market. When a merger between hotels leads to cross-selling and shared customer bases, it may cause the market demand to expand. This expansion is represented by a parameter ${\varsigma }_l>1$, reflecting the increased market demand due to merger synergy.

  $${\varsigma }_l·d_l\left({\rho }_l^{\ast }\right)=\left\{\begin{array}{cc}\le \sum _{i=1}^m{q}_{il}^{H\ast }+\sum _{j=1}^n{q}_{jl}^{OTA\ast },\hfill & \mathrm{if}{\rho }_l^{\ast }=0,\hfill \\ =\sum _{i=1}^m{q}_{il}^{H\ast }+\sum _{j=1}^n{q}_{jl}^{OTA\ast },\hfill & \mathrm{if}{\rho }_l^{\ast }>0,\hfill \end{array}\right.$$

  (8)

  where ${\varsigma }_l=max({\varsigma }_i,{\varsigma }_j)$ denotes the market expansion index due to hotel merger synergy, and $d_l\left({\rho }_l^{\ast }\right)$ is the original market demand function based on the equilibrium retail price ${\rho }_l^{\ast }$. For this equilibrium condition to hold, the following decision rules must be satisfied by hotels and OTA platforms:
  • For Hotels:

    $${\rho }_{il}^H+c_{il}\left(q_{il}^H\right)\left\{\begin{array}{cc}={\rho }_l^{\ast },\hfill & \mathrm{if}{q}_{il}^{H\ast }>0,\hfill \\ \ge {\rho }_l^{\ast },\hfill & \mathrm{if}{q}_{il}^{H\ast }=0.\hfill \end{array}\right.$$

    (9)
  • For OTA Platforms:

    $${\rho }_{jl}^{OTA}+c_j\left(q_{ij}^{OTA},q_{jl}^{OTA}\right)\left\{\begin{array}{cc}={\rho }_l^{\ast },\hfill & \mathrm{if}{q}_{jl}^{OTA\ast }>0,\hfill \\ \ge {\rho }_l^{\ast },\hfill & \mathrm{if}{q}_{jl}^{OTA\ast }=0.\hfill \end{array}\right.$$

    (10)
  Equations (9) and (10) imply that a supply-side-demand market transaction will only take place if the entire transaction cost is less than the retail market price. Otherwise, no transaction takes place.

4.1.2. The Agency Model with M&A

In the agency model with mergers and acquisitions (M&A), OTA platforms sell hotel services on behalf of hotels and retain a commission, while hotels receive the remaining share of the sales revenue. The commission rate decreases as the number of affiliated hotels increases, reflecting bargaining power and cost synergies created through M&A. This interaction shapes the profit and utility functions of the key players in the supply chain. The model can be decomposed into three interrelated components: hotels, OTA platforms, and demand markets.

• Hotels: Hotels sell directly to demand markets at their own prices, while OTA platforms sell on behalf of hotels and charge a commission fee. This commission decreases with the number of hotels affiliated under OTA j, reflecting bargaining power and synergies from mergers and acquisitions (M&A): ${\alpha }_j\left(N_j\right)={\alpha }_0-{\varphi }_j{N}_j,$ where ${\alpha }_0>0$ is the base commission rate when only one hotel participates, $N_j$ is the number of merged or acquired hotels under OTA j, and ${\varphi }_j$ denotes the per-hotel discount rate.

  $$\begin{array}{cc}\hfill max{\pi }_i^{\mathrm{merging}}(q,Q^1,Q^2)=& \sum _{l=1}^k{q}_{il}^H{\rho }_{il}^H+\sum _{j=1}^n\sum _{l=1}^k(1-{\alpha }_j\left(N_j\right))q_{ij}^{OTA}{\rho }_{jl}^{OTA}-f_i\left(q\right)\hfill \\ \hfill -& \sum _{l=1}^k{c}_{il}\left(q_{il}^H\right)-\sum _{j=1}^n{c}_{ij}\left(q_{ij}^{OTA}\right)+r_i\sum _{M=1}^s{\pi }_M^{\mathrm{acquired}}\hfill \\ \hfill & -C_i(q^{\mathrm{merging}},q^{\mathrm{acquired}}),\hfill \end{array}$$

  (11)

  $$\begin{array}{cc}\hfill max{\pi }_i^{\mathrm{acquired}}(q,Q^1,Q^2)=& \left(1-r_i\right)(\sum _{l=1}^k{q}_{il}^H{\rho }_{il}^H+\sum _{j=1}^n\sum _{l=1}^k{q}_{ij}^{OTA}(1-{\alpha }_j\left(N_j\right))-f_i\left(q\right)\hfill \\ \hfill & -\sum _{l=1}^k{c}_{il}\left(q_{il}^H\right)-\sum _{j=1}^n{c}_{ij}\left(q_{ij}^{OTA}\right)),\hfill \end{array}$$

  (12)

  $$\begin{array}{cc}\hfill max{\pi }_i^{\text{non-M\&A}}(q,Q^1,Q^2)=& \sum _{l=1}^k{q}_{il}^H{\rho }_{il}^H+\sum _{j=1}^n\sum _{l=1}^k(1-{\alpha }_0)q_{ij}^{OTA}{\rho }_{jl}^{OTA}-f_i\left(q\right)\hfill \\ \hfill & -\sum _{l=1}^k{c}_{il}\left(q_{il}^H\right)-\sum _{j=1}^n{c}_{ij}\left(q_{ij}^{OTA}\right).\hfill \end{array}$$

  (13)
• OTA platforms: OTA platforms j sell hotel ETP&S on behalf of hotels, retaining a commission rate ${\alpha }_j\left(N_j\right)$ and transferring $(1-{\alpha }_j\left(N_j\right))$ of the revenue to hotels. When multiple hotels are affiliated with the same OTA, cost synergies reduce commission fees. The optimal decision-making behavior of the OTA platforms under the objective of profit maximization can be defined by the following optimality conditions:

  $$max{\pi }_j^{OTA}(Q^1,Q^3)=\sum _{l=1}^k{\alpha }_j\left(N_j\right)q_{jl}^{OTA}{\rho }_{jl}^{OTA}-c_j(Q^1,Q^3).$$

  (14)
• Demand market: The agency model’s market equilibrium model is similar to the merchant model.

4.2. The Supply Chain Model with Dual Channels, Horizontal Altruism, and Uncertain Demand

Incorporating altruistic preferences modifies the decision-making process. Players consider not only their own profits but also those of others, reflecting behavioral economics perspectives.

• Hotels: Assume that hotels exhibit a horizontal altruistic preference, the degree of altruism for hotel i is denoted by ${\gamma }_i$. This implies that hotel i not only considers its own profit but also accounts for the profits of the remaining $m-1$ hotels:

  $$max{U}_i^H={\pi }_i^H+{\displaystyle \frac{{\gamma }_i}{m-1}}\sum _{p\ne i}{\pi }_p,$$

  (15)

  when ${\gamma }_i=0$, the benchmark is purely selfish.
• OTA platforms: OTAs may also incorporate the average profits of affiliated hotels:

  $$max{U}_j^{OTA}(Q^1,Q^3)={\pi }_j^{OTA}+{\displaystyle \frac{{\lambda }_j}{n-1}}\sum _{p\ne j}{\pi }_p,$$

  (16)

  where ${\lambda }_j\ge 0$ represents OTA altruism.
• Demand market: Market demand can be represented as a random variable ${\tilde{d}}_l\left({\rho }_l\right)$, where ${\rho }_l$ denotes the retail price in market l. The expected value of the demand is $d_l\left({\rho }_l\right)$, and its probability density function is $f_l(s,{\rho }_l)$. The corresponding cumulative distribution function is defined as follows:

  $$F_l(s,{\rho }_l)={\int }_{-\infty }^s{f}_l(s,{\rho }_l)ds.$$

  (17)

Let $s_l$ denote the total quantity of goods and services provided by hotels and OTA platforms to market l, i.e., $s_l={\sum }_{i=1}^m{q}_{il}^{H\ast }+{\sum }_{j=1}^n{q}_{jl}^{OTA\ast }.$ The realized demand is given by ${\tilde{d}}_l$, and the actual sales volume is $min\{s_l,{\tilde{d}}_l\}$. Define the excess supply and excess demand as follows:

$$\begin{array}{cc}\hfill {\Delta }_l^{+}& =max\{0,s_l-{\tilde{d}}_l\},\hfill \\ \hfill {\Delta }_l^{-}& =max\{0,{\tilde{d}}_l-s_l\}.\hfill \end{array}$$

Let ${ϵ}_l^{+}$ be the unit penalty cost of excess supply, and ${ϵ}_l^{-}$ be the unit penalty cost of excess demand, as proposed by [24].

Accordingly, the market equilibrium condition with demand uncertainty and market expansion becomes

$${\varsigma }_l·{\tilde{d}}_l\left({\rho }_l^{\ast }\right)=\left\{\begin{array}{cc}\le \sum _{i=1}^m{q}_{il}^{H\ast }+\sum _{j=1}^n{q}_{jl}^{OTA\ast },\hfill & \mathrm{if}{\rho }_l^{\ast }=0,\hfill \\ =\sum _{i=1}^m{q}_{il}^{H\ast }+\sum _{j=1}^n{q}_{jl}^{OTA\ast },\hfill & \mathrm{if}{\rho }_l^{\ast }>0,\hfill \end{array}\right.$$

(18)

Moreover, the market clearing conditions are

$${\rho }_{il}^H+c_{il}\left(q_{il}^H\right)\left\{\begin{array}{cc}={\rho }_l^{\ast },\hfill & \mathrm{if}{q}_{il}^{H\ast }>0,\hfill \\ \ge {\rho }_l^{\ast },\hfill & \mathrm{if}{q}_{il}^{H\ast }=0,\hfill \end{array}\right.$$

(19)

$${\rho }_{jl}^{OTA}+c_j(q_{ij}^{OTA},q_{jl}^{OTA})\left\{\begin{array}{cc}={\rho }_l^{\ast },\hfill & \mathrm{if}{q}_{jl}^{OTA\ast }>0,\hfill \\ \ge {\rho }_l^{\ast },\hfill & \mathrm{if}{q}_{jl}^{OTA\ast }=0.\hfill \end{array}\right.$$

(20)

Given the aforementioned circumstances, it is evident that market transactions only take place when the retail price is more than the entire cost of the hotels or OTA platforms across all marketing channels. The incorporation of demand uncertainty into the model allows for a more realistic reflection of market behavior.

4.3. Variational Inequality (VI)

A technique used to express the dual-channel hotel supply chain’s equilibrium is as a variational inequality. Let the decision vector be

$$x=(Q^{1\ast },Q^{2\ast },q^{\ast },{\delta }^{\ast },Q^{3\ast },{\theta }^{\ast },{\rho }_l^{\ast })\in {\mathbb{R}}^{mn+mk+m+m}\times {\mathbb{R}}^{nk+n}\times {\mathbb{R}}^k,$$

Define $F\left(x\right)$ as the mapping of marginal profits and costs for hotels, OTA platforms, and demand markets. The equilibrium problem can then be expressed as follows:

$$\mathrm{Find}{x}^{\ast }\in K\mathrm{such}\mathrm{that}\langle F\left(x^{\ast }\right),x-x^{\ast }\rangle \ge 0,\forall x\in K,$$

(21)

where K denotes the feasible set of decision variables.

These conditions provide the final variational inequality (VI) system that describes the equilibrium and decision behavior of the supply chain model with dual channels under both the agency and merchant models (for the full formulation, see Appendix A).

4.4. Existence of the Supply Chain Network Model with Dual Channels and Its Uniqueness Results

The nonlinear complementarity problem (NCP), which is to find a vector $x\in {\mathbb{R}}^n$ satisfying the system of equations and inequalities

$$x\ge 0,F\left(x\right)\ge 0,x^{T}F\left(x\right)=0$$

or, equivalently,

$$x_i\ge 0,F_i\left(x\right)\ge 0,x_i{F}_i\left(x\right)=0\mathrm{for}i=1,\dots ,n.$$

Here, $F:\mathbf{X}\to {\mathbb{R}}^n$ is a given function defined on a subset $\mathbf{X}\subseteq {\mathbb{R}}^n$ containing at least the non-negative orthant.

NCP was introduced by Cottle [39], and related variational inequality problem (VIP) was introduced by Hartman and Stampacchia [40], primarily with the goal of computing stationary points for nonlinear programs.

The following nonlinear complementarity problem (NCP) may be derived using the Formulas (A1)–(A4), which is obviously non-negative.

The following theorem provides conditions to ensure that the solutions of (A1)–(A4) are existing and unique in accordance with the existence theory of NCP [41], as stated in [42].

5. Algorithm and Numerical Results

We assume that the hotel supply chain network consists of 3 hotels ($i=1,2,3$), where hotels 1 and 3 are large-sized hotels, and hotel 2 is a medium-sized hotel. There are 3 OTA platforms ($j=1,2,3$) and 3 consumer markets ($l=1,2,3$). The transaction cost function between hotel i and OTA j is defined as follows:

$$c_{ij}\left(q_{ij}^{OTA}\right)=0.5{\left(q_{ij}^{OTA}\right)}^2+3.5q_{ij}^{OTA},$$

where $i=1,2,3$ and $j=1,2,3$. The transaction cost function between hotel i and market l is given by the following:

$$c_{il}\left(q_{il}^H\right)=0.5{\left(q_{il}^H\right)}^2+5q_{il}^H,$$

where $i=1,2,3$ and $l=1,2,3$. The operating cost function of OTA j is expressed as follows:

$$c_j(Q^1,Q^3)=0.5{\left(\sum _{i=1}^3{q}_{ij}^{OTA}+\sum _{l=1}^3{q}_{jl}^{OTA}\right)}^2,$$

where $j=1,2,3$. The cost function after greenhouse gas emission reduction is

$$f_i\left(q_i\right)=q_i+0.5q_i^2+5,$$

where $i=1,2,3$. The cost function for mergers is formulated as follows:

$$C(q,t)=\left(q+3q^2-5\right)-{\displaystyle \frac{q+3q^2-5}{5}}t,$$

where t is the number of months and $q=q^{\mathrm{merging}}+q^{\mathrm{acquired}}$.

In this study, the projection extragradient method algorithm is applied to obtain the equilibrium solution of the problem. It was first introduced by Korpelevich [43], described as a projection extragradient method algorithm for equilibrium decision-making under altruism preferences and demand uncertainty in a dual-channel environmental hotel supply chain network (Algorithm 1).

Algorithm 1 Projection extragradient method algorithm

Input: Initial decision variable values $X={(Q^1,Q^2,Q^3,q,\rho ,\delta ,\theta )}^T$; Set the initial vector x Begin While $e>{10}^{-3}$ Set the step size $\sigma$ and compute: $y={\Pi }_{[0,u]}(x-\sigma F\left(x\right))$ Compute: $x_{\mathrm{new}}={\Pi }_{[0,u]}(x-\sigma F\left(y\right))$ Compute the error: $A=x_{\mathrm{new}}-x$,    $e=A^{T}A$ If $e\le {10}^{-3}$ then return $x_{\mathrm{new}}$, else set $x=x_{\mathrm{new}}$ and continue the algorithm End

Note: ${\Pi }_{[0,u]}(·)$ denotes the projection function mapping a value into the domain $[0,u]$ for each variable to ensure feasibility with respect to the constraints.

We set the step size $\sigma =0.0001$, the initial error $e_0=4$, and the initial vector of decision variables as follows: $x_0={(1,1,1,\dots ,1)}_{1\times 39}$ with the projection bounds which have $\mathrm{Lower}\mathrm{bound}={(0,0,0,\dots ,0)}_{1\times 39}$ and Upper bound = (500, 500, 500, 50, 50, 50, 500, 500, 500, 500, 500, 500, 50, 50, 50, 500, 500, 500, 525, 525, 525, 525, 525, 525, 525, 525, 525, 1100, 1100, 1100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100)_1×39.

5.1. Basic Merchant Model and Agency Model

The demand function in the merchant basic model is given by $d_l\left({\rho }_l\right)=1000-{\phi }^g{\rho }_l,$ where $(\phi ,g,h)=(1,1,1),(\phi ,g,h)=(0.75,1,1),(\phi ,g,h)=(0.5,1,1),(\phi ,g,h)=(0.75,0.75,0.75),(\phi ,g,h)=(0.75,1,0.75),(\phi ,g,h)=(0.75,0.75,1)$, ${\rho }_{il}^H$, ${\rho }_{jl}^{OTA}$ = 2500 and ${\omega }_{ij}^{OTA}$ = 1250 for $i,j,l=1,2,3$. Python 3 is used to run the program, and

Table 1. Results under different parameter values of $(\phi ,h,g)$ without M&A.

	(1, 1, 1)	(0.75, 1, 1)	(0.5, 1, 1)	(0.75, 0.75, 0.75)	(0.75, 1, 0.75)	(0.75, 0.75, 1)
Hotel 1	608,492.90	605,796.01	528,672.68	607,439.22	588,098.78	598,802.75
Hotel 2	175,140.67	172,213.33	138,464.04	132,777.10	126,076.79	126,249.35
Hotel 3	594,134.20	572,984.90	495,861.56	574,104.14	554,539.13	565,243.09
OTA 1	267,943.57	81,878.81	47,637.02	63,960.6	63,960.6	281,110.03
OTA 2	314,670.35	170,090.7	147,232.86	158,120.16	158,120.16	307,442.66
OTA 3	145,069.37	100,536.14	71,042.03	85,035.17	85,035.17	282,957.02

displays its results.

From Table 1 which presents the results under different parameter settings of $(\phi ,h,g)$, we define $e=0(\phi =1)$ and $e=1(\phi =0.75)$, representing the level of carbon emissions after reduction. The findings indicate that decreasing the value of $\phi$ influences the profits of hotels and OTA platforms. In particular, when $\phi$ increases from 0.5 to 1, the profits of hotel 1, hotel 2, OTA 1, OTA 2, and OTA 3 all increase as the level of carbon reduction becomes higher. The results indicate that increasing g, reflecting stronger consumer preferences for low-carbon products, reduces hotel profits but increases OTA profits. Comparing $(\phi ,h,g)=(0.75,0.75,0.75)$ with $(0.75,0.75,1)$, hotels experience profit declines, as the higher costs of low-carbon practices outweigh additional revenues. In contrast, OTAs consistently gain higher profits.

The impact of carbon-reduction cost sensitivity (h) on profitability. When h decreases from 1 to 0.75, the profits of all hotels increase. Furthermore, OTA platforms also achieve higher profits under lower h. All hotels achieve their maximum profits when the parameters are set at $(1,1,1)$, while OTA 1 and OTA 3 reach their highest profits when $g=1$ and $h=0.75$, which indicates that hotels achieve their maximum profits when all three factors fully support sustainability, whereas some OTAs benefit more under conditions where the cost sensitivity of carbon reduction remains moderate, and the parameter values influence profitability.

The agency basic model assumes that $(\phi ,g,h)=(1,1,1)$ and $\alpha =0.2, \alpha =0.25,$ $\alpha =0.3, \alpha =0.35$ and $\alpha =0.40$. The results of the calculation are shown in

Table 2. The impact of commissions under the agency model.

	$\mathit{\alpha }$ = 0.20	$\mathit{\alpha }$ = 0.25	$\mathit{\alpha }$ = 0.30	$\mathit{\alpha }$ = 0.35	$\mathit{\alpha }$ = 0.40
Hotel 1	844,862.31	833,512.05	807,084.58	780,687.18	754,332.76
Hotel 2	353,519.92	336,742.92	317,922.48	299,100.23	280,278.01
Hotel 3	1,576,557.23	1,385,528.74	1,280,405.61	1,180,542.36	1,085,973.32
OTA 1	147,573.6	196,043.01	253,477.22	317,199.13	387,298.87
OTA 2	153,805.57	203,361.65	262,433.65	327,881.39	399,817.09
OTA 3	131,582.16	181,928.42	237,578.86	299,889.34	368,967.34

.

When OTAs charge higher commissions as shown in Table 2, the net profits of hotels decrease accordingly, reflecting that OTAs directly benefit from the increase in commission rates. As $\alpha$ rises, OTA profits increase correspondingly. The results highlight the structural mechanism of the agency model, which strategically favors OTAs, while hotels face the opposite outcome.

5.2. Sensitivity Analysis

To assess the robustness of the proposed model, a sensitivity analysis was conducted by varying the key parameters, namely, the reduction degree of carbon emissions ($\phi$), cost sensitivity (h), and consumer low-carbon preference (g). Table 1 reports the resulting profits for hotels and OTAs under different parameter settings. The results indicate that sustainability-related parameters significantly shape equilibrium outcomes, with hotel profitability maximized when all three parameters strongly support sustainability, while OTA profitability benefits more under moderate cost sensitivity.

5.3. The Impact of Mergers and Acquisitions (M&A) of Merchant Model and Agency Model

It is assumed that $(\phi ,g,h)=(1,1,1)$ and ${\rho }_{il}^H,{\rho }_{jl}^{OTA}$ = 2500 when comparing the merchant model with the agency model under the basic case and the scenario integrating altruism along with demand uncertainty (U&A). The OTA commission rate is set at 40% in the agency model, whereas ${\omega }_{ij}^{OTA}$ = 1250 in the merchant model. From

Table 3. Comparison of profits under the merchant and agency models without M&A.

	Merchant Model		Agency Model
	Basic	U&A	Basic	U&A
Hotel 1	608,492.90	852,761.12	754,332.76	1,685,720.50
Hotel 2	175,140.67	364,618.68	280,278.01	679,331.45
Hotel 3	594,134.20	809,271.60	1,085,973.32	1,629,651.89
OTA 1	267,943.57	271,481.04	387,298.87	1,888,791.87
OTA 2	314,670.35	337,874.56	399,817.09	1,920,271.74
OTA 3	282,929.77	266,566.31	368,967.34	1,954,899.59

, the analysis highlights significant structural differences in outcomes for hotels and OTA platforms.

For the merchant model, the factors of altruism and demand uncertainty lead to a substantial increase in hotel profits, whereas OTAs gain only marginal benefits or even face adverse effects. By contrast, the agency model exhibits markedly different results, as both hotels and OTAs experience higher profits, but OTAs capture the majority of the benefits, with profits rising substantially compared to the merchant model. These findings indicate that integrating altruistic preferences and demand uncertainty strengthens the strategic advantage of the agency model, particularly in favor of OTAs.

The net profits of hotels and OTA platforms are analyzed under two scenarios: (i) without merger results in Table 3, and (ii) with merger. In the merger case, it is assumed that hotel 1 acquires hotel 2 under the following conditions:

• Profit-sharing ratio: Hotel 2 receives 90% of the total post-merger profits, while hotel 1 receives 10%.
• Unified OTA system: Post-merger, both hotels operate under a single OTA booking channel, reducing operational costs. The OTA grants a 5% commission discount for each additional hotel integrated into the system.
• Merger cost: Integration incurs merger-related costs as a function of time (in months, t), following the specified merger cost function.

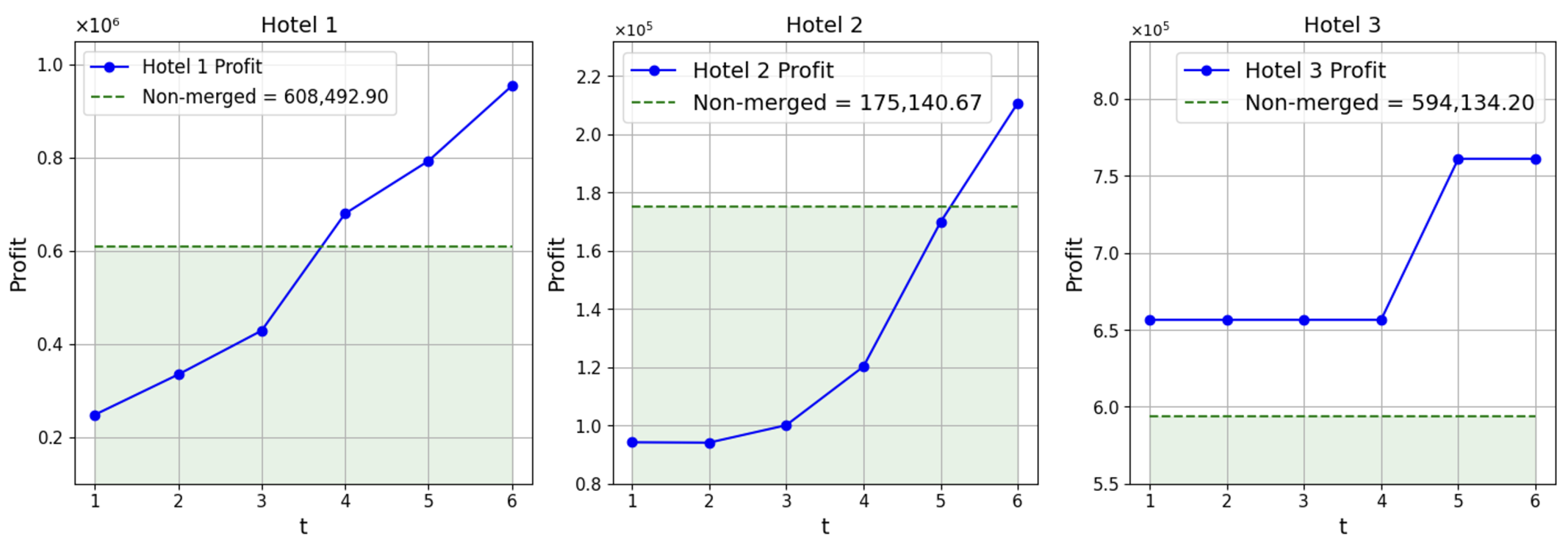
From

Table 4. Monthly profit (t = Month 1 to 6) under merchant model (basic).

	t = 1	t = 2	t = 3	t = 4	t = 5	t = 6
Hotel 1	247,997.4	334,273.49	428,347.61	679,274.2	792,266.14	953,076.74
Hotel 2	94,204.66	94,074.11	100,050.11	120,159.86	169,781.97	210,653.44
Hotel 3	656,430.57	656,430.57	656,430.57	656,430.57	761,108.76	761,108.76

and Figure 3, under the merchant model, hotel 1 which merged with hotel 2 experienced lower net profits in the early stages ($t=1$ to $t=3$) compared to the non-merger case due to merger costs. However, profits grew steadily afterward, breaking even at $t=4$ and significantly surpassing the non-merger case at $t=6$ (953076.74). Hotel 2, despite starting with relatively low profits, adapted and improved substantially, reflecting the benefits of synergy, while hotel 3 remained relatively stable in the early stages before showing notable growth after $t=4$.

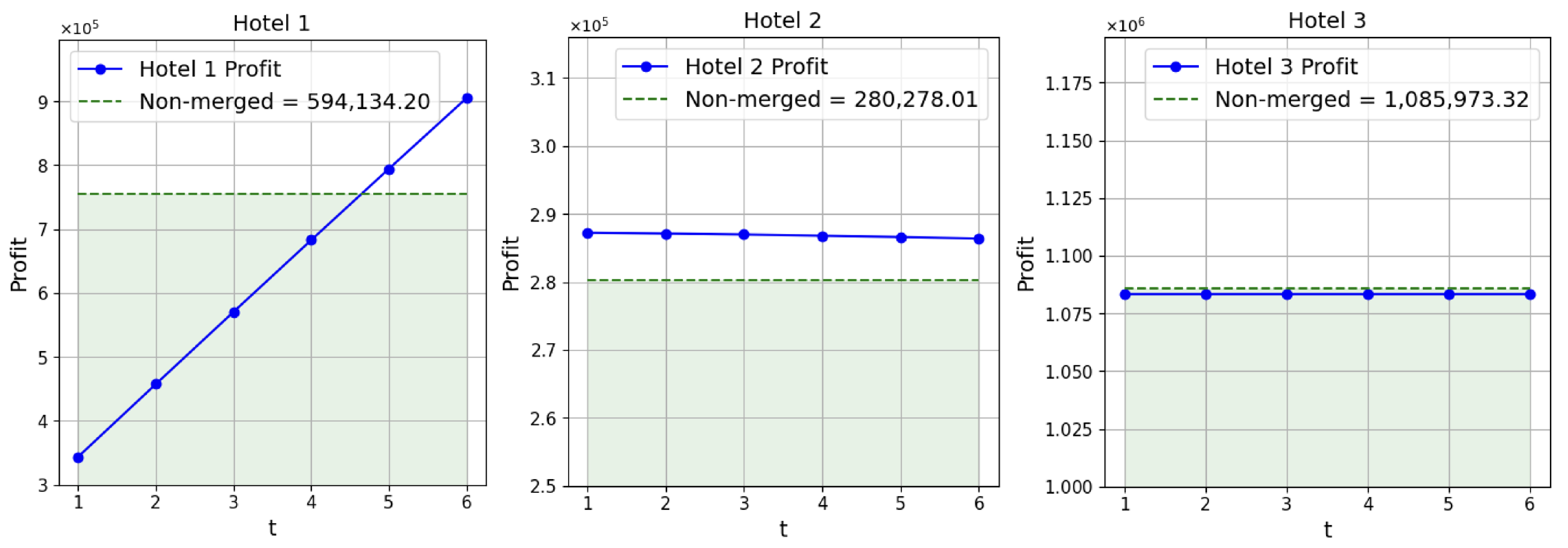
Similarly, from

Table 5. Monthly profit (t = Month 1 to 6) under agency model (basic).

	t = 1	t = 2	t = 3	t = 4	t = 5	t = 6
Hotel 1	343,968.02	457,594.35	570,552.94	682,795.9	794,275.18	904,943.6
Hotel 2	287,246.72	287,118.06	286,969.39	286,797.57	286,598.98	286,369.43
Hotel 3	1,083,569.57	1,083,569.57	1,083,569.57	1,083,569.57	1,083,569.57	1,083,569.57

and Figure 4, under the agency model, hotel 1 also experienced continuous profit growth, exceeding the non-merger case at $t=5$ (794,275.18 compared to 754,332.76). Hotel 2 maintained relatively stable profits with slight adjustments, while hotel 3 remained consistent but earned slightly less than in the non-M&A case, reflecting the equilibrium effect of the merger between hotels 1 and 2.

In conclusion, the merchant model demonstrates greater potential for long-term profit growth, whereas the agency model provides more stability and predictability.

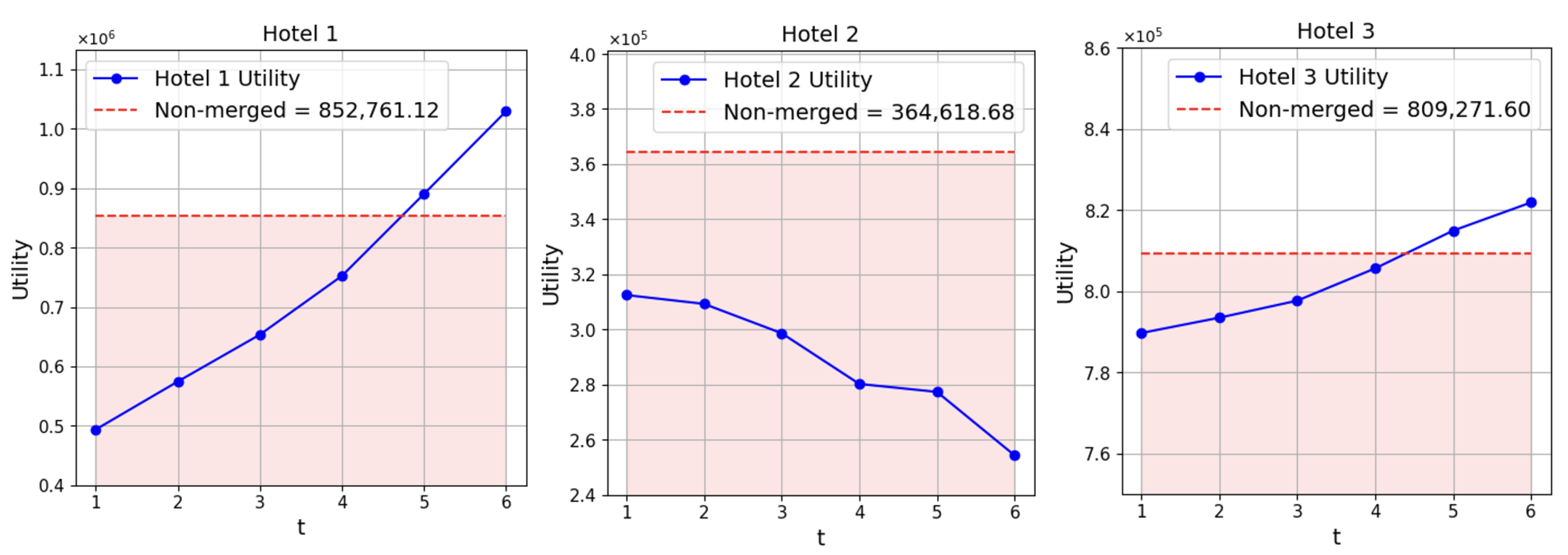
According to

Table 6. Total monthly utility (t = month 1 to 6) under merchant model (U&A).

	t = 1	t = 2	t = 3	t = 4	t = 5	t = 6
Hotel 1	493,756.60	574,517.26	653,421.06	752,365.86	890,279.28	1,029,476.57
Hotel 2	312,489.39	309,292.98	298,644.58	280,244.12	277,356.55	254,312.6
Hotel 3	789,653.74	793,428.2	797,633.57	805,596.99	814,912.61	821,872.3

and Figure 5 under the merchant model and

Table 7. Total monthly utility (t = month 1 to 6) under agency model (U&A).

	t = 1	t = 2	t = 3	t = 4	t = 5	t = 6
Hotel 1	1,879,401.03	1,887,574.94	1,958,257.66	2,033,285.56	2,103,340.80	2,159,968.31
Hotel 2	409,753.19	409,239.45	413,015.50	416,503.03	419,583.20	422,069.95
Hotel 3	1,709,366.49	1,708,952.79	1,712,887.68	1,716,604.57	1,720,087.21	1,727,907.84

and Figure 6 under the agency model, in the case of altruism coupled with demand uncertainty, it is revealed that the agency model consistently yields higher overall benefits than the merchant model. For hotel 1, the non-merger case produced utility of 852,761.12 and 1,685,720.50, while the merger initially reduced benefits under the merchant model to 493,756.60 due to high integration costs before recovering steadily. Notably, at $t=5$, the utility under M&A surpasses that of the non-merged case, highlighting the network advantages and long-term benefits derived from the merger. In contrast, the agency model utility shows a clear upward trend across periods $t=1$ to $t=6$, with values under M&A consistently surpassing those of the non-M&A case. This indicates that hotel 1 benefits significantly from network synergies created through consolidation.

In contrast, hotel 2, the acquired hotel, the merchant model showed utility starts below the non-merged baseline and declines steadily as t increases. This suggests that, despite profitability gains, the M&A reduces perceived utility for hotel 2, indicating limited cooperative or altruistic benefits compared with the non-merged case, whereas the agency model demonstrates notably lower utility under M&A, remaining nearly constant around 400,000–420,000, while the non-M&A case sustains a substantially higher level (679,331.45). This outcome reflects the disadvantages imposed on acquired entities in the agency model. Hotel 3 shows that its utility under M&A rises steadily, surpassing the non-merged benchmark of 809,271.60 at $t=4$. By t = 6, it reaches around 821,872.3, reflecting consistent gains from M&A through network effects, though the agency model produced slightly higher and more consistent values.

When comparing the performance of the three hotels under the merchant model and agency model in both the basic case and the U&A scenario from Table 4, Table 5, Table 6 and Table 7, Figure 3, Figure 4, Figure 5 and Figure 6, it is evident that the agency model demonstrates greater advantages in terms of overall benefits and stability. In the merchant model, hotels 1 and 3 generate steadily increasing profits, whereas hotel 2 shows consistently low returns. Although the addition of U&A improves the aggregate utility, hotel 2 continues to perform at a considerably lower level. By contrast, the agency model clearly outperforms, with hotels 1 and 3 achieving stable and significantly higher benefits, while hotel 2, though still the lowest among the three, secures notably higher returns compared to the merchant model. This effect is particularly pronounced under the U&A scenario, where the agency model enables smaller hotels such as hotel 2 to improve more substantially relative to the basic case. These findings indicate that the agency model not only strengthens the competitive position of larger hotels but also reduces the disadvantages faced by smaller ones, thereby fostering a more balanced distribution of benefits across the system.

5.4. An OTA Altruism Preference and a Hotel Altruism Preference Under a Merchant and Agency Model

Consider the results that change when hotels exhibit altruistic behavior in terms of pricing decisions, market segmentation, and balancing individual profits with the overall benefits of the network between the merchant model and agency model of hotels and OTAs. Assume that $(\phi ,g,h)=(1,1,1)$ under the merchant model, and that ${\tilde{d}}_l\left({\rho }_l\right)=1000-{\phi }^g{\rho }_l+ϵ,$ where $ϵ\sim \mathcal{N}(0,1)$ For excess supply $\left({ϵ}_l^{+}\right)$ and excess demand $\left({ϵ}_l^{-}\right)$, the unit penalties are both set at 1. The parameters are given as $\lambda =0.1,\gamma =0.1,0.2,0.3,0.4,0.5,0.6$ which are used in the computations. The results are presented in Figure 7, Figure 8 and Figure 9.

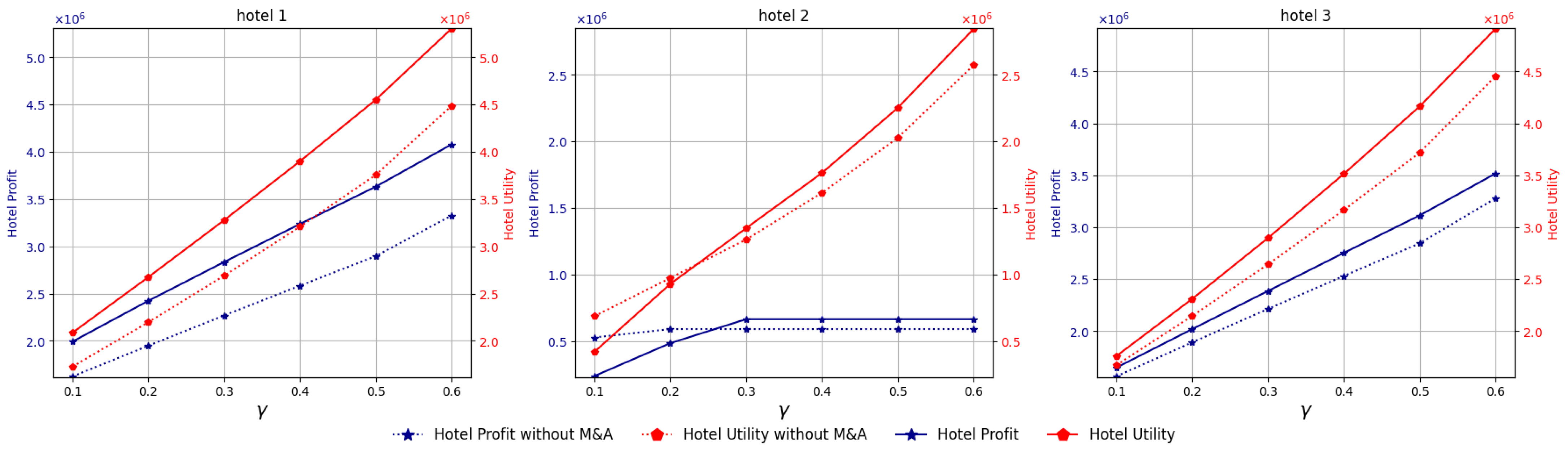
When considering the results under the merchant model in Figure 7, which compares M&A with non-M&A for the three hotels, clear differences can be observed in both profit and utility. For hotels 1 and 3, both profit and utility increase with the degree of altruistic preference ($\gamma$). However, the M&A case consistently lies below the non-M&A case, indicating that mergers do not yield superior outcomes and may even constrain the potential for enhancing hotel profitability and utility.

For hotel 2, which is the acquired hotel, utility increases with higher values of $\gamma$, while profit rises initially but stabilizes and gradually declines once $\gamma \ge 0.4$. Both profit and utility remain below the non-M&A benchmark, suggesting that mergers fail to generate genuine economic advantages for hotel 2.

The analysis of the results from the agency model which sets $\alpha =0.4$, in Figure 8, particularly as the parameter $\gamma$ increases. For hotels 1 and 3, profits under both scenarios tend to rise, profits under M&A accelerate significantly as $\gamma$ grows larger, accompanied by consistently higher overall utility, reflecting the network advantages generated by the merger. In contrast, hotel 2 (the acquired hotel) shows a slight profit increase initially, stabilizing after $\gamma \approx 0.3$. Although profits under M&A slightly exceed the non-M&A case in the later stages, the utility continues to rise throughout the period. Despite starting at a lower level than the non-M&A case, it gradually increases as $\gamma$ grows, indicating that the acquired hotel benefits from network effects even though its direct profit does not surge. Therefore, as the parameter $\gamma$ increases, the M&A scenario delivers superior outcomes in terms of both profit and utility for all hotels.

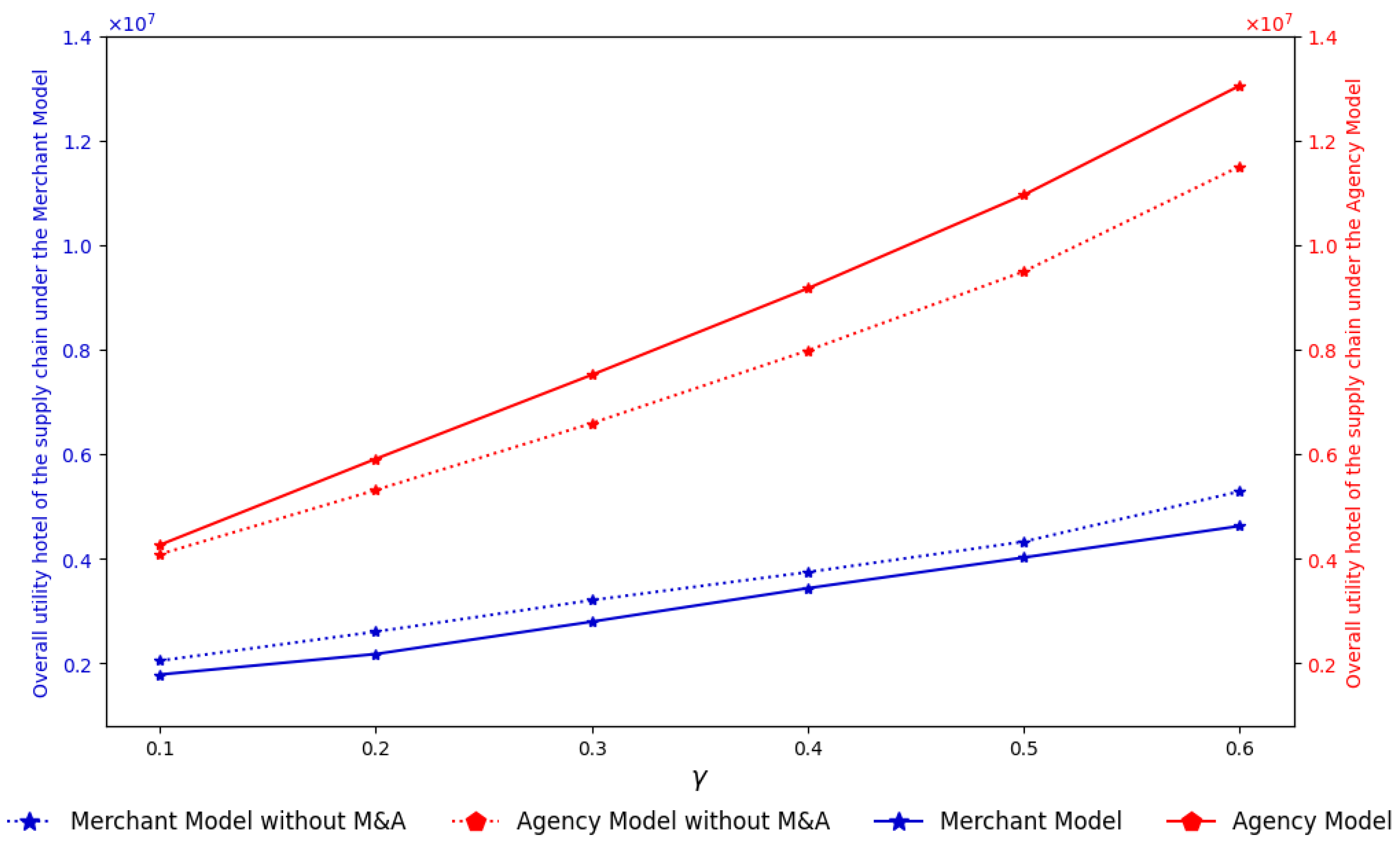
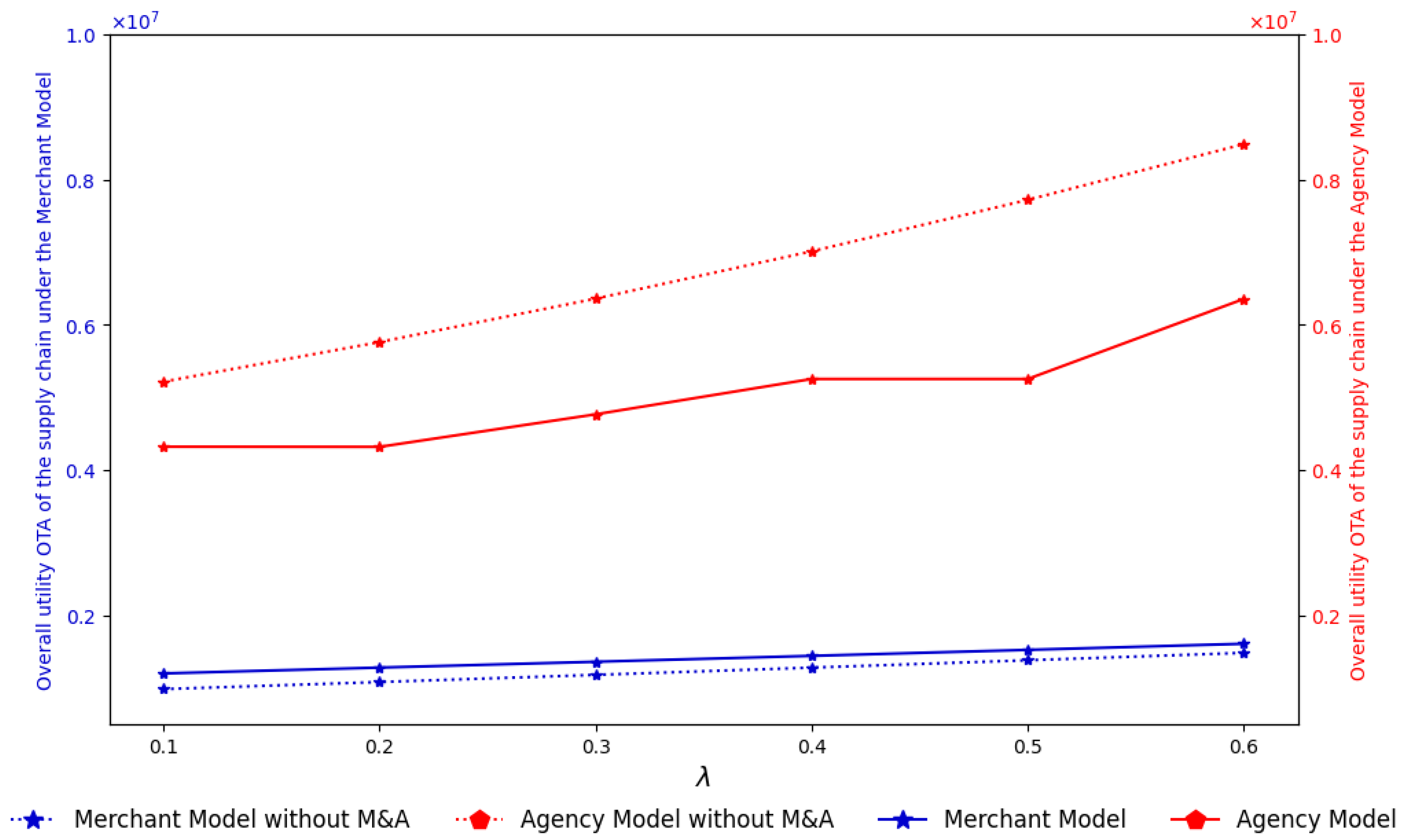
From Figure 9 comparing the overall profits and utilities of the merchant model and the agency model, both under M&A and non-M&A scenarios, it is evident that the agency model yields significantly higher hotel utility across all levels of the parameter $\gamma$ when compared with the merchant model. In particular, in the case of M&A, the utility of the agency model grows steadily and remains higher than both the merchant model and the non-M&A agency model. Meanwhile, the merchant model also shows an increasing trend as $\gamma$ rises, but it still remains at a lower level. This graph clearly indicates that, as the parameter $\gamma$ increases, the agency model under M&A provides the highest overall utility among all cases.

The analysis of OTA altruism preference, the parameters are given as $\gamma =0.1,$$\lambda =0.1,0.2,0.3,0.4,0.5,0.6$ and the results are presented in Figure 10, Figure 11 and Figure 12.

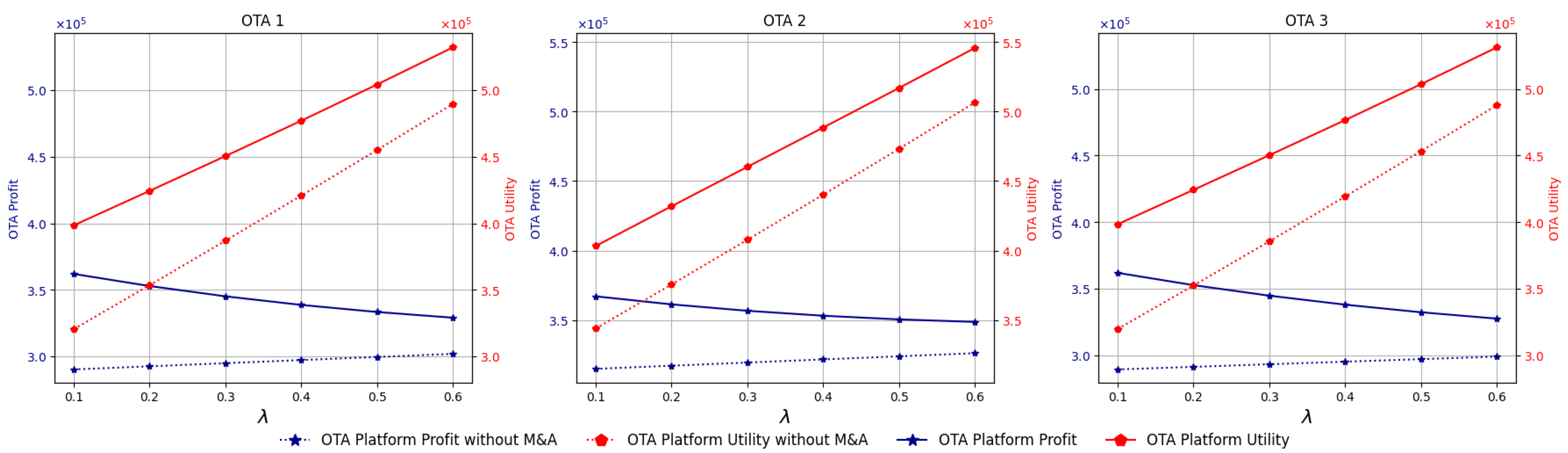
Figure 10 illustrates that, for all three OTAs, a consistent pattern emerges: profits under M&A exhibit either gradual decline or stabilization as $\lambda$ increases, indicating that rising altruistic preference reduces the direct profitability of OTAs when hotels consolidate. By contrast, the overall utility under M&A grows continuously with higher $\lambda$ and remains higher than in the non-M&A case across all levels. This outcome suggests that, although direct profits may stagnate, OTAs derive substantial network-related benefits from altruistic interactions in the system.

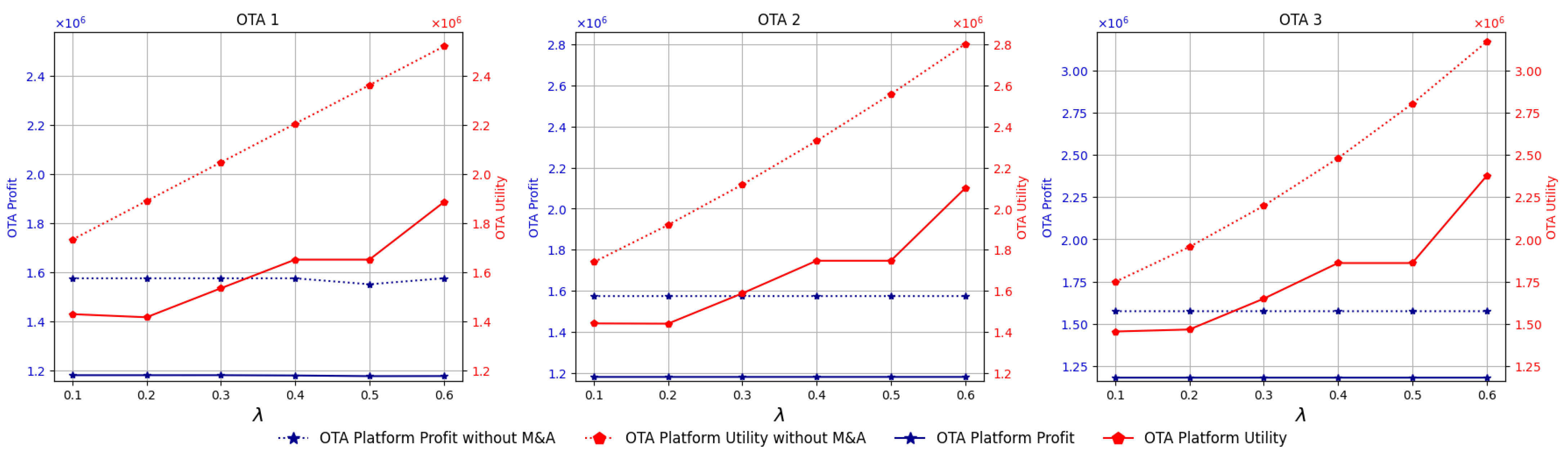
In contrast, under the agency model, as shown in Figure 11, the utility in the non-M&A case grows continuously and is significantly higher than in the M&A case at all levels of $\lambda$. This indicates that non-M&A contributes more effectively to enhancing the platform’s utility. Meanwhile, the profit of each OTA platform remains relatively similar and fairly stable, showing little increase with higher $\lambda$, with the non-M&A case yielding slightly higher profit than the M&A case. This reflects that, in the agency model, mergers and acquisitions do not provide substantial advantages in terms of either profit or utility for the OTA platforms.

From the results in Figure 12, it is observed that the agency model consistently generates a higher utility for OTAs compared to the merchant model across all levels of $\lambda$. In particular, the non-M&A case shows a continuously higher utility than the M&A case. In contrast, within the merchant model, mergers and acquisitions (M&A) contribute only a slight increase in utility when compared to non-M&A. Overall, it can be concluded that the agency model enhances the overall utility of the supply chain more effectively, while mergers and acquisitions of hotel do not provide additional benefits.

6. Managerial Implications

This study provides several managerial insights for key stakeholders in the hotel supply chain.

For hotel managers, mergers and acquisitions (M&A) can be leveraged to pool resources, enhance cooperation, and expand market demand. To maximize profitability, these strategies should be complemented by sustainability initiatives such as carbon reduction practices, which also improve reputation and long-term competitiveness. Furthermore, altruistic behaviors among hotel partners can stabilize collaborations and mitigate risks under demand uncertainty.

For OTA platforms, the results confirm the structural advantage of the agency model, particularly under higher commission rates. However, excessive reliance on commissions may weaken long-term partnerships with hotels. Incorporating altruistic elements into governance strategies can strengthen trust, reputation, and efficiency, ensuring sustainable profitability.

For policy makers, the findings highlight the importance of promoting sustainable tourism through incentives for low-carbon adoption and designing fairer commission structures. Such policies can balance bargaining power between hotels and OTAs, thereby supporting a more resilient and sustainable hospitality industry.

7. Discussion

This study highlights the interdependence of sustainability, altruistic behavior, and M&A in shaping the equilibrium of dual-channel hotel supply chains. By analyzing both the merchant and agency models under demand uncertainty, the results demonstrate that governance structures, cooperative strategies, and consumer preferences jointly determine profitability and utility distribution across hotels, online travel agencies (OTAs), and demand markets.

The numerical results provide four key insights. Sustainability-related factors, such as the extent of carbon emission reduction, cost sensitivity to emission reduction, and consumer low-carbon preferences, primarily determine profit distribution. Hotels achieve maximum profitability when these factors fully support sustainability, while OTAs benefit more when cost sensitivity remains mild. Second, commission structures under the agency model show a structural bias: hotel earnings fall as commission rates climb, but OTA profits significantly rise, hence strengthening OTAs’ competitive edge. Third, there are different results when comparing the merchant and agency models without M&A. The agency model increases profitability for both partners but disproportionately advantages OTAs, while the merchant model benefits hotels, particularly in situations of altruism and demand volatility. The agency model consistently provides the maximum total utility, as demonstrated by the integration of M&A and philanthropy. Improved OTA altruism boosts efficiency and stability, while stronger hotel altruism encourages collaboration and demand growth. In contrast to the benefits derived from altruistic preferences, the advantages of M&A for OTAs are comparatively limited.

These findings extend prior research. Earlier studies (see [23,24]) examined stochastic demand and multi-criteria decision-making but excluded M&A and sustainability. More recent work, such as Wang et al. [4] on altruistic fairness and He et al. [31] on dual-channel supply chains, emphasized behavioral and structural elements. The present study advances this literature by jointly integrating M&A, sustainability, altruism, and OTA governance into a unified equilibrium framework, confirming that altruism mitigates demand uncertainty and improves cooperative efficiency—consistent with behavioral economics, which suggests altruism enhances outcomes relative to the selfish benchmark.

Theoretically, this study enriches the application of variational inequality (VI) models by embedding M&A and altruism into dual-channel hotel supply chains. Altruism acts as a stabilizing force in uncertain environments, reducing mismatches between supply and demand and enabling more balanced profit allocation.

From a managerial perspective, hotels can use M&A to strengthen cooperation and expand market demand, but complementary sustainability practices are essential to maximize profitability. Altruistic collaboration within hotel alliances also stabilizes business relationships under uncertainty. For OTAs, the agency model offers strong profitability advantages, particularly under high commissions; however, excessive commission dependence may erode long-term partnerships. Integrating altruism into platform governance can build trust and foster sustainable collaboration. Policymakers, meanwhile, should promote sustainable tourism through incentives for carbon reduction and ensure fair commission structures to balance bargaining power between hotels and OTAs.

8. Conclusions

This study examined the equilibrium of dual-channel hotel supply chains under demand uncertainty by explicitly considering mergers and acquisitions (M&A), consumer low-carbon preferences, and altruistic behavior. By integrating these elements into a variational inequality framework, the study provides new insights into how governance mechanisms, particularly the merchant and agency models, shape the distribution of profits and utilities among hotels, OTA platforms, and demand markets.

The findings reveal that sustainability related factors, such as carbon emission reduction and consumer low-carbon preferences, significantly influence profit outcomes. The agency model, with its commission-based structure, systematically advantages OTAs, while the merchant model produces more favorable outcomes for hotels under conditions of altruism and demand uncertainty. When M&A and altruism are incorporated, the agency model consistently generates the highest overall utility, although the additional benefits for OTAs derived from M&A remain limited compared to those gained from altruistic preferences.

The contribution of this study is threefold. Theoretically, it advances the application of variational inequality theory by embedding sustainability, M&A, and altruism into dual-channel hotel supply chains. From a managerial perspective, it provides guidance for hotels to pursue M&A and cooperative strategies alongside sustainable practices, while also emphasizing the importance for OTAs to balance commission-driven profitability with long-term partnerships. From a policy standpoint, the study highlights the need to promote sustainable tourism by supporting carbon reduction initiatives and establishing fair commission structures to ensure an equitable balance between hotels and OTAs.

This study has limitations, numerical experiments rely on stylized parameters rather than empirical data, and the static equilibrium framework omits dynamic features such as adaptive pricing and learning. Furthermore, assuming homogeneous consumer preferences simplifies real-world heterogeneity.

Future research could address these gaps by incorporating dynamic and stochastic demand shocks (e.g., pandemics or crises), empirically calibrating parameters with hotel and OTA data, and extending the analysis to multi-OTA and cross-border supply chains. Experimental or survey-based approaches could also validate the role of altruism and sustainability preferences in practice.