Exploring Non-Linear Effects of a Station-Area Built Environment on Origin–Destination Flow in a Large-Scale Urban Metro Network
Abstract
1. Introduction
2. Data and Variables
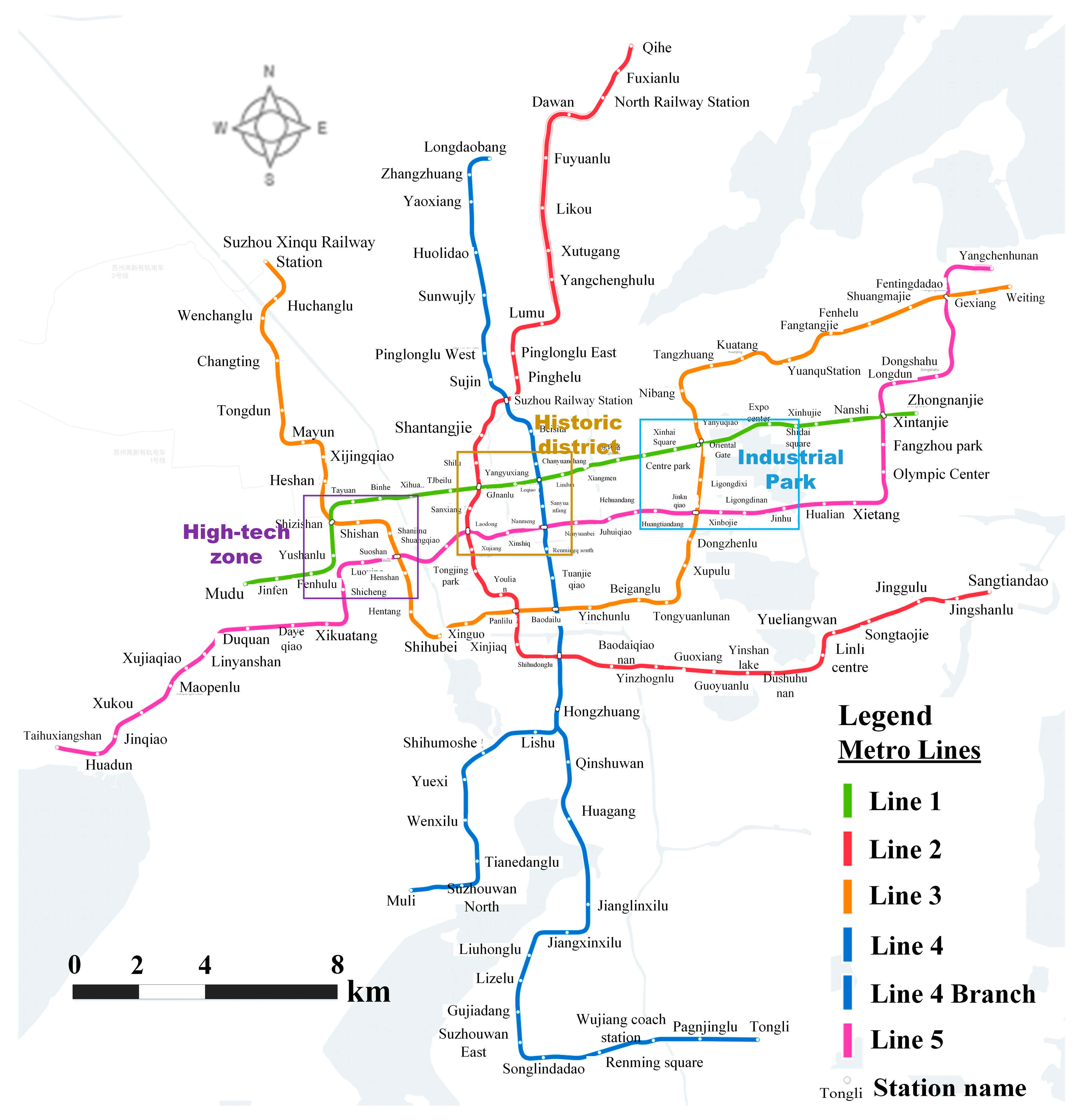
2.1. Study Area
2.2. Dependent Variables
2.3. Independent Variables
2.3.1. Density
2.3.2. Diversity
2.3.3. Design
2.3.4. Station Centrality
3. Methodology
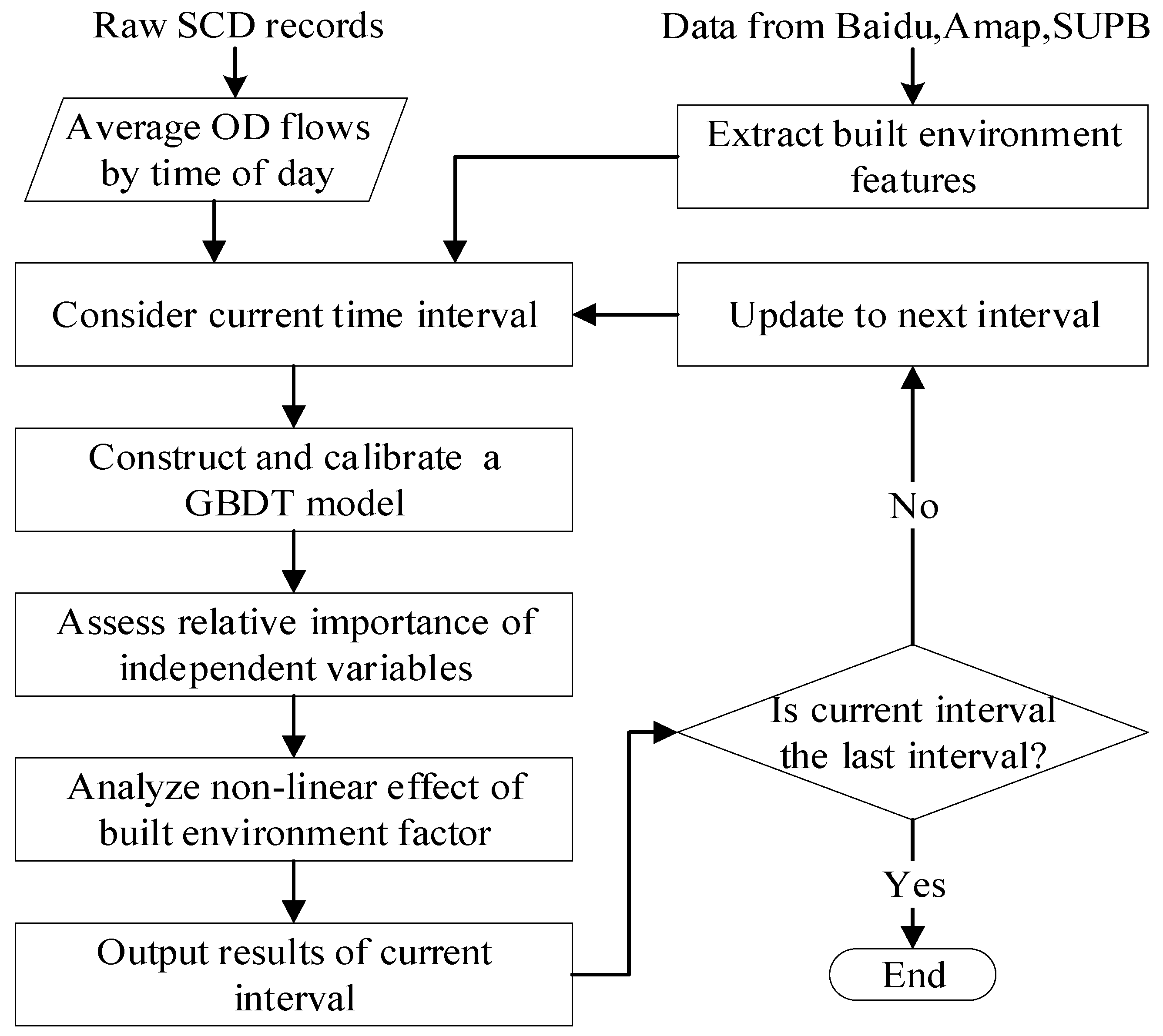
3.1. Framework
3.2. Modelling Approach
4. Results and Discussion
4.1. Model Training and Evaluation
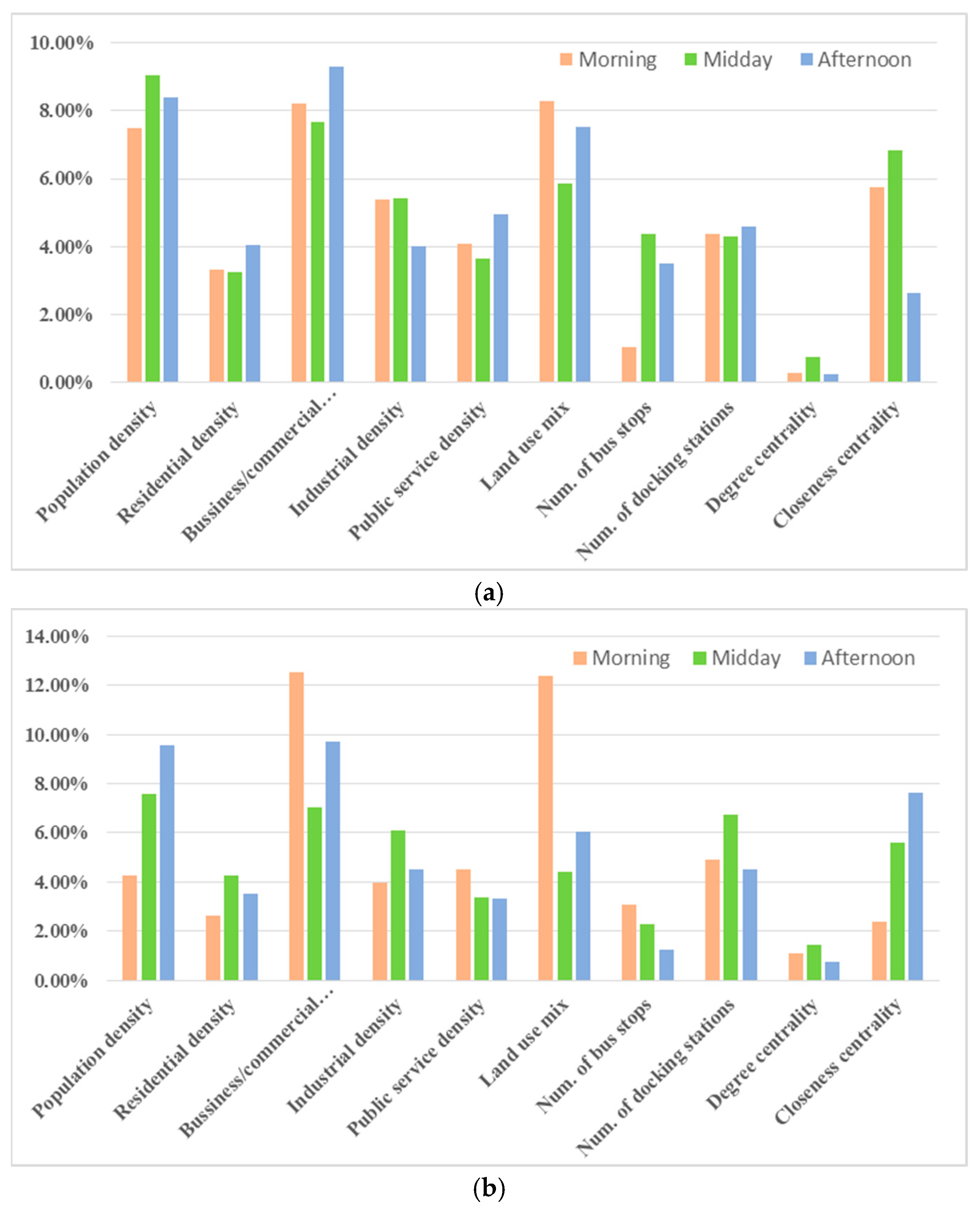
4.2. Contributions of Independent Variables
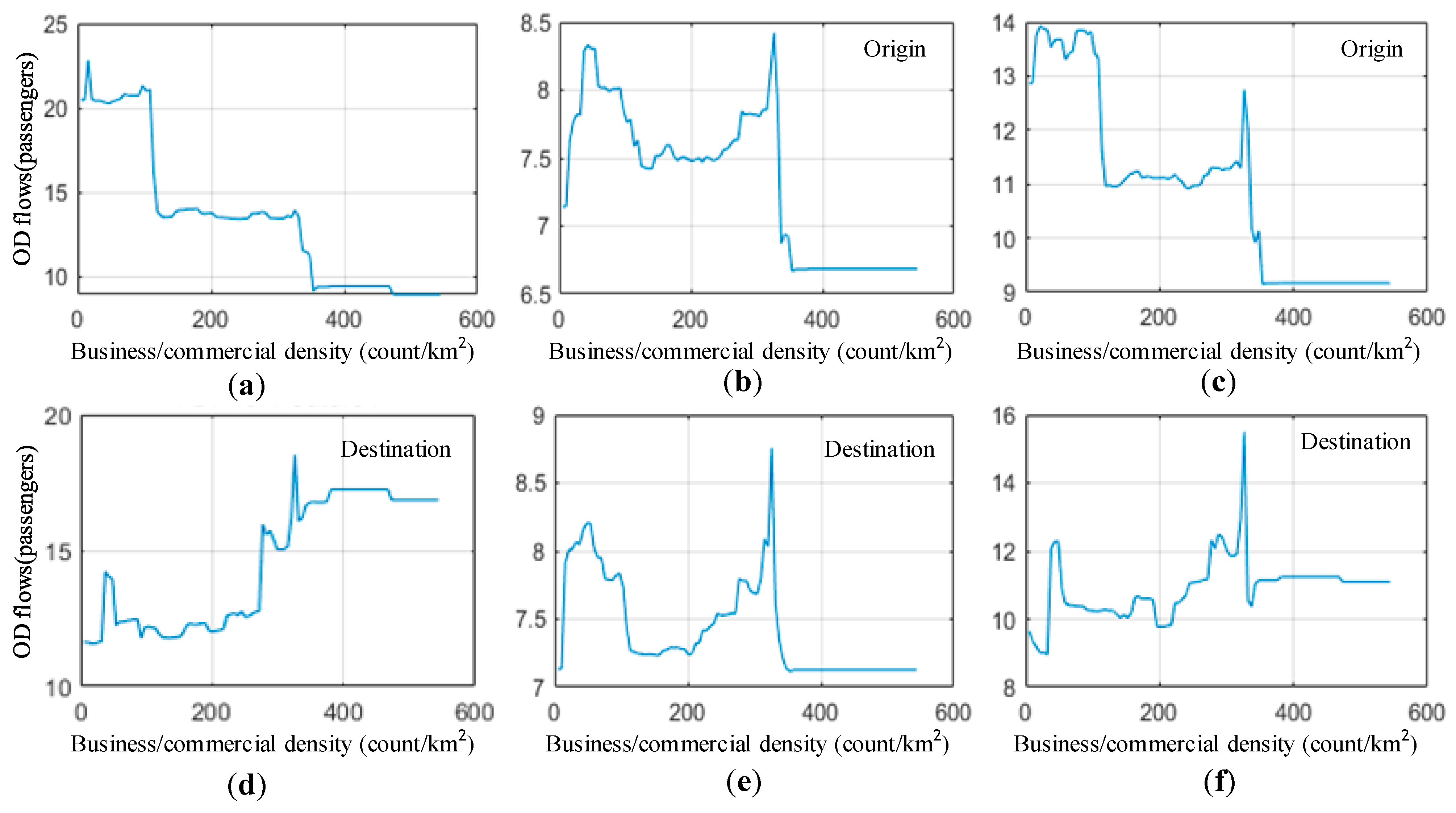
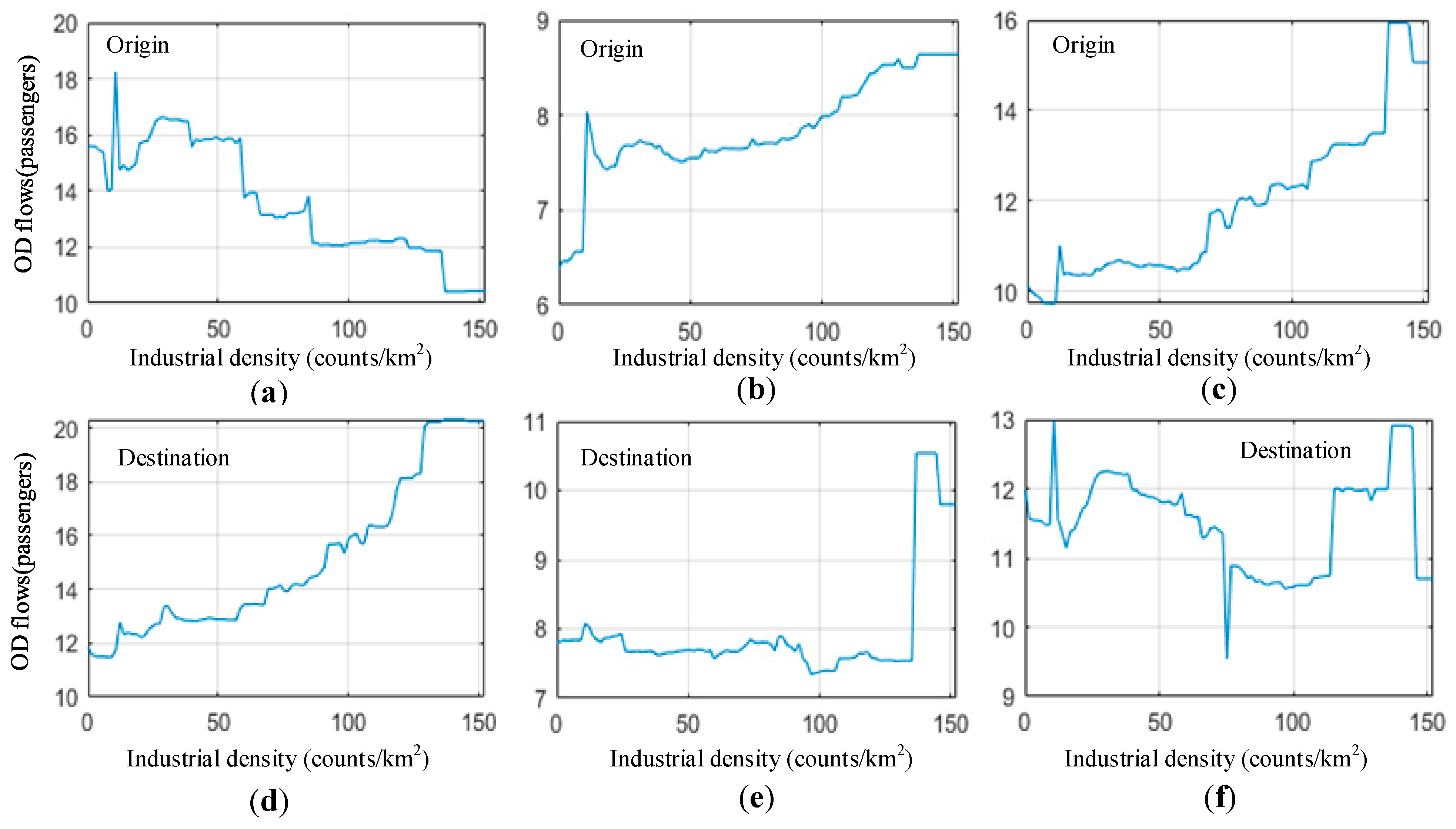
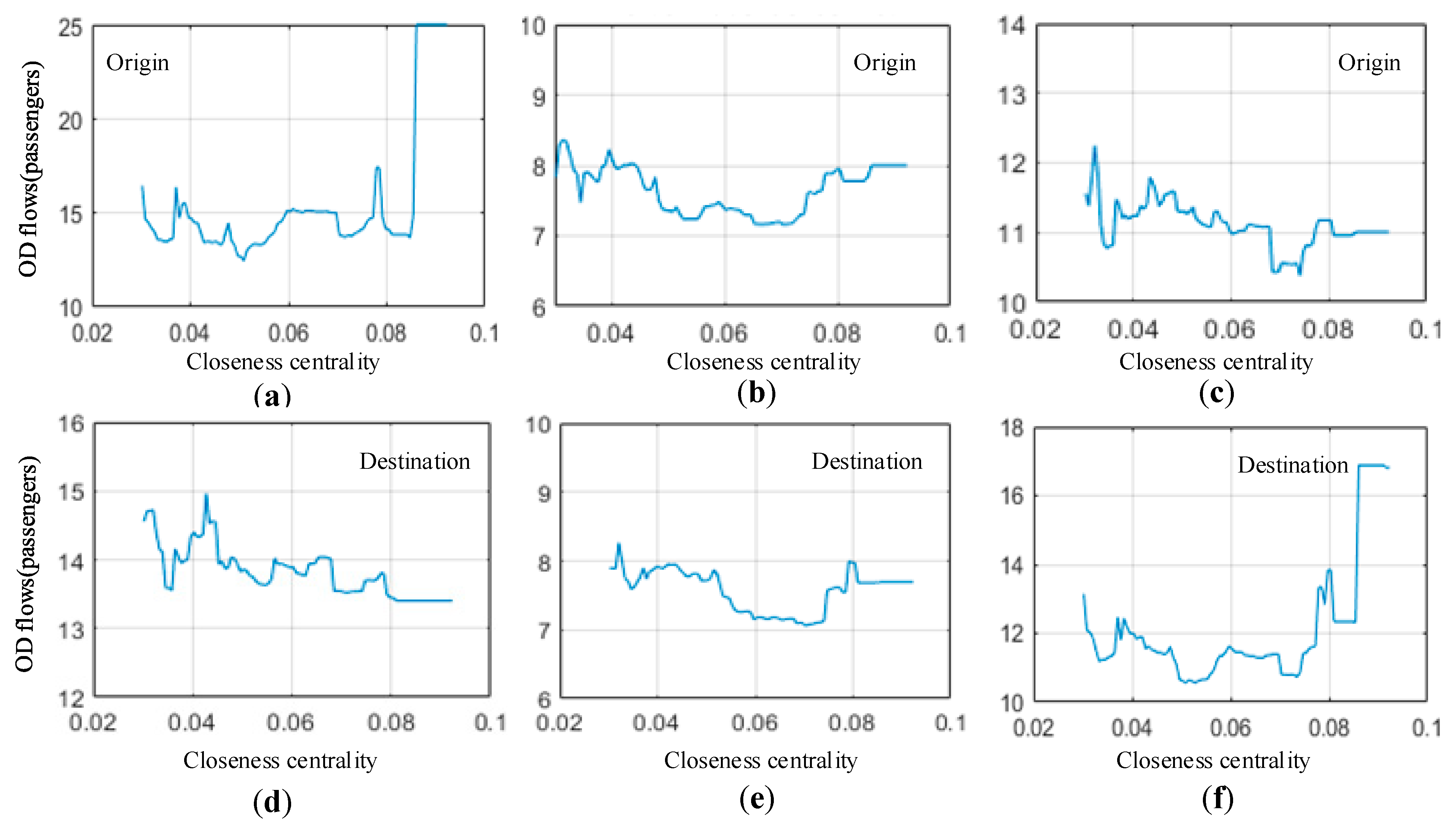
4.3. Non-Linear Effects of Built Environment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, J.; Deng, W.; Song, Y. Analysis of metro ridership at station level and station-to-station level in Nanjing: An approach based on direct demand models. Transportation 2014, 41, 133–155. [Google Scholar] [CrossRef]
- Durning, M.; Townsend, C. Direct Ridership Model of Rail Rapid Transit Systems in Canada. Transp. Res. Rec. J. Transp. Res. Board 2015, 2537, 96–102. [Google Scholar] [CrossRef]
- Estupinan, N.; Rodriguez, D.A. The relationship between urban form and station boardings for Bogota’s BRT. Transp. Res. Part A Policy Pract. 2008, 42, 296–306. [Google Scholar] [CrossRef]
- Gutierrez, J.; Cardozo, O.; Garcia-Palomares, J. Transit ridership forecasting at station level: An approach based on distance-decay weighted regression. J. Transp. Geogr. 2011, 19, 1081–1092. [Google Scholar] [CrossRef]
- Choi, J.; Lee, Y.; Kim, T. An analysis of metro ridership at the station-to-station level in Seoul. Transportation 2012, 39, 705–722. [Google Scholar] [CrossRef]
- Thompson, G.; Brown, J.; Bhattacharya, T. What really matters for increasing transit ridership: Understanding the determinants of transit ridership demand in Broward County, Florida. Urban Stud. 2012, 49, 3327–3345. [Google Scholar] [CrossRef]
- Li, S.; Lyu, D.; Liu, X. The varying patterns of rail transit ridership and their relationships with fine-scale built environment factors: Big data analytics from Guangzhou. Cities 2020, 99, 102580. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X.; Chen, J. What factors influence ridership of station-based bike sharing and free-floating bike sharing at rail transit stations? Inter. J. Sustain. Transp. 2022, 16, 357–373. [Google Scholar] [CrossRef]
- Peng, J.; Fu, X.; Wu, C.; Dai, Q.; Yang, H. Comparative analysis of nonlinear impacts on the built environment within station areas with different metro ridership segments. Travel Behav. Soc. 2025, 38, 100898. [Google Scholar] [CrossRef]
- Cordera, R.; Coppola, P.; dell’Olio, L.; Ibeas, Á. Is accessibility relevant in trip generation? Modelling the interaction between trip generation and accessibility taking into account spatial effects. Transportation 2017, 44, 1577–1603. [Google Scholar] [CrossRef]
- Ewing, R.; Cervero, R. Travel and the built environment. J. Amer. Plan. Assoc. 2010, 76, 265–294. [Google Scholar] [CrossRef]
- Cardozo, O.; García-Palomares, J.; Gutiérrez, J. Application of geographically weighted regression to the direct forecasting of transit ridership at station-level. App. Geogr. 2012, 34, 548–558. [Google Scholar] [CrossRef]
- Sung, H.; Choi, K.; Lee, S. Exploring the impacts of land use by service coverage and station-level accessibility on rail transit ridership. J. Transp. Geogr. 2014, 36, 134–140. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, F.; Wang, Z. Spatio-temporal analysis of rail station ridership determinants in the built environment. Transportation 2019, 46, 2269–2289. [Google Scholar] [CrossRef]
- Jun, M.; Choi, K.; Jeong, J.; Kwon, K.; Kim, H. Land use characteristics of subway catchment areas and their influence on subway ridership in Seoul. J. Transp. Geogr. 2015, 48, 30–40. [Google Scholar] [CrossRef]
- Yu, H.; Peng, Z. Exploring the spatial variation of ridesourcing demand and its relationship to built environment and socioeconomic factors with the geographically weighted Poisson regression. J. Transp. Geogr. 2019, 75, 147–163. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, N.; Liu, Y. Exploring spatiotemporal variation in hourly metro ridership at station level: The influence of built environment and topological structure. Sustainability 2018, 10, 4564. [Google Scholar] [CrossRef]
- Liu, X.; Wu, J.; Huang, J. Spatial-interaction network analysis of built environmental influence on daily public transport demand. J. Transp. Geogr. 2021, 92, 102991. [Google Scholar] [CrossRef]
- van Wee, B.; Handy, S. Key research themes on urban space, scale, and sustainable urban mobility. Int. J. Sustain. Transp. 2016, 10, 18–24. [Google Scholar] [CrossRef]
- Ding, C.; Cao, X.; Næss, P. Applying gradient boosting decision trees to examine non-linear effects of the built environment on driving distance in Oslo. Transp. Res. Part A Policy Pract. 2018, 110, 107–117. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, L.; Song, Y.; Wang, C.; Yu, Z. Nonlinear influence of urban environment on dockless shared bicycle travel patterns. Sustainability 2025, 17, 4575. [Google Scholar] [CrossRef]
- Ding, C.; Cao, X.; Liu, C. How does the station-area built environment influence Metrorail ridership? Using gradient boosting decision trees to identify non-linear thresholds. J. Transp. Geogr. 2019, 77, 70–78. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Tian, M. Effects of built environment on metro ridership considering stage of growth. J. Transp. Syst. Eng. Inf. Technol. 2023, 23, 121–127. [Google Scholar]
- Du, Q.; Zhou, Y.; Huang, Y. Spatiotemporal exploration of the non-linear impacts of accessibility on metro ridership. J. Transp. Geogr. 2022, 102, 103380. [Google Scholar] [CrossRef]
- Li, P.; Chen, X.; Lu, W. Research on nonlinear relationship between subway built environment and travel distance of stations based on XGBoost-SHAP. J. Railw. Sci. Eng. 2024, 21, 1624–1633. [Google Scholar]
- Li, P.; Yang, Q.; Lu, W.; Xi, S.; Wang, H. An improved machine learning framework considering spatiotemporal heterogeneity for analyzing the relationship between subway station-level passenger flow resilience and land use-related built environment. Land 2024, 13, 1887. [Google Scholar] [CrossRef]
- Pang, L.; Ren, L.; Jiang, Y.; Yun, Y. Mechanism of impact of the built environment of urban rail transit origin and destination stations on network ridership during peak hours. Prog. Geogr. 2024, 43, 1785–1797. [Google Scholar]
- Gan, Z.; Yang, M.; Feng, T.; Timmermans, H. Examining the relationship between built environment and metro ridership at station-to-station level. Transp. Res. Part D. Transp. Environ. 2020, 82, 102332. [Google Scholar] [CrossRef]
- Liu, B.; Xu, Y.; Guo, S. Examining the nonlinear impacts of origin-destination built environment on metro ridership at station-to-station level. Inter. J. Geo-Inform. 2023, 12, 59. [Google Scholar] [CrossRef]
- The Website of Suzhou Municipal Transport Bureau. Available online: http://jtj.suzhou.gov.cn/szjt/xwfbmtjj/202302/43216ef0f3414deab37f86df42314b4f.shtml (accessed on 9 February 2023).
- Shannon, C.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Cervero, R.; Kockelman, K. Travel demand and the 3Ds: Density, diversity, and design. Transp. Res. Part D Transp. Environ. 1997, 2, 199–219. [Google Scholar] [CrossRef]
- Liu, R.; Xu, J.; Iris, C.; Chen, J. Dynamic rebalancing strategies for dockless bike-sharing systems. Inter. J. Prod. Econ 2025, 285, 109634. [Google Scholar] [CrossRef]
- Basak, E.; Iris, Ç. Urban Life Matters: The Heterogeneous Effects of On-Demand Bike Sharing Platforms on Urban Transit. 2023. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4391093 (accessed on 29 March 2023).
- Arentze, T.; Timmermans, H. A learning-based transportation oriented simulation system. Transp. Res. Part B Methodol. 2004, 38, 613–633. [Google Scholar] [CrossRef]
- Friedman, J. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Wang, W.; Wang, H.; Xu, J.; Liu, C.; Wang, S.; Miao, Q. Interpretable GBDT Model for analysing Ridership Mechanisms in Urban Rail Transit: A Case Study in Shenzhen. Appl. Sci. 2025, 15, 3835. [Google Scholar] [CrossRef]
- Li, L.; Huang, C.; Liu, Y. Detecting the contribution of transport development to urban construction land expansion in the Beijing-Tianjin-Hebei region of China based on machine learning. Land Use Policy 2025, 157, 107622. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ian, D.; McCourt, M.; Clark, S. Bayesian Optimization for Machine Learning: A Practical Guidebook; SigOpt: San Francisco, CA, USA, 2024. [Google Scholar]
- Sun, G.; Zacharias, J.; Ma, B.; Oreskovic, N. How do metro stations integrate with walking environments? Results from walking access within three types of built environment in Beijing. Cities 2016, 56, 91–98. [Google Scholar] [CrossRef]
- Wehbi, L.; Bektaş, T.; Iris, Ç. Optimising vehicle and on-foot porter routing in urban logistics. Transp. Res. Part D Transp. Environ. 2022, 109, 103371. [Google Scholar] [CrossRef]



| Variable Name | Data Source | Mean | St. Dev. |
|---|---|---|---|
| Dependent variables | |||
| OD flows | |||
| Morning peak (7:00–9:00) | SMC | 14.02 | 27.65 |
| Midday off-peak (11:00–13:00) | SMC | 7.73 | 8.28 |
| Afternoon peak (16:30–18:30) | SMC | 11.30 | 16.96 |
| Build environment characteristics | |||
| Density | |||
| Population density (persons/km2) | Baidu map, SUPB | 2727 | 1176 |
| Residential density (counts/km2) | AMap | 36 | 39 |
| Business/commercial density(counts/km2) | AMap | 210 | 119 |
| Industrial density (counts/km2) | AMap | 54 | 38 |
| Public service density (counts/km2) | AMap | 137 | 99 |
| Diversity | |||
| Land use mix | Calculated | 0.79 | 0.12 |
| Design | |||
| Number of bus stops (counts) | AMap | 6.1 | 2.4 |
| Number of bike-sharing docking stations (counts) | AMap | 5.6 | 5.3 |
| Station centrality | |||
| Degree centrality | Measured from metro network | 2.30 | 0.82 |
| Closeness centrality | Calculated | 0.050 | 0.013 |
| Time Periods | Sample Size | Number of Trees | Learning Rate | Maximum Tree Depth | Evaluation Metrics | |||
|---|---|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | R2 | |||||
| Morning peak | 10,198 | 968 | 0.02 | 6 | 4.90 | 75.98 | 8.72 | 0.90 |
| Midday off-peak | 5390 | 695 | 0.02 | 7 | 1.81 | 8.21 | 2.87 | 0.88 |
| Afternoon peak | 9786 | 867 | 0.02 | 6 | 3.63 | 37.89 | 6.16 | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, W.; Yao, Y.; Ke, S.; Liu, Z. Exploring Non-Linear Effects of a Station-Area Built Environment on Origin–Destination Flow in a Large-Scale Urban Metro Network. Sustainability 2025, 17, 8829. https://doi.org/10.3390/su17198829
Rao W, Yao Y, Ke S, Liu Z. Exploring Non-Linear Effects of a Station-Area Built Environment on Origin–Destination Flow in a Large-Scale Urban Metro Network. Sustainability. 2025; 17(19):8829. https://doi.org/10.3390/su17198829
Chicago/Turabian StyleRao, Wenming, Yuan Yao, Siping Ke, and Zhao Liu. 2025. "Exploring Non-Linear Effects of a Station-Area Built Environment on Origin–Destination Flow in a Large-Scale Urban Metro Network" Sustainability 17, no. 19: 8829. https://doi.org/10.3390/su17198829
APA StyleRao, W., Yao, Y., Ke, S., & Liu, Z. (2025). Exploring Non-Linear Effects of a Station-Area Built Environment on Origin–Destination Flow in a Large-Scale Urban Metro Network. Sustainability, 17(19), 8829. https://doi.org/10.3390/su17198829






