Abstract
Pipeline systems are essential across various industries for transporting fluids over various ranges of distances. A notable application is natural circulation through thermo-syphoning, driven by temperature-induced density variations that generate fluid flow in closed loops. This passive mechanism is widely employed in sectors such as process engineering, oil and gas, geothermal energy, solar water heaters, fertilizers, etc. Natural Circulation Loops eliminate the need for mechanical pumps. While this passive mechanism reduces energy consumption and maintenance costs, maintaining stability and efficiency under varying operating conditions remains a challenge. This study investigates thermo-syphoning in a rectangular closed-loop system and develops optimal control strategies like using a Linear Quadratic Regulator (LQR) and Model Predictive Control (MPC) to ensure stable and efficient heat removal while explicitly addressing physical constraints. The results demonstrate that MPC improves system stability and reduces energy usage through optimized control actions by nearly one-third in the initial energy requirement. Compared to the LQR and unconstrained MPC, MPC with active constraints effectively manages input limitations, ensuring safer and more practical operation. With its predictive capability and adaptability, the proposed MPC framework offers a robust, scalable solution for real-time industrial applications, supporting the development of sustainable and adaptive natural circulation pipeline systems.
1. Introduction
Pipelines are basically a network of interconnected pipes linked with pumps, control valves, instruments, etc., which are used to transport fluids from one location to another [1]. The pipeline systems are integral to various industries as they enable the transportation of fluids over long distances. There are various applications of these pipelines as they are abundantly used in chemical industries, geothermal systems, solar water heating systems, oil and gas sector, water distribution, wastewater management, power generation, and many more.
Various geometries and conditions were employed in such investigations, each possessing its own significance. The literature pertaining to these issues can be categorized based on the geometries and investigation methods utilized. Regarding geometry classification, it may involve either an open-loop or closed-loop configuration. Different methods for conducting these studies can be characterized into various numerical techniques, diverse analytic approaches, and various experimental methods.
This particular section encompasses the literature review on these items with respect to the (a) effect of using various configurations for natural circulation, (b) effect of varying boundary and operating conditions, (c) process dynamics and control of thermo-syphoning loops, and (d) recent use of MPC in thermal systems.
Natural circulation or thermo-syphoning loops are broadly categorized into two main types: single-phase thermo-syphoning loops and two-phase thermo-syphoning loops. This literature review primarily focuses on single-phase natural circulation in thermo-syphoning loops, where heat is transferred from a heat source to a heat sink. The orientation of the thermo-syphoning loop significantly influences its performance [2]. Schematic representations of some of these loops are provided in Figure 1 [3].
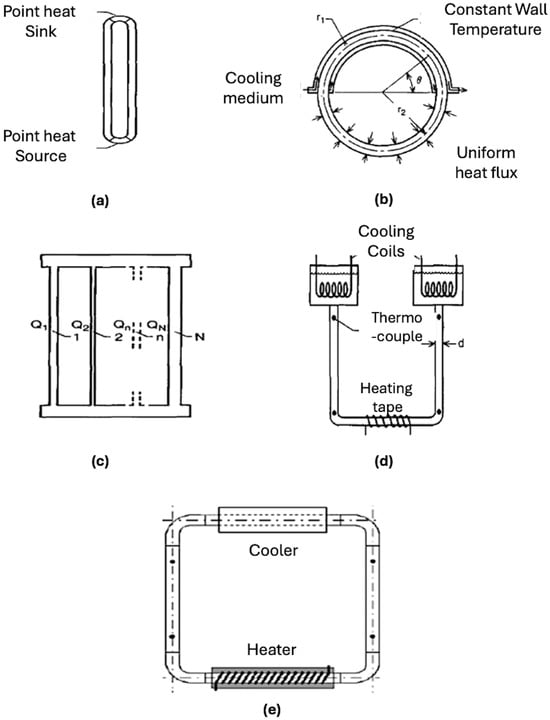
Figure 1.
Various Experimental Setups studied for Natural Circulation Loops. (a) Vertical loop; (b) Toroidal loop; (c) Parallel branches; (d) Open Square loop; (e) Closed Square/Rectangular Loop.
In Figure 1a, a typical vertical loop is depicted, comprising a heat source and a heat sink. Heat moves from the source to the sink due to density or buoyancy gradients. Its applications can be found in atmospheric and ocean flows, refrigeration cycles, cryogenic systems, solar water heaters, etc. Figure 1b illustrates toroidal loops, where constant heat flux is typically applied to the bottom half while the upper half maintains a constant wall temperature boundary condition. Once again, heat transfer occurs through natural circulation driven by density or buoyancy gradients. Such toroidal loops can be found for cooling purposes in industrial processes. Figure 1c demonstrates parallel branches with various heat or cooling fluxes of different magnitudes, facilitating the natural circulation phenomenon. Its applications can be found in nuclear reactors, boilers, and liquid-cooled gas turbine blades. Figure 1d displays an open square loop with heating coils at the bottom and two cooling coils open-ended at the top. Cold water flows from cold storage tanks under gravity, passing through heating coils, and warm water flows in the same legs towards cold storage tanks. Such open loops are found in geological applications such as in the cooling of porous materials in the oceanic and continental crust. In Figure 1e, a closed square loop is shown, featuring a heating section at the bottom and a cooling section at the top. Closed loops are found in solar water heating systems, nuclear power plants, passive cooling of engines, turbines, and electronic components.
However, the performance of the rectangular closed loop was compared with a toroidal loop by Basu et al. [4] and it was concluded that rectangular loops induce larger fluid flows than the toroidal loops under identical dimensions and operating and boundary conditions; however, the stability span for toroidal geometry was found to be wider as compared to rectangular geometry.
Fichera et al. [5] compared the dynamics of two rectangular loops with different tube diameters and lengths, importantly reporting that the loop with a smaller diameter demonstrate more periodic behavior as compared to the loop with larger dimensions whose behavior is relatively more chaotic.
The effect of varying thermal boundary conditions was studied by Misale et al. [6], and it was inferred that varying the heat sink temperature could lead to crossing the stability threshold, highlighting the significance of this thermal boundary condition in influencing the system’s dynamics. In another study [7], it was noticed that as heater power increases, there is a notable shift in the dynamics of fluid flow within the loop. Initially, loop characteristics remain stable up to a specific heater power level. However, beyond this threshold, the system transitions from steady behavior to periodic oscillations and eventually to chaotic patterns.
The dynamics of a rectangular closed loop was compared by subjecting it to different types of input powers such as step, ramp, and exponential profiles [8]. Modified exponential signals were found to outperform the others in terms of stability both during increasing and decreasing power levels. Hashemi-Tilehnoee et al. [9] emphasized the role of natural circulation loops in passive heat transfer across diverse applications, highlighting advances in working fluids, configurations, and modeling techniques to improve efficiency, stability, and safety in next-generation thermal systems.
A neural network-based NARMAX model [10] was developed to capture the unstable dynamics of a closed-loop thermosyphon from experimental input–output data, showing much closer agreement with measurements than an existing mathematical model. However, experimental and theoretical studies on thermal convection loops have shown that optimal and adaptive controllers can effectively suppress chaotic convection, outperforming neural network controllers in stability and efficiency, though the latter offer advantages in handling unknown nominal conditions and time delays [11].
Muscato et al. [12] derived a low-order non-linear model aligned with experimental observations, validated through simulation–experiment comparisons. It was observed that the dynamics of the natural circulation become unstable at higher heat fluxes; however, at lower heat fluxes, the flow in the rectangular loop is less efficient in terms of heat exchange in the cooling section. This model facilitated the controller design for fluid motion stabilization, thus ensuring effective heat dissipation. Both conventional proportional and proportional-derivative controllers, considering the fluid velocity or temperature difference as feedback, were designed for various heating powers. Simulation results confirmed the controllers’ effectiveness in stabilizing the system at the desired equilibrium points.
A. Fichera et al. [13] developed a finite-order model of rectangular natural circulation loops by reducing a Fourier-series-based formulation of the momentum and energy equations to seven equations capturing the first three dynamic modes. In contrast with Muscato et al.’s [12] lower-order lumped-parameter model, which targeted specific nominal equilibrium points, Fichera’s higher-fidelity approach reproduced complex oscillatory behavior more accurately and supported controller design for a broader range of unstable dynamics.
Cammarata et al. [14] implemented an optimal control in the rectangular configuration and reported that the adopted strategy for the optimal controller is quite capable of minimizing a function considering both system stability and control cost, appropriately weighted. Simulations and experimental implementation confirmed the effectiveness of the optimal controller in suppressing hazardous oscillations and flow reversals, guiding the system to the desired steady state. A summary of control strategies applied to Natural Circulation Loops (NCLs) is given in Table 1.

Table 1.
Summary of control strategies employed in NCL.
Tarragona et al. [15] explored the use of Model Predictive Control (MPC) in managing active thermal energy storage systems, highlighting its ability to anticipate demand and weather conditions more effectively than conventional methods. It summarizes technical parameters, computational approaches, and objective functions while discussing strengths, limitations, and future research directions. Tang et al. [16] proposed an MPC-based demand-side management strategy for heat pump and thermal energy storage (HPTES) systems, combining flexibility assessment through tailored MPC constraints with flexibility exploitation via mixed-integer MPC. Numerical results from a real-world installation demonstrate its effectiveness in enabling demand response and supporting renewable integration. Tomás et al. [17] demonstrated the real-world feasibility of applying MPC to heat pumps in a non-residential building, using price-based control with weather forecasts and a grey-box model. Results from a 7-day test show MPC shifts operation to low-price periods, reducing energy costs by 40% and improving grid support, though at the expense of system efficiency.
In geothermal pipeline or solar water heating systems based on Natural Circulation Loops (NCLs), where the primary objective is to extract maximum heat with cooling water, stable and efficient operation is fundamental for ensuring long-term sustainability of energy extraction. Due to their reliance on buoyancy-driven flow without mechanical pumping, NCLs are inherently sensitive to variations in thermal and hydraulic conditions, making them vulnerable to instabilities, oscillations, and thermal stresses. Although advanced control methods have been investigated for various renewable energy systems, the application of MPC to NCL-driven geothermal pipelines has not, to the best of our knowledge, been reported in the literature. This study addresses this research gap by introducing a predictive, optimization-based control strategy that utilizes an NCL dynamic model to forecast system responses and implement optimal control actions. The proposed approach enhances thermal stability and mitigates flow oscillations to prevent excessive material stresses, thereby supporting both operational efficiency and the sustainable exploitation of geothermal or solar resources.
A key strength of the proposed MPC framework lies in its ability to explicitly incorporate operational and physical constraints into the control optimization problem. These constraints include maximum allowable temperatures and pressures to preserve material integrity, flow rate limits to minimize erosion and scaling, and bounds on heat extraction rates to prevent reservoir over-exploitation. Unlike conventional control methods, MPC ensures that these safety and sustainability criteria are respected at all times, even under variable operating conditions. By integrating predictive control with constraint handling, this work offers a novel pathway to improve process reliability, extend infrastructure lifespan, and enhance the environmental compatibility of geothermal energy systems. In this particular study, the test assembly consists of a rectangular loop with a heating section in the bottom horizontal leg and a cooling section in the top horizontal leg, connected by the adiabatic vertical riser and downcomer tubes. The primary objective is to develop an MPC framework capable of achieving effective and stable heat removal by regulating the cooling rate, while explicitly incorporating physical constraints such as maximum and minimum coolant flow capacity. To evaluate the performance of the proposed MPC framework, the authors also employ LQR and MPC with and without constraints in the natural circulating rectangular closed-loop system. These baseline strategies provide well-established references for stability and performance, against which the advantages of MPC in handling constraints and ensuring robust operation can be clearly demonstrated. By leveraging MPC’s predictive capabilities, the proposed approach aims to enhance system stability, improve operational safety, and optimize equipment sizing, ultimately contributing to energy efficiency, reduced maintenance requirements, and the broader adoption of sustainable technologies and practices in industrial applications.
2. Configuration of the Experimental Setup
Figure 2 illustrates the experimental arrangement for a single-phase natural circulation system [12]. This setup resembles the system as represented in Figure 1e, which primarily comprises heating and cooling sections positioned in the lower and upper horizontal parts of the loop, respectively, interconnected via vertical adiabatic glass tubes. The heating section utilizes a variable heater with adjustable heating power, while the cooling section incorporates a double-pipe heat exchanger. Here, the main water flow passes through the inner copper tube, while tap water is injected into the annular pipe to extract heat from the inner fluid. The flow rate of tap water is regulated by a controller.
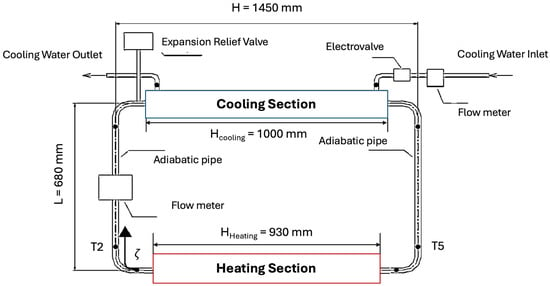
Figure 2.
Experimental Setup for Natural Circulation Loops.
The dimensions of the entire experimental setup are outlined in Table 2.

Table 2.
Dimensions of the experimental setup [13].
3. Mathematical Modeling for Natural Circulation Loops (NCLs)
The assumptions that have been made for the natural circulation model are that (i) the bulk fluid flow is only in the axial direction and (ii) the system behaves isothermally in the entire loop except for the heating and cooling sections. Therefore, the heat supplied by the heating section will be extracted in the cooling section, (iii) the cross-sectional area of the loop remains constant throughout the axial direction, and (iv) the fluid in the loop remains single phase during the entire operation. The mathematical model for natural circulation, based on the fundamental conservation laws of momentum and energy, can be described as follows [12].
We consider a spatial coordinate and time . Here, T denotes the fluid temperature in the loop (), v is the fluid velocity (), is the thermal diffusivity (), D is the inner tube diameter (), g is the gravitational acceleration (), is the volumetric expansion coefficient (), is the reference temperature (), and is the initial velocity ().
The functions and depend on the geometry of the rectangular closed-loop system and are given by
where and in Equation (5) can be defined as follows:
where q is the heat flux, is the temperature gradient between the entrance and exit of the cooling section, is the mass flow rate, is the fluid density at the reference temperature, and is the heat capacity of the cooling water.
A key physical assumption that ensures the existence of equilibrium points is that the total thermal energy transferred to the fluid as it passes through the heat source is exactly balanced by the heat removed as it flows through the heat sink. Based on this principle, we have
which in turn implies
The main model Equations (1) and (2) can be further simplified by introducing Fourier series expansion [18] for the representation of state variables T as follows:
Here, is a complex number. From Equation (5) and geometrical considerations, where (that is, the set of all nonzero integers), substituting Expressions (9)–(11) into Equations (1) and (2) yields the following system of infinite ordinary differential equations:
where , , and . Note that modes are not included in K decay, while modes in K but not in J are dependent variables.
For the rectangular loops considered here, the coefficients from the expansion of are obtained from the following expression:
For simplification, we introduce the following substitutions:
With these substitutions applied and the specific form of , the coefficients for the rectangular geometry simplify to
The coefficients vanish when k is even. Consequently, the set J consists only of odd integers. Furthermore, some coefficients may also vanish for odd k if the circuit’s aspect ratio is rational.
In a similar fashion, the coefficients arising from the expansion of can be computed as:
Again by applying substitution (15) and introducing the following definitions, the following is obtained:
The expressions for in the present case are given by
Notably, since, from the earlier result, , it follows that all even-mode coefficients vanish. Therefore, the set K again consists solely of odd integers.
Now, after plugging Equations (10)–(12) into the main model Equations (1) and (2), and by subsequently calculating the respective coefficients, truncating the Fourier series expansion at its third mode (k = 3), and applying the method of residuals for the separation of the real and imaginary parts of same order [12], we might be able to obtain the following seven ODEs to represent the overall system, as follows:
where
According to our second assumption mentioned earlier in this section, the existence of an equilibrium point is ensured.
Usually, the first step after formulating the model equations is to determine the equilibrium points, followed by linearization of the system around these equilibrium points. The working fluid considered here is pure single phase water. The properties of the working fluid at a reference temperature used in this study are presented in Table 3.

Table 3.
Model Fixed Parameters [12].
Some adaptation parameters, which depend on the operating conditions, particularly on the heating power, were also incorporated in the model. These parameters are difficult to derive analytically; therefore, the authors determined them experimentally by fitting the model to measured data under different heating power conditions. Details of the adaptation parameters are shown in the following Table 4.

Table 4.
Model Adaptation Parameters [13].
The Jacobian matrix of the system is a square matrix, where each element represents the partial derivative of the kth equation with respect to the jth variable.
Similarly, the matrix was calculated as follows:
So, the linearized system in continuous-time settings can be written as
For model validation purposes, the maximum real part of the eigenvalues obtained from the linearized model was compared with the reported eigenvalues of the validated model by Fichera et al. [13], as shown in Figure 3. The slight discrepancies observed, particularly at heater powers exceeding 900 W, can be attributed to uncertainties in operating conditions. In general, the proposed model agrees well with the reference results.
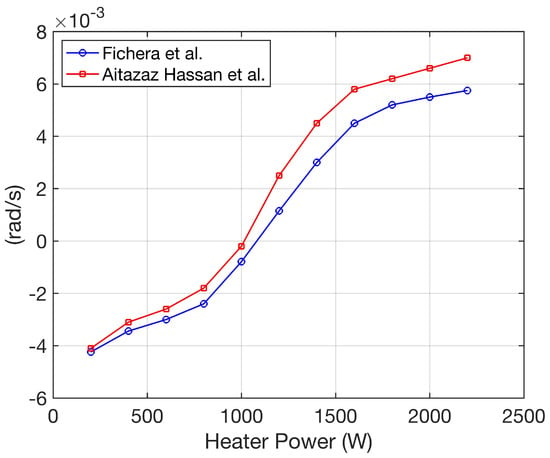
Figure 3.
Comparison of the maximum real part of an eigenvalue of the linearized model at different heater power levels [13].
A comparison of the reference velocity (m/s) obtained from steady states is also shown in the following Table 5.

Table 5.
Reference velocity for model validation.
The above system can be discretized using an appropriate time step and represented as follows:
The controllability matrix is similarly defined as [19]
Controllability Condition
The system is said to be controllable if and only if
where n is the dimension of the state vector x. In our case at P = 1800 W, the system was not found to be fully controllable, as the rank of the controllability matrix was five. However, for such systems that are not fully controllable, it is always recommended to check the stabilizability. From the PBH test (procedure details can be seen in Appendix A.1), it was found that all the uncontrolled eigenvalues are stable. The details of eigenvalues through controllability and stability analysis are shown in the following Figure 4. Three of the eigenvalues (green) are stable and controllable, two (pink) are unstable but controllable, and the remaining two eigenvalues (blue) are uncontrollable but are stable.
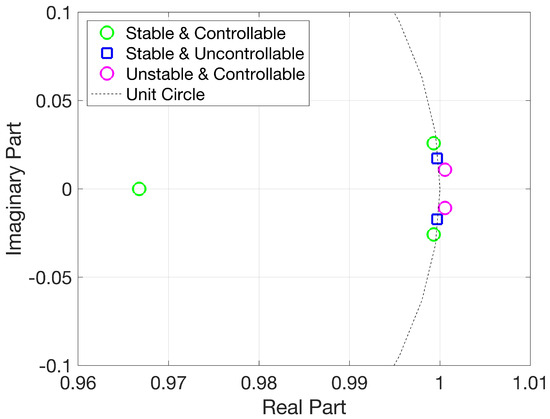
Figure 4.
Eigenmode representation of the system at P =1800 W: Stability and Controllability (PBH Test).
4. Discrete-Time Linear Quadratic Regulator (dLQR)
To develop an optimal control strategy for the discrete system, a dLQR was designed [20]. The discrete-time linearized model, characterized by the state-space matrices and , was used for the controller design. The performance index for the dLQR is defined as
Here, Q and R are the weighting matrices used to penalize state deviations and control effort, respectively. In this work, they were selected as
The dLQR gain is obtained by solving the Discrete-Time Algebraic Riccati Equation (DARE):
The matrix P can be computed using the “dare” command in MATLAB® R2023a. The optimal state-feedback gain matrix K is then given by
The corresponding optimal control input is
When this control law is applied to the discrete-time state-space model, the resulting closed-loop dynamics are given by
Once the model states have been computed, the final step is to reconstruct the temperature function from these model states, i.e., and using the following equation [13]:
5. Linear Model Predictive Control (LMPC)
To extend the optimal control framework for this multivariable system, an LMPC strategy was implemented. MPC is particularly effective for multiple-input multiple-output (MIMO) systems and for directly handling system constraints [21]. These features make MPC a natural choice for this case study.
5.1. Discrete-Time Linear Model
The continuous-time nonlinear dynamics were linearized and discretized with a sampling time of dt = 0.1 s, producing the following discrete-time state-space model:
5.2. MPC Cost Function with Terminal Penalty
The finite-horizon quadratic cost function is defined as [22]
Here, penalizes state deviations, penalizes control effort, and P is the terminal cost matrix obtained from the Discrete Algebraic Riccati Equation (DARE) for the unconstrained infinite-horizon LQR problem. This choice of P guarantees closed-loop stability when constraints are inactive.
5.3. Prediction Model for the Quadratic Programming (QP) Formulation
For the LMPC framework, MATLAB’s built-in program quadprog was used [23]. Let us now define the stacked control sequence and the predicted states over the prediction horizon (N) as
The states can be expressed in terms of initial conditions and as
where
5.4. Quadratic Program (QP) Matrices H and f
The cost function can be expressed as [22]
where the Hessian matrix H and the linear cost vector are defined by
Here, and define the stacked state prediction model, while and are block-diagonal matrices formed from , and the terminal cost P where
and
Here, and represent the stacked state and input setpoints over the prediction horizon. The details of derivation of quadratic cost function for MPC can be found in Appendix A.2.
5.5. Constraints
In this study, only input constraints were considered, as follows:
These are expressed in the following compact form:
where G and are constructed to represent the bounds on each input over the prediction horizon.
6. Results and Discussions
This section will be used to display results obtained from dLQR and LMPC with and without constraints implemented on the natural circulation pipeline system. The estimated states and control input, represented as deviation variables, obtained using LQR, unconstrained MPC, and constrained linear MPC, are illustrated in Figure 5. The dLQR and unconstrained MPC yield identical responses. However, due to the imposed input constraints (Umin = −0.6385 and Umax = 1.277), the constrained MPC exhibits an initial overshoot in the temperature state. Despite this, the system reaches steady state within 130 s, and the overall response remains smooth and free from oscillations. The control input from Equation (18), used by all controllers, is also plotted in Figure 5.
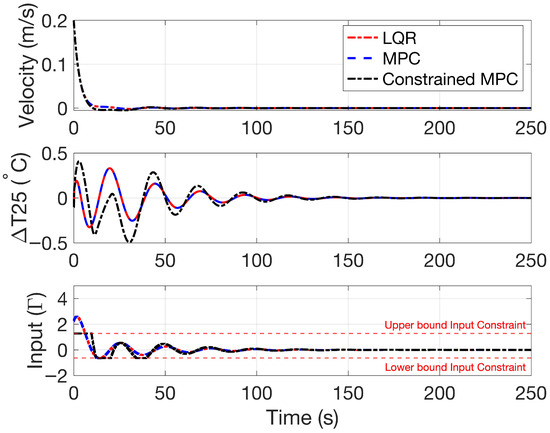
Figure 5.
Estimated states and control input variables for optimal controllers.
The observed variations in system behavior are attributed to the activation of input constraints in the constrained MPC during the initial transient response.
Remarks on dLQR vs. MPC
When the constraints are inactive, the optimal solution from LMPC coincides with the discrete-time LQR (dLQR) control law [24], as follows:
where K is obtained from DARE. The primary advantage of LMPC is realized when constraints become active, as the optimizer adjusts future inputs to satisfy them while minimizing the cost, enabling safe and feasible operation under system limits. The performance of MPC is highly sensitive to initial conditions, with greater deviations from the steady state requiring correspondingly higher control effort. This effect was examined by initiating control after different durations of open-loop operation. Due to the inherent instability of the system, longer delays resulted in the system state moving further from the steady state, thereby increasing the control effort demanded from the controller. The resulting comparison is presented in Figure 6. The observed differences in system behavior are primarily due to the enforcement of control actions by different controllers, namely LQR, unconstrained MPC, and constrained MPC at various time instants (100, 200, 400, and 600 s, respectively). In Figure 6a,b, the control action is applied at 100 s, where all controllers produce nearly identical responses since the input constraints are not activated. In Figure 6c, control actions are introduced at 400 s, and although the input constraints are just reached, the responses remain largely similar. In contrast, Figure 6d demonstrates significant violations of input constraints, leading the constrained MPC to exhibit slightly more oscillatory behavior compared to the LQR and unconstrained MPC. The main advantage in this case is the reduction in control cost without compromising performance. As a result, physical constraints may be violated by conventional LQR or unconstrained MPC; whereas, constrained MPC effectively enforces them, making it a valuable tool for systems with operational limits.
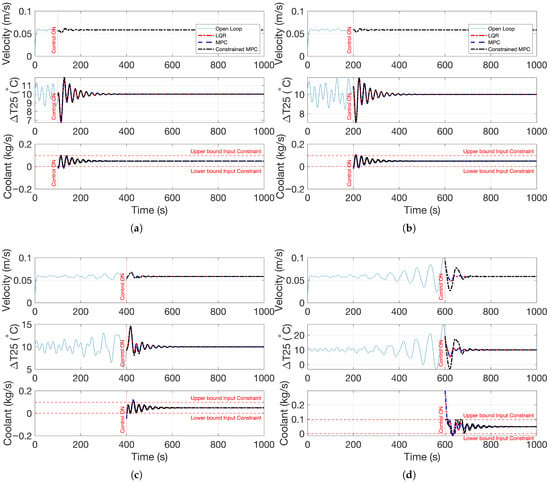
Figure 6.
States and input profiles applying control actions after (a) 100 s; (b) 200 s; (c) 400 s; (d) 600 s.
The control input consists of both the coolant flow rate and the heater power. In this study, the heater power in the heating section is assumed to remain fixed, while the coolant flow rate is manipulated as the control input. Such applications, with a fixed heat source, are commonly found in geothermal systems. In our case, the estimated coolant flow rate (kg/s) as the control input, with fixed heater power , is shown in Figure 6.
In this example, the primary physical constraint is the maximum flow capacity of the coolant pump. As Figure 6 illustrates, when the initial conditions deviate further from the steady state, the controller must exert greater control effort to stabilize the system. This increased demand can lead to the physical constraint being reached or exceeded, effectively surpassing the pump’s maximum flow capacity. Consequently, a pump with higher capacity may be required to meet the control objectives under such conditions. One significant advantage of constrained MPC is that it enables the appropriate selection of pump capacity, ensuring maximum heat removal from the Natural Circulation Loop while respecting system limitations.
For instance, as shown in Figure 6d, at 600 s, when the control action is applied, the required coolant flow rate reaches 0.3 kg/s under LQR and unconstrained MPC. In contrast, the constrained MPC, with an imposed upper limit on the control input, reduces the flow rate to 0.1 kg/s, which represents a substantial reduction in the initial energy requirement. Therefore, even if the pump is designed for 0.2 kg/s while maintaining safe operating margins, the energy demand can still be reduced by nearly one-third compared with that estimated using LQR or unconstrained MPC. By explicitly accounting for such constraints during controller design, MPC can prevent operational violations, improve system safety, and optimize equipment sizing for both performance and cost-effectiveness.
In most existing studies on natural circulation, the manipulated variable is typically the heater power; whereas, in our case study, the control focuses on regulating the coolant flow to maximize heat extraction. This difference precludes a direct quantitative comparison of control actions. Nonetheless, a qualitative comparison highlights the significance of our strategy. Prior studies [12] indicate that a sufficiently high coolant flow rate is necessary to maintain equilibrium. In contrast, MPC allows equilibrium to be maintained either by enforcing constraints or by using as an additional control input. Unlike conventional P and PD controllers deployed by Fichera et al. [13], which are applied separately to individual feedback variables such as velocity or temperature, MPC inherently handles MIMO systems, providing a clear advantage. Furthermore, the optimization of the objective function at each time step, while accounting for input and state constraints, is a distinguishing feature of MPC.
7. Conclusions
Pipeline systems are fundamental to a wide range of industrial operations, and ensuring their reliability is essential for maintaining both safety and efficiency. Among these systems, natural circulation loops present distinct challenges due to their reliance on buoyancy-driven flow rather than mechanical pumping. This inherent characteristic makes them particularly susceptible to disturbances, where flow instabilities can significantly impact both performance and operational safety.
- This study investigates the use of MPC as an effective approach for heat removal in the natural circulation pipelines used in geothermal systems. The findings show that MPC not only stabilizes system dynamics but also optimizes control efforts, which are closely tied to heating or cooling costs. Compared with conventional methods such as the Linear Quadratic Regulator (LQR), MPC provides the additional advantage of enforcing physical constraints on control actions;
- One of MPC’s key advantages is its ability to explicitly manage input constraints. This allows for more practical and safer control actions that respect the physical and operational boundaries of system components such as valves, actuators, sensors, and the maximum voltage capacity of motors or pumps, which may exhibit nonlinear behaviors or operational limits. Furthermore, MPC’s predictive capabilities enable it to respond proactively to dynamic conditions such as process fluctuations, thermal feedback, and variable flow rates;
- From an implementation perspective, the control framework proposed in this research emphasizes both computational efficiency and ease of deployment, making it well-suited for industrial applications. By utilizing scalable control logic and adaptable system models, the approach effectively translates theoretical control concepts into practical, field-ready solutions.
In conclusion, incorporating MPC into natural circulation pipeline systems represents a promising strategy for improving process reliability and operational safety. Beyond its role as a control method, MPC has the potential to serve as a core component of advanced pipeline management systems.
8. Limitations and Future Scope
Although this research highlights the potential of MPC to improve stability and safety in natural circulation pipeline systems, several limitations should be acknowledged. The current analysis is based on simplified linearized models, which do not fully capture the nonlinear behavior, parameter uncertainties, and complex thermo-hydraulic interactions that occur in real systems. The study also assumes ideal sensor and actuator performance, whereas in practice, factors such as measurement noise, delays, and actuator saturation can influence control performance. While computational efficiency was considered, scaling MPC to larger or real-time applications may still present challenges. Looking ahead, there are several opportunities to build on this work. Developing robust or adaptive versions of MPC would make the controller more resilient to uncertainties, variations, and disturbances. Combining MPC with fault detection and diagnostic tools could further enhance system reliability in abnormal operating scenarios. Experimental validation on pilot-scale or industrial natural circulation loops will be a critical step toward translating the proposed approach into practice.
Author Contributions
Conceptualization, A.H. and S.D.; methodology, A.H., G.O.C., and S.D.; software, A.H.; validation, A.H. and G.O.C.; investigation, A.H. and S.A.B.; resources, S.D.; data curation, A.H.; writing—original draft preparation, A.H.; writing—review and editing, A.H. and S.D.; visualization, A.H., G.O.C., and S.D.; supervision, S.D.; project administration, G.O.C. and S.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to acknowledge the support of the University of Alberta. The first author gratefully acknowledges the scholarship received from Higher Education Commission (HEC), Pakistan, and the Pipeline Simulation Interest Group (PSIG) for supporting the pursuit of his doctoral studies at the University of Alberta.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CT | Continuous Time |
| LQR | Linear Quadratic Control |
| MIMO | Multi Input Multi Outputs |
| MPC | Model Predictive Control |
| ID | Inner Diameter |
Appendix A
Appendix A.1. Details of PBH Test for Stabilizability [25]
Consider the following discrete-time linear system:
where , .
- 1.
- Compute the eigenvalues of the system matrix : denote them as ;
- 2.
- For each eigenvalue such that , verify controllability using the Popov–Belevitch–Hautus (PBH) test, as follows:where n is the number of states in the system.
- 3.
- If the PBH test is satisfied for all unstable (or marginally unstable) eigenvalues, then the system is said to be stabilizable.
Appendix A.2. Derivation of the Quadratic Cost Function in MPC
The stage cost at time step k is given by
where and are weighting matrices for states and inputs, respectively.
Define the stacked input vector over the prediction horizon N, as follows:
and the stacked predicted states as follows:
The system dynamics in discrete-time linear form are
Stacked over the horizon, the states can be predicted from the initial state and the input sequence as
where and are appropriately defined matrices capturing system evolution.
Construct block-diagonal weighting matrices as follows:
and stacked reference vectors as follows:
The total cost over the horizon is
Substituting gives
Expanding and grouping terms yields a quadratic form in , as follows:
Identifying the Hessian matrix and linear term gives the following:
Thus, the MPC cost is equivalently expressed as
which forms the objective function of the quadratic program solved at each control step.
References
- Liu, H. Pipeline Engineering; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Misale, M.; Garibaldi, P.; Passos, J.C.; Bitencourt, G.G.D. Experiments in a single-phase natural circulation mini-loop. Exp. Therm. Fluid Sci. 2007, 31, 1111–1120. [Google Scholar] [CrossRef]
- Zvirin, Y. A review of natural circulation loops in pressurized water reactors and other systems. Nucl. Eng. Des. 1981, 67, 203–225. [Google Scholar] [CrossRef]
- Basu, D.N.; Bhattacharyya, S.; Das, P.K. Performance comparison of rectangular and toroidal natural circulation loops under steady and transient conditions. Int. J. Therm. Sci. 2012, 57, 142–151. [Google Scholar] [CrossRef]
- Fichera, A.; Froghieri, M.; Pagano, A. Comparison of the dynamical behaviour of rectangular natural circulation loops. Proc. Inst. Mech. Eng. E 2001, 215, 273–281. [Google Scholar] [CrossRef]
- Misale, M.; Garibaldi, P.; Tarozzi, L.; Barozzi, G.S. Influence of thermal boundary conditions on the dynamic behaviour of a rectangular single-phase natural circulation loop. Int. J. Heat Fluid Flow 2011, 32, 413–423. [Google Scholar] [CrossRef]
- Saha, R.; Ghosh, K.; Mukhopadhyay, A.; Sen, S. Dynamic characterization of a single phase square natural circulation loop. Appl. Therm. Eng. 2018, 128, 1126–1138. [Google Scholar] [CrossRef]
- Basu, D.N.; Bhattacharyya, S.; Das, P.K. Dynamic response of a single-phase rectangular natural circulation loop to different excitations of input power. Int. J. Heat Mass Transf. 2013, 65, 131–142. [Google Scholar] [CrossRef]
- Hashemi-Tilehnoee, M.; Misale, M.; Seyyedi, S.M.; del Barrio, E.P.; Marchitto, A.; Hosseini, S.R.; Sharifpur, M. Overview of fundamental aspects of natural circulation loops. Appl. Therm. Eng. 2025, 276, 126936. [Google Scholar] [CrossRef]
- Fichera, A.; Pagano, A. Neural network-based prediction of the oscillating behaviour of a closed loop thermosyphon. Int. J. Heat Mass Transf. 2002, 45, 3875–3884. [Google Scholar] [CrossRef]
- Yuen, P.K.; Bau, H.H. Optimal and adaptive control of chaotic convection—Theory and experiments. Phys. Fluids 1999, 11, 1435–1448. [Google Scholar] [CrossRef]
- Muscato, G.; Xibilia, M.G. Modeling and control of a natural circulation loop. J. Proc. Control 2003, 13, 239–251. [Google Scholar] [CrossRef]
- Fichera, A.; Pagano, A. Modelling and control of rectangular natural circulation loops. Int. J. Heat Mass Transf. 2003, 46, 2425–2444. [Google Scholar] [CrossRef]
- Cammarata, L.; Fichera, A.; Pagano, A. Designing an optimal controller for rectangular natural circulation loops. Proc. Inst. Mech. Eng. E 2003, 217, 171–180. [Google Scholar] [CrossRef]
- Tarragona, J.; Pisello, A.L.; Fernández, C.; de Gracia, A.; Cabeza, L.F. Systematic review on model predictive control strategies applied to active thermal energy storage systems. Renew. Sustain. Energy Rev. 2021, 149, 111385. [Google Scholar] [CrossRef]
- Tang, W.; Li, Y.; Walker, S.; Keviczky, T. Model Predictive Control Design for Unlocking the Energy Flexibility of Heat Pump and Thermal Energy Storage Systems. In Proceedings of the 2024 IEEE Conference on Control Technology and Applications (CCTA), Newcastle upon Tyne, UK, 21–23 August 2024; pp. 433–439. [Google Scholar]
- Tomás, L.; Lämmle, M.; Pfafferott, J. Demonstration and Evaluation of Model Predictive Control (MPC) for a Real-World Heat Pump System in a Commercial Low-Energy Building for Cost Reduction and Enhanced Grid Support. Energies 2025, 18, 1434. [Google Scholar] [CrossRef]
- Rodríguez-Bernal, A.; Van Vleck, E.S. Diffusion induced chaos in a closed loop thermosyphon. J. Appl. Math. 1998, 58, 1072–1093. [Google Scholar] [CrossRef]
- Respondek, J. Controllability of dynamical systems with constraints. Syst. Control Lett. 2005, 54, 293–314. [Google Scholar] [CrossRef]
- Tran, T.V.; Yoon, S.J.; Kim, K.H. An LQR-based controller design for an LCL-filtered grid-connected inverter in discrete-time state-space under distorted grid environment. Energies 2018, 11, 2062. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Constrained model predictive control. In Model Predictive Control; Springer: London, UK, 2007; pp. 177–216. [Google Scholar]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Fink, M. Implementation of Linear Model Predictive Control–Tutorial. arXiv 2021, arXiv:2109.11986. [Google Scholar]
- Zanon, M.; Bemporad, A. Constrained controller and observer design by inverse optimality. IEEE Trans. Autom. Control 2021, 67, 5432–5439. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, F. Design of Optimal Output Regulators for Dual-Rate Linear Discrete-Time Systems Based on the Lifting Technique. Math. Probl. Eng. 2016, 1, 2879724. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).