Multi-Objective Optimization Study on Capture Performance of Diesel Particulate Filter Based on the GRA-MLR-WOA Hybrid Method
Abstract
1. Introduction
2. Methodology
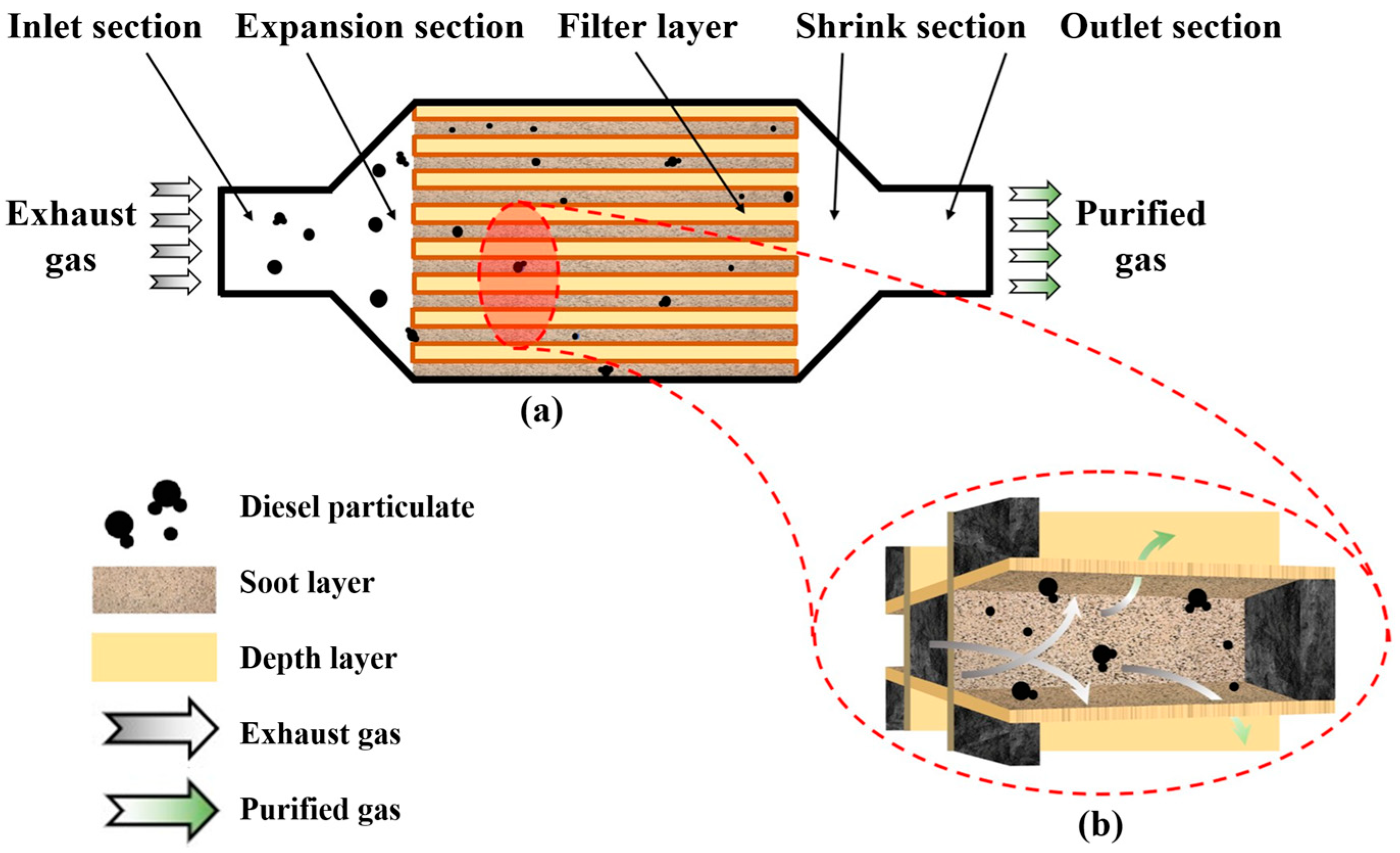
2.1. Physical Model
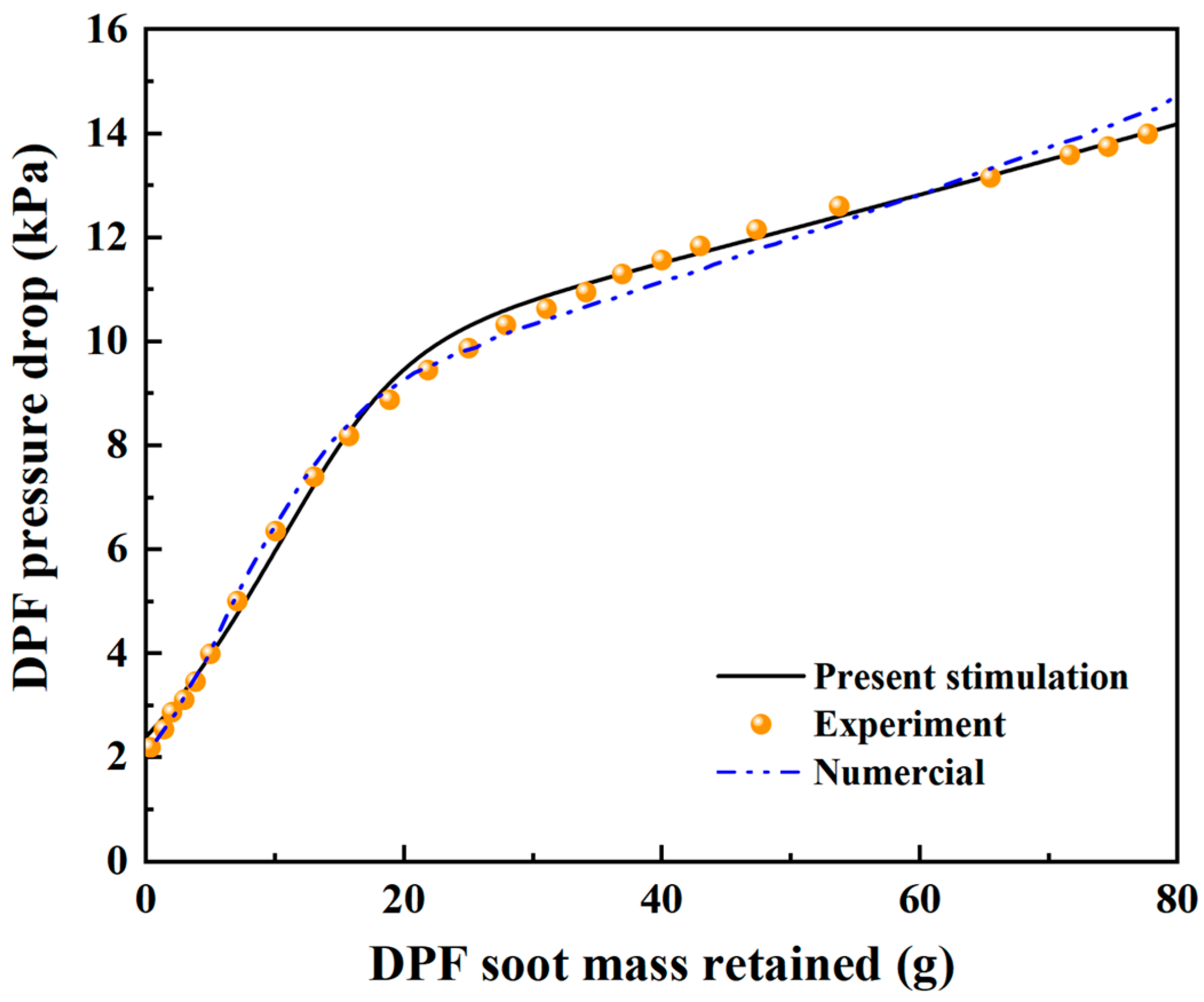
2.2. Numerical Model
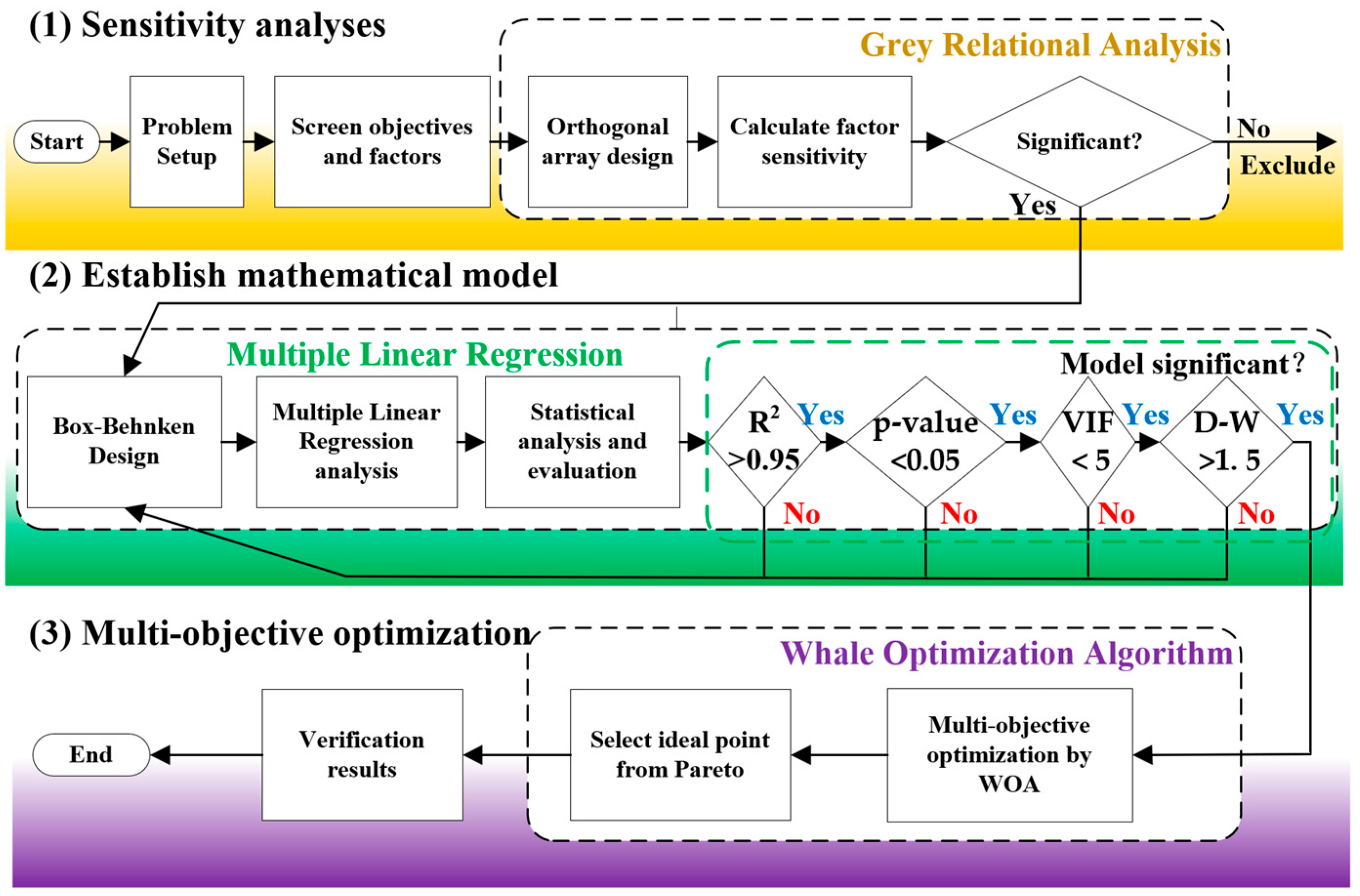
2.3. Multi-Objective Optimization Framework of the Hybrid Method
2.3.1. Grey Relational Analysis
2.3.2. Multiple Linear Regression
2.3.3. Whale Optimization Algorithm
2.3.4. Screening of Optimization Objectives and Indicators
3. Results and Discussion
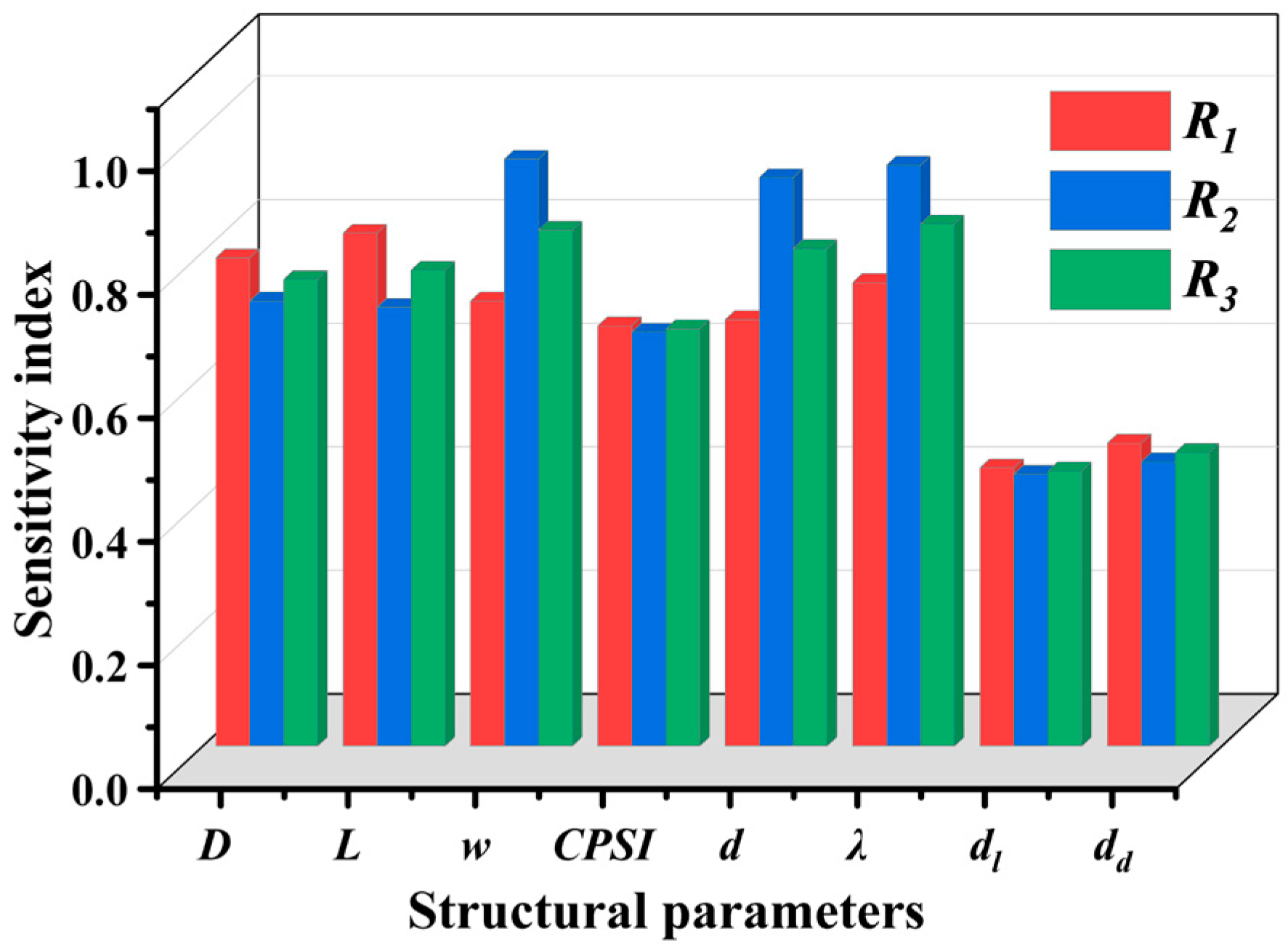
3.1. Parameter Sensitivity Analysis
3.2. Regression Prediction
3.3. Statistical and Diagnostic Methods
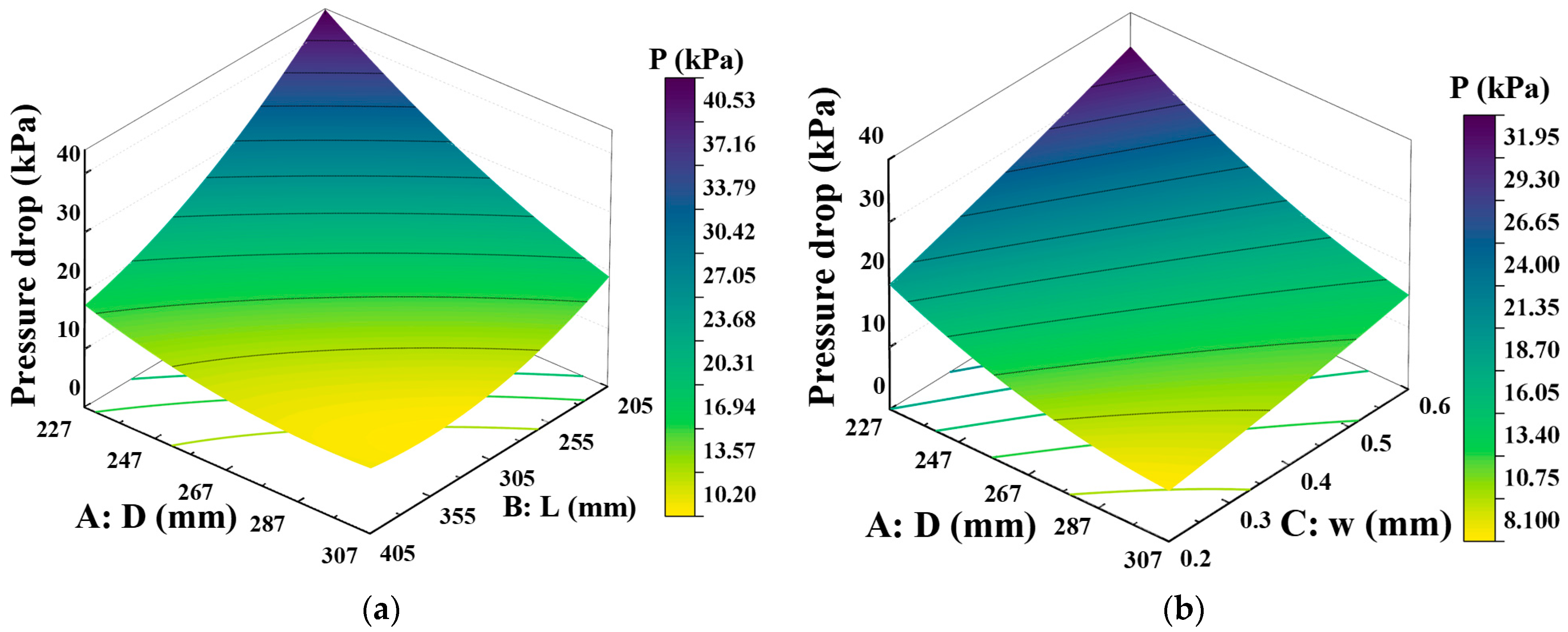
3.4. Interactive Effects of Parameters
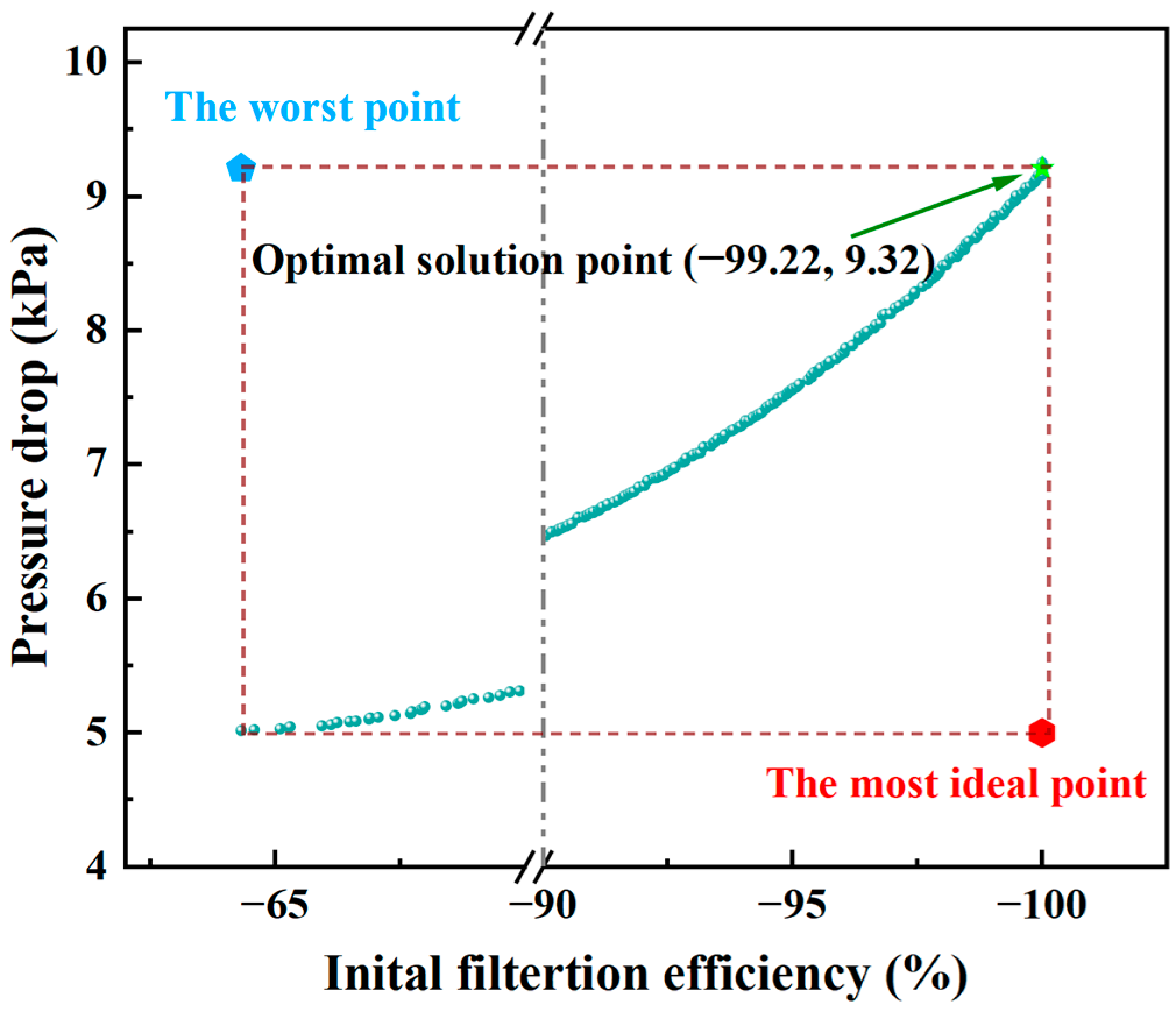
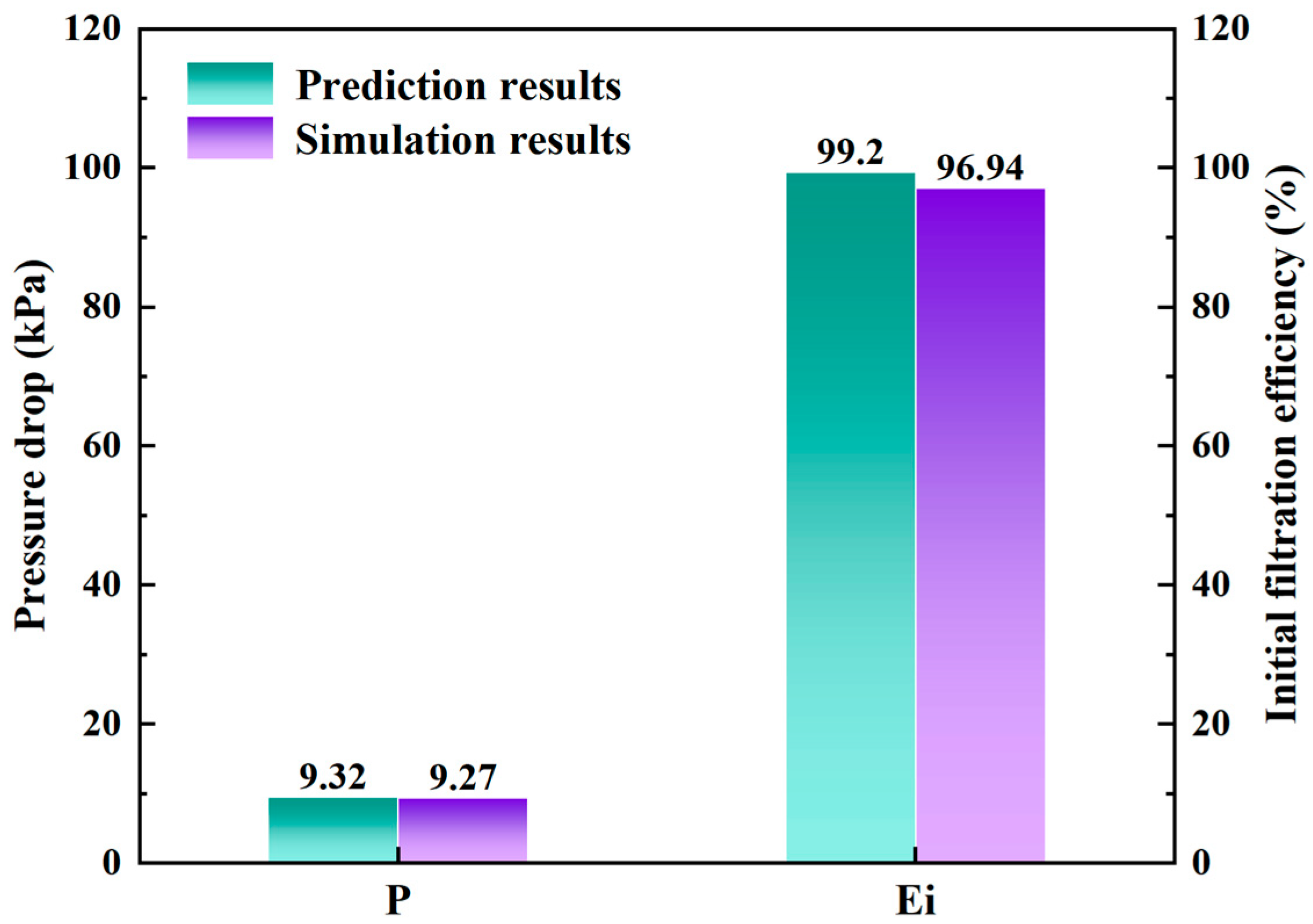
3.5. Optimization Results of the Whale Optimization Algorithm
4. Conclusions
- (1)
- The sensitivity ranking based on GRA indicates that diameter, length, wall thickness, porosity, and pore diameter are the five key variables dominating the comprehensive performance of DPF, with their comprehensive sensitivity coefficients R3 being 0.755, 0.770, 0.835, 0.845, and 0.805, respectively. Among them, length is the most critical factor affecting initial filtration efficiency, while wall thickness is the most critical factor affecting pressure drop.
- (2)
- For the model in this paper, MLR is reliable. For initial filtration efficiency, the coefficient of determination R2 = 0.979 and D-W = 1.717; for pressure drop, R2 = 0.957 and D-W = 1.825; the VIF of all independent variables is <2 and p < 0.01. Under interaction, pressure drop is more sensitive to overall dimensions, while initial filtration efficiency is more sensitive to filter substrate characteristics.
- (3)
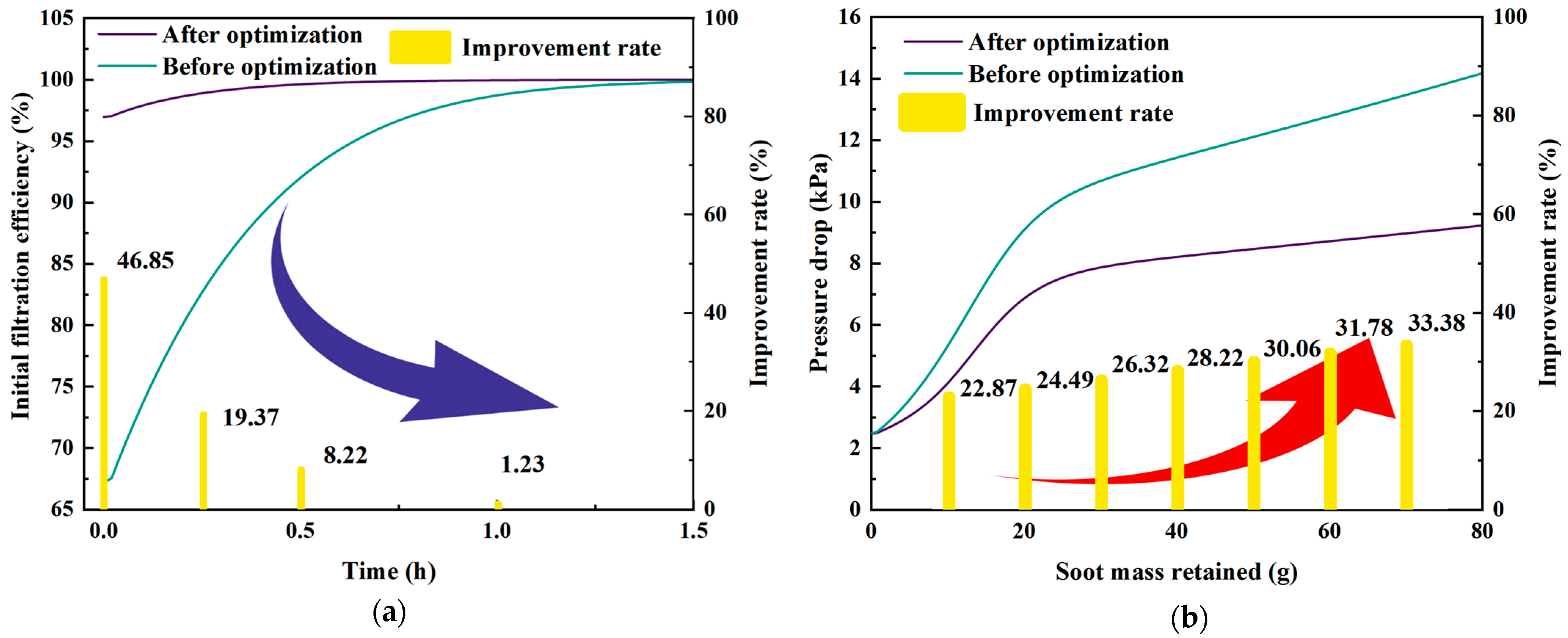
- The ideal solution selected from the Pareto frontier based on the principle of prioritizing emission compliance increases the initial filtration efficiency of the DPF by 46.85% compared with the baseline scheme, while reducing the pressure drop at an 80 g soot load by 34.88%. The deviation between the optimized prediction and simulation results is controlled within 5%, verifying the reliability of the hybrid optimization framework in terms of accuracy and generalization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, J.; Zhang, J.; Jiang, G.; Xie, K. Using DPF to Control Particulate Matter Emissions from Ships to Ensure the Sustainable Development of the Shipping Industry. Sustainability 2024, 16, 6642. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhong, W.; Tan, D.; Cui, S.; Pan, M.; Zhao, Z.; Zhang, J.; Hu, J. Hydrocarbon adsorption mechanism of modern automobile engines and methods of reducing hydrocarbon emissions during cold start process: A review. J. Environ. Manag. 2024, 353, 120188. [Google Scholar] [CrossRef]
- Rrustemi, D.N.; Ganippa, L.C.; Axon, C.J. Investigation of boost pressure and spark timing on combustion and NO emissions under lean mixture operation in hydrogen engines. Fuel 2023, 353, 129192. [Google Scholar] [CrossRef]
- Zhang, B.; Zuo, H.; Huang, Z.; Tan, J.; Zuo, Q. Endpoint forecast of different diesel-biodiesel soot filtration process in diesel particulate filters considering ash deposition. Fuel 2020, 272, 117678. [Google Scholar] [CrossRef]
- Shi, Y.; Hou, D.; Luo, Y.; Kaiqi, Z.; Yang, Y.; Ding, Z.; Cai, Y.; Li, X.; Wang, J.; Wang, J. Degradation of particulate matter utilizing non-thermal plasma: Evolution laws of morphological micro-nanostructure and elemental occurrence state. J. Environ. Chem. Eng. 2024, 12, 114772. [Google Scholar] [CrossRef]
- Tian, J.; Wang, L.; Xiong, Y.; Wang, Y.; Yin, W.; Tian, G.; Wang, Z.; Cheng, Y.; Ji, S. Enhancing combustion efficiency and reducing nitrogen oxide emissions from ammonia combustion: A comprehensive review. Process Saf. Environ. Prot. 2024, 183, 514–543. [Google Scholar] [CrossRef]
- Liu, S.; Kang, Y.; Deng, Z.; Yin, Z.; Ye, Z.; Xue, J.; Zhang, J. Study on the effect of blending hydrocarbon-based biodiesel on the performance of SCR system and urea calibration method for marine engines. Energy 2024, 292, 130473. [Google Scholar] [CrossRef]
- Algayyim, S.J.M.; Saleh, K.; Wandel, A.P.; Fattah, I.M.R.; Yusaf, T.; Alrazen, H.A. Influence of natural gas and hydrogen properties on internal combustion engine performance, combustion, and emissions: A review. Fuel 2024, 362, 130844. [Google Scholar] [CrossRef]
- Zhao, K.; Lou, D.; Zhang, Y.; Fang, L.; Tan, P.; Hu, Z. Flame propagation and NO formation characteristics of hydrogen-air mixture combustion due to dilution effect. Renew. Energy 2025, 241, 122249. [Google Scholar] [CrossRef]
- Xie, F.; Liang, Z.; Lai, K.; Liu, Y.; Wang, Z.; Li, X. Influence of operating parameters on hydrogen DISI engine at injection pressure-drop by experimental investigation and Taguchi method. Fuel 2024, 362, 130840. [Google Scholar] [CrossRef]
- E, J.; Zhang, Z.; Chen, J.; Pham, M.; Zhao, X.; Peng, Q.; Zhang, B.; Yin, Z. Performance and emission evaluation of a marine diesel engine fueled by water biodiesel-diesel emulsion blends with a fuel additive of a cerium oxide nanoparticle. Energy Convers. Manag. 2018, 169, 194–205. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, Z.; Sun, B.; Zhang, S.; Lai, F.; Ma, N.; Ju, X.; Luo, Q.; Bao, L. Experimental investigation of the working boundary limited by abnormal combustion and the combustion characteristics of a turbocharged direct injection hydrogen engine. Energy Conv. Manag. 2024, 299, 117861. [Google Scholar] [CrossRef]
- Buzzi, L.; Biasin, V.; Galante, A.; Gessaroli, D.; Pesce, F.; Tartarini, D.; Vassallo, A.; Scalabrini, S.; Sacco, N.; Rossi, R. Experimental investigation of hydrogen combustion in a single cylinder PFI engine. Int. J. Engine Res. 2024, 25, 358–372. [Google Scholar] [CrossRef]
- Tian, J.; Liu, P.; Liu, Z.; Tang, J.; Yin, W.; Cheng, Y. Investigation on the effects of nanosecond pulsed discharge on combustion characteristics of C3H8/air mixtures using a rapid compression machine. J. Energy Inst. 2025, 119, 101983. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, Y.; Liu, Z.; Wang, L.; Wang, Y.; Yin, W.; Cheng, Y.; Zhao, Q. Experimental study on the discharge characteristics of high-voltage nanosecond pulsed discharges and its effect on the ignition and combustion processes. Appl. Energy 2024, 374, 124011. [Google Scholar] [CrossRef]
- Lee, S.; Jeon, J.; Park, S. Optimization of combustion chamber geometry and operating conditions for compression ignition engine fueled with pre-blended gasoline-diesel fuel. Energy Convers. Manag. 2016, 126, 638–648. [Google Scholar] [CrossRef]
- You, H.; Gao, R.; Hu, P.; Liang, K.; Zhou, X.; Huang, X.; Pan, M. Sensitivity analysis of diesel particulate filters to geometric parameters during soot loading and its multi-objective optimization. Process Saf. Environ. Prot. 2022, 159, 251–265. [Google Scholar] [CrossRef]
- Zhang, Z.; Dong, R.; Tan, D.; Duan, L.; Jiang, F.; Yao, X.; Yang, D.; Hu, J.; Zhang, J.; Zhong, W.; et al. Effect of structural parameters on diesel particulate filter trapping performance of heavy-duty diesel engines based on grey correlation analysis. Energy 2023, 271, 127025. [Google Scholar] [CrossRef]
- Gao, J.; Wang, Y.; Li, X.; Wang, S.; Ma, C.; Wang, X. Catalytic effect of diesel PM derived ash on PM oxidation activity. Chemosphere 2022, 299, 134445. [Google Scholar] [CrossRef]
- Fang, J.; Meng, Z.; Li, J.; Pu, Y.; Du, Y.; Li, J.; Jin, Z.; Chen, C.; Chase, G.G. The influence of ash on soot deposition and regeneration processes in diesel particular filter. Appl. Therm. Eng. 2017, 124, 633–640. [Google Scholar] [CrossRef]
- Lu, Y.; Que, J.H.; Xia, Y.; Li, X.Q.; Jiang, Q.L.; Feng, L.Y. A comparative study of the effects of EGR on combustion and emission characteristics of port fuel injection and late direct injection in hydrogen internal combustion engine. Appl Energy 2024, 375, 123830. [Google Scholar] [CrossRef]
- Luo, Y.; Shi, Y.; Zhuang, K.; Ji, R.; Chen, X.; Huang, Y.; Wang, Z.; Cai, Y.; Li, X. Study on the Evolution of Physicochemical Properties of Carbon Black at Different Regeneration Stages of Diesel Particulate Filters Regenerated by Non-Thermal Plasma. Processes 2024, 12, 1113. [Google Scholar] [CrossRef]
- Lupše, J.; Campolo, M.; Soldati, A. Modelling soot deposition and monolith regeneration for optimal design of automotive DPFs. Chem. Eng. Sci. 2016, 151, 36–50. [Google Scholar] [CrossRef]
- Tan, Y.; Zheng, P.; E, J.; Han, D.; Feng, C. Effects of inlet velocity and structure parameters on the performance of a rotary diesel particulate filter for truck diesel engine based on fuzzy grey relational analysis. Chemosphere 2022, 307, 135843. [Google Scholar] [CrossRef]
- Ye, J.; E, J.; Peng, Q. Effects of porosity setting and multilayers of diesel particulate filter on the improvement of regeneration performance. Energy 2023, 263, 126063. [Google Scholar] [CrossRef]
- Xiao, G.; Li, B.; Tian, H.; Leng, X.; Long, W. Numerical study on flow and pressure drop characteristics of a novel type asymmetric wall-flow diesel particulate filter. Fuel 2020, 267, 117148. [Google Scholar] [CrossRef]
- Konstandopoulos, A.G. In Flow Resistance Descriptors for Diesel Particulate Filters: Definitions, Measurements and Testing; Sae World Congress & Exhibition: Thessaloniki, Greece, 2003. [Google Scholar]
- Jisieike, C.F.; Ishola, N.B.; Latinwo, L.M.; Betiku, E. Crude rubber seed oil esterification using a solid catalyst: Optimization by hybrid adaptive neuro-fuzzy inference system and response surface methodology. Energy 2023, 263, 125734. [Google Scholar] [CrossRef]
- Yang, J.; Stewart, M.; Maupin, G.; Herling, D.; Zelenyuk, A. Single wall diesel particulate filter (DPF) filtration efficiency studies using laboratory generated particles. Chem. Eng. Sci. 2009, 64, 1625–1634. [Google Scholar] [CrossRef]
- Wang, Y.; Ghosh, R.S.; Gong, J.; Nikodem, A.; Kutschi, S.; Zokoe, J.; Xue, E.J.; Wang, Z.; Honda, T.; Wells, A.; et al. Modeling the filtration performance of ceramic filters over transient cycles of natural gas and diesel engines. Appl. Energy 2023, 337, 120895. [Google Scholar] [CrossRef]
- Liu, X.; Matti Maricq, M.; Dobson, D.A. Statistical capillary tube model for porous filter media: An application in modeling of gasoline particulate filter. Sep. Purif. Technol. 2022, 286, 120393. [Google Scholar] [CrossRef]
- Houston, A.J.; Boubert, D.; Clyne, T.W. The Permeability of Novel Hybrid Fiber Composite Material for Use as Diesel Particulate Filters. Adv. Eng. Mater. 2020, 22, 2000562. [Google Scholar] [CrossRef]
- E, J.; Zhao, X.; Liu, G.; Zhang, B.; Zuo, Q.; Wei, K.; Li, H.; Han, D.; Gong, J. Effects analysis on optimal microwave energy consumption in the heating process of composite regeneration for the diesel particulate filter. Appl. Energy 2019, 254, 113736. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Y.; Zhang, Z.; Tan, D.; Li, J.; Yin, Z.; Hu, J.; Zhao, Z. Multi-objective optimization of the combustion chamber geometry for a highland diesel engine fueled with diesel/n-butanol/PODEn by ANN-NSGA III. Energy 2023, 282, 128793. [Google Scholar] [CrossRef]
- Ozturk, S.; Erol, H. Multi-objective optimization of a diesel particulate filter: An acoustic approach. Part. Sci. Technol. 2022, 40, 465–474. [Google Scholar] [CrossRef]
- Zhang, B.; E, J.; Gong, J.; Yuan, W.; Zuo, W.; Li, Y.; Fu, J. Multidisciplinary design optimization of the diesel particulate filter in the composite regeneration process. Appl. Energy 2016, 181, 14–28. [Google Scholar] [CrossRef]
- Seo, J.; Yun, B.; Kim, J.; Shin, M.; Park, S. Development of a cold-start emission model for diesel vehicles using an artificial neural network trained with real-world driving data. Sci. Total Environ. 2022, 806, 151347. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, B.; Gundlapally, S.R.; Koutsivitis, P.; Wahiduzzaman, S. Performance evaluation of neural networks in modeling exhaust gas aftertreatment reactors. Chem. Eng. J. 2022, 433, 134366. [Google Scholar] [CrossRef]
- Qiang, T.P.; Peng, L.Y.; De Yuan, W.; Yuan, H.Z.; Di Ming, L. Effects of Catalyst Structural Parameters on the Performance of Exhaust Gas Aftertreatment System of Diesel Engines. Int. J. Automot. Technol. 2022, 23, 1085–1097. [Google Scholar] [CrossRef]
- Chen, X.; Shi, Y.; Cai, Y.; Xie, J.; Yang, Y.; Hou, D.; Fan, Y. Effect of non-thermal plasma injection flow rate on diesel particulate filter regeneration at room temperature. Carbon Lett. 2024, 34, 1075–1089. [Google Scholar] [CrossRef]
- Guan, B.; Zhan, R.; Lin, H.; Huang, Z. Review of the state-of-the-art of exhaust particulate filter technology in internal combustion engines. J. Environ. Manag. 2015, 154, 225–258. [Google Scholar] [CrossRef]
- Yin, Z.; Liu, S.; Tan, D.; Zhang, Z.; Wang, Z.; Wang, B. A review of the development and application of soot modelling for modern diesel engines and the soot modelling for different fuels. Process Saf. Environ. Prot. 2023, 178, 836–859. [Google Scholar] [CrossRef]
- Zhang, Z.; Dong, R.; Tan, D.; Zhang, B. Multi-objective optimization of performance characteristic of diesel particulate filter for a diesel engine by RSM-MOPSO during soot loading. Process Saf. Environ. Prot. 2023, 177, 530–545. [Google Scholar] [CrossRef]
- Konstandopoulos, A.G.; Kostoglou, M.; Skaperdas, E.; Papaioannou, E.; Kladopoulou, E. Fundamental Studies of Diesel Particulate Filters: Transient Loading, Regeneration and Aging, SAE 2000-01-1016. Sae Pap. 2000, 109, 683–705. [Google Scholar]
- Mafarja, M.M.; Mirjalili, S. Hybrid Whale Optimization Algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Goyal, H.; Jones, P.; Bajwa, A.; Parsons, D.; Akehurst, S.; Davy, M.H.; Leach, F.C.P.; Esposito, S. Design trends and challenges in hydrogen direct injection (H2DI) internal combustion engines-A review. Int. J. Hydrogen Energy 2024, 86, 1179–1194. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, J.; Wang, Y.; Pan, M.; Lu, K.; Ye, Y.; Yin, Z. An artificial intelligence-based strategy for multi-objective optimization of diesel engine fueled with ammonia-diesel-hydrogen blended fuel. Energy 2025, 318, 134701. [Google Scholar] [CrossRef]
- Bibiloni-Ipata, S.; Vielmo-Cogo, V.; Frizzo-Prante, G.; Martinez-Boggio, S. Design and study of the effects of retrofitting diesel engines in hydrogen trucks through simulation. Int. J. Hydrogen Energy 2025, 163, 150806. [Google Scholar] [CrossRef]
- Ding, Y.F.; Chen, Z.J.; Zhang, H.W.; Wang, X.; Guo, Y. A short-term wind power prediction model based on CEEMD and WOA-KELM. Renew. Energy 2022, 189, 188–198. [Google Scholar] [CrossRef]
- Zhou, P.J.; Wen, Z.P.; Wang, Y.; Wu, Y.Z.; Wu, D.H.; Huang, R.F.; Yao, Z.F. Improving the energy performance of vortex pump based on whale optimization algorithm. Eng. Appl. Comp. Fluid Mech 2025, 19, 2441344. [Google Scholar] [CrossRef]
- Ma, R.Z.; Fu, K.L.; Yan, T.H. Dynamic double mutation whale differential algorithms and applications to multi-constrained global optimization engineering problems. Expert Syst. Appl. 2026, 296, 129128. [Google Scholar] [CrossRef]


| Parameter | Value | Unit |
|---|---|---|
| Diameter | 267 | mm |
| Length | 305 | mm |
| Wall thickness | 0.43 | mm |
| Channels per square inch | 100 | 1/in2 |
| Pore diameter | 24.4 | μm |
| Porosity | 0.5 | - |
| Parameter | Symbol | Initial Values | Varying Ranges [Lower Bound, Upper Bound] [36] |
|---|---|---|---|
| Diameter (mm) | D | 267 | [227, 307] |
| Length (mm) | L | 305 | [205, 405] |
| Wall thickness (mm) | w | 0.43 | [0.23, 0.63] |
| Channels per square inch (1/in2) | CPSI | 100 | [50, 200] |
| Pore diameter (μm) | d | 24.4 | [18.4, 30.4] |
| Porosity (-) | λ | 0.5 | [0.3, 0.7] |
| Length of exhaust pipe (mm) | dl | 100 | [50, 200] |
| Diameter of exhaust pipe (mm) | dd | 133 | [83, 183] |
| Serial Number | D (mm) | L (mm) | w (mm) | CPSI (1/in2) | d (μm) | λ (-) | dl (mm) | dd (mm) | P (kPa) | Ei (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 227 | 205 | 0.23 | 50 | 18.4 | 0.3 | 100 | 83 | 24.54 | 30.80 |
| 2 | 227 | 205 | 0.23 | 100 | 24.4 | 0.5 | 200 | 183 | 20.55 | 36.65 |
| 3 | 227 | 205 | 0.23 | 200 | 30.4 | 0.7 | 50 | 133 | 23.20 | 44.97 |
| 4 | 227 | 305 | 0.63 | 50 | 24.4 | 0.7 | 100 | 133 | 77.56 | 84.60 |
| 5 | 227 | 305 | 0.63 | 100 | 30.4 | 0.3 | 200 | 83 | 22.62 | 42.83 |
| 6 | 227 | 305 | 0.63 | 200 | 18.4 | 0.5 | 50 | 183 | 68.44 | 79.65 |
| 7 | 227 | 405 | 0.43 | 50 | 30.4 | 0.5 | 100 | 183 | 23.98 | 53.57 |
| 8 | 227 | 405 | 0.43 | 100 | 18.4 | 0.7 | 200 | 133 | 22.16 | 93.70 |
| 9 | 227 | 405 | 0.43 | 200 | 24.4 | 0.3 | 50 | 83 | 11.06 | 51.54 |
| 10 | 267 | 205 | 0.63 | 50 | 30.4 | 0.5 | 200 | 133 | 35.67 | 54.63 |
| 11 | 267 | 205 | 0.63 | 100 | 18.4 | 0.7 | 100 | 83 | 45.39 | 95.98 |
| 12 | 267 | 205 | 0.63 | 200 | 24.4 | 0.3 | 50 | 183 | 46.82 | 53.93 |
| 13 | 267 | 305 | 0.43 | 50 | 18.4 | 0.3 | 200 | 183 | 9.41 | 64.90 |
| 14 | 267 | 305 | 0.43 | 100 | 24.4 | 0.5 | 100 | 133 | 11.55 | 71.26 |
| 15 | 267 | 305 | 0.43 | 200 | 30.4 | 0.7 | 50 | 83 | 22.90 | 74.65 |
| 16 | 267 | 405 | 0.23 | 50 | 24.4 | 0.7 | 200 | 83 | 11.04 | 68.55 |
| 17 | 267 | 405 | 0.23 | 100 | 30.4 | 0.3 | 100 | 183 | 4.52 | 30.94 |
| 18 | 267 | 405 | 0.23 | 200 | 18.4 | 0.5 | 50 | 133 | 7.23 | 72.51 |
| 19 | 307 | 205 | 0.43 | 50 | 24.4 | 0.7 | 100 | 183 | 28.15 | 79.97 |
| 20 | 307 | 205 | 0.43 | 100 | 30.4 | 0.3 | 50 | 133 | 9.04 | 39.31 |
| 21 | 307 | 205 | 0.43 | 200 | 18.4 | 0.5 | 200 | 83 | 12.33 | 86.65 |
| 22 | 307 | 305 | 0.23 | 50 | 30.4 | 0.5 | 100 | 83 | 7.19 | 39.97 |
| 23 | 307 | 305 | 0.23 | 100 | 18.4 | 0.7 | 50 | 183 | 7.78 | 89.03 |
| 24 | 307 | 305 | 0.23 | 200 | 24.4 | 0.3 | 200 | 133 | 4.50 | 45.42 |
| 25 | 307 | 405 | 0.63 | 50 | 18.4 | 0.3 | 100 | 183 | 5.86 | 87.43 |
| 26 | 307 | 405 | 0.63 | 100 | 24.4 | 0.5 | 50 | 133 | 10.83 | 89.47 |
| 27 | 307 | 405 | 0.63 | 200 | 30.4 | 0.7 | 200 | 83 | 37.27 | 80.84 |
| Structural Parameters | R1 | R2 | R3 |
|---|---|---|---|
| D | 0.79 | 0.72 | 0.755 |
| L | 0.83 | 0.71 | 0.770 |
| w | 0.72 | 0.95 | 0.835 |
| CPSI | 0.68 | 0.67 | 0.675 |
| d | 0.69 | 0.92 | 0.805 |
| λ | 0.75 | 0.94 | 0.845 |
| dl | 0.45 | 0.44 | 0.445 |
| dd | 0.49 | 0.46 | 0.475 |
| D (mm) | L (mm) | w (mm) | λ (-) | d (μm) | P (kPa) | Ei (%) |
|---|---|---|---|---|---|---|
| 227 | 205 | 0.43 | 0.5 | 24.4 | 42.85 | 48.65 |
| 307 | 205 | 0.43 | 0.5 | 24.4 | 16.41 | 63.23 |
| 227 | 405 | 0.43 | 0.5 | 24.4 | 15.60 | 63.98 |
| 307 | 405 | 0.43 | 0.5 | 24.4 | 6.67 | 78.82 |
| 267 | 305 | 0.23 | 0.3 | 24.4 | 7.19 | 30.94 |
| 267 | 305 | 0.63 | 0.3 | 24.4 | 13.32 | 59.23 |
| 267 | 305 | 0.23 | 0.7 | 24.4 | 15.58 | 62.07 |
| 267 | 305 | 0.63 | 0.7 | 24.4 | 35.63 | 90.42 |
| 267 | 205 | 0.43 | 0.5 | 18.4 | 23.24 | 73.48 |
| 267 | 405 | 0.43 | 0.5 | 18.4 | 9.04 | 86.92 |
| 267 | 205 | 0.43 | 0.5 | 30.4 | 27.47 | 43.72 |
| 267 | 405 | 0.43 | 0.5 | 30.4 | 10.67 | 59.04 |
| 227 | 305 | 0.23 | 0.5 | 24.4 | 16.87 | 38.32 |
| 307 | 305 | 0.23 | 0.5 | 24.4 | 6.55 | 52.01 |
| 227 | 305 | 0.63 | 0.5 | 24.4 | 30.39 | 69.07 |
| 307 | 305 | 0.63 | 0.5 | 24.4 | 12.90 | 83.07 |
| 267 | 305 | 0.43 | 0.3 | 18.4 | 9.46 | 64.84 |
| 267 | 305 | 0.43 | 0.7 | 18.4 | 24.04 | 93.43 |
| 267 | 305 | 0.43 | 0.3 | 30.4 | 10.39 | 36.48 |
| 267 | 305 | 0.43 | 0.7 | 30.4 | 25.96 | 69.62 |
| 267 | 205 | 0.23 | 0.5 | 24.4 | 18.64 | 37.48 |
| 267 | 405 | 0.23 | 0.5 | 24.4 | 6.83 | 51.61 |
| 267 | 205 | 0.63 | 0.5 | 24.4 | 33.21 | 67.96 |
| 267 | 405 | 0.63 | 0.5 | 24.4 | 13.49 | 82.70 |
| 227 | 305 | 0.43 | 0.3 | 24.4 | 16.94 | 40.77 |
| 307 | 305 | 0.43 | 0.3 | 24.4 | 6.42 | 54.60 |
| 227 | 305 | 0.43 | 0.7 | 24.4 | 36.86 | 74.45 |
| 307 | 305 | 0.43 | 0.7 | 24.4 | 17.94 | 87.42 |
| 267 | 305 | 0.23 | 0.5 | 18.4 | 9.13 | 61.98 |
| 267 | 305 | 0.63 | 0.5 | 18.4 | 17.67 | 90.36 |
| 267 | 305 | 0.23 | 0.5 | 30.4 | 11.04 | 34.38 |
| 267 | 305 | 0.63 | 0.5 | 30.4 | 20.57 | 63.97 |
| 227 | 305 | 0.43 | 0.5 | 18.4 | 21.18 | 74.38 |
| 307 | 305 | 0.43 | 0.5 | 18.4 | 8.63 | 87.36 |
| 227 | 305 | 0.43 | 0.5 | 30.4 | 25.02 | 44.87 |
| 307 | 305 | 0.43 | 0.5 | 30.4 | 10.29 | 59.31 |
| 267 | 205 | 0.43 | 0.3 | 24.4 | 18.65 | 39.66 |
| 267 | 405 | 0.43 | 0.3 | 24.4 | 6.85 | 54.37 |
| 267 | 205 | 0.43 | 0.7 | 24.4 | 39.91 | 73.56 |
| 267 | 405 | 0.43 | 0.7 | 24.4 | 18.28 | 86.98 |
| 267 | 305 | 0.43 | 0.5 | 24.4 | 13.52 | 65.98 |
| 267 | 305 | 0.43 | 0.5 | 24.4 | 14.77 | 65.03 |
| 267 | 305 | 0.43 | 0.5 | 24.4 | 14.26 | 66.14 |
| 267 | 305 | 0.43 | 0.5 | 24.4 | 13.56 | 65.24 |
| 267 | 305 | 0.43 | 0.5 | 24.4 | 14.71 | 65.01 |
| 267 | 305 | 0.43 | 0.5 | 24.4 | 13.49 | 65.97 |
| B | Standard Error | Beta | t-Value | p-Value | VIF | |
|---|---|---|---|---|---|---|
| Constant | −27.885 | 6.033 | - | −3.363 | 0.002 | - |
| 226.7 | 0.173 | 0.017 | 0.240 | 10.415 | 0.002 | 1.005 |
| 205 | 0.072 | 0.007 | 0.252 | 10.920 | 0.001 | 1.005 |
| 0.43 | 74.369 | 3.198 | 0.535 | 23.251 | 0.008 | 1.000 |
| 0.5 | 80.335 | 3.198 | 0.378 | 25.117 | 0.003 | 1.000 |
| 24.4 | −2.306 | 0.107 | −0.497 | −21.626 | 0.009 | 1.000 |
| R2 | 0.979 | |||||
| F | F(5,39) = 370.471, p = 0.000 | |||||
| D-W | 1.717 | |||||
| B | Standard Error | Beta | t-Value | p-Value | VIF | |
|---|---|---|---|---|---|---|
| Constant | 52.026 | 6.878 | - | 7.244 | 0.005 | - |
| 226.7 | −0.170 | 0.019 | −0.462 | −8.985 | 0.003 | 1.005 |
| 205 | −0.076 | 0.008 | −0.317 | −10.066 | 0.001 | 1.005 |
| 0.43 | 26.677 | 3.647 | 0.375 | 7.315 | 0.010 | 1.000 |
| 0.5 | 39.052 | 3.647 | 0.149 | 10.709 | 0.001 | 1.000 |
| 24.4 | 0.198 | 0.122 | 0.084 | 1.630 | 0.007 | 1.000 |
| R2 | 0.957 | |||||
| F | F(5,39) = 68.267, p = 0.000 | |||||
| D-W | 1.825 | |||||
| D (mm) | L (mm) | w (mm) | λ (-) | d (μm) | P (kPa) | Ei (%) | |
|---|---|---|---|---|---|---|---|
| Original | 266.7 | 305 | 0.43 | 0.5 | 24.4 | 14.18 | 65.90 |
| Optimized | 307 | 405 | 0.57 | 0.55 | 18.1 | 9.32 | 99.22 |
| Comparison | −34.27% | 50.56% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nian, M.; Dong, R.; Zhong, W.; Zhang, Y.; Lou, D. Multi-Objective Optimization Study on Capture Performance of Diesel Particulate Filter Based on the GRA-MLR-WOA Hybrid Method. Sustainability 2025, 17, 8777. https://doi.org/10.3390/su17198777
Nian M, Dong R, Zhong W, Zhang Y, Lou D. Multi-Objective Optimization Study on Capture Performance of Diesel Particulate Filter Based on the GRA-MLR-WOA Hybrid Method. Sustainability. 2025; 17(19):8777. https://doi.org/10.3390/su17198777
Chicago/Turabian StyleNian, Muxin, Rui Dong, Weihuang Zhong, Yunhua Zhang, and Diming Lou. 2025. "Multi-Objective Optimization Study on Capture Performance of Diesel Particulate Filter Based on the GRA-MLR-WOA Hybrid Method" Sustainability 17, no. 19: 8777. https://doi.org/10.3390/su17198777
APA StyleNian, M., Dong, R., Zhong, W., Zhang, Y., & Lou, D. (2025). Multi-Objective Optimization Study on Capture Performance of Diesel Particulate Filter Based on the GRA-MLR-WOA Hybrid Method. Sustainability, 17(19), 8777. https://doi.org/10.3390/su17198777