A Multi-Stage Resilience Enhancement Method for Distribution Networks Employing Transportation and Hydrogen Energy Systems
Abstract
1. Introduction
- (1)
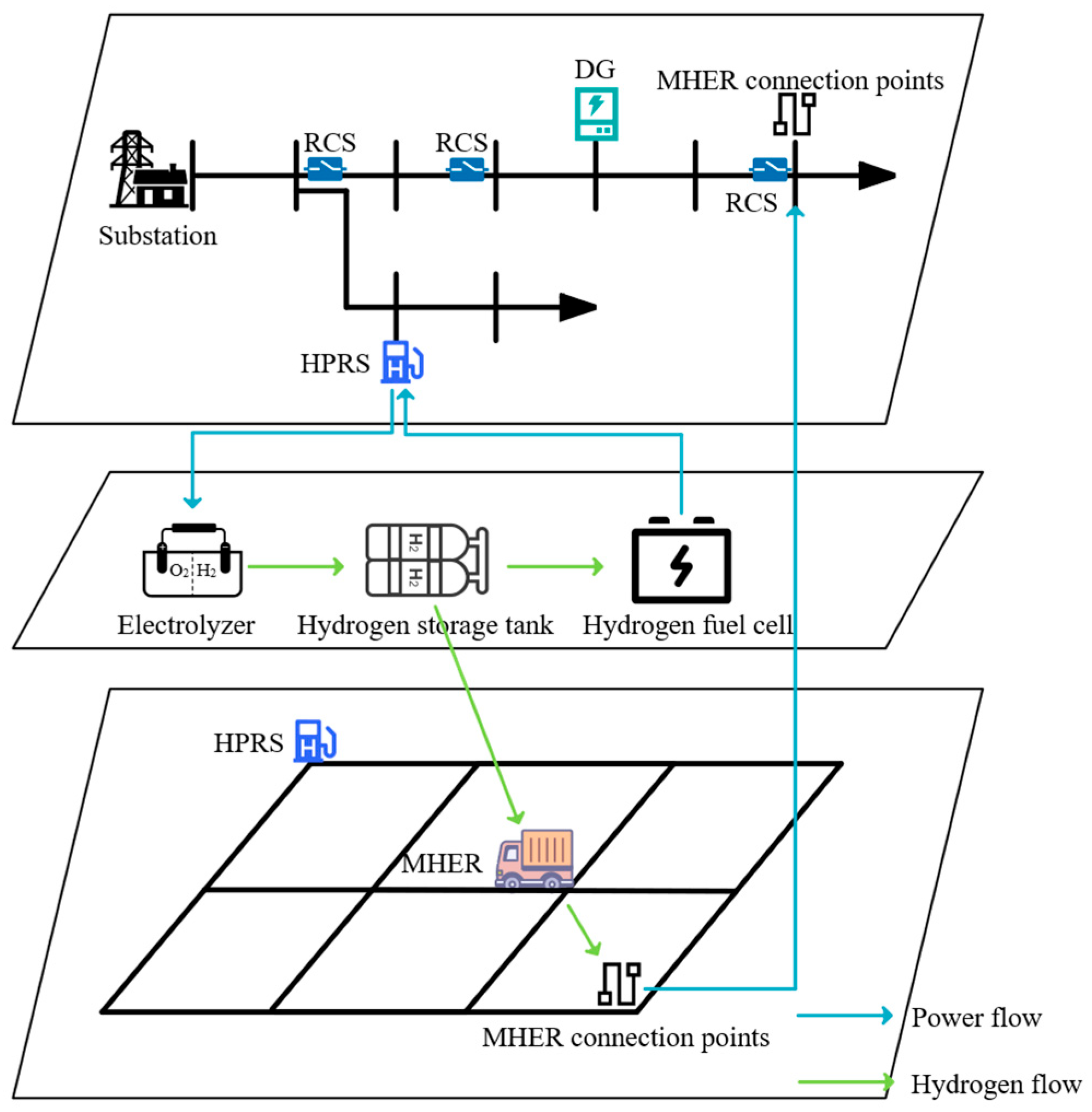
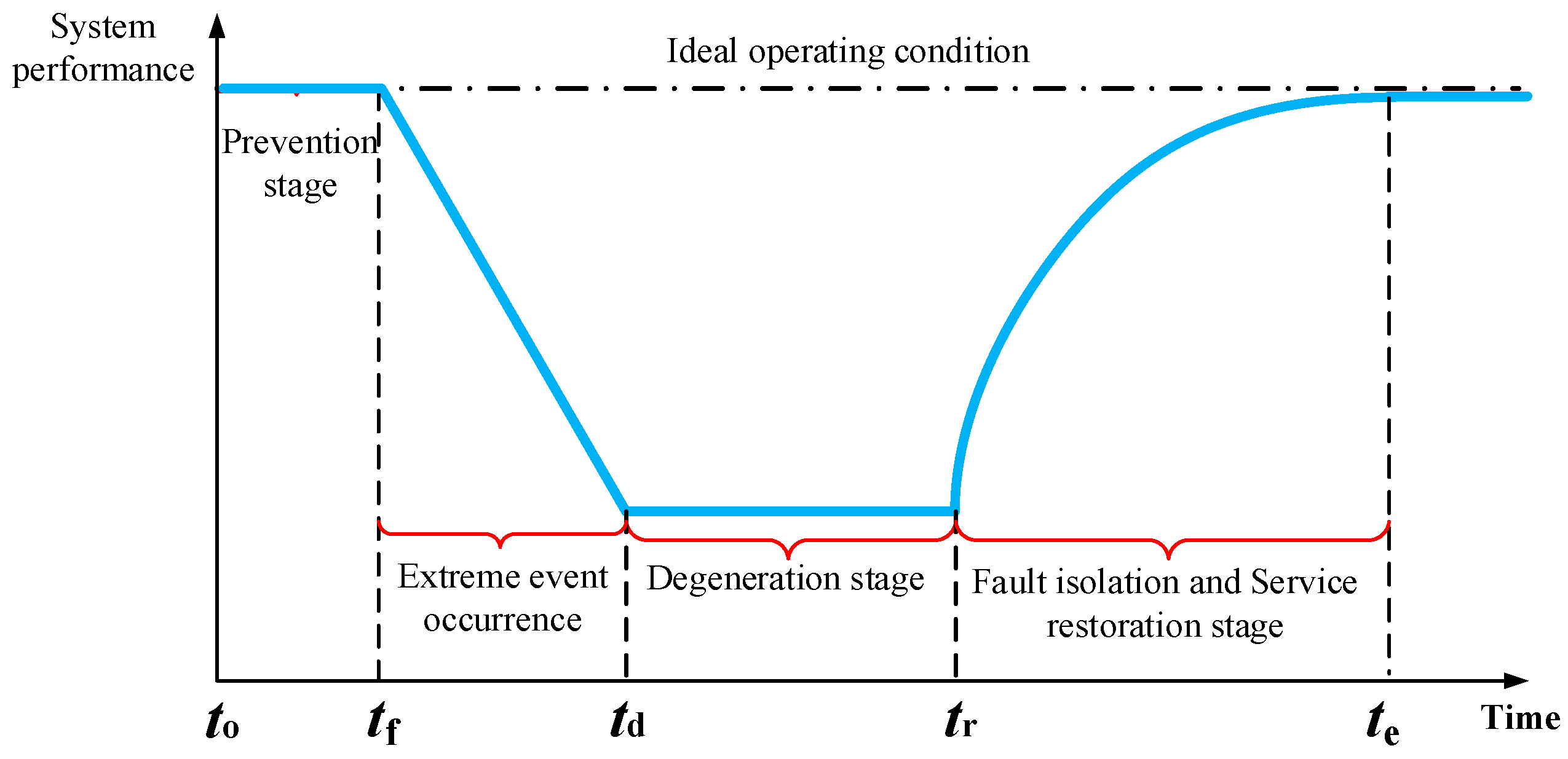
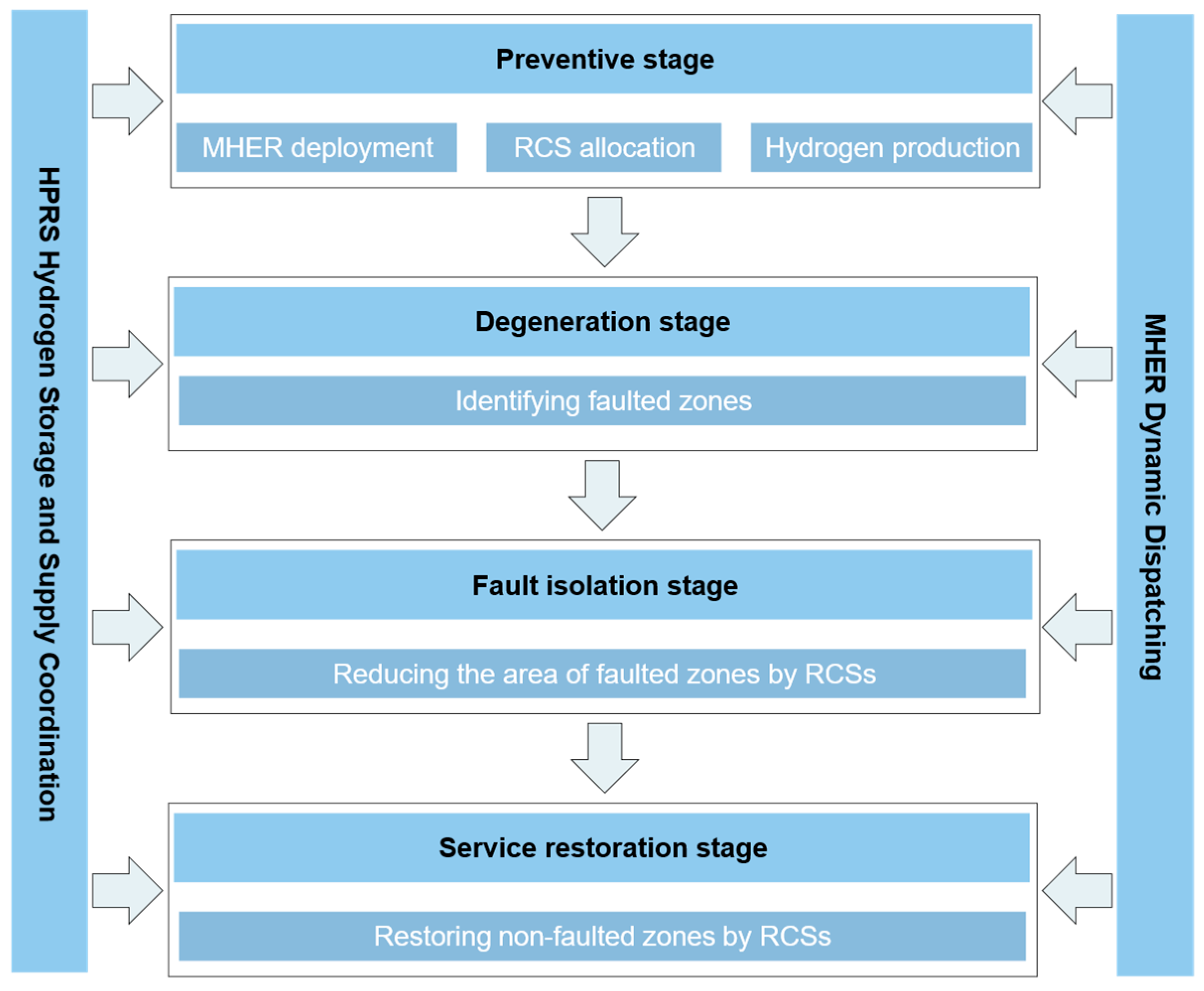
- Based on a multi-stage coordinated framework considering prevention–degradation–fault isolation–power restoration, restoration resources for multiple systems are modeled, achieving coordinated scheduling of diverse restoration resources throughout various stages. During the prevention stage, the system’s capability to defend against extreme events is improved through pre-planned deployment of RCSs and mobile hydrogen emergency resources (MHERs) and by optimizing the distribution network to form preventive islands; after extreme events occur, the response process is divided into detailed stages to achieve precise fault section isolation and rapid power restoration in non-fault zones through coordinated utilization of multi-type resources, such as hydrogen production and refueling stations (HPRSs).
- (2)
- A coordinated dispatching model for three types of recovery resources (power distribution, transportation, and hydrogen energy systems) is established. The transportation systems enable dynamic dispatching of emergency resources, the hydrogen energy systems provide clean energy storage and allocation, and the power distribution system implements global optimal control.
2. Problem Statement
3. Model Formulation
3.1. Preventive Stage Model
3.2. Degradation Stage Model
3.3. Fault Isolation Stage Model
3.4. Service Restoration Stage Model
3.5. HPRS and DG Model
3.6. MHER Model
3.7. System Operational Model
3.8. Objective
4. Case Study
4.1. Parameter Settings
4.2. Restoration Strategies for Different Scenarios
4.3. Comparison of Various Approaches
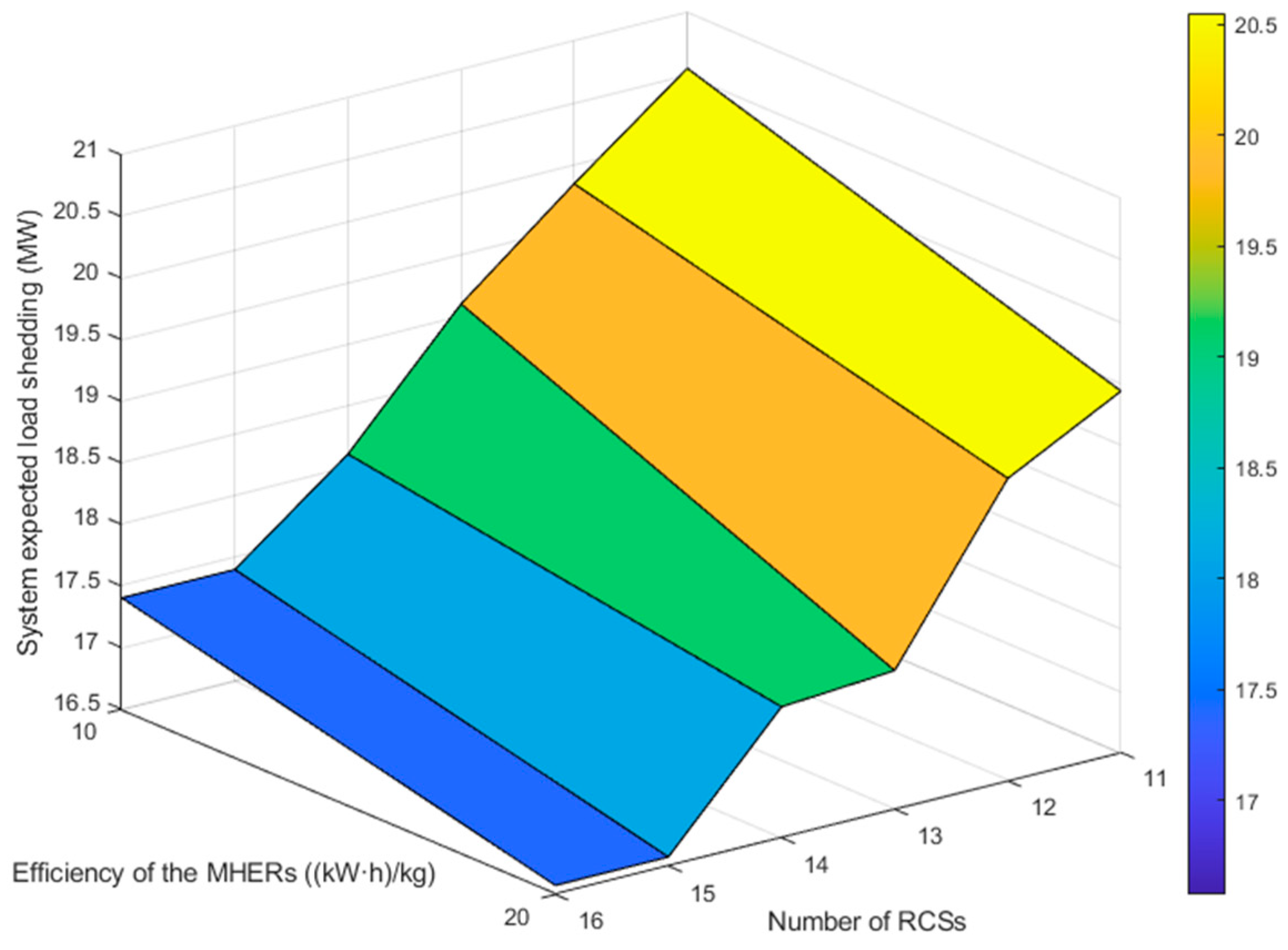
4.4. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sets: | |
| / | Set of buses/set of buses at both ends of line l |
| Set of time periods | |
| / | Set of lines/set of lines connected to bus i |
| Set of fault scenarios | |
| Set of MHERs | |
| Set of candidate locations | |
| Parameters: | |
| Number of RCSs | |
| Maximum capacity for MHER deployment | |
| Number of buses | |
| Large number | |
| Reference voltage magnitude | |
| Binary: 1 if line l fails at time t in scenario c | |
| / | Active and reactive loads at bus i |
| / | Resistance and reactance of line l |
| / | Maximum and minimum voltage magnitudes of bus i |
| / | Active and reactive loads at line l |
| Calorific value of hydrogen | |
| Efficiency of the electrolyzer at bus i | |
| Power-to-hydrogen conversion coefficient | |
| Efficiency of the hydrogen fuel cell | |
| / | Maximum active and reactive power outputs of the HPRS at bus i |
| / | Maximum and minimum allowable hydrogen storage capacities at bus i |
| / | Maximum and minimum active power outputs of the DG at bus i |
| / | Maximum and minimum reactive power outputs of the DG at bus i |
| / | Equivalent distance and real distance between buses m and n |
| / | Zero-flow speed and actual speed |
| Congestion level | |
| Equivalent time from bus m to bus n | |
| / | Maximum active and reactive power outputs of the kth MHER |
| Maximum allowable hydrogen storage capacity at the kth MHER | |
| Efficiency of the kth MHER | |
| / | Maximum and minimum allowable hydrogen storage capacities of the kth MHER |
| Weight coefficient of bus i | |
| Time period | |
| Variables | |
| ,, | Binary: 1 if line l is closed, 0 otherwise |
| ,, | Binary: 1 if the i-end of line l is closed, 0 otherwise |
| Binary: 1 if end i of the line is equipped with an RCS | |
| , | Binary: 1 if bus i is a source bus, 0 otherwise |
| , | Commodity flow through line l |
| ,, | Active power flow through line l |
| ,, | Reactive power flow through line l |
| ,, | Active load shedding at bus i |
| ,, | Reactive load shedding at bus i |
| ,, | Voltage at bus i |
| , | Binary: 1 if bus i is in the fault zone |
| Binary: used for linearization | |
| Hydrogen production of the HPRS at bus i | |
| Active power demand of the HPRS at bus i | |
| Hydrogen storage level of the HPRS at bus i | |
| Refueling capacity of the kth MHER at bus i | |
| / | Active and reactive power outputs of the HPRS at bus i |
| / | Active and reactive power outputs of the DG at bus i |
| Binary: 1 if the kth MHER is pre-deployed at bus m | |
| Binary: 1 if the kth MHER arrives at bus m at time t | |
| / | Active and reactive power outputs of the kth MHER at bus i |
| Hydrogen storage level of the kth MHER | |
| Resilience level | |
| Total load shedding in scenario c | |
| Probability of fault scenario c |
References
- Hu, J.; Liu, X.; Shahidehpour, M.; Xia, S. Optimal operation of energy hubs with large-scale distributed energy resources for distribution network congestion management. IEEE Trans. Sustain. Energy 2021, 12, 1755–1765. [Google Scholar] [CrossRef]
- Poudyal, A.; Poudel, S.; Dubey, A. Risk-based active distribution system planning for resilience against extreme weather events. IEEE Trans. Sustain. Energy 2023, 14, 1178–1192. [Google Scholar] [CrossRef]
- Ma, S.; Chen, B.; Wang, Z. Resilience enhancement strategy for distribution systems under extreme weather events. IEEE Trans. Smart Grid 2018, 9, 1442–1451. [Google Scholar] [CrossRef]
- Wu, D.; Zheng, X.; Xu, Y.; Olsen, D.; Xia, B.; Singh, C.; Xie, L. An open-source extendable model and corrective measure assessment of the 2021 texas power outage. Adv. Appl. Energy 2021, 4, 100056. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). State of the Global Climate 2022; WMO: Geneva, Switzerland, 2022. [Google Scholar]
- Deng, H.; Yang, B.; Chow, M.Y.; Zhu, D.; Yao, G.; Chen, C.; Guan, X.; Srinivasan, D. A decision-dependent hydrogen supply infrastructure planning approach considering causality between vehicles and stations. IEEE Trans. Sustain. Energy 2024, 15, 1914–1932. [Google Scholar] [CrossRef]
- He, X.; Zhang, B.L.; Jia, H.Y.; Xin, K.; Wang, Y.; Yu, C.; Zhang, B. Regret-aware optimization of hydrogen-assisted congestion control in a renewable-dominated reconfigurable distribution network. Renew. Energy 2025, 250, 123084. [Google Scholar] [CrossRef]
- Lian, X.; Qiu, L.; Song, C.; Liu, L.; Xu, Z. Enhancing resilience of power-transportation coupled networks to typhoons: A tri-stage integration strategy of multi-resources. IEEE Trans. Sustain. Energy Grids Netw. 2025, 43, 101747. [Google Scholar] [CrossRef]
- Liu, J.; Qin, C.; Yu, Y. Enhancing distribution system resilience with proactive islanding and RCS-based fast fault isolation and service restoration. IEEE Trans. Smart Grid 2020, 11, 2381–2395. [Google Scholar] [CrossRef]
- Lei, C.; Bu, S.; Wang, Q.; Liang, L. Observability defense-constrained distribution network reconfiguration for cyber-physical security enhancement. IEEE Trans. Smart Grid 2024, 15, 2379–2382. [Google Scholar] [CrossRef]
- Li, Y.; Lei, S.; Sun, W.; Hu, C.; Hou, Y. A distributionally robust resilience enhancement strategy for distribution networks considering decision-dependent contingencies. IEEE Trans. Smart Grid 2024, 15, 1450–1465. [Google Scholar] [CrossRef]
- Liu, J.; Lin, G.; Huang, S.; Zhou, Y.; Rehtanz, C.; Li, Y. Collaborative EV routing and charging scheduling with power distribution and traffic networks interaction. IEEE Trans. Power Syst. 2022, 37, 3923–3936. [Google Scholar] [CrossRef]
- Li, J.; Xu, X.; Yan, Z.; Wang, H.; Shahidehpour, M.; Chen, Y. Coordinated optimization of emergency response resources in transportation-power distribution networks under extreme events. IEEE Trans. Smart Grid 2023, 14, 4607–4620. [Google Scholar] [CrossRef]
- Yan, M.; Shahidehpour, M.; Paaso, A.; Zhang, L.; Alabdulwahab, A.; Abusorrah, A. Distribution system resilience in ice storms by optimal routing of mobile devices on congested roads. IEEE Trans. Smart Grid 2021, 12, 1314–1328. [Google Scholar] [CrossRef]
- Cao, Y.; Zhou, B.; Chung, C.Y.; Zhou, K.; Zhu, L.; Shuai, Z. Resilience-oriented coordinated topology reconfiguration of electricity and drainage networks with distributed mobile emergency resources. IEEE Trans. Smart Grid 2025, 16, 786–800. [Google Scholar] [CrossRef]
- Liu, X.; Soh, C.B.; Zhao, T.; Wang, P. Stochastic scheduling of mobile energy storage in coupled distribution and transportation networks for conversion capacity enhancement. IEEE Trans. Smart Grid 2021, 12, 117–130. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, J.; Song, Y.; Xu, Y. A robust microgrid formation strategy for resilience enhancement of hydrogen penetrated active distribution networks. IEEE Trans. Power Syst. 2024, 39, 2735–2748. [Google Scholar] [CrossRef]
- Cao, X.; Cao, T.; Xu, Z.; Zeng, B.; Gao, F.; Guan, X. Resilience constrained scheduling of mobile emergency resources in electricity-hydrogen distribution network. IEEE Trans. Sustain. Energy 2023, 14, 1269–1284. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, J.; Song, Y.; Xu, Y. A hierarchical strategy for restorative self-healing of hydrogen-penetrated distribution systems considering energy sharing via mobile resources. IEEE Trans. Power Syst. 2023, 38, 1388–1404. [Google Scholar] [CrossRef]
- Lei, S.; Chen, C.; Zhou, H.; Hou, Y. Routing and scheduling of mobile power sources for distribution system resilience enhancement. IEEE Trans. Smart Grid 2019, 10, 5650–5662. [Google Scholar] [CrossRef]
- Lin, Y.; Bie, Z. Tri-level optimal hardening plan for a resilient distribution system considering reconfiguration and DG islanding. Appl. Energy 2018, 210, 1266–1279. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Y.; He, J.; Su, M.; Ni, P. Resilience-oriented distribution system restoration considering mobile emergency resource dispatch in transportation system. IEEE Access 2019, 7, 73899–73912. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Wang, J.; Feng, J.; Gao, Z.; Zheng, S. Rechargeable battery cabinet deployment for public bike system. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20309–20322. [Google Scholar] [CrossRef]


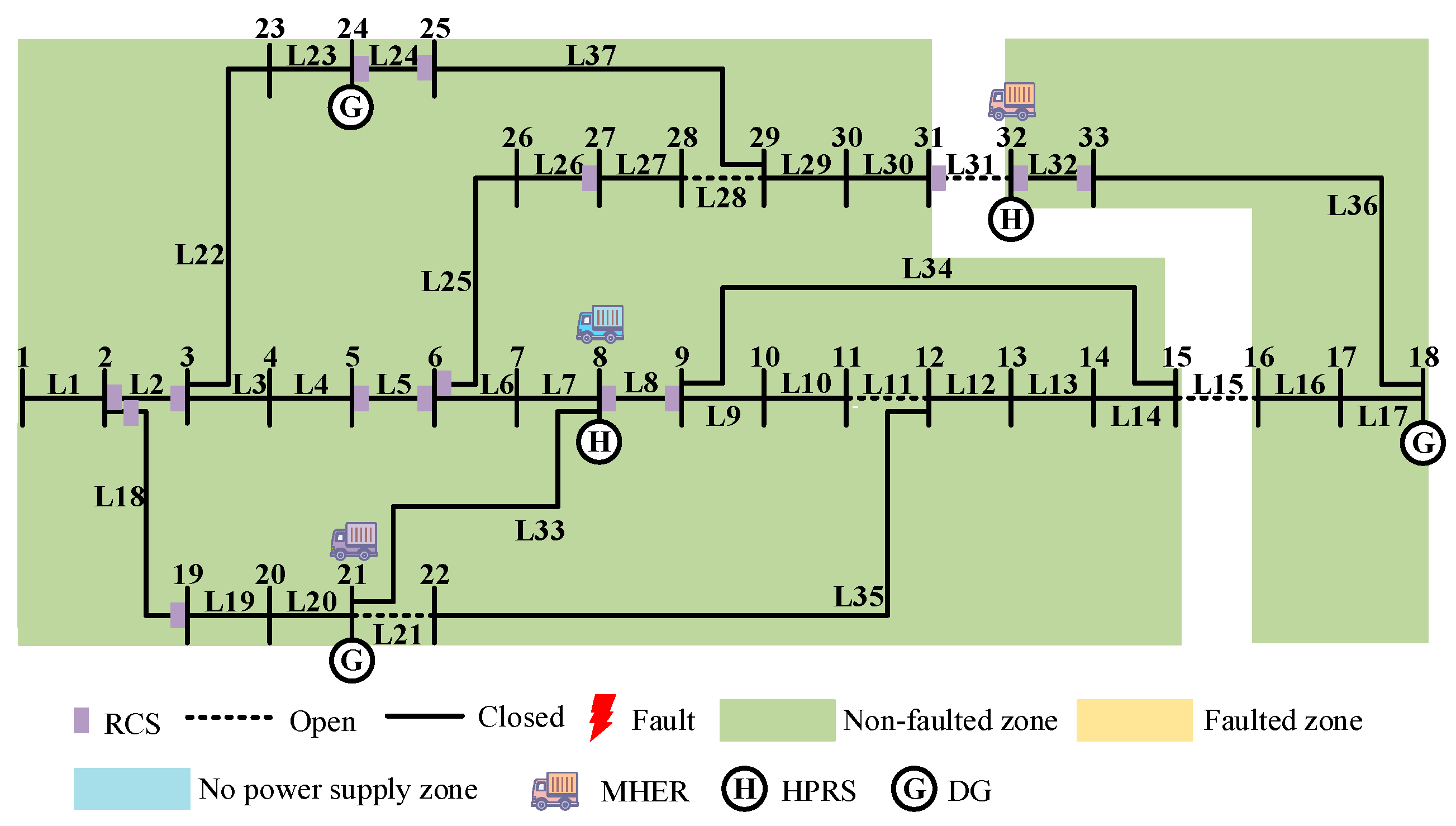
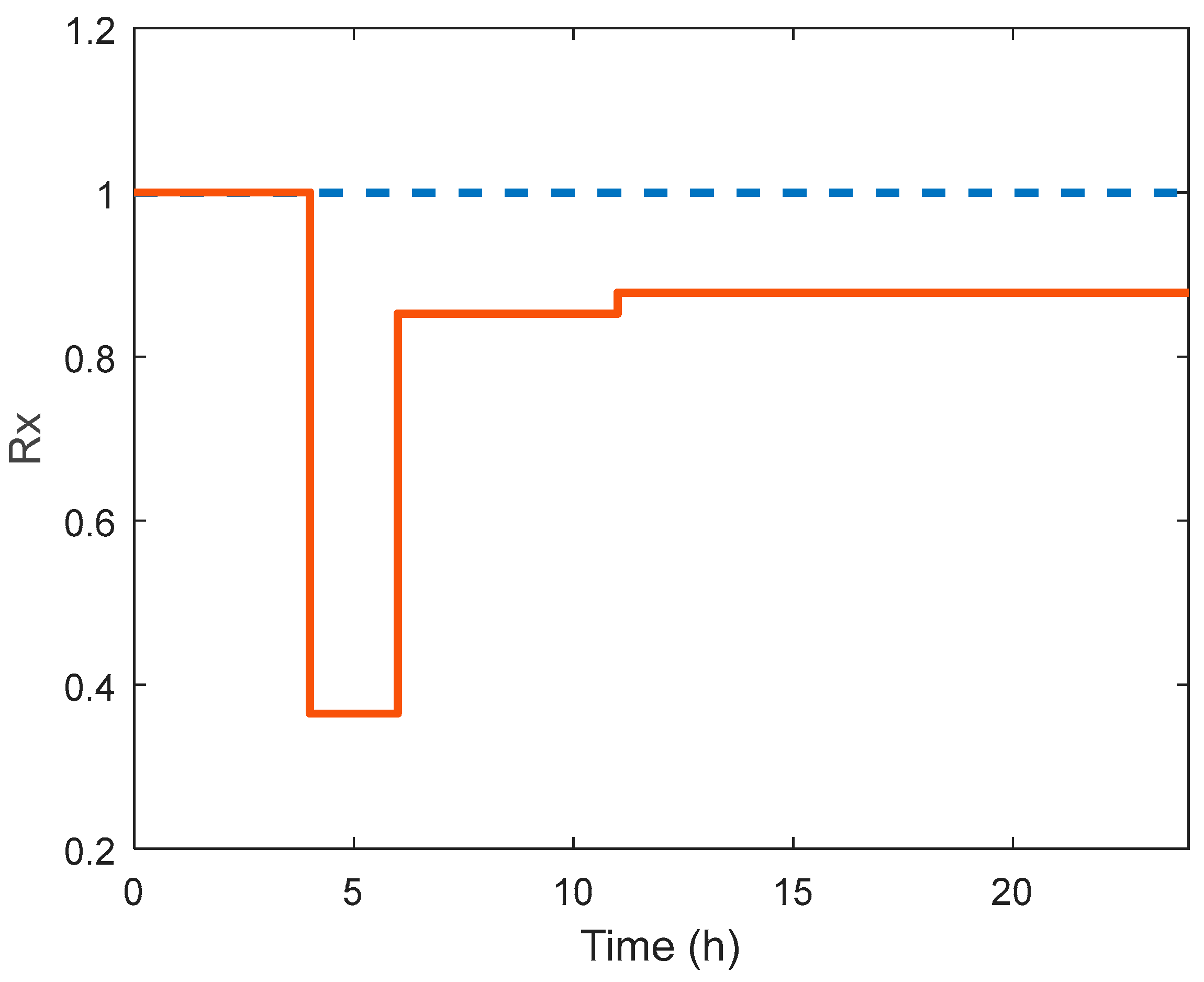
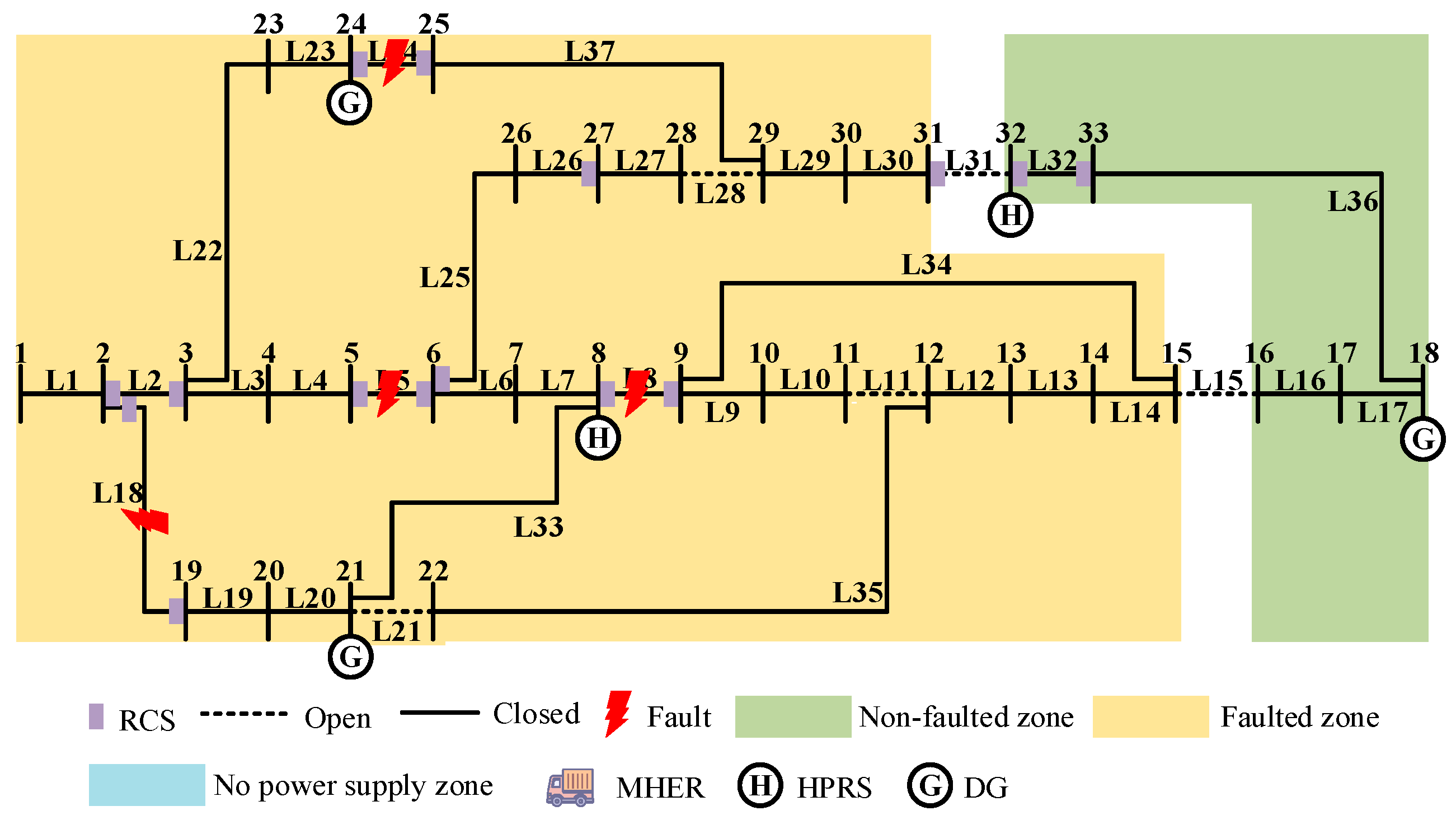


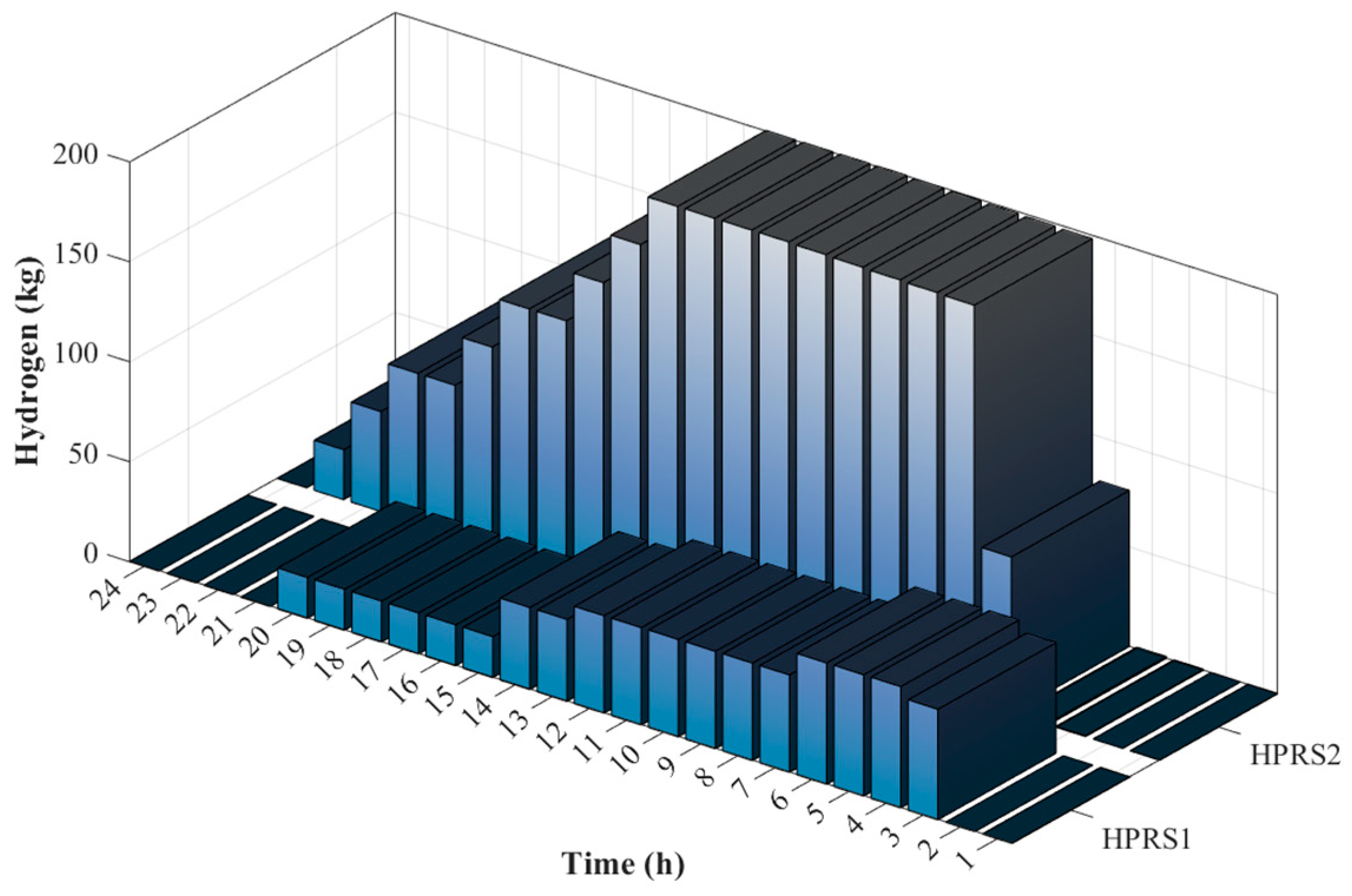
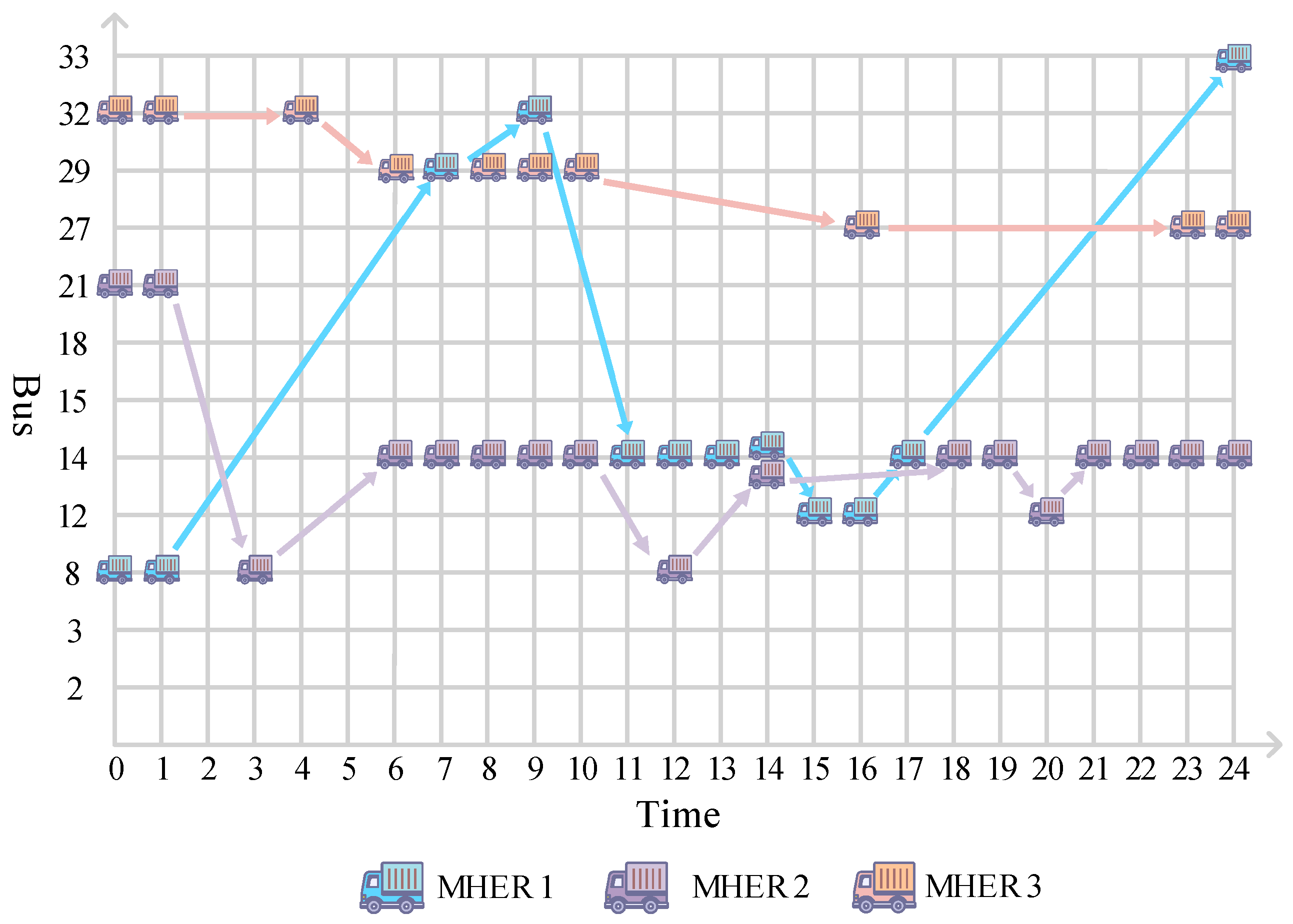
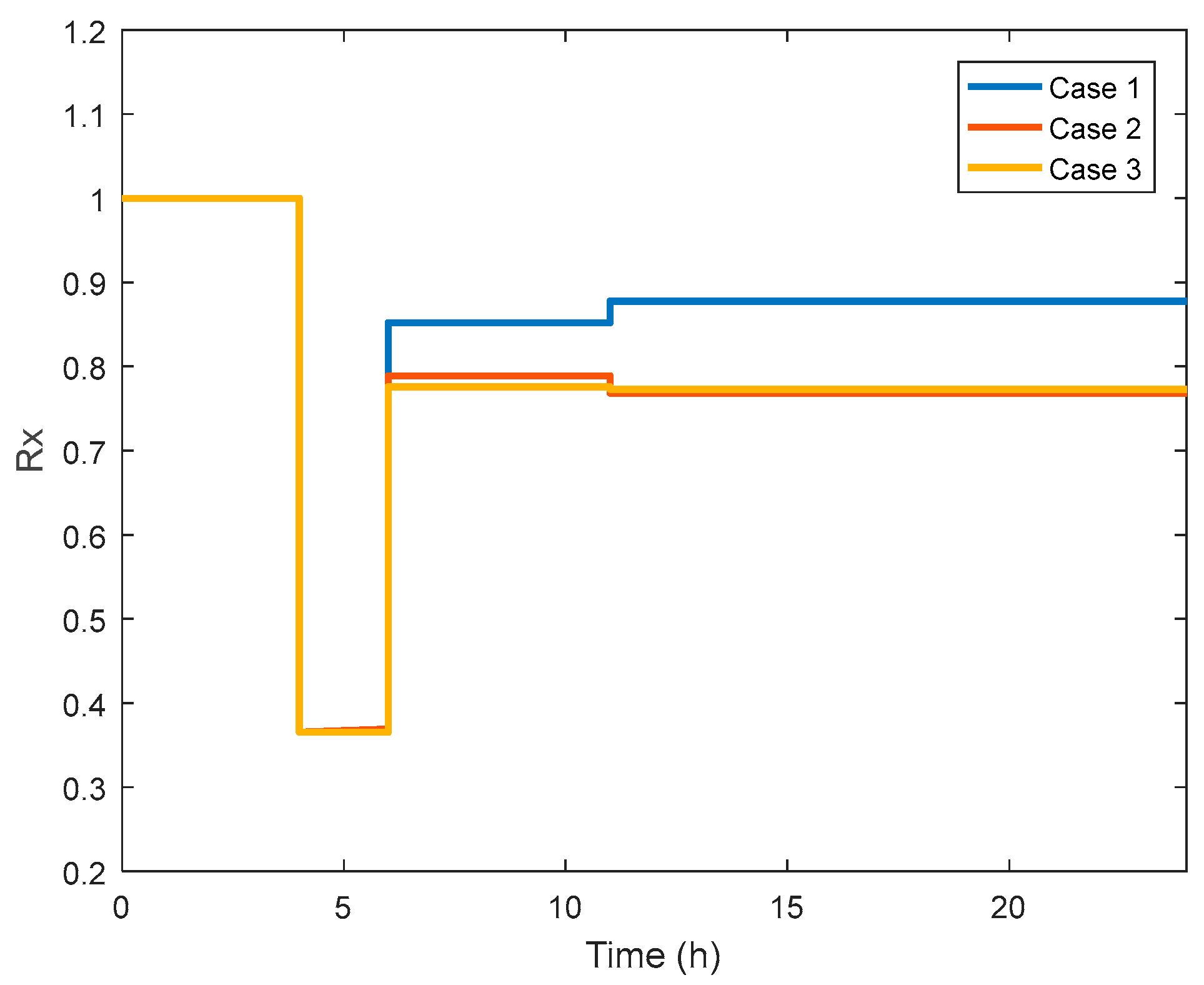
| Scenario Number | Faulty Lines |
|---|---|
| 1 | L2, L11, L25, L26 |
| 2 | L15, L21, L28, L32 |
| 3 | L5, L8, L18, L24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Liu, J.; Li, P.; Ren, J.; Zhang, D.; Zhou, X. A Multi-Stage Resilience Enhancement Method for Distribution Networks Employing Transportation and Hydrogen Energy Systems. Sustainability 2025, 17, 8691. https://doi.org/10.3390/su17198691
Chen X, Liu J, Li P, Ren J, Zhang D, Zhou X. A Multi-Stage Resilience Enhancement Method for Distribution Networks Employing Transportation and Hydrogen Energy Systems. Sustainability. 2025; 17(19):8691. https://doi.org/10.3390/su17198691
Chicago/Turabian StyleChen, Xi, Jiancun Liu, Pengfei Li, Junzhi Ren, Delong Zhang, and Xuesong Zhou. 2025. "A Multi-Stage Resilience Enhancement Method for Distribution Networks Employing Transportation and Hydrogen Energy Systems" Sustainability 17, no. 19: 8691. https://doi.org/10.3390/su17198691
APA StyleChen, X., Liu, J., Li, P., Ren, J., Zhang, D., & Zhou, X. (2025). A Multi-Stage Resilience Enhancement Method for Distribution Networks Employing Transportation and Hydrogen Energy Systems. Sustainability, 17(19), 8691. https://doi.org/10.3390/su17198691






