Continuous Wavelet Analysis of Water Quality Time Series in a Rapidly Urbanizing Mixed-Land-Use Watershed in Ontario, Canada

Abstract

Urbanization and mixed-land-use development significantly impact water quality dynamics in watersheds, necessitating continuous monitoring and advanced analytical techniques for sustainable water management. This study employs continuous wavelet analysis to investigate the temporal variability and correlations of real-time water quality parameters in the Credit River watershed, Ontario, Canada. The Integrated Watershed Monitoring Program (IWMP), initiated by the Credit Valley Conservation (CVC) Authority, has facilitated long-term real-time water quality monitoring since 2010. Fundamental and exploratory statistical analyses were conducted to identify patterns, trends, and anomalies in key water quality parameters, including pH, specific conductivity, turbidity, dissolved oxygen (DO), chloride, water temperature ($T_{H_{2}O}^{°}$), air temperature ($T_{air}^{°}$), streamflow, and water level. Continuous wavelet transform and wavelet coherence techniques revealed significant temporal variations, with “1-day” periodicities for DO, pH, ($T_{H_{2}O}^{°}$), and ($T_{air}^{°}$) showing high power at a 95% confidence level against red noise, particularly from late spring to early fall, rather than throughout the entire year. These findings underscore the seasonal influence on water quality and highlight the need for adaptive watershed management strategies. The study demonstrates the potential of wavelet analysis in detecting temporal patterns and informing decision-making for sustainable water resource management in rapidly urbanizing mixed-land-use watersheds.

1. Introduction

In the field of water resources engineering, real-time water quality data can offer detailed insights into water quality parameters’ temporal variability, enabling the exploration of seasonal patterns and the influence of external factors such as hydrologic variables (e.g., stream flow and water level) [1,2,3]. This information can help water quality managers in decision-making processes. However, the high-resolution nature of real-time water quality datasets, characterized by significant variation, presents challenges in interpreting large datasets spanning months to years. Making sense of such extensive data over extended time periods can prove to be quite challenging [1,2,4,5,6].

Previous investigators have applied multivariate statistical analysis (e.g., principal component analysis and factor analysis, positive matrix factorization, self-organizing maps, and weighted regression approach), non-parametric time series statistical analysis, artificial neural network modeling, and variable consistency dominance-based rough set methods to analyze water quality and hydrologic datasets. Most surface water quality research has focused on temporal and spatial variations in different catchments using multivariate statistics and trend analysis to investigate major contributing factors to water quality changes (e.g., mixed land use, land cover, and climate change). Studies of spatial and seasonal variability of water quality have shown that water quality degradation is predominantly linked to agricultural activities and urban sprawl [7,8,9,10]. However, these methods do not always offer insight into the temporal variation of a time series or multiple series’ intercorrelations on a temporal scale. The most common and effective statistical methods for analysis of real-time water quality data in a traditional statistical framework are non-parametric methods for detecting monotonic trends (e.g., Mann–Kendall and seasonal Mann–Kendall methods). Significant correlations between water quality parameters can also be determined via the non-parametric Kendall rank correction test and Spearman partial rank correlation test [9,10].

Time series analysis requires both exploratory data analysis and hypothesis testing. Exploratory data analysis consists of understanding the data’s basic characteristics (e.g., mean, variance, and skewness) and completing transformations to understand whether a parametric or non-parametric method should be selected. In statistical analysis, the characteristics of the data determine which method is best suited. Parametric methods can only be used if the data or data transformations follow a normal distribution and meet normality assumptions; otherwise, the method is invalid, and its use would result in errors. Water quality data is typically positively skewed, with unequal variance, and is unlikely to follow a normal distribution (even with transformations). Quantile-quantile plots are generally used to check for normality [11]. In addition, non-point source water quality is highly correlated with time and influenced by various climatic, mixed-land-use, hydrologic, and human factors [12]. Usually, such data does not follow a normal distribution and is inherently correlated with time. Accordingly, non-parametric methods are used; however, such methods have their own limitations, being more applicable to assessing monotonous shifts in data over time, returning a yes or no answer and not offering much resolution [13].

Wavelet analysis has emerged as a popular method for interpreting real-time data parameters, offering a comprehensive yet straightforward snapshot of their behavior. In this approach, data is viewed as a non-stationary signal across both time and scale [4,5,6,14,15]. For instance, the fast continuous wavelet transformation (FCWT) offers an improved balance between speed and accuracy, enabling real-time, wide-band, high-quality, time–frequency analysis of non-stationary noisy signals [16]. This technique facilitates a multiresolution decomposition of a time series into various scales through a wavelet transform and wavelet filters [17]. In general, wavelet analysis is a method that changes the representation of a signal to another form in order to highlight some of its characteristics [17,18]. There are two main categories of wavelet analysis: continuous and discrete. Continuous wavelets transform plots into the power of a feature in the time series as a function of time, relative to the power of the original time series, whereas discrete wavelet analysis decomposes a time series into approximations and details [17,19,20]. Wavelet analysis has been used to study electrical signals and climatic and geophysical datasets [19,21]. Emerging studies have illustrated the application of wavelet analysis in examining and assessing daily and hourly water quality and stream flow time series [2,4,14,22]. The analysis is localized in both space and time and hence offers an advantage over Fourier transform, which assumes a signal that is stationary and invariant of time [17,20,23].

Making the interpretation of real-time data easier to understand, without substantial loss of resolution, wavelet analysis has been applied to hydrological variables and water quality time series, with the goal of detecting temporal patterns [1,24]. Using MATLAB, and filling data gaps via linear cubic interpolation, Rajwa-Kuligiewicz et al. [2] performed wavelet analysis on a three-year hydrologic and water quality time series by implementing continuous wavelet transform, wavelet coherence, and cross-spectrum. This afforded them insight into the variability of dissolved oxygen (DO) in relation to water temperature ($T_{H_{2}O}^{°}$), and water level of the Narew River in Poland. Their study identified time series characteristics on various temporal scales ranging from sub-daily to annual. Cross wavelets and wavelet coherences of dissolved oxygen, water temperature, and water level were computed to help understand the types of factors having an impact on dissolved oxygen. Moreover, they describe the significance and relative length of these impacts over time [2]. Several similar studies have been conducted on wavelet theory [3,4,19,25,26,27].

In addition to the background literature review, guidance on employing statistical methods in the analysis of water quality monitoring data exhibiting non-normal distributions in specific applications within surface water resources was also examined. The United States Geological Survey (USGS) publication on statistical methods in water resources (Helsel and Hirsch, [11]), as well as the time series modeling of water resources and environmental systems (Hipel and McLeod, [28]) and statistical tools for analyzing water quality data (Fu and Wang, [29]) were incorporated in the assessment.

With the advancement in monitoring technology, conservation authorities and regulatory agencies can measure surface water quality in real time at various stream locations within a given urbanizing mixed-land-use watershed. The Credit Valley Conservation (CVC) Authority began the implementation of a long-term real-time water quality monitoring program in the winter of 2010. Real-time data is plotted over time, and alerts are automatically issued if water quality readings exceed permissible ranges. This allows water resource managers to investigate the issue in real time and, if necessary, inform the Ontario Ministry of the Environment, Conservation, and Parks (MECP). This process ensures that spills and abnormal discharges are detected in real time and helps ensure public confidence in the quality of the surface water (CVC, 2017, and reported in Ontario Nature 2023 media release) [30,31]. There are currently 11 active stations at various locations throughout the Credit River watershed. The high-resolution nature of real-time water quality datasets offers valuable insights into the temporal variations of the measured parameters and their intercorrelations. However, a key challenge lies in simplifying the data without losing critical information while still extracting meaningful patterns. This study initially tests the hypothesis that real-time water quality and streamflow data do not conform well to normal or lognormal statistical distributions. Consequently, the primary objective is to assess and model the temporal variations and correlations of real-time water quality parameters and streamflow across multiple temporal scales (ranging from hours to one year) over the monitoring period. This is achieved using an innovative approach known as continuous wavelet transformation, which enables the identification of dominant temporal patterns and relationships within the dataset.

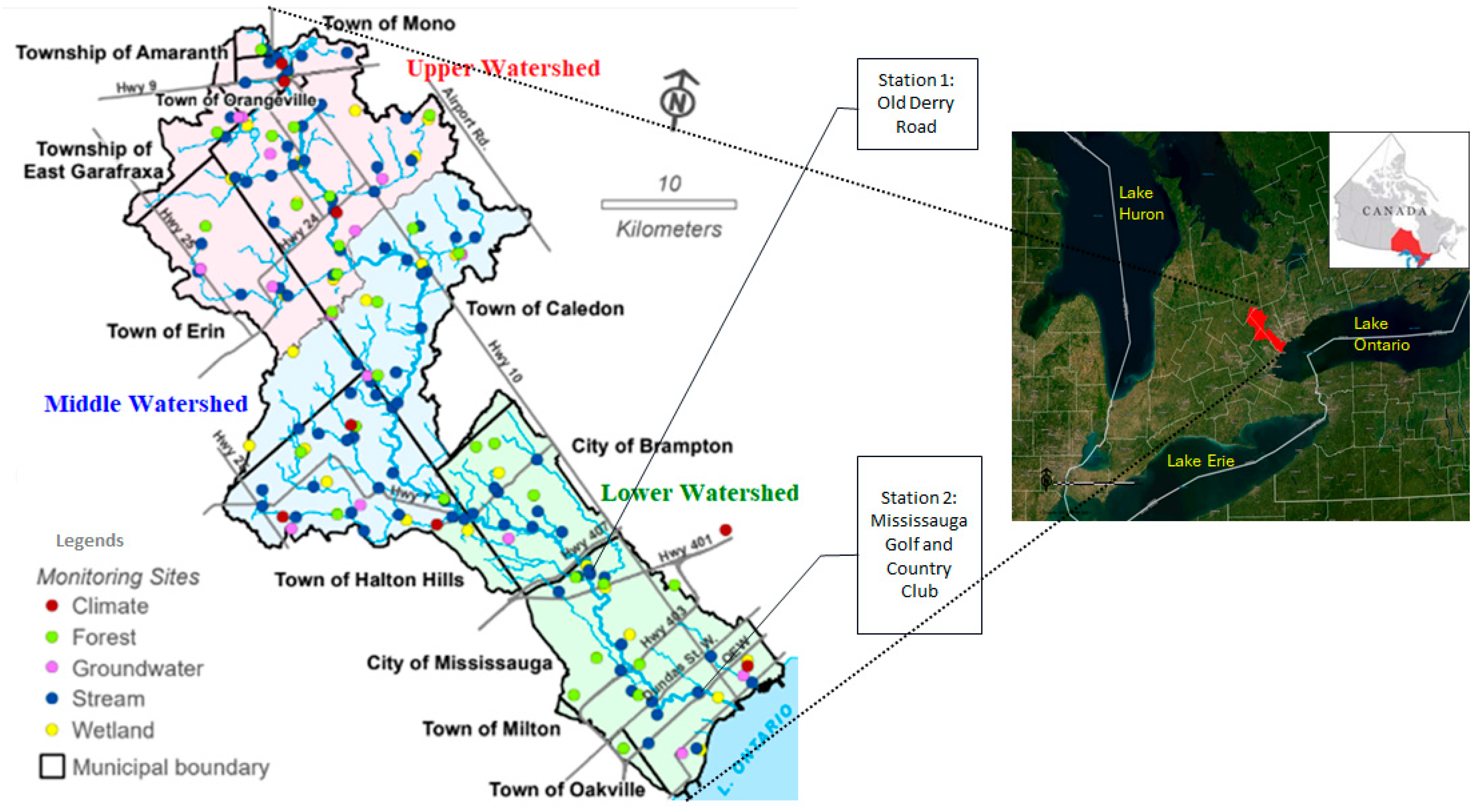
2. Study Area and Datasets

This section provides a brief overview of the study area and the real-time datasets. The study area is located in the Credit River watershed, which is approximately 1000 km² in size [30] and drains into Lake Ontario, one of the five Great Lakes of North America. The Credit River watershed is governed by the Credit Valley Conservation (CVC) Authority. The watershed is divided into the Upper, Middle, and Lower watersheds, as shown in Figure 1.

The Lower watershed is mainly urbanized, while the Upper and Middle watersheds are rural; hence, it is representative of most watersheds across Southern Ontario that drain to Lake Ontario. The watershed is predominantly shaped by agriculture (31,158 ha) and urban development (31,151 ha), which together dominate about 66% of the area. Forests and wetlands (5896 ha), though significant, make up only 23% of the watershed and have been increasingly fragmented by the expansion of agricultural and urban lands. Another notable feature is the presence of meadows, spanning 9917 hectares, or roughly 10% of the watershed. These meadows represent areas of natural regeneration, often recovering from past human activities like abandoned farm fields. This mixed land use highlights the ongoing tension between human development and natural ecosystems in the watershed [32]. However, the Credit Valley River watershed’s protected lands officially contribute to Canada’s goal of protecting 30% of our lands and waters by 2030 as part of the Global Biodiversity Framework. This encompasses an area greater than the Toronto Islands combined [31].

Real-time water quality plays an integral part in the health of the watershed and safeguards our natural resources and these protected areas. With good to fair surface water quality, the Upper and Middle portions of the watershed are predominantly rural and include large portions of the towns of Orangeville, Erin, Halton Hills, and Caledon, as described in CVC’s 2017 report [30,32]. In contrast, tributaries in the Lower watershed have poor to very poor surface water quality, attributable to the region being mainly urbanized. It includes a small portion of the town of Halton Hills, and most of the cities of Brampton, Oakville, and Mississauga [30,33]. Surface water quality is graded on phosphorus levels, coliforms, and benthic macroinvertebrates. The Credit River watershed also features an Integrated Watershed Monitoring Program (IWMP), which includes monitoring terrestrial and aquatic systems. It consists of 47 real-time monitoring stations for precipitation, streamflow, and water quality.

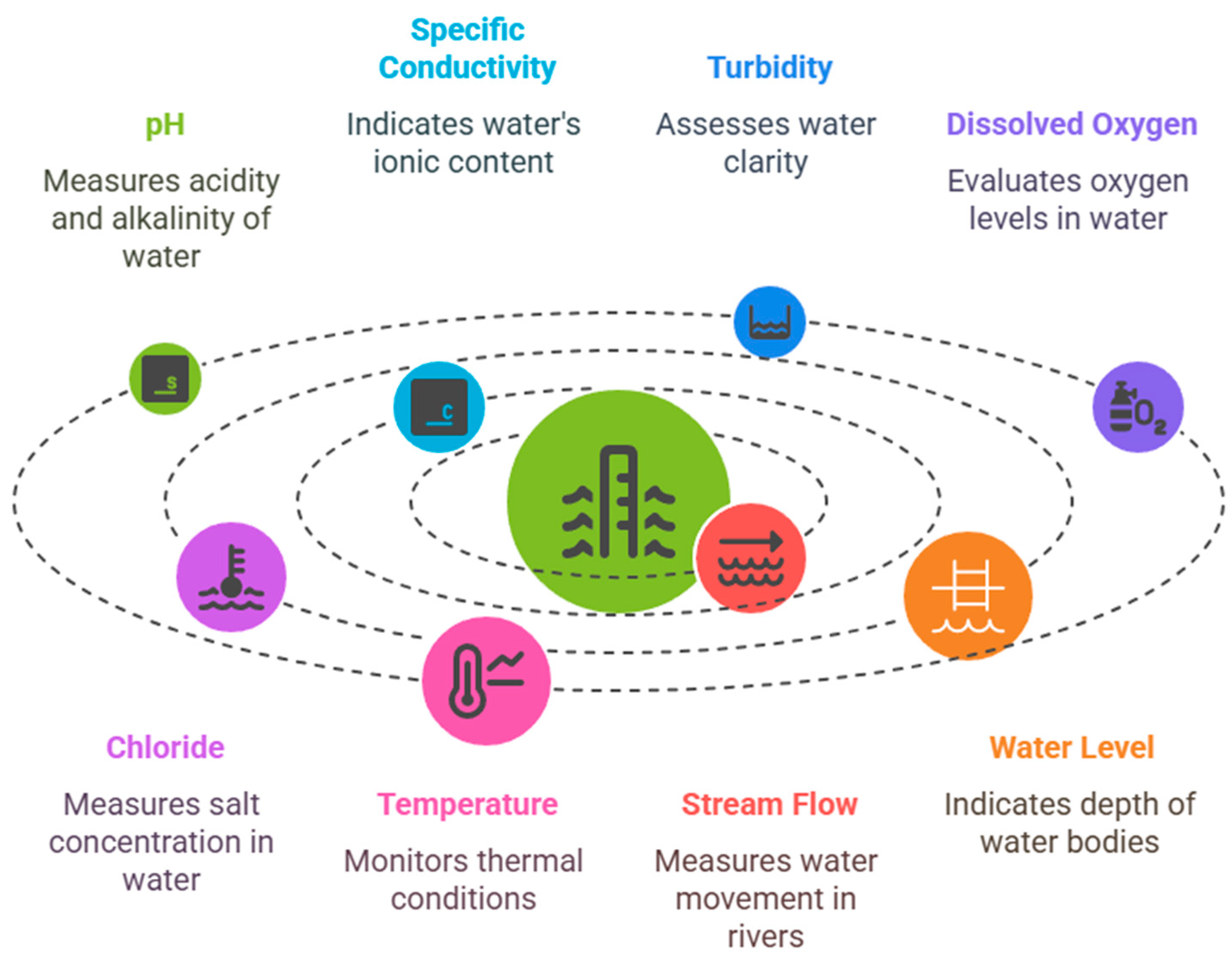
Water quality parameters, including turbidity, specific conductivity, pH, total dissolved solids, water temperature, dissolved oxygen, and chloride, were measured using the multi-parameter probe Hydrolab DX5 (Manufacturer is OTT HydroMet, Loveland, CO, USA), represented in

Table 1. Real-time water quality and stream flow data monitored at each monitoring station.

Parameter				Period of Measurement
Type	Name	Abbreviation	Units
Water quality	$-{\mathit{log}}_{10}\left[H_3{O}^{+}\right]$	pH	Range 1–14	Winter 2010 to Fall 2016
	Specific conductivity	$\kappa$	µS cm−1
	Turbidity	—	Nephelometric Turbidity Units
	Dissolved oxygen	[DO]	mg L−1 or %
	Chloride	$\left[{Cl}^{-}\right]$	mg L−1
	Temperature	$T_{H_{2}O}^{°}$	°C
Hydrological	Stream flow	Q	m3 min−1	Spring 2014 to Fall 2016
	Water level	—	m
Air	Temperature	$T_{air}^{°}$	°C	Fall 2010 to Fall 2016

. Hydrolab DX5 is a field-deployable water quality sonde equipped with multiple sensors that allow simultaneous and continuous measurement of key physical and chemical parameters. Turbidity reflects water clarity and suspended particles, specific conductivity indicates the ionic content of water, pH measures the degree of acidity or alkalinity, total dissolved solids (TDS) represent the concentration of dissolved substances, water temperature influences chemical reactions and biological activity, dissolved oxygen (DO) is critical for aquatic life, and chloride is a common indicator of urban and road-salt influences on water quality. All the data were obtained from the Credit Valley Conservation Authority (CVC), Ontario, Canada (https://cvc.ca/), accessed on 6 April 2017.

The scope of this study included the assessment of 15 min interval real-time surface water quality, stream flow, and air temperature data at two CVC stations over the length of the monitoring period (Table 1). These stations were located at the upstream (Old Derry Rd.) and downstream (Mississauga Golf and Country Club) ends of the Credit River Watershed (

Table 2. Real-time water quality parameter monitoring stations situated on the Lower Credit River watershed.

Station					Period Recorded		Hydrological Site
Name	Number		Location
	City of Mississauga	CVC	Lat. (N)	Long. (W)	Start	End	On	Drains to
Old Derry Road	13,502	8,090,015	43.622°	79.733°	20/2/2010	11/12/2016	Main channel of the Credit River	Credit River, ultimately to Lake Ontario
Mississauga Golf and Country Club	13,506	8,090,002	43.554°	79.620°	6/10/2011	11/12/2016	Main channel of the Credit River	Lake Ontario

). Also, Figure 2 illustrates the description of real-time parameters used for statistical and wavelet analysis.

Pre-Processed Data for Wavelet Analysis

Prior to using MathWorks MATLAB R2017a to run wavelet analysis, data were pre-processed, converting all real-time data received to equal time steps of 15 min. Much of the sensor data was in unequal time steps, as time steps with no values were not always inserted in the data; moreover, some data time steps were simply missing random entries throughout the datasets. Also, on occasion, the seconds and minutes in the data changed, so that two datasets with the same time length would have different times allocated within them. In Excel, all time series in the data were manually reconstructed to equal and identical time steps. Furthermore, due to technical difficulties in running the analysis with such a large dataset (e.g., software would freeze), the data was aggregated to a one-hour interval.

In addition to filter out missing data gaps that spanned several weeks to several months, the following time period data was selected for the seven water quality variables at all stations: (a) Dated 19 April 2012; 3:00 p.m. to 4 November 2016; 7:00 p.m. (referred to as the Spring 2012 to Fall 2016 dataset from hereon). Likewise, the following time periods were selected for the flow and water level data: (b) Dated 28 March 2014; 3:00 p.m. to 31 December 2014; 11:00 p.m. (referred to as the Spring 2014 to Fall 2014 dataset from hereon), and (c) Dated 28 March 2015; 3:00 p.m. to 31 December 2015; 11:00 p.m. (referred to as the Spring 2015 to Fall 2015 dataset from hereon). However, some missing values in the above datasets were still present and were approximated using the moving average method in statistical software R (3.3 version), followed by cubic interpolation to complete the time series (Rajwa-Kuligiewicz et al., 2016 [2]). Thus, this approach helps in maintaining data continuity; the interpolation technique may introduce distortions in the power spectra. In particular, the spectral slope obtained through this method may exhibit a bias toward lower values.

3. Materials and Methods

The real-time data was analyzed in two steps: (i) exploratory and non-parametric statistical analysis to describe the data and (ii) continuous wavelet analysis to provide insight into the temporal variability of real-time data over time and in relation to hydrologic variables. Fundamental statistics served to gain a basic understanding of the data. For each individual dataset, these statistics included exploratory statistics (boxplots), computations of fundamental statistical parameters, normality tests, and plots with LOWESS lines. The non-parametric Kendall rank correlation between different parameters was also calculated.

Statistical analysis of water quality data from February 2010 to December 2016 was conducted using non-parametric methods in R (version 3.3), as such data typically does not follow a normal distribution, even after transformation. Kendall rank correlation (tau) tests were used due to their robustness against missing values. The analysis involved visual inspection through boxplots and Q-Q plots to assess distribution, skewness, outliers, and seasonality. Scatterplots with LOWESS regression were used to examine the relationships between water quality parameters and other factors (e.g., streamflow, climate). Although the seasonal Mann–Kendall test is commonly applied to detect trends, it was not feasible here due to incomplete datasets and the short duration of flow records. Consequently, flow-adjusted concentrations and related trend tests were not performed (for more details, refer to Supplementary Materials).

This study provides a fundamental overview of wavelet analysis used to interpret Credit River watershed quality parameters and streamflow results. Wavelet analysis involves translating and dilating a mother wavelet (combination of Morlet, Confluence of Influence (COI), and Monto Carlo methods), a localized waveform with finite energy and zero mean across a time series, to analyze signals in both time and frequency domains [19]. The continuous wavelet transform (CWT) of a signal is computed using the wavelet’s complex conjugate, while the inverse transform reconstructs the signal using the original wavelet. Key concepts include the admissibility constant (Cg), the total energy of the wavelet, and the scalogram, which represents the signal’s energy at different times and scales. The wavelet power spectrum shows energy per unit time, and wavelet variance captures energy variability at different scales. The frequency–scale relationship is defined mathematically and helps interpret results in terms of characteristic frequencies. Wavelet analysis was conducted in MATLAB (R2007b version) using the wavelet coherency toolbox for continuous analysis and the wavelet toolbox for discrete transforms, with results summarized in Table S1.

Continuous wavelet transformation was applied to all available datasets, as indicated in Table 1 and Table 2. Given water quality and $T_{air}^{°}$ data lacunae, spanning several weeks to over three months, during the Spring 2012 to Fall 2016 period, missing values were filled using the moving average method with linear cubic interpolation. Moreover, to compare water quality parameters and hydrologic variables for which data was only available from 2014 onward, with significant missing data gaps during the winters of each consecutive year, continuous wavelet transform was performed for all the given parameters on two groups of shorter datasets (Spring 2014 to December 2014, and Spring 2015 to December 2015). This allowed for a closer examination of the temporal variation of the data during the critical low-flow summer months. The continuous wavelet transform analysis also included the use of wavelet coherency plots between select water quality parameters to assess their intercorrelation at multiple temporal scales. Therefore, in this study, the power spectrum was computed using the Fourier Transform algorithm available in MATLAB (R2007b version) for more details, refer to Supplementary Materials.

4. Results

The results from the wavelet analysis were complemented by the statistical analysis, and vice versa. This section summarizes the statistical results in Section 4.1 and the wavelet analysis in Section 4.2.

4.1. Basic Summary Statistics of Real-Time Water Quality and Hydrology Data

A statistical summary of real-time water quality and hydrological parameters at Old Derry Road and MGCC from 2010 to 2016 highlights key differences and seasonal trends influenced by natural and anthropogenic factors (

Table 3. Summary statistics of real-time water quality and hydrology data.

Statistics *	Real Time Water Quality and Hydrological Parameters
	${\mathit{T}}_{\mathbf{a}\mathbf{i}\mathbf{r}}^{°}$ (°C)		${\mathit{T}}_{{\mathbf{H}}_2\mathbf{O}}^{°}$ (°C)		$\left[{\mathbf{C}\mathbf{l}}^{-}\right]$ (mg L−1)		Dissolved O2 (mg L−1)		pH		$\mathbf{Specific} \mathbf{Conductivity} \left(\mathsf{\mu }\mathbf{S}{\mathbf{c}\mathbf{m}}^{-2}\right)$		Turbidity (NTU)		Water Level (m)		Flow (m3 s−1)
	Old Derry	MGCC	Old Derry	MGCC	Old Derry	MGCC	Old Derry	MGCC	Old Derry	MGCC	Old Derry	MGCC	Old Derry	MGCC	Old Derry	MGCC	Old Derry	MGCC
No. obs.	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759	238,759
NAs	61,900	69,852	29,750	69,154	55,153	94,805	41,414	91,454	70,205	98,219	48,629	80,707	54,183	88,639	153,554	161,060	153,551	160,537
Minimum	−20.56	−28.42	−0.20	−0.13	0.78	0	5.11	0	7.1	0	20	180	0	0	162.374	75.497	1.608	1.888
Maximum	37.93	37.95	30.99	32.43	1582	5396.08	16.64	16.73	9	9	2968	5013	2688	1966.78	163.81	76.844	66.014	86.254
1st Quartile	4.03	2.86	2.55	3.84	73.4	110.3	8.92	8.86	8.2	8.2	680	757	1	1.4	162.474	75.606	3.664	4.03
3rd Quartile	19.88	19.51	19.52	20.82	118.9	200.3	12.68	12.7	8.4	8.5	763	923	13.1	21.3	162.64	75.811	8.202	11.12
Mean	11.76	10.94	11.41	12.63	110.81	239.28	10.76	10.74	8.29	8.29	720.70	936.30	17.19	24.07	162.59	75.53	7.33	9.34
LCL Mean	11.71	10.89	11.37	12.59	110.46	237.57	10.75	10.73	8.29	8.29	720.15	934.32	16.94	23.75	162.59	73.75	7.28	9.27
UCL Mean	11.81	10.89	11.45	12.68	111.17	240.99	10.77	10.75	8.29	8.29	721.25	938.28	17.45	24.40	162.59	75.73	7.37	9.40
Median	12.24	11.87	11.17	13.39	95.05	136.8	10.93	10.83	8.3	8.3	719	822	4.93	5.8	162.533	75.671	5.131	5.863
Sum (×106)	2.08	1.85	2.83	2.14	20.3	34.4	2.12	1.58	1.40	1.17	137	148	3.17	3.61	13.9	5.88	0.62	0.73
Std. Dev.	10.14	10.76	8.78	9.04	77.31	330.61	2.30	2.20	0.23	0.24	123.23	401.24	55.43	63.55	0.18	0.19	6.72	9.24
Std. Err.	0.024	0.026	0.019	0.022	0.180	0.871	0.005	0.006	0.001	0.001	0.283	1.009	0.129	0.164	0.001	0.001	0.023	0.033
Variance	102.88	115.85	77.12	81.72	5976.46	109,304.70	5.27	4.86	0.05	0.06	15,184.68	160,997.00	3072.84	4038.34	0.03	0.04	45.16	85.33
Coeff. of Variation (%)	86	98	77	72	70	138	21	21	3	3	17	43	322	264	0	0	92	99
Skewness	−0.17	−0.33	0.08	−0.05	4.78	6.10	−0.18	−0.14	−0.71	−0.93	2.14	3.81	14.64	8.16	2.27	1.76	3.22	2.75
Kurtosis	−0.66	−0.47	−1.40	−1.39	40.26	56.07	−0.97	−1.09	207	11.50	22.37	20.34	384.71	103.06	6.51	3.45	13.27	8.97

* No. Observation, Total number of observations; NAs, Not available data points; LCL, Lower confidence limit; UCL, Upper confidence limit.

). Air and water temperatures ${(T}_{air}^{°}$ and $T_{H_{2}O}^{°})$ show similar trends at both sites, with mean $T_{air}^{°}$ around 11 °C and mean $T_{H_{2}O}^{°}$ slightly higher at MGCC. Chloride concentrations are significantly higher at MGCC (mean: 239.28 mg/L) compared to Old Derry Road (110.81 mg/L), likely due to road salt application in urban areas. Dissolved oxygen (DO) levels remain relatively stable at both sites, with means around 10.7 mg/L. The pH values are consistent, with a mean of 8.29, indicating a slightly basic water system. Specific conductivity is markedly higher at MGCC (mean: 936.30 μS/cm) compared to Old Derry Road (720.70 μS/cm), suggesting greater ionic content from urban influences. Turbidity exhibits high variability, with extreme values reaching 2688 NTU at Old Derry Road and 1966.78 NTU at MGCC, highlighting stormwater-driven sediment transport. Water levels and flow rates are notably higher at Old Derry Road, reflecting hydrological differences in catchment response. The high skewness and kurtosis in chloride $\left[{Cl}^{-}\right]$, turbidity, and specific conductivity ($\kappa$) indicate episodic pollution events and non-normal data distributions (Table 3). Overall, the outcomes suggest that MGCC experiences stronger anthropogenic impacts, particularly from urban runoff, while Old Derry Road demonstrates greater hydrological variability, which is likely influenced by natural watershed characteristics.

4.2. Mann–Kendall (MK) Test Summary and Other Statistical Analyses, Including Boxplots and Quantile–Quantile Plots

The statistical analyses, including MK test summaries, boxplots, quantile–quantile plots, etc., were conducted using data collected from October 2010 to December 2016, irrespective of any missing data gaps.

Table 4. Summary of Kendall’s rank correlation test correlation coefficients.

Parameters Correlated	Kendall’s (Non-Parametric) Rank Correlation Test Statistics by Station
	Old Derry Road				MGCC
	Z	τ	p-Value (×10−16)	Correlation?	Z	τ	p-Value (×10−16)	Correlation?
$T_{air}^{°}$ vs. DO	−294	−0.46	<2.2	Yes, negative	−322	−0.52	<2.2	Yes, strong negative
$T_{H_{2}O}^{°}$ vs. DO	−425	0.61	<2.2	Yes, strong negative	−405	−0.65	<2.2	Yes, strong negative
$T_{air}^{°}$ vs. $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$	−174	−0.28	<2.2	Yes, negative	−221	−0.37	<2.2	Yes, negative
Spec. conductivity vs. $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$	287	0.44	<2.2	Yes, positive	367	0.62	<2.2	Yes, strong positive
Spec. conductivity vs. pH	8	0.01	<18	No	42	0.07	<2.2	No
$\left[{\mathrm{C}\mathrm{l}}^{-}\right]$ vs. flow	52	0.12	<2.2	Yes, weak	19	0.05	<2.2	Yes, negative
Turbidity vs. flow	142	0.36	<2.2	Yes, positive	114	0.30	<2.2	Yes, negative
DO vs. pH	173	0.28	<2.2	Yes, positive	189	0.34	<2.2	Yes, negative

provides the results of the Kendall rank correlation (τ) test. The results indicate significant relationships between various water quality parameters at both Old Derry Road and MGCC stations. Air temperature and dissolved oxygen ($T_{air}^{°}$ vs. DO) exhibited a strong negative correlation at both stations, with MGCC showing a slightly stronger relationship (τ = −0.52) compared to Old Derry Road (τ = −0.46). Similarly, $T_{H_{2}O}^{°}$ vs. DO demonstrated a strong negative correlation at both locations (τ = −0.61 and τ = −0.65), suggesting that higher water temperatures reduce DO concentrations. Chloride $\left[{Cl}^{-}\right]$ and air temperature ${(T}_{air}^{°})$ showed a moderate negative correlation, while $\kappa$ and ${Cl}^{-}$ exhibited a strong positive correlation (τ = 0.44 and τ = 0.62, respectively), indicating that chloride concentrations significantly influence conductivity levels. Interestingly, turbidity and flow correlated positively at Old Derry Road (τ = 0.36), while a weak negative correlation was found at MGCC (τ = −0.30), likely due to the different hydrological conditions at the two sites. Additionally, DO and pH showed a positive correlation at Old Derry Road but a negative one at MGCC, suggesting site-specific differences in water chemistry. In contrast, no significant correlation was observed between specific conductivity and pH at either station (Table 4). These findings highlight the complex interactions between temperature, dissolved oxygen, and water quality parameters, emphasizing the need for site-specific analyses in urbanizing watersheds.

The boxplots illustrate the monthly variations in $T_{air}^{°}$ and $T_{H_{2}O}^{°}$, $\left[{Cl}^{-}\right]$ concentration, and DO at the two monitoring stations, Old Derry Road and MGCC, from 2010 to 2016 (Figure 3). Air and water temperatures exhibit a clear seasonal pattern, peaking in summer (June–August) and reaching their lowest values in winter (December–February). Chloride $\left[{Cl}^{-}\right]$ concentrations show a strong seasonal variation, with significantly higher values in winter and early spring, likely due to road salt application, followed by a steady decline in summer and fall. This pattern is more pronounced at MGCC, where $\left[{Cl}^{-}\right]$ concentrations reach extreme levels, indicating potential urban influences. DO follows an inverse trend to temperature, with higher concentrations in winter and lower values in summer, which aligns with the well-known temperature-dependent solubility of oxygen. The presence of numerous outliers, especially in chloride and dissolved oxygen levels, suggests episodic events such as runoff or pollution spikes.

Similarly, Figure 4 depicts the monthly boxplot variations in turbidity, instantaneous flow, pH, and specific conductivity ($\kappa$) at Old Derry Road and MGCC. Turbidity levels exhibit high variability, with pronounced spikes in certain months, particularly during spring and late fall, likely due to storm events and surface runoff. Instantaneous flow follows a similar seasonal pattern, peaking in spring (March–May) due to snowmelt and precipitation and declining during summer and fall. The pH levels remain relatively stable throughout the year, with minor fluctuations and a few outliers, indicating consistent buffering capacity in the water. The $\kappa$ shows a strong seasonal trend, with elevated values in winter and early spring, likely attributed to road salt application and subsequent runoff. MGCC exhibits higher specific conductivity values compared to Old Derry Road, suggesting a greater influence of urbanization activities. The presence of numerous outliers in turbidity and conductivity suggests episodic pollution events or storm-driven variability. Overall, these findings highlight the seasonal and anthropogenic influences on water quality parameters in the study area.

Additionally, Figure 5 presents quantile–quantile (Q-Q) plots comparing the empirical distributions of water quality parameters and flow rates with their corresponding lognormal transformations for the Old Derry Road and MGCC monitoring stations over the 2010–2016 period. Furthermore, Figure 6 visualizes temporal trends by plotting the original datasets with locally weighted scatterplot smoothing (LOWESS) curves, providing insights into variations in water quality parameters and flow dynamics at both stations. A comprehensive discussion of these findings can be found in Section 5.

4.3. Wavelet Analysis

Wavelet analysis produced graphical results: (i) wavelet coherency results are presented in Figure 7 and Figure 8, while (ii) continuous wavelet transform results are presented in Figures S2–S5 (Supplementary File). The continuous wavelet transform consisted of three groups of datasets: Spring 2012 to Fall 2016, Spring 2014 to Fall 2014, and Spring 2015 to Fall 2015. The results are summarized in a power spectrum plot, where various periods are plotted on a log scale on the ordinate, with more extended periods of time at the bottom and shorter periods of time at the top. The abscissa is plotted in equal steps of time intervals.

The power spectra plots in Figure 9, Figure 10, Figure 11 and Figure 12 depict temporal scales on the ordinate, ranging from hours to one year for the Spring 2012 to Fall 2016 dataset. The scale is logarithmic, with the largest scale (approximately one year) at the bottom and the smallest scale (approximately 4 h) at the top. The abscissa represents time in 1 h increments from Spring 2012 to Fall 2016. In contrast, for the Spring 2014 to Fall 2014 and Spring 2015 to Fall 2015 datasets shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, temporal scales on the ordinate range from hours to approximately 3 months. The abscissa still represents time in 1 h increments from Spring 2014/2015 to Fall 2014/2015. The power spectra are color-coded to represent the relative contribution of the frequency of measured parameters to the overall signal power, with yellow and orange indicating the highest power, green indicating moderate power, and navy blue indicating low power. The black contours in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 indicate 95% significance against red noise, typical in environmental datasets. The transparent white shaded areas outside each image represent cones of influence, where the results may be less accurate due to smearing and edge effects. In Figure 9, Figure 10, Figure 11 and Figure 12, the results for the Old Derry Road Station are displayed in the top half, while the MGCC results are shown in the bottom half. The larger figure on the left represents the Spring 2012 to Fall 2016 results, while the smaller, stacked figures to the right depict the Spring 2014 to Fall 2014 and Spring 2015 to Fall 2015 plots (Figures S2–S5 represent similar outcomes for other parameters in Supplementary Materials). The arrows in Figure 7 and Figure 8 indicate the phase of correlation, detailed in Table S1. Further insights into Figure 7 and Figure 8 are available in Section 5. Additionally, Figure 13 depicts wavelet power spectra using monthly real-time data from May to October 2015 for both stations, along with corresponding monthly wavelet coherence for air temperature and dissolved oxygen at the Old Derry Road and MGCC stations. (Similarly, Figure S6 in Supplementary Materials depicts monthly wavelet spectra and wavelet coherence for flow and turbidity at both the Old Derry Road and MGCC stations.)

5. Discussion

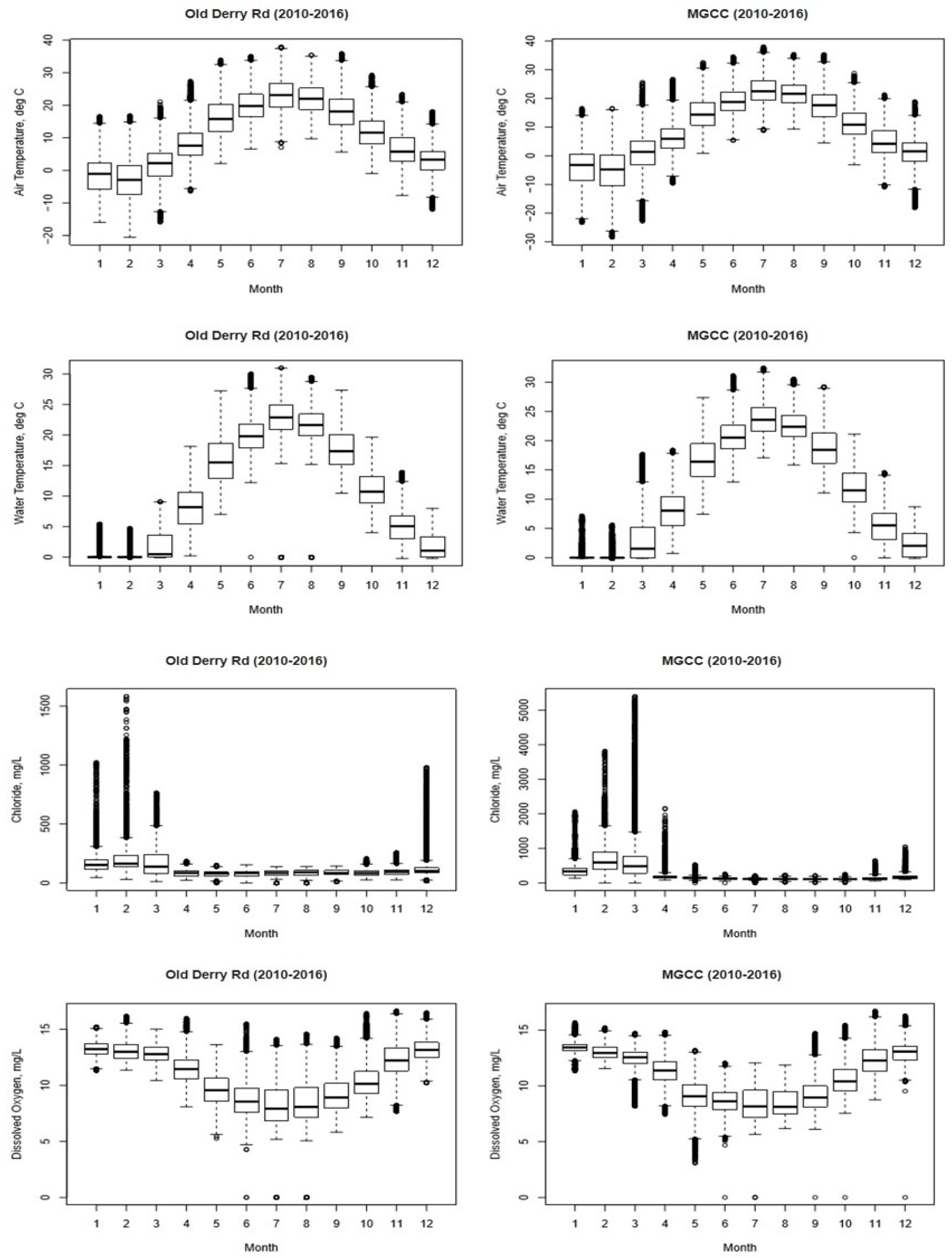
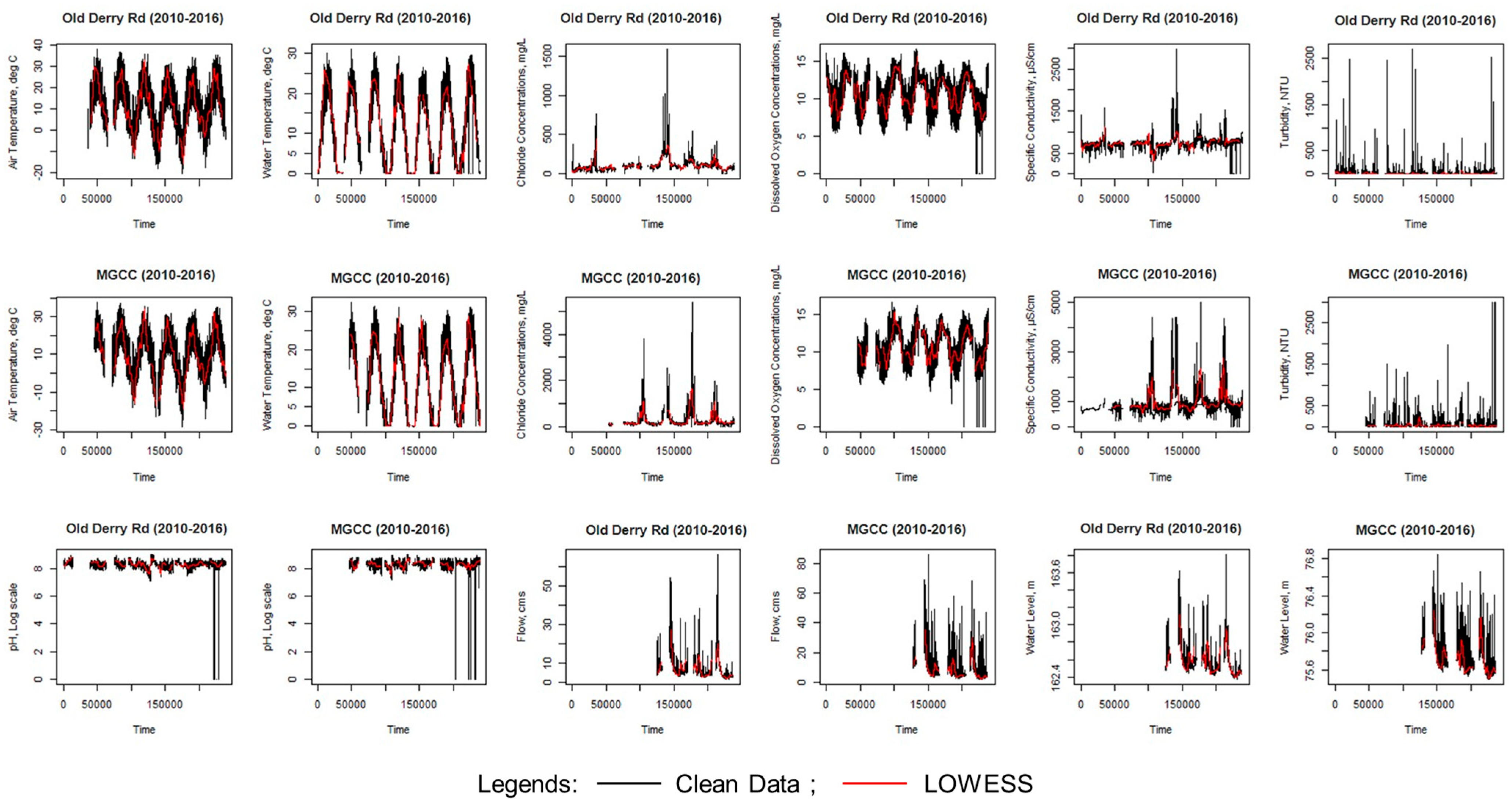
The Old Derry Road and Mississauga Golf Country Club stations generally exhibited similar statistical trends. Figure 3 depicts notable monthly fluctuations in $T_{air}^{°}$, $T_{H_{2}O}^{°}$, and DO means. While the spread of air temperature remains relatively consistent across months, water temperature shows greater variance during the spring and fall compared to July and August. Dissolved oxygen (DO) levels seem to decrease with rising water temperatures, possibly due to heightened oxygen consumption by biological activities. Notably, DO exhibited more variability during the summer months. 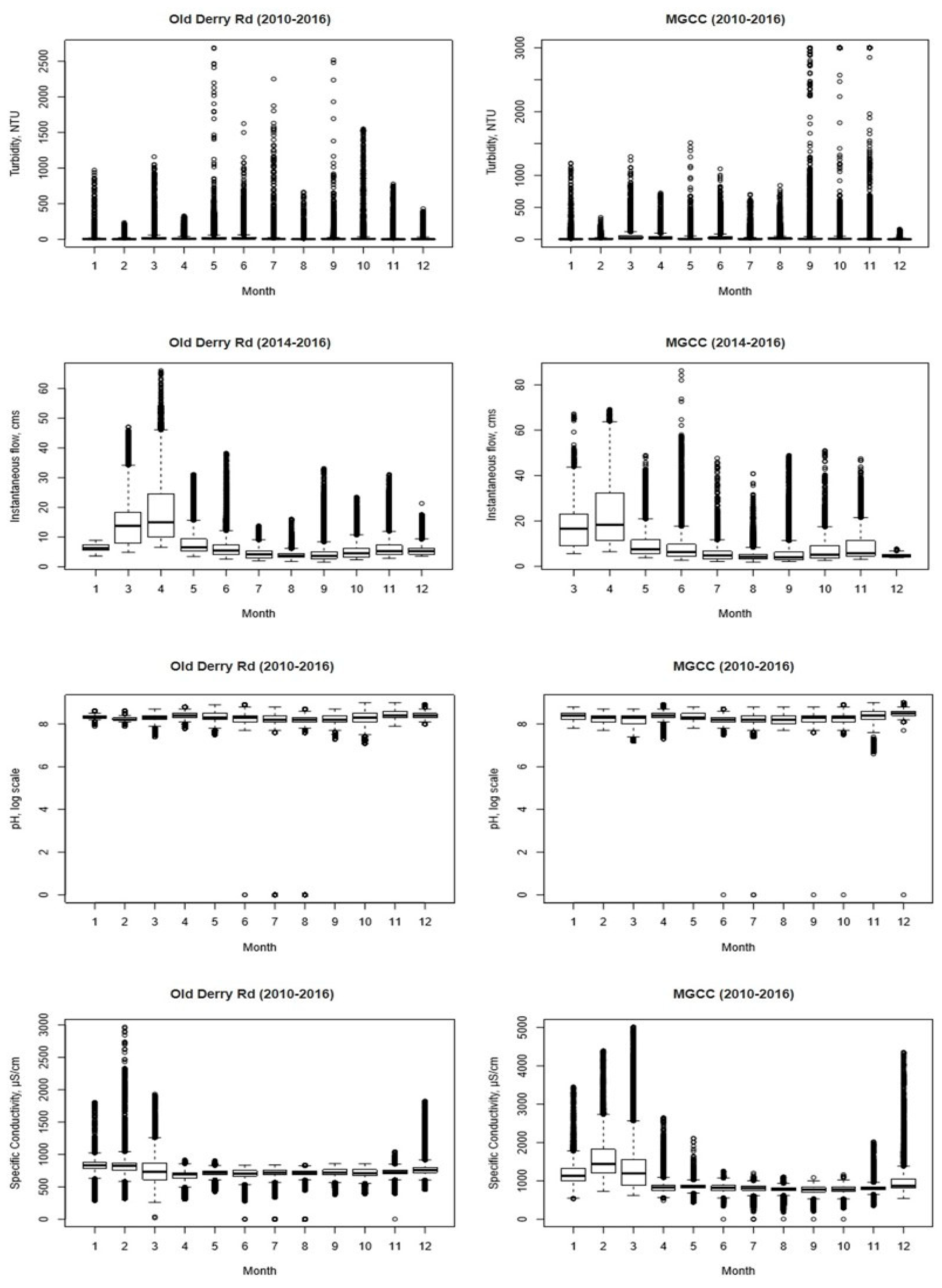Winter months often featured outliers in $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$, likely attributable to road salt application. Turbidity and flow exhibited numerous outliers (Figure 4). Flow peaked in March and April, likely due to snowmelt, with lower flows observed in summer. Mean pH remained stable at around 8.0, across all months. Specific conductivity ($\kappa$) was higher in winter months. 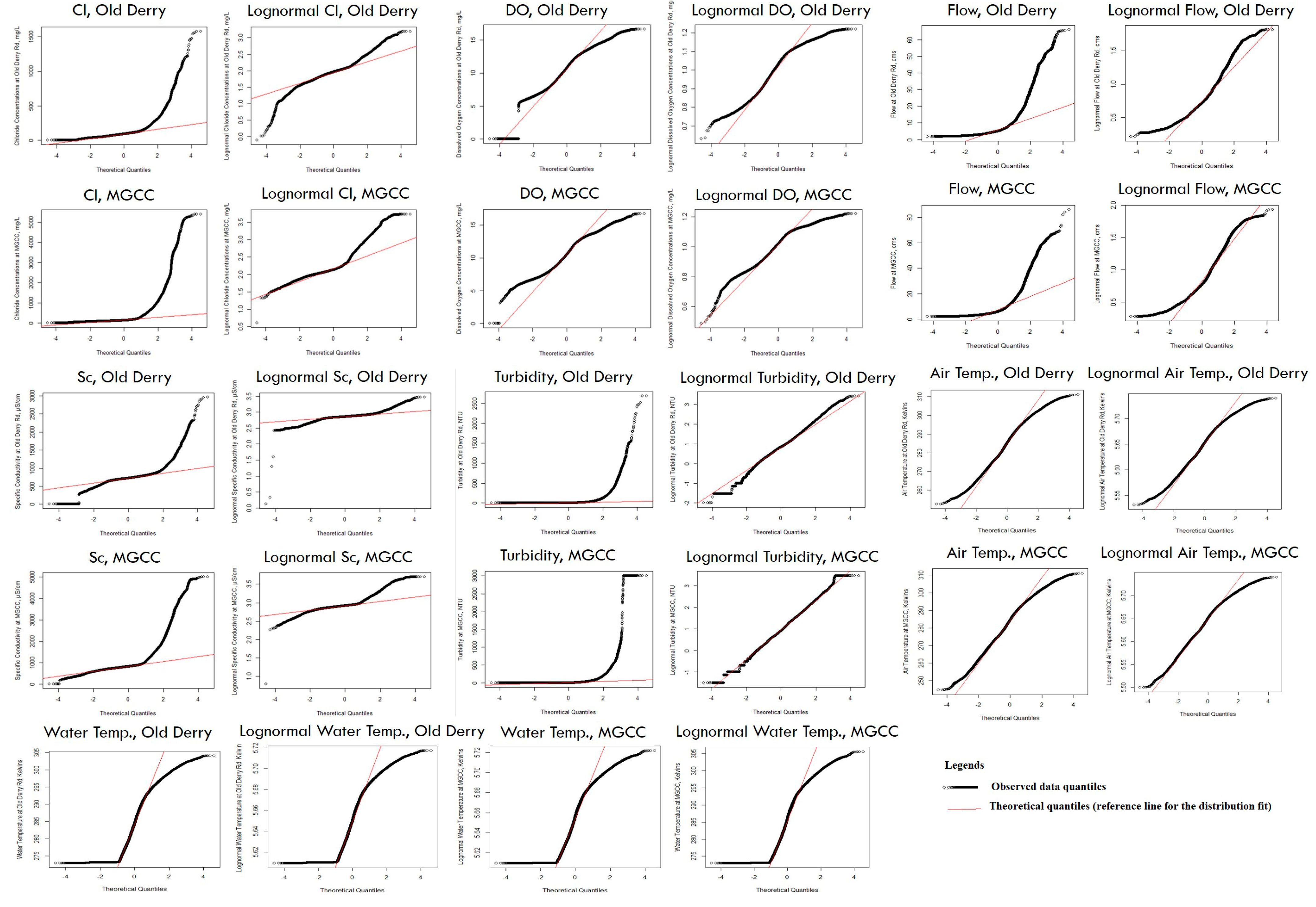Both MGCC and Old Derry Rd show similar patterns in means, spreads, and outliers (Figure 3 and Figure 4). Quantile–quantile plots (Figure 5) reveal right-skewed or heavy-tailed distributions, with turbidity closely fitting a lognormal distribution. Both flow and $T_{air}^{°}$ also approximate a lognormal distribution but show heavy tails. However, $T_{H_{2}O}^{°}$, $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$, and DO do not fit this model well. Data lacunae are evident in Figure 6, particularly with regard to seasonal variations in DO linked to $T_{H_{2}O}^{°}$ and $T_{air}^{°}$. Peaks are frequent in turbidity, $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$, $\kappa$, and flow. Table 4 highlights significant negative correlations between DO and $T_{air}^{°}$ or $T_{H_{2}O}^{°}$, with the correlation stronger for $T_{H_{2}O}^{°}$. Specific conductivity shows a strong positive correlation with $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$, and $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$ also exhibits positive correlations with $T_{air}^{°}$, with a weaker correlation to flow, particularly during snowmelt. Turbidity correlates positively with flow, and DO correlates positively with pH. These statistics offer a basic overview of the datasets, while the subsequent wavelet analysis delves deeper into temporal variations and intercorrelations in the data.

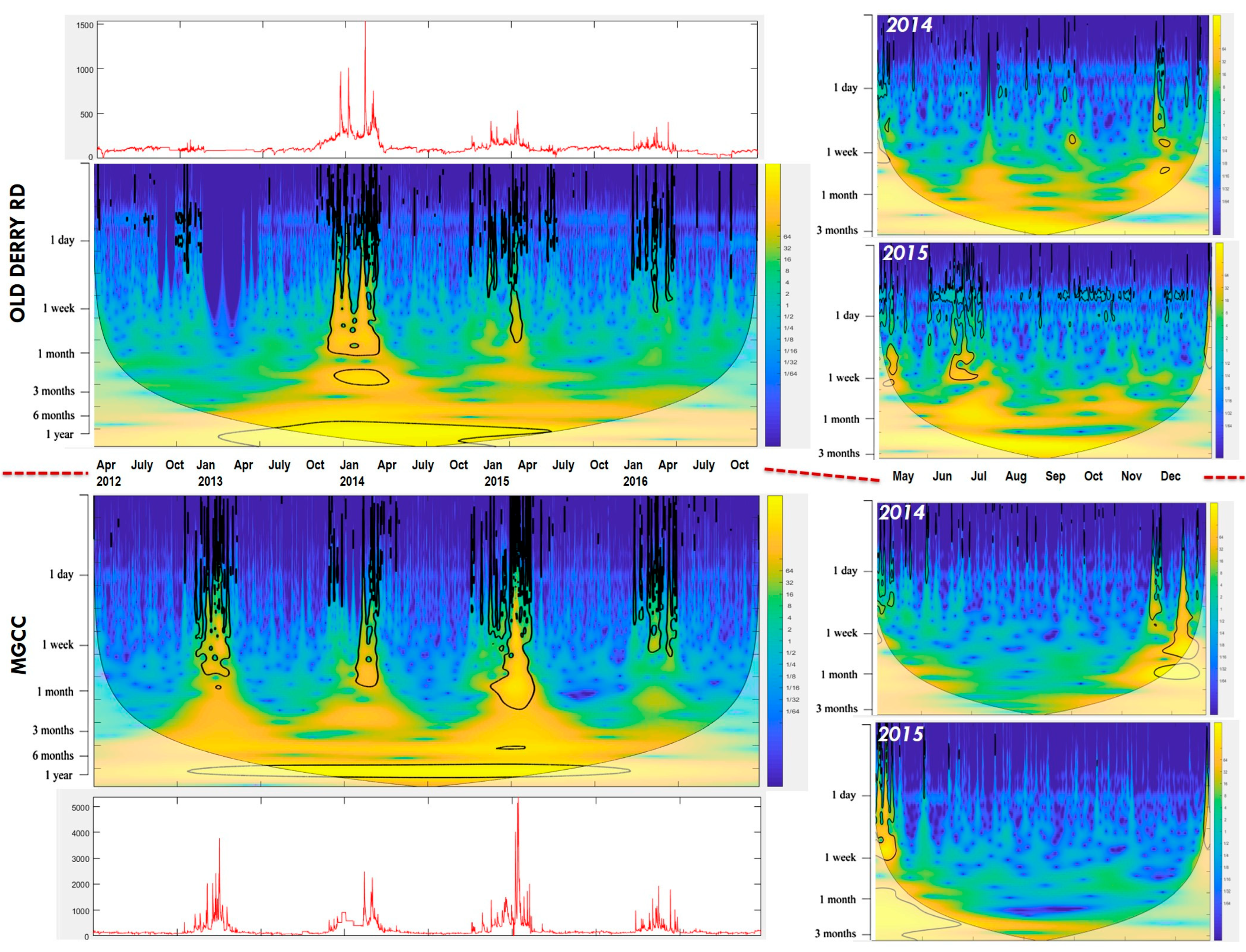
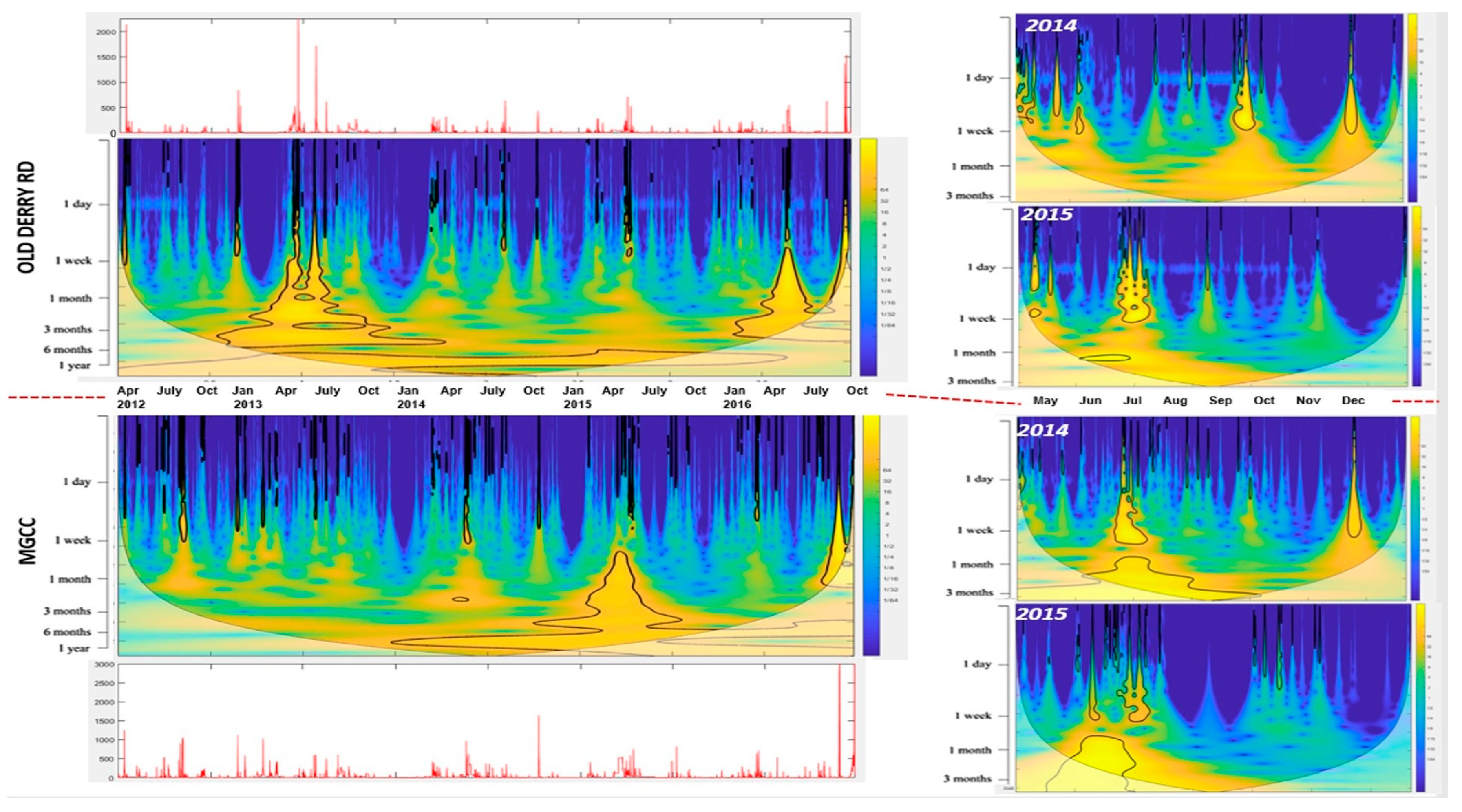
The continuous wavelet transform offers a significant advantage over discrete wavelet analysis, as it allows computations to be made for each temporal scale, enabling identification of dominant temporal patterns. Figure 9, Figure 11 and Figure 13, representing $T_{air}^{°}$, DO, and pH (similarly Figure S4, in Supplementary Materials, represents $T_{H_{2}O}^{°})$, respectively, display similar characteristics and will be discussed together. Conversely, Figure 10 and Figure 12, representing $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$ and turbidity (similarly, Figures S3 and S5 in Supplementary Materials correspond to specific conductivity and stream flow/water level) respectively, exhibit similar traits and were also analyzed together. In Figure 9 and Figure 11, Figures S2 and S4 (in Supplementary Materials), there is notable power at the “1 day” temporal scale with 95% confidence against red noise. The green color in the Spring 2012 to Fall 2016 plots and the yellow-green color in the Spring 2014/2015 to Fall 2014/2015 plots indicate this moderate power. Interestingly, shorter time periods allocate more power to the “1 day” temporal scale. Additionally, as $T_{air}^{°}$ rises, power at this scale increases, whereas it diminishes below ≈5 °C from late fall to winter, as indicated by the blue color. Notably, the continuous wavelet transform was conducted on the absolute values of temperature in Kelvin to prevent interference from negative numbers.

In Figure 11, the low summer values of DO contributed to the greatest energy on the “1 day” temporal scale, illustrating that lower magnitudes do not necessarily mean lower power. This pattern holds true for $T_{air}^{°}$, pH (Figure S5), and $T_{H_{2}O}^{°}$ (Figure S4). High power with 95% confidence against red noise is found at the “one year” temporal scale in Figure 9 and Figure 11, Figures S2 and S4 (in Supplementary Materials), indicating consistent patterns year after year. Overall, Figure 9 and Figure 11, Figures S2 and S4 show significant power at both the “1 day” scale during spring to early fall and the “one year” scale, highlighting the influence of seasonal variation and daily fluctuations. Additionally, the similarity between the Old Derry Rd and MGCC plots across all datasets suggests no significant changes in temporal variation from upstream to downstream.

Similar findings were observed by Rajwa-Kuligiewicz et al. [2], who also used continuous wavelet transform on hydrologic and dissolved oxygen time series measured on rivers in northeast Poland. They noted that DO exhibited concentrated power in the 6-month to one-year band, with moderate power at the one-day band. They emphasized that while power tends to be heightened for longer time scales, the specific location of high power is unique to each time series. They also found, in the same study, that during peak biological activity from March to November, DO showed increased power at higher frequencies on the daily temporal scale, correlating with fluctuations in $T_{H_{2}O}^{°}$; however, the greatest power was concentrated at longer time scales.

In the present study, fluctuations in $T_{H_{2}O}^{°}$ were primarily influenced by $T_{air}^{°}$ and insolation, with consistent temperatures observed during winters. The study also observed greater inter-annual variability in $T_{H_{2}O}^{°}$ and numerous short-term temporal patterns between periods greater than one week and less than one month. These results indicate that wavelet analysis goes beyond 95% confidence levels, typically significant from a statistical point of view, whereas related results were also observed in the Rajwa-Kuligiewicz et al. [2] study.

Also, in the existing study, variations in data at “1 day” temporal scales showed low to no power, but at temporal scales of less than “3 months,” they occasionally did hold power (Figure 10 and Figure 11) (Figures S3 and S5 also represent the same kind of output in Supplementary Materials). Peaks of $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$, during the winter months, held the greatest power, with 95% confidence against red noise (Figure 10). For the Old Derry Rd station, most of the power was held in a single peak from Fall 2013 to the onset of Spring 2014, indicating a significantly greater contribution to $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$, within that time frame rather than at any other time. In contrast, every winter, the MGCC station showed peaks that held significant power. In general, the MGCC station has significantly higher $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$ and peaks than the Old Derry Rd Station. Figure S6, showing specific conductivity, illustrates results similar to those shown in Figure S4, with a greater hold in the winter peaks. 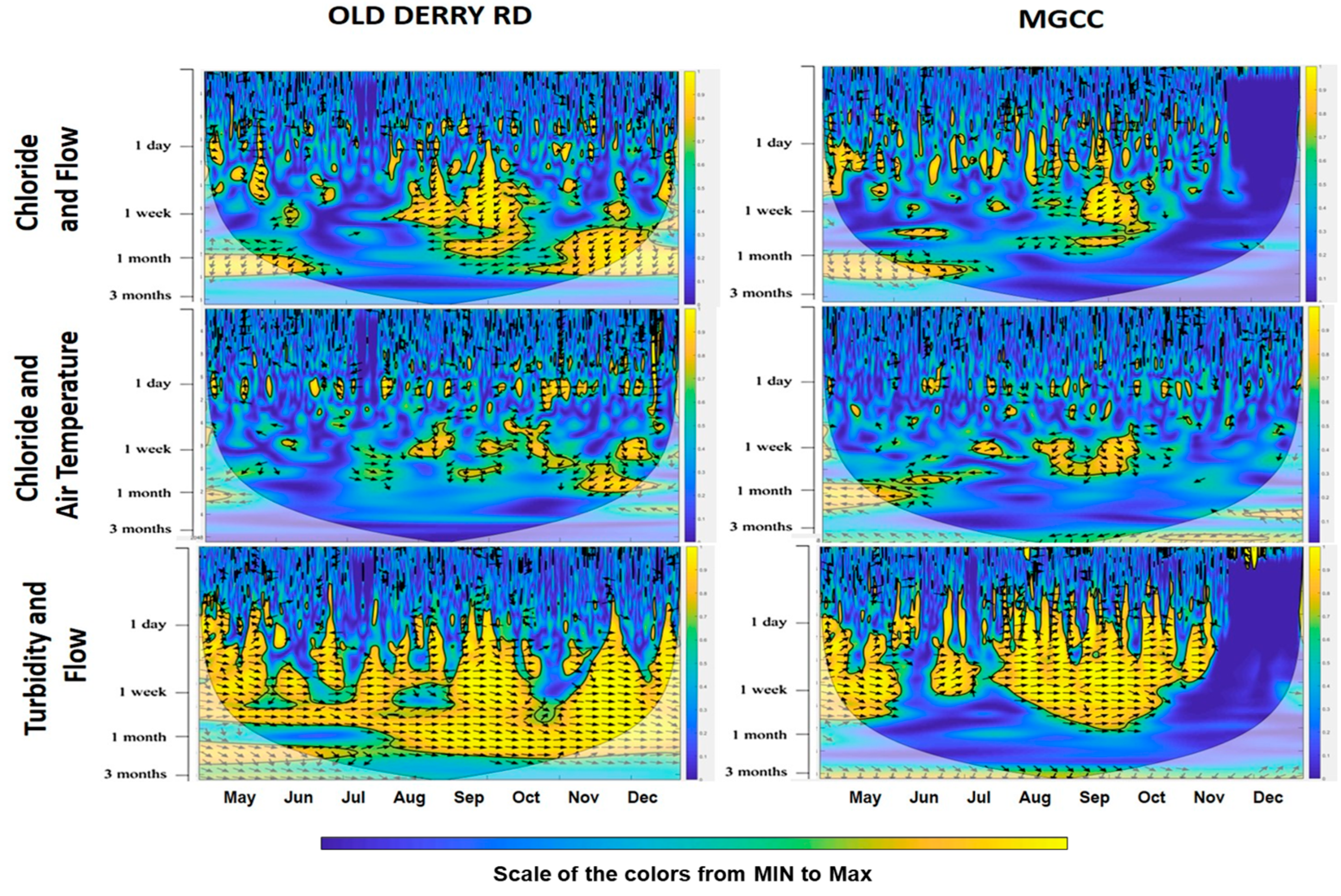Figure 12 for turbidity shows significant fluctuations in power throughout the year related to significant peaks of turbidity around the “1 month” to “6 month” temporal scales—in this case, the greater magnitude of the turbidity peaks contributes to greater power; in contrast, the greater magnitude of DO during the winter months does not contribute to greater power. Comparing Figure 12 for turbidity and Figure S5 (in Supplementary Materials) for flow, it becomes apparent that the turbidity peaks are directly linked to flow.

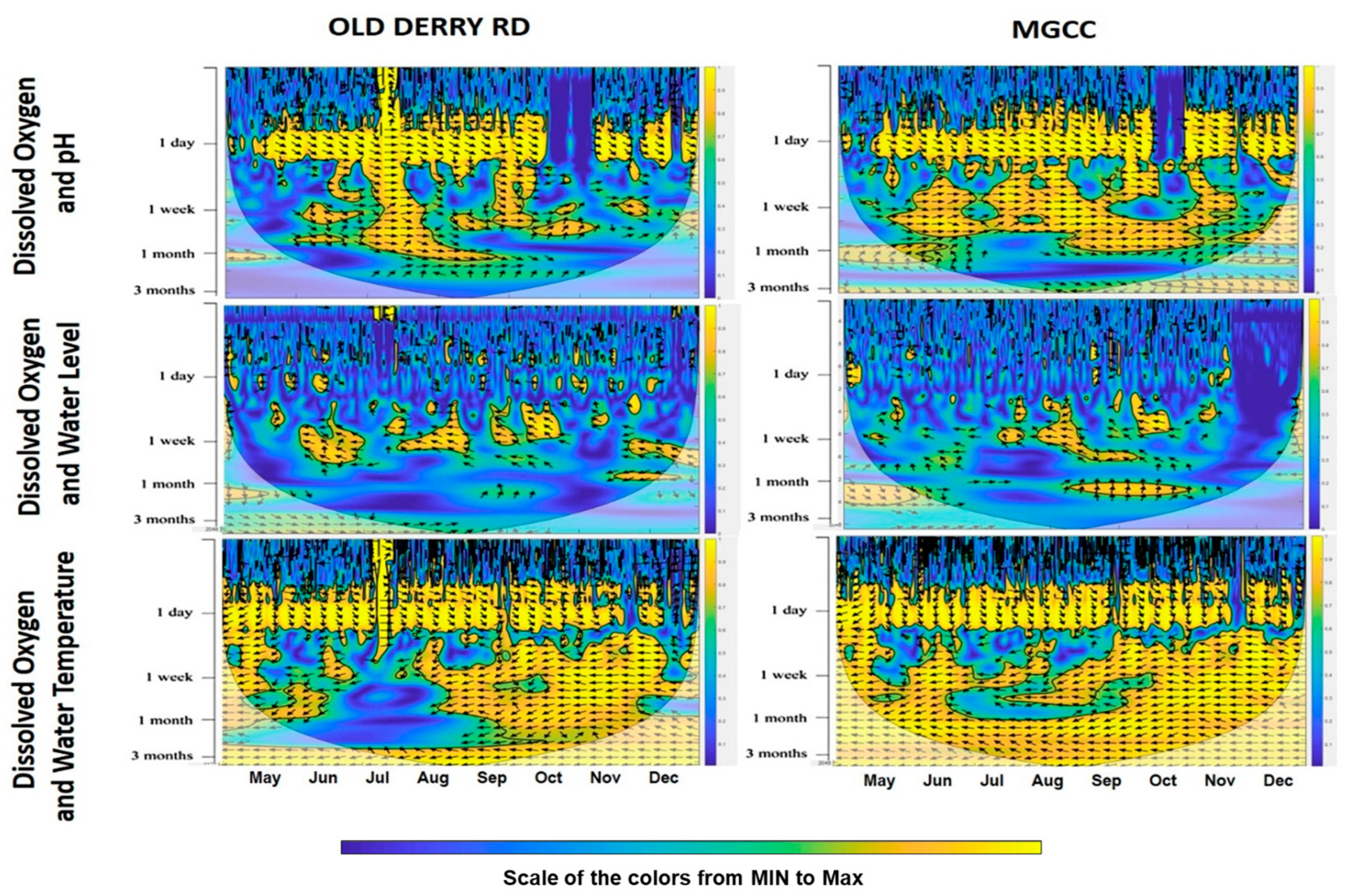
Figure 7 illustrates wavelet coherency between DO and pH, water level, and $T_{H_{2}O}^{°}$ at the Old Derry Rd and MGCC stations during the Spring 2014/2015 to Fall 2014/2015 period. The DO and pH showed a high power correlation at the “1 day” temporal scale with a 45° phase angle, indicating a lag period. Additionally, at Old Derry Rd, a high power correlation existed between “1 day” and “1 month” periods in July, while at MGCC, it extended from July to November. At both stations, DO and water level exhibited a poor correlation. Moreover, DO and $T_{H_{2}O}^{°}$ showed a 45° and 90° lagged correlation at the “1 day” scale and an out-of-phase correlation at other scales. However, a weak correlation existed between DO and $T_{H_{2}O}^{°}$ at temporal scales greater than “1 day” but less than “3 months” during May to August, suggesting a weak relationship between the two parameters in late spring and summer. Figure 8 displays wavelet coherency between $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$, $T_{air}^{°}$, flow, and turbidity for the Old Derry Rd and MGCC stations during the Spring 2014/2015 to Fall 2014/2015 period. A lagged correlation existed between $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$ and flow, particularly at the Old Derry Rd Station, at roughly weekly temporal scales in August and September, and “1 month” scales in the winter months. Little to no correlation was observed between $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$ and $T_{air}^{°}$ at any temporal scale. Turbidity and flow exhibited high power phase correlations, primarily within the “1 day” to “1 month” range at both stations, indicating that flow peaks in daily to monthly timeframes correspond to turbidity peaks.

In general, the wavelet analysis attributed more power to greater fluctuations in the magnitudes of frequency and less power to lower fluctuations in the magnitudes of frequency on a “1 day” scale. These greater fluctuations caused the DO, pH, $T_{air}^{°}$, and $T_{H_{2}O}^{°}$ datasets to exhibit greater power during the spring to fall period vs. the winter. In addition, periodicity in the data over an annual basis (due to seasonality) and data that hovered over a constant value (such as pH) were all represented by a horizontal straight line, indicating no change over time.

Outliers in the data, such as those found in the boxplots of turbidity, $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$, and specific conductivity, were all well captured by the continuous wavelet transform. When the magnitude of the peaks was at extreme values, high power was attributed to these extremes as they held significant power in the entire time series.

The continuous wavelet analysis provided an effective representation of the behavior of the measured parameters. The method can be used for quick feature extraction of irregularities; however, the mechanisms that provide the power, such as the increase in the magnitude of frequency, periodicity, or hovering over a constant value or an extreme magnitude relative to the rest of the dataset, need to be kept in mind when assessing the data over the various temporal scales. The temporal scale resolution is innovative, as most time series analysis is limited to plots of the measured parameters over time.

The continuous wavelet transform is computationally efficient in MATLAB; however, estimating continuous wavelet coherency becomes increasingly inefficient when applied to large real-time datasets. For instance, generating wavelet coherency plots for the Spring 2014/2015 to Fall 2014/2015 period took approximately 15 min each, while attempts to analyze the full Spring 2012 to Fall 2016 dataset caused the program to freeze. To address data continuity issues, we filtered out periods with extensive missing data and applied a moving average method in R, followed by cubic interpolation to approximate the remaining gaps. However, these steps were necessary to maintain a continuous dataset for wavelet analysis. In this study, interpolation may have introduced distortions in the power spectra and potentially bias the spectral slope, especially toward lower frequencies. Furthermore, it should be noted that wavelet coherency, which estimates the localized correlation between two time series in time–frequency space, is distinct from wavelet cross-spectrum, which merely conjugates the two wavelet transforms and can yield inconsistent results (Rajwa-Kuligiewicz et al. [2]; Grinsted et al. [19]). Due to these computational and methodological constraints, the analysis was limited to selected periods and focused exclusively on wavelet coherency, as detailed in Table S1.

In general, the continuous wavelet analysis showed that the two stations, Old Derry Rd and MGCC, had similar temporal variations and correlations for DO, pH, $T_{air}^{°}$, and $T_{H_{2}O}^{°}$, while slightly different temporal variations were seen for $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$, flow, turbidity, and specific conductivity. It should be noted that the magnitude of the measured parameters differed between the two stations; however, the wavelet analysis is only concerned with the power relative to the original signal. As such, it appears that, for example, the high-power single peak in $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$ at Old Derry Rd around January 2014 was much greater than the high-power single peak at MGCC around the same time. However, the time series indicate that the MGCC peak was of greater magnitude than Old Derry Rd. Hence, a power spectra plot alone can only serve to compare temporal variation between the stations, and not between the magnitude or the numerical value of data at that time. Therefore, the actual or numerical value or magnitude of a value is not automatically transferred into a power spectra plot. If we only did statistical analysis without wavelet analysis, only the magnitude or actual value of the data would be observed, but with the power spectra (in which higher power indicates dominant features), the temporal variation between the stations was also observed.

In addition, as detailed above, it should be noted that when producing a wavelet power plot, longer time periods of data attribute less power to events of a smaller scale than do shorter time periods. The geographic area between the Old Derry Rd and MGCC stations had a significant impact on MGCC $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$ during the winters. The greatest peak in MGCC occurred during the winter of 2015. The winter 2014 peak in $\left[{\mathrm{C}\mathrm{l}}^{-}\right]$ at Old Derry Rd was reflected downstream at the MGCC station as well (Figure 8).

Figure 13 displays results on a smaller temporal scale, using monthly datasets from $T_{air}^{°}$ and DO for the year 2015 (May to October). Similarly, Figure S6 in Supplementary Materials depicts flow and turbidity at both the stations. In addition, similar patterns around the 1-day to 1-week scale are observed for these variables, with $T_{air}^{°}$ and DO showing strong correlation at smaller temporal scales. However, on a monthly basis, the wavelet analysis is also investigated from 1-day to 1-week scale in the graphs shown in Figure 13. Peaks in flow coincide with peaks in turbidity, likely due to storm event runoff, with slight variations within each month. However, these figures do not offer significantly greater insight compared to wavelet analysis of several years of real-time data, which provides a comprehensive view of patterns across various temporal scales. Wavelet analysis with long-term data ensures that resolution is not lost at smaller scales, and power spectra indicate the significance of individual data points relative to the entire series. It should be noted that the results from wavelet analysis for one month are not directly comparable to other months. For detailed insights at monthly or weekly levels, it is recommended to zoom in on wavelet power spectra or coherence plots generated from complete real-time datasets, rather than breaking down data into smaller intervals for analysis. Therefore, the approach used in Figure 13 is not advised. In fact, wavelet analysis with several years of real-time data provides the greatest insight into changes in patterns in the time series over a wide range of temporal scales ranging from one day to greater than a year. In addition, the logarithmic scale of the wavelet power spectra ensures that the resolution of the real-time data time series is not lost at smaller scales of 1 day to 1 week. In addition, the wavelet analysis power spectra show the power relative to the length of the time series. As such, performing wavelet analysis on a large dataset of several years without breaking it down into smaller components allows for the wavelet power spectra to indicate the significance and power of the individual data points in the time series relative to the entire time series.

6. Conclusions

This study examined water quality and streamflow at Old Derry Road and MGCC from 2010 to 2016. Seasonal and site-specific differences were observed. MGCC showed stronger human impacts, with higher chloride, conductivity, and turbidity from urban runoff. Old Derry Road reflected more natural hydrological variability. Road salt use and storm events played a major role in water quality changes. CWT revealed dominant daily and annual cycles for DO, pH, and temperature, along with lagged and in-phase correlations between the parameters. Turbidity and flow were strongly linked to stormwater events, while chloride dynamics were seasonal and site-specific. The results were consistent with the Kendall rank correlation, except for a few cases such as [Cl⁻] and air temperature. The study shows that real-time water quality and flow data do not always follow traditional statistical distributions. CWT proved highly effective in detecting localized, non-stationary patterns often missed by standard methods. These findings improve our understanding of watershed behavior in urbanizing landscapes and can guide better water resource management and policy decisions.