Frilled Lizard Optimization Control Strategy of Dynamic Voltage Restorer-Based Power Quality Enhancement
Abstract
1. Introduction
- To design a DVR to improve power quality in a grid-connected system.
- To improve Dynamic Voltage Restorer’s (DVR) ability to minimize total harmonic distortion, this work proposes an optimized fuzzy PI controller.
- To optimize the control parameters, Frilled Lizard Optimization is utilized.
2. Literature Survey
3. Proposed Methodology
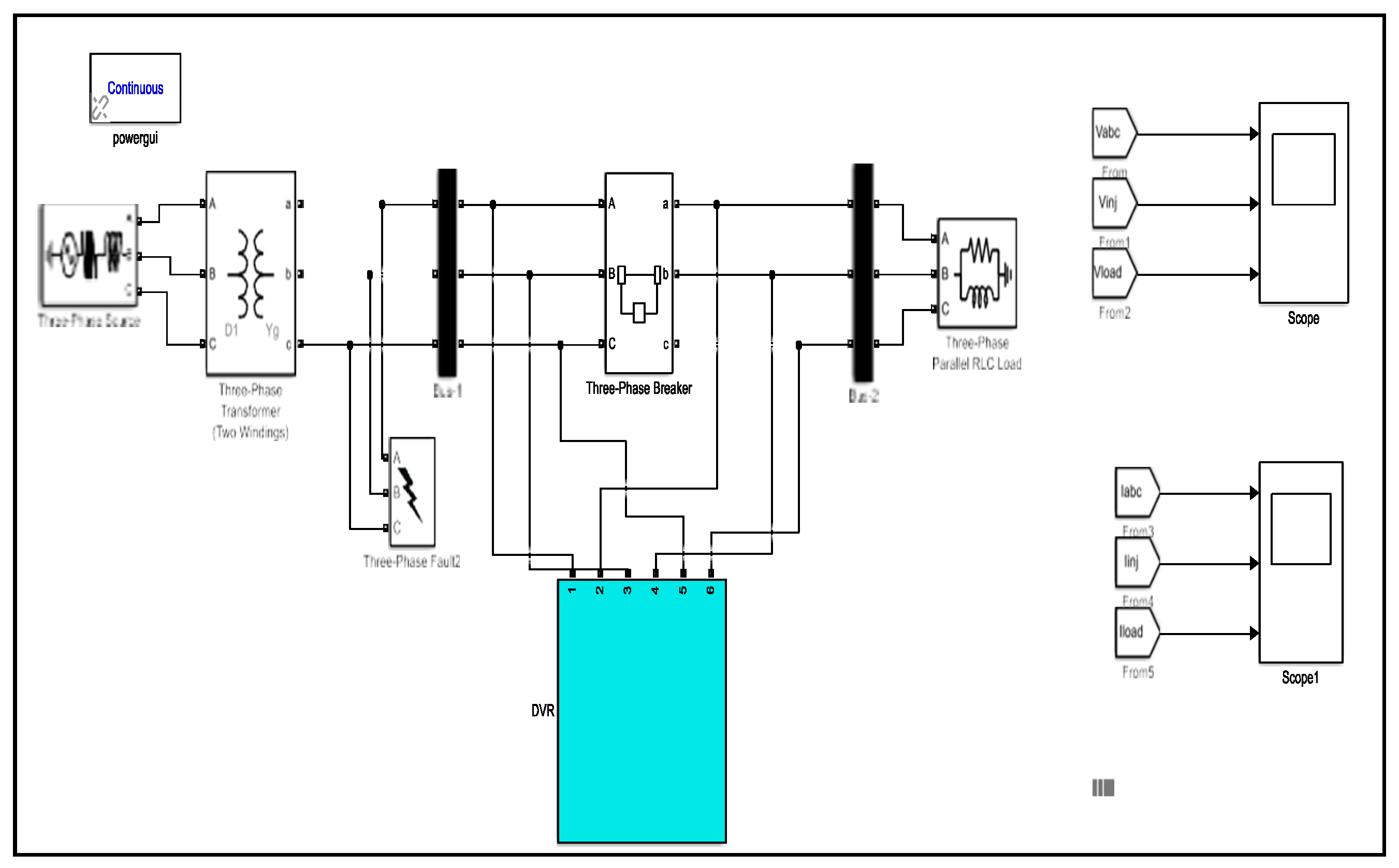
3.1. Dynamic Voltage Restorer (DVR)
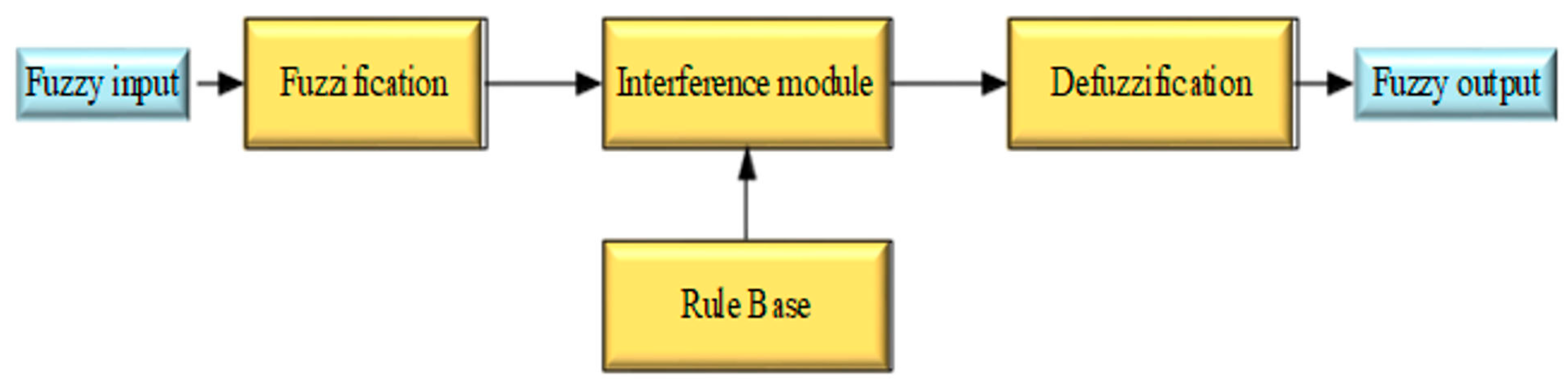
3.2. Proposed Fuzzy-Based Control Techniques
3.3. Frilled Lizard Optimization
3.3.1. Exploration Phase (Hunting Strategy)
3.3.2. Exploitation Phase (Moving up the Tree)
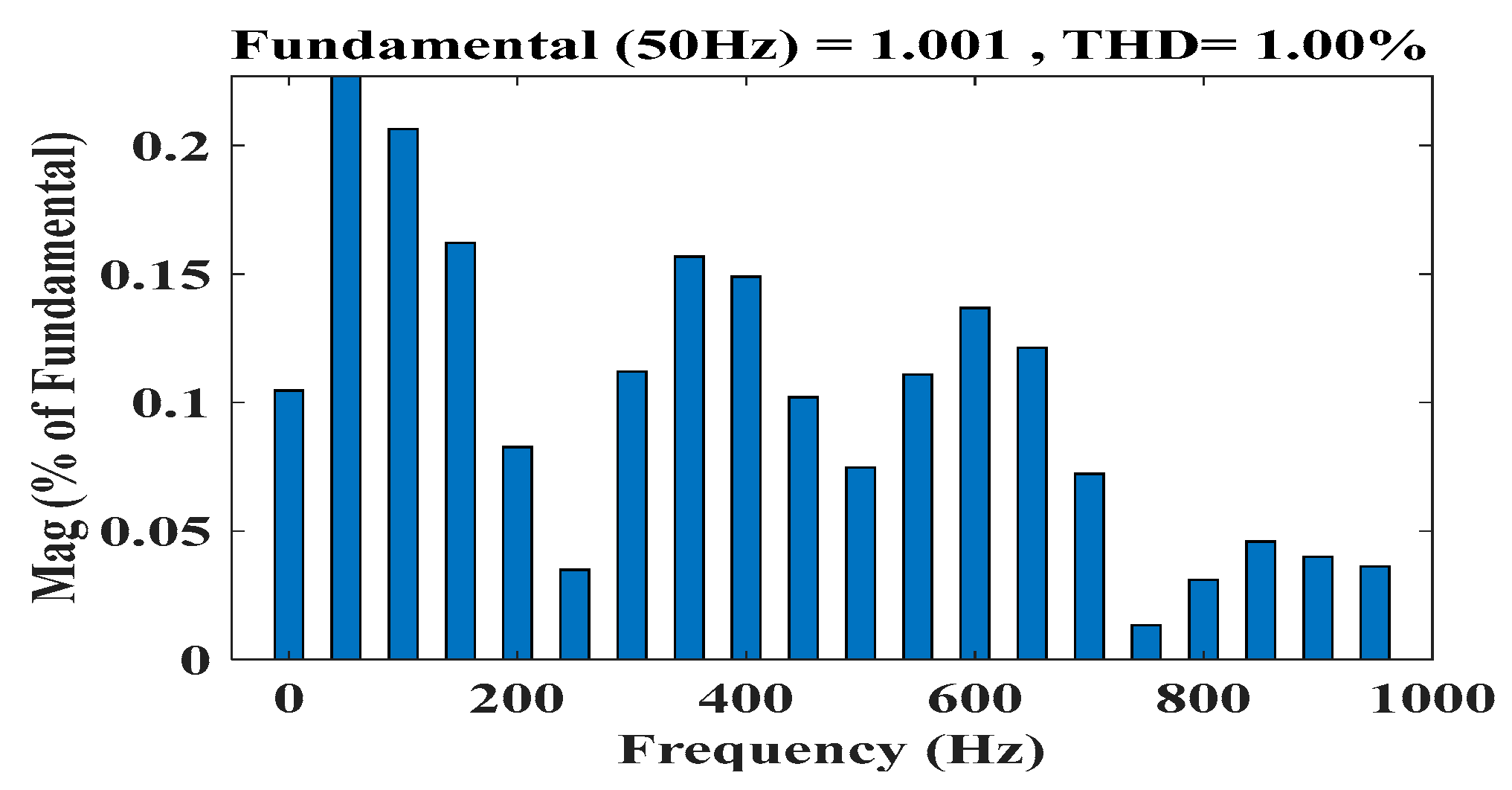
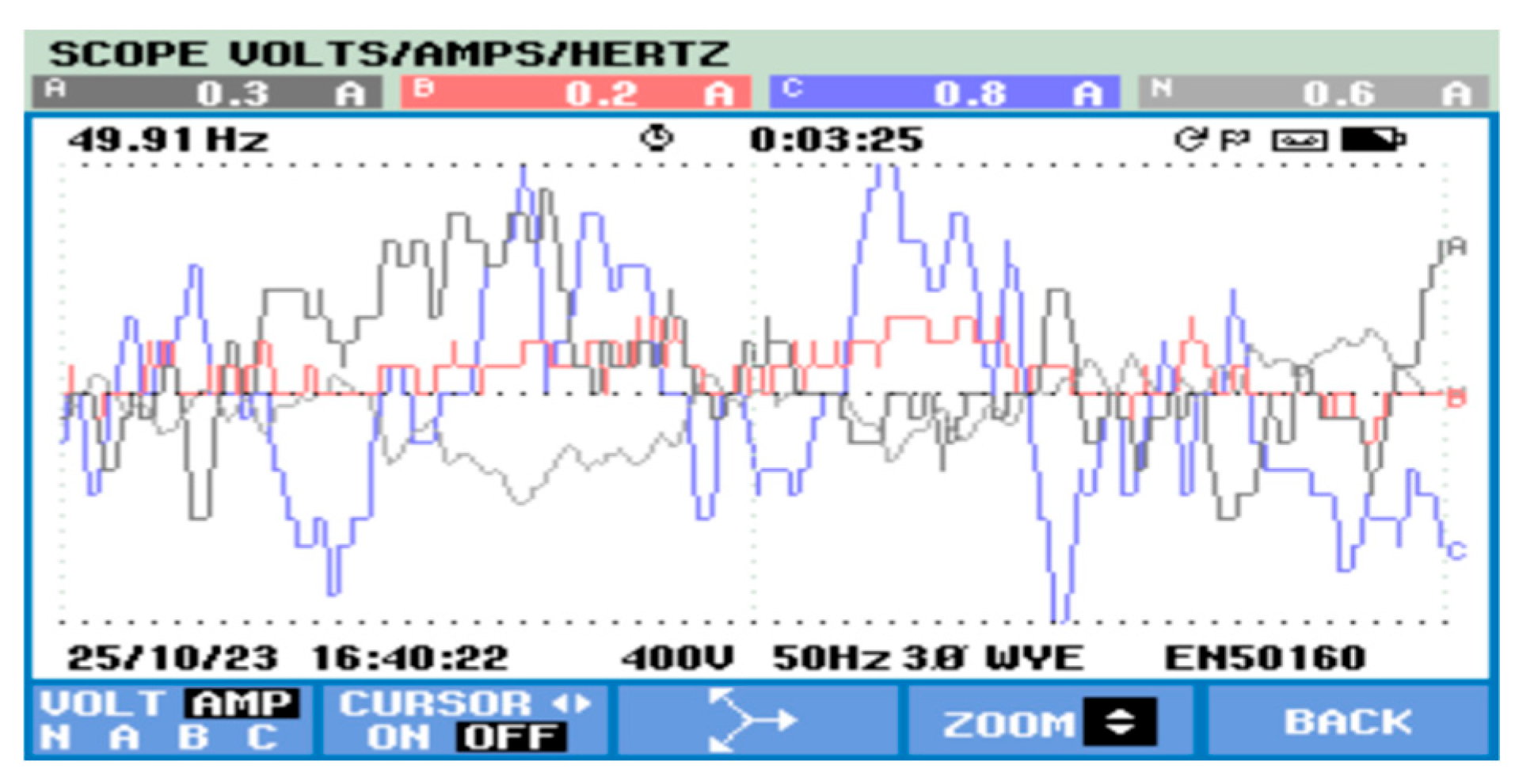
4. Results and Discussion
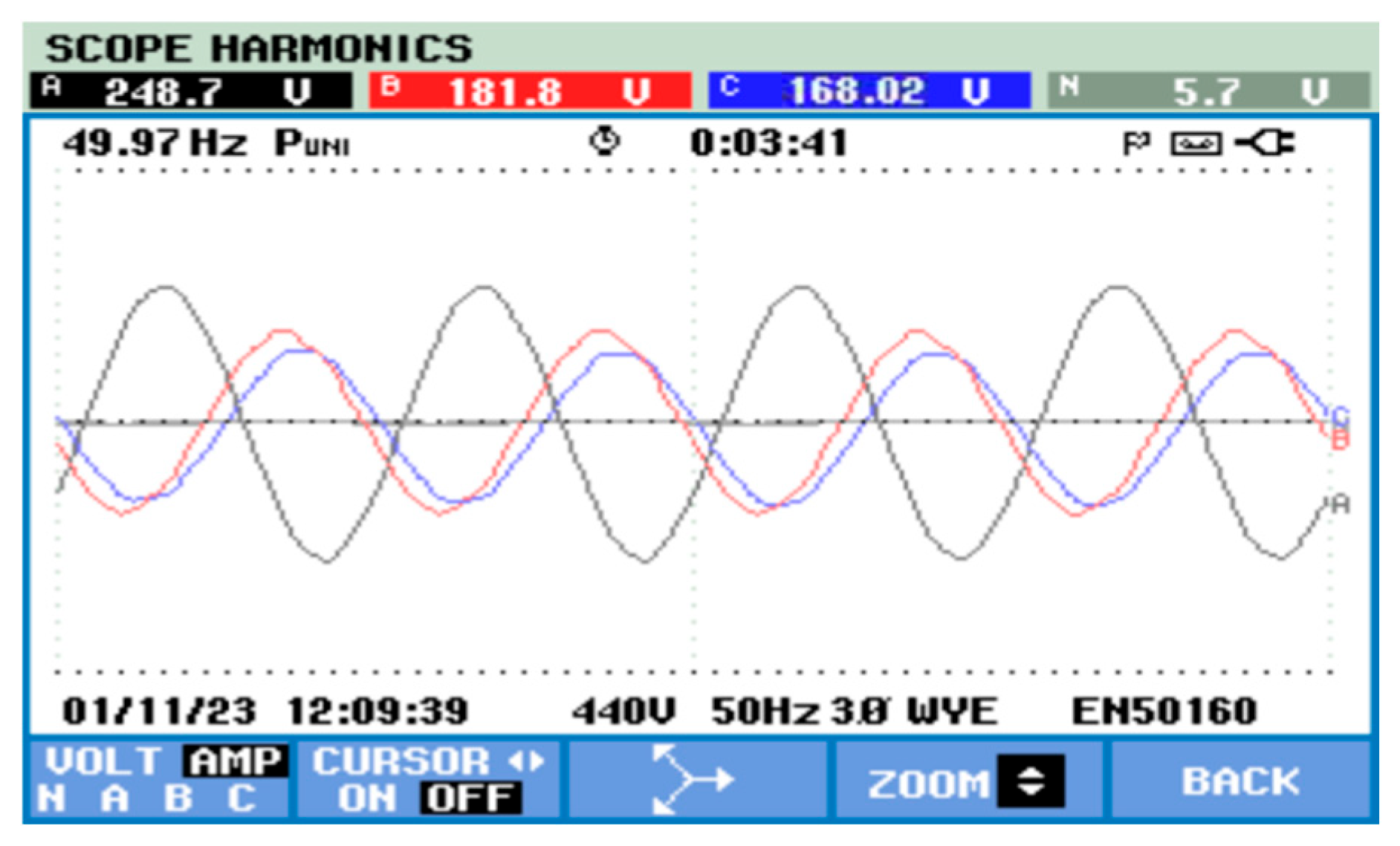
Hardware Design and Output
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sepasi, S.; Talichet, C.; Pramanik, A.S. Power quality in microgrids: A critical review of fundamentals, standards, and case studies. IEEE Access 2023, 11, 108493–108531. [Google Scholar] [CrossRef]
- Yadav, M.P.; Sujatha, P.; Kumar, P.B. Design and analysis of PV-DVR For Interconnected Wind System using Fuzzy Logic Controller. In Proceedings of the 2023 International Conference on Signal Processing, Computation, Electronics, Power and Telecommunication (IConSCEPT), Karaikal, India, 25–26 May 2023. [Google Scholar]
- Kumar, C.; Ghosh, P.; Chatterjee, S. Enhancement of Power Quality by mitigating of sag and swell problem in power system using DVR. IFAC-Pap. Line 2023, 55, 131–137. [Google Scholar] [CrossRef]
- Iqbal, A.; Ayoub, A.; Waqar, A.; Ul-Haq, A.; Zahid, M.; Haider, S. Voltage stability enhancement in grid-connected microgrid using enhanced dynamic voltage restorer (EDVR). AIMS Energy 2024, 9, 150–177. [Google Scholar] [CrossRef]
- Benali, A.; Khiat, M.; Denai, M. Voltage profile and power quality improvement in photovoltaic farms integrated medium voltage grid using dynamic voltage restorer. Int. J. Power Electron. Drive Syst. 2023, 11, 1481–1490. [Google Scholar] [CrossRef]
- Deshpande, C.; Chilipi, R.; Arya, S.R. A multi-convex composition of adaptive LMS filter-based control for dynamic voltage restorer with SSO-optimized PI gains. Electr. Eng. 2024, 107, 8243–8257. [Google Scholar] [CrossRef]
- Roja, S. A Fuzzy controlled grid connected Solar PV-Fed Multilevel Inverter with Series Compensator for Power Quality Improvement. J. Eng. Sci. 2024, 15, 81203–81219. [Google Scholar]
- Sowmyashree, N.; Kulkarni, H.; Shashikala, M.; Veeramanju, K.T. Review of Voltage Sag\Swell Mitigation Control Techniques with Dynamic Voltage Restorer in a Grid Integrated Distribution System. In Advances in Renewable Energy & Electric Vehicles. AREEV 2022; Springer: Singapore, 2024. [Google Scholar] [CrossRef]
- Siddique, A.; Mujahid, A.; Aslam, W.; Sajid, M.; Arfeen, Z.A. Improvements in Voltage Profile of JDW Sugar Mills’ Jawar Distribution Feeder RYK Pakistan Using ANN Based Dynamic Voltage Restorer. J. Eur. Syst. Autom. 2024, 57, 1–8. [Google Scholar] [CrossRef]
- Liu, A.; Wang, Y.; Zhu, Y.; Park, S.J. Research on power quality improvement system based on dynamic voltage restorer. IET Power Electron. 2024, 17, 1399–1410. [Google Scholar] [CrossRef]
- Anitha, P.; Kamaraja, A.S.; Karthik Kumar, K.; Bhuvanesh, A. Load voltage balancing using marine predator algorithm for power system quality improvement. J. Electr. Eng. Technol. 2024, 19, 73–82. [Google Scholar] [CrossRef]
- Reddy, S.G.; Ganapathy, S.; Manikandan, M. Three phase four switch inverter based DVR for power quality improvement with optimized CSA approach. IEEE Access 2022, 10, 72263–72278. [Google Scholar] [CrossRef]
- Kumar, P.; Arya, S.R.; Mistry, K.D. Performance enhancement of DVR using adaptive neural fuzzy and extreme learning machine-based control strategy. Int. J. Fuzzy Syst. 2022, 24, 3416–3430. [Google Scholar] [CrossRef]
- Gopal, B.; Murthy, P.K. Power Quality Improvement Using DVR Control DesignedWith Ann-Fuzzy In MATLAB. Webology 2020, 17, 573–592. [Google Scholar]
- Setty, S.N.; Shashikala, M.S.D.; Veeramanju, K.T. Hybrid control mechanism-based DVR for mitigation of voltage sag and swell in solar PV-based IEEE 33 bus system. Int. J. Power Electron. Drive Syst. 2023, 14, 209. [Google Scholar] [CrossRef]
- Singh, O.J.; Winston, D.P. Enhanced Method of Mitigating Voltage Sags and Swells Using Optimized Fuzzy Controlled DVR. Iran. J. Sci. Technol. Trans. Electr. Eng. 2023, 47, 147–158. [Google Scholar] [CrossRef]
- Abdelkader, A.B.; Mouloudi, Y.; Soumeur, M.A. Integration of renewable energy sources in the dynamic voltage restorer for improving power quality using ANFIS controller. J. King Saud Univ.-Eng. Sci. 2023, 35, 539–548. [Google Scholar] [CrossRef]
- Ghamari, S.M.; Narm, H.G.; Mollaee, H. Fractional-order fuzzy PID controller design on buck converter with antlion optimization algorithm. IET Control. Theory Appl. 2023, 16, 340–352. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, X.; Wang, W.; Liu, W.; Liao, M.; Fu, Z. Power Source Converter Based on a Variable-Domain Fuzzy PI Control. Electronics 2024, 13, 674. [Google Scholar] [CrossRef]
- Falahah, I.A.; Al-Baik, O.; Alomari, S.; Bektemyssova, G.; Gochhait, S.; Leonova, I.; Malik, O.P.; Werner, F.; Dehghani, M. Frilled Lizard Optimization: A Novel Nature-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Preprint 2024. [Google Scholar] [CrossRef]







| Ce/e | NB | NM | Z | PS | PS | PM | PB |
| NB | NB | NB | NB | NM | NM | NS | Z |
| NM | NB | NB | NM | NM | NS | Z | PS |
| NS | NB | NM | NM | NS | Z | PS | PM |
| Z | NM | NM | NS | Z | PS | PM | PM |
| PS | MN | MS | Z | PS | PM | PM | PB |
| PM | NS | Z | PS | PM | PM | PB | PB |
| PB | Z | PS | PM | PM | PB | PB | PB |
| Parameter | Rated Values | Per Unit Values |
|---|---|---|
| MAX.LOAD | 50 KVA | 1 P.U |
| DVR RATING | 10 KVA | 0.5 P.U |
| LOAD VOLTAGE | 230 V | 1 P.U |
| DVR VOLTAGE | 0.115 V | 0.05 P.U |
| DC LINK VOLTAGE | 560 V | - |
| SUPPLY FREQUENCY | 50 Hz | 1 P.U |
| SWITCHING FREQUENCY | 20 KHZ | 400 P.U |
| Controller | THD% |
|---|---|
| Without DVR | 22.4% |
| With PI DVR | 1.98% |
| With Fuzzy DVR | 1.74% |
| Proposed controller | 1.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamalini, C.P.; Suganyadevi, M.V. Frilled Lizard Optimization Control Strategy of Dynamic Voltage Restorer-Based Power Quality Enhancement. Sustainability 2025, 17, 8573. https://doi.org/10.3390/su17198573
Kamalini CP, Suganyadevi MV. Frilled Lizard Optimization Control Strategy of Dynamic Voltage Restorer-Based Power Quality Enhancement. Sustainability. 2025; 17(19):8573. https://doi.org/10.3390/su17198573
Chicago/Turabian StyleKamalini, C. Pearline, and M. V. Suganyadevi. 2025. "Frilled Lizard Optimization Control Strategy of Dynamic Voltage Restorer-Based Power Quality Enhancement" Sustainability 17, no. 19: 8573. https://doi.org/10.3390/su17198573
APA StyleKamalini, C. P., & Suganyadevi, M. V. (2025). Frilled Lizard Optimization Control Strategy of Dynamic Voltage Restorer-Based Power Quality Enhancement. Sustainability, 17(19), 8573. https://doi.org/10.3390/su17198573





