Sustainable Distilled Water Production Using a Solar Parabolic Dish: Hybrid Nanofluids, Numerical Analysis, and Explainable AI

Abstract

This research offers valuable improvements in the efficiency and water yield of a parabolic dish concentrator (PDC) solar distillation system, contributing to more sustainable and effective renewable energy solutions. Three hybrid nanofluids were evaluated, and their performance was measured through experiments and simulations. The numerical model is within 5% agreement with the measurements. Daily distilled water production increases by 25.7% with hybrid nanofluids (from 4.50 L to 5.67 L). The average exergy efficiency is approximately 19%. Furthermore, an interpretable, rule-based AI controller optimized with the Coati algorithm was integrated; this controller suggested operating setpoints and revealed transparent decision thresholds. This work is the first systematic PDC study where three different hybrid nanofluids were examined and explainable artificial intelligence (XAI) was applied within a single framework. The results demonstrate that higher performance and more predictable operation are achievable for producing distilled water based on PDC.

1. Introduction

Today, energy is an increasingly important concept that affects everyone. In particular, the problems of global warming and environmental pollution caused by the fact that fossil fuels essentially meet the energy demand and the prediction that fossil fuels will run out in the not-too-distant future have led to the proliferation of renewable energy studies [1,2]. Renewable energy is derived from the energy flow available in continuous natural processes. Solar energy is considered to have the highest potential among existing renewable energy sources [3]. Parabolic dish concentrators (PDCs) are one of the most common ways to focus solar radiation [4]. The PDC directs the solar radiation and helps it accumulate in an absorber. With the accumulated high temperature, the thermal fluid in the receiver can be used in many heat processes. One of them is the distilled water production process. Researchers have extensively studied distilled water production with a PDC system.

Anil Kumar et al. studied a single-tilt solar still’s distilled water production performance with a parabolic concentrator. They produced distilled water in varying quantities of 3.2–4.1 L/day [5]. Amin et al. investigated the distilled water production performance of a tubular distillation device using a parabolic trough collector to which they added a heat exchanger. They produced 5.32 L of distilled water during their six-hour experiment [6]. Mohamed Elashmawy experimentally studied a tubular distillation system with a parabolic concentrator and solar tracking system. He carried out his experiments in Saudi Arabia. He obtained 3.53–4.71 L/day distilled water production for different weather conditions [7]. In their study, Zhoue et al. produced distilled and hot water in a solar hybrid system using a superconducting gas double-evacuated vacuum tube and heat storage device. Based on the thermodynamic behavior of water vapor in the evaporation–condensation process, they designed and tested a pilot plant for solar hot water and distilled water cogeneration systems. They produced an average of 6.5 L of distilled water daily during the summer in Jinan, China. Similarly, they obtained an average of 3.86 L of hot water for daily use [8]. Omara and Eltawil used dish concentrators for distilled water production in their study. Using a 1 m² parabolic dish, they produced 6.7 L of distilled water daily. They added PLC-controlled solar tracking to the system [9]. In their study, Prado et al. correlated the dish surface area with the distilled water capacity that can be produced. They found that a 1 m² parabolic dish produced 4.11–4.95 L of distilled water daily [10].

Researchers have used various nanofluid concentrations to improve the thermal performance of distilled water production applications using PDCs. Most of these studies have been performed numerically.

Table 1. Some studies using nanofluids in PDC systems.

Researchers	Fluids	Turbulence	Type/Prog.	Study
Bin Suja et al. [11]	Al2O3-water and CuO-water	SST k-ω turbulence model	ANSYS FLUENT 2020R1	High concentrator photovoltaic cells (HCPVw)
Ahnaf Pratik et al. [12]	Slytherin, Xceltherm, ParathermHR™ and water	Realizable k-ε	ANSYS Fluent	Enhancing the thermal performance of a PDC system
An Alnaqi et al. [13]	Oil-based hybrid nanofluid	Standard k-ε model	ANSYS Fluent	Enhancement of parabolic dish solar concentrator filled with an oil-based hybrid nanofluid
Navid Aslfattahi et al. [14]	Soybean oil-based MXene	-	Experimental	The authors studied a novel nanofluid (soybean oil-based MXene) in a solar dish concentrator.
Mohammad Hosseinzadeh et al. [15]	MWCNT-oil nanofluid	-	Experimental	Performance enhancement of nanofluid-based indirect solar cooker
Addisu Bekele et al. [16]	Nanofluids comprise Al2O3 and ZnO nanoparticles	-	Experimental	Performance investigation of PDC systems for solar cooking

lists some numerical and experimental studies of nanofluids used in systems with PDCs.

In terms of completeness, broader CFD developments (SMR, TES, PCM, tower systems) that are related to CSP but outside the scope of our focus on PDC desalination are briefly described below.

Aydın and Yücel conducted CFD modeling of a solar-assisted steam methane reformer (SMR). They integrated the CFD modeling with the SMR kinetic model. The effects of steam/carbon ratio and solar heat transferred to the reactor wall on hydrogen production were investigated [17]. Lou et al. studied the flow distribution by CFD to observe the system performance of optimized perforated baffles in a single-tank thermocline TES system applied to concentrated solar power (CSP). They improved performance by adding optimized perforated baffles [18]. Barreto et al. performed three-dimensional CFD modeling and thermal performance analysis of porous volumetric receivers connected to solar concentrator systems. They found that increased porosity and pore size significantly reduced pressure drop and increased thermal efficiency [19]. In their study, Sole et al. performed the geometric optimization of a heat storage system for PCM power plants using CFD. They geometrically optimized a phase change material (PCM) heat storage system for concentrating solar power applications. They applied the point-to-volume structure theory to find the optimal shape factor. They found that by optimizing the presented PCM system, the obtained power can be increased up to 200% [20]. Using CFD, Reddy and Nataraj conducted a thermal analysis of porous volumetric receivers of the concentrated solar dish and tower systems. They also studied the effects of different Gaussian flux, porosity, and thermal conductivity. They concluded that higher performance can be achieved if the receiver material has higher bulk conductivity and porosity [21]. Qiu et al. proposed a new parabolic channel for parabolic concentrating solar power systems. They aimed to reduce the wasted radiation in conventional receivers. They developed a numerical model and analyzed it in ANSYS 18.2. They have reduced the lost energy rate between 0.32 and 5.04% and increased the collector efficiency by 0.30–4.74% [22]. Wang et al., 2018, used a parabolic trough concentrator in CSP. They conducted experimental and CFD analysis studies to minimize the energy loss of parabolic trough collectors at high temperatures. For the receiver model they designed, the receiver surface temperature increased by an average of 15%, and the thermal oil temperature increased by 3% [23].

This study aims to address global distilled water demand by enhancing solar-powered distilled water production, specifically using PDC systems. Recognizing the limitations of current PDC systems’ low thermal efficiency due to conventional thermal oils, the research proposes utilizing hybrid nanofluids (silver (Ag), copper (Cu), alumina (Al₂O₃), and multi-walled carbon nanotubes (MWCNTs)) to improve heat transfer. Through numerical and experimental methods, the study is investigating the impact of these nanofluids at various concentrations on thermal performance, energy efficiency, and exergy analysis, seeking to increase distilled water production capacity and establish a new benchmark in renewable energy-based water treatment.

When CFD studies to improve the performance of PDC systems are examined, beneficial solutions have been produced with CFD analysis to reduce energy loss and increase thermal conductivity to increase system performance. The following shortcomings have been identified when analyzing the studies on distilled water production with solar energy systems in the literature:

• Parabolic dish concentrator systems consist of a single dish,
• Lack of applications using new generation hybrid nano (thermal oil, carbon nanotube, and metal alloy) working fluids to increase the thermal efficiency of conventional systems,
• Depending on the size of the system and the location where it is used, the daily distilled water production varies between 3 and 7 L,
• For the first time, three distinct hybrid nanofluids comprising carbon nanotube material and thermal oil were employed in a PDC system both experimentally and numerically in this study. MWCNTs doped with silver, copper, and aluminum oxide improved the system’s thermal performance in numerical analysis.

This research utilized a state-of-the-art distilled water PDC system with six solar dishes to address the identified gaps in the literature. Extensive numerical analysis was performed to enhance distilled water production using three innovative hybrid nanoprocessing fluids: Al₂O₃-MWCNT thermal oil, Cu-MWCNT thermal oil, and Ag-MWCNT thermal oil. This research identified the working fluid with superior performance in the system. Subsequently, experimental studies on distilled water production using the selected hybrid nanofluid were carried out, and the data obtained were in close agreement with the numerical analysis findings. Experimental results corroborate the numerical predictions and contribute significantly to understanding distilled water production methods, effectively filling the gaps identified in previous research.

The specific objective of this study is to compare the effects of three different hybrid nanofluids (experimental and numerical) in a multi-tank PDC system; to demonstrate energy-exergy performance using a validated CFD model; and to derive operational thresholds in a field-transferable manner using a rule-based, optimization-supported explainable AI framework.

With the rapid proliferation of artificial intelligence applications in energy systems, the need to explicitly establish interpretability and governance dimensions is emphasized. Recent review studies show that methods such as tree-based rules, SHAP/LIME-based explanations, and fuzzy rule bases strengthen decision-maker confidence and the transition from model to action, from building energy management to the grid level. However, in many applications, the methodological standard of explainability, data governance, and stakeholder communication remains fragmented [24]. This study follows the principles proposed in the literature to concretize explanations based on rules and operational thresholds, thereby establishing the “prediction–action” bridge in the application context.

Previous studies on PDC-based distillation systems have primarily focused on single nanofluids or binary mixtures in single-tray configurations, with limited validation/uncertainty analysis. While energy metrics were prioritized, exergy-based analysis and the derivation of actionable decision rules using interpretable AI were neglected. This study systematically compares three hybrid nanofluids within the same experimental–numerical framework, comprehensively addressing the aforementioned gaps in the literature through a multi-tray architecture, uncertainty-focused validation, mesh–cost trade-offs, and rule-based, optimization-supported explainable AI.

The original contribution of this study in the artificial intelligence component is that it goes beyond classic “black box” approaches and provides a hybrid, rule-based learner with the new coati optimization algorithm (COA), which can be directly converted into operational decisions and is explainable. The motivation for this study is to maintain optimal performance under variable solar irradiation, thermal inertia, and flow conditions in a PDC–hybrid nanofluidic distillation unit, while also providing rapid diagnosis, reliable adjustment, and ease of maintenance in the field. The proposed framework generates compact and controllable rules linked to environmental derived from sensor data, enabling the operator to directly answer the question, “How does the range of climatic parameters affect distilled water production?” COA identifies the most efficient operating regions by performing efficient searches in the parameter space; the rule-based layer then reduces these regions to simple, controllable expressions that can be used as decision thresholds. As a result, instead of deep learning-based models that promise high accuracy but are difficult to interpret, a decision support system with similar accuracy (e.g., 87.5%) and high transparency is achieved. This approach establishes a data-efficient, reliable, and sustainable optimization–control bridge to ensure scalable, network-independent, and resource-constrained distilled water production. This study examines a solar-driven system, not a “zero energy” system; the energy input is solar flux.

2. Materials and Methods

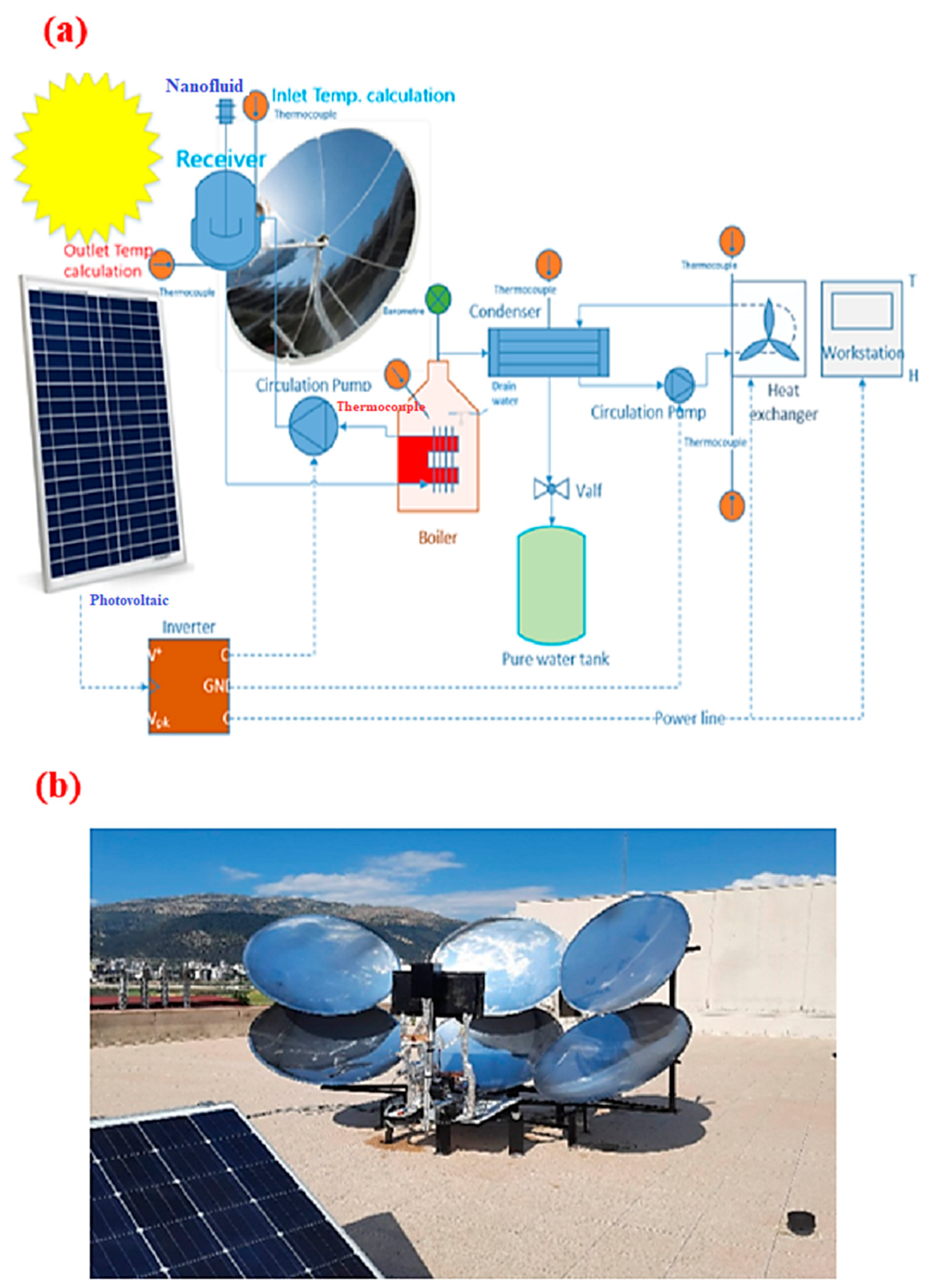
Figure 1 shows a schematic representation of the existing experimental setup and working principle.

Table 2. Some features of a distilled water generator with a parabolic dish concentrator.

Feature	Measurement
Dish concentrator diameter, D	1 m
Reflection field, An	0.785 m2
Focal distance, f	1.041 m
Edge angle, ψ	23.6°
Receiver dimensions	0.5 m·0.3 m·0.02 m
Reflection rate	0.9
Focal length to receiver	0.87 m

gives the specific and dimensional characteristics of the parabolic dish type (PDC) solar system. In the literature, the mirror reflectance ratio is greater than 0.90 in some studies.

There are six solar concentrators in the test set. In the experiments carried out in the existing system, the thermal oil (working fluid) is superheated in the solar receiver. The superheated oil (closed circuit) is sent to the boiling tank by a circulation pump, and the superheat is reduced by transferring its energy to water. This process takes place in three stages: the radiant heat is transferred from the sun and the heat is transferred in the internal flow from the oil to the water in the copper pipe in the boiling tank. At this stage, boiling heat transfer occurs on the tube’s outer surface. In the third stage, the evaporated water goes to the condenser and condenses into distilled water. The experiment starts to track the sun with the first sunrise (the system dynamically tracks the sun). The control and automation of the tracking system and the measurements are PLC-based. The power required for the PLC system and the circulation pumps is provided by the PV panel located next to the experimental set. In the literature, some studies have combined photovoltaic systems with PDC systems [25].

The distilled water produced in this study meets FDA (Food and Drug Administration) standards. According to these standards, the conductivity of distilled water at 25 °C should be no more than 1.3 µS/cm, and the total organic carbon (TOC) value should be no more than 500 ppb [26]. The pH value should be in the range of approximately 5.0–7.0, and the microbial load should not exceed ≤100 CFU/mL for purified water and ≤10 CFU/100 mL for water for injection (WFI) [27].

CFD analyses were performed in advance to observe the performance of the hybrid nanofluids used in the experimental set on the system. The method used for the CFD analysis is described below:

Momentum equation [28].

$$\rho \left(\overrightarrow{V}·\nabla \overrightarrow{V}\right)=-\nabla p+\nabla ·\left(\mu \nabla \overrightarrow{V}\right)$$

(1)

Continuity equation [28].

$$\nabla \overrightarrow{V}=0$$

(2)

Energy equation [28].

$$\rho c_p\left(\overrightarrow{V}·\nabla T\right)=k{\nabla }^{2}T$$

(3)

where $\overrightarrow{V}$ is the fluid velocity, P is the pressure, and T is the temperature. The symbols k, µ, c_p, and ρ refer to the thermal conductivity, dynamic viscosity, specific heat, and fluid density, respectively. The following equation expresses radiative transfer [28].

$${\displaystyle \frac{dI(\overrightarrow{r},\overrightarrow{s})}{ds}}+\left(a+{\sigma }_s\right)I\left(\overrightarrow{r},\overrightarrow{s}\right)=a{n}^2{\displaystyle \frac{\sigma T^4}{\pi }}+{\displaystyle \frac{{\sigma }_s}{4\pi }}{\int }_0^{4\pi }I(\overrightarrow{r},\stackrel{’}{\overrightarrow{s}})\Phi (\overrightarrow{s},\stackrel{’}{\overrightarrow{s}})d\stackrel{’}{\Omega }$$

(4)

The expressions in this equation are given respectively. $\overrightarrow{r}$ = position vector, = direction vector, $\overrightarrow{s}$ = scattering direction vector, σ_s = scattering coefficient, a = absorption coefficient, s = path length, n = refractive index, σ = Stefan–Boltzmann constant (5.669 × 10⁻⁸ W/m²·K⁻⁴), T = local temperature, Φ = phase function, I = radiation intensity, Ω’ = solid angle.

The initial and boundary conditions used in the CFD analysis for the receiver are given in

Table 3. Initial and boundary conditions for receiver numerical analysis method.

Definition	Description
Flow profile	Laminar
Energy	Solved
Gravity	Active (y, −9.81 m/s2)
Receiver side surfaces	Insulation
Energy analysis residuals	10−9
Other residues	10−6
Receiver material	Aluminum
Velocity and pressure equation	Simple (All discretizing second order upwind)
Heat flux	P1 module (solar ray tracing)
Inlet temperature	Ti = constant (373 K)
Output pressure	0 Pa
Mass flow	Fixed
Direction indication method	Normal to borderline
Calculation	Steady

. Within the study’s framework, it was determined that changing the working fluid in the circuit to a fluid with a better thermal capacity could increase the distilled water generator’s efficiency. The equations used to study the system’s experimental results are given below. The calculations are based on the assumption of uniform heat dissipation.

Radiation Calculation

The amount of radiation in PDC systems is calculated using the following equations.

$$Q_s=A_a·G_b$$

(5)

“C” The reflectivity of the concentrator is the ratio of the available aperture to the receiving area “A_a”:

$$C={\displaystyle \frac{A_a}{A_r}}$$

(6)

The proportion of heat absorbed by the receiver is calculated using the optical efficiency (η_opt) of the absorber:

$${Q_{abs}=\eta }_{opt}·Q_s$$

(7)

Thermal Analysis

The thermal analysis model developed is based on the energy balance at the receiver. The absorbed solar radiation is divided into useful energy and thermal losses to the environment:

$$Q_{abs}=Q_u+Q_{loss}$$

(8)

The useful heat output is calculated from the energy balance in the fluid volume as follows [29].

$$Q_u=\dot{m}·c_p·\left(T_{out}-T_{in}\right)$$

(9)

Thermal losses consist of radiation and convection heat losses:

$$Q_{rad}=A_{ro}·{\epsilon }_r·\sigma ·\left({T_r}^4-{T_{am}}^4\right)$$

(10)

$$Q_{conv}=A_{ro}·h_{air}·\left(T_r-T_{am}\right)$$

(11)

The following equation calculates the convection heat transfer coefficient between the absorber and the medium [30].

$$h_{air}=2.8+3·V_{air}$$

(12)

The energy efficiency of the receiver is calculated as the ratio of proper heat to available solar radiation:

$${\eta }_{th}={\displaystyle \frac{Q_u}{Q_s}}$$

(13)

Another indicator used to describe the efficiency of solar energy is the coefficient of performance (COP). The receiver’s COP can be expressed in the following equations.

$$COP={\displaystyle \frac{Q_u}{W_p}}$$

(14)

Here, W_p is the pump power, which can be calculated as follows: in the following equation, P_p is the pump power (Watt), and t is the time (s).

$$W_p=P_p·t$$

(15)

Equation (13) was used for the energy efficiency of the installed PDC distilled water production system, and the following calculations were made for the exergy efficiency. Exergy analysis is frequently performed, mainly in solar energy systems. The exergy output E_xo [31], exergy input E_xi [32], and exergy efficiency ɳ_ex [33] of the system can be calculated by Equations (16)–(18), respectively.

$$E_{xo}=\dot{m}·c_p·\left({T_{out}-T_{in}-T}_{am}·ln\left[{\displaystyle \frac{T_{out}}{T_{in}}}\right]\right)-\dot{m}·T_{am}·{\displaystyle \frac{∆P}{\rho ·T_{fm}}}$$

(16)

$$E_{xi}=Q_s·\left[1-{\displaystyle \frac{4}{3}}\left({\displaystyle \frac{T_{am}}{T_{sun}}}\right)+{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{T_{am}}{T_{sun}}}\right)}^4\right]$$

(17)

$${\eta }_{ex}=\sum E_{xo}/\sum E_{xi}$$

(18)

For the uncertainty of the parameters calculated in the system, Holman [34] developed Equation (19) [35].

$${\beta }_R={\left[{\left({\displaystyle \frac{\delta R}{\delta x_1}}{\beta }_1\right)}^2+{\left({\displaystyle \frac{\delta R}{\delta x_2}}{\beta }_2\right)}^2\dots {\left({\displaystyle \frac{\delta R}{\delta x_n}}{\beta }_n\right)}^2\right]}^{0.5}$$

(19)

β₁, β₂, β₃, …, β_n are the uncertainties in the independent variables, and β_R is the total uncertainty in the results. R is a function of the independent variables x₁, x₂, x₃, … x_n. The maximum uncertainties of the solar radiation and oil flow rate calculated previously in the current system are 0.5% and 2%, respectively. The uncertainty of the system elements is given in

Table 4. Measurement devices and accuracy rates.

Parameter	Measurement Device	Model	Country	Accuracy Rate
Solar radiation	Radiation meter	CEM DT-1307	Türkiye	±10 W/m2
Air velocity	Anemometer	BENETECH	China	±0.1 m/s
Air temperature	Thermometer	GM8901	China	±0.1 °C
Fluid temperature	Thermocouple	Elinco- K-Type	India	±0.1 °C
Volumetric Flow	Oil flow meter	Gentek	Türkiye	±0.1 L/min
Weight	Load cell	HX711	China	±0.5 g/s

.

The pyrometer was verified by short-term field calibration against a reference-class sensor. K-type thermocouples were two-point calibrated at 0 °C and ~100 °C. The flowmeter was verified using the gravimetric (time-mass) method. The balance was checked using traceable reference weights.

In the last 5 years, many scientists have used nanofluids in desalination systems to increase thermal performance [36]. This paper used three different hybrid nanofluids containing carbon nanotube material and thermal oil experimentally and numerically for the first time in a PDC system. In numerical analysis, silver-, copper-, and aluminum oxide-doped MWCNTs increased the system’s thermal performance. The thermophysical properties of the hybrid nanofluid obtained by mixing thermal oil and (Ag/Cu/Al₂O₃) + MWCNTs) The different concentration ratios of 0.3 wt.%, 1 wt.%, 2 wt.%, and 4 wt.% as the working fluid to be used in the distilled water production system are given in

Table 5. Thermophysical properties of the components that will make up the hybrid nano-doped work fluid.

Feature	Thermal Oil (100–150 °C)	Cu Nanoparticles	Ag Nanoparticles	Al2O3 Nanoparticles	MWCNT
Density (kg/m3)	772	8933	10,500	3970	2100
Specific heat capacity (kJ/kg·K)	2.619	0.385	0.235	0.765	0.711
Thermal conductivity (W/m·K)	0.125	401	429	40	1500

.

Figure 2 shows the schematic preparation of the hybrid nanofluid. The viscosity of the hybrid nanofluids targeted for use in this study was calculated using the following equation [37]. Esfe et al. experimentally investigated the thermal conductivity and dynamic viscosity of Ag-MgO/water hybrid nanofluid [38]. They compared their experimental results with five dynamic viscosity equations frequently used in the literature. The best result was obtained by Chen et al. [37]. In this study, the viscosity, thermal conductivity coefficient, and specific heat parameters to be used in the thermal analysis of the working fluid by the CFD method were calculated by Equations (20)–(23).

Nanofluid preparation procedure

The following procedures were followed in the preparation of the nanofluid to be used as the working fluid in the experiments:

• A total of 0.5 wt.% Ag and 0.1 wt.% MWCNTs (multi-walled carbon nanotubes) nanomaterials were tried in 5 L of thermal oil in an ultrasonic mixer and precipitation was observed.
• The work was then continued by diluting the nanofluid.
• No precipitation was observed in the mixture of 0.3 wt.% Ag and 0.1 wt.% MWCNT + 5 L of thermal oil during the 20-day waiting period.

Figure 3 shows the preparation processes of hybrid nanofluids containing different concentrations of Ag (silver) and MWCNT and the stability of the resulting mixtures; this image provides critical information about the mixing processes. The figure clearly shows that precipitation was observed during the preparation process of hybrid nanofluids containing different ratios of Ag and MWCNT, with precipitation occurring after a certain period in the mixture containing 0.5 wt.% Ag and 0.1 wt.% MWCNT, but no precipitation was observed in the mixture containing 0.3 wt.% Ag and 0.1 wt.% MWCNT for 20 days. This reveals that the ratios of 0.3 wt.% Ag and 0.1 wt.% MWCNT are optimal in terms of blend stability and offer a more suitable formulation for long-term use.

In this study, the hybrid nanofluid scope was designed in two planes: In the Experimental section, the Ag–MWCNT hybrid nanofluid prepared on a thermal oil base was used in the 0.3 wt.% Ag + 0.1 wt.% MWCNT composition, which showed non-settling behavior after stability and dispersibility tests. In the computational (CFD) section, three hybrid nanofluids—Ag–MWCNT, Cu–MWCNT, and Al₂O₃–MWCNT—were investigated at 0.3, 1, 2, and 4 levels as the total nanoparticle mass fraction (wt.%) for comparative analysis. Experimental data were used as a reference to validate the numerical model; after validation, the entire hybrid set was parametrically scanned under the same boundary conditions and property relations. This arrangement preserves the field reality of the experimentally tested fluid, while computational comparative analysis reveals the performance potential of the other hybrids.

In general, the thermal conductivity of nanofluids is determined by experiments or simulation models as well as from correlations, where the thermal conductivity of the selected working fluid is calculated by an empirical correlation based on temperature, volume fraction, and particle conductivity [39].

$${\displaystyle \frac{{\mu }_{nf}}{{\mu }_{bf}}}=\left(1+10.6\phi +{\left(10.6\phi \right)}^2\right)$$

(20)

$$k_{nf}\left(T,\phi ,k_{bf}\right)=\left(3.9\times {10}^{-5}T-0.0305\right){\phi }^2+\left(0.086-1.6\times {10}^{-4}T\right)\times \phi +3.1\times {10}^{-4}T+0.129-5.77\times {10}^{-6}{k}_{bf}-40\times {10}^{-4}$$

(21)

This study calculated the hybrid nanofluid’s density (ρ_nf) and specific heat capacity (c_nf).

$${\rho }_{nf}={\phi }_1{\rho }_{p1}+{\phi }_2{\rho }_{p2}+\left(1-\left({\phi }_1+{\phi }_2\right)\right){\rho }_{bf}$$

(22)

$$c_{nf}={\displaystyle \frac{{\phi }_1{\rho }_{p1}{c}_{p1}+{\phi }_1{\rho }_{p2}{c}_{p2}+\left({1-\phi }_1-{\phi }_2\right)c_{bf}}{{\rho }_{nf}}}$$

(23)

Fourier transform infrared spectroscopy (FTIR) spectrums of silver nanoparticles (AgNPs) show a high transmittance percentage across most of the wavenumber range, indicating minimal absorption in the infrared region (Figure 4A). A significant absorption band is observed at the lower wavenumber region, around 500 cm⁻¹, which is attributed to the Ag-O stretching vibration. This suggests the presence of silver oxide on the nanoparticle surface, likely due to partial oxidation of silver. The absence of strong peaks in the higher wavenumber region indicates that there are no significant organic functional groups attached to the nanoparticles.

The particle size of silver nanoparticles was determined using the dynamic light scattering (DLS) method. Measurements were performed using the PSS-Nicomp 380 ZLS Zeta Potential/Particle Sizer (Particle Sizing Systems, Santa Barbara, CA, USA) device. The samples were dispersed in a suitable solvent prior to measurement to obtain a homogeneous suspension. The device calculates the size distribution using light scattering data resulting from the Brownian motion of the particles. Initial evaluations showed that the standard deviation value was greater than 3, and therefore, the results were obtained using the Nicomp algorithm instead of the Gaussian distribution. The Nicomp method provides a more accurate particle size distribution thanks to its advantage of being able to resolve multiple peaks. The measurement results were reported as a density-weighted distribution, and the average diameter and polydispersity index were evaluated. In addition, the device software was set to automatically adjust the baseline, thereby increasing data reliability. Thus, the size distributions of silver nanoparticles were determined reliably and in accordance with standards.

Figure 4B provides information about the descriptive statistics, properties, and potential applications of silver nanoparticle (AgNP) size distribution. The mean particle size is calculated as 53.61 nm and the median value is 59.22 nm. The standard deviation of 31.95 nm indicates that AgNP has a polydisperse structure. It is understood that nanoparticles have different size distributions in the fluid. This distribution indicates that AgNP may have a behavior that may affect the heat transfer properties in solar energy conversion applications. Although the mean particle diameter is around 50–60 nm, it is understood that larger clusters tend to be present, as seen in the graph. Such a distribution may affect properties such as thermal conductivity, optical absorption, and reaction kinetics in applications such as solar water distillation.

The findings emphasize the importance of particle size control in improving performance, stability, and efficiency in various nanotechnology-based applications. Nicomp distribution is more flexible, capable of modeling asymmetric and multimodal distributions, making it ideal for polydisperse systems like nanoparticle suspensions. Nicomp distribution uses cumulative analysis and dynamic light scattering data, providing a more accurate representation of real-world particle size variations. Given the broad size range and polydisperse nature of the AgNPs in this study, their size distribution was determined using the Nicomp distribution, ensuring a more precise and realistic analysis of particle size variations.

Analysis via Coati Optimization and Rule-Based Method

In addition to experimental and numerical investigations, this study incorporates an artificial intelligence (AI)-based analysis to optimize system performance and provide interpretable decision support. A rule-based method was integrated to enhance transparency by explicitly identifying the influence of operational parameters on system efficiency. For this purpose, the recently developed coati optimization algorithm (COA) [40] was employed as the core optimization engine, offering a balance between exploration and exploitation in the search for optimal rule sets.

Coati Optimization Algorithm

COA is a novel bioinspired meta-heuristic algorithm that basically mimics the behavior of raccoon animals in nature [40]. This algorithm solves optimization problems by simulating the coati’s behavior of hunting (e.g., hunting iguanas) and escaping from dangers. The basic logic of COA is based on two main phases: exploration and exploitation. The exploration phase refers to the algorithm’s ability to traverse the search space to find the global optimum. Here, coati provides a wide variety of solutions by avoiding danger or exploring new areas. The exploitation phase focuses on quickly obtaining the best solution by performing exhaustive searches on the found solutions. Coati’s natural instinctive behavior tries to balance these two phases. For example, when danger is detected, the coati at the edge will quickly move to the safe zone, while the coatis in the middle will randomly move closer to the others. Each coati individual in the algorithm represents a potential solution in the solution space of the problem.

The basic stages of the algorithm are as follows:

a- 

Creating the Initial Population

The algorithm starts with a randomly generated initial population of coati. The position of each coati represents the values of the decision variables in the problem. This initial population consists of candidate solutions distributed over the entire search space.

b- 

Objective Function Evaluation

The position of each coati in the initial population is given as input to the objective function (fitness function) of the problem. This results in an objective function value for each coati, which determines the solution quality of that coati. The coati with the best objective function value in the population is designated as the iguana’s location.

c- 

Population Splitting

The population is divided into two groups: the tree-climbing coati that go after the iguana and the ground coati that wait for the iguana to fall to the ground. This grouping allows the algorithm to both discover the best available solution (exploitation) and to explore the search space more broadly (exploration).

d- 

Location Updates

Both groups of coati update their positions with different strategies:

Tree Climbing Coati: This group moves towards the iguana’s position. This movement is modeled by mathematical equations and allows an intensive study of the search space around the best solution.

Coati Waiting on the Ground: The iguana is simulated to fall to the ground and they move according to this new random location. This helps the algorithm to explore different search regions and avoid local optima.

e- 

Updating the Best Member

After the location updates, the new objective function values of the population are recalculated. Based on these new values, the coati with the best objective function value for that iteration is designated as the new iguana. This cycle continues until a stopping criterion (such as a certain number of iterations or reaching a desired solution quality) is met.

Important Advantages

• It takes an adaptive approach to the solution search process by mimicking coati’s natural behavior.
• Position updates and a hazard detection mechanism help prevent the algorithm from getting stuck at local minima.
• The chaos sequence mechanism ensures a wider and higher quality distribution of initial positions, the adaptive T-distribution increases the diversity of individuals with low fitness values, and the alert update mechanism ensures that the algorithm searches efficiently in the domain.
• It has been used in many constrained optimization problems, such as industrial engineering problems.

The pseudo-code of the coati optimization algorithm is given in Algorithm 1.

Algorithm 1. The pseudo-code of the coati optimization algorithm
Input	Objective function f(X) Bounds for decision variables: Xmin, Xmax Population size: N Maximum number of iterations: MaxIter
Output	Best solution Xbest Best objective value Fbest
1.	Initialize population Xi for i = 1 to N using chaotic sequences within bounds
2.	Evaluate fitness Fi = F(Xi) for each individual
3.	Set Xbest as the individual with the best fitness value
4.	For t = 1 to MaxIter do:
4.1.	For each coati Xi in the population do:
4.1.1.	If Xi is at the edge (risk zone):
	Calculate distance to safe zone
	Move Xi towards safe zone
4.1.2.	Else (Xi is in the middle of population):
	Select a random coati Xj
	Update Xi position using both exploitation and exploration based on Xbest and Xj
4.1.3.	Apply boundaries to ensure Xi stays within [Xmin, Xmax]
4.2.	Evaluate updated fitness Fi = F(Xi)
4.3.	Update Xbest and Fbest if improved solution found
5.	Return Xbest and Fbest

Proposed Coati-Based Rule Mining System

In some classification methods, the relationship between the result and the data may not be clear. Even if the result is correct, the factors that influence the result remain unclear, making it difficult to understand the working principle of the method [41]. Such methods are often referred to as black boxes. As the number of parameters increases, especially in data sets containing numerical information, it becomes difficult to reveal the relationships between parameters, and this complexity increases even more in large data sets. Rule mining aims to discover the rules that define the relationships in the data set [42]. In this process, it is clearly determined which parameters in the data set affect the result and in which value ranges these parameters are effective. Thus, the understandability of the results is increased and a transparent decision mechanism is created on the data set. In this study, a specially adapted COA is used to solve the rule mining problem. The innovative aspect of the proposed approach is that it is the first time that the COA, which has been proven in the literature, is applied in the rule mining domain. COA’s optimization mechanism, which mimics the behavior of coati in nature, ensures that solutions are balanced in both the exploration and exploitation phases, allowing for the discovery of optimal or near-optimal rules. In rule-based methods, rule extraction takes place by expressing patterns in the dataset in the form of certain condition-consequence relationships. A rule is usually in the format “If [conditions] then [result]”. Conditions define certain value ranges or thresholds of attributes. This process determines which attributes are to be included in the rule and which value ranges they are to be represented by. Thus, rule sets derived from the dataset provide explainability in classification and decision support systems.

Coati is based on a different representation format for each solution in a population of $n$ individuals. A $d$ (number of attributes) dimensional $x_i$ solution consists of three subcomponents ($x_i={\left\{y\right.}_i^t,y_i^a,\left.y_i^h\right\},i=\mathrm{1,2},\dots ,n$). ${\left\{y\right.}_i^t,y_i^a,\left.y_i^h\right\}$ holds a binary value for each attribute in the solution. This value determines whether an $j$. attribute should be added to the rule or not. In the initial population, $y_i^t$ values are assigned with a random number generator function ($y_i^t=random\left(\mathrm{0,1}\right)$). They are then compared against a predefined threshold value ($\delta ϵ \left[\mathrm{0,1}\right]$) (Equation (24)) to select the attribute.

$$y_j=\left\{\begin{array}{c}1,if y_j^t>\delta (feature is included in the rule)\\ 0,else (feature is not included in the rule)\end{array}\right.$$

(24)

$y_i^a=(y_1^a,y_2^a,\dots ,y_d^a)$ denotes the lower limit of each attribute for the rules in the solution $y_i^h=(y_1^h,y_2^h,\dots ,y_d^h)$ denotes the upper limit of each attribute for the rules in the solution. The lower and upper thresholds in the rules were initially generated randomly; however, during the iterations, they were progressively updated and finalized according to the dataset values. Consequently, the thresholds are ultimately data-driven, without the involvement of domain expertise. The value space of an attribute is defined in the interval $[N^a,N^h$]. In each iteration, the lower and upper limits must satisfy the condition of Equation (25).

$$N^a\le y_j^a\le y_j^h\le N^b$$

(25)

During the iterations, each candidate solution updates its $y_i^t,y_i^a,y_i^h$ values. At the end of the process, all attributes that satisfy the $y_j=1$ condition are included in the $x_i$ rule of the corresponding solution. This calculation is used to determine the fitness value of the objective function. In this study, the accuracy of the classification is chosen as the objective function. For each solution x_i, each candidate rule, classification performance was evaluated using standard metrics (TP, TN, FP, FN), from which accuracy was calculated as the objective function. The algorithm operates in two phases: training and testing. In the training phase, COA is run on the training dataset to obtain the rule sets. These rules are then re-evaluated on the test dataset and analyzed using the same criteria to obtain the final performance results.

The coati optimization algorithm (COA) is a recently developed and effective metaheuristic optimization method. It has been chosen in this study for its robust performance in balancing exploration and exploitation phases. Notably, COA is applied to rule mining for the first time, enabling both high accuracy and interpretable results. These numbers are obtained by evaluating the two parts of the rule separately, as shown in

Table 6. TP, TN, FP, and FN calculation rules in rule-based classification.

“IF” Unit	“THEN” Unit	The Operation
True	True	Add 1 (one) to TP
False	False	Add 1 (one) to TN
True	False	Add 1 (one) to FP
False	True	Add 1 (one) to FN

. These values are used to calculate the “accuracy” ratio, which is used as the objective function

$$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(26)

where

True Positive (TP): If both the “If” (left-hand side) and “Then” (right-hand side) parts of the rule are true, this data sample is considered a true positive.

True Negative (TN): If both the “If” and “Then” parts of the rule are false, this data sample is considered a true negative.

False Positive (FP): If the “If” part of the rule is true, but the “Then” part is false, this is classified as a false positive.

False Negative (FN): If the “If” part of the rule is false, but the “Then” part is true, this data sample is classified as a false negative.

The operation of the algorithm consists of two phases: training and testing. In the first phase, the coati algorithm is adapted to the fitness values and run on the training data sets. The rules obtained at the end of the iterations of the algorithm are retested on the test datasets and the test data are analyzed with the same evaluation criteria. The results obtained relate to the test data set experiments.

Data Set

The dataset used in this study consists of numerical data obtained from multi-sensor measurements and environmental variables. There are 14 independent attributes and 1 dependent variable (class label) in the dataset. Attributes can be analyzed in three main groups:

• Thermal measurements (T1–T9): They represent temperature or power-based measurements obtained from various sensors.
• Pressure parameters (P1–P2): Represent metrics related to the operational outputs of the system.
• Environmental factors:
  • Solar Radiation (solar radiation, W/m²),
  • Ambient Temperature (ambient temperature, °C),
  • Wind Speed (wind speed, m/s).

The class attribute, the dependent variable, categorizes the data into three categories: The data set used in the study has been classified based on experimentally obtained distilled water production values. In this context, three separate classes have been defined to characterize system performance: the amount of distilled water produced for the H (High) class is 25 g and above, for the M (Medium) class it is 25 g > M ≥ 10 g, and for the L (Low) class it is less than 10 g. Thus, this classification based on the amount of distilled water obtained more clearly reveals the effect of environmental and operational parameters on production capacity and allows the rules established to be directly related to quality parameters. In addition, the balanced distribution among the classes prevents the learning algorithms from producing biased results. Sample records are given in

Table 7. Sample records from the data set.

T1	T2	T3	T4	T5	T7	T8	T9	P1	P2	Solar Radiation	Ambient Temperature	Wind Speed	Class
118.74	117.44	151.59	111.22	66.89	74.09	66.27	65.11	35.23	35.33	680	31.4	2.1	L
111.27	121.67	174.37	118.65	80.92	86.1	80.51	78.67	36.24	35.69	682.3	31.77	2.08	L
109.29	123.84	168.83	120.25	90.23	93.68	88.72	88.13	36.69	36.11	685	32.13	2.07	L
111.39	128.99	159.16	121.08	96.56	98.8	94.69	94.71	37.09	36.24	687.2	32.5	2.05	M
113.99	131.67	160.75	130.05	100.48	103.39	98.89	98.45	37.34	36.44	690	32.87	2.03	M
117.36	130.82	167.26	140.18	103.98	107.88	102.36	98.83	37.37	36.65	692.7	33.23	2.02	M
118.14	128.05	160.36	138.81	104.91	109.13	102.97	98.86	37.44	36.66	695	33.6	2	H
113.19	119.71	149.58	133.2	102.42	105.68	99.5	99.27	37.24	36.43	854.1	37.57	3.55	H
109.49	117.08	147.44	136.68	102.19	104.99	99.55	99.23	37.15	36.32	861.7	37.8	3.7	H

. This dataset provides a suitable basis for classifying multidimensional measurement data and extracting interpretable rules. Especially when used in combination with a COA-based rule mining approach, it can be clearly and transparently revealed in which value ranges the measurements obtained from the sensors play a critical role in the classes.

AI Experiments

In the experimental studies, one dataset was used. This dataset has a total of 14 attributes and the data is categorized into three different classes: high, medium, and low energy consumption. The proposed COA-based rule mining approach is compared with two different groups of methods:

• Classical rule extraction methods and classification algorithms
  • Rule extraction methods: JRIP, FURIA, OneR, ConjunctiveRule, DecisionTable, ZeroR
  • Classification methods: Naive Bayes, support vector machine (SVM), KStar, Vote, HyperPipes, J48, RandomTree
• Advanced methods
  • RbA-SFO (rule-based sunflower optimization) [43]
  • Multi-layer perceptron (MLP)
  • TabNet
  • NODEs (neural oblivious decision ensembles)
  • Transformer-based classifier

80% of the dataset was used for training and 20% for testing. Candidate rules were obtained by running the proposed method on the training data. Since a large number of rules can be extracted during the experiments, only a certain number of rules with the best performance are selected in each experiment and evaluated in the testing phase. The success of the rules was measured using the accuracy metric. The accuracy value of each candidate rule was calculated based on comparisons of the test dataset. All applications were performed using the Python 3.10 programming language on a computer with an Intel(R) Core(TM) i5 processor and 8.00 GB memory capacity. Other parameters used in the COA-based approach are presented in

Table 8. Parameters used in coati optimization algorithm.

Parameter	Value
Population Size	50
Max. Iteration	200
Experiment Repetition	20
Leader Fraction	0.15
Follow Coefficient (β)	1.6
Exploration Coefficient (γ)	2
Local Step Size (δ)	0.2
Climb Probability	0.1
Climb Strength	0.5

.

3. Results

Numerical analysis was first performed to demonstrate the applicability of the presented method to the experimental system. Then, the hybrid nanofluid + thermal oil work fluid with the highest receiver outlet temperature was determined. The hybrid nanofluid produced was tested in the experimental set. The first part of the Results Section mentions numerical analysis and results. In the second part, experimental applications and comparative results are noted.

In this study, we present the receiver geometry and the receiver mesh model of the system in Figure 5. We believe that a clear understanding of these elements is crucial for understanding the system. In this figure, all dimensions are provided in millimeters.

Different element sizes were used to determine the optimal mesh for the model analysis. Experiments were performed by reducing the minimum element size by 25% each time to monitor processor performance.

Table 9. Mesh statistics.

Model	Number of Elements	Max. Mesh and Norm. Element Size (mm)	Min. Element Quality	Grow Rate	Max. Skewness	Average Skewness	Min. Orthogonal Quality	Average Orthogonal Quality	Number of Boundary Layers
1	7,318,741	1.2	0.15	1.1	0.79	0.19	0.20	0.81	8
2	4,233,458	1.5	0.086	1.1	0.79	0.19	0.20	0.81	8
3	2,420,018	1.9	0.05	1.1	0.79	0.19	0.20	0.81	8

presents the statistical data of different mesh models and compares the quality and performance of the mesh structures used in the numerical analysis. This table plays a critical role in evaluating the accuracy and quality of the analysis of the meshes used in the numerical analysis of the receiver model of the parabolic dish concentrator (PDC) system. The table lists the parameters of the three models: number of elements, maximum mesh size, minimum element quality, growth rate, maximum and average skewness, minimum and orthogonal quality, and number of boundary layers. Although Model 1 has the highest number of elements (7.318,741), its minimum element quality is 0.15, which is higher than the other models. However, although Model 2 has fewer elements (4.233,458), the minimum element quality is measured as 0.086, which provides enough precision for a more complex and detailed analysis. Model 3 has the lowest number of elements (2.420,018); the minimum element quality remains the lowest at 0.05. It is understood that this model requires less computational power but offers less precision in the analysis. Model 2’s minimum element quality, skewness value of 0.79, and orthogonal quality of 0.20 are within acceptable limits in the analysis. Furthermore, the required precision in the receiver model is maintained using eight boundary layers.

The mesh independence study showed that Model 2 produced only negligible differences in key outputs such as outlet temperature, useful heat flux, and exergy efficiency compared to the finer mesh Model 3; these differences remained within both the numerical convergence tolerance and the experimental uncertainty band. However, Model 3 significantly increases computational time and memory requirements. Model 2 maintains accuracy by providing sufficient wall resolution and cell quality thresholds, while enabling comprehensive parameter scans at a reasonable cost.

The most striking result of Table 9 is the selection of Model 2 as the most appropriate mesh model. This model improves the accuracy of the analysis by providing a sufficient number of elements and appropriate mesh quality while keeping the computational load at a reasonable level. The higher number of elements of Model 1 increases the solution time, while the lower number of elements of Model 3 may negatively affect the accuracy of the solution. Therefore, Model 2 was chosen as the model that provides the best trade-off between accuracy and computational time. This table highlights the importance of the grid used to improve the reliability of the numerical analysis. Careful selection of the grid to ensure that the receiver model operates with optimal performance enhances the accuracy of the thermal analysis, allowing a more accurate calculation of the system efficiency.

Figure 6 is a graph visualizing the effect of the number of mesh elements on the numerical analysis results and solution independence, which helps to assess the reliability of the results obtained for different mesh models. The graph shows how the receiver outlet temperatures change as the number of elements increases, and this analysis reveals that the number of elements does not cause a significant change in the solution results after reaching a certain level. Initially, there is a noticeable increase in the output temperatures as the number of grid elements is increased, but after a certain number of elements, the temperatures stabilize, and the solution becomes mesh-independent. This is observed when the number of elements reaches around 4 million, and the graph curve begins to flatten out, indicating that adding more elements does not significantly improve the analysis results and reduces the uncertainty in the solution. Model 2 was chosen as it has the optimum number of elements and solution accuracy and is the most appropriate model that minimizes computational time and cost while maintaining solution accuracy. This graph emphasizes that the number of mesh elements should be carefully adjusted to achieve a balance between computational time and analysis accuracy and contribute to reliable, accurate, and efficient analysis.

Numerical Analysis Results

In this study, since the flow conditions inside the receiver remained below the transition threshold when experimental flow rates and characteristic dimensions were considered, the basic solutions were performed using the laminar flow model. To accurately capture near-wall heat transfer, a refined mesh structure (y⁺ ≈ 1) was used in the boundary layer. In contrast, radiative heat transfer was solved using the P1 approach due to the accuracy-computational cost balance. To exclude possible turbulence effects, sensitivity studies were performed with SST k–ω (and k–ε for comparison); since deviations below 5% were observed in the main outputs (heat flux, outlet temperature, exergy terms), the laminar model was preferred in the main results. This choice enabled a comprehensive parameter sweep by reducing the computational cost without any significant loss in accuracy.

The receiver model was subjected to numerical analysis of the hybrid nanofluids under the same conditions.

Table 10. Numerical analysis output temperatures for the receiver when the nanofluids are mixed at 1 wt.%.

Time	Receiver Inlet Temperature (K)	Receiver Outlet Temperature (K) [1% Al2O3-MWCNT]	Receiver Outlet Temperature (K) [1% Cu-MWCNT]	Receiver Outlet Temperature (K) [1% Ag-MWCNT]
10.00	373.15	381.16	381.47	381.57
10.30	373.15	381.62	382.02	382.29
11.00	373.15	381.91	382.71	382.9
11.30	373.15	382.69	383.14	383.33
12.00	373.15	382.92	383.45	383.68
12.30	373.15	383.11	383.58	383.78
13.00	373.15	382.99	383.57	383.75
13.30	373.15	382.88	383.34	383.54
14.00	373.15	382.5	382.62	383.1
14.30	373.15	382.04	382.46	382.64
15.00	373.15	381.15	381.78	381.84
15.30	373.15	380.65	381.01	381.16
16.00	373.15	379.38	379.92	379.97
16.30	373.15	378.8	379.07	379.18
17.00	373.15	377.28	377.65	377.75

shows the effect of mixing different hybrid nanofluid types with 1 wt.% thermal oil on the receiver outlet temperatures and comparatively evaluates the thermal performance of Al₂O₃-MWCNT, Cu-MWCNT, and Ag-MWCNT-based nanofluids. The table shows that the receiver inlet temperature is constant at 373.15 K, and the outlet temperatures vary depending on the type of nanofluid at specific periods. The results reveal that the Ag-MWCNT-based hybrid nanofluid provides the highest outlet temperatures at all periods, with Cu-MWCNT coming second and Al₂O₃-MWCNT third. For example, at 12 h, the receiver outlet temperatures were 382.92 K for Al₂O₃-MWCNT, 383.45 K for Cu-MWCNT, and 383.68 K for Ag-MWCNT. These results indicate that silver nanoparticles (Ag) have high thermal conductivity, increasing the heat transfer efficiency and resulting in higher outlet temperatures than other nanofluids. An important finding of Table 10 is that the performance differences between the hybrid nanofluid types are significant even at 1% concentration, proving that the nanofluid components directly affect their performance in thermal systems.

Although there have been studies in the literature where nanomaterial volume concentration ranging from 1% to 10% [44], the highest nanomaterial total volume concentration in this study was 4.1%. In connection with

Table 11. Numerical analysis results of hybrid nano Ag-MWCNT-thermal oil mixing.

Time	Receiver Inlet Temperature (K)	Receiver Outlet Temperature (K) [0.3% Ag-0.1% MWCNT]	Receiver Outlet Temperature (K) [1% Ag-0.1% MWCNT]	Receiver Outlet Temperature (K) [2% Ag-0.1% MWCNT]	Receiver Outlet Temperature (K) [4% Ag-0.1% MWCNT]
10.00	373.15	381.1	381.57	382.4	384.06
10.30	373.15	381.77	382.29	383.27	385.43
11.00	373.15	382.4	382.9	384	386.2
11.30	373.15	382.86	383.33	384.58	387.08
12.00	373.15	383.2	383.68	384.85	387.19
12.30	373.15	383.29	383.78	385.54	388.36
13.00	373.15	383.25	383.75	385.02	387.96
13.30	373.15	383.06	383.54	384.76	387.205
14.00	373.15	382.7	383.1	384.02	385.86
14.30	373.15	382.21	382.64	383.76	385.53
15.00	373.15	381.2	381.84	383	385.18
15.30	373.15	380.79	381.16	382.1	383.98
16.00	373.15	379.25	379.97	381.04	383.72
16.30	373.15	378.9	379.18	380.1	381.94
17.00	373.15	377.4	377.75	378.65	380.45

, it can be seen that Table 10 only compares different hybrid nanofluids at 1% concentration. In comparison, Table 11 examines the performance of the same Ag-MWCNT nanofluid at different concentrations from 0.3 wt.% to 4 wt.%. While Table 10 shows which type of hybrid nanofluid is more efficient, Table 11 analyzes the effect of this superior-performing nanofluid at different concentration levels. In particular, considering that 4 wt.% Ag-MWCNT reaches the highest outlet temperatures in Table 11, the superior performance of Ag-MWCNT, even at 1 wt.% concentration in Table 10, indicates that this effect will become more pronounced as the concentration increases.

These results show that when hybrid nanofluids are used at higher concentrations, they absorb more solar energy and provide higher temperature output from the receiver. Therefore, the heat transfer mechanism works more efficiently. However, it should be taken into account that the viscosity may increase with increasing concentration, which may increase the system’s energy consumption by increasing the pump power requirement. In this context, 0.3 wt.% and 1 wt.% Ag-MWCNT mixtures offer a more balanced performance and are at the optimum level in terms of energy efficiency.

Table 12. Numerical analysis results of receiver thermal oil and Hybrid nano Ag-MWCNT-Thermal oil.

Time	Receiver Inlet Temperature (K)	Receiver Outlet Temperature Thermal Oil (K)	Receiver Outlet Temperature 4% Ag-MWCNT-Thermal Oil (K)	Output Temperature Rise (∆T)
10.00	373.15	379.65	385.76	6.11
10.30	373.15	380.35	387.29	6.94
11.00	373.15	380.85	388.03	7.18
11.30	373.15	381.05	388.99	7.94
12.00	373.15	381.25	389.25	8
12.30	373.15	381.45	389.67	8.22
13.00	373.15	381.15	389.26	8.01
13.30	373.15	381.05	389.05	8
14.00	373.15	380.85	388.73	7.88
14.30	373.15	380.65	388.13	7.48
15.00	373.15	380.45	387.8	7.35
15.30	373.15	379.45	385.6	6.15
16.00	373.15	378.85	385.36	6.51
16.30	373.15	377.85	383.55	5.7
17.00	373.15	376.55	382.08	5.53

compares the receiver outlet temperatures obtained using conventional thermal oil and the hybrid nanofluid (4 wt.% Ag-MWCNT-thermal oil blend), providing a concrete demonstration of the contribution of hybrid nanofluids to heat transfer efficiency. The table shows the outlet temperatures measured at different periods at a constant receiver inlet temperature of 373.15 K and clearly shows that the hybrid nanofluid system provides higher outlet temperatures compared to the conventional thermal oil in every measurement. Especially in the morning, the temperature difference hovers around 5.5 K. In contrast, at noon, this difference reaches a maximum of 8 K. This situation shows that the hybrid nanofluids’ high thermal conductivity coefficient allows for more efficient heat transfer and more heat to be extracted from the receiver under the same radiation conditions. At noon, when solar radiation reaches its highest level, thermodynamic efficiency is maximized, and hybrid nanofluids’ performance improvement becomes more pronounced. At 12:30 pm, the receiver outlet temperature using the hybrid nanofluid was 389.67 K, while the thermal oil system recorded 381.45 K, a temperature difference of 8.22 K. Even when the solar radiation starts to decrease in the afternoon, the thermal performance advantage of the hybrid nanofluid is maintained, and the receiver outlet temperatures remain at higher levels than those of conventional thermal oil.

These results are directly related to Table 10 and Table 11. In Table 10, the performance of different types of hybrid nanofluids at 1 wt.% concentration was compared, and it was observed that the Ag-MWCNT-based hybrid nanofluid achieved the highest outlet temperatures compared to the other nanofluids (Al₂O₃-MWCNT and Cu-MWCNT). Table 11 showed how the receiver outlet temperatures changed when the same hybrid nanofluid was used in different concentrations (0.3–4 wt.%) and showed that the 4 wt.% Ag-MWCNT blend achieved the highest outlet temperatures. Table 12 takes these findings further and directly compares the most efficient hybrid nanofluid with conventional thermal oil, proving that hybrid nanofluids provide a significant performance improvement compared to conventional methods when used at 4% concentration. Table 12’s outstanding contribution is that it presents not only different nanofluid concentrations but also a direct comparison of hybrid nanofluids and conventional thermal oils, clearly demonstrating the potential of hybrid nanofluids to improve heat transfer in solar concentrator systems.

Figure 7A shows the pressure distribution inside the receiver in three dimensions and details the pressure changes experienced by the hybrid nanofluid as it travels through the receiver. This graph shows how the pressure changes from when the fluid enters the receiver to when it leaves the receiver and the effects of this change on the flow dynamics.

The figure shows that the pressure is highest in the receiver inlet region. This means the working fluid enters the receiver at high velocity, and a pressure build-up occurs at the inlet. As the fluid moves through the receiver, the pressure gradually decreases. This decrease is due to the fluid losing some energy as it moves through the receiver through friction, heat transfer, and interaction with obstacles. At the receiver outlet, the pressure drops to near atmospheric pressure. This situation is an indication of the pressure loss through the receiver.

Notably, the pressure distribution is more complex in the areas of obstacles inside the receiver. A pressure increase is observed just before the obstacles, while a sudden pressure drop occurs behind the obstacle. This situation indicates that pressure imbalances occur due to the resistance experienced by the fluid as it overcomes the obstacles and the subsequent turbulent zone. Such turbulent zones can increase heat transfer by causing the fluid to remain in the receiver longer, but excessive pressure losses can negatively affect system efficiency.

By visualizing the effect of hybrid nanofluids on pressure distribution, this graph provides important insights into the optimizations needed in receiver design to minimize pressure losses. Keeping the pressure loss in the receiver within certain limits saves the system energy and increases overall efficiency by reducing pump power. The pressure distribution shown in Figure 6 demonstrates that improvements in the design of the receiver can be made to ensure that the fluid exhibits a more stable pressure profile across the receiver.

Figure 7B shows the velocity distribution inside the receiver in three dimensions and details the velocity variations experienced by the working fluid (hybrid nanofluid) as it passes through the receiver. This graph visualizes how the fluid moves through the receiver and how the velocity profiles change. The figure shows that the working fluid has the highest velocity in the receiver inlet region. This is because the fluid has maximum energy and acceleration when entering the receiver. However, as the fluid moves along the receiver, a gradual decrease in velocity is observed. This is due to the friction and resistance caused by the fluid coming into contact with obstacles or surfaces inside the receiver. The velocity of the fluid approaches almost zero, incredibly close to the receiver walls and obstacles inside the receiver. This is expected in areas where the fluid contacts surfaces and loses velocity due to friction.

As the fluid moves through the receiver, the velocity is more stable and homogeneously distributed in the regions between the obstacles. This indicates that the fluid flows steadily through the receiver. However, in some regions, especially just behind the obstacles, low-velocity vortices (vortices) are formed. In these regions, the fluid’s movement slows down, and in some cases, backflow can be observed. Such vortices increase heat transfer and allow the fluid to stay in the receiver longer.

This graph shows that using hybrid nanofluids increases the homogeneity of the flow inside the receiver and optimizes the heat transfer by keeping the fluid inside the receiver for a longer time. Analysis of the velocity distribution inside the receiver provides critical data for improvements in receiver design. It shows that longer fluid residence time in the receiver improves thermal efficiency.

Figure 7C shows the temperature distribution inside the receiver in three dimensions and details the temperature changes the working fluid (hybrid nanofluid) undergoes during its movement inside the receiver. This figure visualizes how heat transfer occurs and how the temperature profiles are distributed as the working fluid passes through the receiver.

The graph shows a gradual increase in the temperature of the working fluid as it enters the receiver. This increase can be explained by the direct contact of the fluid with the solar energy as it travels along the receiver surfaces and absorbs the heat. Notably, the temperature is higher, especially in the regions closest to the receiver surface. As the velocity of the liquid traveling along the receiver decreases, the liquid is in contact with the surfaces for a more extended period, increasing the temperature of the liquid. This factor increases the system’s efficiency because it allows the fluid to absorb more heat.

In contrast, in regions where the fluid’s velocity increases, the temperature distribution is lower. This is because the fluid passes through the receiver faster, so it is in contact with the surfaces for a shorter time. Furthermore, temperature differences become more pronounced in regions where the flow is turbulent or where the fluid encounters obstacles. In these zones, fluid flow slows down and heat transfer becomes more efficient.

This figure highlights the importance of optimization in the receiver design and the use of hybrid nanofluids as the working fluid. In particular, the high thermal conductivity of hybrid nanofluids makes the temperature distribution more homogeneous and increases the system’s overall efficiency. Such analysis of the temperature distribution allows the receiver geometry to be designed to be more efficient and further improve the system’s performance.

Experimental applications and comparative results

The experiments were carried out for three consecutive 3-day periods in June 2024. Experiments were conducted with n ≥ 3 repetitions; values are reported as mean ± k = 2 uncertainty. To assess the effect of seasonality, the model was run over wide ranges for G, T∞, wind, and RH; it was observed that daily production scaled approximately linearly with G at fixed setpoints, and that wind/RH affected thermal matching. Multi-seasonal validation will be addressed in a future field campaign. The one-day results were obtained by taking the average of 3 days. For the experiments, the system is activated at 8.45 in the morning. The system is continuously monitored remotely with the help of sensors. The experimental set directs the solar energy to the receiver, and energy is stored in the receiver for a while. The experimental set starts to produce distilled water around 9.30 am. As seen in Figure 8A, with the improvements made in the system and the use of nanofluid, distilled water production has increased from 4.5 to 5.67 L per day compared to the experiments using thermal oil. This promising increase in performance of 25.7% points to the potential benefits of our research in renewable energy and nanotechnology. This system is not intended to meet the entire drinking and domestic water demand on its own, but is a solution focused on high desalination water production and modeling the environmental parameters that affect this production. In the prototype configuration (D = 1 m, n = 6), 5.67 L/day was obtained; in area scaling, production is roughly proportional to the open area. It has been calculated that ~83 m² of open area would be required for a 100 L/day requirement at the residential scale; therefore, the recommended applications are (i) niche applications requiring critical quality, (ii) hybrid systems (e.g., RO + PDC), and (iii) integrated architectures with waste heat or heat storage. Production per area can be increased by enlarging the D-diameter, using selective coatings, and improving monitoring accuracy.

A detailed interpretation of Figure 8B reveals the direct relationship between solar radiation and the amount of distilled water produced. The graph shows the solar radiation values measured at half-hourly intervals throughout the day and the amount of distilled water produced during this period. As the solar radiation starts to increase in the morning hours, the amount of distilled water produced by the system gradually increases. This shows the sensitivity and efficiency of the system to solar radiation and reveals that distilled water production peaks at noon when solar radiation reaches its maximum level. When solar radiation started to decrease in the afternoon, there was a significant decrease in distilled water production. This trend shows that the system is directly dependent on solar energy, and changes in radiation directly affect the production performance. It is noteworthy from the graph that the amount of distilled water production is higher in the experiments using hybrid nanofluids (especially 0.3 wt.% Ag-0.1 wt.% MWCNT-thermal oil blend) compared to the systems using conventional thermal oil. This situation indicates that solar energy is utilized more efficiently, and heat transfer is more effective due to the higher thermal conductivity of hybrid nanofluids. Especially during the peak hours of solar radiation, a significant increase in distilled water production of the system using hybrid nanofluid was observed. These findings show that hybrid nanofluids can be used as a potential solution in energy-intensive applications and allow more efficient utilization of renewable energy resources in distilled water production.

Figure 9A shows the time-dependent variation of the receiver outlet temperatures by comparing the numerical analysis results of the system using 0.3 wt.% Ag-0.1 wt.% MWCNT hybrid nanofluid with the experimental measurement results and evaluates the agreement between these two data sets; in the graph, it is seen that the outlet temperatures obtained from the numerical analysis largely overlap with the experimental data and the difference between the two data sets remains below 5%. Especially in the morning, when solar radiation and receiver temperatures are still low, the difference between the numerical and experimental data is minimal; later in the day and as temperatures increase, the difference between the measurements increases slightly but remains within the predicted margin of error. Towards noon, when the solar radiation reaches its maximum, the numerical analysis data are very close to the experimental measurements, demonstrating that the numerical model is accurate and successfully reflects the physical dynamics of the system. The error bars in the graph represent the possible uncertainties in the experimental measurements, and it can be seen that with an error rate of 5%, both numerical and experimental data provide reliable results, proving that the developed model works with high accuracy not only theoretically but also in real applications and that hybrid nanofluids offer an effective solution to improve the thermal performance of PDC systems. The most remarkable aspect of Figure 9A is that the strong correlation between numerical analysis and experimental measurements is an important indicator that successful results can be achieved in larger-scale applications in the future, increasing the reliability of models and hybrid nanofluids used in such systems.

Figure 9B is a graph that compares the system’s numerical and experimentally obtained thermal efficiency values using 0.3 wt.% Ag-0.1 wt.% MWCNT hybrid nanofluid and visualizes how the thermal efficiency changes at different times of the day. This data is directly related to the receiver outlet temperatures presented in Figure 9A because the increase in receiver outlet temperatures is directly related to the increase in the thermal efficiency of the system. As the solar radiation starts to increase in the morning hours, the thermal efficiency of the system gradually increases, and as the solar radiation reaches its peak closer to noon, the efficiency reaches maximum levels and stabilizes. In this process, it is noteworthy that the numerical analysis data are generally higher than the experimental measurements. However, this difference is minimized at noon, and the two data sets almost overlap, indicating that the efficiency reaches maximum levels numerically and experimentally at noon when the system reaches the highest temperatures. In the afternoon, a gradual decrease in thermal efficiency is observed with the decrease in solar radiation, at which point the experimental data fluctuates more and the numerical analysis results are more stable, but these fluctuations are within the error bars, indicating that the system is more affected by environmental factors in the afternoon and the measurement accuracy may decrease. In conjunction with Figure 9A, Figure 9B shows that the thermal efficiency values are also at maximum levels during the hours when the outlet temperatures are high, and these two graphs confirm each other; this proves that the thermal performance-enhancing effect of hybrid nanofluids can be measured consistently in terms of both temperature and efficiency and that the system works reliably.

The error bars indicate the expanded uncertainty at the 95% confidence level (k = 2). The combined uncertainty was calculated using the root-sum-square (RSS) approach for the output function R(x) derived from the measured quantities (Holman). The primary sources are: (i) solar radiation measurement (pyranometer ±10 W m⁻²; short-term cloud cover/spectral shift effects), (ii) temperature measurements (K-type thermocouple ±0.1 °C; contact/settlement and calibration drift), (iii) flow and volume measurements (flowmeter ±0.1 L min⁻¹; ±0.02 L equivalent in gravimetric/volumetric tracking of daily production), (iv) tracking and alignment (dish focus/tracking error ±0.2°; wind-induced oscillation), (v) optical–surface parameters (±0.01–0.02 in absorptivity/emissivity and top cover transmittance), (vi) nanofluid concentration and thermo-physical correlations (≈1–2% in property coefficients), and (vii) data acquisition resolution and time stamp drift. These bands indicate that the <5% discrepancy between the numerical model and the experiment remains within the expected error range.

Figure 10 compares the numerical and experimental exergy efficiency values of the system using 0.3 wt.% Ag-0.1 wt.% MWCNT hybrid nanofluid at different times of the day to show how the exergy efficiency of the system changes over time and how the losses in the energy conversion processes tend; In the morning hours, a significant increase in the exergy efficiency of the system is observed with the increase in solar radiation, but it is noteworthy that the exergy efficiency is generally lower compared to the thermal efficiency values shown in Figure 9B because exergy analyses reflect the losses inherent in energy conversion processes, taking into account not only heat transfer efficiency but also entropy production and irreversible energy losses within the system. Towards noon, when the system’s thermal efficiency reaches its maximum, the exergy efficiency also reaches its highest levels. However, these values remain at a lower peak than the thermal efficiency, indicating that even at the moments of maximum thermal performance of the system, exergy losses cannot be eliminated. Irreversible losses are present in the energy conversion process. In the afternoon, as the solar radiation decreases and the system starts to cool down, a sharp decrease in the exergy efficiency is observed, during which the numerical analysis data shows a more stable trend compared to the experimental measurements; fluctuations in the experimental data can be attributed to measurement uncertainties, environmental factors and possible sudden losses in the system. In conjunction with Figure 9B, it is observed that the increase in thermal efficiency directly leads to a similar trend in the exergy efficiency. However, the curve in the exergy efficiency remains at lower levels than the thermal efficiency, proving that hybrid nanofluids play an important role in reducing irreversible losses in energy systems by improving the heat transfer performance and increasing the thermal efficiency but not eliminating the exergy losses.

The reported exergy efficiency of approximately 19% for PDC-based distillation systems is competitive in the literature when similar scales and conditions are considered. Indeed, a theoretical upper limit of approximately 21.1% has been demonstrated for an ideal single-effect solar distiller; in this context, our obtained value is close to this threshold [45]. On the other hand, in multi-stage distillation applications where PDC is used as a thermal source, collector/unit-based second-law efficiencies generally remain low; for example, in a PDC–MSF study, the collector exergy efficiency was reported to be 0.7–1.3%, while the total exergy efficiency of the MSF unit was 0.07% Similarly, in solar fields integrated with membrane distillation, collector exergy efficiency is often in the single-digit percentage range (e.g., ≈4–6.5%), indicating the dominance of in-field irreversibilities [46]. In dish–Stirling systems, a different application of PDC, exergy efficiencies of up to ≈41.5% can be achieved at the collector level, but the overall system efficiency is around ≈13.2%; exergy losses in multi-stage thermal chains limit the overall performance [47]. This wide distribution demonstrates that the definition of exergy efficiency (input–output vs. consumed–produced) and system boundaries significantly affect the results; it has been reported in detail that the MSF efficiency for the same process can vary from a few percentage points to >10% depending on the approach [48]. Therefore, the improvement in receiver–evaporator thermal matching, enhanced transport with hybrid nanofluids, and reduced irreversibilities through rule-based operating thresholds indicate a competitive performance at an application-scale level of approximately 19% for PDC-based distillation.

Artificial Intelligence Model Results

In addition to the experimental and numerical evaluations, the previously introduced coati optimization algorithm (COA), combined with a rule-based method, was applied to the system data to assess its optimization capability. The outcomes of this AI-based analysis are summarized below.

Table 13. Some rules and accuracy values extracted by the proposed method.

Accuracy	Rule	Class
0.962	If (73 ≤ T7 ≤ 108) and (66 ≤ T8 ≤ 101) and (19 ≤ P1 ≤ 38) and (680 ≤ SolarRadiation ≤ 782)	L
0.957	If (85 ≤ T2 ≤ 134) and (70 ≤ T7 ≤ 109) and (33 ≤ P1 ≤ 37) and (679 ≤ SolarRadiation ≤ 761)	L
0.929	If (29 ≤ P1 ≤ 37) and (28 ≤ AmbientTemperature ≤ 40) and (3 ≤ WindSpeed ≤ 6))	M
0.929	If (67 ≤ T5 ≤ 98) and (53 ≤ T9 ≤ 97)	L
0.929	If (90 ≤ T5 ≤ 105) and (105 ≤ T7 ≤ 109) and (37 ≤ P1 ≤ 38) and (824 ≤ SolarRadiation ≤ 927) and (3 ≤ WindSpeed ≤ 6)	H
0.929	If (99 ≤ T4 ≤ 134) and (612 ≤ SolarRadiation ≤ 787)	L
0.857	If (120 ≤ T1 ≤170) and (90 ≤ T7 ≤ 109) and (843 ≤ SolarRadiation ≤ 927) and (2 ≤ WindSpeed ≤ 5)	H
0.857	If (113 ≤ T1 ≤ 171) and (107 ≤ T4 ≤ 135) and (73 ≤ T5 ≤ 105) and (99 ≤ T7 ≤ 109) and (30 ≤ P1 ≤ 38) and (905 ≤ SolarRadiation ≤ 927)	H
0.786	If (105 ≤ T1 ≤ 172) and (92 ≤ T2 ≤ 120) and (91 ≤ T3 ≤ 176) and (113 ≤ T4 ≤ 140) and (89 ≤ T7 ≤ 109) and (33 ≤ P1 ≤ 38)	M
0.714	If (95 ≤ T2 ≤ 123) and (91 ≤ T3 ≤ 176) and (91 ≤ T4 ≤ 133) and (76 ≤ T5 ≤ 105) and (31 ≤ AmbientTemperature ≤ 41)	M

presents representative rules obtained through the coati-based rule mining approach together with their classification accuracy values. These results indicate not only which operational conditions lead to specific performance classes but also demonstrate that the proposed RB coati method achieves high accuracy while generating interpretable and meaningful rules for the dataset.

Figure 11 compares the accuracy of the proposed RB coati method with the rule-based classification algorithms commonly used in the literature. When the results obtained are analyzed, it is seen that the RB coati method (87.51% accuracy rate) shows by far the highest performance. This value is almost double the 47.61% accuracy rate achieved by JRip, FURIA, and ConjunctiveRule algorithms, which are in second place, and the fact that the ZeroR algorithm also has an accuracy of 47.61% indicates that the distribution between classes may be unbalanced, since ZeroR is a very simple method that predicts only the most frequent class. On the other hand, methods such as DecisionTable (38.09%), RIDOR (28.57%), and OneR (23.80%) achieved very low accuracy rates, indicating their inability to capture complex structures in the dataset. In conclusion, the proposed RB Coati method significantly outperforms both classical and modern rule-based methods. This finding demonstrates the effectiveness of the method in terms of rule extraction and classification accuracy.

In Figure 12, the proposed RB coati method is presented in comparison with different machine learning algorithms. The results show that the RB coati method (with an accuracy of 87.51%) clearly outperforms the other methods. Notably, the traditional statistical classifiers, Naive Bayes (28.57%) and SVM (39.09%), performed significantly worse. Similarly, KStar (39.09%), HyperPipes (33.33%) and scikit-learn based method (42.85%) also performed poorly compared to the proposed method. Among the rule-based methods, the frequently used C4.5 (J48) and Random Tree algorithms gave relatively better results with an accuracy of 47.61%, but they were far behind the 87.51% success rate achieved by the proposed RB coati method. This shows that the proposed method offers higher accuracy, better generalization ability, and adaptability to the dataset compared to both rule-based and statistical approaches. Hence, RB coati provides a significant advantage not only over classical classification methods but also over the widely used rule-based approaches. This result shows that the proposed method offers a more reliable and effective classification alternative for complex datasets.

Figure 13 compares the accuracy performance of the proposed RB coati method and some popular machine learning models. As can be seen from the table, the RB coati method achieves the highest accuracy (87.51%) and outperforms both rule-based and modern deep learning methods. This shows that the proposed method can extract highly effective rules from the dataset and increase the classification accuracy. The Transformers-based model performed close to RB coati with 85.71% accuracy, but RB coati achieved slightly better results. The RbA SFO, multilayer perceptron (MLP), and NODE (neural oblivious decision ensemble) methods show moderate performance with accuracies around 78% respectively. This reveals that the proposed RB coati method is more competitive compared to both rule-based and neural network-based approaches. On the other hand, TabNet lags behind the other methods with an accuracy of 64.3%, indicating that TabNet may have a limited advantage depending on the structure of the dataset. Overall, Figure 3 highlights the superiority of the RB coati method in terms of classification accuracy and that it is an effective choice, especially among rule-based models.

Compared to the following studies, the COA + rule-based hybrid approach in the PDC-based system presented in this study stands out by moving beyond the “prediction-oriented black box” line in the use of artificial intelligence, providing explainable rules and operating range recommendations that directly generate decision support. Effective examples in the literature include HHO-ANN [49], for active/concerted systems, ANN-HWO and PSO comparisons in a stepwise arrangement [49], Taguchi + ML (DT/RF) and independent ABC optimization [50] in a dual-slope scheme, and comprehensive ML comparisons in hemispherical distillers [51]; these studies primarily focus on accuracy metrics such as high R²/MAE; however, the ability to explain the model’s internal logic and which operational parameter improves the output within which range is limited (e.g., while DT’s ability to perform class separation partially enhances explanation, it does not provide a unified framework that combines rule extraction and optimization). In contrast, the COA-rule-based framework proposed in this study achieves classification performance (87.5%) while simultaneously extracting rules to clarify the effects of parameters and automatically determining optimal ranges, thereby internally establishing the “prediction → action” bridge. Thus, unlike the meta-heuristic fine-tuned black-box predictors prevalent in the solar-powered water production literature, reliability (explainability) and operation-oriented optimization are integrated into a single explainable decision support layer (see comparisons in [49,50,51,52,53]).

Our findings align with the trend in recent studies on explaining errors/conditions with XAI in PV and smart energy applications: explanations should not only answer the question “which variable is important?” but also provide clear thresholds that can be translated into operational settings. Our framework (a rule-based system optimized with COA) meets this requirement by producing field-applicable threshold-valued decision rules and maintaining the performance–understandability balance. Thus, as recent reviews suggest, it shifts explanations to a maintenance/operational perspective and integrates them with decision support; it exemplifies the transferability of explainable error detection approaches demonstrated in PV-focused XAI studies to the PDC-based distillation context [54].

4. Conclusions and Recommendations

Essential considerations for PDC systems are production costs, complexity, efficiency, uniform temperature distribution, and choice of working fluid. This study uses an experimental and numerical investigation of a low-cost PDC distilled water generator with a parabolic dish concentrator and rectangular receiver to improve its performance. Additionally, a coati optimization approach is adapted as a rule-based explainable artificial intelligence method to optimize operational parameters with relevant intervals and identify performance-enhancing patterns, further supporting system efficiency improvements. The conclusions of this study, including bullet points, are provided below.

Verified integrated approach: Three hybrid nanofluids were investigated in a multi-tray PDC setup; experimental–CFD results agreed within 5%. The mesh independence study showed that Model 2 is the most suitable choice in terms of accuracy–computational cost balance.

Performance gain: Daily distilled water production increased by 25.7% (4.50 → 5.67 L) with the use of hybrid nanofluids. The average exergy efficiency was ≈19%, indicating enhanced thermal/optical coupling.

Operating with XAI: The coati-based rule-generation framework provided transparent thresholds that automatically suggested setpoints, offering a decision support mechanism directly transferable to field applications. Applicability and reliability: extended uncertainty bands are ≤4–5% for key outputs. Findings provide practical design and operational guidance for fluid selection, tracking/alignment, and flow–temperature adjustments.

In the future planning of the study, the verification of the produced water’s drinkability (conductivity/TDS, pH, turbidity, TOC, and basic microbiology) will be prioritized, Ag and MWCNT ratios will be jointly optimized between heat transfer, viscosity, and economy using design-experiment/response surface approaches, a detailed cost–benefit analysis will be conducted for all candidate (single/hybrid) fluids, and long-term stability/rheology and multi-season field/pilot-scale tests will be performed to evaluate XAI-based closed-loop control capabilities.