Active Distribution Network Bi-Level Programming Model Based on Hybrid Whale Optimization Algorithm
Abstract
1. Introduction
- Demand response is introduced into the ADN planning problem to realize “source-load-network” collaborative planning, which can effectively reduce the network loss and cost of the system.
- A hybrid improved whale algorithm is proposed to optimize the algorithm structure and search method of the whale algorithm through co-evolution and adaptive mutation, which effectively improves its convergence speed and optimization accuracy.
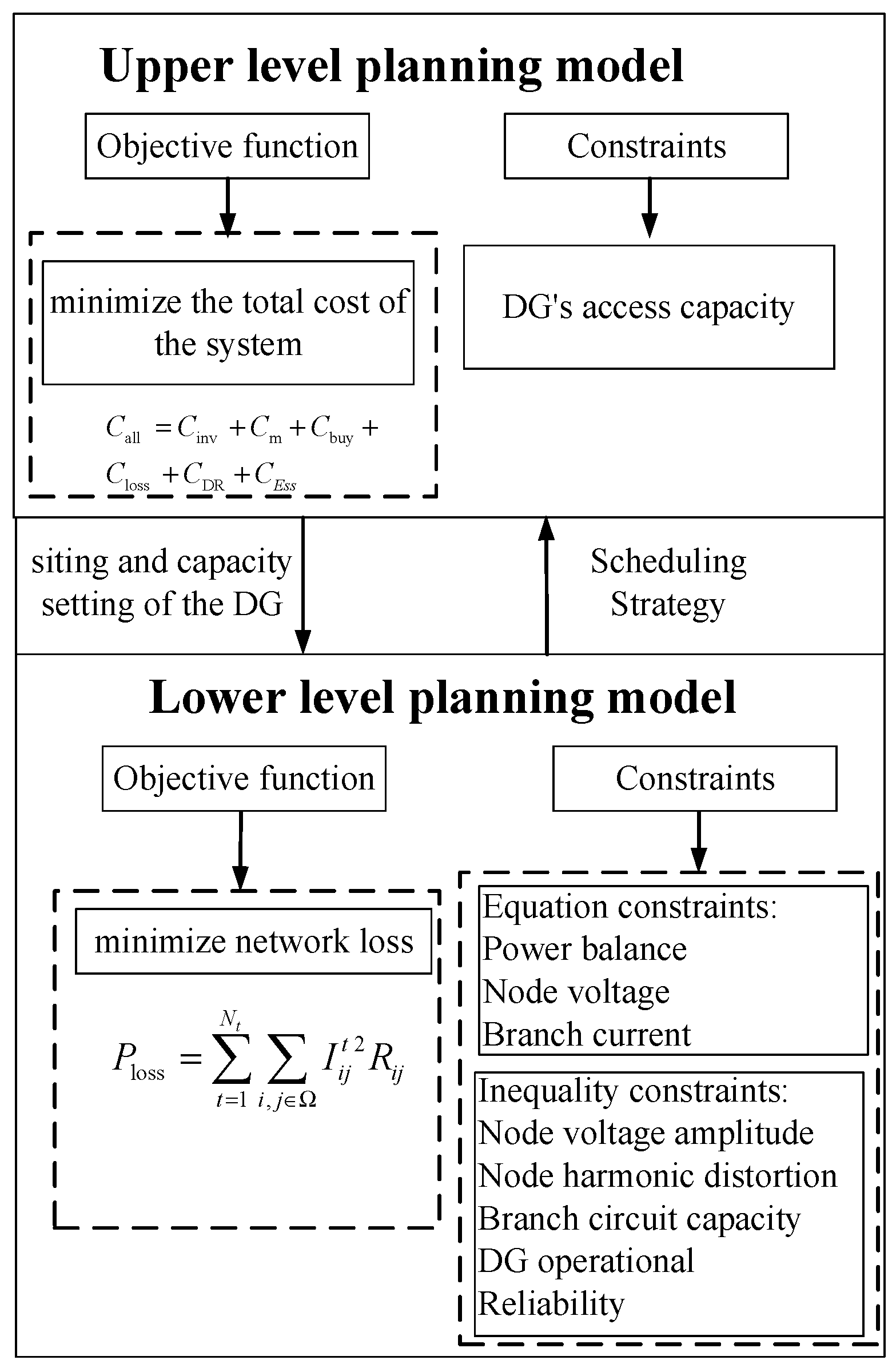
2. ADN “Source-Load-Network” Two-Tier Planning Model
2.1. Upper-Level Planning Model
2.1.1. Objective Function
2.1.2. Constraints
2.2. Lower-Level Planning Model
2.2.1. Objective Function
2.2.2. Constraints
- (i)
- Equation constraints
- (ii)
- Inequality constraints
3. Hybrid Whale Optimization Algorithm
3.1. Basic WOA
3.1.1. Whale Encircling Prey Stage
3.1.2. Stages of the Bubble Web Attack
3.1.3. Search and Predation Phase
3.2. Improvement in WOA
3.2.1. Optimization of Algorithm Structure Based on Co-Evolution
3.2.2. Optimization of Search Method Based on Adaptive Mutation
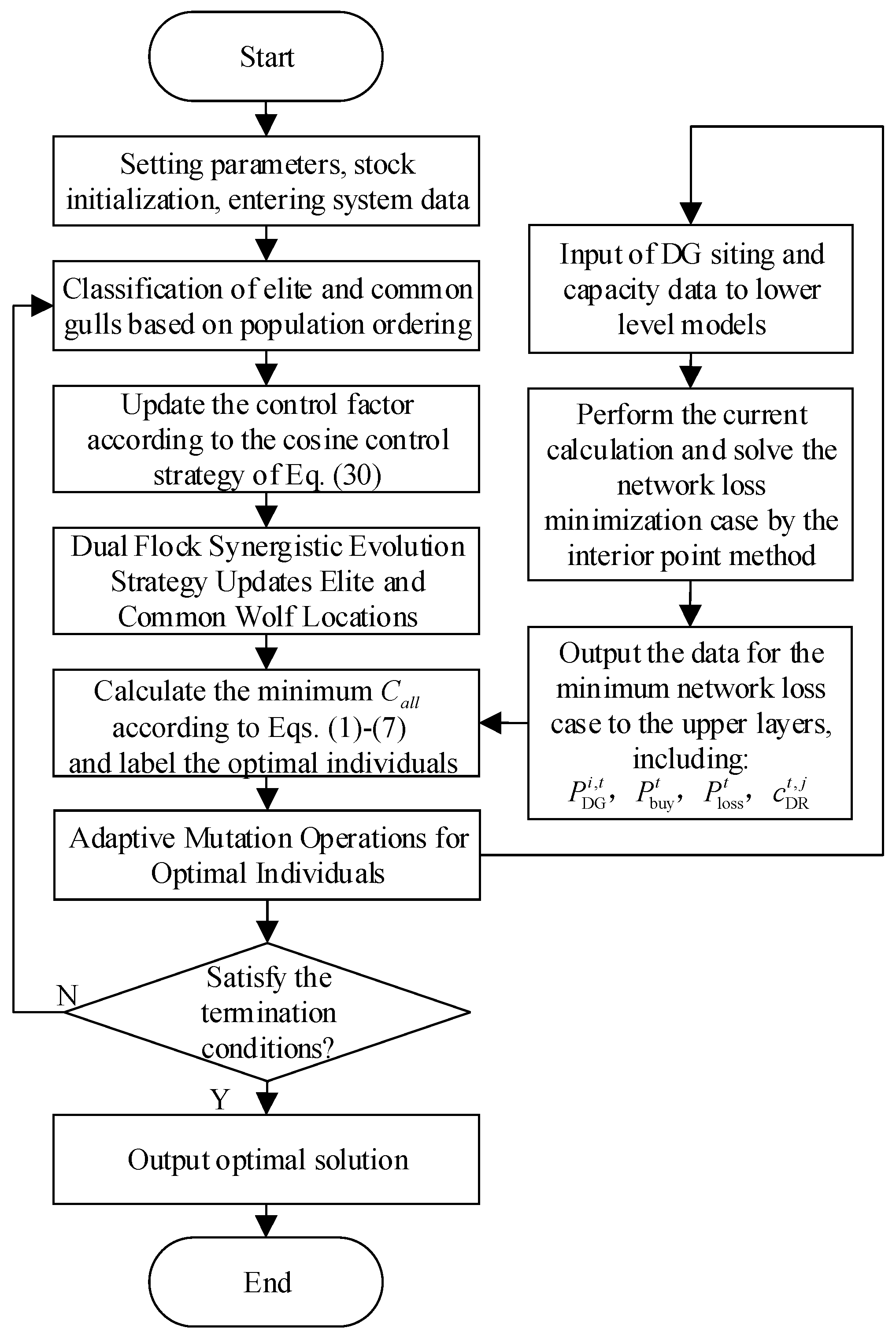
- The algorithm parameters were set according to Equations (19) and (20) to randomly generate the initial population;
- The initial population fitness values were calculated and ranked to mark the optimal individuals;
- Flocks of gulls were categorized into elite and common gull flocks based on sorting, with the proportion of elites generated by a feedback-adjusted formula;
- The control factors were updated according to the cosine control strategy of Equation (30);
- Updating elite gulls, establish common gull positions according to the dual-flock co-evolution strategy;
- The ranking of the gull flock is updated, and the optimal individuals are determined by calculating the fitness value of the new population using Equations (21)–(29);
- Mutation and update operations are performed on the optimal individuals according to Equations (33) and (34);
- Check if the maximum iteration limit has been reached; if so, cease iteration and output the optimal value. Otherwise, proceed to step 3 to resume iteration.
3.3. Model Solving Process
4. Example Analysis
4.1. Parameterization
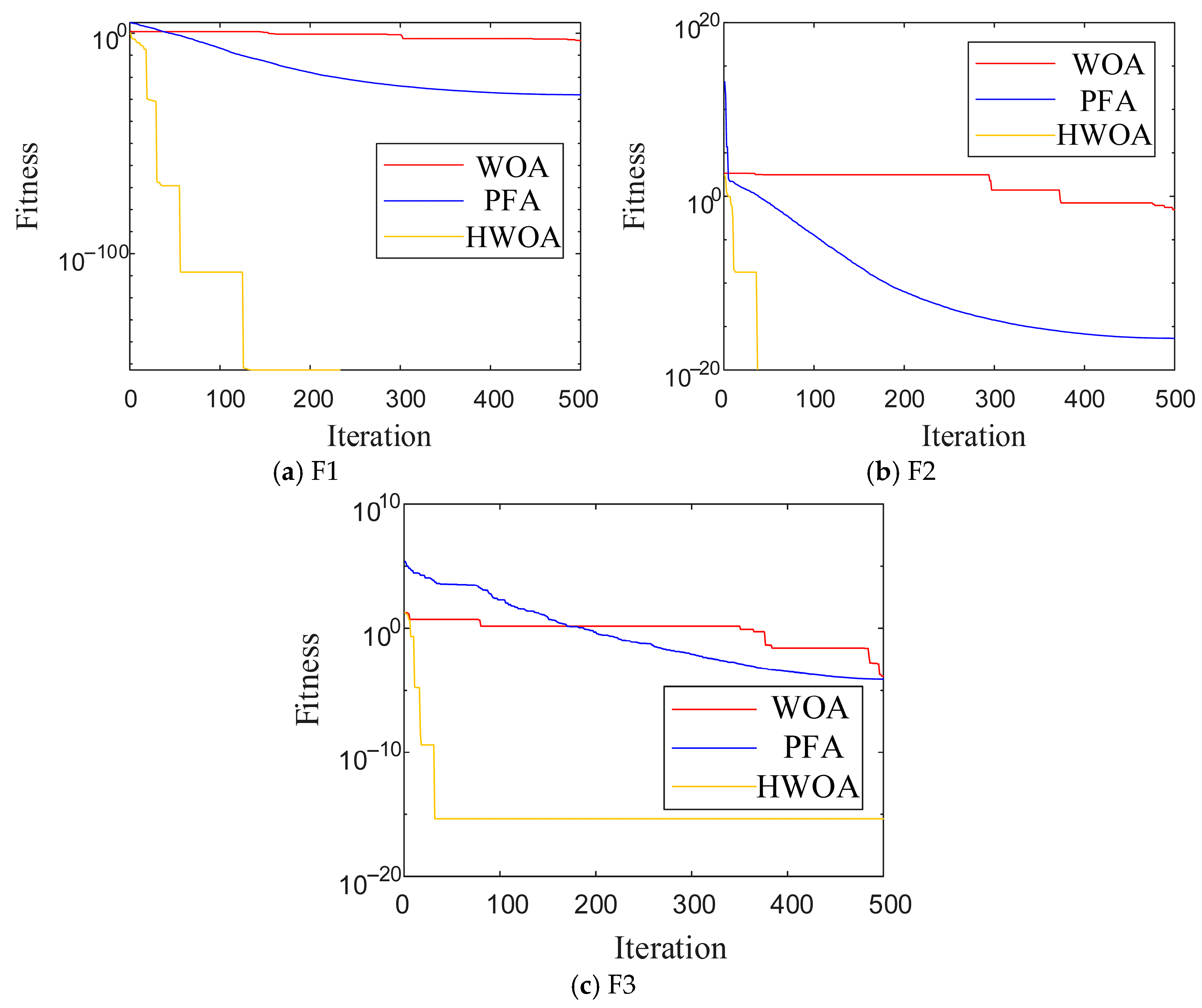
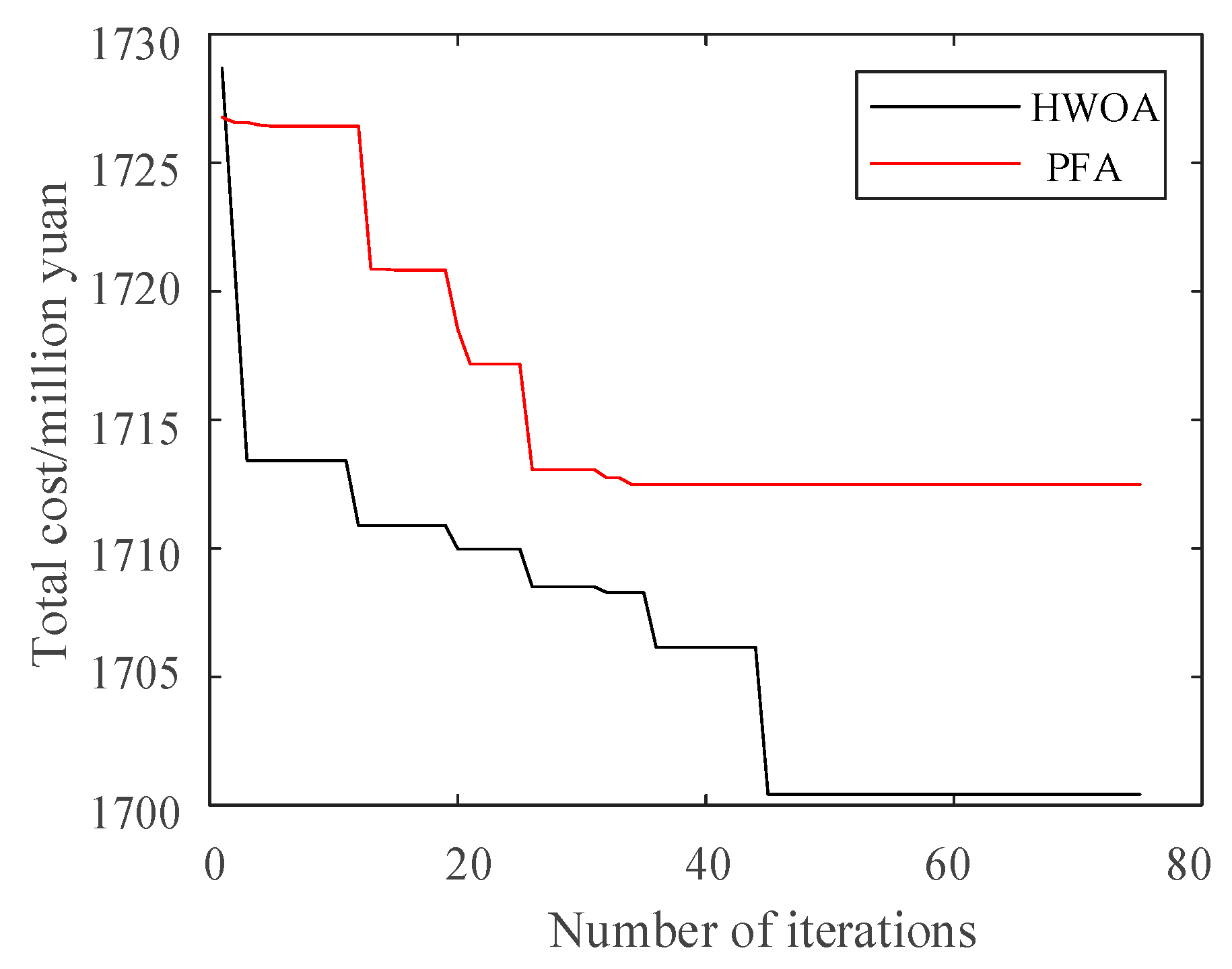
4.2. Algorithm Performance Analysis
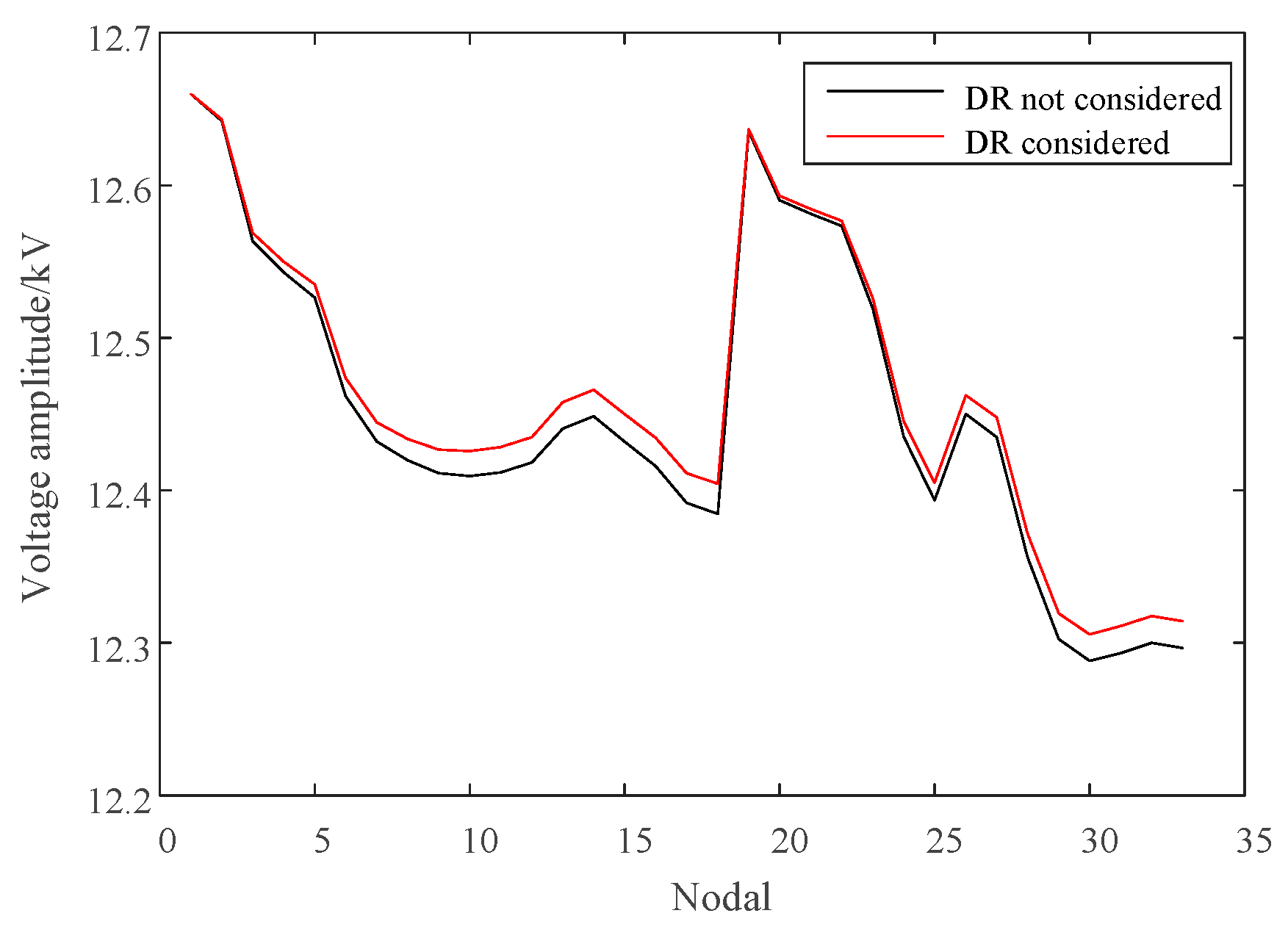
4.3. Analysis of Optimization Results
5. Conclusions
- By incorporating demand response into the ADN planning process, distributed energy consumption can be effectively improved by 88.77 MWh, network loss can be reduced by 6.8 MWh, and the comprehensive cost can be decreased by CNY 3.62 million. This enables the system to operate economically, efficiently, safely, and stably.
- The HWOA, which considers both global search and local exploration, exhibits excellent optimization performance, with higher accuracy and faster speed in solving the double-layer planning problem for ADNs. Compared to PFA, the algorithm’s efficiency is improved by 18.92%, resulting in a reduction of CNY 120.6 thousand in system assembly derived from optimization and a decrease of CNY 24.2 thousand in network loss cost.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, M.; Zheng, H.; Shen, Z. Whether the Carbon Emissions Trading System Improves Energy Efficiency—Empirical Testing Based on China’s Provincial Panel Data. Energy 2023, 275, 127465. [Google Scholar] [CrossRef]
- Li, Y.; Feng, B.; Wang, B.; Sun, S. Joint Planning of Distributed Generations and Energy Storage in Active Distribution Networks: A Bi-Level Programming Approach. Energy 2022, 245, 123226. [Google Scholar] [CrossRef]
- Razavi, S.-M.; Momeni, H.-R.; Haghifam, M.-R.; Bolouki, S. Multi-Objective Optimization of Distribution Networks via Daily Reconfiguration. IEEE Trans. Power Deliv. 2022, 37, 775–785. [Google Scholar] [CrossRef]
- Han, F.; Zhang, X.; Li, M.; Li, F.; Zhao, W. Stability Control for Grid-Connected Inverters Based on Hybrid-Mode of Grid-Following and Grid-Forming. IEEE Trans. Ind. Electron. 2024, 71, 10750–10760. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, Z.; Liu, X.; Yang, L.; Dan, Y.; Zhu, Y.; Ding, Y.; Wang, Q. Bi-Level Coordinated Planning of Active Distribution Network Considering Demand Response Resources and Severely Restricted Scenarios. J. Mod. Power Syst. Clean Energy 2021, 9, 1088–1100. [Google Scholar] [CrossRef]
- Haghifam, S.; Najafi-Ghalelou, A.; Zare, K.; Shafie-khah, M.; Arefi, A. Stochastic Bi-Level Coordination of Active Distribution Network and Renewable-Based Microgrid Considering Eco-Friendly Compressed Air Energy Storage System and Intelligent Parking Lot. J. Clean. Prod. 2021, 278, 122808. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Y.; Zheng, F.; Lin, J.; An, X.; Shi, H. Day-Ahead and Real-Time Energy Management for Active Distribution Network Based on Coordinated Optimization of Different Stakeholders. Power Syst. Technol. 2021, 45, 2299–2307. [Google Scholar]
- Zhang, Z.; Lei, D.; Li, J.; Xu, Y.; Luo, J. Source-Network-Load-Storage Bi-Level Collaborative Planning Model of Active Distribution Network with SOP Based on Adaptive Epsilon-Dominating Multi-Objective Particle Swarm Optimization Algorithm. Power Syst. Technol. 2022, 46, 2199–2209. [Google Scholar]
- Tian, X.; Yang, H.; Ge, Y.; Yuan, T. Site Selection and Capacity Determination of Electric Hydrogen Charging Integrated Station Based on Voronoi Diagram and Particle Swarm Algorithm. Energies 2024, 17, 418. [Google Scholar] [CrossRef]
- Yang, M.; Li, J.; Li, J.; Yuan, X.; Xu, J. Reconfiguration Strategy for DC Distribution Network Fault Recovery Based on Hybrid Particle Swarm Optimization. Energies 2021, 14, 7145. [Google Scholar] [CrossRef]
- Sun, Q.; Yu, Y.; Li, D.; Hu, X. A Distribution Network Reconstruction Method with DG and EV Based on Improved Gravitation Algorithm. Syst. Sci. Control Eng. 2021, 9, 6–13. [Google Scholar] [CrossRef]
- Javadi, M.; Gough, M.; Mansouri, S.; Ahmarinejad, A.; Nematbakhsh, E.; Santos, S.; Catalao, J. A Two-Stage Joint Operation and Planning Model for Sizing and Siting of Electrical Energy Storage Devices Considering Demand Response Programs. Int. J. Electr. Power Energy Syst. 2022, 138, 107912. [Google Scholar] [CrossRef]
- Xie, H.; Wang, W.; Wang, W.; Tian, L. Optimal Dispatching Strategy of Active Distribution Network for Promoting Local Consumption of Renewable Energy. Front. Energy Res. 2022, 10, 826141. [Google Scholar] [CrossRef]
- Xu, X.; Niu, D.; Peng, L.; Zheng, S.; Qiu, J. Hierarchical Multi-Objective Optimal Planning Model of Active Distribution Network Considering Distributed Generation and Demand-Side Response. Sustain. Energy Technol. Assess. 2022, 53, 102438. [Google Scholar] [CrossRef]
- Purlu, M.; Turkay, B.E. Optimal Allocation of Renewable Distributed Generations Using Heuristic Methods to Minimize Annual Energy Losses and Voltage Deviation Index. IEEE Access 2022, 10, 21455–21474. [Google Scholar] [CrossRef]
- Xiao, H.; Pei, W.; Deng, W.; Ma, T.; Zhang, S.; Kong, L. Enhancing Risk Control Ability of Distribution Network for Improved Renewable Energy Integration through Flexible DC Interconnection. Appl. Energy 2021, 284, 116387. [Google Scholar] [CrossRef]
- Yang, Y.; Bian, R.; Wang, T.; Wei, W.; Jun, Z. Inverse Time Overcurrent Optimization of Distribution Network with DG Based on Improved Gray Wolf Algorithm. Energy Rep. 2022, 8, 237–246. [Google Scholar] [CrossRef]
- Hao, J.; Feng, X.; Chen, X.; Jin, X.; Wang, X.; Hao, T.; Hong, F.; Du, X. Optimal Scheduling of Active Distribution Network Considering Symmetric Heat and Power Source-Load Spatial-Temporal Characteristics. Appl. Energy 2024, 373, 123974. [Google Scholar] [CrossRef]
- Sperr, F.; Stai, E.; Venkatraman, A.; Krause, T.; Hug, G. Service Restoration in the Medium Voltage Grid Minimizing the SAIDI Contribution After Primary Substation Failures. IEEE Trans. Power Syst. 2024, 39, 66–82. [Google Scholar] [CrossRef]
- Mirshekali, H.; Mortensen, L.K.; Shaker, H.R. Reliability-Aware Multi-Objective Approach for Predictive Asset Management: A Danish Distribution Grid Case Study. Appl. Energy 2024, 358, 122556. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Yuan, Q.; Shi, H.; Han, M. Multi-Strategy Improved Seagull Optimization Algorithm. Int. J. Comput. Intell. Syst. 2023, 16, 154. [Google Scholar] [CrossRef]
- Liu, J.; Wang, H.; Li, X.; Chen, K.; Li, C. Robotic Arm Trajectory Optimization Based on Multiverse Algorithm. Math. Biosci. Eng. 2023, 20, 2776–2792. [Google Scholar] [CrossRef]
- Chen, B.; Zou, H. Self-Conclusion and Self-Adaptive Variation Particle Swarm Optimization. Comput. Eng. Appl. 2022, 58, 67–75. [Google Scholar]
- Wang, H.; Schulz, N. A Revised Branch Current-Based Distribution System State Estimation Algorithm and Meter Placement Impact. IEEE Trans. Power Syst. 2004, 19, 207–213. [Google Scholar] [CrossRef]
- Sun, P.; Luo, M.; Sun, Z.; Zhou, K.; Luo, Y.; Liu, T.; Tang, H.; Wang, W. An Improved Approach Based on Cuckoo Search Algorithm for Bi-Level Distributed Wind Generation Planning in Active Distribution Network. Power Syst. Technol. 2016, 40, 2743–2749. [Google Scholar]
- Liu, X.; Hayati, H. CCHP Optimization for a Building through Optimal Size of the Prime Mover Considering Energy, Exergy, Economics, and Environmental Aspects. CASE Stud. Therm. Eng. 2022, 39, 102403. [Google Scholar] [CrossRef]
- Ghiaskar, A.; Amiri, A.; Mirjalili, S. Polar Fox Optimization Algorithm: A Novel Meta-Heuristic Algorithm. Neural Comput. Appl. 2024, 36, 20983–21022. [Google Scholar] [CrossRef]
| Project Type | Unit | Correlation Coefficient |
|---|---|---|
| DG unit investment cost | CNY/kVA | 13 |
| DG discount rate | % | 8 |
| DG lifecycle | years | 25 |
| DG unit operating cost | CNY/kWh | 0.03 |
| Purchase price of electricity | CNY/kWh | 0.4 |
| Grid loss tariff | CNY/kWh | 0.35 |
| DR compensation | CNY/kWh | 1 |
| No. | Function Name | Expression | Variable Range | Theory Extreme Value |
|---|---|---|---|---|
| F1 | Sphere | 0 | ||
| F2 | Rastrigin | 0 | ||
| F3 | Ackley | 0 |
| Test Function | Performance Indicators | WOA | PFA | HWOA |
|---|---|---|---|---|
| F1 | Optimum value | 1.9 × 10−9 | 1.7 × 10−34 | 0 |
| Average value | 1.9 × 10−7 | 2.0 × 10−33 | 0 | |
| Standard deviation | 2.6 × 10−7 | 2.6 × 10−33 | 0 | |
| F2 | Optimum value | 8.4 × 10−9 | 5.7 × 10−14 | 0 |
| Average value | 3.8 × 10−1 | 1.1 × 100 | 0 | |
| Standard deviation | 1.9 × 100 | 2.9 × 100 | 0 | |
| F3 | Optimum value | 4.1 × 10−6 | 4.0 × 10−14 | 8.9 × 10−16 |
| Average value | 4.4 × 10−5 | 4.3 × 10−14 | 8.9 × 10−16 | |
| Standard deviation | 6.1 × 10−5 | 4.3 × 10−15 | 0 |
| Optimization Results | Unit | HWOA | PFA |
|---|---|---|---|
| DG access point | / | 6, 32, 14 | 27, 12, 25 |
| DG capacity | kVA | 905, 693, 804 | 1048, 837, 803 |
| DG Investment costs | k CNY | 2874.0 | 3282.9 |
| DG Running costs | k CNY | 364.3 | 401.1 |
| Power purchase costs | k CNY | 12,716.7 | 12,075.7 |
| Net loss cost | k CNY | 364.6 | 388.8 |
| DR cost | k CNY | 684.6 | 976.3 |
| Total cost | k CNY | 17,004.2 | 17,124.8 |
| Optimization Results | Option 1 | Option 2 |
|---|---|---|
| DG consumption (MWh) | 1125.56 | 1214.33 |
| DR volume (MWh) | 0 | 68.46 |
| Total system cost (thousand CNY) | 20,629.8 | 17,005.8 |
| Network loss (MWh) | 110.97 | 104.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Che, Y. Active Distribution Network Bi-Level Programming Model Based on Hybrid Whale Optimization Algorithm. Sustainability 2025, 17, 8560. https://doi.org/10.3390/su17198560
Guo H, Che Y. Active Distribution Network Bi-Level Programming Model Based on Hybrid Whale Optimization Algorithm. Sustainability. 2025; 17(19):8560. https://doi.org/10.3390/su17198560
Chicago/Turabian StyleGuo, Hao, and Yanbo Che. 2025. "Active Distribution Network Bi-Level Programming Model Based on Hybrid Whale Optimization Algorithm" Sustainability 17, no. 19: 8560. https://doi.org/10.3390/su17198560
APA StyleGuo, H., & Che, Y. (2025). Active Distribution Network Bi-Level Programming Model Based on Hybrid Whale Optimization Algorithm. Sustainability, 17(19), 8560. https://doi.org/10.3390/su17198560






