Integrating Rainwater Harvesting and Solar Energy Systems for Sustainable Water and Energy Management in Low Rainfall Agricultural Region: A Case Study from Gönyeli, Northern Cyprus
Abstract
1. Introduction
1.1. Background
1.2. Rainwater Harvesting (RWH) System
1.3. Solar Energy
1.4. Importance of the Study
- First, to design an RWH system to meet North Cyprus’s rainfall characteristics. RWH was designed to be utilized for irrigation. The RWH design is based on historical daily rainfall data from 1981 to 2023. Obtaining detailed and suitable rainfall data to have a good design of the RWH system is a challenge in developing countries like Cyprus. Therefore, nine satellite precipitation products were selected for this study’s evaluation of their accuracy in comparison to ground-based gauge rainfall data. Based on the best dataset, finding the distribution function that best fits rainfall data is crucial to designing a successful rainwater harvesting system. It enables accurate projections of both typical and atypical rainfall occurrences, which helps with overflow management and tank size selection. By simulating the frequency of rainfall, the system may be adapted to local patterns, ensuring sufficient capacity for heavy rain while reducing costs. This statistical knowledge supports a reliable, sustainable design that maximizes water availability and system resilience. According to the authors’ review, only a few scientific studies [57,58,59,60,61] have statistically examined the rainfall time series in several Cyprus regions. Michaelides et al. [57] utilized a gamma distribution function to investigate the characteristics of Cyprus’s annual rainfall frequency distribution. Stamatatou et al. [58] examined the characteristics of the annual maximum rainfall depth and storm duration at the Limassol station in Cyprus employing a variety of distribution functions, including generalized extreme value (GEV), Gumbel, and generalized Pareto, gamma, exponential, and log-normal. The findings showed that the generalized extreme value distribution was chosen to describe the storm duration and yearly maximum rainfall depth at the chosen station. Zaifoglu et al. [59] conducted a regional frequency analysis of the annual maximum daily precipitation in Northern Cyprus using traditional cluster analysis and time series clustering techniques. Generalized logistic, generalized normal, and Pearson Type III distributions were determined to be the best fits for the various Northern Cyprus subregions. Besides, in the Güzelyurt region of Northern Cyprus, Kassem et al. [60] determined the best distribution model for monthly and total rainfall. The findings demonstrated that the Nakagami and Wakeby distributions provided the best fit for the actual total and monthly rainfall data. Furthermore, the best-fit probability distribution for monthly rainfall in seven Northern Cyprus locations was identified by Kassem et al. [61]. The findings show that the Gumbel Max best distribution and the generalized extreme value distribution performed effectively in examining the characteristics of average rainfall data. Therefore, 65 frequency distributions and three goodness-of-fit test statistics were applied in this study to determine the best-fit probability distributions in the case of average and maximum daily rainfall.
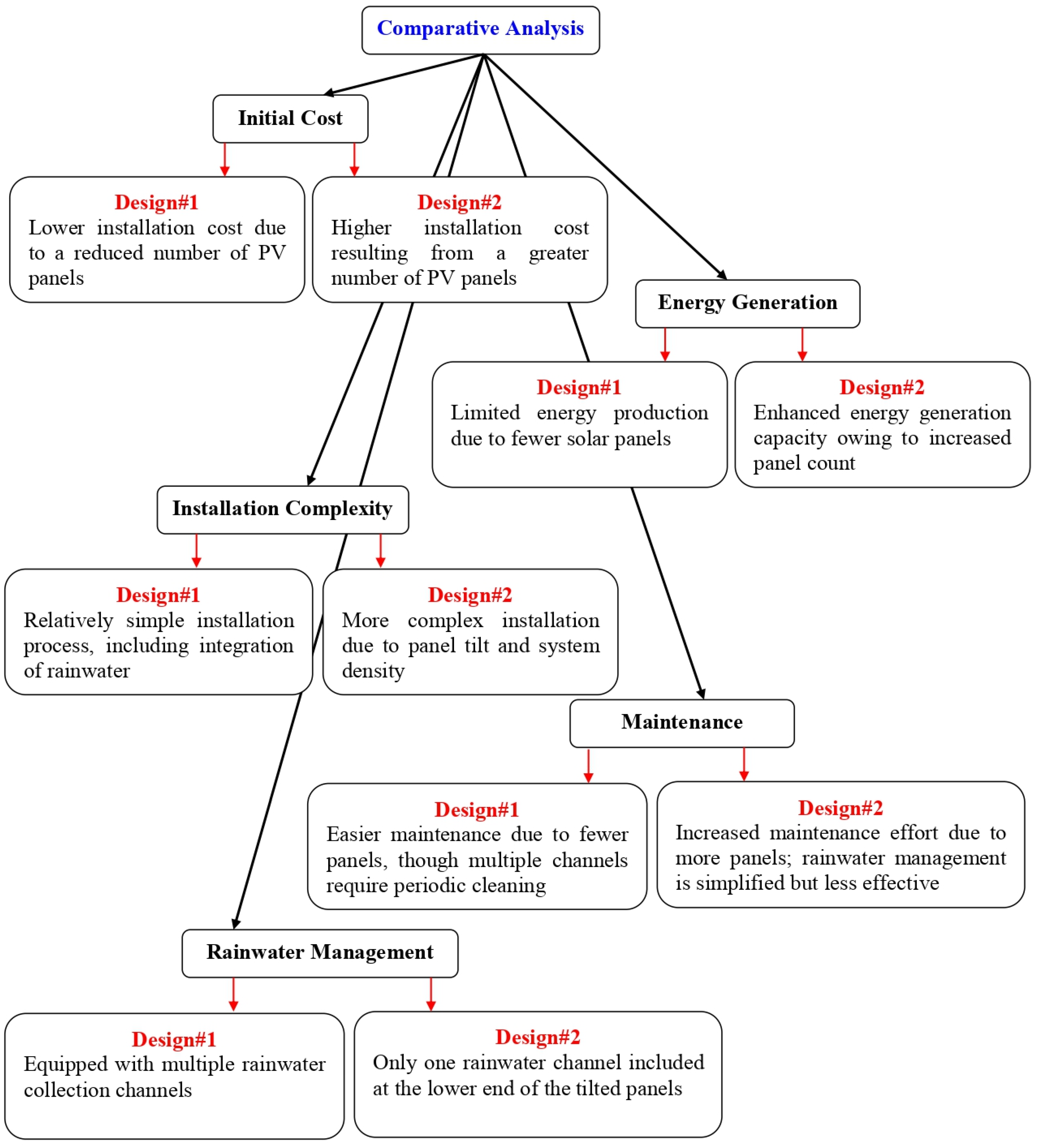
- Second, to evaluate the potential of water savings from the use of the solar system for irrigation purposes and generating electricity for the building.
- Third, to evaluate the technical performance, environmental impact, and economic feasibility of patented hybrid systems using RETScreen Expert software (version 9.1, 2023) to provide a comprehensive understanding of the system’s performance and financial feasibility.
2. Materials and Methods
2.1. Study Area
2.2. Dataset
2.2.1. Ground-Based Gauge Rainfall Data
2.2.2. Satellite-Based Rainfall Data
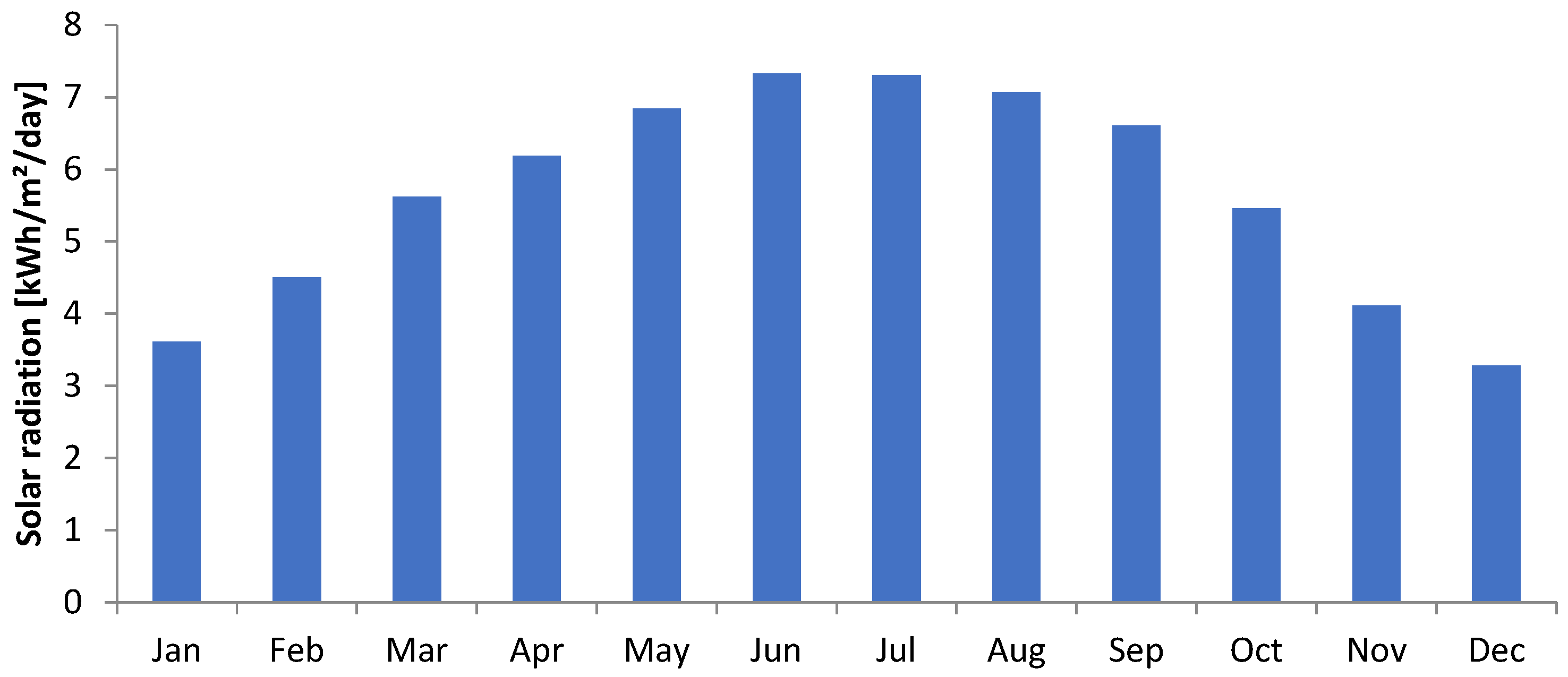
2.2.3. Solar Radiation Dataset
2.3. System Design
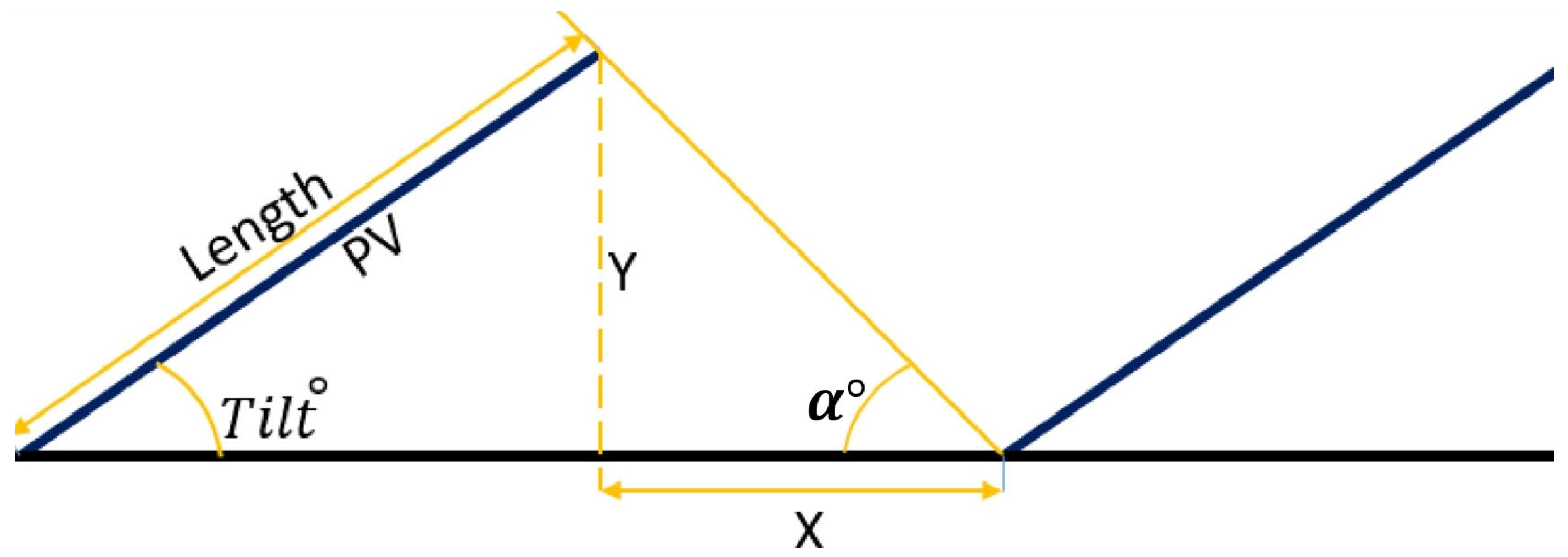
2.3.1. Shading Distance Calculations
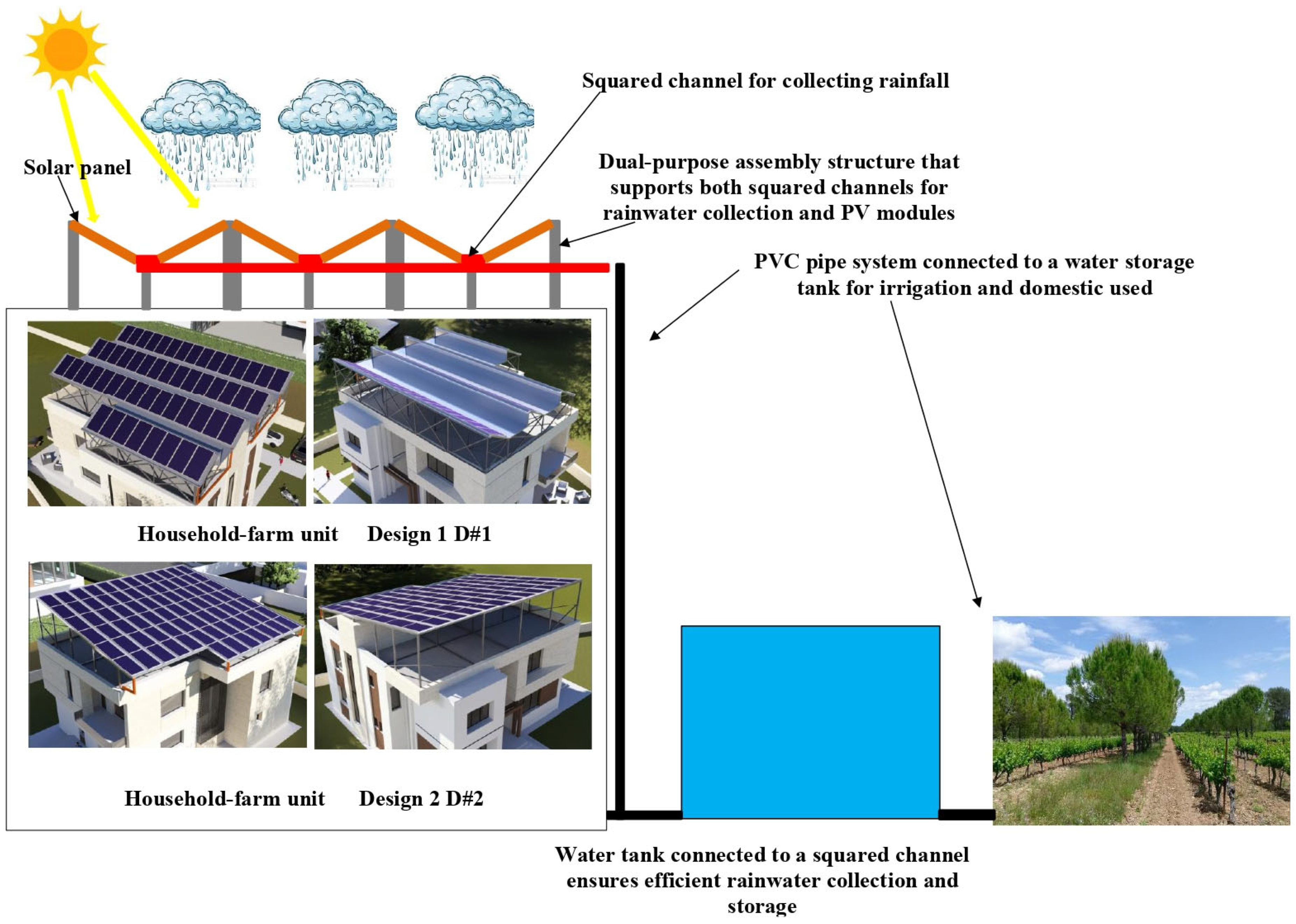
2.3.2. Description of System
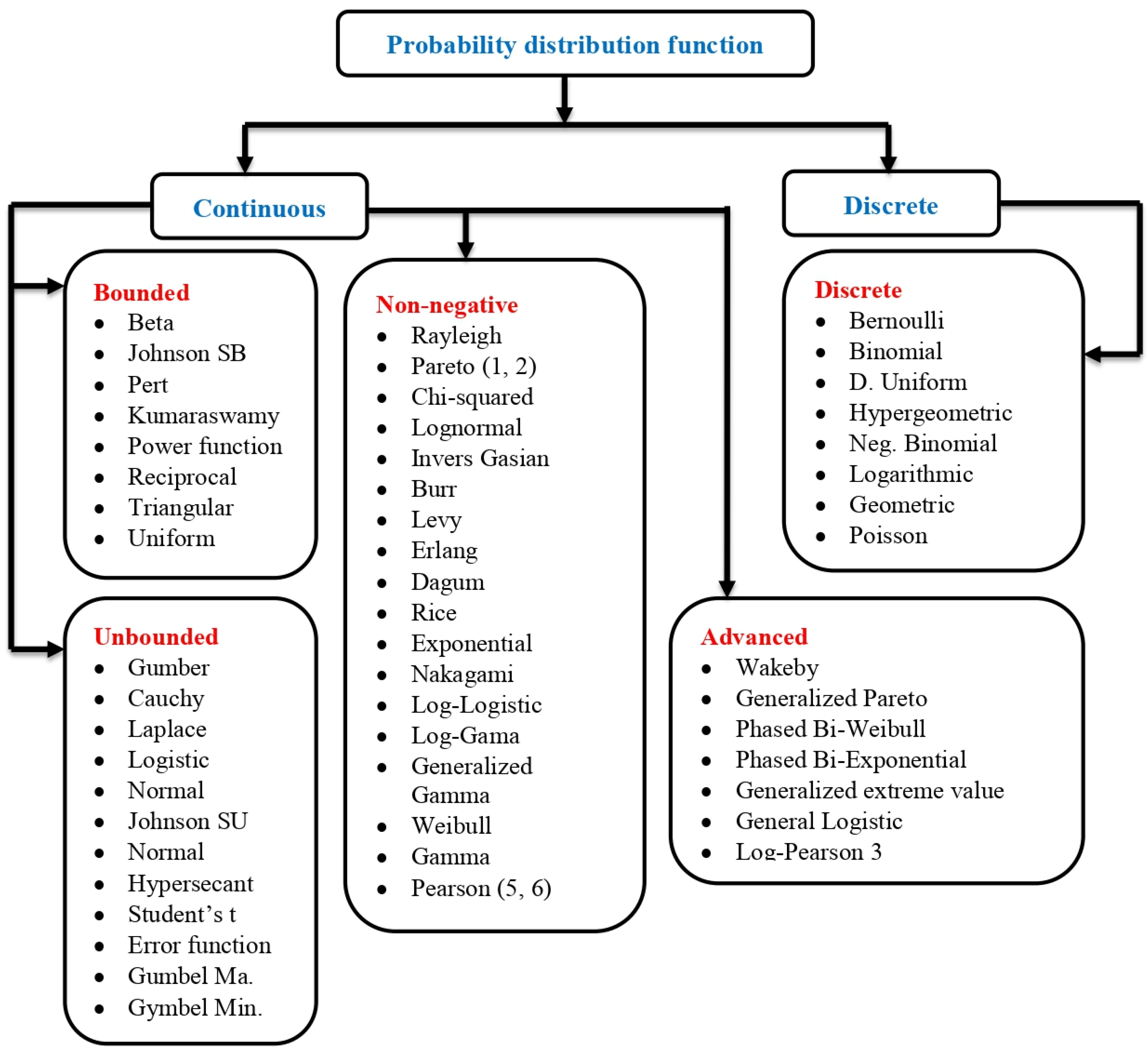
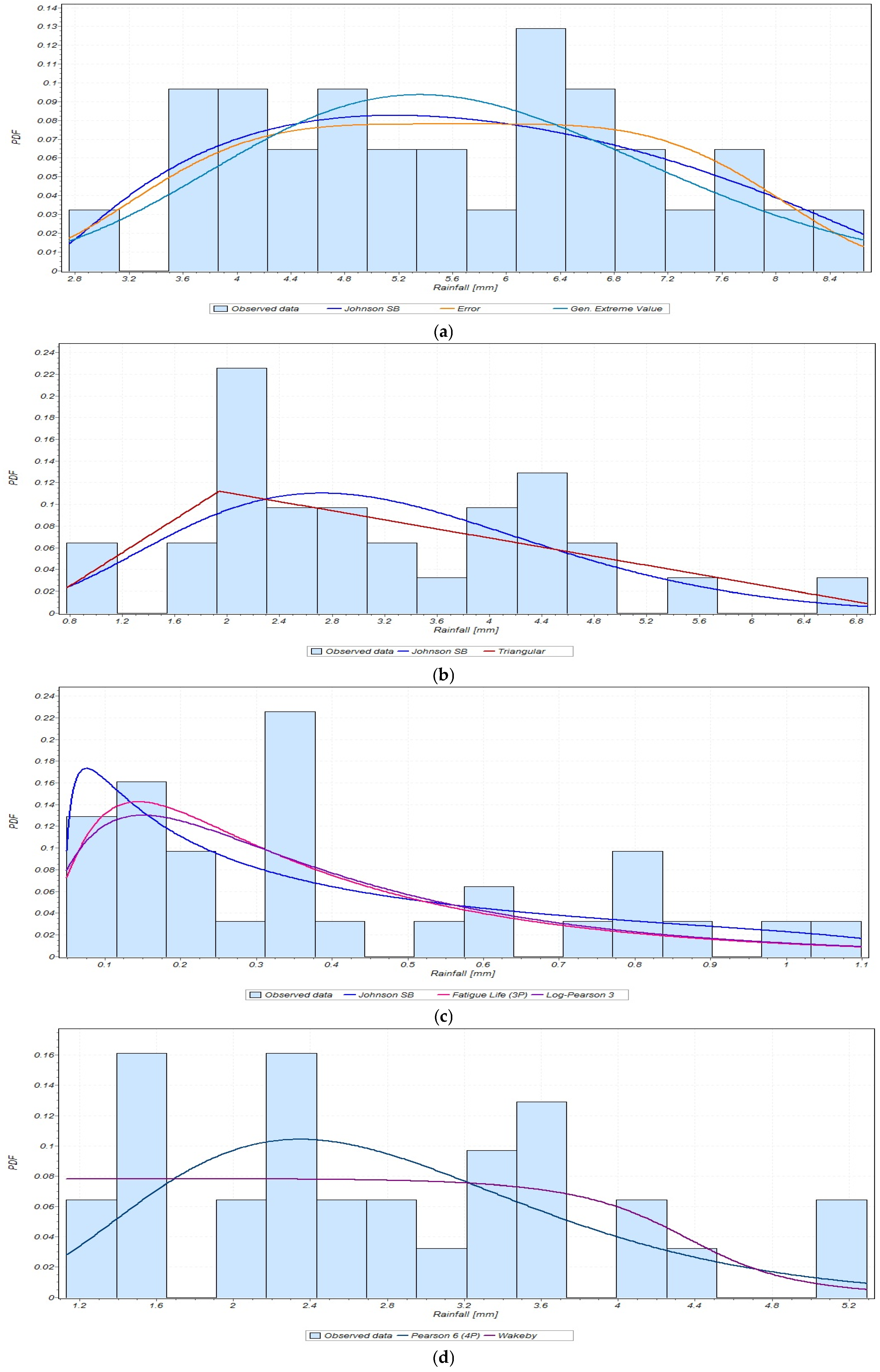
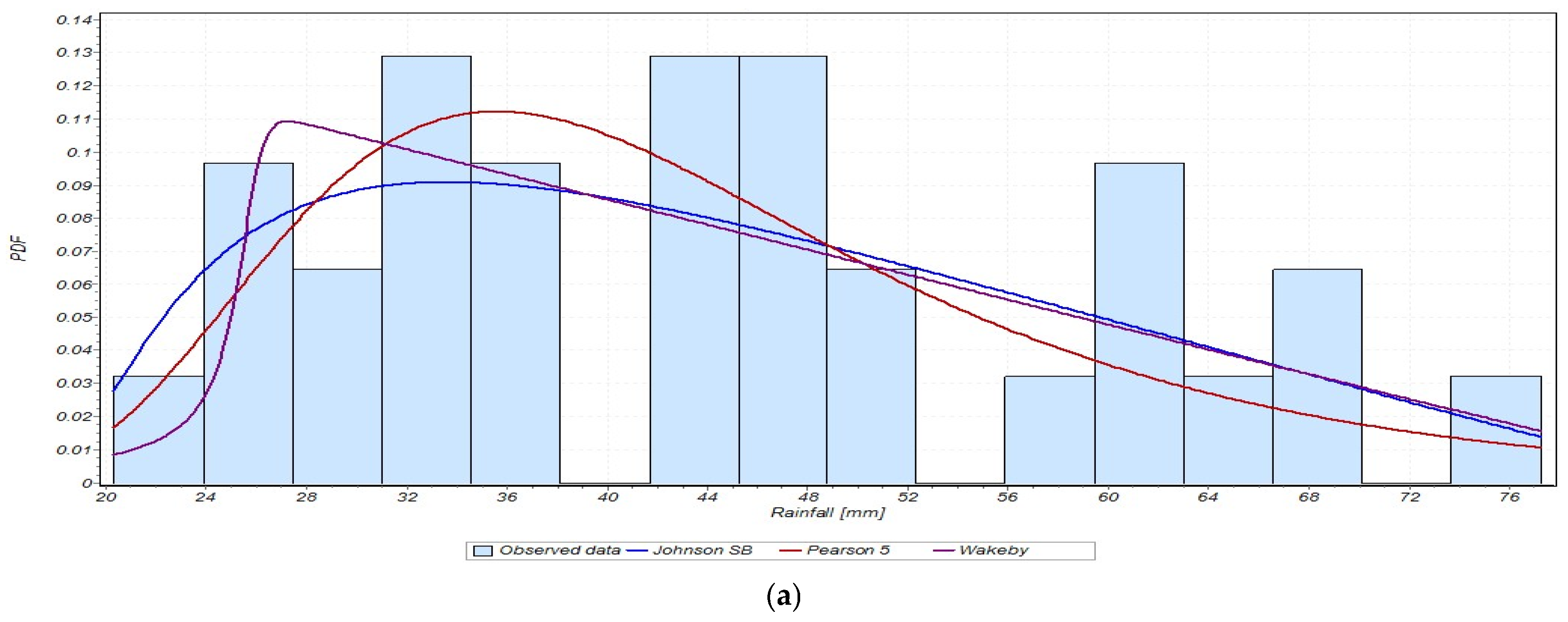
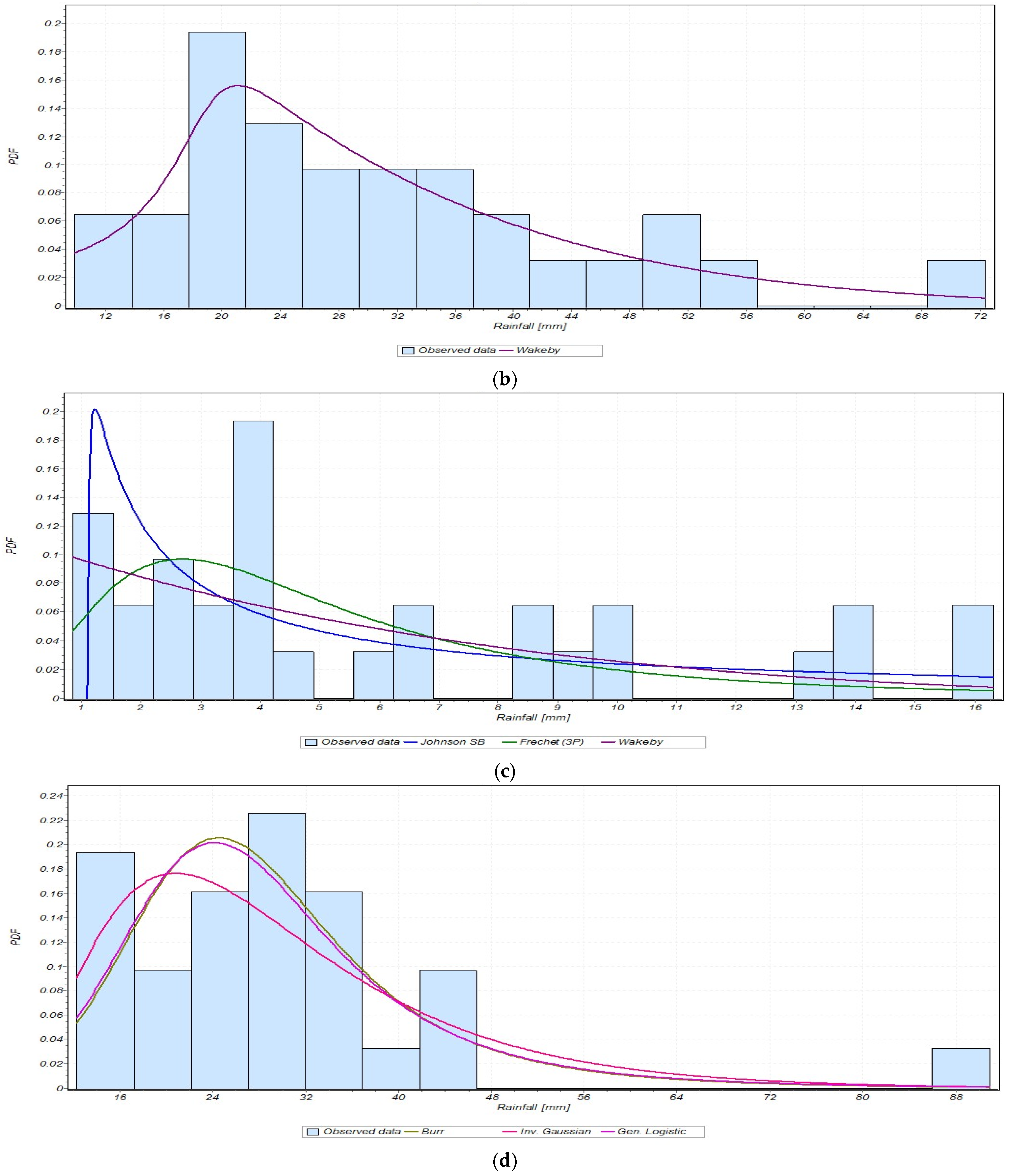
2.4. Analyzing the Distribution of Rainfall
2.5. Assessment of Rainwater Harvesting Potential
2.6. Economic Model
3. Results and Discussion
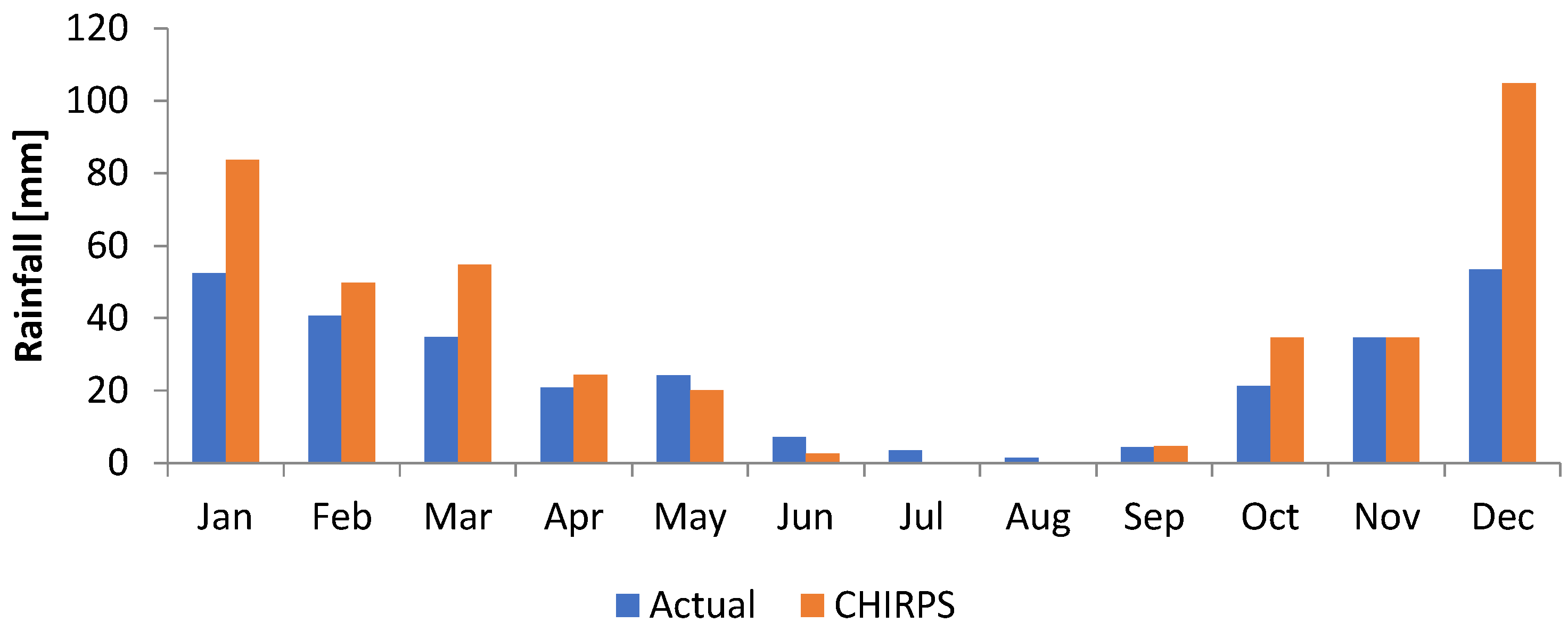
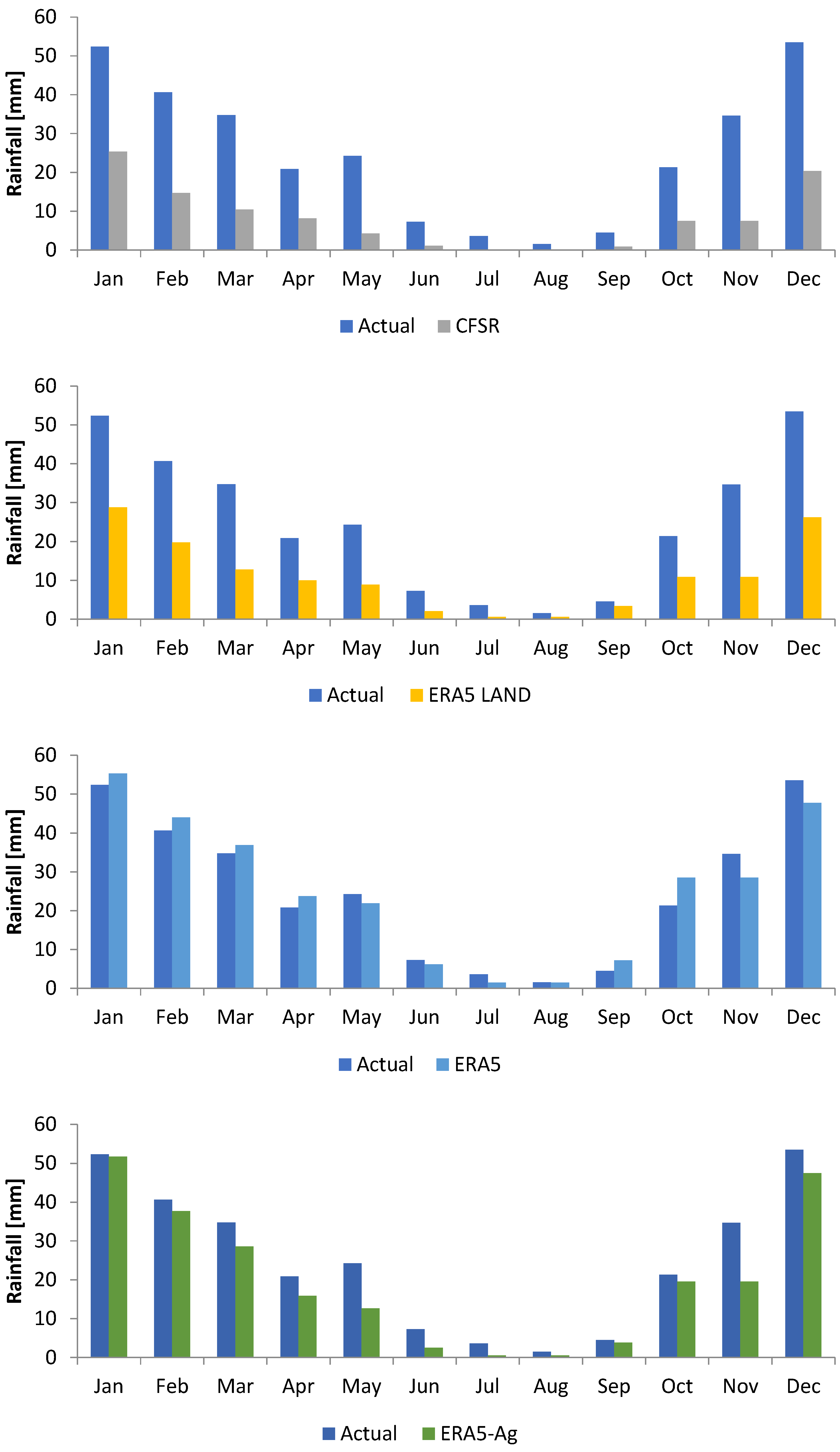
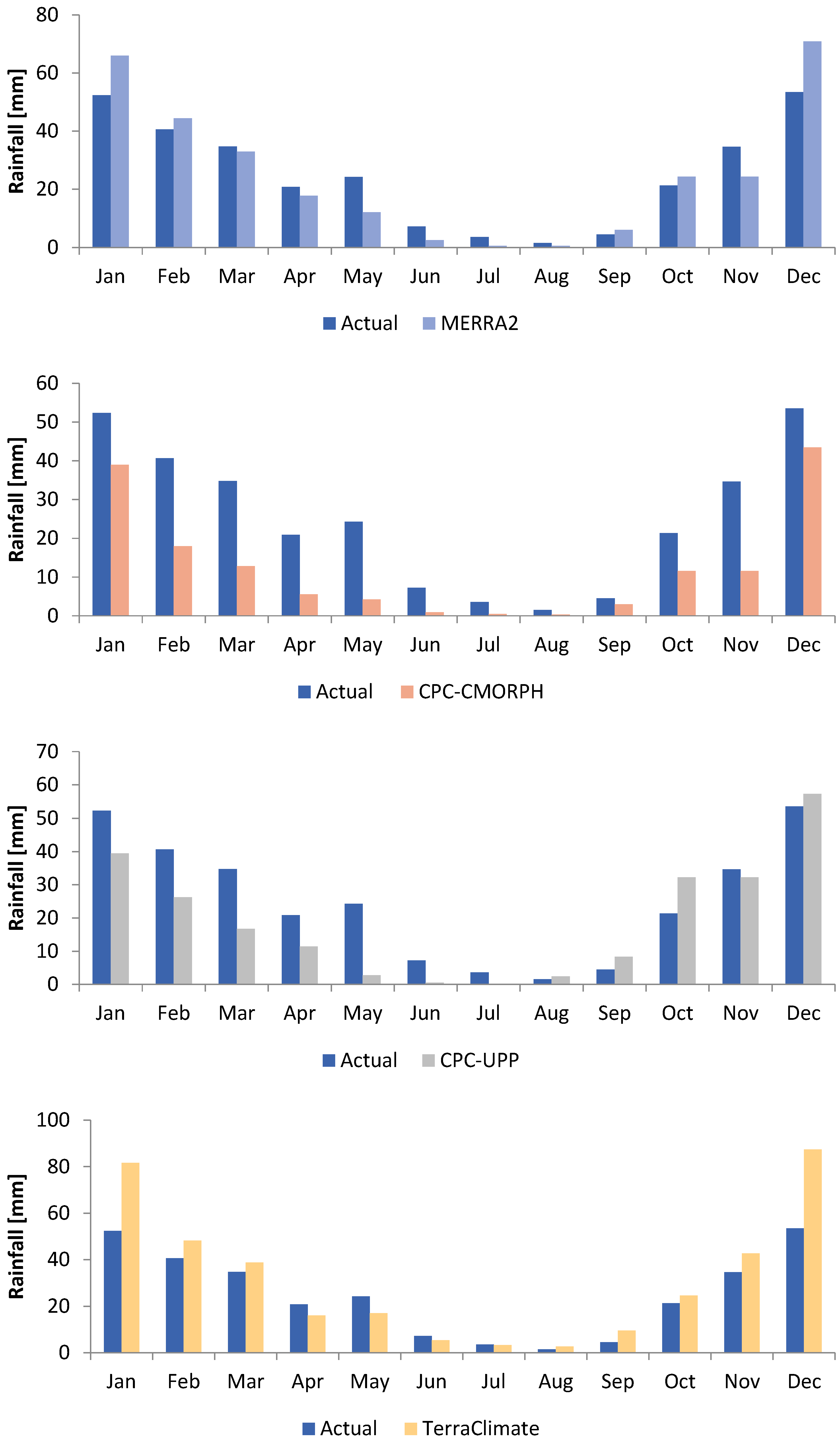
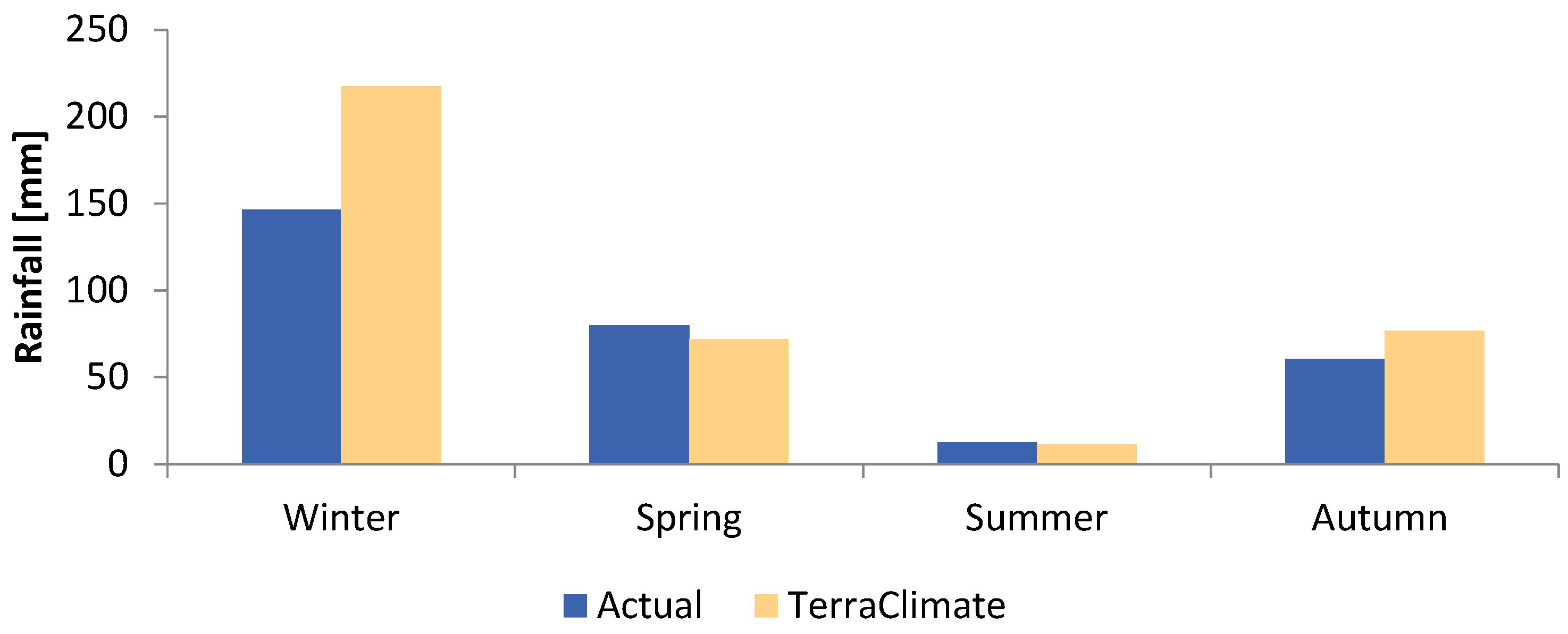
3.1. Comparison of Nine Satellite Rainfall Products
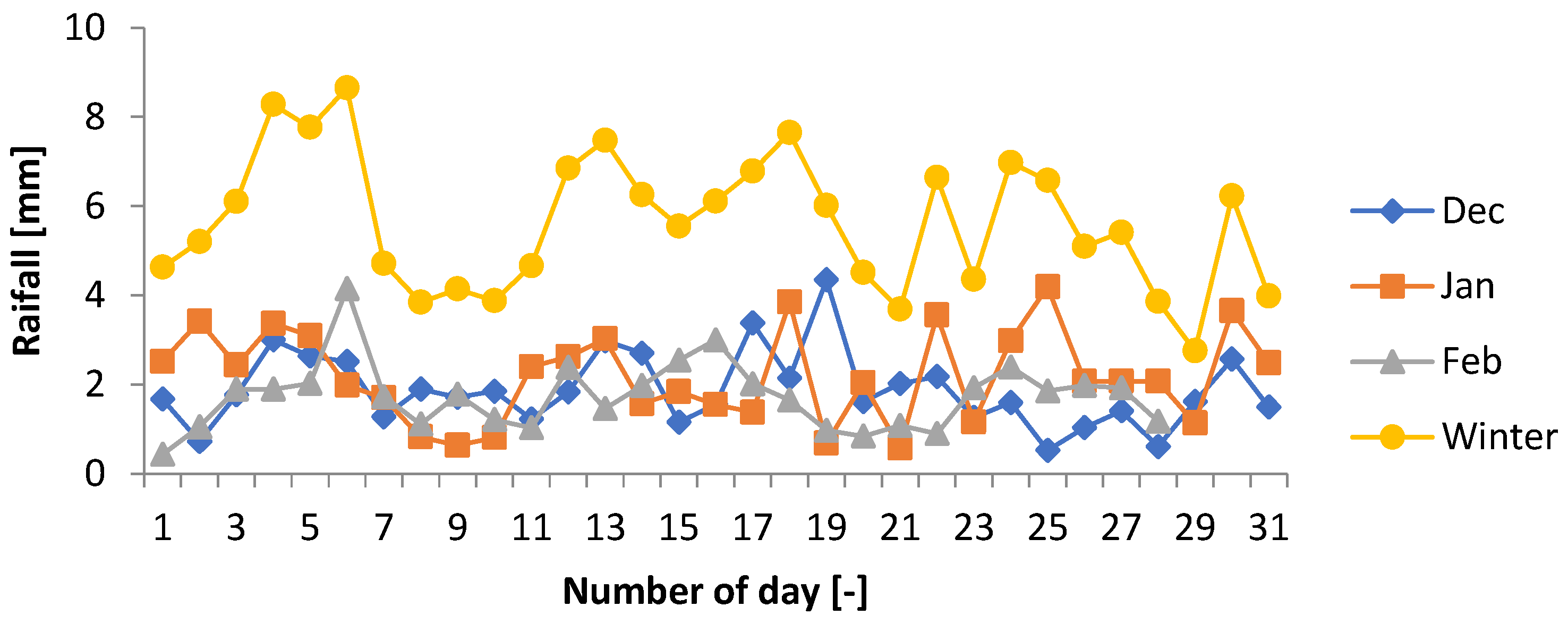
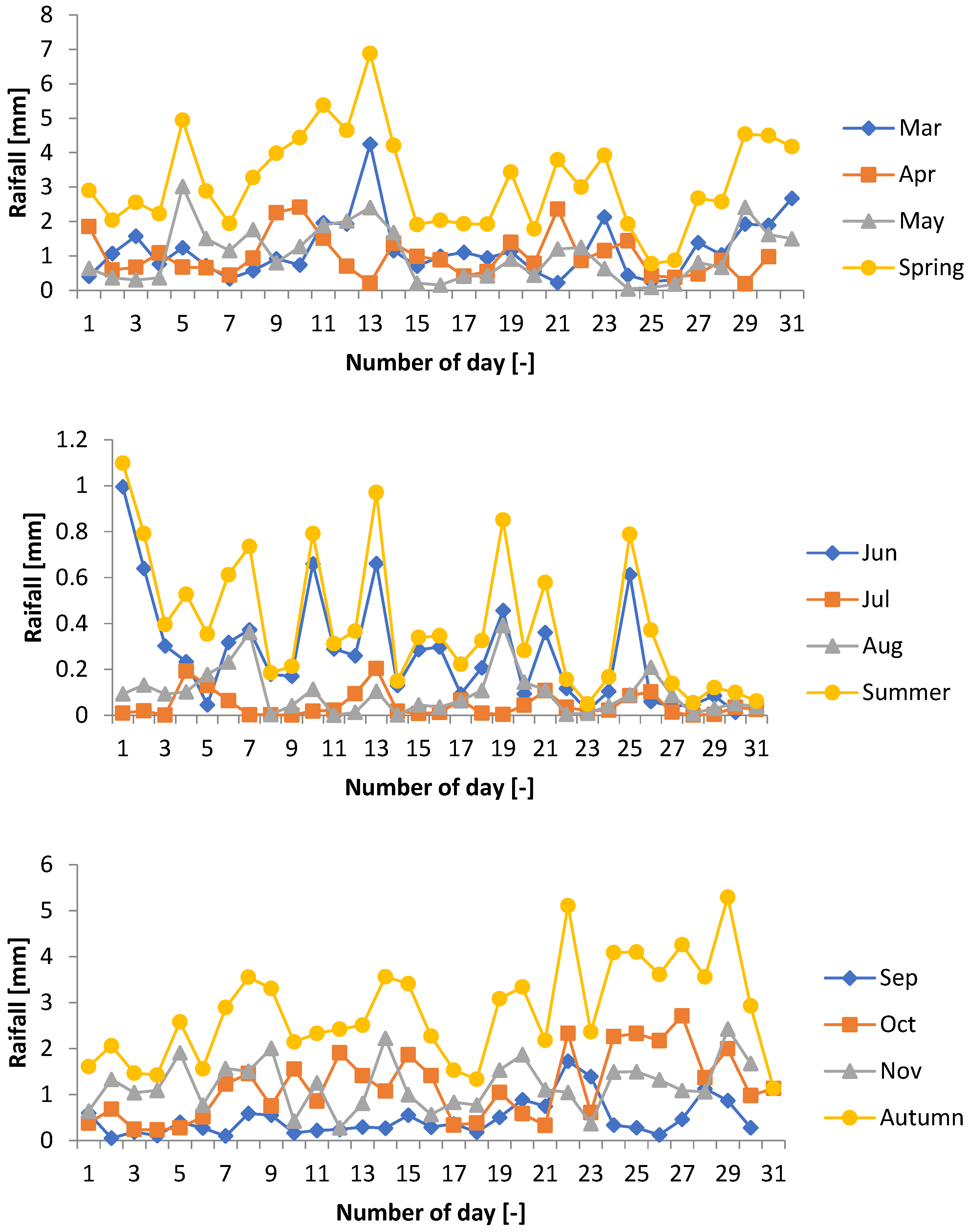
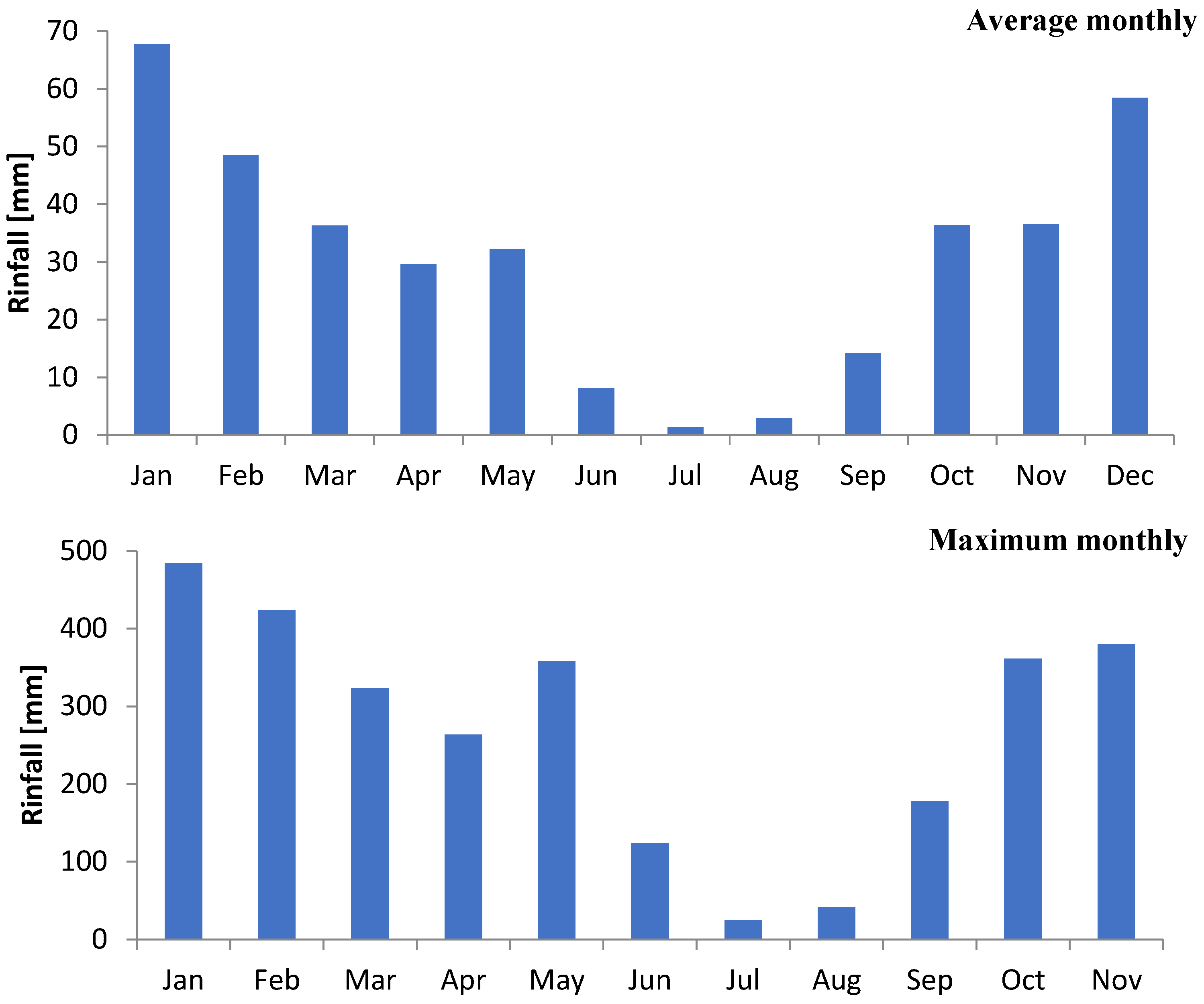
3.2. Characteristics of Rainfall in the Selected Location
3.2.1. Selecting the Best-Fit Results for Average Daily and Seasonally Rainfall
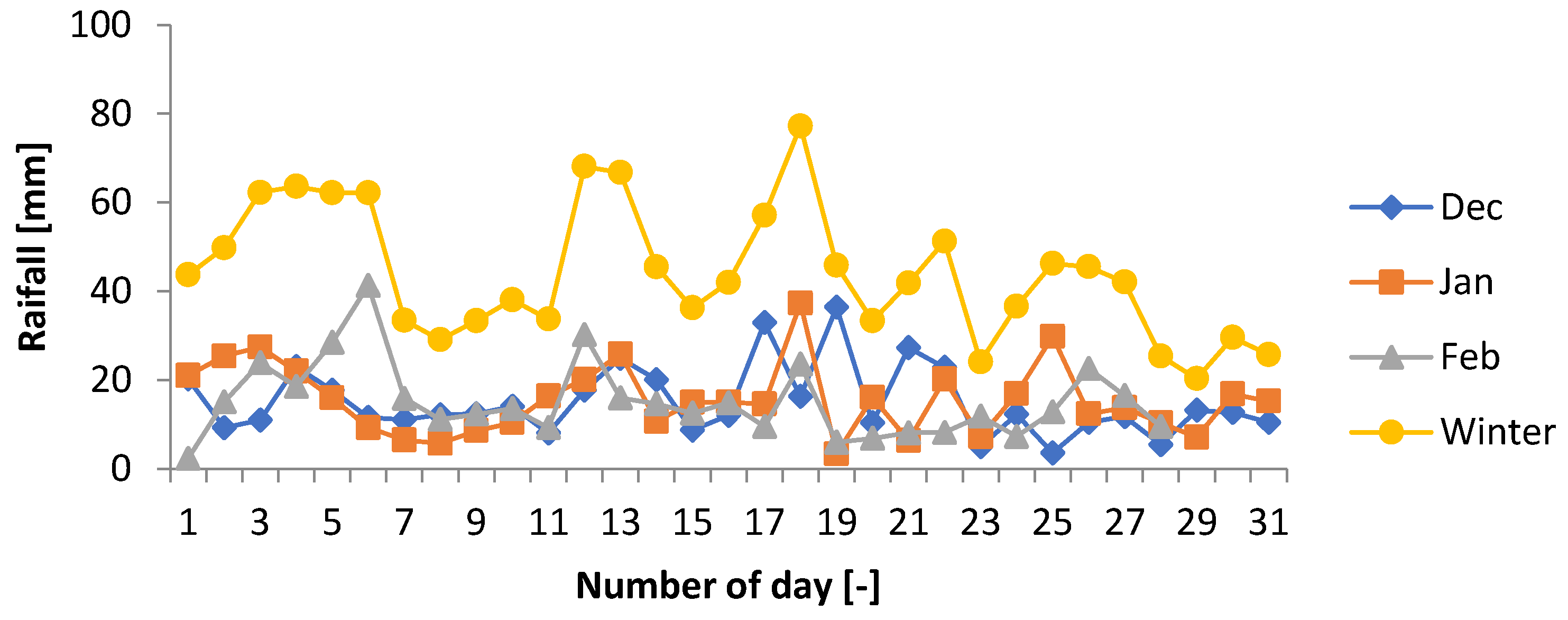
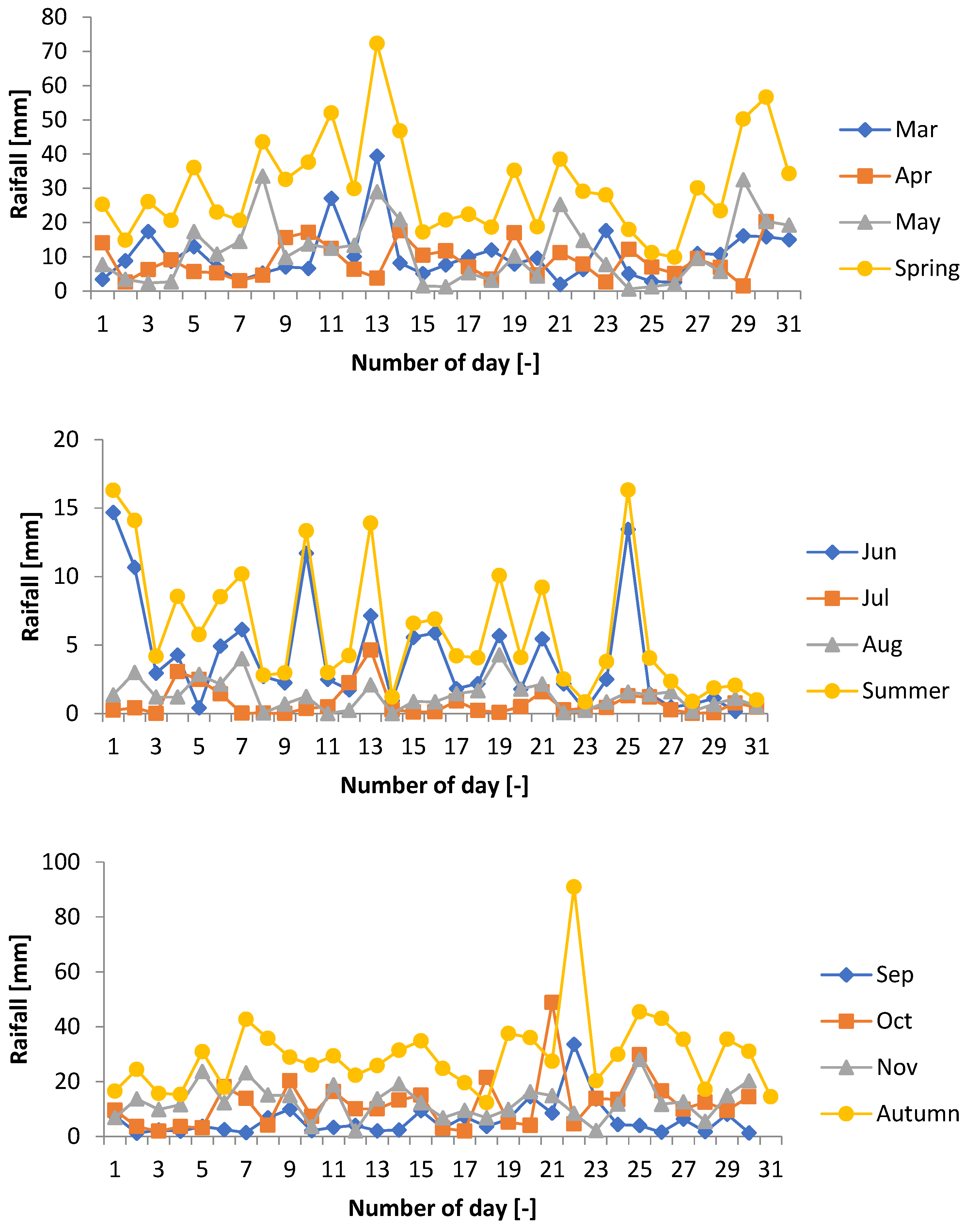
3.2.2. Selecting the Best-Fit Results for Maximum Daily and Seasonal Rainfall
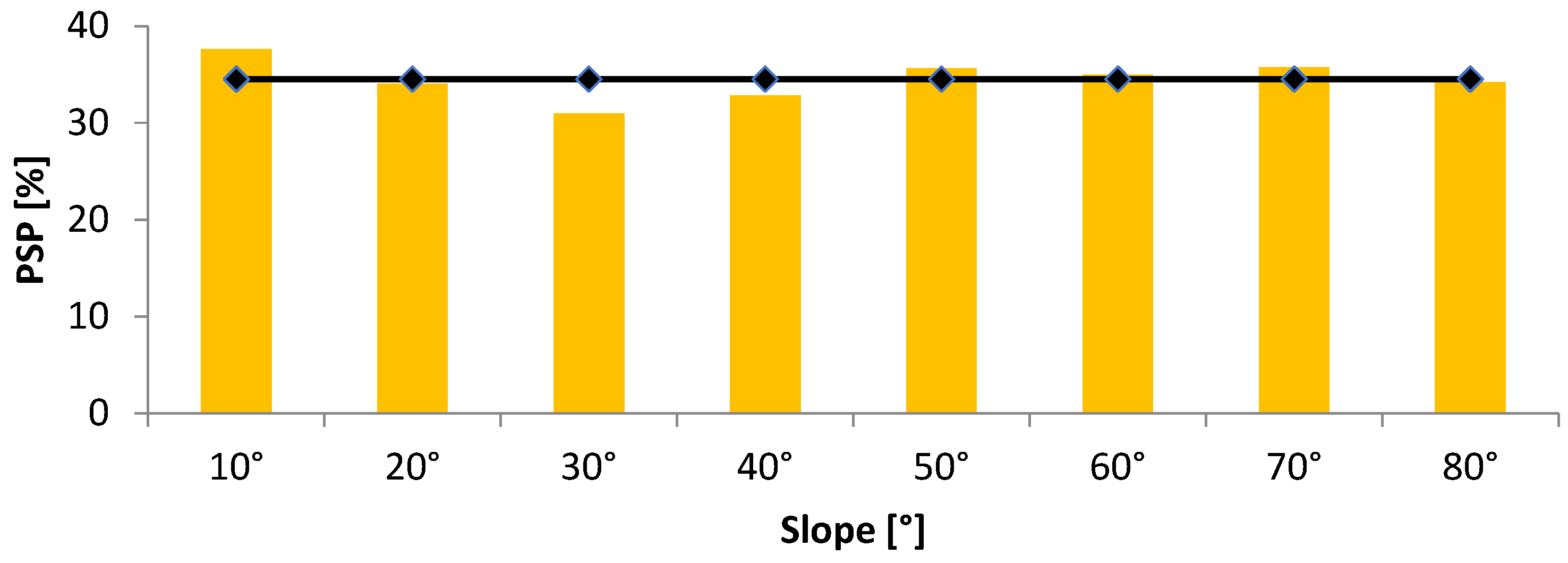
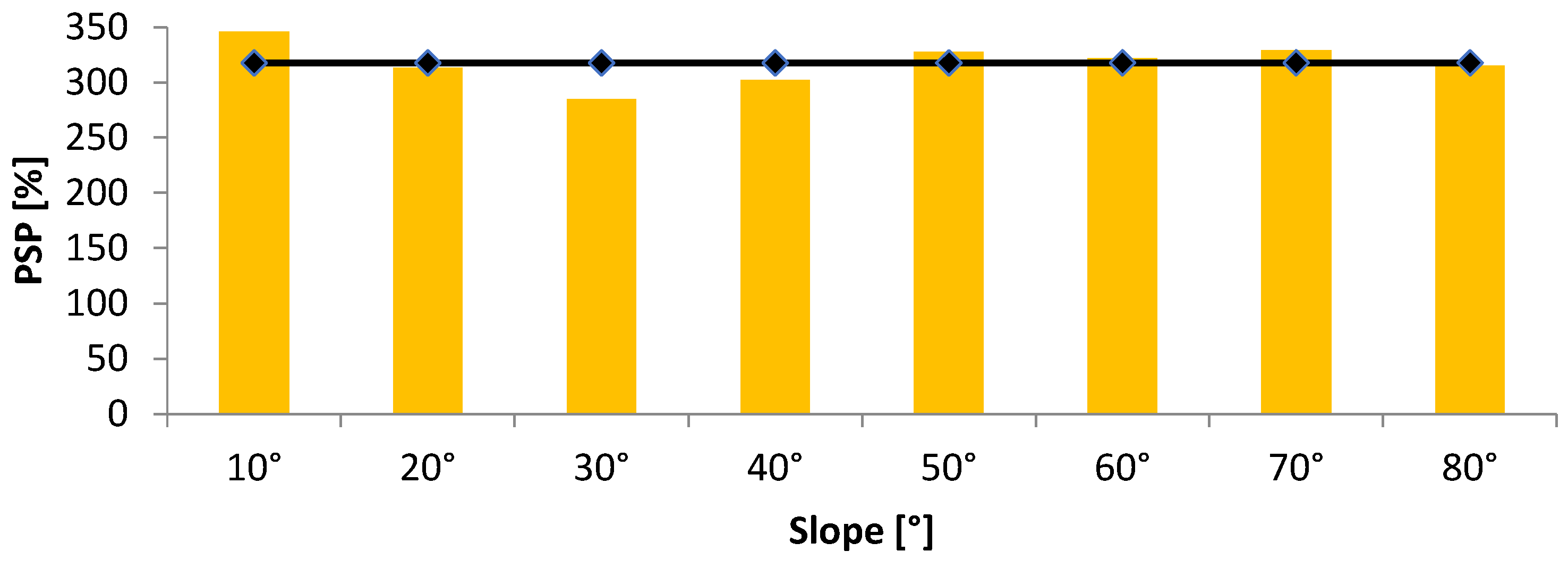
3.3. Potential Rainwater Harvesting
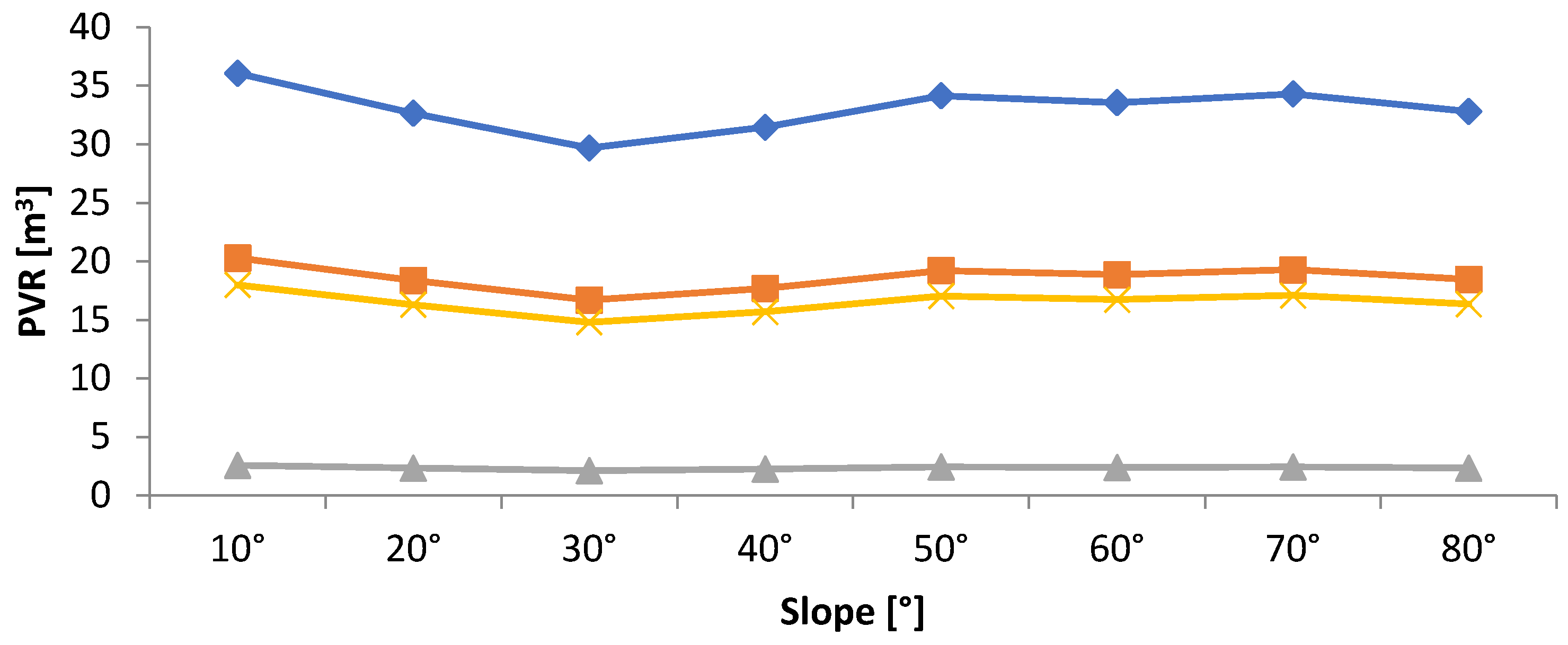
- It is found that the value of rainwater that can be collected from the roof of the selected building is 30–36 m3, 17–20m3, 2–3 m3, and 15–18m3 for winter, spring, summer, and autumn, respectively, based on the average daily data.
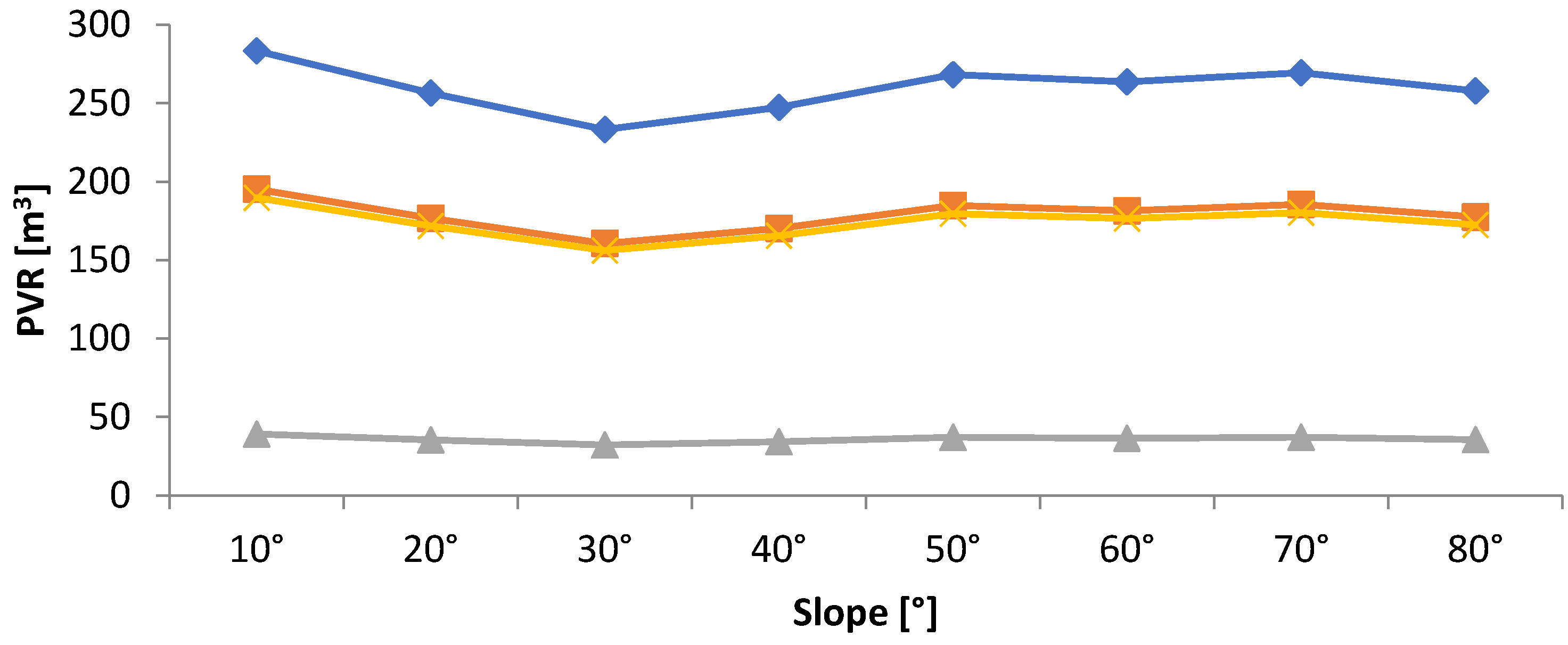
- Based on the maximum daily statistics, it is determined that the amount of rainwater that can be gathered from the rooftop of the building selected is 283–233 m3, 195–161 m3, 39–32 m3, and 190–156 m3 for winter, spring, summer, and fall, respectively.
- Besides, the highest of 36 m3 and 283 m3 of rainwater that can be collected from the roof of the selected buildings at the tilt angle of 10° is found in the winter season.
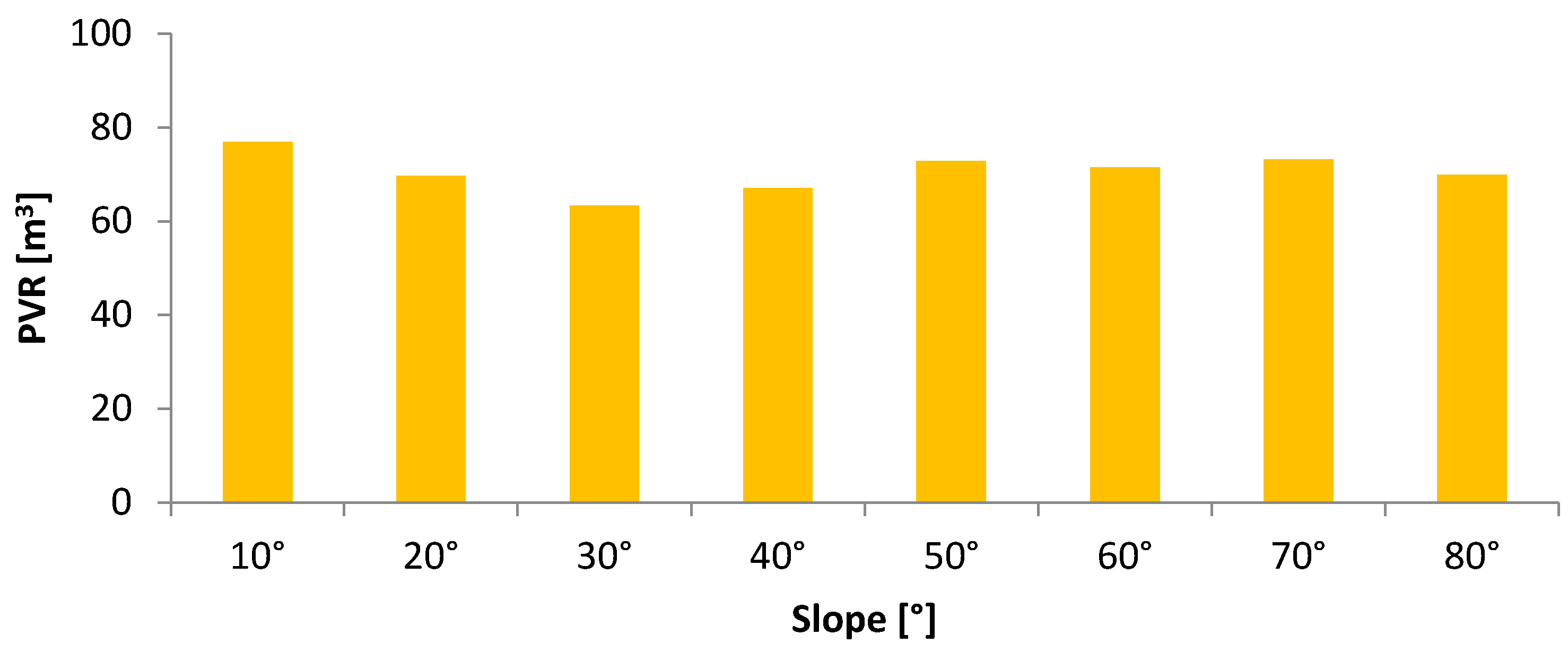
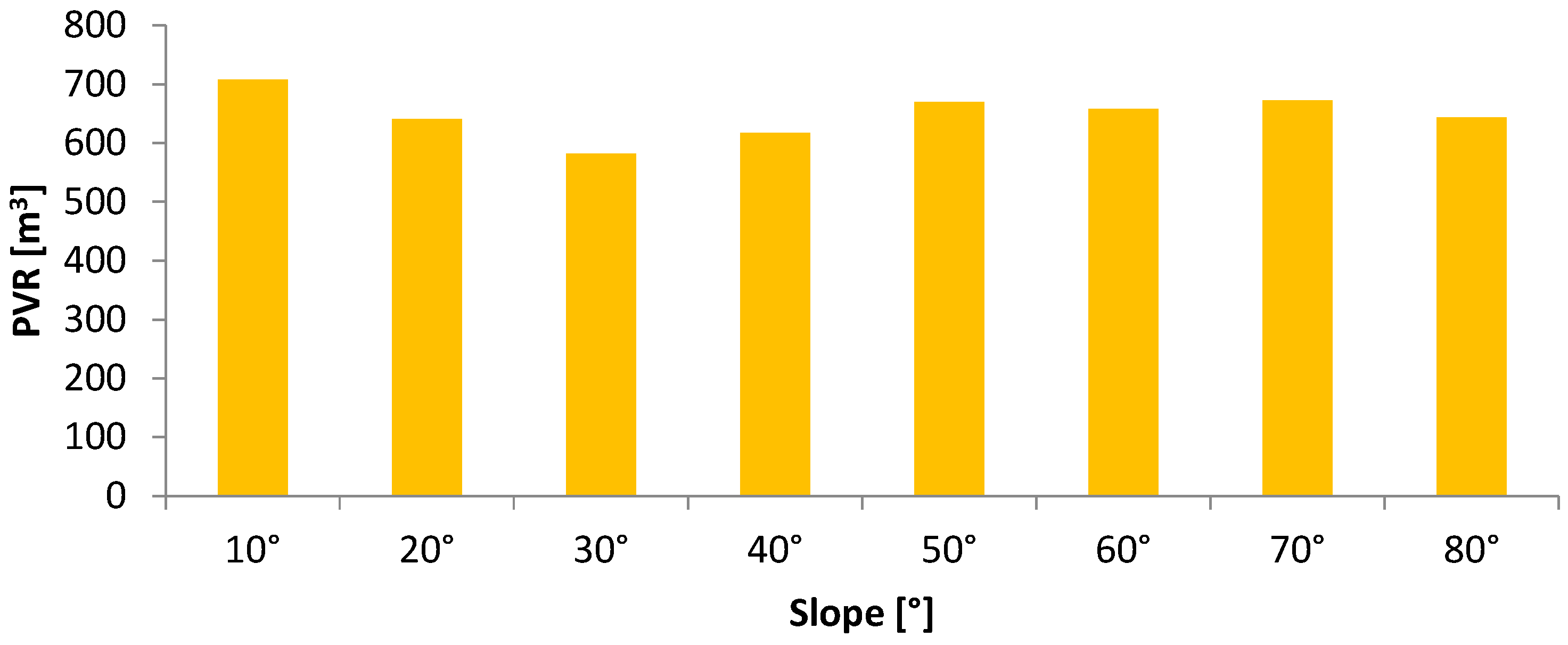
- Moreover, the annual rainwater that can be gathered from the rooftop is estimated to vary from 77 m3 to 63 m3, with an average of 71 m3, based on the average daily data and from 708 m3 to 582 m3, with an average of 649 m3, based on the maximum daily data.
3.4. Techno-Economic Feasibility of the Proposed System
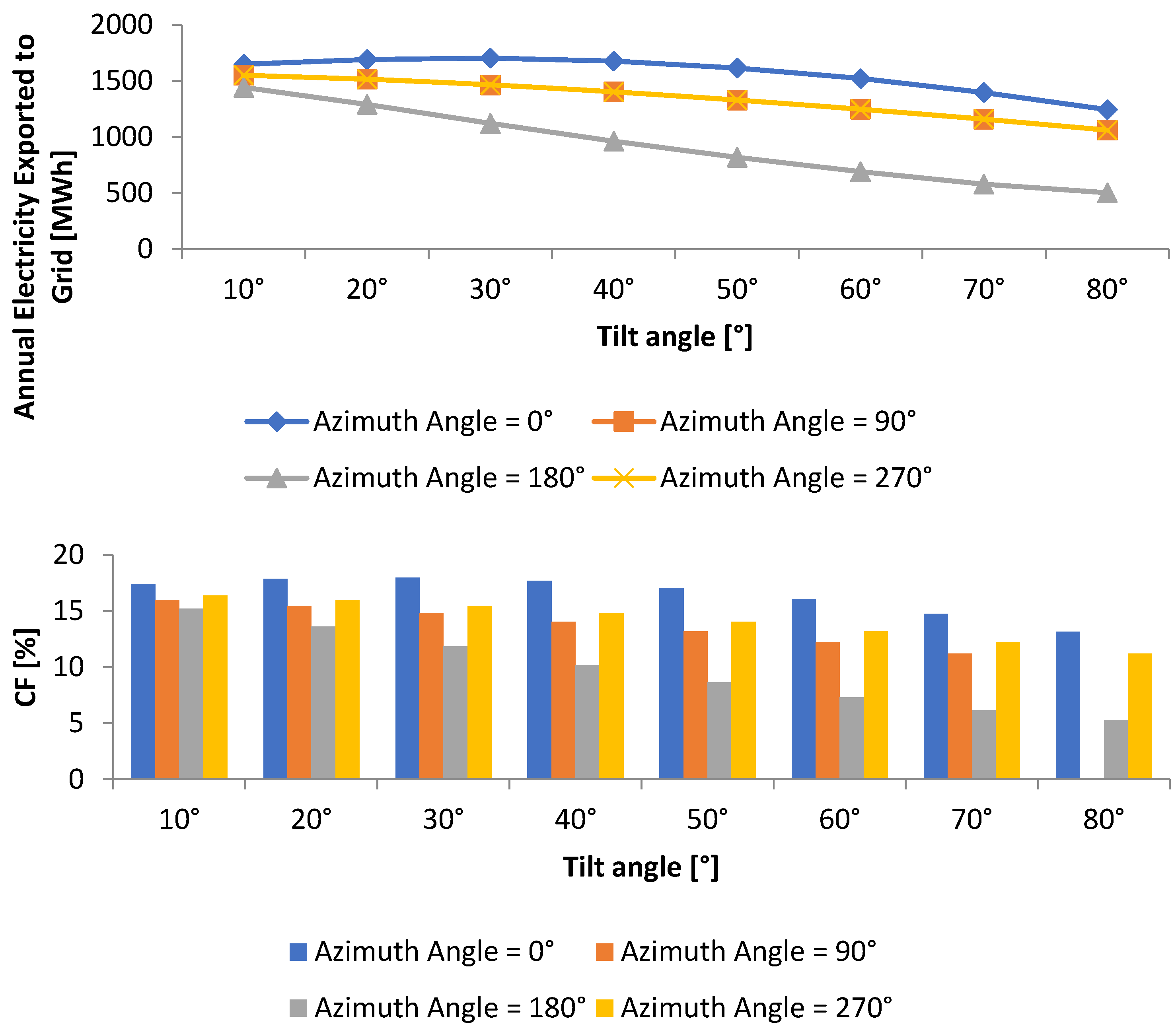
3.4.1. Optimum Tilt and Azimuth Angle of the Proposed System
3.4.2. Techno-Economic Feasibility of the Proposed System
4. Conclusions
5. Limitations and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morante-Carballo, F.; Montalván-Burbano, N.; Quiñonez-Barzola, X.; Jaya-Montalvo, M.; Carrión-Mero, P. What do we know about water scarcity in semi-arid zones? A global analysis and research trends. Water 2022, 14, 2685. [Google Scholar] [CrossRef]
- Jha, M.K.; Dev, M. Impacts of climate change. In Smart Internet of Things for Environment and Healthcare; Springer Nature: Cham, Switzerland, 2024; pp. 139–159. [Google Scholar]
- Shemer, H.; Wald, S.; Semiat, R. Challenges and solutions for global water scarcity. Membranes 2023, 13, 612. [Google Scholar] [CrossRef] [PubMed]
- Elhassnaoui, I.; Moumen, Z.; Tvaronavičienė, M.; Ouarani, M.; Ben-Daoud, M.; Serrari, I.; Hasnaoui, M.D. Management of water scarcity in arid areas: A case study (Ziz Watershed). Insights Reg. Dev. 2021, 3, 80–103. [Google Scholar] [CrossRef] [PubMed]
- Biswas, A.; Sarkar, S.; Das, S.; Dutta, S.; Choudhury, M.R.; Giri, A.; Bera, B.; Bag, K.; Mukherjee, B.; Banerjee, K.; et al. Water scarcity: A global hindrance to sustainable development and agricultural production–A critical review of the impacts and adaptation strategies. Camb. Prism. Water 2025, 3, e4. [Google Scholar] [CrossRef]
- Lepcha, R.; Patra, S.K.; Ray, R.; Thapa, S.; Baral, D.; Saha, S. Rooftop rainwater harvesting a solution to water scarcity: A review. Groundw. Sustain. Dev. 2024, 26, 101305. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M. Water use and stress. Our World in Data. 2018. Available online: https://ourworldindata.org/water-use-stress?utm_source=gonpath-newsletter.beehiiv.com&utm_medium=referral&utm_campaign=economias-hidricas (accessed on 3 September 2025).
- Tiwari, K.; Goyal, R.; Sarkar, A. GIS-based methodology for identification of suitable locations for rainwater harvesting structures. Water Resour. Manag. 2018, 32, 1811–1825. [Google Scholar] [CrossRef]
- Ezzeldin, M.; Konstantinovich, S.E.; Igorevich, G.I. Determining the suitability of rainwater harvesting for the achievement of sustainable development goals in WadiWatir, Egypt using GIS techniques. J. Environ. Manag. 2022, 313, 114990. [Google Scholar] [CrossRef]
- Velis, M.; Conti, K.I.; Biermann, F. Groundwater and human development: Synergies and trade-offs within the context of the sustainable development goals. Sustain. Sci. 2017, 12, 1007–1017. [Google Scholar] [CrossRef]
- Mperejekumana, P.; Shen, L.; Zhong, S.; Muhirwa, F.; Gaballah, M.S.; Nsigayehe, J.M.V. Integrating climate change adaptation into water-energy-food-environment nexus for sustainable development in East African Community. J. Clean. Prod. 2024, 434, 140026. [Google Scholar] [CrossRef]
- Hoang, A.T.; Nguyen, X.P. Integrating renewable sources into energy system for smart city as a sagacious strategy towards clean and sustainable process. J. Clean. Prod. 2021, 305, 127161. [Google Scholar] [CrossRef]
- Ghadami, N.; Gheibi, M.; Kian, Z.; Faramarz, M.G.; Naghedi, R.; Eftekhari, M.; Fathollahi-Fard, A.M.; Dulebenets, A.A.; Tian, G. Implementation of solar energy in smart cities using an integration of artificial neural network, photovoltaic system and classical Delphi methods. Sustain. Cities Soc. 2021, 74, 103149. [Google Scholar] [CrossRef]
- Kumar, C.M.S.; Singh, S.; Gupta, M.K.; Nimdeo, Y.M.; Raushan, R.; Deorankar, A.V.; Ananda Kumar, T.M.; Rout, P.K.; Chanotiya, C.S.; Nannaware, A.D.; et al. Solar energy: A promising renewable source for meeting energy demand in Indian agriculture applications. Sustain. Energy Technol. Assess. 2023, 55, 102905. [Google Scholar] [CrossRef]
- Kanwal, S.; Mehran, M.T.; Hassan, M.; Anwar, M.; Naqvi, S.R.; Khoja, A.H. An integrated future approach for the energy security of Pakistan: Replacement of fossil fuels with syngas for better environment and socio-economic development. Renew. Sustain. Energy Rev. 2022, 156, 111978. [Google Scholar] [CrossRef]
- Yu, J.; Tang, Y.M.; Chau, K.Y.; Nazar, R.; Ali, S.; Iqbal, W. Role of solar-based renewable energy in mitigating CO2 emissions: Evidence from quantile-on-quantile estimation. Renew. Energy 2022, 182, 216–226. [Google Scholar] [CrossRef]
- Belaïd, F.; Al-Sarihi, A.; Al-Mestneer, R. Balancing climate mitigation and energy security goals amid converging global energy crises: The role of green investments. Renew. Energy 2023, 205, 534–542. [Google Scholar] [CrossRef]
- Bouckaert, S.; Pales, A.F.; McGlade, C.; Remme, U.; Wanner, B.; Varro, L.; D’Ambrosio, D.; Spencer, T. Net Zero by 2050: A Roadmap for the Global Energy Sector; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2021. [Google Scholar]
- Rahman, A. Recent advances in modelling and implementation of rainwater harvesting systems towards sustainable development. Water 2017, 9, 959. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Jing, X.; Wang, Y.; Wang, Y.; Yue, T. Water saving efficiency and reliability of rainwater harvesting systems in the context of climate change. J. Clean. Prod. 2018, 196, 1341–1355. [Google Scholar] [CrossRef]
- Harka, A.E.; Roba, N.T.; Kassa, A.K. Modelling rainfall runoff for identification of suitable water harvesting sites in Dawe River watershed, Wabe Shebelle River basin, Ethiopia. J. Water Land Dev. 2020, 47, 186–195. [Google Scholar] [CrossRef]
- Elewa, H.H.; Zelenakova, M.; Nosair, A.M. Integration of the analytical hierarchy process and GIS spatial distribution model to determine the possibility of runoff water harvesting in dry regions: WadiWatir in Sinai as a case study. Water 2021, 13, 804. [Google Scholar] [CrossRef]
- Rahmat, S.N.; Al-Gheethi, A.A.S.; Ayob, S.; MohdShahli, F. Development of dual water supply using rooftop rainwater harvesting and groundwater systems. SN Appl. Sci. 2020, 2, 85. [Google Scholar] [CrossRef]
- Leong, J.Y.C.; Chong, M.N.; Poh, P.E.; Hermawan, A.; Talei, A. Longitudinal assessment of rainwater quality under tropical climatic conditions in enabling effective rainwater harvesting and reuse schemes. J. Clean. Prod. 2017, 143, 64–75. [Google Scholar] [CrossRef]
- Wartalska, K.; Grzegorzek, M.; Bełcik, M.; Wdowikowski, M.; Kolanek, A.; Niemierka, E.; Jadwiszczak, P.; Kaźmierczak, B. The potential of rainwater harvesting systems in Europe–Current state of Art and future perspectives. Water Resour. Manag. 2024, 38, 4657–4683. [Google Scholar] [CrossRef]
- Lasage, R.; Verburg, P.H. Evaluation of small scale water harvesting techniques for semi-arid environments. J. Arid Environ. 2015, 118, 48–57. [Google Scholar] [CrossRef]
- Snelling, A.M.; Lamond, J.; Everett, G.; O’Donnell, E.C.; Ahilan, S.; Thorne, C. Public perceptions of rainwater harvesting (RWH): Comparing users and non-users of RWH systems. Urban Water J. 2024, 21, 181–189. [Google Scholar] [CrossRef]
- Lee, K.E.; Mokhtar, M.; Hanafiah, M.M.; Halim, A.A.; Badusah, J. Rainwater harvesting as an alternative water resource in Malaysia: Potential, policies and development. J. Clean. Prod. 2016, 126, 218–222. [Google Scholar] [CrossRef]
- Raimondi, A.; Quinn, R.; Abhijith, G.R.; Becciu, G.; Ostfeld, A. Rainwater harvesting and treatment: State of the art and perspectives. Water 2023, 15, 1518. [Google Scholar] [CrossRef]
- Crosson, C.; Tong, D.; Zhang, Y.; Zhong, Q. Rainwater as a renewable resource to achieve net zero urban water in water stressed cities. Resour. Conserv. Recycl. 2021, 164, 105203. [Google Scholar] [CrossRef]
- Alim, M.A.; Rahman, A.; Tao, Z.; Samali, B.; Khan, M.M.; Shirin, S. Suitability of roof harvested rainwater for potential potable water production: A scoping review. J. Clean. Prod. 2020, 248, 119226. [Google Scholar] [CrossRef]
- Alim, M.A.; Rahman, A.; Tao, Z.; Samali, B.; Khan, M.M.; Shirin, S. Feasibility analysis of a small-scale rainwater harvesting system for drinking water production at Werrington, New South Wales, Australia. J. Clean. Prod. 2020, 270, 122437. [Google Scholar] [CrossRef]
- de Sá Silva, A.C.R.; Bimbato, A.M.; Balestieri, J.A.P.; Vilanova, M.R.N. Exploring environmental, economic and social aspects of rainwater harvesting systems: A review. Sustain. Cities Soc. 2022, 76, 103475. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Li, X.Y. Water and energy conservation of rainwater harvesting system in the Loess Plateau of China. J. Integr. Agric. 2013, 12, 1389–1395. [Google Scholar] [CrossRef]
- Vargas-Parra, M.V.; Villalba, G.; Gabarrell, X. Applying exergy analysis to rainwater harvesting systems to assess resource efficiency. Resour. Conserv. Recycl. 2013, 72, 50–59. [Google Scholar] [CrossRef]
- Corrêa, J.D.P.; Fernandes, L.L.; Blanco, C.J.C.; Neves, R.R. Proposal of rainwater harvesting coefficient (RWHC) for determination of effectively usable rainfall depth, relevant to rainwater harvesting systems design. RBRH 2018, 23, e15. [Google Scholar] [CrossRef]
- Rahman, A. Rainwater harvesting for sustainable developments: Non-potable use, household irrigation and stormwater management. Water 2021, 13, 3460. [Google Scholar] [CrossRef]
- Campisano, A.; Butler, D.; Ward, S.; Burns, M.J.; Friedler, E.; DeBusk, K.; Fisher-Jeffes, L.N.; Ghisi, E.; Rahman, A.; Furumai, H.; et al. Urban rainwater harvesting systems: Research, implementation and future perspectives. Water Res. 2017, 115, 195–209. [Google Scholar] [CrossRef] [PubMed]
- Lopes, V.A.; Marques, G.F.; Dornelles, F.; Medellin-Azuara, J. Performance of rainwater harvesting systems under scenarios of non-potable water demand and roof area typologies using a stochastic approach. J. Clean. Prod. 2017, 148, 304–313. [Google Scholar] [CrossRef]
- Malinowski, P.A.; Stillwell, A.S.; Wu, J.S.; Schwarz, P.M. Energy-water nexus: Potential energy savings and implications for sustainable integrated water management in urban areas from rainwater harvesting and gray-water reuse. J. Water Resour. Plan. Manag. 2015, 141, A4015003. [Google Scholar] [CrossRef]
- Gokcekus, H.; Kassem, Y.; Alijl, N. Enhancing Co-Benefits and reducing Flood Risks through Nature-based Solutions and Assessments: A Case Study in the Dead Sea Region of Jordan. Eng. Technol. Appl. Sci. Res. 2024, 14, 16450–16459. [Google Scholar] [CrossRef]
- Nandi, S.; Gonela, V. Rainwater harvesting for domestic use: A systematic review and outlook from the utility policy and management perspectives. Util. Policy 2022, 77, 101383. [Google Scholar] [CrossRef]
- Prăvălie, R.; Patriche, C.; Bandoc, G. Spatial assessment of solar energy potential at global scale. A geographical approach. J. Clean. Prod. 2019, 209, 692–721. [Google Scholar] [CrossRef]
- Hosseini, S.E.; Wahid, M.A. Hydrogen from solar energy, a clean energy carrier from a sustainable source of energy. Int. J. Energy Res. 2020, 44, 4110–4131. [Google Scholar] [CrossRef]
- Fang, H.; Li, J.; Song, W. Sustainable site selection for photovoltaic power plant: An integrated approach based on prospect theory. Energy Convers. Manag. 2018, 174, 755–768. [Google Scholar] [CrossRef]
- Yan, J.; Yang, Y.; EliaCampana, P.; He, J. City-level analysis of subsidy-free solar photovoltaic electricity price, profits and grid parity in China. Nat. Energy 2019, 4, 709–717. [Google Scholar] [CrossRef]
- Hao, D.; Qi, L.; Tairab, A.M.; Ahmed, A.; Azam, A.; Luo, D.; Pan, Y.; Zhang, Z.; Yan, J. Solar energy harvesting technologies for PV self-powered applications: A comprehensive review. Renew. Energy 2022, 188, 678–697. [Google Scholar] [CrossRef]
- Ahmadi, E.; McLellan, B.; Mohammadi-Ivatloo, B.; Tezuka, T. The role of renewable energy resources in sustainability of water desalination as a potential fresh-water source: An updated review. Sustainability 2020, 12, 5233. [Google Scholar] [CrossRef]
- Kassem, Y.; Gokcekus, H.; AbAlbakoush, I.A.; Abdullah, K.S.B. Solar-Powered Solutions for the Water and Energy Shortage Problem: The Case Study of Nahr El Bared, Lebanon. Eng. Technol. Appl. Sci. Res. 2023, 13, 10861–10869. [Google Scholar] [CrossRef]
- Verma, S.; Mishra, S.; Chowdhury, S.; Gaur, A.; Mohapatra, S.; Soni, A.; Verma, P. Solar PV powered water pumping system–A review. Mater. Today Proc. 2021, 46, 5601–5606. [Google Scholar] [CrossRef]
- Saim, M.A.; Khan, I. Problematizing solar energy in Bangladesh: Benefits, burdens, and electricity access through solar home systems in remote islands. Energy Res. Soc. Sci. 2021, 74, 101969. [Google Scholar] [CrossRef]
- Chong, W.T.; Naghavi, M.S.; Poh, S.C.; Mahlia, T.M.I.; Pan, K.C. Techno-economic analysis of a wind–solar hybrid renewable energy system with rainwater collection feature for urban high-rise application. Appl. Energy 2011, 88, 4067–4077. [Google Scholar] [CrossRef]
- Chong, W.T.; Fazlizan, A.; Poh, S.C.; Pan, K.C.; Ping, H.W. Early development of an innovative building integrated wind, solar and rain water harvester for urban high rise application. Energy Build. 2012, 47, 201–207. [Google Scholar] [CrossRef]
- Chong, W.T.; Wang, X.H.; Wong, K.H.; Mojumder, J.C.; Poh, S.C.; Saw, L.H.; Lai, S.H. Performance assessment of a hybrid solar-wind-rain eco-roof system for buildings. Energy Build. 2016, 127, 1028–1042. [Google Scholar] [CrossRef]
- Wang, X.; Chong, W.; Wong, K.; Lai, S.; Saw, L.; Xiang, X.; Wang, C.T. Preliminary techno–environment–economic evaluation of an innovative hybrid renewable energy harvester system for residential application. Energies 2019, 12, 1496. [Google Scholar] [CrossRef]
- Cao, H.; Zeng, X.; Wu, L.; Wu, X.; Zhang, Z. A hybrid wind and rainwater energy harvesting system for applications in sea-crossing bridges. Ocean Eng. 2021, 234, 109267. [Google Scholar] [CrossRef]
- Michaelides, S.; Tymvios, F.; Michaelidou, T. Spatial and temporal characteristics of the annual rainfall frequency distribution in Cyprus. Atmos. Res. 2009, 94, 606–615. [Google Scholar] [CrossRef]
- Stamatatou, N.; Vasiliades, L.; Loukas, A. The effect of sample size on bivariate rainfall frequency analysis of extreme precipitation. Proceedings 2018, 7, 19. [Google Scholar] [CrossRef]
- Zaifoglu, H.; Akintug, B.; Yanmaz, A.M. Regional frequency analysis of precipitation using time series clustering approaches. J. Hydrol. Eng. 2018, 23, 05018007. [Google Scholar] [CrossRef]
- Kassem, Y.; Gökçekuş, H.; Gökçekuş, R. Identification of the most suitable probability distribution models for monthly and annual rainfall series in Güzelyurt Region, Northern Cyprus. Desalination Water Treat. 2021, 215, 427–451. [Google Scholar] [CrossRef]
- Kassem, Y.; Gökçekuş, H.; Çamur, H.; Esenel, E. Statistical analysis and determination of best-fit probability distribution for monthly rainfall in Northern Cyprus. Desalination Water Treat. 2021, 215, 347–379. [Google Scholar] [CrossRef]
- Elkiran, G.; Dahiru, A.; Gokcekus, H. Water resources management and trend of water use in North Cyprus. Desalination Water Treat. 2020, 177, 264–274. [Google Scholar] [CrossRef]
- Ilseven, S. The edaphic, topographic, climatologic and lithologic factors that affect plant endemism on Troodos (Cyprus) Mountain. In Proceedings of the ICGE-2023, Antalya, Turkey, 5–8 October 2023; pp. 509–517. [Google Scholar]
- Saner, S. Geotectonic Evolution of the Island of Cyprus. In Climate Change and Natural Resources: Environmental Management and Sustainable Development; Springer: Berlin/Heidelberg, Germany, 2025; p. 287. [Google Scholar]
- Papadaskalopoulou, C.; Giannakopoulos, C.; Lemesios, G.; Zachariou-Dodou, M.; Loizidou, M. Challenges for water resources and their management in light of climate change: The case of Cyprus. Desalination Water Treat. 2015, 53, 3224–3233. [Google Scholar] [CrossRef]
- Gökçekuş, H.; Kassem, Y.; Rizza, T. Groundwater quality assessment for irrigation in coastal region (Güzelyurt), Northern Cyprus and importance of empirical model for predicting groundwater quality (electric conductivity). Environ. Earth Sci. 2025, 84, 224. [Google Scholar] [CrossRef]
- Delipetrou, P.; Makhzoumi, J.; Dimopoulos, P.; Georghiou, K. Cyprus. In Mediterranean Island Landscapes: Natural and Cultural Approaches; Springer: Dordrecht, The Netherlands, 2008; pp. 170–203. [Google Scholar]
- Lentini, A. The biodiversity of Cyprus Island. J. Environ. Sci. Engneering 2015, 4, 125–131. [Google Scholar]
- Kassem, Y.; Gökçekuş, H.; Çamur, H.; Esenel, E. Application of artificial neural network, multiple linear regression, and response surface regression models in the estimation of monthly rainfall in Northern Cyprus. Desalination Water Treat. 2021, 215, 328–346. [Google Scholar] [CrossRef]
- Hisam, E.; Mehr, A.D.; Alganci, U.; Seker, D.Z. Comprehensive evaluation of Satellite-Based and reanalysis precipitation products over the Mediterranean region in Turkey. Adv. Space Res. 2023, 71, 3005–3021. [Google Scholar] [CrossRef]
- Macharia, J.M.; Ngetich, F.K.; Shisanya, C.A. Comparison of satellite remote sensing derived precipitation estimates and observed data in Kenya. Agric. For. Meteorol. 2020, 284, 107875. [Google Scholar] [CrossRef]
- Sun, S.; Shi, W.; Zhou, S.; Chai, R.; Chen, H.; Wang, G.; Shen, H. Capacity of satellite-based and reanalysis precipitation products in detecting long-term trends across Mainland China. Remote Sens. 2020, 12, 2902. [Google Scholar] [CrossRef]
- Setiya, P.; Singh, M.; Nain, A.S. Evaluating the performance of Grid IMD, NASA POWER, and MarkSimtimeseries weather dataset for Uttarakhand Climatic Condition. Theor. Appl. Climatol. 2024, 155, 2657–2668. [Google Scholar] [CrossRef]
- Kassem, Y.; Camur, H.; Ghoshouni, E.G. Assessment of a Hybrid (Wind-Solar) System at High-Altitude Agriculture Regions for achieving Sustainable Development Goals. Eng. Technol. Appl. Sci. Res. 2024, 14, 12595–12607. [Google Scholar] [CrossRef]
- Kassem, Y.; Camur, H.; Adamu, M.T.; Chikowero, T.; Apreala, T. Prediction of Solar Irradiation in Africa using Linear-Nonlinear Hybrid Models. Eng. Technol. Appl. Sci. Res. 2023, 13, 11472–11483. [Google Scholar] [CrossRef]
- Kassem, Y.; Abdalla, M.H.A. Modeling predictive suitability to identify the potential of wind and solar energy as a driver of sustainable development in the Red Sea state, Sudan. Environ. Sci. Pollut. Res. 2022, 29, 44233–44254. [Google Scholar] [CrossRef]
- Hamad, J.; Ahmad, M.; Zeeshan, M. Solar energy resource mapping, site suitability and techno-economic feasibility analysis for utility scale photovoltaic power plants in Afghanistan. Energy Convers. Manag. 2024, 303, 118188. [Google Scholar] [CrossRef]
- Bandira, P.N.; Tan, M.L.; Teh, S.Y.; Samat, N.; Shaharudin, S.M.; Mahamud, M.A.; Tangang, F.; Juneng, L.; Chung, J.X.; Samsudin, M.S. Optimal solar farm site selection in the george town conurbation using GIS-based multi-criteria decision making (MCDM) and NASA POWER data. Atmosphere 2022, 13, 2105. [Google Scholar] [CrossRef]
- Kassem, Y.; Çamur, H.; Alhuoti, S.M.A. Solar energy technology for Northern Cyprus: Assessment, statistical analysis, and feasibility study. Energies 2020, 13, 940. [Google Scholar] [CrossRef]
- Almorox, J.; Voyant, C.; Bailek, N.; Kuriqi, A.; Arnaldo, J.A. Total solar irradiance’s effect on the performance of empirical models for estimating global solar radiation: An empirical-based review. Energy 2021, 236, 121486. [Google Scholar] [CrossRef]
- Gairaa, K.; Bakelli, Y. Solar energy potential assessment in the Algerian south area: Case of Ghardaïa region. J. Renew. Energy 2013, 2013, 496348. [Google Scholar] [CrossRef]
- Bhatia, S.C. Advanced Renewable Energy Systems; Woodhead: New Delhi, India, 2014. [Google Scholar]
- Al-Najideen, M.I.; Alrwashdeh, S.S. Design of a solar photovoltaic system to cover the electricity demand for the faculty of Engineering-Mu’tah University in Jordan. Resour.-Effic. Technol. 2017, 3, 440–445. [Google Scholar] [CrossRef]
- Kassem, Y.; Gökçekuş, H.; Gökçekuş, R. Towards Sustainable Energy Solutions: Evaluating the Impact of Floating PV Systems in Reducing Water Evaporation and Enhancing Energy Production in Northern Cyprus. Energies 2024, 17, 5300. [Google Scholar] [CrossRef]
- Parchure, A.S.; Gedam, S.K. Probability distribution analysis of extreme rainfall events in a flood-prone region of Mumbai, India. Arab. J. Geosci. 2019, 12, 369. [Google Scholar] [CrossRef]
- Bajirao, T.S. Comparative performance of different probability distribution functions for maximum rainfall estimation at different time scales. Arab. J. Geosci. 2021, 14, 2138. [Google Scholar] [CrossRef]
- Nedaei, M.; Assareh, E.; Walsh, P.R. A comprehensive evaluation of the wind resource characteristics to investigate the short term penetration of regional wind power based on different probability statistical methods. Renew. Energy 2018, 128, 362–374. [Google Scholar] [CrossRef]
- Phien, H.N.; Ajirajah, T.J. Applications of the log Pearson type-3 distribution in hydrology. J. Hydrol. 1984, 73, 359–372. [Google Scholar] [CrossRef]
- Tortorelli, R.; Asquith, W.; Alan, R. Depth-Duration Frequency of Precipitation for Oklahoma; Water Resources Investigation Report 99-4232; US Geological Survey: Reston, VA, USA, 1999. [Google Scholar]
- Şen, Z.; Eljadid, A.G. Rainfall distribution function for Libya and rainfall prediction. Hydrol. Sci. J. 1999, 44, 665–680. [Google Scholar] [CrossRef]
- Ogunlela, A. Stochastic Analysis of Rainfall Events in Ilorin, Nigeria. J. Agric. Res. Dev. 2001, 1, 36–50. [Google Scholar] [CrossRef]
- Zalina, M.; Desa, M.; Nguyen, V.-T.-A.; Kassim, A. Selecting a probability distribution for extreme rainfall series in Malaysia. Water Sci. Technol. 2002, 45, 63–68. [Google Scholar] [CrossRef]
- Tao, D.Q.; Nguyen, V.T.; Bourque, A. On selection of probability distributions for representing extreme precipitations in Southern Quebec. In Proceedings of the Annual conference of the Canadian Society for Civil Engineering, Montreal, QC, Canada, 5–8 June 2002; pp. 1–8. [Google Scholar]
- Lee, C. Application of rainfall frequency analysis on studying rainfall distribution characteristics of Chia-nan plain in Southern Taiwan. J. Crops Environ. Bioinform. 2005, 2, 31–38. [Google Scholar]
- Fadhilah, Y.; Md, Z.; Vâ, N.; Suhaila, S.; Zulkifli, Y. Fitting The Best–Fit Distribution For The Hourly Rainfall Amount In The Wilayah Persekutuan. J. Teknol. 2012, 46, 49–58. [Google Scholar] [CrossRef][Green Version]
- Kwaku, X.; Duke, O. Characterization and frequency analysis of one day annual maximum and two to five consecutive days maximum rainfall of Accra, Ghana. ARPN J. Eng. Appl. Sci. 2007, 2, 27–31. [Google Scholar][Green Version]
- Hanson, L.S.; Vogel, R. The Probability Distribution of Daily Rainfall in the United States. In Proceedings of the World Environmental and Water Resources Congress 2008, Honolulu, HI, USA, 12–16 May 2008. [Google Scholar] [CrossRef]
- Sharma, M.; Singh, J. Use of probability distribution in rainfall analysis. N. Y. Sci. J. 2010, 3, 40–49. [Google Scholar]
- Johnson, F.; Haddad, K.; Rahman, A.; Green, J. Application of Bayesian GLSR to estimate sub-daily rainfall parameters for the IDF revision project. In Proceedings of the Hydrology and Water Resources Symposium, Sydney, Australia, 19–22 November 2012. [Google Scholar]
- Green, J.; Xuereb, K.; Johnson, F.; Moore, G. The revised intensity–frequency–duration (IFD) design rainfall estimates for Australia—An overview. In Proceeding of the 34th Hydrology and Water Resources Symposium, Sydney, Australia, 19–22 November 2012. [Google Scholar]
- Khudri, M.; Sadia, F. Determination of the Best Fit Probability Distribution for Annual Extreme Precipitation in Bangladesh. Eur. J. Sci. Res. 2013, 103, 391–404. [Google Scholar]
- Mamoon, A.A.; Joergensen, N.E.; Rahman, A.; Qasem, H. Derivation of new design rainfall in Qatar using L-moment based index frequency approach. Int. J. Sustain. Built Environ. 2014, 3, 111–118. [Google Scholar] [CrossRef]
- Montaseri, M.; Amirataee, B.; Rezaei, H. Assessment of Goodness of Fit Methods in Determining the Best Regional Probability Distribution of Rainfall Data. Int. J. Eng. 2014, 27, 1537–1546. [Google Scholar] [CrossRef]
- Mandal, S.; Choudhury, B.U. Estimation and prediction of maximum daily rainfall at Sagar Island using best fit probability models. Theor. Appl. Climatol. 2014, 121, 87–97. [Google Scholar] [CrossRef]
- Subyani, A.M.; Al-Amri, N.S. IDF curves and daily rainfall generation for Al-Madinah city, western Saudi Arabia. Arab. J. Geosci. 2015, 8, 11107–11119. [Google Scholar] [CrossRef]
- Hassan, Z.; Shamsudin, S.; Harun, S. Choosing The Best Fit Distribution For Rainfall Event Characteristics Based On 6H-Ietd Within Peninsular Malaysia. J. Teknol. 2015, 75, 145–157. [Google Scholar] [CrossRef][Green Version]
- Mamoon, A.A.; Rahman, A. Selection of the best fit probability distribution in rainfall frequency analysis for Qatar. Nat. Hazards 2016, 86, 281–296. [Google Scholar] [CrossRef]
- Amin, M.T.; Rizwan, M.; Alazba, A.A. A best-fit probability distribution for the estimation of rainfall in northern regions of Pakistan. Open Life Sci. 2016, 11, 432–440. [Google Scholar] [CrossRef]
- Mohamed, T.; Ibrahim, A. Fitting Probability Distributions of Annual Rainfall in Sudan. SUST J. Eng. Comput. Sci. 2016, 17, 35–39. [Google Scholar]
- Agbonaye, A.I.; Izinyon, O.C. Best-Fit Probability Distribution Model for Rainfall Frequency Analysis of Three Cities in South Eastern Nigeria. Niger. J. Environ. Sci. Technol. 2017, 1, 34–42. [Google Scholar] [CrossRef]
- Yuan, J.; Emura, K.; Farnham, C.; Alam, M.A. Frequency analysis of annual maximum hourly precipitation and determination of best fit probability distribution for regions in Japan. Urban. Clim. 2018, 24, 276–286. [Google Scholar] [CrossRef]
- Alam, M.; Farnham, C.; Emura, K. Best-Fit Probability Models for Maximum Monthly Rainfall in Bangladesh Using Gaussian Mixture Distributions. Geosciences 2018, 8, 138. [Google Scholar] [CrossRef]
- Alam, M.; Emura, K.; Farnham, C.; Yuan, J. Best-Fit Probability Distributions and Return Periods for Maximum Monthly Rainfall in Bangladesh. Climate 2018, 6, 9. [Google Scholar] [CrossRef]
- Meena, R.K.; Dubey, S.; Basak, S.M. Use of Different Probability Distribution in Rainfall Analysis for RRS, Pundiari, Cooch Behar. Int. J. Curr. Microbiol. Appl. Sci. 2019, 8, 1325–1337. [Google Scholar] [CrossRef]
- Yadav, K.; Jain, S. Frequency Analysis of Rainfall Data Using Probability Distribution Models. Int. J. Curr. Microbiol. Appl. Sci. 2019, 8, 1390–1396. [Google Scholar] [CrossRef]
- Kassem, Y.; Gökçekuş, H. Water resources and rainfall distribution function: A case study in Lebanon. Desalination Water Treat. 2020, 177, 306–321. [Google Scholar] [CrossRef]
- Kassem, Y.; Gökçekuş, H.; Hassan, M.E.E.E. Daily Rainfall Characteristics in Sudan: Statistical Analysis and Modeling. In International Conference on Water Problems in Mediterranean Countries; Springer Nature: Cham, Switzerland, 2023; pp. 145–156. [Google Scholar]
- Sukrutha, A.; Dyuthi, S.; Desai, S. Probability distribution for monthly precipitation data in India. arXiv 2017, arXiv:1708.03144. [Google Scholar]
- Abdulla, F. Rainwater harvesting in Jordan: Potential water saving, optimal tank sizing and economic analysis. Urban. Water J. 2020, 17, 446–456. [Google Scholar] [CrossRef]
- Asamoah, S.S.; Parbey, J.; Yankey, I.K.; Awuah, A. Techno-economic assessment of a central grid-connected wind farm in Ghana using RETScreen® Expert. Heliyon 2023, 9, e12902. [Google Scholar] [CrossRef]
- Kassem, Y.; Gökçekuş, H.; Güvensoy, A. Techno-economic feasibility of grid-connected solar PV system at Near East University hospital, Northern Cyprus. Energies 2021, 14, 7627. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the SWAT Model on a Large River Basin with Point and Nonpoint Sources. JAWRA 2001, 37, 1169–1188. [Google Scholar]
- Van Liew, M.W.; Arnold, J.G.; Garbrecht, J.D. Hydrologic simulation on agricultural watersheds: Choosing between two models. Trans. ASAE 2003, 46, 1539. [Google Scholar] [CrossRef]
- Kokkalis, P.; Al Jassar, H.K.; Al Sarraf, H.; Nair, R.; Al Hendi, H. Evaluation of ERA5 and NCEP reanalysis climate models for precipitation and soil moisture over a semi-arid area in Kuwait. Clim. Dyn. 2024, 62, 4893–4904. [Google Scholar] [CrossRef]
- Ntagkounakis, G.; Nastos, P.T.; Kapsomenakis, Y. Creating High-Resolution Precipitation and Extreme Precipitation Indices Datasets by Downscaling and Improving on the ERA5 Reanalysis Data over Greece. Eng 2024, 5, 1885–1904. [Google Scholar] [CrossRef]
- Salih, W.; Epule, T.E.; EL Khalki, E.M.; Ouatiki, H.; Erraki, S.; Achli, S.; Chehbouni, A. A comprehensive assessment of satellite precipitation products over a semi-arid region: Focus on extreme events. Nat. Hazards 2024, 120, 3037–3065. [Google Scholar] [CrossRef]
- Hassler, B.; Lauer, A. Comparison of reanalysis and observational precipitation datasets including ERA5 and WFDE5. Atmosphere 2021, 12, 1462. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Lavers, D.A.; Hersbach, H.; Rodwell, M.J.; Simmons, A. An improved estimate of daily precipitation from the ERA5 reanalysis. Atmos. Sci. Lett. 2024, 25, e1200. [Google Scholar] [CrossRef]
- Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of several rainfall products used for hydrological applications over West Africa using two high-resolution gauge networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Jae Lim, K.; Ballabio, C. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef]
- Peng, J.; Liu, T.; Huang, Y.; Ling, Y.; Li, Z.; Bao, A.; Chen, X.; Kurban, A.; De Maeyer, P. Satellite-based precipitation datasets evaluation using gauge observation and hydrological modeling in a typical arid land watershed of Central Asia. Remote Sens. 2021, 13, 221. [Google Scholar] [CrossRef]
- Wang, Q.; Xia, J.; She, D.; Zhang, X.; Liu, J.; Zhang, Y. Assessment of four latest long-term satellite-based precipitation products in capturing the extreme precipitation and streamflow across a humid region of southern China. Atmos. Res. 2021, 257, 105554. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrea, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Ahsan, A.; Naser, J.; Rahman, A. Reliability analysis of rainwater tanks in Melbourne using daily water balance model. Resour. Conserv. Recycl. 2011, 56, 80–86. [Google Scholar] [CrossRef]
- Ahmad, M.I.; Sinclair, C.D.; Spurr, B.D. Assessment of flood frequency models using empirical distribution function statistics. Water Resour. Res. 1988, 24, 1323–1328. [Google Scholar] [CrossRef]
- Tasker, G. Regional frequency analysis: An approach based on L-moments. J. Am. Stat. Assoc. 1998, 93, 1233. [Google Scholar] [CrossRef]
- Gwenzi, W.; Nyamadzawo, G. Hydrological impacts of urbanization and urban roof water harvesting in water-limited catchments: A review. Environ. Process. 2014, 1, 573–593. [Google Scholar] [CrossRef]
- Domènech, L.; Saurí, D. A comparative appraisal of the use of rainwater harvesting in single and multi-family buildings of the Metropolitan Area of Barcelona (Spain): Social experience, drinking water savings and economic costs. J. Clean. Prod. 2011, 19, 598–608. [Google Scholar] [CrossRef]
- Ndeketeya, A.; Dundu, M. Maximising the benefits of rainwater harvesting technology towards sustainability in urban areas of South Africa: A case study. Urban Water J. 2019, 16, 163–169. [Google Scholar] [CrossRef]
- Fernandes, L.F.S.; Terêncio, D.P.; Pacheco, F.A. Rainwater harvesting systems for low demanding applications. Sci. Total Environ. 2015, 529, 91–100. [Google Scholar] [CrossRef]
- Imam, A.A.; Al-Turki, Y.A.; R., S.K. Techno-Economic Feasibility Assessment of Grid-Connected PV systems for residential buildings in Saudi Arabia—A case Study. Sustainability 2019, 12, 262. [Google Scholar] [CrossRef]
- Kebede, K.Y. Viability study of grid-connected solar PV system in Ethiopia. Sustain. Energy Technol. Assess. 2015, 10, 63–70. [Google Scholar] [CrossRef]
- Mohammadi, K.; Naderi, M.; Saghafifar, M. Economic feasibility of developing grid-connected photovoltaic plants in the southern coast of Iran. Energy 2018, 156, 17–31. [Google Scholar] [CrossRef]
- Owolabi, A.B.; Nsafon, B.E.K.; Roh, J.W.; Suh, D.; Huh, J.S. Validating the techno-economic and environmental sustainability of solar PV technology in Nigeria using RETScreen Experts to assess its viability. Sustain. Energy Technol. Assess. 2019, 36, 100542. [Google Scholar] [CrossRef]
- Rehman, S.; Ahmed, M.A.; Mohamed, M.H.; Al-Sulaiman, F.A. Feasibility study of the grid connected 10 MW installed capacity PV power plants in Saudi Arabia. Renew. Sustain. Energy Rev. 2017, 80, 319–329. [Google Scholar] [CrossRef]
- Abd-ur-Rehman, H.M.; Al-Sulaiman, F.A. Optimum selection of solar water heating (SWH) systems based on their comparative techno-economic feasibility study for the domestic sector of Saudi Arabia. Renew. Sustain. Energy Rev. 2016, 62, 336–349. [Google Scholar] [CrossRef]
- Eke, R.; Demircan, C. Shading effect on the energy rating of two identical PV systems on a building façade. Sol. Energy 2015, 122, 48–57. [Google Scholar] [CrossRef]
- Bernadette, D.; Twizerimana, M.; Bakundukize, A.; Pierre, B.J.; Theoneste, N. Analysis of shading effects in solar PV system. Int. J. Sustain. Green Energy 2021, 10, 47–62. [Google Scholar] [CrossRef]
- Zomer, C.; Rüther, R. Simplified method for shading-loss analysis in BIPV systems–Part 1: Theoretical study. Energy Build. 2017, 141, 69–82. [Google Scholar] [CrossRef]
- Kader, K.A.; Rahman, F.; Nahid, N.I.; Abedin, Z.; Mannan, M.A. Design and Analysis of an On-Grid Solar System Using PVsyst Software for Commercial Application. Int. J. Sci. Eng. Res. 2021, 12, 8. [Google Scholar]
- Mishra, P.R.; Rathore, S.; Jain, V. PVSyst enabled real time evaluation of grid connected solar photovoltaic system. Int. J. Inf. Technol. 2024, 16, 745–752. [Google Scholar] [CrossRef]
- Saha, A.; Setu, S.; Das, S.; Hossain, M.I.; Rahman, A.K.; Rahman, M.M. Decision support system for community managed rainwater harvesting: A case study in the salinity-prone coastal region of Bangladesh. Heliyon 2024, 10, e30455. [Google Scholar] [CrossRef]
- Li, R.; Zhang, S.; Guo, Y.; Zhang, F.; Zhang, W.; Yan, J.; Li, H. Impacts of compatibility between rainwater availability and water demand on water saving performance of rainwater harvesting systems. J. Environ. Manag. 2024, 370, 122722. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, G.C.R.; Alves, C.D.M.A. The performance of rainwater harvesting systems in the context of deep uncertainties. Proc. IAHS 2024, 385, 11–16. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, A.; Samali, B. Evaluation of climate change impacts on rainwater harvesting. J. Clean. Prod. 2016, 137, 60–69. [Google Scholar] [CrossRef]
- Ali, S.; Zhang, S.; Chandio, F.A. Impacts of rainfall change on stormwater control and water saving performance of rainwater harvesting systems. J. Environ. Manag. 2021, 280, 111850. [Google Scholar] [CrossRef]
- Del Pero, C.; Aste, N.; Leonforte, F. The effect of rain on photovoltaic systems. Renew. Energy 2021, 179, 1803–1814. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Stojkov, M.; Katinić, M.; Lacković, I. Effects of extreme weather conditions on pv systems. Sustainability 2023, 15, 16044. [Google Scholar] [CrossRef]
- Jackson, N.D.; Gunda, T. Evaluation of extreme weather impacts on utility-scale photovoltaic plant performance in the United States. Appl. Energy 2021, 302, 117508. [Google Scholar] [CrossRef]
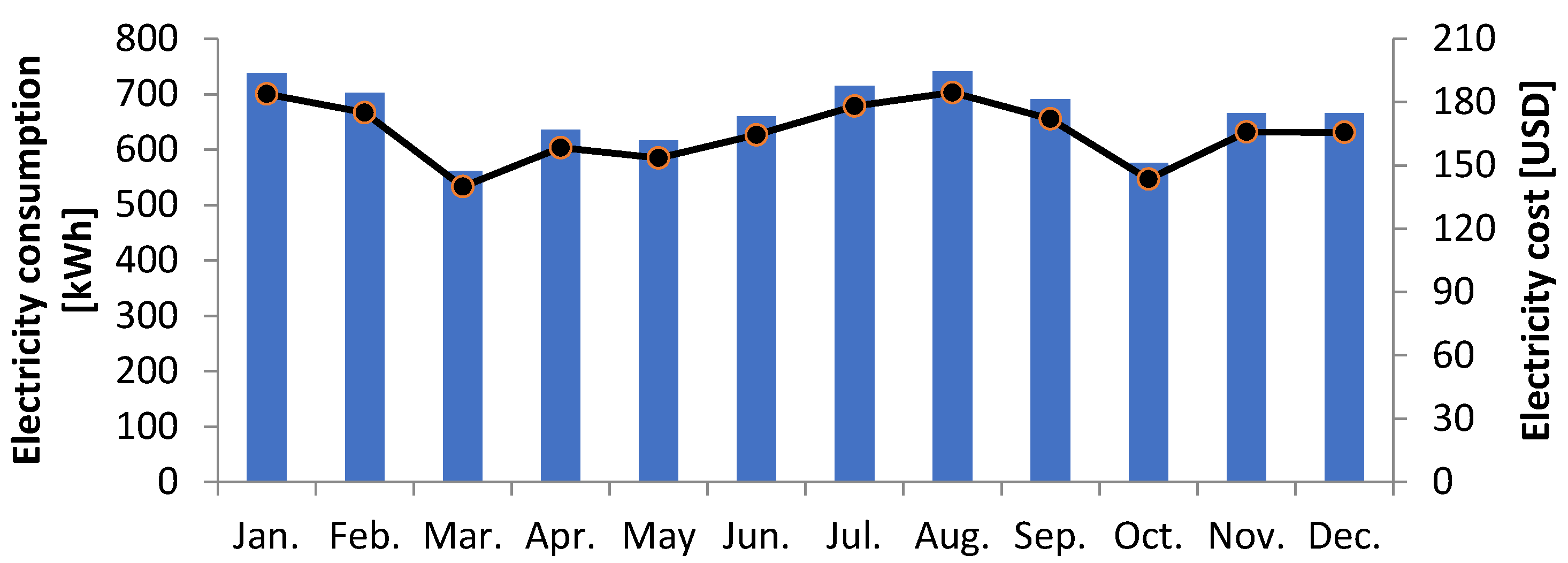
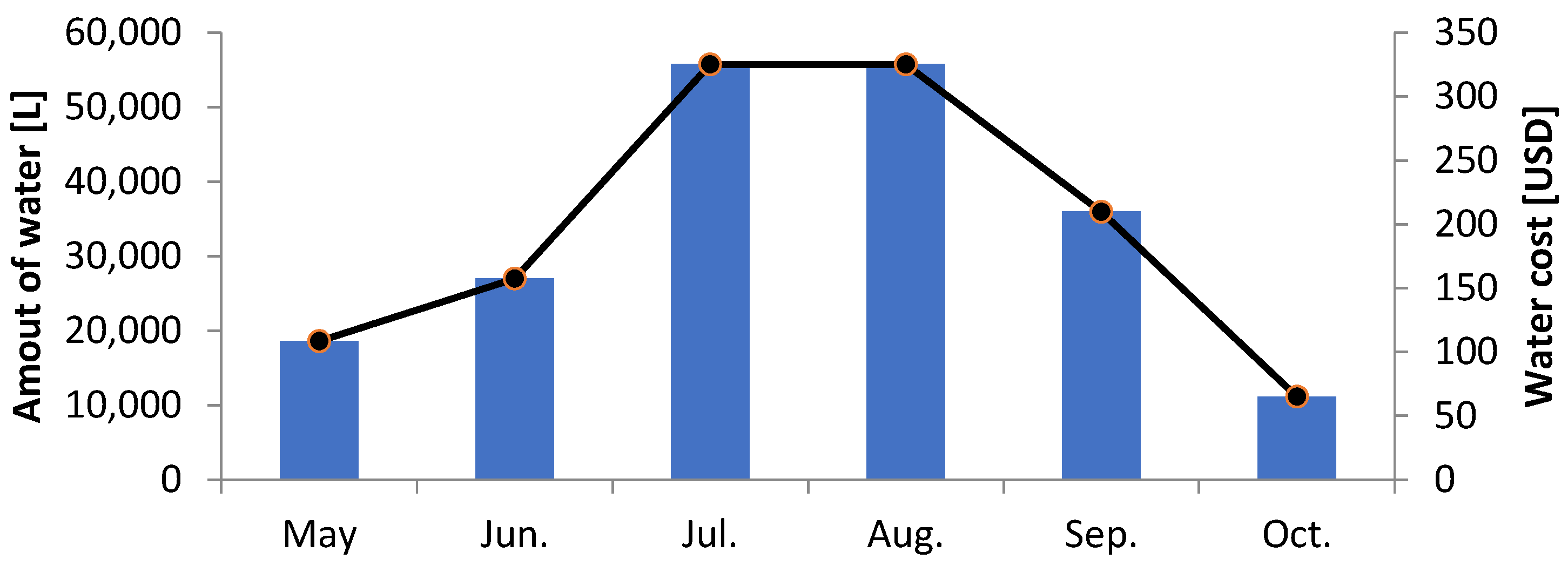
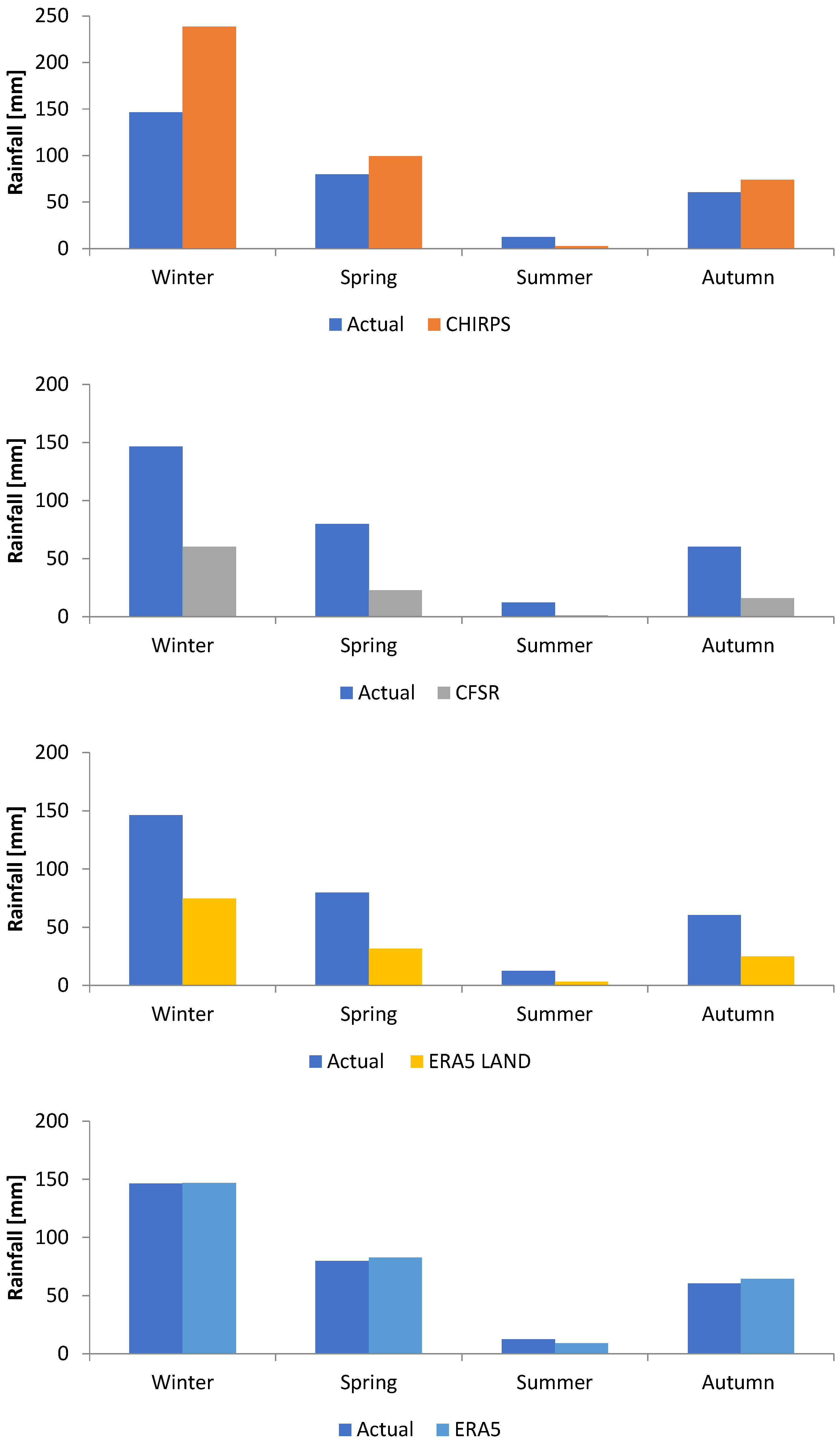
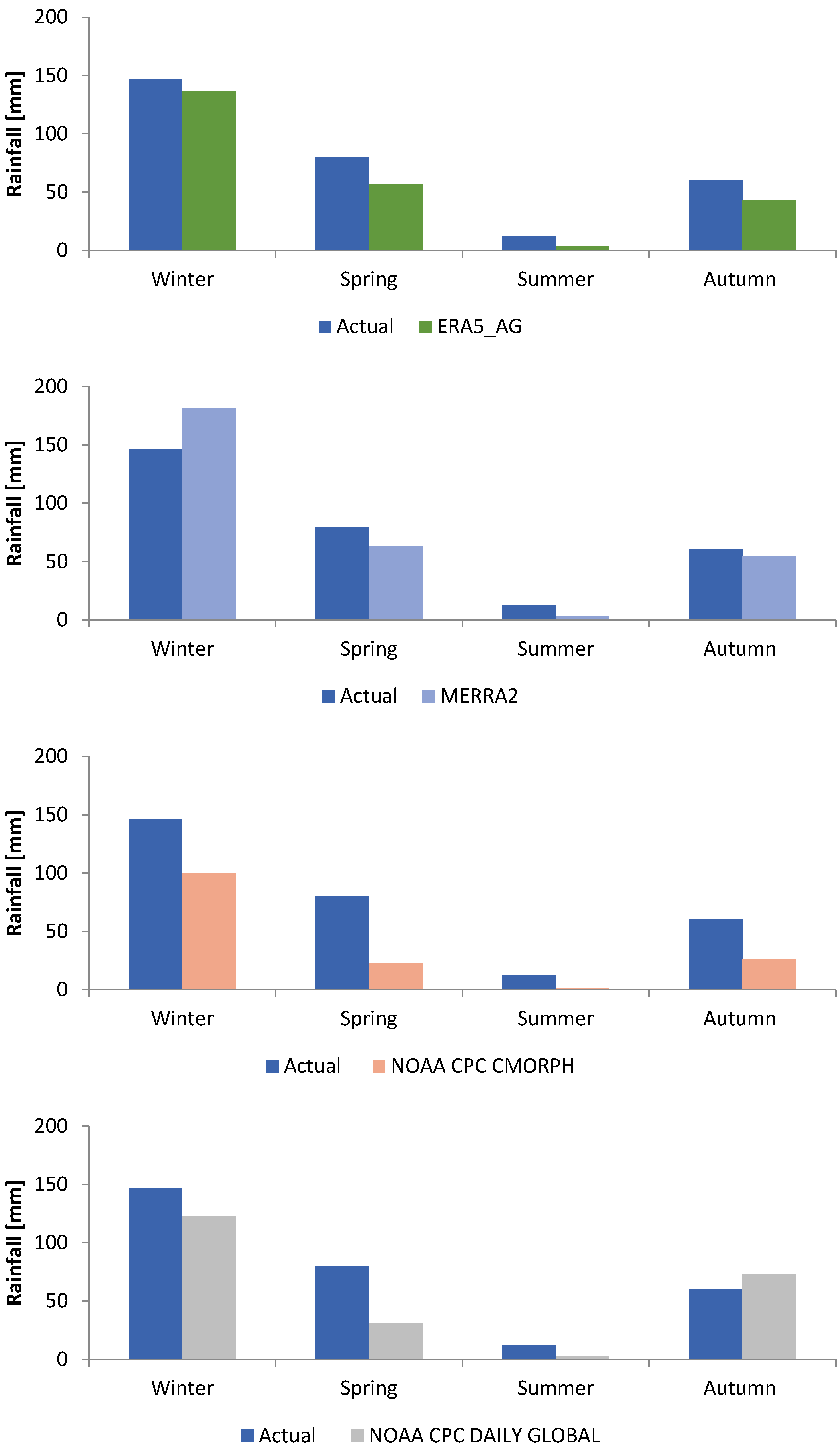
| Reference | Year | Description of the Study | A Schematic of the Proposed System | Main Findings |
|---|---|---|---|---|
| [52] | 2011 | Present the techno-economic feasibility of a wind–solar hybrid renewable energy generation system with a rainwater collection feature for electrical energy generation. |  | A building’s energy consumption can be mainly fulfilled by a developed system, which helps to make the building independent (or partially independent) from the urban electricity grid. |
| [53] | 2012 | Design a 3-in-1 wind–solar hybrid renewable energy and rainwater harvester. |  | The Power-Augmentation-Guide-Vane improved wind turbine performance by 73.2% at low wind speed (3 m/s). Combining solar panels with rainwater collection improved resource efficiency and energy capture. |
| [54] | 2016 | Present a technical feasibility study of a hybrid solar–wind–rain eco-roof system with natural ventilation and skylight for electrical energy generation and saving. | 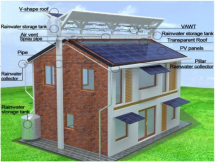 | The hybrid eco-roof technology increased wind turbine efficiency by implementing a V-shaped roof that accelerated airflow via the Venturi effect. An automated water-based system enhanced solar PV performance by cooling and cleaning. Skylighting and integrated ventilation improved the performance of sustainable buildings, reduced the demand for artificial lighting, and improved interior comfort. |
| [55] | 2019 | Conduct a technical, environmental, and economic feasibility study for a hybrid renewable energy harvester system for residential applications. | 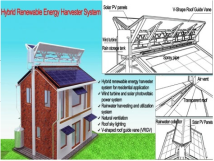 | The developed system can help partially meet a building’s energy needs. Besides, wind turbine performance is significantly enhanced by the hybrid energy harvesting system’s integration of a V-shaped roof guiding vane, which speeds up wind flow. |
| [56] | 2021 | Propose a hybrid wind and rainfall energy harvesting system that would be mounted on the sea-crossing bridge’s pipe to capture both types of energy. | 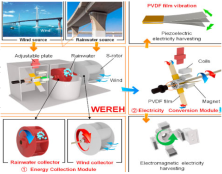 | By combining piezoelectric and electromagnetic phenomena, the hybrid wind and rainwater energy harvesting achieves efficient dual energy harvesting. The S-rotor and water wheel operate independently, enabling real-time wind energy capture and delayed rainfall energy generation, allowing the sea-crossing bridge’s sensors to operate continuously under a range of weather conditions. |
| Property | Description/Value |
|---|---|
| Sensor/transducer type | Tipping bucket/reed switch |
| Precipitation type | Liquid |
| Accuracy | ±2% |
| Sensitivity | 0.2 mm |
| Closure time | <100 ms (for 0.2 mm of rain) |
| Capacity | Unlimited |
| Funnel diameter | 225 mm |
| Standard | 400 cm2 |
| With the expander unit | 1000 cm2 |
| Max. current rating | 500 mA |
| Breakdown voltage | 400 VDC |
| Capacity open contacts | 0.2 pF |
| Life (operations) | 108 closures |
| Material | Non-corrosive aluminum alloy LM25 |
| Dimensions | 390 (h) × 300 (Ø) mm |
| Weight | 2.5 kg |
| Temperature range (operating) | 085 °C |
| Product | Description/Full Name of the Dataset | Resolution | Period |
|---|---|---|---|
| ERA5 | Fifth-generation reanalysis product of the European Centre for Medium-Range Weather Forecasts | 0.05°/1 d | 1979–present |
| ERA5-Land | ERA5-Land has been produced by replaying the land component of the ECMWF ERA5 climate reanalysis | 0.125° 0.125° | 1963–present |
| ERA5 -Ag | Agriculture-specific dataset of the ECMWF ERA5 | 0.1°0.1° | 1979–present |
| MERRA-2 | Second-generation Modern-ERA Retrospective Analysis for Research and Applications | 0.5° 0.625° | 1980–present |
| TerraClimate | Global gridded dataset of meteorological and water balance for global terrestrial surfaces | 0.0420.042° | 1958–present |
| CHIRPS | A new land-only climatic database for precipitation, obtained through the Climate Hazards Group of the University of California at Santa Barbara (UCSB) | 0.05°0.05° | 1981–present |
| CFSR | NCEP (NOAA NWS National Centers for Environmental Prediction) Climate Forecast System Reanalysis dataset | 1/5° | 1979–present |
| CPC-CMORPH | The Satellite Precipitation—CMORPH Climate Data Record (CDR) consists of satellite precipitation estimates that have been bias-corrected and reprocessed using the Climate Prediction Center (CPC) Morphing Technique (MORPH) to form a global, high-resolution precipitation analysis | 0.5°0.5° | 1998–present |
| CPC-UPP | This data set is part of the products suite from the Climate Prediction Center (CPC) Unified Precipitation Project (UPP) that is underway at NOAA CPC | 0.5°0.5° | 1979–present |
| Specification | Value | |
|---|---|---|
| Mechanical Characteristics | ||
| Module type | JKM360M-66H | |
| Cell type | Mono PERC 158.75 × 158.75mm | |
| Number of cells | 132 (6 × 22) | |
| Weight | 20.0 kg | |
| Electrical Characteristics | STC | NOCT |
| Maximum power (Pmax) | 360 Wp | 268 Wp |
| Maximum power voltage (Vmp) | 36.97 V | 33.78 V |
| Maximum power current (Imp) | 9.74 A | 7.93 A |
| Open-circuit voltage (Voc) | 43.58 V | 41.04 V |
| Short-circuit current (Isc) | 10.48 A | 8.46 A |
| Module efficiency STC (%) | 19.52% | |
| Operating temperature (°C) | −40 °C~+85 °C | |
| Temperature coefficients of Pmax | −0.35%/°C | |
| Temperature coefficients of Voc | −0.28%/°C | |
| Temperature coefficients of Isc | 0.048%/°C | |
| Nominal operating cell temperature (NOCT) | 45 ± 2 °C | |
| Tilt Angle [°] | Shading Distance [M] |
|---|---|
| 10 | 0.3 |
| 20 | 0.6 |
| 30 | 0.9 |
| 40 | 1.1 |
| 50 | 1.3 |
| 60 | 1.5 |
| 70 | 1.6 |
| 80 | 1.7 |
| Parameter | Unit | Value |
|---|---|---|
| PV module cost | USD/Watt | 0.30 |
| The lifetime of the PV module | Year | 25 |
| Cost of the inverter | USD | 2600 |
| Cost of plastic tank | USD | 792 |
| Support structure for solar panel | USD/kW | 150 |
| Rainwater collection channel | USD/m2 | 25 |
| Miscellaneous/contingency fund | % of the total initial cost | 3 |
| Installation and spare parts | % of the total initial cost | 8.6 |
| The lifetime of the inverter | Year | 10 |
| Feasibility study, development, and engineering cost | % of the total initial cost | 0.6 |
| Inverter replacement periodic cost | Every ten years | Equal to the inverter’s cost |
| Inflation rate | % | 8 |
| Discount rate | % | 6 |
| Project life | Year | 25 |
| Energy cost increase rate | % | 5 |
| Reinvestment rate | % | 9 |
| Debt ratio | % | 70 |
| Debt interest rate | % | 0 |
| Debt term | Year | 20 |
| Dataset | Monthly | Seasonally | ||||
|---|---|---|---|---|---|---|
| R-Squared | RMSE [mm] | MAE [mm] | R-Squared | RMSE [mm] | MAE [mm] | |
| CHIRPS | 0.91 | 19.06 | 11.90 | 0.99 | 47.72 | 33.62 |
| CFSR | 0.89 | 19.67 | 16.57 | 0.97 | 56.49 | 49.71 |
| ERA5 LAND | 0.93 | 16.56 | 13.72 | 0.99 | 46.95 | 41.16 |
| ERA5 | 0.95 | 3.81 | 3.23 | 1.00 | 2.87 | 2.60 |
| ERA5-Ag | 0.94 | 6.50 | 4.89 | 0.99 | 15.75 | 14.66 |
| MERRA2 | 0.91 | 8.22 | 6.28 | 0.96 | 20.03 | 16.54 |
| CPC-CMORPH | 0.81 | 14.70 | 12.36 | 0.90 | 40.92 | 37.08 |
| CPC-UPP | 0.74 | 11.02 | 9.01 | 0.79 | 28.20 | 23.49 |
| TerraClimate | 0.92 | 13.74 | 8.89 | 0.94 | 36.59 | 24.06 |
| Month | DF | Test | Classification | Parameter |
|---|---|---|---|---|
| Jan | Johnson SB | KS | Continuous-Bounded | γ = 0.18753 δ = 0.92797 λ = 4.6823 ξ = 0.03519 |
| Johnson SB | AD | Continuous-Bounded | γ = 0.18753 δ = 0.92797 λ = 4.6823 ξ = 0.03519 | |
| Normal | C-s | Continuous-Unbounded | σ = 1.0229 μ = 2.1858 | |
| Feb | Dagum (4P) | KS | Continuous-Non-negative | k = 0.30979 α = 5.685 β = 1.9334 γ = 0.32815 |
| Dagum (4P) | AD | Continuous-Non-negative | k = 0.30979 α = 5.685 β = 1.9334 γ = 0.32815 | |
| Levy | C-s | Continuous-Non-negative | σ = 1.4103 | |
| Mar | Log-Logistic (3P) | KS | Continuous-Non-negative | α = 2.3899 β = 0.90586 γ = 0.04141 |
| Wakeby | AD | Continuous-Advanced | α = 1.6205 β = 3.0465 γ = 0.51091 δ = 0.19898 ξ = 0.13324 | |
| Log-Logistic (3P) | C-s | Continuous-Non-negative | α = 2.3899 β = 0.90586 γ = 0.04141 | |
| Apr | Inv. Gaussian (3P) | KS | Continuous-Non-negative | λ = 3.6049 μ = 1.1232 γ = −0.1355 |
| Wakeby | AD | Continuous-Advanced | α = 8.3601 β = 26.197 γ = 0.75358 δ = −0.10774 ξ = 0 | |
| Weibull (3P) | C-s | Continuous-Non-negative | α = 1.3339 β = 0.88001 γ = 0.17673 | |
| May | Wakeby | KS | Continuous-Advanced | α = 1.4478 β = 0.37189 γ = 0 δ = 0 ξ = −0.01538 |
| Wakeby | AD | Continuous-Advanced | α = 1.4478 β = 0.37189 γ = 0 δ = 0 ξ = −0.01538 | |
| Johnson SB | C-s | Continuous-Bounded | γ = 0.91051 δ = 0.89552 λ = 3.9419 ξ = −0.16837 | |
| Jun | Johnson SB | KS | Continuous-Bounded | γ = 1.572 δ = 0.91146 λ = 1.534 ξ = −0.02936 |
| Wakeby | AD | Continuous-Advanced | α = 0.29902 β = 0.10448 γ = 0 δ = 0 ξ = 9.5636 × 10−4 | |
| Erlang (3P) | C-s | Continuous-Non-negative | m = 1 β = 0.25206 γ = 0.0135 | |
| Jul | Log-Pearson 3 | KS | Continuous-Advanced | α = 18.887 β = −0.35822 γ = 2.7703 |
| Phased Bi-Weibull | AD | Continuous-Advanced | α1 = 0.99972 β1 = 0.01554 γ1 = 0 α2 = 0.67204 β2 = 0.03706 γ2 = 0.00261 | |
| Log-Logistic | C-s | Continuous-Non-negative | α = 1.0305 β = 0.01698 | |
| Aug | Log-Pearson 3 | KS | Continuous-Advanced | α = 2.2362 β = −1.0863 γ = −0.67154 |
| Dagum | AD | Continuous-Non-negative | k = 0.21083 α = 3.154 β = 0.18395 | |
| Gen. Logistic | C-s | Continuous-Advanced | k = 0.33186 σ = 0.04097 μ = 0.06905 | |
| Sep | Lognormal | KS | Continuous-Non-negative | σ = 0.79939 μ = −1.057 |
| Lognormal (3P) | AD | Continuous-Non-negative | σ = 0.77923 μ = −1.0317 γ = −0.00649 | |
| Wakeby | C-s | Continuous-Advanced | α = 2.4861 β = 24.442 γ = 0.32909 δ = 0.11924 ξ = 0 | |
| Oct | Johnson SB | KS | Continuous-Bounded | γ = 0.42553 δ = 0.64897 λ = 2.7761 ξ = 0.09971 |
| Johnson SB | AD | Continuous-Bounded | γ = 0.42553 δ = 0.64897 λ = 2.7761 ξ = 0.09971 | |
| Weibull | C-s | Continuous-Non-negative | α = 1.505 β = 1.2768 | |
| Nov | Burr (4P) | KS | Continuous-Non-negative | k = 410.35 α = 2.2025 β = 19.348 γ = 0.10019 |
| Gen. Extreme Value | AD | Continuous-Advanced | k = −0.16419 σ = 0.51505 μ = 0.99221 | |
| Dagum | C-s | Continuous-Non-negative | k = 0.30935 α = 6.5299 β = 1.6691 | |
| Dec | Wakeby | KS | Continuous-Non-negative | α = 15.39 β = 14.166 γ = 0.89436 δ = −0.07454 ξ = 0.03718 |
| Wakeby | AD | Continuous-Advanced | α = 15.39 β = 14.166 γ = 0.89436 δ = −0.07454 ξ = 0.03718 | |
| Wakeby | C-s | Continuous-Advanced | α = 15.39 β = 14.166 γ = 0.89436 δ = −0.07454 ξ = 0.03718 |
| Season | DF | Test | Classification | Parameter |
|---|---|---|---|---|
| Winter | Error | KS | Continuous-Unbounded | k = 4.0395 σ = 1.511 μ = 5.6338 |
| Johnson SB | AD | Continuous-Bounded | γ = 0.23375 δ = 1.004 λ = 7.3287 ξ = 2.3215 | |
| Gen. Extreme Value | C-s | Continuous-Advanced | k = −0.20079 σ = 1.4778 μ = 5.03 | |
| Spring | Johnson SB | KS | Continuous-Bounded | γ = 2.0689 δ = 2.1565 λ = 15.213 ξ = −1.1827 |
| Johnson SB | AD | Continuous-Bounded | γ = 2.0689 δ = 2.1565 λ = 15.213 ξ = −1.1827 | |
| Triangular | C-s | Continuous-Bounded | m = 1.9374 a = 0.47754 b = 7.2821 | |
| Summer | Log-Pearson 3 | KS | Continuous-Advanced | α = 20.475 β = −0.18999 γ = 2.6709 |
| Wakeby | AD | Continuous-Advanced | α = 0.47551 β = 0.27013 γ = 0 δ = 0 ξ = 0.02749 | |
| Fatigue Life (3P) | C-s | Continuous-Non-negative | α = 0.77395 β = 0.33182 γ = −0.03038 | |
| Autumn | Wakeby | KS | Continuous-Advanced | α = 3.2617 β = 1.0513 γ = 0.07273 δ = 0.53543 ξ = 1.0616 |
| Wakeby | AD | Continuous-Advanced | α = 3.2617 β = 1.0513 γ = 0.07273 δ = 0.53543 ξ = 1.0616 | |
| Pearson 6 (4P) | C-s | Continuous-Non-negative | α1 = 6.2001 α2 = 133.47 β = 56.203 γ = 0.17101 |
| Month | DF | Test | Classification | Parameter |
|---|---|---|---|---|
| Jan | Dagum | KS | Continuous-Non-negative | k = 0.47664 α = 4.5829 β = 19.002 |
| Johnson SB | AD | Continuous-Bounded | γ = 1.9767 δ = 1.599 λ = 72.121 ξ = −1.8612 | |
| Log-Pearson 3 | C-s | Continuous-Advanced | α = 17.449 β = −0.13141 γ = 4.9063 | |
| Feb | Gen. Logistic | KS | Continuous-Advanced | k = 0.25388 σ = 4.0656 μ = 13.288 |
| Burr (4P) | AD | Continuous-Non-negative | k = 0.95673 α = 3.9551 β = 15.408 γ = −2.3151 | |
| Gen. Logistic | C-s | Continuous-Advanced | k = 0.25388 σ = 4.0656 μ = 13.288 | |
| Mar | Gen. Logistic | KS | Continuous-Advanced | k = 0.31917 σ = 3.2124 μ = 8.5246 |
| Wakeby | AD | Continuous-Advanced | α = 18.346 β = 3.4325 γ = 3.4914 δ = 0.32051 ξ = 1.1552 | |
| Frechet (3P) | C-s | Continuous-Non-negative/Unbounded | α = 4.4227 β = 18.71 γ = −11.865 | |
| Apr | Gamma (3P) | KS | Continuous-Non-negative | α = 1.9461 β = 3.9671 γ = 1.0613 |
| Triangular | AD | Continuous-Bounded | m = 2.6375 a = 1.0479 b = 22.451 | |
| Log-Logistic (3P) | C-s | Continuous-Non-negative | α = 2.7315 β = 7.6946 γ = −0.19962 | |
| May | Johnson SB | KS | Continuous-Bounded | γ = 0.95882 δ = 0.76586 λ = 44.446 ξ = −0.82892 |
| Johnson SB | AD | Continuous-Bounded | γ = 0.95882 δ = 0.76586 λ = 44.446 ξ = −0.82892 | |
| Levy (2P) | C-s | Continuous-Non-negative | σ = 3.7662 γ = 0.15548 | |
| Jun | Log-Pearson 3 | KS | Continuous-Advanced | α = 12.186 β = −0.32963 γ = 4.922 |
| Log-Pearson 3 | AD | Continuous-Advanced | α = 12.186 β = −0.32963 γ = 4.922 | |
| Frechet (3P) | C-s | Continuous-Non-negative/Unbounded | α = 2.0452 β = 3.8148 γ = −1.9001 | |
| Jul | Pareto 2 | KS | Continuous-Non-negative | α = 2.1788 β = 1.0299 |
| Burr | AD | Continuous-Non-negative | k = 38.604 α = 0.76293 β = 78.059 | |
| Lognormal | C-s | Continuous-Non-negative | σ = 1.5801 μ = −1.1549 | |
| Aug | Wakeby | KS | Continuous-Advanced | α = 2.5662 β = 1.3486 γ = 0.25904 δ = 0.41054 ξ = −0.19362 |
| Wakeby | AD | Continuous-Advanced | α = 2.5662 β = 1.3486 γ = 0.25904 δ = 0.41054 ξ = −0.19362 | |
| Gen. Pareto | C-s | Continuous-Non-negative/Unbounded | k = −0.3155 σ = 1.8361 μ = −0.05725 | |
| Sep | Gen. Gamma (4P) | KS | Continuous-Non-negative | k = 0.81775 α = 0.92604 β = 5.0817 γ = 1.1591 |
| Gen. Pareto | AD | Continuous-Non-negative/Unbounded | k = 0.25254 σ = 3.6722 μ = 1.0147 | |
| Wakeby | C-s | Continuous-Advanced | α = 51.126 β = 44.732 γ = 3.489 δ = 0.27459 ξ = 0 | |
| Oct | Phased Bi-Weibull | KS | Continuous-Advanced | α1 = 1.0577 β1 = 13.578 γ1 = 1 α2 = 1.7341 β2 = 13.127 γ2 = 12.453 |
| Gen. Pareto | AD | Continuous-Non-negative/Unbounded | k = −0.11597 σ = 11.494 μ = 1.3564 | |
| Reciprocal | C-s | Continuous-Bounded | a = 1.8756 b = 48.89 | |
| Nov | Wakeby | KS | Continuous-Advanced | α = 51.208 β = 5.7024 γ = 5.5576 δ = −0.04698 ξ = −0.29588 |
| Wakeby | AD | Continuous-Advanced | α = 51.208 β = 5.7024 γ = 5.5576 δ = −0.04698 ξ = −0.29588 | |
| Error function | C-s | Continuous-Unbounded | k = 1.8886 σ = 6.3089 μ = 12.653 | |
| Dec | Wakeby | KS | Continuous-Advanced | α = 174.22 β = 23.352 γ = 7.8323 δ = 0.00332 ξ = 0 |
| Wakeby | AD | Continuous-Advanced | α = 174.22 β = 23.352 γ = 7.8323 δ = 0.00332 ξ = 0 | |
| Nakagami | C-s | Continuous-Non-negative | m = 0.85455 Ω = 284.19 |
| Season | DF | Test | Classification | Parameter |
|---|---|---|---|---|
| Winter | Wakeby | KS | Continuous-Advanced | α = 2105.9 β = 87.559 γ = 30.657 δ = −0.49652 ξ = 0 |
| Johnson SB | AD | Continuous-Bounded | γ = 0.59032 δ = 0.95127 λ = 71.693 ξ = 17.303 | |
| Pearson 5 | C-s | Continuous-Non-negative | α = 8.9676 β = 355.01 | |
| Spring | Wakeby | KS | Continuous-Advanced | α = 119.98 β = 13.908 γ = 17.447 δ = −0.1198 ξ = 6.8618 |
| Wakeby | AD | Continuous-Advanced | α = 119.98 β = 13.908 γ = 17.447 δ = −0.1198 ξ = 6.8618 | |
| Wakeby | C-s | Continuous-Advanced | α = 119.98 β = 13.908 γ = 17.447 δ = −0.1198 ξ = 6.8618 | |
| Summer | Johnson SB | KS | Continuous-Bounded | γ = 0.77046 δ = 0.53354 λ = 17.666 ξ = 1.0915 |
| Wakeby | AD | Continuous-Advanced | α = 6.5362 β = 0.16191 γ = 0 δ = 0 ξ = 0.50184 | |
| Frechet (3P) | C-s | Continuous-Non-negative/Unbounded | α = 2.7693 β = 7.4869 γ = −4.0114 | |
| Autumn | Burr | KS | Continuous-Non-negative | k = 1.082 α = 4.2353 β = 27.892 |
| Gen. Logistic | AD | Continuous-Advanced | k = 0.23139 σ = 6.4346 μ = 27.028 | |
| Inv. Gaussian | C-s | Continuous-Non-negative | λ = 123.57 μ = 29.637 |
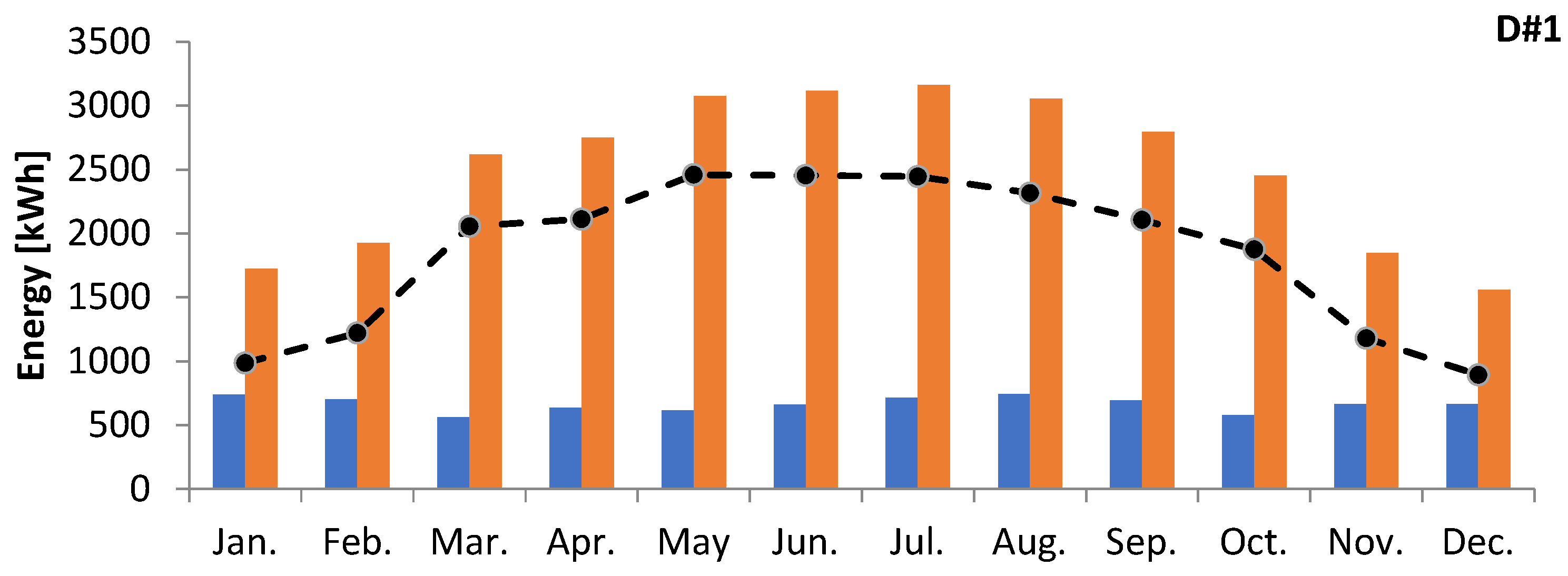
| Economic Performance of D#1 | |||||
| NPV [USD] | EP [year] | SP [year] | LCOE [USD/kWh] | B-C | ALCS [USD/year] |
| 31744 | 2.8 | 7.4 | 0.041 | 5.75 | 2483 |
| Net annual reduction of GHG emissions of D#1 | |||||
| Net annual GHG emission reduction [tCO2] | Cars and light trucks are not used | People are reducing energy use by 20% | Hectares of forest absorbing carbon | ||
| 19.4 | 3.6 | 19.4 | 1.8 | ||
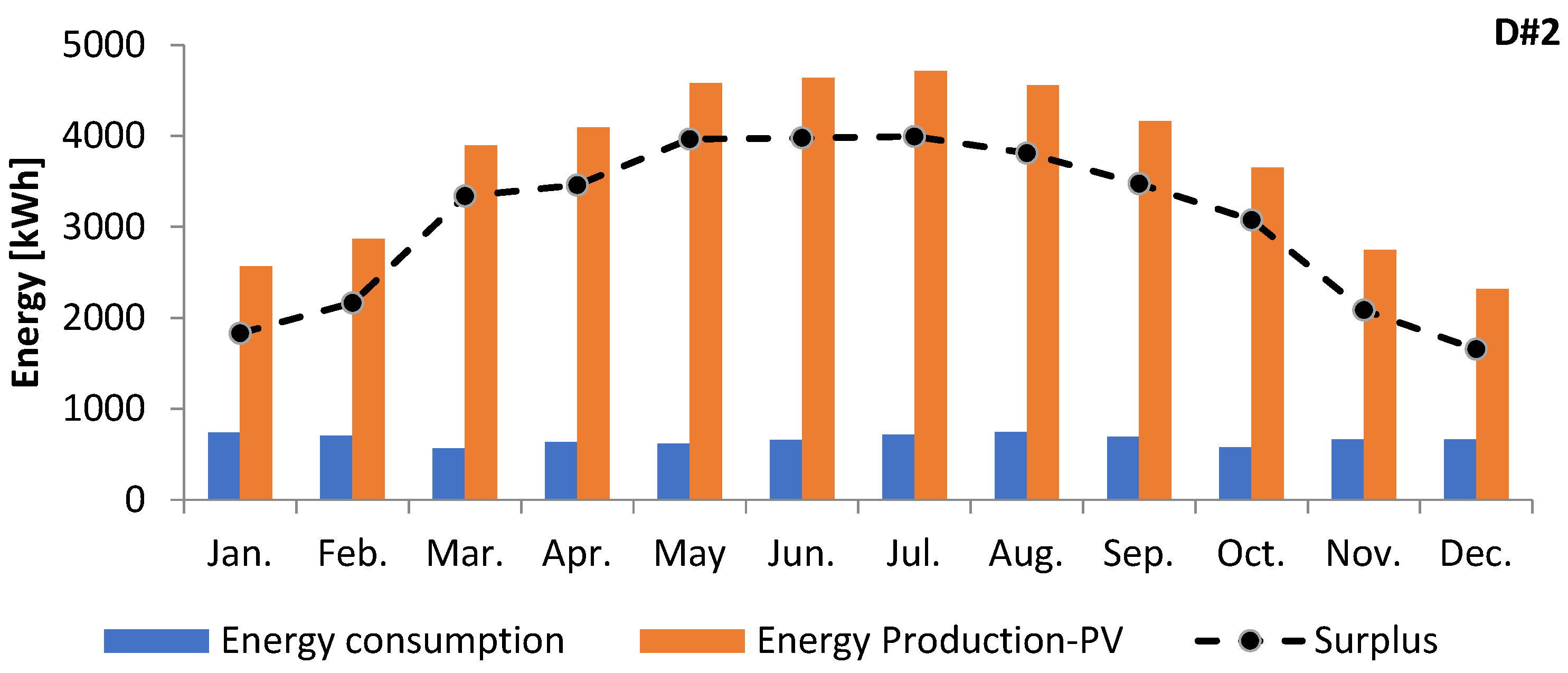
| Economic Performance of D#2 | |||||
| NPV [USD] | EP [year] | SP [year] | LCOE [USD/kWh] | B-C | ALCS [USD/year] |
| 54827 | 1.8 | 5.0 | 0.028 | 9.10 | 4289 |
| Net annual reduction of GHG emissions of D#2 | |||||
| Net annual GHG emission reduction [tCO2] | Cars and light trucks are not used | People are reducing energy use by 20% | Hectares of forest absorbing carbon | ||
| 29.0 | 5.3 | 29.0 | 10.0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kassem, Y.; Gökçekuş, H.; Kiraz, A.; Abdelnaby, A.H.A. Integrating Rainwater Harvesting and Solar Energy Systems for Sustainable Water and Energy Management in Low Rainfall Agricultural Region: A Case Study from Gönyeli, Northern Cyprus. Sustainability 2025, 17, 8508. https://doi.org/10.3390/su17188508
Kassem Y, Gökçekuş H, Kiraz A, Abdelnaby AHA. Integrating Rainwater Harvesting and Solar Energy Systems for Sustainable Water and Energy Management in Low Rainfall Agricultural Region: A Case Study from Gönyeli, Northern Cyprus. Sustainability. 2025; 17(18):8508. https://doi.org/10.3390/su17188508
Chicago/Turabian StyleKassem, Youssef, Hüseyin Gökçekuş, Aşkın Kiraz, and Abdalla Hamada Abdelnaby Abdelnaby. 2025. "Integrating Rainwater Harvesting and Solar Energy Systems for Sustainable Water and Energy Management in Low Rainfall Agricultural Region: A Case Study from Gönyeli, Northern Cyprus" Sustainability 17, no. 18: 8508. https://doi.org/10.3390/su17188508
APA StyleKassem, Y., Gökçekuş, H., Kiraz, A., & Abdelnaby, A. H. A. (2025). Integrating Rainwater Harvesting and Solar Energy Systems for Sustainable Water and Energy Management in Low Rainfall Agricultural Region: A Case Study from Gönyeli, Northern Cyprus. Sustainability, 17(18), 8508. https://doi.org/10.3390/su17188508








