A Hybrid Deep Learning and Model Predictive Control Framework for Wind Farm Frequency Regulation

Abstract

To enhance wind farm frequency regulation in renewable-dominant power systems, this paper proposes a bi-level hybrid framework integrating deep learning and model predictive control (MPC) by retaining the critical wake propagation delay while neglecting higher-order turbulence effects. The upper layer employs a synthetic inertial intelligent control strategy based on contractive autoencoder (CAE) and deep neural network (DNN). Particle swarm optimization (PSO) obtains optimal synthetic inertial parameters for dataset construction, CAE extracts features from multi-dimensional inputs, and DNN outputs optimal coefficients to determine the total power deficit the wind farm needs to supply. The lower layer uses a nonlinear model predictive control (NMPC) strategy with the discretized rotor motion equation as the prediction model and optimization under constraints to allocate the total power deficit to each turbine. MATLAB/Simulink case studies show that, compared with fixed-coefficient synthetic inertial control, the proposed framework raises the frequency nadir by 0.01–0.02 Hz, shortens the settling time by over 200 s under 2–4% load disturbances, and maintains rotor speed within the safe range. This work significantly enhances the wind farm’s frequency regulation performance, contributing to power system and energy sustainability.

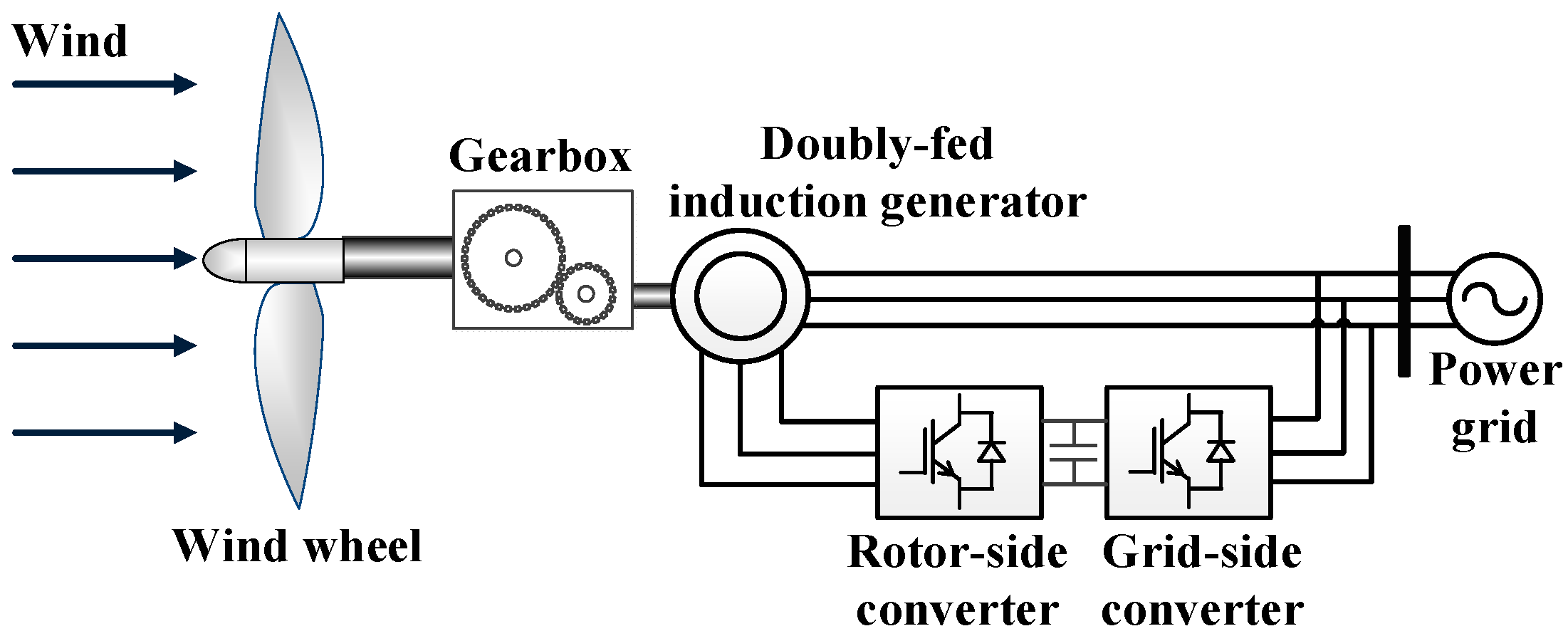
1. Introduction

Driven by the global push for energy sustainability and decarbonization, renewable energy is gradually replacing traditional energy sources and assuming a dominant role in modern power systems [1]. As a clean and pollution-free renewable energy source, wind power effectively alleviates energy shortages and mitigates environmental pollution caused by conventional energy utilization and is a key link in achieving a sustainable energy future [2]. According to the statistics in June 2025, the global share of grid-connected renewable generation had exceeded 38%, establishing it as a cornerstone of global electricity networks [3,4]. In recent years, advancements in wind power technology have led to a steady increase in its global penetration. The global newly installed wind power capacity reached 117 GW, while the cumulative capacity exceeded 1136 GW, spanning 55 countries and regions worldwide [5]. China plays a leading role, accounting for 70% of global new capacity in 2024 and ranking first in offshore wind installations [6]. Germany approved 11 GW of onshore wind in 2024—a 70% year-on-year increase—and commissioned 2.2 GW in the first half of 2025, the highest level since 2017 [7]. While this extensive integration of wind power has advanced global energy structure optimization and decarbonization, it has also introduced new challenges to the stable operation of power systems [8].

The high-penetration integration of wind power and other renewables has markedly reduced the overall inertia of power systems, weakening the grid’s resilience to power fluctuations and exacerbating challenges to grid frequency stability [9,10]. The high-speed rotational kinetic energy stored in wind turbine (WT) rotors provides a unique physical basis for power system frequency regulation. Through rotor kinetic energy control technologies, this inertial energy can be instantaneously released or absorbed with millisecond-level response speeds, directly suppressing frequency disturbances. Additionally, WTs can actively reserve a 5–10% power margin via overspeed deluding or pitch angle control, enabling bidirectional flexible adjustment of output. Endowed with dual capabilities of inertial response and power reserve, wind power has emerged as a key controllable resource for enhancing frequency stability in high-renewable power systems, making its frequency regulation technology a current research focus [11].

Research on wind power frequency regulation technologies has been extensively explored at both the WT and farm levels. For the turbine level, most studies focus on synthetic inertial control and its improved methods. Reference [12] adopts the internal point method to coordinate the axial induction coefficients of each WT, optimize the output of the wind farm, and designs an adaptive droop control strategy. During the frequency regulation process, the sag coefficient is adjusted according to the WT operating conditions to enable the wind farm to optimally participate in the primary frequency regulation. Reference [13] proposes an improved WT droop control strategy considering turbulent wind speed fluctuations across dual time scales. By combining parameter tuning and online learning, it achieves adaptive adjustment and online correction of WT droop coefficients under turbulent winds. Reference [14] utilizes an improved PSO algorithm to optimize virtual inertia and droop control parameters, conducting wind speed adaptability analysis across three scenarios. Results confirm that the proposed strategy significantly enhances frequency regulation performance. Reference [15] formulates an objective function minimizing the sum of the first and second frequency dips, derives analytical expressions, and employs PSO and backpropagation neural networks to solve for optimal synthetic inertial control parameters. However, turbine-level studies often overlook wake effects in practical wind farms and the mutual interactions between WTs. Reference [16] proposes an MPC weight coefficient correction method and an MPC strategy considering wind speed, which can effectively increase the active power output of the WT and promote the recovery of rotational speed. However, current turbine-level research often overlooks the dynamic interactions between WTs, and struggles to adapt to the complex and diverse operation scenarios in renewable-dominant power systems.

For the wind farm level, the existing research primarily focuses on WT grouping and coordinated control. Reference [17] develops a framework based on WT installation positions and wind directions, utilizing MPC and K-means clustering to group WTs. A collaborative control strategy accounting for spatiotemporal uncertainty is designed to optimize the overall frequency regulation capability, enabling WTs to connect to or disconnect from the grid in an orderly manner based on wind speed, active power increments, and duration. Reference [18] employs a clustering algorithm to dynamically group fans exhibiting similar frequency regulation performance and developed a fuzzy adaptive comprehensive inertial controller. By utilizing frequency deviation and the rate of frequency change as inputs, while designating the droop control coefficient and virtual inertial control coefficient as outputs, a synthetic inertial control loop is established.

Reference [19] proposes a wind farm frequency control method based on WT regulating capacity. During rapid frequency drops, wind farms prioritize reducing the frequency change rate and maximum deviation by rapidly injecting active power. As frequency begins to recover, they simulate synchronous generator characteristics for further adjustment. Reference [20] proposes a frequency control scheme for doubly fed induction generators considering wake effects, which is achieved by integrating virtual inertia control and primary frequency control in an overall manner. This scheme enables frequency regulation under time-varying conditions and effectively alleviates the maximum frequency variation rate and frequency deviation. Reference [21] clusters the WTs based on their similar frequency regulation capabilities, defined the frequency regulation capability factor as the clustering index, and took the system frequency deviation and frequency change rate as input and the inertia control coefficient as output, thus achieving effective frequency support for the power system.

Existing research on wind farm frequency control predominantly centers on WT grouping and coordinated control strategies, aiming to optimize frequency regulation capability through dynamic grouping, spatiotemporal uncertainty management, and simulation of synchronous generator characteristics. However, existing studies largely overlook the time-delay coupling effects induced by wake interactions during frequency regulation. This oversight impedes accurate modeling of dynamic relationships in wind farms, particularly in renewable-dominant systems with complex and abrupt frequency fluctuations.

To address the aforementioned challenges, this paper proposes a hybrid framework integrating deep learning and MPC for wind farm frequency regulation in renewable-dominant power systems. Specifically, a bi-level control architecture is customized for this scenario to synergistically enhance regulation performance—drawing on established techniques to target the unique complexities of wind farm dynamics. The upper layer establishes a synthetic inertial control strategy using CAE and DNN: first, PSO is utilized to generate optimal synthetic inertial parameters under diverse operating scenarios, forming a comprehensive dataset; CAEs then extract robust features from multi-dimensional inputs, and DNN—trained on these features—enables real-time output of optimal inertial and droop coefficients, determining the total power deficit required for frequency support. The lower layer employs an NMPC strategy, which takes the discretized rotor motion equation as its prediction model, allocates the total power deficit to individual turbines under constraints of rotor speed and electromagnetic power, and ensures coordinated operation by minimizing deviations in rotor kinetic energy and power fluctuations. Through case studies in MATLAB/Simulink, this framework is validated to outperform conventional strategies in key metrics such as frequency nadir improvement, stabilization acceleration, and adaptability to varying load disturbances and wind speeds. By leveraging the complementary strengths of deep learning—and organizing these tools into a structure tailored to wind farm frequency regulation—the proposed framework effectively captures complex dynamic relationships within wind farms. It is this targeted integration of existing techniques that provides a robust solution for enhancing wind farm frequency regulation performance, contributing to power system and energy sustainability.

2. Wind Farm Modeling for Frequency Regulation

2.1. Wind Turbine Mathematical Model

A doubly fed induction generator (DFIG) primarily comprises three components: the wind rotor, transmission chain, and converter. Figure 1 illustrates the structural schematic of the DFIG [22,23]. The incoming wind flows across the rotor blades, driving the gearbox to rotate and converting wind energy into mechanical energy. This mechanical energy is subsequently converted into usable electrical energy by the generator. Given the intermittent nature of wind energy, integration with a converter is necessary to transform it into stable power suitable for grid injection.

The aerodynamic power converted from wind energy after the wind passes through the turbine blades is as follows [24]:

$$P_m=0.5\rho \pi C_P(\lambda ,\beta )R^2{\nu }^3$$

(1)

where $\rho$ is the density of air; $C_P(\lambda ,\beta )$ is the wind energy utilization coefficient; $\lambda$ is the tip speed ratio; $\beta$ is the pitch moment Angle; R is the radius of WT; v represents the incoming wind speed. The calculation formula for the wind energy utilization coefficient $C_p(\lambda ,\beta )$ is as follows:

$$\left\{\begin{array}{l}{C}_P(\lambda ,\beta )=0.22({\displaystyle \frac{116}{{\lambda }_i}}-0.4\beta -5)e^{{\displaystyle \frac{-12.5}{{\lambda }_i}}}\\ {\lambda }_i={\displaystyle \frac{1}{\frac{1}{\lambda +0.08\beta }-\frac{0.035}{{\beta }^3+1}}}\end{array}\right.$$

(2)

where $\lambda$ is the tip speed ratio, which is defined as the ratio of the blade tip linear velocity to the wind speed, $\lambda =\omega R/\nu$, and $\omega$ represents the rotational speed of WT.

When wind speed is at or below the rated value, the blade pitch angle is typically maintained at $\beta =0^{\circ }$, and the power coefficient becomes a function solely of the tip speed ratio $\lambda$. Under normal operation, each wind speed corresponds to an optimal rotational speed ${\omega }_{opt}$ at which the power coefficient reaches its maximum value $C_{p\max }$, thereby yielding the maximum extractable power $P_{\max }$ for that specific wind speed. The associated tip speed ratio under this condition is defined as the optimal tip speed ratio ${\lambda }_{opt}$, which is unique to the given turbine model. Consequently, the turbine operates in maximum power point tracking (MPPT) mode. For all turbines of the same type, ${\lambda }_{opt}$ remains constant. By connecting the maximum power points corresponding to their respective optimal speeds across the full range of wind speeds, the optimal speed–power characteristic of the turbine is derived, as illustrated in Figure 2.

Combining Equation (1), the mechanical power $P_{MPPT}$ of WT operating in the MPPT mode can be calculated as:

$$P_{MPPT}=k_{opt}{\omega }^3$$

(3)

where $k_{opt}$ is the optimal torque gain, $k_{opt}=0.5\pi \rho C_{P\max }{R}^5/{\lambda }_{opt}^3$.

Neglecting the dynamic effects of the gearbox and approximating the drive train as a rigid shaft, a simplified single mass drive train model is obtained:

$$\left\{\begin{array}{l}{J}_t{\displaystyle \frac{d\omega }{dt}}=T_m-T_e={\displaystyle \frac{P_m}{\omega }}-{\displaystyle \frac{P_e}{\omega }}\\ J_t=J_r+N_g^2{J}_g\end{array}\right.$$

(4)

where $J_r$ and $J_g$ are the rotor and generator moments of inertia, respectively; $J_t$ is the equivalent total moment of inertia of WT referred to the low speed side; $N_g$ is the gearbox ratio; $T_m$ represents the aerodynamic torque; $T_e$ is the generator electromagnetic torque referred to the low speed side; and $P_e$ is the generator electromagnetic power.

2.2. Wind Farm Dynamic Equivalent Modeling Considering Wake Effect and Time Delay

With the continuous expansion of wind farm scales, the impacts of wake effect among turbines on frequency regulation have become increasingly significant. The wake effect refers to the phenomenon where airflow passing through a turbine’s rotor creates a downstream region with reduced wind speed and increased turbulence intensity. Downstream turbines located within the wake of upstream units thus experience heightened fatigue loads and diminished extractable wind energy, leading to reduced wind farm generation efficiency, increased maintenance costs, and higher failure rates. Thus, the main hypothesis of this study is that the first-row WTs operate under constant wind speed, with high-order turbulence effects neglected while the core characteristic of wake propagation delay is retained. The Jensen wake model, an analytical wake model widely adopted in WT frequency regulation studies [25], is distinguished by three salient features: (1) the initial diameter of the wake boundary equals the rotor diameter; (2) the wake cross sectional area increases in direct proportion to the downstream propagation distance; (3) the wake wind speed is uniform across any plane perpendicular to the wind direction.

A schematic of the Jensen single turbine wake model is presented in Figure 3. It is evident that the wake expands uniformly on both sides of the rotor with a constant expansion coefficient. Under these assumptions, the wake wind speed at a downstream distance x is expressed as:

$$\nu ={\nu }_0\left(1-{\displaystyle \frac{\sqrt{1-C_T(\lambda ,\beta )}}{{\left(1+2k\frac{x}{D}\right)}^2}}\right)$$

(5)

where ${\nu }_0$ is the free stream wind speed; $C_T(\lambda ,\beta )$ is the turbine thrust coefficient; k represents the wake decay coefficient, whose classical value for onshore WT wake calculations is 0.075; and D is the rotor diameter of the turbine.

In wind farms with numerous turbines, downstream units may be simultaneously affected by wakes generated by several upstream turbines. Consequently, the superposition of multiple wake effects at the location of downstream turbines must be accounted for. Four wake superposition methods are currently commonly used: the geometric sum model, linear sum model, energy conservation model, and square sum model [26]. This study employs the widely adopted square sum model. Under this framework, the incident wind speed at the jth turbine within the wind farm is expressed as:

$$\left\{\begin{array}{l}{\nu }_j={\nu }_0[1-\sqrt{{\displaystyle \sum _{i=1}^{j-1}{(1-\frac{{\nu }_{ij}}{{\nu }_i})}^2}}]\\ {\nu }_{ij}={\nu }_{0i}\{1-[{\displaystyle \frac{1-\sqrt{1-C_T}}{{(1+2k\frac{x_{ij}}{D})}^2}}]\cdot [{\displaystyle \frac{A_{shadow,ij}}{A_{0j}}}]\}\end{array}\right.$$

(6)

where ${\nu }_{ij}$ is the wake induced wind speed at downstream turbine $j$ originating from upstream turbine $i$; ${\nu }_{0i}$ is the incident wind speed at the rotor of upstream turbine $i$; $x_{ij}$ represents the along wind distance between upstream turbine $i$ and downstream turbine $j$; $A_{shadow,ij}$ is the wake shadow area cast by turbine $i$ on turbine $j$; and $A_{0j}$ is the rotor swept area of downstream turbine $j$.

When a turbine’s control action alters the wake wind speed, the modified flow field does not reach downstream turbines instantaneously. Instead, the propagation delay, termed the inter-turbine time lag, must be considered. The calculation of this time lag is given by:

$${\tau }_{ij}={\displaystyle \frac{x_{ij}}{{\nu }_i}}$$

(7)

where ${\tau }_{ij}$ is the wake propagation time lag from upstream turbine $i$ to downstream turbine $j$; $x_{ij}$ is the along wind distance between upstream turbine $i$ and downstream turbine $j$; and ${\nu }_i$ is the initial wind speed at the rotor of upstream turbine $i$.

Combining the above with the wake equations, the wake superposition formulation accounting for the propagation time lag is obtained as:

$${\nu }_j(t)={\nu }_0(t)[1-\sqrt{{\displaystyle \sum _{i=1}^{j-1}{(1-\frac{{\nu }_{ij}(t-{\tau }_{ij})}{{\nu }_i(t)})}^2}}]$$

(8)

In wind farms, the large number of WTs necessitates simplification to reduce computational complexity. Typically, turbines operating under identical conditions are treated as equivalent units. The operational status of WTs in a farm is primarily influenced by wind speed, with variations in wind speed leading to differences in their active power output and rotor speeds. To address this, this paper combines wake effect considerations with the congruent equivalence method to group turbines based on wind speed magnitudes. Within each group, turbines having the same wind speed are equivalent to a single representative turbine. Through this approach, a wind farm containing multiple turbines can be simplified to an equivalent model composed of these representative units, thereby reducing the complexity of large-scale wind farm analysis.

The rated capacity and rated active power of the equivalent generator after equivalence are:

$$\left\{\begin{array}{c}{S}_{eq}={\displaystyle \sum _{i=1}^{N_r}{S}_i}\\ P_{eq}={\displaystyle \sum _{i=1}^{N_r}{P}_i}\end{array}\right.$$

(9)

where $S_i(i=1,\dots ,N_r)$ is the rated capacity of each generator; $P_i(i=1,\dots ,N_r)$ is the rated active power of each generator.

The impedance parameters of the equivalent generator can be obtained by the capacity-weighted average method, with the weighting coefficient being:

$${\rho }_i=S_i/{\displaystyle \sum _1^{N_r}{S}_i}$$

(10)

This chapter develops a wind farm model considering the time-delay effect of wake propagation, aiming to profoundly reveal the mechanism of how wind power integration influences power system dynamics. This work thereby provides a robust modeling foundation for the subsequent frequency regulation strategy design and optimization. This paper establishes a multi-turbine dynamic model that explicitly incorporates inter-turbine interaction characteristics, with a key focus on wake effect modeling. Specifically, the Jensen wake model with square-sum superposition is adopted to quantify the wake impact of upstream turbines on downstream ones. In the modeling process, the operational state of each turbine is considered independently—constraints such as rotor speed limits and power ramp rates are tailored to the unique working conditions of each turbine, rather than applying uniform settings to the entire farm, which fully reflecting the dynamic interaction between multiple turbines in the wind farm.

3. Synthetic Inertial Control Based on Deeping Learning

3.1. Synthetic Inertial Control Based on DNN and CAE

From the perspective of the overall synthetic inertial control process, frequency regulation performance is primarily determined by the magnitudes of the droop and virtual inertia coefficients. For a given power system with fixed wind speed, wind power penetration level, and load disturbance characteristics, there always exists a unique set of optimal synthetic inertia parameters that yields the best possible frequency response. However, traditional time-domain simulations rely on manual parameter tuning based on engineering experience, which is time-consuming and may not guarantee convergence to the global optimum. To address this challenge, this paper proposes a deep learning-based wind farm inertial control strategy. This architecture has the ability to process and extract key features from high-dimensional, coupled input data through CAE’s denoising and dimensionality reduction, while DNN’s deep layers provide strong nonlinear fitting to map these features to optimal control parameters, enabling millisecond-level online output that meets grid frequency regulation’s real-time demands. The CAE-DNN model takes key frequency regulation factors as inputs, including grid-side real-time frequency deviation, rate of frequency change, and wind farm-side first-row wind speed, rotor speeds, and total power deficit. Its expected outputs are the optimal equivalent inertial coefficient and droop coefficient for the wind farm, which guide the lower-layer MPC in power deficit allocation to ensure grid frequency stability and WT safety. 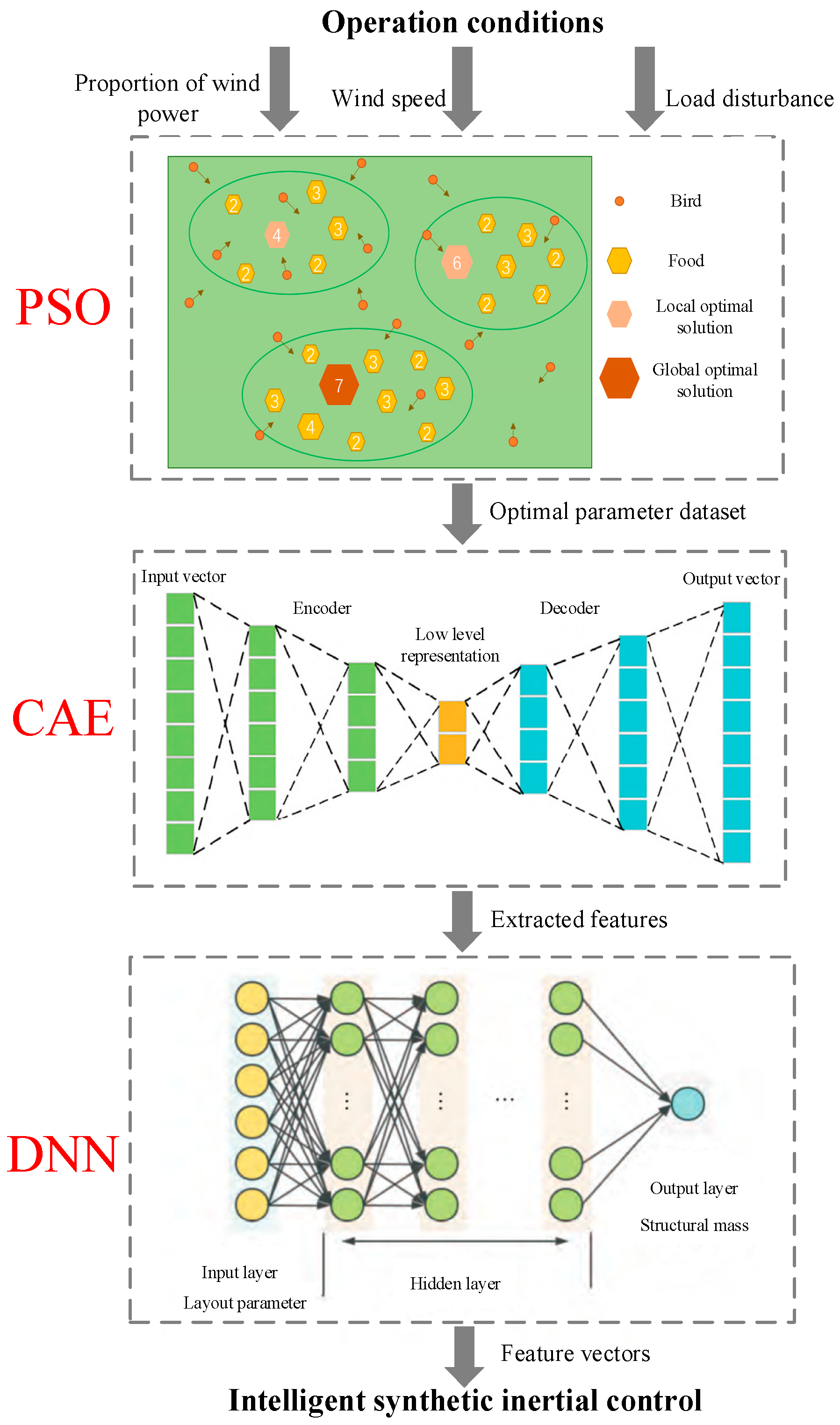Figure 4 illustrates this architecture.

The DNN-based synthetic inertia intelligent control framework for WT frequency regulation encompasses three critical stages: data acquisition, feature extraction, and parameter prediction. First, the PSO algorithm is employed in simulations to identify optimal synthetic inertia parameters under various operating conditions. These parameters are then coupled with corresponding scene data to construct an integrated multi-dimensional training dataset. Once the dataset is established, a CAE is applied to learn and extract latent features, preserving key information while reducing dimensionality and data redundancy. This process ensures well-conditioned inputs for the subsequent DNN. Finally, the DNN learns the complex mapping between wind farm synthetic inertia parameters and system states from the extracted features. By approximating the optimal parameter mapping function, the network can rapidly and accurately output the wind farm’s optimal synthetic inertia parameters in real time during online operation. This approach significantly enhances the adaptability and robustness of the control strategy while shortening online decision-making time, enabling real-time response to power system frequency variations.

In practical wind farm operation, when extreme conditions occur such as drastic wind speed changes exceeding the cut-out wind speed or compound faults involving multiple system failures, wind turbines prioritize their own stability and safety through protective mechanisms including pitch control and generator disconnection. Under such circumstances, the turbines withdraw from frequency regulation to focus on self-preservation. Therefore, our validation focuses on the frequency regulation performance within safe operating ranges where wind speeds remain within normal thresholds and no major equipment failures occur. This operating envelope covers over 95% of typical wind farm operation scenarios. Regarding control strategies under extreme conditions beyond the training dataset, our framework incorporates dedicated safety protocols: when wind speed exceeds predefined safety limits or critical component faults are detected, the upper-layer DNN control coefficient generator automatically freezes its output, transitioning control authority to the lower-layer MPC for minimum power maintenance strategy execution.

3.2. Feature Extraction with Contractive Autoencoders

In the combined inertial frequency regulation process, regulation performance is predominantly governed by the droop control parameter $K_{\mathrm{pf}}$ and the virtual inertial control parameter $K_{\mathrm{df}}$. For a given system, a unique optimal parameter pair always exists under fixed wind speed, wind power proportion, and load disturbance conditions. The collection of such optimal pairs, obtained across variations in these three variables, forms a high-dimensional dataset. The predictive phase’s efficacy hinges critically on appropriate input data selection, rigorous preprocessing, and effective feature learning. To enhance predictive accuracy, this study employs a deep feature learning method known as the CAE, which not only reconstructs input signals with high fidelity but also demonstrates robustness against input perturbations.

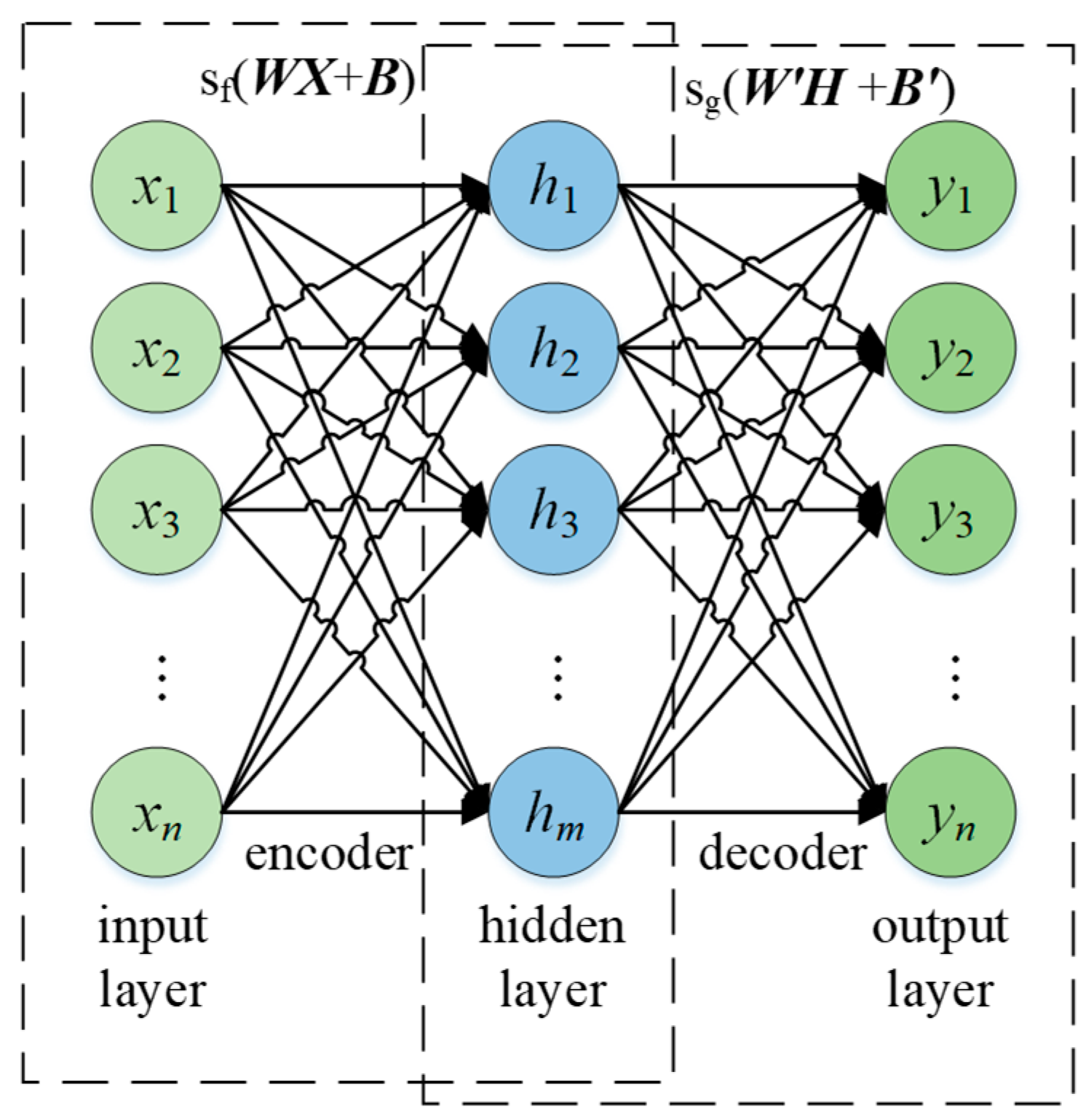
The network architecture of the autoencoder is illustrated in Figure 5. An encoder maps the input vector to a latent feature vector, and a decoder then reconstructs the original input vector from these latent features.

The input sample set, denoted by X, consists of N samples $x_1,x_2,x_3,\dots ,x_n$. The latent feature vector set of the hidden layer, denoted by H, contains M samples $h_1,h_2,h_3,\dots ,h_m$. The relationship between X and H can be expressed as:

$$H=s_f(WX+B)$$

(11)

where W is the input-to-hidden layer weight matrix, B is the corresponding bias matrix, and $s_f$ is the activation function of the encoder neurons, typically implemented as the sigmoid function.

$$s_f(z)={\displaystyle \frac{1}{1+\exp (-z)}}$$

(12)

where z is the input vector.

The decoder performs the inverse operation of the encoder, reconstructing the original input from the latent feature vectors in the hidden layer. Let Y denote the output vector set, consisting of N samples, each of dimension n. The decoding relationship between H and Y can be expressed as:

$$Y=s_g(W^{\prime }H+B^{\prime })$$

(13)

where $W^{\prime }$ represents the weight matrix that connects the hidden layer to the output layer, $B^{\prime }$ represents the corresponding bias matrix, and $s_g$ is the activation function of the decoder neurons.

The autoencoder accomplishes feature learning by minimizing the discrepancy between the reconstructed outputs and the initial input data, as follows:

$$L(X,Y)={\displaystyle \frac{1}{N}}{‖X-Y‖}^2$$

(14)

Gradient descent algorithms are employed to iteratively update network weights and biases, aiming to minimize the reconstruction error, which is expressed as follows:

$$\left\{\begin{array}{l}W\leftarrow W-l{\displaystyle \frac{\partial L(X,Y)}{\partial W}}\\ B\leftarrow B-l{\displaystyle \frac{\partial L(X,Y)}{\partial B}}\end{array}\right.$$

(15)

where l denotes the learning rate. However, during autoencoder training, the model may only retain information from the initial input data. This does not necessarily ensure an effective representation of the underlying feature information.

Building upon the conventional autoencoder, the CAE augments the loss function with a contraction regularization term. This adjustment forces the encoder to learn feature extraction mapping with more prominent contractive properties and improved resilience to minor perturbations in the training data neighborhood. Let $\lambda$ denote the contraction regularization factor, and let $J_f(x)$ represent the Jacobian matrix of hidden layer outputs with respect to input samples. The CAE loss function is then expressed as:

$$J_{CAE}(W,B)=J(X,Y)+\lambda {\left|J_f(x)\right|}_F^2$$

(16)

where ${\left|J_f(x)\right|}_F^2$ is the squared Frobenius norm of the Jacobian matrix, expressed as:

$${\left|J_f(x)\right|}_F^2={{\displaystyle \sum _{i,j}(\frac{\partial h_j(x)}{\partial x_i})}}^2$$

(17)

With respect to the loss function, the CAE extracts abstract features by balancing the reconstruction error and the contraction regularization term. Contraction regularization compels the learned mapping to show small gradients against the input, whereas the reconstruction error mandates the CAE to retain full information. Under their combined influence, the gradients of the feature extraction function are mostly small, with only a few having larger magnitudes. As a result, minor input perturbations are attenuated by the small gradients, thereby enhancing the CAE’s robustness. During the pre-training phase, the CAE continuously learns and extracts data features while providing well-posed initial parameters for the DNN.

3.3. Deep Neural Network Training and Optimization

DNN is composed of an input layer, a hidden layer and an output layer, where the input layer and the output layer are respectively located at the two ends of the network and the middle layer is collectively referred to as the hidden layer. This architecture requires full connection between all adjacent layers, specifically manifested as a complete neuron mapping from layer i to layer i + 1, as shown in Figure 6.

The DNN is a multilayer architecture that uses unsupervised learning to initialize the weights of each layer. Through layer-wise feature mapping, it projects input features into successive feature spaces, refining their representation and enabling effective approximation of complex functions. The core principles of the DNN can be summarized in three aspects. First, each layer undergoes unsupervised pre-training. Second, during this unsupervised layer-wise training, the output features of one layer serve as the input to the next. Third, a supervised learning phase is subsequently applied to fine-tune all layers. Compared with conventional networks such as the backpropagation neural network, the DNN leverages its pre-training mechanism to achieve faster convergence and mitigate overfitting.

At the local level, a DNN functions similarly to a perceptron: each neuron performs the linear operation $z={\displaystyle \sum _{i=1}^m{w}_i{x}_i+b}$, followed by an activation function $\sigma (z)$. Given the DNN’s multiple layers and numerous parameters, consistent conventions are needed to define the linear coefficients $w$ and biases $b$. For the linear coefficient $w$: the weight connecting the first neuron in layer 2 to the second neuron in layer 3 is denoted $w_{21}^3$; the superscript 2 indicates the layer to which $w$ belongs, while the subscripts correspond to the output index (second neuron in layer 3) followed by the input index (first neuron in layer 2). Placing the output index first eliminates the need for transposition, simplifying the forward pass to $wx+b$. Note that the input layer has neither $w$ nor bias parameters $b$. For the bias $b$: the bias for the first neuron in layer 2 is defined as $b_1^2$, where the superscript 1 denotes its layer and the subscript 1 denotes the index of the neuron to which it applies.

3.4. Procedure and Steps

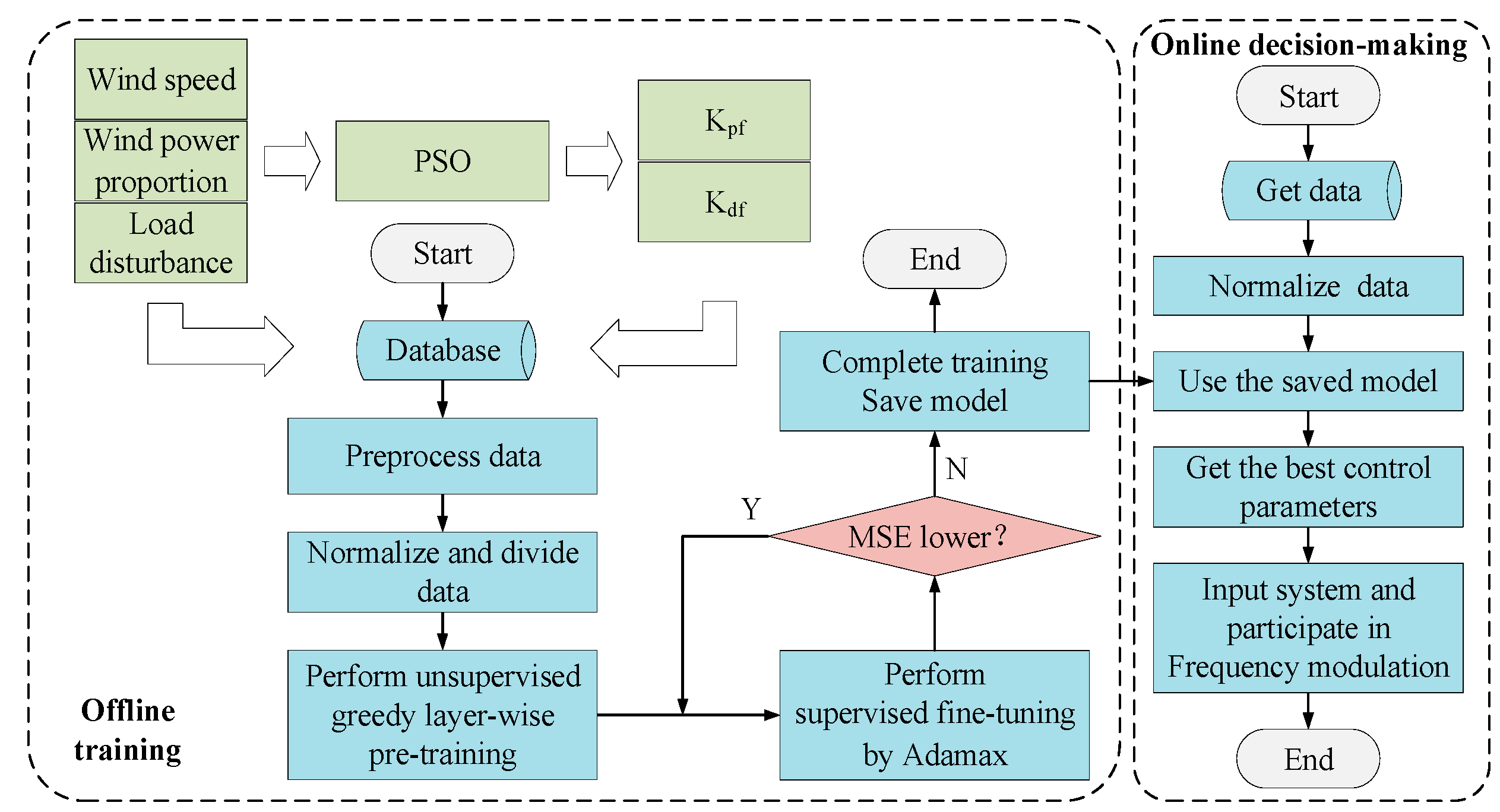
The synthetic inertial intelligent control scheme for wind power frequency regulation is divided into three parts: data acquisition, feature extraction, and parameter prediction. By extracting and learning features from the original combined inertia controller, the strategy is refined and optimized. The overall framework consists of an offline training phase and an online decision phase, as shown in Figure 7.

Offline training aims to establish a highly robust mapping model for the online stage, capable of rapidly extracting scenario features and feeding them into the decision process. The offline procedure is as follows:

Step 1: Define the PSO objective function and constraints, and perform time domain simulations. Use PSO to obtain optimal combined inertia parameter sets and pair them with wind speed, wind power penetration, and load disturbance; build a dataset with these three variables under the corresponding scenarios.

Step 2: Pre-process the dataset using CAE to perform feature extraction and denoising. This enhances data quality by removing noise artifacts while preserving essential features for subsequent DNN training.

Step 3: Normalize the CAE-processed data to a standardized scale, then partition it into training (90%) and validation (10%) subsets to facilitate proper model evaluation and prevent overfitting.

Step 4: Implement greedy pre-training in an unsupervised layer-wise manner, where feature vectors extracted by the CAE are progressively fed through each network layer while employing dropout to deactivate neurons stochastically, diminish co-dependence among nodes, boost generalization capability, and avoid model overfitting, with successive iterations yielding initialized weight matrices and bias vectors.

Step 5: Carry out supervised parameter optimization through fine-tuning, utilizing the Adamax optimization algorithm to adjust and enhance the weight matrix at the input layer, feature representations in hidden layers, and the weight matrix at the output layer.

Step 6: Take the mean square error (MSE) as the evaluation metric. If MSE decreases, return to Step 5; when MCE ceases to decrease, training terminates and the model is saved.

After offline training, whenever a new load disturbance occurs, scenario data can be matched instantly, and the trained network can rapidly deliver the optimal combined inertia parameters to achieve superior control and arrest frequency decline. The online procedure is as follows:

Step 1: Acquire real-time operational parameters including wind velocity profiles, renewable energy penetration levels, and grid disturbance characteristics to construct the online dataset.

Step 2: Apply standardization procedures to normalize the acquired online dataset to a consistent scale.

Step 3: Feed the normalized data into the saved DNN model; the optimal combined inertia parameter set is produced promptly and accurately.

Step 4: Implement the complete frequency regulation strategy in the power system to realize efficient and stable frequency control.

By separating multidimensional, complex operating conditions into an offline training stage and leveraging the trained model for rapid online decisions, the proposed dual phase architecture avoids repetitive online optimization required by traditional rolling horizon or fixed coefficient methods. This significantly accelerates wind farm response within the power system and enhances overall stability.

4. Power Allocation Based on Model Predictive Control

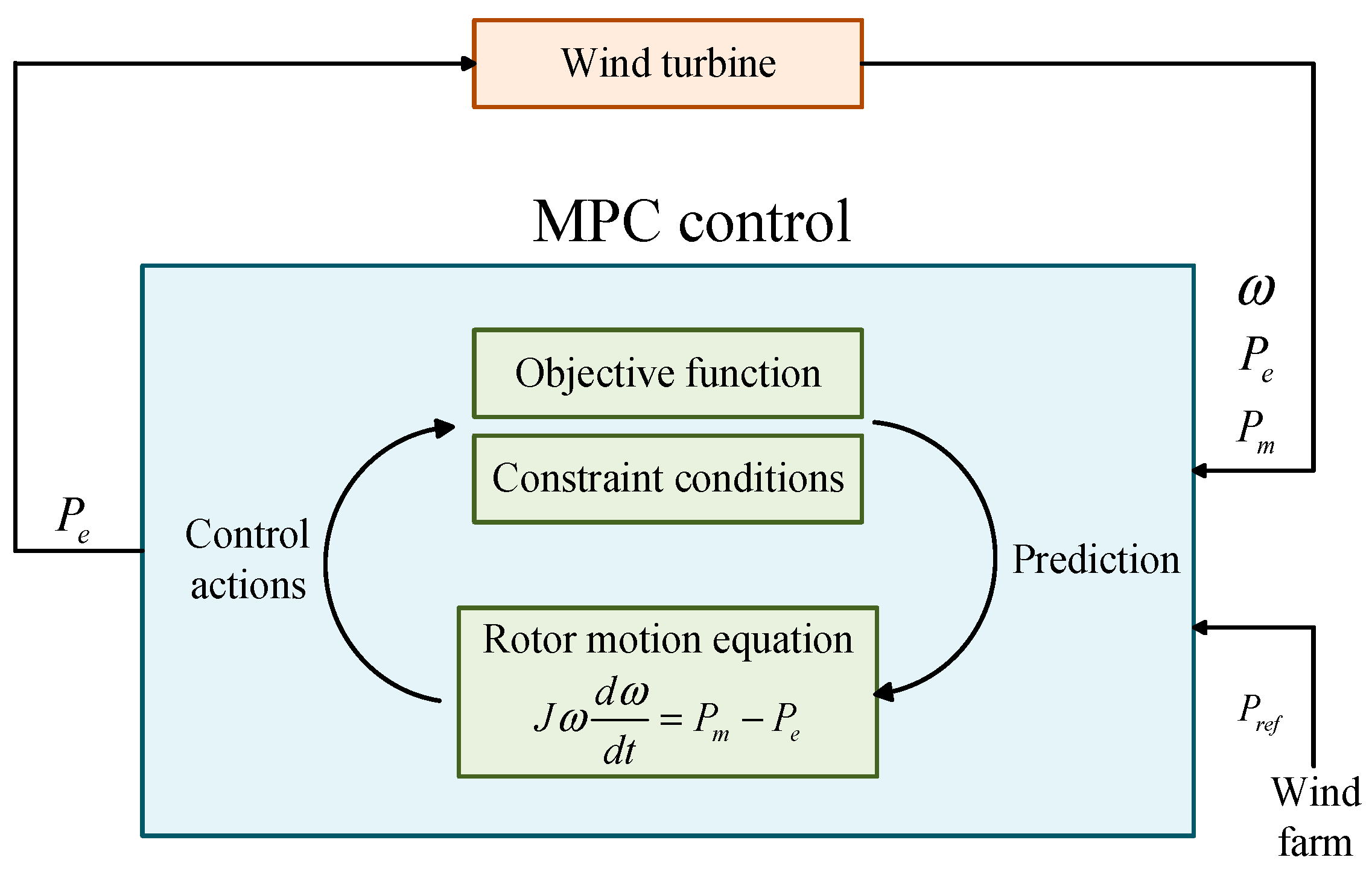
4.1. MPC Based Power Allocation Strategy

The improved synthetic inertial control proposed in the preceding section provides the wind farm with an aggregate power reference for grid frequency regulation. However, this reference must be allocated to individual turbines considering their specific operating conditions to realize coordinated control across the entire farm. MPC, a finite-horizon, receding-horizon optimization strategy with real-time feedback (schematic shown in Figure 8), has been increasingly adopted for active power control in wind-integrated systems due to its excellent control performance, modest model accuracy requirements, and strong robustness. To ensure both the overall frequency response of the wind farm and rational power distribution among turbines, the CAE- and DNN-based synthetic inertial control developed in Section 3 is employed as the reference input to a lower-layer NMPC scheme. This NMPC allocates the reference power and achieves effective frequency regulation.

The lower layer NMPC constructs its prediction model from the rotor motion equations of WTs. The wind farm incremental power reference generated by the upper layer is treated as a hard constraint in the NMPC. Turbine rotational speeds within the farm are selected as state variables, while mechanical powers act as disturbance inputs. Through rolling optimization, the NMPC generates distinct control signals to govern the electromagnetic power of each turbine. In this manner, electromagnetic power is rationally apportioned among all turbines according to their operating states, preventing disconnection caused by excessive rotor kinetic energy extraction. Moreover, the nonlinear turbine dynamics are decoupled from the system frequency dynamic equations and subjected to dedicated predictive control, significantly reducing the computational burden while ensuring stable frequency regulation performance.

4.2. MPC Design and Implementation

In designing the lower layer MPC, three key considerations must be addressed. First, the model’s nonlinearities should be retained to enhance control accuracy while simultaneously improving computational efficiency and shortening the response time to frequency drop events. Second, rotational speed and electromagnetic power constraints must be imposed on each turbine to prevent disconnection caused by excessive rotor kinetic energy release, ensuring smoother rotor response and reliable support during frequency declines. Finally, the MPC strategy must distribute the wind farm power deficit computed by the upper layer deep learning-based synthetic inertia controller, continuously generating distinct control signals to regulate the active power output of each turbine throughout the frequency regulation process.

The rotor motion equation of WT can be written as:

$${\omega }_{r,j}{J}_i{\displaystyle \frac{d{\omega }_{r,j}}{dt}}=P_{m,i}-P_{w,i}$$

(18)

where ${\omega }_{r,j}$ is the rotor speed of the $i^{th}$ WT, $J_i$ is moment of inertia, $P_{m,i}$ is mechanical power, and $P_{w,i}$ is electromagnetic power.

Expressing the powers in Equation (18) as deviations, let $\Delta P_{m,i}$ and $\Delta P_{w,i}$ denote the changes in mechanical and electromagnetic power, respectively. The rotor motion equation then becomes:

$${\omega }_{r,j}{J}_i{\displaystyle \frac{d{\omega }_{r,j}}{dt}}=\Delta P_{m,i}-\Delta P_{w,i}$$

(19)

To align with the state space formulation of MPC, the rotor motion equation can be expressed as:

$${\displaystyle \frac{d{\omega }_{r,j}}{dt}}={\displaystyle \frac{1}{{\omega }_{r,j}{J}_i}}(\Delta P_{m,i}-\Delta P_{w,i})$$

(20)

Tailoring the MPC design to practical requirements yields the state space representation:

$$\left\{\begin{array}{l}\dot{x}(t)=f(x(t),u(t),w(t))\\ y(t)=u(t)\end{array}\right.$$

(21)

where the state variable vector is composed of the rotor speeds of all turbines within the wind farm:

$$x={[{\omega }_{r,j}]}^T$$

(22)

The control vector $u$ comprises the electromagnetic power outputs of each WT in the wind farm delivered to the power system, the disturbance vector comprises the variations in mechanical power of each turbine, and the output vector comprises the additional electromagnetic power each turbine must inject after the disturbance, as follows:

$$u={[\Delta P_{w,i}]}^T$$

(23)

$$w={[\Delta P_{m,i}]}^T$$

(24)

$$y={[\Delta P_{w,i}]}^T$$

(25)

Discretizing the continuous time state space model via the forward Euler method yields the discrete rotor motion equation as:

$${\omega }_{r,i}(k+1)={\omega }_{r,i}(k)+T_s\cdot {\displaystyle \frac{\Delta P_{m,i}(k)-\Delta P_{w,i}(k)}{J_i\cdot {\omega }_{r,i}(k)}}$$

(26)

That is:

$$x(k+1|k)=x(k|k)+T_s\cdot f(x(k|k),u(k|k),w(k|k))$$

(27)

At this point, the MPC output equation becomes:

$$y(k)=u(k)$$

(28)

With a prediction horizon of p, the system state p steps ahead of the current state is predicted as:

$$\left\{\begin{array}{l}x(k+1|k)=x(k|k)+T_{s}f(x(k|k),u(k|k),w(k|k))\\ x(k+2|k)=x(k+1|k)+T_{s}f(x(k+1|k),u(k+1|k),w(k+1|k))\\ ⋮\\ x(k+p|k)=x(k+p-1|k)+T_{s}f(x(k+p-1|k),u(k+p-1|k),w(k+p-1|k))\end{array}\right.$$

(29)

The MPC scheme designed for WTs in this paper aims to maximize the wind farm’s economic benefits during frequency regulation while minimizing changes in rotor kinetic energy. To simplify the solution, the MPC objective function must be properly formulated and explicitly expressed in terms of the control variables.

The objective function is designed with two considerations: first, to ensure the economic efficiency and normal operation of WTs, the rotor kinetic energy should be kept as close as possible to a given reference value; second, to maintain turbine stability, the variation in electromagnetic power output should be minimized—i.e., kept as close as possible to its steady-state value. Accordingly, the optimization objective function for WT’s MPC is formulated as follows:

$$\begin{array}{cc}\hfill \min J=& {\displaystyle \sum _{k=1}^p{\displaystyle \sum _{i=1}^j{P}_i\times \frac{1}{2}{J}_i\times {({\omega }_{r,i}(k)-{\omega }_{r,iref})}^2}}\hfill \\ & +{\displaystyle \sum _{k=1}^p{\displaystyle \sum _{i=1}^j{Q}_i\times {(\Delta P_{w,i}(k)-\Delta P_{w,iref})}^2}}\hfill \end{array}$$

(30)

where ${\omega }_{r,iref}$ is the rotor speed reference for the $i^{th}$ turbine, $\Delta P_{w,iref}$ the reference increment of electromagnetic power output for the $i^{th}$ turbine (here $\Delta P_{w,iref}=0$), $P_i$ the weighting penalty coefficient for the rotor speed of the $i^{th}$ turbine, and $Q_i$ is the weighting penalty coefficient for the electromagnetic power of the $i^{th}$ turbine.

In actual wind farm operation, constraints on both state and control variables must be imposed to ensure turbine safety. For state variables, rotor speed is typically maintained within the range of 0.7 p.u. to 1.3 p.u. Speeds below 0.7 p.u. render the turbine unable to provide frequency support, leading to tripping. Speeds exceeding 1.3 p.u. exceed the rated operating range, degrading power quality and risking drivetrain damage. Denoting the upper and lower rotor speed limits for the $i^{th}$ turbine as ${\omega }_{r,i\max }$ and ${\omega }_{r,i\min }$ respectively, the state variable constraints are given by:

$${\omega }_{r,i\min }\le {\omega }_{r,i}\le {\omega }_{r,i\max }$$

(31)

The electromagnetic power output of each WT directly affects grid frequency. Therefore, its variation must be constrained. An upper limit prevents excessive power from raising grid voltage or driving frequency outside permissible ranges, while a lower limit guarantees sufficient power to maintain stable grid frequency and voltage, avoiding frequency drops or voltage instability that would compromise supply reliability and power quality. Let $\Delta P_{w,i\max }$ and $\Delta P_{w,i\min }$ denote, respectively, the upper and lower bounds on the electromagnetic power increment for the ith turbine; the control variable constraints are then expressed as:

$$\Delta P_{w,i\min }\le \Delta P_{w,i}\le \Delta P_{w,i\max }$$

(32)

Moreover, the wind farm power reference $P_{ref}$ obtained in Section 3 must be enforced as an equality constraint on the electromagnetic power outputs of all turbines, requiring their total to match the prescribed reference:

$${\displaystyle \sum _{i=1}^j\Delta P_{w,i}}=P_{ref}$$

(33)

After solving, the required electromagnetic power sequence for WTs in the farm is obtained as $u={(u(1),u(2),\dots ,u(p))}^T$. Accounting for model mismatch and external disturbances, only the first element u(1) is applied as the control variable at the next time step. Through continuous receding horizon optimization and feedback correction, the electromagnetic power of each turbine is ultimately allocated appropriately throughout the frequency regulation process.

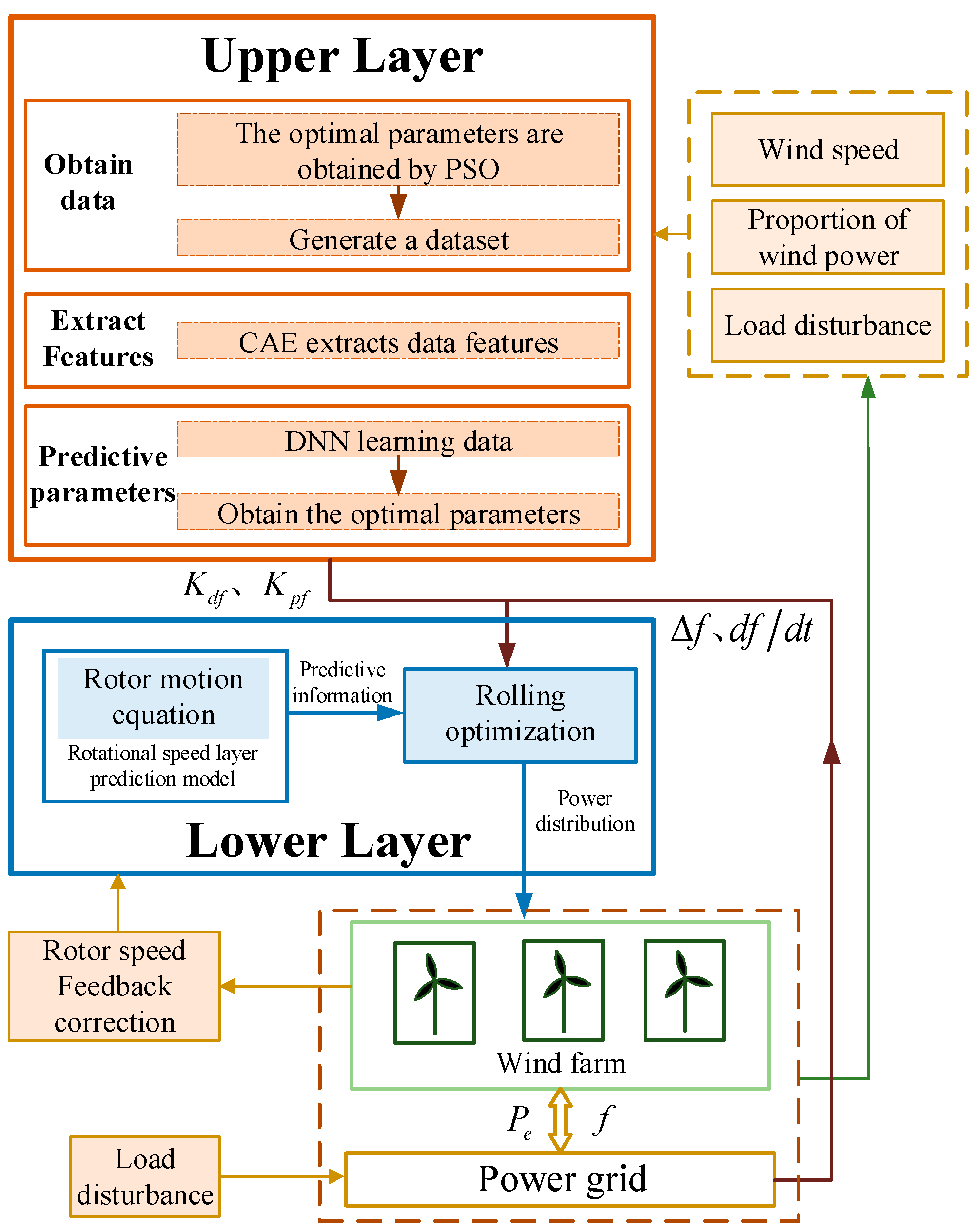
4.3. Overall Framework of This Paper

This paper proposes a hybrid deep learning and model predictive control framework that integrates a bi-level control model for wind farm frequency regulation, as illustrated in Figure 9. The upper layer adopts the synthetic inertial intelligent control strategy based on CAE and DNN presented in Section 3. Specifically, PSO is first employed to obtain optimal synthetic inertia parameters and construct a dataset. This dataset then undergoes preprocessing. CAE extracts features from multi-dimensional inputs (wind speed, wind power penetration, load disturbance) and their corresponding outputs, eliminating observation noise induced by wake and time-delay effect. The resulting feature vectors are fed into the CAE-trained network, which instantly outputs optimal synthetic inertia coefficients. These coefficients include droop and virtual inertia gains. Combined with real-time frequency deviation and its rate of change in the power system, these coefficients determine the aggregate power deficit that the wind farm must supply, thus finalizing the upper layer decision. In the proposed framework, the upper-layer surrogate model outputs optimal virtual inertia coefficients, which directly correspond to the dynamic simulation of the system’s inertia constant. Meanwhile, the droop coefficients determined by the framework are linked to the system’s damping coefficient. By embedding these physical insights into the integration of deep learning and MPC, the framework ensures that its decision-making process adheres to the fundamental principles of inertia and damping in power systems, bridging data-driven optimization with physical system characteristics.

The lower layer introduces an NMPC strategy to convert the above-determined aggregate power deficit into the required incremental electromagnetic power for each turbine. Using the discretized rotor motion equation as the prediction model, NMPC continuously takes rotor speed, mechanical power, and electromagnetic power of each turbine as state, disturbance, and control variables, respectively. Through receding horizon optimization and under the constraints of rotor speed and electromagnetic power, the scheme ensures that the sum of all turbines’ power increments equals the total deficit calculated by the upper layer. Simultaneously, it minimizes deviations in rotor kinetic energy and power fluctuations. The first element of the resulting optimal power adjustment sequence is selected as the control action, enabling closed-loop rolling correction. This not only smooths turbine output but also significantly suppresses secondary frequency dips caused by wake effects.

5. Case Study and Analysis

5.1. Simulation System and Parameters

To verify the effectiveness of the proposed frequency regulation framework of wind farm, a typical power system is built in MATLAB/Simulink platform (Version 2022b), comprising a 350-MW thermal unit and a 150-MW wind farm, as shown in Figure 10. The wind farm consists of three rows of ten NREL 5-MW turbines each (NREL, Golden, CO, USA). The incoming wind blows perpendicular to these rows, so all turbines within the same row experience identical wind speeds. By combining the equivalent parts in Section 2.2, ten WTs in each row can be equivalent to one. All WTs are set to maintain a constant blade pitch angle of 0 degrees during the frequency regulation dynamics. The system-frequency-response (SFR) model is adopted to simulate the frequency dynamics of power grids with wind power, which is a widely recognized model in power system frequency stability research. This model embeds a wind farm dynamic model inside that explicitly captures inter-turbine wake effects and their propagation delays. The wind farm dynamic model is solved using MATLAB/Simulink and MPC, enabling the SFR framework to not only provide the necessary transparency for control benchmarking but also ensure an accurate and physically consistent estimation of the wind farm’s response through the aforementioned wind farm dynamic model (

Table 1. System Parameters.

Types	Data
Rated Wind Speed	11 m/s
Rated Power	5 MW
Roter Diameter	126 m
Moment of Inertia	11,776,047 kg·m2
Rated Generator Speed	1230 rpm
Gearbox	97:1

).

5.2. Verification of the Proposed Framework

The incoming wind speed is 11 m/s, and the system experiences a 2% step disturbance at t = 100 s. This scene is denoted as Scene 1. Under this scene, the following control strategies are compared (

Table 2. Quantitative comparisons of three strategies in Scene 1.

Strategy	fnadir/Hz	Lowest Speed of WT1/p.u.	Time to Steady State/s
Strategy 1	49.9065	-	-
Strategy 2	49.9149	0.961	508
Strategy 3	49.9179	0.982	278

):

Strategy 1: WTs do not participate in frequency regulation.

Strategy 2: synthetic inertial control with fixed coefficients.

Strategy 3: the proposed synthetic inertial control based on deep learning and MPC.

After the disturbance, Strategy 3 enables the controller to issue a timely boost command $P_{ref}$ to the rotor-side converter, converting rotor kinetic energy into active power and suppressing frequency fluctuations. Consequently, when turbines are not involved in frequency regulation, a larger frequency drop occurs after load fluctuations. Once frequency regulation control is applied, rotor kinetic energy becomes coupled with system frequency, resulting in a marked improvement.

Figure 11 shows that after the disturbance, the frequency nadir under Strategy 1 is 49.9065 Hz, whereas under Strategy 2 it is 49.9149 Hz. The proposed control strategy, leveraging the synergy of DNN and MPC, rapidly identifies system changes and optimizes control parameters, raising the frequency nadir to 49.9179 Hz. This improvement is significant. A deeper analysis reveals that the traditional fixed-coefficient strategy, which ignores complex factors such as wake effects, cannot adjust frequency promptly or precisely. After the initial drop, the system undergoes several large-amplitude oscillations due to insufficient regulation energy and rotor speed recovery, stabilizing only 408 s after the disturbance. In contrast, the proposed strategy, with the deep network’s powerful data processing and feature extraction capabilities combined with MPC’s accurate prediction and optimization, determines the optimal control scheme rapidly. System frequency stabilizes within 178 s, 230 s faster than the conventional strategy. This substantial difference demonstrates the superior performance of the proposed control strategy in raising the frequency nadir and accelerating stabilization.

From Figure 11, it can be found the entire frequency regulation process lasted for approximately several hundred seconds. This is caused by the large spacing between WTs, the propagation of wake effects and the elimination of their impacts require a certain amount of time, which is an inevitable physical process in large-scale wind farm operations. The proposed hybrid framework, after offline training of the upper-layer CAE-DNN model, achieves rapid online response: the DNN can output optimal inertial and droop coefficients in milliseconds once a grid frequency disturbance or wake effect is detected, and the lower-layer nonlinear MPC completes power deficit allocation within seconds. This rapid online response enables the framework to quickly adapt to grid frequency changes and the dynamic impacts of wake effects, effectively improving the stability of grid frequency and ensuring the safe operation of WTs.

The simulation platform hardware is configured for a laptop with Intel^® Core™ i7-8750H processor and 8 GB of RAM (Intel, Santa Clara, CA, USA). In the simulation program of this paper, the MPC is solved by writing a Function module using the M-language in Simulink, rather than using solvers. According to the actual simulation results, the solution time for a single NMPC is approximately 0.49 ms, which demonstrates the proposed strategy can meet the actual control cycle requirements of frequency regulation in wind farms. Meanwhile, its performance in terms of increasing the lowest point of frequency, shortening the stabilization time, robustness and adaptability is significantly better than that of the comparison strategy.

Further inspection of Figure 11c–e shows that compared with Strategy 2, the proposed control strategy exhibits more efficient energy control during frequency regulation. It supports system frequency by releasing less rotor kinetic energy, thanks to the deep network’s accurate system state assessment and MPC’s optimal allocation. This precise energy release prevents turbine tripping due to excessively low rotor speed and reduces the impact of wake-induced wind speed disturbances. During regulation, rotor speed recovers quickly and remains stable, ensuring safe turbine operation and reliable power supply. In summary, the proposed control strategy significantly enhances system robustness and adaptability under diverse load disturbances, providing strong assurance for wind farms to participate efficiently in power system frequency regulation.

5.3. Robustness and Adaptability Analysis

5.3.1. Analysis Under Different Disturbances

To verify the adaptability of the proposed method under diverse load disturbances, scenes with different load disturbances are simulated in this section with an identical wind speed of 11 m/s. Scene 2 involves a 3% step load disturbance at t = 100 s, and Scene 3 further increases the disturbance to 4%. The simulation curves for the three scenarios are presented in Figure 12.

A lateral comparison of the three disturbance intensities under the same wind speed reveals the excellent adaptability of the proposed Strategy 3 to varying load magnitudes. As the disturbance increases from 2% to 4%, the frequency nadir under Strategy 3 decreases proportionally. It drops from 49.9197 Hz to 49.8773 Hz and then to 49.8341 Hz, yet it consistently outperforms Strategies 1 and 2. Meanwhile, the frequency settling time with Strategy 3 remains nearly constant at 178–179 s after each disturbance, demonstrating its robustness under different load disturbances.

Figure 12b,c confirm the same result. When the disturbance increases from 2% to 4%, Strategy 3 raises the aggregated wind power peak by 0.011 p.u. and 0.021 p.u., respectively. Rotor speed excursions are always confined within the safe operating range of 0.7 p.u. to 1.3 p.u. There is no rotor speed approaching the tripping limit, which often occurs with fixed-coefficient Strategy 2. At the 4% disturbance, Strategy 3 still limits frequency deviation to within 0.2 Hz, whereas the deviation under Strategy 2 grows to 0.2084 Hz, significantly widening the stability margin.

These results consistently demonstrate that Strategy 3 can adaptively adjust its droop and virtual inertia coefficients over a broad range of load disturbances. It maintains optimal frequency support under all examined conditions, fully validating its strong adaptability to complex disturbance environments.

5.3.2. Analysis Under Different Wind Speeds

To further validate the adaptability and effectiveness of the proposed synthetic inertial control strategy based on the deep neural network and MPC, Scene 4 and Scene 5 are devised for comparative analysis. In Scene 4, the wind speed entering the wind farm is reduced to 10.5 m/s while a 2% load disturbance is imposed on the system; in Scene 5, the inflow wind speed is further decreased to 10 m/s, thereby emulating more severe and challenging operating conditions. By comparing the performance of the fixed coefficient synthetic inertial control strategy with that of the improved synthetic inertial control strategy proposed herein under these scenes, the robustness and adaptability of the proposed approach across varying wind speed conditions can be comprehensively assessed.

The comparison of Scene 1, Scene 4, and Scene 5 shows that as wind speed decreases from rated values, the available rotor kinetic energy diminishes markedly. Under the proposed strategy, the frequency nadir falls from 49.9204 Hz (Scene 1) to 49.9199 Hz (Scene 4) and further to 49.9179 Hz (Scene 5), confirming superior frequency support at higher wind speeds. Figure 9 and Figure 12a reveal that the fixed-coefficient approach, constrained by reduced inflow wind speed and limited rotor kinetic energy, struggles to damp oscillations caused by wake-induced time lags. In contrast, the proposed control effectively suppresses these oscillations and restores frequency stability rapidly. Moreover, the settling time shortens as wind speed declines. It decreases from 216 s in Scene 1 to 190 s in Scene 4 and 178 s in Scene 5, indicating that stronger wake effects accompany higher wind speeds. Figure 13b shows that total wind farm output decreases with wind speed, yet the proposed strategy delivers sufficient electromagnetic power increments at the instant of disturbance and attenuates subsequent wake-driven fluctuations. This demonstrates its ability to adapt energy release intensity to wind speed: it fully utilizes rotor kinetic energy margins at low wind speeds while avoiding over-regulation at high speeds. Rotor speed trajectories confirm that across all three wind speed levels, the proposed strategy keeps every turbine strictly within the safe 0.7 to 1.3 p.u. range, with smooth recovery and minimal overshoot. By preventing tripping due to excessively low rotor speed, it avoids secondary frequency dips and economic losses. Compared with conventional synthetic inertial control, the proposed strategy accelerates rotor speed stabilization, allowing turbines to resume normal operation more quickly and better meeting the power system’s frequency regulation needs.

The comparative analyses across Scenes 1–5 collectively validate the strong adaptability and robustness of the improved synthetic inertial control strategy based on deep neural networks and MPC under varying wind speeds and load disturbances. Whether at high or low wind speeds, the strategy significantly enhances the wind farm’s frequency regulation performance, providing solid technical support for wind farms to play a more pivotal role in frequency control within renewable energy-dominated modern power systems.

To verify the adaptability of the proposed strategy in more complex wind speed conditions, turbulent wind speed is added for scene 6, and the frequency regulation control strategies of Strategy 2 and Strategy 3 are compared in this scene. The results are shown in Figure 14. As can be seen from the figure, the grid frequency fluctuates continuously under turbulent wind speeds, but the fluctuations of the proposed method are generally smaller than those of Strategy 2. The lowest frequency point of Strategy 2’s curve is 49.6524 Hz, while that of the proposed method is 49.74 Hz. In addition, the wind turbine power fluctuations of the proposed method are also relatively smaller, which helps reduce the mechanical load on wind turbines and extend their service life. The above result analysis verifies the feasibility and superiority of the proposed method under turbulent wind conditions, providing a technical reference for its subsequent application in actual wind speed scenarios.

6. Conclusions

This paper addresses the challenges to power system sustainability caused by high wind power penetration, particularly the neglect of wake effects, time-delay coupling, and complex dynamic interactions within wind farms. To this end, a hybrid framework integrating deep learning and MPC is proposed for wind farm frequency regulation, featuring a bi-level control architecture. The main contributions and findings are summarized as follows.

(1) A dynamic wind-farm model has been derived, which explicitly incorporates the Jensen wake model with square-sum superposition and an analytical expression for the inter-turbine time delay caused by wake propagation. Congruent equivalence is then applied to aggregate turbines operating under identical wind conditions, resulting in a tractable yet accurate representation that is suitable for real-time control design while preserving the essential wake physics.

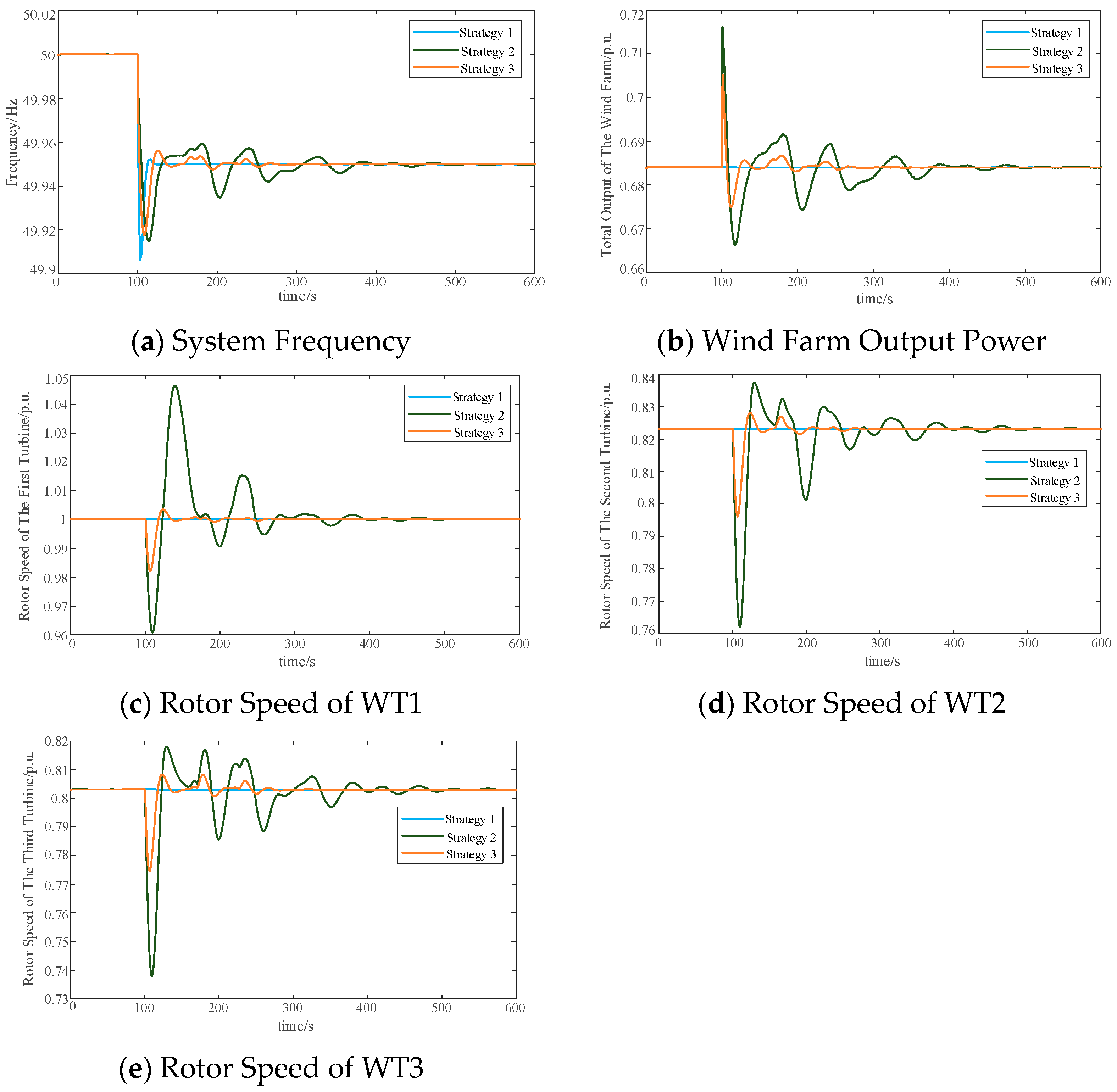
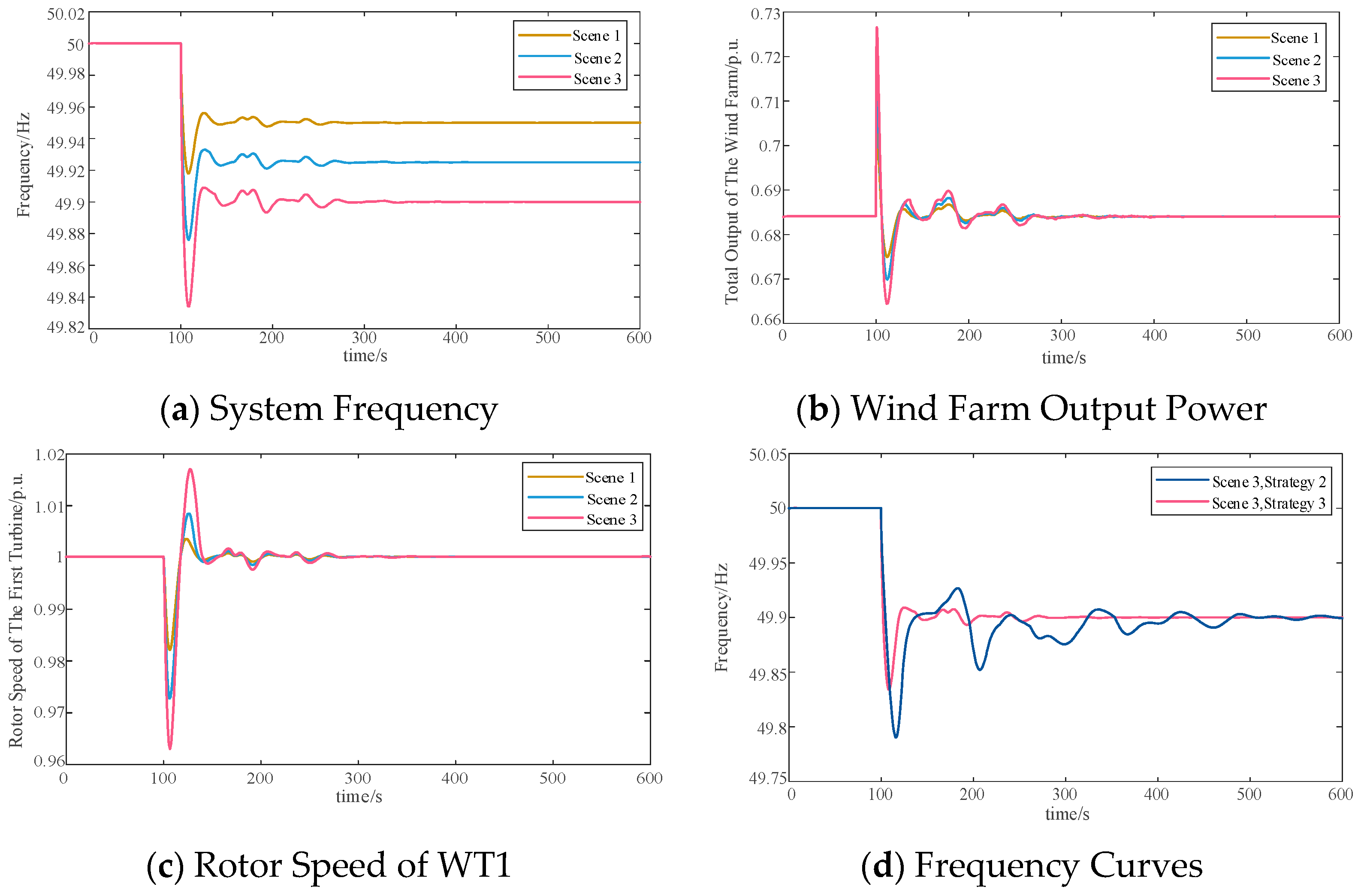
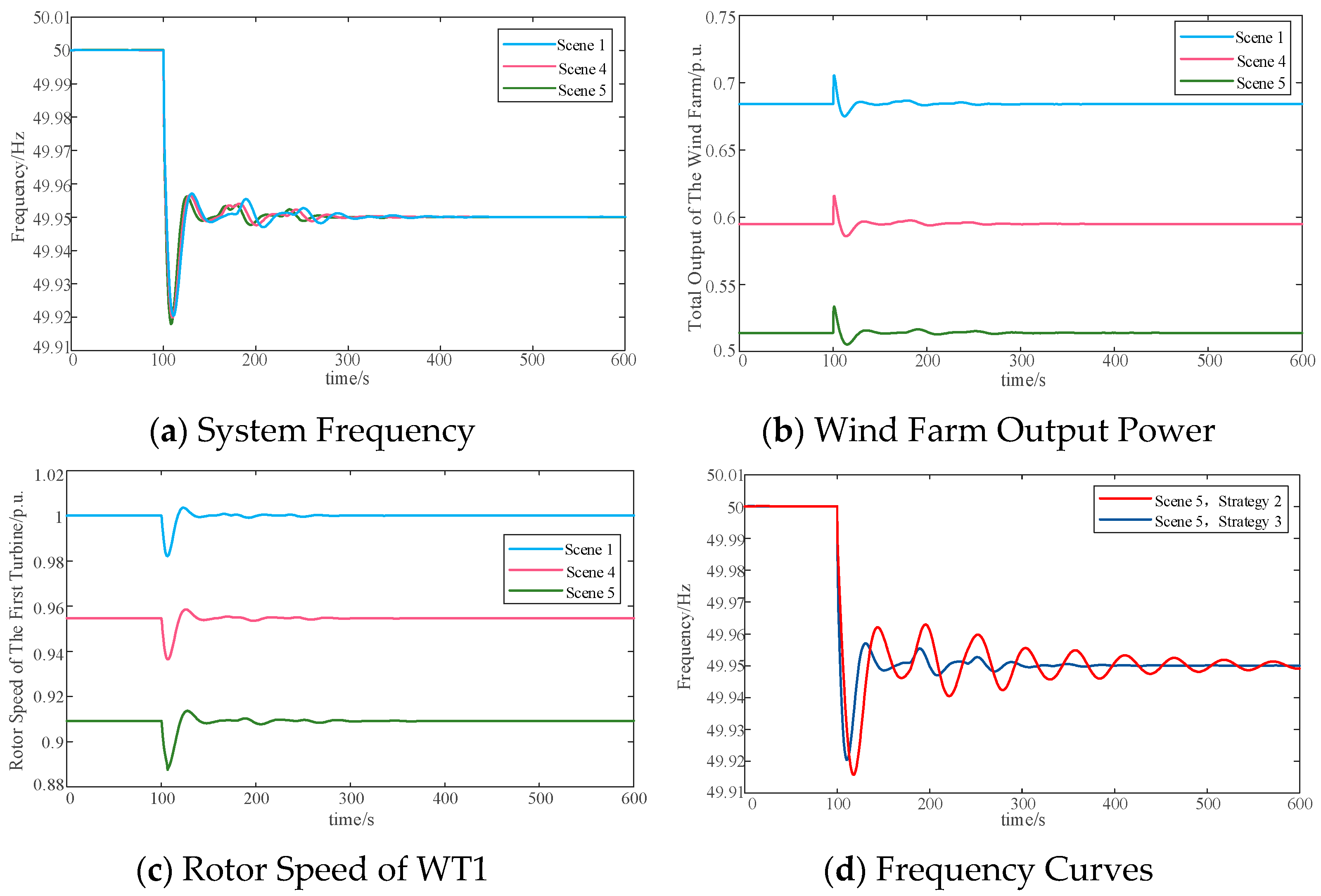
(2) A bi-level control architecture is proposed, where the upper layer employs a CAE–DNN surrogate trained offline to map wind speed, renewable-penetration level, and load-disturbance magnitude (2–4%) into optimal droop and virtual-inertia coefficients—under typical operating conditions, the coefficients optimized by this model can reduce the initial grid frequency drop amplitude by 0.008–0.012 Hz compared with empirically set coefficients. The lower layer utilizes a nonlinear MPC that continuously allocates the requested power deficit to individual DFIGs, using the discretized rotor-motion equation as the prediction model and enforcing hard limits (e.g., rotor speed ≤ 1.05 p.u., power ramp rate ≤ 0.1 p.u./s); with receding-horizon optimization, this layer not only smooths turbine power output fluctuations (controlling deviations within ±3% of rated power) but also mitigates secondary frequency dips induced by wake delays, reducing the amplitude of such dips by 0.005–0.007 Hz.

(3) Extensive MATLAB/Simulink simulations on a 350-MW system with a 150-MW wind farm demonstrate that the proposed DL-MPC framework raises the frequency nadir by 0.01–0.02 Hz compared with fixed-coefficient synthetic-inertia control, shortens the settling time after a 2–4% load disturbance by more than 200 s, and maintains rotor speed excursions within ≤5% of rated speed under wind-speed variations from 10 m/s to 11 m/s and load disturbances up to 4%. Additionally, the framework reduces the wind farm’s power tracking error relative to grid frequency regulation demands by 15–20%, thus comprehensively confirming its robustness in dynamic operating conditions and adaptability to multi-factor disturbances, as well as its ability to ensure WT operational safety.

(4) Compared with conventional energy sources like thermal, hydro, and nuclear power, wind power has certain advantages in inertial response but is constrained by factors such as cost and controllability, especially when wind speed changes rapidly. Nevertheless, this does not diminish the potential of wind power in frequency regulation but instead highlights the need to optimize frequency regulation strategies. Based on this, this study proposes a hybrid deep learning and MPC framework. It aims to fully utilize the inertial advantages of WT while reducing the impact of costs and controllability of wind power. This provides technical support for efficient and low-cost wind power frequency regulation, promoting a larger role for wind power in grid frequency regulation.

For real-world applications, future extensions could focus on multi-farm coordinated control to adapt to large-scale renewable integration, while long-term operation may benefit from adaptive tuning of MPC weights to balance regulation performance and turbine maintenance costs—further enhancing its practical value for sustainable power systems. To improve the generalization of this pethood, future work should also focus on integrating real-time operational data into DNN with real-time operational data and leveraging transfer learning approaches to pre-train models using historical data from geographically comparable wind farms.