Analysis of Traffic Conflict Characteristics and Key Factors Influencing Severity in Expressway Interchange Diverging Areas: Insights from a Chinese Freeway Safety Study

Abstract

Conflicts in freeway interchange diverging areas remain poorly understood, particularly their characteristics and severity determinants. To address this gap, we extracted over 20,000 vehicle trajectories from UAV footage at 16 interchange divergence zone across five multi-lane expressways using a YOLOX–DeepSORT method. From these trajectories, we identified longitudinal and lateral conflicts and classified their severity into minor, moderate, and severe levels using a two-dimensional extended time-to-collision metric. Subsequently, we incorporated 19 macroscopic traffic-flow and microscopic driver-behavior variables into four conflict-severity models–multivariate logistic regression, random forest, CatBoost, and XGBoost—and conducted to identify the key determinants of conflict severity based on the optimal models. The results indicate that lateral conflicts last longer and pose higher collision risks than longitudinal ones. Furthermore, moderate conflicts are most prevalent, whereas severe conflicts are concentrated within 300 m upstream of exit ramps. Specifically, for longitudinal conflicts, the most influential factors include speed difference, target-vehicle speed, truck involvement, traffic density, and exit behavior. In contrast, for lateral conflicts, the most critical factors include lane-change frequency, speed difference, target-vehicle speed, distance to the exit ramp, and truck proportion. Overall, these findings support the development of hazardous-driving warning systems and proactive safety management strategies in interchange diverging areas.

1. Introduction

With the rapid expansion of highway networks, the diverge area of interchanges—where vehicles exit the mainline—has become a critical bottleneck bearing extremely high traffic volumes [1]. This is particularly pronounced on mountainous highways, where terrain constraints often shorten the available distance for diverging operations, forcing drivers to perform rapid lateral lane changes and longitudinal braking [2]. Recent studies have documented that crash rates per unit length in these areas can be 2–5 times higher than those on basic highway segments, marking them as high-risk zones that disproportionately contribute to overall road fatalities and injuries [3].

Previous studies [4,5] have found that, unlike other sections of highways where rear-end (longitudinal) collisions mainly occur due to speed variations, diverging areas are characterized by frequent lane-changing behaviors, resulting in a higher proportion of lateral collision accidents. These lateral collisions differ in their formation mechanisms—often arising from weaving and merging interactions—and exhibit unique spatiotemporal distributions and risk factors compared with the more straightforward rear-end risks in basic road segments [6]. Therefore, accurately identifying the collision risk factors in highway diverging areas is crucial for advancing targeted proactive safety interventions and reducing the socioeconomic burden associated with traffic accidents.

Traditional safety analysis relies on historical collision data, which are often sparse and passive, thereby limiting the effectiveness of proactive risk assessment [7]. In recent years, emerging studies have sought to address this issue by adopting surrogate safety measures, such as traffic conflicts, which precede collisions and provide richer datasets for evaluation [8]. However, much of this research has focused on urban roads or highways in flat terrain, with limited attention to mountainous environments, where highway alignment indicators and environmental conditions exacerbate collision risks [9,10]. Recent investigations into driving behavior on tunnel–interchange sections of mountainous highways have highlighted elevated accident rates due to restricted maneuvering space, yet they often overlook the spatiotemporal distribution of conflicts, their severity determinants, and the distinctions between lateral and longitudinal types—such as differences in formation mechanisms, hotspot locations, durations, and dominant risk contributors [11]. Existing research has not yet delved into these aspects, leaving a critical gap: a comprehensive, data-driven comparison of lateral and longitudinal conflicts in interchange diverging areas of mountainous highways, including their unique influencing factors relative to ordinary segments.

Advances in roadside sensing technologies—such as high-resolution video, unmanned aerial vehicles (UAVs), and radar—have revolutionized traffic data collection, enabling precise measurement of indicators such as time headway (THW), time to collision (TTC), post-encroachment time (PET), and acceleration [12]. These fine-grained datasets provide a solid foundation for identifying factors that affect safety. Given that traffic conflicts occur more frequently than collisions and can be observed in real time within confined spaces, conflict-based analyses are increasingly replacing traditional collision records for safety evaluation. This shift promotes proactive management strategies, as conflicts, being reliable precursors to accidents, offer larger sample sizes and earlier insights [7].

To address these gaps, our study aims to leverage high-precision trajectories obtained from UAVs to capture fine-grained potential risk factors. By integrating advanced computer vision techniques (e.g., YOLOX–DeepSORT) with machine learning models, we dissect the spatiotemporal distribution characteristics of lateral and longitudinal conflicts, as well as the distinctions in key influencing factors of their severity.

Our contributions include identifying hotspot areas and durations of various conflict severity types in diverging zones, elucidating the formation mechanisms and key influencing factors of lateral and longitudinal conflicts, and providing targeted guidance for the development of intelligent early-warning systems and improvements in proactive safety management measures. The remainder of this paper is structured as follows: Section 2 provides a detailed review of related research; Section 3 and Section 4 describe the data processing methods, including data extraction from UAV videos and conflict identification with severity classification; Section 5 elaborates on the modeling methodology; Section 6 presents the results on conflict spatiotemporal distribution characteristics and key influencing factors; Section 7 and Section 8 discusses the implications of the findings for safety management and offers recommendations for future improvements.

2. Literature Review

Based on the research scope, this paper primarily conducted investigations in three areas: traffic conflict measurement indicators, conflict modeling methods, and analysis of conflict influencing factors in interchange diverge areas.

2.1. Traffic Conflict Measurement Indicators

Traffic conflict indicators are widely recognized as surrogate safety measures. Arun et al. [13] classified them into four categories: evasive behavior, Space/Time-Based, motion-based, and energy-based indicators (as shown in Table 1).

• Evasive behavior indicators (e.g., emergency braking, sharp steering) directly capture drivers’ avoidance responses. While they intuitively reflect safety-critical behavior, their dependence on subjective judgment limits applicability to observational surveys or small-scale experiments.
• Space/Time-Based indicators such as Time-to-Collision (TTC) and Post-Encroachment Time (PET) are computationally straightforward and widely used. However, their reliance on assumptions of constant speed and aligned trajectories restricts their applicability to rear-end scenarios, with poor performance in lane-changing and lateral conflict situations.
• Motion-based indicators (e.g., Deceleration Rate to Avoid Conflict, DRAC) integrate vehicle kinematics, enhancing sensitivity to dynamic interactions. Yet, they still depend on trajectory assumptions and require high-resolution trajectory data.
• Energy-based indicators combine both the likelihood and severity of conflicts by incorporating kinetic energy. This makes them conceptually closer to real crash risk assessment, though their reliance on continuous microscopic data severely limits practical applications.

Overall, each indicator has specific strengths and weaknesses, and their applicability varies by scenario. Most studies focus on one-dimensional measures (temporal or spatial), whereas complex two-dimensional interactions—particularly common in mountainous interchange divergence zones—remain underexplored.

Table 1. Comparison of Single Traffic Conflict Measurement Indicators.

Classification		Typical Indicators	Definition	Data Type/Resolution	Focus	Strengths	Limitations
Evasive Behavior [14]		Operational Behaviors Causing Traffic Conflicts	Observable driver avoidance responses	Video/manual observation	Conflict occurrence	Intuitive; easy to detect in surveys	Subjective; not scalable
Spatial/Temporal Proximity Indicators	Time-Based Indicator TTC and Its Derived Indicators [15]	Time-to-Collision (TTC), Exposure Collision Time (ECT), Cumulative Hazardous Collision Time (CHCT)	Time until collision if speed/trajectory maintained	Vehicle trajectories/aggregated data	Conflict counts	Simple; interpretable	Assumes constant speed/trajectory; limited to rear-end
	Time-Based Indicator PET and Its Derived Indicators [16]	Post Encroachment Time (PET), Time in Advance of Collision (TAdv)	Time gap between vehicles crossing same point	Video or trajectory data	Conflict exposure	Captures crossing conflicts	Ignores real-time driver reaction
	Distance-Based [17]	Conflict Distance (CD), Non-Full Braking Distance (NFBD)	Distance margins between vehicles	Trajectory or flow data	Distance safety margin	Physically intuitive	Sensitive to reaction assumptions
Traffic Entity Intrinsic Motion Characteristics [18]		Deceleration Rate to Avoid Conflict (DRAC)	Required deceleration to avoid crash	High-resolution trajectory data	Conflict severity proxy	Reflects vehicle dynamics	High data demand
Conflict Energy Indicators [19]		Collision energy	Kinetic energy at potential collision	High-resolution microscopic data	Likelihood and severity	Integrates probability and severity	Extremely high data requirements

Table 1. Comparison of Single Traffic Conflict Measurement Indicators.

Classification		Typical Indicators	Definition	Data Type/Resolution	Focus	Strengths	Limitations
Evasive Behavior [14]		Operational Behaviors Causing Traffic Conflicts	Observable driver avoidance responses	Video/manual observation	Conflict occurrence	Intuitive; easy to detect in surveys	Subjective; not scalable
Spatial/Temporal Proximity Indicators	Time-Based Indicator TTC and Its Derived Indicators [15]	Time-to-Collision (TTC), Exposure Collision Time (ECT), Cumulative Hazardous Collision Time (CHCT)	Time until collision if speed/trajectory maintained	Vehicle trajectories/aggregated data	Conflict counts	Simple; interpretable	Assumes constant speed/trajectory; limited to rear-end
	Time-Based Indicator PET and Its Derived Indicators [16]	Post Encroachment Time (PET), Time in Advance of Collision (TAdv)	Time gap between vehicles crossing same point	Video or trajectory data	Conflict exposure	Captures crossing conflicts	Ignores real-time driver reaction
	Distance-Based [17]	Conflict Distance (CD), Non-Full Braking Distance (NFBD)	Distance margins between vehicles	Trajectory or flow data	Distance safety margin	Physically intuitive	Sensitive to reaction assumptions
Traffic Entity Intrinsic Motion Characteristics [18]		Deceleration Rate to Avoid Conflict (DRAC)	Required deceleration to avoid crash	High-resolution trajectory data	Conflict severity proxy	Reflects vehicle dynamics	High data demand
Conflict Energy Indicators [19]		Collision energy	Kinetic energy at potential collision	High-resolution microscopic data	Likelihood and severity	Integrates probability and severity	Extremely high data requirements

2.2. Traffic Conflict Modeling Methods

Conflict modeling has evolved significantly since the seminal work of Salman and Al-Maital [20], who first linked conflict indicators to traffic volume through regression analysis. Current approaches fall into two broad categories: aggregate models and disaggregate models, as summarized in Table 2.

• Aggregate models treat conflicts as count data aggregated over space and time, relating them to crashes through traditional statistical frameworks such as Poisson and negative-binomial models. Their strengths lie in simplicity and interpretability, making them suitable for long-term safety performance evaluation. However, their coarse resolution fails to account for the variability of individual driver behavior, thereby limiting their explanatory power for conflict severity and temporal dynamics [21,22,23].
• Disaggregate models, by contrast, focus on individual conflict events, allowing a finer-grained analysis of contributing factors. These models represent a major methodological advancement, enabling researchers to capture the influence of human, vehicle, roadway, and environmental conditions. Probabilistic frameworks and generalized linear models are frequently employed, and more recently, machine learning algorithms such as random forests, support vector machines, and neural networks have been applied to capture complex nonlinear relationships [24,25].

While most existing models predict conflict frequency, relatively few address conflict severity. Furthermore, traditional statistical models excel in interpretability but struggle with nonlinear dynamics, whereas machine learning methods offer higher predictive accuracy at the cost of interpretability [26]. Striking a balance between accuracy and explanatory power remains a central challenge in conflict modeling.

Table 2. Summary of Traffic Conflict Modeling Methods.

Model Category	Features/Conditions	Data Type/Resolution	Outcome/Focus	Strengths	Limitations
Linear/Nonlinear Regression [27,28]	Relates conflicts to explanatory variables	Aggregate counts	Conflict frequency	Transparent; easy to interpret	Poor fit for rare/severe events
Poisson/NB [29,30,31]	Standard count models; NB handles overdispersion	Aggregate counts	Conflict frequency	Statistically robust; widely applied	Cannot capture severity
Zero-Inflated Models [32,33,34]	Accommodates excessive zero-conflict periods	Aggregate counts with excess zeros	Conflict frequency	Effective for sparse data	Still limited to frequency
Poisson-Log-Normal Models [35,36]	Models correlation and flexible variance	Panel or aggregate data	Conflict frequency	Robust with dispersion	Computationally demanding
Grey Models [37]	Forecast with incomplete or small datasets	Time-series/small samples	Conflict frequency	Effective with limited data	Oversimplified assumptions
Fuzzy Models [38,39]	Incorporates uncertainty via subjective rules	Small or mixed datasets	Conflict severity	Handles ambiguity	Subjective; limited generalizability
Markov Models [40]	Captures transitions across conflict states	Sequential conflict data	Conflict progression/type	Captures dynamic processes	Requires large sequential datasets
Probabilistic Models [41]	Estimates conflict likelihood under varying conditions	Disaggregate trajectory data	Frequency and severity	Flexible; accounts for uncertainty	High data quality required
Machine Learning (RF, SVM, NN) [42,43]	Learns nonlinear, multi-factor relationships	High-resolution trajectory data	Frequency and severity	High predictive accuracy	Black-box; limited interpretability

Table 2. Summary of Traffic Conflict Modeling Methods.

Model Category	Features/Conditions	Data Type/Resolution	Outcome/Focus	Strengths	Limitations
Linear/Nonlinear Regression [27,28]	Relates conflicts to explanatory variables	Aggregate counts	Conflict frequency	Transparent; easy to interpret	Poor fit for rare/severe events
Poisson/NB [29,30,31]	Standard count models; NB handles overdispersion	Aggregate counts	Conflict frequency	Statistically robust; widely applied	Cannot capture severity
Zero-Inflated Models [32,33,34]	Accommodates excessive zero-conflict periods	Aggregate counts with excess zeros	Conflict frequency	Effective for sparse data	Still limited to frequency
Poisson-Log-Normal Models [35,36]	Models correlation and flexible variance	Panel or aggregate data	Conflict frequency	Robust with dispersion	Computationally demanding
Grey Models [37]	Forecast with incomplete or small datasets	Time-series/small samples	Conflict frequency	Effective with limited data	Oversimplified assumptions
Fuzzy Models [38,39]	Incorporates uncertainty via subjective rules	Small or mixed datasets	Conflict severity	Handles ambiguity	Subjective; limited generalizability
Markov Models [40]	Captures transitions across conflict states	Sequential conflict data	Conflict progression/type	Captures dynamic processes	Requires large sequential datasets
Probabilistic Models [41]	Estimates conflict likelihood under varying conditions	Disaggregate trajectory data	Frequency and severity	Flexible; accounts for uncertainty	High data quality required
Machine Learning (RF, SVM, NN) [42,43]	Learns nonlinear, multi-factor relationships	High-resolution trajectory data	Frequency and severity	High predictive accuracy	Black-box; limited interpretability

2.3. Influencing Factors of Traffic Conflicts in Interchange Divergence Areas

Existing studies highlight the effects of geometric design and traffic conditions on safety in freeway interchange divergence areas.

Geometric factors play a central role. Weaving-zone length, in particular, has consistently emerged as one of the most influential variables [26,38,44,45]. Empirical evidence shows that shorter weaving zones compel drivers to change lanes more frequently and with sharper maneuvers [46], thereby increasing both the likelihood and severity of lateral conflicts [47]. Beinum et al. [48] further emphasized the interaction between weaving-zone length and traffic disorder, noting that insufficient design standards combined with operational turbulence substantially heighten collision risk.

Traffic condition factors also contribute significantly. Sarhan et al. [49] demonstrated that higher traffic volumes are positively associated with crash frequency in weaving zones, especially during peak hours when short headways constrain gap acceptance and intensify merging pressures. These findings suggest that operational conditions can amplify or mitigate the risks introduced by geometric design, underscoring the need for integrated design-operation analyses [43,48].

Driver behavior serves as the critical mechanism linking geometry and operations to conflicts. Under constrained spatial conditions, drivers tend to accept smaller gaps, perform higher-frequency lane changes, and make more abrupt maneuvers. This behavioral adaptation explains why even modest increases in traffic volume or reductions in weaving length can disproportionately increase conflict risk [50].

Despite these insights, two critical research gaps remain. First, most studies have focused on basic freeway segments or urban expressways, leaving mountainous freeway divergence zones largely underexplored. These zones differ substantially in geometry, traffic patterns, and operational constraints, making direct extrapolation problematic. Second, the vast majority of studies emphasize conflict frequency over severity, neglecting the fact that severity—not just frequency—determines the actual safety outcomes [51].

2.4. Summary of Current Research Status and Research Objectives

Existing research has identified key factors that contribute to collisions on basic freeway segments and urban expressways; however, interchange divergence zones on mountainous freeways remain understudied. Because they serve as critical nodes, interchange divergence zones experience more complex traffic conditions than other freeway segments. The rugged terrain and limited land in mountainous regions result in inherently short divergence areas, which further elevate collision risk. Consequently, the characteristics of traffic conflicts and the determinants of conflict severity in these zones are still poorly understood. The heightened probability of lateral conflicts also calls for extending surrogate safety indicators into two-dimensional space to capture a wider range of conflict scenarios. To reflect their unique traffic patterns, conflict-identification thresholds for mountainous interchange divergence zones should be recalibrated using empirical vehicle-trajectory data.

Accordingly, this study used drones to collect vehicle-trajectory data in mountainous interchange divergence areas, analyzed the spatiotemporal distribution of lateral and longitudinal conflicts, and developed conflict-severity models that identifies the key factors driving these conflicts. The results provide a theoretical foundation for proactive safety management in such zones.

3. Methodology

To address the above research gap, we developed a systematic methodological framework that integrates data collection, trajectory extraction, conflict identification, severity classification, statistical modeling, and key risk factor analysis into a logically coherent workflow, as illustrated in Figure 1. The overall approach is to base the analysis on high-precision vehicle trajectory data collected by drones, quantify traffic safety risks through conflict identification and severity classification metrics, and then employ multiple modeling methods and interpretability tools to explore the relationships between influencing factors and risk levels. The overall research design follows a step-by-step progression, where the output of each stage supports the subsequent stage, thereby ensuring consistency and traceability throughout the research process. The methodological framework consists of three main stages:

• Data Collection and Processing
  • For data collection, drone-based traffic operation videos were obtained at 16 interchange divergence areas on mountainous expressways in southern China, which served as the study sites.
  • Vehicle trajectories were extracted using a YOLOX–DeepSORT detection and tracking framework, with coordinate transformation and signal smoothing applied for noise reduction.
  • The accuracy of trajectory extraction was validated through on-road driving experiments to ensure compliance with the precision requirements for traffic conflict analysis.
• Conflict Event Extraction and Severity Classification
  • To capture lateral interactions in interchange divergence areas, an extended time-to-collision (ETTC) metric was designed as the criterion for conflict assessment.
  • A lane-based proximity-matching method was employed to identify interacting vehicles, and ETTC thresholds were applied to extract longitudinal or lateral conflicts. In this study, a traffic conflict was defined when ETTC remained below 3 s for more than 20 consecutive frames.
  • Extracted conflicts were classified into three categories—severe, moderate, and minor—based on ETTC distributions, using the 15th and 85th percentiles of the cumulative frequency as thresholds to achieve statistically objective classification.
• Modeling and Influential Factor Analysis
  • Based on refined trajectory data, 19 explanatory variables were derived, covering macroscopic traffic flow conditions, microscopic kinematic features, geometric attributes, congestion index, and vehicle driving intentions.
  • Multiple predictive models were constructed, including multinomial logistic regression (LR), random forest (RF), CatBoost, and XGBoost, with comparative evaluation to identify the optimal model.
  • Feature importance analysis (Gini index, SHAP values) was conducted to assess the contributions of each variable to conflict severity, identify key influencing factors for longitudinal and lateral conflicts, and further examine the differences in their underlying mechanisms.

Each methodological step is logically interrelated and firmly aligned with the study’s objectives. The process of data collection and trajectory extraction provides reliable vehicle-level information, thereby establishing a solid empirical foundation. The extraction and classification of conflict events transform raw trajectories into quantifiable indicators of traffic safety risk. Building on these outcomes, modeling and factor analysis uncover the mechanisms through which traffic conditions, vehicle characteristics, and driving behavior influence conflict severity, ultimately identifying the key factors that contribute to elevated risk.

Figure 1. The Technical Approach of This Study.

Figure 1. The Technical Approach of This Study.

4. Data Collection and Processing

4.1. Acquisition of Drone Video Data

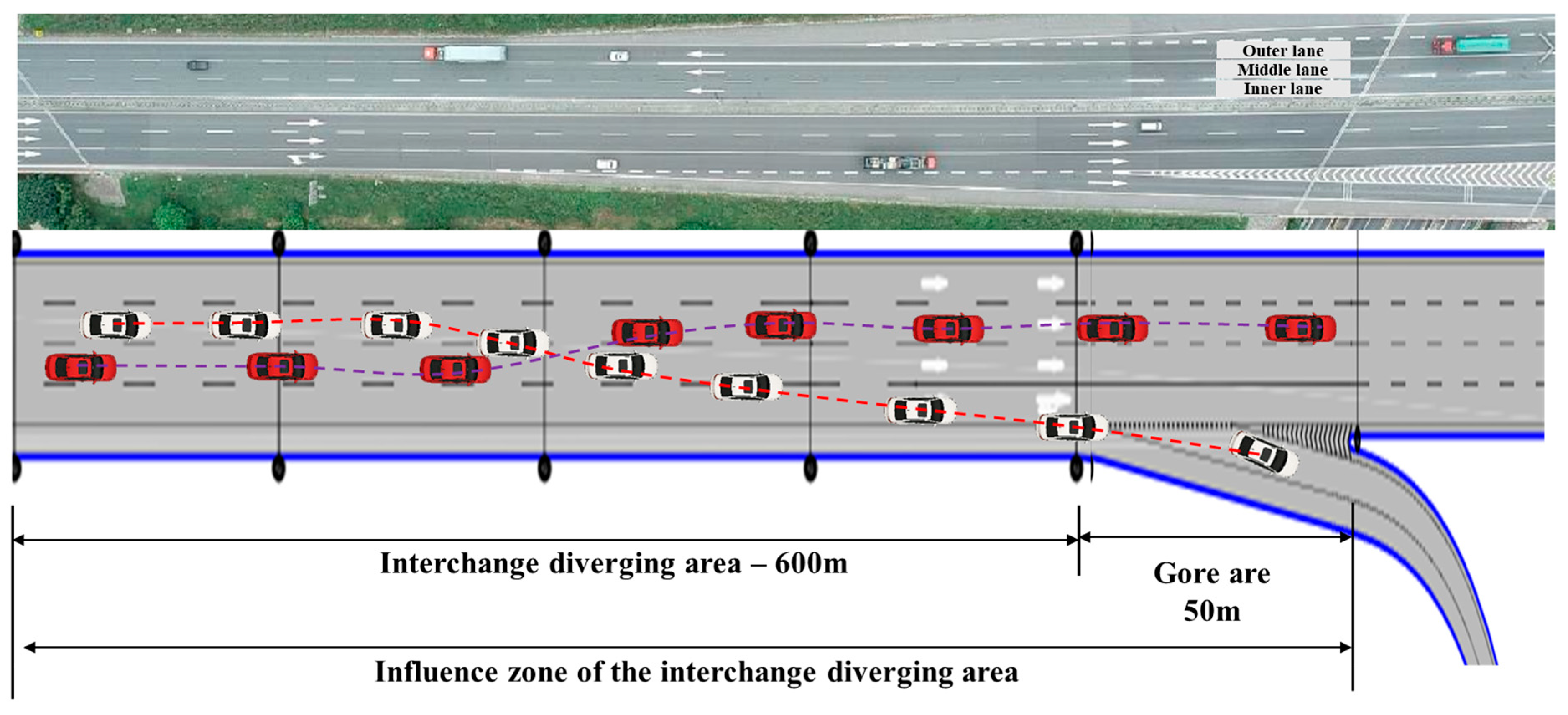
To collect data from expressway interchange divergence areas, we surveyed 16 interchanges on two mountainous expressways in southern China. Data were recorded over the 600 m upstream of each exit ramp (Figure 2). Video footage was captured during three periods (07:00–09:00, 12:00–14:00, and 16:00–18:00) across seven weekdays in April 2025, yielding 212 h of recordings.

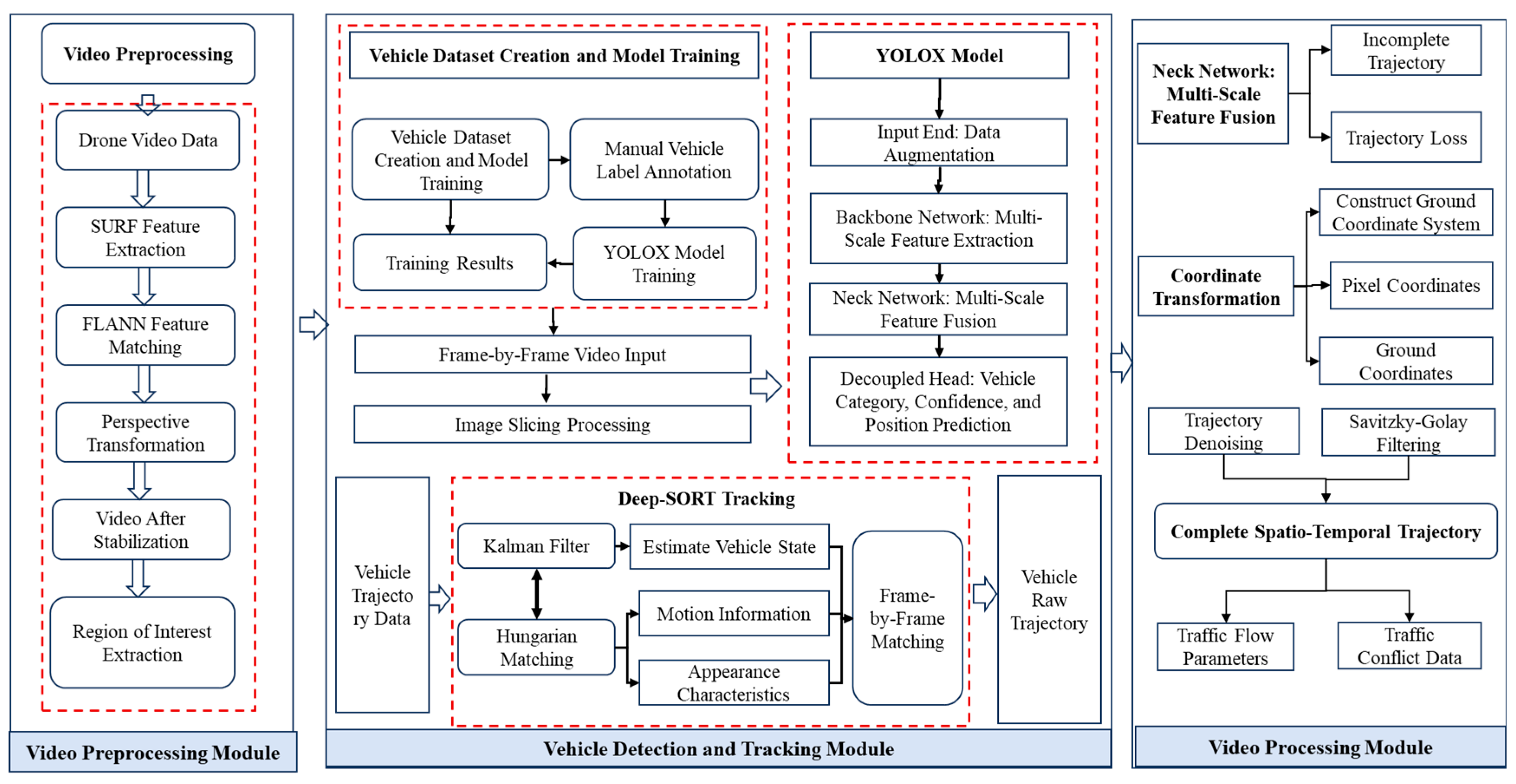
4.2. Vehicle Trajectory Extraction and Processing

Based on vehicle detection and tracking technology, a video-based vehicle trajectory extraction algorithm was developed. The algorithm comprises two primary modules, as shown in Figure 3.

4.2.1. Vehicle Detection and Tracking Module

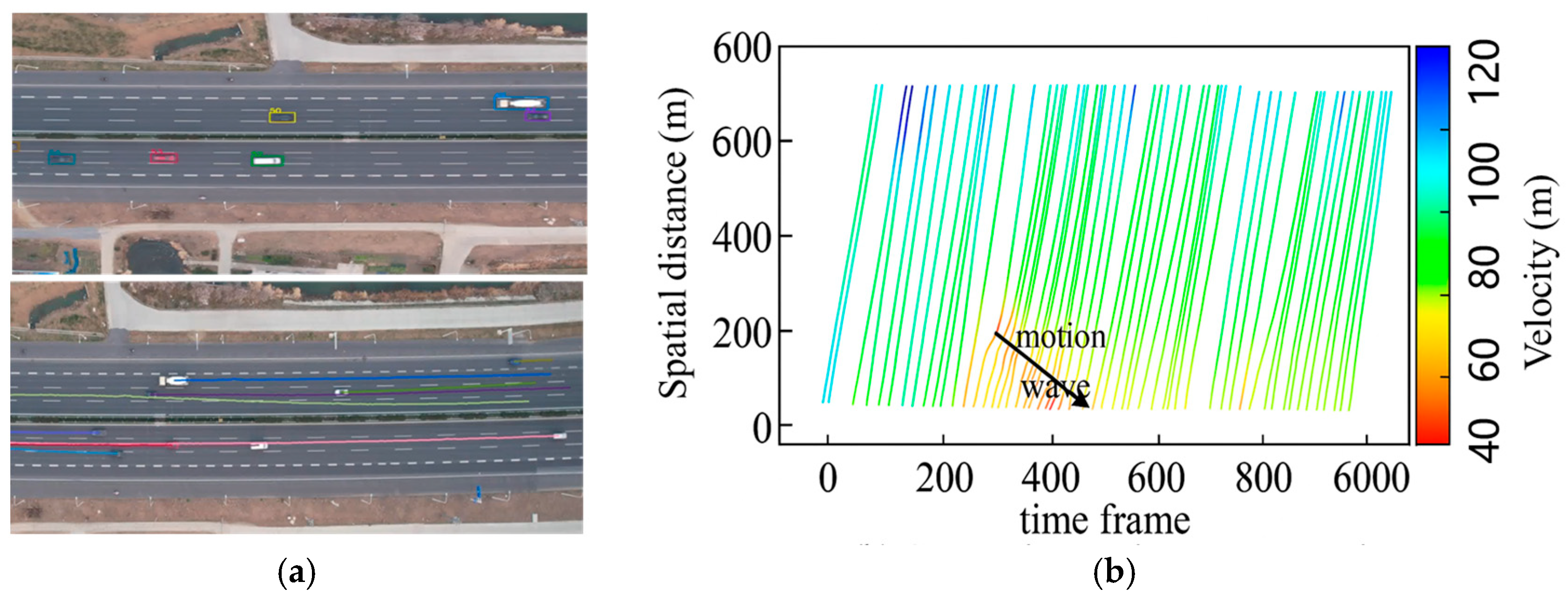
We developed a vehicle-detection and -tracking framework that integrates the YOLOX object-detection network with the DeepSORT tracker. YOLOX consists of an input layer, backbone, neck, and decoupled head, which together support multi-scale feature extraction and robust feature fusion. DeepSORT uses a Kalman filter to predict vehicle states in the next frame and the Hungarian algorithm to fuse motion and appearance cues, enabling reliable object matching and continuous trajectory tracking. We curated a traffic dataset of 32,283 images from freeway-interchange divergence areas captured in real-world video. All vehicles were manually labeled to train the YOLOX detector. Representative detection and tracking results are shown in Figure 4a.

4.2.2. Trajectory Processing Module

Some trajectories were incomplete because frame loss and matching errors occurred in the raw detection data. Statistical analysis showed that invalid trajectories represented < 1.7% of all data; they were therefore discarded. We established a fixed ground coordinate system to convert pixel positions into ground coordinates and standardize trajectory locations. Savitzky–Golay filtering was then applied to smooth raw position and velocity signals, producing noise-reduced spatiotemporal trajectories (Figure 4b).

After processing, we extracted complete trajectories for 20,437 vehicles at 1/30 s temporal resolution and 0.05 m per pixel spatial resolution.

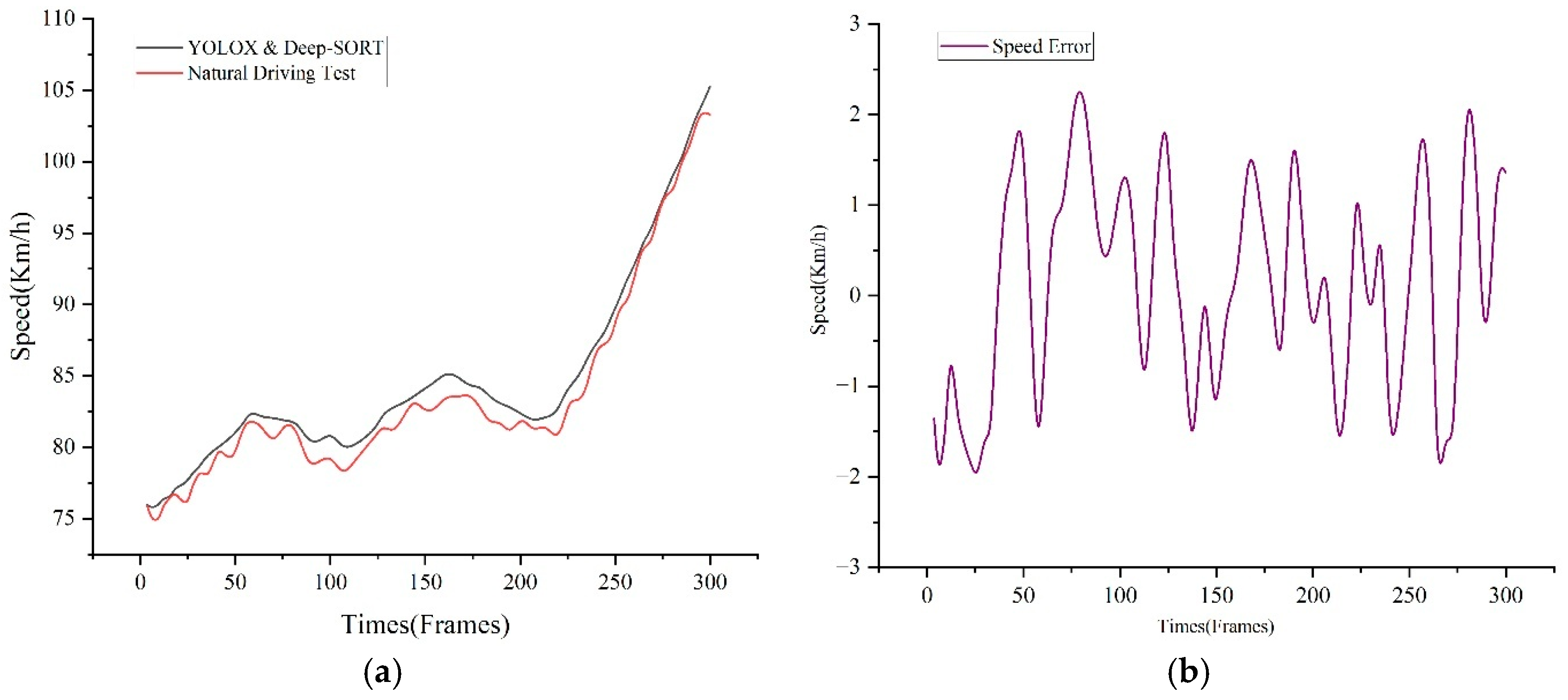
4.2.3. Data Accuracy Validation

Applying the proposed extraction framework, we obtained 32,917 complete vehicle trajectories. To verify extraction accuracy, we conducted an on-road experiment in a representative interchange divergence area and compared the extracted trajectory of a test vehicle with ground-truth measurements. High-precision onboard sensors recorded the vehicle’s true positions and speeds, yielding distance errors < 5 cm and a speed accuracy of 0.04 m s⁻¹. Figure 5 compares the speeds estimated by our algorithm with those measured during the field test in the same divergence scenario. The algorithm reproduced vehicle speed within 5 km h⁻¹ of the ground truth, achieving an overall accuracy of 91.6%.

4.3. Extraction of Traffic Conflict Events and Severity Classification

4.3.1. Extraction of Conflict Events

The conventional time-to-collision (TTC) metric describes longitudinal conflicts between vehicles traveling in a car-following sequence within the same lane. In interchange divergence areas, vehicles that exit the mainline and those that continue straight must change lanes within a short distance, which often triggers lateral conflicts [37]. The standard TTC is therefore unsuitable for quantifying the risk associated with these lateral interactions [7,52].

To address these limitations, we introduce the extended time-to-collision (ETTC) metric, originally proposed by Wojke et al. [53], which evaluates conflicts in a two-dimensional space. Unlike TTC, which assumes interactions strictly along a single lane, ETTC captures unconstrained vehicle motion and accounts for both longitudinal and lateral relative dynamics. It is based on the closest-point principle and vehicle approach rate in a planar coordinate system, allowing it to dynamically estimate the minimum time margin before potential collision regardless of whether interactions occur head-to-head, side-by-side, or diagonally [47]. Furthermore, ETTC incorporates vehicle geometry by considering the distance between contour points rather than centroids alone, thereby enhancing the accuracy of conflict detection in heterogeneous traffic with varying vehicle sizes and orientations. These features make ETTC particularly well suited for complex diverging zones, where irregular lane-changing maneuvers and dense interactions render the conventional TTC insufficient [32].

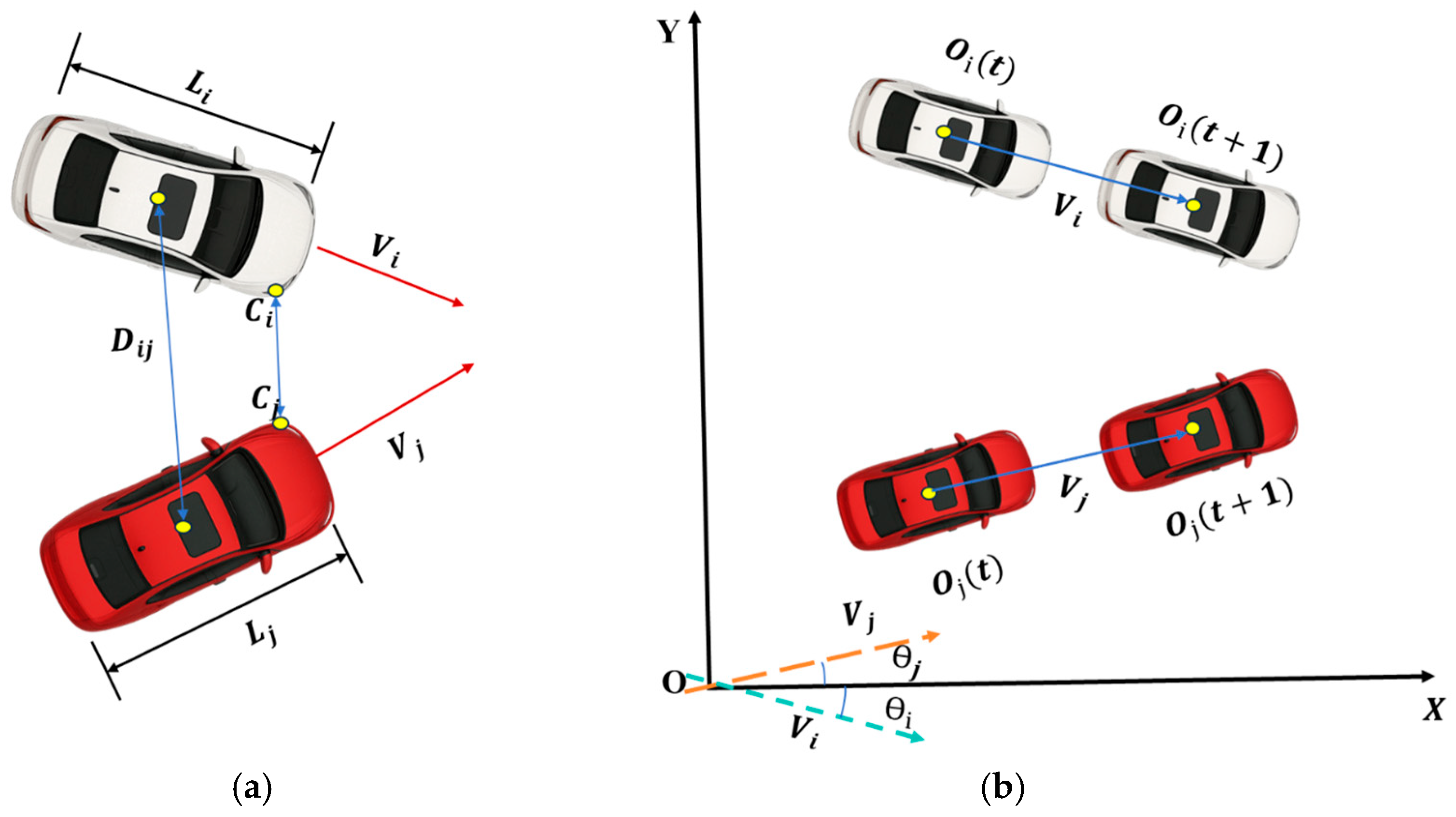
ETTC based on closest-point analysis and vehicle approach rate: In this study, each trajectory point extracted from a detection box corresponds to the vehicle’s geometric center. For computational simplicity, we assume that the approach rate at the vehicle centroids equals that at the closest points and that the difference between the centroid distance $d_{i,j}$ and the closest-point distance equals one-half the sum of the vehicle lengths. Accordingly, the ETTC for a weaving zone is computed as follows.

$$R_{ETTC}={\displaystyle \frac{d_{ij}}{d_{ij}^{\prime }}}=-{\displaystyle \frac{\sqrt{{(O}_i-O_j){{(O}_i-O_j)}^T}}{{{(O}_i-O_j)}^T{(V}_i-V_j)}}\left[\sqrt{{(O}_i-O_j){{(O}_i-O_j)}^T}-{\displaystyle \frac{L_i-L_j}{2}}\right]$$

(1)

where $d_{ij}$ represents the distance between the closest points of vehicles $i$ and $j$, i.e., the linear distance between the closest points $C_i$ and $C_j$ on the outer contours of the vehicle bodies at that moment; $d_{ij}^{\prime }$ denotes the approach rate of the closest points, i.e., the first-order derivative of $d_{ij}$; $O_i$ and $O_j$ are the position vectors of the center points of the two vehicles, respectively; $V_i$ and $V_j$ are the velocity vectors of the two vehicles, respectively; $L_i$ and $L_j$ are the lengths of the two vehicles, respectively. The specific meanings of these parameters are illustrated in Figure 6, where θ represents the vehicle’s heading angle; $t$ is the time variable, indicating the state of the vehicles at a given moment; and $D$ denotes the distance between the centroids of the vehicles.

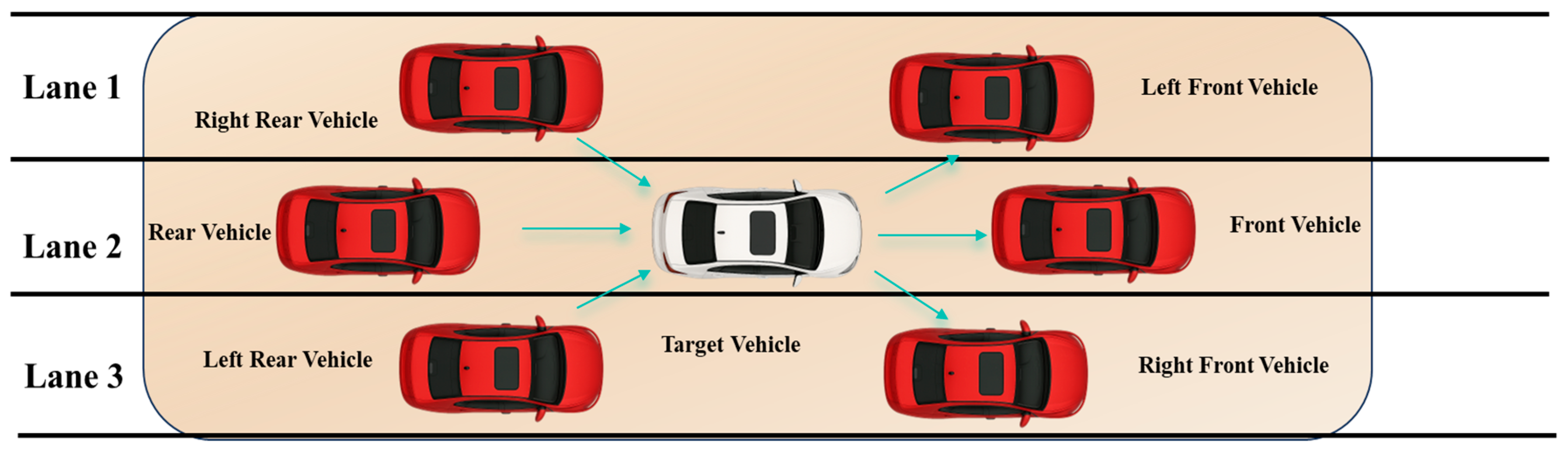
To identify critical interactions, we propose a lane-based proximity-matching method that locates interacting vehicles and their orientations (Figure 7). A moving vehicle can interact with others in up to six directions. Interactions with the immediately preceding or following vehicle in the same lane are deemed longitudinal, whereas interactions with vehicles in adjacent lanes are deemed lateral. We use the ETTC metric to decide whether an interaction constitutes a conflict. Previous studies regard a TTC below 1–3 s as indicative of a conflict [27]. To capture the full development of an event, we set the ETTC threshold at 3 s. A conflict is logged when the ETTC drops below this threshold and remains there for at least 20 consecutive frames.

4.3.2. Traffic Conflict Severity Classification

Using the conflict-identification criteria, we extracted 11,030 events: 5701 longitudinal and 5329 lateral. Thus, lateral conflicts represent a large share of events in interchange-divergence zones compared with basic segments and tunnels [23,31]. Figure 8 plots the ETTC distributions for the two conflict types. Clear differences emerge between longitudinal and lateral conflicts. For longitudinal conflicts, ETTC follows a skewed normal distribution concentrated at 1.8–2.7 s, peaking at 2.3 s. In contrast, ETTC for lateral conflicts approximates a normal distribution, centered between 0.9 and 2.1 s, with a peak at 1.4 s. At any given cumulative probability, lateral conflicts exhibit consistently smaller ETTC values than longitudinal ones, implying a higher collision risk. This elevated risk reflects the intensive lane-changing activity typical of divergence zones [26,47].

Criteria for classifying conflict severity vary with traffic scenarios. Reference [26] identifies the cumulative-frequency method as a common approach to severity classification. Accordingly, we used the 15th and 85th percentiles of the ETTC cumulative-frequency curve as thresholds, creating three levels—severe, moderate, and minor. The corresponding ETTC ranges are listed in Table 3. The rationale for choosing these percentile cut-offs includes:

• Nonparametric robustness: ETTC typically follows skewed distributions that depend on scale and sample size. Percentile thresholds are insensitive to these factors and avoid assumptions about distributional form [26].
• Consistency with traffic engineering practice: Percentiles—especially the 85th percentile—are long used for identifying upper operating limits (e.g., speed setting and operational assessments). By symmetry, the 15th percentile captures the lower extreme, yielding a 70% middle band flanked by two 15% tails. This approach balances sensitivity to extremes with stability of subgroup sizes. In conflict research, there are precedents of using the 85th percentile of cumulative-frequency curves to identify “critical” or “severe” conflict thresholds, which confirms its applicability [22].

In summary, after extracting conflict events and classifying their severity, a total of 6274 conflict events were extracted in this study, including 3726 minor conflicts, 2187 moderate conflicts, and 674 severe conflicts.

Figure 8. ETTC Distribution of Traffic Conflict Events. (a) Longitudinal conflicts. (b) Lateral conflict.

Figure 8. ETTC Distribution of Traffic Conflict Events. (a) Longitudinal conflicts. (b) Lateral conflict.

Table 3. ETTC Intervals for Different Conflict Types.

Conflict Types	Severe Conflicts	Moderate Conflicts	Minor Conflicts
Longitudinal Conflicts	(0, 1.07]	(1.07, 2.46]	(2.46, 3.00]
Lateral Conflicts	(0, 1.09]	(1.09, 2.31]	(3.31, 3.00]

Table 3. ETTC Intervals for Different Conflict Types.

Conflict Types	Severe Conflicts	Moderate Conflicts	Minor Conflicts
Longitudinal Conflicts	(0, 1.07]	(1.07, 2.46]	(2.46, 3.00]
Lateral Conflicts	(0, 1.09]	(1.09, 2.31]	(3.31, 3.00]

5. Influential Factors and Their Modeling on Conflict Severity

5.1. Conflict Explanatory Variables

Traffic-conflict severity depends on both macroscopic flow conditions and microscopic interaction behavior [26]. Using trajectory data collected in the divergence zone, we identified 19 candidate variables that may influence conflict severity (as shown in Table 4). The main considerations are summarized below.

(1)

Reference [49] shows that the mass and momentum of trucks heighten conflict severity; therefore, the truck proportion, in addition to flow, density and mean speed, is retained.

(2)

For microscopic features, we consider motion variables (speed, speed differential, acceleration) and geometric variables (length, width) for both the subject and interacting vehicles.

(3)

We also include conflict location: proximity to the exit ramp modulates lane-change urgency and thus shapes acceleration patterns and maneuver abruptness.

(4)

Finally, we incorporate the Congestion Index (CI) proposed by Dias et al. [54]—an indicator related to CIRS that measures segment congestion on a 0–1 scale, where free-flow speed is the 85th-percentile speed at the detector. The CI is computed as follows:

$$P_{CI}=\left\{\begin{array}{cc}{\displaystyle \frac{V_{free}-V_{actual}}{V_{free}}},& P_{CI}>0\\ 0,& P_{CI}<0\end{array}\right.$$

(2)

where $P_{CI}$ is the Congestion Index, $V_{free}$ was the free-flow speed, and $V_{actual}$ was the actual vehicle speed.

(5)

Due to the unique location of the interchange divergence area, this study considers the driving condition of the target vehicle, specifically whether the vehicle intends to exit the main expressway. This factor may significantly influence the type and severity of traffic conflicts.

Table 4. Explanatory Variables for Traffic Conflict Severity.

Variables	Description of Variables	Units	Means	S.D.	Min. Values	Max. Values
TD	Traffic Density within the Road Segment	$\mathrm{V}\mathrm{e}\mathrm{h}/\mathrm{k}\mathrm{m}$	19.42	2.84	10.55	28.91
TF	Traffic Flow within the Road Segment	$\mathrm{V}\mathrm{e}\mathrm{h}/\mathrm{h}$	1137	127	794	1496
AS	Average Speed within the Road Segment	$\mathrm{K}\mathrm{m}/\mathrm{h}$	98.9	11.8	39.27	123.64
ST	Speed of the Target Vehicle	$\mathrm{K}\mathrm{m}/\mathrm{h}$	73.22	5.8	40.57	107.43
AT	Acceleration of the Target Vehicle	$\mathrm{m}/{\mathrm{s}}^2$	−0.14	0.06	−0.37	−0.05
SIV	Speed of the Interacting Vehicles	Km/h	87.27	12.57	56.55	107.23
SDB	Speed Difference Between the Target Vehicle and the Interacting Vehicle	$\mathrm{K}\mathrm{m}/\mathrm{h}$	18.37	2.65	0.23	27.44
LTV	Length of the Target Vehicle	$\mathrm{m}$	5.44	0.89	3.5	17.5
WTV	Width of the Target Vehicle	$\mathrm{m}$	2.12	0.23	1.6	2.55
LIV	Length of the Interacting Vehicle	$\mathrm{m}$	5.37	1.04	3.5	17.5
WIV	Width of the Interacting Vehicles	$\mathrm{m}$	1.97	0.17	1.6	2.55
LAPT	Lateral Position of the Traffic Conflict	$\mathrm{m}$	312.57	23.56	0	1000
LOPT	Longitudinal Position of the Traffic Conflicts	$\mathrm{m}$	7.243	0.234	1.255	15
AHT	Average Headway Times	s	3.72	0.34	1.51	6.23
CIRS	Congestion Index of the Road Segment Within 30 s Before the Conflict Event	/	0.67	0.04	0.07	0.92
PTRS	Proportion of trucks on the road segment 30 s before the conflict	%	17.27	1.23	6.23	32.57
LCRS	Number of Lane Changes in the Road Segment 30 s Before the Conflict Event	/	16.91	3.27	6	29
IT	Whether the conflict vehicle includes a truck: 1 if a truck is included, 0 otherwise	/	0.325	0.085	0	1
TVE	Whether the motion condition of the target vehicle is exiting the mainline: 1 if exiting the mainline, 0 otherwise	/	0.287	0.047	0	1

Table 4. Explanatory Variables for Traffic Conflict Severity.

Variables	Description of Variables	Units	Means	S.D.	Min. Values	Max. Values
TD	Traffic Density within the Road Segment	$\mathrm{V}\mathrm{e}\mathrm{h}/\mathrm{k}\mathrm{m}$	19.42	2.84	10.55	28.91
TF	Traffic Flow within the Road Segment	$\mathrm{V}\mathrm{e}\mathrm{h}/\mathrm{h}$	1137	127	794	1496
AS	Average Speed within the Road Segment	$\mathrm{K}\mathrm{m}/\mathrm{h}$	98.9	11.8	39.27	123.64
ST	Speed of the Target Vehicle	$\mathrm{K}\mathrm{m}/\mathrm{h}$	73.22	5.8	40.57	107.43
AT	Acceleration of the Target Vehicle	$\mathrm{m}/{\mathrm{s}}^2$	−0.14	0.06	−0.37	−0.05
SIV	Speed of the Interacting Vehicles	Km/h	87.27	12.57	56.55	107.23
SDB	Speed Difference Between the Target Vehicle and the Interacting Vehicle	$\mathrm{K}\mathrm{m}/\mathrm{h}$	18.37	2.65	0.23	27.44
LTV	Length of the Target Vehicle	$\mathrm{m}$	5.44	0.89	3.5	17.5
WTV	Width of the Target Vehicle	$\mathrm{m}$	2.12	0.23	1.6	2.55
LIV	Length of the Interacting Vehicle	$\mathrm{m}$	5.37	1.04	3.5	17.5
WIV	Width of the Interacting Vehicles	$\mathrm{m}$	1.97	0.17	1.6	2.55
LAPT	Lateral Position of the Traffic Conflict	$\mathrm{m}$	312.57	23.56	0	1000
LOPT	Longitudinal Position of the Traffic Conflicts	$\mathrm{m}$	7.243	0.234	1.255	15
AHT	Average Headway Times	s	3.72	0.34	1.51	6.23
CIRS	Congestion Index of the Road Segment Within 30 s Before the Conflict Event	/	0.67	0.04	0.07	0.92
PTRS	Proportion of trucks on the road segment 30 s before the conflict	%	17.27	1.23	6.23	32.57
LCRS	Number of Lane Changes in the Road Segment 30 s Before the Conflict Event	/	16.91	3.27	6	29
IT	Whether the conflict vehicle includes a truck: 1 if a truck is included, 0 otherwise	/	0.325	0.085	0	1
TVE	Whether the motion condition of the target vehicle is exiting the mainline: 1 if exiting the mainline, 0 otherwise	/	0.287	0.047	0	1

5.2. Traffic Conflict Models

5.2.1. Multinomial Logistic Regression Model

Logistic regression (LR) is a widely used model for binary outcomes and a standard tool in traffic-safety analysis because it can reveal latent relationships among variables. Here, we classify conflict events into three severity levels—severe, moderate, and minor. Accordingly, we construct an independent LR model for each severity class. For each class (m = 0, 1, 2), the predicted probability is computed as follows:

$$p\left(Y=m|X_i\right)={\displaystyle \frac{\mathit{exp}\left(w_m+{\sum }_{i=1}^k{\beta }_{i,m}{X}_i\right)}{1+\mathit{exp}\left(w_m+{\sum }_{i=1}^k{\beta }_{i,m}{X}_i\right)}}$$

(3)

where $w_m$ is the intercept; $k$ is the number of feature variables; ${\beta }_{i,m}$ represents the model parameter for event $m$; and $X_i$ is the $i$-th variable.

5.2.2. Random Forest Model

Random forest (RF) is an ensemble learning algorithm composed of multiple decision trees. It builds a “forest” of Classification and Regression Trees (CART) generated with random samples and feature subsets; each tree operates independently, and their aggregated votes form the final prediction. RF models have been widely applied to traffic-conflict assessment [47]. Node splits in a CART are commonly evaluated with the Gini index, defined as:

$$G\left(t_q\right)=1-\sum _{j=1}^n{p}^2\left(j\right|t_1)$$

(4)

where $G\left(t_1\right)$ is the Gini index for node $t_1$; $n$ is the number of classes; and $p\left(j\right|t_1)$ is the estimated probability of the $j$-th class.

5.2.3. CatBoost Model

CatBoost, introduced by Prokhorenkova in 2018, is a machine learning algorithm based on Gradient Boosting Decision Trees (GBDT) [55]. The GBDT algorithm employed Classification and Regression Trees (CART) as weak learners, iteratively computed model gradients to identify the direction of steepest descent for the loss function, and thereby continuously refined the model through iterative training. Building on the GBDT framework, CatBoost utilized symmetric binary trees as base learners and implemented an ordered boosting approach to mitigate prediction bias. This method excelled in handling complex variable relationships and heterogeneous feature data. The basic steps were outlined as follows:

Input Data: A traffic conflict dataset D with n samples is provided, denoted as $D=\left\{\right(x_v, y_w), v = 1,2, \cdots ,l\}$, where $x_v = (x_{v1}, \cdots ,x_{vN})$ represents the feature contribution factors, and $y_i$ is the corresponding output value;

Initialization: Input $I$ CARTs and a random permutation $\sigma \{1,2, \cdots ,l\}$;

Residual Calculation: For each sample $x_v$ in the $u$-th tree, train a model $M_v$ excluding $x_v$, and compute the residual $r_v = y_v - M_{\sigma \left(v\right)}-1\left(x_v\right)$;

Base Learner Training: Train a base learner using the residuals $r_v$, producing an output $\Delta M=A\left[\right(x_v,r_w), \sigma (w)\le v]$. Update the model as $M_v$ = $M_v+\Delta M$;

Iteration: Repeat the above process until all I trees have been trained.

5.2.4. XGBoost Model

XGBoost, proposed by Chen et al. [56], is an ensemble algorithm that uses decision trees as base learners and boosting for aggregation. A decision tree is a tree-structured model consisting of nodes connected by branches. Each internal node tests a feature of the input sample and routes it along the corresponding branch, and the prediction—class label or continuous value—is output at the leaf nodes. Boosting builds the ensemble iteratively, adding one tree at each step and weighting it to form an increasingly accurate model.

In the XGBoost algorithm, each sample was assigned to a single leaf node in each tree, with each leaf node associated with a specific leaf weight. Let the leaf weight for sample $x$ on the $k$-th tree be denoted as $f_k\left(x_i\right)$. The predicted outcome of the ensemble model after $k$ iterations, ${\widehat{y}}_i\left(k\right)$, was calculated as the sum of the leaf weights across all base evaluators, expressed as follows:

$${\widehat{y}}_i(k)=\sum _k^K{f}_k\left(x_i\right)$$

(5)

The loss function of XGBoost consisted of two components: the traditional loss function and the model complexity.

$$O_{bj}=\sum _{i=1}^{m}l\left(y_i,{\widehat{y}}_i\right)+\sum _{k=1}^k{f}_k\Omega f_k$$

(6)

In the equation, the term ${\sum }_{i=1}^{m}l\left(y_i,{\widehat{y}}_i\right)+{\sum }_{k=1}^k{f}_k\Psi f_k$ represented the conventional loss function, where $m$ denoted the total number of samples entering the $k$-th tree. The term ${\sum }_{k=1}^k{f}_k\Psi f_k$ indicated the model complexity, which was introduced to minimize generalization error and mitigate overfitting. The loss function was ultimately transformed into the following form:

$$O_{bj}=-{\displaystyle \frac{1}{2}}\sum _{j=1}^N{\displaystyle \frac{G_j^2}{H_j+\lambda }}+\gamma N$$

(7)

$$G_j=\sum _{i\in I_j}{g}_i, H_j=\sum _{i\in I_j}{h}_i$$

(8)

where, $n$ denoted the $n$-th iteration, and a tree comprised a total of $N$ leaf nodes. The terms $g_i$ and $h_i$ represented the first- and second-order derivatives, respectively, of the loss function $l\left(y_i^n,{\widehat{y}}_i^{n-1}\right)$ with respect to ${\widehat{y}}_i^{n-1}$, collectively referred to as the gradient statistics for each sample. Additionally, a greedy algorithm was employed to solve the aforementioned objective function, controlling local optima to achieve global optimality.

5.3. Evaluation Metrics

The study utilized Accuracy, Recall, Precision, and Mean Area Under the Curve (MAUC) as metrics to comprehensively compare the overall performance of the models.

5.3.1. Accuracy

Accuracy quantifies overall predictive performance as the ratio of correctly classified samples to the total sample size. For traffic-conflict severity prediction, accuracy captures how well the model assigns events to the correct severity class (minor, moderate, or severe). It is computed as follows:

$$Accuracy={\displaystyle \frac{{\sum }_{i=1}^{k}T{P}_i}{N}}$$

(9)

where $k=3$ represented the number of categories for the dependent variable, namely minor, moderate, and severe conflicts. $T{P}_i$ denoted the number of samples correctly predicted for the $i$-th category. Accuracy was suitable for quickly assessing the overall performance of the model; however, when severe conflict samples were scarce, it could have obscured the model’s predictive deficiencies for minority classes. Therefore, it was necessary to combine accuracy with other metrics for analysis.

5.3.2. Recall

Recall (also called sensitivity) quantifies a model’s ability to identify the positive class; it is the ratio of correctly predicted positive samples to all actual positives. In traffic-conflict prediction, recall is especially important because failing to detect severe conflicts (false negatives) can introduce safety risks. For multiclass problems, recall is computed individually for each class as:

$${Recall}_i={\displaystyle \frac{{TP}_i}{{TP}_i+{FN}_i}}$$

(10)

where ${Recall}_i$ denoted the recall for the $i$-th category, ${TP}_i$ represented the number of samples correctly predicted for the $i$-th category, and ${FN}_i$ indicated the number of samples in the $i$-th category incorrectly predicted as other categories. In traffic conflict classification, the recall for severe conflicts was a critical metric. Missing severe conflicts could result in accidents not being promptly warned, necessitating model optimization to enhance the recall for the severe class.

5.3.3. Precision

Precision measures the reliability of predictions by quantifying the fraction of predicted positives that are truly positive. In traffic conflict prediction, high precision indicates that the model’s severe-conflict alerts are reliable and minimize false positives. Precision for each class is computed as follows:

$${Precision}_i={\displaystyle \frac{{TP}_i}{{TP}_i+{FP}_i}}$$

(11)

where ${Precision}_i$ denoted the precision for the $i$-th category, and ${FP}_i$ represented the number of samples from other categories incorrectly predicted as the $i$-th category. In proactive traffic safety management systems, a high precision for severe conflicts was essential to avoid frequent false alarms that could undermine system credibility. The trade-off between precision and recall required adjustment based on the application scenario; for instance, prioritizing higher recall for severe conflicts might have come at the expense of some precision.

5.3.4. Mean Area Under the Curve (MAUC)

The Area Under the Curve (AUC) represented the area under the Receiver Operating Characteristic (ROC) curve, used to evaluate the model’s ability to distinguish between different categories (e.g., conflict severity levels). The ROC curve was plotted with the true positive rate ($TPR=Recall$) on the vertical axis and the false positive rate ($FPR={\displaystyle \frac{FP}{FP+TN}}$) on the horizontal axis. AUC values ranged from 0 to 1, with values closer to 1 indicating stronger discriminative ability. In multi-class tasks, the AUC for each category was calculated using the “One-vs-Rest” approach, and the mean AUC was obtained by averaging these values. The AUC was computed by integrating the ROC curve:

$$AUC={\int }_0^{1}TPR\left(FPR\right)d\left(FPR\right)$$

(12)

For multi-class tasks, the mean AUC was calculated as the weighted average of the AUCs for each category:

$$Mean AUC=\sum _{i=1}^c{w}_i {AUC}_i$$

(13)

where $C$ represented the number of categories, which was 3 in this study (minor, moderate, and severe conflicts), ${AUC}_i$ denoted the AUC for the $i$-th category, and $w_i$ was the weight for the $i$-th category, typically determined based on the proportion of samples in that category.

The selected metrics capture different aspects of performance: accuracy reflects overall correctness, while recall and precision measure how effectively positive cases—especially severe conflicts—are identified. Training time assesses computational efficiency, and mean AUC summarizes the model’s discriminative ability. When applied to traffic-conflict prediction in interchange-divergence zones, this suite of metrics provides a comprehensive evaluation of accuracy, sensitivity, and operational practicality.

6. Results

6.1. Conflict Distribution Characteristics

6.1.1. Temporal Distribution Characteristics

Hazardous vehicle interactions are continuous processes; therefore, traffic conflicts display pronounced temporal characteristics. Study [32] defines conflict duration as the interval during which a vehicle remains in a hazardous state—from the moment the enhanced time-to-collision (ETTC) drops below a threshold until it rises above it again. Conflict duration is directly linked to collision risk: longer conflicts keep drivers in hazardous states for more time and therefore entail higher risk.

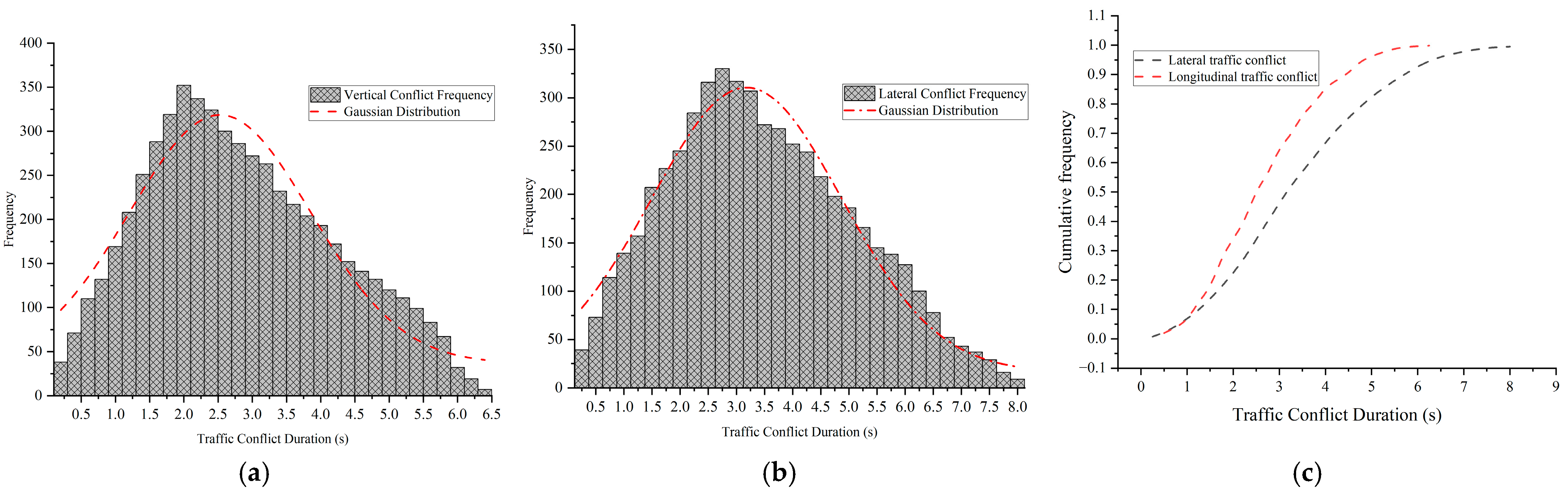
Figure 9 depicts the duration distributions for longitudinal and lateral conflicts. Both distributions share a similar shape, approximating a skewed normal curve. This pattern indicates that once drivers recognize a hazardous interaction, they promptly adjust their behavior, thereby limiting most conflicts to short durations. Specifically, longitudinal conflicts cluster between 1 and 4 s (mean = 2.46 s), whereas lateral conflicts cluster between 1.5 and 4.7 s (mean = 2.73 s). The cumulative-frequency curves rise steeply at first and then level off, with an inflection near the 85th percentile. Before this point, for any given cumulative probability, longitudinal conflicts are consistently shorter than lateral ones, indicating that lateral conflicts generally persist longer and therefore entail greater collision risk.

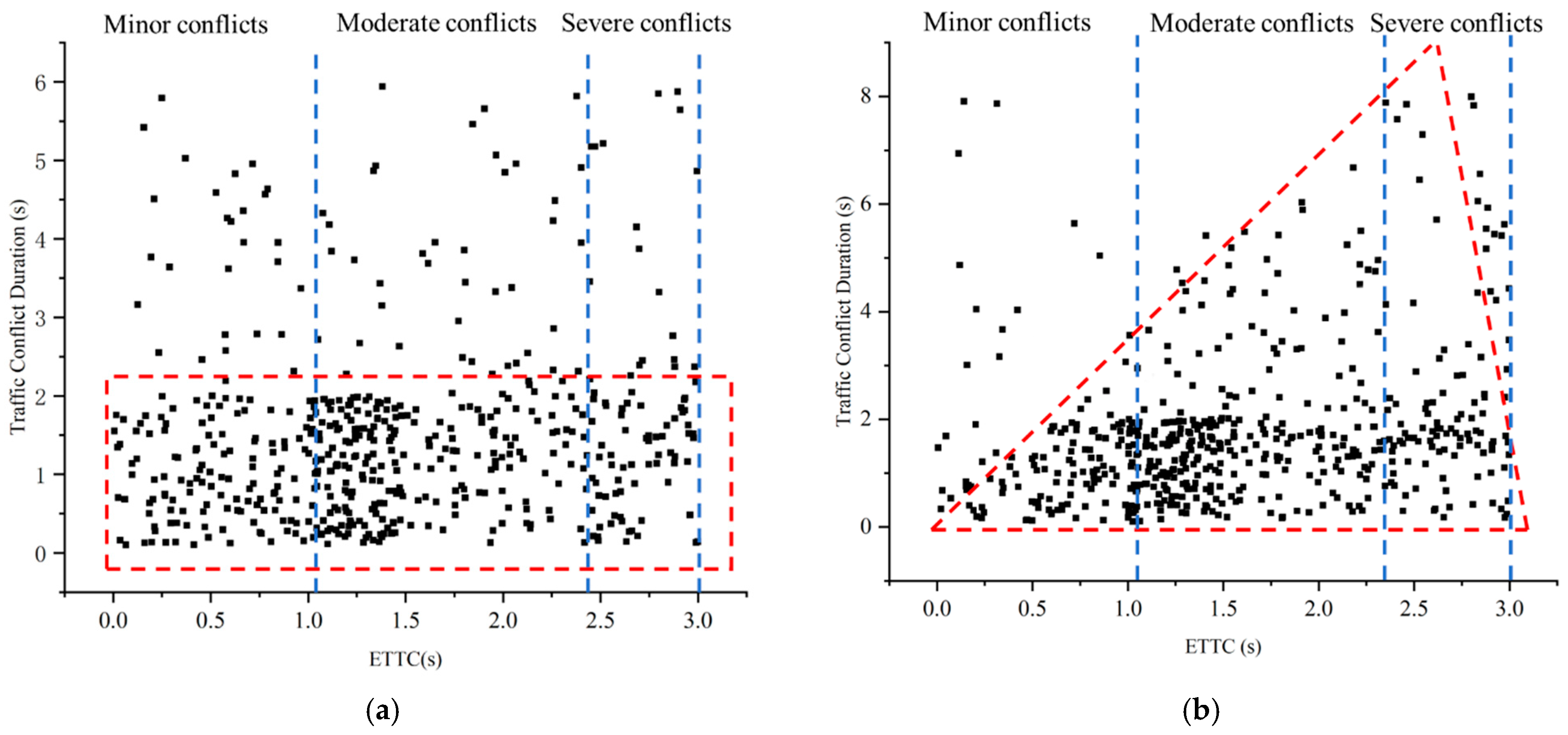
Figure 10 illustrates the correlation between conflict event duration and Enhanced Time-to-Collision (ETTC), with each scatter point representing an individual conflict event. Longitudinal conflict events were primarily moderate, with severe conflicts being least frequent and typically lasting less than 2 s. In car-following scenarios, drivers’ high sensitivity to the leading vehicle’s distance facilitated rapid avoidance of short-range longitudinal conflicts. Lateral conflict events were mainly moderate or minor, with severe conflicts occurring infrequently. The scatter plot for lateral conflicts showed a triangular contour, indicating that more severe conflicts had longer durations. Specifically, minor lateral conflicts lasted within 2 s, moderate conflicts within 3 s, and severe conflicts within 5 s.

6.1.2. Spatial Distribution Characteristics

The interchange diverge area was divided into five zones (Zone 1 to Zone 5) based on driving behavior, with proximity increasing toward the exit ramp. Zones 1 to 4 each spanned 150 m, and Zone 5 spanned 50 m [27,54]. Figure 11 maps the spatial distribution of traffic conflict events in a specific interchange diverge area across these zones. Figure 11 shows that conflict frequency increased with longitudinal displacement. Zones 3 and 4 had significantly higher conflict frequencies than Zones 1 and 2, especially at the Zone 4 and exit ramp intersection. Vehicles exiting the mainline in Zones 3 and 4 frequently performed lane changes, causing longitudinal conflicts from abrupt speed changes and lateral conflicts from lane maneuvers. The middle and outer lanes had significantly higher conflict frequencies than the inner lane. Conflicts were most prevalent at the boundaries between the middle and outer lanes and between the outer lane and the hard shoulder. Lane 1 was less affected by the weaving zone, resulting in lower collision risk. General conflicts were the most common, occurring across all zones and lanes. Severe conflicts were primarily concentrated in Zones 4 and 5. The short length of the weaving zone restricted lane-change preparation time, causing frequent forced lane changes and increased severe conflicts.

Figure 12 presents bar charts illustrating the longitudinal and transverse frequency distributions of conflict events across all observation points. The charts show that minor and severe conflict frequencies followed the order: Zone 4 > Zone 3 > Zone 2 > Zone 5 > Zone 1. Closer to the upstream divergence point, abrupt lane-changing behavior increased minor and severe conflict frequencies. Downstream of the exit ramp, where divergence-related lane changes were absent, conflict probability gradually decreased. General conflicts were more widespread, increasing then decreasing along the driving direction, peaking in Zone 3. Zone 3, at a moderate distance from the exit ramp, provided longer safe lane-changing times but involved hesitant maneuvers, leading to more general conflicts [32,44].

The conflict patterns in Zone 5 differed from those in Zones 1–4. In Zones 1–4, especially Zones 3 and 4, conflicts were largely driven by active lane-changing maneuvers as vehicles prepared to exit, resulting in high frequencies of both longitudinal and lateral conflicts. By contrast, Zone 5, located downstream of the ramp, no longer experienced active divergence-related lane changes. The conflicts in this zone primarily stemmed from residual traffic flow disturbances, such as abrupt speed variations between vehicles that had already completed lane changes and those continuing straight, as well as insufficient adjustments caused by compressed weaving distances upstream. Consequently, although the overall conflict frequency in Zone 5 was lower than in Zones 3 and 4, the conflicts that did occur were often more severe due to limited space for corrective maneuvers.

The transverse frequency ranking was: middle lane > outer lane > inner lane > middle–outer lane boundary > outer lane–hard shoulder boundary > inner–middle lane boundary. Conflict probability increased closer to the outer lanes. Traffic signs prompted through-traffic vehicles to stay in the inner lanes, reducing lane changes in the divergence zone. Vehicles exiting the expressway moved to the middle and outer lanes upstream to prepare for lane changes, increasing conflicts near the outer lanes [7,11,42].

6.2. Model Performance Evaluations

6.2.1. Comparison of Candidate Model Performance

A grid search algorithm optimized model parameters, while cross-validation was used to train and test the models. Model performance metrics were evaluated and presented in

Table 5. Performance Comparison of Candidate Models.

Type of Traffic Conflicts	Evaluation Metrics	Candidate Models
		LR	RF	CatBoost	XGBoost
Longitudinal Traffic Conflicts	Accuracy (%)	83.22	79.79	91.34	90.27
	Recall (%)	62.54	67.33	80.27	79.34
	Precision (%)	75.26	69.43	80.92	77.82
	MAUC	0.849	0.813	0.857	0.902
Lateral Traffic Conflicts	Accuracy (%)	81.40	79.51	87.07	88.24
	Recall (%)	61.65	63.55	74.29	78.18
	Precision (%)	72.92	71.67	75.37	79.21
	MAUC	0.829	0.807	0.843	0.881

and Figure 13.

For longitudinal conflict severity, the CatBoost and XGBoost models achieved accuracies above 90%, with comparable performance. The Logistic Regression (LR) model had an accuracy of 83.27%, while the Random Forest (RF) model had the lowest at 77.23%. For recall, CatBoost and XGBoost models outperformed others, achieving 80.27% and 79.34%, respectively, while the LR model had the lowest recall. For mean Area Under the Curve (MAUC), CatBoost and XGBoost models outperformed RF and LR models, with CatBoost slightly surpassing XGBoost. Thus, the CatBoost model showed the best performance for longitudinal conflict severity.

For lateral conflict severity, the XGBoost model achieved the highest accuracy, recall, and precision. Its MAUC value exceeded that of the LR, RF, and CatBoost models by 6.24%, 10.95%, and 5.25%, respectively. Thus, the XGBoost model demonstrated optimal performance for lateral conflict severity.

In summary, the CatBoost and XGBoost models were selected to examine the relationships between longitudinal and lateral conflict severity and key parameters, respectively.

6.2.2. Verification of Sample Balancing Strategies

In this dataset, severe conflicts are relatively rare compared to moderate and mild conflicts. This paper will further explore whether sample imbalance affects the model’s performance.

Based on the clues provided by references [23,26], this paper uses the optimal CatBoost and XGBoost models to validate the effectiveness of two classical sample balancing strategies: Synthetic Minority Over-sampling Technique (SMOTE) and Cost-sensitive Learning (CSL). SMOTE is an oversampling method that increases the number of minority class samples by interpolating and synthesizing new samples between minority class instances. Cost-sensitive learning addresses class imbalance by adjusting the cost of misclassification. The model assigns higher penalties to the minority class (e.g., severe conflict) based on class weights, thereby increasing its focus on the minority class. The specific implementation process for each technique is as follows:

• SMOTE

Step 1: Identification of Minority and Majority Classes

The conflict severity dataset is first categorized into minor, moderate, and severe conflicts. The severe conflict category represents the minority class, while minor and moderate conflicts represent the majority class.

Step 2: Selection of K-nearest Neighbors

SMOTE operates by selecting $K$ nearest neighbors for each minority class sample and generating new synthetic samples between them. In this study, $K$ = 5 is chosen, meaning that for each minority class sample, five nearest neighbors are selected, and new samples are generated by interpolating between them.

Step 3: Generation of Synthetic Samples

For each minority class sample, SMOTE generates new synthetic samples using the following formula:

$${new}_{sample}={minority}_{sample}+\lambda (neighbor-{minority}_{sample})$$

(14)

where $\lambda$ is a random value between 0 and 1, which determines the position of the new sample in relation to the original sample and its neighbor.

Step 4: Balancing the Dataset

The number of minority class samples is increased to match the number of majority class samples. In this case, the number of severe conflict samples is augmented by creating synthetic samples, effectively balancing the dataset.

2.

CSL

Step 1: Setting Class Weights

In Cost-sensitive Learning, each class is assigned a weight to adjust the misclassification cost. For the minority class (severe conflict), a higher weight is assigned to ensure the model focuses more on these samples during training.

In this study, the class weights are set as follows: for severe conflict (minority class), the weight is set to 2. For minor and moderate conflicts (majority class), the weight is set to 1.

Step 2: Adjusting the Loss Function

The loss function is adjusted so that higher penalties are applied when the minority class is misclassified. Specifically, the model is penalized more heavily for misclassifying severe conflict events, encouraging the model to focus on correctly identifying severe conflicts.

Step3: Model Training

The class weights are incorporated into the training process of both the CatBoost and XGBoost models. The weighted loss function ensures that the model places more emphasis on the minority class (severe conflict), addressing the imbalance and improving the model’s performance in predicting the less frequent class.

The model performance under different sample balancing strategies is shown in

Table 6. Overall Model Performance under Different Sample Balancing Strategies.

Type of Traffic Conflicts	Evaluation Metrics	Candidate Models
		CatBoost			XGBoost
		Raw Sample	SMOTE	CSL	Raw Sample	SMOTE	CSL
Longitudinal Traffic Conflicts	Accuracy	0.913	0.893	0.890	0.903	0.912	0.909
	Recall	0.803	0.811	0.803	0.793	0.803	0.820
	Precision	0.809	0.754	0.786	0.778	0.777	0.770
	MAUC	0.857	0.851	0.827	0.902	0.892	0.901
Lateral Traffic Conflicts	Accuracy	87.07	87.21	88.21	88.24	87.98	92.31
	Recall	74.29	75.27	75.01	78.18	80.21	79.27
	Precision	75.37	75.07	75.68	79.21	81.23	79.88
	MAUC	0.843	0.823	0.821	0.881	0.862	0.884

and

Table 7. Class-wise Model Performance Comparison under Original Distribution and Balancing Strategies.

Methods	CatBoost				XGBoost
	Severe Conflicts
	Accuracy	Precision	Recall	MAUC	Accuracy	Precision	Recall	MAUC
Raw sample	0.865	0.822	0.771	0.794	0.876	0.823	0.752	0.762
SMOTE	0.862	0.861	0.788	0.787	0.871	0.847	0.786	0.755
CSL	0.869	0.865	0.796	0.809	0.863	0.81	0.772	0.739
Moderate conflicts
Raw sample	0.905	0.852	0.792	0.828	0.912	0.847	0.804	0.874
SMOTE	0.875	0.831	0.768	0.821	0.901	0.836	0.813	0.843
CSL	0.886	0.827	0.772	0.829	0.897	0.809	0.809	0.862
Minor conflict
Raw sample	0.927	0.864	0.834	0.794	0.902	0.892	0.824	0.897
SMOTE	0.902	0.867	0.852	0.787	0.886	0.867	0.842	0.863
CSL	0.873	0.804	0.829	0.809	0.892	0.878	0.853	0.844

.

As can be seen from the table, although the two sample balancing techniques improve the recall rate of severe traffic conflict categories, the improvement is limited (only between 0.05 and 0.3), which has a very limited effect in practical applications. Furthermore, the use of balancing techniques also brings some trade-offs, such as a slight decrease in overall precision and MAUC, as well as mild overfitting in small sample subsets. In addition, the literature [43] reveals the reasons why sample balancing techniques are not significant for the data in this study:

(1)

SMOTE, when creating new samples, is based on linear interpolation of existing samples, which may result in insufficient differences between the generated samples and the original severe conflict samples. Therefore, the model may overfit these synthetic samples, particularly in small sample subsets, leading to overfitting and affecting the model’s generalization ability on the test set.

(2)

Additionally, cost-sensitive learning increases the misclassification cost of severe conflicts, making the model more focused on the severe category. Although this method improves the recall rate of the severe category to some extent, its excessive focus on the minority class may cause the model to neglect the balance of other classes, thereby affecting overall precision and the model’s generalization performance.

(3)

In many real-world datasets, severe categories are inherently rare, and balancing the samples does not always solve the inherent problem of class imbalance. For predicting severe conflict classes, the model may need to rely more on deep feature learning rather than just increasing sample size. This is one of the reasons why simple oversampling methods do not significantly improve model performance.

Overall, balancing techniques did not provide significant advantages in this study’s dataset. In the process of modeling and key risk factor analysis, we are still working based on the original sample.

6.3. Analysis of Key Influencing Factors

6.3.1. Longitudinal Conflicts

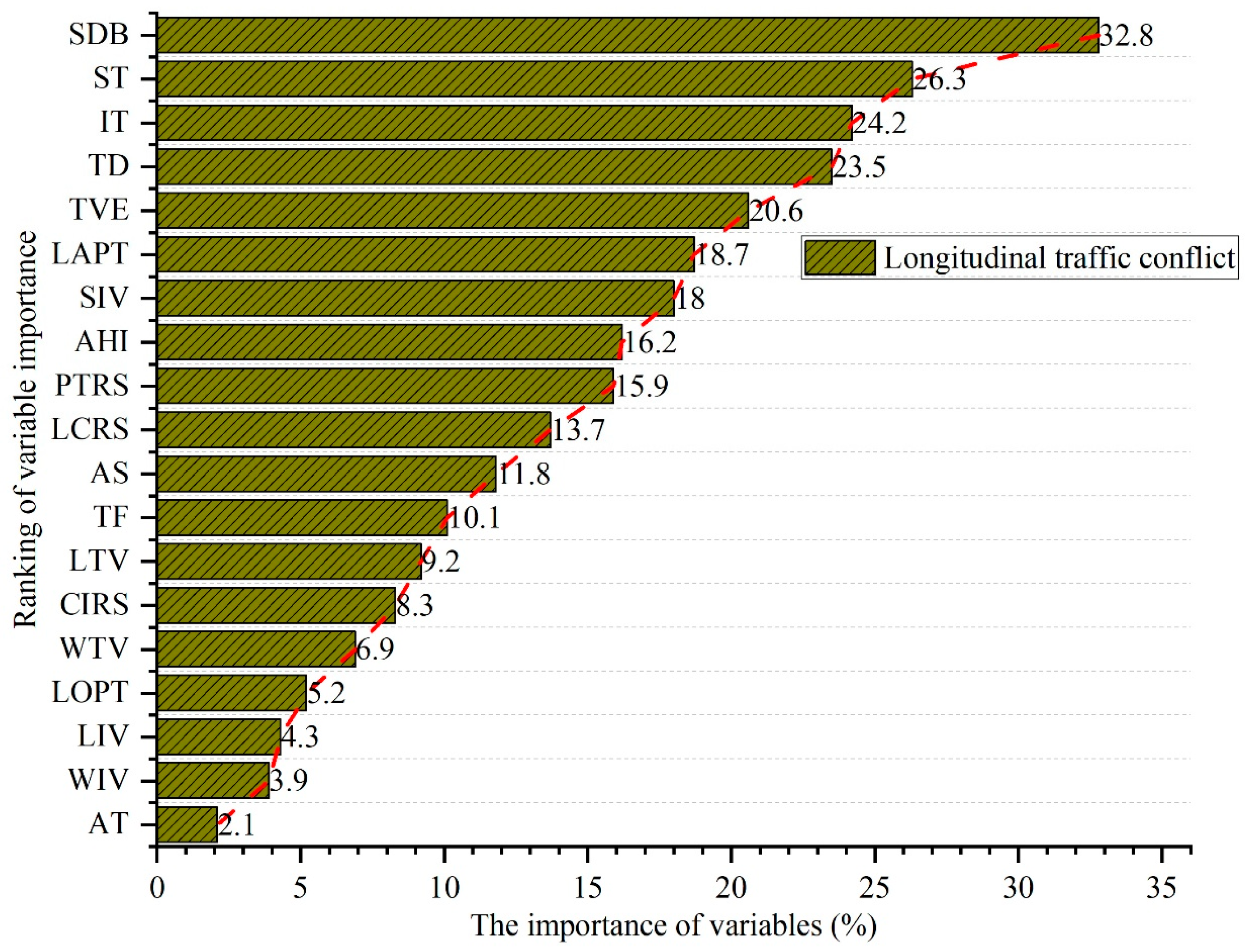
The optimal CatBoost model was used to analyze the impact of risk factors on longitudinal conflict severity. The importance of independent variables was assessed using the average Gini index decrease from the CatBoost algorithm. Figure 14 presents a ranking of factors influencing lateral conflict severity based on feature importance.

Figure 14 lists the key features for predicting lateral conflict severity in descending order: SDB, ST, IT, TD, TVE, LAPT, SIV, AHI, PTRS, LCRS, AS, TF, LTV, CIRS, WTV, LOPT, LIV, WIV, AT. The five most influential variables for longitudinal conflict severity were speed difference between target and interacting vehicles, target vehicle speed, truck-involved conflicts, traffic density, and diverging conditions. Speed difference and target vehicle speed directly influenced lateral collisions in ETTC calculations. Higher values of these metrics reduced safe operation time, increasing collision likelihood [27]. Truck-involved conflicts were more severe due to greater mass, size, and maneuverability differences, which increased kinetic energy, extended braking distances, and heightened blind spot risks, reducing ETTC values and elevating conflict hazards [26]. Traffic density significantly influenced ETTC-based conflict severity, as high density reduced inter-vehicle distances, shortened reaction times, and limited operational space, increasing collision probability. Congested traffic, frequent speed changes, and lane changes destabilized driving patterns, increasing conflict risks [48]. Despite lower vehicle speeds, significant relative speed differences increased impact forces, leading to more severe conflicts [13]. Diverging conditions significantly influenced conflict severity, as vehicles exiting the mainline performed mandatory lane changes and decelerated, creating speed differences and reduced headways with following vehicles. These actions increased longitudinal collision risks, reducing ETTC values and elevating conflict severity. Study [32] found that frequent mandatory lane changes by vehicles exiting the mainline increased speed fluctuations by 61.11% (standard deviation) and maximum deceleration by 18.60%. These actions, combined with traffic density and signage, further intensified longitudinal conflicts.

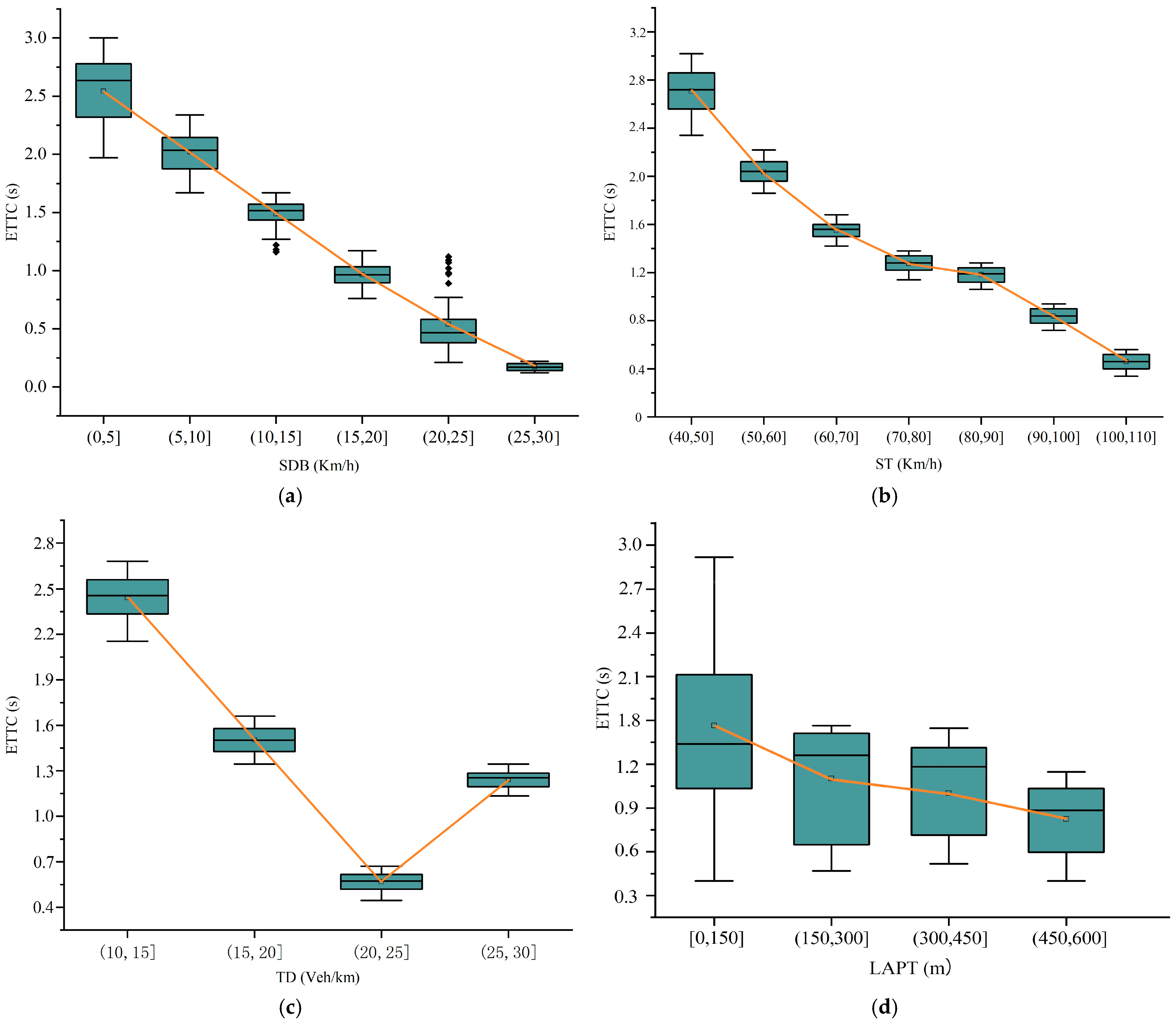
As the CatBoost model’s feature importance could not quantify relationships between variables and outcomes, a quantitative analysis of top-ranked continuous variables was conducted to assess their impact on longitudinal conflict risk (Figure 15).

(1)

Relative speed was segmented at 5 km·h⁻¹ intervals, and ETTC distribution for longitudinal conflicts was analyzed per segment (Figure 15a). Longitudinal conflict risk increased with SDB, and ETTC distribution became more concentrated. Conflict severity rose sharply in the [0, 20] km·h⁻¹ range but slowed in the [20, 30] km·h⁻¹ range, where conflicts were typically severe. For safety management in divergence zones, roadside and onboard units should warn drivers when relative speeds exceed 20 km·h⁻¹ to ensure cautious lane changes [30].

(2)

Target vehicle speed was segmented at 10 km·h⁻¹ intervals, and ETTC distribution for longitudinal conflicts was analyzed per segment (Figure 15b). Longitudinal conflict risk increased sharply with target vehicle speed, and ETTC distribution became more concentrated. ETTC trends showed three stages: rapid conflict severity increase in [40, 70] km·h⁻¹; stable ETTC around 1.9 s in [70, 90] km·h⁻¹; and pronounced risk increase in [90, 110] km·h⁻¹. Most samples in [40, 100] km·h⁻¹ were general or minor conflicts, while severe conflicts were concentrated in [100, 110] km·h⁻¹.

(3)

Traffic density was segmented at 5 veh·km⁻¹ intervals, and ETTC distribution for longitudinal conflicts was analyzed per segment (Figure 15c). ETTC showed a V-shaped pattern across traffic density segments. In [10, 25] veh·km⁻¹, increasing traffic density sharply reduced mean ETTC, increasing conflict severity. Mean ETTC was lowest in [20, 25] veh·km⁻¹. In [25, 30] veh·km⁻¹, mean ETTC increased slightly but remained below the [15, 20] veh·km⁻¹ mean. An ETTC warning threshold of 1.7–2 s could be set for divergence zones.

(4)

Longitudinal conflict positions were segmented at 150 m intervals from the exit ramp, and ETTC distribution was analyzed per segment (Figure 15d). ETTC values increased with LAPT, and their distribution range expanded. The [300, 600] m segment had mostly minor and general conflicts, with fewer severe conflicts. Severe conflicts were concentrated in [0, 300] m. Particular attention should focus on road sections within 300 m of the ramp exit in divergence zones.

Figure 15. The Impact of Key Variables on Longitudinal Conflicts. (a) The Impacts of SDB on Longitudinal Conflicts. (b) The Impacts of ST on Longitudinal Conflicts. (c) The Impacts of TD on Longitudinal Conflicts. (d) The Impacts of LAPT on Longitudinal Conflicts.

Figure 15. The Impact of Key Variables on Longitudinal Conflicts. (a) The Impacts of SDB on Longitudinal Conflicts. (b) The Impacts of ST on Longitudinal Conflicts. (c) The Impacts of TD on Longitudinal Conflicts. (d) The Impacts of LAPT on Longitudinal Conflicts.

6.3.2. Lateral Conflicts

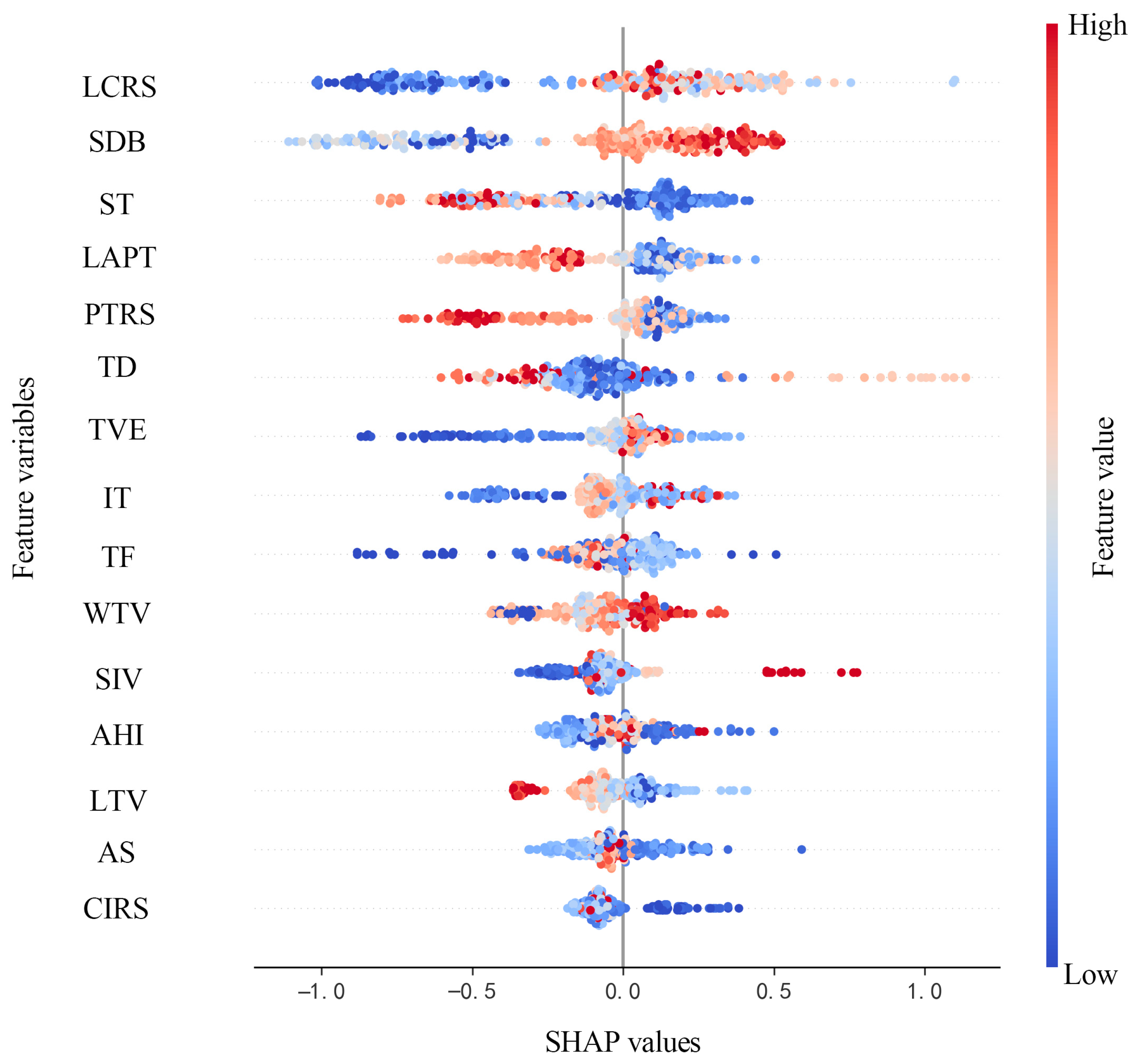
SHAP (SHapley Additive exPlanations) was specifically employed within the XGBoost framework to improve model interpretability by quantifying feature contributions. Figure 16 shows the ranked importance of factors influencing lateral conflict severity. The horizontal axis displays SHAP values, with larger values indicating greater contributions to conflict severity prediction. Each dot represents a sample, with colors indicating feature value magnitude (red for higher, blue for lower).

Figure 16 lists the most influential features for predicting lateral conflict severity in descending order: LCRS, SDB, ST, LAPT, PTRS, TD, TVE, IT, TF, WTV, SIV, AHI, LTV, AS, CIRS. The top five variables influencing lateral conflict severity were lane change frequency, speed differential, target vehicle speed, longitudinal conflict position, and truck proportion.

Frequent lane changes increased lateral conflict severity by intensifying vehicle interactions and reducing reaction time for surrounding drivers. Lane-changing maneuvers caused lateral disturbances, often triggering abrupt braking or evasive actions, particularly in high-density diverging zones with limited space. Previous studies linked increased lane-changing activity to higher crash risk and conflict intensity [34,49]. Speed differential magnitude was a key predictor of conflict severity. Large speed differences reduced time-to-collision (TTC) during merging or lane changes, increasing high-impact lateral crash risks. Research shows that greater velocity variance increases conflict frequency and severity [29,33]. Target vehicle speed directly influenced the complexity of lateral interactions. High target vehicle speeds reduced gap acceptance and increased severe conflict likelihood due to limited deceleration or avoidance time. Low target speeds prompted abrupt maneuvers by faster vehicles, increasing rear-end and sideswipe risks. Empirical evidence confirms that target vehicle speed influences conflict probability and severity [27,41,48]. Longitudinal conflict location in the diverging zone determined available temporal and spatial resources for evasive actions. Conflicts near the diverging zone’s end provided limited response time, increasing lateral interaction severity. Studies indicate that proximity to exit gore or taper regions increases severity due to constrained geometry and limited decision-making time [26,28,44]. A higher truck proportion in traffic flow increased lateral conflict severity due to larger size, limited maneuverability, and extended blind zones. Truck-involved interactions were more dangerous due to higher impact forces and reduced visibility. Literature confirms that truck presence increases the likelihood and severity of lateral conflicts, particularly in merging and diverging segments [33,37].

Figure 16. Ranking of the Contribution Degrees of Key Influencing Factors on Lateral Conflicts.

Figure 16. Ranking of the Contribution Degrees of Key Influencing Factors on Lateral Conflicts.

Similarly, to quantitatively analyze the impact of key influencing factors on lateral conflict risk, several top-ranked continuous variables were selected, and the distribution of ETTC scores across different value intervals was examined, as illustrated in Figure 17.

(1)

Lane changes within 30 s before a lateral conflict were segmented into intervals of five, and ETTC score distribution was analyzed per interval (Figure 17a). Lateral conflict severity increased with higher LCRS values, and ETTC score distribution became more concentrated. In the [0, 25] range, conflict severity rose sharply with each lane change increment, but in the [25, 30] range, the increase slowed, and conflicts were typically severe. For safety management in diverging zones, a threshold of over 25 lane changes in 30 s could serve as a risk warning, prompting roadside and in-vehicle units to alert drivers to lane change cautiously.

(2)

Relative speed was segmented at 5 km/h intervals, and ETTC score distribution was analyzed per interval (Figure 17b). Lateral conflict risk increased with higher SDB values, and ETTC distribution became more concentrated. In the [0, 25] km/h range, lateral conflict severity rose sharply, but the increase slowed in the [25, 30] km/h range. For proactive safety management in diverging zones, a relative speed threshold of 25 km/h could serve as a risk monitoring indicator.

(3)

Target vehicle speed was segmented at 10 km/h intervals, and ETTC distribution for lateral conflicts was analyzed per interval (Figure 17c). Mean ETTC for lateral conflicts decreased with increasing ST, indicating rising collision risk. The ETTC decline occurred in two stages. In the [40, 60] km/h range, mean ETTC remained high, primarily corresponding to minor conflicts with no notable decline. In the [60, 70] km/h range, mean ETTC dropped sharply to approximately 1.7 s. In the [70, 110] km/h range, mean ETTC continued to decrease, indicating high collision risk. On three-lane unidirectional expressways, vehicles in diverging zones traveling at 90–110 km/h faced higher conflict probability, necessitating cautious driving and speed control.

(4)

Lateral conflict positions were segmented at 150 m intervals from the exit ramp, and ETTC score distribution was analyzed per interval (Figure 17d). LAPT affected lateral conflicts oppositely to longitudinal conflicts. The [450, 600] m range from the exit ramp was the primary zone for severe lateral conflicts, while most conflicts in the [0, 150] m range were minor, with few severe cases. This pattern resulted from exit reminder signs on Chinese expressways, typically located at 0 m, 500 m, and 1 km before the exit. In the [450, 600] m interval, drivers likely noticed signs and began lane changes from inner lanes, increasing weaving behavior and lateral conflict likelihood and severity.

Figure 17. The Impact of Key Variables on Longitudinal Conflicts. (a) The Impacts of LCRS on lateral conflicts. (b) The Impacts of SDB on lateral conflicts. (c) The Impacts of ST on lateral conflicts. (d) The Impacts of LAPT on lateral conflicts.

Figure 17. The Impact of Key Variables on Longitudinal Conflicts. (a) The Impacts of LCRS on lateral conflicts. (b) The Impacts of SDB on lateral conflicts. (c) The Impacts of ST on lateral conflicts. (d) The Impacts of LAPT on lateral conflicts.

6.3.3. Comparative Analysis of Key Determinants

In diverging areas, longitudinal and lateral conflicts share some determinants, but their manifestations and mechanisms differ significantly. Speed differential (SDB) and subject vehicle speed (ST) are critical predictors for both conflict types; larger differentials and higher speeds compress reaction time and increase closing speed, thereby reducing ETTC and raising collision energy. Truck proportion (IT/PTRS) also elevates risk, but longitudinal conflicts are exacerbated by mass and braking distance, whereas lateral conflicts are intensified by limited maneuverability and blind-spot effects. Traffic density (TD) and diverging context (TVE) determine the space–time budget for evasive maneuvers; high density shortens headways and reduces acceptable gaps, thereby lowering ETTC. Although both conflict types are influenced by speed and trucks, longitudinal conflicts are governed more by car-following and braking dynamics, showing high risk within 0–300 m near the ramp due to mandatory deceleration and short headways; lateral conflicts, by contrast, are dominated by gap acceptance and lane-changing competition, often intensifying within 450–600 m as signage prompts large-scale weaving.

Further comparison reveals differences in the spatiotemporal distribution and speed regimes of conflict severity. Longitudinal conflict severity is concentrated in high-speed braking scenarios at ST = 100–110 km/h, whereas lateral conflict risk escalates earlier, with ETTC dropping to about 1.7 s at ST = 60–70 km/h and continuing to deteriorate at higher speeds. Warning thresholds for relative speed also differ: SDB ≥ 20 km/h is more suitable for identifying longitudinal risks, while SDB ≥ 25 km/h better discriminates lateral risks. Density affects longitudinal conflicts in a V-shaped manner, with ETTC minimized at 20–25 veh/km; although lateral conflicts are still influenced by density, once active weaving occurs, its marginal role is overtaken by lane-change rate (LCRS) and speed differentials.

Safety management should adopt differentiated strategies sensitive to position and maneuver type: focusing on rear-end risk mitigation near ramps and lane-change safety upstream; applying variable speed control and inter-vehicle communication to damp speed differentials; and emphasizing lane discipline and blind-spot assistance for trucks. Overall, longitudinal risks concentrate near ramp gore areas under mandatory deceleration and short headways, while lateral risks are most pronounced upstream where signage triggers weaving; hence, implementing fine-grained interventions tailored to location and maneuver is more reasonable than adopting a single uniform strategy.

7. Conclusions

Using a YOLOX and DeepSORT framework, vehicle trajectories were extracted with high precision from roadside video footage at multiple expressway diverging zones. Traffic conflict types and severity were classified based on the two-dimensional positions of interacting vehicles and the ETTC indicator. The spatiotemporal distribution of traffic conflicts was analyzed, along with key factors influencing longitudinal and lateral conflicts.

Spatiotemporal analysis of traffic conflicts established severity classification thresholds for longitudinal and lateral conflicts in unidirectional three-lane expressway diverging zones. ETTC thresholds for longitudinal conflicts were 2.46 s (slight/moderate) and 1.07 s (severe), and for lateral conflicts, 2.31 s (slight/moderate) and 1.09 s (severe).

CatBoost and XGBoost models identified key factors influencing longitudinal and lateral conflicts in diverging zones. The top five factors for longitudinal conflicts were speed difference, target vehicle speed, heavy truck involvement, traffic density, and mainline exit status. For lateral conflicts, the top five factors were lane change frequency within 30 s, speed difference, target vehicle speed, distance to the exit ramp, and heavy truck proportion.

This study’s findings offered two key implications for engineering applications. First, quantitative classification of traffic conflict severity provided a reliable basis for real-time safety monitoring in multilane expressway diverging zones. Integration of roadside video, radar, and other sensors with artificial intelligence enabled automatic identification of traffic conflict types and ETTC indicators. For prolonged severe conflicts, the system issued early warnings via variable message signs, roadside broadcasts, or in-vehicle units to promote cautious driving.

Second, this study identified key factors influencing longitudinal and lateral conflicts in expressway diverging zones, offering insights for proactive safety management strategies. To address speed-related conflicts, dynamic speed limit signs or variable speed limit (VSL) systems could adjust mainline and ramp speeds based on real-time traffic conditions. Deceleration alert zones could prompt drivers to reduce speed differentials proactively. Lane-level intelligent guidance systems could encourage early lane changes for faster vehicles, preventing abrupt deceleration in diverging zones. To mitigate heavy truck conflicts, time- or lane-based restrictions could prevent mixed traffic during peak periods. Dedicated truck lanes or early diversion zones could control heavy truck movements near diverging zones. In high traffic density scenarios, buffer segments and queuing areas could extend lane-changing distances, reducing sudden lane changes and longitudinal conflict risks. Vehicle-to-infrastructure (V2I) systems could provide real-time traffic and conflict warnings. To reduce conflicts from mainline-exiting vehicles, high-definition maps and navigation data could provide personalized lane-change suggestions proactively.

Regarding technical and economic feasibility, the implementation of these measures depends heavily on regional development levels and traffic management conditions. From a technical perspective, systems such as variable speed limits (VSL) and vehicle-to-infrastructure (V2I) can already be integrated with existing monitoring and information platforms as well as in-vehicle systems, making it possible to achieve real-time collision risk monitoring and warning in complex scenarios. However, from an economic perspective, the construction and maintenance costs remain high, making full-scale deployment particularly challenging in developing regions. To address this, a phased implementation path can be adopted: initially promoting low-cost measures (such as deceleration alert zones and optimized signage/markings), followed by pilot deployment of V2I systems on key road segments in the medium term, and gradually introducing advanced strategies such as lane-level guidance and dedicated truck lanes in the later stages. With the declining costs of sensors, communications, and artificial intelligence technologies, along with policy support and the establishment of multi-stakeholder cooperation mechanisms, these measures will gain stronger potential for wider adoption. This gradual and context-specific approach not only ensures financial sustainability but also secures the progressive realization of safety benefits, making the proposed strategies realistically feasible and valuable for expressways in diverse regions and stages of development.

8. Limitations and Future Studies

This study has several limitations, which also present opportunities for future research: (1) The UAV-based trajectory data were collected only during daytime windows (07:00–09:00, 12:00–14:00, 16:00–18:00) under normal weather, excluding nighttime, adverse weather, and weekend conditions that may involve distinct traffic patterns and risk dynamics (e.g., reduced visibility, lower friction, or varying demand structures). (2) Moreover, conflict severity was classified solely by kinematic indicators such as ETTC, which, although widely used, do not account for vehicle-specific characteristics, driver behavior, or actual crash outcomes, and their generalizability to other road geometries or regions remains uncertain. (3) While SHAP was applied to improve model interpretability, other explainable AI methods (e.g., Explainable Boosting Machines) may yield complementary insights, yet systematic comparisons of their performance and consistency in identifying risk factors are still lacking.

Building upon these limitations, future research should focus on (1) expanding UAV data collection to incorporate nighttime, adverse weather, and weekend conditions, thereby improving the robustness and generalizability of conflict detection models; (2) incorporating additional variables such as driver demographics, behavioral traits, and vehicle types to enrich the depth of conflict mechanism analysis; (3) developing and validating practical safety interventions (e.g., dynamic guidance systems) through traffic simulations and controlled field experiments to assess their real-world applicability; (4) conducting comparative studies of different interpretable machine learning models, with particular attention to their performance differences in identifying key determinants of traffic conflicts under diverse operating environments.

By systematically addressing these issues, future studies can refine the external validity of UAV-based conflict analysis and strengthen the potential of explainable machine learning for traffic safety management.