Fracture Process in Conceptual Numerical Geological Rock Mass System Model and Its Implications for Landslide Monitoring and Early Warning
Abstract
1. Introduction
2. Establishment of Heterogeneous Geological Rock Mass System Model and Experimental Process
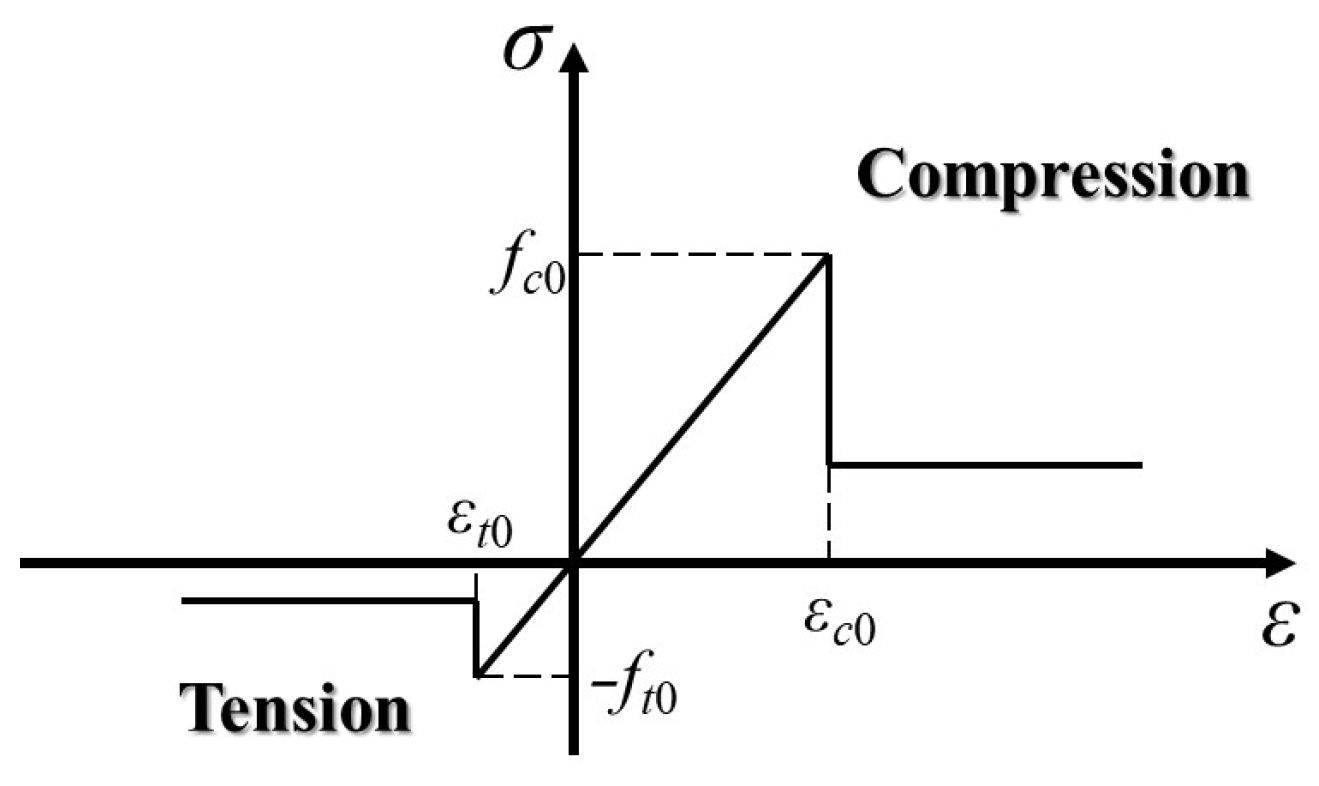
2.1. Basic Principles of RFPA Numerical Method
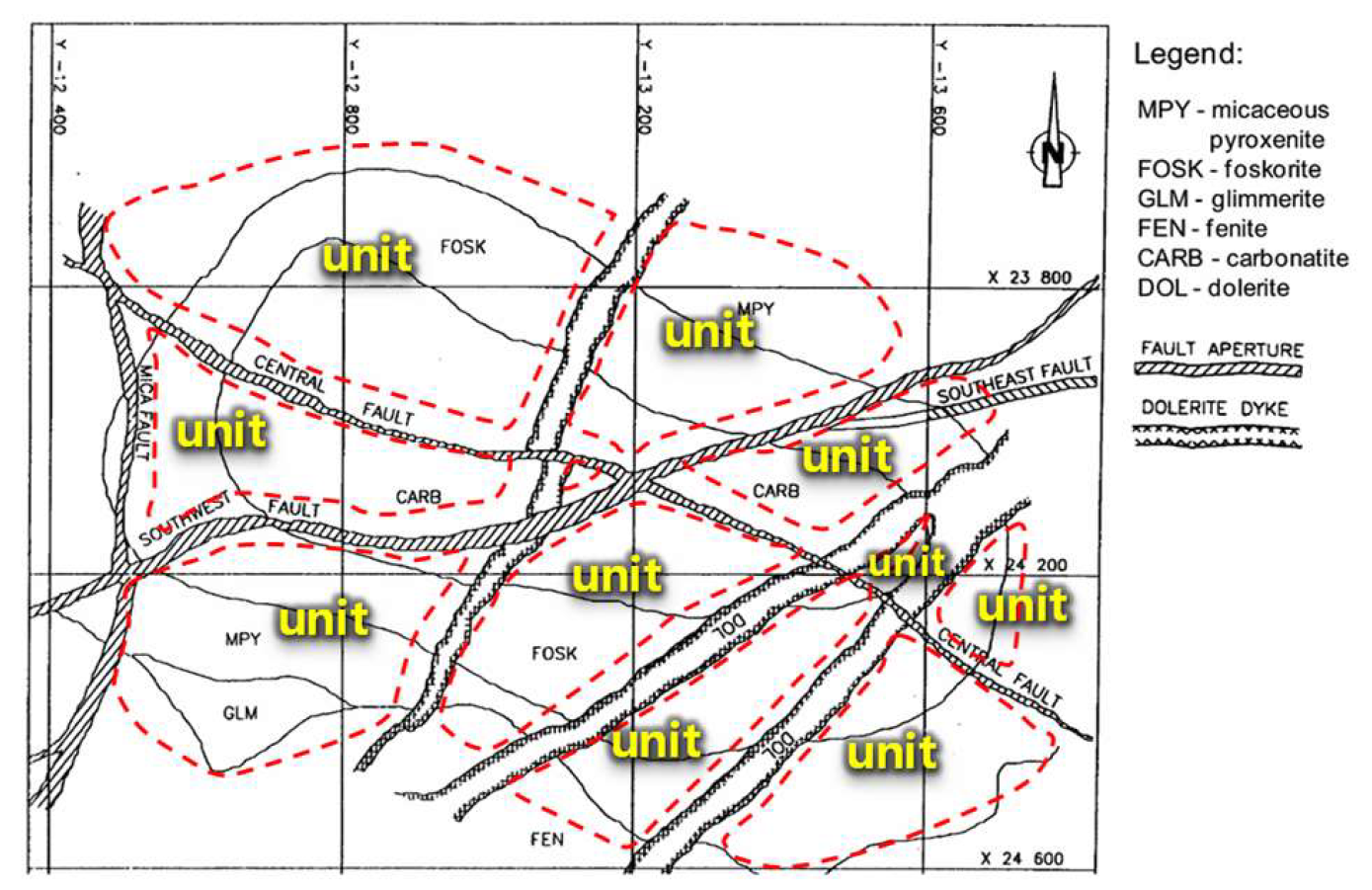
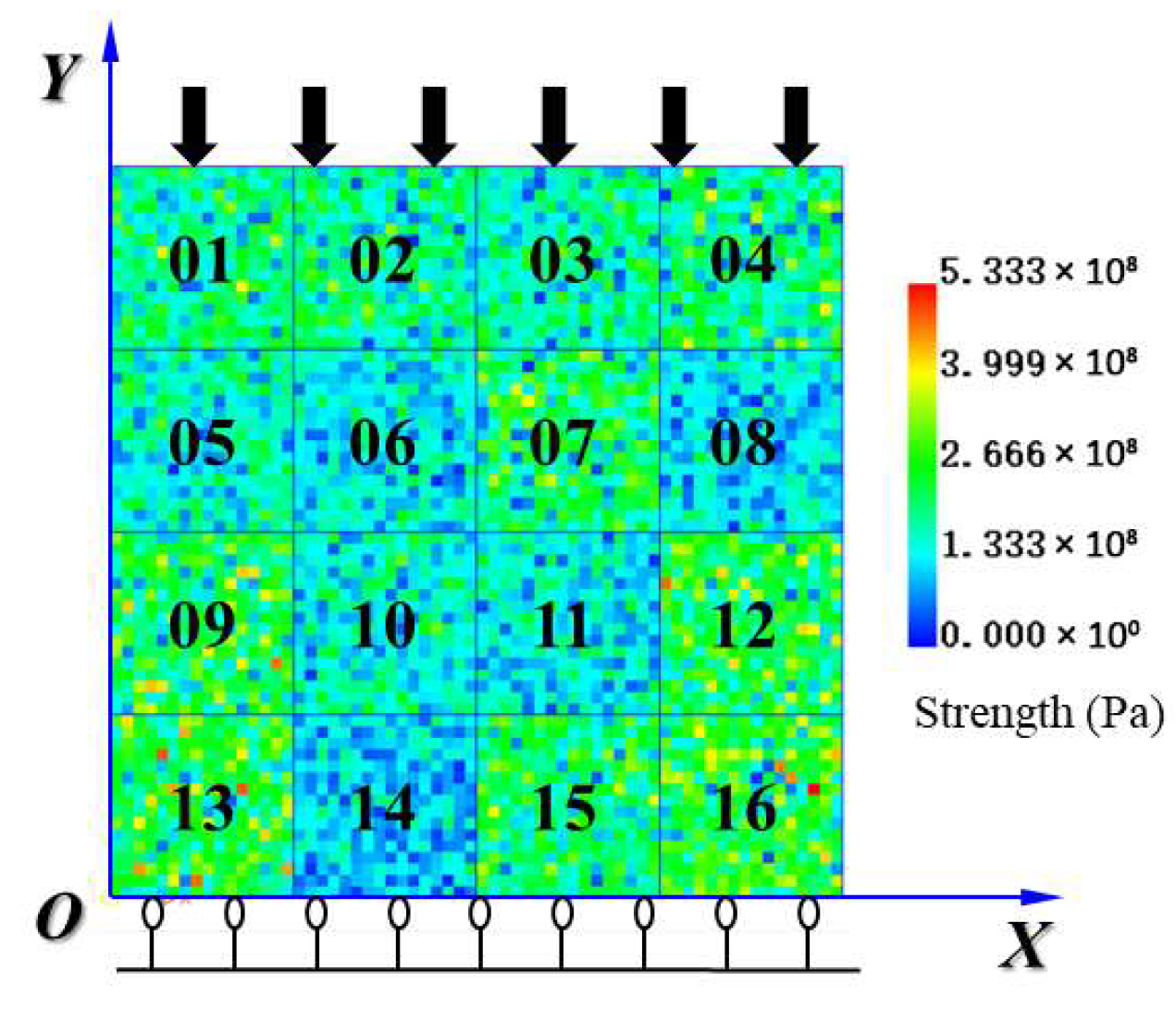
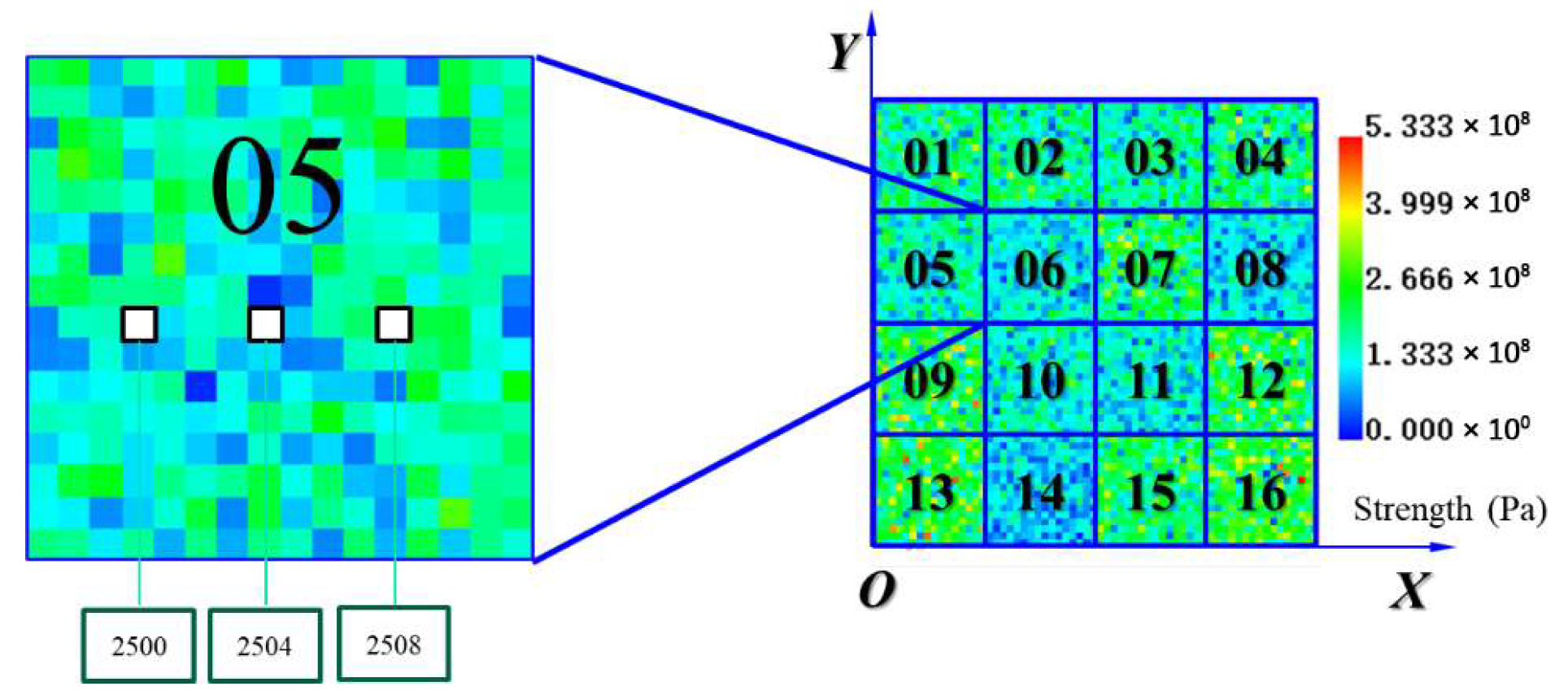
2.2. Establishment of Heterogeneous Geological Rock Mass System Model and Test Scheme
3. Evolutionary Characteristics of Fracture Process for Heterogeneous Geological Rock Mass System Model
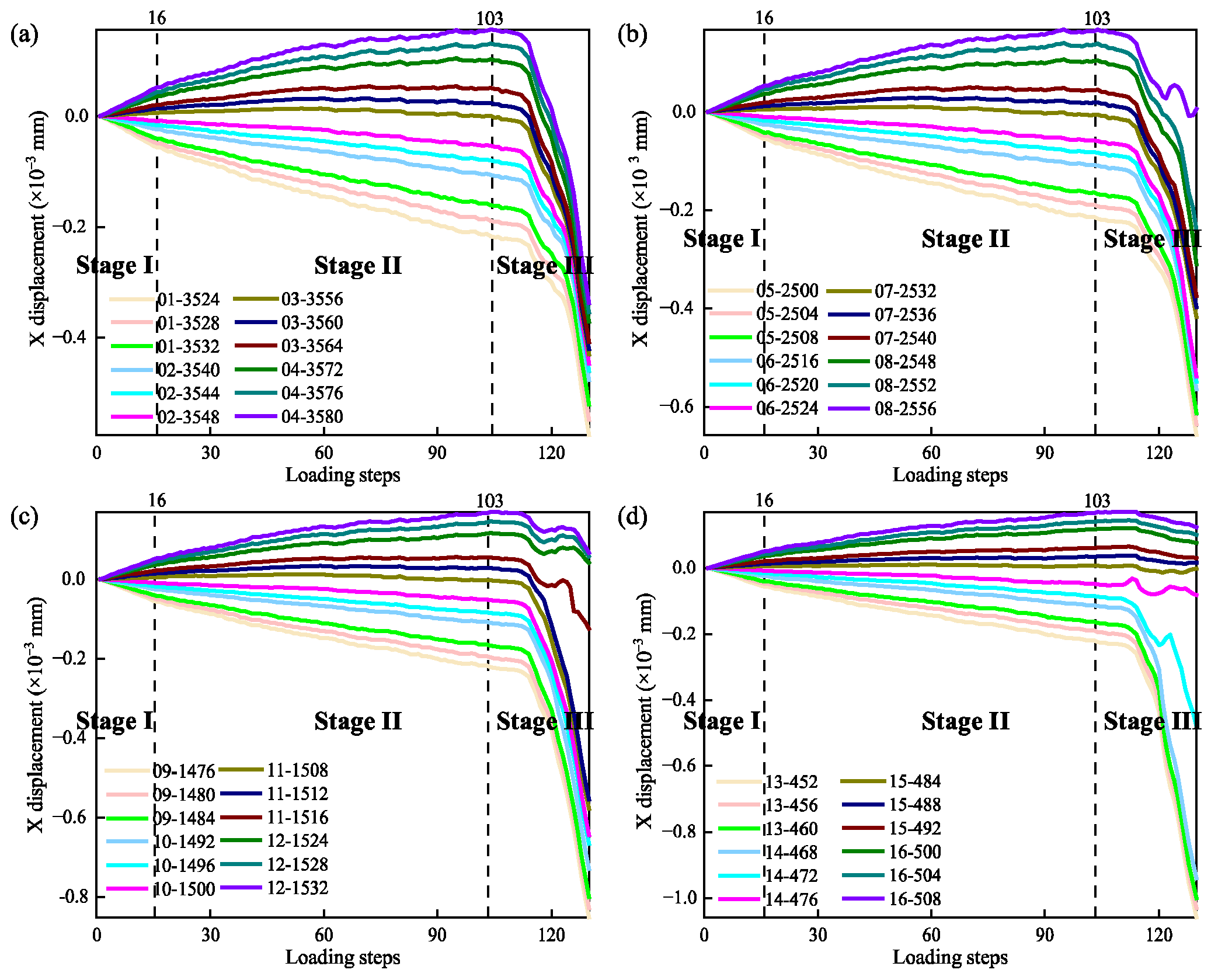
3.1. Evolution Characteristics of Displacement in X Direction
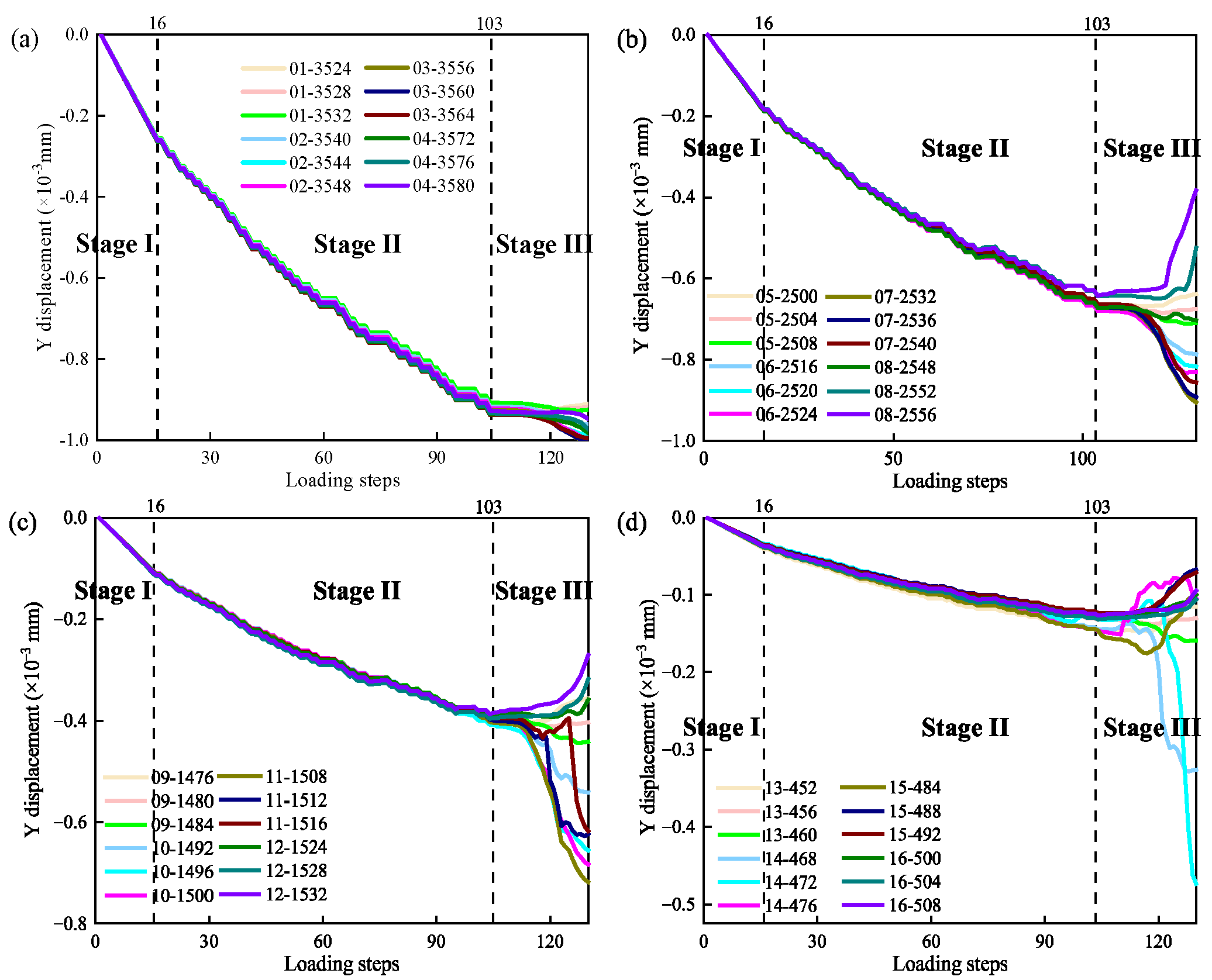
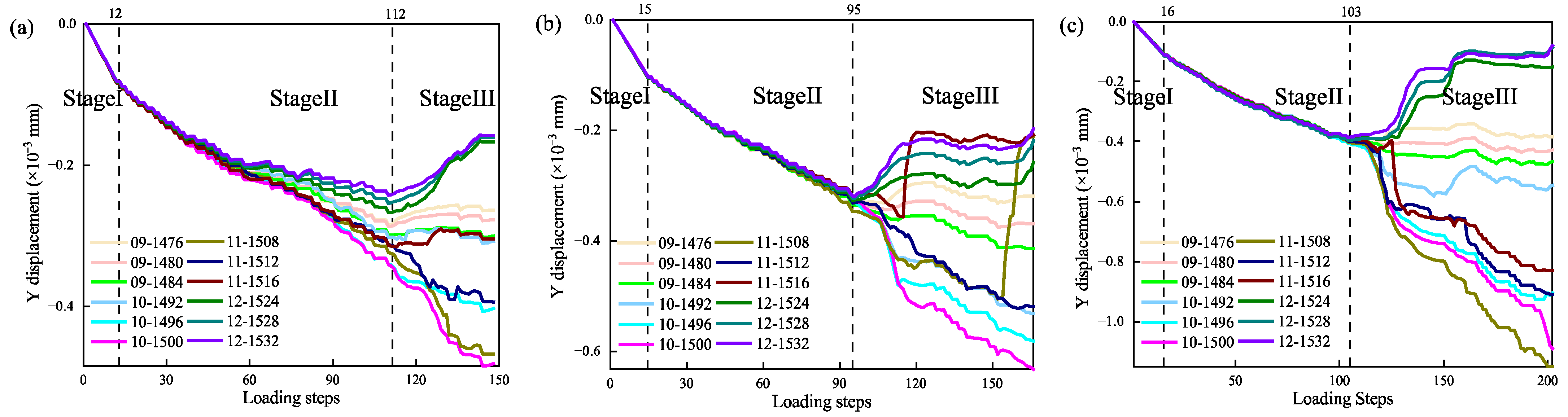
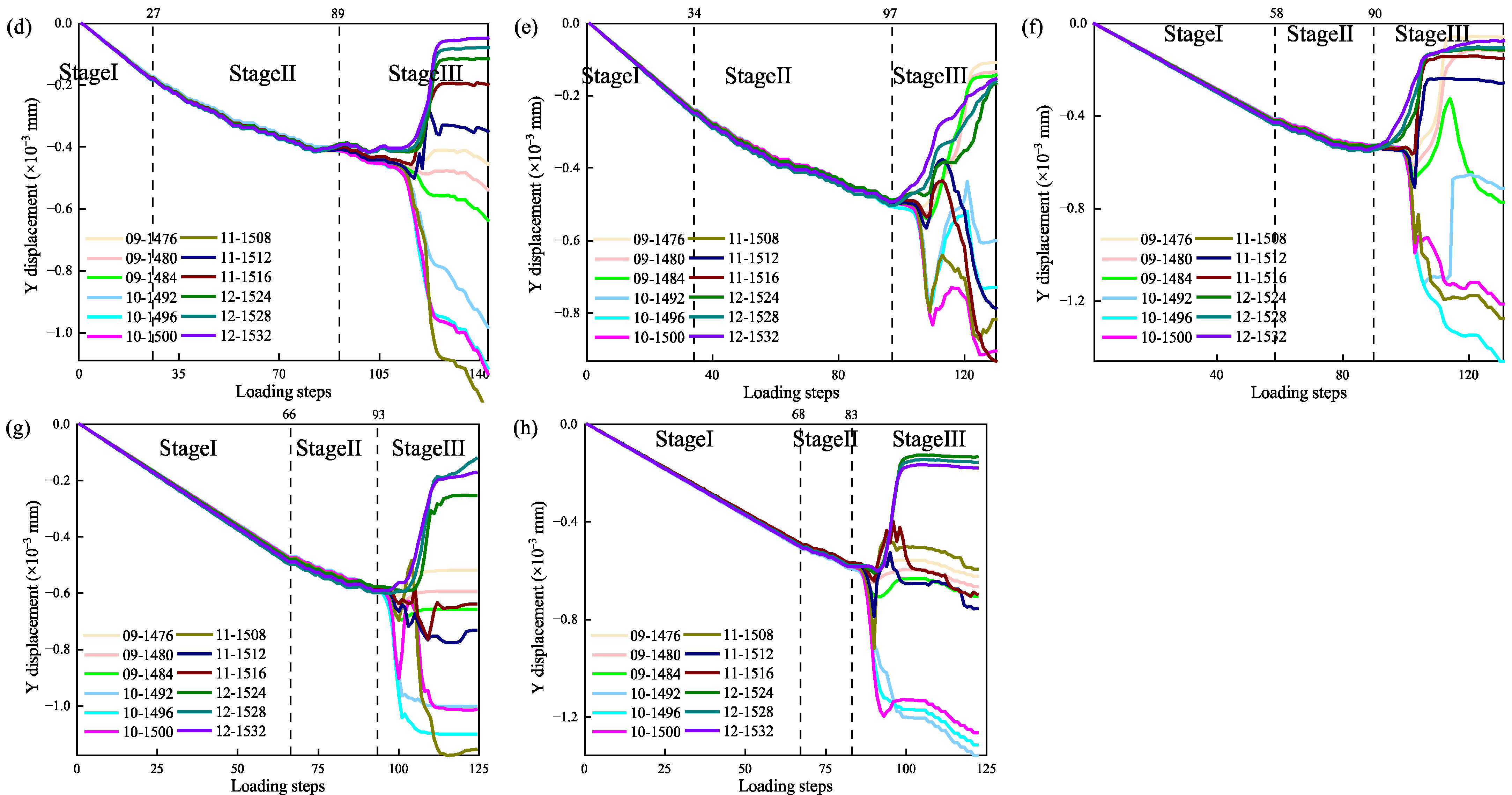
3.2. Evolution Characteristics of Displacement in Y Direction
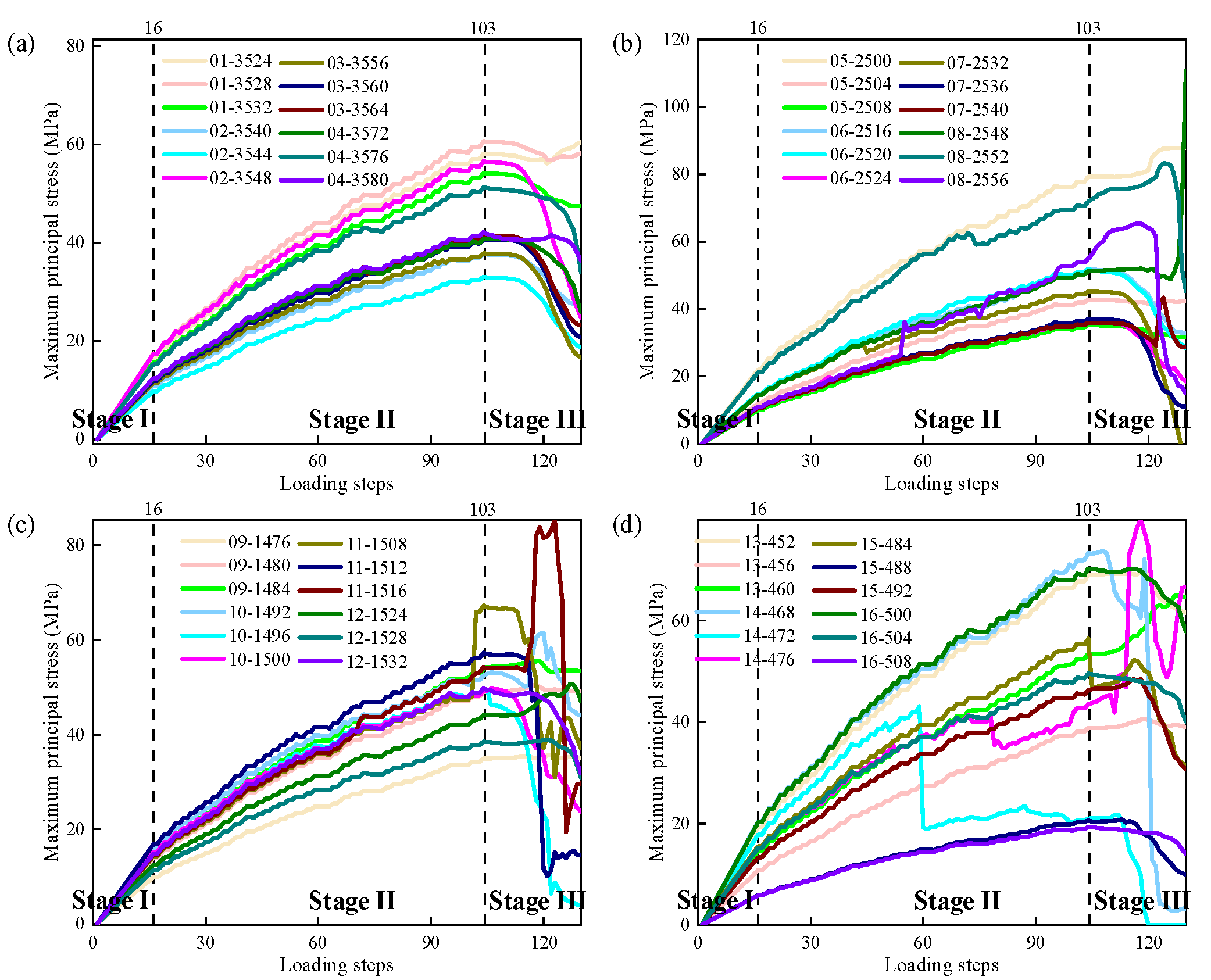
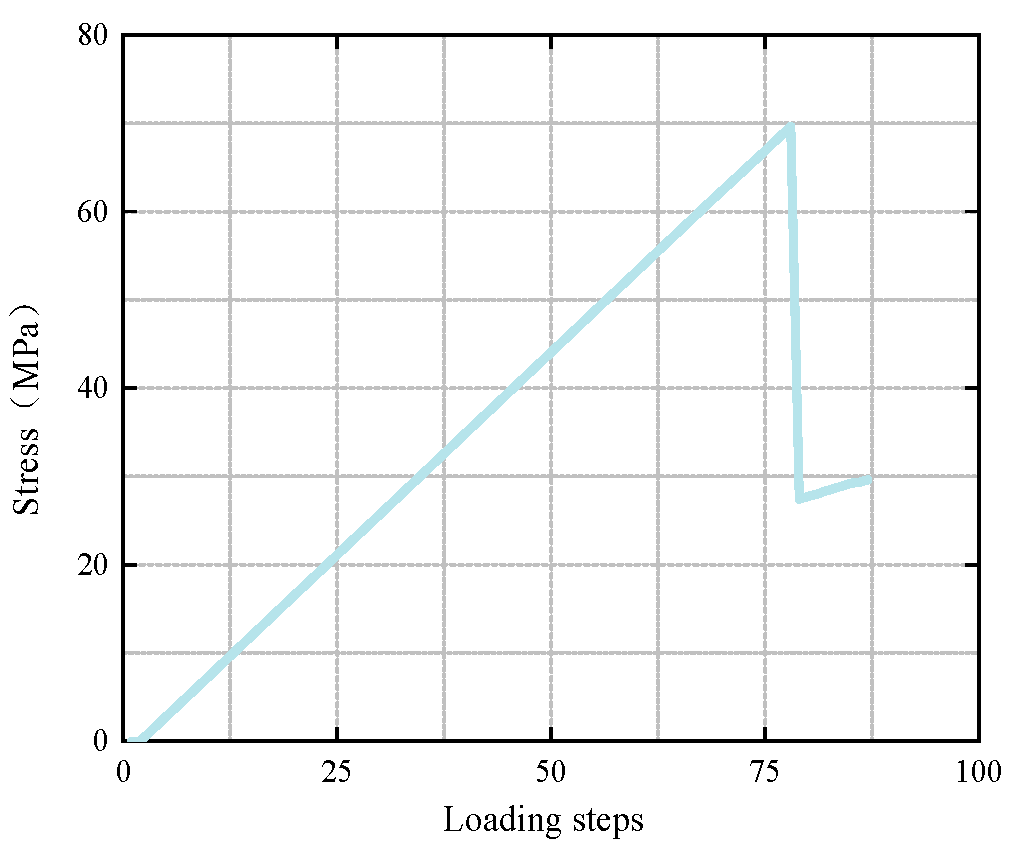
3.3. Evolution Characteristics of the Maximum Principal Stress
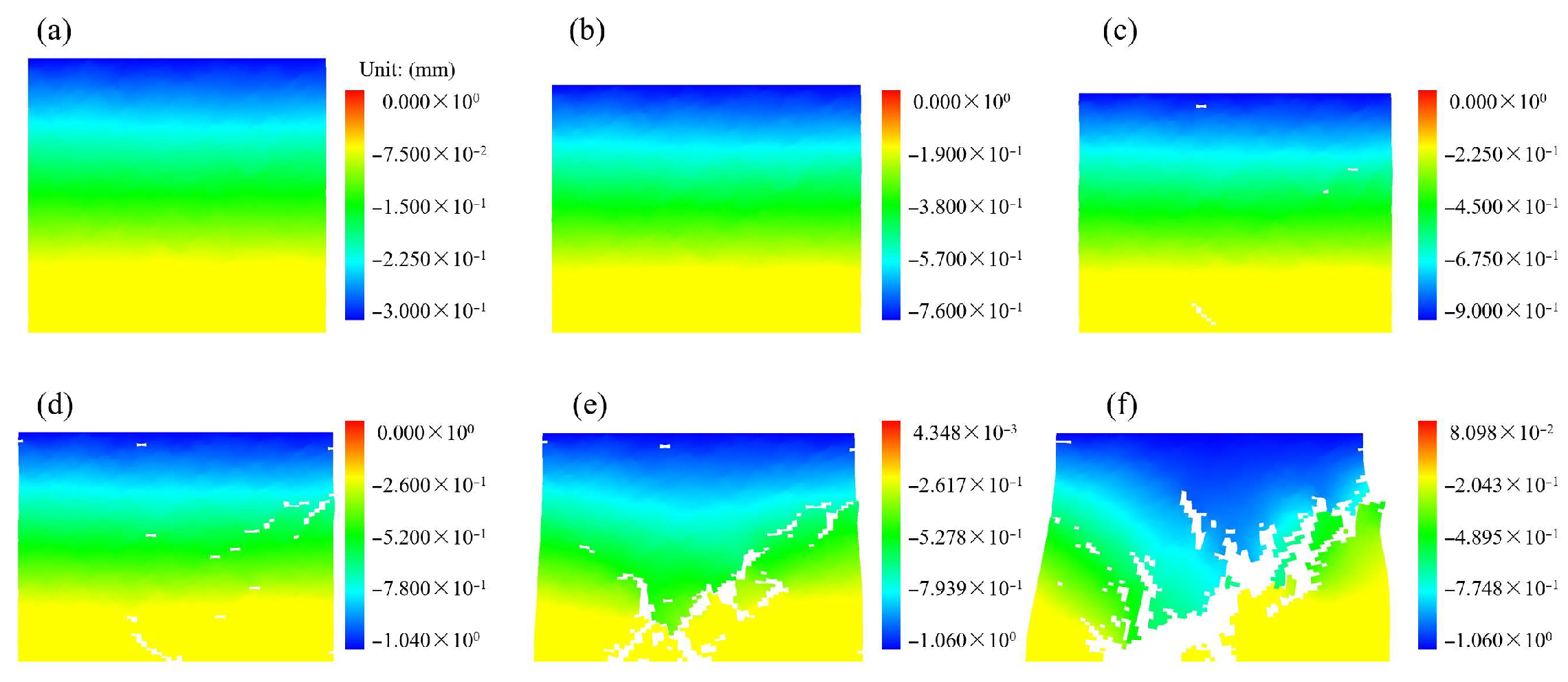
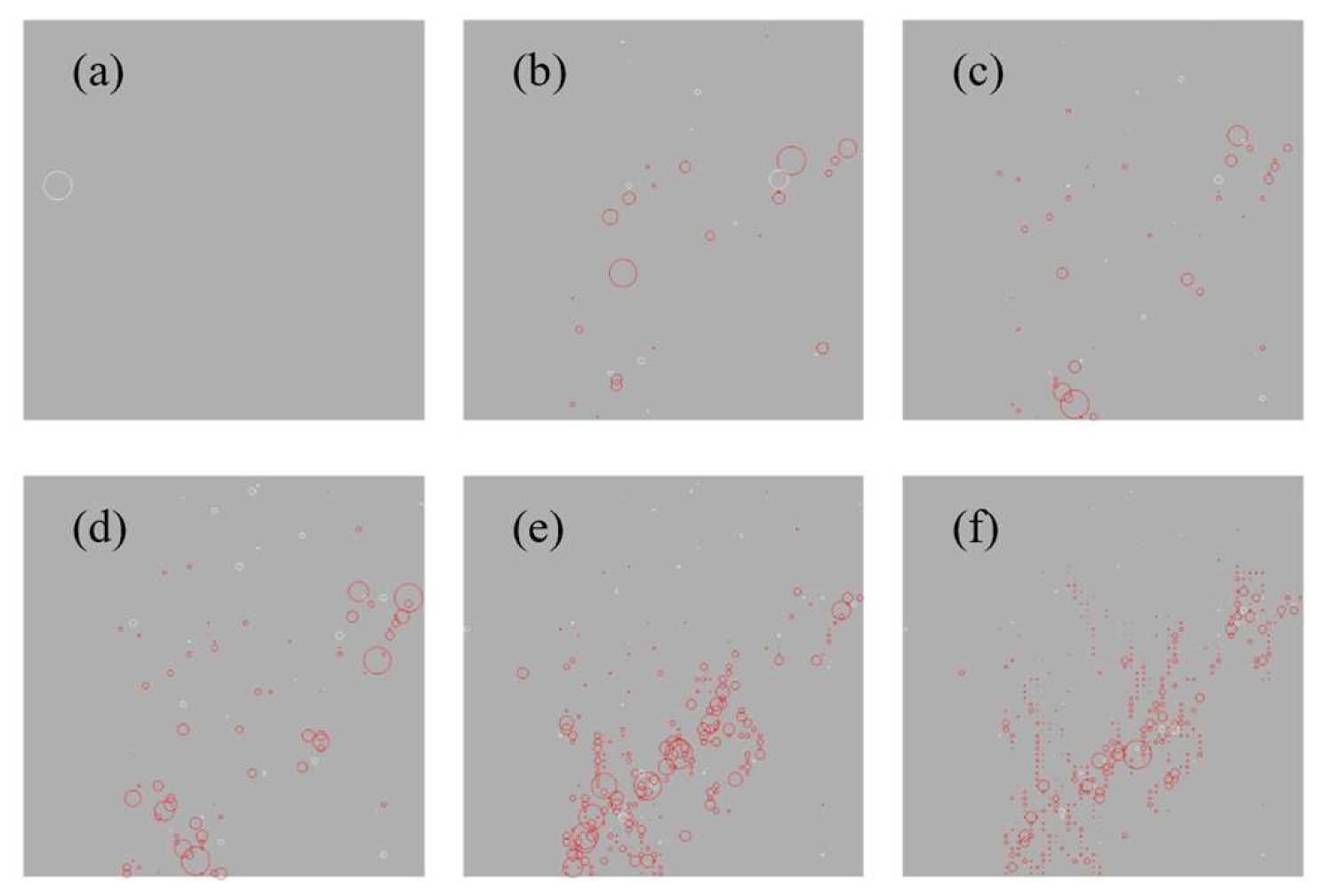
3.4. Evolution Characteristics of Acoustic Emission Signals
4. Discussion
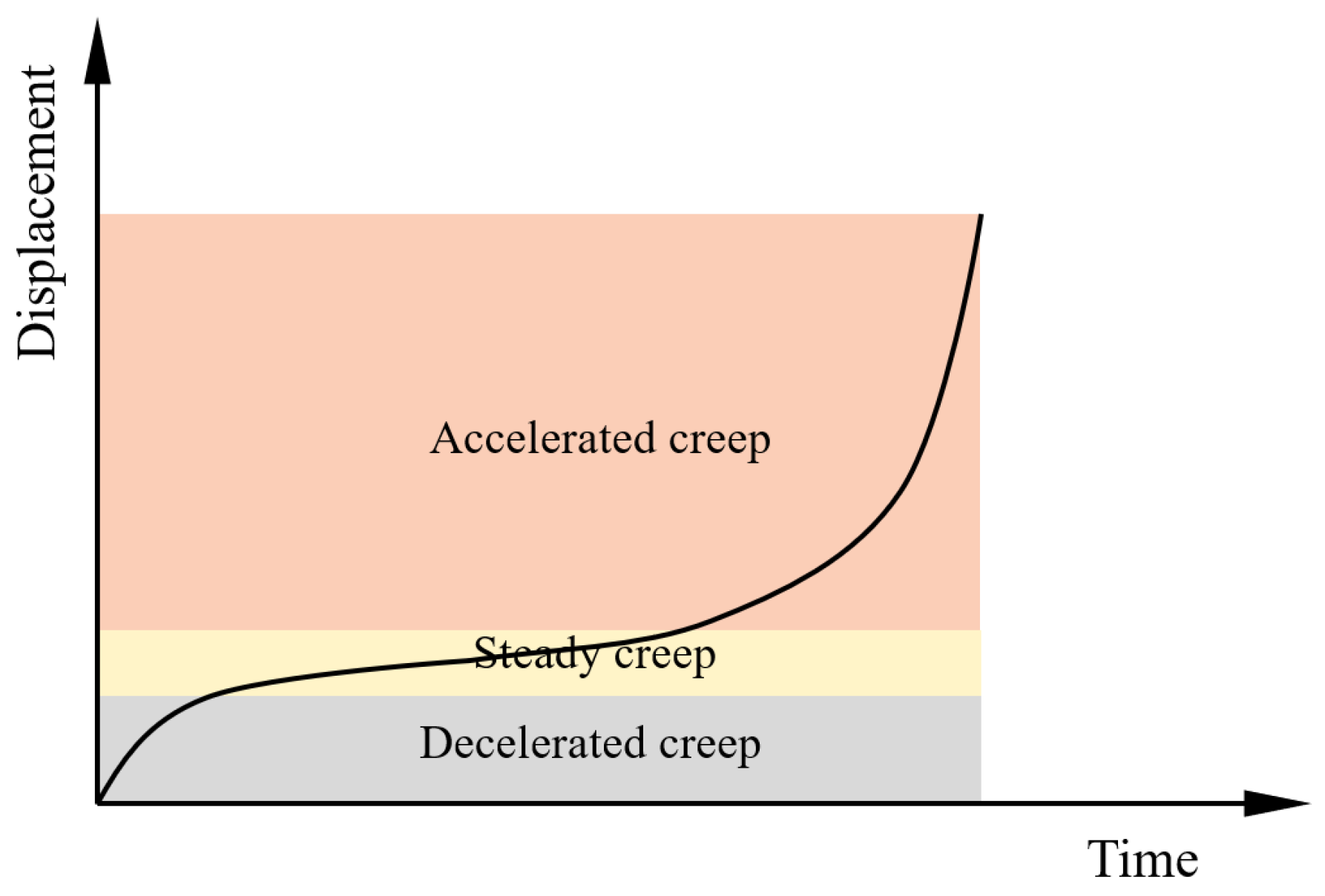
4.1. Implications of the Evolution Characteristics of Heterogeneous Geological Rock Mass Model Fracture Processes for Rockslide Monitoring and Early Warning
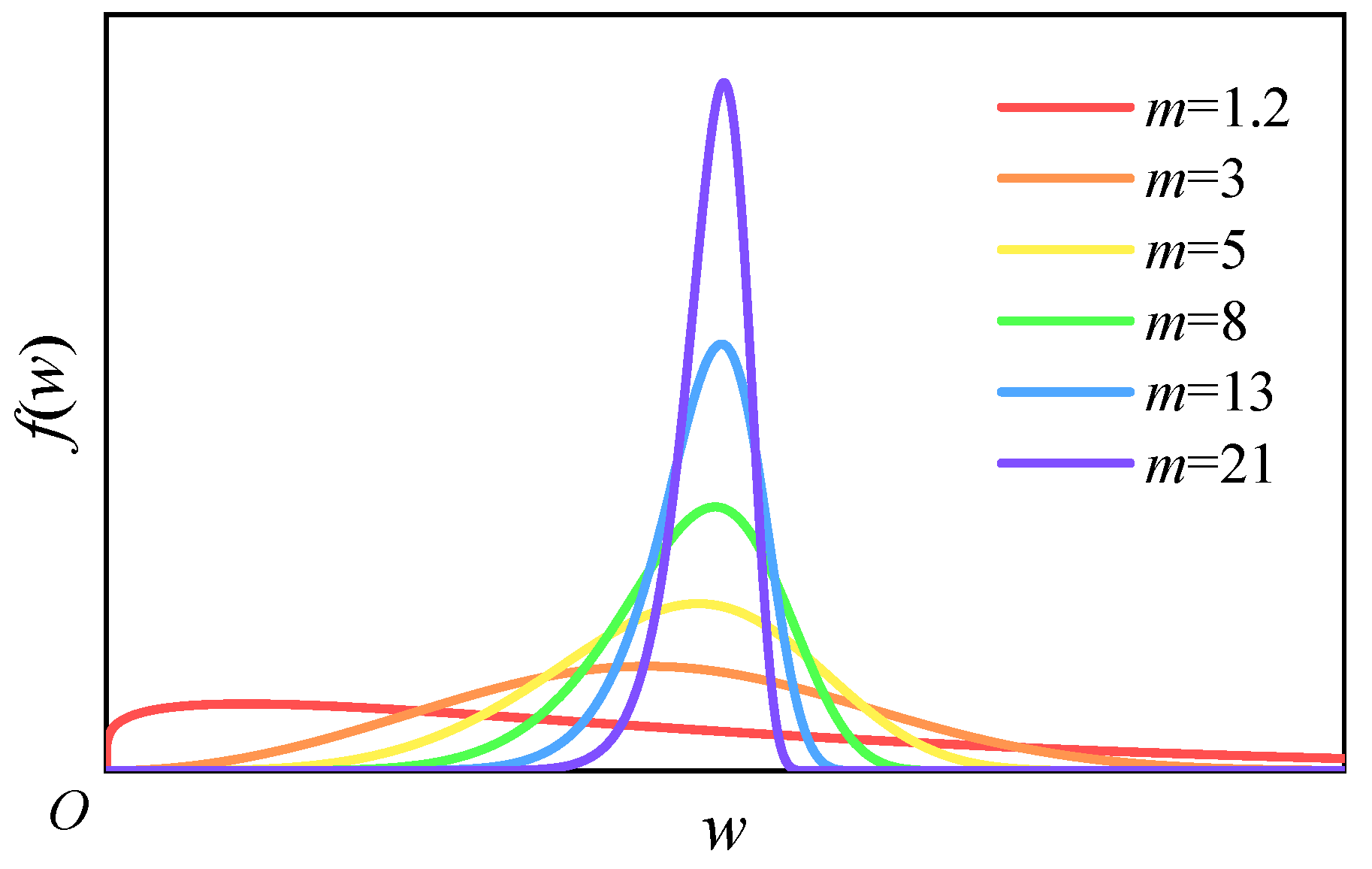
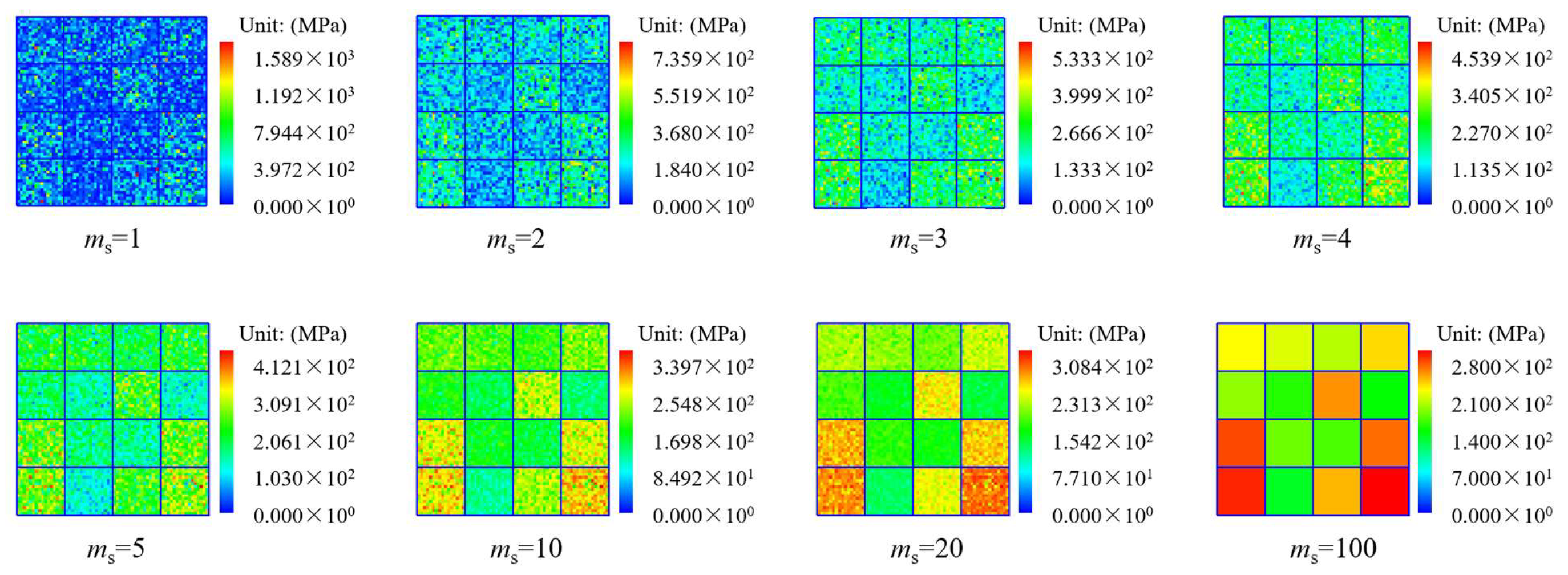
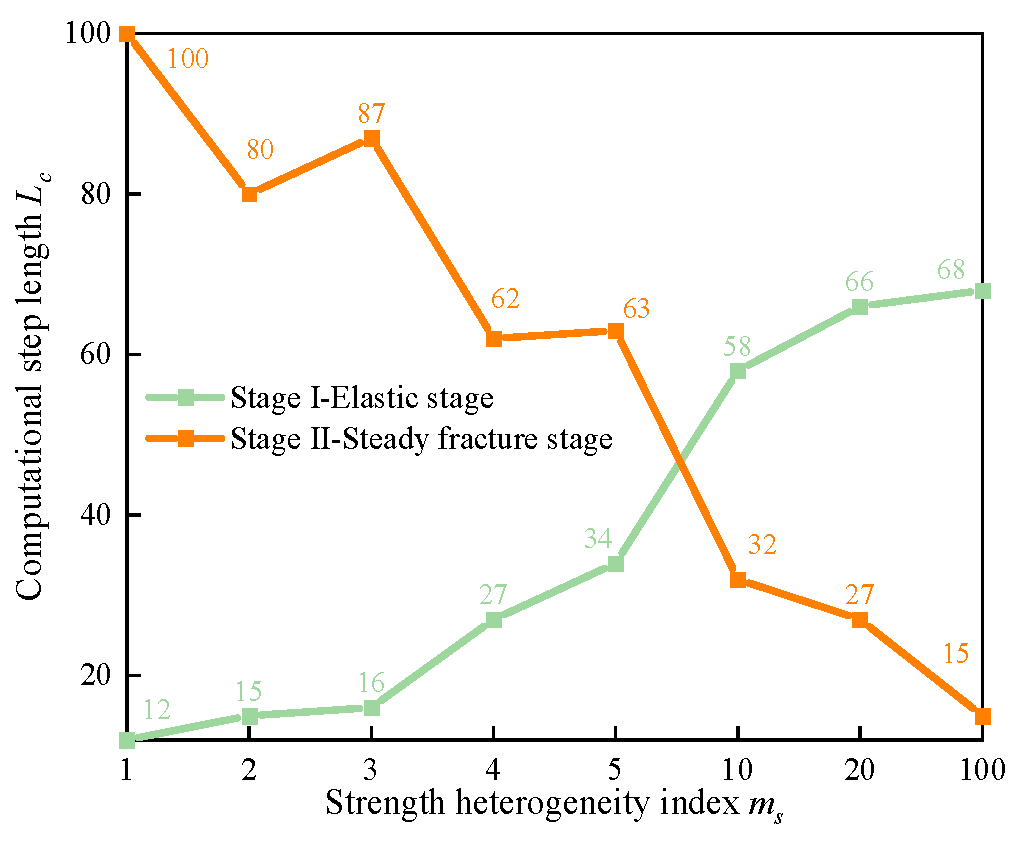
4.2. Effects of Rock Mass Homogeneity Index ms on Fracturing Process and Its Implications for Landslide Early Warning
4.3. Limitations and Prospects of Geological Rock Mass System Models
5. Conclusions
- (1)
- Before the fracture and instability of the heterogeneous geological rock mass system model, there is evident “differentiation” in the magnitude and direction of both displacement and stress increments. Additionally, a sudden increase in the number of acoustic emission events occurs, with their concentration near macroscopic cracks. Such a phenomenon could serve as an early warning indicator for predicting rock landslides.
- (2)
- Although displacement differentiation, stress differentiation, and acoustic emission (AE) nucleation appear in the heterogeneous geological rock mass system model before its fracture, the lack of uniformity and regular patterns of these phenomena across elements at different locations suggests that an integrated approach involving displacement monitoring, stress monitoring, and acoustic monitoring is insufficient for the accurate prediction of rock landslides.
- (3)
- Expanding the quantity and spatial distribution of monitoring points, along with diversifying and integrating monitoring techniques, can substantially improve the accuracy of early warning for landslides.
- (4)
- It is precisely because of the heterogeneous characteristics of rock masses that many precursor signals appear before the main fracture occurs. Effectively capturing these precursor signals enables monitoring and obtaining early warning of rock landslides.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Zhang, C.; Wang, Y.; Lin, H. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Lian, S.; Zhang, L.; Zhao, Y.; Wu, Q.; Du, C.; Wan, W. Evolution characteristics of unfrozen water content and damage for saturated sandstone during freezing–thawing cycle process based on the in-situ nuclear magnetic resonance. Bull. Eng. Geol. Environ. 2025, 84, 296. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Zuo, J.P.; Zhu, F.; Liu, H.Y.; Xu, C.Y. Non-orthogonal Failure Behavior of Roadway Surrounding Rock Subjected to Deep Complicated Stress. Rock Mech. Rock Eng. 2023, 56, 6261–6283. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Wang, W.; Wan, W.; Tang, J. Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. Int. J. Rock Mech. Min. Sci. 2017, 93, 66–75. [Google Scholar] [CrossRef]
- Yu, W.; Guo, H.; Li, K.; Pan, B. Experimental Study on Uniaxial Compression Mechanics and Failure Characteristics of Non-Through Fractured Rock. Sustainability 2023, 15, 4968. [Google Scholar] [CrossRef]
- Saito, M. Forecasting Time of Slope Failure by Tertiary Creep. In Proceedings of the 7th International Conference on Soil Mechanics and Foundations Engineering, Montreal, QC, Canada, 17–23 August 1969; Pergamon Press: Oxford, UK, 1969; pp. 667–683. [Google Scholar]
- Intrieri, E.; Carlà, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth-Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
- Solari, L.; Del Soldato, M.; Raspini, F.; Barra, A.; Bianchini, S.; Confuorto, P.; Casagli, N.; Crosetto, M. Review of Satellite Interferometry for Landslide Detection in Italy. Remote Sens. 2020, 12, 1351. [Google Scholar] [CrossRef]
- Song, J.; Leng, J.; Li, J.; Wei, H.; Li, S.; Wang, F. Application of Acoustic Emission Technique in Landslide Monitoring and Early Warning: A Review. Appl. Sci. 2025, 15, 1663. [Google Scholar] [CrossRef]
- Yin, Y.; Zheng, W.; Liu, Y.; Zhang, J.; Li, X. Integration of GPS with InSAR to monitoring of the Jiaju landslide in Sichuan, China. Landslides 2010, 7, 359–365. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Q.; Alonso-Rodriguez, A.; Subramanian, S.S.; Li, W.; Zheng, G.; Dong, X.; Huang, R. Successive landsliding and damming of the Jinsha River in eastern Tibet, China: Prime investigation, early warning, and emergency response. Landslides 2019, 16, 1003–1020. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Q.; Liu, J.; Subramanian, S.S.; He, C.; Zhu, X.; Zhou, L. Successful early warning and emergency response of a disastrous rockslide in Guizhou province, China. Landslides 2019, 16, 2445–2457. [Google Scholar] [CrossRef]
- Guo, F.; Meng, X.; Qi, T.; Dijkstra, T.; Thorkildsen, J.K.; Yue, D.; Chen, G.; Zhang, Y.; Dou, X.; Shi, P. Rapid onset hazards, fault-controlled landslides and multi-method emergency decision-making. J. Mountain Sci. 2022, 19, 1357–1369. [Google Scholar] [CrossRef]
- Huang, G.; Du, S.; Wang, D. GNSS techniques for real-time monitoring of landslides: A review. Satell. Navig. 2023, 4, 5. [Google Scholar] [CrossRef]
- Wang, G.; Kearns, T.J.; Yu, J.; Saenz, G. A stable reference frame for landslide monitoring using GPS in the Puerto Rico and Virgin Islands region. Landslides 2013, 11, 119–129. [Google Scholar] [CrossRef]
- Shu, B.; He, Y.; Wang, L.; Zhang, Q.; Li, X.; Qu, X.; Huang, G.; Qu, W. Real-time high-precision landslide displacement monitoring based on a GNSS CORS network. Measurement 2023, 217, 113056. [Google Scholar] [CrossRef]
- He, M.; Tao, Z.; Zhang, B. Application of remote monitoring technology in landslides in the Luoshan mining area. Min. Sci. Technol. 2009, 19, 609–614. [Google Scholar] [CrossRef]
- Tao, Z.; Zhu, C.; Zheng, X.; He, M. Slope stability evaluation and monitoring of Tonglushan ancient copper mine relics. Adv. Mech. Eng. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, Y.; Zhu, C.; Xu, H.; Li, G.; He, M. Mechanical evolution of constant resistance and large deformation anchor cables and their application in landslide monitoring. Bull. Eng. Geol. Environ. 2019, 78, 4787–4803. [Google Scholar] [CrossRef]
- Chae, B.-G.; Park, H.-J.; Catani, F.; Simoni, A.; Berti, M. Landslide prediction, monitoring and early warning: A concise review of state-of-the-art. Geosci. J. 2017, 21, 1033–1070. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Z.; Deng, W.; Yang, T.; Zhou, J.; Yu, Q.; Mao, Y. Rock landslide early warning system combining slope stability analysis, two-stage monitoring, and case-based reasoning: A case study. Bull. Eng. Geol. Environ. 2021, 80, 8433–8451. [Google Scholar] [CrossRef]
- Uhlemann, S.; Smith, A.; Chambers, J.; Dixon, N.; Dijkstra, T.; Haslam, E.; Meldrum, P.; Merritt, A.; Gunn, D.; Mackay, J. Assessment of ground-based monitoring techniques applied to landslide investigations. Geomorphology 2016, 253, 438–451. [Google Scholar] [CrossRef]
- Feng, Z.; Zhao, Y.; Feng, Z. Indeterminacy of displacement and stress of geologic rock mass system in the critically non-stationary state: Implication on prediction of geo-hazards. Nat. Hazards 2021, 107, 1105–1124. [Google Scholar] [CrossRef]
- Carlà, T.; Farina, P.; Intrieri, E.; Botsialas, K.; Casagli, N. On the monitoring and early-warning of brittle slope failures in hard rock masses: Examples from an open-pit mine. Eng. Geol. 2017, 228, 71–81. [Google Scholar] [CrossRef]
- Paronuzzi, P.; Bolla, A.; Rigo, E. Brittle and Ductile Behavior in Deep-Seated Landslides: Learning from the Vajont Experience. Rock Mech. Rock Eng. 2015, 49, 2389–2411. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, C.; He, M.; Dong, M.; Zhang, G.; Zhang, F. Failure Mechanism and Long Short-Term Memory Neural Network Model for Landslide Risk Prediction. Remote Sens. 2021, 14, 166. [Google Scholar] [CrossRef]
- Xu, Q.; Peng, D.; Zhang, S.; Zhu, X.; He, C.; Qi, X.; Zhao, K.; Xiu, D.; Ju, N. Successful implementations of a real-time and intelligent early warning system for loess landslides on the Heifangtai terrace, China. Eng. Geol. 2020, 278, 105817. [Google Scholar] [CrossRef]
- Feng, Z.; Lo, C.; Lin, Q. The characteristics of the seismic signals induced by landslides using a coupling of discrete element and finite difference methods. Landslides 2016, 14, 661–674. [Google Scholar] [CrossRef]
- Ye, B.; Qiu, H.; Tang, B.; Liu, Y.; Liu, Z.; Jiang, X.; Yang, D.; Ullah, M.; Zhu, Y.; Kamp, U. Creep deformation monitoring of landslides in a reservoir area. J. Hydrol. 2024, 632, 12. [Google Scholar] [CrossRef]
- Wu, Y.; Niu, R.; Wang, Y.; Chen, T. A Fast Deploying Monitoring and Real-Time Early Warning System for the Baige Landslide in Tibet, China. Sensors 2020, 20, 6619. [Google Scholar] [CrossRef]
- Tang, J.; Yang, S.; Yang, K.; Tian, W.; Liu, G.; Duan, M. Discrete Element Modeling of Thermally Damaged Sandstone Containing Two Pre-Existing Flaws at High Confining Pressure. Sustainability 2023, 15, 6318. [Google Scholar] [CrossRef]
- Lin, P.; Wong, R.H.C.; Tang, C.A. Experimental study of coalescence mechanisms and failure under uniaxial compression of granite containing multiple holes. Int. J. Rock Mech. Min. Sci. 2015, 77, 313–327. [Google Scholar] [CrossRef]
- Wang, T.; Li, P.; Tang, C.a.; Zhang, B.; Yu, J. Finite Element Analysis for the Mechanism of Stress Wave Propagation and Crack Extension Due to Blasting of a Frozen Rock Mass. Sustainability 2023, 15, 4616. [Google Scholar] [CrossRef]
- Tang, C.; Tang, S.; Gong, B.; Bai, H. Discontinuous deformation and displacement analysis: From continuous to discontinuous. Sci. China Technol. Sci. 2015, 58, 1567–1574. [Google Scholar] [CrossRef]
- Tang, C.A.; Tham, L.G.; Wang, S.H.; Liu, H.; Li, W.H. A numerical study of the influence of heterogeneity on the strength characterization of rock under uniaxial tension. Mech. Mater. 2007, 39, 326–339. [Google Scholar] [CrossRef]
- Tang, C.; Webb, A.A.G.; Moore, W.; Wang, Y.; Ma, T.; Chen, T. Breaking Earth’s shell into a global plate network. Nat. Commun. 2020, 11, 3621. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Yao, W.; Xia, K. Numerical study on tensile failures of heterogeneous rocks. J. Rock Mech. Geotech. Eng. 2020, 12, 50–58. [Google Scholar] [CrossRef]
- Bolla, A.; Paronuzzi, P. Numerical Investigation of the Pre-collapse Behavior and Internal Damage of an Unstable Rock Slope. Rock Mech. Rock Eng. 2019, 53, 2279–2300. [Google Scholar] [CrossRef]
- Vyazmensky, A.; Stead, D.; Elmo, D.; Moss, A. Numerical Analysis of Block Caving-Induced Instability in Large Open Pit Slopes: A Finite Element/Discrete Element Approach. Rock Mech. Rock Eng. 2009, 43, 21–39. [Google Scholar] [CrossRef]
- Xu, Q. Understanding the landslide monitoring and early warning: Consideration to practical issues. J. Eng. Geol. 2020, 28, 360–374. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, Y. Retrospection on the development of rock mass mechanics and the summary of some unsolved centennial problems. Chin. J. Rock Mech. Eng. 2021, 40, 1297–1336. (In Chinese) [Google Scholar] [CrossRef]
- Guo, Q.; Hong, W.; Xi, X.; Pan, J.; Zhang, Y.; Wang, S. Effect of Heterogeneity on the Failure of Rock with an Initial Crack under Uniaxial Compressions: A Numerical Study. Lithosphere 2022, 2022, 6518010. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Chen, X.; Huang, C.; Tang, C. Fracture Process in Conceptual Numerical Geological Rock Mass System Model and Its Implications for Landslide Monitoring and Early Warning. Sustainability 2025, 17, 8408. https://doi.org/10.3390/su17188408
Tang L, Chen X, Huang C, Tang C. Fracture Process in Conceptual Numerical Geological Rock Mass System Model and Its Implications for Landslide Monitoring and Early Warning. Sustainability. 2025; 17(18):8408. https://doi.org/10.3390/su17188408
Chicago/Turabian StyleTang, Liming, Xu Chen, Chao Huang, and Chunan Tang. 2025. "Fracture Process in Conceptual Numerical Geological Rock Mass System Model and Its Implications for Landslide Monitoring and Early Warning" Sustainability 17, no. 18: 8408. https://doi.org/10.3390/su17188408
APA StyleTang, L., Chen, X., Huang, C., & Tang, C. (2025). Fracture Process in Conceptual Numerical Geological Rock Mass System Model and Its Implications for Landslide Monitoring and Early Warning. Sustainability, 17(18), 8408. https://doi.org/10.3390/su17188408







