Evaluating and Optimizing Water Resources Carrying Capacity in Anji County, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Data Source
2.3. Research Methods
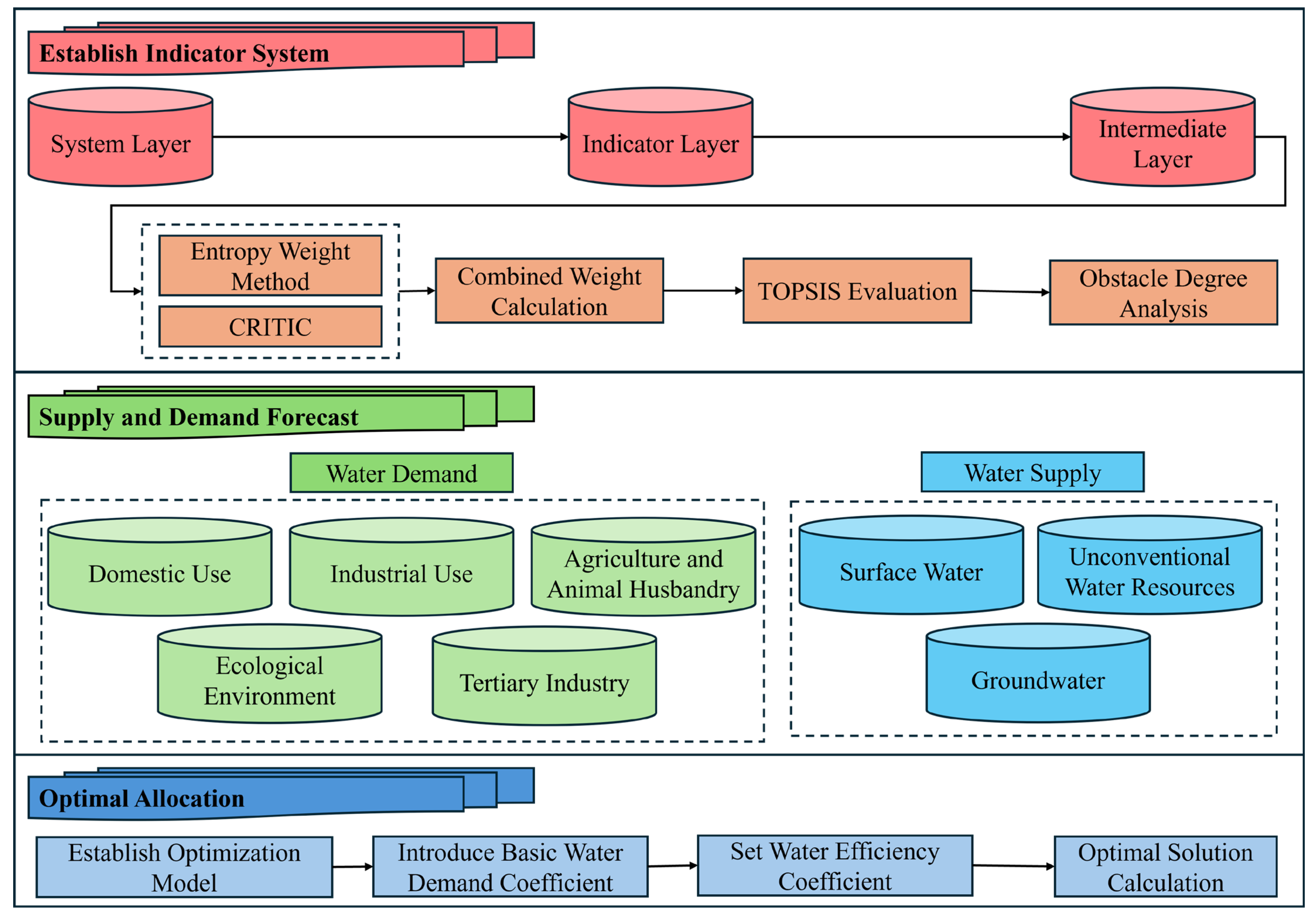
2.3.1. WRCC Evaluation Method
Indicator System Construction
Entropy Weight Method
CRITIC Method
Calculation of Combined Weights
TOPSIS Model Evaluation and Calculation
Obstacle Factor Analysis of WRCC
2.3.2. Methods for Forecasting Water Supply and Demand
Water Demand Forecasting
Water Supply Forecast
2.3.3. Water Resource Optimization Allocation Method
3. Results
3.1. Evaluation of WRCC
3.1.1. Analysis of Indicator Influence in the Evaluation
3.1.2. Analysis of Evaluation Results
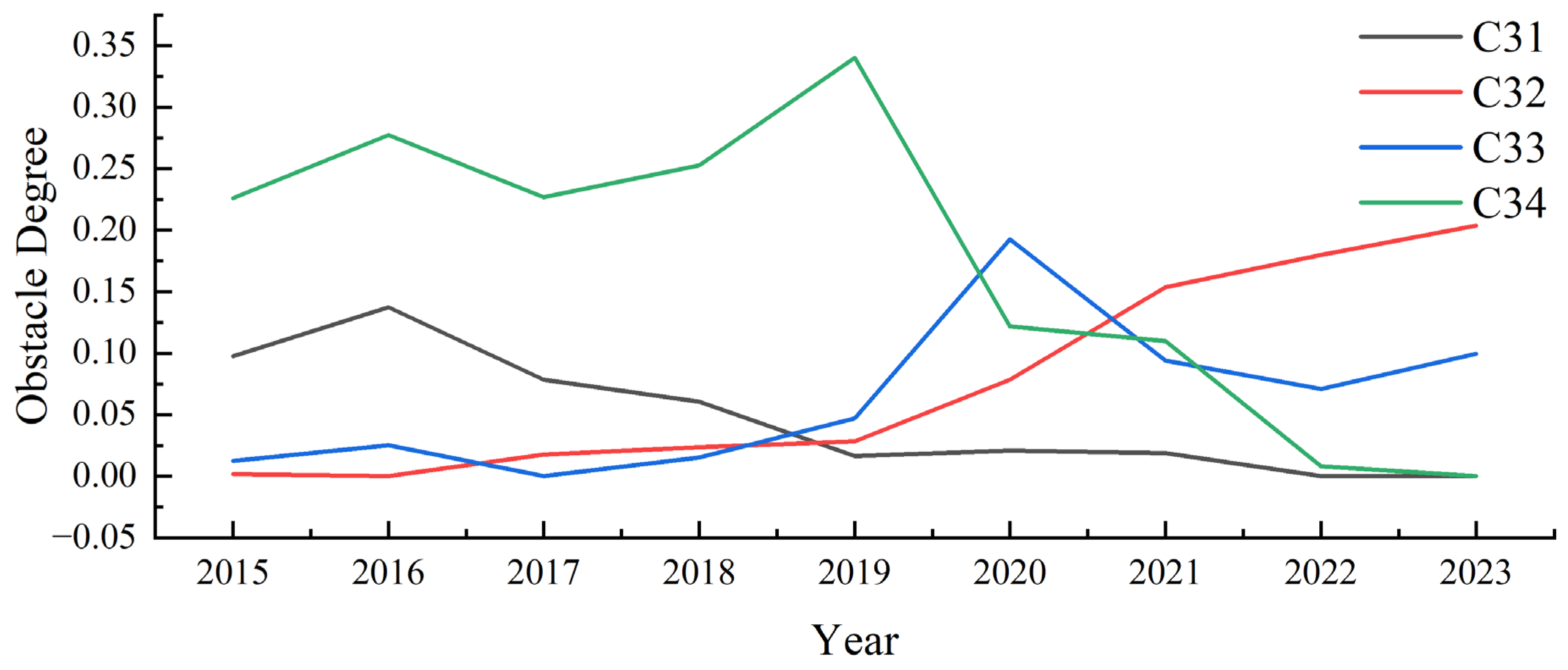
3.1.3. Analysis of Obstacle Degree Results
3.2. Analysis of Water Supply–Demand Balance
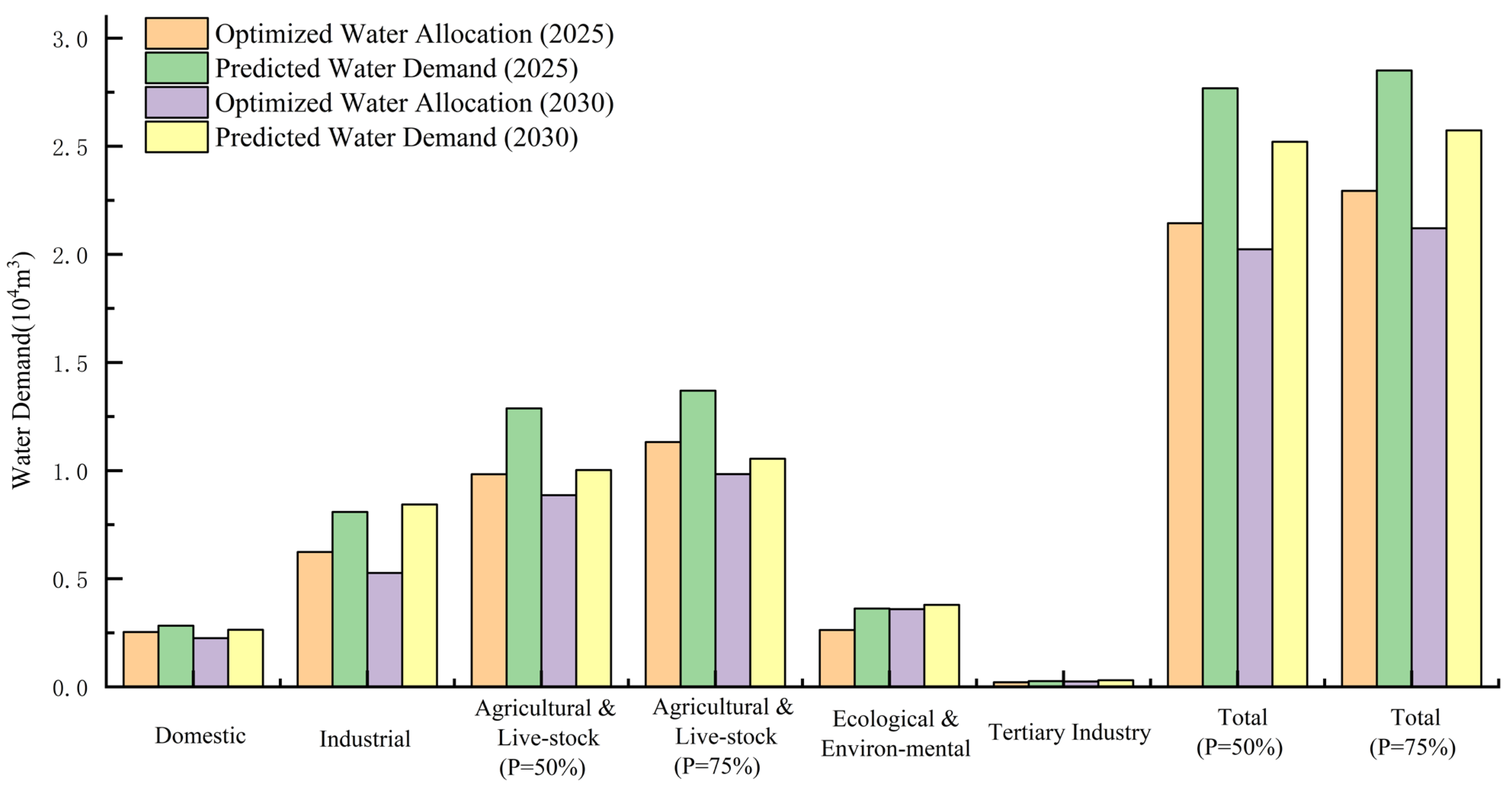
3.3. Optimal Allocation of Water Resources
4. Discussion
5. Conclusions
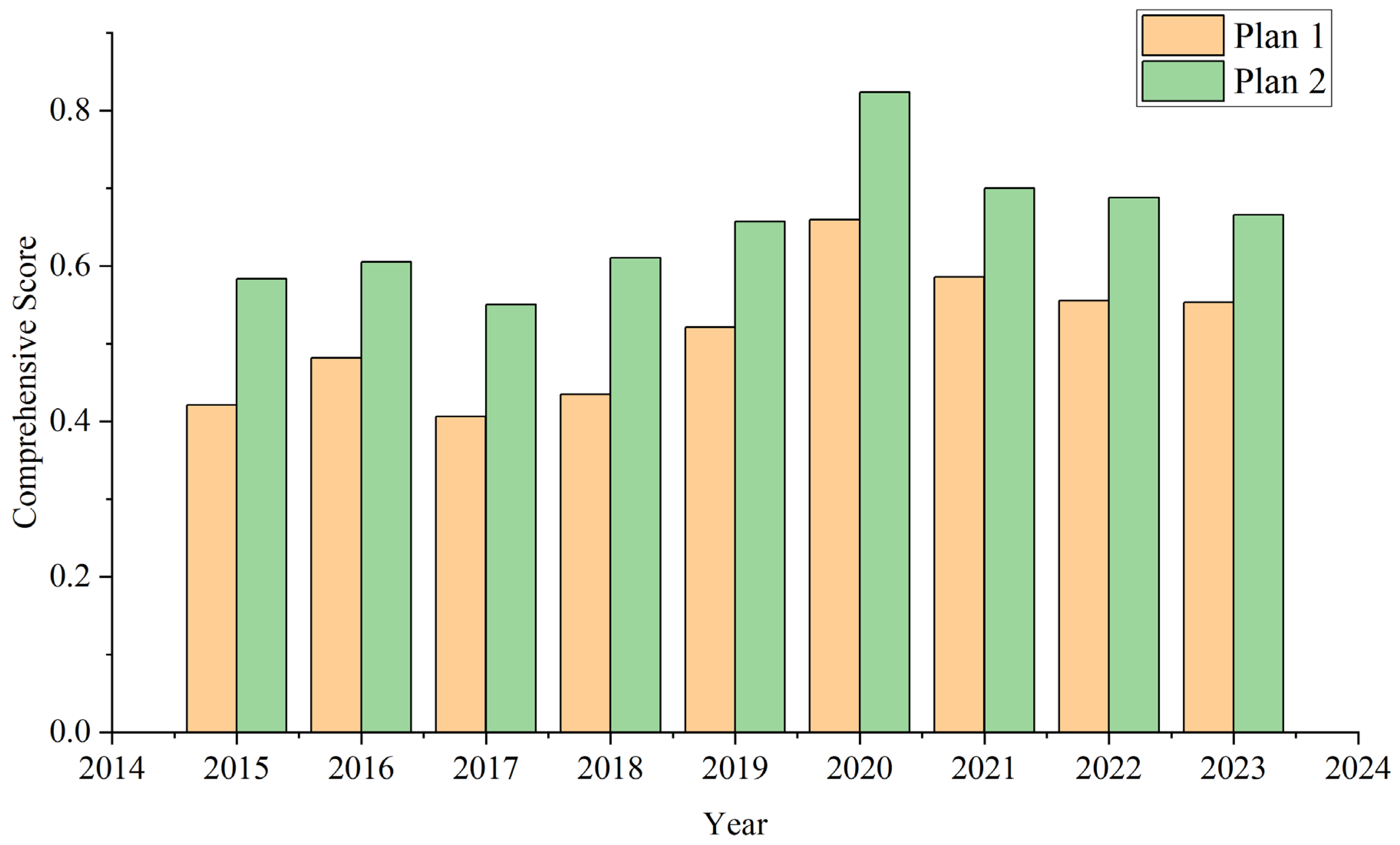
- Water resource carrying capacity is tight and exhibits significant volatility. During the study period, Anji County was classified as being in a “near overload” state for most years, with an average comprehensive evaluation score of 0.5135, indicating that the water supply–demand relationship was approaching saturation. While performance in 2020 was relatively favorable, a decline was observed again in 2023, highlighting the region’s periodic vulnerability and the dynamic imbalance risks of its water resource system.
- Key constraint factors are concentrated in wastewater reuse and water consumption per unit output. Obstacle degree analysis revealed that the wastewater reuse rate (C34) and water consumption per unit of industrial output (C24) were major limiting factors for improving water resource carrying capacity in multiple years, indicating substantial room for enhancing water use efficiency. Additionally, since 2021, the per capita water resource availability (C11) has gradually emerged as a major constraint and warrants close attention.
- Forecasts show phased supply–demand balance improvement, yet structural weaknesses remain. Under average hydrological conditions (P = 50%), Anji County is projected to achieve a water surplus by 2030. However, dry-year water shortages persist (P = 75%). The situation is especially acute in 2025, with a projected shortage rate of 23%, reflecting the limited capacity of the water supply system to withstand extreme climatic events.
- Optimized water resource allocation significantly enhances system carrying capacity. By developing a multi-source, multi-objective linear programming model based on maximizing net benefits, the study achieved rational allocation across domestic, industrial, agricultural, ecological, and tertiary-sector water uses, thereby maximizing resource utilization efficiency. After optimization, water allocation became more balanced, TOPSIS evaluation scores improved overall, and the water resource carrying capacity levels were notably enhanced, demonstrating the effectiveness of scientific allocation in alleviating water resource constraints.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, B.; Jiang, H.; Zou, Y.; Liu, Y.; Mu, R.; Wang, H. An Integrated Model for Optimal Water Resources Allocation under “3 Redlines” Water Policy of the Upper Hanjiang River Basin. J. Hydrol-Reg. Stud. 2022, 42, 101167. [Google Scholar] [CrossRef]
- Chen, H.; Huang, S.; Qiu, H.; Xu, Y.P.; Teegavarapu, R.S.V.; Guo, Y.; Nie, H.; Xie, H.; Xie, J.; Shao, Y.; et al. Assessment of Ecological Flow in River Basins at a Global Scale: Insights on Baseflow Dynamics and Hydrological Health. Ecol. Indic. 2025, 178, 113868. [Google Scholar] [CrossRef]
- Li, P.; Wu, J. Water Resources and Sustainable Development. Water 2023, 16, 134. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Wang, Y. Comprehensive Evaluation and Influencing Factors of Urban Agglomeration Water Resources Carrying Capacity. J. Clean. Prod. 2021, 288, 125097. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, S.; Gao, C. Dynamic Simulation and Comprehensive Evaluation of the Water Resources Carrying Capacity in Guangzhou City, China. Ecol. Indic. 2022, 135, 108528. [Google Scholar] [CrossRef]
- Chen, H.; Xu, B.; Qiu, H.; Huang, S.; Teegavarapu, R.S.V.; Xu, Y.P.; Guo, Y.; Nie, H.; Xie, H. Adaptive Assessment of Reservoir Scheduling to Hydrometeorological Comprehensive Dry and Wet Condition Evolution in a Multi-Reservoir Region of Southeastern China. J. Hydrol. 2025, 648, 132392. [Google Scholar] [CrossRef]
- Gao, J.; Wang, L. Embedding Spatiotemporal Changes in Carbon Storage into Urban Agglomeration Ecosystem Management-A Case Study of the Yangtze River Delta, China. J. Clean. Prod. 2019, 237, 117764. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Xi, S.; Liu, J.; Li, J.; Hou, S.; Chen, B. Multi-Objective Optimization of Energy-Water Nexus from Spatial Resource Reallocation Perspective in China. Appl. Energy 2022, 314, 118919. [Google Scholar] [CrossRef]
- Li, J.; Meng, Z.; Zhang, J.; Chen, Y.; Yao, J.; Li, X.; Qin, P.; Liu, X.; Cheng, C. Prediction of Seawater Intrusion Run-Up Distance Based on K-Means Clustering and ANN Model. J. Mar. Sci. Eng. 2025, 13, 377. [Google Scholar] [CrossRef]
- Chu, J.; Wang, Z.; Bao, X.; Yao, Z.; Cui, X. Addressing the Contradiction between Water Supply and Demand: A Study on Multi-Objective Regional Water Resources Optimization Allocation. Environ. Dev. Sustain. 2024. [Google Scholar] [CrossRef]
- Li, J.; Xia, F.; Yang, D.; Huo, J. Comprehensive Evaluation of Water Resource Carrying Capacity in Northwest China. Water 2024, 17, 67. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Song, Y. Comprehensive Comparison and Assessment of Three Models Evaluating Water Resource Carrying Capacity in Beijing, China. Ecol. Indic. 2022, 143, 109305. [Google Scholar] [CrossRef]
- Li, W.; Jiang, S.; Zhao, Y.; Li, H.; Zhu, Y.; Ling, M.; Qi, T.; He, G.; Yao, Y.; Wang, H. Comprehensive Evaluation and Scenario Simulation of Water Resources Carrying Capacity: A Case Study in Xiong’an New Area, China. Ecol. Indic. 2023, 150, 110253. [Google Scholar] [CrossRef]
- Yang, Z.; Song, J.; Cheng, D.; Xia, J.; Li, Q.; Ahamad, M.I. Comprehensive Evaluation and Scenario Simulation for the Water Resources Carrying Capacity in Xi’an City, China. J. Environ. Manag. 2019, 230, 221–233. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Xiao, C.; Qi, Z.; Meng, F.; Liang, X. Development Tendency Analysis for the Water Resource Carrying Capacity Based on System Dynamics Model and the Improved Fuzzy Comprehensive Evaluation Method in the Changchun City, China. Ecol. Indic. 2021, 122, 107232. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, X.; Wang, X.; Jin, Z.; Chen, F. Multi-Level Fuzzy Comprehensive Evaluation for Water Resources Carrying Capacity in Xuzhou City, China. Sustainability 2023, 15, 11369. [Google Scholar] [CrossRef]
- Zhou, K. Comprehensive Evaluation on Water Resources Carrying Capacity Based on Improved AGA-AHP Method. Appl. Water Sci. 2022, 12, 103. [Google Scholar] [CrossRef]
- Su, Y.; Xu, X.; Dai, M.; Hu, Y.; Li, Q.; Shu, S. A Comprehensive Evaluation of Water Resource Carrying Capacity Based on the Optimized Projection Pursuit Regression Model: A Case Study from China. Water 2024, 16, 2650. [Google Scholar] [CrossRef]
- Deng, L.; Yin, J.; Tian, J.; Li, Q.; Guo, S. Comprehensive Evaluation of Water Resources Carrying Capacity in the Han River Basin. Water 2021, 13, 249. [Google Scholar] [CrossRef]
- Liu, D.; Chen, X.; Lou, Z. A Model for the Optimal Allocation of Water Resources in a Saltwater Intrusion Area: A Case Study in Pearl River Delta in China. Water Resour. Manag. 2010, 24, 63–81. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, P.; Zhang, G. Multi-Objective Optimal Allocation of Water Resources in Yangchangwan Mining Area Based on Ecological Priority. E3S Web Conf. 2021, 260, 01004. [Google Scholar] [CrossRef]
- Li, C.; Tian, X.; Cao, Z.; Wang, Y. Research on Optimal Allocation of Water Resources in the Western Mining Area of China Based on WEAP. Appl. Water Sci. 2022, 12, 113. [Google Scholar] [CrossRef]
- Ma, J.; Liu, H.; Wu, W.; Zhang, Y.; Dong, S. Research on Optimal Allocation of Water Resources in Handan City Based on the Refined Water Resource Allocation Model. Water 2022, 15, 154. [Google Scholar] [CrossRef]
- Luo, Y.; Sha, J.; Liu, B.; Zhang, Y.; Yang, J. Optimal Allocation of Water Resources Based on GWAS Model in Handan, China. Water 2023, 15, 1090. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, J.; Feng, K. Optimal Allocation of Regional Water Resources Based on Simulated Annealing Particle Swarm Optimization Algorithm. Energy Rep. 2022, 8, 9119–9126. [Google Scholar] [CrossRef]
- Guo, W.; Sha, J.; Xu, D.; Liu, S.; Wang, C.; Li, K. Application of MOHUS in Multi-Objective Optimal Allocation of Water Resources for the Central Route South-to-North Water Diversion Project in Hebei Province, China. Water 2025, 17, 1612. [Google Scholar] [CrossRef]
- He, H.; Chen, A.; Yin, M.; Ma, Z.; You, J.; Xie, X.; Wang, Z.; An, Q. Optimal Allocation Model of Water Resources Based on the Prospect Theory. Water 2019, 11, 1289. [Google Scholar] [CrossRef]
- De Paula Fontainhas Bandeira, A.; Mendes, C.A.B. Optimization Water Allocation Model to Natural Resources Exploration. In Proceedings of the World Environmental and Water Resources Congress, Austin, TX, USA, 17 May 2015; American Society of Civil Engineers: Reston, VA, USA, 2015; pp. 2320–2329. [Google Scholar] [CrossRef]
- Wang, J.; Hou, B.; Jiang, D.; Xiao, W.; Wu, Y.; Zhao, Y.; Zhou, Y.; Guo, C.; Wang, G. Optimal Allocation of Water Resources Based on Water Supply Security. Water 2016, 8, 237. [Google Scholar] [CrossRef]
- Liu, P.; Lü, S.; Han, Y.; Wang, F.; Tang, L. Comprehensive Evaluation on Water Resources Carrying Capacity Based on Water-Economy-Ecology Concept Framework and EFAST-Cloud Model: A Case Study of Henan Province, China. Ecol. Indic. 2022, 143, 109392. [Google Scholar] [CrossRef]
- Yang, G.; Dong, Z.; Feng, S.; Li, B.; Sun, Y.; Chen, M. Early Warning of Water Resource Carrying Status in Nanjing City Based on Coordinated Development Index. J. Clean. Prod. 2021, 284, 124696. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R. A Novel Plithogenic TOPSIS- CRITIC Model for Sustainable Supply Chain Risk Management. J. Clean. Prod. 2020, 247, 119586. [Google Scholar] [CrossRef]
- Al-Aomar, R. A Combined AHP-ENTROPY Method for Deriving Subjective and Objective Criteria Weights. Int. J. Ind. Eng. Theory Appl. Pract. 2010, 17, 12–24. [Google Scholar] [CrossRef]
- Keyvanfar, M.; Janatrostami, S.; Ashrafzadeh, A. A Comprehensive Assessment of Water Resources Carrying Capacity in Anzali Wetland Using AHP-Entropy-CRITIC Combined Weighting Method and TOPSIS-GRA Model. Iran. J. Soil. Water Res. 2025, 56, 105–126. [Google Scholar] [CrossRef]
- Zafar, S.; Alamgir, Z.; Rehman, M.H. An Effective Blockchain Evaluation System Based on Entropy-CRITIC Weight Method and MCDM Techniques. Peer-to-Peer Netw. Appl. 2021, 14, 3110–3123. [Google Scholar] [CrossRef]
- Wei, Z.; Ji, D.; Yang, L. Comprehensive Evaluation of Water Resources Carrying Capacity in Henan Province Based on Entropy Weight TOPSIS—Coupling Coordination—Obstacle Model. Environ. Sci. Pollut. Res. 2023, 30, 115820–115838. [Google Scholar] [CrossRef]
- Zhang, Q.; Qian, H.; Xu, P.; Hou, K.; Yang, F. Groundwater Quality Assessment Using a New Integrated-Weight Water Quality Index (IWQI) and Driver Analysis in the Jiaokou Irrigation District, China. Ecotox Environ. Safe 2021, 212, 111992. [Google Scholar] [CrossRef]
- Lv, B.; Liu, C.; Li, T.; Meng, F.; Fu, Q.; Ji, Y.; Hou, R. Evaluation of the Water Resource Carrying Capacity in Heilongjiang, Eastern China, Based on the Improved TOPSIS Model. Ecol. Indic. 2023, 150, 110208. [Google Scholar] [CrossRef]
- Du, L.; Niu, Z.; Zhang, R.; Zhang, J.; Jia, L.; Wang, L. Evaluation of Water Resource Carrying Potential and Barrier Factors in Gansu Province Based on Game Theory Combined Weighting and Improved TOPSIS Model. Ecol. Indic. 2024, 166, 112438. [Google Scholar] [CrossRef]
- Chung, E.-S.; Abdulai, P.J.; Park, H.; Kim, Y.; Ahn, S.R.; Kim, S.J. Multi-Criteria Assessment of Spatial Robust Water Resource Vulnerability Using the TOPSIS Method Coupled with Objective and Subjective Weights in the Han River Basin. Sustainability 2017, 9, 29. [Google Scholar] [CrossRef]
- Xia, B.; Juliang, J.; Rongxing, Z.; Chengguo, W.; Yuliang, Z.; Libing, Z.; Yi, C. Coordination Evaluation and Obstacle Factors Recognition Analysis of Water Resource Spatial Equilibrium System. Environ. Res. 2022, 210, 112913. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, Z.; Di, D.; Wang, H. Water Resources Allocation Based on Water Resources Supply-Demand Forecast and Comprehensive Values of Water Resources. J. Hydrol. Reg. Stud. 2023, 47, 101421. [Google Scholar] [CrossRef]
- Ruijs, A.; Kortelainen, M.; Wossink, A.; Schulp, C.J.E.; Alkemade, R. Opportunity Cost Estimation of Ecosystem Services. Environ. Resour. Econ. 2017, 66, 717–747. [Google Scholar] [CrossRef]
- Cui, Y.; Feng, P.; Jin, J.; Liu, L. Water Resources Carrying Capacity Evaluation and Diagnosis Based on Set Pair Analysis and Improved the Entropy Weight Method. Entropy 2018, 20, 359. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, H.; Wang, Y.; Yang, Y. Evaluation of Water Environmental Carrying Capacity of City in Huaihe River Basin Based on the AHP Method: A Case in Huai’an City. Water Resour. Ind. 2017, 18, 71–77. [Google Scholar] [CrossRef]
- Yang, M.; Qu, D.; Shen, Y.; Yang, S.; Liu, B.; Lu, W. Evaluation of Water Resources Carrying Capacity of Zhangye City Based on Combined Weights and TOPSIS Modeling. Water 2023, 15, 4229. [Google Scholar] [CrossRef]
- Ren, B.; Zhang, Q.; Ren, J.; Ye, S.; Yan, F. A Novel Hybrid Approach for Water Resources Carrying Capacity Assessment by Integrating Fuzzy Comprehensive Evaluation and Analytical Hierarchy Process Methods with the Cloud Model. Water 2020, 12, 3241. [Google Scholar] [CrossRef]
- Peng, T.; Deng, H. Comprehensive Evaluation on Water Resource Carrying Capacity in Karst Areas Using Cloud Model with Combination Weighting Method: A Case Study of Guiyang, Southwest China. Environ. Sci. Pollut. Res. 2020, 27, 37057–37073. [Google Scholar] [CrossRef] [PubMed]
- Chi, M.; Zhang, D.; Fan, G.; Zhang, W.; Liu, H. Prediction of Water Resource Carrying Capacity by the Analytic Hierarchy Process-Fuzzy Discrimination Method in a Mining Area. Ecol. Indic. 2019, 96, 647–655. [Google Scholar] [CrossRef]
- Deng, L.; Guo, S.; Yin, J.; Zeng, Y.; Chen, K. Multi-Objective Optimization of Water Resources Allocation in Han River Basin (China) Integrating Efficiency, Equity and Sustainability. Sci. Rep. 2022, 12, 798. [Google Scholar] [CrossRef]
- Feng, T.; Liu, B.; Ren, H.; Yang, J.; Zhou, Z. Optimized Model for Coordinated Development of Regional Sustainable Agriculture Based on Water–Energy–Land–Carbon Nexus System: A Case Study of Sichuan Province. Energ. Convers. Manag. 2023, 291, 117261. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, K.; Li, L.; Lei, Y.; Wu, S.; Wang, F.; Luo, J. The Optimal Allocation and the Evaluation of Water Resources Carrying Capacity in Shendong Mining Area. Resour. Policy 2022, 77, 102738. [Google Scholar] [CrossRef]
- Zhu, Q.; Cao, Y. Research on Provincial Water Resources Carrying Capacity and Coordinated Development in China Based on Combined Weighting TOPSIS Model. Sci. Rep. 2024, 14, 12497. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Fu, Z.; Fang, Y.; Zhao, X.; Ding, X.; Huang, J.; Liu, Z.; Fu, X.; Liu, J. Spatial-Temporal Evaluation and Prediction of Water Resources Carrying Capacity in the Xiangjiang River Basin Using County Units and Entropy Weight TOPSIS-BP Neural Network. Sustainability 2024, 16, 8184. [Google Scholar] [CrossRef]
- Fu, Z.; Dong, J.; Zhang, J.; Guo, Y.; Zhang, Y.; Jiang, X.; Wang, H.; Wang, S. A Novel Energy-Water-Carbon Coupling System Optimization Management Model Based on Water Environmental Carrying Capacity under the Influence of Climate Change. Energy Strateg. Rev. 2024, 53, 101424. [Google Scholar] [CrossRef]
- Wu, L.; Su, X.; Ma, X.; Kang, Y.; Jiang, Y. Integrated Modeling Framework for Evaluating and Predicting the Water Resources Carrying Capacity in a Continental River Basin of Northwest China. J. Clean. Prod. 2018, 204, 366–379. [Google Scholar] [CrossRef]

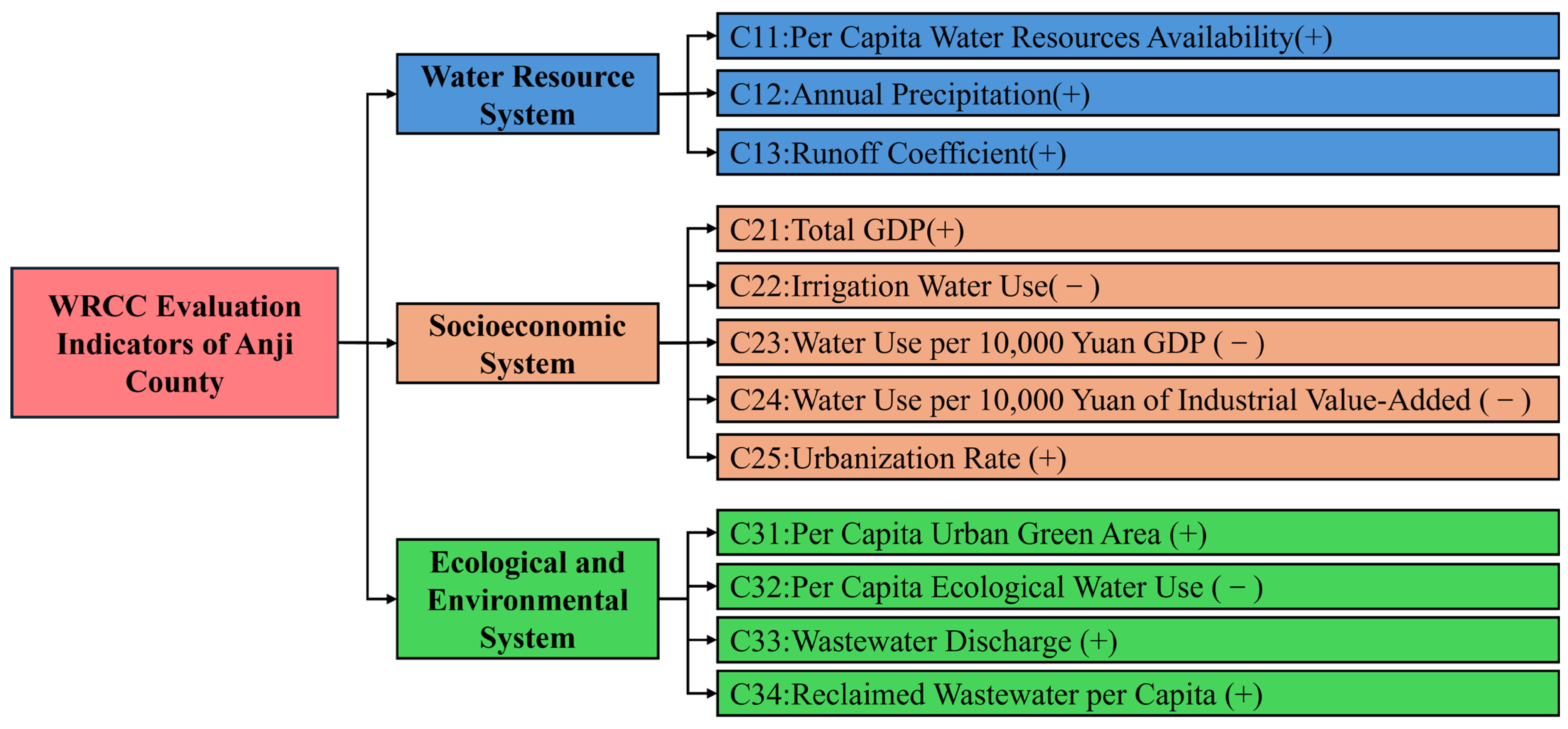
| Data Category | Main Indicators | Data Sources | Years |
|---|---|---|---|
| Water Resource System | Per capita water resources (C11), annual precipitation (C12), water yield coefficient (C13) | Anji County Water Resources Bulletin, https://www.anji.gov.cn/xxgk/bmxxgk/xtjj/fdzdgknr/jjhshfztjxx/tjgb/index.html (accessed on 15 March 2024) | 2019–2023 |
| Socioeconomic System | Total GDP (C21), irrigation water use for farmland (C22), water consumption per 10,000 RMB GDP (C23), water consumption per 10,000 RMB of industrial added value (C24), urbanization rate (C25) | Huzhou Statistical Yearbook, https://tjj.huzhou.gov.cn/col/col1229208257/index.html (accessed on 15 March 2024) | 2019–2023 |
| Ecological and Environmental System | Per capita public green space area (C31), per capita ecological and environmental water use (C32), return water volume (C33), reclaimed wastewater volume (C34) | Huzhou Bureau of Ecology and Environment, Anji County Statistics, Anji County “14th Five-Year” Water Resources Development Plan | 2019–2023 |
| Closeness Coefficient Interval | Level | Description |
|---|---|---|
| (0, 0.2) | Severely Overloaded | The region has a very low level of WRCC, with significant contradictions and imbalances. |
| [0.2, 0.4) | Slightly Overloaded | Water resource utilization efficiency in certain areas needs improvement, and the current state of water resources has suffered to some extent. |
| [0.4, 0.6) | Near Overload | The carrying capacity is moderate but shows signs of gradual weakening. |
| [0.6, 0.8) | Well-Carrying | The region has a relatively strong water supply capacity, sufficient to support the expansion and prosperity of socioeconomic activities. |
| [0.8, 1) | Surplus Carrying | The area possesses abundant water resources, which are highly conducive to promoting socioeconomic development. |
| Year | Domestic Water Demand | Industrial Water Demand | Agricultural & Livestock Water Demand | Ecological & Environmental Water Demand | Tertiary Industry Water Demand | Total Water Demand | ||
|---|---|---|---|---|---|---|---|---|
| P = 50% | P = 75% | P = 50% | P = 75% | |||||
| 2025 | 0.2828 | 0.8088 | 1.2876 | 1.3695 | 0.3624 | 0.0267 | 2.7683 | 2.8502 |
| 2030 | 0.2644 | 0.8437 | 1.0023 | 1.0551 | 0.3796 | 0.0305 | 2.5206 | 2.5733 |
| Year | Surface Water Supply | Groundwater Supply | Non-Conventional Water Supply | Total Supply | ||
|---|---|---|---|---|---|---|
| P = 50% | P = 75% | P = 50% | P = 75% | |||
| 2025 | 2.0727 | 1.9535 | 0.0800 | 0.2190 | 2.3417 | 2.1525 |
| 2030 | 2.3831 | 1.6698 | 0.1000 | 0.3650 | 2.8481 | 2.1348 |
| Sector | Domestic Water Use | Agricultural Water Use | Industrial Water Use | Ecological and Environmental Water Use | Tertiary Industry Water Use |
|---|---|---|---|---|---|
| Water Use Benefit Coefficient | 1.00 | 0.36 | 4.43 | 0.18 | 10.00 |
| Goal Level (A) | Criterion Level (B) | Indicator (C) | Entropy Method Weight (w1) | CRITIC Method Weight (w2) | Multiplicative Method | Additive Method |
|---|---|---|---|---|---|---|
| WRCC of Anji County | Water Resource System | Per Capita Water Resource Availability (C11) | 0.0992 | 0.1215 | 0.1084 | 0.1068 |
| Annual Precipitation (C12) | 0.0901 | 0.0760 | 0.0848 | 0.0831 | ||
| Water Yield Coefficient (C13) | 0.0896 | 0.0796 | 0.0865 | 0.0846 | ||
| Production and Living System | Total GDP (C21) | 0.0778 | 0.0688 | 0.0750 | 0.0733 | |
| Irrigation Water Use for Farmland (C22) | 0.0686 | 0.0701 | 0.0710 | 0.0694 | ||
| Water Consumption per 10,000 RMB of GDP (C23) | 0.0705 | 0.0703 | 0.0735 | 0.0718 | ||
| Water Consumption per 10,000 RMB of Industrial Added Value (C24) | 0.0833 | 0.0780 | 0.0825 | 0.0806 | ||
| Urbanization Rate (C25) | 0.0501 | 0.0743 | 0.0625 | 0.0622 | ||
| Ecological and Environmental System | Per Capita Public Green Space Area (C31) | 0.0629 | 0.0743 | 0.0700 | 0.0686 | |
| Per Capita Ecological and Environmental Water Use (C32) | 0.0605 | 0.1051 | 0.0816 | 0.0828 | ||
| Return Water Volume (C33) | 0.0424 | 0.0894 | 0.0630 | 0.0659 | ||
| Reclaimed Wastewater Volume (C34) | 0.2119 | 0.0898 | 0.1413 | 0.1509 |
| Year | Distance to Positive Ideal Solution | Distance to Negative Ideal Solution | Comprehensive Score Index | Evaluation Grade |
|---|---|---|---|---|
| 2015 | 0.2256 | 0.1644 | 0.4215 | On the Verge of Overload |
| 2016 | 0.2069 | 0.1923 | 0.4817 | On the Verge of Overload |
| 2017 | 0.2269 | 0.1555 | 0.4067 | On the Verge of Overload |
| 2018 | 0.1986 | 0.1535 | 0.4359 | On the Verge of Overload |
| 2019 | 0.1689 | 0.1840 | 0.5215 | On the Verge of Overload |
| 2020 | 0.1109 | 0.2147 | 0.6595 | Well Within Carrying Capacity |
| 2021 | 0.1443 | 0.2042 | 0.5859 | On the Verge of Overload |
| 2022 | 0.1770 | 0.2211 | 0.5554 | On the Verge of Overload |
| 2023 | 0.1824 | 0.2261 | 0.5535 | On the Verge of Overload |
| Year | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 2015 | C34 | C24 | C21 | C23 | C22 |
| 2016 | C34 | C24 | C31 | C21 | C23 |
| 2017 | C34 | C12 | C13 | C22 | C24 |
| 2018 | C34 | C25 | C13 | C24 | C21 |
| 2019 | C34 | C12 | C25 | C21 | C24 |
| 2020 | C33 | C34 | C12 | C25 | C13 |
| 2021 | C11 | C32 | C13 | C34 | C12 |
| 2022 | C11 | C13 | C12 | C32 | C33 |
| 2023 | C11 | C13 | C32 | C12 | C33 |
| Year | Water Demand | Water Supply | Supply–Demand Balance (Surplus (−)/Deficit (+)) | Water Shortage Rate (%) | ||||
|---|---|---|---|---|---|---|---|---|
| P = 50% | P = 75% | P = 50% | P = 75% | P = 50% | P = 75% | P = 50% | P = 75% | |
| 2025 | 2.7683 | 2.8502 | 2.3417 | 2.1525 | 0.4266 | 0.6977 | 17.3% | 23.0% |
| 2030 | 2.5206 | 2.5733 | 2.8481 | 2.1348 | −0.0527 | 0.1385 | / | 6.1% |
| Planning Year | Supply–Demand Balance | Domestic Use | Industrial Use | Agricultural Use | Ecological Use | Tertiary Industry | Total | ||
|---|---|---|---|---|---|---|---|---|---|
| 50% | 75% | 50% | 75% | ||||||
| 2025 | Water Demand | 0.2534 | 0.6234 | 0.9832 | 1.1322 | 0.2633 | 0.021 | 2.1443 | 2.2933 |
| Surface Water | 0.2534 | 0.3334 | 0.7247 | 0.8320 | 0.1623 | 0.021 | 1.4948 | 1.7021 | |
| Groundwater | 0 | 0.06 | 0 | 0 | 0 | 0 | 0.06 | 0.06 | |
| Reclaimed Water from Wastewater Treatment | 0 | 0 | 0.0585 | 0.0002 | 0.101 | 0 | 0.1595 | 0.1012 | |
| Water Shortage | 0 | 0.23 | 0.1 | 0.3 | 0 | 0 | 0.33 | 0.53 | |
| 2030 | Water Demand | 0.2257 | 0.5266 | 0.8864 | 0.9838 | 0.3596 | 0.025 | 2.0233 | 2.1207 |
| Surface Water | 0.2257 | 0.2286 | 0.7042 | 0.7864 | 0.2017 | 0.025 | 1.3852 | 1.5656 | |
| Groundwater | 0 | 0.08 | 0 | 0 | 0 | 0 | 0.08 | 0.08 | |
| Reclaimed Water from Wastewater Treatment | 0 | 0 | 0.0822 | 0.0074 | 0.1579 | 0 | 0.2401 | 0.2053 | |
| Water Shortage | 0 | 0.218 | 0.1 | 0.19 | 0 | 0 | 0.318 | 0.408 | |
| Sector | Optimized 2025 | Predicted 2025 | Δ2025 | Optimized 2030 | Predicted 2030 | Δ2030 |
|---|---|---|---|---|---|---|
| Domestic | 0.2534 | 0.2828 | −0.0294 | 0.2257 | 0.2644 | −0.0387 |
| Industrial | 0.6234 | 0.8088 | −0.1854 | 0.5266 | 0.8437 | −0.3171 |
| Agricultural (P = 50%) | 0.9832 | 1.2876 | −0.3044 | 0.8864 | 1.0023 | −0.1159 |
| Agricultural (P = 75%) | 1.1322 | 1.3695 | −0.2373 | 0.9838 | 1.0551 | −0.0713 |
| Ecological & Environmental | 0.2633 | 0.3624 | −0.0991 | 0.3596 | 0.3796 | −0.0200 |
| Tertiary Industry | 0.021 | 0.0267 | −0.0057 | 0.025 | 0.0305 | −0.0055 |
| Total (P = 50%) | 2.1443 | 2.7683 | −0.6240 | 2.0233 | 2.5206 | −0.4973 |
| Total (P = 75%) | 2.2933 | 2.8502 | −0.5569 | 2.1207 | 2.5733 | −0.4526 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, H.; Liu, W.; Wei, F.; Chen, Y.; Xu, C.; Wang, Z.; Wang, Y.; Tan, J.; Wei, W.; Chen, H. Evaluating and Optimizing Water Resources Carrying Capacity in Anji County, China. Sustainability 2025, 17, 8383. https://doi.org/10.3390/su17188383
Qiu H, Liu W, Wei F, Chen Y, Xu C, Wang Z, Wang Y, Tan J, Wei W, Chen H. Evaluating and Optimizing Water Resources Carrying Capacity in Anji County, China. Sustainability. 2025; 17(18):8383. https://doi.org/10.3390/su17188383
Chicago/Turabian StyleQiu, Haodong, Wenlong Liu, Fusen Wei, Yijing Chen, Chuyu Xu, Zhongwei Wang, Yukun Wang, Jiaqi Tan, Wencheng Wei, and Hao Chen. 2025. "Evaluating and Optimizing Water Resources Carrying Capacity in Anji County, China" Sustainability 17, no. 18: 8383. https://doi.org/10.3390/su17188383
APA StyleQiu, H., Liu, W., Wei, F., Chen, Y., Xu, C., Wang, Z., Wang, Y., Tan, J., Wei, W., & Chen, H. (2025). Evaluating and Optimizing Water Resources Carrying Capacity in Anji County, China. Sustainability, 17(18), 8383. https://doi.org/10.3390/su17188383






