Scenario Simulation and Comprehensive Evaluation of Coupling Coordination Relationship Between Regional Water Use and Water Environmental Protection: A Case Study of Tianjin, China
Abstract
1. Introduction
2. Materials and Methods
2.1. The Study Area
2.2. Simulation Model Based on SD
2.2.1. Analysis of the System Structure
- (1)
- Water resources subsystem (WR)
- (2)
- Social economy subsystem (SE)
- (3)
- Water environment subsystem (WE)
2.2.2. Design of the System Dynamics Model
2.3. Design of Scenarios
- (1)
- Business as usual (BAU)
- (2)
- Water conservation prioritization (WCP)
- (3)
- Social–economic advancement (SEA)
- (4)
- Water environmental protection (WEP)
- (5)
- Integrated balanced development (IBD)
2.4. Selection of Evaluation Indicators
2.4.1. Factor Analysis
2.4.2. Cluster Analysis
2.4.3. Final Indicator Selection
2.5. Coupling Coordination Degree Evaluation Model
2.5.1. Entropy Weight Method
2.5.2. Coupling Coordination Calculation
2.5.3. Obstacle Degree Model
3. Results
3.1. Validation of System Dynamics Model
3.1.1. Structural Verification
3.1.2. Behavioral Adequacy
3.1.3. Sensitivity Analysis
3.1.4. Historical Validation
3.2. Simulation Results Under Different Scenarios
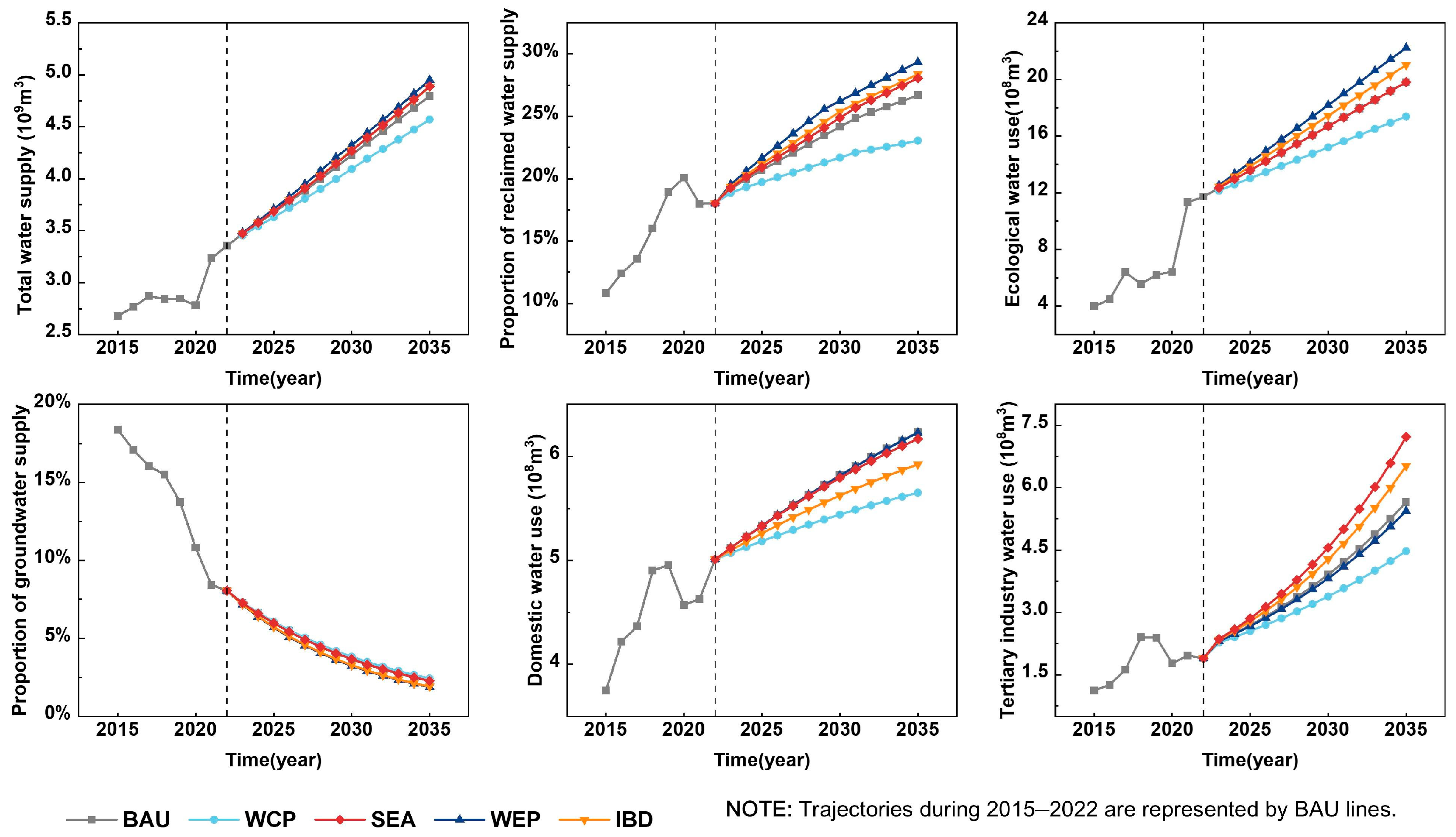
3.2.1. Simulation Results of the Water Resources Subsystem
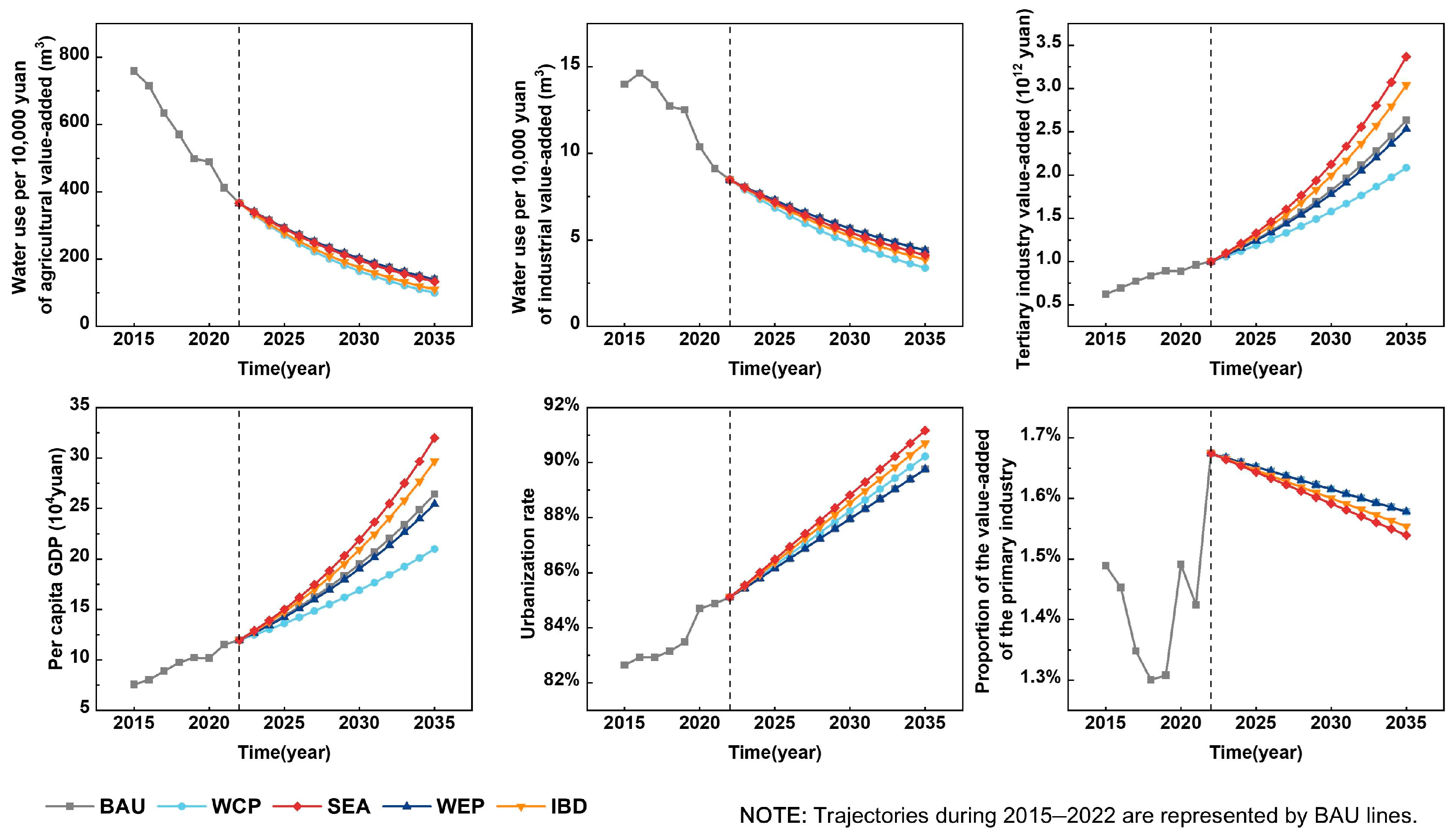
3.2.2. Simulation Results of the Social Economy Subsystem
3.2.3. Simulation Results of the Water Environment Subsystem
3.3. Results of Entropy Weight Quantification of Indicators
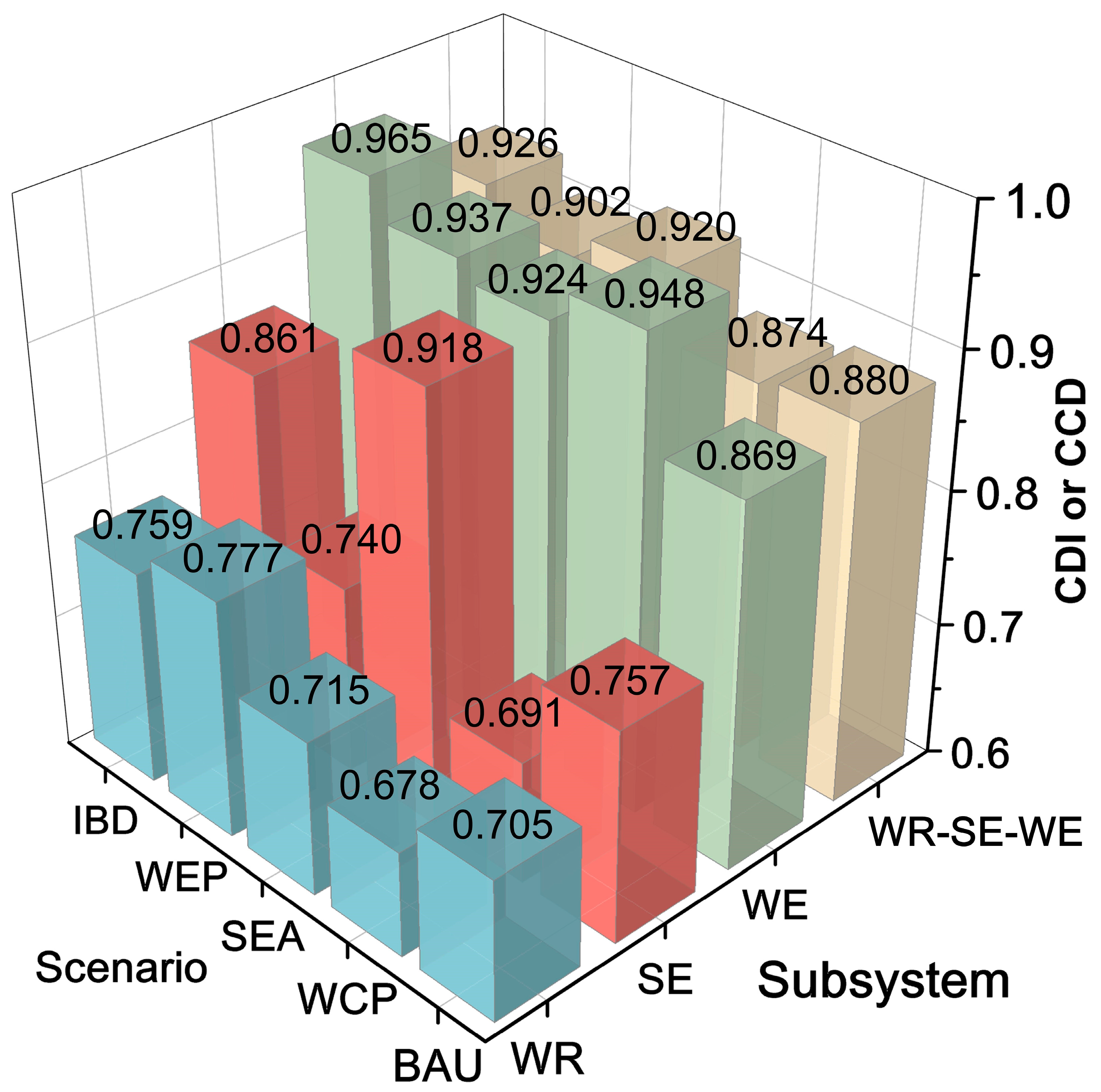
3.4. Analysis of CDI and CCD Evolution of the System Under Different Scenarios
3.5. Comparative Analysis of Subsystems Under Different Scenarios in 2035
3.6. Obstacle Factor Diagnosis of WR-SE-WE System Coupling Coordination
4. Discussion
4.1. Analysis of the Coupling Coordination for Regional Water Use and Water Environmental Protection
4.2. Recommendations
4.3. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WR-SE-WE | The water resources–social economy–water environment system |
| WR | The water resources subsystem |
| SE | The social economy subsystem |
| WE | The water environment subsystem |
| BAU | The business-as-usual scenario |
| WCP | The water conservation prioritization scenario |
| SEA | The social–economic advancement scenario |
| WEP | The water environmental protection scenario |
| IBD | The integrated balanced development scenario |
| CCD | The coupling coordination degree |
| CCDM | The coupling coordination degree model |
References
- Chen, K.; Liu, X.; Ding, L.; Huang, G.; Li, Z. Spatial Characteristics and Driving Factors of Provincial Wastewater Discharge in China. Int. J. Environ. Res. Public Health 2016, 13, 1221. [Google Scholar] [CrossRef] [PubMed]
- Wang, H. Regional assessment of human-caused ecological risk in the Poyang Lake Eco-economic Zone using production–living–ecology analysis. PLoS ONE 2021, 16, e246749. [Google Scholar] [CrossRef]
- Chen, B.; Zhao, B.; Li, Y.; Yu, Q.; Zhao, B.; Tan, J.; Wen, C. Spatiotemporal evolution and factors influencing ecological civilization development in Chinese watersheds. Int. J. Environ. Res. Public Health 2022, 19, 10728. [Google Scholar] [CrossRef] [PubMed]
- Eckstein, G.; Paisley, R.K.; Burchi, S.; Curlier, M.; Stephan, R. The Greening of Water Law: Managing Freshwater Resources for People and the Environment; UNEP: Nairobi, Kenya, 2010. [Google Scholar]
- Wei, F.; Cui, S.; Liu, N.; Chang, J.; Ping, X.; Ma, T.; Xu, J.; Swaisgood, R.R.; Locke, H. Ecological civilization: China’s effort to build a shared future for all life on Earth. Natl. Sci. Rev. 2021, 8, a279. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, Q.; Taylor, J.A. A balanced calibration of water quantity and quality by multi-objective optimization for integrated water system model. J. Hydrol. 2016, 538, 802–816. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, Z. A prediction method of regional water resources carrying capacity based on artificial neural network. Earth Sci. Res. J. 2021, 25, 169–177. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, V. A Comprehensive Review on Multi-objective Optimization Techniques: Past, Present and Future. Arch. Comput. Methods Eng. 2022, 29, 5605–5633. [Google Scholar] [CrossRef]
- Şan, M.; Nacar, S.; Kankal, M.; Bayram, A. Daily precipitation performances of regression-based statistical downscaling models in a basin with mountain and semi-arid climates. Stoch. Environ. Res. Risk Assess 2023, 37, 1431–1455. [Google Scholar] [CrossRef]
- Ning, X.; He, Y.; Zhang, J.; Wu, C.; Zhang, Y. Analysis of Carbon Emission Projections and Reduction Potential of Resource-Dependent Urban Agglomerations from the Perspective of Multiple Scenarios—A Case Study of Hu-Bao-O-Yu Urban Agglomeration. Int. J. Environ. Res. Public Health 2023, 20, 4250. [Google Scholar] [CrossRef]
- Li, T.; Yang, S.; Tan, M. Simulation and optimization of water supply and demand balance in Shenzhen: A system dynamics approach. J. Clean. Prod. 2019, 207, 882–893. [Google Scholar] [CrossRef]
- Dai, D.; Sun, M.; Lv, X.; Hu, J.; Zhang, H.; Xu, X.; Lei, K. Comprehensive assessment of the water environment carrying capacity based on the spatial system dynamics model, a case study of Yongding River Basin in North China. J. Clean. Prod. 2022, 344, 131137. [Google Scholar] [CrossRef]
- Dong, Q.; Zhang, X.; Chen, Y.; Fang, D. Dynamic Management of a Water Resources-Socioeconomic-Environmental System Based on Feedbacks Using System Dynamics. Water Resour. Manag. 2019, 33, 2093–2108. [Google Scholar] [CrossRef]
- Liu, T.; Yang, X.; Geng, L.; Sun, B. A Three-Stage Hybrid Model for Space-Time Analysis of Water Resources Carrying Capacity: A Case Study of Jilin Province, China. Water 2020, 12, 426. [Google Scholar] [CrossRef]
- Zhu, C.; Fang, C.; Zhang, L.; Wang, X. Simulating the interrelationships among population, water, ecology, and economy in urban agglomerations based on a system dynamics approach. J. Clean. Prod. 2024, 439, 140813. [Google Scholar] [CrossRef]
- Xin, R.; Skov-Petersen, H.; Zeng, J.; Zhou, J.; Li, K.; Hu, J.; Liu, X.; Kong, J.; Wang, Q. Identifying key areas of imbalanced supply and demand of ecosystem services at the urban agglomeration scale: A case study of the Fujian Delta in China. Sci. Total Environ. 2021, 791, 148173. [Google Scholar] [CrossRef]
- Wan, H.; He, G.; Li, B.; Zeng, J.; Cai, Y.; Shen, X.; Yang, Z. Coupling coordination relationship between urbanization and water environment in China. J. Clean. Prod. 2024, 472, 143423. [Google Scholar] [CrossRef]
- Peng, J.; Tong, H.; Liu, X.; Feng, Y.; Zhu, Y.; Wu, Y.; Chu, Z.; Zheng, B. Comprehensive evaluation of water resources and environmental carrying capacity based on dualistic water cycle analysis and its application in the Tuo River Basin, China. Ecol. Indic. 2023, 146, 109897. [Google Scholar] [CrossRef]
- Xu, L.; Chen, S.S. Coupling coordination degree between social-economic development and water environment: A case study of Taihu lake basin, China. Ecol. Indic. 2023, 148, 110118. [Google Scholar] [CrossRef]
- Sun, Y.S.; Wang, Y.L.; Zhang, W.; Ye, S.G. Regional water resources carrying capacity in China based on analytic hierarchy process and system dynamics model: A case study of Golmud City. Front. Environ. Sci. 2024, 12, 1450747. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Z. Exploiting temporal features in water resource carrying capacity assessment based on extended VIKOR. Sustain. Cities Soc. 2024, 114, 105801. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, Z. Assessment of coupling coordination degree and water resources carrying capacity of Hebei Province (China) based on WRESP2D2P framework and GTWR approach. Sustain. Cities Soc. 2022, 82, 103862. [Google Scholar] [CrossRef]
- Wu, X.; Hu, F. Analysis of ecological carrying capacity using a fuzzy comprehensive evaluation method. Ecol. Indic. 2020, 113, 106243. [Google Scholar] [CrossRef]
- Xu, H.; Ren, Y.; Zheng, H.; Ouyang, Z.; Jiang, B. Analysis of Runoff Trends and Drivers in the Haihe River Basin, China. Int. J. Environ. Res. Public Health 2020, 17, 1577. [Google Scholar] [CrossRef]
- Wu, L.; Qiu, X.; Wang, T.; Tao, K.; Bao, L.; Zeng, E.Y. Water Quality and Organic Pollution with Health Risk Assessment in China: A Short Review. ACS ES&T Water 2022, 2, 1279–1288. [Google Scholar] [CrossRef]
- Kong, Y.; He, W.; Yuan, L.; Shen, J.; An, M.; Degefu, D.M.; Gao, X.; Zhang, Z.; Sun, F.; Wan, Z. Decoupling Analysis of Water Footprint and Economic Growth: A Case Study of Beijing–Tianjin–Hebei Region from 2004 to 2017. Int. J. Environ. Res. Public Health 2019, 16, 4873. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Shen, Z.; Liu, G.; Jin, Z.; Liu, R. The effect of social economy-water resources-water environment coupling system on water consumption and pollution emission based on input-output analysis in Changchun city, China. J. Clean. Prod. 2023, 423, 138719. [Google Scholar] [CrossRef]
- Mao, C.; Wang, Z.; Yue, A.; Liu, H.; Peng, W. Evaluation of smart city construction efficiency based on multivariate data fusion: A perspective from China. Ecol. Indic. 2023, 154, 110882. [Google Scholar] [CrossRef]
- Shen, R.; Yao, L. Exploring the Regional Coordination Relationship between Water Utilization and Urbanization Based on Decoupling Analysis: A Case Study of the Beijing–Tianjin–Hebei Region. J. Environ. Res. Public Health 2022, 19, 6793. [Google Scholar] [CrossRef]
- Wuijts, S.; Driessen, P.P.J.; Van Rijswick, H.F.M.W. Towards More Effective Water Quality Governance: A Review of Social-Economic, Legal and Ecological Perspectives and Their Interactions. Sustainability 2018, 10, 914. [Google Scholar] [CrossRef]
- Zhong, Q.; Fu, H.; Yan, J.; Li, Z. How does energy utilization affect rural sustainability development in traditional villages? Re-examination from the coupling coordination degree of atmosphere-ecology-socioeconomics system. Build. Environ. 2024, 257, 111541. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Y.; Fu, Y.; Xu, Z.; Li, Q.; Wang, H. A framework of ecological sensitivity assessment for the groundwater system in the Mi River basin, Eastern China. Environ. Earth Sci. 2023, 82, 334. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Song, J.X.; Cheng, D.D.; Xia, J.; Li, Q.; Ahamad, M.I. Comprehensive evaluation and scenario simulation for the water resources carrying capacity in Xi’an city, China. J. Environ. Manag. 2019, 230, 221–233. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Zhou, C.; Liu, B.; Wang, D.; Zhao, X.; Yang, X.; Zhu, X.; Lin, Z. Study on water resources carrying capacity in Zhuanglang River Basin. Environ. Monit. Assess 2022, 194, 390. [Google Scholar] [CrossRef]
- Zhou, R.; Jin, J.; Zhou, Y.; Cui, Y.; Wu, C.; Zhang, Y.; Zhou, P. Spatial difference analysis and driving factor diagnosis for regional water resources carrying capacity based on set pair analysis. Heliyon 2024, 10, e38251. [Google Scholar] [CrossRef]
- Liu, Y.; Han, B.; Lu, F.; Gong, C.; Ouyang, Z.; Jiang, C.Q.; Zhang, X. Improving water efficiency is more effective in mitigating water stress than water transfer in Chinese cities. iScience 2024, 27, 109195. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Xu, X.; Wu, J.; Jarvie, S.; Li, F.; Han, P.; Zhang, Q. Comprehensive evaluation and scenario simulation of carrying capacity of water resources in Mu Us Sandy Land, China. Water Supply 2022, 22, 7256–7271. [Google Scholar] [CrossRef]
- Li, Z.; Sun, Z.; Zhang, L.; Zhan, N.; Lou, C.; Lian, J. Investigation of water quality and aquatic ecological succession of a newly constructed river replenished by reclaimed water in Beijing. Heliyon 2023, 9, e17045. [Google Scholar] [CrossRef]
- Hu, W.; Tian, J.; Zang, N.; Gao, Y.; Chen, L. Study of the development and performance of centralized wastewater treatment plants in Chinese industrial parks. J. Clean. Prod. 2019, 214, 939–951. [Google Scholar] [CrossRef]
- Zhu, L.; Bai, Y.; Zhang, L.; Si, W.; Wang, A.; Weng, C.; Shu, J. Water–Land–Food Nexus for Sustainable Agricultural Development in Main Grain-Producing Areas of North China Plain. Foods 2023, 12, 712. [Google Scholar] [CrossRef] [PubMed]
- Qian, C.; Xu, C.; Kong, F. Spatio-Temporal Pattern of Green Agricultural Science and Technology Progress: A Case Study in Yangtze River Delta of China. Int. J. Environ. Res. Public Health 2022, 19, 8702. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, F.; Li, Y. Spatial difference analysis and dynamic evolution prediction of urban industrial integrated water use efficiency in China. Heliyon 2024, 10, e23797. [Google Scholar] [CrossRef]
- Cheshmehzangi, A.; Tang, T. Tianjin: From Coastal Advantages to Large-Scale Urban Transformation. In 30 Years of Urban Change in China’s 10 Core Cities; Springer: Singapore, 2024; pp. 187–203. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, H.; Ye, H. Multidimensional multiscale complexity analysis of sediment dynamics in the Yanhe Watershed of the loess Plateau, China. J. Environ. Manag. 2024, 370, 122928. [Google Scholar] [CrossRef] [PubMed]







| Subsystem | Indicator Category | Indicator | Specific Meaning of the Indicator |
|---|---|---|---|
| Water resources | Effect of water resources protection | Ecological water use | During a certain period, the amount of water resources that need to be guaranteed to maintain the structure and function of ecosystems. |
| Proportion of groundwater supply | The proportion of groundwater supply in the total regional water supply, reflecting the degree of dependence on groundwater in water resources development. | ||
| Water use scale | Tertiary industry water use | The amount of water consumed in the production and operation processes of service industries. | |
| Domestic water use | The total amount of water resources consumed in the daily life of urban and rural residents. | ||
| Water supply capacity and structure | Total water supply | The total amount of water resources provided by various water supply projects such as surface water, groundwater, and reclaimed water in the region, reflecting the water supply guarantee capacity. | |
| Proportion of reclaimed water supply | The proportion of reclaimed water supply in the total water supply, reflecting the level of wastewater recycling. | ||
| Social economy | Economic water use efficiency | Water use per 10,000 CNY of agricultural value added | The amount of water resources consumed per 10,000 CNY of added value created in agriculture, measuring the level of water conservation and water use efficiency in agriculture. |
| Water use per 10,000 CNY of industrial value added | The amount of water resources consumed per 10,000 CNY of added value created in industry, reflecting the water-saving capacity of industrial production. | ||
| Achievements of structural transfer | Urbanization rate | The proportion of urban permanent population in the total regional population, reflecting the degree of urban-rural population structure transformation. | |
| Proportion of the value added of the primary industry | The proportion of the added value of the primary industry in GDP, reflecting the status of agriculture in the industrial structure and its transformation trend. | ||
| Scale of economic development | Per capita GDP | Regional GDP divided by the total population, measuring the level of economic development and per capita production capacity. | |
| Tertiary industry value added | The total output value of the service industry, reflecting the development scale of the largest service industry in the economic structure. | ||
| Water environment | Level of wastewater generation | Agricultural wastewater generation | The total amount of wastewater generated from agricultural production, reflecting the pollution load of agricultural activities. |
| Industrial wastewater generation | The total amount of wastewater discharged during industrial production, reflecting the intensity of industrial pollution generation. | ||
| Degree of water pollutants | Industrial COD generation | The content of chemical oxygen demand in industrial wastewater, measuring the degree of organic pollution in industrial wastewater. | |
| Residential NH3-N generation | The content of ammonia nitrogen in domestic sewage, reflecting the nitrogen pollution level of domestic sewage. | ||
| Efficiency of pollution treatment | Wastewater collection and treatment rate | The proportion of the total amount of wastewater collected and treated to the total amount of wastewater generated, reflecting the coverage capacity of the wastewater collection system. | |
| COD concentration in wastewater treatment plant effluent | The concentration of chemical oxygen demand in the effluent of wastewater treatment plants, reflecting the pollutant removal effect of wastewater treatment facilities. |
| Subsystem | Selected Variable | Error in 2022 (%) | Average Error from 2012 to 2022 (%) | Annotation |
|---|---|---|---|---|
| Social Economy | Total GDP | 0.32 | 2.43 | The average error is only calculated from 2016 to 2022. |
| Value added of industry | 3.95 | 2.92 | ||
| Value added of tertiary industry | 1.60 | 5.16 | ||
| Urbanization rate | 0.02 | 0.10 | ||
| Population | 0.09 | 2.10 | ||
| Urban population | 0.11 | 2.00 | ||
| Water Resources | Groundwater supply | 2.42 | 7.62 | |
| Surface water supply | 7.35 | 0.18 | ||
| Industrial water use | 2.59 | 8.16 | ||
| Socioeconomic water use | 2.54 | 3.80 | ||
| Domestic water use | 3.51 | 0.60 | ||
| Water Environment | Wastewater treatment rate | 0.71 | 0.40 | The average error is only calculated for the years 2020 to 2022. |
| Wastewater reuse | 5.34 | 5.42 | ||
| Total wastewater generation | 1.35 | 1.75 | ||
| Total COD generation | 3.90 | 0.82 | ||
| Total NH3-N generation | 4.25 | 2.02 |
| Subsystem | Indicator | Entropy | Redundancy | Weight | Orientation |
|---|---|---|---|---|---|
| WR | Ecological water use | 0.9512 | 0.0488 | 0.2073 | Positive |
| Proportion of groundwater supply | 0.9646 | 0.0354 | 0.1502 | Negative | |
| Tertiary industry water use | 0.9853 | 0.0147 | 0.0626 | Negative | |
| Domestic water use | 0.9578 | 0.0422 | 0.1793 | Negative | |
| Total water supply | 0.9371 | 0.0629 | 0.2670 | Positive | |
| Proportion of reclaimed water supply | 0.9685 | 0.0315 | 0.1336 | Positive | |
| SE | Water use per 10,000 CNY of agricultural value added | 0.9687 | 0.0313 | 0.1059 | Negative |
| Water use per 10,000 CNY of industrial value added | 0.9589 | 0.0411 | 0.1389 | Negative | |
| Urbanization rate | 0.9425 | 0.0575 | 0.1943 | Positive | |
| Proportion of the value added of the primary industry | 0.9687 | 0.0313 | 0.1059 | Negative | |
| Per capita GDP | 0.9354 | 0.0646 | 0.2184 | Positive | |
| Tertiary industry value added | 0.9300 | 0.0700 | 0.2366 | Positive | |
| WE | Agricultural wastewater generation | 0.9995 | 0.0005 | 0.0029 | Negative |
| Industrial wastewater generation | 0.9516 | 0.0484 | 0.3115 | Negative | |
| Industrial COD generation | 0.9571 | 0.0429 | 0.2761 | Negative | |
| Residential NH3-N generation | 0.9853 | 0.0147 | 0.0949 | Negative | |
| Wastewater collection and treatment rate | 0.9995 | 0.0005 | 0.0029 | Positive | |
| COD concentration in wastewater treatment plant effluent | 0.9516 | 0.0484 | 0.3115 | Negative |
| Year | Scenario | WR Subsystem | SE Subsystem | WE Subsystem | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Indicator 1 Obstacle Degree (%) | Indicator 2 Obstacle Degree (%) | Indicator 3 Obstacle Degree (%) | Indicator 1 Obstacle Degree (%) | Indicator 2 Obstacle Degree (%) | Indicator 3 Obstacle Degree (%) | Indicator 1 Obstacle Degree (%) | Indicator 2 Obstacle Degree (%) | Indicator 3 Obstacle Degree (%) | ||
| 2015 | TWS | Eco-WU | GWS% | TI-VA | GDP/cap | Urban% | COD-Conc (Eff) | Agri-WWG | COD-G (Ind) | |
| 10.21 | 7.92 | 5.74 | 9.05 | 8.35 | 7.43 | 7.14 | 6.87 | 6.80 | ||
| 2020 | TWS | Eco-WU | GWS% | TI-VA | GDP/cap | Urban% | Agri-WWG | Ind-WWG | COD-G (Ind) | |
| 12.12 | 8.54 | 3.87 | 10.17 | 9.29 | 7.01 | 7.39 | 6.56 | 6.22 | ||
| 2025 | BAU | TWS | DWU | Eco-WU | TI-VA | GDP/cap | Urban% | Agri-WWG | Ind-WWG | COD-G (Ind) |
| 9.64 | 7.36 | 6.31 | 11.71 | 10.14 | 7.33 | 8.87 | 5.96 | 5.09 | ||
| WCP | TWS | Eco-WU | DWU | TI-VA | GDP/cap | Urban% | Agri-WWG | Ind-WWG | COD-Conc (Eff) | |
| 10.32 | 6.95 | 6.90 | 12.49 | 10.93 | 7.42 | 7.04 | 5.20 | 5.01 | ||
| SEA | TWS | DWU | Eco-WU | TI-VA | GDP/cap | Urban% | Agri-WWG | Ind-WWG | COD-G (Ind) | |
| 9.75 | 7.49 | 6.44 | 11.52 | 9.96 | 6.99 | 9.54 | 5.82 | 4.97 | ||
| WEP | TWS | DWU | Eco-WU | TI-VA | GDP/cap | Urban% | Agri-WWG | Ind-WWG | COD-G (Ind) | |
| 9.98 | 7.82 | 6.28 | 12.51 | 10.85 | 7.79 | 9.27 | 6.21 | 5.30 | ||
| IBD | TWS | DWU | Eco-WU | TI-VA | GDP/cap | Urban% | Agri-WWG | Ind-WWG | COD-G (Ind) | |
| 10.21 | 7.50 | 6.52 | 12.25 | 10.59 | 7.49 | 8.92 | 6.02 | 5.14 | ||
| 2030 | BAU | DWU | TWS | Eco-WU | TI-VA | GDP/cap | PIVA% | Agri-WWG | Ind-WWG | COD-G (Ind) |
| 13.36 | 7.61 | 5.62 | 11.91 | 10.01 | 7.96 | 10.27 | 5.21 | 4.45 | ||
| WCP | DWU | TWS | Eco-WU | TI-VA | GDP/cap | PIVA% | COD-Conc (Eff) | Agri-WWG | Ind-WWG | |
| 11.77 | 9.69 | 7.69 | 14.86 | 13.00 | 8.58 | 4.60 | 4.31 | 3.07 | ||
| SEA | DWU | TWS | Eco-WU | TI-VA | GDP/cap | PIVA% | Agri-WWG | COD-Conc (Eff) | Ind-WWG | |
| 14.36 | 7.81 | 6.12 | 10.42 | 8.77 | 8.01 | 12.98 | 4.64 | 4.59 | ||
| WEP | DWU | TWS | Eco-WU | TI-VA | GDP/cap | PIVA% | Agri-WWG | Ind-WWG | COD-G (Ind) | |
| 14.87 | 7.34 | 4.57 | 13.64 | 11.56 | 8.87 | 10.89 | 5.40 | 4.61 | ||
| IBD | DWU | TWS | Eco-WU | TI-VA | GDP/cap | PIVA% | Agri-WWG | Ind-WWG | COD-G (Ind) | |
| 14.51 | 8.51 | 5.83 | 12.70 | 10.62 | 9.09 | 10.24 | 5.00 | 4.27 | ||
| 2035 | BAU | DWU | TIWU | Eco-WU | PIVA% | TI-VA | GDP/cap | Agri-WWG | COD-Conc (Eff) | Ind-WWG |
| 25.08 | 6.50 | 3.85 | 10.99 | 8.84 | 6.98 | 13.10 | 4.22 | 3.77 | ||
| WCP | DWU | Eco-WU | RWS% | TI-VA | GDP/cap | PIVA% | COD-Conc (Eff) | NH3-G (Res) | Agri-WWG | |
| 20.67 | 8.29 | 6.82 | 16.64 | 14.82 | 11.82 | 4.54 | 0.51 | 0.00 | ||
| SEA | DWU | TIWU | Eco-WU | PIVA% | Ind-WU/10k | Agri-WU/10k | Agri-WWG | COD-Conc (Eff) | Ind-WWG | |
| 32.51 | 11.65 | 5.13 | 12.58 | 1.69 | 1.00 | 22.64 | 5.62 | 1.74 | ||
| WEP | DWU | TIWU | TWS | PIVA% | TI-VA | GDP/cap | Agri-WWG | Ind-WWG | COD-G (Ind) | |
| 29.38 | 7.27 | 0.00 | 12.89 | 11.78 | 9.63 | 14.04 | 3.59 | 3.06 | ||
| IBD | DWU | TIWU | Eco-WU | PIVA% | TI-VA | GDP/cap | Agri-WWG | Ind-WWG | COD-G (Ind) | |
| 33.52 | 11.83 | 2.94 | 15.31 | 6.04 | 4.45 | 14.05 | 2.42 | 2.06 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Liu, K.; Chen, W.; Liu, H. Scenario Simulation and Comprehensive Evaluation of Coupling Coordination Relationship Between Regional Water Use and Water Environmental Protection: A Case Study of Tianjin, China. Sustainability 2025, 17, 8220. https://doi.org/10.3390/su17188220
Li B, Liu K, Chen W, Liu H. Scenario Simulation and Comprehensive Evaluation of Coupling Coordination Relationship Between Regional Water Use and Water Environmental Protection: A Case Study of Tianjin, China. Sustainability. 2025; 17(18):8220. https://doi.org/10.3390/su17188220
Chicago/Turabian StyleLi, Bohong, Kaili Liu, Wenkai Chen, and Hongbo Liu. 2025. "Scenario Simulation and Comprehensive Evaluation of Coupling Coordination Relationship Between Regional Water Use and Water Environmental Protection: A Case Study of Tianjin, China" Sustainability 17, no. 18: 8220. https://doi.org/10.3390/su17188220
APA StyleLi, B., Liu, K., Chen, W., & Liu, H. (2025). Scenario Simulation and Comprehensive Evaluation of Coupling Coordination Relationship Between Regional Water Use and Water Environmental Protection: A Case Study of Tianjin, China. Sustainability, 17(18), 8220. https://doi.org/10.3390/su17188220






