Next Article in Journal
The Impact of Renewable Energy Diversity on Inflation: A Case Study Based on China
Previous Article in Journal
Mapping Flood-Prone Areas Using GIS and Morphometric Analysis in the Mantaro Watershed, Peru: Approach to Susceptibility Assessment and Management
Previous Article in Special Issue
Musée des Civilisations de l’Europe et de la Méditerranée: A Sustainable Fusion of Heritage and Innovation Through Ultra-High-Performance Concrete
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 17
Issue 17
10.3390/su17177808
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Optimizing Carbon Footprint and Strength in High-Performance Concrete Through Data-Driven Modeling

by
Saloua Helali
1,
Shadiah Albalawi
2,
Maer Alanazi
2,
Bashayr Alanazi
3 and
Nizar Bel Hadj Ali
4,*
1
Research and Technology Center of Energy, Technoparc Borj Cedria, Hammam Lif BP 095, Tunisia
2
Department of Physics, Faculty of Science, University of Tabuk, King Faisal Road, Tabuk 47512, Saudi Arabia
3
Department of Physics, College of Science, Northern Border University, Arar 73213, Saudi Arabia
4
Modeling in Civil Engineering and Environment (MCEE), National School of Engineers, University of Gabes, Street Omar Elkhattab, Zrig, Gabes 6029, Tunisia
*
Author to whom correspondence should be addressed.
Sustainability 2025, 17(17), 7808; https://doi.org/10.3390/su17177808
Submission received: 23 July 2025 / Revised: 26 August 2025 / Accepted: 26 August 2025 / Published: 29 August 2025
(This article belongs to the Special Issue Advancements in Concrete Materials for Sustainable Construction)
Browse Figures
Versions Notes

Abstract

High-performance concrete (HPC) is an essential construction material used for modern buildings and infrastructure assets, recognized for its exceptional strength, durability, and performance under harsh situations. Nonetheless, the HPC production process frequently correlates with elevated carbon emissions, principally attributable to the high quantity of cement utilized, which significantly influences its carbon footprint. In this study, data-driven modeling and optimization strategies are employed to minimize the carbon footprint of high-performance concretes while keeping their performance properties. Starting from an experimental dataset, artificial neural networks (ANNs), ensemble techniques (ETs), and Gaussian process regression (GPR) are employed to yield predictive models for compressive strength of HPC mixes. The model’s input variables are the various components of HPC: cement, water, superplasticizer, fly ash, blast furnace slag, and coarse and fine aggregates. Models are trained using a dataset of 356 records. Results proved that the GPR-based model exhibits excellent accuracy with a determination coefficient of 0.90. The prediction model is used in a double objective optimization task formulated to identify mix configurations that allow for high mechanical performance aligned with a reduced carbon emission. The multi-objective optimization task is undertaken using genetic algorithms (GAs). Promising results are obtained when the machine learning prediction model is associated with GA optimization to identify strong yet sustainable mix configurations.

1. Introduction

Massive worldwide urbanization and industrialization caused an increasing demand for building materials such as wood, steel, and concrete. Amongst the various kinds of construction materials, concrete is a fundamental component in modern buildings and infrastructure assets [1]. Research into cementitious matrix materials has led to the introduction of relatively new generations of concretes such as highnormalncrete (HPC) and ultra-high-performance concrete (UHPC), offering higher mechanical properties and excellent durability compared with normal strength concrete (NSC) [2,3]. In addition, high-performance concretes offer excellent compactness and impermeability [4]. HPC was also proven to have better fluidity and segregation resistance compared with NSC, which leads to rational use of construction material associated with shorter construction time [5]. The high mechanical performance of HPC is mainly due to an elevated cement content combined with the usage of several auxiliary cementitious materials such as fly ash, blast furnace slag, and silica fume [6]. From NSC to UHPC, each concrete mixture is formulated to meet specific design requirements defined by engineering codes and practices. Among the various concrete properties, compressive strength is a key parameter in the design of civil engineering structures such as buildings and bridges. It is considered the most widely used measurement of performance in concrete structure design. Cylindrical concrete specimens are frequently fractured in compression testing apparatus to ascertain the compressive strength. The empirical formula can also be used to estimate the compressive strength for a defined mixture configuration. However, the determination of concrete compressive strength using empirical methods tends to be inaccurate and requires more exploration, especially when dealing with recent concrete types such as HPC [7,8]. This situation is common in many engineering fields, and it represents a typical situation where Machine Learning (ML) can be used to fill the gap in scientific knowledge by offering data-driven estimate models [9,10,11].
Figure 1 illustrates the number of articles dealing with ML and HPC. According to this diagram, the number of publications in this topic is increasing, with the majority of contributions coming from engineering, materials science, and computer science. ML-based prediction of HPC compressive strength has been extensively investigated in the last few years; most studies focused on improving the performance of prediction models using various ML algorithms combined, in some cases, with optimization methods. In a pioneering study, Yeh et al. [12] used artificial neural networks (ANNs) to build a predictive model of HPC compressive strength. The model was trained using a database collected from literature. Yu et al. [13] suggested a predictive model using support vector machine (SVM). The model was trained using 1761 data records collected from existing literature. Bui et al. [14] tackled the prediction task using an artificial neural network combined with a modified firefly algorithm. Moayedi et al. [15] combined ANN with three metaheuristic optimization methods to develop an estimate model for HPC compressive strength. Han et al. [16] used random forest (RF) for HPC strength prediction. Hameed et al. [17] achieved relatively high accuracy in the prediction of HPC compressive strength using ANN combined with cross-validation techniques and principal component analyses (PCA). Recent research works also investigated boosting the smooth transition regression trees method (BooST) [18], ensemble learners [19,20,21], and the cascade forward neural network (CFNN) [22] for the compressive strength prediction of HPC.
Most research works on HPC focus largely on achieving high mechanical performance in terms of compressive strength and durability. Achieving this typically requires high cement contents in concrete mixes [1,23], which inevitably have negative environmental impacts. In fact, the building and construction activity is the biggest source of greenhouse gas emissions, contributing an astounding 37% of global emissions [24]. Concrete buildings are responsible for 7% of the world’s greenhouse gas emissions, which makes it imperative to reduce their global warming potential [24]. The concrete design mix and cement type have been shown to have a significant impact on the environmental effects. Due to the increasing global demand for reducing concrete environmental impact, alternative binders, such as slag, silica fume, and fly ash, have been developed specifically for HPC and are used in place of cement [25,26]. In the most recent research, Rajagopal et al. [27] compared the environmental footprints of high-performance concrete and standard concrete, concentrating on important environmental parameters such as waste generation during construction, energy consumption, water usage, and carbon footprint. They underscored the significance of making well-informed material selection choices in the building industry, suggesting that while HPC may be beneficial for structural integrity, its higher environmental footprint necessitates careful consideration.
The increasing global focus on environmental sustainability has made the reduction of carbon emissions a critical objective for the construction industry. Even if concrete has proven essential and affordable for modern societies, its carbon footprint tends to be massive. In parallel to all studies focusing on its mechanical properties, concrete’s carbon footprint has received wide coverage during the last decade [28,29,30,31]. In this context, ML has developed as a distinct tool for investigating carbon emissions of concrete mixtures. For instance, Jin et al. [32] employed a long short-term memory (LSTM) network and multi-objective particle swarm optimization (MOPSO) algorithm to optimize concrete mix ratios, focusing on minimizing carbon emissions while achieving required compressive strength, thus addressing the carbon footprint of high-performance concrete effectively. Physics-informed neural networks (PINNs) have been successfully employed to model chemical processes in cement hydration, allowing for precise predictions of carbon emissions during concrete production. Rahman and Lu [33] used a PINN to show that industrial by-products such as fly ash and slag can be used in place of cement to save CO2 emissions by 60–80% without sacrificing strength. This approach bridges the gap between theoretical models and real-world applications, providing a strong framework for eco-friendly concrete models. Li et al. [34] developed a concrete design model using ML techniques focused on optimizing alkali-activated slag-fly ash geopolymer concrete. The optimization process led to notable reductions in both production costs and carbon emissions, achieving carbon emission reductions of 77.3% to 80.7% at C30 strength and 76.9% to 81.3% at C50 strength.
By training models on large datasets of concrete properties and environmental impacts, researchers can predict the performance of different mixtures and identify those with the lowest carbon footprint. Conversely, few studies were found to exploit the prediction model in the optimization of HPC mixture in order to achieve a satisfactory compromise between the mechanical properties and the carbon footprint. Motivated by these limitations, the aim of the study described in this paper is to build prediction models for both the compressive strength and the carbon footprint of high-performance concrete and to use the obtained model in mixture design optimization. Prediction models are built on a dataset of 356 records. Trained models are obtained by applying Gaussian process regression (GPR), ensemble techniques (ETs), and artificial neural networks (ANNs). ML algorithms are tested and compared using common performance metrics. The prediction models are used in a double objective optimization task formulated to identify mix configurations that allow for high mechanical performances aligned with a reduced environmental cost. The multi-objective optimization challenge is undertaken employing genetic algorithms (GAs): a global search optimization method, biology-inspired, that belongs to the member of the stochastic search algorithm class [35].
The arrangement of the paper reminder is as follows: Section 1 contains the data collected. Section 2 introduces the ML algorithms and the methodology adopted to build the predictive model. The formulation of the mix design optimization task is presented in Section 3. In Section 4, the data-based prediction models are presented and compared. Mix design optimization results are also presented. Mix optimization results are discussed and compared. Finally, conclusions are exposed in Section 5.

2. Data Collection

To investigate the compressive strength and the carbon footprint of HPC, an existing mix dataset is employed. The dataset comprises 356 concrete mixtures gathered from experimental works [12,36]. Each mixture is defined through eight attributes (7 input variables and 1 model output). The input variables are the mass fraction of the principal components used for the fabrication of one cubic meter of HPC. Each mixture configuration is characterized by its content of cement, superplasticizer, fine aggregate, water, coarse aggregate, fly ash, and blast furnace slag. The sole output variable is the 28-day compressive strength of HPC measured by breaking cylindrical concrete specimens with a size of 300 mm height and 150 mm diameter in a compression testing machine. The 28-day compressive strength is usually considered the design strength. In fact, concrete is known to gain strength rapidly in the first two weeks after casting. Generally, concrete gains approximately 90% of its final strength after 14 days. It continues to gain strength and reaches 99% of its final strength in 28 days. After that, the rate at which the concrete’s strength grows is significantly reduced compared to the first 28 days. In the studied HPC mix, the 28-day compressive strength ranges between 20.6 and 81.75 MPa with an average value of 39.7 MPa. Preprocessing of the dataset was only limited to removing duplicate records. There were no outliers in the original dataset, mainly because it was gathered from experimental results.
Investigating some relationships between the dataset variables shows a clear correlation between the water-to-cement ratio and the compressive strength. In Figure 2, the compressive strength values of all mix configurations are displayed with respect to the ratio between water and cement content. This figure reveals a clear trend between these two parameters. In fact, the highest strength values are associated with relatively small water-to-cement ratios ranging between 0.25 and 0.6. A similar trend is noticed when studying the distribution of compressive strength with respect to the water-to-binder ratio where high compressive strength values are associated with water-to-binder ratios ranging between 0.2 and 0.45 (Figure 3).
Relatively small water to cement and water-to-binder ratios in HPC are obvious consequences of the use of superplasticizers in the concrete mix. In fact, using superplasticizers in HPC leads to enhanced workability, increased compressive strength, and improved durability compared to conventional concrete [37]. Consequently, superplasticizers allow for lower water-cement ratios while maintaining high fluidity, facilitating the production of concrete with a high level of compressive strength. Figure 4 illustrates the distribution of the compressive strength values with respect to the superplasticizer-to-binder ratio. This figure shows no clear correlation between the superplasticizer content and the strength of HP concrete.
Table 1 presents general statistical information about the dataset. This table shows the ranges of components of the dataset as well as the range of the measured compressive strength.
The presented dataset is used to yield a predictive model for the compressive strength of high-performance concrete at 28 days. Obviously, there is no need to train a model for the carbon footprint of various HPC mixes since it can be simply calculated using carbon emission factors for the various components. The carbon footprint of HPC is influenced by several key factors, primarily related to its composition and life cycle. CO2 emissions are largely caused by the manufacturing of cement, a key ingredient in concrete. Therefore, the type and amount of cement used in HPC are critical determinants of its carbon footprint. The incorporation of additional cementitious materials (SCMs), like fly ash, ground granulated blast-furnace slag (GGBS), and silica fume, can mitigate these emissions by reducing cement consumption and enhancing the concrete’s durability and mechanical properties. The sum of the CO2 emissions from each component in the mix is used to determine the carbon footprint of the different HPC mixes in the dataset. Carbon emissions data are gathered from previous studies [8,38] and from available databases [39]. The emission factors in kg CO2 per ton for each HPC component are displayed in Table 2. Note that carbon dioxide emissions of HPC generated during production (mixing) or transportation are not included in the calculated carbon footprint. Thus, calculated carbon CO2 emissions are only employed to compare various HPC mixes and should not be considered as the absolute carbon footprint of HPC mix configurations.

3. ML Training and Testing

In the past few decades, machine learning algorithms have emerged as efficient alternatives to traditional physics-based modeling methods in many engineering fields. A diversity of machine learning methods have recently been employed to disclose nonlinear and complex relationships between high-performance concrete input components and output metrics describing the performance of the produced concrete, such as its compressive strength.
In this context, well-established ML algorithms are tested and compared to predict the compressive strength of HPC. The experimental dataset (356 records) is trained using a model for the 28-day compressive strength of HPC. All proposed models are trained from the collected datasets using the MATLAB® Regression Learner application (version 2021a) [40]. K-fold cross-validation [41] is used with k = 5 for all training instances. The training set is divided into k equal pieces (referred to as folds) after this validation procedure. Four folds are employed for training in each training iteration, with the remaining fold serving as the test set. Until every fold has been used, this process is repeated. Since training and testing are performed on many dataset segments, the model is validated on each fold after k iterations, which is thought to produce more reliable and consistent results [42].

3.1. ML Algorithms

The Regression Learner Matlab® application is used to perform automated training for the studied dataset. In this work, trained models were obtained by applying ensemble techniques (ETs), artificial neural networks (ANNs), and Gaussian process regression (GPR). Each dataset’s optimal prediction model is distributed as a Matlab® function that can be applied to produce expected answers for new input data. The employed ML techniques are briefly described in the subsequent sections.

3.1.1. Gaussian Process Regression

One non-parametric Bayesian method for statistical inference is Gaussian process regression [43]. It is a powerful tool for modeling intricate and ambiguous interactions between input and output variables. The GPR is built upon the assumption that a Gaussian process with defined mean and covariance functions describes the relationship between the inputs and the outputs. Typically, kernel functions are used to define the mean and covariance functions. Bayesian inference is then applied to determine the distribution that is most likely to have produced the data given a set of training records. By increasing the likelihood of the data, the covariance function’s hyperparameters are optimized. Finally, the GPR-trained model is a normal distribution, with the variance serving as a gauge of the model’s confidence and the mean value representing the expected output [44].

3.1.2. Ensemble Techniques

Ensembles are collections of machine learning algorithms that, instead of combining a single model, combine a number of simpler, reduced models or single learners. The main idea behind ensemble models is that a group of weak learners can be associated to form a strong learner. For instance, the performance of ensemble-based techniques, such as bootstrap aggregating (bagging) and boosting, is typically superior to that of single models. Common implementations of extreme gradient boosting (XGBoost) [45] and bagging and boosting are random forest (RF) [46]. These two methods use decision trees (DTs) as the base learner.

3.1.3. Artificial Neural Networks

Artificial neural networks are constructed by connecting multiple layers, containing an input layer, one or more hidden layers, and an output layer [47]. The input data that has to be analyzed or learned about by the neural network is sent to the first layer. The input is changed into data that is useful for the output layer by means of hidden layers. When the input data is supplied, the output layer generates the ANN’s response.

3.2. Model Performance Evaluation Criteria

Three metrics are employed to estimate the developed machine learning models: the mean absolute error (MAE), root mean squared error (RMSE), and determination coefficient (R2). Generally, MAE and RMSE typically aim for lower levels. Better model performance is indicated by determination coefficient values that are close to one. Equations (1)–(3) provide expressions for these performance criteria.
R 2 = 1 − ∑ i = 1 N y i , p − y i , o 2 ∑ i = 1 N y i , o − y o , m 2
M A E = 1 N   ∑ i = 1 N y i , p − y i , o
R M S E = ∑ i = 1 N y i , p − y i , o 2 N  
where N is the total number of data points, and y i , 0 ,   y i , p   and   y o , m are the HPC compressive strength’s observed, predicted, and average observed values.

4. HPC Mix Optimization

Having the best performance model for predicting the compressive strength of high-performance concrete, it is envisioned to recognize the volumetric fraction of each component, resulting in the maximum compressive strength while minimizing the carbon footprint of the mix. This task is expressed as a multi-objective optimization problem where the variables are the volumetric fractions of the seven components (cement, fine aggregate, water, fa, bls, superplasticizer, and coarse aggregate) forming concrete mixtures. The target of this optimization task is to recognize the mix configuration that maximizes the concrete compressive strength and minimizes the carbon emission of the mix. The fitness of a defined mix configuration is evaluated using two objective functions. The first objective function uses the ML-based prediction model established for the 28-day concrete compressive strength (as described in Section 3). The second objective function is the carbon footprint calculated as a linear combination of the CO2 emission factors multiplied by the mass quantity of each component in the HPC mix. For the component volumetric fractions, boundary values are considered as displayed in Table 3.
Genetic algorithms (GAs) are used to address the optimization challenge: a global search optimization technique that falls within the category of stochastic search algorithms. John Holland was the first to propose GA optimization, although Goldberg’s work is largely responsible for its success [48]. Even if many biology-inspired optimization techniques have been proposed in the last two decades, genetic algorithms are still a reference optimization technique for both discrete and continuous optimization problems.
A genetic algorithm mimics the principles of natural evolution and employs biology-inspired mechanisms such as mutation, crossover, and selection [49]. A search begins with an initial set of possible solutions (a population of solutions in GA terminology). The population evolves iteratively through reproduction utilizing mutation operators and crossover. Based on the evaluation of the objective function for candidate solutions in the population, new solutions are produced. In order to guarantee a steady development in the quality of the solutions, the finest solutions are given further chances to develop. By gradually changing the population’s makeup, this approach facilitates convergence towards the best answers.
Seven volumetric fractions, which represent the concrete components, are involved in a concrete mixture configuration as mentioned in the optimization problem. Consequently, there is an infinite number of possible mix configurations. A GA is usually capable of efficiently exploring large and complex search spaces to identify optimal solutions, the primary justification for selecting this method to tackle the mix design optimization in this study.

5. Results and Discussion

5.1. ML Prediction Models

Based on the collected experimental data, models are trained using GPR, ET, and ANN algorithms. The performances of the ML procedures in modeling the compressive strength of HPC were assessed, with the results presented in Table 4.
The results displayed in Table 4 show that Gaussian process regression (GPR) yields better efficiency compared with ensemble techniques and artificial neural networks. The prediction model obtained using GPR uses an isotropic exponential function as the covariance function describing the relationship between the input variables and the model output. The optimized model results in a determination coefficient of 0.93, which is in line with values found in related studies published in the literature [10,22]. GPR outperforms ETs and ANNs based on the values of the three statistical metrics, indicating the model’s prediction performance. The GPR model was obtained using a basic linear function and an anisotropic exponential kernel function (kernel scale of 0.45606). For the ET, the predictive model was created using optimized bagged and boosted trees with a minimum leaf size of one and 492 learners. The tested ANN is a tri-layered feedforward, fully connected neural network with each layer having a size of 10.
The predicted values of the concrete compressive strength are shown with respect to the actual determined values for the datasets studied. In Figure 5, the predicted and measured values of the 28-day compressive strength are compared. The results indicate a strong relationship between the measured and anticipated values. A high correlation between the expected values derived from GPR was demonstrated by a determination coefficient of 0.93. The link between the measured and predicted values is more pronounced for compressive strengths between 20 and 50 MPa. A higher discrepancy between model predictions and measurements is noticed for high-strength mixes. This result may be attributed to the distribution of dataset points, including a relatively small percentage of mix configurations having a compressive strength higher than 60 MPa (only 9%). Nevertheless, the regression findings in Figure 5 indicate that the GPR-based model has a significant generalization potential and a high prediction performance. The GPR-based model also has comparable efficiency metrics with recent HPC prediction models reported in recent published research works by Zhang et al. [50], Vu-Bac et al. [51], and Kang et al. [52]. The obtained prediction model presents excellent prospects for usage as a basis for optimizing mix design, avoiding expensive and time-consuming experimental studies, and the errors associated with empirical formulations.

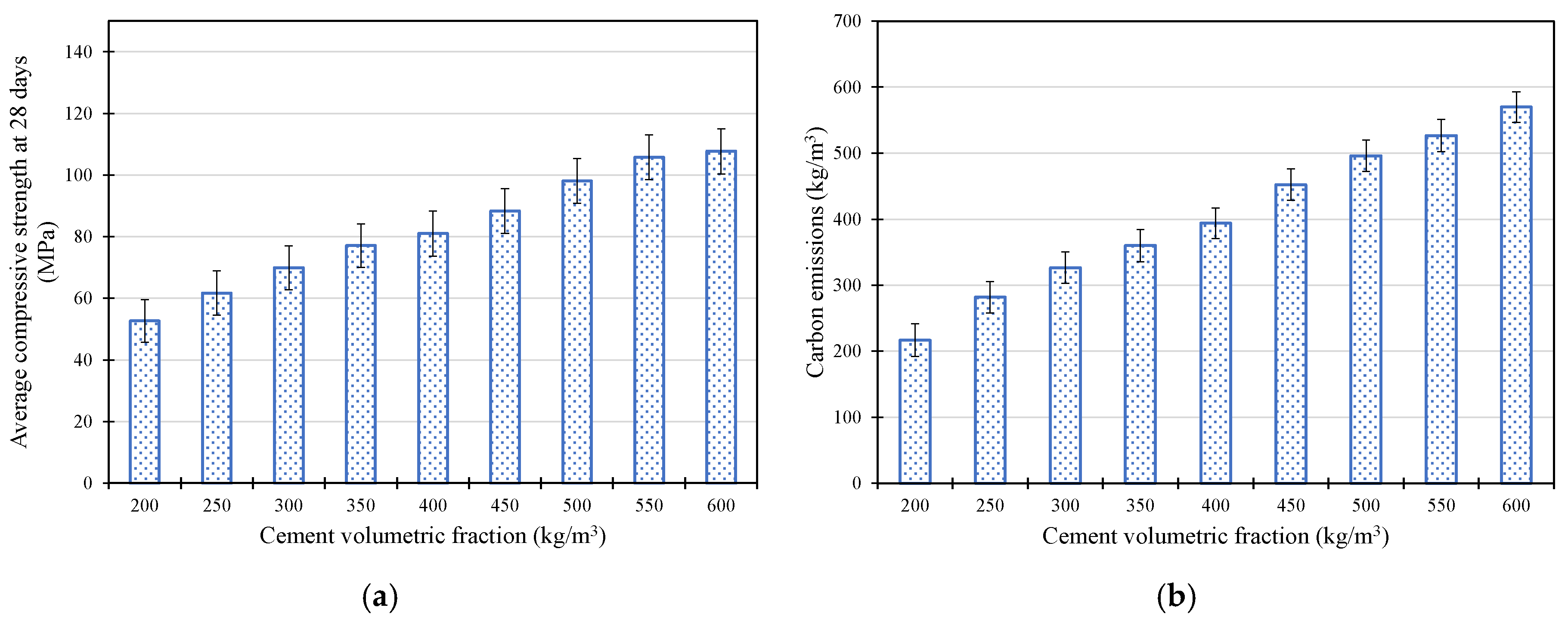
5.2. Parametric Study

The data-driven model is further employed to investigate the main correlations between the components of HPC mixes and their strength and sustainability features.
A key parameter in concrete design is the proportion of water to cement. This parameter is further investigated here using the GPR model. Figure 6a shows the evolution of the compressive strength of HP concrete mixes in relation to the water-to-concrete proportion. Evaluation of the compressive strength is performed for three configurations, including three different cement contents per cubic meter of concrete. The first class includes a cement content ranging between 200 and 300 kg. The second class includes a cement content ranging between 300 and 400 kg, and the last class includes a higher cement content ranging between 400 and 500 kg. For all three HPC classes, results showed a strong relationship between the ratio of water to cement and compressive strength, with an approximate linear trend showing a progressive decrease in the compressive strength as the ratio increased.
The investigation of the water-to-binder ratio shows a similar trend (Figure 6b), with a more pronounced decrease in HPC compressive strength with respect to increasing water-to-binder ratio. The results reveal that increasing the water-to-binder ratio from 0.2 to 0.7 can cause HPC to lose 1/3 of its compressive strength.
The SCM content of the various HPC mixes is also studied. For this, the ratio between the SCMs (blast furnace slag and fly ash) and the cement content is investigated. Figure 7a displays the evolution of the HPC compressive strength with respect to the SCM-to-cement ratio. The SCM-to-cement proportion varies from 0.3 to 1.6 for varying values of the cement content. The displayed results reveal no clear trend between these two parameters. In contrast, when the carbon footprint is investigated (Figure 7b), a strong correlation is exposed. Results show that carbon emissions decrease by a third when the SCM-to-cement ratio is increased from 0.3 to 1.6. These results emphasize the importance of SCMs in HPC. In fact, obtained results clearly showed that while the compressive strength is not affected, reduced cement content directly lowers CO2 emissions and environmental impact.
The data-driven model also shows that superplasticizers do not have a direct effect on the compressive strength of the studied HPC mixes. In Figure 8, the evolution of compressive strength with respect to the superplasticizer-to-binder ratio is displayed. The ratio varies between 0 and 0.06. Results reveal no clear trend or correlation between HPC compressive strength and the superplasticizer content in various HPC mixes.

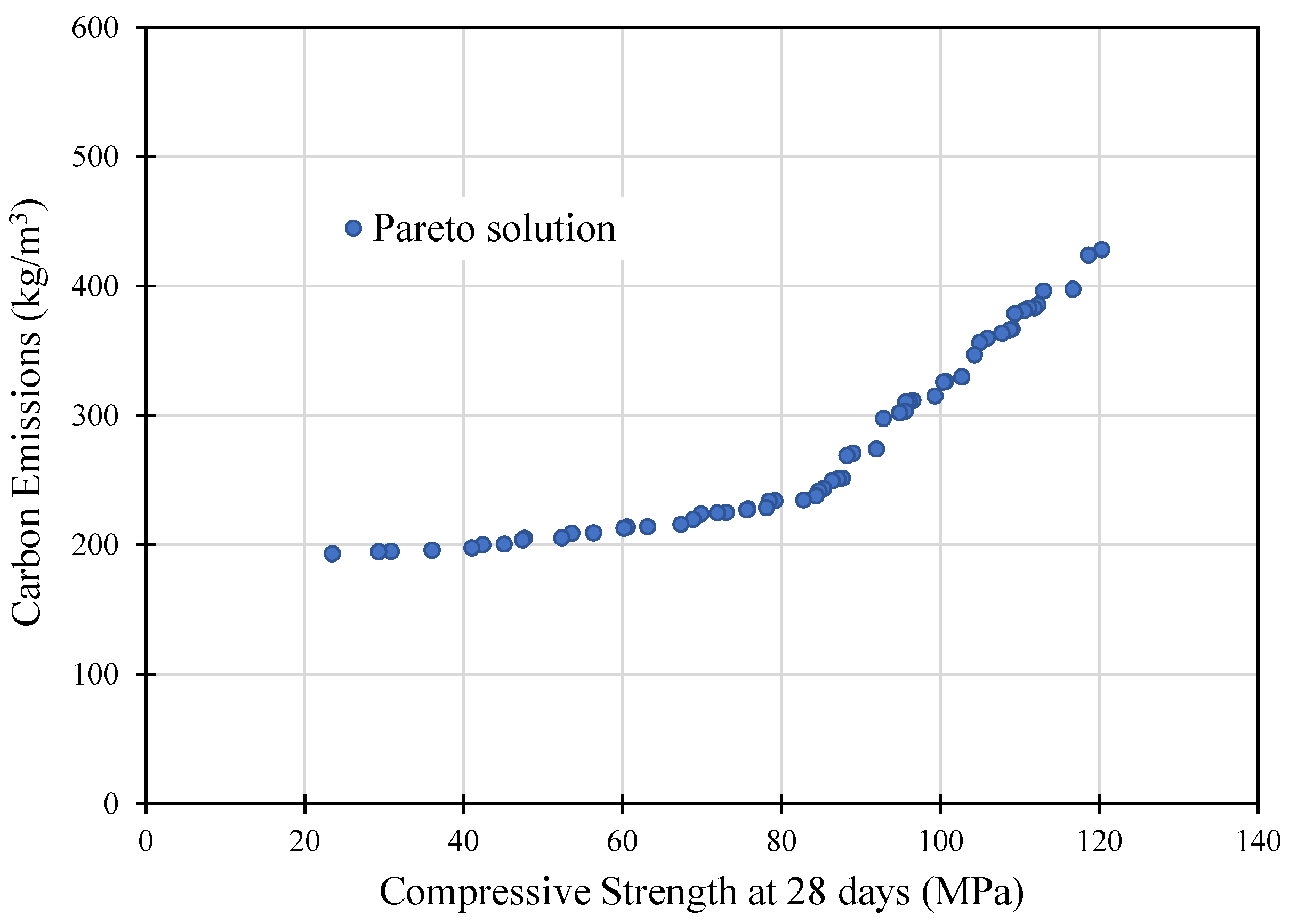
5.3. Mix Optimization Results

HPC mix design optimization is performed following the formulation presented earlier. Genetic algorithm optimization is used. The prediction model obtained using the GPR algorithm is used to evaluate the 28-day compressive strength for the various mix configurations generated through the optimization method. Carbon emission is also determined for each generated mix configuration following the method presented earlier. Strength is maximized while carbon emission is minimized under the boundary conditions applied on the volumetric fractions of the various components (Table 3). The GA optimizer was run with a population size of 200 individuals and a maximum iteration number of 3000. The crossover and mutation rates were fixed at 0.8 and 0.05, respectively. Convergence was assumed when simulations showed no improvement for 30 successive iterations.
As a multi-objective problem, the optimization task under consideration necessitates the generation of a comprehensive set of potential solutions, which are delineated as those capable of optimally fulfilling the dual objectives (compressive strength and carbon footprint), each exhibiting varying degrees of performance. These solutions are referred to as Pareto optimal or nondominated solutions. In the context of a multi-objective minimization problem, a possible solution is classified as Pareto optimal if there exists no feasible vector of optimization variables that can enhance the values of any objective function without simultaneously inducing a deterioration in the values of other objectives [53,54]. Consequently, the selection of the solution occurs from among the mutually nondominated candidates. Pareto analysis is the only mathematical means to deal with the results of a multi-objective optimization task [55]. Figure 9 displays the Pareto optimal solutions for the two objectives that were found using GA optimization.
In order to investigate some of the generated Pareto solutions, some optimized mix designs are displayed in Figure 10. Optimization results are displayed for nine values of the cement volumetric fractions ranging from 200 kg/m3 to 600 kg/m3. Each bar in Figure 10a represents the maximum compressive strength obtained for the corresponding cement content. Values are averaged over five optimization runs using GA optimization. The standard variation in the maximum compressive strength is also displayed for each bar. Carbon emissions are also displayed with respect to the cement content for the optimal solutions. It is noticed that compressive strength exceeding 80 MPa can be obtained with an optimized mix for cement content starting from 400 kg/m3. Results also show a strong correlation between cement volumetric fraction and both compressive strength and carbon footprint.
A sample optimized mix configuration is presented in Table 5. The mix configuration corresponds to a cement content of 500 kg/m3 which is a typical value for high-strength concretes [56]. Using this mix configuration, the model predicts a compressive strength of 95 MPa at 28 days and carbon emissions that approximate 498 kg/m3.
The GPR-based models trained using the employed dataset (356 records) show promising potential to be generalized and used for mix design optimization. There are still great improvement possibilities of the suggested methodology through the amelioration of the ML model and its prediction performance. In the first place, the dataset can be enriched by including new records based on recently published experimental studies dealing with the compression strength of HPC. Secondly, the data-driven model can be optimized for a higher prediction performance using the great advancements realized in machine learning. The study’s initial findings highlight the promise of data-driven models that can be used for little to no expense in place of costly and time-consuming experimental research. Furthermore, data-driven models based on actual experimental data are obviously more accurate than simple empirical formulations. As for the concrete mix optimization methodology, although high compressive strength may be obtained, this is achieved at the cost of a high cement volumetric fraction. Unfortunately, high cement content is not only expensive but also harmful to the environment because of the high carbon footprint of cement. This aspect is handled in this study and could be part of future research into mix design optimization that considers financial and environmental aspects of HPC production.

6. Conclusions

In this paper, data-driven models are proposed to predict the compressive strength of high-performance concrete. The proposed models are trained based on experimental datasets collected from recently published studies. Three ML algorithms are employed and compared for data training: artificial neural networks (ANNs), ensemble techniques (ETs), and Gaussian process regression (GPR). The data-driven models are then employed to perform multi-objective mix design optimization, allowing for the determination of the volumetric fractions of the various concrete components leading to a maximized compressive strength and a reduced carbon footprint. The main conclusions of this research work are summarized hereafter.
-
The ML algorithms tested all showed comparable performance, with the determination coefficient ranging between 0.88 and 0.93. For the reduced dataset, the determination coefficients were slightly lower but still showing a good correlation (R2 ranging from 0.8 to 0.89).
-
The best predictive performance was obtained using the GPR algorithm. The model trained using 356 records has a determination coefficient of 0.93, which is comparable with the findings of many published research works using similar datasets. The compressive strength at 28 days is typically considered the design strength, which justifies the investigation of a data-driven model to predict the compressive strength specifically after 28 days from concrete casting.
-
The prediction model is used as the fitness function, and boundary constraints are defined based on the lower and the upper limits for the volumetric fraction of the concrete components. Optimization employing genetic algorithms allowed for the determination of the Pareto optimal mix configuration, leading to the best compromise between the concrete compressive strength and its carbon footprint. The proposed optimization framework can be improved through the consideration of financial and environmental aspects.
-
Performance differences in supplementary cementitious materials (SCMs) from different regions may affect the stability of the model. In addition, mix proportioning or workability could be optimized in a more comprehensive view of the HPC optimization task. These points could be part of future endeavors.
Finally, the limitations associated with experimentally obtaining physical quantities and the errors typically related to simple analytical models can be overcome by adapting the data-driven modeling and optimization methodology proposed here for the compressive strength of high-performance concrete to be effectively used for other physical properties.

Author Contributions

Conceptualization, S.H.; methodology, N.B.H.A.; software, N.B.H.A.; validation, S.H.; formal analysis, B.A. and N.B.H.A.; writing—original draft, S.H. and N.B.H.A.; writing—review and editing, S.H., S.A., M.A. and B.A.; visualization, S.H., S.A. and M.A.; supervision, N.B.H.A.; funding acquisition, S.A., M.A. and B.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. O’Hegarty, R.; Kinnane, O.; Newell, J.; West, R. High performance, low carbon concrete for building cladding applications. J. Build. Eng. 2021, 43, 102566. [Google Scholar] [CrossRef]
  2. El-Abbasy, A.A. Production, behaviour and mechanical properties of ultra-high-performance fiber concrete—A comprehensive review. Case Stud. Constr. Mater. 2022, 17, e01637. [Google Scholar] [CrossRef]
  3. Wang, S.; Wang, B.; Zhu, H.; Chen, G.; Li, Z.; Yang, L.; Zhang, Y.; Zhou, X. Ultra-high performance concrete: Mix design, raw materials and curing regimes-A review. Mater. Today Commun. 2023, 35, 105468. [Google Scholar] [CrossRef]
  4. Han, Y.; Zhou, T. Performance Analysis of High-Performance Concrete Materials in Civil Construction. Materials 2023, 16, 5711. [Google Scholar] [CrossRef] [PubMed]
  5. Zhang, Y.; Sun, W.; Liu, S. Study on the hydration heat of binder paste in high-performance concrete. Cem. Concr. Res. 2002, 32, 1483–1488. [Google Scholar] [CrossRef]
  6. Dushimimana, A.; Niyonsenga, A.A.; Nzamurambaho, F. A review on strength development of high performance concrete. Constr. Build. Mater. 2021, 307, 124865. [Google Scholar] [CrossRef]
  7. Jibril, M.M.; Zayyan, M.A.; Malami, S.I.; Usman, A.G.; Salami, B.A.; Rotimi, A.; Abba, S.I. Implementation of nonlinear computing models and classical regression for predicting compressive strength of high-performance concrete. Appl. Eng. Sci. 2023, 15, 100133. [Google Scholar] [CrossRef]
  8. Moula, S.; Ben Fraj, A.; Wattez, T.; Bouasker, M.; Hadj Ali, N.B. Mechanical properties, carbon footprint and cost of ultra-high performance concrete containing ground granulated blast furnace slag. J. Build. Eng. 2023, 79, 107796. [Google Scholar] [CrossRef]
  9. Naser, M.Z.; Kodur, V.; Thai, H.-T.; Hawileh, R.; Abdalla, J.; Degtyarev, V.V. StructuresNet and FireNet: Benchmarking databases and machine learning algorithms in structural and fire engineering domains. J. Build. Eng. 2021, 44, 102977. [Google Scholar] [CrossRef]
  10. Naser, M.Z. Machine learning for all! Benchmarking automated, explainable, and coding-free platforms on civil and environmental engineering problems. J. Infrastruct. Intell. Resil. 2023, 2, 100028. [Google Scholar] [CrossRef]
  11. Wan, S.; Li, S.; Chen, Z.; Tang, Y. An ultrasonic-AI hybrid approach for predicting void defects in concrete-filled steel tubes via enhanced XGBoost with Bayesian optimization. Case Stud. Constr. Mater. 2025, 22, e04359. [Google Scholar] [CrossRef]
  12. Yeh, I.C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
  13. Yu, Y.; Li, W.; Li, J.; Nguyen, T.N. A novel optimised self-learning method for compressive strength prediction of high performance concrete. Constr. Build. Mater. 2018, 184, 229–247. [Google Scholar] [CrossRef]
  14. Bui, D.-K.; Nguyen, T.; Chou, J.-S.; Nguyen-Xuan, H.; Ngo, T.D. A modified firefly algorithm-artificial neural network expert system for predicting compressive and tensile strength of high-performance concrete. Constr. Build. Mater. 2018, 180, 320–333. [Google Scholar] [CrossRef]
  15. Moayedi, H.; Foong, L.K.; Le, B.N. Three intelligent computational models to predict the high-performance concrete mixture. Neural Comput. Appl. 2023, 36, 3479–3498. [Google Scholar] [CrossRef]
  16. Han, Q.; Gui, C.; Xu, J.; Lacidogna, G. A generalized method to predict the compressive strength of high-performance concrete by improved random forest algorithm. Constr. Build. Mater. 2019, 226, 734–742. [Google Scholar] [CrossRef]
  17. Hameed, M.M.; AlOmar, M.K.; Baniya, W.J.; AlSaadi, M.A. Incorporation of artificial neural network with principal component analysis and cross-validation technique to predict high-performance concrete compressive strength. Asian J. Civ. Eng. 2021, 22, 1019–1031. [Google Scholar] [CrossRef]
  18. Anyaoha, U.; Zaji, A.; Liu, Z. Soft computing in estimating the compressive strength for high-performance concrete via concrete composition appraisal. Constr. Build. Mater. 2020, 257, 119472. [Google Scholar] [CrossRef]
  19. Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modeling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
  20. Li, Q.-F.; Song, Z.-M. High-performance concrete strength prediction based on ensemble learning. Constr. Build. Mater. 2022, 324, 126694. [Google Scholar] [CrossRef]
  21. Liu, X.; Zhang, Y.; Lei, S.; Yang, S. Estimating the mechanical properties of high-performance concrete via automated and ensembled machine learning methods. Mater. Today Commun. 2023, 37, 107386. [Google Scholar] [CrossRef]
  22. Imran, M.; Khushnood, R.A.; Fawad, M. A hybrid data-driven and metaheuristic optimization approach for the compressive strength prediction of high-performance concrete. Case Stud. Constr. Mater. 2023, 18, e01890. [Google Scholar] [CrossRef]
  23. Fantilli, A.P.; Mancinelli, O.; Chiaia, B. The carbon footprint of normal and high-strength concrete used in low-rise and high-rise buildings. Case Stud. Constr. Mater. 2019, 11, e00296. [Google Scholar] [CrossRef]
  24. United Nations Environment Programme. Building Materials and the Climate: Constructing a New Future; United Nations Environment Programme: Paris, France, 2023. [Google Scholar]
  25. Adhikari, S.; Chougale, J.B.; Radke, A. A Review on the Investigation of Durability Performance of High-Performance Concrete with Cementitious Materials. Int. Res. J. Adv. Eng. Hub (IRJAEH) 2024, 2, 622–628. [Google Scholar] [CrossRef]
  26. Wałach, D.; Mach, A. Effect of Concrete Mix Composition on Greenhouse Gas Emissions over the Full Life Cycle of a Structure. Energies 2023, 16, 3229. [Google Scholar] [CrossRef]
  27. Rajagopal, M.R.; Pamu, Y.; Anusha, I. Comparative analysis of environmental footprints: Conventional versus high-strength concrete in construction. IOP Conf. Ser. Earth Environ. Sci. 2024, 1409, 012007. [Google Scholar] [CrossRef]
  28. Golafshani, E.M.; Behnood, A.; Kim, T.; Ngo, T.; Kashani, A. A framework for low-carbon mix design of recycled aggregate concrete with supplementary cementitious materials using machine learning and optimization algorithms. Structures 2024, 61, 106143. [Google Scholar] [CrossRef]
  29. Wang, M.; Du, M.; Jia, Y.; Chang, C.; Zhou, S. Carbon Emission Optimization of Ultra-High-Performance Concrete Using Machine Learning Methods. Materials 2024, 17, 1670. [Google Scholar] [CrossRef]
  30. Sun, C.; Wang, K.; Liu, Q.; Wang, P.; Pan, F. Machine-Learning-Based Comprehensive Properties Prediction and Mixture Design Optimization of Ultra-High-Performance Concrete. Sustainability 2023, 15, 15338. [Google Scholar] [CrossRef]
  31. Wakjira, T.G.; Kutty, A.A.; Alam, M.S. A novel framework for developing environmentally sustainable and cost-effective ultra-high-performance concrete (UHPC) using advanced machine learning and multi-objective optimization techniques. Constr. Build. Mater. 2024, 416, 135114. [Google Scholar] [CrossRef]
  32. Jin, L.; Zhang, Y.; Liu, P.; Fan, T.; Wu, T.; Wu, Q. Carbon-footprint based concrete proportion design using LSTM and MOPSO algorithms. Mater. Today Commun. 2024, 38, 107837. [Google Scholar] [CrossRef]
  33. Rahman, M.A.; Lu, Y. EcoBlendNet: A physics-informed neural network for optimizing supplementary material replacement to reduce the carbon footprint during cement hydration. J. Clean. Prod. 2024, 464, 142777. [Google Scholar] [CrossRef]
  34. Li, Y.; Shen, J.; Lin, H.; Li, Y. Optimization design for alkali-activated slag-fly ash geopolymer concrete based on artificial intelligence considering compressive strength, cost, and carbon emission. J. Build. Eng. 2023, 75, 106929. [Google Scholar] [CrossRef]
  35. Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
  36. UCI. UC Irvine Machine Learning Repository. Available online: https://archive.ics.uci.edu/ (accessed on 22 July 2025).
  37. Wang, L.; Ma, Y.; Li, L. Uncovering the role of superplasticizer in developing nano-engineered ultra-high-performance concrete. Front. Mater. 2023, 10, 1177189. [Google Scholar] [CrossRef]
  38. Wang, X.-Y. Simulation for optimal mixture design of low-CO2 high-volume fly ash concrete considering climate change and CO2 uptake. Cem. Concr. Compos. 2019, 104, 103408. [Google Scholar] [CrossRef]
  39. Jones, C.; Hammond, G. Embodied Carbon—The ICE Database. Available online: https://circularecology.com/embodied-carbon-footprint-database.html (accessed on 22 July 2025).
  40. Ciaburro, G. MATLAB for Machine Learning: Practical Examples of Regression, Clustering and Neural Networks; Packt Publishing: Birmingham, UK, 2017. [Google Scholar]
  41. James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2014. [Google Scholar]
  42. Wong, T.T.; Yang, N.Y. Dependency Analysis of Accuracy Estimates in k-Fold Cross Validation. IEEE Trans. Knowl. Data Eng. 2017, 29, 2417–2427. [Google Scholar] [CrossRef]
  43. Williams, C.K.I.; Rasmussen, C.E. Gaussian processes for regression. In Proceedings of the Advances in Neural Information Processing Systems 8, San Francisco, CA, USA, 13–17 August 2016; pp. 290–297. [Google Scholar]
  44. Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
  45. González, S.; García, S.; Del Ser, J.; Rokach, L.; Herrera, F. A practical tutorial on bagging and boosting based ensembles for machine learning: Algorithms, software tools, performance study, practical perspectives and opportunities. Inf. Fusion 2020, 64, 205–237. [Google Scholar] [CrossRef]
  46. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
  47. Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
  48. Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
  49. Yang, X.-S. Chapter 5—Genetic Algorithms. In Nature-Inspired Optimization Algorithms; Yang, X.-S., Ed.; Elsevier: Oxford, UK, 2014; pp. 77–87. [Google Scholar]
  50. Zhang, Y.; Ren, W.; Chen, Y.; Mi, Y.; Lei, J.; Sun, L. Predicting the compressive strength of high-performance concrete using an interpretable machine learning model. Sci. Rep. 2024, 14, 28346. [Google Scholar] [CrossRef] [PubMed]
  51. Vu-Bac, N.; Le-Anh, T.; Rabczuk, T. A Machine Learning based uncertainty quantification for compressive strength of high-performance concrete. Front. Struct. Civ. Eng. 2025, 19, 824–836. [Google Scholar] [CrossRef]
  52. Kang, J.; Gao, J.; Liu, X. Machine learning for predicting the compressive strength of high-performance concrete materials. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 403. [Google Scholar] [CrossRef]
  53. Selmi, M.; Kormi, T.; Ali, N.B.H. Comparison of multi-criteria decision methods through a ranking stability index. Int. J. Oper. Res. 2016, 27, 165–183. [Google Scholar] [CrossRef]
  54. Coello, C.A.C.; Lamont, G.B.; Veldhuizen, D.A.V. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
  55. Selmi, M.; Kormi, T.; Ali, N.B.H. Comparing Multi-Criteria Decision aid methods through a ranking stability index. In Proceedings of the 2013 5th International Conference on Modeling, Simulation and Applied Optimization (ICMSAO), Hammamet, Tunisia, 28–30 April 2013; pp. 1–5. [Google Scholar]
  56. Leung, C.K.Y. Concrete as a Building Material. In Encyclopedia of Materials: Science and Technology; Buschow, K.H.J., Cahn, R.W., Flemings, M.C., Ilschner, B., Kramer, E.J., Mahajan, S., Veyssière, P., Eds.; Elsevier: Oxford, UK, 2001; pp. 1471–1479. [Google Scholar]
Sustainability 17 07808 g001
Figure 1. Data was obtained from the Scopus database by utilizing the keywords “high-performance concrete” and “machine learning”. (a) The number of papers published each year and (b) the distribution of these publications among the many disciplines of study.
Figure 1. Data was obtained from the Scopus database by utilizing the keywords “high-performance concrete” and “machine learning”. (a) The number of papers published each year and (b) the distribution of these publications among the many disciplines of study.
Sustainability 17 07808 g001
Sustainability 17 07808 g002
Figure 2. Compressive strength of the dataset mixes with respect to the water-to-cement ratio.
Figure 2. Compressive strength of the dataset mixes with respect to the water-to-cement ratio.
Sustainability 17 07808 g002
Sustainability 17 07808 g003
Figure 3. Compressive strength of the dataset mixes with respect to the water-to-binder ratio.
Figure 3. Compressive strength of the dataset mixes with respect to the water-to-binder ratio.
Sustainability 17 07808 g003
Sustainability 17 07808 g004
Figure 4. Compressive strength of the dataset mixes with respect to the superplasticizer-to-binder ratio.
Figure 4. Compressive strength of the dataset mixes with respect to the superplasticizer-to-binder ratio.
Sustainability 17 07808 g004
Sustainability 17 07808 g005
Figure 5. Predicted versus measured compressive strengths for HPC using Gaussian process regression.
Figure 5. Predicted versus measured compressive strengths for HPC using Gaussian process regression.
Sustainability 17 07808 g005
Sustainability 17 07808 g006
Figure 6. Evolution of HPC compressive strength with respect to the water-to-cement ratio (a) and with respect to the binder-to-cement ratio (b) for different cement content classes.
Figure 6. Evolution of HPC compressive strength with respect to the water-to-cement ratio (a) and with respect to the binder-to-cement ratio (b) for different cement content classes.
Sustainability 17 07808 g006
Sustainability 17 07808 g007
Figure 7. Evolution of HPC compressive strength (a) and carbon emissions (b) with respect to the SCM-to-cement ratio.
Figure 7. Evolution of HPC compressive strength (a) and carbon emissions (b) with respect to the SCM-to-cement ratio.
Sustainability 17 07808 g007
Sustainability 17 07808 g008
Figure 8. Evolution of HPC compressive strength with respect to the superplasticizer-to-binder ratio.
Figure 8. Evolution of HPC compressive strength with respect to the superplasticizer-to-binder ratio.
Sustainability 17 07808 g008
Sustainability 17 07808 g009
Figure 9. Optimal values of the 28-day compressive strength with respect to the cement volumetric fraction.
Figure 9. Optimal values of the 28-day compressive strength with respect to the cement volumetric fraction.
Sustainability 17 07808 g009
Sustainability 17 07808 g010
Figure 10. (a) Average compressive strength and (b) carbon footprint with respect to cement content for nine Pareto optimal solutions.
Figure 10. (a) Average compressive strength and (b) carbon footprint with respect to cement content for nine Pareto optimal solutions.
Sustainability 17 07808 g010
Table 1. Statistics of dataset variables.
Table 1. Statistics of dataset variables.
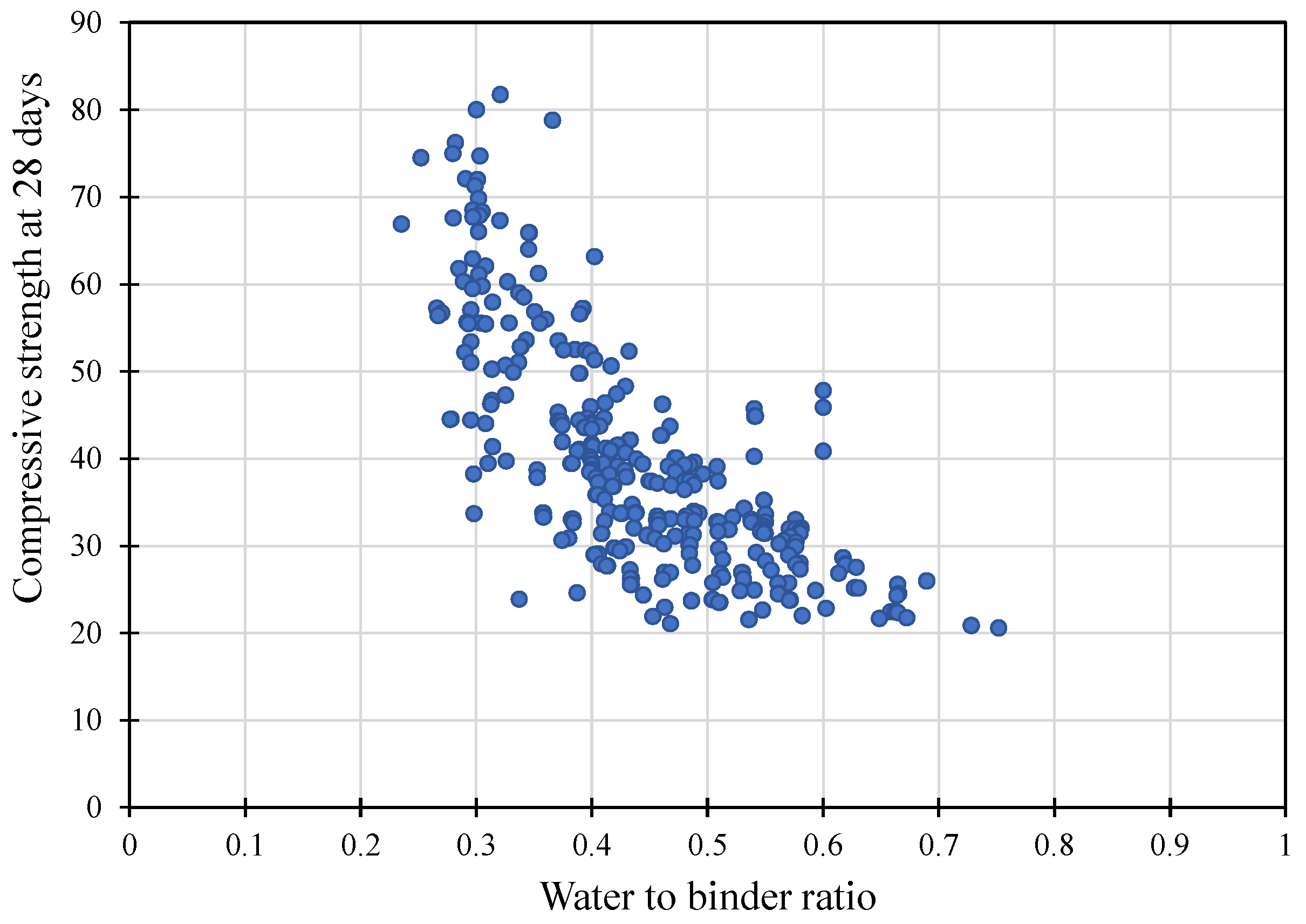
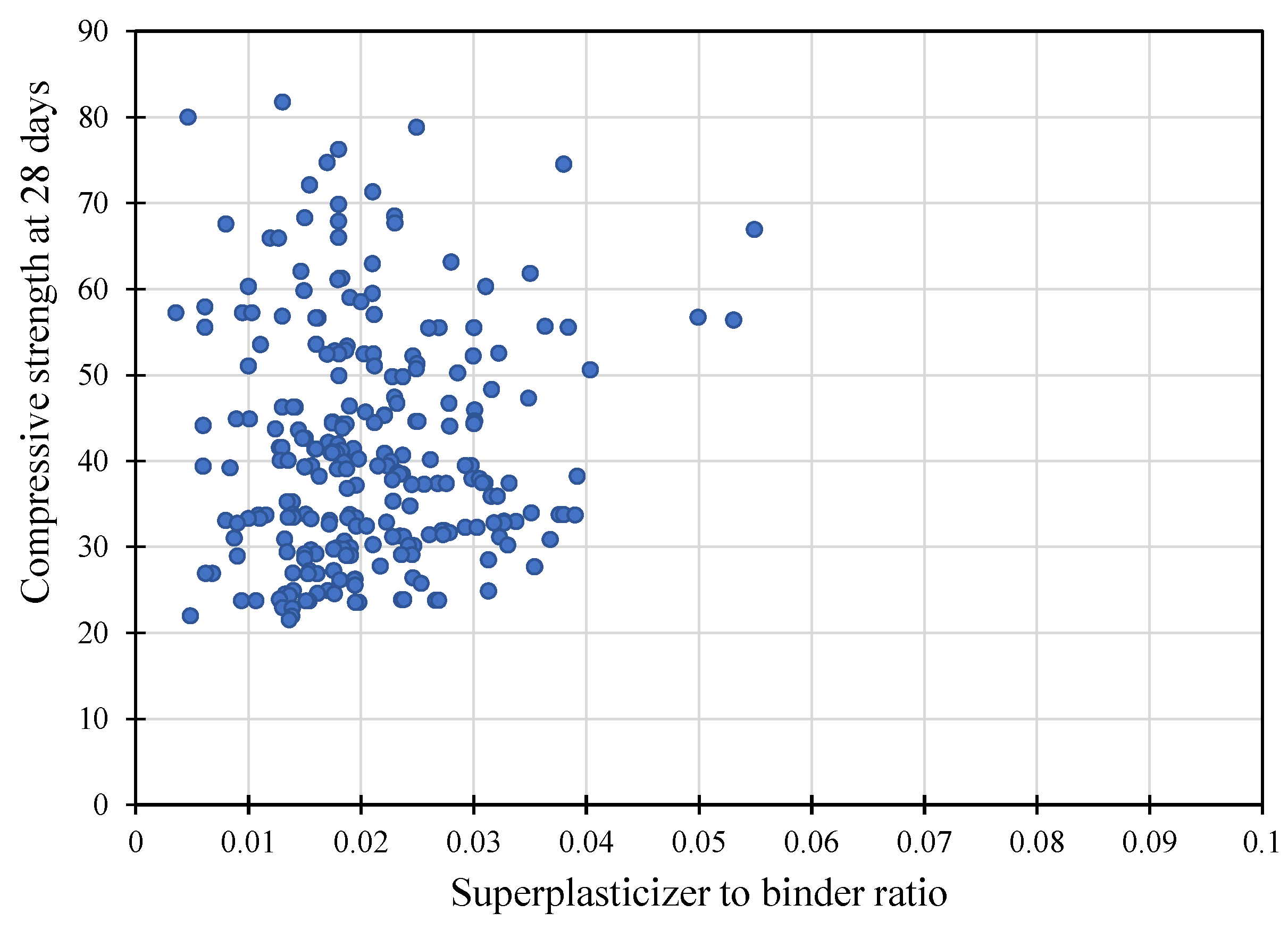
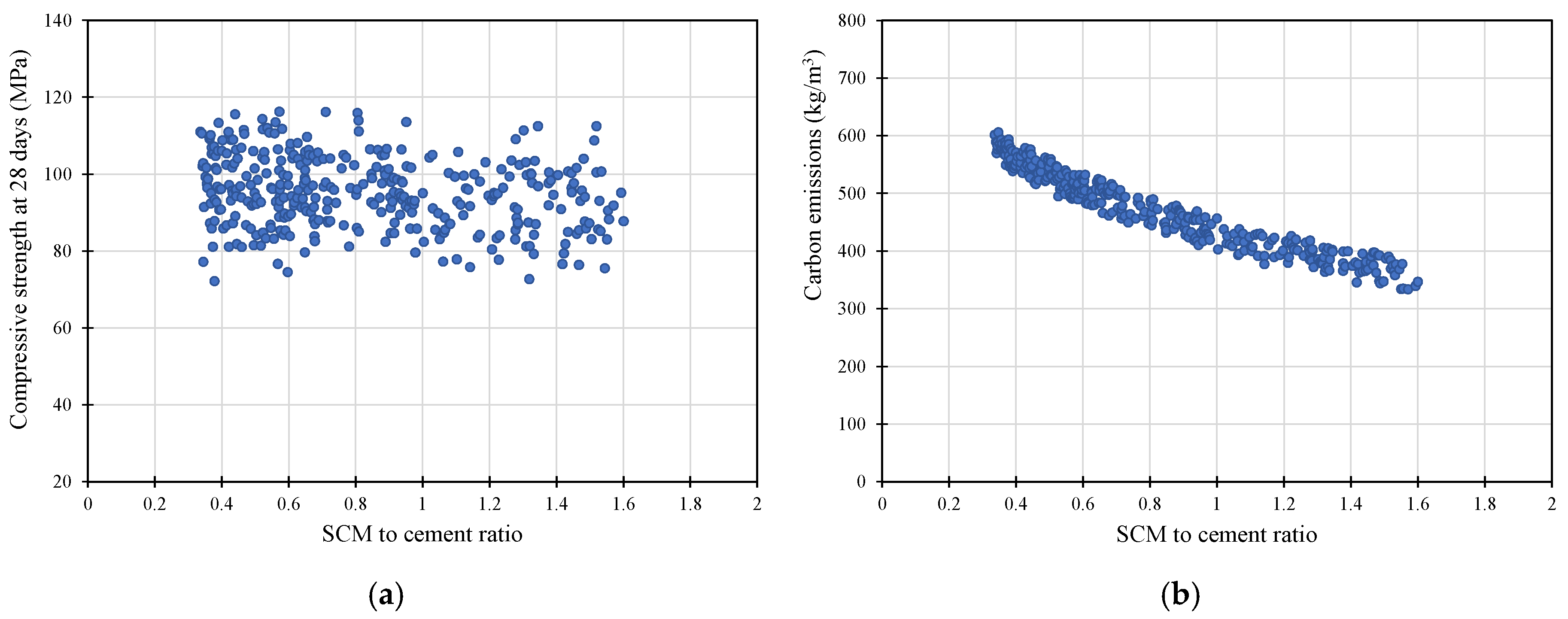
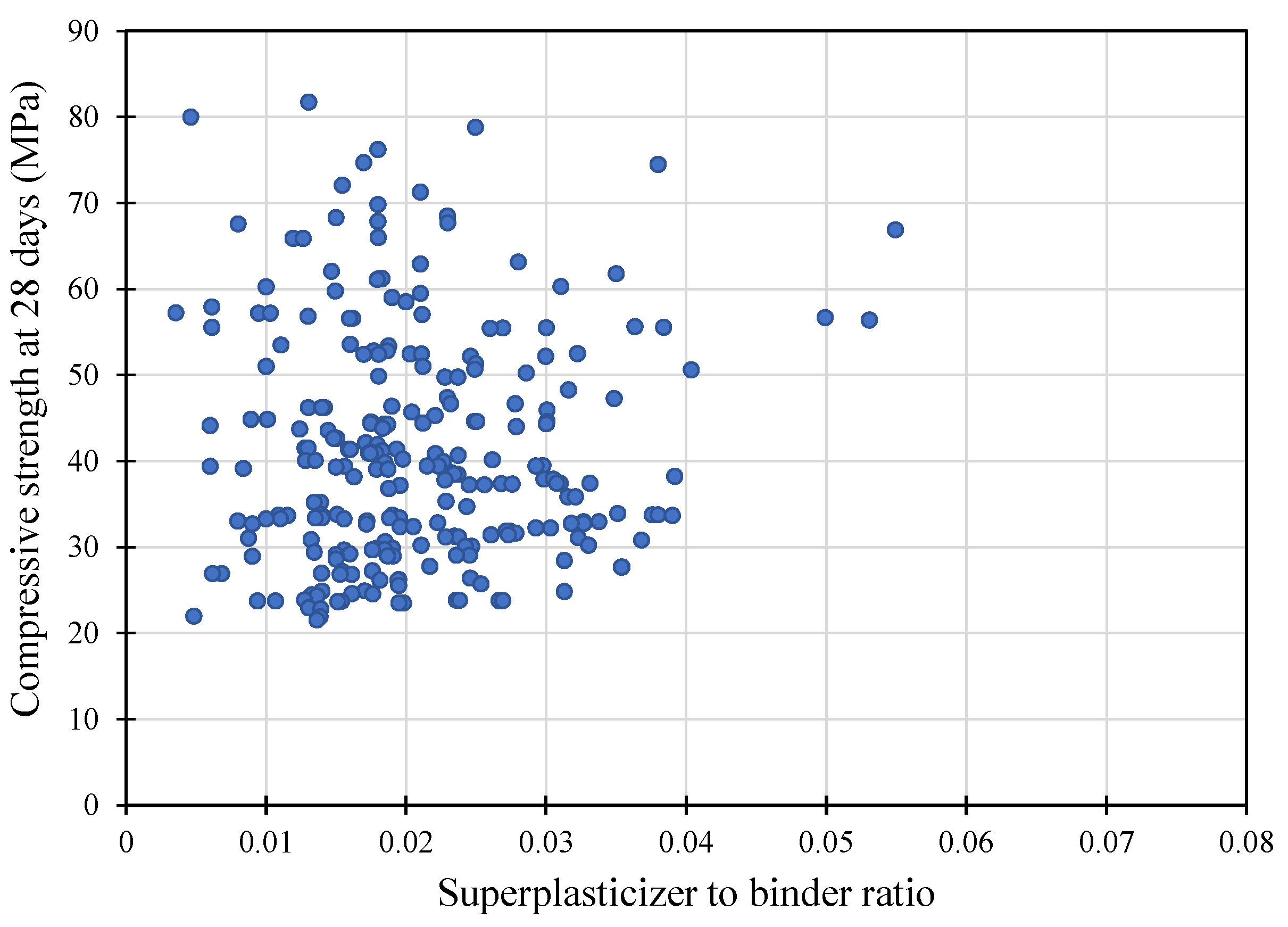
VariableMinMaxMedianMeanStd. Dev.
Cement (kg/m3)108.3540282.5279.3103.1
Blast Furnace Slag (kg/m3)0359.4100.592.788.4
Fly Ash (kg/m3)019512.258.362.4
Water (kg/m3)126.6247185182.819.6
Superplasticizer (kg/m3)032.27.056.95.3
Coarse Aggregate (kg/m3)8011134.3950.4951.582.3
Fine Aggregate (kg/m3)594992.6764.2760.171.9
28-day Compressive Strength (MPa)20.681.737.439.713.0
Table 2. Carbon emissions from HPC components.
Table 2. Carbon emissions from HPC components.
MaterialsCarbon Emission (kg/ton)References
Cement880[8,38]
Blast Furnace Slag100[8]
Fly Ash19.6[29,38]
Superplasticizer1880[39]
Coarse Aggregate7.5[39]
Fine Aggregate7.5[39]
Water0.2[29,38]
Table 3. Boundary values for the optimization variables.
Table 3. Boundary values for the optimization variables.
VariableMinMax
Cement (kg/m3)100550
Blast Furnace Slag (kg/m3)0400
Fly Ash (kg/m3)0200
Water (kg/m3)120250
Superplasticizer (kg/m3)040
Coarse Aggregate (kg/m3)8001200
Fine Aggregate (kg/m3)5001000
Table 4. Performances of the studied ML algorithms in modeling the compressive strength of HPC.
Table 4. Performances of the studied ML algorithms in modeling the compressive strength of HPC.
OutputML AlgorithmMetrics
RMSER2MAE
Compressive Strength
(28 days)		Gaussian Process Regression4.56450.933.0930
Ensemble Technique5.00020.913.5314
Artificial Neural Network5.76470.884.1764
Table 5. Optimized mix configuration for a typical HPC.
Table 5. Optimized mix configuration for a typical HPC.
Concrete ComponentVolumetric Fraction (kg/m3)
Cement (kg/m3)500
Blast Furnace Slag (kg/m3)364.2
Fly Ash (kg/m3)17.9
Water (kg/m3)156.55
Superplasticizer (kg/m3)18.161
Coarse Aggregate (kg/m3)1113.9
Fine Aggregate (kg/m3)917.88
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Helali, S.; Albalawi, S.; Alanazi, M.; Alanazi, B.; Bel Hadj Ali, N. Optimizing Carbon Footprint and Strength in High-Performance Concrete Through Data-Driven Modeling. Sustainability 2025, 17, 7808. https://doi.org/10.3390/su17177808

AMA Style

Helali S, Albalawi S, Alanazi M, Alanazi B, Bel Hadj Ali N. Optimizing Carbon Footprint and Strength in High-Performance Concrete Through Data-Driven Modeling. Sustainability. 2025; 17(17):7808. https://doi.org/10.3390/su17177808

Chicago/Turabian Style

Helali, Saloua, Shadiah Albalawi, Maer Alanazi, Bashayr Alanazi, and Nizar Bel Hadj Ali. 2025. "Optimizing Carbon Footprint and Strength in High-Performance Concrete Through Data-Driven Modeling" Sustainability 17, no. 17: 7808. https://doi.org/10.3390/su17177808

APA Style

Helali, S., Albalawi, S., Alanazi, M., Alanazi, B., & Bel Hadj Ali, N. (2025). Optimizing Carbon Footprint and Strength in High-Performance Concrete Through Data-Driven Modeling. Sustainability, 17(17), 7808. https://doi.org/10.3390/su17177808

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop