Estimating the Niche Breadth of Tomicus piniperda L. on Breeding Material: A Statistical Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Climatic Conditions in the Study Area
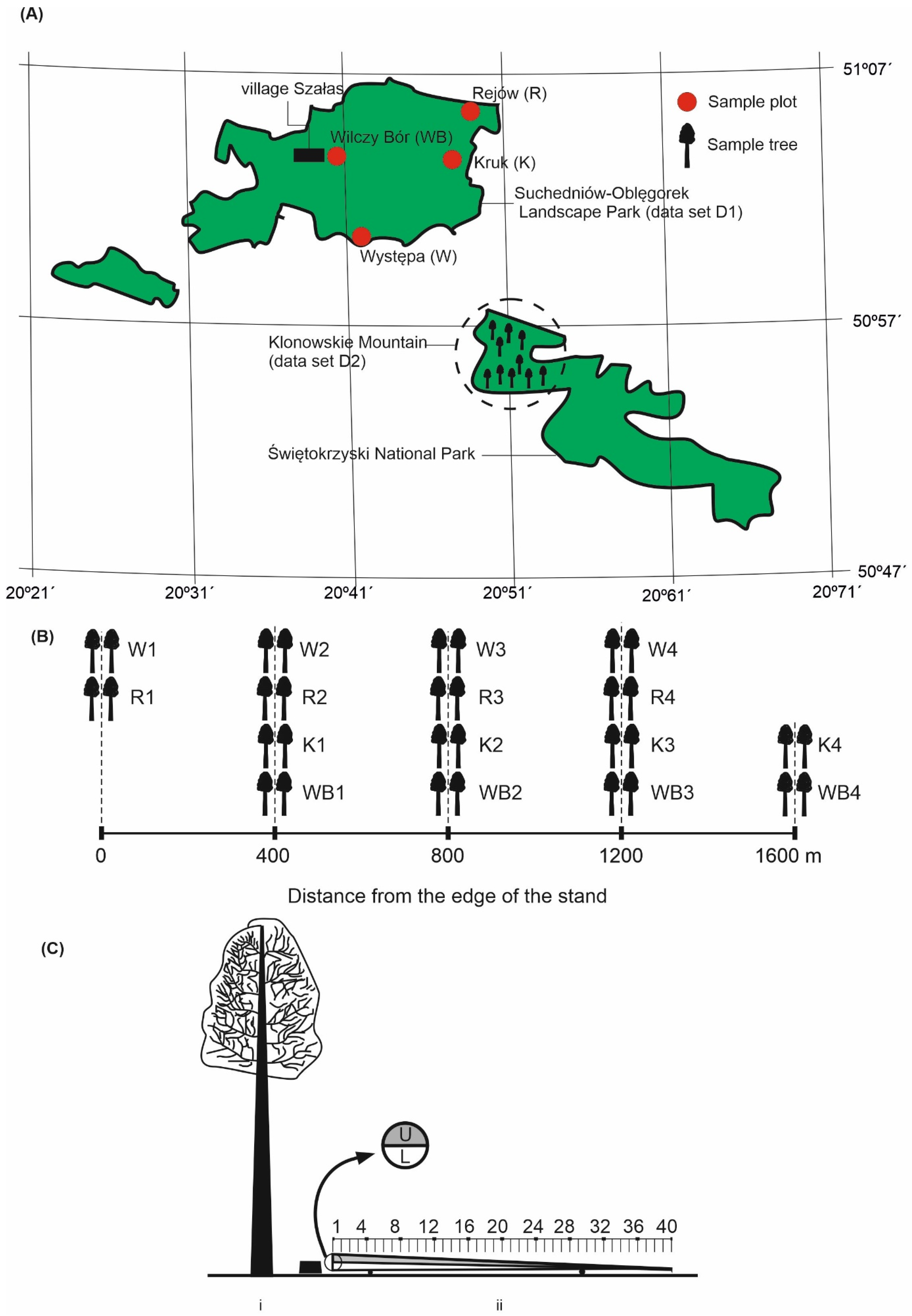
2.2. Sample Tree Dataset D1
- i.
- The initial and final stem diameter;
- ii.
- The initial diameter of the unit stem;
- iii.
- The total length;
- iv.
- The thickness of the bark at the midpoint of each stem unit, using the same method as was used to measure the bark thickness at breast height.
2.3. Sample Tree Dataset D2
2.4. Measures Used to Describe the Niche Breadth of Bark Beetles
2.5. Analysis of the Distribution of T. piniperda Galleries on Stems
2.6. Model Construction Procedure for T. piniperda Niche on Stems
2.6.1. Stepwise Regression Model Construction Process
2.6.2. Model Parameterisation Stages
- Infestation density (number of galleries/m2) for stem units (du) and upper sections (dhu).
- Stem characteristics:
- -
- Initial diameter of the stem;
- -
- Stem diameter and bark thickness at breast height;
- -
- Length of the stem with a bark thickness greater than 1, 2, …, 20 mm (l>1, l>2, …, l>20).
- i.
- The relationship between the independent variables and the dependent variable;
- ii.
- The relationships between independent variables were examined by calculating the variance inflation factor (VIF) [57]:
- iii.
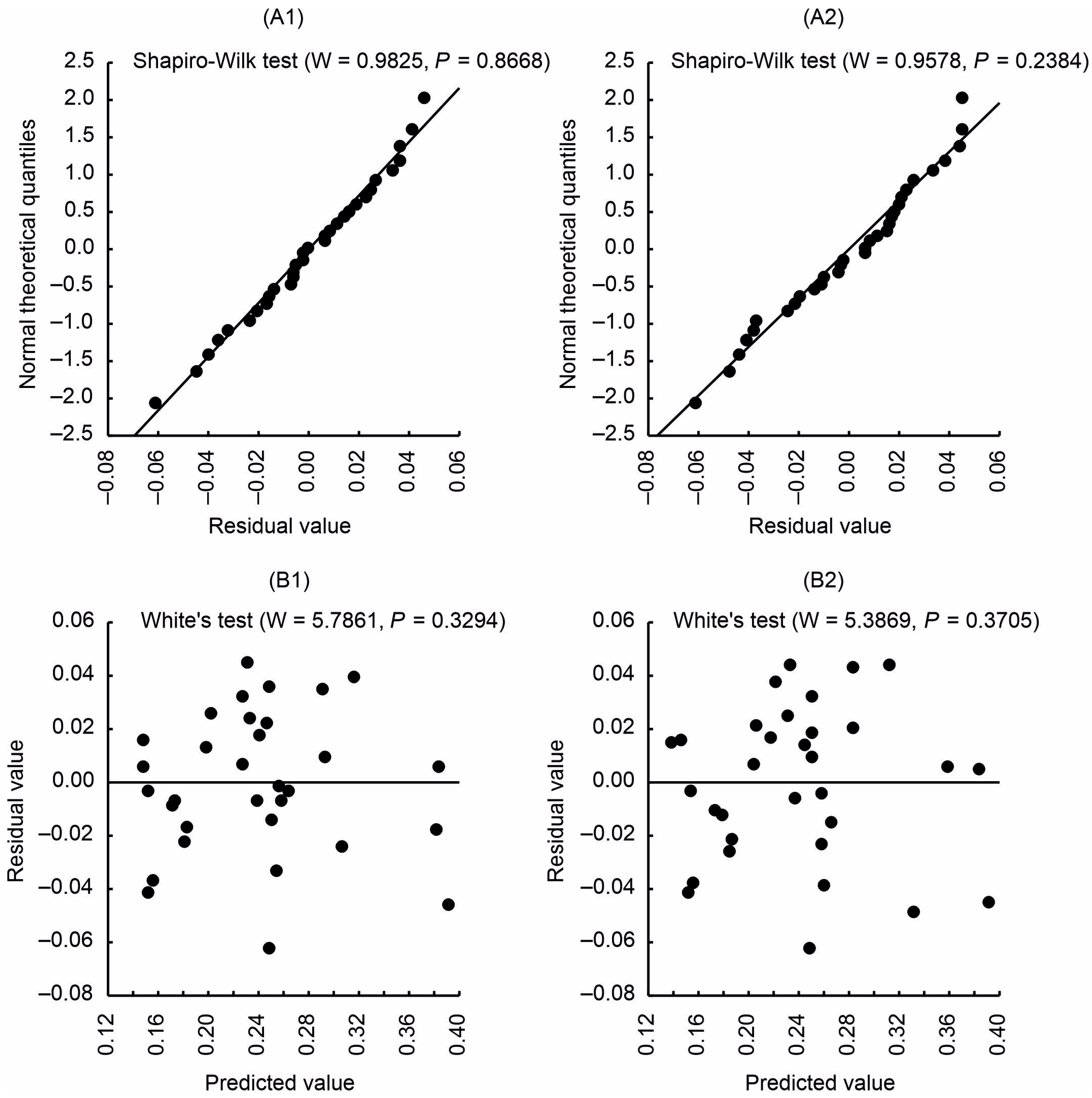
- The distribution of regression residuals was analysed using White’s test [58]:
- iv.
- The Shapiro–Wilk test was used to check whether the residuals were normally distributed.
2.6.3. Assessment of the Accuracy of the Constructed Model
3. Results
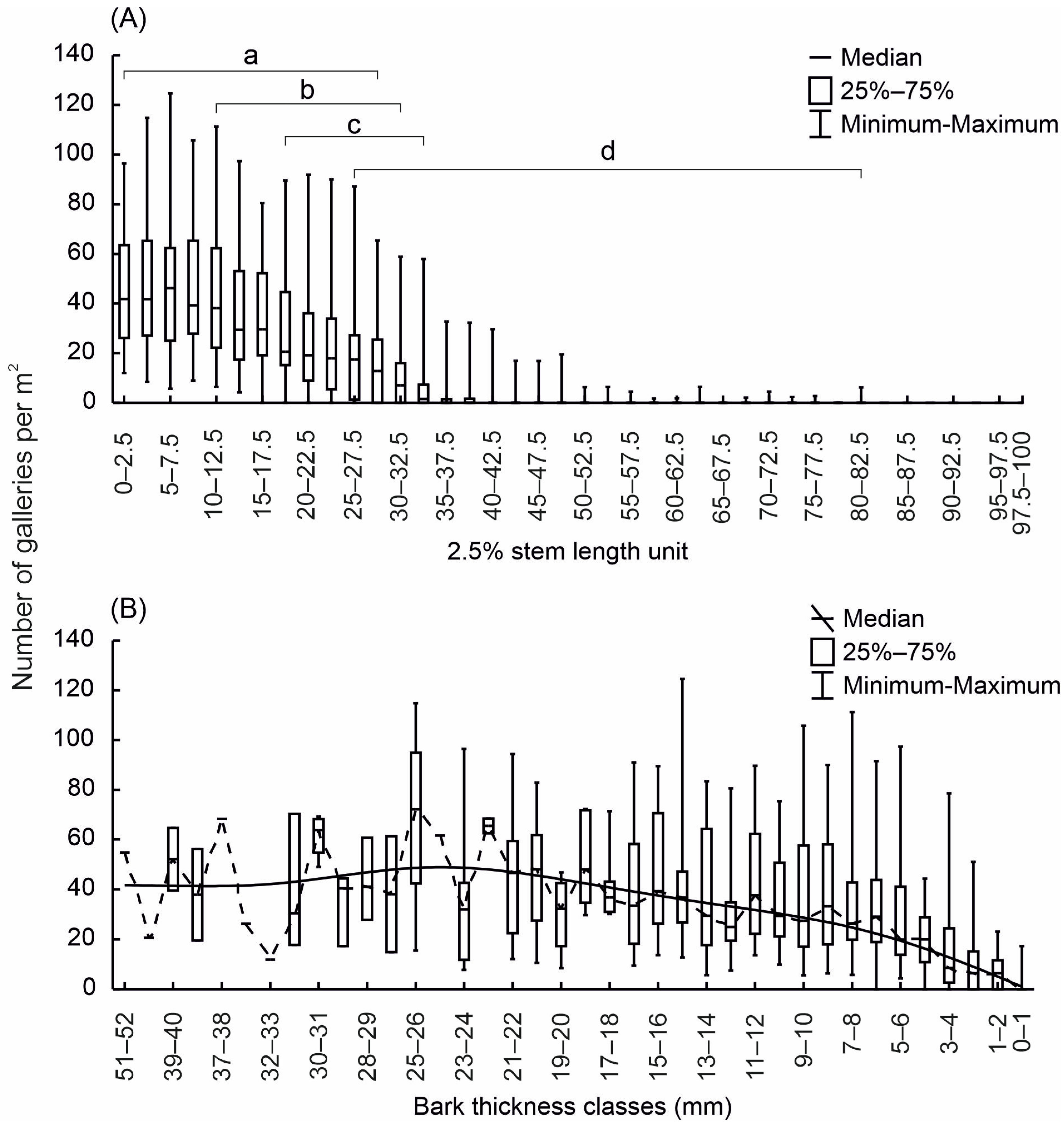
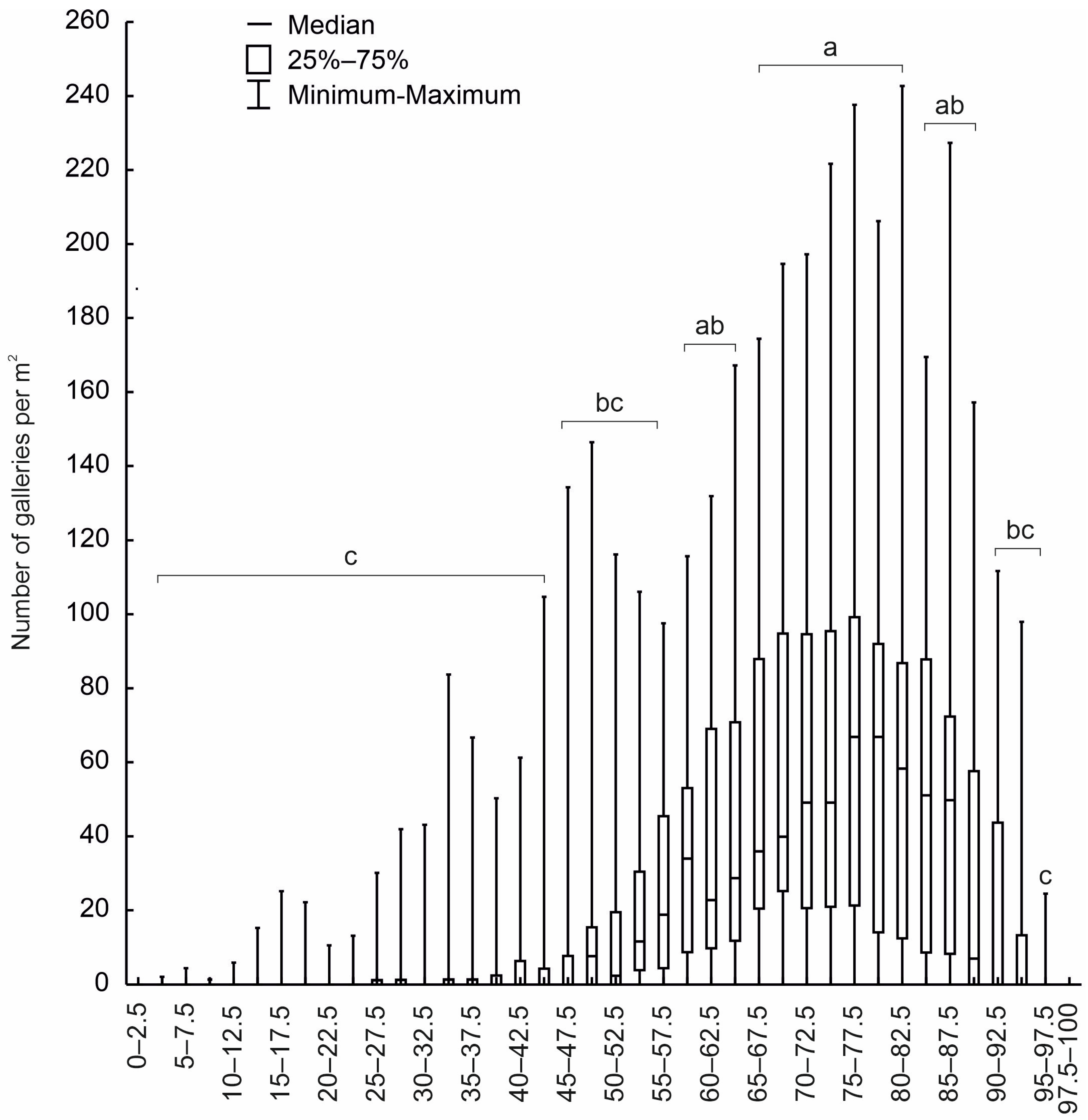
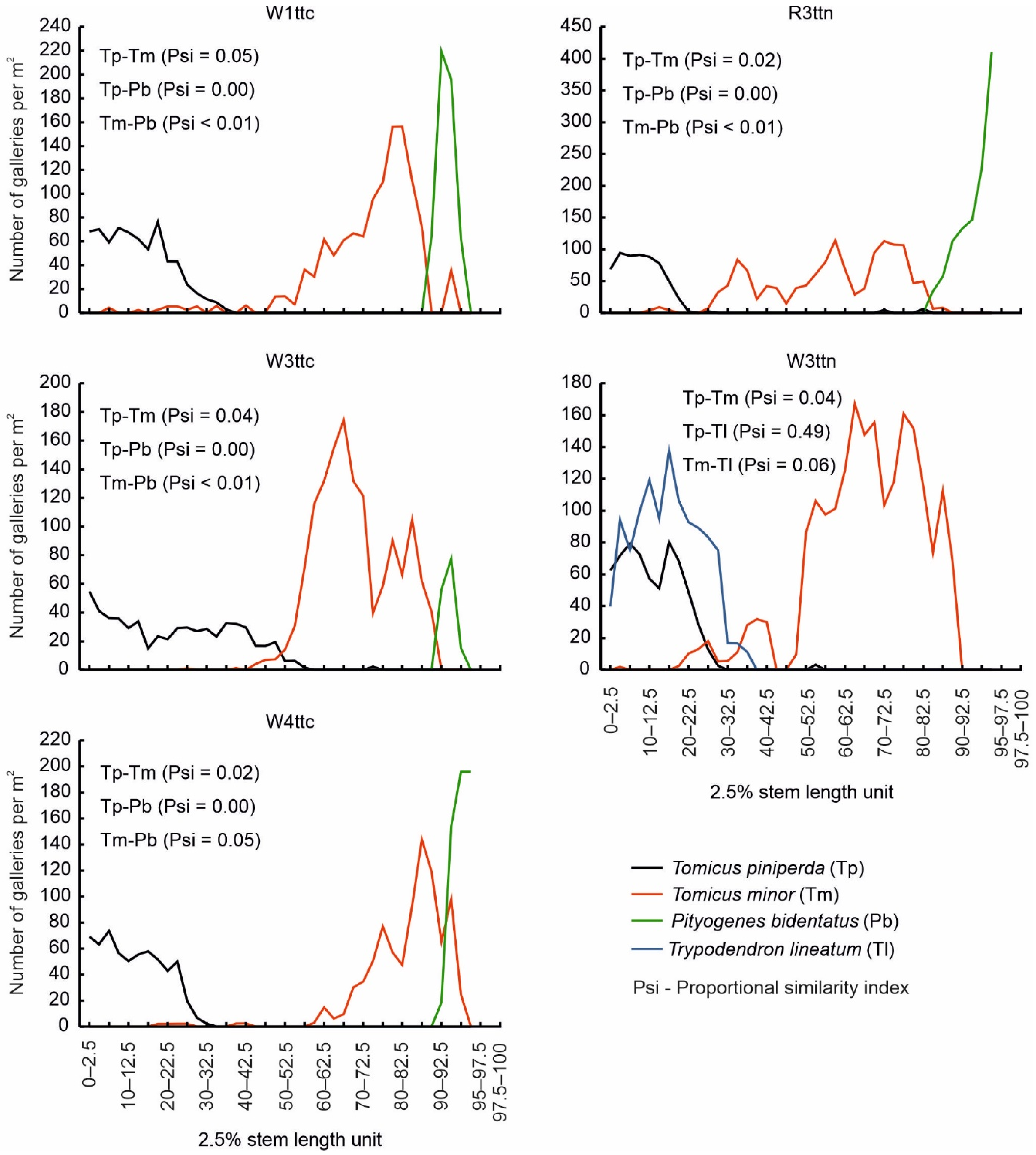
3.1. Analysis of the Colonisation of Trap Trees by Bark Beetles (Dataset D1)
3.2. Analysis of the Colonisation of Windfalls by Tomicus piniperda (Dataset D2)
3.3. Evaluation of Tomicus Piniperda Niche Breadth on Stems
3.3.1. Parameterisation of the Model
- -
- Length of stems with a bark thickness greater than 4 mm (l>4);
- -
- Density of T. piniperda galleries on the 11th unit du11 (model I) and on the 11th upper section dhu11 (model II) of the stem.
3.3.2. Validation of the Model
4. Discussion
4.1. Methodological Assumptions
4.2. Evaluation and Validation of the Model
4.3. Application in the Analysis of T. piniperda Population Density
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The Intergovernmental Panel on Climate Change. Summary for Policymakers. In Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2018; pp. 3–24. [Google Scholar] [CrossRef]
- Rissanen, K.; Hölttä, T.; Bäck, J.; Rigling, A.; Wermelinger, B.; Gessler, A. Drought effects on carbon allocation to resin defences and on resin dynamics in old-grown Scots pine. Environ. Exp. Bot. 2021, 185, 104410. [Google Scholar] [CrossRef]
- McDowell, N.G.; Sapes, G.; Pivovaroff, A.L.; Adams, H.D. Mechanisms of woody-plant mortality under rising drought, CO2 and vapour pressure deficit. Nat. Rev. Earth Environ. 2022, 3, 294–308. [Google Scholar] [CrossRef]
- Patacca, M.; Lindner, M.; Lucas-Borja, M.E.; Cordonnier, T.; Fidej, G.; Gardiner, B.; Hauf, Y.; Jasinevičius, G.; Labonne, S.; Linkevičius, E.; et al. Significant increase in natural disturbance impacts on European forests since 1950. Glob. Change Biol. 2023, 29, 1359–1376. [Google Scholar] [CrossRef] [PubMed]
- Jaime, L.; Batllori, E.; Lloret, F. Bark beetle outbreaks in coniferous forests: A review of climate change effects. Eur. J. For. Res. 2023, 143, 1–17. [Google Scholar] [CrossRef]
- Georgiev, G.; Georgieva, M.; Dimitrov, S.; Iliev, M.; Trenkin, V.; Mirchev, P.; Belilov, S. Remote sensing assessment of the expansion of Ips typographus attacks in the Chuprene Reserve, Western Balkan Range. Forests 2022, 13, 39. [Google Scholar] [CrossRef]
- Marini, L.; Økland, B.; Jönsson, A.M.; Bentz, B.; Carroll, A.; Forster, B.; Grégoire, J.C.; Hurling, R.; Nageleisen, L.M.; Netherer, S.; et al. Climate drivers of bark beetle outbreak dynamics in Norway spruce forests. Ecography 2017, 40, 1426–1435. [Google Scholar] [CrossRef]
- Cullingham, C.I.; Cooke, J.E.K.; Dang, S.; Davis, C.S.; Cooke, B.J.; Coltman, D.W. Mountain pine beetle host-range expansion threatens the boreal forest. Mol. Ecol. 2011, 20, 2157–2171. [Google Scholar] [CrossRef]
- Biedermann, P.H.W.; Müller, J.; Grégoire, J.C.; Gruppe, A.; Hagge, J.; Hammerbacher, A.; Hofstetter, R.W.; Kandasamy, D.; Kolarik, M.; Kostovcik, M.; et al. Bark Beetle Population Dynamics in the Anthropocene: Challenges and Solutions. Trends Ecol. Evol. 2019, 34, 914–924. [Google Scholar] [CrossRef]
- Sexton, J.P.; Montiel, J.; Shay, J.E.; Stephens, M.R.; Slatyer, R.A. Evolution of ecological niche breadth. Ann. Rev. Ecol. Evol. Syst. 2017, 48, 183–206. [Google Scholar] [CrossRef]
- Krebs, C.J. (Ed.) Niche measures and resource preferences. In Ecological Methodology; Harper & Row: New York, NY, USA, 2014; pp. 597–653. [Google Scholar]
- Niemelä, J. Biodiversity monitoring for decision-making. Ann. Zool. Fen. 2000, 37, 307–317. [Google Scholar]
- Ankeny, R.A.; Leonelli, S. Model Organisms, 1st ed.; Cambridge University Press: Cambridge, UK, 2020; pp. 1–83. [Google Scholar] [CrossRef]
- Raffa, K.F.; Grégoire, J.C.; Lindgren, B.S. Natural history and ecology of bark beetles. In Bark Beetles: Biology and Ecology of Native and Invasive Species; Vega, F.E., Hofstetter, R.W., Eds.; Elsevier Academic Press: Amsterdam, The Netherlands, 2015; pp. 1–40. [Google Scholar] [CrossRef]
- Schelhaas, M.J.; Nabuurs, G.J.; Schuck, A. Natural disturbances in the European forests in the 19th and 20th centuries. Glob. Change Biol. 2003, 9, 1620–1633. [Google Scholar] [CrossRef]
- Jaramillo, J.; Muchugu, E.; Vega, F.E.; Davis, A.; Borgemeister, C.; Chabi-Olaye, A. Some like it hot: The influence and implications of climate change on coffee berry borer (Hypothenemus hampei) and coffee production in East Africa. PLoS ONE 2011, 6, e24528. [Google Scholar] [CrossRef]
- Meddens, A.J.; Hicke, J.A.; Ferguson, C.A. Spatiotemporal patterns of observed bark beetle-caused tree mortality in British Columbia and the western United States. Ecol. Appl. 2012, 22, 1876–1891. [Google Scholar] [CrossRef] [PubMed]
- Thom, D.; Seidl, R.; Steyrer, G.; Krehan, H.; Formayer, H. Slow and fast drivers of the natural disturbance regime in Central European forest ecosystems. For. Ecol. Manag. 2013, 307, 293–302. [Google Scholar] [CrossRef]
- Lieutier, F.; Långström, B.; Faccoli, M. The Genus Tomicus. In Bark Beetles: Biology and Ecology of Native and Invasive Species; Vega, F.E., Hofstetter, R.W., Eds.; Elsevier Academic Press: Amsterdam, The Netherlands, 2015; pp. 371–426. [Google Scholar]
- Ritzerow, S.; Konrad, H.; Stauffer, C. Phylogeography of the Eurasian pine shoot beetle Tomicus piniperda L. (Coleoptera, Scolytidae). Eur. J. Entomol. 2004, 101, 13–19. [Google Scholar] [CrossRef]
- Haack, R.A.; Kucera, D. New Introduction-Common Pine Shoot Beetle, Tomicus piniperda L.; Pest Alert NATP-05-93; U.S.D.A. Forest Service, Northeastern Area: Milwaukee, WI, USA, 1993; pp. 1–2. [Google Scholar]
- Eager, T.A.; Berisford, C.W.; Dalusky, M.J.; Nielsen, D.G.; Brewer, J.W.; Hilty, S.J.; Haack, R.A. Suitability of some southern and western pines as hosts for the pine shoot beetle, Tomicus piniperda (Coleoptera: Scolytidae). J. Econ. Entomol. 2004, 97, 460–467. [Google Scholar] [CrossRef]
- Humble, L.M.; Allen, E.A. Forest biosecurity: Alien invasive species and vectored organisms. Can. J. Plant Pathol. 2006, 28, 256–269. [Google Scholar] [CrossRef]
- Kirkendall, L.R.; Faccoli, M.; Ye, H. Description of the Yunnan shoot borer, Tomicus yunnanensis Kirkendall & Faccoli sp. n. (Curculionidae, Scolytinae), an unusually aggressive pine shoot beetle from southern China, with a key to the species of Tomicus. Zootaxa 2008, 1819, 25–39. [Google Scholar] [CrossRef]
- Borkowski, A. Regression equations for estimating populations of Tomicus piniperda (L.) on Scots pine (Pinus sylvestris L.). For. Ecol. Manag. 2019, 453, 117578. [Google Scholar] [CrossRef]
- Zubek, K.; Czerwik-Marcinkowska, J.; Borkowski, A. A non-invasive method of estimating populations of Tomicus piniperda on Scots pine (Pinus sylvestris L.). Insects 2022, 13, 1071. [Google Scholar] [CrossRef]
- Öhrn, P. Seasonal Flight Patterns of the Spruce Bark Beetle (Ips typographus) in Sweden. Phenology, Voltininsm and Development. Bachelor’s Thesis, Swedish University of Agricultural Sciences, Uppsala, Sweden, 2012. [Google Scholar]
- Dobbertin, M.; Wermelinger, B.; Bigler, C.; Bürgi, M.; Carron, M.; Forster, B.; Gimmi, U.; Rigling, A. Linking increasing drought stress to Scots pine mortality and bark beetle infestations. Sci. World J. 2007, 7, 231–239. [Google Scholar] [CrossRef]
- Wermelinger, B.; Rigling, A.; Schneider Mathis, D.; Dobbertin, M. Assessing the role of bark- and wood-boring insects in the decline of Scots pine (Pinus sylvestris) in the Swiss Rhone valley. Ecol. Entomol. 2008, 33, 239–249. [Google Scholar] [CrossRef]
- Rankin, L.J.; Borden, J.H. Competitive interactions between the mountain pine beetle and the pine engraver in lodgepole pine. Can. J. For. Res. 1991, 21, 1029–1036. [Google Scholar] [CrossRef]
- Flechtmann, C.A.H.; Dalusky, M.J.; Berisford, C.W. Bark and ambrosia beetle (Coleoptera: Scolytidae) responses to volatiles from aging loblolly pine billets. Environ. Entomol. 1999, 28, 638–648. [Google Scholar] [CrossRef]
- Saint-Germain, M.; Drapeau, P.; Buddle, C.M. Landing patterns of phloem- and wood-feeding Coleoptera on Black spruce of different physiological and decay states. Environ. Entomol. 2009, 38, 797–802. [Google Scholar] [CrossRef] [PubMed]
- Carscadden, K.A.; Emery, N.C.; Arnillas, C.A.; Cadotte, M.W. Niche breadth: Causes and consequences for ecology, evolution, and conservation. Quart. Rev. Biol. 2020, 95, 179–214. [Google Scholar] [CrossRef]
- Paine, T.D.; Birch, M.C.; Švihra, P. Niche breadth and resource partitioning by four sympatric species of bark beetles (Coleoptera: Scolytidae). Oecologia 1981, 48, 1–6. [Google Scholar] [CrossRef]
- Grünwald, M. Ecological segregation of bark beetles (Coleoptera, Scolytidae) of spruce. Zeit. Angew. Entomol. 1986, 101, 176–187. [Google Scholar] [CrossRef]
- Amezaga, I.; Rodríguez, M.A. Resource partitioning of four sympatric bark beetles depending on swarming dates and tree species. For. Ecol. Manag. 1998, 109, 127–135. [Google Scholar] [CrossRef]
- Ayres, B.D.; Ayres, M.P.; Abrahamson, M.D.; Teale, S.A. Resource partitioning and overlap in three sympatric species of Ips bark beetles (Coleoptera: Scolytidae). Oecologia 2001, 128, 443–453. [Google Scholar] [CrossRef]
- Wallin, K.F.; Kolb, T.E.; Skov, K.R.; Wagner, M. Forest management treatments, tree resistance, and bark beetle resource utilization in ponderosa pine forests of northern Arizona. For. Ecol. Manag. 2008, 255, 3263–3269. [Google Scholar] [CrossRef]
- Borkowski, A.; Skrzecz, I. Ecological segregation of bark beetles (Col., Curculionidae, Scolytinae) in Scots pine. Ecol. Res. 2016, 31, 135–144. [Google Scholar] [CrossRef]
- Borkowski, A. Resource partitioning of Scots pine by pine shoot beetles in stands under conditions of stress. Forests 2021, 12, 1336. [Google Scholar] [CrossRef]
- Bentz, B.J.; Jönsson, A.M. Modeling bark beetle responses to climate change. In Bark Beetles. Biology and Ecology of Native and Invasive Species; Vega, F.E., Hofstetter, R.W., Eds.; Elsevier Academic Press: San Diego, CA, USA, 2015; pp. 533–553. [Google Scholar]
- Pureswaran, D.S.; Meurisse, N.; Rassati, D.; Liebhold, A.M.; Faccoli, M. Climate change and invasions by nonnative bark and ambrosia beetles. In Bark Beetle Management Ecology, and Climate Change; Hofstetter, R.W., Gandhi, K.J.K., Eds.; Academic Press: London, UK, 2022; pp. 3–30. [Google Scholar] [CrossRef]
- Grodzki, B.W.; Jakus, R.; Gazda, M. Patterns of bark beetle occurrence in Norway spruce stands of national parks in Tatra Mts. in Poland and Slovakia. J. Pest Sci. 2003, 76, 78–82. [Google Scholar] [CrossRef]
- Kärvemo, S.; van Boeckel, T.P.; Gilbert, M.; Grégoire, J.C.; Schroeder, M. Large-scale risk map ping of an eruptive bark beetle–Importance of forest susceptibility and beetle pressure. For. Ecol. Manag. 2014, 318, 158–166. [Google Scholar] [CrossRef]
- Pasztor, F.; Matulla, C.; Rammer, W.; Lexer, M.J. Drivers of the bark beetle disturbance regime In Alpine forests in Austria. For. Ecol. Manag. 2014, 318, 349–358. [Google Scholar] [CrossRef]
- Olszewski, J.L.; Szałach, G.; Żarnowiecki, G. Klimat. In Monografia Świętokrzyskiego Parku Narodowego; Cieśliński, S., Kowalkowski, A., Eds.; ŚPN Bodzentyn: Kraków, Poland, 2000; pp. 129–145. [Google Scholar]
- Grégoire, J.C.; Evans, H.F. Damage and control of BAWBILT organisms an overview. In Bark and Wood Boring Insects in Living Trees in Europe, a Synthesis; Lieutier, F., Day, K.R., Battisti, A., Grégoire, J.C., Evans, H.F., Eds.; Springer: Dordrecht, The Netherlands, 2004; pp. 19–39. [Google Scholar]
- Levins, R. Evolution in Changing Environments, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1968; 132p. [Google Scholar]
- Hurlbert, S.H. The measurement of niche overlap and some relatives. Ecology 1978, 59, 67–77. [Google Scholar] [CrossRef]
- Bolnick, D.I.; Yang, L.H.; Fordyce, J.A.; Davis, J.M.; Svanbäck, R. Measuring individual-level resource specialization. Ecology 2002, 83, 2936–2941. [Google Scholar] [CrossRef]
- Hutchinson, G.E. Homage to Santa Rosalia, or why are there so many kinds of Animals? Am. Nat. 1959, 93, 145–159. [Google Scholar] [CrossRef]
- TIBCO Software Inc. Statistica, version 13.3 (Data Analysis Software System); TIBCO Software Inc.: Tulsa, OK, USA, 2021. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. Biometry: The Principles and Practice of Statistics in Biological Research, 4th ed.; W.H. Freeman and Company: New York, NY, USA, 2013; 915p. [Google Scholar]
- Anderson, V.L.; McLean, R.A. Design of Experiments: A Realistic Approach; Taylor & Francis: London, UK, 2019; p. 440. [Google Scholar] [CrossRef]
- Kleinbaum, D.G.; Nizam, A.; Rosenberg, E. Applied Regression Analysis and Other Multi-Variable Methods, 5th ed.; Cengage Learning: Boston, MA, USA, 2013; 1072p. [Google Scholar]
- Kozak, A.; Kozak, R. Does cross validation provide additional information in the evaluation of regression models? Can. J. For. Res. 2003, 33, 976–987. [Google Scholar] [CrossRef]
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example, 5th ed.; Wiley: Hoboken, NJ, USA, 2012; 389p. [Google Scholar] [CrossRef]
- White, H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 1980, 48, 817–838. [Google Scholar] [CrossRef]
- Thompson, S.K. Sampling, 3rd ed.; Wiley: New York, NY, USA, 2012; 472p. [Google Scholar]
- Barak, A.V.; McGrevy, D.; Tokaya, G. Dispersal and re-capture of marked, overwintering Tomicus piniperda (L.) (Coleoptera: Scolytidae) from Scotch pine bolts. Great Lakes Entomol. 2000, 33, 69–80. [Google Scholar] [CrossRef]
- Tetko, I.V.; Livingstone, D.J.; Luik, A.I. Neural network studies. 1. Comparison of Overfitting and Overtraining. J. Chem. Inf. Comput. Sci. 1995, 35, 826–833. [Google Scholar] [CrossRef]
- Saarenmaa, H. Modeling the spatial pattern and intraspecific competition in Tomicus piniperda (Coleoptera: Scolytidae). In Communicationes Instituti Forestalis Fenniae (Finland); Finnish Forest Research Institute: Helsinki, Finland, 1983; pp. 1–40. ISBN 951-40-0634-8. [Google Scholar]
- Långström, B. Distribution and production of Tomicus piniperda in pine wood stacks. Sver. Skogsv. Tidsk. 1984, 1, 23–35. [Google Scholar]
- Bouhot, L.; Lieutier, F.; Debouzie, D. Spatial and temporal distribution of attacks by Tomicus piniperda L. and Ips sexdentatus Boern. (Col., Scolytidae) on Pinus sylvestris. J. Appl. Entomol. 1988, 106, 356–371. [Google Scholar] [CrossRef]
- Jamin, J.K. Contribution à L’étude du Dépérissement Provoqué par les Coléoptères Scolytides sur le Pin Sylvestre en Région Centre; Ecole Nationale des Ingénieurs des Travaux des Eaux et Forêts: Nogent-sur-Vernisson, France, 1977; pp. 1–90. [Google Scholar]
- Price, P.W. Insect Ecology, 3rd ed.; Wiley: New York, NY, USA, 1997; 868p. [Google Scholar]
- Mayers, C.G.; McNew, D.L.; Harrington, T.C.; Roeper, R.A.; Fraedrich, S.W.; Biedermann, P.H.W.; Castrillo, L.A.; Reed, S.E. Three genera in the Ceratocystidaceae are the respective symbionts of three independent lineages of ambrosia beetles with large, complex mycangia. Fung. Biol. 2015, 19, 1075–1092. [Google Scholar] [CrossRef]
- Långström, B.; Hellqvist, C. Pinus contorta as a potential host for Tomicus piniperda L. and T. minor (Hart.) (Col., Scolytidae) in Sweden. Zeitsch. Angew. Entomol. 1985, 99, 174–181. [Google Scholar] [CrossRef]
- Niemeyer, H.; Watzek, G.; Lu, N.; Niu, J. Freilandtest zur Attraktivitat von Monoterpenen und Ethanol fur den Borkenkäfer Tomicus piniperda L. (Col., Scolytidae). J. Appl. Entomol. 1996, 120, 265–267. [Google Scholar] [CrossRef]
- Poland, T.M.; Groot, P.; Burke, S.; Wakarchuk, D.; Haack, R.A.; Nott, R.; Scarr, T. Development of an improved attractive lure for the pine shoot beetle, Tomicus piniperda (Coleoptera: Scolytidae). Agric. For. Entomol. 2003, 5, 293–300. [Google Scholar] [CrossRef]
- Rudinsky, J.A.; Ryker, L.C. Sound production in Scolytidae: Rivalry and premating stridulation of male Douglas-fir beetle. J. Insect Physiol. 1976, 22, 997–1003. [Google Scholar] [CrossRef]
- Nilssen, A.C. Spatial attack pattern of the bark beetle Tomicus piniperda L. (Coleoptera: Scolytidae). Norweg. J. Entomol. 1978, 25, 171–175. [Google Scholar]
- Långström, B. Windthrown Scots pines as brood material for Tomicus piniperda and T. minor. Silva Fen. 1984, 18, 187–198. [Google Scholar] [CrossRef]
- Gilbert, M.; Nageleisen, L.M.; Franklin, A.; Grégoire, J.C. Post storm surveys reveal large-scale spatial patterns and influences of site factors, forest structure and diversity in endemic bark-beetle populations. Lands Ecol. 2005, 20, 35–49. [Google Scholar] [CrossRef]
- Komonen, A.; Laatikainen, A.; Similä, M.; Martikainen, P. Ytimennävertäjien kasvainsyönti trombin kaataman suojelumännikön ympäristössä Höytiäisen saaressa Pohjois-Karjalassa. Mets. Aikak. 2009, 2, 127–134. [Google Scholar] [CrossRef][Green Version]
- Öhrn, P.; Björklund, N.; Långström, B. Occurrence, performance and shoot damage of Tomicus piniperda in pine stands in southern Sweden after storm-felling. J. Appl. Entomol. 2018, 142, 854–861. [Google Scholar] [CrossRef]





| Forest Subdistrict | Distance a (m) | Trap Tree Code b | Length (m) | Diameter c (cm) | DBH d (cm) | Thickness of the dbh Bark (mm) |
|---|---|---|---|---|---|---|
| Występa (W) | 0 | W1ttc | 22.0 | 31.75 | 27.00 | 19.01 |
| W1ttn | 17.0 | 27.25 | 20.25 | 14.94 | ||
| 400 | W2ttc | 26.2 | 42.75 | 39.75 | 32.98 | |
| W2ttn | 21.6 | 30.75 | 22.75 | 21.89 | ||
| 800 | W3ttc | 29.0 | 55.50 | 43.00 | 26.41 | |
| W3ttn | 22.6 | 31.00 | 26.50 | 16.63 | ||
| 1200 | W4ttc | 26.0 | 33.50 | 28.50 | 19.71 | |
| W4ttn | 22.8 | 27.75 | 22.25 | 17.18 | ||
| Rejów (R) | 0 | R1ttc | 23.2 | 30.75 | 25.00 | 22.80 |
| R1ttn | 19.2 | 20.75 | 17.75 | 11.22 | ||
| 400 | R2ttc | 29.6 | 51.75 | 45.25 | 21.31 | |
| R2ttn | 25.6 | 23.75 | 21.00 | 13.07 | ||
| 800 | R3ttc | 28.0 | 52.00 | 45.50 | 28.37 | |
| R3ttn | 24.8 | 31.25 | 27.00 | 16.14 | ||
| 1200 | R4ttc | 27.2 | 35.25 | 30.25 | 18.01 | |
| R4ttn | 21.2 | 26.25 | 21.75 | 8.71 | ||
| Wilczy Bór (WB) | 400 | WB1ttc | 25.6 | 35.25 | 32.25 | 19.05 |
| WB1ttn | 22.0 | 26.25 | 20.75 | 10.97 | ||
| 800 | WB2ttc | 27.6 | 48.50 | 41.75 | 21.97 | |
| WB2ttn | 24.4 | 32.50 | 24.50 | 17.64 | ||
| 1200 | WB3ttc | 28.4 | 57.00 | 49.25 | 20.95 | |
| WB3ttn | 22.8 | 30.25 | 25.50 | 17.12 | ||
| 1600 | WB4ttc | 24.8 | 33.75 | 30.75 | 19.34 | |
| WB4ttn | 24.0 | 27.00 | 23.75 | 19.47 | ||
| Kruk (K) | 400 | K1ttc | 30.4 | 55.75 | 51.25 | 40.72 |
| K1ttn | 26.4 | 33.25 | 30.75 | 18.57 | ||
| 800 | K2ttc | 29.5 | 47.00 | 40.25 | 28.51 | |
| K2ttn | 25.5 | 40.00 | 33.75 | 18.21 | ||
| 1200 | K3ttc | 31.2 | 67.00 | 53.00 | 20.88 | |
| K3ttn | 26.8 | 40.00 | 34.00 | 21.78 | ||
| 1600 | K4ttc | 27.6 | 60.00 | 47.25 | 38.97 | |
| K4ttn | 22.0 | 29.50 | 24.50 | 15.41 |
| Windfall No. | Length (m) | Diameter Outsider Bark at Thicker End (cm) | Diameter at Breast Height (cm) | Thickness of the dbh Bark (mm) |
|---|---|---|---|---|
| 1 | 27.9 | 48.25 | 39.25 | 24.38 |
| 2 | 30.2 | 52.25 | 43.75 | 24.96 |
| 3 | 23.5 | 28.75 | 23.25 | 10.01 |
| 4 | 26.1 | 33.75 | 29.25 | 18.42 |
| 5 | 25.1 | 31.25 | 25.25 | 16.58 |
| 6 | 30.1 | 55.25 | 46.50 | 23.15 |
| 7 | 25.6 | 32.25 | 29.50 | 20.01 |
| 8 | 25.1 | 28.50 | 25.50 | 19.68 |
| 9 | 28.9 | 45.25 | 37.75 | 29.64 |
| 10 | 29.5 | 58.75 | 46.75 | 35.82 |
| No. Equation | Name of Variable | Value of Parameter | SE | Value t-Statistics | p | VIF | R | R2adj | RMSE | ANOVA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F Value | p Level | ||||||||||
| 11 | Intercept | 0.0953 | 0.0142 | 6.7071 | <0.001 | ||||||
| l>4 | 0.0147 | 0.0021 | 6.9233 | <0.001 | 1.45 | 0.9295 | 0.8546 | 0.0276 | 92.113 | <0.001 | |
| du11 | 0.0018 | 0.0003 | 5.8524 | <0.001 | |||||||
| 12 | Intercept | 0.0885 | 0.0154 | 5.7544 | <0.001 | ||||||
| l>4 | 0.0165 | 0.0022 | 7.5117 | <0.001 | 1.29 | 0.9148 | 0.8257 | 0.0302 | 74.405 | <0.001 | |
| dhu11 | 0.0015 | 0.0003 | 4.8729 | <0.001 | |||||||
| Tree No. | l>4 a | Equation (11) b | Equation (12) c | |||||
|---|---|---|---|---|---|---|---|---|
| du11 d | Relative Error (%) | dhu11 e | Relative Error (%) | |||||
| 1 | 0.296 | 9.36 | 27.34 | 0.282 | 4.73 | 20.60 | 0.274 | 7.52 |
| 2 | 0.248 | 7.40 | 37.64 | 0.272 | 9.78 | 35.29 | 0.264 | 6.43 |
| 3 | 0.217 | 5.12 | 17.35 | 0.202 | 6.96 | 16.85 | 0.198 | 8.59 |
| 4 | 0.191 | 5.76 | 11.69 | 0.201 | 5.03 | 11.45 | 0.201 | 4.87 |
| 5 | 0.244 | 7.40 | 16.18 | 0.233 | 4.39 | 16.93 | 0.236 | 3.24 |
| 6 | 0.252 | 8.04 | 20.46 | 0.250 | 0.80 | 17.32 | 0.247 | 2.06 |
| 7 | 0.202 | 7.40 | 10.23 | 0.222 | 10.40 | 9.45 | 0.225 | 11.54 |
| 8 | 0.255 | 8.53 | 14.54 | 0.247 | 3.28 | 16.59 | 0.254 | 0.43 |
| 9 | 0.186 | 6.90 | 5.73 | 0.207 | 11.30 | 0.00 | 0.202 | 8.78 |
| 10 | 0.345 | 9.36 | 87.19 | 0.390 | 12.99 | 93.01 | 0.382 | 10.84 |
| Mean ± SD | 0.244 ± 0.05 | 0.251 ± 0.06 | 0.248 ± 0.05 | |||||
| t-test | t = −0.2974, p = 0.7696 | t = −0.2034, p = 0.8411 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borkowski, A. Estimating the Niche Breadth of Tomicus piniperda L. on Breeding Material: A Statistical Approach. Sustainability 2025, 17, 7744. https://doi.org/10.3390/su17177744
Borkowski A. Estimating the Niche Breadth of Tomicus piniperda L. on Breeding Material: A Statistical Approach. Sustainability. 2025; 17(17):7744. https://doi.org/10.3390/su17177744
Chicago/Turabian StyleBorkowski, Andrzej. 2025. "Estimating the Niche Breadth of Tomicus piniperda L. on Breeding Material: A Statistical Approach" Sustainability 17, no. 17: 7744. https://doi.org/10.3390/su17177744
APA StyleBorkowski, A. (2025). Estimating the Niche Breadth of Tomicus piniperda L. on Breeding Material: A Statistical Approach. Sustainability, 17(17), 7744. https://doi.org/10.3390/su17177744






