Neural Network-Based Approaches for Predicting Construction Overruns with Sustainability Considerations

Abstract

This research focuses on developing neural network-based models for predicting time and cost overruns in construction projects during the construction phase, incorporating sustainability considerations. Previous studies have identified seven key performance areas that affect the final outcome: productivity, quality, time, cost, safety, team satisfaction, and client satisfaction. Although the interconnections among these performance areas are recognized, their exact relationships and impacts are not fully understood. Hence, the utilization of a neural networks proves to be highly beneficial in predicting the outcome of future construction projects, as it can learn from data and identify patterns, without requiring a complete understanding of these mutual influences. The neural network was trained and tested on the data collected on five completed construction projects, each analyzed at three distinct stages of execution. A total of 182 experiments were conducted to explore different neural network architectures. The most effective configurations for predicting time and cost overruns were identified and evaluated, demonstrating the potential of neural network-based approaches to support more sustainable and proactive project management. The time overrun prediction model demonstrated high accuracy, achieving a MAPE of 10.93%, RMSE of 0.128, and correlation of 0.979. While the cost overrun model showed a lower predictive accuracy, its MAPE (166.76%), RMSE (0.4179), and correlation (0.936) values indicate potential for further refinement. These findings highlight the applicability of neural network-based approaches in construction project management and their potential to support more proactive and informed decision-making.

1. Introduction

1.1. Problem Definition

The construction sector is considered one of the most vital and profitable industries worldwide, yet it is fraught with uncertainties and risk. Despite numerous attempts to improve processes, construction projects frequently fail to achieve the desired outcomes due to various challenges.

Earlier research and an extensive analysis of the literature have highlighted the key performance areas essential for the success of construction projects. Some of them are inherently challenging to quantify. Nevertheless, they are all fundamental in achieving projects’ success, including productivity, quality, time, cost, safety, team satisfaction and client satisfaction [1].

Five completed construction projects with a financial value between 15 and 25 million euros were analyzed using the multiple case study method. Interviews were conducted with key project stakeholders to gather their opinions about the project’s progress and to gain detailed insights into the situation, such as circumstances, causes of problems, reasons for work stoppages, and the presence of identified performance areas in their projects. Communication was established with representatives of clients, consultants, and contractors, and comprehensive project documentation was collected. The analysis revealed that none of the projects exceeded the contractual deadline to the extent of requiring penalty payments, but the deadlines were significantly extended compared to the initial contracts. In each analyzed project, the contractor and the client signed annexes to extend the deadlines, primarily due to significant off-budget works and exceeding the anticipated scope of works. Although some projects did not show significant deviations in total costs, there were notable changes in the cost structure, which could pose problems for the contractor in certain cases. By comparing the opinions of key project stakeholders and analyzing the agreed and realized deadlines and costs, it was found that there is a significant gap between key project stakeholder expectations and the realized performance of construction projects. This finding underscores the necessity of further research and efforts to achieve more sustainable project outcomes [2].

This gap between stakeholder expectations and actual project performance highlights the need for predictive tools that can anticipate deviations in time and cost during the execution phase, rather than reacting after issues occur. Such tools would provide project managers and other key project stakeholders with timely insights to help steer projects toward successful completion. Each of these stakeholders enters the project with clearly defined expectations. Any significant deviation from the original plan can disrupt those expectations and lead to operational or financial losses. This research addresses the problem by developing data-driven neural network models that learn from historical project data, incorporating both technical indicators and stakeholder-related performance variables. By identifying potential overruns early, the models aim to support proactive decision-making and reduce the risk of misalignment between planned and realized outcomes.

Despite extensive efforts to improve project control and risk management, current methodologies often fall short in capturing the dynamic and interdependent nature of construction processes. Traditional models struggle with handling incomplete or imprecise data and frequently lack the flexibility to adapt to complex on-site conditions. As a result, there is growing interest in advanced data-driven approaches that can offer more accurate and timely predictions.

The structure of this paper is as follows. Section 1 provides the research background, introduces the use of neural networks in the construction context, and outlines the main objectives and hypotheses of this study. Section 2 describes the research methodology, including the development of the neural network model and the evaluation approach. Section 3 presents the results and a discussion, organized into three subsections that focus on the prediction models for cost and time overruns, followed by a comparative analysis and suggestions for future research. Finally, Section 4 summarizes the key findings and discusses practical implications.

1.2. Research Background on Artificial Neural Networks

Artificial neural networks (ANNs) have emerged as a promising solution due to their ability to model nonlinear relationships, learn from historical data, and generalize to new, unseen data [3,4]. Their application in construction management has been steadily increasing, particularly in areas requiring predictive analysis such as schedule and cost estimations. ANNs have proven particularly effective in addressing complex problems, and their application in construction project management research has been growing over recent years [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Unlike traditional regression models or decision trees, which often rely on predefined assumptions or struggle with nonlinear, high-dimensional data, ANNs can flexibly adapt to complex patterns typical of construction project dynamics, learn from vast and heterogeneous datasets, and capture hidden correlations between variables [7]. Trijeti et al. [8], Al Mnaseer et al. [9], and Velumani et al. [10] further reinforced the superiority of ANN approaches over traditional models in construction forecasting tasks.

For instance, Jha and Chockalingam [11] developed a quality performance prediction model using ANNs with “MATLAB”, demonstrating that the model could achieve the desired project performance by managing identified critical factors. Alaloul et al. [12] created an ANN model to assess the impact of coordination factors on construction projects’ performance, showing a high accuracy in predicting cost, time, and quality outcomes. Car-Pušić et al. [13] developed ANN-based models for predicting highway construction times and costs in Croatia, achieving significant improvements in estimation accuracy and practical applicability.

Tijanić et al. [14] demonstrated that an artificial neural network, specifically GRNN, can significantly improve the accuracy of cost estimates for road construction projects, particularly during the initial design phase, with results surpassing MLP, RBFNN, and linear regression models. El-Sawah and Moselhi [15] evaluated different neural network types for cost estimations, reporting MAPEs between 16.83% and 19.35%, which were more accurate than regression models. These studies highlight the effectiveness of neural networks in enhancing prediction accuracy across various aspects of construction projects. Han et al. [16] introduced a BIM-integrated cost prediction model using a Gray Backpropagation Neural Network (PGNN) optimized via the Sparrow Search Algorithm. Their model, based on BIM-derived quantities, material prices, and time-series inputs, achieved an R² of 0.9819 and a maximum relative error of 2.99%. Zhang and Mo [17] developed a BIM–Elman Neural Network enhanced with Particle Swarm Optimization, reaching an over 95% prediction accuracy by incorporating geometric, material, and change-order data. Zhang and Zhang [18] proposed an additional model, Deep CostNet for Building Engineering Techniques (DCN-BET), that used historical cost records and project attributes for dynamic learning, although specific performance metrics were not detailed. Another innovative approach by Liu et al. [19] applied hypergraph deep learning to model multidimensional interrelationships between economic and project variables, significantly improving early-stage cost forecasting.

Alsugair et al. [20] developed a feedforward ANN model using only three input variables (contract cost, duration, and sector) achieving a MAPE of 12.22%, which outperformed standard regression techniques. Ji et al. [21] proposed a hybrid model combining K-means clustering, genetic algorithms, and BP neural networks to forecast residential project durations, delivering high accuracy even with a relatively small dataset. Anaraki et al. [22] introduced a composite ANN architecture integrating feedforward and Long Short-Term Memory (LSTM) networks to capture both static and temporal dependencies in project data, significantly improving dynamic prediction performance. Furthermore, Shihadeh et al. [23] presented a neural network-based model focused on predicting construction timeframes, further reinforcing the practical viability of such techniques. Petruseva et al. [24] created a model for predicting time overruns based on variables such as structure type, construction year, contracted and realized construction time, contracted and realized construction cost, and reasons for deadline non-compliance. Their study achieved impressive accuracy with metrics of R² = 0.970 and MAPE = 2.50%.

1.3. Research Objectives

Given the promising results of artificial neural networks in predicting construction projects’ performance, this study aims to develop models for predicting time and cost overruns, with a focus on critical performance areas essential for projects’ success and sustainability. The process of designing and selecting the optimal neural network architecture for predicting these overruns is established as part of this research. A series of experiments is conducted to determine the most effective architectures by analyzing the performance metrics of the developed models. The accuracy of these predictive models is evaluated using a dataset collected from completed construction projects. The hypotheses tested in this research include

• Artificial neural networks can provide a high accuracy in predicting time and cost overruns in construction projects by analyzing critical performance areas.
• Evaluating various performance metrics will lead to the identification of the most effective neural network architectures for predicting construction project overruns.

Achieving these objectives would contribute to the development of predictive models that enable early identification of cost and time overruns in construction projects. This would support more informed decision-making during projects’ execution, helping key project stakeholders to proactively mitigate risks, optimize resource allocation, and ultimately improve overall project outcomes.

2. Research Methodology

To ensure the consistency and comparability of the collected data, specific criteria were applied when selecting the five projects analyzed in this study. First, all projects were publicly funded, which ensured a uniform regulatory, administrative, and procurement environment, as well as better availability and reliability of documentation. Second, projects were required to have a contracted value between EUR 15 and EUR 25 million. This range was chosen to focus on mid-scale construction projects, significant in scope but not so large as to introduce exceptional complexity or singular influence. Finally, only projects contracted from 2016 onward were included, ensuring that the data reflects current legal, economic, and technological conditions in the construction sector.

In addition, the sample intentionally included different types of construction projects, such as buildings, roads, and municipal infrastructure, to examine whether common factors and performance patterns could be identified across distinct project categories. This diversity allowed for a broader exploration of shared influences on cost and time overruns, regardless of project type.

2.1. Model for Predicting Cost and Time Overruns in Construction Projects

The research was conducted using RapidMiner Studio 10.2.000. Although there are many advanced software tools available for similar purposes, such as Keras, TensorFlow, Weka, and Chainer, the user-friendly visual interface of RapidMiner Studio makes it accessible even to those with limited programming experience. It allows quick testing and modification of models without writing code, using graphical representations. One of the key advantages of RapidMiner is its intuitive drag-and-drop interface, where operators (functions and processes) are represented as icons that can be easily connected into workflows. This visual programming approach significantly speeds up models’ development and improves clarity in the model structure. Additionally, it offers extensive documentation and examples that aid in learning and troubleshooting. These resources have proven to be extremely helpful during this research.

The process of creating and selecting the most optimal neural network architecture in predicting overruns is shown in Figure 1. It begins with assigning values to the input data presented in

Table 1. Attributes—list of applied and evaluated input data.

	Input Data
1	Planned payment amount
2	Realized amount charged
3	Off-budget work cost
4	Project documentation quality
5	Project change management
6	Dynamic plan analysis
7	Adherence to activity deadlines
8	Cost ratio
9	Trend of changes and additional works
10	Hazard identification
11	Incident and accident frequency
12	Workforce
13	Employee turnover
14	Conflict management
15	Client satisfaction with communication (with the contractor)
16	Client satisfaction with contractor expertise and work quality
17	Client satisfaction with costs
18	Client satisfaction with work progress
19-1	Time overrun
19-2	Cost overrun

.

The input data consist of objectives, numerically defined project data, and subjective indicators derived from stakeholder interviews. Quantitative variables such as planned payment amount, realized amount charged, off-budget work cost, cost ratio, and incident frequency were collected directly from project documentation and records. On the other hand, attributes related to conflict management and various aspects of client satisfaction were assessed through structured interviews conducted with key project stakeholders [2]. Each respondent rated the relevant items on a 5-point Likert scale. In cases where multiple participants were interviewed for the same project, the mean value of their responses was used to create a single representative score for that attribute. This hybrid approach ensured that both technical and experiential dimensions of project performance were included in the model.

Since the goal of this research was to create two models, one to predict cost overrun and the other to predict time overrun, slightly different input data were used. The previously defined performance areas and evaluation approaches [1,2] were refined and corrected in order to make the input data of better quality. The final set of input variables (Table 1) was determined based on an extensive literature review and discussions with experts.

Attributes 1–18 are common in both models. To create the cost overrun prediction model, it needs to be provided with data about cost overruns from past projects. Similarly, to develop the time overrun prediction model, the model must be supplied with information regarding time overruns from previous projects. It was crucial to limit this attribute, because if the model proves to be useful and is utilized in the initial phase of the work, all necessary data must be enterable into the process.

For each of the five projects, three specific points during the project timeline were identified and analyzed in detail, corresponding to approximately one-third intervals of the total project duration on the construction site.

At the beginning of the RapidMiner process, the input data has to be evaluated and imported. No missing values were present in the dataset, so no imputation techniques were required. It is essential to determine the attributes to be used for further prediction. In this research, it was decided to utilize all the collected data shown as attributes 1–18 and attribute 19 depending on model. Only regular and label roles were assigned to the attributes. Regular attributes are used as input variables for learning tasks. The label role, on the other hand, is a special role that serves as the target attribute for learning operators and is often referred to as the “target variable.” Two separate models were developed for predicting outcomes, with minor differences starting from this point. In one model, the label was defined as time overrun, while in the other model, the label was defined as cost overrun.

The input dataset was divided into two parts: 70% for model training and the remaining 30% for model testing. After the training, the model was applied to the test dataset to generate predictions and verify its performance. This approach helps evaluate the model’s performance by ensuring that the model is tested on unseen data. In this example of predicting time and cost overruns, a neural network was applied that learns a model by means of a feedforward neural network trained by a backpropagation algorithm (multi-layer perceptron). In this study, a 70/30 train–test split was applied without additional k-fold cross-validation. This decision was primarily motivated by the relatively small dataset size, which would have made each fold in a cross-validation process too small to reliably capture the diversity of project conditions. While this approach is acceptable for exploratory, small-sample studies, it may limit the robustness of the findings. Future work will employ k-fold cross-validation once a larger dataset becomes available.

A total of 182 experiments were conducted to evaluate the effectiveness of different neural network architectures in predicting time and cost overruns in construction projects. The testing approach was structured and aimed at achieving a balance between models’ complexity and generalization capacity. The initial phase focused on analyzing simpler architectures with a single hidden layer, where the number of neurons was gradually reduced from 18 to 5. The purpose of this phase was to assess the baseline performance of less complex models and to identify suitable starting points for more advanced configurations.

Following this, two-layer architectures were evaluated, where the number of neurons in the first hidden layer was progressively reduced, beginning with a higher number of neurons in the first layer (e.g., 16) and combining it with a decreasing number in the second layer, thus covering a representative range of more complex network structures (e.g., 16–15, 16–14, …, 16–4). This gradual and systematic approach enabled a detailed exploration of how the model behaves across different levels of architectural complexity. As a result, it was possible to identify how many layers and neurons were optimal for the specific prediction task, considering the limited dataset and the desired level of accuracy.

Experiments were conducted to select the optimal prediction model architecture. In general, the effectiveness of a neural network model is influenced by the balance between the number of input attributes and the complexity of the network’s architecture, specifically the number of hidden layers and nodes. Deeper architectures were avoided in order to minimize the risk of overfitting, as the dataset used in this study was relatively small. An excessive number of hidden layers or nodes can lead to a phenomenon known as overfitting [25]. The implications of these experiments are discussed further in the Results and Discussion chapter.

Beyond limiting the number of hidden layers to reduce models’ complexity, additional overfitting mitigation strategies were considered. Given the dataset size, methods such as dropout regularization, L2 weight regularization, and early stopping were evaluated. Preliminary tests with L2 regularization (λ = 0.01) and dropout (p = 0.2) showed no consistent improvement in predictive accuracy, likely due to the already small network configurations used. Early stopping was deemed less applicable, as the default training duration (200 cycles) did not result in substantial divergence between training and testing errors. These results suggest that, while such techniques can be effective with larger datasets, their benefits in the present small-sample context were limited.

After several iterations of adjusting the number of training cycles, it was ultimately decided to adhere to the default program setting of 200 training cycles for training the neural network. During backpropagation, the predicted outputs are compared to the actual target values to determine the error using a predefined loss function. This error is then propagated backward through the network, and the weights of the connections are updated accordingly in small increments to gradually minimize the error. The learning rate specifies the size of the weight updates in each iteration. The most commonly used learning rate values are between 0.0 and 0.2. For the purposes of this model, a value of 0.01 was determined. Momentum (0.9) adjusts the current weight update by adding a fraction of the previous update, which helps in overcoming local maxima and smoothest optimization directions.

2.2. Evaluating Model

In models’ evaluation, understanding the learning process and adjustment mechanisms of a model is crucial. The backpropagation algorithm is a supervised learning method used for optimizing weights in artificial neural networks. This algorithm consists of two main phases: propagation and weight update. During the propagation phase, the network’s output is compared to the expected results to compute the error using a specified error function. This error is then propagated backward through the network, with incremental adjustments made to the weights of connections to minimize the error. This process is repeated over numerous training iterations until the network’s performance reaches an acceptable level. A multi-layer perceptron (MLP) is a type of feedforward artificial neural network designed to map input data to appropriate output values. The network structure includes several layers of nodes organized in a directed graph, where each layer is fully connected to the subsequent one. Except for the input layer, each node in the network functions as a neuron and employs a nonlinear activation function, such as the sigmoid function. MLPs utilize backpropagation as their learning mechanism, adjusting weights across the network’s multiple layers to enhance prediction accuracy. For evaluating the performance of an MLP, it is essential to use relevant metrics. By analyzing errors, one can determine how well the model generalizes to new data and identify potential areas for improvement [30,31,32].

The performance of each model was evaluated using Mean Absolute Percentage Error, Root Mean Squared Error, and correlation values (

Table 2. Measures to evaluate model.

Performance Measure	Formula
Mean Absolute Percentage Error	$MAPE={\displaystyle \frac{{\sum }_{i=1}^n\frac{\left|X_i-Y_i\right|}{Y_i}}{n}}$
Root Mean Squared Error	$RMSE=\sqrt[2]{{\displaystyle \frac{{\sum }_{i=1}^n{\left(X_i-Y_i\right)}^2}{n}}}$
Pearson’s Correlation Coefficient	$r={\displaystyle \frac{\sum \left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{\sum {\left(X_i-\overline{X}\right)}^2\sum {\left(Y_i-\overline{Y}\right)}^2}}}$

Where X_i is the value predicted by the ANN; Y_i is actual value; n is the number of data points; $\overline{\mathrm{X}}$ and $\overline{\mathrm{Y}}$ are the mean values of predicted and actual data, respectively.

).

Mean Absolute Percentage Error (MAPE) is a measure that indicates the average deviation of model predictions from the actual values, relative to the magnitude of the measured item [31]. Expressed as a percentage, it provides insight into the accuracy of experimental measurements by illustrating how close the predicted values are to the true values. A smaller percentage signifies higher accuracy and better model performance. Interpretation of MAPE values is shown in

Table 3. Interpretation of MAPE values [33].

MAPE Value	Prediction Accuracy
MAPE ≤ 10%	High
10% < MAPE < 20%	Good
20% < MAPE ≤ 50%	Reasonable
MAPE > 50%	Low

.

The Root Mean Squared Error (RMSE) quantifies the average deviation between the predicted values and the actual values, providing an estimate of the model’s predictive accuracy. It indicates how well the model is able to predict the target value. RMSE values range from zero to infinity. A lower RMSE signifies smaller differences between the predicted and observed values, reflecting better model performance [34,35].

Correlation represents the relationship between predicted and observed values. The Pearson Correlation Coefficient was used, which measures the strength and direction of the linear relationship between two variables. A higher correlation value (close to 1) indicates a stronger relationship, meaning that the value of one variable can be predicted with greater certainty based on the value of another variable. A lower correlation value (close to 0) signifies a weak connection and low predictability [32]. Interpretation of correlation values is shown in

Table 4. Interpretation of correlation values [36].

Correlation Value	Prediction Accuracy
0 < r < 0.2	Very low
0.2 ≤ r < 0.4	Low
0.4 ≤ r < 0.6	Moderate
0.6 ≤ r < 0.8	High
0.8 ≤ r ≤ 1.0	Very high

.

The Coefficient of Determination (R²) indicates the proportion of the variance in the dependent variable that is predictable from the independent variables. It provides a measure of the goodness of fit, where values closer to 1 signify that the model explains a greater portion of the variability in the data, indicating a more accurate prediction [37].

3. Results and Discussion

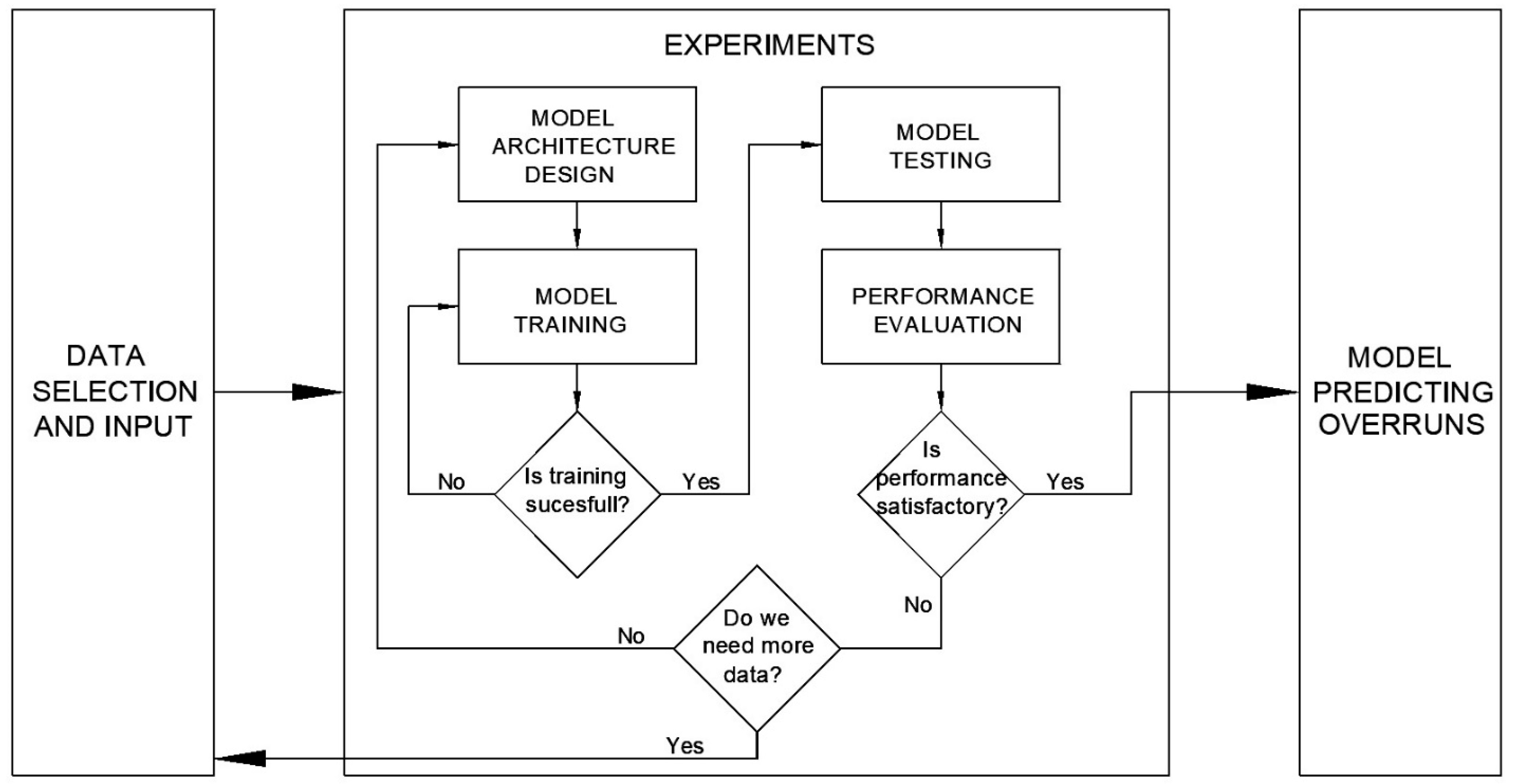
3.1. Cost Overrun Prediction Model

Ninety-one experiments were conducted to determine the optimal model for predicting cost overruns. Various configurations with different numbers of hidden layers and nodes were tested. The initial setup began with a single hidden layer featuring 18 nodes, progressively reducing the number of nodes by one in each subsequent experiment until only 5 nodes remained. Additionally, experiments included configurations with two hidden layers, exploring different combinations of nodes across these layers.

After analyzing the results from all 91 experiments, it was observed that the RMSE values are relatively low, suggesting that the models are generally accurate in their predictions. However, the MAPE values across all experiments were found to be extremely high, with some experiments reaching up to 523%, indicating extremely low prediction accuracy.

Table 5. Experiments for determining the optimal architecture for the cost overrun prediction model.

Hidden Nodes (Layer 1)	Hidden Nodes (Layer 2)	MAPE (%)	RMSE	Correlation	R2
16	5	172.43	0.441	0.929	0.863
15	5	179.90	0.393	0.938	0.880
11	10	166.76	0.417	0.936	0.876
11	9	163.59	0.437	0.939	0.882
8	6	179.81	0.440	0.941	0.885
7	5	169.17	0.400	0.955	0.912
6	2	177.45	0.441	0.969	0.939
5	4	173.44	0.443	0.971	0.943
4	3	171.83	0.439	0.936	0.876
4	2	172.99	0.442	0.919	0.845

highlights 10 experiments where the MAPE values are below 180%.

The RMSE values, ranging from 0.393 to 0.443 for the 10 most successful experiments, are acceptable but fell short of expectations. Although the correlation values are reasonably good, MAPE values are too high, indicating that the models are not suitable for practical application. According to Table 3, the calculated values mean low prediction accuracy.

Nevertheless, the three most optimal solutions were selected for further detailed analysis and commentary (

Table 6. The best model architectures for cost overrun prediction.

Hidden Nodes (Layer 1)	Hidden Nodes (Layer 2)	MAPE (%)	RMSE	Correlation	R2
15	5	179.90	0.393	0.938	0.880
11	10	166.76	0.417	0.936	0.876
11	9	163.59	0.437	0.939	0.882

). These models are characterized by having two hidden layers. Based on the RMSE values, the optimal model appears to be the first model, which consists of 15 nodes in the first hidden layer and 5 nodes in the second hidden layer. According to the MAPE values, the third model, which utilizes 11 nodes in the first hidden layer and 9 nodes in the second hidden layer, demonstrates the best performance among the models tested. However, despite this model achieving the best MAPE value in the set of experiments, this value remains exceptionally high. A MAPE value of 163.59% signifies that, on average, the model’s predictions deviate from the actual values by 163.59%. This exceptionally high MAPE indicates significant inaccuracies in the model’s predictions, suggesting that the model’s overall predictive performance is poor, pointing to the model’s instability and substantial variability in its predictions. This variability suggests that the model is inconsistent and that its predictions lack reliability. On the other hand, the correlation metric provides favorable results across all models, with the most optimal correlation observed in the model featuring 11 nodes in the first hidden layer and 10 nodes in the second hidden layer.

Considering all the presented parameters, the model with 11 nodes in the first hidden layer and 10 nodes in the second hidden layer was selected as the most optimal architecture for the cost overrun prediction model at this stage of the research. Although the RMSE and correlation values suggest that the model could be capable of accurate predictions, the high MAPE indicates that significant adjustments to the model are necessary. The presented values might indicate that the dataset used for training was too small, potentially failing to capture sufficient variability.

3.2. Time Overrun Prediction Model

Parallel experiments were conducted to identify the best model for predicting time overruns, following the same procedure for hidden layers and node combinations.

Table 7. Experiments for determining the optimal architecture for the time overrun prediction model.

Hidden Nodes (Layer 1)	Hidden Nodes (Layer 2)	MAPE (%)	RMSE	Correlation	R2
14	8	81.35	0.068	0.985	0.970
13	5	81.88	0.206	0.981	0.962
12	8	65.97	0.119	0.968	0.937
12	7	76.73	0.093	0.978	0.956
10	8	68.81	0.106	0.975	0.951
9	7	29.29	0.121	0.973	0.947
7	5	45.25	0.173	0.986	0.972
6	4	55.34	0.169	0.982	0.964
6	3	17.90	0.121	0.983	0.966
5	3	10.93	0.128	0.979	0.958

presents the ten models that demonstrated the best prediction performance.

The experimental results showed Root Mean Squared Error values ranging from 0.068 to 0.394, indicating strong performance. The correlation coefficients were excellent, ranging from 0.968 to 1.000. However, the Mean Absolute Percentage Error was notably high in many cases, reaching a maximum of 320.05%. Although some of the top 10 optimal architectures for the time overrun prediction model included variants with a larger number of hidden nodes, it was found that models with fewer hidden nodes per layer provided a much better predictive performance.

Table 8. The best model architectures for time overrun prediction.

Hidden Nodes (Layer 1)	Hidden Nodes (Layer 2)	MAPE (%)	RMSE	Correlation	R2
9	7	29.29	0.121	0.973	0.947
6	3	17.90	0.121	0.983	0.966
5	3	10.93	0.128	0.979	0.958

presents the results of the three experiments with the highest potential for correctly predicting time overruns.

Based on the results of the experiments, there is strong potential for accurately predicting time overruns. Two models exhibit an RMSE value of 0.121, one with 9 nodes in the first hidden layer and 7 nodes in the second hidden layer and another with 6 nodes in the first hidden layer and 3 nodes in the second hidden layer. The latter model also exhibited the highest correlation value. Despite this, the model featuring five nodes in the first hidden layer and three nodes in the second hidden layer was selected as the most optimal architecture. This choice was made based on the fact that, despite having a slightly higher RMSE of 0.128, it achieved a significantly lower MAPE of just 10.93%.

3.3. Discussion

The time overrun prediction model demonstrates a significantly superior performance compared to the cost overrun prediction model when applied to the same set of input data. Based on the optimal neural network architecture selected and the MAPE values presented in Table 3, it is evident that the model achieves a MAPE of 10.93%, which is classified as good and approaches the boundary of high accuracy (MAPE ≤ 10%). Furthermore, the prediction accuracy for correlations, with a value of 0.979, is rated as very high, indicating exceptional performance. These results strongly support the efficacy of the approach taken and suggest that further refinements could substantially enhance the model’s performance.

In recent years, numerous studies have demonstrated the effectiveness of artificial neural networks (ANNs) for predicting construction project costs and duration.

Han et al. [16] introduced a BIM-integrated cost prediction model based on a Gray BP Neural Network (PGNN) optimized with the Sparrow Search Algorithm. By extracting engineering quantities from BIM models and incorporating material prices and time-series data, their model achieved a maximum relative error of only 2.99%, an RMSE of 0.1358, and an R² of 0.9819. Similarly, Zhang and Mo [17] developed a BIM–Elman Neural Network (ENN) optimized through Particle Swarm Optimization. Their model utilized a combination of geometric, material, and design-change data from BIM and achieved a prediction accuracy exceeding 95%, with R² values above 0.95. Zhang and Zhang [18] proposed the Deep CostNet for Building Engineering Techniques (DCN-BET), a deep learning-based framework designed for real-time construction cost optimization. Leveraging historical cost records and structured project attributes, the model dynamically updated predictions as new project data became available. Liu et al. [19] introduced a hypergraph deep learning approach for predicting actual construction costs, modeling complex interdependencies among project features and economic variables. By capturing high-order relationships that traditional neural networks typically overlook, the model demonstrated a high early-stage prediction accuracy and improved generalization, particularly for multidimensional data inputs.

In addition to cost prediction, several recent studies have also explored the use of neural networks to forecast construction projects’ duration, particularly in the early planning phases. Alsugair et al. [20] proposed a straightforward feedforward ANN model using only three input variables: contract cost, duration, and sector. Despite its simplicity, the model outperformed linear regression, achieving a MAPE of 12.22%. Ji et al. [21] proposed a hybrid model combining K-means clustering, genetic algorithms, and BP neural networks to forecast residential project durations based on structured numeric inputs. Their method demonstrated a strong predictive accuracy and generalization even on a relatively small dataset. Another advanced study by Anaraki et al. [22] integrated feedforward and Long Short-Term Memory (LSTM) neural networks to capture both time-independent and sequential time-dependent variables, significantly improving the prediction quality in dynamic project environments.

All these models rely heavily on structured, quantitative data, such as contract values, floor areas, or predefined schedules, and aim to predict the total planned cost or timeline rather than track or anticipate deviations. The outputs are typically overall cost estimates or duration forecasts, with little to no integration of qualitative or stakeholder-driven project dynamics. In contrast, the models presented in this study are specifically designed to predict time and cost overruns during the execution phase, enabling more proactive risk management. Rather than forecasting the total contract duration, they aim to detect emerging delays based on technical and stakeholder performance indicators, such as dynamic plan adherence, change management, client satisfaction, and incident rates. This study recognizes that successful project delivery involves more than accurate forecasting of total cost or duration. It requires the ability to detect early signs of deviation, particularly those rooted in human factors such as team satisfaction, communication quality, and client expectations. The models were trained on a small but highly detailed dataset comprising five real-world infrastructure projects, each evaluated at three stages of execution.

While the time overrun prediction model achieved strong results (MAPE = 10.93%, RMSE = 0.128, correlation = 0.979), the cost overrun model presented challenges, with a high MAPE (166.76%) but a solid RMSE (0.4179) and correlation (0.936). These seemingly conflicting results are largely attributable to the nature of the target variable, cost overruns expressed as percentages, where very small actual cost deviations can produce disproportionately large percentage errors. This highlights a known limitation of MAPE as a metric and reinforces the importance of considering RMSE and correlation alongside it. Unlike other models that rely primarily on technical inputs, this model integrates both quantitative data and qualitative insights. This allows it to capture dimensions of projects’ performance often ignored in traditional cost models. Rather than predicting total cost or duration, the models focus on identifying potential deviations, which are more relevant during the execution phase for real-time decision-making. Furthermore, by including key performance areas like safety, quality, and team satisfaction, the model supports a more holistic, sustainability-aware view of projects’ success. Most importantly, the model emphasizes real-world relevance. Grounded in stakeholder interviews and actual case documentation, the dataset captures the lived complexity of projects’ execution, something not always reflected in BIM or structured contract data.

In summary, while existing studies have shown excellent predictive accuracy, they typically operate in well-defined, data-rich environments and aim to estimate final cost and budget values. This research, though facing challenges in prediction accuracy (particularly with MAPE in the cost overrun prediction model), offers a more dynamic and context-sensitive model. It reflects the realities of construction projects’ execution and contributes a novel perspective by integrating subjective performance indicators and focusing on overruns rather than static totals. These attributes make it highly relevant for advancing proactive, sustainability-informed construction project management.

Although the current progress in developing cost and time overrun prediction models is promising, the models do not yet achieve the desired predictive accuracy. Since MAPE values are crucial for assessing models’ accuracy, the high MAPE value (e.g., 163.59% in the case of cost overrun prediction) clearly indicates significant deviations and a lack of reliability in practical applications. Therefore, significant improvements are required to enhance their practical applicability through the expansion of the dataset and improvement in standardization methods to ensure greater stability and accuracy in predictions. The identified optimal models provide a foundation for future research aimed at advancing the accuracy and utility of cost and time predictions in construction projects. It is anticipated that continued research efforts will yield substantially better results.

Given the comparisons with other models in the literature, it is evident that while the developed models show promise, further adjustments and optimizations are required. The current model, based on a dataset of five projects, has offered valuable insights into its performance. However, its scalability to larger datasets and diverse project types remains uncertain. To address this, future research will focus on expanding the dataset within the defined project selection attributes and retraining the model on a broader sample to empirically test its robustness and generalization capacity. Future work may also involve increasing the number of training experiments to better explore the space of possible neural network architectures, parameters, and hyperparameters. Furthermore, the model can be fine-tuned by adjusting input data attributes to examine how reducing the number of attributes impacts the model’s predictive performance. In this context, feature selection techniques will be applied to systematically identify the most relevant input variables, using both algorithmic methods and domain-specific knowledge to retain the most informative and practically significant features. Although ANN was the sole modeling technique explored in this study, future work will consider additional algorithms to determine whether comparable or improved results can be achieved with alternative methods.

While the current models were developed using a relatively small, domain-specific dataset, their underlying architecture is adaptable to larger and more heterogeneous data sources. Scaling to broader datasets would involve fine-tuning of hyperparameters and potentially deeper architectures to capture greater variability. Once the database is expanded, the models could also be explored in the context of transfer learning, where knowledge gained from construction-related data could be adapted to other industries with similar project execution characteristics.

In parallel, one of the key challenges identified during this study relates to models’ evaluation and interpretability. The high MAPE values in the cost overrun model, despite an acceptable RMSE and correlation, limit the model’s immediate applicability in practice. In real-world project environments, such inconsistency in prediction accuracy can undermine key project stakeholders’ trust and reduce the model’s usefulness as a decision-support tool. Until further improvements are made, this model should be used with caution, ideally in combination with expert judgment. Identifying this challenge highlights the importance of carefully selecting performance measures and considering their limitations when applying predictive models in complex construction scenarios. Future research will therefore consider integrating alternative metrics such as Symmetric Mean Absolute Percentage Error (SMAPE), Mean Absolute Error (MAE), and Mean Squared Error (MSE), which can offer a more balanced view of models’ performance.

4. Conclusions

4.1. Concluding Remarks

This research contributes to the understanding of predicting cost and time overruns in construction projects by presenting a comprehensive overview of an artificial neural network model’s generation and the selection of optimal architectures. By employing advanced techniques and performance evaluation this study offers new insights that could enhance prediction accuracy in practical applications.

This research confirms that various metrics are crucial for identifying the most effective neural network architectures. Utilizing data from previous research and refining input quality, two models were created to predict these overruns. A total of 182 experiments were conducted to evaluate various neural network architectures. This process identified the most effective neural network architectures for predicting construction project overruns based on a range of performance metrics. However, achieving a high accuracy in predicting both time and cost overruns remains challenging, indicating areas for further refinement and opening opportunities for more sustainable construction project management.

For predicting time overruns, the optimal model was characterized by two hidden layers, with five nodes in the first layer and three nodes in the second layer. This architecture demonstrated exemplary performance, achieving an RMSE of 0.128, a MAPE of 10.93%, a correlation of 0.979, and an R² value of 0.958. These metrics indicate good accuracy and reliability.

In contrast, the model for predicting cost overruns, featuring two hidden layers with 11 nodes in the first layer and 10 nodes in the second layer, showed less satisfactory results. Despite a reasonable correlation of 0.936, R² value of 0.876, and an acceptable RMSE of 0.417, the high MAPE of 166.76% revealed significant challenges in accuracy and stability. This disparity between the low RMSE and high MAPE suggests potential issues with dataset balance and highlights the need for further refinement of the model. A deeper analysis indicates that this discrepancy stems from the fact that many actual cost overrun values in the dataset are very close to zero. In such cases, even minor absolute prediction errors can result in disproportionately large percentage errors when using MAPE, thereby significantly inflating its value. This is a known limitation of MAPE, especially in low-magnitude outcome domains, and it illustrates why RMSE and correlation remain important complementary metrics. The model’s performance underscores the necessity of improving the quality of input data and refining model parameters to achieve more reliable predictions.

4.2. Practical Implications

The practical value of this research lies in the development of a tool that enables reliable predictions, reduces the time required for data collection and analysis, and supports decision-making during the execution phase of construction projects. By integrating a multi-stakeholder perspective, a comprehensive dataset, and advanced machine learning methods, a model can be developed that is both robust and suited to everyday practice. Its primary purpose is to provide timely predictions of contract time and cost overruns, at a stage when corrective measures can still be taken to minimize risks and prevent significant deviations. The project manager could input the most recent performance indicators into the time overrun prediction model. If the model predicts a high probability of exceeding the contractual completion date, the manager could proactively allocate additional resources, adjust scheduling sequences, or renegotiate specific milestones with stakeholders. Similarly, even though the cost overrun model currently shows a lower predictive accuracy, a significant deviation alert could still prompt early financial audits or targeted cost-control measures. This kind of predictive intervention could help reduce the risk of severe overruns, thereby improving both economic and sustainability outcomes.

These advancements have important implications for the construction industry, where accurate predictions of time and cost overruns are crucial for effective project planning and management. Improved prediction tools will enable project managers to enhance planning and control, thereby mitigating the risks associated with time and cost overruns and ultimately contributing to more successful project outcomes.