Explaining and Predicting Microbiological Water Quality for Sustainable Management of Drinking Water Treatment Facilities
Abstract
1. Introduction
2. Study Area and Data Description

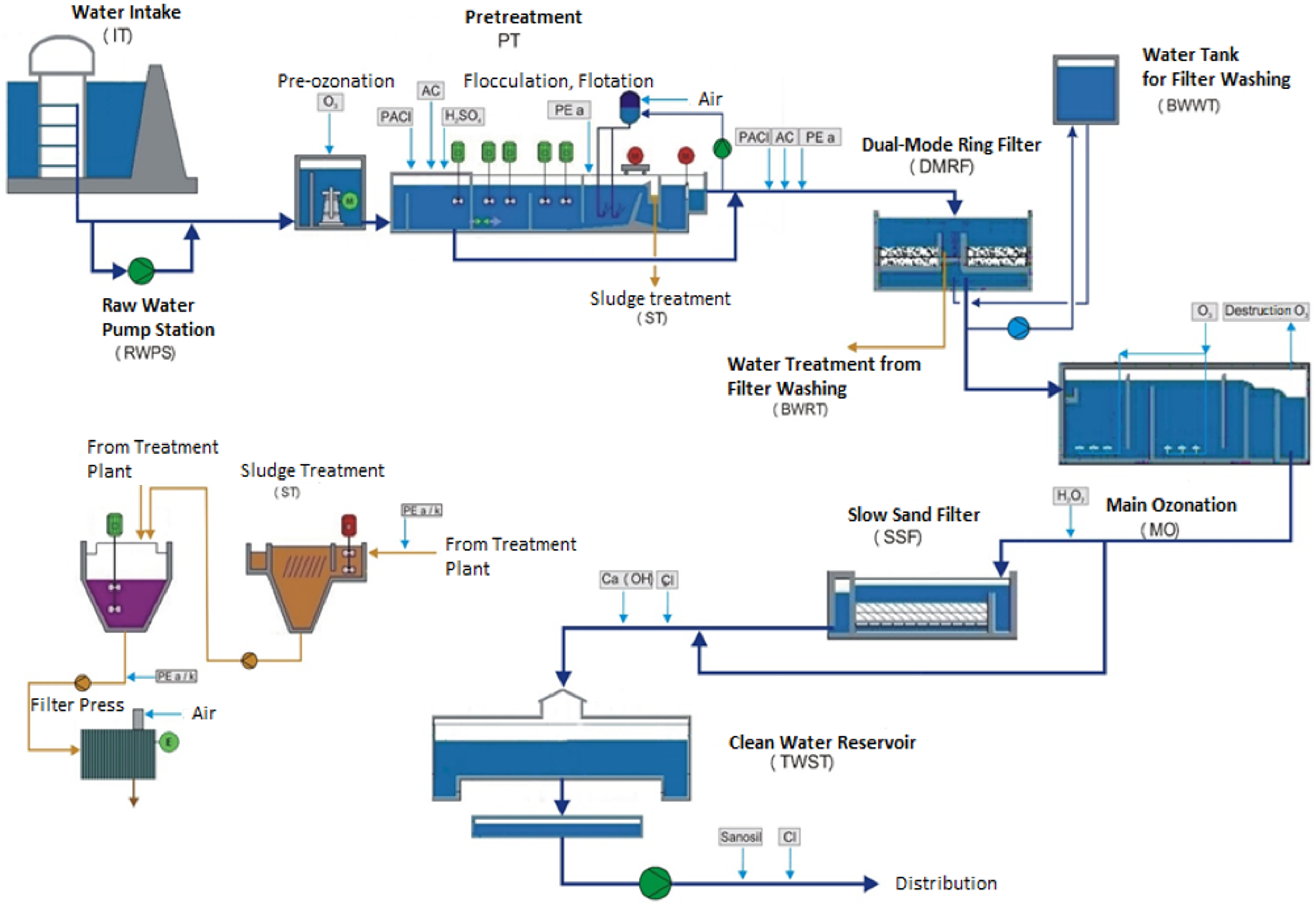
| Symbol | Description | Unit |
|---|---|---|
| Temp | Water temperature | °C |
| O2 | Oxygen concentration | mg/L |
| pH | pH | - |
| Tur | Water turbidity | NTU |
| TOC | Total organic carbon | mg/L |
| KMnO4 | Potassium permanganate | mg/L |
| UV 254 | Concentration of the organic matter in the water | 1/cm |
| NH4 | Ammonia | mg/L |
| Mn | Manganese | mg/L |
| Al | Aluminum | mg/L |
| Fe | Iron | mg/L |
| Tot. coliforms 1 | Total coliforms | CFU/100 mL |
| E. coli 2 | Escherichia coli | CFU/100 mL |
3. Materials and Methods
3.1. Modeling Methods
3.2. Building Decision and Model Trees
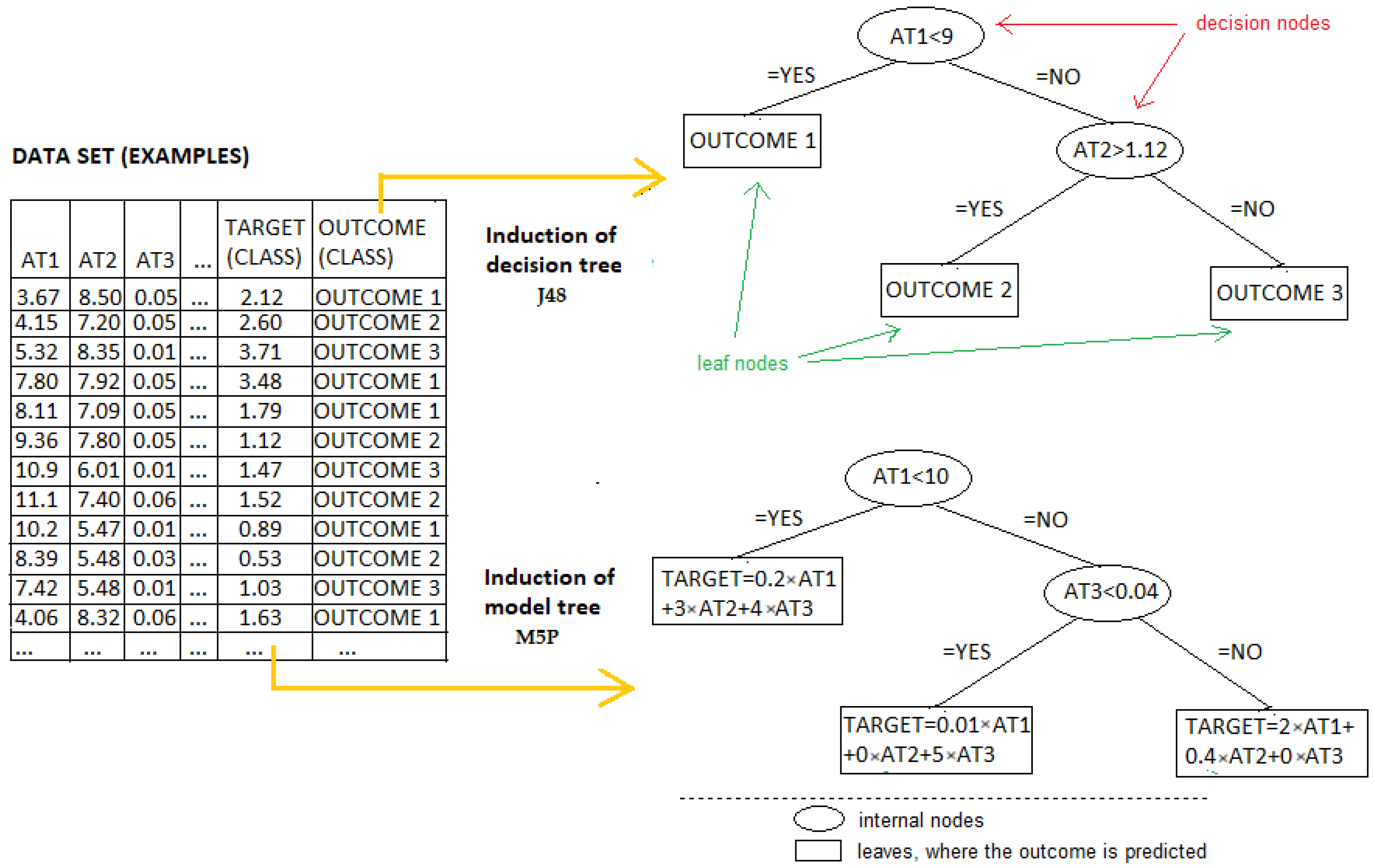
3.3. Model Evaluation and Assessment
3.4. Statistical Analysis and Experimental Setup


| Total Coliforms | E. coli Bacteria | |||||||
|---|---|---|---|---|---|---|---|---|
| Classes | Mean | STDEV | k-Means | Selected | Mean | STDEV | k-Means | Selected |
| Class 0 | 0–136.91 | 0–99.46 | 0–113.81 | 0–100 | 0–5.06 | 0–5.04 | 0–8.47 | 0–5 |
| Class 1 | 136.91–417.38 | 99.46–356.74 | 113.81–476.77 | 100–500 | 5.06–47.69 | 5.06–44.88 | 8.47–57.08 | 5–50 |
| Class 2 | >417.38 | >356.74 | >476.77 | >500 | >47.69 | >44.88 | >57.08 | >50 |


4. Results and Discussion
4.1. Descriptive Models
4.1.1. Descriptive Model for Total Coliforms

4.1.2. Descriptive Model for E. coli Bacteria

4.2. Predictive Models
| Total Coliforms | E. coli Bacteria | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Measures | Model Trees | RF | M-LP | Bagging | XGBoost | Model Trees | RF | M-LP | Bagging | XGBoost |
| R | 0.72 | 0.80 | 0.45 | 0.73 | 0.89 | 0.48 | 0.60 | 0.42 | 0.55 | 0.78 |
| MAE | 205.28 | 138.79 | 273.17 | 165.94 | 111.82 | 26.5 | 17.41 | 28.87 | 20.13 | 15.11 |
| RMSE | 267.32 | 203.19 | 350.37 | 230.66 | 185.06 | 57.7 | 50.10 | 58.96 | 51.89 | 46.62 |
| RAE (%) | 70.06 | 48.70 | 95.84 | 58.22 | 44.56 | 69.3 | 55.89 | 92.70 | 64.63 | 49.62 |
| RRSE (%) | 78.8 | 59.94 | 103.37 | 68.05 | 53.47 | 73.8 | 80.30 | 94.51 | 83.19 | 75.23 |
4.2.1. Predictive Model for Total Coliforms

| Equation No. | Equation |
|---|---|
| 1. | Tot. coliforms pred = 0.1099 × Temp − 12.6543 × pH − 1.514 × TOC + 20.0651 × UV 254 − 14.1254 × NH4 + 0.0189 × Tot. coliforms + 286.8738 |
| 2. | Tot. coliforms pred = 0.1099 × Temp − 14.835 × pH − 1.514 × TOC + 20.0651 × UV 254 − 5.2055 × NH4 + 0.0189 × Tot. coliforms + 262.9118 |
| 3. | Tot. coliforms pred = 0.1099 × Temp − 12.0872 × pH − 1.514 × TOC + 20.0651 × UV 254 − 5.2055 × NH4 + 0.0189 × Tot. coliforms + 175.9947 |
| 4. | Tot. coliforms pred = 0.351 × Temp − 0.8502 × pH − 4.4381 × TOC + 78.196 × UV 254 − 0.551 × NH4 + 0.0125 × Tot. coliforms + 226.4315 |
| 5. | Tot. coliforms pred = 0.1619 × Temp − 0.8502 × pH − 5.5019 × TOC + 160.9756 × UV 254 − 0.551 × NH4 + 0.0125 × Tot. coliforms + 246.5877 |
| 6. | Tot. coliforms pred = 0.1619 × Temp − 0.8502 × pH − 5.9023 × TOC + 90.2781 × UV 254 − 0.551 × NH4 + 0.0125 × Tot. coliforms + 373.1973 |
| 7. | Tot. coliforms pred = 0.1619 × Temp − 0.8502 × pH − 11.999 × TOC + 90.2781 × UV 254 − 0.551 × NH4 + 0.0125 × Tot. coliforms + 288.8409 |
| 8. | Tot. coliforms pred = − 0.0978 × Temp − 0.4027 × pH − 0.4387 × TOC + 7.7413 × UV 254 + 0.0143 × Tot. coliforms + 532.73 |
| 9. | Tot. coliforms pred = − 0.1405 × Temp − 0.4027 × pH − 0.4387 × TOC + 7.7413 × UV 254 + 0.0143 × Tot. coliforms + 23.2427 |
| 10. | Tot. coliforms pred = 0.0508 × Temp − 0.4027 × pH − 0.4387 × TOC + 7.7413 × UV 254 + 0.0189 × Tot. coliforms + 727.1597 |

4.2.2. Predictive Model for E. coli Bacteria

| Equation No. | Equation |
|---|---|
| 1. | E. coli pred = − 0.0094 × O2 − 1.0048 × pH + 0.0719 × KMnO4 − 0.302 × NH4 + 0.6454 × Fe + 0.0017 × E. coli + 27.4774 |
| 2. | E. coli pred = − 0.0094 × O2 − 1.7702 × pH + 0.0719 × KMnO4 − 0.6939 × NH4 + 0.6454 × Fe + 0.0017 × E. coli + 23.4384 |
| 3. | E. coli pred = − 0.0094 × O2 − 1.4932 × pH + 0.0719 × KMnO4 − 0.3272 × NH4 + 0.6454 × Fe + 0.0017 × E. coli + 19.8177 |
| 4. | E. coli pred = − 0.0094 × O2 − 1.5966 × pH + 0.0719 × KMnO4 − 0.3272 × NH4 + 0.6454 × Fe + 0.0017 × E. coli + 17.6368 |
| 5. | E. coli pred = − 0.0445 × O2 − 0.4569 × pH + 0.2575 × Turbidity − 0.1558 × KMnO4 + 1.4384 × Fe + 0.0014 × E. coli + 47.3177 |
| 6. | E. coli pred = − 0.0445 × O2 − 0.4569 × pH + 0.2575 × Turbidity − 0.1558 × KMnO4 + 1.4384 × Fe + 0.0014 × E. coli + 35.5702 |
| 7. | E. coli pred = − 0.0445 × O2 − 0.4569 × pH + 0.6061 × Turbidity − 0.744 × KMnO4 + 1.4384 × Fe + 0.0014 × E. coli + 90.2576 |
| 8. | E. coli pred = − 0.0445 × O2 − 0.4569 × pH + 0.3106 × Turbidity + 0.0609 × KMnO4 + 1.4384 × Fe + 0.0014 × E. coli + 69.5288 |
| 9. | E. coli pred = − 0.0525 × O2 − 0.5132 × pH + 0.0291 × Turbidity + 0.0609 × KMnO4 + 3.8009 × Fe + 0.0014 × E. coli + 20.6872 |
| 10. | E. coli pred = − 0.0525 × O2 − 0.5132 × pH + 0.0291 × Turbidity + 0.0609 × KMnO4 + 3.3453 × Fe + 0.0014 × E. coli + 39.9425 |

4.3. Final Discussion and Remarks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Al | Aluminum |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANN | Artificial Neural Network |
| ARIMA | Autoregressive Integrated Moving Average |
| CART | Classification and Regression Tree |
| CNN | Convolutional Neural Network |
| R2 | Coefficient of Determination |
| CT | Classification Tree |
| DNN | Deep Neural Network |
| DSS | Decision Support System |
| DT | Decision Tree |
| DWTF | Drinking Water Treatment Facility |
| E. coli | Escherichia coli |
| EUDWD | European Union Drinking Water Directive |
| ERT | Extremely Randomized Tree |
| Fe | Iron |
| GBM | Gradient Boosting |
| GBR | Gradient Boosting Regression |
| ID3 | Iterative Dichotomiser |
| KMnO4 | Potassium permanganate |
| kNN | k-Nearest Neighbor |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LightGBM | Light Gradient Boosting Machine |
| LR | Linear Regression |
| MAC | Maximum Allowable Concentration |
| MAE | Mean Absolute Error |
| MAX | Maximum |
| MIN | Minimum |
| ML | Machine Learning |
| M-LP | Multi-Layer Perceptron |
| MT | Model Tree |
| Mn | Manganese |
| NH4 | Ammonia |
| O2 | Oxygen Concentration |
| R | Correlation Coefficient |
| RAE | Relative Absolute Error |
| RMSE | Root Mean-Squared Error |
| RF | Random Forest |
| RT | Regression Tree |
| SDG | Sustainable Development Goal |
| SGB | Stochastic Gradient Boosting |
| STDEV | Standard Deviation |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| TDIDT | Top-Down Induction of Decision Trees |
| TDSs | Total Dissolved Solids |
| Temp | Temperature |
| TOC | Total Organic Carbon |
| TPOT | Tree-based Pipeline Optimization Tool |
| UV 254 | Concentration of Organic Matter in Water |
| XGBoost | Extreme Gradient Boosting |
| ZI | Zero-Inflated Regression Model |
References
- Pachepsky, Y.A.; Allende, A.; Boithias, L.; Cho, K.; Jamieson, R.; Hofstra, N.; Molina, M. Microbial Water Quality: Monitoring and Modeling. J. Environ. Qual. 2018, 47, 931–938. [Google Scholar] [CrossRef] [PubMed]
- Shahid Iqbal, M.; Nauman Ahmad, M.; Hofstra, N. The Relationship between Hydro-Climatic Variables and E. coli Concentrations in Surface and Drinking Water of the Kabul River Basin in Pakistan. AIMS Environ. Sci. 2017, 4, 690–708. [Google Scholar] [CrossRef]
- EU Drinking Water Directive Directive. (EU) 2020/2184 of the European Parliament and of the Council of 16 December 2020 on the Quality of Water Intended for Human Consumption. Available online: https://eur-lex.europa.eu/eli/dir/2020/2184/oj/eng (accessed on 18 October 2024).
- Odonkor, S.T.; Ampofo, J.K. Escherichia coli as an indicator of bacteriological quality of water: An overview. Microbiol. Res. 2013, 4, e2. [Google Scholar] [CrossRef]
- Ministry of Health. Regulation on compliance parameters, methods of analysis and monitoring of water intended for human consumption. National Newspapers, 15 December 2017. Available online: https://narodne-novine.nn.hr/clanci/sluzbeni/2017_12_125_2848.html (accessed on 14 October 2024).
- Stocker, M.D.; Pachepsky, Y.A.; Hill, R.L. Prediction of E. coli Concentrations in Agricultural Pond Waters: Application and Comparison of Machine Learning Algorithms. Front. Artif. Intell. 2022, 4, 768650. [Google Scholar] [CrossRef] [PubMed]
- Seo, M.; Lee, H.; Kim, Y. Relationship between Coliform Bacteria and Water Quality Factors at Weir Stations in the Nakdong River, South Korea. Water 2019, 11, 1171. [Google Scholar] [CrossRef]
- Sokolova, E.; Ivarsson, O.; Lillieström, A.; Speicher, N.K.; Rydberg, H.; Bondelind, M. Data-driven models for predicting microbial water quality in the drinking water source using E. coli monitoring and hydrometeorological data. Sci. Total Environ. 2022, 802, 149798. [Google Scholar] [CrossRef] [PubMed]
- Khan, F.M.; Gupta, R.; Sekhri, S. Superposition learning-based model for prediction of E. coli in groundwater using physico-chemical water quality parameters. Groundw. Sustain. Dev. 2021, 13, 100580. [Google Scholar] [CrossRef]
- Volf, G.; Sušanj Čule, I.; Zorko, S. Influence of the physiochemical parameters on the occurrence of E. coli bacteria in a small and shallow reservoir. J. Water Health 2024, 22, 2206. [Google Scholar] [CrossRef] [PubMed]
- Hannan, A.; Anmala, J. Classification and Prediction of Fecal Coliform in Stream Waters Using Decision Trees (DTs) for Upper Green River Watershed, Kentucky, USA. Water 2021, 13, 2790. [Google Scholar] [CrossRef]
- Li, L.; Qiao, J.; Yu, G.; Wang, L.; Li, H.-Y.; Liao, C.; Zhu, Z. Interpretable Tree-Based Ensemble Model for Predicting Beach Water Quality. Water Res. 2022, 211, 118078. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Wang, J.; Yang, X.; Zhang, Y.; Zhang, L.; Ren, H.; Wu, B.; Ye, L. A review of the application of machine learning in water quality evaluation. Eco-Environ. Health 2022, 1, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Godo-Pla, L.; Emiliano, P.; Valero, F.; Sin, G.; Monclus, H. Predicting the oxidant demand in full-scale drinking water treatment using an artificial neural network: Uncertainty and sensitivity analysis. Process Saf. Environ. Prot. 2019, 125, 317–327. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, T.; Du, W.; Meng, Q.; Xu, X.; Zhao, X. A Comprehensive Review of Machine Learning for Water Quality Prediction over the Past Five Years. J. Mar. Sci. Eng. 2024, 12, 159. [Google Scholar] [CrossRef]
- de Lacerda, M.C.; Batista, G.S.; de Souza, A.F.N.; Aragão, D.P.; Cabral de Araújo, M.M.; Cunha, P.H. Predicting the Presence of Total Coliforms and Escherichia coli in Water Supply Reservoirs Using Machine Learning Models. J. Water Process Eng. 2025, 76, 108146. [Google Scholar] [CrossRef]
- Kaur, I.; Gulati, A.; Lamba, P.S.; Jain, A.; Taneja, H.; Syal, J.S. Water Quality Assessment Using Machine Learning: A Focus on Coliform Prediction in Water. Asian J. Water Environ. Pollut. 2024, 21, 19–26. [Google Scholar] [CrossRef]
- Suh, S.M.; Moon, J.G.; Jung, S.; Pyo, J.C. Improving Fecal Bacteria Estimation Using Machine Learning and Explainable AI in Four Major Rivers, South Korea. Sci. Total Environ. 2024, 957, 177459. [Google Scholar] [CrossRef] [PubMed]
- Hajduk Černeha, B. Akumulacija Butoniga u Istri-Prva iskustva u korištenju za vodoopskrbu. In Proceedings of the Vodni dnevi, Rimske Toplice, Slovenia, 17–18 September 2021. [Google Scholar]
- Zorko, S. Akumulacija Butoniga-pritisci u slijevu i zaštita voda. In Proceedings of the Upravljanje jezerima i akumulacijama u Hrvatskoj i Okrugli stol o aktualnoj problematici Vranskog jezera kod Biograda na Moru, Biograd na Moru, Croatia, 4–6 May 2017. [Google Scholar]
- HRN EN ISO 5667-3:2024; Water Quality-Sampling-Part 3: Preservation and Handling of Water Samples (ISO 5667-3:2024; EN ISO 5667-3:2024). Croatian Standards Institute, HZN e-Glasilo 5/2024: Zagreb, Croatia, 2024.
- HRN EN ISO 9308-2:2014; Water Quality-Enumeration of Escherichia coli and Coliform Bacteria-Part 2: Most Probable Number Method (ISO 9308-2:2012; EN ISO 9308-2:2014). Croatian Standards Institute, HZN e-Glasilo 5/2014: Zagreb, Croatia, 2014.
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Brooks/Cole, Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann: San Francisco, CA, USA, 2016. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 1996, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 2001, 24, 123–140. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd ed.; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Wang, Y.; Witten, I.H. Inducing model trees for continuous classes. In Proceedings of the European Conference on Machine Learning. 9th European Conference on Machine Learning, Prague, Czech Republic, 23–25 April 1997. [Google Scholar]
- Blaustein, R.A.; Pachepsky, Y.; Hill, R.L.; Shelton, D.R.; Whelan, G. Escherichia coli survival in waters: Temperature dependence. Water Res. 2013, 47, 569–578. [Google Scholar] [CrossRef] [PubMed]
- Wahyuni, E.A. The Influence of pH Characteristics on The Occurance of Coliform Bacteria in Madura Strait. Procedia Environ. Sci. 2015, 23, 130–135. [Google Scholar] [CrossRef]
- Smith, P.R.; Paiba, G.A.; Ellis-Iversen, J. Short Communication: Turbidity as an Indicator of Escherichia coli Presence in Water Troughs on Cattle Farms. J. Dairy Sci. 2008, 91, 2082–2085. [Google Scholar] [CrossRef] [PubMed]
- Aram, S.A.; Saalidong, B.M.; Lartey, P.O. Comparative assessment of the relationship between coliform bacteria and water geochemistry in surface and ground water systems. PLoS ONE 2021, 16, e0257715. [Google Scholar] [CrossRef] [PubMed]
- Džeroski, S. Machine learning applications in habitat suitability modelling. In Artificial Intelligence Methods in the Environmental Sciences II; Springer: New York, NY, USA, 2009; pp. 397–411. [Google Scholar]
- Domingos, P. A Few Useful Things to Know About Machine Learning. Commun. ACM 2012, 55, 78–87. [Google Scholar] [CrossRef]
- Gharari, S.; Hrachowitz, M.; Fenicia, F.; Savenije, H.H.G. Hydrological Model Calibration Using Multi-Objective Optimization. Water Resour. Res. 2013, 49, 8356–8376. [Google Scholar] [CrossRef]
- Biau, G. Analysis of a Random Forests Model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Wang, X.; Li, Y.; Qiao, Q.; Tavares, A.; Liang, Y. Water Quality Prediction Based on Machine Learning and Comprehensive Weighting Methods. Entropy 2023, 25, 1186. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, H.; Hameed, I.A.; Seidu, R. Comparative predictive modelling of the occurrence of faecal indicator bacteria in a drinking water source in Norway. Sci. Total Environ. 2018, 628–629, 1178–1190. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volf, G.; Sušanj Čule, I.; Atanasova, N.; Zorko, S.; Ožanić, N. Explaining and Predicting Microbiological Water Quality for Sustainable Management of Drinking Water Treatment Facilities. Sustainability 2025, 17, 6659. https://doi.org/10.3390/su17156659
Volf G, Sušanj Čule I, Atanasova N, Zorko S, Ožanić N. Explaining and Predicting Microbiological Water Quality for Sustainable Management of Drinking Water Treatment Facilities. Sustainability. 2025; 17(15):6659. https://doi.org/10.3390/su17156659
Chicago/Turabian StyleVolf, Goran, Ivana Sušanj Čule, Nataša Atanasova, Sonja Zorko, and Nevenka Ožanić. 2025. "Explaining and Predicting Microbiological Water Quality for Sustainable Management of Drinking Water Treatment Facilities" Sustainability 17, no. 15: 6659. https://doi.org/10.3390/su17156659
APA StyleVolf, G., Sušanj Čule, I., Atanasova, N., Zorko, S., & Ožanić, N. (2025). Explaining and Predicting Microbiological Water Quality for Sustainable Management of Drinking Water Treatment Facilities. Sustainability, 17(15), 6659. https://doi.org/10.3390/su17156659








