Predicting Soil Fertility in Semi-Arid Agroecosystems Using Interpretable Machine Learning Models: A Sustainable Approach for Data-Sparse Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Soil Sampling
2.2. Calculation of Soil Fertility Index
2.3. Modeling Approach
2.3.1. Dataset Preparation
2.3.2. Establishment of Modeling Architecture
2.3.3. Hyperparameter Optimization (GridSearchCV)
2.3.4. Model Validation and Performance Metrics
2.3.5. Interpretation and Recording of Coefficients
2.4. Statistical Analysis
3. Results
3.1. Descriptive Statistics
3.2. Model Evaluation
3.3. Accuracy Assessment
3.4. Model-Based Spatial Predictions
4. Discussion
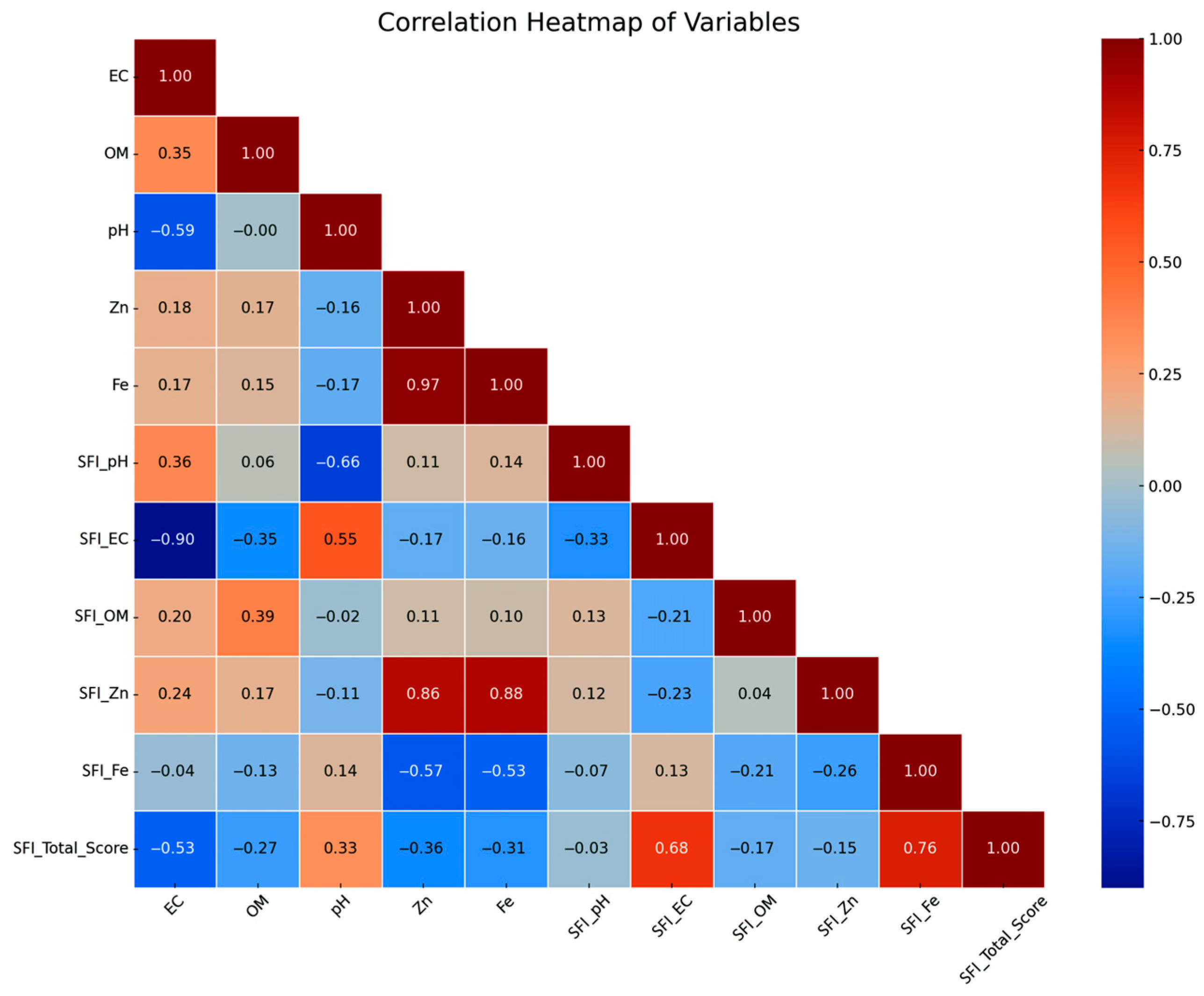
4.1. Exploring Zinc and Iron Mobility Under the Influence of Alkaline pH and Organic Matter in Cultivated Soils
4.2. Data-Driven Identification of Critical Soil Fertility Drivers Using Regularized Regression Models
4.3. Trade-Offs in Regularization, Spatial Realism, and Practical Implications for Soil Fertility Modeling
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krasilnikov, P.; Taboada, M.A.; Amanullah. Fertilizer use, soil health and agricultural sustainability. Agriculture 2022, 12, 462. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Digital soil mapping: A brief history and some lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Liptzin, D.; Norris, C.E.; Cappellazzi, S.B.; Mac Bean, G.; Cope, M.; Greub, K.L.; Rieke, E.L.; Tracy, P.W.; Aberle, E.; Ashworth, A.; et al. An evaluation of carbon indicators of soil health in long-term agricultural experiments. Soil Biol. Biochem. 2022, 172, 108708. [Google Scholar] [CrossRef]
- Tunçay, T.; Kılıç, Ş.; Dedeoğlu, M.; Dengiz, O.; Başkan, O.; Bayramin, I. Assessing soil fertility index based on remote sensing and GIS techniques with field validation in a semiarid agricultural ecosystem. J. Arid Environ. 2021, 190, 104525. [Google Scholar] [CrossRef]
- Adhikari, K.; Hartemink, A.E. Linking soils to ecosystem services—A global review. Geoderma 2016, 262, 101–111. [Google Scholar] [CrossRef]
- Jia, X.; Fang, Y.; Hu, B.; Yu, B.; Zhou, Y. Development of Soil Fertility Index Using Machine Learning and Visible–Near Infrared Spectroscopy. Land 2023, 12, 2155. [Google Scholar] [CrossRef]
- Adeniyi, O.D.; Brenning, A.; Maerker, M. Spatial prediction of soil organic carbon: Combining machine learning with residual kriging in an agricultural lowland area (Lombardy region, Italy). Geoderma 2024, 448, 116953. [Google Scholar] [CrossRef]
- Matyunin, G.; Ogorodnikova, S.; Murmantseva, E.; Rozanov, V.; Palyga, R. Assessment of soil fertility indicators based on remote sensing data. In BIO Web of Conferences, Proceedings of the XVII International Scientific and Practical Conference "State and Development Prospects of Agribusiness" (INTERAGROMASH 2024), Rostov-on-Don, Russia, 22–25 May 2024; EDP Sciences: London, UK, 2024; Volume 113, p. 04013. [Google Scholar] [CrossRef]
- Demir, S.; Sahin, E.K. The effectiveness of data pre-processing methods on the performance of machine learning techniques using RF, SVR, Cubist and SGB: A study on undrained shear strength prediction. Stoch. Environ. Res. Risk Assess. 2024, 38, 3273–3290. [Google Scholar] [CrossRef]
- Kebonye, N.M.; John, K.; Chakraborty, S.; Agyeman, P.C.; Ahado, S.K.; Eze, P.N.; Němeček, K.; Drábek, O.; Borůvka, L. Comparison of multivariate methods for arsenic estimation and mapping in floodplain soil via portable X-ray fluorescence spectroscopy. Geoderma 2021, 384, 114792. [Google Scholar] [CrossRef]
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Rahman Nur, A.; Jaya, A.K.; Siswanto, S. Comparative Analysis of Ridge, Lasso and Elastic Net Regularization Approaches in Handling Multicollinearity for Infant Mortality Data in South Sulawesi. J. Mat. Stat. Dan Komputasi 2024, 20, 311–319. [Google Scholar] [CrossRef]
- General Directorate of Meteorology. 2025. Available online: https://www.mgm.gov.tr/veridegerlendirme/il-ve-ilceler-istatistik.aspx?m=BATMAN (accessed on 10 May 2025).
- Eren, Y. General Assessment of the Geology, Tectonics, Seismicity, and New Settlement Area Selection of the Immediate Vicinity of Batman Province. Tech. Rep. 2011. [Google Scholar] [CrossRef]
- Loiseau, T.; Arrouays, D.; Richer-de-Forges, A.C.; Lagacherie, P.; Ducommun, C.; Minasny, B. Density of soil observations in digital soil mapping: A study in the Mayenne region, France. Geoderma Reg. 2021, 24, e00358. [Google Scholar] [CrossRef]
- Gee, G.W.; Bouder, J.W. Particle size analysis. In Methods of Soil Analysis. Part I, Agronomy No. 9; Clute, A., Ed.; American Society of Agronomy: Madison, WI, USA, 1986. [Google Scholar]
- Rhoades, J.; Chandavi, D.; Lesch, S.F. Soil Salinity Assessment Methods and Interpretation of Electrical Conductivity Measurements; FAO Irrigation and Drainage Paper 57; Food and Agriculture Organization of the United Nations: Rome, Italy, 1999; Available online: https://openknowledge.fao.org/handle/20.500.14283/x2002e (accessed on 20 August 2025).
- Nelson, D.W.; Sommers, L.E. Methods of Soil Analysis, Part 2. Chemical and Microbiological Properties, 2nd ed.; Page, A.L., Miller, R.H., Keeney, D.R., Eds.; SSSA Inc.: Madison, WI, USA, 1982. [Google Scholar]
- Lindsay, W.L.; Norvell, W. Development of a DTPA soil test for zinc, iron, manganese, and copper. Soil Sci. Soc. Am. J. 1978, 42, 421–428. [Google Scholar] [CrossRef]
- Saraswat, A.; Ram, S.; AbdelRahman, M.A.E.; Raza, M.B.; Golui, D.; HC, H.; Lawate, P.; Sharma, S.; Dash, A.K.; Scopa, A.; et al. Combining Fuzzy, Multicriteria and Mapping Techniques to Assess Soil Fertility for Agricultural Development: A Case Study of Firozabad District, Uttar Pradesh, India. Land 2023, 12, 860. [Google Scholar] [CrossRef]
- Merumba, M.S.; Semu, E.; Semoka, J.M.; Msanya, B.M. Soil Fertility Status in Bukoba, Missenyi and SharmaBiharamulo Districts in Kagera Region, Tanzania. Int. J. Appl. Agric. Sci. 2020, 6, 96. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning. In Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Roozbeh, M. Shrinkage ridge estimators in semiparametric regression models. J. Multivar. Anal. 2015, 136, 56–74. [Google Scholar] [CrossRef]
- Shen, X.; Alam, M.; Fikse, F.; Rönnegård, L. A novel generalized ridge regression method for quantitative genetics. Genetics 2013, 193, 1255–1268. [Google Scholar] [CrossRef]
- Xing, L.; Pittman, J.J.; Inostroza, L.; Butler, T.J.; Munoz, P. Improving predictability of multisensor data with nonlinear statistical methodologies. Crop Sci. 2018, 58, 972–981. [Google Scholar] [CrossRef]
- Huang, S.; Wu, Y.; Wang, Q.; Liu, J.; Han, Q.; Wang, J. Estimation of chlorophyll content in pepper leaves using spectral transmittance red-edge parameters. Int. J. Agric. Biol. Eng. 2022, 15, 85–90. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Dehmer, M. High-dimensional LASSO-based computational regression models: Regularization, shrinkage, and selection. Mach. Learn. Knowl. Extr. 2019, 1, 359–383. [Google Scholar] [CrossRef]
- Ruan, Y.; Huang, G.; Zhang, J.; Mai, S.; Gu, C.; Rong, X.; Huang, L.; Zeng, W.; Wang, Z. Risk analysis of noise-induced hearing loss of workers in the automobile manufacturing industries based on back-propagation neural network model: A cross-sectional study in Han Chinese population. Br. Med. J. Open 2024, 14, 079955. [Google Scholar] [CrossRef]
- Ternès, N.; Rotolo, F.; Michiels, S. Empirical extensions of the lasso penalty to reduce the false discovery rate in high-dimensional Cox regression models. Stat. Med. 2016, 35, 2561–2573. [Google Scholar] [CrossRef]
- Sancar, N.; Onakpojeruo, E.P.; Inan, D.; Uzun Ozsahin, D. Adaptive Elastic Net Based on Modified PSO for Variable Selection in Cox Model with High-Dimensional Data: A Comprehensive Simulation Study. IEEE Access 2023, 11, 127302–127316. [Google Scholar] [CrossRef]
- Suzuki, T.; Tomioka, R.; Sugiyama, M. Sharp Convergence Rate and Support Consistency of Multiple Kernel Learning with Sparse and Dense Regularization. arXiv 2011. [Google Scholar] [CrossRef]
- Wei, B.; Liu, Y.; Liu, X.; Wei, C. Commentary: Analysis of Risk Factors for Painful Diabetic Peripheral Neuropathy and Construction of a Prediction Model Based on Lasso Regression. Front. Endocrinol. 2025, 16, 1519556. [Google Scholar] [CrossRef]
- Hartemink, A.E.; Barrow, N.J. Soil pH-Nutrient Relationships: The Diagram. Plant Soil 2023, 486, 209–215. [Google Scholar] [CrossRef]
- Malathi, P.; Babu, B.G.; Sellamuthu, K.M. Zinc Availability in Calcareous Soil as Influenced by Various Levels, Sources of Zn and Zn Solubilizing Bacteria. Asian Res. J. Agric. 2024, 17, 1123–1133. [Google Scholar] [CrossRef]
- He, Y.; Zhang, J.; Li, C.; Zhang, L.; Fu, D. The Effect of Biochar Application Rates on Soil Fertility and Phyto-Availability of Heavy Metals is Dependent on Soil Type and pH. Commun. Soil Sci. Plant Anal. 2025, 56, 1291–1305. [Google Scholar] [CrossRef]
- Sary, D.H.; Abd EL-Rahman, Z.M.; El-Sedfy, O.M.F. Impact of Irrigation Regimes and Organic Amendments on Soil Physical Properties, Nutrient Availability, and Productivity in Calcareous Soil. Asian J. Soil Sci. Plant Nutr. 2024, 10, 830–851. [Google Scholar] [CrossRef]
- Tarolli, P.; Luo, J.; Park, E.; Barcaccia, G.; Masin, R. Soil Salinization in Agriculture: Mitigation and Adaptation Strategies Combining Nature-Based Solutions and Bioengineering. iScience 2024, 27, 108830. [Google Scholar] [CrossRef]
- Safdar, H.; Amin, A.; Shafiq, Y.; Ali, A.; Yasin, R.; Shoukat, A.; Ul Hussan, M.; Sarwar, M.I. A Review: Impact of Salinity on Plant Growth. Nat. Sci. 2019, 17, 34–40. [Google Scholar] [CrossRef]
- Carlos, F.S.; Marcolin, É.; Kunde, R.J.; Weinert, C.; Pasa, E.H.; Schäffer, N.; de Sousa, R.O.; dos Reis, R.B.; Andreazza, R.; de Oliveira, J.R.; et al. Long-Term No-Tillage Increases Soil Organic Matter and Cation Exchange Capacity, but Reduces P and K, in Irrigated Rice. Soil Use Manag. 2025, 41, e70016. [Google Scholar] [CrossRef]
- Van Eynde, E.; Fendrich, A.N.; Ballabio, C.; Panagos, P. Spatial Assessment of Topsoil Zinc Concentrations in Europe. Sci. Total Environ. 2023, 892, 164512. [Google Scholar] [CrossRef]
- Chen, J.; Liu, R.; Jian, Y.; Ma, T. Spatial Distribution and Factors Influencing the Various Forms of Iron in Alluvial–Lacustrine Clayey Aquitard. Water 2023, 15, 3934. [Google Scholar] [CrossRef]
- Sun, G.; Liu, H.; Cui, D.; Chai, C. Spatial Heterogeneity of Soil Nutrients in Yili River Valley. PeerJ 2022, 10, e13311. [Google Scholar] [CrossRef] [PubMed]
- Noulas, C.; Tziouvalekas, M.; Karyotis, T. Zinc in Soils, Water and Food Crops. J. Trace Elem. Med. Biol. 2018, 49, 252–260. [Google Scholar] [CrossRef] [PubMed]
- Singh, A. Soil Salinity: A Global Threat to Sustainable Development. Soil Use Manag. 2022, 38, 39–67. [Google Scholar] [CrossRef]
- Busoms, S.; Almira-Casellas, M.; Barceló, J.; Poschenrieder, C. Plant Tolerance to Alkaline Salinity: A Gordian Knot to Untie. In Plant Stress Tolerance; CRC Press: Boca Raton, FL, USA, 2025; pp. 37–69. [Google Scholar] [CrossRef]
- Yang, S.; Xu, Y.; Tang, Z.; Jin, S.; Yang, S. The Impact of Alkaline Stress on Plant Growth and Its Alkaline Resistance Mechanisms. Int. J. Mol. Sci. 2024, 25, 13719. [Google Scholar] [CrossRef]
- Hoffland, E.; Kuyper, T.W.; Comans, R.N.; Creamer, R.E. Eco-Functionality of Organic Matter in Soils. Plant Soil 2020, 455, 1–22. [Google Scholar] [CrossRef]
- Kabelka, D.; Konvalina, P.; Kopecký, M.; Klenotová, E.; Šíma, J. Assessment of Soil Organic Matter and Its Microbial Role in Selected Locations in the South Bohemia Region (Czech Republic). Land 2025, 14, 183. [Google Scholar] [CrossRef]
- Laik, R.; Awad Eltahira, E.B.; Pramanick, B.; Nidhi, N.; Singh, S.K.; van Es, H.M. Enhancing Soil Health in Rice Cultivation: Optimized Zn Application and Crop Residue Management in Calcareous Soils. Sustainability 2025, 17, 489. [Google Scholar] [CrossRef]
- Alloway, B.J. Micronutrients and Crop Production: An Introduction. In Micronutrient Deficiencies in Global Crop Production; Springer: Dordrecht, The Netherlands, 2008; pp. 1–39. [Google Scholar] [CrossRef]
- Singh, P.; Saini, S.P. Micronutrients Availability in Soil–Plant System as Influenced by Long-Term Integrated Nutrient Management under Rice–Wheat Cropping. J. Plant Nutr. 2022, 45, 457–470. [Google Scholar] [CrossRef]
- Mossa, A.W.; Gashu, D.; Broadley, M.R.; Dunham, S.J.; McGrath, S.P.; Bailey, E.H.; Young, S.D. The effect of soil properties on zinc lability and solubility in soils of Ethiopia–an isotopic dilution study. Soil 2021, 7, 255–268. [Google Scholar] [CrossRef]
- Munns, R.; Gilliham, M. Salinity tolerance of crops—What is the cost? New Phytol. 2015, 208, 668–673. [Google Scholar] [CrossRef] [PubMed]
- Voltr, V.; Menšík, L.; Hlisnikovský, L.; Hruška, M.; Pokorný, E.; Pospíšilová, L. The soil organic matter in connection with soil properties and soil inputs. Agronomy 2021, 11, 779. [Google Scholar] [CrossRef]
- Bünemann, E.K.; Bongiorno, G.; Bai, Z.; Creamer, R.E.; De Deyn, G.; de Goede, R.; Fleskens, L.; Geissen, V.; Kuyper, T.W.; Mäder, P.; et al. Soil quality—A critical review. Soil Biol. Biochem. 2018, 120, 105–125. [Google Scholar] [CrossRef]
- Majumder, S.; Shankar, T.; Maitra, S.; Kumar, A.; Gudade, B.A.; Sagar, L.; Sairam, M.; Das, S.; Dash, S. Effect of Nutrient Omission Plot Technique Based Nutrient Management in Rabi Rice (Oryza sativa) on Crop Productivity, Nutrient Uptake and Soil Health. Indian J. Agron. 2024, 69, 357–363. [Google Scholar] [CrossRef]
- Gawande, Y.D.; Hadole, S.S.; Mankar, E.P. Effect of Different Sources and Levels of Zinc on the Nutrient Content, Uptake and Fertility Status of Wheat. Int. J. Plant Soil Sci. 2025, 37, 288–309. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, S.; Mohapatra, T. Interaction Between Macro- and Micro-Nutrients in Plants. Front. Plant Sci. 2021, 12, 665583. [Google Scholar] [CrossRef]
- Thapa, S.; Bhandari, A.; Ghimire, R.; Xue, Q.; Kidwaro, F.; Ghatrehsamani, S.; Maharjan, B.; Goodwin, M. Managing Micronutrients for Improving Soil Fertility, Health, and Soybean Yield. Sustainability 2021, 13, 11766. [Google Scholar] [CrossRef]
- Feng, B.; Ma, J.; Liu, Y.; Wang, L.; Zhang, X.; Zhang, Y.; Zhao, J.; He, W.; Chen, Y.; Weng, L. Application of Machine Learning Approaches to Predict Ammonium Nitrogen Transport in Different Soil Types and Evaluate the Contribution of Control Factors. Ecotoxicol. Environ. Saf. 2024, 284, 116867. [Google Scholar] [CrossRef] [PubMed]
- Dhaliwal, S.S.; Naresh, R.K.; Mandal, A.; Walia, M.K.; Gupta, R.K.; Singh, R.; Dhaliwal, M.K. Effect of manures and fertilizers on soil physical properties, build-up of macro and micronutrients and uptake in soil under different cropping systems: A review. J. Plant Nutr. 2019, 42, 2873–2900. [Google Scholar] [CrossRef]
- Kaur, T.; Sehgal, S.K.; Singh, S.; Sharma, S.; Dhaliwal, S.S.; Sharma, V. Assessment of seasonal variability in soil nutrients and its impact on soil quality under different land use systems of lower Shiwalik foothills of Himalaya, India. Sustainability 2021, 13, 1398. [Google Scholar] [CrossRef]
- Athokpam, H.; Wani, S.H.; Kamei, D.; Athokpam, H.S.; Nongmaithem, J.; Kumar, D.; Singh, Y.K.; Naorem, B.S.; Devi, T.R.; Devi, L. Soil macro-and micro-nutrient status of Senapati district, Manipur (India). Afr. J. Agric. Res. 2013, 8, 4932–4936. [Google Scholar] [CrossRef]
- Swaminathan, B.; Palani, S.; Vairavasundaram, S. Fertility Level Prediction in Precision Agriculture Based on an Ensemble Classifier Model. Int. J. Sustain. Agric. Manag. Inform. 2021, 7, 270. [Google Scholar] [CrossRef]
- Birol, M.; Günal, H. Field Scale Variability in Soil Properties and Silage Corn Yield. Soil Stud. 2022, 11, 27–34. [Google Scholar] [CrossRef]
- Kujawska, J.; Kulisz, M.; Cel, W.; Kwiatkowski, C.A.; Harasim, E.; Bandura, L. Evaluating and Predicting CO2 Flux from Agricultural Soils Treated with Organic Amendments: A Comparative Study of ANN and ElasticNet Models. J. Soils Sediments 2025, 25, 864–882. [Google Scholar] [CrossRef]
- Zhao, Z.; Luo, S.; Zhao, X.-X.; Zhang, J.; Li, S.; Luo, Y.; Dai, J. A Novel Interpolation Method for Soil Parameters Combining RBF Neural Network and IDW in the Pearl River Delta. Agronomy 2024, 14, 2469. [Google Scholar] [CrossRef]
- Tekin, A.B.; Gunal, H.; Sindir, K.; Balci, Y. Spatial structure of available micronutrient contents and their relationships with other soil characteristics and corn yield. Fresenius Environ. Bull. 2011, 20, 783–792. [Google Scholar]
- Vasu, D.; Sahu, N.; Tiwary, P.; Chandran, P. Modelling the spatial variability of soil micronutrients for site specific nutrient management in a semi-arid tropical environment. Model. Earth Syst. Environ. 2021, 7, 1797–1812. [Google Scholar] [CrossRef]
- Dharumarajan, S.; Lalitha, M.; Niranjana, K.V.; Hegde, R. Evaluation of digital soil mapping approach for predicting soil fertility parameters—A case study from Karnataka Plateau, India. Arab. J. Geosci. 2022, 15, 386. [Google Scholar] [CrossRef]
- Srinivasan, R.; Shashikumar, B.N.; Singh, S.K. Mapping of soil nutrient variability and delineating site-specific management zones using fuzzy clustering analysis in eastern coastal region, India. J. Indian Soc. Remote Sens. 2022, 50, 533–547. [Google Scholar] [CrossRef]
- Mohammed, S.; Arshad, S.; Bashir, B.; Ata, B.; Al-Dalahmeh, M.; Alsalman, A.; Ali, H.; Alhennawi, S.; Kiwan, S.; Harsanyi, E. Evaluating machine learning performance in predicting sodium adsorption ratio for sustainable soil-water management in the eastern Mediterranean. J. Environ. Manag. 2024, 370, 122640. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Metwaly, M.M.; Metwalli, M.R.; AbdelRahman, M.A.; Badreldin, N. Integrating active and passive remote sensing data for mapping soil salinity using machine learning and feature selection approaches in arid regions. Remote Sens. 2023, 15, 1751. [Google Scholar] [CrossRef]
- Mohammadifar, A.; Gholami, H.; Golzari, S. Assessment of the uncertainty and interpretability of deep learning models for mapping soil salinity using DeepQuantreg and game theory. Sci. Rep. 2022, 12, 15167. [Google Scholar] [CrossRef]
- Bouslihim, Y.; Bouasria, A.; Jelloul, A.; Khiari, L.; Dahhani, S.; Mrabet, R.; Moussadek, R. Baseline high-resolution maps of soil nutrients in Morocco to support sustainable agriculture. Sci. Data 2025, 12, 1389. [Google Scholar] [CrossRef] [PubMed]
- Khosravani, P.; Moosavi, A.A.; Baghernejad, M.; Kebonye, N.M.; Mousavi, S.R.; Scholten, T. Machine Learning Enhances Soil Aggregate Stability Mapping for Effective Land Management in a Semi-Arid Region. Remote Sens. 2024, 16, 4304. [Google Scholar] [CrossRef]
- Ozturk, M.; Kilic, M.; Günal, H. Digital Mapping of Soil pH and Electrical Conductivity: A Comparative Analysis of Kriging and Machine Learning Approaches. MAS J. Appl. Sci. 2024, 9, 1168–1185. [Google Scholar] [CrossRef]
- Abakay, O.; Kılıç, M.; Günal, H.; Kılıç, O.M. Tree-based algorithms for spatial modeling of soil particle distribution in arid and semi-arid region. Environ. Monit. Assess. 2024, 196, 264. [Google Scholar] [CrossRef]
- Gunal, H.; Kılıç, M.; Altındal, M.; Gündoğan, R. Rapid spatial estimation of soil pH using machine learning under limited covariate conditions. Levantine J. Appl. Sci. 2021, 1, 30–37. [Google Scholar] [CrossRef]




| Parameter | 1 | 0.8 | 0.5 | 0.2 | 0 |
|---|---|---|---|---|---|
| pH | 6.5–7.5 | 7.4–8.5 | 5.5–6.4 | 4.5–5.4 | <4.5 or >8.5 |
| EC (dS m−1) | 0–2 | 2.1–4 | 4.1–6 | 6.1–8 | >8 |
| OM (g kg−1) | >30 | 20.1–30 | 10.1–20 | 5.1–10 | 0–5 |
| Zn (mg kg−1) | 0.71–2.41 | 2.4–8.0 | 0.2–0.7 | >8 | <0.2 |
| Fe (mg kg−1) | 2.1–4.5 | 1.1–2.0 | 0.2–1.0 | >4.5 | <0.2 |
| Variable | Unit | Mean | Std Dev | Minimum | 1.Quartile | Median | 3.Quartile | Maximum |
|---|---|---|---|---|---|---|---|---|
| EC | dS/m | 5.39 | 3.30 | 1.33 | 3.22 | 4.47 | 6.20 | 15.71 |
| Organic Matter | g/kg | 59.99 | 15.13 | 26.10 | 49.53 | 61.47 | 68.98 | 97.13 |
| pH | 7.90 | 0.13 | 7.54 | 7.81 | 7.92 | 7.99 | 8.19 | |
| Zn | mg/kg | 0.03 | 0.04 | 0.00 | 0.01 | 0.02 | 0.04 | 0.25 |
| Fe | 27.22 | 39.62 | 0.35 | 6.13 | 13.79 | 31.73 | 248.97 | |
| SFI pH | 0.76 | 0.08 | 0.60 | 0.80 | 0.80 | 0.80 | 0.80 | |
| SFI EC | 0.60 | 0.26 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | |
| SFI OM | 0.99 | 0.04 | 0.80 | 1.00 | 1.00 | 1.00 | 1.00 | |
| SFI Zn | 0.22 | 0.06 | 0.20 | 0.20 | 0.20 | 0.20 | 0.60 | |
| SFI Fe | 0.49 | 0.27 | 0.20 | 0.20 | 0.50 | 0.80 | 1.00 | |
| SFI Score | 0.61 | 0.07 | 0.48 | 0.56 | 0.60 | 0.68 | 0.76 |
| Model | Ridge | Lasso | ElasticNet |
|---|---|---|---|
| Best Alpha | 100 | 0.01 | 0.1 |
| l1 ratio | 0.2 | ||
| MSE Train | 0.00 | 0.00 | 0.00 |
| RMSE Train | 0.06 | 0.06 | 0.06 |
| R2 Train | 0.83 | 0.89 | 0.78 |
| MSE Test | 0.00 | 0.00 | 0.00 |
| RMSE Test | 0.06 | 0.06 | 0.07 |
| R2 Test | 0.63 | 0.75 | 0.68 |
| RPD Test | 1.07 | 1.15 | 1.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acir, N. Predicting Soil Fertility in Semi-Arid Agroecosystems Using Interpretable Machine Learning Models: A Sustainable Approach for Data-Sparse Regions. Sustainability 2025, 17, 7547. https://doi.org/10.3390/su17167547
Acir N. Predicting Soil Fertility in Semi-Arid Agroecosystems Using Interpretable Machine Learning Models: A Sustainable Approach for Data-Sparse Regions. Sustainability. 2025; 17(16):7547. https://doi.org/10.3390/su17167547
Chicago/Turabian StyleAcir, Nurullah. 2025. "Predicting Soil Fertility in Semi-Arid Agroecosystems Using Interpretable Machine Learning Models: A Sustainable Approach for Data-Sparse Regions" Sustainability 17, no. 16: 7547. https://doi.org/10.3390/su17167547
APA StyleAcir, N. (2025). Predicting Soil Fertility in Semi-Arid Agroecosystems Using Interpretable Machine Learning Models: A Sustainable Approach for Data-Sparse Regions. Sustainability, 17(16), 7547. https://doi.org/10.3390/su17167547






