Multi-Channel Graph Convolutional Network for Evaluating Innovation Capability Toward Sustainable Seed Enterprises

Abstract

The innovation capability of seed enterprises reflects their core competitiveness and serves as a vital foundation for sustainable agricultural development and modernization. Therefore, evaluating this capability is of great importance. However, existing evaluation methods primarily focus on internal enterprise attributes, overlooking the complex inter-enterprise relationships and lacking sufficient feature fusion capabilities to capture latent information. To address these limitations, this paper proposes a Multi-Channel Graph Convolutional Network (MGCN) model that integrates enterprise attributes with three types of relational graphs. The model adopts a multi-channel architecture for feature extraction and employs a gated attention mechanism for cross-graph feature fusion, jointly considering node features and relation information to improve prediction accuracy. Experimental results demonstrate that MGCN achieves an average accuracy of 83.59% under five-fold cross-validation, outperforming several mainstream models such as Random Forest and traditional GCN. Case studies further reveal that MGCN not only captures key features of individual enterprises but also leverages features and label distribution from neighboring enterprises, facilitating more context-aware classification decisions. In conclusion, the MGCN model provides an effective method for the intelligent evaluation of innovation capability in seed enterprises and supports the formulation of sustainable strategic plans at both the national and enterprise level.

1. Introduction

As key players in agricultural innovation, seed enterprises play a vital role in driving technological progress in the industry. However, under the globalized economic landscape, they are faced with unprecedented competitive pressure [1]. Innovation capacity is a key determinant of enterprise competitiveness and is crucial for maintaining market position and ensuring sustainable development. Therefore, it is essential to evaluate the innovation capacity of seed enterprises. Evaluating seed enterprise capabilities can assist governments in formulating policies. At present, China is prioritizing support for 276 key seed enterprises with sustainable development potential. By continuously monitoring and assessing seed enterprises, it is possible to adjust national support policies and target beneficiaries accordingly. For seed enterprises, evaluating their innovation capabilities can help them to gain an understanding of themselves, develop sustainable strategic plans, strengthen overall enterprise capacity, and enhance competitiveness. Currently, enterprises evaluation methods are generally classified into three types, including classical statistical models [2], machine learning models [3], and deep learning models [4].

Commonly used classical statistical models include the Balanced Scorecard (BSC) [5], Key Performance Indicators (KPI) [6], Analytic Hierarchy Process (AHP) [7], Data Envelopment Analysis (DEA) [8], and Grey Relational Analysis (GRA) [9], among others. Compared with earlier DuPont analysis [10], these approaches are no longer limited to financial indicators but evaluate enterprises from multiple dimensions, providing more comprehensive and scientific assessment results. For example, Xiang employed the DEA method to evaluate the innovation efficiency of listed companies, analyzing the relationship between innovation inputs and outputs, and proposed improvement suggestions [11]. Yu applied the AHP to evaluate the credit level of technology-based small and medium-sized enterprises, pointing out deficiencies in the existing credit index system, such as an excessive focus on financial capacity while neglecting technical and talent indicators [12].

Machine learning has become an increasingly important tool in enterprise evaluation, especially as the volume and complexity of enterprise data grow and the limitations of traditional statistical methods become more evident. Machine learning techniques can handle large-scale datasets and capture complex, non-linear relationships. Methods such as Support Vector Machine (SVM) [13] and Random Forest (RF) [14] have been introduced into the field of enterprise evaluation. For example, Zhang constructed a credit risk evaluation index system and proposed a model based on SVM to predict default behavior in small and medium-sized enterprise [15]. In some cases, researchers face incomplete data. To address the issue of missing evaluation labels, Akman applied Principal Component Analysis (PCA) and the k-means clustering algorithm to determine data labels and then employed algorithms such as RF to predict enterprise innovation capacity. This method integrates unsupervised and supervised machine learning techniques, offering a relatively objective approach for label generation while providing a fast and accurate evaluation procedure [16].

Deep learning is increasingly applied in enterprise evaluation due to its capabilities in automatic feature extraction and modeling complex, non-linear relationships in data. For example, Lian employed an artificial neural network with a multilayer perceptron (MLP) architecture to assess the credit risk of listed companies in China based on financial indicators, and found that fixed asset turnover was the most influential factor in bank lending decisions [17]. Shang proposed an enterprise performance evaluation model for cross-border e-commerce based on deep learning. The model integrates a multidimensional indicator system with recurrent neural networks, deep belief networks, and attention mechanisms, which together improve both prediction accuracy and the efficiency of performance classification [18]. Hosaka introduced a novel method that converts financial ratios into grayscale images and applies a convolutional neural network to predict corporate bankruptcy. This image-based representation of financial data improved the accuracy of corporate financial health assessment [19].

Graph neural networks (GNNs) effectively capture both node features and relational dependencies in graph-structured data, making them well-suited for tasks involving complex inter-entity interactions [20]. For example, Feng represented each enterprise’s individual features as nodes within separate graph structures, analyzing the relationships between these feature nodes and the information flow among them to perform corporate credit prediction [21]. However, early studies mainly focused on the internal attributes of individual enterprises, overlooking the complex inter-enterprise interactions that influence prediction outcomes. To address this limitation, Wei modeled all seed enterprises as nodes in a single graph, where each node encodes basic attributes and litigation information, while heterogeneous edges represent investment, stakeholder, and related connections. By leveraging hypergraph neural networks to capture shared risk factors across industry sectors, regions, and stakeholders, the accuracy of enterprise bankruptcy prediction was significantly improved [22]. Bi considered the contributions of different types of inter-enterprise relationships by applying attention mechanisms to assign weights to both neighboring enterprises and relationship types. The fused features are then used to determine the risk category of the target enterprise, enabling more effective risk assessment within the context of industrial supply chains [23]. It is evident that graph neural networks play a crucial role, such as Graph Convolutional Networks (GCN) [24] and Graph Attention Networks (GAT) [25], all of which effectively capture the topological information of graphs. However, when both node features and graph topology impact the task, these models still face challenges in adaptively balancing their relative importance. To address this issue, Wang proposed the AM-GCN model, which performs graph convolutions simultaneously on both the topology and feature graphs, adaptively adjusting their contributions to generate more robust and scalable embeddings [26].

Effectively leveraging various types of inter-enterprise relationships, rather than relying solely on intrinsic enterprise features, and accurately capturing their distinct impacts remain key challenges in evaluating the innovation capacity of seed enterprises. This paper proposes the MGCN model, which integrates multi-channel graph convolution with a gated attention [27] to fully exploit both the intrinsic attributes of seed enterprises and various types of inter-enterprise relationships. The model takes three types of relational graph as the input and processes them through four parallel GCN channels: three dedicated to extracting features from specific relations, and one designed to capture common patterns. Compared with approaches that merge all relations into a single heterogeneous graph, this architecture enables clearer separation and modeling of individual relationship effects, reducing information interference and enhancing representational capacity. Channel outputs are adaptively fused via a gated attention mechanism, allowing context-aware feature selection that emphasizes relationship information most relevant to innovation capability prediction. By integrating multi-source information and comprehensively modeling complex inter-enterprise connections, MGCN significantly improves the accuracy of innovation capability assessment for seed enterprises, providing a powerful tool to enhance enterprise competitiveness and promote sustainable agricultural development.

To validate the effectiveness of the proposed model, we conducted extensive experiments, including comparisons with nine baseline methods, ablation studies to evaluate the contribution of each model component, relational graph analysis to assess the impact of removing specific relationship types on prediction accuracy, feature analysis based on top-k correlated features to examine their influence on model performance, and case studies to explore the model’s decision-making logic and practical utility.

2. Materials and Methods

2.1. Data Collection and Preprocessing

Prior to the evaluation of seed enterprises’ innovation capacity, data collection and organization were conducted as essential preparatory steps. The data used in this study were mainly obtained from the China Seed Industry Big Data Platform and the Aiqicha website. These datasets included both internal enterprise information and external relational data, ensuring comprehensiveness and accuracy.

In total, 1000 enterprise records were collected, covering leading seed enterprises in China, along with large, medium, and small enterprises engaged in breeding. After data processing, 981 valid samples were retained. Based on innovation capacity, the samples were categorized into four levels: “Excellent”, “Good”, “Moderate”, and “Poor”, with corresponding sample sizes of 86, 304, 356, and 235, respectively.

The internal data of seed enterprises mainly include basic information, innovation outputs, qualifications, and honors, as detailed in

Table 1. Description of internal feature data in seed enterprises.

Type	Features
Basic Information	year of establishment; registered province; registered capital; paid-in capital; number of insured employees.
Innovation Output	number of variety approval applications; number of variety registration applications; number of plant variety protection applications; number of transformants; number of patents; number of published papers.
Qualifications and Honors	number of national-level awards; designation as a national leading enterprise in a dominant variety cluster; designation as a national supplementary enterprise in a weak link cluster; designation as a national breakthrough enterprise in a bottleneck cluster; status as a national enterprise technology center; status as a provincial enterprise technology center; recognition as a “Little Giant” Enterprises with Specialization, Refinement, Distinctiveness, and Innovation.

.

The external relational data were primarily composed of shareholding and cooperation relationships among seed enterprises, while an additional set of innovation similarity data was constructed based on the enterprises’ primary innovation outputs. These various forms of relational information were subsequently utilized for the construction of enterprise relationship graphs, which served as the structural foundation for downstream modeling and analysis.

During data preprocessing, strict screening procedures were applied to ensure the representativeness and consistency of the research samples. Non-market-oriented seed-related entities, including agricultural research institutions, agricultural technology service centers, and agricultural technology extension centers, were excluded.

Some collected data on seed enterprises showed strong right-skewness, contained categorical variables, and had inconsistent measurement units, which could adversely affect model performance if left unprocessed. To ensure feature comparability and improve model learning efficiency, the following steps were applied:

Variables such as registered capital, paid-in capital, and number of insured employees exhibited large value ranges and significant right-skewness. To reduce skewness, a log transformation was applied using the following formula:

$$n^{\prime }=\ln \left(n+1\right)$$

(1)

where $n$ denotes any single value from registered capital, paid-in capital, or number of insured employees.

The categorical variable “province” was converted into a numerical format using one-hot encoding, whereby each province is represented as a separate binary feature.

The Z-score normalization method was applied to standardize the data to a distribution with a mean of 0 and a standard deviation of 1, thereby eliminating the differences in scales among different features. The formula is given by:

$$x={\displaystyle \frac{X-\mu }{\sigma }}$$

(2)

where $X$ represents a feature in the dataset, $\mu$ is the mean of that feature, and $\sigma$ is its standard deviation.

2.2. Construction of Inter-Enterprise Relationship Graphs

To more accurately evaluate the innovation capacity of seed enterprises, three inter-enterprise relationship graphs—namely the shareholding graph, the collaboration graph, and the innovation similarity graph—were constructed based on a curated dataset of 981 seed enterprises. These graphs capture diverse relational structures within the seed industry. Inter-enterprise relationships, such as equity holdings and strategic collaborations, are critical for the flow of innovation resource [28,29,30], and may exert an indirect but significant impact on innovation capacity. The innovation similarity graph is intended to reveal latent connections among enterprises, identify innovation clusters, and further enhance the model’s predictive performance.

In the shareholding graph, an edge is established between two seed enterprises if a shareholding relationship exists, reflecting ownership or investment ties that may facilitate the transfer of innovation resources, technologies, and strategic advantages. Given that this study focuses on evaluating the innovation capacity of seed enterprises, the number of variety approvals, variety registrations, and variety protections are considered key indicators of innovation performance [31,32]. Accordingly, in the collaboration relationship graph, an edge is created between two enterprises if they have jointly applied for any of the three aforementioned activities. Similarly, in the innovation similarity graph, cosine similarity is computed based on the three indicators. For each enterprise, those with an innovation similarity exceeding 80% are identified, from which the top three are selected to form edges with the focal enterprise. The cosine similarity between two enterprises (Enterprise A and Enterprise B) is calculated as follows:

$$c\left(A,B\right)={\displaystyle \frac{A·B}{‖A‖‖B‖}}$$

(3)

Using the aforementioned methods, three types of graphs were constructed: the shareholding relationship graph (Graph-S), the collaboration relationship graph (Graph-C), and the innovation similarity relationship graph (Graph-I) of seed enterprises. These three graphs share an identical node set, with each node corresponding to the same enterprise across all graphs; however, they differ substantially in their edge configurations, which reflect different forms of relational information. The number of nodes and edges in each graph is shown in

Table 2. Seed enterprise shareholding relationship graph (Graph-S); seed enterprise cooperation relationship graph (Graph-C); seed enterprise innovation similarity relationship graph (Graph-I).

Graph	Nodes	Edges	Classes	Features
Graph-S	981	89	4	48
Graph-C	981	678	4	48
Graph-I	981	2261	4	48

.

To provide a more intuitive and comprehensive understanding of their structural characteristics, the graphs were visualized using the spring layout algorithm, which generates graphical representations where the distances and spatial arrangements between nodes clearly reflect their connectivity within the network. It can clearly be observed that the edges in Graph-S and Graph-C are relatively sparse, especially in Figure 1a, where most nodes lack connecting edges or form isolated components. Therefore, Graph-S may have a limited impact on the subsequent evaluation of innovation capacity. Given that innovation resources can be transferred between shareholder and investee enterprises [30,33], thereby affecting their innovation capability, the shareholding graph is modeled as an undirected graph in this study.

2.3. Evaluation Model

2.3.1. Overall Framework

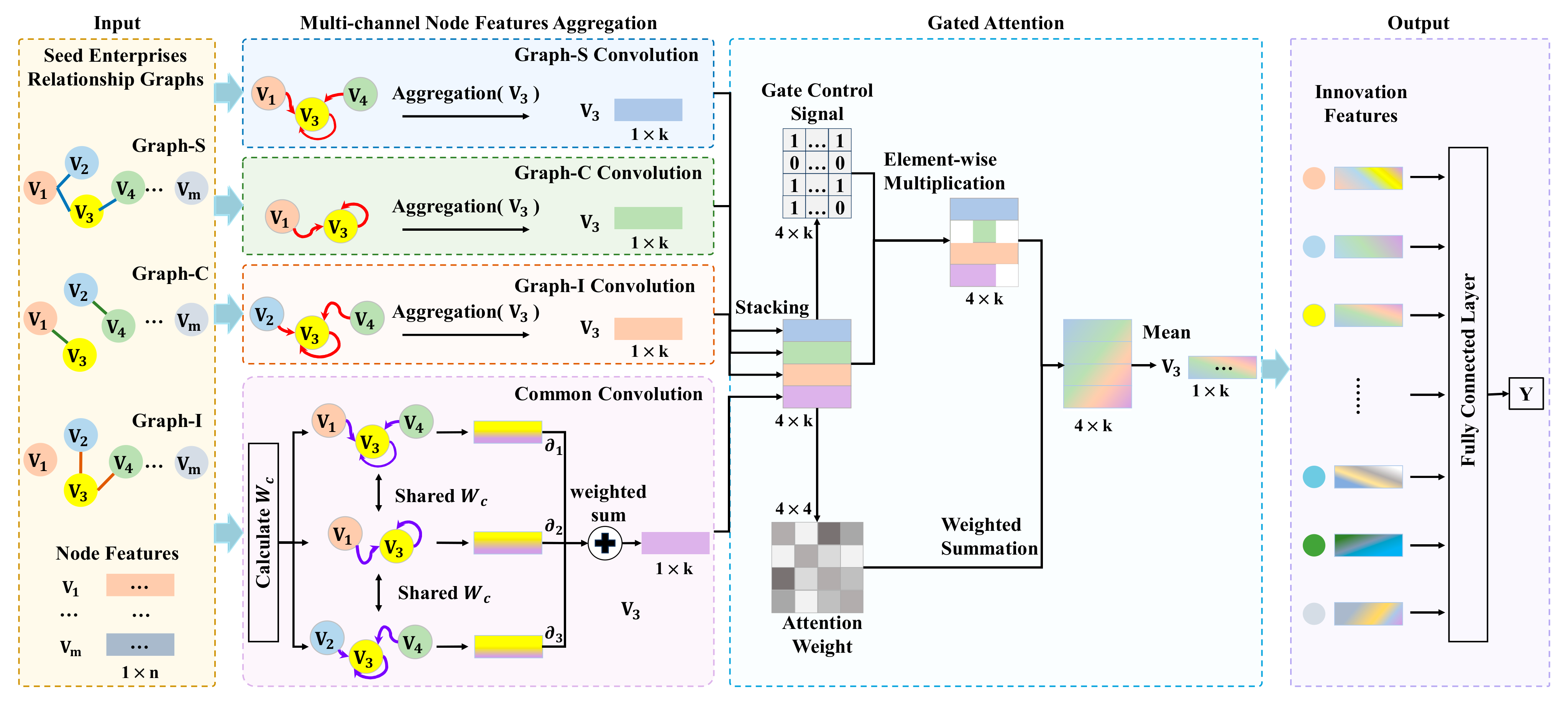
This study constructs an innovation capacity evaluation model for seed enterprises based on a multi-channel graph convolutional network. The overall architecture of the proposed MGCN model is illustrated in Figure 2.

The model takes as input three heterogeneous relationship graphs representing shareholding (Graph-S), collaboration (Graph-C), and innovation similarity (Graph-I) among seed enterprises. These graphs are processed through four parallel graph convolutional channels: three dedicated to extracting relationship-specific features, and one common feature processing channel that aggregates features across all graphs using shared convolutional weights. Each channel propagates innovation-related information along the edges of its corresponding graph, allowing each node to integrate features from its neighbors. This message-passing mechanism ensures that a node’s embedding reflects both its own attributes and the structural context of connected enterprises. As shown in the “Multi-channel Node Features Aggregation” section of Figure 2, each channel generates a feature vector for each node (e.g., $V_3$) via GCN-based aggregation, thereby encoding information related to the enterprise’s innovation capacity into vector representations. The Common Convolution module applies shared weights $W_c$ to capture relationally invariant patterns. All four outputs are then stacked and passed into a Gated Attention module, which generates gating signals and attention weights to adaptively regulate the contribution of each feature. This allows the model to emphasize informative features while suppressing irrelevant ones. Finally, as shown in the “Output” block, the fused embeddings are fed into a fully connected layer to predict innovation capacity. This architecture enables the dynamic integration of multiple heterogeneous relationships and allows the model to adaptively adjust to diverse feature compositions, enhancing its capability to handle complex and varied data and supporting an accurate and comprehensive assessment of seed enterprises’ innovation capacity.

2.3.2. Specific Feature Processing Channel for Single Graph

In this channel, Graph Convolutional Networks (GCNs) are used to update node features by aggregating information from each node and its neighbors. In standard GCNs, each neighboring node contributes equally, and through multi-layer propagation, nodes can indirectly capture information from more distant nodes. The update rule is defined as

$$H^{\left(l+1\right)}=\sigma \left(D^{-{\displaystyle \frac{1}{2}}}\left(A+I\right)D^{-{\displaystyle \frac{1}{2}}}{H}^{\left(l\right)}{W}^{\left(l\right)}\right)$$

(4)

Here, $l$ denotes the layer number of the GCN, $\sigma$ is a non-linear activation function, $A$ is the original adjacency matrix, and $I$ is the identity matrix used to introduce self-loops. $D$ is the degree matrix, where the diagonal elements represent the degree of each node, and $W^{\left(l\right)}$ is the trainable weight matrix at layer $l$. Based on this formulation, the embeddings obtained from the feature processing channels for the shareholding graph, the collaboration graph, and the innovation similarity graph are denoted as $H_s$, $H_p$, and $H_o$.

2.3.3. Common Feature Processing Channel for Multiple Graphs

To capture shared patterns across different graphs, a common feature processing channel applies a shared weight matrix $W_c^{\left(l\right)}$ to all graphs. The GCN update rule is applied independently to each graph using this shared weight, Taking the shareholding graph (Graph-S) as an example, the node embedding update is computed as

$$H_{cs}^{\left(l+1\right)}=\sigma \left(D_s^{-{\displaystyle \frac{1}{2}}}\left(A_s+I\right)D_s^{-{\displaystyle \frac{1}{2}}}{H}_{cs}^{\left(l\right)}{W}_c^{\left(l\right)}\right)$$

(5)

Using this method, embeddings $H_{cs}$, $H_{cp}$ and $H_{co}$. for the shareholding, collaboration, and innovation similarity graphs are obtained and combined via weighted fusion to produce the common channel output:

$$H_c=w_1{H}_{cs}+w_2{H}_{cp}+w_3{H}_{co}$$

(6)

The parameters $w_1$, $w_2$, $w_3$ are trainable weights bounded between 0 and 1, satisfying the condition that their sum equals 1.

2.3.4. Gated Attention for Feature Fusion

The four embeddings $H_s$, $H_p$, $H_o$ and $H_c$. are stacked to form $H_z$, which is input into a gated attention mechanism. This mechanism adaptively weighs the contribution of each channel through a combination of attention scores and gating signals. Specifically, linear projections are applied to derive query, key, value, and gate matrices:

$$Q=w_q{H}_z , K=w_k{H}_z , V=w_v{H}_z, G=\sigma \left(w_g{H}_z\right)$$

(7)

Here, $w_q$, $w_k$, $w_v$, and $w_g$ represent the linear transformation weight matrices for the Query, Key, Value, and Gate, respectively. The function $\sigma$ denotes the Sigmoid activation function, which constrains the gating signal to a range between 0 and 1. Next, the attention scores are computed using the Query and Key:

$$Scores={\displaystyle \frac{Q{K}^T}{\sqrt{D^{\prime }}}}$$

(8)

Here, $K^T$ is the transpose of the Key matrix, $D^{\prime }$ is set to the dimensionality of the hidden layer in the gated attention mechanism and $\sqrt{D^{\prime }}$ is a scaling factor used to prevent the dot-product results from becoming too large. Attention scores are normalized via softmax to obtain $Attn$. The gated value is computed by element-wise multiplying the Value matrix with the gate

$$V_g=V\odot G$$

(9)

The final output is obtained by a weighted sum followed by a linear transformation:

$$output=W_f\left({\sum }_{x=1}^{X}Attn{V}_g\right)$$

(10)

Among them, $W_f$ is the weight matrix of the final linear transformation. $\sum _{x=1}^{X}Attn{V}_g$ represents the sum of the features of all sequence positions and combines the features of all sequence positions for each sample into one feature vector.

2.3.5. Multi-Objective Loss Function

To guide training, a multi-objective loss is defined with three components: classification loss, consistency constraint, and diversity constraint. These components work together to optimize the overall performance of the model.

The classification loss measures the difference between the model’s predictions and ground-truth labels. To address sample imbalance, Weighted Cross-Entropy Loss is used, with class weights based on the number of training samples per class. This helps the model focus more on minority classes during training, enhancing robustness to imbalanced data. The class weights are set as follows:

$${\tilde{w}}_n={\displaystyle \frac{\frac{1}{{support}_n}}{\sum _{k=1}^N\frac{1}{{support}_k}}}$$

(11)

Here, $N$ denotes the number of classes, ${support}_n$ represents the number of samples in class $n$, and ${\tilde{w}}_n$ is the normalized weight for class $n$. The weighted cross-entropy loss is formulated as

$$L_{cls}=-\sum _{i\in trainnodes}{w}_{y_i}\log \left(p_{i,y_i}\right)$$

(12)

where $w_{y_i}$ denotes the weight corresponding to the true class $y_i$ of node $i$ and $p_{i,y_i}$ represents the predicted probability that node $i$ belongs to its true class $y_i$, which is obtained from the output layer of the model.

Encourages embeddings from different graphs in the common feature channel to be similar. For each embedding $H_{cs}$, $H_{cp}$, $H_{co}$, a similarity matrix $S=H{H}^T$, is computed and normalized. The consistency loss is

$$L_c={‖S_{cs}-S_{cp}‖}_F^2+{‖S_{cp}-S_{co}‖}_F^2$$

(13)

We ensure distinctiveness between embeddings from the specific and common channels of the same graph using HSIC [34]:

$$HSIC\left(H_s,H_{cs}\right)={\displaystyle \frac{1}{{\left(n-1\right)}^2}}trace\left(K_{s}H{K}_{cs}H\right)$$

(14)

Here, trace denotes the trace of a matrix. $K_s$ and $K_{cs}$ are the Gram matrices defined as $K_s=H_s{H}_s^T$, $K_{cs}=H_{cs}{H}_{cs}^T$, respectively. The matrix $H$ is the centering matrix given by $H=I-{\displaystyle \frac{1}{n}}E{E}^T$, where $I$ is the identity matrix and $E$ is a column vector of all ones. The total diversity loss is:

$$L_d=HSIC\left(H_s,H_{cs}\right)+HSIC\left(H_p,H_{cp}\right)+HSIC\left(H_o,H_{co}\right)$$

(15)

The overall loss function is formulated as a weighted sum of the classification loss, the consistency constraint, and the diversity constraint:

$$L=L_{cls}+\alpha L_c+\beta L_d$$

(16)

Here, $\alpha$ and $\beta$ are hyperparameters used to control the weights of the consistency and diversity constraints, respectively. During training, α decreases while β increases. Early on, a higher α helps the model stabilize faster by emphasizing consistency. Later, reducing α and increasing β encourages more diversity in embeddings, improving the model’s generalization.

2.3.6. Seed Enterprise Innovation Capability Prediction

The $output$ from the gated attention mechanism is used for the multi-class classification task. Specifically, it is fed into a fully connected layer to obtain the raw scores for each class:

$${\widehat{y}}_{logits}=W_{fc}·output+b_{fc}$$

(17)

where ${\widehat{y}}_{logits}$ denotes the output of the fully connected layer, while $W_{fc}$ and $b_{fc}$ are the weight matrix and bias vector, respectively. The raw scores ${\widehat{y}}_{logits}$ are then transformed into a probability distribution using the softmax function, which ensures that each class score is between 0 and 1, and the sum of all class scores equals 1. The softmax function is defined as

$${\widehat{y}}_i={\displaystyle \frac{exp\left({\widehat{y}}_{logits,i}\right)}{\sum _{j=1}^{N}exp\left({\widehat{y}}_{logits,j}\right)}}$$

(18)

where $N$ denotes the number of classes, and $\widehat{y}$ represents the predicted probability for the $i$-th class.

2.4. Evaluation Metrics

To comprehensively evaluate the performance of the model, 5-fold cross-validation was conducted, and the average values of various evaluation metrics were calculated. These metrics include accuracy, precision, recall, and F1-score. specifically, precision, recall, and F1-Score were computed using the Macro-average method [35], resulting in Macro Precision, Macro Recall, and Macro F1-Score, Macro-averaging is performed by calculating the metric independently for each class and then taking the average of these values. This method assigns equal weight to all classes, regardless of the number of instances in each individual class, making it particularly suitable for imbalanced classification scenarios. The mathematical formulations of these evaluation metrics are presented as follows:

$$ACC={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(19)

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(20)

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(21)

$$F1-Score=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}$$

(22)

TP refers to the number of instances correctly predicted as positive by the model; TN refers to the number of instances correctly predicted as negative; FP refers to the number of instances incorrectly predicted as positive; and FN refers to the number of instances incorrectly predicted as negative.

3. Results

3.1. Experimental Setup

A series of experiments were designed and conducted in this study, including model comparison experiments, ablation studies on the model architecture, analysis of the effectiveness of relation graphs, and feature analysis. The proposed model was evaluated against nine representative baselines: LR [36], SVM [15], RF [37], MLP [38], GCN [24], GAT [25], GraphSAGE [39], GraphTransformer [40], and R-GCN [41]. Since LR, SVM, RF, and MLP cannot process graph data, only node features of seed enterprises were used as input in these experiments. GCN, GAT, GraphSAGE, GraphTransformer, and R-GCN support graph structures, so the three types of relationships were merged into a single graph as input.

Due to the presence of class imbalance in the data, targeted handling methods were applied to different models to enhance their robustness and overall learning performance. For the LR, SVM, and RF models, the SMOTETomek method was used on the training data. This hybrid approach addresses class imbalance by both increasing the number of minority class samples through interpolation and reducing noise by removing majority class samples near the decision boundary. For the GCN, GAT, GraphSAGE, GraphTransformer, R-GCN, and MGCN models, conventional sampling methods may disrupt the graph topology; therefore, a weighted cross-entropy loss function was employed, assigning weights to different classes to improve the models’ ability to handle imbalanced data. In addition, focal loss was also explored as an alternative loss function to further enhance the model’s sensitivity to hard-to-classify minority samples. The MLP model adopted both approaches simultaneously.

All experiments were conducted using 5-fold stratified cross-validation to mitigate potential bias from random data partitioning, ensuring each fold maintained a class distribution consistent with the overall dataset. To guarantee reproducibility, a fixed random seed of 33 was used throughout.

To determine the optimal configuration for each model, an exhaustive grid search was carefully performed. The final hyperparameter settings used in our experiments are summarized in

Table 3. Parameters setting.

Model	Setting
LR	max_iter = 500; multi_class = multinomial; penalty = ‘l2’; solver = lbfgs.
SVM	C = 10; kernel = linear; decision_function_shape = ovr.
RF	n_estimators = 200; max_depth = 10; min_samples_leaf = 2; min_samples_split = 2.
MLP	hidden layer = 2; hidden1 = 16, hidden2 = 16; optimizer = Adam; learning rate = 0.001; weight decay = 1 × 10−4; activation function = relu; epochs = 200, loss = ‘focal’.
GCN	hidden layer = 2; hidden1 = 64, hidden2 = 16; activation function = relu; dropout rate = 0.5; optimizer = Adam; learning rate = 0.01; weight decay = 1 × 10−5; epochs = 200; loss = ‘cross entropy’.
GAT	hidden layer = 2; hidden1 = 16, hidden2 = 16; heads = 4; activation function = relu; dropout rate = 0.6; optimizer = Adam; learning rate = 0.001; weight decay = 1 × 10−5; epochs = 300, loss = ‘focal’.
GraphSAGE	hidden layer = 2; hidden1 = 32, hidden2 = 32; aggr = ‘max’; activation function = relu; dropout rate = 0.4; optimizer = Adam; learning rate = 0.01; weight decay = 1 × 10−5; epochs = 200; loss = ‘cross entropy’.
GraphTransformer	hidden layer = 2; hidden1 = 16, hidden2 = 16; heads = 4; activation function = relu; dropout rate = 0.5; optimizer = Adam; learning rate = 0.001; weight decay = 1 × 10−3; epochs = 300, loss = ‘ cross entropy’.
R-GCN	hidden layer = 2; hidden1 = 16, hidden2 = 32; activation function = relu; dropout rate = 0.6; optimizer = Adam; learning rate = 0.01; weight decay = 1 × 10−3; epochs = 400; loss = ‘cross entropy’.
MGCN	hidden layer = 2; hidden1 = 32, hidden2 = 64; activation function = relu; dropout rate = 0.6; optimizer = Adam; learning rate = 0.01; weight decay = 1 × 10−3; epochs = 200; loss = ‘cross entropy’.

. The full range of hyperparameter values explored during the search process is provided in Appendix A.

3.2. Comparative Experiments

By comparing with various classical machine learning models (LR, SVM, RF), neural network models (MLP), and graph neural network models (GCN, GAT, GraphSAGE, GraphTransformer, R-GCN), we comprehensively evaluated the proposed MGCN model in terms of performance, stability, and node embedding quality. The results demonstrate its significant advantages and robustness in assessing the innovation capability of seed enterprises, establishing it as an effective and powerful technical tool.

In

Table 4. Prediction results of the innovation ability of seed enterprises by different methods.

Method	ACC	Macro Precision	Macro Recall	Macro F1-Score
LR	0.7717 ± 0.0304	0.7736 ± 0.0384	0.7568 ± 0.0367	0.7580 ± 0.0317
SVM	0.7737 ± 0.0299	0.7556 ± 0.0306	0.7645 ± 0.0373	0.7556 ± 0.0315
RF	0.7880 ± 0.0387	0.7790 ± 0.0295	0.8043 ± 0.0389	0.7852 ± 0.0343
MLP	0.7605 ± 0.0255	0.7492 ± 0.0322	0.7389 ± 0.0311	0.7412 ± 0.0308
GCN	0.8063 ± 0.0191	0.7824 ± 0.0330	0.7718 ± 0.0314	0.7729 ± 0.0278
GAT	0.8135 ± 0.0286	0.7850 ± 0.0303	0.8206 ± 0.0309	0.7951 ± 0.0279
GraphSAGE	0.8033 ± 0.0302	0.7800 ± 0.0257	0.7990 ± 0.0445	0.7840 ± 0.0316
GraphTransformer	0.7992 ± 0.0142	0.7981 ± 0.0102	0.7986 ± 0.0378	0.7941 ± 0.0219
R-GCN	0.8145 ± 0.0166	0.7859 ± 0.0225	0.8249 ± 0.0212	0.7974 ± 0.0239
MGCN	0.8359 ± 0.0273	0.8173 ± 0.0316	0.8277 ± 0.0536	0.8186 ± 0.0398

, the MGCN model achieved the best performance, with an accuracy (ACC) of 0.8359 ± 0.0273, Macro Precision of 0.8173 ± 0.0316, Macro Recall of 0.8277 ± 0.0536, and Macro F1-Score of 0.8186 ± 0.0398. These results indicate that the model achieves high accuracy while effectively identifying positive classes and maintaining strong overall performance. This superiority is attributed to the model’s multi-channel architecture, which processes different relation graphs separately to capture the varied impacts of each relationship type on innovation capability. Moreover, the gated attention mechanism enables efficient feature selection and fusion based on multi-channel embeddings, allowing the model to integrate node features and graph topology. This suggests that innovation capability predictions are influenced by both internal attributes and inter-enterprise relationships.

In comparison, RF performed best among traditional machine learning models, achieving 78.8% accuracy. However, it cannot process graph data and thus ignores topological structure information, limiting its effectiveness. LR, a simple linear classifier, performed worse due to its limited capacity to model complex data. The SVM model, with a linear kernel, outperformed other kernels, suggesting that the relationship between features and labels tends to be more linear. By using the kernel trick to project data into higher-dimensional space and finding a margin-maximizing hyperplane, SVM is more effective than LR. However, it is sensitive to outliers and may underperform when the sample size greatly exceeds the number of features, as it relies on samples to define the decision boundary.

In Table 4, graph neural networks clearly outperform traditional models due to their ability to exploit structural information. GCN achieves 80.63% accuracy by aggregating fixed-weight neighborhood features, but this rigidity limits its ability to capture complex graph variations. GAT improves F1 score to 79.51% by assigning attention weights dynamically, though it is more sensitive to noisy neighbors and still processes only a single homogeneous graph. GraphSAGE attains 80.33% accuracy by sampling neighbors and using max pooling, which boosts efficiency but fails to distinguish edge types, weakening relational modeling. GraphTransformer utilizes multi-head attention to capture global graph patterns, achieving an accuracy of 79.92%. However, due to the simple graph structure and limited number of nodes and features, the advantages of global attention are limited and prone to introducing noise, which affects performance improvement. R-GCN explicitly models multiple relation types through relation-specific transformations, achieving a high recall of 82.49%, which highlights the importance of relation awareness. However, due to the lack of a gating fusion mechanism, it lacks flexibility in integrating multi-relational information. In contrast, MGCN attains higher accuracy (83.59%) and F1 score (81.86%). Its multi-channel design independently processes each relation’s subgraph, allowing it to better capture the distinct features and structural differences displayed by each relation. The dynamic fusion of features and topology enables MGCN to integrate multi-relational information more flexibly.

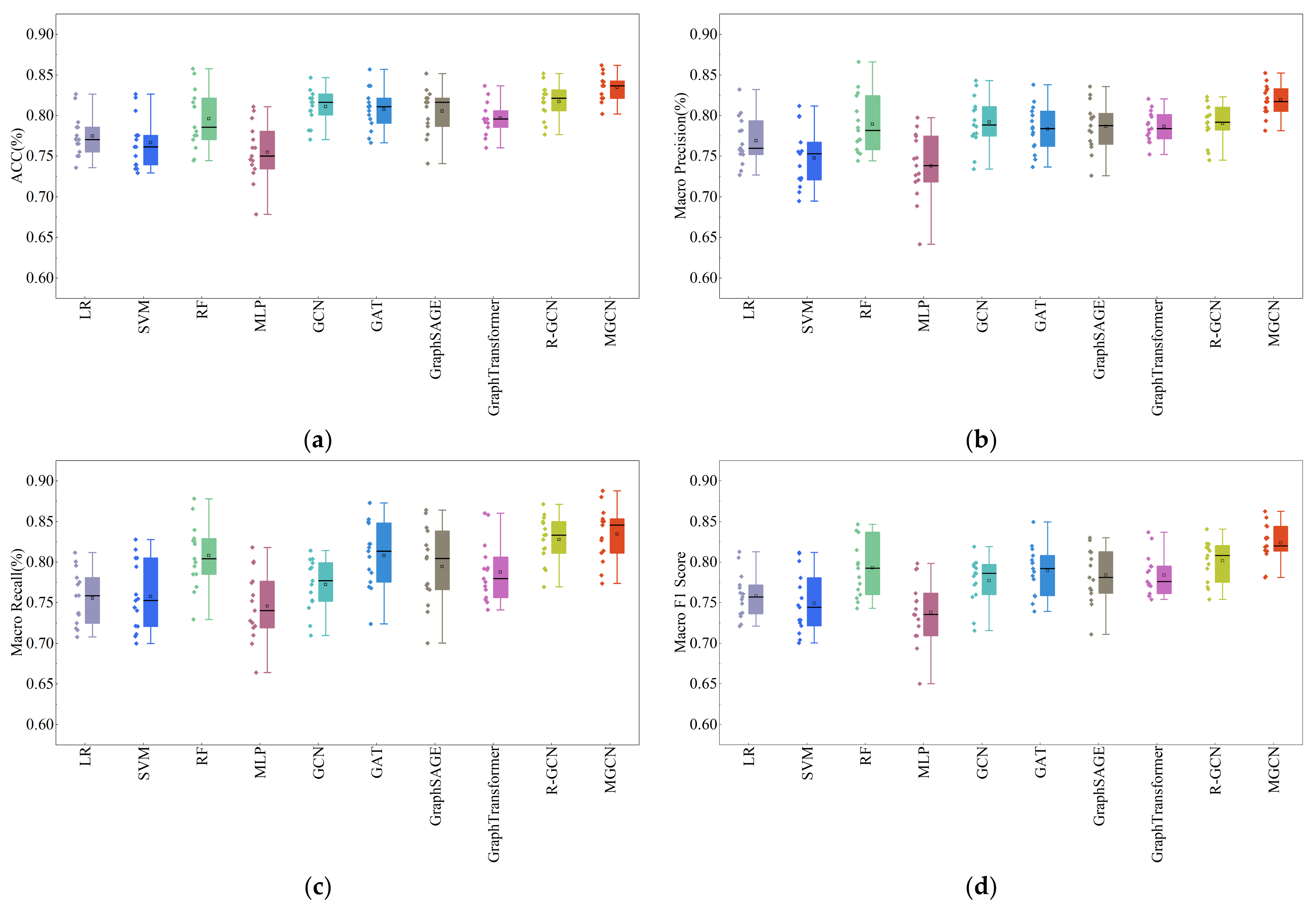
All models exhibited varying degrees of performance fluctuation in their prediction results (Table 4), mainly due to dataset differences across 5-fold cross-validation. To further assess model stability, three rounds of 5-fold cross-validation with different random seeds were conducted, generating 15 results per model. In Figure 3, the box represents the interquartile range (IQR) of the data, with the line inside indicating the median, reflecting the central tendency of the dataset. A small square within the box marks the mean value, allowing comparison with the median to assess data skewness. The whiskers show the range of non-outlier data. The overlaid scatter points represent all individual data values, helping to visualize the spread and distribution of the data.

In Figure 3, the scatter plots display the individual results from multiple runs of each model, while the height and spread of the box plots reflect the models’ central tendency and robustness, highlighting those that are both efficient and stable. MGCN consistently shows the highest medians and the narrowest interquartile ranges across accuracy, precision, recall, and F1-score, indicating superior performance with low variability. GCN, R-GCN, and GraphTransformer also exhibit relatively high medians and compact distributions, suggesting stable results attributed to their effective graph representation learning mechanisms. In contrast, SVM, RF, and MLP have wider box plots and more dispersed scatter points, especially in recall and F1-score, reflecting greater fluctuations and lower stability in their performance, possibly because these models lack the ability to fully exploit graph relational information, making them more sensitive to data variability.

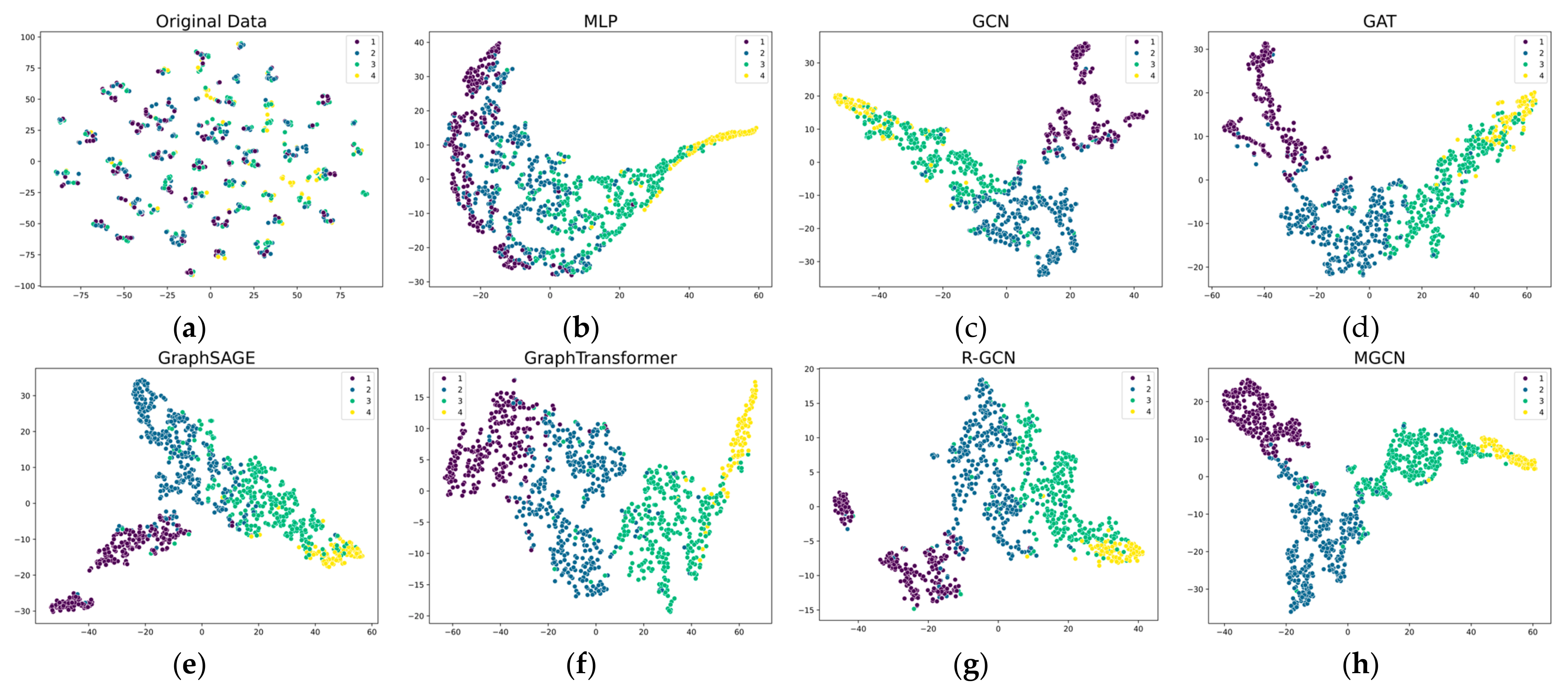
To demonstrate model effectiveness in feature processing, t-SNE was used to reduce dimensionality and visualize the standardized input features and final-layer node embeddings from various neural network models. In Figure 4, nodes are colored by innovation capability labels, where Classes 1, 2, 3, and 4 correspond to innovation levels of “Poor”, “Moderate “, “Good”, and “Excellent”, respectively.

In Figure 4a, the original input features produce a highly fragmented distribution in the embedding space, forming multiple small and scattered clusters. Nodes from different classes are intermixed without clear boundaries. In Figure 4b, the node embeddings learned by the Multi-Layer Perceptron (MLP) model exhibit a certain degree of class separation, with improved intra-class similarity compared to the original input features. However, there is still significant overlap between different classes—particularly between classes 2 and 3. This indicates that the MLP, lacking access to graph structural information, is limited in its ability to model complex inter-enterprise relationships, resulting in suboptimal node representations in multi-relational contexts. Graph-based models generally produce better results, showing clearer class separation compared to non-graph models. However, overlap between classes 2 and 3 remains a common issue across several methods. Overall, the MGCN model demonstrates the best class separability, with more distinct and compact clusters. R-GCN and GraphSAGE also achieve relatively good performance in clustering. Additionally, nodes belonging to class 4 consistently form well-defined clusters across different graph models, suggesting that the innovation capability represented by this class is more easily distinguishable from others.

3.3. Ablation Experiments of MGCN Components

The contributions of the main components of the MGCN model to the overall performance were evaluated by removing each component individually. Specifically, the following variants were tested:

MGCN-noF: the specific feature processing channels were removed;

MGCN-noC: the common feature processing channel was removed;

MGCN-noG: the gated attention mechanism was replaced with average weighting;

MGCN-noLc: the consistency constraint was removed from the loss function;

MGCN-noLd: the diversity constraint was removed from the loss function.

Table 5. The test results of the validity of the model structure.

Method	ACC	Macro Precision	Macro Recall	Macro F1
MGCN	0.8359 ± 0.0273	0.8173 ± 0.0316	0.8277 ± 0.0536	0.8186 ± 0.0398
MGCN-noF	0.8084 ± 0.0300	0.8000 ± 0.0367	0.8179 ± 0.0279	0.8036 ± 0.0290
MGCN-noC	0.8166 ± 0.0288	0.7967 ± 0.0323	0.8214 ± 0.0256	0.8043 ± 0.0295
MGCN-noG	0.8003 ± 0.0341	0.7926 ± 0.0323	0.8137 ± 0.0347	0.7994 ± 0.0317
MGCN-noLc	0.8094 ± 0.0049	0.7979 ± 0.0139	0.8157 ± 0.0203	0.8015 ± 0.0056
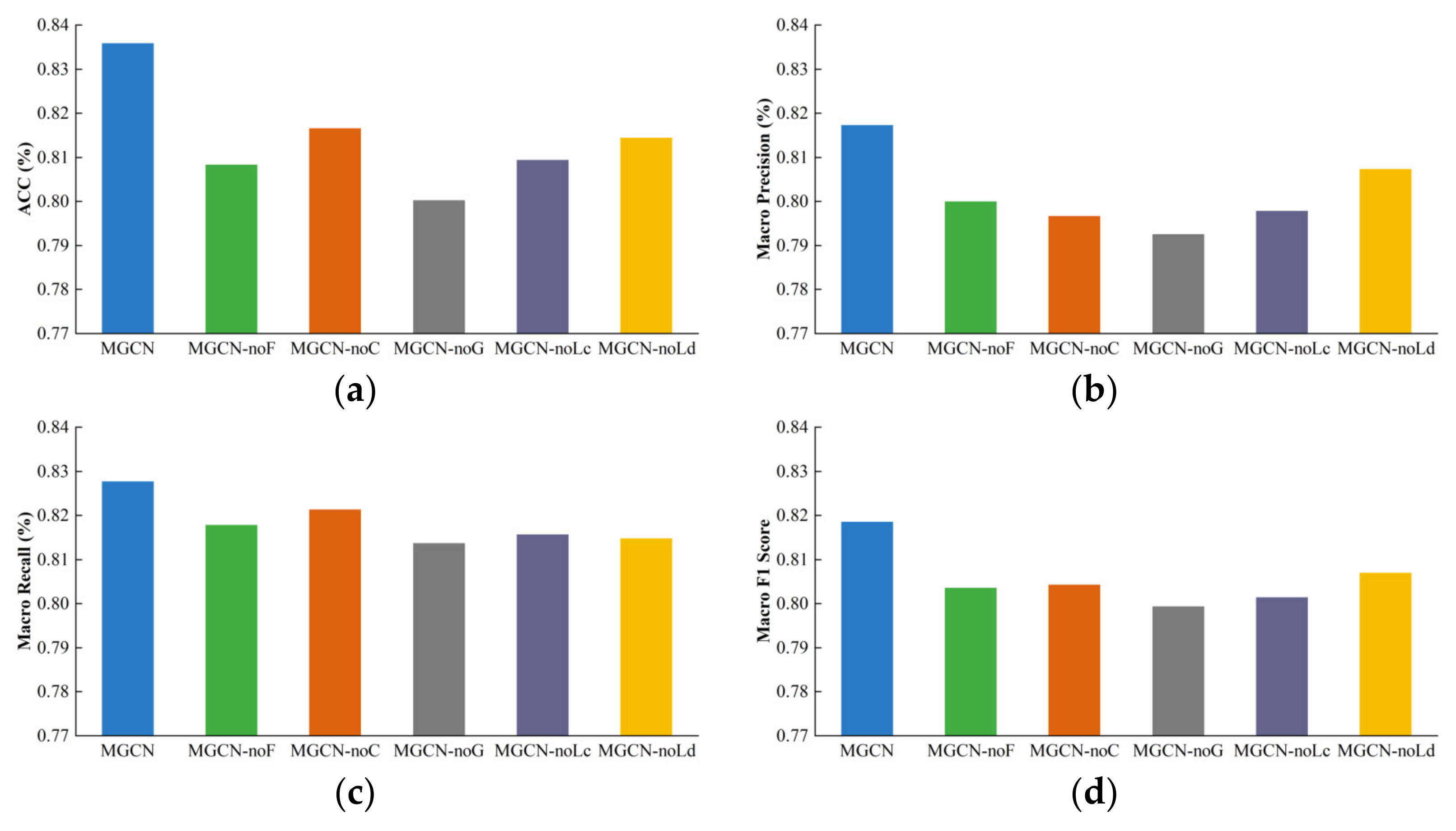
MGCN-noLd	0.8145 ± 0.0372	0.8074 ± 0.0379	0.8148 ± 0.0382	0.8070 ± 0.0375

presents the experimental results of these variants as well as the complete MGCN model. To provide a more intuitive comparison of the models’ performance, the results were visualized using a bar chart (Figure 5). In Figure 5, the complete MGCN model outperforms all its variants across all evaluation metrics, indicating that each component contributes positively to the overall performance. Notably, the MGCN-noG variant shows the most significant performance drop, highlighting the powerful role of the gated attention mechanism in dynamically selecting and integrating features.

The performance of the MGCN-noF variant also drops considerably, indicating that capturing structural information specific to each relational graph is essential. Without these dedicated channels, the model fails to fully exploit the heterogeneity across different relation types, thereby limiting its representational capacity. Removing the common feature channel (MGCN-noC) results in a smaller but still noticeable decline in performance. This suggests that although the overlap among the three relational graphs is limited, the common channel still provides valuable integrative information that complements the specific channels. Their combined effect enables the MGCN model to balance the trade-off between relation-specific information and generalization.

The MGCN-noLc and MGCN-noLd variants, which remove the consistency and diversity constraints, respectively, also exhibit slight performance declines. The consistency constraint ensures that the common channel learns coherent and stable features across different relational graphs, while the diversity constraint encourages the specific channels to capture distinctive and discriminative features. These constraints contribute to a more effective optimization process, enhancing the model’s overall robustness and generalization capability.

In summary, the ablation study results clearly demonstrate that each component of the MGCN model plays a critical and indispensable role in improving the accuracy of innovation capability prediction for seed enterprises. The specific and common feature processing channels enhance the model’s feature extraction from both specificity and commonality perspectives. The gated attention mechanism significantly improves feature utilization efficiency by dynamically adjusting feature fusion and emphasizing key features. The consistency and diversity constraints optimize the loss function to enhance the aggregation of node features in both channels from the perspectives of commonality and specificity, further boosting the model’s performance. These findings not only validate the effectiveness of the model architecture but also provide guidance for future improvements and optimizations.

3.4. Analysis of the Effectiveness of Relational Graphs

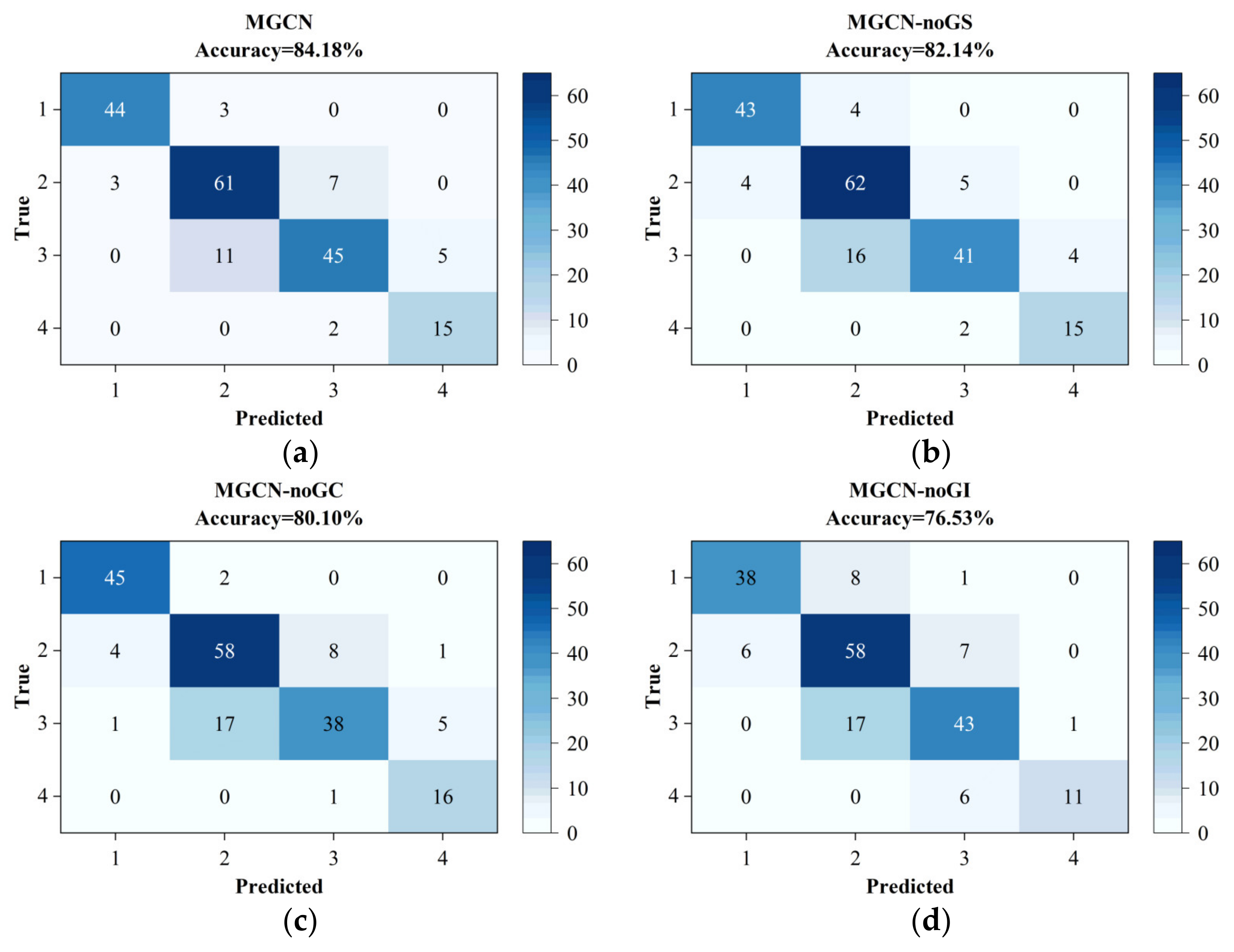
To investigate the impact of different relational graphs on innovation capability evaluation, we conducted an analysis by removing, respectively, the shareholding graph (MGCN-noGS), the cooperation graph (MGCN-noGC), and the innovation similarity graph (MGCN-noGI) from the MGCN model.

As shown in

Table 6. The test results of the validity analysis of the relationship diagram.

Method	ACC	Macro Precision	Macro Recall	Macro F1
MGCN	0.8359 ± 0.0273	0.8173 ± 0.0316	0.8277 ± 0.0536	0.8186 ± 0.0398
MGCN-noGS	0.8155 ± 0.0253	0.7930 ± 0.0290	0.8165 ± 0.0338	0.7997 ± 0.0297
MGCN-noGC	0.7911 ± 0.0249	0.7807 ± 0.0235	0.8125 ± 0.0284	0.7883 ± 0.0248
MGCN-noGI	0.7533 ± 0.0337	0.7561 ± 0.0287	0.7370 ± 0.0399	0.7433 ± 0.0331

, the model using the complete set of relational graphs outperforms all its variants across all evaluation metrics, indicating that each relational graph plays a critical role in enhancing the accuracy of innovation capability evaluation. In particular, the MGCN-noGI model exhibits the most significant performance degradation, highlighting the importance of the innovation similarity graph in identifying clusters of enterprises with similar innovation capabilities. Innovation similarity graph is constructed based on the number of variety approvals, registrations, and protections, indirectly verifying the importance of these features. The performance drop in the MGCN-noGS model is relatively smaller, likely due to the limited number of edges in the shareholding graph, which reduces the amount of information propagated through the graph. Nonetheless, shareholding relationships still have a certain impact on innovation prediction. The performance degradation in MGCN-noGC is more notable, suggesting that cooperation relationships facilitate the flow of innovation resources among enterprises, underscoring their importance in improving prediction accuracy.

Moreover, to provide a clearer and more intuitive understanding of the classification effectiveness of each model, the outcomes from the third fold of the five-fold cross-validation are presented in the form of confusion matrices, thereby facilitating a detailed analysis of performance variations and classification accuracy across different categories.

In Figure 6a, the MGCN model achieves an accuracy of 84.18%, demonstrating strong predictive performance. Misclassifications are primarily concentrated around the diagonal of the confusion matrix, suggesting that most errors occur between similar or neighboring classes. Notably, no misclassification is observed between class 1 and class 4 or between class 2 and class 4, which highlights clear distinctions between these categories and a reduced likelihood of confusion.

For the MGCN-noGS model (Figure 6b), the accuracy drops slightly to 82.14%, indicating a modest decline in overall predictive performance compared to the full MGCN model. Notably, the classification performance for class 3 deteriorates, with more instances being misclassified into adjacent categories. This observation suggests that the inclusion of the shareholding graph contributes positively to distinguishing between classes 2 and 3, thereby enhancing the model’s ability to capture nuanced relational information that aids in more accurate categorization.

In the MGCN-noGC model (Figure 6c), the accuracy decreases to 80.10%. Although classification performance for classes 1 and 2 remains relatively strong, misclassifications between classes 2 and 3 increase significantly—particularly with many samples labeled as “Good” (class 3) being predicted as “Moderate” (class 2). This indicates that cooperation relationships are especially important for distinguishing between these two categories, and that inter-enterprise cooperation may help improve innovation capabilities in mid-level seed enterprises.

The MGCN-noGI model (Figure 6d) achieved an accuracy of 76.53%, with overall classification performance inferior to that of the other models. In particular, its ability to distinguish between class 1 and class 2 significantly declined, leading to frequent misclassifications between these two categories. This indicates that some seed enterprises in class 1 and class 2 are relatively similar. The similarity relationships—constructed based on the number of variety approvals, registrations, and protections—focus on the similarity of innovation outputs among seed enterprises, which helps the model better distinguish between class 1 and class 2. Moreover, a number of class 4 enterprises were misclassified as class 3, indicating the model’s limited capacity to identify enterprises with outstanding innovation capabilities when similarity-based innovation output signals are removed.

In summary, the shareholding graph, cooperation graph, and innovation similarity graph all have significant impacts on the model’s performance. Among them, the innovation similarity graph proves to be the most important, contributing the most to predictive accuracy. It is particularly effective when enterprises share similar features, as it helps highlight the differences in their innovation outcomes. Although the cooperation and shareholding graphs have relatively smaller contributions, they remain indispensable. These relationship graphs capture the complex inter-enterprise connections from different perspectives, and their combined effect enhances the predictive capability of the model.

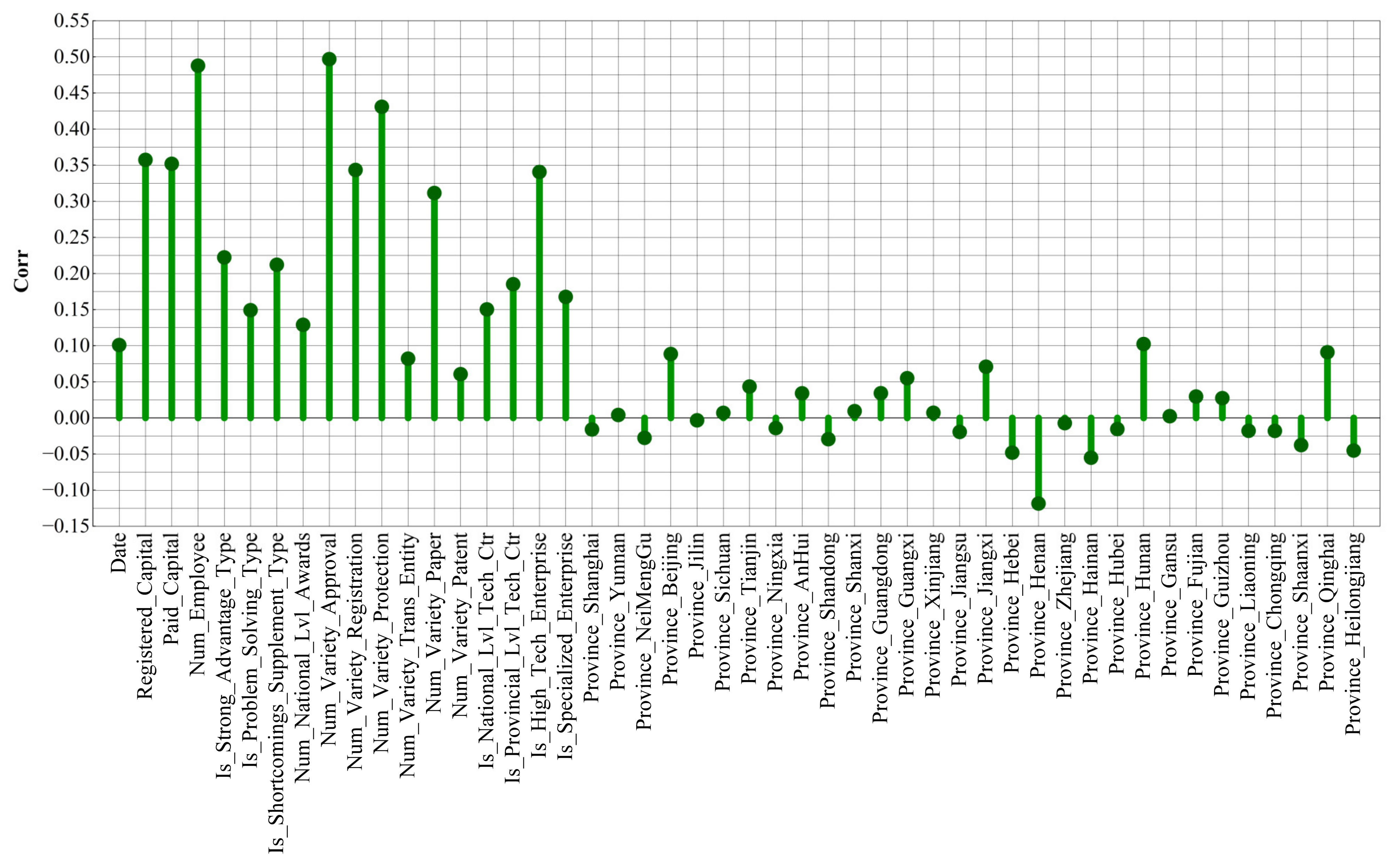
3.5. Analysis of Enterprises Features

In the evaluation of innovation capability in seed enterprises, it is important to recognize that not all features contribute equally to the final prediction results. Therefore, to gain a more comprehensive and deeper understanding of the role and significance of each individual feature, Pearson correlation coefficients were computed, allowing for an objective assessment of the correlation between each feature and the categorized levels of innovation capability, as illustrated in Figure 7.

As shown in Figure 7, features such as the number of approved varieties, number of insured employees, number of protected varieties, and registered capital exhibit strong correlations with innovation capability, indicating their significant influence in the evaluation process. The “province” feature, to some extent, implicitly reflects geographic location and regional policy support. For example, Hunan Province, compared to more remote areas, is more suitable for crop cultivation and field trials, which may explain its stronger correlation with innovation performance. In contrast, features from certain provinces show weaker or even negative correlations with innovation capability. In fact, the number of transformants—a result of transgenic technology—also serves as an important indicator of enterprise innovation capability [42], However, due to the high complexity and difficulty of transformations development, the number of transformations currently developed by enterprises remains very limited, resulting in a low Pearson correlation coefficient that does not fully reflect their potential value in evaluating innovation capability.

To further validate the impact of feature selection on model performance, we conducted a series of controlled experiments using subsets of features ranked by the absolute value of their Pearson correlation coefficients. Specifically, we selected the top 10 (MGCN-F10), top 20 (MGCN-F20), top 30 (MGCN-F30), and top 40 (MGCN-F40) most relevant features for testing, thereby examining how varying the quantity of features affects the predictive accuracy of the model.

As shown in

Table 7. Prediction results of the innovation ability of seed enterprises based on different numbers of characteristics.

Method	ACC	Macro Precision	Macro Recall	Macro F1
MGCN-F10	0.7931 ± 0.0258	0.7784 ± 0.0299	0.7808 ± 0.0332	0.7775 ± 0.0301
MGCN-F20	0.8084 ± 0.0385	0.7966 ± 0.0475	0.7874 ± 0.0391	0.7869 ± 0.0399
MGCN-F30	0.8186 ± 0.0142	0.7989 ± 0.0145	0.8110 ± 0.0222	0.8023 ± 0.0155
MGCN-F40	0.8257 ± 0.0190	0.8108 ± 0.0245	0.8246 ± 0.0307	0.8136 ± 0.0254
MGCN	0.8359 ± 0.0273	0.8173 ± 0.0316	0.8277 ± 0.0536	0.8186 ± 0.0398

, the MGCN model using all features achieved the best performance, indicating that a more comprehensive feature input leads to higher model accuracy, The performance of MGCN-F10, which used only the top 10 features, still reached an accuracy of 79.31%. As the number of selected features increased, model performance improved steadily. Additionally, it was observed that performance improvement was more pronounced when the number of features was relatively low; however, the rate of improvement diminished as more features were added. This suggests that features with a high correlation with innovation capability play a dominant role in prediction, while features with a lower Pearson correlation, though individually less informative, provide supplementary information that enhances the model’s generalization ability and predictive accuracy.

3.6. Case Analysis

Understanding the innovation capabilities of seed enterprises is crucial for both government policy formulation and enterprise strategic planning. Such evaluations can help governments identify strong and weak enterprises, allocate resources effectively, and implement targeted support, while enabling enterprises to develop strategies that foster sustainable innovation and enhance competitiveness. The proposed Multi-Channel Graph Convolutional Network (MGCN) model provides an accurate and comprehensive assessment of innovation capabilities, offering reliable technical support for these policies and strategic initiatives.

To better illustrate the practical value and interpretability of the proposed model, we conduct a case study on representative enterprises from each innovation capability category, including both correctly and incorrectly classified cases. A summary of the selected cases is presented in

Table 8. Case Details.

Enterprise	True Label	Predicted Label	Correct Prediction
Enterprise 1	Poor	Poor	TRUE
Enterprise 2	Moderate	Moderate	TRUE
Enterprise 3	Good	Good	TRUE
Enterprise 4	Excellent	Excellent	TRUE
Enterprise 5	Poor	Moderate	FALSE
Enterprise 6	Moderate	Good	FALSE
Enterprise 7	Good	Moderate	FALSE
Enterprise 8	Excellent	Good	FALSE

.

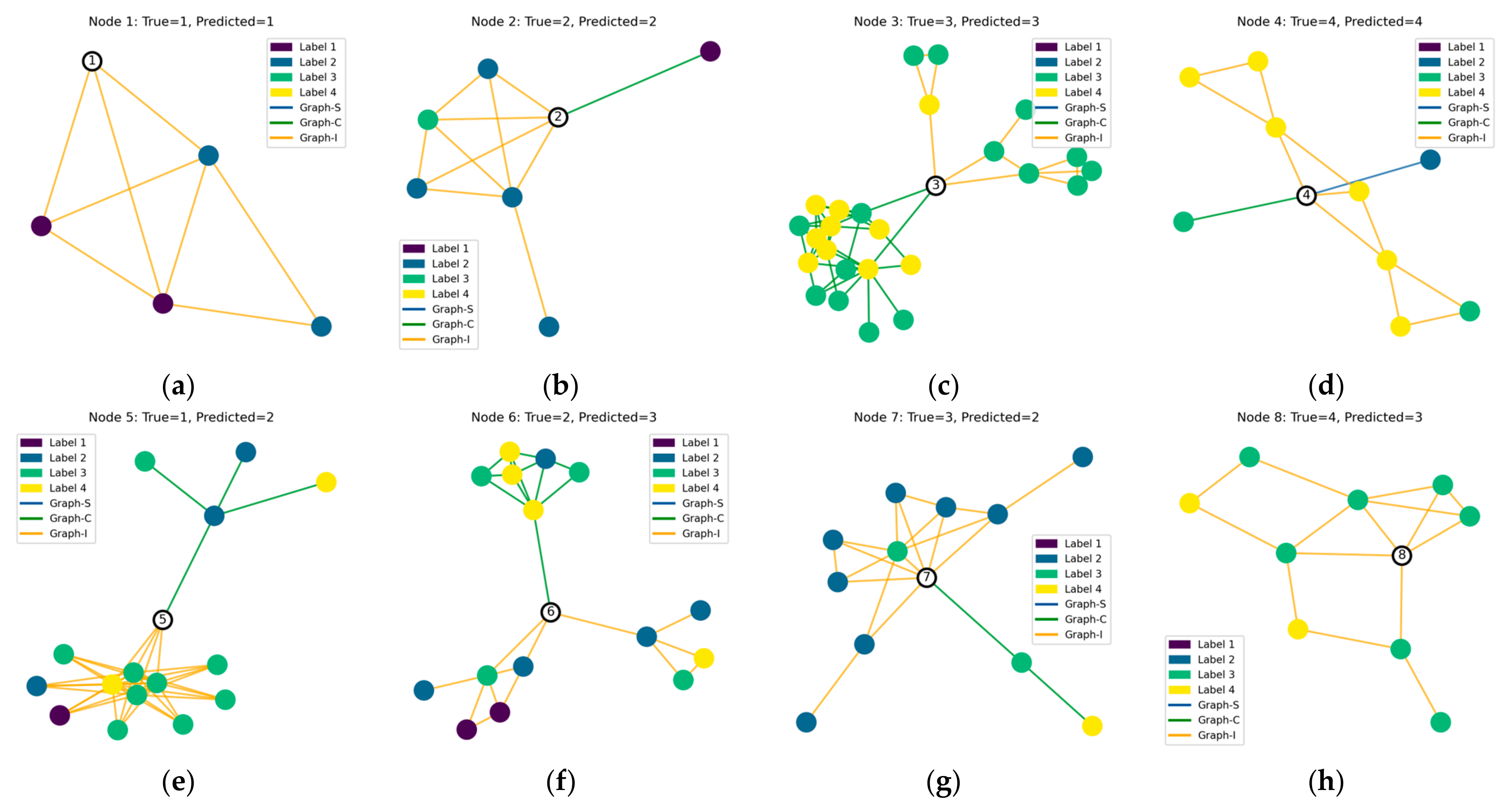
To gain deeper insight into how the model makes decisions across different scenarios, we visualize the two-hop neighborhoods of eight representative nodes. As shown in Figure 8, in each subgraph, the target node is represented as a blank node, while all other nodes are colored according to their ground-truth labels: Label 1 (Poor), Label 2 (Moderate), Label 3 (Good), and Label 4 (Excellent). Edges in the subgraphs correspond to three types of relationships: Graph-S (blue) for shareholding, Graph-C (green) for cooperation, and Graph-I (orange) for innovation output similarity. These visualizations help us understand how the model aggregates information from heterogeneous relations and multi-hop neighbors.

In graph-structured data, the connections between nodes play a critical role in both information propagation and pattern recognition. By examining the model’s prediction outcomes, we observe a clear trend: when a target node is surrounded by a large proportion of neighbors from a particular class, the model tends to assign the target node to that same class.

For instance, as shown in Figure 8c, the feature representation of Enterprise 3 is relatively inconspicuous, lacking strong signals indicative of either extremely high or extremely low innovation capability. In such cases, information from neighboring nodes becomes a key reference for the model’s decision-making. Since Enterprise 3 is connected via cooperation and innovation similarity relations to several highly innovative enterprises, the model classifies it as belonging to the “Good” innovation capability category. This outcome demonstrates that when node-level features are insufficient or ambiguous, the surrounding graph structure provides valuable support for the model’s inference.

In most cases, the model is able to correctly identify the class of the target node, particularly when the node’s features are distinctive and consistent with those of its neighbors. For example, in Figure 8d, Enterprise 4 is accurately classified. This enterprise is characterized by outstanding innovation capability: it is large in scale, has a substantial number of employees, holds 196 approved new varieties, and has been designated as a national-level enterprise technology center. With a well-recognized leadership position in the industry and strong innovation achievements, the enterprise presents highly distinctive features and is surrounded by neighbors with consistent labels, making it easy for the model to make a correct prediction.

However, classification based on graph structure is not always reliable. In some cases, the model may over-rely on the label distribution of neighboring nodes while neglecting the intrinsic features of the target node, leading to misclassification. For example, in Figure 8e, Enterprise 5 is incorrectly classified as Label 2 (Moderate), although its ground-truth label is Label 1 (Poor). Upon examining the enterprise’s profile, we find that it has published only two scientific papers and lacks other key indicators of innovation such as new variety development or patents, suggesting weak innovation capability. Nevertheless, in the graph, it maintains a cooperation relationship with one Label 2 node and shares innovation similarity with several Label 3 nodes, which likely misled the model due to neighborhood influence. A similar case appears in Figure 8g, where Enterprise 7 is misclassified as Label 2 (Moderate) instead of its true label, Label 3 (Good). Structural analysis shows that this node is surrounded predominantly by nodes of Label 2, which likely exerted a strong influence on the model’s decision, preventing it from accurately identifying the enterprise’s true level of innovation.

These visualizations reveal how the model performs relational reasoning within a multi-relational graph and how structural information contributes to classification decisions. At the same time, they highlight potential risks, such as over-dependence on local neighborhood signals, underscoring the importance of balancing structural context with node features in graph neural network applications. Although a few misclassifications occur, the overall results indicate that the model reliably captures key innovation patterns and provides informative assessments of enterprise innovation capabilities.

In practice, target enterprises for evaluation can first be identified, and their relationship graphs can be constructed based on relevant data, or an industry-wide graph covering all seed enterprises can be directly built. The MGCN model is then applied to assess the innovation capabilities of these enterprises. The resulting innovation capability ratings can help governments optimize support policies, allocate resources more effectively, and track the progress of key enterprises. Enterprises can also use the assessment results for self-positioning, formulate targeted improvement measures, and plan strategies for sustainable enhancement of their innovation capabilities.

4. Discussion

Seed enterprises play a crucial role in agricultural innovation and sustainable development, contributing to food security and industry growth [43]. Accurately evaluating their innovation capability is essential for guiding resource allocation and fostering industrial development. However, most existing methods primarily focus on the intrinsic characteristics of individual enterprises, while neglecting the complex inter-enterprise relationships that significantly influence innovation performance. Moreover, they often suffer from limited feature integration, failing to capture the multifaceted factors embedded in enterprise networks.

To address these challenges, we propose a Multi-Channel Graph Convolutional Network (MGCN) model that effectively integrates multi-source relational data and intrinsic enterprise features. Unlike traditional models that rely on manually crafted features or single-graph structures, MGCN leverages three types of enterprise relational graphs. By leveraging graph-based data structures, the proposed model effectively overcomes the inability of traditional approaches to represent the heterogeneous and structurally complex interactions among enterprises, which often results in the omission of critical relational features during modeling [44]. The model employs four parallel channels to process node and structural features independently and uses a gated attention mechanism for dynamic cross-graph feature fusion. This multi-channel architecture [45] enables the extraction of diverse local and multi-level factors influencing innovation capability, while gated attention helps in the integration of node features and graph structural features, as validated by our ablation studies. Prior studies have demonstrated the advantages of attention mechanisms in multimodal fusion and graph-structured learning [46,47].

Traditional approaches such as logistic regression (LR) and support vector machines (SVM) typically rely on manually constructed features and exhibit limited capacity for modeling relational structures [48]. These methods often lack effective mechanisms for feature integration [49], which constrains their performance—especially under the high-dimensional, heterogeneous, and unstructured data environment characteristics of agricultural big data. Although such models may demonstrate reasonable interpretability and stability on small to medium-sized datasets [50], their generalization and representational power remain insufficient in more complex settings. Graph neural networks (GNNs), by contrast, offer inherent advantages in modeling structured data and have shown promise in capturing the intricate relational patterns among enterprises. However, most existing GNN-based models rely on a single graph structure, limiting their ability to capture the multiple types of relationships of real-world enterprise network [51]. In comparison, the proposed MGCN model integrates multi-channel node feature embeddings and deep feature fusion to effectively leverage diverse information sources associated with seed enterprises. This enables MGCN to address several key limitations of both traditional machine learning methods and existing GNNs in the context of modeling agricultural enterprises. Specifically, under five-fold cross-validation, MGCN obtains an average accuracy of 83.59% ± 2.73%, surpassing traditional models such as logistic regression (77.17%), SVM (77.37%), random forest (78.80%), and multilayer perceptron (76.05%). It also outperforms classical GNN models, including GCN (80.63%), GAT (81.35%), GraphSAGE (80.33%), GraphTransformer (79.92%), and R-GCN (81.45%). The improvement over R-GCN, the strongest among baselines, is approximately 2.14 percentage points. These results underscore MGCN’s advantage in integrating multi-relational structures and capturing complex inter-enterprise dynamics, which are crucial for evaluating innovation capability in real-world agricultural networks.

While the proposed MGCN model exhibits superior predictive performance, it comes with increased computational cost due to its multi-channel architecture and gated attention mechanism. Specifically, the average running time per fold reaches 95.95 s, significantly higher than those of GAT (6.08s), GraphSAGE (7.89s), and R-GCN (21.39s). This increase is primarily attributed to the added model capacity and cross-graph fusion components. However, to mitigate potential overfitting risks associated with such complexity, we employ Dropout regularization and validate model robustness through five-fold cross-validation. Experimental results show stable performance across all folds, suggesting that the added complexity brings net performance gains without evident overfitting. Nevertheless, future work will explore more lightweight architectures to further balance accuracy and efficiency.

To deepen understanding of MGCN’s behavior, we conducted case analyses on correctly and incorrectly classified seed enterprises. The results show that the model not only leverages target enterprise features but also strongly depends on neighboring nodes’ features and predicted labels. Frequently, a target node is assigned the category dominant among its neighbors, highlighting the influence of local relational structure. While this reflects effective graph topology utilization, it also reveals potential vulnerability to misclassification when neighbors’ labels are mixed or noisy. These insights suggest future directions to refine neighborhood aggregation and enhance robustness against label noise.

The MGCN model also has limitations related to data and interpretability. First, it is based on static graphs, which represent the enterprise relationships at a fixed point in time and are simpler to construct and analyze. Static graphs effectively capture the overall relational structure and are less computationally intensive, making them a practical choice when temporal data are limited or unavailable. However, static graphs cannot model the temporal evolution of enterprise relationships, such as changing collaborations, equity transfers, or shifting innovation trajectories, which are common in real-world settings. Dynamic graphs offer the advantage of explicitly capturing such temporal patterns, potentially improving the accuracy and timeliness of innovation capability evaluation [52]. Due to current data constraints and modeling complexity, this study uses static graphs, with future research planned to incorporate dynamic graph neural networks—using temporal convolutional or sequential modeling layers—to better represent temporal dynamics.

Moreover, current node features are mainly derived from public statistical data and lack important innovation-related indicators like technology commercialization rates and research team composition. Expanding feature dimensionality and diversity could improve characterization depth. Finally, despite GNNs’ power in modeling complex structures, their “black-box” nature limits interpretability, hindering adoption in policy and management. Future studies may integrate explainability methods [53] to enhance transparency and trustworthiness, facilitating broader practical application.

5. Conclusions

As a fundamental driver of agricultural productivity, the innovation capability of seed enterprises plays a critical role in promoting sustainable agricultural development. Accordingly, precise evaluation of this capability is key to identifying their developmental stages and informing targeted resource allocation. Existing approaches tend to emphasize enterprise-level attributes in isolation, overlooking the complex relational dynamics among enterprises that critically shape innovation outcomes. In addition, their limited capacity for feature integration constrains their ability to capture the high-order, multi-source information embedded within enterprise networks.

To address these limitations, we propose a Multi-Channel Graph Convolutional Network (MGCN) model that integrates internal enterprise attributes with three types of inter-enterprise relational graphs—shareholding, collaboration, and innovation similarity. The model adopts a multi-channel architecture and a gated attention mechanism to enable cross-graph feature fusion, effectively combining node-level features with structural information. Experimental results show that MGCN achieves an average accuracy of 83.59% under five-fold cross-validation, outperforming nine baseline models, including Random Forest, MLP, and several GCN variants. Ablation studies further confirm that the gated attention mechanism contributes most significantly to performance improvements. Among the three types of relational graphs, innovation similarity exerts the most significant influence on prediction accuracy. It facilitates the formation of meaningful innovation clusters and enhances the model’s ability to capture and infer complex relational patterns. Beyond quantitative metrics, the case analysis demonstrates that MGCN not only learns the intrinsic features of individual enterprises but also leverages the structural context and label distribution of neighboring nodes. The model tends to classify target nodes into the predominant category within their local subgraphs. This observation highlights the critical role of graph topology in prediction, while also revealing potential vulnerabilities—such as sensitivity to noisy or inconsistent neighbor labels. In practical applications, such evaluations can guide governments in optimizing support policies, allocating resources more effectively, and monitoring the progress of key enterprises, while enterprises themselves can leverage the results to identify weaknesses, plan targeted improvements, and design strategies for sustainable innovation and enhanced competitiveness.

Although the MGCN model demonstrates strong performance, it still has some limitations. First, it relies on static graphs and cannot capture the temporal evolution of enterprise relationships, such as changing collaborations or equity structures. Integrating dynamic graph models could better reflect real-world variations. Second, node features are primarily derived from publicly available data, which may not fully capture certain innovation-related aspects, such as team composition or technology commercialization activities. Finally, the interpretability of MGCN remains limited, potentially constraining its adoption in policymaking and management practices. Future work will explore the integration of temporal modeling, enriched feature sets, and explainability techniques.