Co-Optimization and Interpretability of Intelligent–Traditional Signal Control Based on Spatiotemporal Pressure Perception in Hybrid Control Scenarios
Abstract
1. Introduction
- (1)
- Holistic Traffic Dynamo State (HTDS): A novel state representation that holistically captures both incoming and outgoing lane conditions by integrating three key elements classified using the Intelligent Driver Model (IDM)—real-time queue lengths, predicted vehicle merging patterns, and approaching traffic flows through downstream state propagation.
- (2)
- Neighbor–Pressure–Adaptive Reward Weighting (NP-ARW) mechanism: A reward engineering mechanism is introduced, which calculates pressure differences between corresponding connecting lanes of the DRL-controlled intersection and its neighboring max-pressure intersections. It dynamically adjusts queue penalty weights and adapts reward contributions to redistribute congestion toward lower-pressure regions.
- (3)
- Comparative Explainable Control via Phase Decision Logic Analysis: Leveraging our Strategy Imitation–Mechanism Attribution framework, which employs XGBoost for strategy imitation and Decision Trees for mechanism attribution. We develop a post hoc interpretation module. This module quantifies feature importance for both cooperative and non-cooperative agents, explicitly uncovers systematic differences in phase-switching logic during conflicting traffic movements, and analyzes decision-making rationale across diverse traffic scenarios. Furthermore, it provides the complete distilled decision tree structure as interpretable decision logic.
2. Related Work
2.1. Traditional Signal Control
2.2. Intelligent Signal Control
2.3. Hybrid Control Scenario
2.4. Interpretability of DRL-Based Traffic Signal Control
- (1)
- Model Distillation and Surrogate Models: These techniques extract interpretable approximations (e.g., decision trees, symbolic rules) from complex RL policies. Verma et al.’s PIRL framework [49] uses domain-specific languages and neural-guided search for symbolic strategies. Alternatively, Ault et al. [50] directly constrained policies to interpretable polynomial functions by custom Deep Q-learning. Their derived functions, which are structurally comparable to weighted sums of traffic features resembling fixed-time control rules, achieved performance comparable to deep neural networks in minimizing delay at single intersections.
- (2)
- Feature Attribution Methods: These approaches quantify the influence of state features on agent decisions. Approaches like SHAP (Shapley Additive exPlanations) and LIME (Local Interpretable Model-agnostic Explanations) identify critical features impacting control logic. For instance, Rizzo et al. [51] pioneered SHAP for RL-controlled roundabouts, revealing detector state impact on phase choice. Schreiber et al. [52] showed that features like “left-turn vehicle count” significantly boosted corresponding phase Q-values in DQN control.
- (3)
- Visualization: Tools such as MARLens [53] offer intuitive insights in comparative scenarios and interactive analysis. Researchers could observe agent behavior evolution, test hypotheses, and identify training anomalies through coordinated views of metrics like rewards and queue lengths.
- (4)
- Counterfactual Explanation: It answers “what-if” questions by simulating modified states and actions to assess impact on outcomes. While traffic RL-specific applications are emerging, concepts like “minimal counterfactuals” [54] offer valuable approaches.
3. Methodology
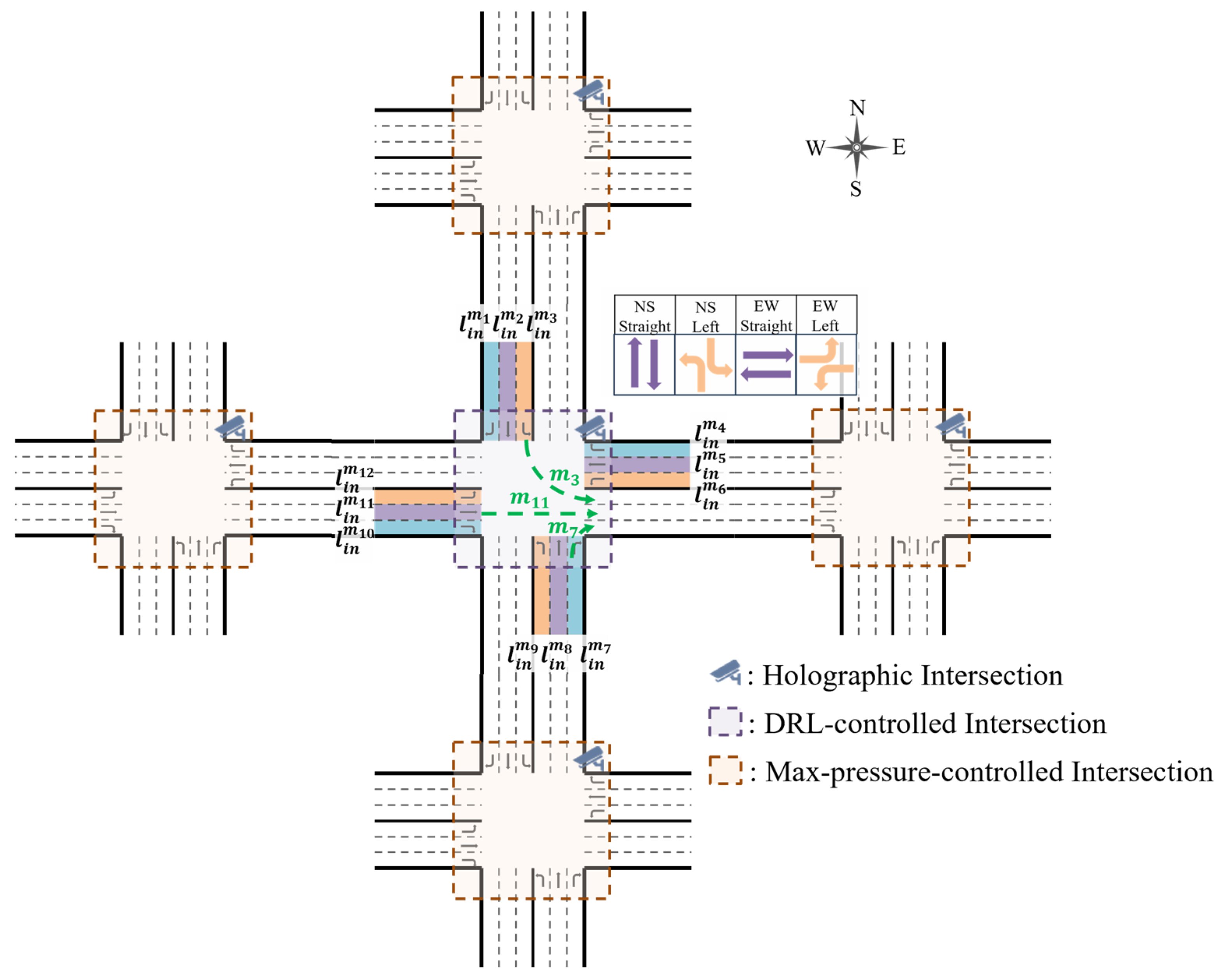
3.1. Traffic Terminology
3.2. Problem Formulation
3.3. Spatiotemporal Pressure Perception Agent Design
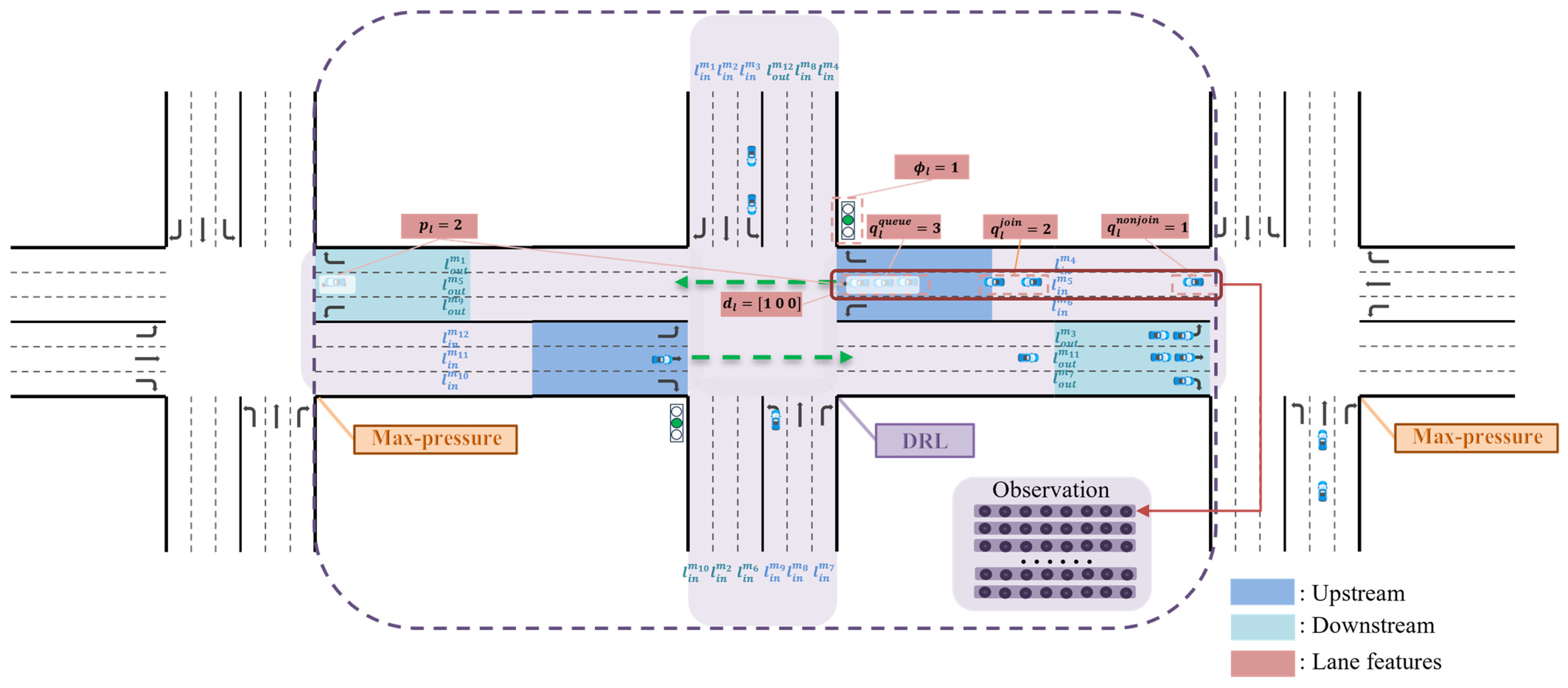
3.3.1. State
3.3.2. Action
3.3.3. Reward
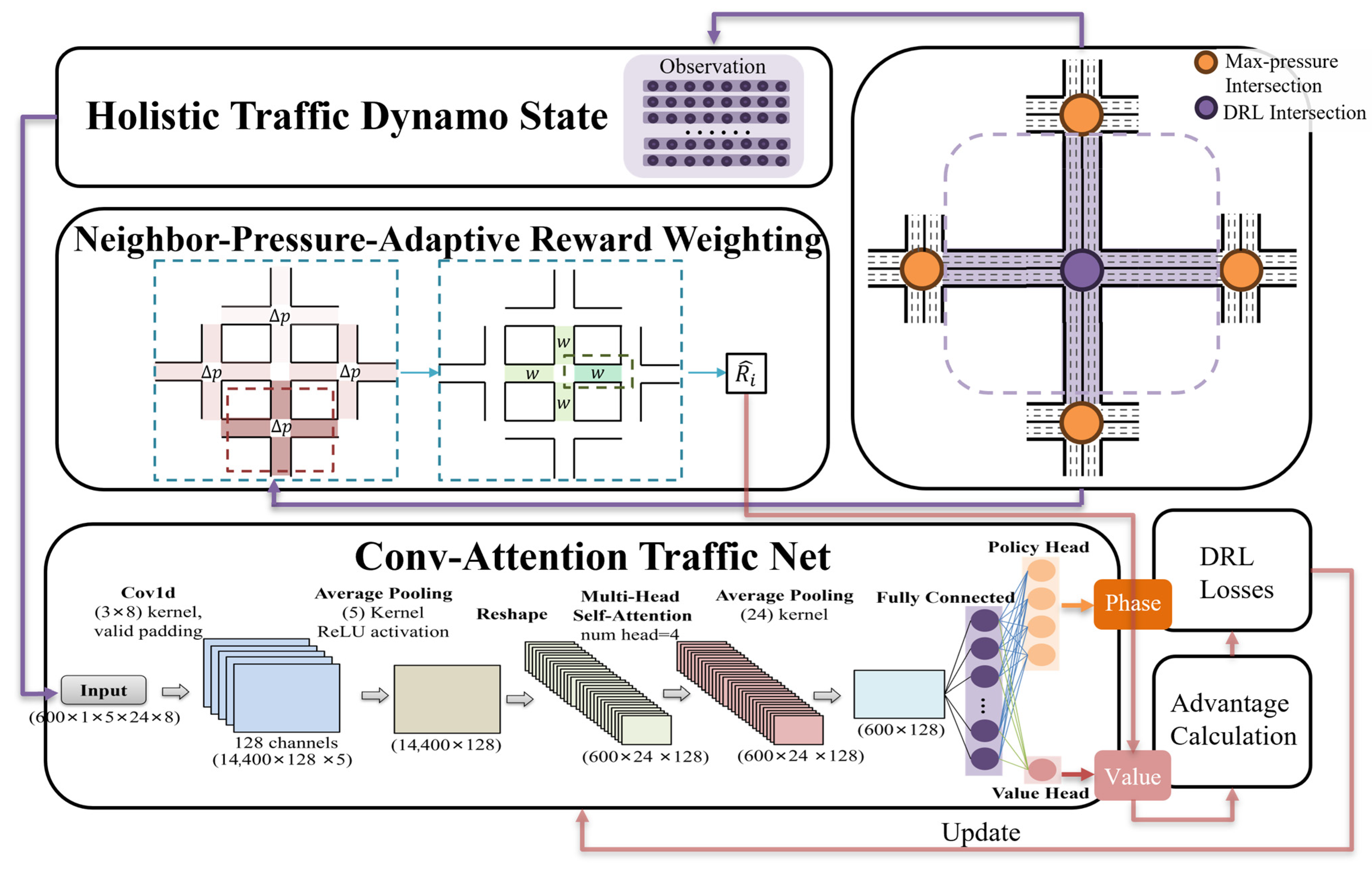
3.4. Holistic Traffic Dynamo State (HTDS)
3.4.1. Vehicle State Tripartite Decomposition
3.4.2. State Representation
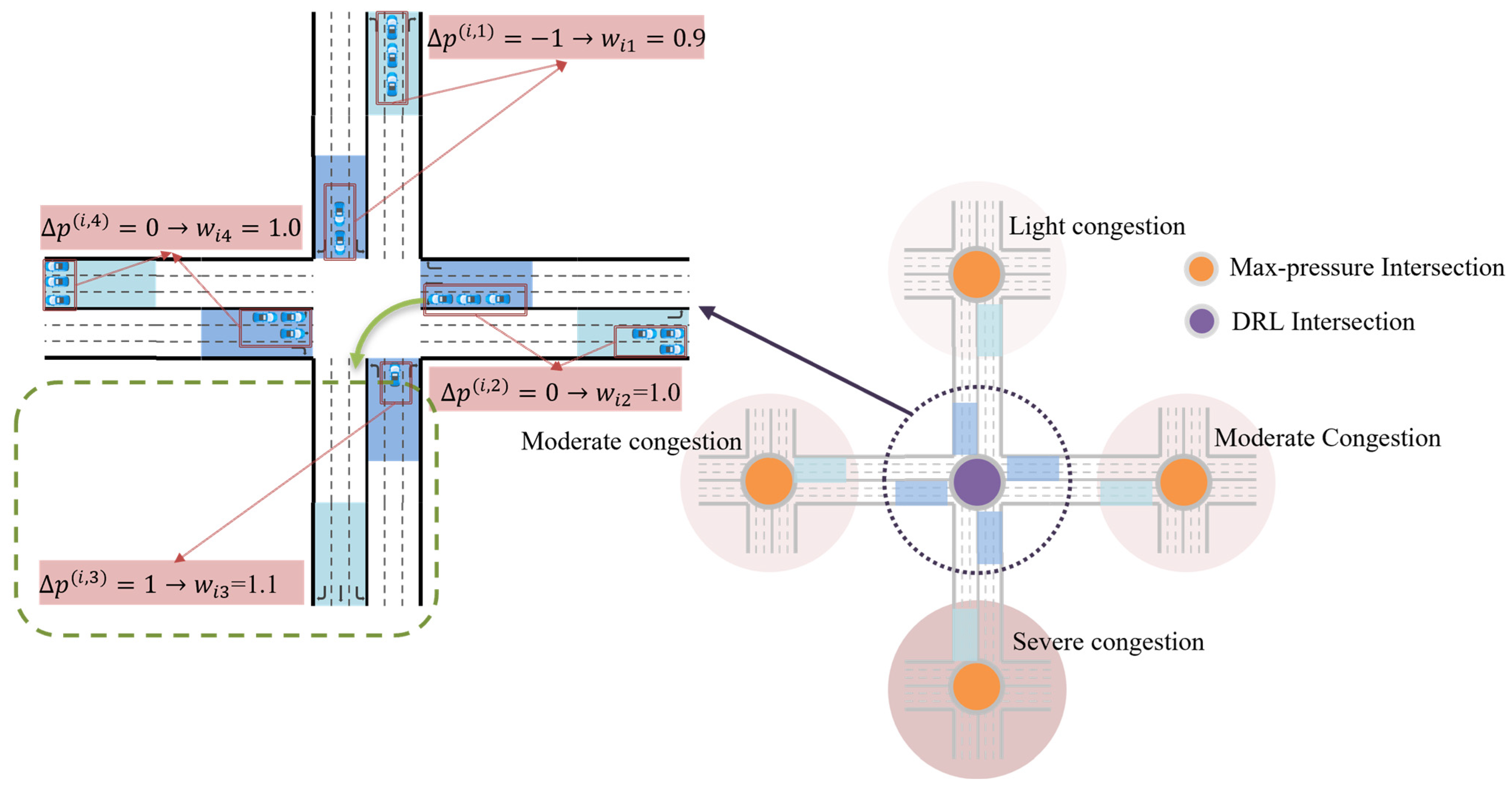
3.5. Neighbor–Pressure–Adaptive Reward Weighting (NP-ARW)
3.5.1. Neighbor Pressure Perception
3.5.2. Reward Reshaping
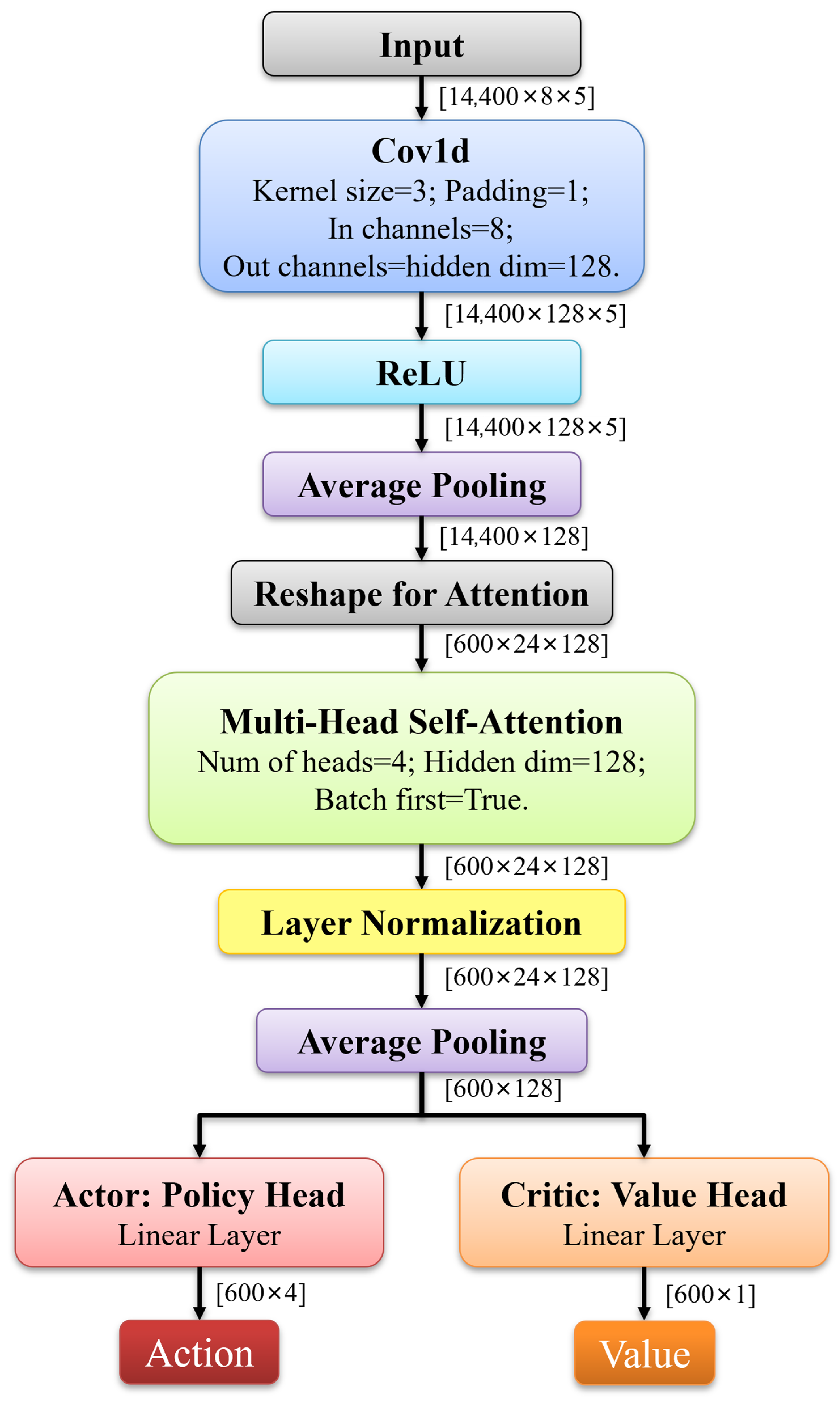
3.6. Conv-Attention Traffic Net (CAT-Net)
| Algorithm 1. Spatiotemporal Pressure Perception PPO with HTDS−NP−ARW | |
| Require: | Env: (SUMO); Model: Hidden dim , Attention heads , Time series , Movements , Features ; Training: Parallel envs , Batch size , Epochs , Minibatch , Learning rate , Clip range , Discount factor , Value loss coeff , Entropy coeff . |
| Ensure: | Trained policy network and value network (shared backbone). |
| Initialization | |
| 1: | Init , with random params; Adam optimizers; buffer (cap=), collector (), logger . |
| Main Loop | |
| 2: | for iter to do |
| 1. Collect Trajectories via Parallel Environment | |
| 3: | Reset envs to ; . |
| 4: | for to do |
| 5: | for each Agent do |
| 6: | [HTDS] Observe (Eq.(4)-(6)); |
| 7: | Sample action ; |
| 8: | end for |
| 9: | Execute ; Observe next state and ; |
| 10: | [NP-ARW] Compute (Eq.(7)) and (Eq.(8)-(9)), |
| 11: | append (). |
| 12: | end for |
| 13: | .add (Reshape). |
| 2. Compute Advantages and TD Targets | |
| 14: | Sample all trajectories from ; |
| 15: | and for all ; |
| 16: | TD targets ; |
| 17: | Advantage estimates . |
| 3. Update Policies via PPO | |
| 18: | for epoch to do |
| 19: | (shuffled minibatch, ). |
| 20: | for do |
| 21: | [Actor] Compute ; log; |
| 22: | ; |
| 23: | ; |
| 24: | [Critic] ; ; |
| 25: | ; ; |
| 26: | end for |
| 27: | Average total loss over minibatch: ; |
| 28: | Zero gradients of and ; |
| 29: | Backpropagate ; |
| 30: | Clip gradients to prevent explosion; |
| 31: | Update optimizers for and . |
| 32: | end for |
| 4. Log Metrics and Save Models | |
| 33: | Log training metrics via ; |
| 34: | Save model checkpoints () every 5 iterations. |
| 35: | end for |
3.7. Theoretical Foundations for DRL-Traditional Intersection Coordination
3.8. Mechanistic Analysis of DRL Agent’s Control Strategy
3.8.1. Feature Engineering of Phase Selection Strategies
3.8.2. XGBoost-to-Decision Tree Distillation for Interpretable Control Policies
3.8.3. Quantifying Feature Attribution in Phase Decisions with SHAP Values
4. Experiment and Results
4.1. Experiment Settings
4.2. Compared Methods
4.2.1. Traditional Baselines
4.2.2. DRL Baselines
4.3. Evaluation Metrics
4.4. Results
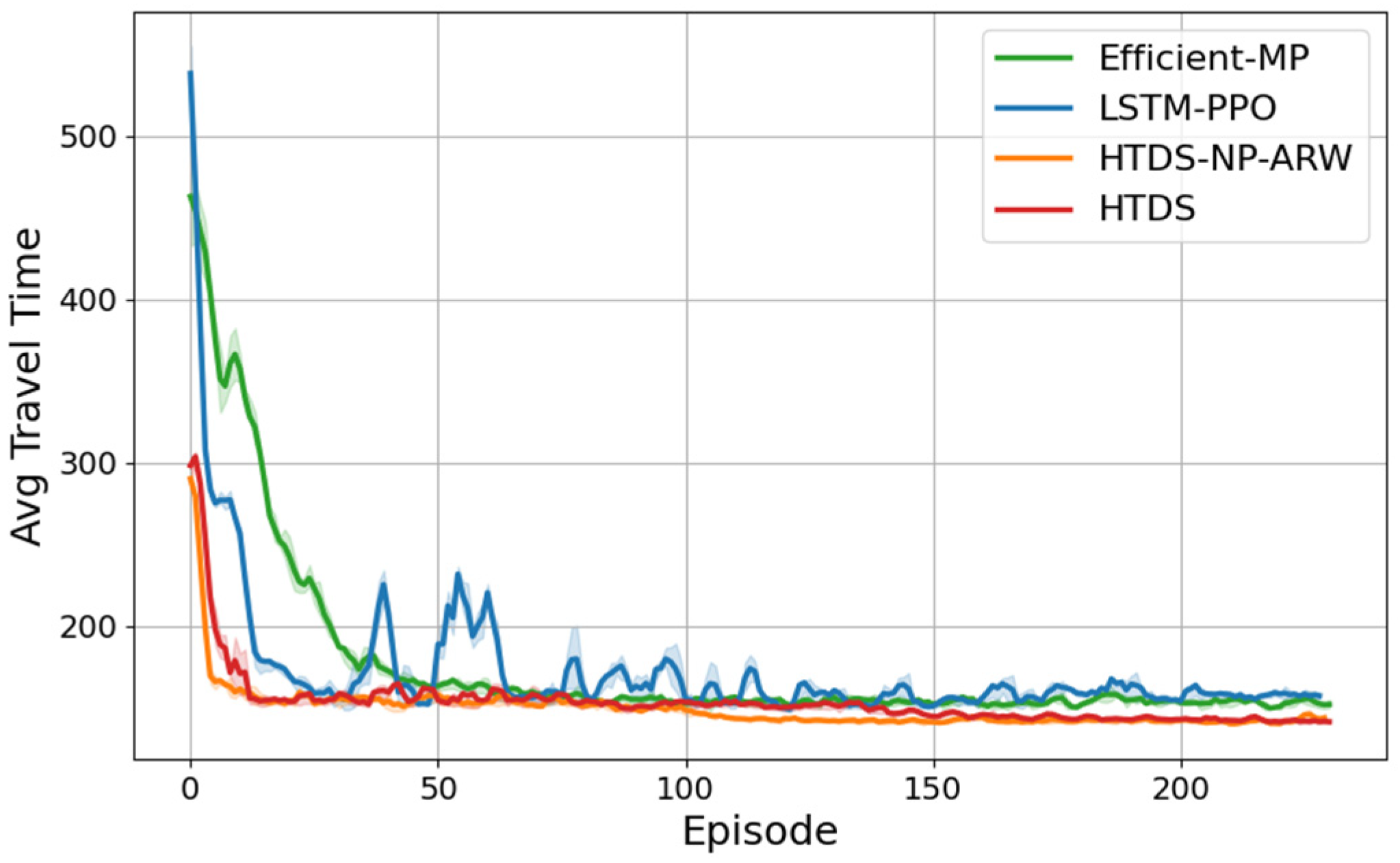
4.4.1. Comparison of Convergence
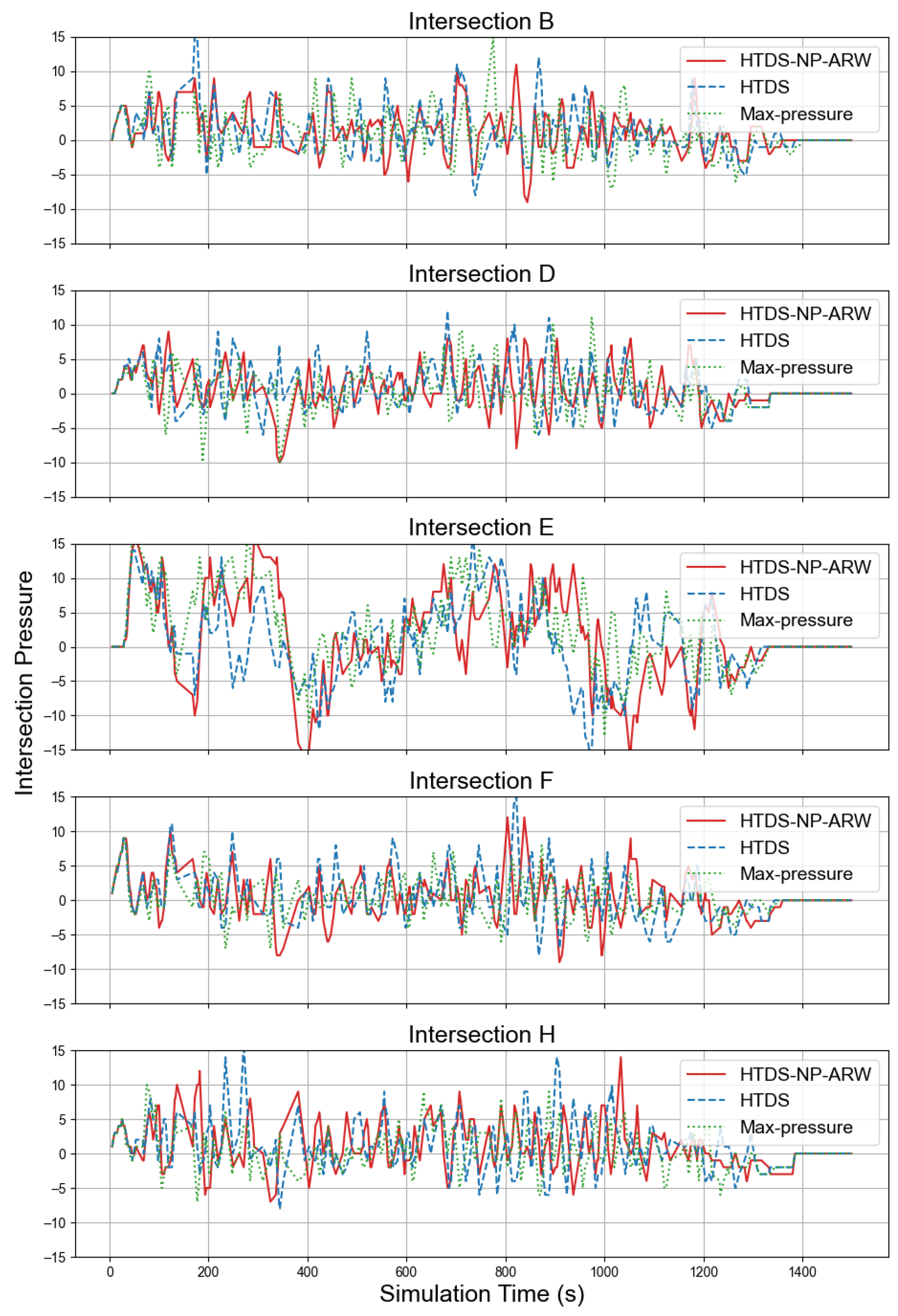
4.4.2. Evaluation of Performance
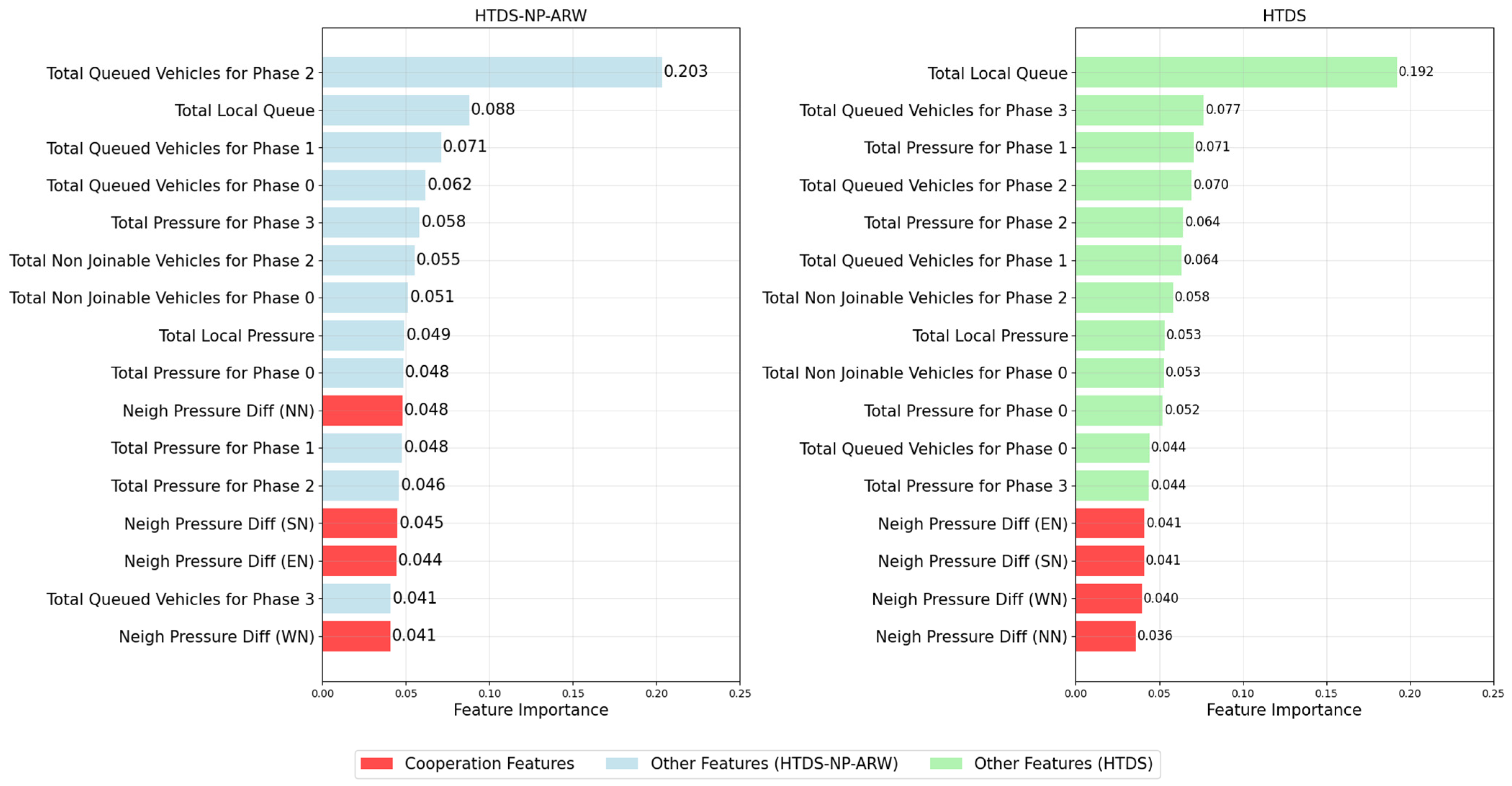
4.4.3. Feature Importance Ranking
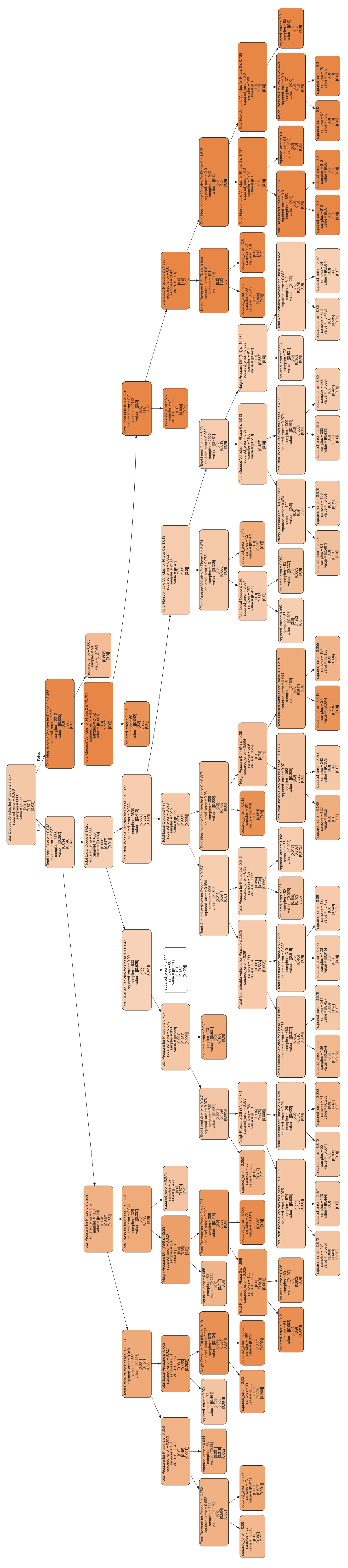
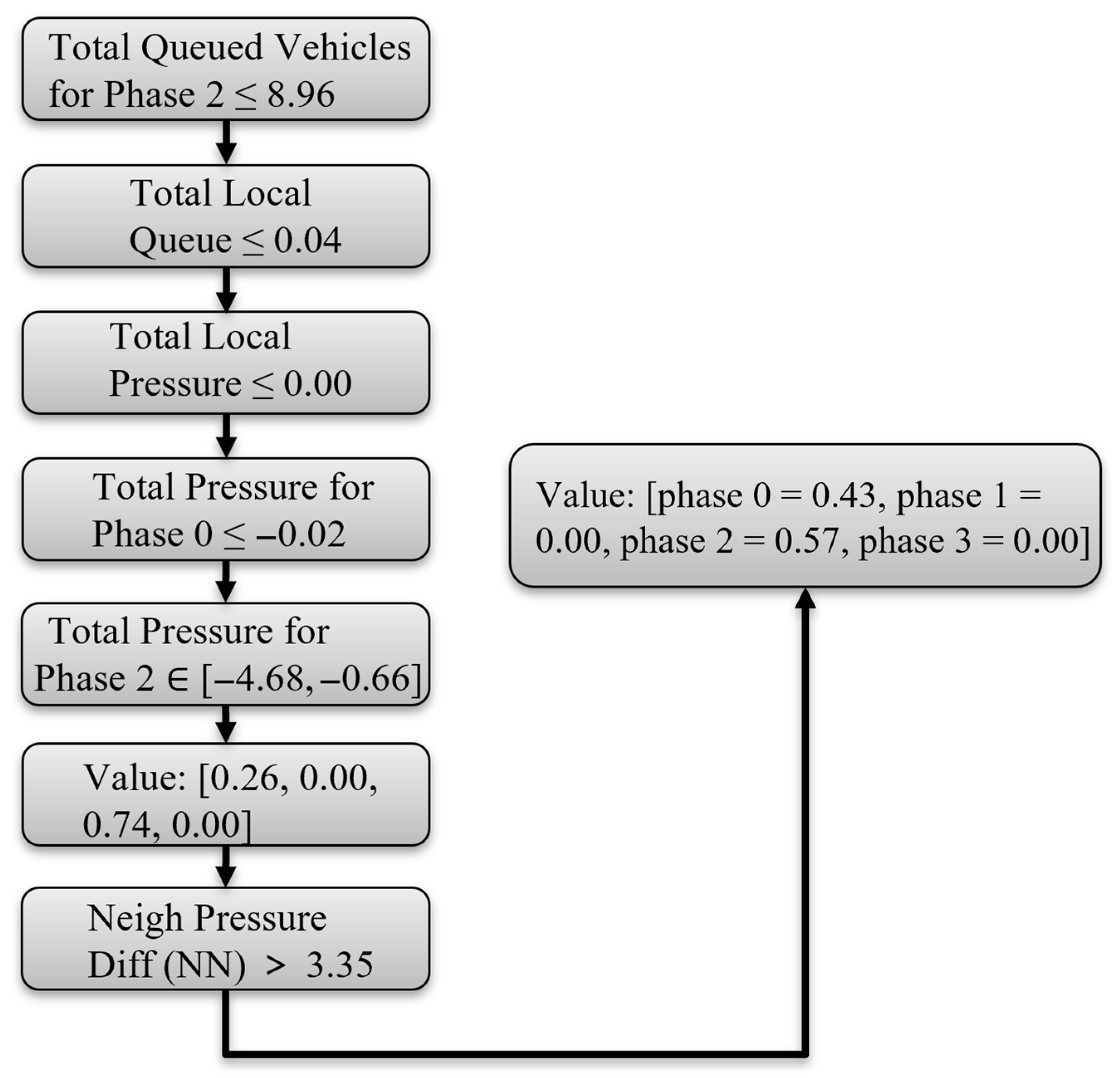
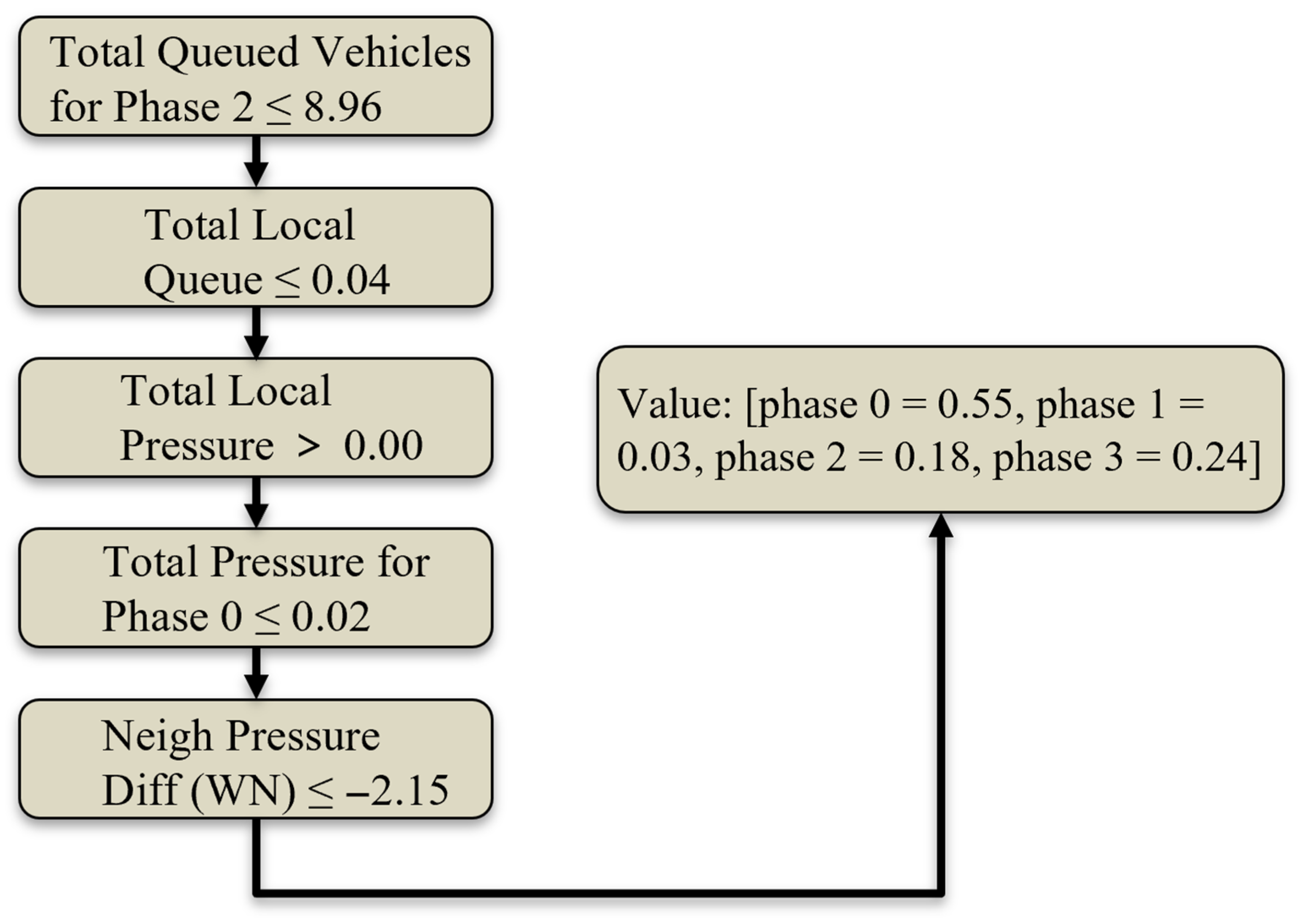
4.4.4. Phase-Action Decision Logic Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Macioszek, E.; Wyderka, A.; Jurdana, I. The bicyclist safety analysis based on road incidents maps. Sci. J. Silesian Univ. Technol. Ser. Transp 2025, 126, 129–147. [Google Scholar] [CrossRef]
- Lowrie, P. Scats, Sydney Co-Ordinated Adaptive Traffic System: A Traffic Responsive Method of Controlling Urban Traffic. 1990. Available online: https://trid.trb.org/View/488852 (accessed on 15 August 2025).
- Cools, S.-B.; Gershenson, C.; D’Hooghe, B. Self-organizing traffic lights: A realistic simulation. In Advances in Applied Self-Organizing Systems; Springer: London, UK, 2008; pp. 41–50. [Google Scholar]
- Little, J.D.; Kelson, M.D.; Gartner, N.H. MAXBAND: A Versatile Program for Setting Signals on Arteries and Triangular Networks. 1981. Available online: https://dspace.mit.edu/bitstream/handle/1721.1/1979/SWP-1185-08951478.pdf?sequence=1 (accessed on 15 August 2025).
- Varaiya, P. The max-pressure controller for arbitrary networks of signalized intersections. In Advances in Dynamic Network Modeling in Complex Transportation Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 27–66. [Google Scholar]
- Varaiya, P. Max pressure control of a network of signalized intersections. Transp. Res. Part C-Emerg. Technol. 2013, 36, 177–195. [Google Scholar] [CrossRef]
- Hunt, P.; Robertson, D.; Bretherton, R.; Royle, M.C. The SCOOT on-line traffic signal optimisation technique. Traffic Eng. Control 1982, 23, 190–192. [Google Scholar]
- Lowrie, P. Scats—A Traffic Responsive Method of Controlling Urban Traffic; Roads and Traffic Authority: Darlinghurst, NSW, Australia, 1992.
- Li, L.; Lv, Y.; Wang, F.-Y. Traffic signal timing via deep reinforcement learning. IEEE/CAA J. Autom. Sin. 2016, 3, 247–254. [Google Scholar] [CrossRef]
- Liang, X.; Du, X.; Wang, G.; Han, Z. A deep reinforcement learning network for traffic light cycle control. IEEE Trans. Veh. Technol. 2019, 68, 1243–1253. [Google Scholar] [CrossRef]
- Wei, H.; Xu, N.; Zhang, H.; Zheng, G.; Zang, X.; Chen, C.; Zhang, W.; Zhu, Y.; Xu, K.; Li, Z. Colight: Learning network-level cooperation for traffic signal control. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 1913–1922. [Google Scholar]
- Garg, D.; Chli, M.; Vogiatzis, G. Deep reinforcement learning for autonomous traffic light control. In Proceedings of the 2018 3rd IEEE International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 3–5 September 2018; pp. 214–218. [Google Scholar]
- Chu, T.; Wang, J.; Codecà, L.; Li, Z. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1086–1095. [Google Scholar] [CrossRef]
- Chen, C.; Wei, H.; Xu, N.; Zheng, G.; Yang, M.; Xiong, Y.; Xu, K.; Li, Z. Toward a thousand lights: Decentralized deep reinforcement learning for large-scale traffic signal control. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3414–3421. [Google Scholar] [CrossRef]
- Prashanth, L.; Bhatnagar, S. Reinforcement learning with average cost for adaptive control of traffic lights at intersections. In Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 1640–1645. [Google Scholar]
- Zhang, Y.; Goel, H.; Li, P.; Damani, M.; Chinchali, S.; Sartoretti, G. Coordlight: Learning decentralized coordination for network-wide traffic signal control. IEEE Trans. Intell. Transp. Syst. 2025, 26, 8034–8049. [Google Scholar] [CrossRef]
- Goel, H.; Zhang, Y.; Damani, M.; Sartoretti, G. Sociallight: Distributed cooperation learning towards network-wide traffic signal control. arXiv 2023, arXiv:2305.16145. [Google Scholar]
- Wang, Y.; Xu, T.; Niu, X.; Tan, C.; Chen, E.; Xiong, H. STMARL: A spatio-temporal multi-agent reinforcement learning approach for cooperative traffic light control. IEEE Trans. Mob. Comput. 2020, 21, 2228–2242. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, Y.; Liu, L.; Liu, Y.; Li, G.; Lin, L. Denselight: Efficient control for large-scale traffic signals with dense feedback. arXiv 2023, arXiv:2306.07553. [Google Scholar]
- Wei, H.; Zheng, G.; Yao, H.; Li, Z. Intellilight: A reinforcement learning approach for intelligent traffic light control. In Proceedings of the the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2496–2505. [Google Scholar]
- Cai, C.; Wei, M. Adaptive urban traffic signal control based on enhanced deep reinforcement learning. Sci. Rep. 2024, 14, 14116. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Wang, Y.; Yu, Y.; Zhou, M. Mixlight: Mixed-agent cooperative reinforcement learning for traffic light control. IEEE Trans. Ind. Inf. 2023, 20, 2653–2661. [Google Scholar] [CrossRef]
- Koonce, P. Traffic Signal Timing Manual; Federal Highway Administration: Washington, DC, USA, 2008.
- Webster, F.V. Traffic Signal Settings; Transportation Research Board: Washington, DC, USA, 1958. [Google Scholar]
- Roess, R.P.; Prassas, E.S.; McShane, W.R. Traffic Engineering; Pearson/Prentice Hall: Hoboken, NJ, USA, 2004. [Google Scholar]
- Papageorgiou, M.; Diakaki, C.; Dinopoulou, V.; Kotsialos, A.; Wang, Y. Review of road traffic control strategies. Proc. IEEE 2003, 91, 2043–2067. [Google Scholar] [CrossRef]
- Papageorgiou, M. An integrated control approach for traffic corridors. Transp. Res. Part C-Emerg. Technol. 1995, 3, 19–30. [Google Scholar] [CrossRef]
- Stevanovic, A. Adaptive Traffic Control Systems: Domestic and Foreign State of Practice; The National Academies Press: Washington, DC, USA, 2010. [Google Scholar]
- Henry, J.-J.; Farges, J.L.; Tuffal, J. The PRODYN real time traffic algorithm. In Control in Transportation Systems; Elsevier: Amsterdam, The Netherlands, 1984; pp. 305–310. [Google Scholar]
- Zheng, Y.; Luo, J.; Gao, H.; Zhou, Y.; Li, K. Pri-DDQN: Learning adaptive traffic signal control strategy through a hybrid agent. Complex Intell. Syst. 2025, 11, 47. [Google Scholar] [CrossRef]
- Bouktif, S.; Cheniki, A.; Ouni, A.; El-Sayed, H. Deep reinforcement learning for traffic signal control with consistent state and reward design approach. Knowl.-Based Syst. 2023, 267, 110440. [Google Scholar] [CrossRef]
- Cai, S.; Fang, J.; Xu, M. XLight: An interpretable multi-agent reinforcement learning approach for traffic signal control. Expert Syst. Appl. 2025, 273, 126938. [Google Scholar] [CrossRef]
- Koohy, B.; Stein, S.; Gerding, E.; Manla, G. Reward Function Design in Multi-Agent Reinforcement Learning for Traffic Signal Control. 2022. Available online: https://ceur-ws.org/Vol-3173/1.pdf (accessed on 15 August 2025).
- Rafique, M.T.; Mustafa, A.; Sajid, H. Reinforcement Learning for Adaptive Traffic Signal Control: Turn-Based and Time-Based Approaches to Reduce Congestion. arXiv 2024, arXiv:2408.15751. [Google Scholar]
- Zhang, L.; Wu, Q.; Shen, J.; Lü, L.; Du, B.; Wu, J. Expression might be enough: Representing pressure and demand for reinforcement learning based traffic signal control. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 26645–26654. [Google Scholar]
- Azfar, T.; Ke, R. Traffic Co-Simulation Framework Empowered by Infrastructure Camera Sensing and Reinforcement Learning. arXiv 2024, arXiv:2412.03925. [Google Scholar] [CrossRef]
- Xia, X.; Gao, L.; Chen, Q.A.; Ma, J.; Zheng, Z.; Luo, Y.; Alshammari, F.; Xiang, X. Enhanced Perception with Cooperation Between Connected Automated Vehicles and Smart Infrastructure. 2025. Available online: https://escholarship.org/uc/item/7sd5c485 (accessed on 15 August 2025).
- Wei, H.; Chen, C.; Zheng, G.; Wu, K.; Gayah, V.; Xu, K.; Li, Z. Presslight: Learning max pressure control to coordinate traffic signals in arterial network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1290–1298. [Google Scholar]
- Liu, J.; Zhang, H.; Fu, Z.; Wang, Y. Learning scalable multi-agent coordination by spatial differentiation for traffic signal control. Eng. Appl. Artif. Intell. 2021, 100, 104165. [Google Scholar] [CrossRef]
- Chu, T.; Chinchali, S.; Katti, S. Multi-agent reinforcement learning for networked system control. arXiv 2020, arXiv:2004.01339. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, Y.; Zhang, Z.; Xue, W.; Xie, X.; Yang, T.; Ge, X.; Chen, R. Neighborhood cooperative multiagent reinforcement learning for adaptive traffic signal control in epidemic regions. IEEE Trans. Intell. Transp. Syst. 2022, 23, 25157–25168. [Google Scholar] [CrossRef]
- Tseng, Y.-T.; Ferng, H.-W. Adaptive DRL-Based Traffic Signal Control with an Infused LSTM Prediction Model. In Proceedings of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, Kitakyushu, Japan, 1–4 July 2025; pp. 291–302. [Google Scholar]
- Huang, P.; Wang, P.; Li, X.; Jin, X.; Yao, S. Adaptive Distributed Training for Multi-Agent Reinforcement Learning in Multi-Objective Traffic Signal Control. 2025. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5332828 (accessed on 15 August 2025).
- Lin, W.-Y.; Song, Y.-Z.; Ruan, B.-K.; Shuai, H.-H.; Shen, C.-Y.; Wang, L.-C.; Li, Y.-H. Temporal difference-aware graph convolutional reinforcement learning for multi-intersection traffic signal control. IEEE Trans. Intell. Transp. Syst. 2023, 25, 327–337. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inform. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Zheng, G.; Zang, X.; Xu, N.; Wei, H.; Yu, Z.; Gayah, V.; Xu, K.; Li, Z. Diagnosing reinforcement learning for traffic signal control. arXiv 2019, arXiv:1905.04716. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, G.; Yang, Q.; Han, T. An adaptive traffic signal control scheme with Proximal Policy Optimization based on deep reinforcement learning for a single intersection. Eng. Appl. Artif. Intell. 2025, 149, 110440. [Google Scholar] [CrossRef]
- Haddad, T.A. Deep Reinforcement Learning for Multi-intersection Traffic Signal Control: A New Cooperative Approach. In Proceedings of the Sixth International Symposium on Informatics and Its Applications (ISIA), Msila, Algeria, 10–December 2024. [Google Scholar]
- Verma, A.; Murali, V.; Singh, R.; Kohli, P.; Chaudhuri, S. Programmatically interpretable reinforcement learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5045–5054. [Google Scholar]
- Ault, J.; Hanna, J.P.; Sharon, G. Learning an interpretable traffic signal control policy. arXiv 2019, arXiv:1912.11023. [Google Scholar]
- Rizzo, S.G.; Vantini, G.; Chawla, S. Reinforcement learning with explainability for traffic signal control. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 3567–3572. [Google Scholar]
- Schreiber, L.; Ramos, G.d.O.; Bazzan, A.L. Towards explainable deep reinforcement learning for traffic signal control. In Proceedings of the LatinX in AI Workshop@ ICML, Virtually, 19 July 2021. [Google Scholar]
- Zhang, Y.; Zheng, G.; Liu, Z.; Li, Q.; Zeng, H. MARLens: Understanding multi-agent reinforcement learning for traffic signal control via visual analytics. IEEE Trans. Vis. Comput. Graph. 2024, 31, 4018–4033. [Google Scholar] [CrossRef]
- Saulières, L. A Survey of Explainable Reinforcement Learning: Targets, Methods and Needs. arXiv 2025, arXiv:2507.12599. [Google Scholar] [CrossRef]
- Zhang, G.; Chang, F.; Huang, H.; Zhou, Z. Dual-objective reinforcement learning-based adaptive traffic signal control for decarbonization and efficiency optimization. Mathematics 2024, 12, 2056. [Google Scholar] [CrossRef]
- Aslani, M.; Mesgari, M.S.; Wiering, M. Adaptive traffic signal control with actor-critic methods in a real-world traffic network with different traffic disruption events. Transp. Res. Part C-Emerg. Technol. 2017, 85, 732–752. [Google Scholar] [CrossRef]
- Aslani, M.; Seipel, S.; Mesgari, M.S.; Wiering, M. Traffic signal optimization through discrete and continuous reinforcement learning with robustness analysis in downtown Tehran. Adv. Eng. Inf. 2018, 38, 639–655. [Google Scholar] [CrossRef]
- Mannion, P.; Duggan, J.; Howley, E. An experimental review of reinforcement learning algorithms for adaptive traffic signal control. Auton. Road Transp. Support Syst. 2016, 47–66. [Google Scholar]
- Casas, N. Deep deterministic policy gradient for urban traffic light control. arXiv 2017, arXiv:1703.09035. [Google Scholar] [CrossRef]
- Abdoos, M.; Mozayani, N.; Bazzan, A.L. Traffic light control in non-stationary environments based on multi agent Q-learning. In Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 1580–1585. [Google Scholar]
- Wan, C.-H.; Hwang, M.-C. Adaptive traffic signal control methods based on deep reinforcement learning. In Intelligent Transport Systems for Everyone’s Mobility; Springer: Berlin/Heidelberg, Germany, 2019; pp. 195–209. [Google Scholar]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.-P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wießner, E. Microscopic traffic simulation using sumo. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2575–2582. [Google Scholar]
- Wu, Q.; Zhang, L.; Shen, J.; Lü, L.; Du, B.; Wu, J. Efficient pressure: Improving efficiency for signalized intersections. arXiv 2021, arXiv:2112.02336. [Google Scholar] [CrossRef]
- Huang, L.; Qu, X. Improving traffic signal control operations using proximal policy optimization. IET Intel. Transp. Syst. 2023, 17, 592–605. [Google Scholar] [CrossRef]
- Zhang, G.; Chang, F.; Jin, J.; Yang, F.; Huang, H. Multi-objective deep reinforcement learning approach for adaptive traffic signal control system with concurrent optimization of safety, efficiency, and decarbonization at intersections. Accid. Anal. Prev. 2024, 199, 107451. [Google Scholar] [CrossRef]
- Guo, J.; Cheng, L.; Wang, S. CoTV: Cooperative control for traffic light signals and connected autonomous vehicles using deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10501–10512. [Google Scholar] [CrossRef]

| Metrics | Fixed-Time | Webster | Max- Pressure | Efficient-MP | LSTM-PPO | HTDS | HTDS- NP-ARW | ||
|---|---|---|---|---|---|---|---|---|---|
| Average Travel Time () | 405.90 | 215.21 | 147.07 | 148.87 | 151.43 | 142.11 | 140.24 | ||
| Average Loss Time () | 312.66 | 122.04 | 53.54 | 55.1 | 58.9 | 47.76 | 46.77 | ||
| CO2 Emission () | 4.76 | 5.74 | 5.82 | 5.50 | 5.19 | 5.29 | 5.26 | ||
| DRL Intersection | Queue | 23.03 | 15.03 | 4.79 | 4.45 | 8.49 | 3.46 | 3.76 | |
| Pressure | 1.06 | 5.99 | 2.29 | 1.41 | 5.25 | 0.60 | 0.61 | ||
| Neigh Intersection | Queue | NN | 14.32 | 5.13 | 1.57 | 1.25 | 3.14 | 1.35 | 1.54 |
| WN | 14.42 | 5.48 | 0.91 | 1.92 | 1.88 | 1.30 | 0.91 | ||
| EN | 14.66 | 5.20 | 0.82 | 1.48 | 2.06 | 1.07 | 1.05 | ||
| SN | 14.77 | 5.56 | 1.91 | 1.25 | 2.94 | 1.49 | 1.61 | ||
| Pressure | NN | 16.48 | 1.96 | 0.67 | 1.06 | 0.69 | 1.13 | 0.96 | |
| WN | 18.08 | 2.33 | 0.33 | 0.34 | 0.18 | 0.82 | 0.82 | ||
| EN | 18.53 | 2.27 | 0.33 | 0.39 | 0.13 | 0.60 | 0.7 | ||
| SN | 16.17 | 3.00 | 0.55 | 1.11 | 0.579 | 1.04 | 0.84 | ||
| Average Queue of Neigh | 14.54 | 5.34 | 1.30 | 1.47 | 2.51 | 1.30 | 1.28 | ||
| Average Pressure of Neigh | 17.32 | 2.39 | 0.47 | 0.73 | 0.49 | 0.90 | 0.83 | ||
| Features | HTDS-NP-ARW | HTDS | |
|---|---|---|---|
| Collaborative Features | Neigh Pressure Diff (NN) | 0.1069 | 0.0887 |
| Neigh Pressure Diff (WN) | 0.0976 | 0.1297 | |
| Neigh Pressure Diff (EW) | 0.1136 | 0.0730 | |
| Neigh Pressure Diff (SN) | 0.1516 | 0.1441 | |
| SHAP Contribution Percentage | 19.48% | 14.39% | |
| Local Features | Total Local Pressure | 0.1333 | 0.2234 |
| Total Local Queue | 0.2234 | 0.2965 | |
| SHAP Contribution Percentage | 13.16% | 17.41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Y.; Qin, G.; Zeng, J.; Tang, K.; Zhu, H.; Chung, E. Co-Optimization and Interpretability of Intelligent–Traditional Signal Control Based on Spatiotemporal Pressure Perception in Hybrid Control Scenarios. Sustainability 2025, 17, 7521. https://doi.org/10.3390/su17167521
Xiong Y, Qin G, Zeng J, Tang K, Zhu H, Chung E. Co-Optimization and Interpretability of Intelligent–Traditional Signal Control Based on Spatiotemporal Pressure Perception in Hybrid Control Scenarios. Sustainability. 2025; 17(16):7521. https://doi.org/10.3390/su17167521
Chicago/Turabian StyleXiong, Yingchang, Guoyang Qin, Jinglei Zeng, Keshuang Tang, Hong Zhu, and Edward Chung. 2025. "Co-Optimization and Interpretability of Intelligent–Traditional Signal Control Based on Spatiotemporal Pressure Perception in Hybrid Control Scenarios" Sustainability 17, no. 16: 7521. https://doi.org/10.3390/su17167521
APA StyleXiong, Y., Qin, G., Zeng, J., Tang, K., Zhu, H., & Chung, E. (2025). Co-Optimization and Interpretability of Intelligent–Traditional Signal Control Based on Spatiotemporal Pressure Perception in Hybrid Control Scenarios. Sustainability, 17(16), 7521. https://doi.org/10.3390/su17167521







