Analysis of Water Rights Allocation in Heilongjiang Province Based on Stackelberg Game Model and Entropy Right Method
Abstract
1. Introduction
2. Regional Overview
3. Materials and Methods
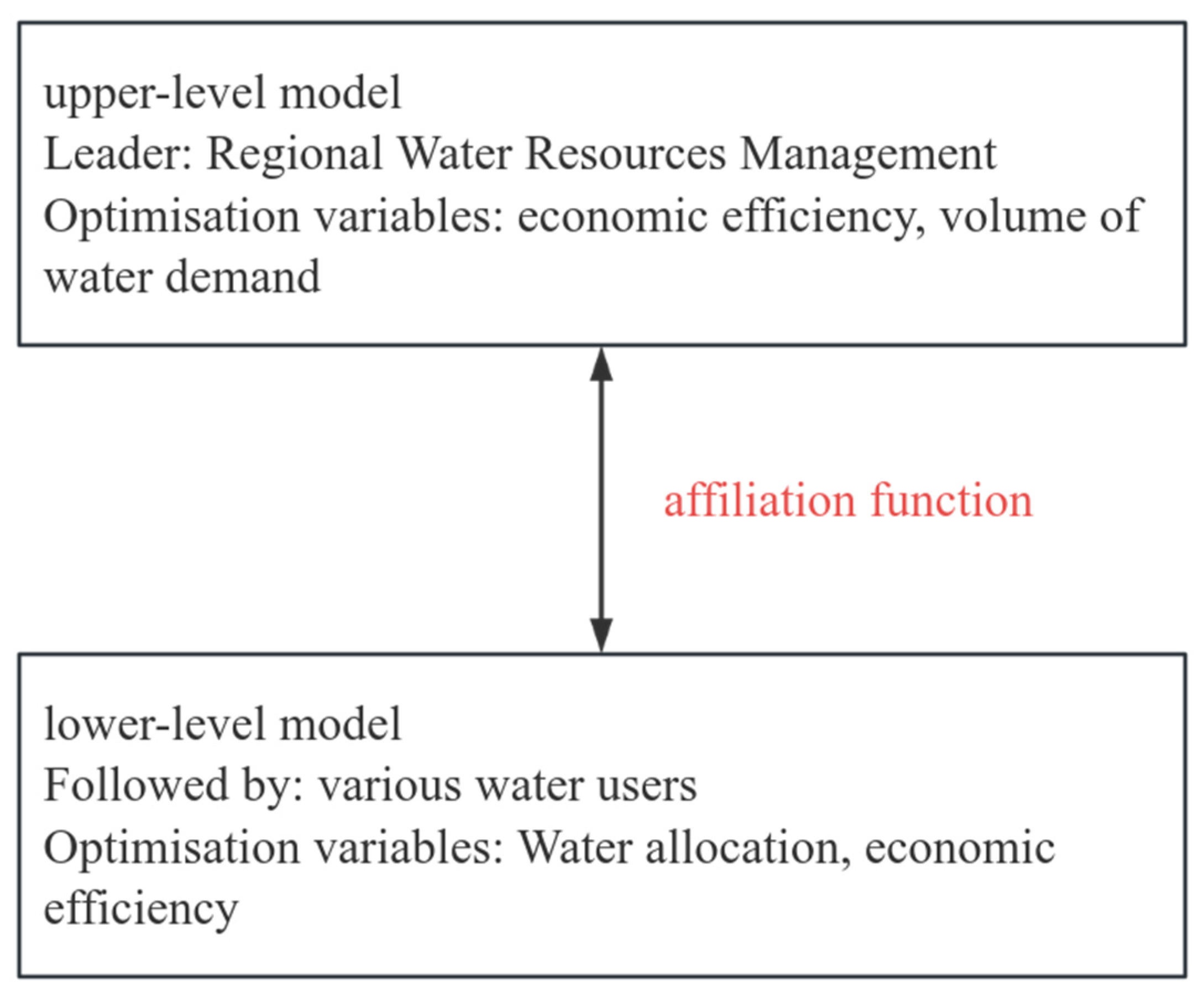
3.1. Stackelberg Game Model
Modeling the Regional Stackelberg Game
3.2. Entropy Weighting (Physics)
3.2.1. Construction of the Indicator System
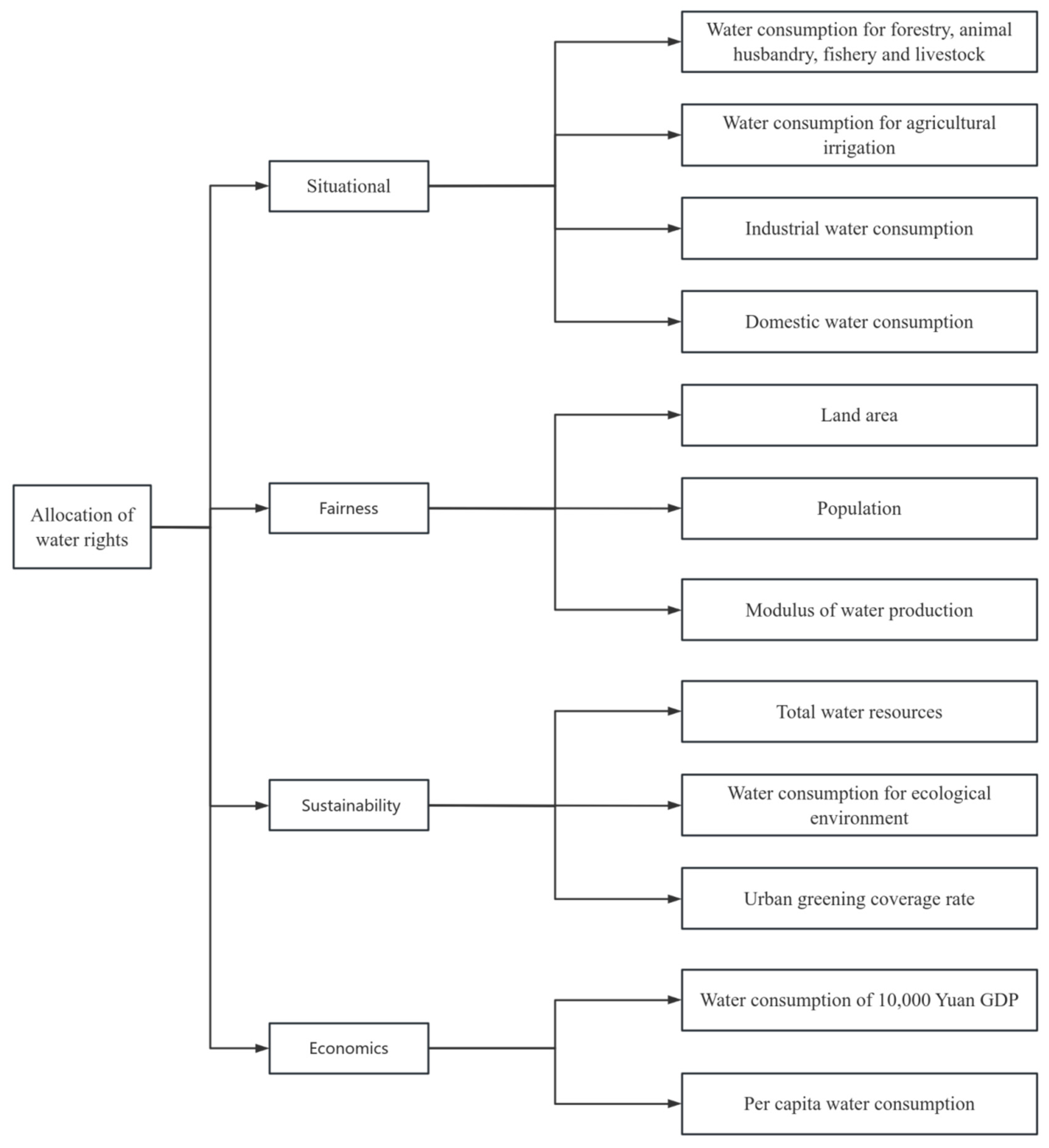
3.2.2. Entropy Weighting Method to Calculate Indicator Weights and Composite Scores
- (1)
- Denote the set of evaluation objects as {Ai} (i = 1,2,…,i) and the set of indicators used for evaluation as {Xj} (j = 1,2,…,j) and denote the raw value of the jth indicator of the ith evaluation object by xij. The evaluation matrix is constructed as follows in the next step.
- (2)
- Normalize the indicators using the extreme difference transformation method. Since the unit of measurement of the indicators is not uniform, before using them to calculate the composite indicators, it is necessary to carry out standardization, that is, the absolute value of the indicators is transformed into the relative value, so as to solve the problem of homogenization of the values of the various different qualitative indicators [38]. In addition, the positive and negative indicator values represent different meanings (the higher the value of the positive indicator, the better, and the lower the value of the negative indicator, the better); therefore, the positive and negative indicators need to use different algorithms for data standardization:
4. Results and Analyses
4.1. Scenario 1 Calculation Process
4.2. Scenario 2 Calculation Process
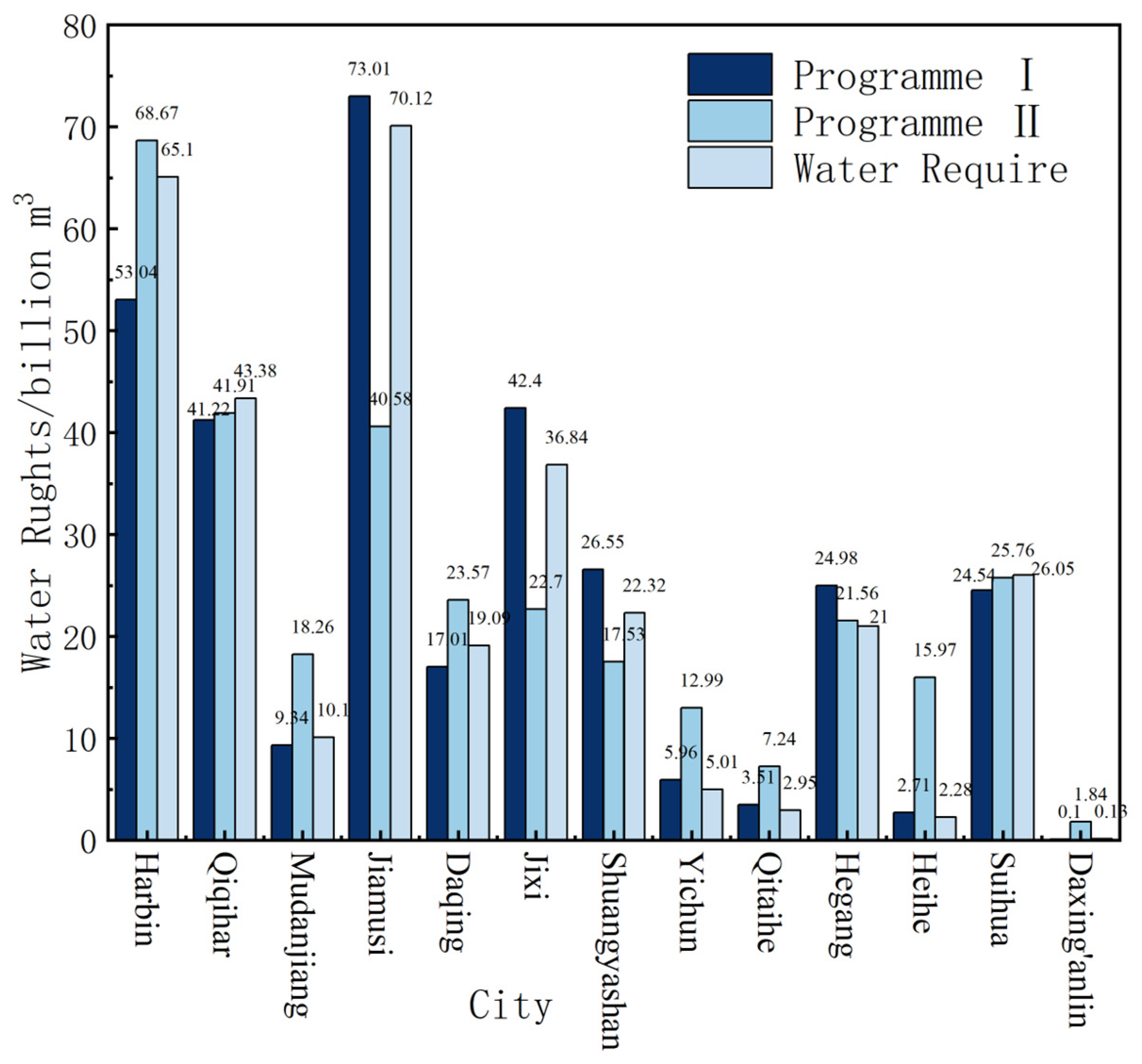
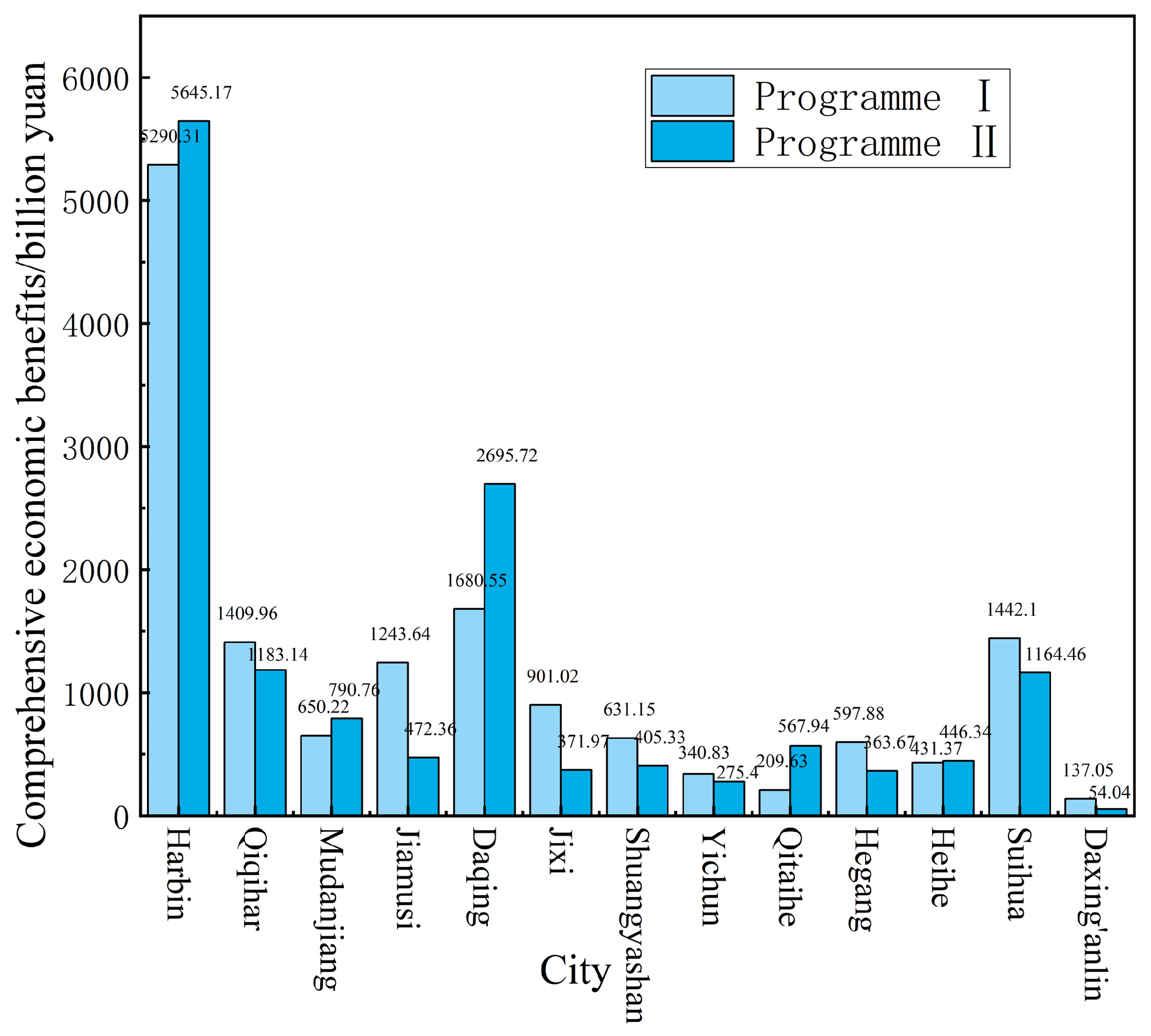
4.3. Comparison of the Results of the Two Scenario Configurations
4.4. Measures for Exceeding Water Quotas
4.5. Method Generalization and Discussion
5. Conclusions
- (1)
- The entropy weight method ensures objectivity in water allocation by assigning weights to each indicator and avoiding human interference. However, its static nature limits its capacity to address dynamic interactions and feedback among stakeholders. In situations of intensified competition, such as water scarcity, it is less effective in coordinating inter-regional conflicts and often fails to achieve maximum overall benefit.
- (2)
- In contrast, the Stackelberg game model demonstrates clear advantages in managing multi-party interest conflicts and supporting dynamic adjustments. By structuring decision making hierarchically between upper-level managers and lower-level users, it adapts allocations in response to actual seasonal and sectoral demands. This flexibility allows prioritization of agricultural water use during peak irrigation periods, industrial supply during production peaks, and maintenance of ecological flows in major river systems. As a result, the Stackelberg model achieves better alignment with real-world conditions, higher adaptability, and stronger capacity to support balanced regional development compared to the entropy weight method.
- (3)
- Based on the comparative analysis, this study provides a practical framework for method selection that can be applied in other regions. For areas with multiple stakeholders, strong regulatory capacity, and dynamic negotiation needs, the Stackelberg game model is more suitable due to its adaptability to changing conditions. In contrast, the entropy weighting method is more appropriate for regions requiring transparent, objective weight assignment where decision making must be stable and data-driven. The application process should include the following: conducting a preliminary assessment of water availability, socio-economic conditions, and ecological constraints; applying each method independently with appropriate parameter settings; validating results against historical allocation patterns and stakeholder responses; and integrating the chosen method into local water management policies with regular reviews. This approach allows decision makers to select the most suitable model for their regional context, improving the applicability and transferability of this study’s findings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Four Billion People Facing Severe Water Scarcity|Science Advances. Available online: https://www.science.org/doi/10.1126/sciadv.1500323 (accessed on 4 June 2025).
- Deng, L.; Guo, S.; Yin, J.; Zeng, Y.; Chen, K. Multi-Objective Optimization of Water Resources Allocation in Han River Basin (China) Integrating Efficiency, Equity and Sustainability. Sci. Rep. 2022, 12, 798. [Google Scholar] [CrossRef]
- Cosgrove, W.J.; Loucks, D.P. Water Management: Current and Future Challenges and Research Directions. Water Resour. Res. 2015, 51, 4823–4839. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Xin, G.; Ying, L. Multi-Attribute Decision-Making Based on Comprehensive Hesitant Fuzzy Entropy. Expert. Syst. Appl. 2024, 237, 121459. [Google Scholar] [CrossRef]
- Chen, L.; Wang, X.; Wang, Y.; Gao, P. Improved Entropy Weight Methods and Their Comparisons in Evaluating the High-Quality Development of Qinghai, China. Open Geosci. 2023, 15, 20220570. [Google Scholar] [CrossRef]
- Lan, J.; Du, Y. Evaluation of Water Resources Carrying Capacity in China Based on Entropy Weight TOPSIS Model. J. Comput. Methods Sci. Eng. 2024, 24, 1981–1991. [Google Scholar] [CrossRef]
- He, G.; Zhao, S.; Du, Y. Evaluation and Dynamic Warning of Ecological Security of Water Resources Based on TQR-EGM Model. J. Water Resour. Water Eng. 2021, 32, 36–42. (In Chinese) [Google Scholar]
- The Coordination of Stakeholder Interests in Environmental Regulation: Lessons from China’s Environmental Regulation Policies from the Perspective of the Evolutionary Game Theory. J. Clean. Prod. 2020, 249, 119385. [CrossRef]
- Jin, J.; Fang, X. Evaluation of Economic Scenarios of Water Allocation Using a Game Theory. Water Supply 2023, 23, 3253–3261. [Google Scholar] [CrossRef]
- Boyd, N.T.; Gabriel, S.A.; Rest, G.; Dumm, T. Generalized Nash Equilibrium Models for Asymmetric, Non-Cooperative Games on Line Graphs: Application to Water Resource Systems. Comput. Oper. Res. 2023, 154, 106194. [Google Scholar] [CrossRef]
- Wang, S.; Fu, L.; Peng, H.; Wang, J.; Hua, Y.; Gui, Z. Study on an Equilibrium Water Price System Based on Cooperative Game Technology. Water 2023, 15, 2354. [Google Scholar] [CrossRef]
- Komasi, M.; Alizadefard, A.; Ahmadi, M. Examination of Players’ Strategies in Determining the Optimal Groundwater Exploitation by Game Theory. Hydrogeol. J. 2024, 32, 691–704. [Google Scholar] [CrossRef]
- Xiang, K.; Chen, J.; Yang, L.; Wu, J.; Shi, P. Equilibrium Interaction Strategies for Integrated Energy System Incorporating Demand-Side Management Based on Stackelberg Game Approach. Energies 2024, 17, 3603. [Google Scholar] [CrossRef]
- Zhang, X.; Castelletti, A.; Wang, X.; Guo, P. Robust Stackelberg Equilibrium Water Allocation Patterns in Shallow Groundwater Areas. Water Resour. Res. 2024, 60, e2023WR035373. [Google Scholar] [CrossRef]
- Huang, Q.; Lv, C.; Feng, Q. Stackelberg Game Based Optimal Water Allocation from the Perspective of Energy-Water Nexus: A Case Study of Minjiang River, China. J. Clean. Prod. 2024, 464, 142764. [Google Scholar] [CrossRef]
- Zarreh, M.; Yaghoubi, S.; Bahrami, H. Pricing of Drinking Water under Dynamic Supply and Demand Based on Government Role: A Game-Theoretic Approach. Water Resour. Manag. 2024, 38, 2101–2133. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, T.; Zhao, R.; Zhang, J.; Min, X. Bi-Level Hybrid Game Model for Optimal Operation of Multi-Function Reservoir Considering Integrated Water Resource Management. Environ. Sci. Pollut. Res. 2024, 31, 54026–54043. [Google Scholar] [CrossRef] [PubMed]
- Shekarforush, S.H.; Sardarshahraki, A.; Ghaffari Moghadam, Z. A Model to Manage the Allocation of Water Resources with the Game Theory Approach under Uncertainty. 2025. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5167027 (accessed on 5 March 2025).
- Liu, S.-B.; Hu, C.-H.; Wang, S.-W.; Guo, X.; Niu, C.-J.; Quan, L.-Y.; Li, M. Pricing Mechanism for Multi-Source–Multi-User Water under a Dynamic Game Model: A Case Study of Yiwu City. China Rural. Water Hydropower 2024, 5, 169–175. [Google Scholar] [CrossRef]
- Jia, X.; Fu, X.; Zhang, X.; Fan, Z. Robust Master–Slave Game Model for Water-Quality Protection and Water-Use Efficiency and Its Application. J. Hydraul. Eng. 2024, 55, 874–882. (In Chinese) [Google Scholar] [CrossRef]
- Xu, Z.; Yao, L.; Zhou, X.; Moudi, M.; Zhang, L. Optimal Irrigation for Sustainable Development Considering Water Rights Transaction: A Stackelberg-Nash-Cournot Equilibrium Model. J. Hydrol. 2019, 575, 628–637. [Google Scholar] [CrossRef]
- Houba, H.; Tomori, F. Stackelberg Social Equilibrium in Water Markets. Games 2023, 14, 54. [Google Scholar] [CrossRef]
- De Frutos Cachorro, J.; Martín-Herrán, G.; Tidball, M. Commitment vs. Noncommitment Behaviors in Natural Resource Conflicts: A Case Study of Groundwater Resources. Econ. Model. 2024, 132, 106652. [Google Scholar] [CrossRef]
- Pan, L.; Chen, X.; Zhao, L.; Xiao, A. Does Information Asymmetry Impact Sub-Regions’ Cooperation of Regional Water Resource Allocation? Int. J. Environ. Res. Public Health 2019, 16, 4292. [Google Scholar] [CrossRef] [PubMed]
- Janjua, S.; An-Vo, D.-A.; Reardon-Smith, K.; Mushtaq, S. Resolving Water Security Conflicts in Agriculture by a Cooperative Nash Bargaining Approach. Agric. Water Manage. 2024, 306, 109205. [Google Scholar] [CrossRef]
- Chu, Y.; Xiao, Y.; Zhu, J. A Bilevel Optimal Water Allocation Model Considering Water Users’ Satisfaction Degree and Water Rights Transaction: A Case Study in Qingzhang River Basin, China. Water 2023, 15, 2650. [Google Scholar] [CrossRef]
- Environmental Water Efficiency: Maximizing Benefits and Minimizing Costs of Environmental Water Use and Management. Available online: https://wires.onlinelibrary.wiley.com/doi/epdf/10.1002/wat2.1285 (accessed on 4 June 2025).
- Yang, Y.; Liu, Y.; Dai, J.; Zeng, Y. Cost-Sharing Mechanism of Water Pollution Control in Main and Subbasins Based on Stackelberg Game Model. Math. Probl. Eng. 2022, 2022, 6559840. [Google Scholar] [CrossRef]
- Men, B.; Wu, Z.; Liu, H.; Li, Y.; Zhao, Y. Research on Hedging Rules Based on Water Supply Priority and Benefit Loss of Water ShortageA Case Study of Tianjin, China. Water 2019, 11, 778. [Google Scholar] [CrossRef]
- Water Resources Utilization Efficiency and Influence Factors under Environmental Restrictions. J. Clean. Prod. 2018, 184, 611–621. [CrossRef]
- De Clercq, D.; Smith, K.; Chou, B.; Gonzalez, A.; Kothapalle, R.; Li, C.; Dong, X.; Liu, S.; Wen, Z. Identification of Urban Drinking Water Supply Patterns across 627 Cities in China Based on Supervised and Unsupervised Statistical Learning. J. Environ. Manage. 2018, 223, 658–667. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, J.; Han, H.; Zhang, J. Study of the Allocation of Regional Flood Drainage Rights in Watershed Based on Entropy Weight TOPSIS Model: A Case Study of the Jiangsu Section of the Huaihe River, China. Int. J. Environ. Res. Public Health 2020, 17, 5020. [Google Scholar] [CrossRef]
- Fei, B.; Min, Z. Assessment of Water Resources Vulnerability in International River Basins Based on Entropy Weight Method. J. Environ. Prot. Ecol. 2020, 21, 865–875. [Google Scholar]
- Li, M.; Sun, H.; Singh, V.P.; Zhou, Y.; Ma, M. Agricultural Water Resources Management Using Maximum Entropy and Entropy-Weight-Based TOPSIS Methods. Entropy 2019, 21, 364. [Google Scholar] [CrossRef] [PubMed]
- Feng, J. Optimal Allocation of Regional Water Resources Based on Multi-Objective Dynamic Equilibrium Strategy. Appl. Math. Model. 2021, 90, 1183–1203. [Google Scholar] [CrossRef]
- Cui, Y.; Feng, P.; Jin, J.; Liu, L. Water Resources Carrying Capacity Evaluation and Diagnosis Based on Set Pair Analysis and Improved the Entropy Weight Method. Entropy 2018, 20, 359. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yang, J.; Xu, Z.; Zhang, C. Effect of Frequency of Multi-Source Water Supply on Regional Guarantee Rate of Water Use. Water 2019, 11, 1356. [Google Scholar] [CrossRef]
- Song, P.; Wang, C.; Zhang, W.; Liu, W.; Sun, J.; Wang, X.; Lei, X.; Wang, H. Urban Multi-Source Water Supply in China: Variation Tendency, Modeling Methods and Challenges. Water 2020, 12, 1199. [Google Scholar] [CrossRef]
- Zhang, S.; Wen, X.; Zhang, R.; Miao, W.; Gan, Z. An Optimal Allocation Model Based on the Regional Ecological Water Requirements and Multi-Water Supply Characteristics: A Case Study of Shandong Province, China. J. Hydrol. Reg. Stud. 2023, 49, 101513. [Google Scholar] [CrossRef]

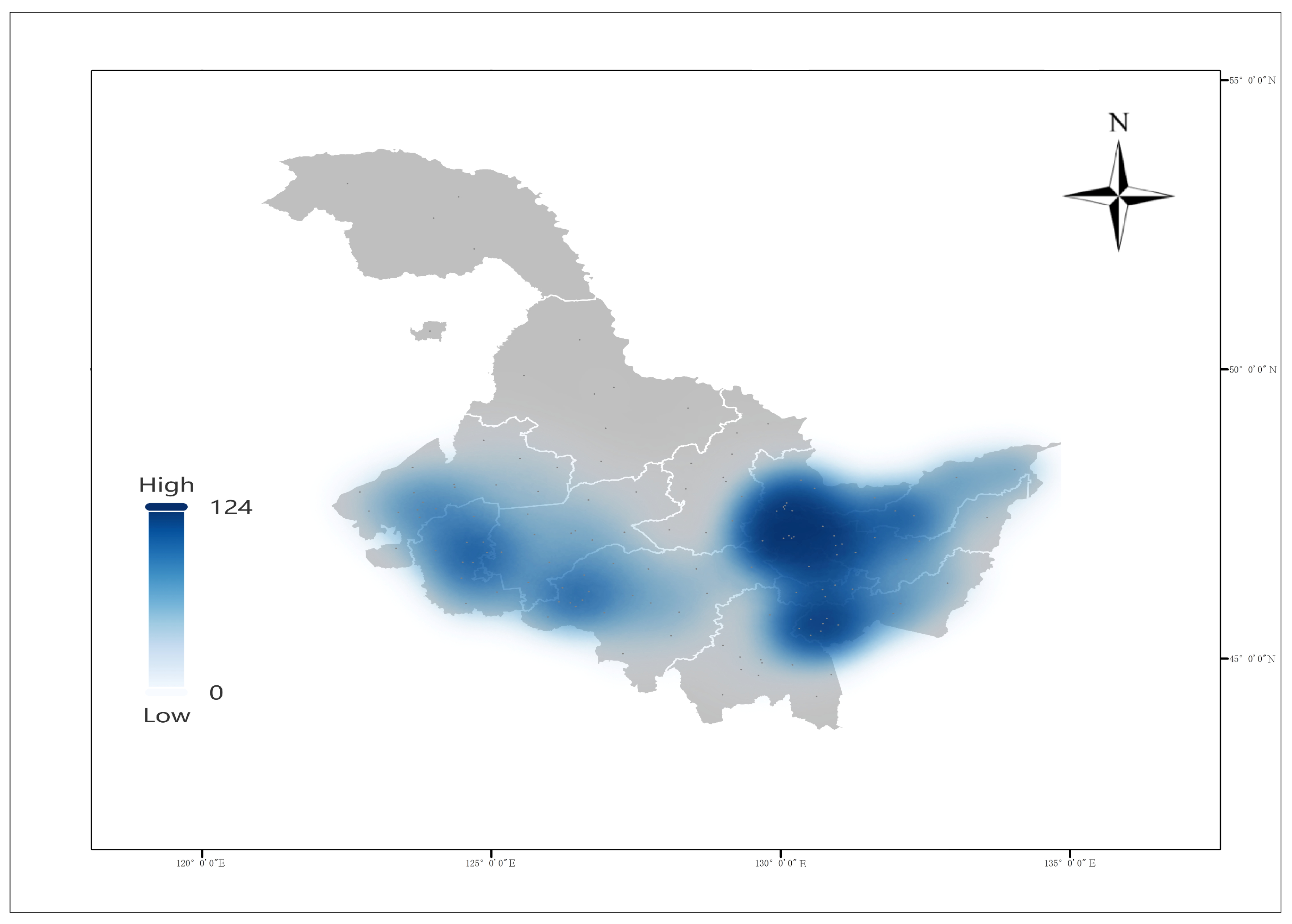

| Indicator | Harbin | Qiqihar | Mudanjiang | Jiamusi | Daqing | Jixi | Shuangyashan | Yichun | Qitaihe | Hegang | Heihe | Suihua | Daxing’anling |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Per capita water consumption/m3 | 690.20 | 839.88 | 413.60 | 3076.79 | 702.35 | 2236.79 | 1629.20 | 462.18 | 392.81 | 2194.36 | 148.24 | 507.50 | 32.75 |
| Population/10,000 people | 943.20 | 516.50 | 244.20 | 227.90 | 271.80 | 164.70 | 137.00 | 108.40 | 75.10 | 95.70 | 153.80 | 513.30 | 39.70 |
| Total water resources/billion m3 | 137.97 | 120.65 | 89.89 | 56.39 | 30.48 | 42.13 | 34.40 | 93.58 | 7.98 | 32.13 | 191.81 | 72.45 | 286.42 |
| Land area/km2 | 53,068 | 42,469 | 38,865 | 32,704 | 21,219 | 22,488 | 22,036 | 32,760 | 6222 | 14,680 | 66,802 | 34,964 | 64,822 |
| Domestic water consumption/billion m3 | 4.19 | 1.48 | 1.02 | 0.87 | 0.92 | 0.63 | 0.43 | 0.34 | 0.21 | 0.40 | 0.42 | 1.47 | 0.08 |
| Water consumption for forestry, animal husbandry, fishery, and livestock | 1.36 | 0.83 | 0.75 | 1.25 | 0.75 | 0.20 | 0.11 | 0.12 | 0.12 | 0.14 | 0.11 | 1.50 | 0.01 |
| Industrial water consumption/billion m3 | 1.86 | 6.43 | 1.15 | 1.80 | 3.90 | 0.34 | 0.44 | 0.32 | 0.37 | 0.57 | 0.15 | 0.40 | 0.02 |
| Water consumption for ecological environment/billion m3 | 1.20 | 0.05 | 0.03 | 0.03 | 0.06 | 0.02 | 0.03 | 0.01 | 0.01 | 0.09 | 0.00 | 0.02 | 0.00 |
| Water consumption for agricultural irrigation/billion m3 | 54.80 | 34.33 | 6.78 | 65.94 | 13.24 | 35.56 | 21.24 | 4.18 | 2.16 | 19.74 | 1.53 | 22.45 | 0.00 |
| Modulus of water production/10,000m3/km2 | 26.00 | 28.41 | 23.13 | 17.24 | 14.37 | 18.73 | 15.61 | 28.57 | 12.83 | 21.89 | 28.71 | 20.72 | 44.19 |
| Water consumption of CNY 10,000 GDP/m3 | 121.64 | 354.27 | 115.43 | 859.10 | 72.86 | 610.24 | 432.56 | 157.20 | 127.48 | 592.89 | 35.79 | 221.19 | 8.49 |
| Urban greening coverage rate/% | 33.07 | 44.21 | 29.20 | 43.50 | 43.89 | 40.10 | 43.69 | 38.76 | 46.17 | 43.09 | 43.12 | 29.10 | 48.60 |
| Year | Harbin | Qiqihar | Mudanjiang | Jiamusi | Daqing | Jixi | Shuangyashan | Yichun | Qitaihe | Hegang | Heihe | Suihua | Daxing’anling |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2014 | 5332.7 | 1238.8 | 1264.1 | 766.0 | 4077.5 | 516.0 | 432.7 | 256.0 | 214.2 | 259.5 | 421.4 | 1190.2 | 128.4 |
| 2015 | 5751.2 | 1270.7 | 1310.7 | 619.4 | 2983.5 | 514.7 | 433.3 | 248.2 | 212.6 | 265.6 | 447.8 | 1272.2 | 134.9 |
| 2016 | 5183.8 | 1325.3 | 1368.1 | 640.5 | 2610.0 | 518.4 | 437.4 | 251.2 | 216.6 | 264.1 | 470.8 | 1316.3 | 143.9 |
| 2017 | 5576.3 | 1353.2 | 1404.7 | 714.8 | 2680.5 | 530.1 | 426.9 | 266.4 | 228.8 | 282.9 | 488.9 | 1336.8 | 149.7 |
| 2018 | 5249.4 | 1340.2 | 1423.0 | 724.1 | 2801.2 | 535.2 | 476.4 | 274.2 | 250.3 | 289.6 | 505.1 | 1359.6 | 129.0 |
| 2019 | 5351.7 | 1128.9 | 825.0 | 762.9 | 2568.3 | 552.0 | 507.0 | 298.8 | 231.0 | 336.0 | 579.0 | 1101.0 | 138.6 |
| 2020 | 5183.8 | 1200.4 | 831.7 | 811.8 | 2301.1 | 572.4 | 493.9 | 295.2 | 206.4 | 340.2 | 614.4 | 1150.2 | 141.9 |
| 2021 | 5351.7 | 1224.5 | 875.0 | 816.2 | 2620.0 | 603.7 | 516.0 | 318.7 | 231.4 | 354.2 | 637.1 | 1177.7 | 153.1 |
| Year | Harbin | Qiqihar | Mudanjiang | Jiamusi | Daqing | Jixi | Shuangyashan | Yichun | Qitaihe | Hegang | Heihe | Suihua | Daxing’anling |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2014 | 70.6 | 48.28 | 10.51 | 59.58 | 27.12 | 39.7 | 26.86 | 6.41 | 3.29 | 23.24 | 4.87 | 28.25 | 0.48 |
| 2015 | 67.06 | 49.17 | 10.66 | 59.22 | 24.73 | 38.12 | 22.49 | 5.51 | 3.14 | 21.2 | 4.47 | 31.05 | 0.33 |
| 2016 | 67.41 | 48.15 | 10.49 | 59.31 | 27.52 | 36.25 | 23.31 | 4.92 | 2.94 | 21.33 | 4.25 | 29.54 | 0.16 |
| 2017 | 67.64 | 48.93 | 10.44 | 75.1 | 25.59 | 37.81 | 24.66 | 5.13 | 3.01 | 20.9 | 3.61 | 30.08 | 0.15 |
| 2018 | 62.31 | 49.67 | 10.32 | 74.68 | 24.98 | 36.83 | 23.44 | 5.05 | 3.01 | 21.52 | 3.55 | 28.43 | 0.15 |
| 2019 | 58.14 | 45.54 | 10.30 | 65.73 | 21.77 | 34.44 | 19.22 | 4.77 | 2.94 | 17.52 | 2.91 | 26.98 | 0.14 |
| 2020 | 62.67 | 46.39 | 10.07 | 65.13 | 20.46 | 34.95 | 19.24 | 4.78 | 2.94 | 19.42 | 2.76 | 25.19 | 0.13 |
| 2021 | 65.1 | 43.38 | 10.1 | 70.12 | 19.09 | 36.84 | 22.32 | 5.01 | 2.95 | 21 | 2.28 | 26.05 | 0.13 |
| Indicator | Weights |
|---|---|
| Per capita water consumption/m3 | 0.0672 |
| Population/10,000 people | 0.0785 |
| Total water resources/billion m3 | 0.0609 |
| Land area/km2 | 0.0360 |
| Domestic water consumption/billion m3 | 0.0835 |
| Water consumption for forestry, animal husbandry, fishery, and livestock | 0.0798 |
| Industrial water consumption/billion m3 | 0.1117 |
| Water consumption for ecological environment/billion m3 | 0.2523 |
| Water consumption for agricultural irrigation/billion m3 | 0.0738 |
| Modulus of water production/10,000m3/km2 | 0.0515 |
| Water consumption of CNY 10,000 GDP/m3 | 0.0695 |
| Urban greening coverage rate/% | 0.0353 |
| City | Harbin | Qiqihar | Mudanjiang | Jiamusi | Daqing | Jixi | Shuangyashan | Yichun | Qitaihe | Hegang | Heihe | Suihua | Daxing’anling |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aggregate score | 0.2049 | 0.1251 | 0.0545 | 0.1211 | 0.0703 | 0.0677 | 0.0523 | 0.0388 | 0.0216 | 0.0643 | 0.0477 | 0.0769 | 0.0548 |
| Allocated water rights/billion m3 | 68.67 | 41.91 | 18.26 | 40.58 | 23.57 | 22.70 | 17.53 | 12.99 | 7.24 | 21.56 | 15.97 | 25.76 | 1.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.; Yang, S.; Wu, Z.; Si, Z. Analysis of Water Rights Allocation in Heilongjiang Province Based on Stackelberg Game Model and Entropy Right Method. Sustainability 2025, 17, 7407. https://doi.org/10.3390/su17167407
Lu K, Yang S, Wu Z, Si Z. Analysis of Water Rights Allocation in Heilongjiang Province Based on Stackelberg Game Model and Entropy Right Method. Sustainability. 2025; 17(16):7407. https://doi.org/10.3390/su17167407
Chicago/Turabian StyleLu, Kaiming, Shang Yang, Zhilei Wu, and Zhenjiang Si. 2025. "Analysis of Water Rights Allocation in Heilongjiang Province Based on Stackelberg Game Model and Entropy Right Method" Sustainability 17, no. 16: 7407. https://doi.org/10.3390/su17167407
APA StyleLu, K., Yang, S., Wu, Z., & Si, Z. (2025). Analysis of Water Rights Allocation in Heilongjiang Province Based on Stackelberg Game Model and Entropy Right Method. Sustainability, 17(16), 7407. https://doi.org/10.3390/su17167407






