Co-Optimization of Charging Strategies and Route Planning for Variable-Ambient-Temperature Long-Haul Electric Vehicles Based on an Electrochemical–Vehicle Dynamics Model

Abstract

Vehicle electrification is one of the main development directions within the automobile industry. However, due to the range limit of electric vehicles, electric vehicle users generally have range anxiety, especially toward long-haul driving. Therefore, there is an urgent need to effectively coordinate route planning and charging during long-haul driving, especially considering factors such as insufficient charging facilities, long charging times, battery aging, and changes in energy consumption under variable-temperature environments. In this study, the goal is to collaboratively optimize route planning and charging strategies. To achieve this goal, a mixed-integer nonlinear model is developed to minimize the total system cost, an electrochemical model is applied to accurately track the battery state, and a two-layer IACO-SA is proposed. Finally, the highway network in five provinces of China is adopted as an example to compare the optimal scheme results of our model with those of three other models. The comparison results prove the effectiveness of the proposed model and solution algorithm for the collaborative optimization of route planning and charging strategies of electric vehicles during long-haul driving.

1. Introduction

Vehicle electrification is one of the main trends in the automotive industry, and it brings many advantages, such as its use of sustainable energy, ensuring clean resources and environmental friendliness. With the growing popularity of electric vehicles, the number of the charging facilities is continuing to increase, and their functionality is also improving. For example, sales of new energy vehicles in China exceeded 11 million in 2024, up by 38.1% year on year, accounting for 40.9% of total vehicle sales. By 2024, the total number of charging facilities for electric vehicles in China had reached 12.818 million, of which 3.579 million were public charging facilities, and 9.239 million were private charging facilities [1]. These charging facilities are mainly located in the urban road network and are already able to meet the daily urban travel needs of electric vehicles.

However, due to the distance between charging stations in the intercity highway network and the range limit of electric vehicles, electric vehicle users still have serious range anxiety toward long-distance driving. This is especially the case in low-temperature environments of −20 °C, wherein the driving range of electric vehicles is reduced by about 30%. Electric vehicle charging power selection is also a problem that users need to consider; if high-power fast charging is used, this will accelerate the aging of the battery, while if low-power slow charging is used, this extends the waiting time. Due to factors such as insufficient charging facilities, long charging times, battery aging, and energy consumption changes in a variable-temperature environment, rationally arranging route planning and charging for long-haul driving is the key to extending driving range, relieving mileage anxiety, and shortening travel times.

At present, there are many research studies on route planning and charging problems related to electric vehicles, and many of these studies have focused on long-haul driving. The authors of [2] developed a path and charging strategy planning model, aiming to achieve the shortest vehicle travel time and taking the state and safe power of charging equipment in the actual road network as constraints. They adopted a genetic algorithm to solve the model. The authors of [3] designed a multi-objective two-layer quadratic optimization model which took into account the interaction between the traffic network and the power network. The authors of [4] proposed an asynchronous decentralized load-restoration method for a resilient electricity transportation network considering the co-response of buildings and electric buses. The model’s aim was to maximize the power supply time of loads and to minimize the driving distances of e-buses. The authors of [5] established an adaptive charging and routing strategy that considered travel time, waiting time, and charging time and developed a multi-standard shortest-path search algorithm using a shrinking hierarchy. Considering real-time traffic information and energy consumption information related to road conditions, the authors of [6] formulated a three-step heuristic algorithm based on pre-processing of the traffic network, charging path planning, and sub-path planning. The authors of [7] described a new cost-effective EV charging–navigation problem and transformed it into a two-stage stochastic optimization problem to investigate EV charging behavior and its interaction with route selection. The authors of [8] designed an improved differential evolution (IDE) algorithm to solve a variant of the EV path-planning problem involving a time window and a partial charge strategy for nonlinear charging, developing an efficient method to guide EV advance charging. The authors of [9] used a hybrid selection model based on nested logit (NL) to study the influence of personal attitude (i.e., planning ability, risk avoidance, and confidence in battery) on the driver’s charging frequency decision-making behavior. The results showed that the initial charging state and attitude had a significant impact on charging frequency decision-making. The authors of [10] used fitness ant colony optimization algorithms to further adjust the available routes based on the vehicle’s braking and battery power to determine the most efficient route and extend the driving range. However, these research considerations are not comprehensive, and the model constraints are often relatively simple, without comprehensive consideration of factors such as the location of the charging station, charging power, battery aging, time-of-use (TOU) price, temperature, and state of charge (SOC).

EV charging problems are usually studied with the objective of minimizing travel time or cost, taking into account factors such as charging station location, charging power, the use of partial or full charging, and the TOU price. The profit distribution and collaborative optimization of multi-agent systems are also of great significance in the field [11]. The authors of [12] established a multilevel optimization model to provide EV drivers with charging strategies for long-distance driving, aiming to minimize travel time and charging cost simultaneously. They determined the optimal charging power for each charging station on the available routes and designed a dynamic planning method to solve the model. The authors of [13] developed a new finite-horizon Markov decision process (FH-MDP) problem to minimize the driving time of an electric vehicle while preventing battery depletion by optimally selecting the charging stations and the number of charges. The authors of [14] modeled the optimal charging and optimal routing problem for EVs as an optimization problem, with the charging variables considered in the optimization model including peak charging demand, daytime usage time tariffs, partial charging, waiting time, and public charging station characteristics. The authors of [15] modeled the charging scheduling problem as a dynamic programming scenario with state-dependent constraints and solved it using fitted-value iterations. They then proposed a multi-stage decoupling algorithm to reduce the dimensionality in the fitted-value iterations in order to reduce the computational complexity. The authors of [16] studied the charging scheduling problem with the objective of minimizing the total charging cost of all electric buses, taking into account two important factors: peak and valley prices and time-varying charging power. Current research studies do not consider battery aging and battery depletion, which are hidden costs that are not readily apparent and difficult to quantify in the short term but account for a significant portion of costs in the long term.

The charging process usually consists of two charging stages, the constant current (CC) and constant voltage (CV) stages, leading to nonlinear charging curves. However, nonlinear curves are difficult to integrate into the optimization problem, so existing studies tend to linearize the nonlinear charging curves. For example, the authors of [17] modeled the battery degradation cost by introducing a wear-out cost function and linearized the nonlinear charging curve using a segmented affine function, which further simplified the model to mixed-integer linear programming and reduced the computational effort. The authors of [18] established two linearization methods to replace the nonlinear part and optimize the selection of fast charging and normal charging modes to maximize the operational revenue and minimize the power cost and battery degradation cost. The authors of [19] investigated the effect of charge state-dependent characteristics and established a nonlinear discharge function, and the experimental results showed that ignoring the effect of charge state may lead to infeasible or inferior solutions. Linearizing the nonlinear charging curve reduces the computational difficulty of the model, but the accuracy is also reduced, so we use an electrochemical model to calculate the battery voltage and SOC, preserving the nonlinearity of the charging and discharging curves and improving model accuracy.

An electrochemical model is a type of lithium-ion battery model, meaning it can more accurately simulate the characteristics of lithium-ion batteries during charging and discharging compared to an equivalent circuit model, in which the parameters during simulation are the same as the actual parameters of lithium-ion batteries. The authors of [20] developed a reduced-order SPMe model that combines electrolyte kinetics and side reactions. The model is a simplification of the DFN model and can accurately capture the key features of the DFN model while significantly reducing the computational complexity. The authors of [21] developed a comprehensive Bayesian parameter identification framework to determine parameter distributions in electrochemical models and estimate the global sensitivity of lithium-ion battery parameters. The authors of [22] designed an efficient identification scheme for electrochemical model parameters based on an agent model. The authors of [23] constructed a new battery model to accurately predict dynamic cyclic content decay by combining enhanced SPM with first-principles chemical/mechanical degradation physics. The authors of [24] proposed an extended single-particle model (ESP) with higher accuracy, and based on this, a novel closed-loop estimation algorithm for the state of charge based on the combination of the ESP model and the amperage-hour integral was proposed. In this paper, the SPMe model of electrochemical modeling is described.

Most studies have shown that the temperature inside the battery pack of electric vehicles is usually maintained between 15 °C and 60 °C. In cold outside environments, electric vehicles use positive temperature coefficient (PTC) to heat the battery pack and compartment, so PTC is the main factor for the elevated energy consumption of electric vehicles at low temperatures. The authors of [25] analyzed the effect of temperature on powertrain efficiency and auxiliary power and predicted the energy consumption of electric buses at driving level, solving the model using a Markov-based Gaussian Processing Regression (M-GPR) model. The authors of [26] predicted the energy consumption of each road segment of the road network, considering auxiliary consumption, and calculated energy-efficient routes. The authors of [27] proposed a comprehensive model for the auxiliary system of electric buses, including heating, ventilation, air conditioning, and other electrical components, and the results showed that the model can predict energy consumption accurately. The authors of [28] analyzed the mechanism of the influence of driving speed and ambient temperature on the power consumption of electric vehicles, elucidating the relationship between these factors and the power consumption per unit mile of electric vehicles. There are many energy consumption models described in the current literature that take into account the effect of temperature, but there is still a lack of research on the driving energy consumption of electric vehicles under changing ambient temperature conditions during long-distance driving across geographical areas.

This study aims to provide a comprehensive modeling framework for route planning and electric vehicle charging during long-haul driving in variable-temperature environments. The goal is to minimize the total system cost, including the charging cost (considering charging time and charging power) and the battery depletion cost (number of charge/discharge cycles). In addition to factors such as TOU price, energy consumption variations in variable-temperature environments are considered, and an electrochemical model is used to track the battery voltage and SOC to improve model accuracy. The problem is a mixed-integer nonlinear programming problem with partial differential functions, and a two-layer IACO-SA is proposed to solve the problem, with an improved artificial ant colony algorithm (IACO) in the outer layer to solve the path planning and charging station selection and a simulated annealing algorithm (SA) in the inner layer to solve the charging strategy.

The main contributions of this paper are as follows:

(1)

A new method is proposed to solve the long-haul driving route planning and charging co-optimization problem of electric vehicles under variable ambient temperature. This method comprehensively considers range limitations under battery voltage and SOC, the change in energy consumption under variable-temperature environmental conditions, variable charging power, TOU price, and battery aging.

(2)

A new electrochemical model is adopted to track the battery voltage and SOC, and it accurately captures the nonlinear process of voltage and SOC changes and improves model accuracy.

(3)

The effect of PTC on energy consumption in low-temperature environments is analyzed. The model for predicting the energy consumption of EVs at different temperatures is improved and applied to calculate energy consumption amidst temperature changes in cross-territory, long-haul EV driving scenarios.

The rest of this paper is organized as follows: In Section 2, the problem is described by transforming the network structure from a road network with charging facilities to a charging scheme super-network, and a mathematical formulation of the problem, in conjunction with an electrochemical model, is described. In Section 3, a two-layer IACO-SA is proposed based on the adjacency–contradiction strategy to solve the model. In Section 4, the performance of the proposed model is examined and a solving algorithm is applied to a highway network related to five provinces in China. Finally, Section 5 provides concluding remarks.

2. Modeling Framework

2.1. Model Description and Preliminaries

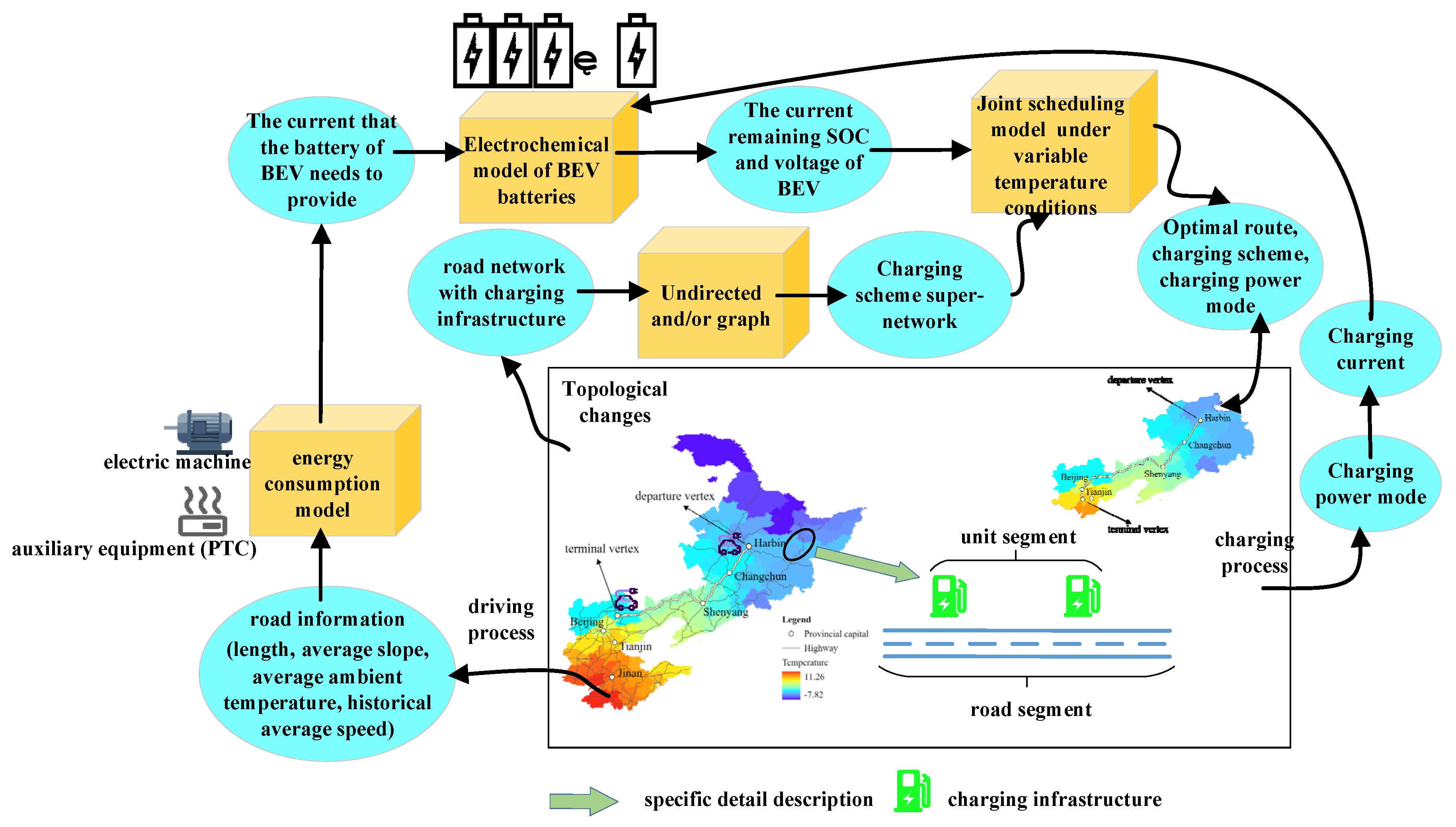
We set out to construct a system for long-haul BEV driving that considers the coupling of BEVs and variable-temperature road networks under economic constraints. The aim of our research is to select the optimal economic scheme under the given temperature conditions of the road network, considering changes in energy consumption and BEV range limitations, necessitating frequent charging. Thus, a joint route optimization, charging infrastructure scheduling, and charging power mode selection problem for long-haul BEV driving is proposed. Hereinafter, this problem is referred to as the long-haul joint scheduling problem. The system is divided into a road network part and a vehicle part to facilitate the description of the system. For the road network part, the topology of the road network is considered—including the basic road network and charging infrastructure; the basic information of the road segment, including the historical average speed, average road slope, and road length; the charging power at the charging infrastructure; and the road segment temperature. Changes in temperature have a great impact on the driving range of electric vehicles, with low-temperature conditions having especially strong effects. Regarding the vehicle part, it considers the state of charge (SOC) and BEV voltage for tracking purposes, as well as BEV energy consumption, including motor energy consumption and auxiliary equipment energy consumption. A schematic drawing of the long-haul BEV driving system, which considers the coupling of BEV and variable-temperature road networks, is shown in Figure 1.

Road network and ambient temperature variations are a fundamental and necessary part of BEV route optimization and charging infrastructure scheduling. For the road network part, a network of long travel roads with temperature and charging infrastructure, unit segments, and the road information of unit segments are described. Define a road network with ambient temperature and charging infrastructure for long travel $G_1=(\delta ,\epsilon ,P_c,T)$, where $\delta$ denotes the set of vertexes, $\epsilon$ denotes the road segment connecting different vertexes, $P_c$ denotes the charging infrastructure of road segment $\epsilon$, and $T$ denotes the set of average temperatures of road segment $\epsilon$. The vertex set $\delta$ includes the departure vertex $o$, where the BEV begins its long-haul drive, and terminal vertex $d$ is where the BEV finishes its long-haul drive; the set of intermediate vertexes is represented by $S$, with each intermediate vertex being $i,j,n\in S$. The road segment set $\epsilon$ includes all feasible road segments, where the vertexes are on both sides of the road segment $i,j,n\in \delta$. Let $P_{cij}$ denote charging infrastructure on road segment $(i,j)$, and $P_{cij}\subset P_c$. Let $P_{cijk}$ denote the charging infrastructure $k$ of road segment $(i,j)$, and $P_{cijk}\in P_{cij}$. Let $T_{ij}$ denote the average ambient temperature of road segment $(i,j)$, and $T_{ij}\in T$. Define the set of unit segment $\theta$; a unit segment is a more detailed division of a road segment. The two nodes of each unit segment can be road vertex or charging infrastructure, and their four cases are expressed as ${\theta }_{ij}$, ${\theta }_{i{P}_{cijk1}}$, ${\theta }_{P_{cijk1}{P}_{cijk2}}$, and ${\theta }_{P_{cijk2}j}$, respectively. The road information under the unit segment includes the length of unit segment $L_{{\theta }_{ij}}$, the average slope of unit segment ${\gamma }_{{\theta }_{ij}}$, the average ambient temperature $T_{{\theta }_{ij}}$, and the historical average speed of unit segment $v_{{\theta }_{ij}}$. Let $\chi$ represent the set of average slope, average ambient temperature, and the historical average speed of the unit segment. For example, ${\chi }_{{\theta }_{ij}}=\{{\gamma }_{{\theta }_{ij}},T_{{\theta }_{ij}},v_{{\theta }_{ij}}\}$.

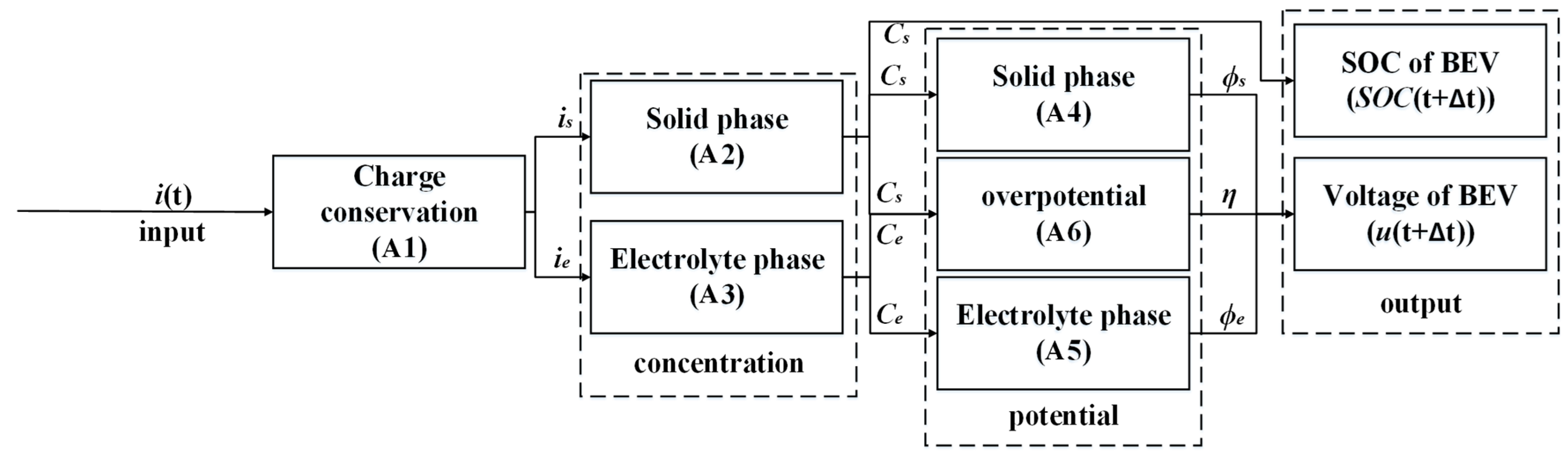
For the vehicle part, the state of charge (SOC) and electric vehicle voltage tracking, as well as the establishment of an energy consumption model under variable ambient temperature conditions, are the keys of the long-haul BEV system. They establish the criteria for route optimization and reasonable scheduling considering charging infrastructure. It can determine the maximum charging amount under different charging powers depending on the charging infrastructure. In order to be able to accurately capture the BEV battery state in the road network, an electrochemical model is adopted to track the BEV charging process and driving process considering the charging infrastructure and road segment. The electrochemical model can exactly describe the internal dynamics of the BEV power battery in the charging process and map the external characteristics of the BEV battery in the charging process. Let current $I$ denote the input of the electrochemical model. Let $ϵ\left(I\right)$ represent the electrochemical model, which can calculate the voltage $V\left(ϵ\left(I\right)\right)$ and the SOC $SoC\left(ϵ\left(I\right)\right)$ when the battery is in the charging process and driving process, serving as the outputs of the electrochemical model. 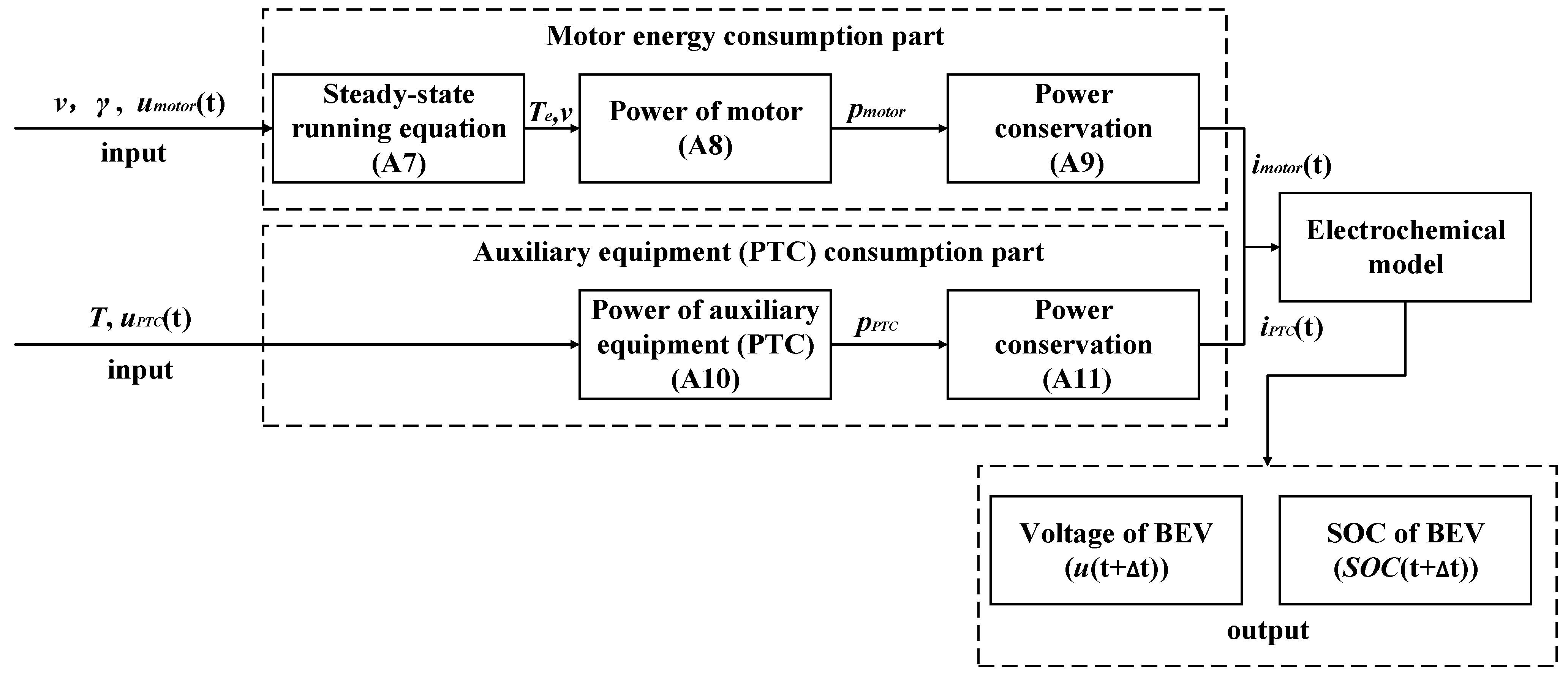The structure and formulas of this specific electrochemical model are shown in Appendix A. The PTC heating energy consumption is an important factor affecting the driving range of BEVs. The dynamic model of motor energy consumption and the empirical model of PTC heating energy consumption are considered for the variable ambient temperature energy consumption. Let road information under the unit segment serve as the input for motor energy consumption and PTC heating energy consumption. Let $\Phi \left(\chi \right)$ represent the energy consumption model, which can calculate the voltage $V\left(ϵ\left(\Phi \left(\chi \right)\right)\right)$ and SOC $SoC\left(ϵ\left(\Phi \left(\chi \right)\right)\right)$ when the battery is in the driving process, serving as the outputs of energy consumption model. The formulas and structure of the motor energy consumption and PTC heating energy consumption model are shown in Appendix B. The output of the energy consumption model is the input of the electrochemical model, which can ensure battery status tracking in the road network with variable ambient temperature.

2.2. Definition of the Pre-Processing of the Road Network Part: The Construction of the Multilateral Network Charging Scheme and the Super-Network Charging Scheme

In order to reduce the complexity of the joint scheduling optimization model, the long-haul road network with charging infrastructure is transformed into a charging scheme multilateral network to deal with route optimization and charging infrastructure scheduling simultaneously. Then, based on the undirected network and/or graph, the charging scheme multilateral network is transformed into a charging scheme super-network, which is convenient for the construction and solution of the joint scheduling model. The charging scheme multilateral network adds the selected charging infrastructure scheme to the long-haul road network.

The kth charging infrastructure $P_{cijk}\in P_{cij}$ that belongs to road segment $(i,j)$ corresponds to a binary 0/1 variable $z_{ijk}$, representing that the charging infrastructure $k$ on the road segment $(i,j)$ is selected to satisfy the BEV charging requirement. The amount of charging infrastructure on a road segment is not unique. The amount of charging infrastructure on the road segment $(i,j)$ is $\left|P_{cij}\right|$. Thus, the charging schemes are diverse in the different road segments, indexed by $q_s,q_t\in \{1,\dots ,2^{\left|P_{cij}\right|}\}$. Let vector $z_{ij}^{\prime }$ represent the charging scheme selected to satisfy the charging requirement on road segment $(i,j)$, which can be denoted as $z_{ij}^{\prime }=\{z_{ij1},\dots ,z_{ij{k}_s},\dots ,z_{ij\left|P_{cij}\right|}\}$.

Figure 2a shows an example including a reduced road network with four vertexes, four road segments, and four aspects of charging infrastructure. In the road segment $(a,b)$, there are two aspects of charging infrastructure, $P_{ab1}$ and $P_{ab2}$, which can be divided into four kinds of charging schemes. These charging schemes include $z_{ab}^{\prime }=\{0,0\}$, $z_{ab}^{\prime }=\{1,0\}$, $z_{ab}^{\prime }=\{0,1\}$, and $z_{ab}^{\prime }=\{1,1\}$, which, respectively, can be interpreted as no charging infrastructure, only charging infrastructure $P_{ab1}$, only charging infrastructure $P_{ab2}$, and both charging infrastructure $P_{ab1}$ and $P_{ab2}$, selected to satisfy the charging requirement on the edge $(a,b)$.

According to the relationship of long-haul road networks with charging infrastructure and charging schemes, a multilateral network $G_2=(\delta ,\epsilon ,Z^{\prime })$ is considered based on $G_1$ to describe the relationship of the road network and charging schemes. $Z^{\prime }$ represents the charging schemes set on the road segment set $\epsilon$. The vertex set $\delta$ and road segment set $\epsilon$ have already been defined in this paper (see Section 2.1). Let set $Z_{ij}^{\prime }$ represent the subset of the charging scheme set on the edge $(i,j)$. Figure 2b is the result of the road network $G_1$ in Figure 2a changing to multilateral network $G_2$. There are 9 kinds of charging schemes of road segments in the multilateral network $G_2$, including the charging situation and straight-through situation on all roads.

The charging scheme multilateral network can clearly show the relationship between the road network with charging infrastructure and each road segment charging scheme, but expressing the road segment charging scheme under the same road segment and the road segment charging scheme under different road segments is more complicated. Thus, a theory, and/or graph, is adopted to transform the multilateral network $G_2$ into a super-network of charging schemes to systematize the expression of the relationship of charging schemes under the same road segment and different road segments. There are three kinds of relationships between different road segment charging schemes: an adjacency relationship, a contradictory relationship, and no relationship. The adjacency relationship kind is defined as two road segment charging schemes on two different road segments which share the same vertex, and two road segment charging schemes can be selected sequentially. A contradictory relationship is found when two charging schemes are on the same road segment and two road segment charging schemes cannot be selected simultaneously. No relationship is noted if the two charging schemes are on two different road segments and there is no similar vertex between the two road segments. For example, in Figure 2c, the charging schemes 1, 2, 3, and 4 on road segment $(a,b)$ have a contradictory relationship. Charging scheme 1 on road segment $(a,b)$ and charging scheme 7 on road segment $(b,c)$ have an adjacency relationship. Charging scheme 1 on road segment $(a,b)$ and charging scheme 9 on road segment $(c,d)$ show no relationship. Let super-network $G_3=(Z^{\prime },\vartheta ,\psi )$ represent the different relationships of all the road segment charging schemes, where $\vartheta$ denotes the set of adjacency relationships for charging scheme set $Z^{\prime }$, and $\psi$ denotes the set of contradictory relationships for charging scheme set $Z^{\prime }$. For the sake of brevity, these are called the adjacency relationship set and contradiction relationship set, respectively. Let ${ha}_{ij{q}_s,jn{q}_t}$ represent the element of adjacency relationship set $\vartheta$, which denotes the relationship between the charging scheme $q_s$ on road segment $(i,j)$ and the charging scheme $q_t$ on road segment $(j,n)$. Element ${ha}_{ijn{q_{s}q}_t}$ can be expressed as

$${ha}_{ijn{q_{s}q}_t}=\left\{\begin{array}{c}1, if charging sheme q_s of the \\ road sement\left(i,j\right)have adjacency \\ relationshipwith charging sheme q_t of \\ the road segment (j,n)\\ 0, otherwise\end{array}\right.$$

(1)

Let ${hc}_{ij{q}_s{q}_t}$ represent the element of contradictory relationship set $\psi$, which denotes the relationship between the charging scheme $q_s$ on the road segment $(i,j)$ and the charging scheme $k_t$ on the road segment $(i,j)$. Element ${hc}_{ij{q}_s,ij{q}_t}$ can be expressed as

$${hc}_{ij{q}_s{q}_t}=\left\{\begin{array}{c}2, if charging sheme q_s on the \\ road segment\left(i,j\right)have contradictory \\ relationship with charging sheme q_t of\\ the road segment (i,j)\\ 0, otherwise\end{array}\right.$$

(2)

Let matrix $F$ represent the incidence matrix, which can be obtained through the incidence relationship between vertex set $\delta$ and charging scheme set $Z^{\prime }$ and sized by ($\left|Z^{\prime }\right|\times \left|\delta \right|$). Let $f_{ij{q}_s,n}$ represent the element of the incidence matrix. The element $f_{ij{q}_s,n}$ can be expressed as

$$f_{ij{q}_{s}n}=\left\{\begin{array}{c}1, if charging sheme q_s on the road\\ segment \left(i,j\right)have incidence relationship \\ with the vertex n,that means i=n or j=n \\ 0, otherwise\end{array}\right.$$

(3)

The adjacency relationship and contradictory relationship of the hypergraph $G_3$ can be calculated by matrix $F$ as follows:

$$H=F\times F^T-2\times E$$

(4)

where $H$ represents the adjacency–contradictory matrix, including the adjacency relationship and contradictory relationship in the road segment charging scheme set $Z^{\prime }$, and the size is $\left(\right|Z^{\prime }|\times |Z^{\prime }\left|\right)$. $F^T$ represents the transpose of the incidence matrix. $E$ is the identity matrix, and the size is $\left(\right|Z^{\prime }|\times |Z^{\prime }\left|\right)$.

2.3. Model Formulation

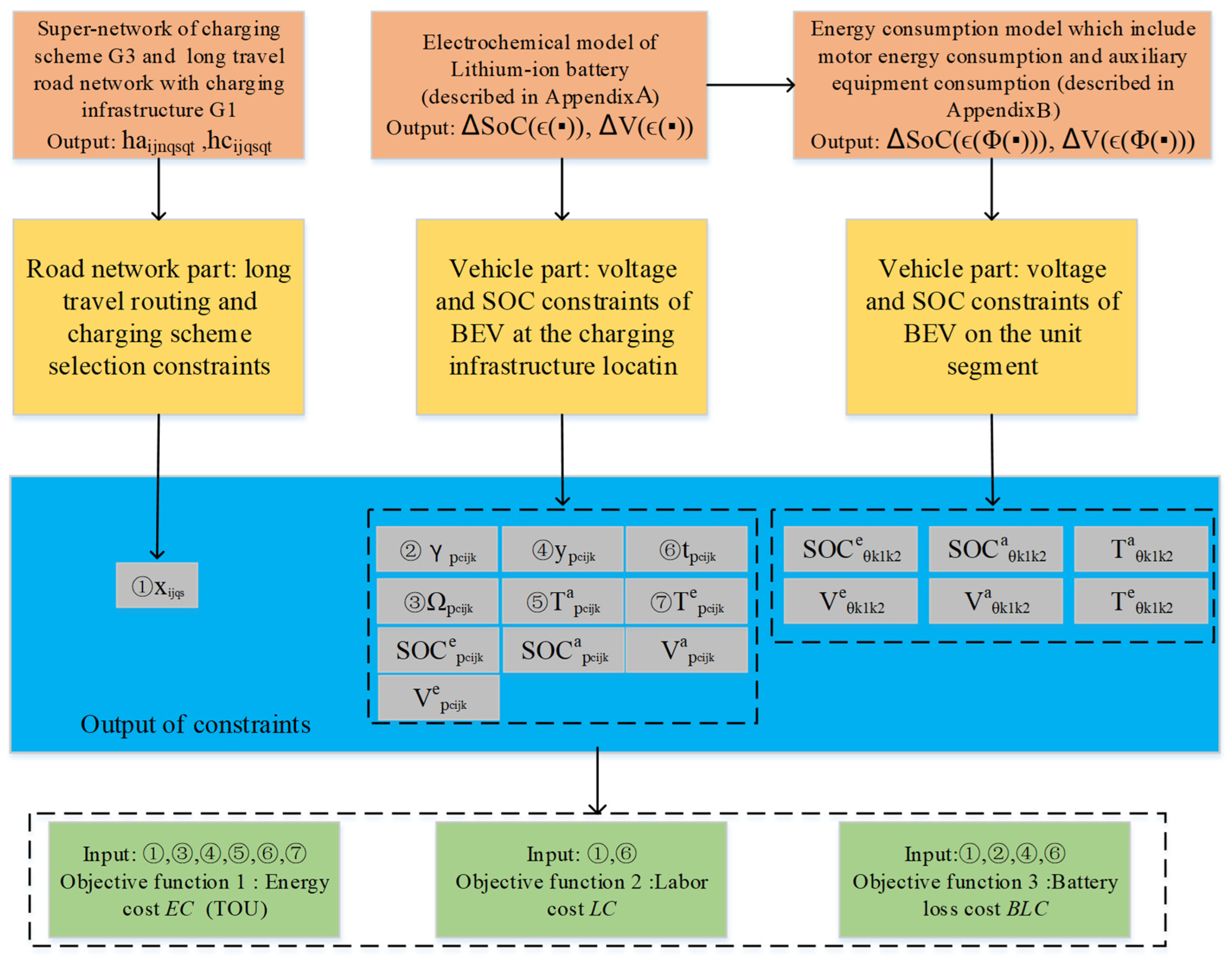
In this subsection, a joint schedule optimization model for long-haul EV driving is developed. A flowchart of the joint scheduling model’s structure is shown in Figure 3.

In the road network part, route continuity should be ensured during long BEV travel, and charging infrastructure should be considered upon driving route planning. Thus, this part’s constraints are described by the super-network of charging scheme $G_3$ and the long-haul road network with charging infrastructure $G_1$. A binary variable $x_{ij{q}_s}$ is introduced to indicate whether the long-haul BEV system adopts charging scheme $q_s\in Z_{ij}^{\prime }$ of road segment $(i,j)\in \epsilon$. $x_{ij{q}_s}$ enables the tracking of each selected road segment in $G_1$ and the corresponding charging scheme. The long-haul driving routing and charging scheme selection constraints are shown below:

$${\sum }_{j,n\in S,q_s\in Z_{oj}^{\prime },q_t\in Z_{jn}^{\prime }}⌊({ha}_{ojn{q_{s}q}_t}+x_{oj{q}_s}\times x_{jn{q}_t})/2⌋=1$$

(5)

$${\sum }_{q_s\in Z_{ij}^{\prime },q_t\in Z_{jn}^{\prime }}⌊({ha}_{ijn{q}_s{q}_t}+x_{ij{q}_s}\times x_{jn{q}_t})/2⌋\le 1$$

(6)

$${\sum }_{i,j\in S,q_s\in Z_{ij}^{\prime },q_t\in Z_{jd}^{\prime }}⌊({ha}_{ijd{q}_s{q}_t}+x_{ij{q}_s}\times x_{jd{q}_t})/2⌋=1$$

(7)

$${\sum }_{q_s\in Z_{ij}^{\prime },q_t\in Z_{ij}^{\prime },q_s\ne q_t}\left({hc}_{ij{q}_s{q}_t}\times x_{ij{q}_s}\times x_{ij{q}_t}\right)=0$$

(8)

$$x_{ij{q}_s}\in \left\{0,1\right\}$$

(9)

Constraints (5)–(7) ensure that the connectivity of the road segment of the BEV long-haul driving route and each road segment have the corresponding charging scheme. Constraint (8) ensures that there is only one charging scheme that can be selected on the road segment. Constraint (9) states that variables $x_{ij{q}_s}$ are binary variables.

Besides satisfying the above route and charging scheme constraints, the joint schedule optimization model needs to also consider the battery voltage and SOC limitations of the BEV in the charging process. To avoid the negative effects over-discharging and over-charging have on battery life, two parameters, ${\overline{SoC}}^{p_c}$ and ${\underset{\_}{SoC}}^{p_c}$, are introduced to set the maximum SOC and minimum SOC for BEV batteries in the charging process, respectively. Due to the relaxation effect, the voltage can be lower than the minimum cut-off voltage or more than the maximum cut-off voltage for a short time, which also affects battery life; two parameters, ${\overline{V}}^{p_c}$ and ${\underset{\_}{V}}^{p_c}$, are introduced to set the maximum battery voltage and minimum battery voltage in the charging process, respectively. The voltage shows nonlinear change during the charging process.

The presence of different charging power values leads to changes in the maximum charging amount of the BEV, with there also being relaxation effects for lithium-ion batteries. The higher the charging power, the lower the maximum BEV charging amount. We assume that every element of charging infrastructure has the same number of charging power modes. Let variable $y_{P_{cijk}}$ represent the current of the charging power mode selected for the charging infrastructure $k\in P_{cij}$ on road segment $(i,j)\in \epsilon$. The set of charging power is $\xi$.

Let $T_{P_{cijk}}^a$ denote the BEV’s time of arrival at the charging infrastructure $k\in P_{cij}$ on road segment $(i,j)\in \epsilon$. Let $t_{P_{cijk}}$ represent the BEV charging duration for the charging infrastructure $k\in P_{cij}$ on road segment $\left(i,j\right)\in \epsilon$. The BEV charging time with the charging infrastructure $k\in P_{cij}$ on road segment $(i,j)\in \epsilon$ can be described by ${\tau }_{P_{cijk}}=[T_{P_{cijk}}^a,T_{P_{cijk}}^a+t_{P_{cijk}}]$. The charging duration is affected by the charging power mode and selected charging infrastructure $z_{ijk}$. If charging infrastructure $k$ is not selected ($z_{ijk}=0$), the charging duration $t_{P_{cijk}}$ of charging infrastructure $k$ is 0. The BEV’s SOC increment at a single charging infrastructure $k\in P_{cij}$ on the road segment $(i,j)\in \epsilon$ can be expressed as

$${\mathsf{{\rm Y}}}_{P_{cijk}}={\int }_{T_{P_{cijk}}^a}^{T_{P_{cijk}}^a+t_{P_{cijk}}}∆SoC\left(ϵ\left(y_{P_{cijk}}\right)\right)dt$$

(10)

The voltage increment of BEV at a single charging infrastructure $k\in P_{cij}$ on the road segment $(i,j)\in \epsilon$ can be expressed as

$${\Lambda }_{P_{cijk}}={\int }_{T_{P_{cijk}}^a}^{T_{P_{cijk}}^a+t_{P_{cijk}}}∆V\left(ϵ\left(y_{P_{cijk}}\right)\right)dt$$

(11)

The changes in voltage and SOC monotonically increase in the charging process, which means that if the voltage and SOC of the BEV battery are reasonable at the time of charging completion, the voltage and SOC of the BEV battery of BEV will remain reasonable at each internal time of the charging process. Let variable ${SoC}_{P_{cijk}}^a$ and ${SoC}_{P_{cijk}}^e$ represent the battery SOC when the BEV arrives at/leaves the charging infrastructure $k\in P_{cij}$ on road segment $(i,j)\in \epsilon$. Let variable $V_{P_{cijk}}^a$ and $V_{P_{cijk}}^e$ represent voltage when the BEV arrives at/leaves the charging infrastructure $k\in P_{cij}$ on road segment $(i,j)\in \epsilon$. The voltage and SOC constraints of the BEV at the charging infrastructure location are as follows:

$${\underset{\_}{V}}^{p_c}\le x_{ij{q}_s}\times V_{P_{cijk}}^a+\left(1-x_{ij{q}_s}\right)\times {\overline{V}}^{p_c}\le {\overline{V}}^{p_c}$$

(12)

$${\underset{\_}{SoC}}^{p_c}\le x_{ij{q}_s}\times {SoC}_{P_{cijk}}^a+\left(1-x_{ij{q}_s}\right)\times {\overline{SoC}}^{p_c}\le {\overline{SoC}}^{p_c}$$

(13)

$${\underset{\_}{V}}^{p_c}\le x_{ij{q}_s}\times V_{P_{cijk}}^e+\left(1-x_{ij{q}_s}\right)\times {\overline{V}}^{p_c}\le {\overline{V}}^{p_c}$$

(14)

$${\underset{\_}{SoC}}^{p_c}\le x_{ij{q}_s}\times {SoC}_{P_{cijk}}^e+\left(1-x_{ij{q}_s}\right)\times {\overline{SoC}}^{p_c}\le {\overline{SoC}}^{p_c}$$

(15)

$$x_{ij{q}_s}\times V_{P_{cijk}}^a\le x_{ij{q}_s}\times V_{P_{cijk}}^e$$

(16)

$$x_{ij{q}_s}\times {SoC}_{P_{cijk}}^a\le x_{ij{q}_s}\times {SoC}_{P_{cijk}}^e$$

(17)

$${SoC}_{P_{cijk}}^e={SoC}_{P_{cijk}}^a+x_{ij{q}_s}\times {\mathsf{{\rm Y}}}_{P_{cijk}}$$

(18)

$$V_{P_{cijk}}^e=V_{P_{cijk}}^a+x_{ij{q}_s}\times {\Lambda }_{P_{cijk}}$$

(19)

$$y_{P_{cijk}}\in \xi$$

(20)

Constraints (12) and (13) guarantee that when the BEV arrives at charging infrastructure $k\in P_{cij}$ on road segment $(i,j)\in \epsilon$, the corresponding battery voltage $V_{P_{cijk}}^a$ and SOC ${SoC}_{P_{cijk}}^a$ are not lower than the minimum voltage limit and minimum SOC limit, respectively. Constraints (14) and (15) ensure that after the BEV finishes charging at charging infrastructure $k\in P_{cij}$ on road segment $(i,j)\in \epsilon$, the corresponding voltage $V_{P_{cijk}}^e$ and SOC ${SoC}_{P_{cijk}}^e$ are not higher than the maximum voltage limit and maximum SOC limit, respectively. Constraints (16) and (17) require that after the BEV has finished charging at charging infrastructure $k\in P_{cij}$ on road segment $(i,j)\in \epsilon$, the corresponding voltage $V_{P_{cijk}}^e$ and SOC ${SoC}_{P_{cijk}}^e$ cannot be lower than the voltage $V_{P_{cijk}}^a$ and SOC ${SoC}_{P_{cijk}}^a$ for when the BEV arrives at the charging infrastructure site $k\in P_{cij}$ on road segment $(i,j)\in \epsilon$. Constraints (18)-(19) ensure the relationship regarding the cumulative voltage increase and cumulative SOC increase in the charging process. Constraint (20) states the range of variable $y_{P_{cijk}}$.

In the driving process, the joint schedule optimization model also considers the BEV’s battery voltage and SOC limitations, also considering a relaxation effect to avoid the negative effects of over-discharging and over-charging. It assumes that the speed of each unit segment is constant, which means that the BEV runs at a uniform speed on each unit segment. The BEV is fully charged when it leaves the departure vertex. Let variable ${\underset{\_}{V}}^{\theta }$ and ${\overline{V}}^{\theta }$ denote the minimum and maximum voltage of the BEV’s battery in the driving process. Let variable ${\underset{\_}{SoC}}^{\theta }$ and ${\overline{SoC}}^{\theta }$ denote the minimum and maximum SOC of the BEV’s battery in the driving process. Let variable $\overline{P}$ denote the maximal output power of the BEV’s battery.

To simplify the expression, ${\theta }_{k1k2}$ is used to represent unit segments ${\theta }_{ij}$, ${\theta }_{i{P}_{cijk1}}$, ${\theta }_{P_{cijk1}{P}_{cijk2}}$, and ${\theta }_{P_{cijk2}j}$. And $k1$ and $k2$ are adjacent charging infrastructure on road segment $\left(i,j\right)\in \epsilon$. Let $t_{{\theta }_{k1k2}}^a$ represent the time at which the BEV departed charging infrastructure $k1$ on unit segment ${\theta }_{k1k2}$ in the driving process. Let $t_{{\theta }_{k1k2}}^e$ represent the time at which the BEV arrived at charging infrastructure $k2$ on unit segment ${\theta }_{k1k2}$ in the driving process. $t_{{\theta }_{k1k2}}^e$ can be expressed as $t_{{\theta }_{k1k2}}^a+L_{{\theta }_{k1k2}}/v_{{\theta }_{k1k2}}$. The BEV’s SOC variation during the driving process on a single unit segment, ${\theta }_{k1k2}$, can be expressed as

$${\mathsf{\Theta }}_{k1k2}={\int }_{t_{{\theta }_{k1k2}}^a}^{t_{{\theta }_{k1k2}}^e}∆SoC\left(ϵ\left(\mathit{\Phi }\left({\chi }_{{\theta }_{k1k2}}\right)\right)\right)dt$$

(21)

The BEV’s voltage variation during the driving process on a single unit segment, ${\theta }_{k1k2}$, can be expressed as

$${\mathsf{\Psi }}_{k1k2}={\int }_{t_{{\theta }_{k1k2}}^a}^{t_{{\theta }_{k1k2}}^e}∆V\left(ϵ\left(\mathit{\Phi }\left({\chi }_{{\theta }_{k1k2}}\right)\right)\right)dt$$

(22)

Let variable $V_{{\theta }_{k1k2}}^a$ denote the battery voltage of the BEV when it arrives at the unit segment ${\theta }_{k1k2}\in \theta$ on road segment $\left(i,j\right)\in \epsilon$. Let variable ${SoC}_{{\theta }_{k1k2}}^a$ denote the BEV battery’s SOC for when the BEV arrives at unit segment ${\theta }_{k1k2}\in \theta$ on road segment $\left(i,j\right)\in \epsilon$. Let variable $V_{{\theta }_{k1k2}}^e$ denote the BEV battery’s voltage for when the BEV leaves unit segment ${\theta }_{k1k2}\in \theta$ on road segment $\left(i,j\right)\in \epsilon$.

Let variable ${SoC}_{{\theta }_{k1k2}}^e$ denote the BEV battery’s SOC for when the BEV leaves unit segment ${\theta }_{{\theta }_{k1k2}}\in \theta$ on road segment $\left(i,j\right)\in \epsilon$. Let parameter $\overline{P}$ represent the maximum BEV driving power. The BEV constraints’ voltage and SOC regarding the unit segment constraints are as follows:

$$V_{P_{coj1}}^a=x_{oj{q}_s}\times {\overline{V}}^{\theta }$$

(23)

$${SoC}_{P_{coj1}}^a=x_{oj{q}_s}\times {\overline{SoC}}^{\theta }$$

(24)

$${\underset{\_}{V}}^{\theta }\le x_{ij{q}_s}\times V_{{\theta }_{k1k2}}^a+\left(1-x_{ij{q}_s}\right)\times {\overline{V}}^{\theta }\le {\overline{V}}^{\theta }$$

(25)

$${\underset{\_}{SoC}}^{\theta }\le x_{ij{q}_s}\times {SoC}_{{\theta }_{k1k2}}^a+\left(1-x_{ij{q}_s}\right)\times {\overline{SoC}}^{\theta }\le {\overline{SoC}}^{\theta }$$

(26)

$${\underset{\_}{V}}^{\theta }\le x_{ij{q}_s}\times V_{{\theta }_{k1k2}}^e+\left(1-x_{ij{q}_s}\right)\times {\overline{V}}^{\theta }\le {\overline{V}}^{\theta }$$

(27)

$${\underset{\_}{SoC}}^{\theta }\le x_{ij{q}_s}\times {SoC}_{{\theta }_{k1k2}}^e+\left(1-x_{ij{q}_s}\right)\times {\overline{SoC}}^{\theta }\le {\overline{SoC}}^{\theta }$$

(28)

$$V_{{\theta }_{k1k2}}^e=V_{{\theta }_{k1k2}}^a-x_{ij{q}_s}\times {\Psi }_{k1k2}$$

(29)

$${SoC}_{{\theta }_{k1k2}}^e={SoC}_{{\theta }_{k1k2}}^a-x_{ij{q}_s}\times {\Theta }_{k1k2}$$

(30)

$$x_{ij{q}_s}\times V_{{\theta }_{k1k2}}^a\ge x_{ij{q}_s}\times V_{{\theta }_{k1k2}}^e$$

(31)

$$x_{ij{q}_s}\times {SoC}_{{\theta }_{k1k2}}^a \ge x_{ij{q}_s}\times {SoC}_{{\theta }_{k1k2}}^e$$

(32)

$$0\le {\displaystyle \frac{v_{{\theta }_{k1k2}}}{\eta }}\left(mgfcos({\gamma }_{{\theta }_{k1k2}})+mgsin({\gamma }_{{\theta }_{k1k2}})+{\displaystyle \frac{C_{D}A}{21.25}}{v_{{\theta }_{k1k2}}}^2\right)\le \overline{P}$$

(33)

Constraints (23) and (24) ensure that the BEV has a fully charged battery before beginning long-haul travel from the departure vertex. Constraints (25)–(28) ensure that, when the BEV arrives at/leaves charging infrastructure location $k1,k2\in P_{cij}$ on unit segment ${\theta }_{k1k2}$ of road segment $\left(i,j\right)\in \epsilon$, the corresponding voltage $V_{{\theta }_{k1k2}}^a$/$V_{{\theta }_{k1k2}}^e$ and SOC ${SoC}_{{\theta }_{k1k2}}^a$/${SoC}_{{\theta }_{k1k2}}^e$ should be in the range of the voltage limit and SOC limit, respectively. Constraints (29)–(30) ensure the relationship of the cumulative voltage reduction and cumulative SOC reduction in the driving process. Constraints (31) and (32) require that, after the BEV leaves the charging point at charging infrastructure location $k2\in P_{cij}$ on unit segment ${\theta }_{k1k2}$ of road segment $\left(i,j\right)\in \epsilon$, the corresponding voltage $V_{{\theta }_{k1k2}}^e$ and SOC ${SoC}_{{\theta }_{k1k2}}^e$ cannot be higher than the voltage $V_{{\theta }_{k1k2}}^a$ and SOC ${SoC}_{{\theta }_{k1k2}}^a$ for when the BEV arrived at charging infrastructure location $k2\in P_{cij}$ on unit segment ${\theta }_{k1k2}$ of road segment $\left(i,j\right)\in \epsilon$. Constraint (33) guarantees the BEV power does not exceed a certain range.

The objective function of the proposed optimization model minimizes the total cost, which consists of two parts: battery loss cost and transportation cost. The transportation cost includes energy cost and labor cost, considering the time-of-use (TOU) electricity price.

Considering the TOU pricing strategy, let ${\mu }_l$ and ${\mu }_h$ represent the off-peak-hour and on-peak-hour electricity rate, respectively. Let $H$ denote 24 h within a day; $H=\{1,\dots ,24\}$. Let $H_l$ and $H_h$ represent the off-peak hour set and on-peak hour set, respectively. The BEV charging volume at a single charging infrastructure point can be expressed as

$${\Omega }_{P_{cijk}}={\int }_0^{t_{P_{cijk}}}{\displaystyle \frac{y_{P_{cijk}}\times V\left(ϵ\left(y_{P_{cijk}}\right)\right)}{1000}}dt$$

(34)

where $y_{ij{p}_c}\times V\left(ϵ\left(y_{P_{cijk}}\right)\right)$ represents charging power. The energy cost in different electricity price time periods can be expressed as follows:

$$\left\{\begin{array}{c}{EC}_1={\mu }_l\left(\sum _{i,j\in S,q_s\in Z_{ij}^{\prime },k\in P_{cij}}{x}_{ij{q}_s}\times {\Omega }_{P_{cijk}}\right),{\tau }_{P_{cijk}}\in H_l\\ {EC}_2={\mu }_h\left(\sum _{i,j\in S,q_s\in Z_{ij}^{\prime },k\in P_{cij}}{x}_{ij{q}_s}\times {\Omega }_{P_{cijk}}\right),{\tau }_{P_{cijk}}\in H_h\end{array}\right.$$

(35)

The energy cost EC can be calculated as

$$EC={EC}_1+{EC}_2$$

(36)

Let ${\pi }_c$ denote labor cost per hour. The labor cost $LC$ can be calculated as

$$LC={\displaystyle \frac{{\pi }_c}{3600}}\times \left({\sum }_{i,j\in S,q_s\in Z_{ij}^{\prime },k\in P_{cij}}{x}_{ij{q}_s}\times t_{P_{cijk}}\right)$$

(37)

The battery loss cost is calculated by the reduced battery life caused by the number of battery discharge cycles. Let ${\alpha }_b$ denote the average battery loss cost under discharge for one cycle. The battery loss cost $BLC$ can be calculated as

$$BLC={\alpha }_b\times \left({\sum }_{i,j\in S,q_s\in Z_{ij}^{\prime },k\in P_{cij}}{x}_{ij{q}_s}\times {\displaystyle \frac{{\mathsf{{\rm Y}}}_{P_{cijk}}}{{\overline{SoC}}^{p_c}-{\underset{\_}{SoC}}^{p_c}}}\right)$$

(38)

With the above definitions and constraints, the below joint schedule optimization model for long-haul travel is formulated as a mathematical optimization model:

$$min.EC+LC+BLC$$

(39)

s.t. constraints (5)–(9), (12)–(20), and (23)–(33) are met.

3. Solution Algorithm

As formulated above, the joint schedule optimization model for long-haul travel is a mixed-integer nonlinear program with a partial differential function which is difficult to solve. In this section, an artificial ant colony algorithm-based approach is proposed to solve the joint schedule optimization model for long-haul travel. The solution procedure includes two modules: (1) an outer module that adopts the artificial ant colony algorithm and adjacency–contradiction strategy to determine the charging scheme of the road segment (i.e., the route and the charging infrastructure) and (2) an inner module that determines the charging power mode at the selected charging infrastructure location based on the charging scheme of the road segment from the outer problem. In the following subsections, detailed descriptions of the outer module and inner module are provided.

3.1. Inner Problem Module

With a given long-haul travel charging scheme, based on road segment scheduling (i.e., the solution of the outer problem), the inner problem aims to optimize the charging power mode at the charging infrastructure location so that the energy cost, labor cost, and battery loss cost can be minimized. Let $x_{ij{q}_s}^{\ast }$ and denote the solutions of $x_{ij{q}_s}$ in the outer problem module. The purpose of considering charging scheme decision-making (i.e., $x_{ij{q}_s}$) in the outer problem is to improve the efficiency of the ant colony algorithm-based solution procedure. All the road segment charging schemes are binary variables. By putting them in the outer problem, the inner problem is guaranteed to be a mixed-integer nonlinear program that can easily be made optimal using a simulated annealing algorithm (SA). The optimal charging power mode at the corresponding charging infrastructure location can be obtained by the following sub-model, which is the charging power mode model ($\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{M}$):

$$\left(\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{M}\right):\mathrm{Min}EC(y_{id{p}_c},x_{ij{q}_s}^{\ast })+LC(x_{ij{q}_s}^{\ast })+BLC(y_{id{p}_c},x_{ij{q}_s}^{\ast })$$

(40)

The CPMM is constrained by (12)–(20). As formulated above, the $\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{M}$ is a trackable-integer nonlinear program. The optimal solution of the $\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{M}$ is used in the outer module to calculate the fitness value.

3.2. Outer Problem Module

The outer problem module adopts an improved ant colony algorithm with an adjacency–contradiction strategy to deal with long-haul travel route optimization travel and charging infrastructure scheduling in the joint schedule optimization model for long-haul travel. This improved ant colony algorithm (IACO) includes heuristic approaches that imitate nature’s natural selection process. The input data of the outer problem module includes a multilateral charging scheme network, a charging scheme super-network, and road information under the unit segment. In the driving process, the electrochemical model and energy consumption model are adopted in the outer problem module. In the following subsection, firstly, we will describe the process for generating a population which can ensure solution feasibility. Then, the fitness value (i.e., the energy cost, labor cost, and BEV battery loss cost) of the population is evaluated. Finally, the article’s proposed ant colony algorithm optimization stage is described, including pheromone update operations, the state transition operation, and the termination condition.

The population generation part encompasses solution vector expression and the process of generating feasible solutions. A single list is adopted to express the solution vector, which can fully describe the choice of road segment charging scheme. The process of generating feasible solutions needs to satisfy long-haul travel routing and charging scheme selection constraints in view of the road network and the BEV’s voltage and SOC constraints on the unit segment. The variable pertaining to road segment charging scheme decisions, $x=\left\{x_{ij{q}_s}\right|i,j\in S,\left(i,j\right)\in \epsilon ,q_s\in Z_{ij}^{\prime }$}, has grouping features, which can be represented by binary encoding. The charging scheme solution can simultaneously represent the long travel route and the selected charging infrastructure $\mathrm{z}=\left\{z_{ijk}\right|i,j\in S,(i,j)\in \epsilon ,k\in P_{cij}\}$.

An adjacent–contradiction strategy-based generation method is adopted to deal with long-haul driving routing and the charging scheme selection constraints. The solution generation process involves three auxiliary sets, including a selected set, an alternative set, and a tabu set. The selected set records all road segment charging schemes that have been selected. All road segment charging schemes that meet constraints (5)–(9) are put into the alternative set. The tabu set includes all the road segment charging schemes in the selected set and those that violate the requirements of constraints (5)–(9). The process of this specific adjacent–contradiction strategy-based generation method is shown in Algorithm 1.

Algorithm 1 Adjacent–contradiction strategy-based generation method
Input: the incidence matrix F of charging scheme network G2 departure vertex o, and terminal vertex d Output: the select set
Step 1:	Calculate the charging scheme adjacent–contradiction matrix of road segment by $H=F\times F^T-2\times E$
Step 2:	The adjacency–contradiction matrix H is divided into adjacency matrix Ha and contradiction matrix Hc, according to Section 2.2
Step 3:	Update the alternative set, according to the incidence matrix F and departure vertex o
Step 4:	Randomly select road segment charging scheme in the alternative set, according to the pheromone matrix and state transition strategy and put it to the selected set
Step 5:	Update the alternative set, according adjacency matrix Ha and the selected set
Step 6:	The charging scheme of road segment that conflicts with the tabu set in the alternative set is eliminated, and update the alternative set
Step 7:	In the alternative set, screen out the charging schemes of road segment that violation of power constraint requirements (30) and update the alternative set
Step 8:	Randomly select the charging scheme of road segment in the alternative set, according to the pheromone matrix and state transition strategy and put it to the selected set
Step 9:	Put the charging scheme of road segment that in the alternative set into the tabu set and put the charging scheme of road segment that have the contradiction relationship into the tabu set
Step 10:	Repeat steps 5–9 until the charging scheme of road segment is associated with the terminal vertex d

Constraints (23)–(33), pertaining to the BEV’s voltage and SOC on the unit segment, are adopted to check the feasibility of the solution vector (road segment charging scheme selected). The selection of charging power mode can influence the feasibility of the solution vector, and this effect, for high charging power, leads to a lower maximum SOC. Thus, maximum charging power mode is adopted to check the feasibility of the solution vector, and this mode can ensure all charging power modes are feasible. If the solution vector violates constraints (23)–(33) on the unit segment, the solution vector is regenerated until they are satisfied.

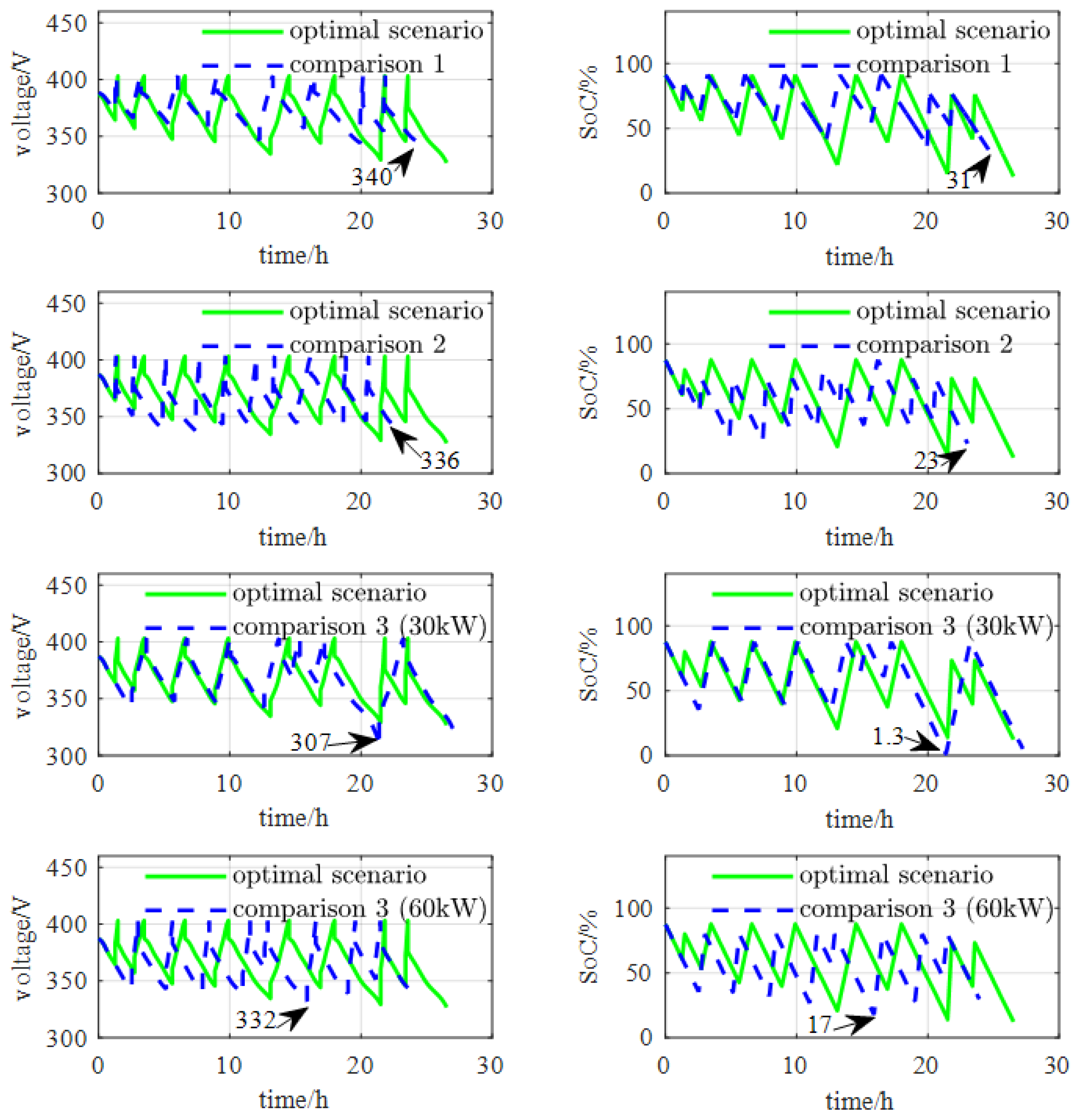
Fitness evaluation is used to judge the quality of solution vectors. Let $y_{P_{cijk}}^{\ast }$ denote the optimal charging power mode for the solution, which can be obtained by the charging power mode model in the inner problem module. According to the charging scheme solution of road segments $x_{ij{q}_s}^{\ast }$ and ${\tilde{x}}_{oj{q}_{s}id{q}_t}^{\ast }$ and the optimal charging power mode solution $y_{P_{cijk}}^{\ast }$, the fitness value can be evaluated. The fitness value can be obtained via the joint schedule optimization model for long-haul travel in the outer problem module. The fitness value calculation formula is $EC+LC+BLC$.

In the process of optimization, there are two types of operations, namely the pheromone update operation type and the state transition operation type. An appropriate strategy can decrease the likelihood of falling into local optimality. The pheromone update operations have two parts, including pheromone volatilization and pheromone increase. Pheromone volatilization is a group operation, in which the pheromones in all locations are reduced by the same percentage to increase the difference between superior and inferior solutions. The pheromone increase occurred in every path the ants took. The paths that match the fitness values will experience larger pheromone increments. The formulation for the pheromone update operation is as follows:

$$\left\{\begin{array}{c}{\tau }_{ij}\left(t+1\right)=\left(1-\rho \right)\times {\tau }_{ij}\left(t\right)+{\sum }_{k=1}^m∆{\tau }_{ij}^k\left(t\right)\\ ∆{\tau }_{ij}^k\left(t\right)=Q/L_k\left(t\right)\end{array}\right.$$

(41)

where ${\tau }_{ij}\left(t+1\right)$ represents the pheromone content in the $\left(t+1\right)$ generation at position $(i,j)$, $\rho$ represents the volatilization coefficient, $m$ represents the maximum number of ants, and $∆{\tau }_{ij}^k\left(t\right)$ represents the pheromone content for ant $k$ at position $(i,j)$ in the $t$ generation. The state transition operation is critical, as it affects the probability of each alternate road segment charging scheme being selected. Thus, in this paper, the roulette selection strategy is adopted, and the correspondence formulation is as follows:

$$P_{ij}^k=\left\{\begin{array}{cc}{\displaystyle \frac{{\tau }_{ij}^{\alpha }(t)\times {\eta }_{ij}^{\beta }(t)}{{\sum }_{s\in {\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{t}}_k}{\tau }_{ij}^{\alpha }(t)\times {\eta }_{ij}^{\beta }(t)}}& j\in {\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{t}}_k\hfill \\ 0& otherwise\hfill \end{array}\right.$$

(42)

where $P_{ij}^k$ represents the probability from the road segment charging scheme $i$ to road segment charging scheme $j$ for ant $k$.

In this paper, the maximum iteration count is selected as the termination rule.

4. Numerical Examples

In this section, in order to verify the developed methodology and solution algorithm, numerical examples are used based on a real-world highway network across five provinces in China, namely Heilongjiang province, Jilin province, Hebei province, Liaoning province, and Shandong province. This section introduces the model parameters and road characteristics and presents a discussion of computational results.

4.1. Model Parameters and Road Characteristics

A highway road network spanning five provinces is considered, as part of the charging infrastructure in China, as shown in Figure 4, which presents the road characteristics of the highway network, indicating that there are 109 vertexes, 183 road segments, and 263 elements of charging infrastructure. Temperature variations are also taken into account by the long-haul driving system, as shown in Figure 5, including spring temperatures ranging from −7.8 °C to 11.2 °C, summer temperatures ranging from 15.3 °C to 29.2 °C, autumn temperatures ranging from 9.2 °C to 23.3 °C, and winter temperatures ranging from −23.2 °C to 0.7 °C. The information for each unit road segment, including the road length, road mean slope road level, and base speed, was obtained from the Baidu map website.

One type of BEV is considered in this numerical study; it has a battery capacity of 60 kWh. We assume that the temperature of the battery pack does not change with the ambient temperature and that the excess electricity consumption is affected by the positive temperature coefficient (PTC) power to keep the temperature in the compartment at a constant value of 25 °C. The PTC power is 9.2 kW. Three charging mode types are considered in this numerical study: one with charging power of 30 kW, one with charging power of 60 kW, and one with charging power of 120 kW. The charging mode with a charging power of 30 kW can guarantee that the SOC is greater than 90% when the BEV has finished charging at the charging infrastructure location. However, it takes about 2 h to finish charging from 10% SOC to 90% SOC. The charging modes with a charging power of 60 kW and a charging power of 120 kW can guarantee SOC values of 83% and 76% and take one hour and half an hour, respectively. The price of electricity usually fluctuates at different times of the day under the TOU scheme; charging the BEV at a time where the price of electricity is low leads to greater cost savings.

Based on the existing TOU policy in China, the peak hours are from 9:00 a.m. to 11:30 a.m. and from 3.30 p.m. to 9:00 p.m.; flat hours are from 6:00 a.m. to 9:00 a.m., from 11:30 a.m. to 12:30 a.m., from 1:30 a.m. to 3:30 a.m., and from 9:00 p.m. to 11:00 p.m.; and valley hours are from 0:00 a.m. to 6:00 a.m., from 12:30 a.m. to 1:30 p.m., and from 11:00 p.m. to 12:00 p.m. The peak hour electricity rate is (CHN) 0.9/kwh, whereas the flat hour electricity price and valley hour electricity price are (CHN) 0.6/kwh and (CHN) 0.3/kwh. The charging provider charges a labor service fee of (CHN) 0.1/kwh.

4.2. Model Results and Analysis

A two-layer structure is used to solve the problem, where the outer layer adopts the improved ant colony algorithm, and the inner layer adopts the simulated annealing (SA) algorithm. The ant colony algorithm-based solution procedure is implemented with the following parameters: $po{p}_{size}=30, maxgeneratio{n}_{ant}=200, rou=0.2, Q=10$. The simulated annealing (SA) algorithm solution procedure is implemented with the following parameters: $T_{max}=1000, T_{min}={10}^{-2}, LL=5, q=0.8$. The parameter selection analysis can be found in the Supplementary Materials. It took about five minutes to complete the solution procedure. Figure 6 shows the convergence performance of the proposed two-layer algorithm in different seasons. Figure 6a describes the cost ranges, along with the number of iterations, of the two-layer algorithm in different seasons. Figure 6b shows the two-layer algorithm’s distribution of costs over five runs in different seasons.

The best obtained solutions as regards average temperature in different seasons are reported in

Table 1. The proposed model’s results across the four seasons.

Item		Value (Spring)	Value (Summer)	Value (Autumn)	Value (Winter)
Total cost of travel		CNY 357.18	CNY 303.75	CNY 335.62	CNY 442.55
Charging costs	Energy costs (TOU)	CNY 224.63	CNY 193.62	CNY 211.10	CNY 273.65
	Labor costs	CNY 45.41	CNY 38.22	CNY 42.61	CNY 57.75
Battery loss costs		CNY 87.15	CNY 71.92	CNY 81.91	CNY 111.14
The number of used charging infrastructure elements		7	7	6	8
Total time of travel		25.39 h	22.86 h	25.25 h	26.54 h
Total Charging time		7.11 h	3.73 h	6.91 h	7.93 h
Mean charging time of each selected charging infrastructure element		1.01 h	0.51 h	1.15 h	0.99 h
Mean charging power of each selected charging infrastructure element		33.84 kW	53.58 kW	32.67 kW	38.67 kW

. In the different seasons, the cost of solving is lowest in summer, while it is highest in winter. The cost of solving is similar in spring and autumn. We also compared individual changes in indicators in summer and winter. In the winter, the total cost of travel increases by 45.70%; the battery loss costs increase by 54.53%; the amount of charging infrastructure used increases by 14.29%; the total travel time increases by 16.10%; the charging time increases by 112.60%; the mean charging time of each selected element of charging infrastructure increases by 94.12%; and the mean charging power of each selected element of charging infrastructure is reduced by 27.83%.

From Figure 7, we can observe each road segment that the BEV goes through and the charging mode correspond to the selected charging infrastructure. The change in voltage embodies the relaxation effect at the boundary position between the charging process and driving process, which elucidates the rapid change in voltage when the BEV starts and finishes charging. Figure 7 also presents important information such as the BEV voltage, which is within the predefined 288–403.2 V range, while the SOC is within the predefined 0–100% range. This demonstrates that this solution for route planning, charging mode selection, and charging infrastructure selection can ensure feasible operation for long-haul travel.

Three algorithms were employed to verify the performance of the proposed algorithm, including an improved ant colony optimization algorithm (IACO), a simulated annealing algorithm (SA), and a particle swarm optimization algorithm (PSO). As shown in

Table 2. Comparison of algorithmic performance across all four seasons.

	Spring (CNY)	Summer (CNY)	Autumn (CNY)	Winter (CNY)
IACO-SA	357.18	303.75	335.62	442.55
IACO	379.88	344.25	353.36	479.54
SA	394.24	374.23	388.94	493.81
PSO	364.23	353.84	343.60	483.25

, during the 10 runs, the proposed algorithm had the lowest average total cost in all cases across all four seasons. The average total cost of the IACO algorithm ranked second, and the average total cost of the SA was the worst, which means that the SA is more prone to getting stuck in local optimal solutions.

4.3. Comparison Model 1: Long-Haul Driving Without Regard for Temperature (PTC) Strategy in Winter

Most previous studies focus on the BEV route planning problem without considering ambient temperature change. They usually assume that BEVs consume the same rates of power at different temperatures, not considering the positive temperature coefficient (PTC) power consumption rate, which is necessary to consider in low-temperature environments. In this section, the results of a model that does not consider winter temperatures and those of the model presented in this paper are compared.

When the BEV does not consider temperature change, the PTC power consumption rate does not work as it does in the proposed model. We assumed that the BEV route, element of charging infrastructure selected, and charging mode selected of comparison model 1 are the same as the model of this paper. The joint schedule optimization model for long-haul travel was solved. The results of comparison model 1 under the conditions of long-haul BEV travel without considering winter PTC are shown in

Table 3. Winter results of comparison model 1, comparison model 2, and comparison model 3.

Item	The Model of This Paper	Comparison Model 1	Comparison Model 2	Comparison Model 3 (30 kW)	Comparison Model 3 (60 kW)
Total cost of travel	CNY 442.55	CNY 366.70	CNY 525.81	CNY 444.11	CNY 543.26
Energy costs (TOU)	CNY 273.65	CNY 248.15	CNY 355.44	CNY 286.05	CNY 372.93
Labor costs	CNY 57.75	CNY 41.09	CNY 59.04	CNY 53.64	CNY 58.01
Battery loss costs	CNY 111.14	CNY 77.46	CNY 111.33	CNY 104.41	CNY 112.31
The number of used charging infrastructure elements	8	8	10	7	8
Total time of travel	26.54 h	24.82 h	23.04 h	27.24 h	23.93 h
Charging time	7.93 h	5.64 h	3.99 h	9.58 h	5.16 h
Mean charging time of on-route charging infrastructure elements	0.99 h	0.71 h	0.40 h	1.37 h	0.64 h
Mean charging power of on-route charging infrastructure elements	38.67 kW	38.06 kW	77.88 kW	30 kW	60 kW

.

Table 3 indicates that when the BEV is restricted, i.e., not considering the temperature in winter, the total cost change is 17.14%, and the change in battery loss cost is more than 30%. Furthermore, compared to the proposed model, the application of comparison model 1 results in a shorter total travel time, with a difference of 6.48%. This is because comparison model 1 misestimates the charging time at the charging infrastructure location.

Figure 8 details the BEV’s voltage and SOC changes obtained using the proposed model and comparison model 1. It can be observed that the voltage and SOC comparison model 1 are higher than the voltage and SOC of the proposed model during long-haul travel. The travel time of comparison model 1 is shorter than that of the proposed model. Thus, long-haul travel without considering temperature (PTC) in winter will cause huge errors, including voltage error, SOC error, and total travel time error.

4.4. Comparison Model 2: Long-Haul Driving with the Shortest Journey Time Strategy in Winter

Total travel time is a key point of focus in the process of long-haul driving. In some cases, a shorter total travel times result in more cost benefits. To compare the optimal total cost and shortest total travel time, as detailed in this subsection, the parameter of winter temperature was adopted, and the joint schedule optimization model for long-haul travel was resolved with the objective of achieving the shortest total travel time. We assumed that the departure vertex, terminal vertex, road network structure, and vehicle information were the same as the model of this paper. We conducted simulations to calculate values such as the shortest total time, economic cost, BEV voltage, and BEV SOC in the process of long-haul travel. Figure 8 details the changes in voltage and SOC experienced by the BEV under the application of the proposed model and comparison model 2.

Comparison model 2’s simulation results are shown in Figure 8, and a comparison of these results with the proposed model’s results is presented in Table 3. The total travel time of comparison model 2 is 23.04 h under the shortest travel time assumption, which is 13.19% lower than the proposed model. The main reason for the decrease in total travel time is the increase in the BEV charging power. The mean charging power of on-route charging infrastructure for comparison model 2 is 77.88 kW, which is 101.40% higher than that for the model of this paper. The number of used charging infrastructure elements for comparison model 2 is 10, which is 25% higher than the model of this paper. The charging time of comparison model 2 is 3.99 h, which is 49.68% lower than the model of this paper. The total travel cost for comparison model 2 is CNY 525.81, which is 18.81% higher than that for the proposed model. The comparison results demonstrate that the proposed model brings economic benefits. Using the joint schedule optimization model for long-haul travel, prioritizing total cost, can result in significant savings in terms of the total cost of travel and energy cost, with only a small amount of total travel time being lost.

4.5. Comparison Model 3: Long-Haul Driving with Fixed Charging Power Mode Strategy in Winter

In most studies, a fixed charge power mode strategy is adopted, which results in inflexible long-haul travel scheduling optimization. Thus, we also compared a model with a fixed charging power mode and the model of this paper to analyze the proposed model’s solution capabilities more effectively. Our simulation assumed that the departure vertex, terminal vertex, road network structure, and vehicle information were the same as those for the model of this paper; however, the comparative model had a fixed charging power of 30 kW/60 kW, which meant that the maximum charge time at any charging infrastructure location was 2 h/1 h, and the maximum SOC was 91.92%/83% when the BEV finished charging at the charging infrastructure location. We applied the joint schedule optimization model for long-haul travel and compared it with a model with fixed charging power mode to obtain the optimal route, charging scheme, and charging mode. This subsection compares the results of each model. Figure 8 details the changes in the BEV’s voltage and SOC when using the proposed model and the comparison model 3. More results are shown in Table 3. With fixed charging powers of 30 kW and 60 kW, the total travel costs are CNY 444.11 and CNY 543.26, respectively, values that are 0.35% and 22.85% higher than the results for this paper’s model. With a fixed charge power of 30 kW, the BEV’s driving range increases, resulting in the need for fewer charging stops. The number of used elements of charging infrastructure for a fixed charge power of 30 kW is 7, 12.50% lower than that for the model of this paper. Nevertheless, the total travel and charging time of the model with a fixed charge power of 30 kW are higher than the model of this paper. With fixed charging powers of 30 kW and 60 kW, the total travel time values are 27.24 h and 23.92 h, respectively, which are 2.64% higher and 9.87% lower than the model of this paper, respectively. The charging time of the model with a fixed charge power of 30 kW is 9.58 h, which is 20.81% higher than the model of this paper. The results of this comparison show that, at a fixed charge power of 30 kW, the route, charging infrastructure selection, and charging mode selection capabilities of the proposed model yield higher cost benefits and lessen the total travel time, leading to a better travel experience. At a fixed charge power of 60 kW, the charging time is shortened, but at the cost of an increase in total expenses.

5. Conclusions

In this paper, we proposed a model framework for solving the route planning and charging problem for electric vehicles during long-haul driving in variable ambient temperatures, using a two-layer IACO-SA based on an adjacency–contradiction strategy to solve the model. The model minimizes the total cost, including charging cost and battery depletion cost. The additional energy consumption of electric vehicle auxiliary equipment (PTC) in low-temperature environments was also taken into account, and an electrochemical model was used to track the battery voltage and SOC of the electric vehicle in different ambient temperatures, improving model accuracy.

After applying the model and the solution algorithm to a real road network spanning five provinces in China and comparing it with three other models, we can draw the following conclusions:

(1)

The total cost and total travel time errors of the model without considering auxiliary equipment (PTC) energy consumption are 17% and 6% better, respectively. Considering the auxiliary equipment (PTC) energy consumption can lead to more accurate estimates of the future energy consumption of EVs, thus rationalizing the charging schedule.

(2)

We compared the results of the proposed model for summer and winter. Using PTC auxiliary equipment in winter results in a 45% increase in total costs, a 54% increase in battery loss costs, a 41% increase in charging costs, and a 38% decrease in average charging power. This means that, in low-temperature conditions, the cost of PTC auxiliary equipment, battery loss, and charging increase significantly, and to ensure the correct electric voltages, a lower charging power mode is needed at the charging infrastructure location to achieve a greater maximum charging capacity and ensure the energy supply for PTC at low temperatures. Moreover, charging the electric vehicle more frequently can accelerate battery aging. At the same time, in the winter, electric vehicle drivers should choose routes with more charging infrastructure to meet power constraints, though this further increases the energy cost and battery aging cost.

(3)

Compared to the model with the objective of minimizing travel time, our proposed model yields cost savings of 18%, and although it increases the travel time by 13%, the model’s application leads to less frequent charging and provides a more comfortable travel experience for users. Compared with a model with a fixed charging power of 30 kW, the proposed model yields cost savings of 0.35%, a 2.64% reduction in travel time, and 20.81% reduction in charging time. Compared with a model with a fixed charging power of 60 kW, the proposed model yields a lower total cost.

In summary, our proposed model is a comprehensive model that can provide more cost-effective route planning and charging strategies for electric vehicle long-haul driving under variable ambient temperature conditions.