Optimizing Sustainable Tourism: A Multi-Objective Framework for Juneau and Beyond
Abstract
1. Introduction
2. Method
2.1. Data Collection and Preparation
2.1.1. Research Hypotheses
2.1.2. Data Collection
2.1.3. Data Preparation
Positive Orientation
- (1)
- The primary purpose of data transformation is to convert inverse indicators (where smaller values are better) into positive indicators (where larger values are better). This unifies the direction of all indicators to facilitate comprehensive evaluation and model optimization.
- (2)
- For non-positive indicators, such as infrastructure pressure, living costs, and carbon footprint, we applied a transformation formula:
- (3)
- For intermediate indicators, such as tourist numbers, population size, and tourism employment, which have optimal ranges, we used
Standardization
2.2. Establishment of the Evaluation Framework
2.2.1. Weight Determination
Analytic Hierarchy Process
- (1)
- Constructing the Judgment Matrix:
- (2)
- Calculating Weights:
- (3)
- Consistency Check:
Entropy Weighting Method
- (1)
- Calculate , the proportion of the (i)-th object for the (j)-th indicator, using the original data matrix:
- (2)
- Compute the entropy value of the (j)-th indicator:
- (3)
- Determine the information utility value of the (j)-th indicator:
- (4)
- Calculate the weight of the (j)-th indicator:
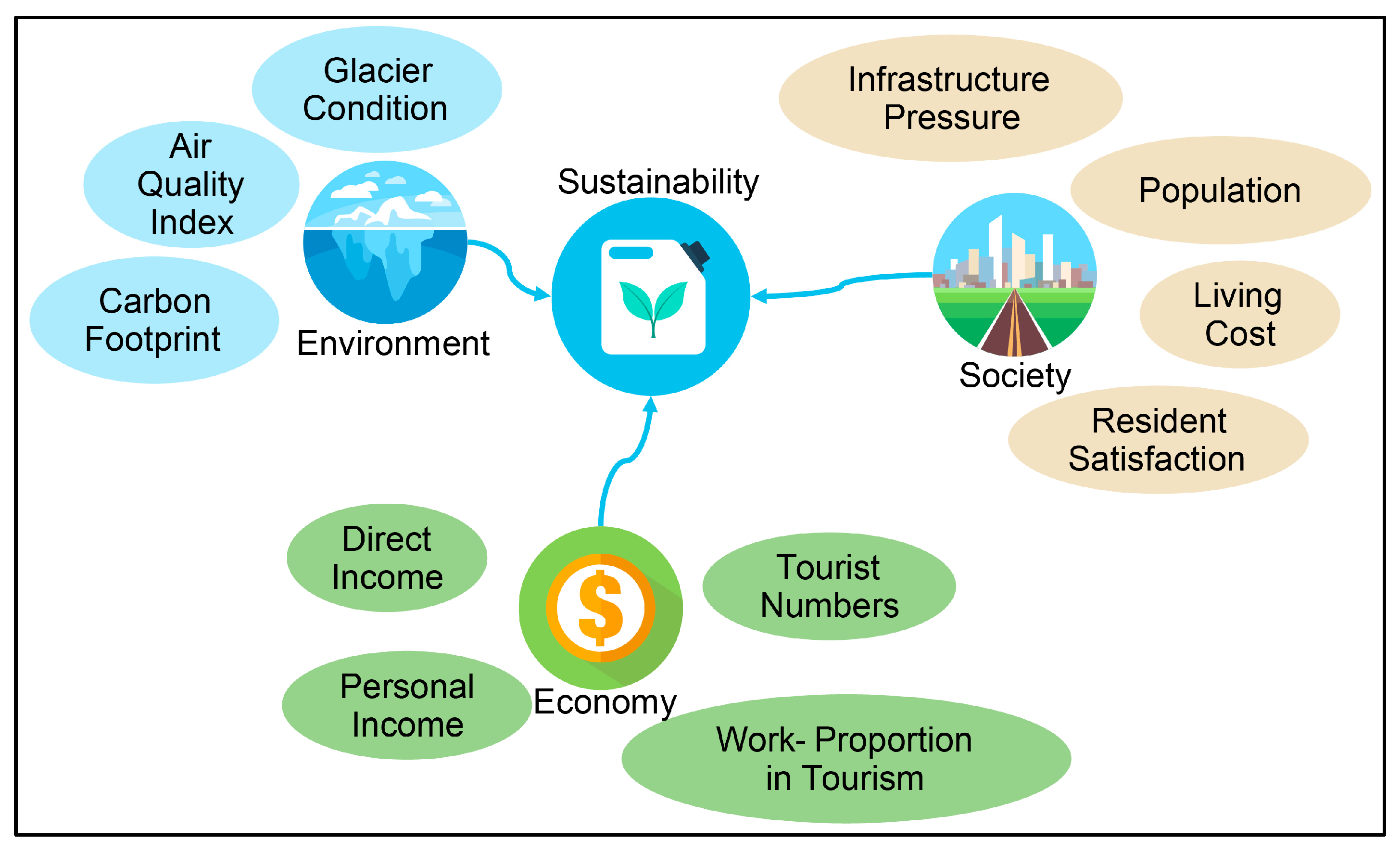
2.2.2. Economic, Social, and Environmental Dimensions
- (1)
- Economic Model
- (2)
- Social Model
- (3)
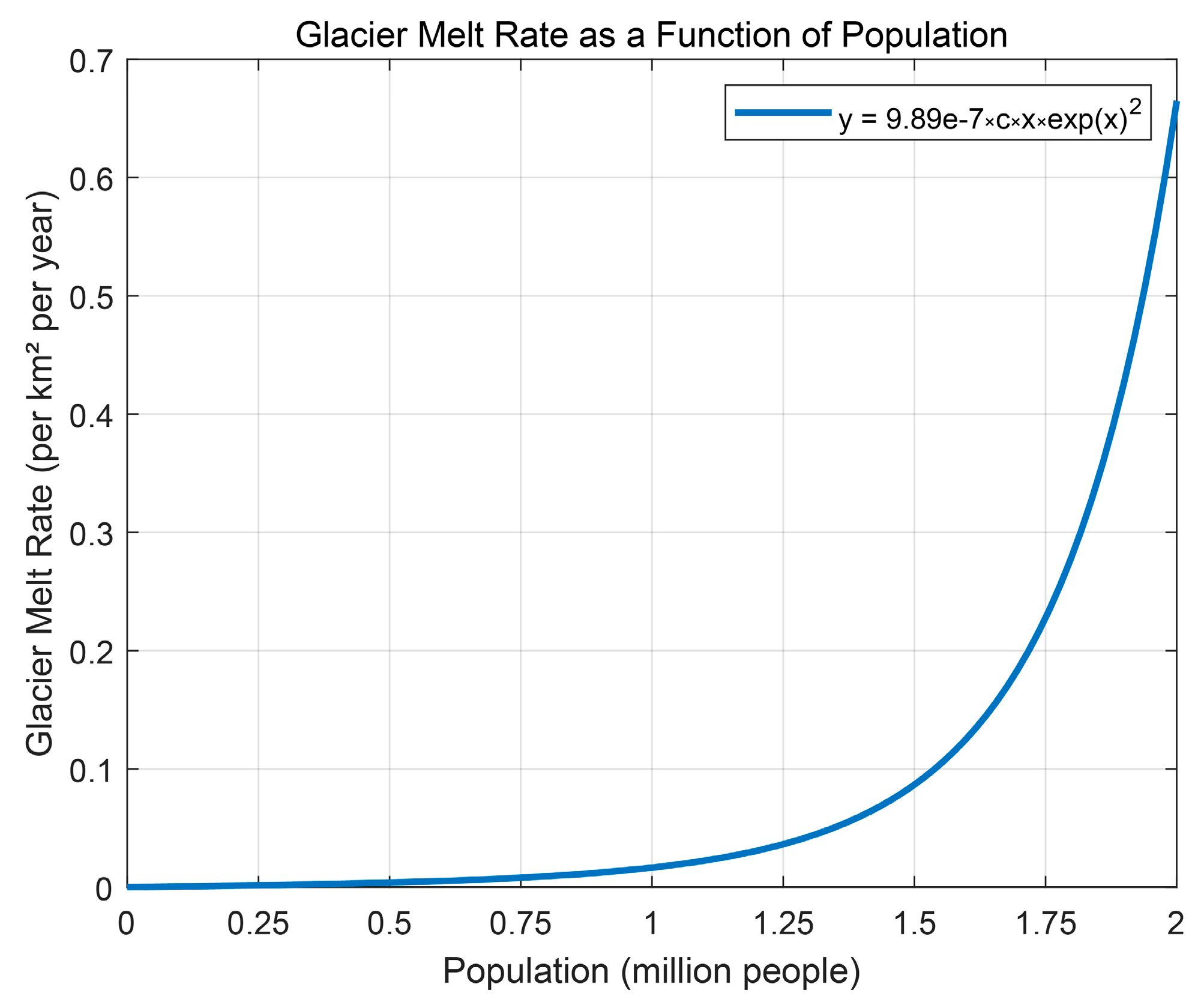
- Environmental Model
- (4)
- Constraints
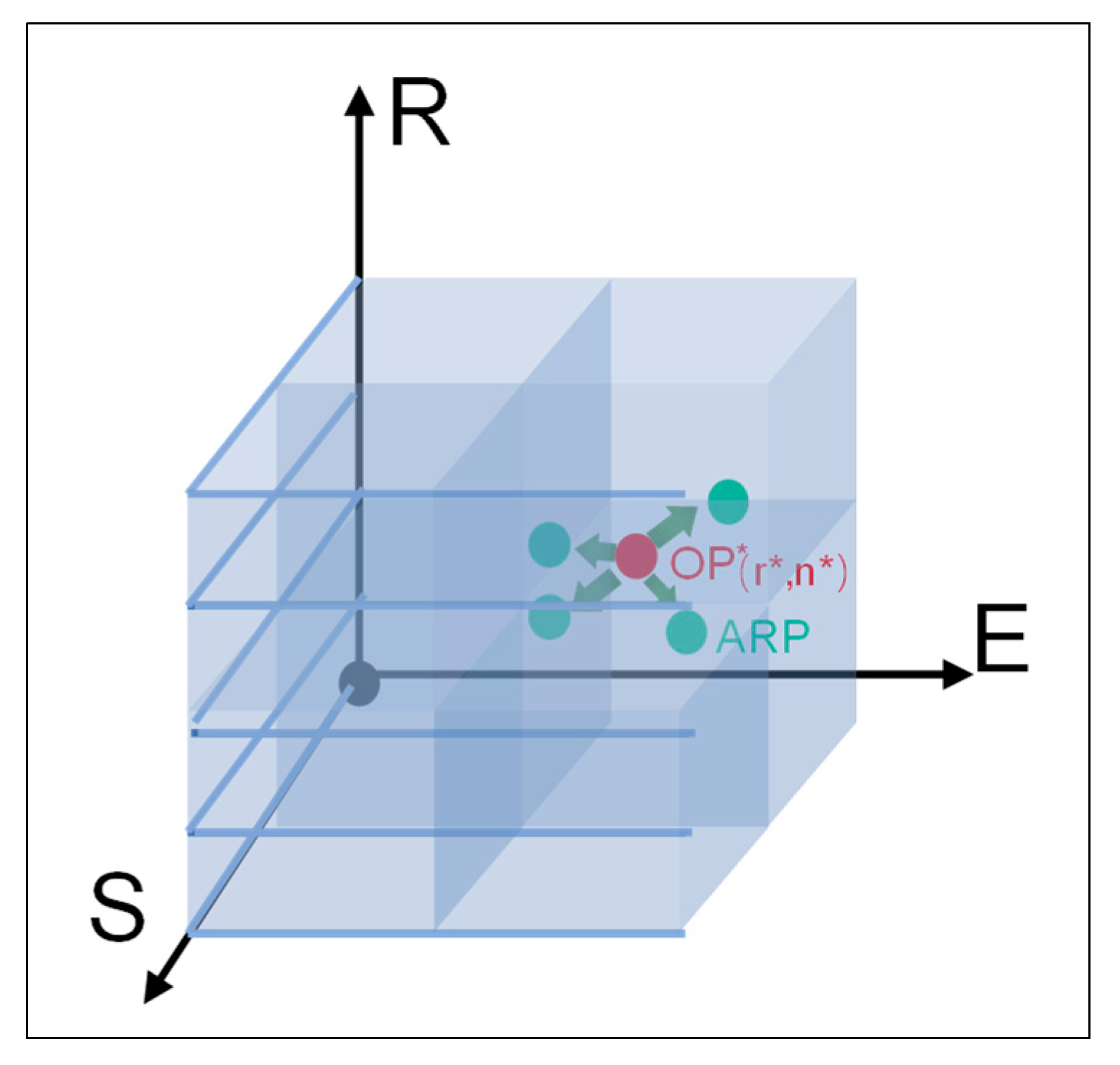
2.2.3. Objective Function
2.3. Multi-Objective Optimization
2.4. Assumptions and Notations
2.5. Model Application to Barcelona
- (1)
- Economic Model
- (2)
- Environmental Cost Model
- (3)
- Social Cost Model
- (4)
- Target Variable
3. Results
3.1. Model Validation and Composite Weight Results
3.2. Evaluation Models for Economic, Social, and Environmental Dimensions
4. Discussion
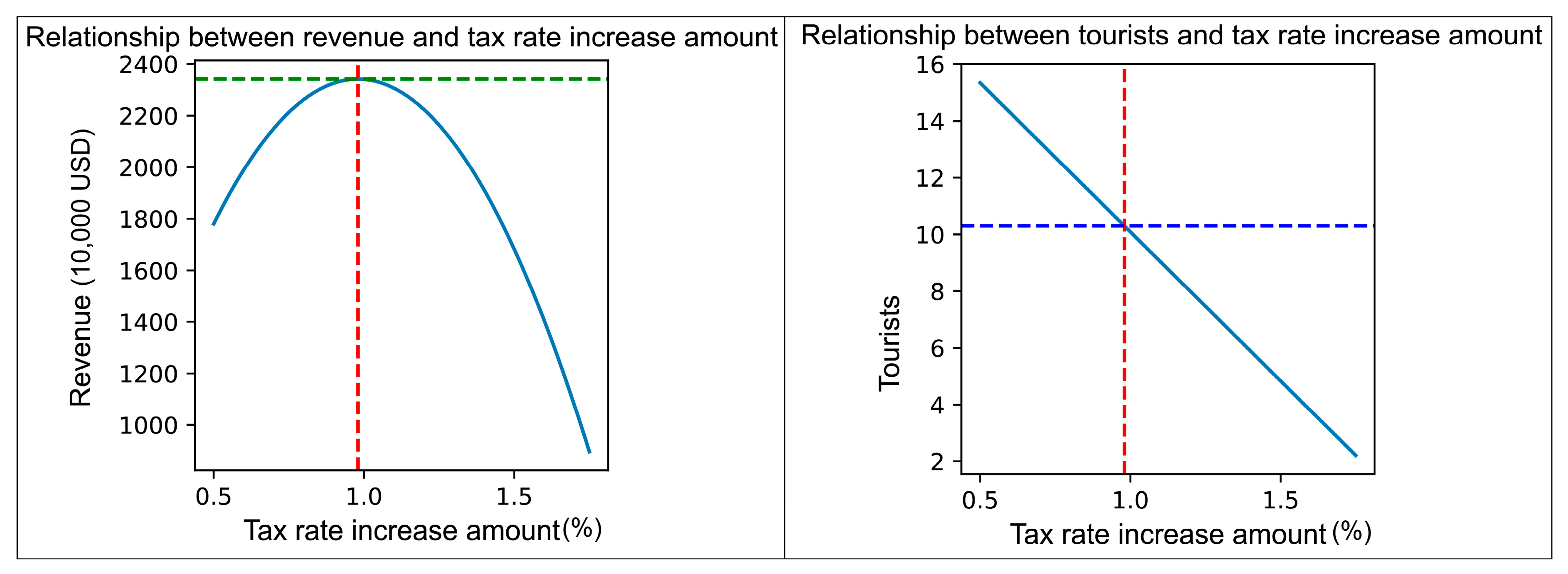
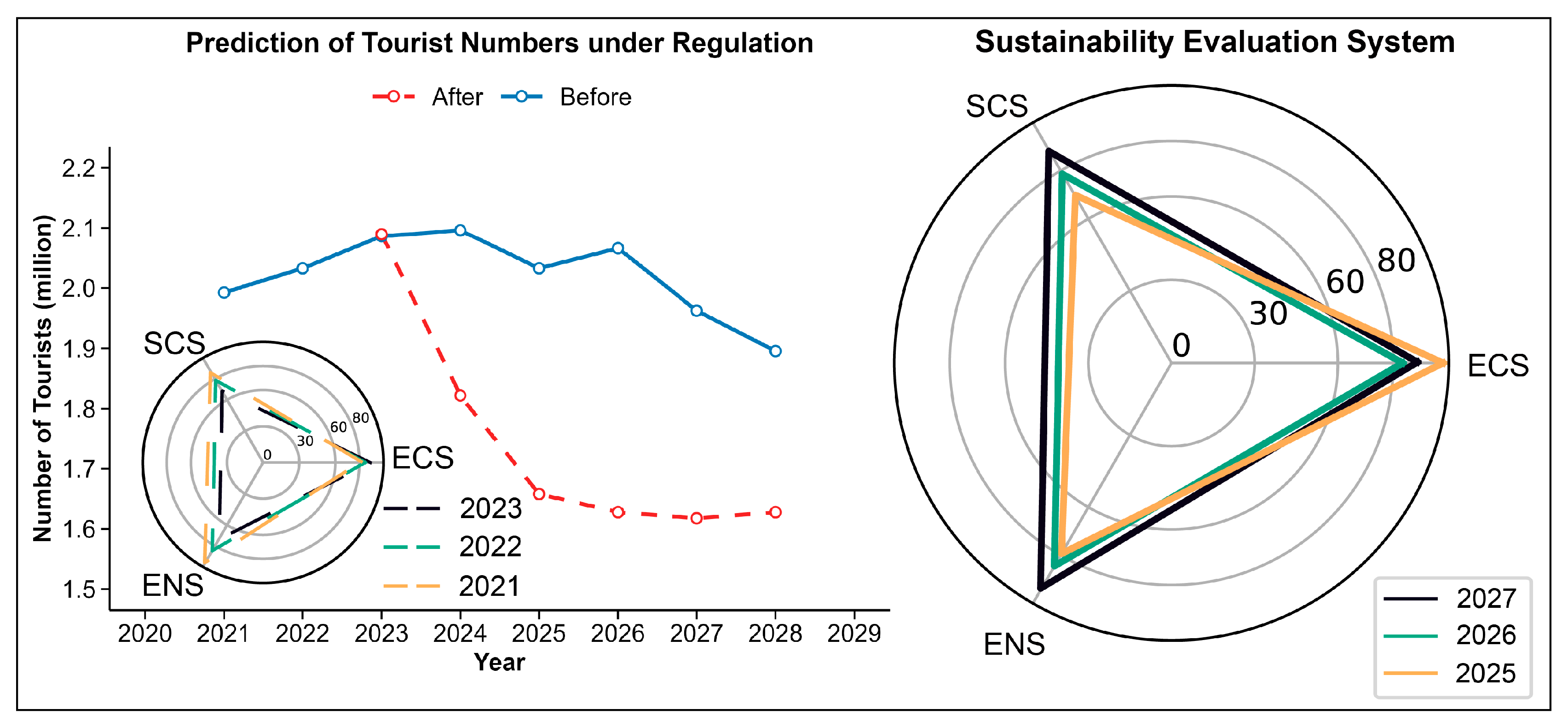
4.1. Optimal Scenario and Feedback Mechanism
4.2. Comparative Analysis and Projections
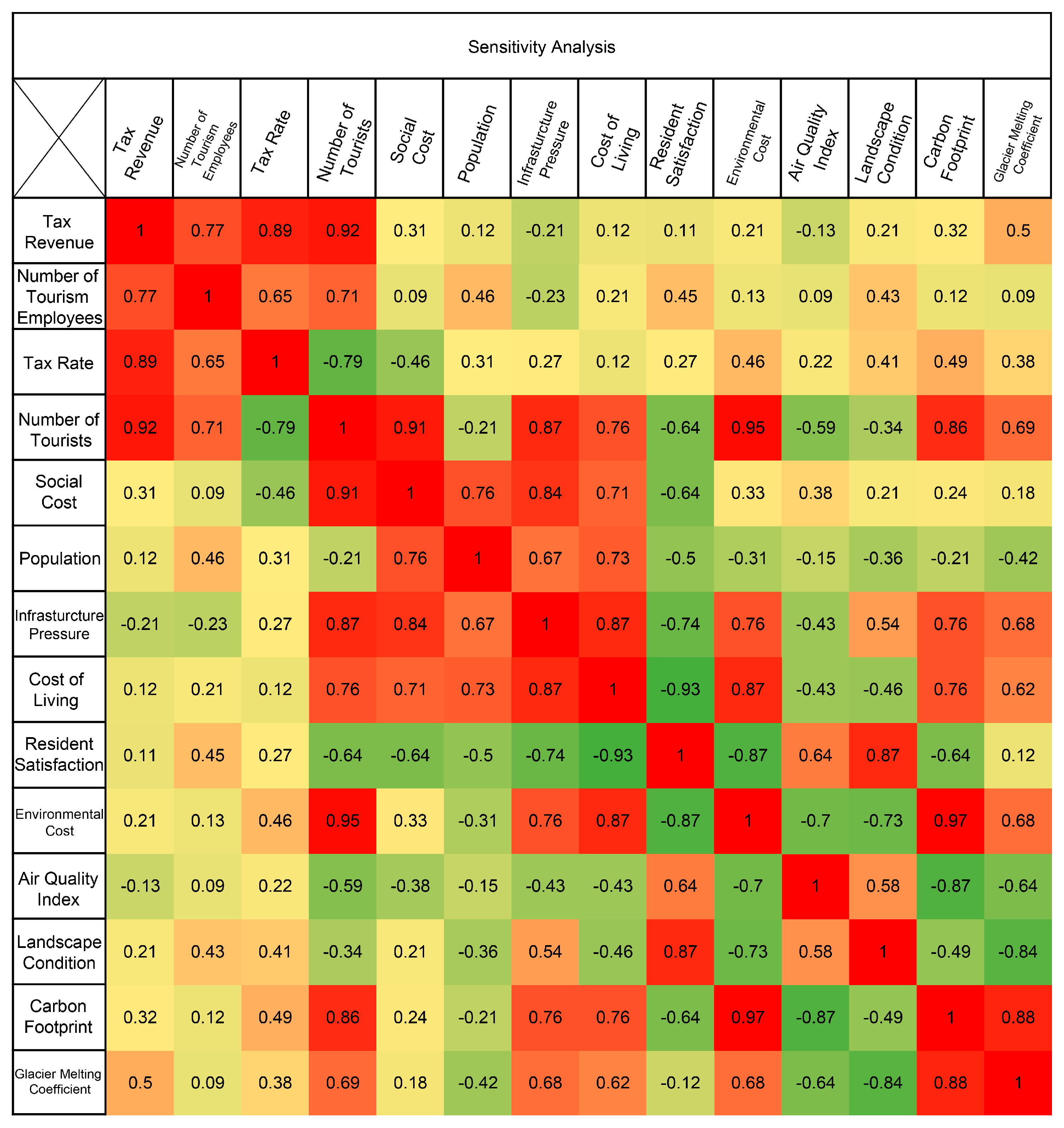
4.3. Sensitivity and Interdependency Analysis
4.4. Cross-Destination Application: Barcelona
4.5. Model Evaluation and Limitations
4.5.1. Strengths and Weaknesses
4.5.2. Limitations and Opportunities for Enhancement
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Subramaniam, N.; Akbar, S.; Situ, H.; Ji, S.; Parikh, N. Sustainable development goal reporting: Contrasting effects of institutional and organisational factors. J. Clean. Prod. 2023, 411, 137339. [Google Scholar] [CrossRef]
- Mackenbach, J.P. Rene Dubos and Jared Diamond dream of Dutch polders. Eur. J. Public Health 2006, 16, 575. [Google Scholar] [CrossRef][Green Version]
- Wagner, F. Cowboy professionalism: A cultural study of big-mountain tourism in the last frontier. J. Philos. Sport 2024, 51, 333–349. [Google Scholar] [CrossRef]
- Williams, A.M.; Chen, J.L.; Li, G.; Balaz, V. Risk, uncertainty and ambiguity amid COVID-19: A multi-national analysis of international travel intentions. Ann. Tour. Res. 2022, 92, 103346. [Google Scholar] [CrossRef]
- Teerlink, S. Humpback Whales and Humans: A Multi-Disciplinary Approach to Exploring the Whale-Watching Industry in Juneau, Alaska; University of Alaska Fairbanks: Fairbanks, AK, USA, 2017. [Google Scholar]
- Timm, K. Nature-Based Tourism Operator Response to Environmental Change in Juneau, Alaska; University of Alaska Fairbanks: Fairbanks, AK, USA, 2014. [Google Scholar]
- Jones, J. Mendenhall in Motion Inscribing Glacial Time and Animating Ecological Thresholds. Master’s Thesis, Harvard University, Cambridge, MA, USA, 2023. [Google Scholar]
- Satrovic, E.; Adedoyin, F.F. The Role of Energy Transition and International Tourism in Mitigating Environmental Degradation: Evidence from SEE Countries. Energies 2023, 16, 1002. [Google Scholar] [CrossRef]
- Mamirkulova, G.; Mi, J.; Abbas, J.; Mahmood, S.; Mubeen, R.; Ziapour, A. New Silk Road infrastructure opportunities in developing tourism environment for residents better quality of life. Glob. Ecol. Conserv. 2020, 24, e01194. [Google Scholar] [CrossRef]
- Mathes-Park, D. The Role of Destination Marketing Organizations in Advancing Stewardship and Sustainability. Master’s Thesis, California State University, Sacramento, CA, USA, 2024. [Google Scholar]
- Hurlimann, A.; Moosavi, S.; Browne, G.R. Urban planning policy must do more to integrate climate change adaptation and mitigation actions. Land Use Policy 2021, 101, 105188. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, A.; Mu, D. Impact of walking speed on tourist carrying capacity: The case of Maiji Mountain Grottoes, China. Tour. Manag. 2021, 84, 104273. [Google Scholar] [CrossRef]
- Vujko, A.; Plavsa, J.; Petrovic, M.D.; Radovanovic, M.; Gajic, T. Modelling of carrying capacity in National Park-Fruska Gora (Serbia) case study. Open Geosci. 2017, 9, 61–72. [Google Scholar] [CrossRef]
- Zango-Palau, A.; Jolivet, A.; Lurgi, M.; Claramunt-Lopez, B. A quantitative approach to the understanding of social-ecological systems: A case study from the Pyrenees. Reg. Environ. Change 2024, 24, 9. [Google Scholar] [CrossRef]
- Bertocchi, D.; Camatti, N.; Salmasi, L.; van der Borg, J. Assessing the tourism sustainability of EU regions at the NUTS-2 level with a composite and regionalised indicator. J. Sustain. Tour. 2023, 31, 1738–1755. [Google Scholar] [CrossRef]
- Dakos, V.; Kefi, S. Ecological resilience: What to measure and how. Environ. Res. Lett. 2022, 17, 043003. [Google Scholar] [CrossRef]
- Koens, K.; Postma, A.; Papp, B. Is Overtourism Overused? Understanding the Impact of Tourism in a City Context. Sustainability 2018, 10, 4384. [Google Scholar] [CrossRef]
- Fernandez, T.V.; Paez, B.G. Indicator system to evaluate the management of training for sustainable tourism management. Rev. Coop. Desarro. COODES 2022, 10, 261–285. [Google Scholar]
- Gorbanev, I.; Cortes, A.; Agudelo-Londono, S. Redesign of the Attention Process of Patients with Rheumatologic Diseases: Assessing the Performance with Analytic Hierarchy Process. Adv. Oper. Res. 2017, 2017, 6367037. [Google Scholar] [CrossRef]
- Ding, J.-F.; Tseng, W.-J.; Hsu, F.-T. An evaluation of key risk factors affecting shipping market operations across the Taiwan Strait for liner carriers. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2014, 228, 302–311. [Google Scholar] [CrossRef]
- Blancas, F.J.; Lozano-Oyola, M.; Gonzalez, M.; Caballero, R. Sustainable tourism composite indicators: A dynamic evaluation to manage changes in sustainability. J. Sustain. Tour. 2016, 24, 1403–1424. [Google Scholar] [CrossRef]
- Jeong, J.Y.; Karimov, M.; Sobirov, Y.; Saidmamatov, O.; Marty, P. Evaluating Culturalization Strategies for Sustainable Tourism Development in Uzbekistan. Sustainability 2023, 15, 7727. [Google Scholar] [CrossRef]
- Martín, J.; Martínez, J.; Fernández, J. An Analysis of the Factors behind the Citizen’s Attitude of Rejection towards Tourism in a Context of Overtourism and Economic Dependence on This Activity. Sustainability 2018, 10, 2851. [Google Scholar] [CrossRef]
- Milano, C.; Novelli, M.; Russo, A. Anti-tourism activism and the inconvenient truths about mass tourism, touristification and overtourism. Tour. Geogr. 2024, 26, 1313–1337. [Google Scholar] [CrossRef]
- Rico, A.; Martinez-Blanco, J.; Montlleo, M.; Rodriguez, G.; Tavares, N.; Arias, A.; Oliver-Sola, J. Carbon footprint of tourism in Barcelona. Tour. Manag. 2019, 70, 491–504. [Google Scholar] [CrossRef]
- Cocola-Gant, A.; Lopez-Gay, A. Transnational gentrification, tourism and the formation of ‘foreign only’ enclaves in Barcelona. Urban Stud. 2020, 57, 3025–3043. [Google Scholar] [CrossRef]
- Frago, L. Impact of COVID-19 Pandemic on Retail Structure in Barcelona: From Tourism-Phobia to the Desertification of City Center. Sustainability 2021, 13, 8215. [Google Scholar] [CrossRef]
- Scott, D.; Gossling, S.; Hall, C.M.; Peeters, P. Can tourism be part of the decarbonized global economy? The costs and risks of alternate carbon reduction policy pathways. J. Sustain. Tour. 2016, 24, 52–72. [Google Scholar] [CrossRef]
- Huss, M.; Hock, R. Global-scale hydrological response to future glacier mass loss. Nat. Clim. Change 2018, 8, 135–140. [Google Scholar] [CrossRef]
- Singh, S. Impact of Smart Tourism Technologies on Technology Engagement, Destination Experiences, and Place Attachment from the Perspectives of Gamification, Engagement and Self-Determination Theory. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2022. [Google Scholar]
- Zarhari, N.A.A.; Mat Som, A.P.; Azinuddin, M.; Hanafiah, M.H. Overtourism and destination branding: The mediating role of functional and emotional values among tourists. Tour. Hosp. Manag. 2023, 29, 303–308. [Google Scholar] [CrossRef]
- Zemla, M. European historic cities and overtourism-conflicts and development paths in the light of systematic literature review. Int. J. Tour. Cities 2024, 10, 353–372. [Google Scholar] [CrossRef]
- Cooper, E. Carbon Making sense of sustainable tourism on the periphery: Perspectives from Greenland. Tour. Geo. 2023, 5, 1303–1321. [Google Scholar] [CrossRef]
- Walker, B.; Hollin, C.S.; Carpenter, S.R.; Kinzig, A. Resilience, adaptability and transformability in social-ecological systems. Ecol. Soc. 2004, 9, 9. [Google Scholar] [CrossRef]
- Radic, V.; Hock, R. Glaciers in the Earth’s Hydrological Cycle: Assessments of Glacier Mass and Runoff Changes on Global and Regional Scales. Surv. Geophys. 2014, 35, 813–837. [Google Scholar] [CrossRef]
- Filimonau, V. Carbon Management in Tourism: Mitigating the Impacts on Climate Change. Tour. Manag. 2015, 46, 62–63. [Google Scholar] [CrossRef]
- Cavalcante, W.Q.d.F.; Coelho, A.; Bairrada, C.M. Sustainability and Tourism Marketing: A Bibliometric Analysis of Publications between 1997 and 2020 Using VOSviewer Software. Sustainability 2021, 13, 4987. [Google Scholar] [CrossRef]
- Gustavsson, P.; Syberfeldt, A. A New Algorithm Using the Non-Dominated Tree to Improve Non-Dominated Sorting. Evol. Comput. 2018, 26, 89–116. [Google Scholar] [CrossRef]
- Lee, S.; O’Leary, J.T. Determinants of Income Inequality in US Nonmetropolitan Tourism- and Recreation-Dependent Communities. J. Travel Res. 2008, 46, 456–468. [Google Scholar] [CrossRef]
- Levi Cupul-Magana, A.; Paola Rodriguez-Troncoso, A. Tourist carrying capacity at Islas Marietas National Park: An essential tool to protect the coral community. Appl. Geogr. 2017, 88, 15–23. [Google Scholar] [CrossRef]
- Psycharis, Y.; Tselios, V.; Pantazis, P. The contribution of Cohesion Funds and nationally funded public investment to regional growth: Evidence from Greece. Reg. Stud. 2020, 54, 95–105. [Google Scholar] [CrossRef]
- Postma, A.; Schmuecker, D. Understanding and overcoming negative impacts of tourism in city destinations: Conceptual model and strategic framework. J. Tour. Futures 2017, 3, 144–156. [Google Scholar] [CrossRef]
- Balsalobre-Lorente, D.; Driha, O.M.; Leitao, N.C.; Murshed, M. The carbon dioxide neutralizing effect of energy innovation on international tourism in EU-5 countries under the prism of the EKC hypothesis. J. Environ. Manag. 2021, 298, 113513. [Google Scholar] [CrossRef]
- Salazar, A.; Cardoso, C. Tourism planning: Impacts as benchmarks for sustainable development plans. Worldw. Hosp. Tour. Themes 2019, 11, 652–659. [Google Scholar] [CrossRef]
- Brochado, A.; Rodrigues, P.; Sousa, A.; Borges, A.P.; Veloso, M.; Gomez-Suarez, M. Resilience and Sustainable Urban Tourism: Understanding Local Communities’ Perceptions after a Crisis. Sustainability 2023, 15, 13298. [Google Scholar] [CrossRef]
- Becken, S.; Simmons, D. Using the concept of yield to assess the sustainability of different tourist types. Ecol. Econ. 2008, 67, 420–429. [Google Scholar] [CrossRef]

| Dimension | Indicator | Location | Source/Agency | Reference/URL |
|---|---|---|---|---|
| Economic | Annual Tourism Revenue | Juneau | City and Borough of Juneau, Finance Department | https://juneau.org/finance (accessed on 15 March 2025) |
| Tourism-Related Employment | Juneau | Alaska Department of Labor and Workforce Development | https://labor.alaska.gov/ (accessed on 15 March 2025) | |
| Annual Tourist Arrivals | Juneau | City and Borough of Juneau, Docks & Harbors | https://juneau.org/harbors (accessed on 15 March 2025) | |
| Tourism Tax Revenue | Barcelona | Barcelona City Council (Ajuntament de Barcelona) | https://ajuntament.barcelona.cat/ (accessed on 15 March 2025) | |
| Social | Resident Satisfaction Index | Juneau | Supplemental Survey Data/Literature | (Specify if from a specific study or survey) |
| Infrastructure Pressure (e.g., traffic) | Juneau | City and Borough of Juneau, Community Development | https://juneau.org/community-development (accessed on 15 March 2025) | |
| Housing Price Index | Barcelona | Spanish National Statistics Institute (INE) | https://www.ine.es/ (accessed on 15 March 2025) | |
| Population Density | Barcelona | Statistical Institute of Catalonia (Idescat) | https://www.idescat.cat/ (accessed on 15 March 2025) | |
| Environmental | Mendenhall Glacier Retreat Rate | Juneau | NOAA, National Centers for Environmental Information | https://www.ncdc.noaa.gov/cdo-web/ (accessed on 15 March 2025) |
| Air Quality Index (AQI) | Juneau | U.S. Environmental Protection Agency (EPA) | https://www.airnow.gov/ (accessed on 15 March 2025) | |
| Air Quality Index (AQI) | Barcelona | European Environment Agency (EEA)/Local Station | https://www.eea.europa.eu/ (accessed on 15 March 2025) | |
| Carbon Emissions (Tourism Sector) | Both | Estimated Based on Transport/Energy Data from Sources Above | (Model-derived) |
| Symbol | Description | Unit |
|---|---|---|
| x | Annual Tourist Numbers | USD 10,000/year |
| M | Average Tourist Expenditure | |
| R | Annual Government Revenue | USD 10,000 |
| r | Tax Rate Increase for Related Industries | % |
| L | Glacier Melting Rate | Tons/year |
| E | Environmental Cost | Dimensionless |
| C | Carbon Emissions | kg/person × day |
| S | Social Cost | Dimensionless |
| Consistency Test Results | |||
|---|---|---|---|
| CI | RI | CR | Result |
| 0.011 | 0.525 | 0.021 | Pass |
| Primary Indicator | Primary Weight | Secondary Indicator | Secondary Weight | Composite Weight |
|---|---|---|---|---|
| Economic | 0.43411 | Direct Revenue | 0.22879 | 0.0993 |
| Personal Income | 0.24824 | 0.1078 | ||
| Tourism Employment Proportion | 0.29450 | 0.1278 | ||
| Tourist Numbers | 0.22845 | 0.0992 | ||
| Social | 0.26323 | Population Size | 0.15325 | 0.0342 |
| Infrastructure Pressure | 0.31346 | 0.0825 | ||
| Living Cost | 0.25181 | 0.0562 | ||
| Resident Satisfaction | 0.27148 | 0.0714 | ||
| Environmental | 0.30266 | Air Quality Index | 0.45399 | 0.1374 |
| Glacier Condition | 0.31049 | 0.0940 | ||
| Carbon Footprint | 0.23552 | 0.0713 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, J.; Yang, H.; Wang, Z.; Peng, B.; Li, S. Optimizing Sustainable Tourism: A Multi-Objective Framework for Juneau and Beyond. Sustainability 2025, 17, 7344. https://doi.org/10.3390/su17167344
Pan J, Yang H, Wang Z, Peng B, Li S. Optimizing Sustainable Tourism: A Multi-Objective Framework for Juneau and Beyond. Sustainability. 2025; 17(16):7344. https://doi.org/10.3390/su17167344
Chicago/Turabian StylePan, Jing, Haoran Yang, Zihao Wang, Bo Peng, and Shaoning Li. 2025. "Optimizing Sustainable Tourism: A Multi-Objective Framework for Juneau and Beyond" Sustainability 17, no. 16: 7344. https://doi.org/10.3390/su17167344
APA StylePan, J., Yang, H., Wang, Z., Peng, B., & Li, S. (2025). Optimizing Sustainable Tourism: A Multi-Objective Framework for Juneau and Beyond. Sustainability, 17(16), 7344. https://doi.org/10.3390/su17167344



_Li.png)


