1. Introduction
With the deepening integration of electricity and carbon trading markets, power system planning is confronted with increasingly complex constraints and challenges. The rapid growth of renewable energy penetration has exacerbated system volatility and uncertainty, leading to severe wind and solar curtailment as well as insufficient flexibility. These issues highlight the urgent need for advanced planning methodologies capable of simultaneously ensuring economic efficiency, achieving low-carbon objectives, and maintaining operational security. The early studies on source-grid-load (SGL) coordinated planning primarily focused on the coordinated operation of generation, the grid, and the load, as well as uncertainty modeling on the supply side [
1]. However, they paid insufficient attention to energy storage resources, which have been widely deployed in recent years to enhance systems’ flexibility [
2,
3]. In response, integrated planning approaches that consider SGLS have gradually emerged. These methods partially incorporate uncertainties on both the supply and demand sides, along with low-carbon development strategies. Nevertheless, most existing research has yet to thoroughly explore the mechanisms of interaction between electricity and carbon markets—referred to as electricity–carbon coupling—nor systematically analyze the impact of achieving a supply–demand balance in flexibility under such a coupling framework on the overall coordinated planning of a SGLS system. Therefore, developing a coordinated SGLS planning method that accounts for both electricity–carbon coupling and system flexibility holds significant theoretical and practical importance.
As a critical terminal component of power systems, the distribution network is characterized by a complex topology, a large scale, and diverse configurations. With the large-scale integration of distributed energy resources (DERs), traditional distribution network structures are increasingly inadequate in managing the power balancing challenges that arise from the combined effects of generation-side intermittency and load-side uncertainty [
4]. Consequently, the planning of modern distribution networks is evolving into a multi-dimensional, complex optimization problem, featuring uncertainty, multi-objectivity, nonlinearity, dynamic behavior, and discrete decision variables [
5]. According to [
6], the widespread deployment of distributed energy and power electronic devices has significantly amplified system uncertainty, thereby increasing the complexity of planning problems. To address these challenges, a meshed distribution network planning approach has been proposed. This method divides the original system into multiple supply zones for partitioned optimization, effectively reducing the modeling dimensionality and simplifying the planning process [
7].
In the field of SGLS coordinated planning, carbon trading mechanisms have been widely adopted to promote carbon emission reduction and optimize power generation structures. References [
8,
9] incorporate carbon trading constraints into generation-side capacity planning to limit the output of high-emission units. Reference [
10] introduces a tiered carbon pricing mechanism in the dispatch of integrated energy systems, significantly enhancing the effectiveness of emission constraints. In [
11,
12], carbon pricing is embedded in system planning models to prioritize the siting of low-carbon technologies, which thereby improves the utilization of renewable energy sources. On the other hand, reference [
13] employs a leader–follower game-theoretic approach to engage both supply and demand sides in demand response programs, achieving both economic efficiency and system load relief through peak shaving and valley filling. Reference [
14] proposes a demand response potential forecasting method based on the electricity–carbon coupling incentive effect, which effectively improves the controllability and economic benefits of the demand response. Reference [
15] introduces an integrated electricity–carbon trading linkage mechanism for the demand side, achieving the dual goals of carbon emission reduction and cost optimization through the joint optimization of electricity and carbon markets. In addition, references [
16,
17] present a weather-aware electricity price interval forecasting method and a large language model-based approach for assisting in bidding behavior and market sentiment analysis, providing new techniques for the joint forecasting of electricity and carbon prices. Across these studies, carbon trading mechanisms control emissions by adjusting carbon prices, while a price-based demand response achieves load shifting through electricity price signals. Both are fundamentally driven by market signals, which indicates an inherent correlation between electricity and carbon prices. However, most of the existing literature still treats the carbon trading mechanism as an independent factor, without thoroughly examining the potential impact of electricity–carbon coupling on integrated system planning.
However, the integration of electricity–carbon coupling mechanisms not only affects generation dispatch and investment but also exacerbates the need for system flexibility. As carbon pricing incentivizes higher renewable energy penetration, the variability and uncertainty of renewable resources increase, leading to significant flexibility challenges. Therefore, it is essential to integrate a flexibility supply–demand balancing framework into electricity–carbon coupled planning to ensure the secure and economic operation of the distribution network. Ensuring a balance between the supply and demand of flexibility has emerged as a core challenge for the sustainable operation of power systems [
18,
19]. A variety of flexibility-oriented planning approaches have been proposed in the literature. For instance, reference [
20] presents a generation expansion model that incorporates flexibility balancing, which significantly enhances the system’s ability to accommodate the uncertainties of wind and solar power. Reference [
21] highlights that neglecting flexibility considerations in planning may result in an inadequate system regulation capacity and even trigger operational risks. To address this, reference [
22] develops a probabilistic flexibility margin model to quantify systems’ regulation capability, which is further extended into a bi-level optimization framework with upper–lower layer interactions [
23,
24]. In addition, some studies introduce flexibility metrics into SGLS coordinated planning models to achieve coordinated regulation of various resources [
25] or to evaluate the flexibility supply capability in the contexts of thermal power retrofitting [
26] and transmission network expansion [
27]. Overall, the current research on system flexibility remains largely focused on the optimal configuration of supply-side resources, with limited attention being paid to demand-side flexibility resources—such as shiftable and interruptible loads—in terms of modeling and dispatch potential. Moreover, few studies incorporate these demand-side resources into a comprehensive flexibility supply–demand balancing framework under electricity–carbon coupling mechanisms. Investigating the influence of electricity–carbon market interactions on system flexibility regulation and developing a joint flexibility balancing model that involves both the demand and supply sides still present significant research opportunities.
In summary, most current approaches only focus on electricity pricing or carbon pricing separately, without fully revealing their intrinsic coupling relationship. Meanwhile, although some works have introduced flexibility-oriented planning concepts, they often neglect demand-side flexibility resources or lack a systematic framework for achieving flexibility supply–demand balance. Moreover, none of the existing studies simultaneously consider the combined effects of electricity–carbon coupling and flexibility supply–demand balance. In addition, conventional optimization algorithms, such as standard PSO or GA, suffer from slow convergence and a tendency to fall into local optima.
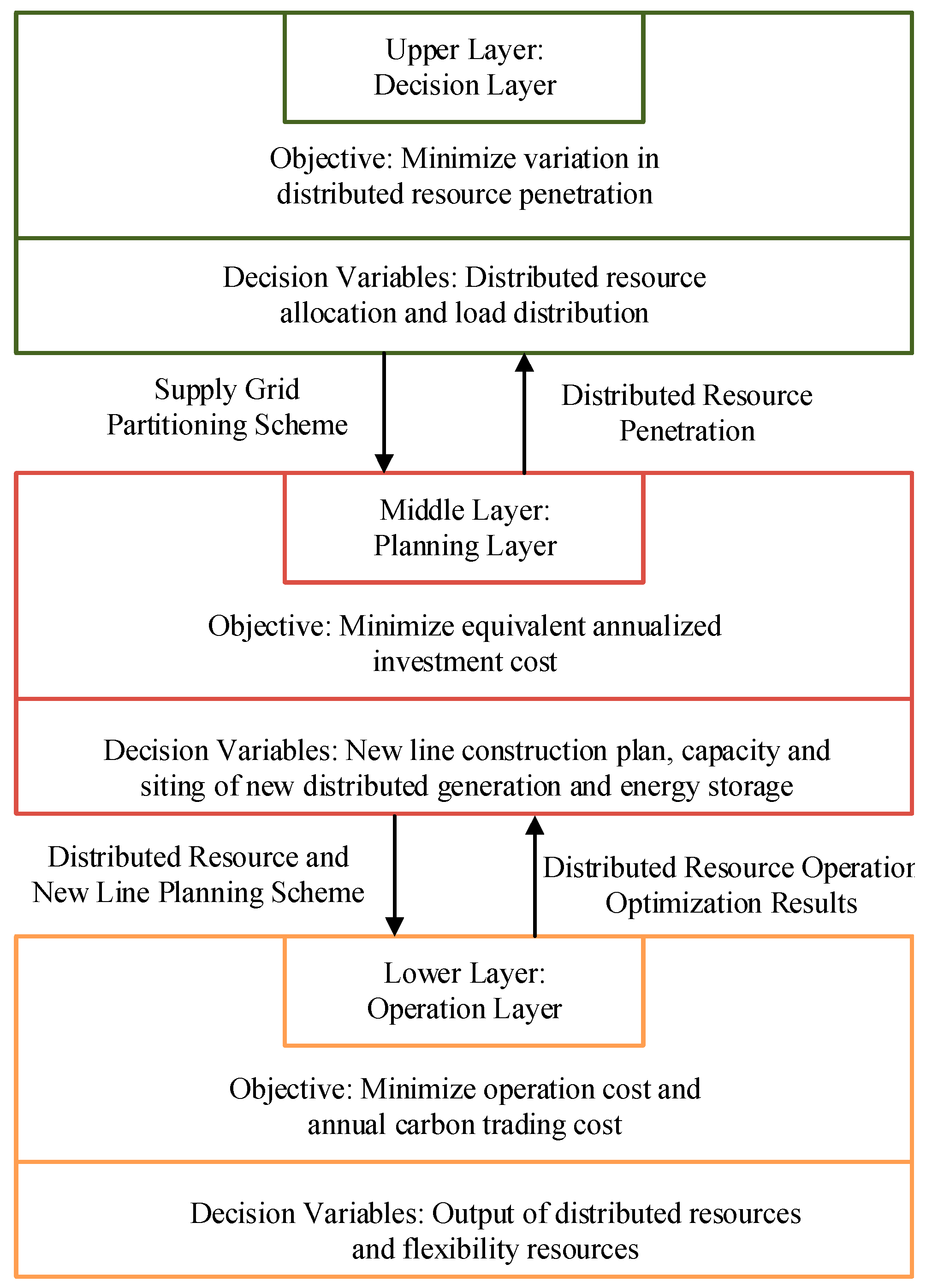
To overcome these limitations, this paper proposes a three-layer coordinated planning model that integrates electricity–carbon coupling and a flexibility supply–demand balance, while also introducing the IAPSO algorithm to enhance both the solution quality and computational efficiency. The main innovations and contributions of this paper are as follows:
- (1)
Three-layer planning model development: a “decision–planning–operation” three-layer coordinated planning model is proposed, which incorporates electricity–carbon coupling and a flexibility supply–demand balance into a unified framework for source–grid–load–storage planning in distribution networks;
- (2)
Electricity–carbon pricing mechanism: a dynamic electricity–carbon coupled pricing model is established to effectively guide resource allocation and investment decisions;
- (3)
Flexibility supply–demand modeling: a comprehensive flexibility quantification approach is proposed that integrates both supply-side and demand-side flexibility resources for coordinated system operation;
- (4)
Algorithmic improvement: an improved adaptive PSO algorithm is designed to accelerate convergence and enhance the global search capability for solving large-scale planning problems.
The remainder of this paper is organized as follows:
Section 2 introduces the electricity–carbon coupled pricing model,
Section 3 presents the flexibility supply–demand quantification model,
Section 4 describes the three-layer coordinated planning model,
Section 5 explains the IAPSO algorithm and solution methodology,
Section 6 provides simulation results and discussions, and
Section 7 concludes this paper.
5. Model Solution
5.1. Improved K-Means Algorithm
The K-means algorithm is a clustering method based on objective function optimization, and commonly uses Euclidean distance as the criterion for power supply grid division. However, Euclidean distance primarily emphasizes spatial proximity and does not account for the electrical coupling between distributed resources and loads, which can significantly affect grid partitioning [
29]. To address this limitation in the context of SGLS coordinated planning in distribution networks, two evaluation indices—the electrical coupling degree and renewable energy accommodation rate—are introduced to comprehensively assess and optimize regional partitioning within the distribution system.
The comprehensive index system for regional division is primarily determined by the objectives and principles of distribution network partitioning. Considering the functional requirements of each region, this study develops an integrated evaluation framework to comprehensively assess and optimize regional partitioning. The system incorporates the electrical coupling degree, which reflects the electrical proximity between nodes; the voltage security margin, which indicates the overall deviation of node voltages during coordinated regulation; and the renewable energy accommodation rate, which evaluates the self-regulation capability of each region under partitioned conditions. The use of these indicators, together, aims to maximize the autonomy and operational efficiency of distribution network regions.
(1) Electrical Coupling Degree
In the architecture design of distribution networks, electrical connections between nodes within the same region are typically strong. The electrical coupling degree is quantified using the following formula:
where
denotes the weight of the edge between nodes
and
, which is represented by the electrical distance between the two nodes;
is half the sum of the weights of all edges within the region;
represents the sum of the weights of all edges connected to node
. If nodes
and
are located in the same region, then
; otherwise,
.
(2) Voltage Security Margin
The voltage security margin is defined as the ability of PV, energy storage, and load resources within a region to regulate active and reactive power to control voltage deviations. The specific calculation formula is as follows:
where
represents the voltage regulation capability index of region
;
denotes the total number of partitioned regions;
is the maximum voltage deviation of node
within the region; and
represents the maximum voltage regulation capacity at node
, considering the active and reactive power margins within the region.
(3) Renewable Energy Accommodation Rate
The renewable energy accommodation rate refers to the ability of controllable sources and net load fluctuations within a region to be smoothed over the scheduling period. This metric helps evaluate and optimize the distribution network’s capacity for renewable energy integration and load regulation across different time intervals. The quantitative expression of this indicator is as follows:
where
,
,
, and
represent the adjustable capacities of distributed PV, wind power, energy storage, and flexible loads, respectively, as well as the net load within the region at time
.
(4) Comprehensive Regional Partitioning Index System for Distribution Networks
Integrating the aforementioned regional division indicators and considering the regulation capabilities of the sources, loads, and storage within each region, the comprehensive partitioning index system for county-level distribution networks is formulated as follows to fully leverage regional autonomy.
where
,
, and
are weighting coefficients, which satisfy the following condition:
The improved K-means algorithm is a hard clustering method based on a predefined number of clusters , with the following steps:
Determine the number of clusters according to the prerequisites of grid partitioning;
Define classification criteria using the spatiotemporal distances of load points and distributed resources;
Calculate weights based on the comprehensive regional partitioning index; smaller weights indicate greater similarity between data points;
Apply the minimum weight matching algorithm [
30] to find the minimum weight set in the graph, and thereby group data points into distinct clusters;
Use the K-means algorithm to separately select cluster centers and load centers.
Edges in the minimum weight matching connect vertices from different clusters, optimizing the matching between nearby cluster centers and load centers to determine the final grid partitioning results.
5.2. Search Method Based on Improved Adaptive Particle Swarm Optimization
Particle swarm optimization (PSO) treats the solution space of a problem as a multi-dimensional search space composed of particles. Each particle represents a potential solution and explores the space by adjusting its own position and velocity. The position of each particle is updated based on both its own best experience and the collective experience of the swarm, with the aim of identifying the optimal solution. Through continuous iterations, the swarm gradually converges toward the global optimum.
The steps of the IAPSO algorithm are as follows:
Initialize the velocity and position of all particles. Evaluate the objective function value for each particle.
- 2.
Determination of Personal Best
During initialization, each particle’s personal best position is set to its current position.
- 3.
Adaptive Inertia Weight Adjustment
In IAPSO, let the solution space be
-dimensional (
). Let
and
denote the velocity and position of each particle, respectively. Based on the current velocity and iteration index
, the position of each particle is updated using the following equation:
For each particle, the velocity and position are updated using Equation (40). In this process, represents the particle’s personal best position, while denotes the global best position found by the entire population. The inertia weight serves to balance the global exploration and local exploitation capabilities. The acceleration coefficients and reflect the particle’s tendency to move toward its personal best and the global best positions, respectively. Additionally, and are uniformly distributed random numbers in the range [0, 1].
The inertia weight critically affects PSO’s search ability and convergence. Larger inertia weights favor global exploration, while smaller ones enhance local exploitation. Conventional PSO uses a fixed inertia weight, often resulting in suboptimal convergence. To improve the method’s stability and performance, this study employs an adaptive inertia weight that varies with each particle’s fitness. The update rules for minimization and maximization problems are given by Equations (41) and (42).
where
and
are the preset minimum and maximum inertia weight coefficients,
is the fitness value of the particle
at iteration
,
and
are the minimum and maximum fitness values among all particles at iteration ttt, and
is the average fitness of all particles at iteration
.
can be expressed as follows:
Taking the example of maximizing fitness using PSO, a higher fitness value indicates a better particle position. When a particle’s fitness is below the average fitness of all particles, it means that the particle is in a relatively poor position; in this case, setting the inertia weight to its maximum enhances the particle’s global search ability, helping it quickly move toward better regions. Conversely, when a particle’s fitness exceeds the average fitness, it indicates a relatively good position; adaptively reducing the inertia weight strengthens the particle’s local search ability, enabling faster convergence to the optimal solution. This inertia weight adjustment effectively balances global exploration and rapid convergence.
- 4.
Adaptive Adjustment of Acceleration Factors
The acceleration factors
and
represent the cognitive ability of particles and their social information-sharing capability, respectively. Proper tuning of these factors can accelerate the search process and help avoid premature convergence to local optima. Therefore, this study improves the setting of acceleration factors
and random constants
, as shown in Equations (44) and (45):
In Equations (44) and (45), denotes the maximum number of iterations, the current iteration, and the inertia weight calculated by Equations (41) and (42); the other parameters share the same meaning as in Equation (40). This design allows particles to be influenced more by their individual best positions in early iterations, enabling rapid convergence to relatively good solutions. As the iterations progress, the influence of individual best positions diminishes, and particles move towards the global best, which promotes overall convergence.
Fixed inertia weights and acceleration coefficients often cause the algorithm to get trapped in local optima, reducing its optimization performance. Therefore, this study dynamically updates the acceleration coefficients based on the adaptive inertia weight, as shown in Equations (46) and (47).
Based on the adaptive inertia weight, the quality of each particle’s position is reflected, which allows appropriate adjustment of the particle’s cognitive and social sharing abilities so that particles can more rapidly converge toward their own historical best positions and the global best position.
- 5.
Crossover and Mutation Operation
To generate new offspring,
random values are drawn from a Gaussian distribution and added to
components of the solution vector. This helps the algorithm escape local optima. For each parent solution vector, the offspring produced by Gaussian mutation at generation
is expressed as follows:
where
and
represent the mean and standard deviation of the Gaussian distribution, respectively.
denotes a Gaussian random variable with a mean of 0 and a standard deviation of 1. The standard deviation for each solution vector is calculated by Equation (49):
where
is the fitness value of the
solution in the population, and
is the minimum fitness value among the current population’s solution vectors.
- 6.
Calculate the fitness of each particle and update the individual best positions.
- 7.
Check if the maximum number of iterations is reached. If yes, output the results; if not, return to step (3).
5.3. Solution Procedure
Preprocess the planning of the power supply partitions, determine the optimal number of clusters, and use the improved K-means clustering algorithm to identify load centers and DG centers. Then, apply minimum weight matching to define the power supply grids. The grid partition results are passed to the middle layer;
Initialize parameters of the IAPSO algorithm and generate the initial population;
Pass the configuration scheme generated by the middle layer to the lower layer as the initial conditions. The lower layer model determines the economic operation cost and environmental governance cost based on distributed resource outputs, and thus identifies the optimal operational strategy for the grid;
Pass the optimal strategy to the middle layer. If the DG penetration meets the requirements, do not return to the upper layer. The middle layer updates the global particle velocities and positions directly based on the optimized scheme;
Check whether the termination condition is met. If yes, the global optimum is the optimal planning scheme; if not, update the particle positions and velocities and return to step 2.
6. Simulation Analysis
To verify the effectiveness of the proposed strategy, simulation experiments were conducted in MATLAB R2024a using the IEEE 33-bus distribution network as an example. The system base voltage is set to 12.66 kV, and the allowable voltage range at the nodes is [0.95 p.u., 1.05 p.u.]. The system is equipped with diesel generators, and the planned types of DG include wind turbines, PV, micro gas turbines, and energy storage devices. The rated capacity of a single DG unit is 50 kW. The unit investment costs per kW are 5000, 6500, 1500, and 2000 RMB for wind energy, PV energy, micro gas turbine energy, and energy storage, respectively; the unit maintenance costs are 0.06, 0.04, 0.04, and 0.05 RMB/kWh, respectively. The unit investment cost for lines is 150,000 RMB/km. The planning investment period is 10 years with a discount rate of 0.1. Each node can accommodate up to 10 units of wind turbines and PV devices. The state of charge (SOC) for the storage devices ranges from 0.1 to 0.9, and they have charge/discharge efficiencies of 0.9.
The electricity purchase prices are segmented as follows: off-peak hours 0:00–8:00 and 11:30–13:30 at 0.25 RMB/kWh; flat hours 8:00–11:30, 13:30–16:30, and 22:30–24:00 at 0.42 RMB/kWh; peak hours 16:30–20:30 at 0.65 RMB/kWh; and sharp peak hours 20:30–22:30 at 0.82 RMB/kWh. The initial carbon trading price is 400 RMB/ton. To ensure the rationality of the parameter settings, the investment and maintenance costs in this study are primarily derived from the relevant literature and typical data from the domestic renewable energy market. The time-of-use electricity prices are based on the pricing structures of regional electricity markets, and the carbon trading price is taken from the recent average market level. These parameters are selected to establish a representative simulation environment for validating the proposed model and methodology.
The partitioning results of the IEEE 33-node network and the line construction plan are shown in
Figure 3. The wind power output and load variation curves for four typical days are shown in
Figure 4.
6.1. Planning Results Analysis
The planning scheme obtained using the IAPSO is presented in
Table 1.
The configuration results indicate that, due to the uncertainty of distributed resources, the planning tends to deploy them in load-intensive areas to achieve local consumption. Considering the variability of PV generation, energy storage devices are preferably allocated in regions with a high concentration of distributed PV units. Through charging and discharging, they help smooth peak loads and valleys, thereby enhancing the stability of the distribution network.
Next, the impact of carbon trading prices on the planning results is analyzed. Under the conditions that the lengths of the positive and negative carbon emission intervals and the carbon quota purchase cost growth coefficient remain unchanged, the electricity–carbon coupling market is considered. The carbon trading price is varied within the range of 0 to 600 RMB/t, and the configuration results of gas turbines, wind power, PV energy, and ESS are shown in
Figure 5.
As the carbon trading price increases, the capacity of the gas turbine units gradually decreases, while the capacities of the DERs and ESS steadily increase. This indicates that higher carbon prices lead to greater carbon emission costs, prompting an expansion in the installed capacity of renewable energy and pure energy systems to reduce system emissions and, consequently, carbon trading costs. With further increases in carbon prices, these capacities approach their respective limits.
6.2. Analysis of Advantages of the IAPSO
The initial parameters of the IAPSO algorithm are configured as follows: the population size is set to 80, and the maximum number of iterations is 100. A constraint is imposed to ensure that the power generation from DERs accounts for more than 50% of the total generation. Taking the total system cost as an example, the convergence curves of the standard PSO algorithm and the IAPSO algorithm are illustrated in
Figure 6.
As shown in the figure, the IAPSO algorithm outperforms the traditional PSO in both convergence speed and convergence quality. The improved algorithm converges in about 28 iterations, whereas the traditional PSO requires approximately 70 iterations to reach convergence.
To more clearly demonstrate the advantages of the IAPSO algorithm, this study compares it with the standard PSO and the traditional genetic algorithm (GA), as well as differential evolution (DE) [
31] and the grey wolf optimizer (GWO) [
32]. The planning results for the investment and operational costs obtained by these methods are summarized in
Table 2.
As shown in
Table 2, the planning scheme based on IAPSO outperforms PSO, the GA, DE, and the GWO across all cost metrics, including investment and operation cost, curtailment penalty, flexibility penalty, carbon trading cost, and total system cost. This advantage arises from three key enhancements in the IAPSO framework. First, the inertia weight is dynamically adjusted based on particle fitness—particles with lower fitness are assigned larger inertia weights to enhance global exploration, while those with better performance receive smaller weights to refine their local search. Second, the acceleration coefficients evolve adaptively throughout the iterations, emphasizing individual cognition in the early stages for rapid exploration and gradually strengthening social collaboration to improve the convergence speed. Third, a Gaussian mutation mechanism is incorporated to increase solution diversity and help the population escape local optima. These combined mechanisms enable IAPSO to achieve faster convergence and more accurate global optimization results, ultimately leading to a more cost-effective planning outcome.
6.3. Analysis of Power Supply Zone Operation
The optimal operation strategies for the three power supply zones on a typical day, derived from the proposed planning scheme, are illustrated in
Figure 7,
Figure 8 and
Figure 9.
Based on the typical daily operation profiles of each power supply zone, the system charges energy storage devices when wind and solar outputs are high, and discharges them during peak demand periods to supply power to the grid. During off-peak hours, electricity is purchased from the grid while the storage units are charged simultaneously. This strategy enables the local consumption of DERs and minimizes operational costs by leveraging time-of-use electricity pricing. In addition, flexible resources, such as shiftable loads, are utilized to further flatten the peak demand and fill valleys.
6.4. Analysis of Planning Results Under Different Scenarios
To more clearly compare and analyze the impacts of considering electricity–carbon coupling and flexibility supply–demand balance on the coordinated planning of SGLS, this study designs four different planning scenarios for validation and comparison:
Scenario 1: Planning considering only time-of-use electricity pricing;
Scenario 2: Planning considering electricity–carbon coupling;
Scenario 3: Planning considering flexibility supply–demand balance.
Scenario 4: Planning considering both electricity–carbon coupling and flexibility supply–demand balance.
The cost planning results of the three scenarios are shown in
Table 3.
Scenario 1, which only considers the electricity pricing mechanism, leads to the highest overall cost, with pronounced flexibility penalties and renewable curtailment. Scenario 2 introduces electricity–carbon coupling, effectively reducing curtailment and carbon trading costs while improving the utilization of distributed resources. Scenario 3 incorporates a flexibility supply–demand balancing mechanism, which further alleviates flexibility shortages and enhances the system’s efficiency. Scenario 4 combines electricity–carbon coupling with flexibility balancing, achieving the best performance in terms of cost reduction, renewable energy integration, and system flexibility and thereby providing a comprehensive and economically efficient solution for modern power system planning.
6.5. Method Consistency Test
Without altering the parameters of the simulation model, the proposed planning method was executed 30 independent times. The resulting new line construction plans and distributed generation configurations were completely identical across all runs. The standard deviation of the total cost obtained from the 30 independent runs was less than 1.4%, whereas the standard deviations for the traditional PSO and GA methods were approximately 4.5% and 5.2%, respectively. These results demonstrate the strong consistency and robustness of the proposed method.
6.6. Validation on a Larger-Scale Network
To further verify the effectiveness of the proposed method, the more complex PG&E 69-bus distribution system [
33] was tested. The parameter settings were kept consistent with those described in this section. The partitioning results of the 69-bus system and the corresponding line construction plans are shown in
Figure 10.
The planning scheme obtained using the IAPSO algorithm is presented in
Table 4.
From the configuration results, it can be observed that, for the 69-bus network, the proposed method still provides an effective planning scheme. Considering the uncertainty of distributed resources, the method tends to allocate them in load-intensive areas to achieve local consumption. These results confirm that the proposed method remains effective and applicable to larger-scale distribution networks.
6.7. Discussion
The simulation results provide several important insights into the effectiveness of the proposed model and the IAPSO algorithm.
First, the integration of the electricity–carbon coupling mechanism substantially improves the planning performance. By establishing a linkage between electricity prices and carbon trading signals, the model creates a coordinated market environment that guides investment towards low-carbon resources while discouraging carbon-intensive generation. This mechanism not only promotes the utilization of renewable energy but also contributes to the reduction of overall system costs through the mitigation of carbon-related expenditures.
Second, the incorporation of a flexibility supply–demand balancing framework proves to be essential for ensuring the secure and economic operation of the system. The explicit quantification of flexibility and the coordinated scheduling of multiple resources, including energy storage and controllable loads, enable the model to effectively accommodate renewable variability. This reduces dependence on conventional thermal generation for balancing purposes and alleviates operational stress, thereby improving both economic efficiency and system reliability.
Third, the proposed IAPSO algorithm exhibits superior convergence performance and robustness relative to conventional metaheuristic approaches. The adaptive adjustment of its parameters and the introduction of Gaussian mutation enhance its global exploration capability while maintaining solution diversity, which ensures stable and high-quality optimization results across repeated runs.
Finally, the successful application of the proposed approach to a larger-scale distribution network validates its scalability and practical applicability. This indicates that the model and algorithm are suitable for complex real-world systems. Future research may extend this work by explicitly modeling equipment degradation and incorporating more detailed representations of demand-side flexibility, thus further improving the accuracy and applicability of the proposed framework.
7. Conclusions
This study proposes a three-layer coordinated planning model for source–grid–load–storage systems considering electricity–carbon coupling and flexibility supply–demand balance. The key contributions and findings can be summarized as follows:
The proposed “Decision–Planning–Operation” structure provides a systematic approach for distribution network planning. By combining grid partitioning, coordinated resource allocation, and multi-scenario operational optimization, the model effectively reduces planning complexity while enhancing cost efficiency and renewable energy integration;
The improved adaptive IAPSO algorithm demonstrates faster convergence and higher solution accuracy compared with conventional metaheuristic techniques, offering robust computational support for large-scale and highly constrained planning problems;
The introduction of a dynamic electricity–carbon pricing mechanism effectively promotes the deployment of low-carbon resources and reduces the total system cost, supporting the low-carbon transition of distribution networks;
By quantifying and coordinating the flexibility contributions of conventional units, energy storage, and controllable loads, the model mitigates flexibility shortages, reduces renewable curtailment, and alleviates the over-reliance on thermal units, thereby improving system operational reliability and economic performance.
These results confirm the scalability and practical applicability of the proposed model and algorithm, providing a feasible solution for future low-carbon and flexibility-oriented distribution network planning. Future work will focus on incorporating equipment degradation and more detailed demand-side flexibility models to further enhance planning accuracy.
In addition, this study contributes to sustainable development by integrating economic, environmental, and operational objectives into a unified planning framework. By promoting the deployment of renewable energy, reducing carbon emissions, and enhancing the efficiency of flexibility resource utilization, the proposed model supports the transition towards cleaner and more resilient energy systems. This aligns with global sustainability goals and provides actionable insights for policymakers and utilities seeking to achieve both economic efficiency and environmental responsibility in power system planning.