Analysis of the Distribution Characteristics and Influencing Factors of Apparent Temperature in Chang–Zhu–Tan

Abstract

Rapid urbanization and climate change have exacerbated urban heat stress, underscoring the importance of research on human thermal comfort for sustainable urban development. This study analyzes the spatiotemporal variation and driving factors of apparent temperature in the Chang–Zhu–Tan urban agglomeration, China. The Humidex index, representing apparent temperature, was derived from multi-source remote sensing data (Landsat 8, MODIS) and meteorological variables (ERA5-Land reanalysis), employing atmospheric correction, random forest modeling, and path analysis. The results indicate pronounced spatiotemporal heterogeneity: apparent temperature reached its maximum in urban centers during summer (mean 52.9 °C) and its minimum in winter (mean 5.99 °C), following a decreasing gradient from urban core to periphery. Land cover emerged as a key driver, with vegetation (NDVI, r = −0.938) showing a strong negative correlation and built-up areas (NDBI, r = +0.8) a positive correlation with apparent temperature. Uniquely, in the Chang–Zhu–Tan region’s persistently high humidity, water bodies (MNDWI, r = +0.616) exhibited a positive correlation with apparent temperature, likely due to humidity-enhanced thermal perception in summer and relatively warmer water temperature in winter. Path analysis revealed that air temperature exerts the strongest direct positive influence on apparent temperature, while relative humidity and NDVI primarily act through indirect pathways. These findings provide scientific evidence to guide climate-adaptive urban planning and enhance human living conditions in humid environments.

1. Introduction

Rapid urbanization and climate change have exacerbated urban heat stress, posing significant challenges to urban livability and public health. Addressing these challenges is paramount for achieving sustainable urban development and enhancing urban resilience in the face of environmental changes. This underscores the critical importance of research on human thermal comfort [1]. To quantify thermal perception, indices including apparent temperature, temperature-humidity index [2], wind efficiency index [3], and discomfort index [4] have been proposed. Apparent temperature serves as a key human comfort indicator [5] by incorporating meteorological elements, such as air temperature, humidity, and wind speed. This metric shows strong associations with urban thermal health, indoor temperature [6], and heat-related mortality [7,8]. Compared to conventional weather station data, apparent temperature more accurately represents actual human thermal sensation and regional climatic comfort [9].

In recent years, research on apparent temperature has intensified, encompassing the development of calculation models, grading methodologies, analyses of spatiotemporal variation, and practical applications. Calculation models now integrate multiple meteorological factors, including temperature, humidity, and solar radiation. Notable models include the Apparent Temperature (AT) model [10], models of perceived temperature based on human thermal equilibrium [11], and methods that calculate perceived temperature in ten-day intervals [12]. Grading methods for apparent temperature have evolved from initial subjective comfort classifications based on surveys [13,14] to more objective approaches utilizing mathematical constructs such as the “golden ratio” (a method deriving comfort thresholds, often linked to core body temperature, using the golden ratio proportion) [15] and the “seasonal anchor method” (a method establishing equivalent thermal sensation thresholds across different indices based on typical seasonal human thermal perception) [16]. Most studies addressing spatiotemporal characteristics have concentrated on analyzing long-term temporal trends and spatial distributions of apparent temperature during summer months (July-August) across various provinces and cities. For instance, Du Jiaming et al. [17] employed daily meteorological data from 31 stations in northern Guangdong (1965–2018) and used GIS technology to examine changes in summer apparent temperature and its distribution. Applications of apparent temperature research are diverse, encompassing tourism climate assessment [18], building energy consumption [19], heating requirements [20], and epidemiological studies [21].

Despite these advances, significant limitations persist in current research. Most studies rely predominantly on sparse meteorological station data [17,21], which, despite providing temporal continuity, fail to capture fine-scale spatial heterogeneity critical for urban-scale analysis [22]. Furthermore, investigations often exhibit a narrow seasonal focus (e.g., summer months) and employ simplified calculation models [10] that inadequately represent synergistic meteorological-environmental interactions. Crucially, models developed for northern China’s drier climates lack generalizability to southern China’s distinct subtropical regime—characterized by intense summer heat-humidity coupling, wet-cold winters, dense vegetation, and pronounced topographic relief [23,24]. This regional complexity remains underexplored. Finally, while environmental drivers (e.g., air temperature, humidity) are recognized as influential [17,22], studies lack systematic quantification of their direct effects versus indirect interactions (e.g., vegetation cooling modulated by urban heat islands), hindering mechanistic understanding of nonlinear pathways.

To address these challenges, this study utilized multi-source remote sensing data, including Landsat 8 OLI/TIRS imagery and MODIS water vapor products, to extract key environmental variables for the Chang–Zhu–Tan region. After atmospheric correction and radiometric calibration, random forest regression was employed to estimate near-surface air temperature from remote sensing parameters. Apparent temperature was then calculated using the Humidex index for subsequent analysis. By integrating inversion results with air temperature and humidity and applying correlation analysis, stepwise regression, and path analysis, we systematically investigated the spatiotemporal distribution and primary environmental drivers of apparent temperature. The contributions of this work are threefold: (1) advancing thermal comfort theory by quantifying multi-factor interactions governing apparent temperature in humid subtropical cities; (2) developing a transferable framework integrating multi-source remote sensing inversion with machine learning for high-resolution apparent temperature mapping; and (3) providing evidence-based guidance for urban heat island mitigation, climate-resilient planning, and public health risk management in southern China.

2. Study Area and Data Sources

2.1. Overview of the Study Area

This paper takes the Chang–Zhu–Tan area as the study region (Figure 1), and the study scope completely covered the main urban area of the Chang–Zhu–Tan and some peripheral areas of the city. The study area is located at the junction of Changsha, Zhuzhou, and Xiangtan, which facilitates the analysis of spatial heterogeneity in apparent temperature among the cities. Geographically, the Chang–Zhu–Tan region is situated in the hilly area in the east-central part of Hunan Province, with Changsha as the center and Zhuzhou and Xiangtan as the secondary centers, in a “zigzag” distribution. The cities are within 40 km of each other, forming a compact structure bordered by Yueyang to the north, Hengyang and Chenzhou to the south, and Yiyang and Loudi to the west. The Chang–Zhu–Tan area belongs to the typical subtropical monsoon climate, with hot summers, cold winters, abundant rainfall, and four distinct seasons. Located in the lower reaches of the Xiangjiang River, the area has an average annual temperature of 16–18 °C, annual precipitation of 1300–1500 mm, and average relative humidity of 80% [23]. Precipitation exceeds 1000 mm annually, with 60–80% concentrated from April to September [24], forming a distinct rainy season. Due to the influence of topography and terrain, the eastern mountainous areas receive relatively more precipitation than the flat areas. The study area extends from 112°49′18″ E to 113°17′22″ E and 27°46′13″ N to 28°17′15″ N.

2.2. Data Sources and Pre-Processing

2.2.1. Remote Sensing Data

The remote sensing data used in this paper included Landsat 8 OLI/TIRS data and MODIS water vapor product data (MOD05-L2). Landsat 8 OLI/TIRS data were obtained from images acquired on 25 September 2016, 26 July 2017, 17 December 2017, and 23 March 2018, representing spring, summer, autumn, and winter, respectively. MOD05-L2 data provide the air column water vapor content on the land surface under clear-sky conditions. Both datasets were georectified, radiometrically and atmospherically corrected, and resampled to a 30 m resolution using ENVI 5.3. To ensure comparable atmospheric water vapor conditions, image pairs with minimal temporal gaps (approximately 22 min between Landsat 8 and MODIS acquisitions) were prioritized. All data were projected to UTM zone 49 (WGS84 datum) for further analysis.

2.2.2. Meteorological Data

Meteorological data were obtained from the ERA5-Land reanalysis dataset, which integrates multiple observational sources (including ground-based and satellite data) through numerical modeling. Hourly data at 11:00 a.m. local time were extracted for the same dates as the Landsat 8 acquisitions (25 September 2016; 26 July 2017; 17 December 2017; and 23 March 2018). A total of 25 grid points were selected, providing spatially interpolated estimates of latitude, longitude, near-surface air temperature, and dew-point temperature derived from assimilated observations and numerical modeling.

2.2.3. Topographic Data

Topographic variables used in this study included the Digital Elevation Model (DEM) and slope. DEM data were obtained from the Geospatial Data Cloud (https://www.gscloud.cn/), providing gridded elevation information for the study area. Slope was derived from the DEM using standard terrain analysis tools in ArcGIS 10.2 GIS software, and represents the rate of elevation change at each grid cell. Both DEM and slope were included as environmental variables to assess their influence on apparent temperature and surface thermal patterns.

3. Research Methods

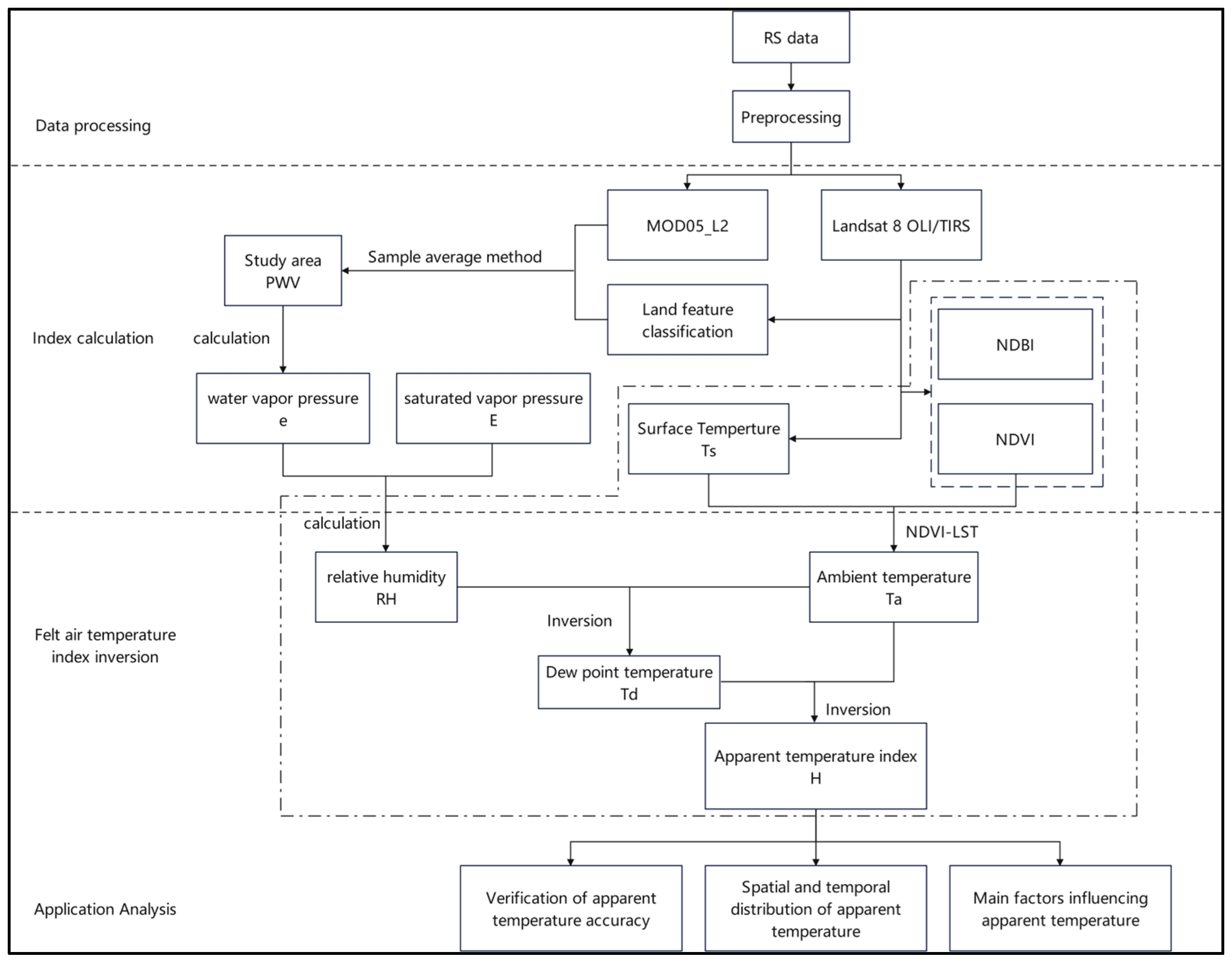
As shown in Figure 2, Landsat 8 and MODIS multi-source remote sensing data were used to obtain surface temperature, relative humidity, and Normalized Difference Vegetation Index (NDVI) information for the Chang–Zhu–Tan area, respectively. Firstly, atmospheric correction was performed on Landsat 8 data to eliminate the effects of atmospheric scattering and absorption, thereby enhancing data accuracy. Secondly, the Random Forest algorithm was used to establish regression models between surface parameters (temperature, humidity, NDVI) and air temperature by combining the observed data from ground meteorological stations to realize the inversion of air temperature. According to the formula of the Humidex apparent temperature index, the air temperature and relative humidity data obtained from the inversion were substituted to obtain the apparent temperature data in the Chang–Zhu–Tan area, and the spatial-temporal distribution of apparent temperature was analyzed. Finally, correlation analysis, stepwise multiple regression, and path analysis methods were used to analyze the apparent temperature influencing factors and acting mechanisms.

3.1. Remote Sensing Inversion Method

3.1.1. Surface Feature Indices Calculation

To explore correlations between apparent temperature and surface features (e.g., buildings, vegetation, water bodies), several indices were calculated from atmospherically corrected Landsat 8 OLI imagery. These include the Normalized Difference Vegetation Index (NDVI) for vegetation, the Modified Normalized Difference Water Index (MNDWI) for water bodies, and the Normalized Difference Built-up Index (NDBI) for built-up areas. These indices collectively characterize the spatial distribution of vegetation, water, and artificial surfaces.

$$NDVI=({\lambda }_{NIR}-{\lambda }_R)/({\lambda }_{NIR}+{\lambda }_R)$$

(1)

$$MNDWI=({\lambda }_G-{\lambda }_{MIR})/({\lambda }_G+{\lambda }_{MIR})$$

(2)

$$NDBI=({\lambda }_{MIR}-{\lambda }_{NIR})/({\lambda }_{MIR}+{\lambda }_{NIR})$$

(3)

where ${\lambda }_{NIR}$ represents the near-infrared band, ${\lambda }_R$ the red spectral band, ${\lambda }_G$ the green spectral band, and ${\lambda }_{MIR}$ the mid-infrared band.

3.1.2. Land Cover Classification Using Random Forest

Random Forest (RF) classification [25] was adopted instead of methods such as Support Vector Machines due to its superior performance with high-dimensional spectral data, robustness to noise, and efficiency in processing large-scale remote sensing datasets. The RF model was configured with 100 decision trees to balance classification accuracy and computational efficiency, with node splits based on Gini impurity minimization and feature subsets selected to reduce correlation and enhance generalizability. Training data were derived from atmospherically corrected Landsat 8 OLI bands, producing a six-class land cover map: urban, industrial, grassland, forest, water bodies, and clouds. Including clouds as a separate class, due to their typically 8–15 °C lower surface temperatures compared to adjacent surfaces, provided critical spatial data for subsequent atmospheric water vapor interpolation.

3.1.3. Near-Surface Temperature Inversion

(1)

Surface temperature inversion

In this paper, the atmospheric correction method [26] was used to invert the surface temperature, which is also called the Radiative Transfer Equation (RTE). The basic principle is to estimate the influence of the atmosphere on the surface thermal radiation and then subtract this part of the atmospheric influence from the total thermal radiation to obtain the surface thermal radiation intensity. This thermal radiation intensity was then converted into the corresponding surface temperature [27]. The calculation formula is as follows:

$$L_{\lambda }=\left[\epsilon B\left(T_s\right)+.\left(1-\epsilon \right).L_{\downarrow }\right]\tau +L_{\uparrow }$$

(4)

$$T_s={\displaystyle \frac{K_2}{\mathit{ln}\left(\frac{K_1}{B\left(T_s\right)}+1\right)}}$$

(5)

where $\epsilon$ is the surface specific radiance, $B\left(T_s\right)$ is the thermal radiant brightness of the blackbody at $T_s$, τ, $L_{\uparrow }$, $L_{\downarrow }$ are the atmospheric profile parameters, and $L_{\lambda }$ is the thermal infrared radiant brightness value; for the Landsat 8 TIR image, K₁ = 774.89 W/(m₂.umk.sr), K₂ = 1321.08 K.

(2)

Inversion of near-surface air temperature

The Temperature Vegetation Index (TVX) method [28] is based on the assumption that the surface temperature at the full vegetation coverage of remote sensing images is approximately equal to the air temperature at the site to estimate the near-surface air temperature. This was achieved by establishing the regression relationship between NDVI and Ts across image arrays (Equation (6)). The surface temperature corresponding to the NDVI value of the full vegetation cover was deduced, and finally the near-surface air temperature for the window was obtained.

$$T_a={NDVI}_{max}\times b+a$$

(6)

where $T_a$ is the near-surface air temperature in °C, and a and b are the intercept and slope of the linear regression coefficients of ${NDVI}_{max}$ and $T_a$, respectively, for each moving window, and ${NDVI}_{max}$ is the theoretical full-coverage NDVI value.

3.1.4. Dew-Point Temperature Inversion

Changes in near-surface air humidity can significantly affect human comfort. At the same temperature, an increase in humidity enhances the sensation of coldness perceived by the human body [29]. In this study, the relative humidity (RH) is calculated using the atmospheric precipitable water volume (PWV) from MOD05_L2, combined with the water vapor pressure (e) and saturated water vapor pressure (E). The dew-point temperature (T_d) is obtained by inverting the RH equation using the near-surface air temperature (T_a). The T_d can be used to characterize the magnitude of the near-surface air humidity, and the calculation formulas are as follows [22,29]:

$$RH={\displaystyle \frac{e}{E}}\ast 100\%$$

(7)

$$T_d=RH\left(A+B\ast t\right)+C\ast t-19.2$$

(8)

In Equation (7), $\mathrm{e}=W/1.7442$;$E=6.112\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{17.67T_a}{T_a+243.5}}\right)$, W is the atmospheric precipitable water (mm), and $T_a$ is the near-surface air temperature (°C). In Equation (8), A = 0.198, B = 0.0017, C = 0.84, $T_d$ is the dew-point temperature (°C), and t is the dry-bulb temperature (°C), i.e., the near-surface air temperature.

3.1.5. Apparent Temperature Inversion

The Humidex index was employed in this study to quantify apparent temperature, comprehensively evaluating human thermal sensation to external environments, especially in hot and humid conditions [30]. It is calculated using air temperature (T_a) and dew-point temperature (T_d) with the following formula [22]:

$$H=T_a+0.5555\ast (6.11\ast {\mathrm{e}}^{5417.753\ast \left({\displaystyle \frac{1}{273.16}}-{\displaystyle \frac{1}{T_d+273.15}}\right)}-10)$$

(9)

where H is the apparent temperature (°C); $T_a$ is the air temperature (°C); $T_d$ is the dew point temperature (°C). The Humidex index was selected for its suitability in the high-humidity climate of Chang–Zhu–Tan and its reliance on parameters that are easily obtained from remote sensing and reanalysis datasets. In contrast to indices such as AT or WBGT, which require additional and less accessible parameters such as wind speed or mean radiant temperature, the Humidex offers a practical and robust measure for regional thermal comfort analysis, especially in environments where humidity strongly influences human perception.

3.2. Correlation Analysis

Correlation analysis is a statistical method used to describe the strength of the linear relationship between two or more variables. In this paper, the Pearson correlation coefficient was used as the index of correlation analysis to calculate the correlation coefficients between apparent temperature and meteorology, ground cover, topography, and geomorphology in the Chang–Zhu–Tan area and to carry out the significance test. The closer the correlation coefficient is to 1 or −1, the stronger the linear relationship between the two variables; the closer the correlation coefficient is to 0, the weaker the linear relationship between the two variables.

3.3. Stepwise Regression Analysis

This paper used the stepwise multiple regression method to screen out the independent variables that have a significant effect on apparent temperature and establish the regression equation. The stepwise multiple regression method can be used to determine the degree of influence of the independent variables on the dependent variable, as well as to establish a prediction model.

Stepwise regression analysis is a statistical method used to screen independent variables and optimize regression models. In this paper, stepwise regression analysis was used to take the apparent temperature as the dependent variable, and the influence factors such as meteorology, surface cover, topography, and geomorphology as the independent variables. According to the standard of F test or t test, the independent variables were selected or eliminated step by step, the main influence factors were screened out, and the optimized regression model was obtained.

3.4. Path Analysis

Pathway analysis is a statistical method used to decompose the total correlation between variables into direct and indirect effects, as well as causal mechanisms [31]. In this paper, we adopted the path analysis method to establish a path model with apparent temperature as the outcome variable and meteorology, ground cover, topography, geomorphology and other influencing factors as cause variables. We calculated the direct effect path coefficients, indirect effect path coefficients, and total effect path coefficients of each cause variable on the outcome variable. The direct effect path coefficient indicates the effect of the causal variable directly through the outcome variable; the indirect effect path coefficient indicates the effect of the causal variable indirectly affecting the outcome variable through other causal variables; and the total effect path coefficient indicates the total effect of the causal variable on the outcome variable [32].

4. Results and Analysis

4.1. Evaluation of Apparent Temperature Retrieval Consistency

This study employed Landsat 8 and MODIS multi-source remote sensing data to retrieve the Humidex index, characterizing apparent temperature across the Chang–Zhu–Tan region. To evaluate the consistency of these retrieved Humidex values, we utilized near-surface air temperature (Ta) and dew-point temperature (Td) products from the ERA5-Land high-resolution reanalysis dataset to calculate a reference Humidex index.

The evaluation process involved several steps: First, Ta and Td data for the study dates (25 September 2016; 26 July 2017; 17 December 2017; and 23 March 2018) were downloaded from the ECMWF ERA5-Land dataset. After preprocessing, 25 spatially representative evaluation points within the study area were selected. Second, Humidex index values for these points were calculated using the ERA5-Land meteorological data and Equation (9). Finally, the corresponding remote sensing-derived Humidex index results were extracted at these 25 evaluation points in ArcGIS 10.2 software, and their average was computed for comparison. Partial comparison results for these evaluation points are presented in

Table 1. Comparison of the Humidex index from remote sensing and ERA5-Land reanalysis data (°C).

Evaluation Point	Spring		Summer		Autumn		Winter
	ERA5-Land HT	RS-Derived HT	ERA5-Land HT	RS-Derived HT	ERA5-Land HT	RS-Derived HT	ERA5-Land HT	RS-Derived HT
1	27.67	24.63	50.48	55.08	45.00	43.98	6.64	7.17
2	27.75	22.93	50.52	49.83	44.96	40.17	6.74	6.53
3	27.96	23.45	50.76	51.21	45.06	40.75	6.92	6.67
4	28.12	23.69	50.68	49.19	45.09	41.79	7.05	6.47
5	28.26	22.69	50.39	50.38	45.10	37.80	7.15	6.48
6	27.94	24.37	50.82	56.38	45.07	43.58	6.82	7.69
7	27.91	24.88	50.74	57.97	44.90	43.58	6.87	7.85
8	28.04	23.36	50.92	55.91	44.91	41.04	7.02	8.06
9	28.20	22.12	50.95	51.42	45.00	41.95	7.17	6.39
10	28.37	21.90	50.80	55.91	45.02	41.04	7.32	8.06
Mean	28.13	22.90	51.27	52.04	44.94	39.99	7.22	6.83

.

The results indicate that the average difference between the remote sensing-derived Humidex index and the Humidex index calculated from ERA5-Land meteorological data was not greater than 6 °C. This suggests that the apparent temperature retrieved in this study is reasonably consistent with the ERA5-Land reference values, adequately representing the thermal conditions for subsequent research. While the remote sensing-derived Humidex index and the ERA5-Land-calculated Humidex index were not identical, with remote sensing results generally being slightly lower than the ERA5-Land calculations, the primary reasons for these discrepancies include: (1) Landsat 8 image acquisition time was 10:57 local time, whereas the ERA5-Land meteorological data acquisition time was 11:00 local time. Under clear-sky conditions, temperature generally increases with time, which could contribute to the observed difference. (2) Surface Temperature (Ts) is a crucial parameter in the apparent temperature retrieval process, and its accuracy directly influences the final Humidex index results. The atmospheric correction method used for Ts retrieval relies on atmospheric transmittance and atmospheric upward and downward radiance parameters derived from calculation models provided by the National Aeronautics and Space Administration (NASA). However, input parameters required by these models (e.g., atmospheric pressure, wind speed, altitude) adopted default values instead of real-time observational data, which can reduce the precision of Ts retrieval.

4.2. Characteristics of the Spatial-Temporal Distribution of Apparent Temperature

4.2.1. Seasonal Variability of Apparent Temperature

In order to analyze the seasonal variability of apparent temperature in Chang–Zhu–Tan, this paper selected Landsat 8 images representing the four seasons of spring, summer, autumn, and winter around 2017, inverted the Humidex index of apparent temperature in the region, and plotted its spatial distribution (Figure 3). In Figure 3, red represents the highest temperature and blue represents the lowest temperature, and the image was processed with tone stretching to enhance the display. Figure 3 shows that the apparent temperature in the Chang–Zhu–Tan area ranged from 48 to 57 °C in summer, from 6 to 8 °C in winter, from 21 to 25 °C in spring, and from 35 to 44 °C in autumn, which presents the four-seasonal change characteristics of hot summer, cold winter, volatile autumn, and pleasant spring. It is important to clarify that these exceptionally high Humidex values indicate a period of severe heat stress, rather than literal air temperatures. This aligns with the index’s purpose of highlighting conditions where the body’s ability to cool itself is severely compromised by high humidity, leading to a much higher ‘felt’ temperature than the actual ambient air temperature. In addition, Figure 3 shows that the apparent temperatures in the three main urban areas of Chang–Zhu–Tan are higher and the apparent temperatures in the areas around the urban areas are lower during spring, summer, and autumn, while the apparent temperatures in the Xiangjiang River Basin are higher and the apparent temperatures in other areas are lower during winter.

In order to quantitatively describe the seasonal variability of apparent temperature in the Chang–Zhu–Tan area, this paper counted the maximum, minimum, average, and maximum temperature difference in apparent temperature in four seasons (

Table 2. Statistical data of apparent temperature in four seasons in the Chang–Zhu–Tan region (°C).

Statistical Data	Maximum Value	Minimum Value	Mean Value	Maximum Temperature Difference	Standard Deviation
Spring	24.99	19.87	23.42	5.12	1.02
Summer	57.97	46.34	52.9	11.63	3.22
Autumn	44	30.69	34.71	13.31	1.87
Winter	8.06	6.83	5.99	1.23	0.71

). Table 2 shows that the maximum temperature differences in spring, summer, autumn, and winter were 5.12 °C, 11.63 °C, 13.31 °C and 1.23 °C, respectively, indicating that the difference in apparent temperature between the main urban area and the surrounding areas is large in summer and autumn, especially in autumn, while the difference in apparent temperature in the whole region is small in spring and winter, especially in winter. These results reflect that the distribution of apparent temperature in the Chang–Zhu–Tan area is characterized by obvious seasonal changes.

4.2.2. Spatial Heterogeneity of Apparent Temperature

Figure 3 shows the apparent temperature in the Chang–Zhu–Tan area. It gradually decreases from the city centers to the surrounding areas. The three main urban areas have higher apparent temperatures, and the surrounding areas have lower apparent temperatures. This spatial pattern relates to the urban heat island effect. The urban center areas are significantly warmer than surrounding areas due to dense buildings, sparse vegetation, poor air circulation, and high heat absorption/emission capacity of surfaces. These factors affect the apparent temperature [20].

Additionally, Figure 3 reveals the seasonal variation in apparent temperature within the Xiangjiang River Basin. In spring, apparent temperatures in the basin are lower compared to those in the main urban areas and their immediate surroundings. During summer, both the Xiangjiang River Basin and the main urban areas experience higher apparent temperatures, with maximum values exceeding 50 °C. This is attributable not only to the urban heat island effect but also to the onset of “three-volt weather” in mid-July, characterized by daytime temperatures nearing 40 °C and elevated relative humidity that exacerbates the perceived heat. In autumn, apparent temperatures in the basin are lower than in the main urban areas but higher than in the surrounding regions. In winter, the apparent temperature in the Xiangjiang River Basin surpasses that of other areas.

In order to quantitatively describe the spatial heterogeneity of apparent temperature in the Chang–Zhu–Tan area, this paper counted the mean values of apparent temperature in the three main urban areas of Changsha, Zhuzhou, and Xiangtan in four seasons (

Table 3. Statistics of average apparent temperature in the three regions of Chang–Zhu–Tan (°C).

Statistical Data	Spring	Summer	Autumn	Winter
Changsha	23.84	54.20	35.26	6.00
Zhuzhou	23.11	51.83	34.34	5.98
Xiangtan	23.31	52.67	34.53	5.99

). Table 3 shows that Changsha has the highest mean apparent temperature, which reaches 54.2 °C in summer, while the apparent temperatures in Zhuzhou and Xiangtan are relatively similar. This indicates that the apparent temperature correlates with the urbanization level, and the higher the urbanization, the higher the apparent temperature. These results reveal the significant spatial heterogeneity and urbanization effect of apparent temperature in Chang–Zhu–Tan.

4.2.3. Difference Analysis Between Apparent Temperature and Air Temperature

Figure 4 shows the distribution of the difference between apparent temperature and near-surface air temperature in the Chang–Zhu–Tan area. It can be clearly seen from the figure that in spring, the apparent temperature in the Xiangjiang River basin is much higher than the near-surface air temperature, with the maximum difference reaching 24.9 °C, while the apparent temperature in some areas around the urban area is lower than the near-surface air temperature; in summer and autumn, the apparent temperature in the whole Chang–Zhu–Tan area is generally higher than the near-surface air temperature, with the maximum difference in the Xiangjiang River basin in summer, as high as 16.4 °C, and that of the main urban area in autumn, which is the largest; in winter, the apparent temperature of the Chang–Zhu–Tan area is higher than the near-surface air temperature. In winter, the apparent temperature in Chang–Zhu–Tan is generally lower than the near-surface air temperature, and the difference is the smallest in the Xiangjiang River Basin.

4.3. Analysis of the Main Influencing Factors of Apparent Temperature

In order to investigate the main influencing factors of apparent temperature distribution in the Chang–Zhu–Tan area, this paper comprehensively considered the meteorology, surface information, topography and geomorphology, and selected eight influencing factors, including air temperature, relative humidity, surface temperature, NDBI, NDVI, MNDWI, DEM (Digital Elevation Model), and slope. Six hundred sample points were randomly selected within the study area using ArcGIS 10.2, and the values of apparent temperature and each index were extracted for each point location. Then, correlation and regression analyses were conducted using SPSS 25.0.

4.3.1. Correlation Analysis

In order to explore the relationship between the apparent temperature and the eight influencing factors, this paper adopted the Pearson correlation analysis method, and the results are shown in

Table 4. Pearson correlation analysis of apparent temperature and influencing factors.

Influencing Factors	Air Temperature	Relative Humidity	Surface Temperature	MNDWI	NDBI	NDVI	DEM	Slope
Pearson correlation coefficient	0.955	−0.884	0.646	0.616	0.8	−0.938	−0.404	−0.308

. Table 4 shows that there is a positive correlation between air temperature, surface temperature, NDBI and MNDWI, and apparent temperature. Among them, air temperature had the highest correlation coefficient with apparent temperature, reaching about 0.955, which is a decisive factor affecting apparent temperature. When the surrounding air temperature is higher than the skin temperature, a person will have a heat sensation, and the higher the air temperature is and the longer it is maintained, the more obvious the heat sensation is. The building index NDBI was used to characterize the building density of the city, and the correlation coefficient was 0.8, which is larger, indicating that the apparent temperature increases with building density. This is because cement, concrete, and other materials in high-density building areas have a strong solar radiation absorption capacity, and it is difficult to dissipate the heat, causing surface temperature increases, and apparent temperature also increases [33]. MNDWI was used to characterize the water distribution and extent; the correlation coefficient was 0.616, which indicates that the apparent temperature increases with MNDWI values. This occurs because water bodies strongly absorb and reflect solar radiation, increasing surface temperature and sensible heat flux (i.e., heat transported from surface to atmosphere). The sensible heat flux affects air temperature and humidity, which in turn affect human apparent temperature. Relative humidity, NDVI, DEM, and slope showed negative correlation with apparent temperature. Among them, relative humidity and NDVI had stronger correlations (−0.884 and −0.938). When air temperature is high, increased relative humidity promotes evaporation, effectively reducing surface temperature and apparent temperature. Vegetation has significant cooling effects; denser vegetation lowers apparent temperature due to enhanced foliar transpiration, reducing surface temperature [34].

4.3.2. Stepwise Regression Analysis

To identify the primary factors influencing apparent temperature, this study employed stepwise regression analysis, using apparent temperature as the dependent variable and eight candidate predictors as independent variables. Stepwise regression iteratively introduces or eliminates variables to optimize model fit. Prior to model construction, multicollinearity among the eight predictors (air temperature, relative humidity, surface temperature, MNDWI, NDBI, NDVI, DEM, and slope) was evaluated using the Variance Inflation Factor (VIF) and tolerance (1/VIF). All variables demonstrated acceptable multicollinearity, with VIF values below 10 (air temperature: 4.92, NDVI: 1.88, relative humidity: 3.15, surface temperature: 5.07, MNDWI: 3.50, NDBI: 4.20, DEM: 1.50, slope: 1.20), ensuring robust coefficient estimates. The Kolmogorov–Smirnov test confirmed that apparent temperature was normally distributed. Stepwise regression was then applied to data from 600 sample points using SPSS 25.0, yielding the parameter estimates presented in

Table 5. Stepwise regression analysis coefficients and models of apparent temperature and its influencing factors, including unstandardized (B) and standardized coefficients, their statistical significance (t, p-values), and overall model fit (R, R²) across different model steps.

Models		Unstandardized Coefficients		Standardized Coefficients	t	p	R	R2
		B	Standard Error
1	(Constant)	3.133	0.354		8.858	0.000	0.955	0.912
	Air Temperature	1.093	0.014	0.955	77.767	0.000
2	(Constant)	16.059	0.384		41.798	0.000	0.987	0.975
	Air Temperature	0.648	0.014	0.566	47.101	0.000
	NDVI	−3.823	0.099	0.099−0.463	−38.573	0.000
3	(Constant)	−6.159	1.324		−4.650	0.000	0.992	0.984
	Air Temperature	1.211	0.034	1.058	35.101	0.000
	NDVI	−3.162	0.089	0.089−0.383	−35.416	0.000
	Relative Humidity	0.173	0.010	0.437	17.263	0.000
4	(Constant)	−6.808	1.268		−5.369	0.000	0.992	0.985
	Air Temperature	1.183	0.033	1.034	35.698	0.000
	NDVI	−3.168	0.085	0.085−0.384	−37.146	0.000
	Relative Humidity	0.177	0.010	0.447	18.475	0.000
	Surface temperature	0.052	0.007	0.051	7.550	0.000

. Four variables—air temperature, relative humidity, surface temperature, and NDVI—were retained in the final model, which describes their relationship with apparent temperature as follows:

$$Y=-6.808+1.183X_1-3.168X_2+0.177X_3+0.052X_4$$

(10)

where Y denotes apparent temperature, X1 denotes air temperature, X2 denotes NDVI, X3 denotes relative humidity, and X4 denotes surface temperature. The coefficient of determination (R²) of the regression model was 0.985, indicating that the model was able to explain 98.5% of the variance in apparent temperature, and the fit was good. The t-test value of each independent variable of the regression model was greater than 2.0 (absolute value), and the significance level was less than 0.05, indicating that each independent variable had a significant effect on apparent temperature. The magnitude and sign of the regression coefficients reflect the degree and direction of the influence of each independent variable on apparent temperature. Air temperature, relative humidity, and surface temperature had a positive correlation with apparent temperature, among which air temperature had the strongest correlation, with a regression coefficient of 1.183; NDVI had a negative correlation with apparent temperature, with a regression coefficient of −3.168. To summarize, this paper established a regression model between the apparent temperature and the four main influencing factors in the Chang–Zhu–Tan area by using a stepwise regression analysis method and carried out parameter estimation and testing of the model. In this paper, a regression model between the apparent temperature and four main influencing factors in Chang–Zhu–Tan area was established by using stepwise regression analysis, and parameter estimation and testing of the model were conducted. The results show that the model fits well, is statistically significant, and can reflect the causal relationship between each influence factor and apparent temperature.

4.3.3. Path Analysis

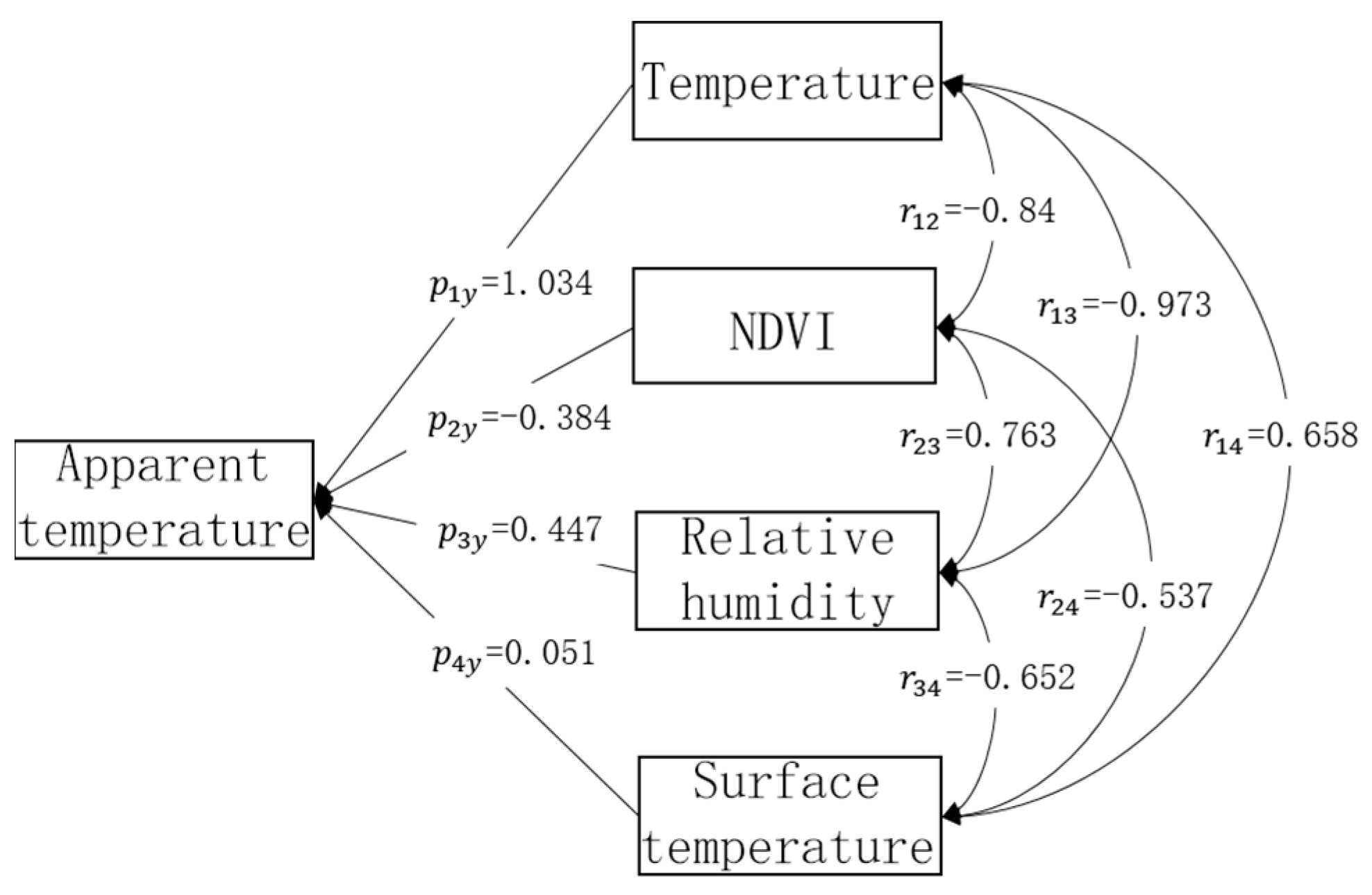
Based on the main influence factors screened by the stepwise regression analysis, this paper carried out the path analysis of air temperature, relative humidity, surface temperature, NDVI, and apparent temperature, and calculated the direct path coefficient and indirect path coefficient. The results of the path analysis are shown in

Table 6. Path analysis of apparent temperature and influence factors.

Apparent Temperature	Correlation Coefficient	Direct Path Coefficient	Indirect Throughput Coefficient
			Air Temperature	NDVI	Relative Humidity	Surface Temperature	Σ
Air temperature	0.955	1.034	—	0.323	−0.435	0.034	−0.075
NDVI	−0.938	−0.384	−0.869	—	0.341	−0.027	−0.555
Relative Humidity	−0.884	0.447	−1.006	−0.293	—	−0.033	−1.332
Surface temperature	0.646	0.051	0.680	0.206	−0.291	—	0.595

and Figure 5. The results of the pathway analysis show that the absolute value of the direct pathway coefficient of air temperature is larger than the absolute value of the sum of the indirect pathway coefficients, which indicates that air temperature mainly affects the apparent temperature directly, whereas the absolute values of the direct pathway coefficients of NDVI, relative humidity, and surface temperature are smaller than the sum of the absolute values of the indirect pathway coefficients, which indicates that NDVI, relative humidity, and surface temperature mainly affect the apparent temperature indirectly. The direct path coefficients of air temperature, relative humidity, NDVI, and surface temperature are 1.034, 0.447, −0.384, and 0.051, respectively, and the direct path coefficient of air temperature is the largest and positive. The indirect path coefficients of relative humidity through air temperature and NDVI were −1.006 and −0.293, respectively, both of which were negative. The indirect path coefficient of NDVI through air temperature was −0.869, which was mainly a negative effect on the sensory temperature through air temperature, and the indirect flux coefficient of relative humidity through air temperature was 0.341, which has a positive effect on apparent temperature. The indirect path coefficient of surface temperature through air temperature is 0.68, which has a positive effect on apparent temperature; the indirect path coefficient through NDVI is 0.206, which has a positive effect on apparent temperature; and the indirect path coefficient through relative humidity is −0.291, which has a negative effect on apparent temperature.

5. Discussion

5.1. Spatiotemporal Characteristics of Apparent Temperature and Dominant Driving Factors

Apparent temperature in the Chang–Zhu–Tan region exhibits significant spatiotemporal heterogeneity. Temporally, apparent temperature varies markedly with seasons, peaking in summer (remote sensing-derived average of 52.9 °C) and reaching its lowest in winter (average of 5.99 °C). Spatially, urban centers and industrial areas show a typical heat island effect, primarily attributed to impermeable urban surfaces. Land cover type is a key driving factor: Normalized Difference Vegetation Index (NDVI) is significantly negatively correlated with apparent temperature (e.g., r = −0.938), while Normalized Difference Built-up Index (NDBI) shows a significant positive correlation (e.g., r = +0.8). These findings are consistent with general understandings in urban thermal environment research.

5.2. Complex Impact of Water Bodies in High-Humidity Regions on Apparent Temperature

Contrary to the general perception of water bodies having a cooling effect, this study found a positive correlation between the Modified Normalized Difference Water Index (MNDWI) and apparent temperature (r = +0.616). This atypical phenomenon results from the combined influence of Chang–Zhu–Tan’s perennially high humidity climate, observation time, seasonality, and urban micro-environmental factors. High humidity amplifies human thermal perception, leading to an “intensified hot” feeling in summer and an “intensified cold” feeling in winter. Specifically, in summer, while water body evaporation consumes latent heat, increased humidity exacerbates the “sauna-like” sensation; in winter, water bodies, due to their high thermal inertia, remain relatively warmer than surrounding land; meanwhile, during spring and autumn, water bodies tend to exhibit a cooling effect. The amplified summer heat perception due to high humidity and the relative warming effect of water bodies in winter collectively contribute to the overall positive correlation between MNDWI and apparent temperature.

5.3. Research Contributions and Uncertainties

This study introduced quantified apparent temperature using the Humidex index and achieved fine-scale retrieval by fusing Landsat 8 and MODIS data. However, discrepancies exist between remote sensing-derived apparent temperature and ERA5-Land reanalysis data (as shown in Table 1, with average differences ranging from approximately 0.39 to 5.23 °C across most seasons). These differences are primarily attributed to (1) inherent mismatches in data source spatial resolution (Landsat 30 m vs. ERA5-Land ~9 km); (2) minor temporal mismatches (Landsat 10:57 vs. ERA5-Land 11:00); and (3) uncertainties in land surface temperature (Ts) retrieval. Despite these variations, the inversion results effectively capture the spatiotemporal patterns of apparent temperature at a regional scale, providing a reasonable representation for urban thermal environment analysis.

6. Conclusions

This study investigated the spatio-temporal distribution and driving factors of apparent temperature (Humidex index) in the Chang–Zhu–Tan urban agglomeration. The key findings are summarized as follows:

(1)

Apparent temperature in the Chang–Zhu–Tan area exhibits distinct seasonal and spatial heterogeneity. Summer experiences extreme heat stress (e.g., an average of 52.9 °C), while winter is cold (an average of 5.99 °C), with notable urban–rural differences in summer and autumn that diminish in spring and winter.

(2)

Spatially, apparent temperature consistently decreases from urban centers (highest in Changsha, followed by Xiangtan and Zhuzhou) to surrounding areas across seasons, directly correlating with urbanization levels.

(3)

The relationship between apparent temperature and air temperature varies seasonally, with apparent temperature often exceeding air temperature in humid conditions (e.g., summer, autumn, and the Xiangjiang River basin in spring) due to humidity’s amplifying effect, and it being lower in winter.

(4)

Apparent temperature is significantly influenced by a range of factors, showing positive correlations with air temperature, surface temperature, and NDBI, and negative correlations with relative humidity, NDVI, DEM, and slope. Air temperature, NDVI, and relative humidity were identified as the primary drivers, exerting both direct and complex indirect influences on apparent temperature through intricate pathways.

In conclusion, this study offers valuable insights into the complex thermal environment of humid urban agglomerations. The identified spatio-temporal patterns and multi-factorial relationships are crucial for informing evidence-based, climate-resilient urban planning strategies that prioritize human well-being and advance urban sustainable development.