Research on the Sustainable Spatio-Temporal Evolution and Driving Factors of Global Transportation Carbon Emissions: Evidence from a Panel of 140 Countries, 1971–2018

Abstract

The rapid development of the global transportation industry has led to increased carbon dioxide emissions, intensifying the pressure to reduce these emissions. On the basis of constructing a global carbon emission analysis framework for the transportation industry, this study used panel data on carbon emissions from the transportation industry in 140 countries or regions for a long-term time series from 1971 to 2018. The standard deviation ellipse, Gini coefficient, and Moran’s I index were used to characterize the spatial patterns of carbon emissions in the global transportation industry. The factors influencing carbon emissions from the global transportation industry were analyzed using quantile regression. The main findings are as follows: (1) From the distribution pattern, the total carbon emissions from the global transportation industry showed a significant upward trend, and the spatial polarization characteristics were particularly significant. (2) The Gini coefficient of global carbon emissions from the transportation industry showed a significant downward trend, characterizing a more balanced spatial distribution. (3) From the perspective of correlation patterns, the spatial distribution of carbon emissions from the global transportation industry was positively correlated. (4) Regarding influencing factors, population size had a significant role in promoting carbon emissions from the transportation industry, and the difference was not apparent. The influence of affluence on carbon emissions was basically in line with the characteristics of the Kuznets curve, technological advances had a significant negative influence on carbon emissions, and participation in the global value chain had a significant influence on carbon emissions from countries or regions with high carbon emissions. In conclusion, it is necessary to enhance international cooperation on carbon emission management in the global transportation industry and adopt differentiated policy measures. For instance, we should accelerate the construction of a multimodal transport system, increase the promotion and support for new energy heavy-duty trucks, implement policies such as priority road rights for new energy heavy-duty trucks and reduce tolls on expressways, and deepen the integration of transportation and energy.

1. Introduction

Reducing carbon emissions and protecting the earth’s environment are imperative and must be jointly pursued worldwide. A significant contributor to global emissions is the transportation industry. This essential industry supports the development of national economies and society and has a fundamental, pioneering role. Rapid economic development has led to increasing economic and social demands for all aspects of the transportation industry, stimulating its development and, thus, increasing its carbon emissions. Therefore, exploring carbon emission reduction in the transportation industry is necessary to achieve global warming control. The research on carbon emissions has mainly focused on the following aspects:

In carbon emission measurement research, methods with the highest academic recognition are the actual measurement method, emission factor method, material balance method, “top-down” method, and “bottom-up” method. For measuring carbon emissions from the transportation industry, ref. [1] proposed a method based on the fundamental theory of “activity-mode of transportation-weight-density-fuel consumption”; ref. [2] combined the measured method with the material balance algorithm and measured the carbon emissions from fossil energy combustion and cement consumption in China from 1950 to 2013; ref. [3] calculated the greenhouse gas emissions from the production, transportation, and on-site construction of building materials in metro stations and shield intervals by using the emission factor method; ref. [4] calculated the greenhouse gas emissions from the production, transportation, and on-site construction of building materials in China’s metro stations constructed from 1995 to 1999 and the shield intervals by applying a “top-down” method from the Intergovernmental Panel on Climate Change (IPCC). “Approach to estimate carbon emissions from the transportation sector in China during 1995–2014. The “top-down” and “bottom-up” approaches are the most widely used in the literature.

The spatial and temporal evolution of carbon emissions in the transportation industry has been broadly investigated. This research is relatively in-depth, with specific research content mainly including the evolution of the spatial pattern of carbon emissions in the transportation industry and the laws and heterogeneity embedded in the evolution [5,6]. Ref. [2] explored the characteristics of the distribution of carbon dioxide emissions from vehicles on major transportation routes in Brazil, using spatial autocorrelation and high-low clustering analysis to explore the spatial distribution characteristics of carbon dioxide emissions from vehicles on major transportation routes in Brazil; ref. [7] analyzed the spatial correlation network evolution characteristics of China’s transportation carbon emission intensity and its driving mechanism by using a modified gravitational model, a social network analysis method, and a time-exponential random graph; ref. [8] analyzed the spatial-temporal evolution characteristics of carbon emissions in a 43-city cluster in the middle reaches of the Bohai Rim Region and explored the spatial agglomeration of carbon emissions by using the spatial autocorrelation model. In studying the spatial and temporal evolution of carbon emissions, many scholars have focused on the evolution of carbon emissions from the transportation industry in terms of temporal and spatial distribution. The driving analysis of the added value and influencing factors of spatial analysis in this article is mainly reflected in two aspects. Theoretically speaking, it can reveal the laws of dynamic evolution. Through spatio-temporal analysis, the spatial pattern of carbon emissions can be identified, the siphon effect and gradient diffusion mechanism between regions can be revealed, and the theoretical framework of the transportation environment system can be improved. At the same time, it is possible to quantify the differences in dominant factors in different regions and construct a multi-dimensional driving model. In addition, the effect of policy intervention can be verified, and the dynamic impact of measures such as traffic restriction policies and the promotion of new energy on the spatio-temporal distribution of carbon emissions can be analyzed, providing methodological support for policy evaluation. From a practical perspective, it mainly has functions such as guiding regional collaborative governance, supporting the implementation of the dual carbon goals, and promoting green technological innovation. Its core value lies in revealing the spatio-temporal heterogeneity of carbon emissions and the driving mechanisms, providing a scientific basis for precise emission reduction.

Researchers have commonly employed three methodologies—Logarithmic Mean Divisia Index (LMDI) factor decomposition, the STIRPAT model, and spatial econometric models—to investigate the factors influencing carbon emissions from the transportation industry [9,10,11]. Ref. [12] examined Asian countries or regions and used the LMDI decomposition method to explore the driving factors of carbon emissions from their transportation industries; ref. [7] used the Tapio model to explore the decoupling relationship between carbon emissions and economic growth at the provincial level and used the LMDI model to decompose the decoupling index and analyze the driving factors affecting the decoupling process; ref. [13] constructed an extended STIRPAT model for empirical analysis, using the carbon emission data of the transportation industry from 1998 to 2017 as the original data.

Most studies on carbon emissions from the transportation industry have focused on the spatial scale below the national or intra-national region. Few studies are from a global perspective, especially spatial correlation studies on carbon emissions from the transportation industry. Notably, the factors influencing carbon emissions from the transportation industry are complex. For example, population, industrial structure, digitalization, and technological innovation may have different degrees of influence on carbon emissions in the transportation industry [14]. Most of the research has neither separated the study of macro- and microeconomic factors nor used an integrated analytical framework that combines both aspects. Moreover, the literature on the analysis and discussion of factors influencing carbon emissions in the transportation industry has mostly relied on the LMDI method, overlooking its susceptibility to subjective influences from researchers.

This study aimed to demonstrate the necessity of investigating carbon emissions in the transportation industry from a global standpoint, showcasing the magnitude of disparities in the temporal and spatial dimensions across countries or regions. Thus, using data sourced from the International Energy Agency (IEA), this study compiled a long-term dataset from 1971 to 2018 on the global carbon emissions from the transportation industry to provide a global perspective and analyze the temporal patterns of carbon emissions in the transportation sector. Next, this study analyzed the spatial distribution pattern, spatial dispersion pattern, and spatial correlation pattern of global carbon emissions from the transportation industry. Finally, this study analyzed the contribution rate of various influencing factors to the countries or regions with carbon emissions from the transportation industry in different quartiles through quantile regression.

2. Theoretical Analysis and Hypothesis

To address the rapid global climate change and alleviate the Earth’s environmental problems, the current development mode that sacrifices the environment must be transformed. Green environmental protection has become the new trend and new banner of The Times. The term “low-carbon economy” first came into the public eye in a document issued by the British government and was subsequently widely applied in the academic circle. Regarding the specific definition of “low-carbon economy”, there is no official statement recognized by all countries or regions internationally, and the academic community also has its own opinions on this [15].

The definition of low-carbon economy in foreign academic circles mostly starts from the perspective of the market economy, is rich in capitalist color, and is more suitable for Western developed countries that have reached a certain stage of economic development [16,17]. The domestic academic circle’s definition of a low-carbon economy takes into account the Marxist thought of harmonious coexistence between humans and nature [18,19]. Refs. [20,21,22,23] defined a low-carbon economy from a fresh perspective of energy flow and resource flow as an economic behavior that achieves low-carbon development of energy flow and recycling of resource flow through innovation and optimization in technology and systems, thereby achieving both economic growth and environmental quality [3,24].

Ref. [13] based on a comprehensive analysis of existing concepts, defined the low-carbon economy from the perspective of human beings, the main body of economic activities [13]. Ref. [4] hold that a low-carbon economy is an environmentally friendly economic form that aims for sustainable development and emerges when productivity and the humanistic environment reach a certain level [4].

Based on the viewpoints of scholars at home and abroad, this article defines a low-carbon economy as follows: humans actively take measures to achieve technological innovation and the upgrading of the humanistic environment, and ultimately reach a harmonious coexistence of human development and the natural environment.

To a certain extent, “low-carbon transportation” can be said to be associated with “low-carbon economy”. After the UK first proposed the concept of “low-carbon economy” in a government document in 2003, the theory of low-carbon economy flourished. Shortly after that, the UK Department for Transport was the first to propose “low-carbon transport” in the “Innovation Strategy for Low-Carbon Transport”.

Regarding the concept of low-carbon transportation, just like low-carbon economy, there is no unified consensus at home and abroad yet, and the academic community also has different opinions on it. Refs. [2,25,26] started from the carbon reduction methods in transportation and held that low-carbon transportation refers to a development approach that uses clean energy at the production source and reduces vehicle carbon emissions during the production process [2,27,28,29]. Ref. [5] starting from the perspectives of enterprises and industries holds that a low-carbon economy should be achieved through enterprise innovation and the optimization of the transportation sector structure to realize green, low-consumption and sustainable development [5]. Ref. [16] started from the characteristics of low-carbon transportation and held that low-carbon transportation is a mode of transportation with low energy consumption, low pollution and high energy combustion rate [16].

Based on the viewpoints of various scholars, this article defines low-carbon transportation as follows: mobilizing the subjective initiative of participants in the transportation industry, including individuals and enterprises, as well as the government, improving technological and humanistic environmental levels, controlling carbon emissions from the source of energy use in the transportation industry, and reducing pollution during the production process of transportation activities, thereby achieving the goal of green and low-carbon transportation.

There are numerous factors influencing carbon emissions within the transportation sector, and the mechanisms of these various factors differ [30]. This article aims to delve into the mechanisms that impact carbon emissions in the transportation industry from five perspectives: scale effect, structural effect, income effect, technology effect, and global value chain effect. The analysis framework is depicted (Figure 1).

• Scale effect

The scale effect refers to the expansion of the total scale of economic and social production, the total scale of population, and the total scale of the transportation industry, which objectively brings about more inputs of production factors and more consumption of energy resources, resulting in an increase in carbon emissions from the transportation industry. Specifically, the expansion of the total scale of economic and social production in a nation or region will stimulate the growth of the total scale of the transportation industry through various aspects and processes of social production activities, thereby causing an increase in carbon emissions from the transportation industry [31,32]. It is important to note that the indirect impacts resulting from scale expansion should not be overlooked. With the expansion of the total scale of economic and social production and the scale of the transportation industry, income will continue to rise. Consequently, both society and the industry itself tend to utilize more resources and funds to achieve technological innovation and improvement, thereby attaining higher profits, such as enhancing energy efficiency and developing green and environmentally friendly clean energy. These actions will contribute to the reduction of carbon emissions [33]. Considering the positive and negative effects of scale effect, this paper proposes the following hypothesis:

Hypothesis 1A. When the direct effect of scale is greater than the indirect effect, the expansion of scale is positively correlated with carbon emissions in the transportation industry.

Hypothesis 1B. When the direct effect of scale is less than the indirect effect, the expansion of scale is negatively correlated with carbon emissions in the transportation industry.

2.

Structure effect

The economic structure of a country or region further affects the level of socio-economic development by influencing changes in factor endowments and resource allocation efficiency [10]. An optimized industrial structure has high added value, low factor input rates, and high production efficiency, which is conducive to achieving more efficient, rational, and environmentally friendly resource allocation, thereby reducing carbon emissions in the transportation industry. In addition, the transportation industry itself is an important component of the service industry, and its own industrial structure adjustment and optimization will inevitably affect carbon emissions. Based on the above analysis, the following hypothesis is proposed:

Hypothesis 2. The optimization of industrial structure is conducive to reducing carbon emissions in the transportation industry.

3.

Income effect

The Environmental Kuznets Curve (EKC) theory posits that, initially, during the early stages of economic development, environmental pollution exhibits a positive correlation with per capita income. However, as economic development attains a certain threshold, this trend reverses, with environmental pollution declining as per capita income increases. Countries or regions with high income levels have a relatively stronger attraction to high-end production factors such as technology and information, which is conducive to improving the technological level of the entire economic society and transportation industry, thus achieving the demand for carbon emission reduction [34]. Simultaneously, individuals with high income levels have more opportunities to receive higher-quality education, and such people tend to be more inclined to select green and environmentally friendly lifestyles and consumption structures, which is conducive to achieving carbon emission reduction in the transportation industry. Conversely, countries or regions with low and medium income levels tend to utilize capital and other production factors to augment economic aggregates and improve basic material life, often at the expense of environmental quality. Based on this, the following hypothesis is formulated:

Hypothesis 3A. When per capita income is at a low level, especially in developing countries or regions, the increase in per capita income will increase carbon emissions in the transportation industry.

Hypothesis 3B. When the per capita income level reaches a certain value, especially in developed countries or regions, the increase in per capita income level will reduce carbon emissions in the transportation industry.

4.

Technical effects

The influence of technological effects on carbon emissions in the transportation industry primarily manifests in three aspects. Firstly, via technological means, it directly impacts the industry that manufactures transportation vehicles, such as the development and utilization of clean energy to power cars, and the employment of magnetic levitation trains, which can curtail high carbon emissions in the transportation industry at the source. Secondly, technology can enhance the efficiency of energy utilization and further diminish carbon emissions in the transportation industry. The effects of the above two aspects can be summarized as the carbon emission intensity effect, signifying that by enhancing technological levels, carbon emissions per unit of output can be reduced. Thirdly, the advancement of clean energy technologies can reduce the usage of high-carbon-emitting fossil fuels, effectively suppressing carbon emissions in the industry through energy structure effects. Hence, the following hypothesis is proposed:

Hypothesis 4. The improvement of technological level is conducive to the reduction of carbon emissions in the transportation industry.

5.

Global value chain effect

Despite the emergence of anti-globalization voices in recent years, the overall trend of international division of labor in the global value chain will not change. The new international division of labor means that the participation and division of labor status of countries or regions in the global value chain will show new changes [8]. On the one hand, with the continuous expansion of the global value chain, more and more countries or regions are actively participating in the process of globalization, and the horizontal coverage area of international intra-product division of labor is constantly expanding, and the degree of foreign trade is constantly strengthening, which provides a steady stream of transportation demand for the transportation industry, leading to an increase in its carbon dioxide emissions level. On the other hand, with the continuous extension of the global value chain, the status of countries or regions in the international division of labor is beginning to change. More developing countries or regions will gradually move closer to higher-level value chains, and continue to achieve clean and green production activities, thus achieving the goal of improving the environment and reducing carbon emissions. Therefore, a hypothesis is proposed:

Hypothesis 5A. When the influence of participation in the global value chain is greater than the influence of division of labor status, the carbon emission level of the transportation industry will increase with the increase in participation in the global value chain.

Hypothesis 5B. When the influence of participation in the global value chain is less than the influence of division of labor status, the carbon emission level of the transportation industry will decrease with the improvement of the division of labor status in the global value chain.

3. Research Methodology and Data Sources

3.1. Standard Deviational Ellipse (SDE)

An SDE analysis can quantitatively analyze the spatial distribution of the research object in terms of centrality, directionality, and spreading by using the following processes and formulas:

$$\begin{gathered} SDEx=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{(x_i-\overline{X})}^2}}{n}}} \\ SDEy=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{(y_i-\overline{Y})}^2}}{n}}} \end{gathered}$$

(1)

$$\begin{gathered} A=({\displaystyle \sum _{i=1}^n{{\tilde{x}}_i}^2}-{\displaystyle \sum _{i=1}^n{\tilde{y}}_i^2}) \\ \tan \theta ={\displaystyle \frac{A+B}{C}} \end{gathered}$$

$$B=\sqrt{{({\displaystyle \sum _{i=1}^n{{\tilde{x}}_i}^2}-{\displaystyle \sum _{i=1}^n{\tilde{y}}_i^2})}^2+4({\displaystyle \sum _{i=1}^n{({\tilde{x}}_i{\tilde{y}}_i)}^2)}}$$

$$\begin{gathered} C=2{\displaystyle \sum _{i=1}^n{\tilde{x}}_i{\tilde{y}}_i} \\ \tan \theta ={\displaystyle \frac{A+B}{C}} \end{gathered}$$

(2)

$${\sigma }_y=\sqrt{2}\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{({\tilde{x}}_i\sin \theta -{\tilde{y}}_i\cos \theta )}^2}}{n}}};{\sigma }_x=\sqrt{2}\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{({\tilde{x}}_i\cos \theta -{\tilde{y}}_i\sin \theta )}^2}}{n}}}$$

(3)

In Equation (1), $x_i$ and $y_i$, respectively, refer to the longitude and latitude coordinates of the spatial positions of countries around the world. $x_i$ is the arithmetic average center of carbon emissions from the transportation industry of a country or region, and n is the number of countries or regions. In Equation (2), among them, $\widetilde{x_i}$ and $\widetilde{y_i}$ is the difference between the average center and the coordinate values of x and y. In Equation (3), ${\sigma }_y$ and ${\sigma }_x$ have determined the specific lengths of the long and short axes.

3.2. Gini Coefficient

In this study, the Gini coefficient was used to further explore the dynamic spatial dispersion evolution of carbon emissions from the global transportation industry. The formula is as follows:

$$G=1-{\displaystyle \sum _{j=1}^m{\mathrm{\mu }}_j}*(2Q_j-S_j)$$

(4)

In Equation (4), G represents the value of the Gini coefficient, with a range of [0,1]. Moreover, the closer the value of the Gini coefficient is to 1, the more obvious the spatial polarization characteristics of the research object are. The closer the value of the Gini coefficient is to 0, the more obvious the discrete characteristics of the research object in space; ${\mu }_j$ is the proportion of carbon emissions from the transportation industry in each country or region when they are evenly distributed globally; $S_j$ is the actual share of carbon emissions from transportation in each country or region; and $Q_j$ is the cumulative share of carbon emissions from the transportation sector in the JTH country or region.

3.3. Moran’s I Index

This study used the complete Moran’s I index and local Moran’s I index to quantify the spatial agglomeration characteristics of the carbon emission values of the transportation industry in each country or region. The formula is as follows:

$$I={\displaystyle \frac{n{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n{w}_{ij}(x_i-\overline{x})(x_j-\overline{x})}}{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n{w}_{ij}}{\displaystyle \sum _{i=1}^n{(x_i-\overline{x})}^2}}}$$

(5)

In Equation (5), n is the total number of countries or regions; x_i and x_j denote the observed values of carbon emissions from the transportation sector of each country or region in spaces i and j, respectively; $\overline{x}$ is the average value of carbon emissions from the global transportation sector; and w_ij is the spatial weight matrix, used in this study as the adjacency weight matrix.

3.4. STIRPAT Model

Ref. [4] conceptualized the pressures and impacts on the environment caused by economic activities in human society; they attempted to analyze them quantitatively and were the first to propose the IPAT model. Ref. [17] modified the IPAT model to create the STIRPAT model, which expresses the impacts of population size, wealth, and technology level on the environment as a stochastic impact regression (Equation (6)).

$$I=a{P}^b{A}^c{T}^d\epsilon$$

(6)

I, P, A, and T, respectively, denote four factors: the pressure on the environment and its impact, population size, affluence, and technology level where the economy and society are located. a is a constant term; b, c, and d are the estimated indices of the population size, affluence, and technology level, respectively; and ɛ is the random error term of the model. In this study, within the framework of the STIRPAT theoretical analysis, both sides of the equation are treated logarithmically; that is, the relationship between environmental pressures and influencing factors is transformed into a linear relationship that can be quantified through the derivation of the equation (Equation (7)).

$$\ln I=\ln a+b\ln P+c\ln A+d\ln T+\ln \epsilon$$

(7)

This study attempted to expand and decompose the STIRPAT model [2,18,19]. The total population at the end of the year (POP) measures the scale effect of the population; gross domestic product (GDP) and total transportation value (T.V.) measure the scale effect of affluence; the share of tertiary industry (FTR) measures the structural effect of affluence; the level of per capita income (PGIN) measures the income effect of affluence; the share of clean energy (CERC) measures the structural effect of energy at the technological level; the carbon dioxide emission (CGDP) measures the intensity effect of carbon emission per unit of value added; total foreign trade measures (IEV) the participation in global value chains; the share of exports of high-tech products and services (TICR) measures the division of labor position in global value chains.

$$\begin{gathered} \ln TC{T}_{it}=\ln C+{\beta }_1\ln P_{it}+{\beta }_2\ln GD{P}_{it}+{\beta }_3\ln T{V}_{it}+{\beta }_{4}FT{R}_{it}+{\beta }_5\ln PGI{N}_{it}+ \\ {\beta }_6\ln CER{C}_{it}+{\beta }_7\ln CGD{P}_{it}+{\beta }_8\ln IE{V}_{it}+{\beta }_9\ln TIC{R}_{it}+{\alpha }_i+{\mu }_{it} \end{gathered}$$

(8)

In Equation (8), α_i is the individual fixed effect, β_i is the parameter to be estimated, lnC is the constant term, i denotes different countries or regions, t denotes different years, and µ_it is the random error term. Because of the significant differences between countries or regions and because the traditional mean regression cannot avoid the influence of extreme values, this study conducted quantile regression. The model expression is as follows:

$$\begin{gathered} Q_{\tau }(\ln TC{T}_{it})={(C)}_{\tau }+{\beta }_{1\tau }\ln P_{it}+{\beta }_{2\tau }\ln GD{P}_{it}+{\beta }_{3\tau }\ln T{V}_{it}+{\beta }_{4\tau }FT{R}_{it}+{\beta }_{5\tau }\ln PGI{N}_{it}+ \\ {\beta }_{6\tau }\ln CER{C}_{it}+{\beta }_{7\tau }\ln CGD{P}_{it}+{\beta }_{8\tau }\ln IE{V}_{it}+{\beta }_{9\tau }\ln TIC{R}_{it}+{\alpha }_i+{\mu }_{it} \end{gathered}$$

(9)

In Equation (9), Q_τ(lnTCT_it) and (C)_τ are the τ-quantile of the total and constant terms of carbon emissions from the transportation sector, and β_1τ, β_2τ, β_3τ, β_4τ, β_5τ, β_6τ, β_7τ, β_8τ, and β_9τ are the regression coefficients of τ-quantile of the respective variables.

3.5. Data Sources and Description

This study analyzed carbon emissions from the transportation industry on a global scale. Based on the IEA CO₂ emissions database, carbon emissions data from the transportation industry of 140 countries or regions and a long time series from 1971 to 2018 were used as the research sample, including the total amount of carbon emissions from the transportation industry, the percentage of fossil fuels in the energy consumption, and the national or regional society-wide CO₂ emissions. The dissolution of the Soviet Union in the early 1990s, which comprised 15 countries or regions, led to a change in the statistical caliber of countries or regions, and the number of samples increased to a certain extent. Additionally, socioeconomic indicators, such as the tertiary industry’s value-added share in total social output, GDP, per capita income level, and total population, were derived from the World Bank’s World Development Indicators database. Because of the relatively large scale of this study, some countries or regions are affected by their political and economic development and geographic environments, and additional data are necessary, such as for South Africa and some countries or regions in the Middle East. Additionally, in elucidating the driving factors of global carbon emissions from the transportation industry, because of the consistency of statistical criteria, data availability, and continuity, this study refers to literature, for example, refs. [20,21], and ref. [22], and others, to conduct data selection and screening. Finally, panel data from 140 countries or regions from 1971 to 2018 were used as the research sample to investigate the factors influencing global carbon emissions from the transportation industry. This sample is representative and typical because it covers countries and regions from five continents with various levels of development and income.

4. Findings

4.1. Spatial Distribution Evolution

Using carbon emissions data from the transportation industry of 140 countries or regions, this study employed ArcGIS10.8 software for visualization processing (Figure 2).

Between 1971 and 2008, global carbon emissions from the transportation sector showed a spatial pattern of “one strong and multiple poles”. The United States is one of the main engines of the global economy, and its transportation demand has been consistently high. Although the proportion of carbon emissions from the transportation industry decreased from 50.45% to 30.03% globally, it still far exceeded that of other countries and regions. In the early 1990s, with the dissolution of the Soviet Union, the statistical scope of International Energy changed. Russia emerged as an independent nation, and its carbon emissions data were collected and recorded separately. As the sole successor of the former Soviet Union, Russia’s carbon emissions from its transportation industry ranked second globally, making it a new growth pole, along with Japan, Canada, China, Mexico, Brazil, Spain, the United Kingdom, France, and other countries or regions.

From 2009 to 2018, global carbon emissions from the transportation sector showed a spatial pattern of “two strengths and multiple poles.” China became one of the world’s largest manufacturing and trade centers, and its transportation demand, foreign trade volume and, thus, carbon emissions from its transportation sector increased significantly. Today, China is the second-largest transportation emitter worldwide. From 2009 to 2018, its share of carbon emissions from the transportation sector increased from 9.36% to 13.48%. Notably, during the same period, the share of US transportation carbon emissions decreased from 28.86% to 25.57%. As shown in Figure 2, the countries or regions that are growth poles showed a clear trend of spreading to the southeast, resulting in a shift in the overall pattern of carbon emissions from the global transportation industry in the almost near west–east direction.

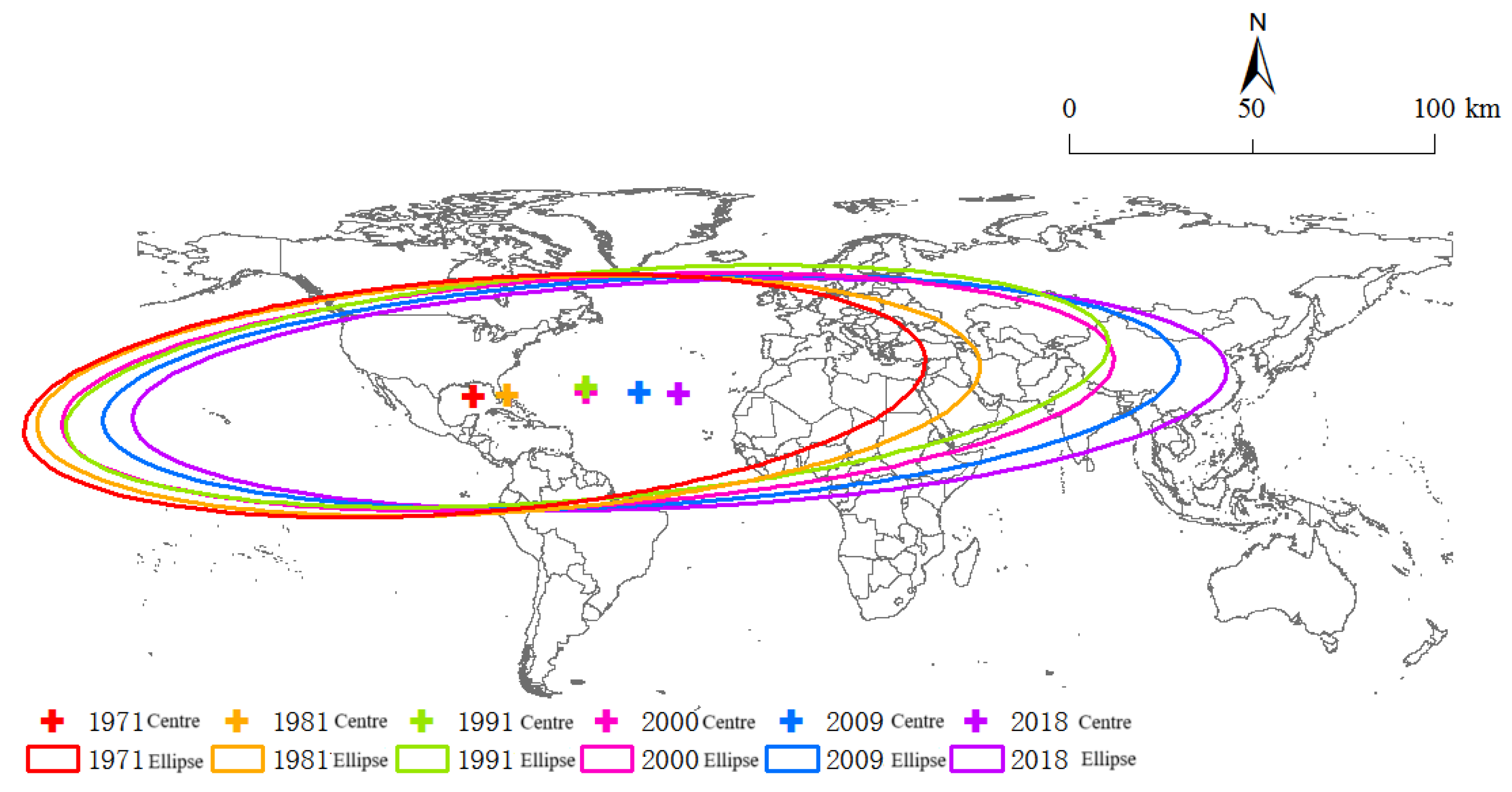
This study used the SDE method to analyze the dynamic evolutionary patterns of global carbon emissions from the transportation industry in spatial distribution. Three aspects of global carbon emissions from the transportation industry—centrality, directionality, and dispersion—are explored in the discussion section of this paper. Furthermore, it further validates this conclusion. Subsequently, using the ArcGIS 10.8 software platform and temporal dynamic evolution analysis, this study selected six years: 1971, 1981, 1991, 2000, 2009, and 2018. On the basis of the carbon emission data from the transportation industry of each country or region for the respective years, six distinct ellipses were generated, and the results were output accordingly (Figure 3).

The center of gravity of global carbon emissions from the transportation sector showed a clear trend of shifting from west to east, closely related to rapid economic development in the Eastern Hemisphere, especially in East Asia, and the north–south direction was unchanged.

Global carbon emissions from the transportation industry are generally distributed in the northwest-southeast direction, with the east–west difference being more evident than the north–south difference. Although the corner shows an inevitable upward trend through the dynamic change in the corner of the ellipse, its angle is not apparent, indicating that the overall global carbon emissions from the transportation industry did not change significantly in the north–south direction.

Regarding spreadability, the area of the global transportation carbon emissions ellipse increased from 12,386.20 to 14,586.68, the perimeter of the ellipse increased from 532.34 to 631.76, and the oblateness of the ellipse increased from 2.88 to 3.84 from 1971 to 2018. The dynamic change in the three values can be seen as a combination of three values. The spatial distribution of the carbon emissions of the global transportation industry is more dispersed and balanced in the east–west direction than in the north–south direction, which is consistent with the conclusion of the dynamic evolution of the time series.

4.2. Spatial Dispersion Evolution

According to the analysis of the evolution of spatial distribution, the characteristics of the “strong pole” agglomeration of global carbon emissions from the transportation industry in space can be obtained. However, the specific dispersion law of any time-ordered change cannot be portrayed. Therefore, this study used the Gini coefficient to further explore the dynamic dispersion of carbon emissions from the transportation industry during the spatial evolution process.

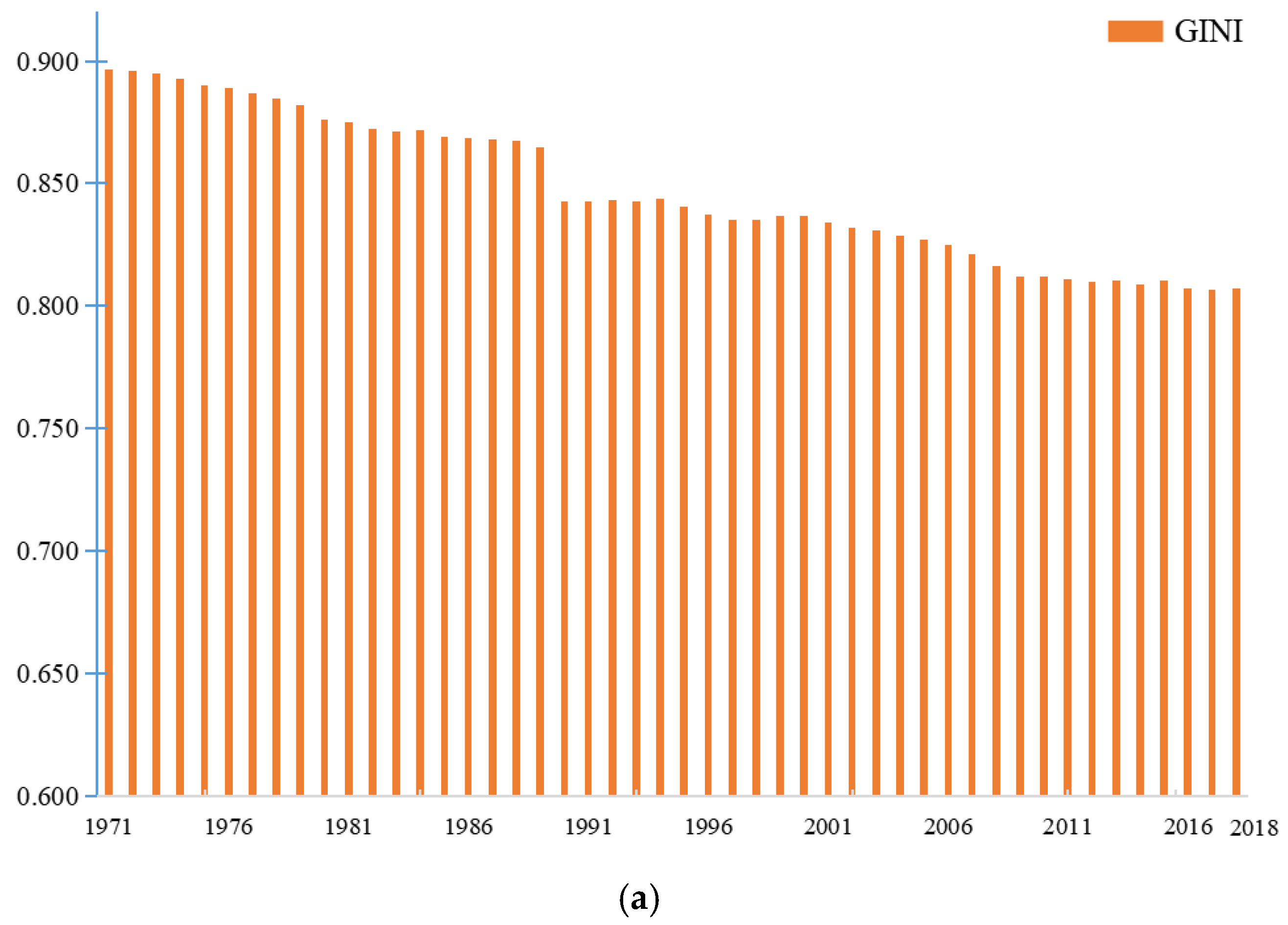
According to the results (Figure 4), from 1971 to 2018, the value of the Gini coefficient was always greater than 0.80, which indicates that the polarization of carbon emissions from the global transportation industry is more obvious. Additionally, the Gini coefficient showed an apparent downward trend, indicating that carbon emissions from the global transportation industry show a balanced distribution trend in space. Notably, under the influence of the world economy and politics, in the early 1990s, the Soviet Union became 15 countries or regions, leading to a significant increase in the number of samples for the study, and from 1989 to 1990, there was a steep decline in the Gini coefficient. The dynamic evolution of the results demonstrated that the overall trend of the Gini coefficient during the long-series study period of 1971–2018 was not affected by this.

Based on the aforementioned, combined with the dynamic evolution of the Gini coefficient, this study divided the spatial dispersion of global transportation carbon emissions into four stages. The Gini coefficient values of global carbon emissions from the transportation industry exhibited a rapid decline from 0.8963 to 0.8646. This trend manifested as a rapid dispersion in spatial distribution, primarily due to a significant decrease in the proportion of carbon emissions from the transportation industry in the United States, coupled with an increasing trend in carbon emissions from transportation industries in other countries or regions.

During the second phase, from 1990 to 2000, the Gini coefficient values of global carbon emissions from the transportation industry exhibited a slow fluctuating decline from 0.8429 to 0.8369. This trend was characterized by an overall slow dispersion in spatial distribution. Notably, this period was characterized by complex and dynamic international political and economic conditions. Influenced by changes in Eastern Europe and the dissolution of the Soviet Union, the global landscape shifted toward a multipolar pattern. Countries or regions mutually constrained each other, and economic development entered a phase of adjustment and recovery.

During the third phase, from 2001 to 2009, global carbon emissions from the transportation industry exhibited an accelerated decline in the Gini coefficient values from 0.8341 to 0.8118. This period showed a renewed acceleration in the dispersion of the spatial distribution. The primary reason for this trend was the significant growth in carbon emissions from China’s transportation industry during this phase. The momentum shifted from being a growth pole to a polarization effect, transitioning from a stage of a “single strong nation” to “dual strong nations.” Moreover, in several countries or regions, especially developing countries or regions in Southeast Asia, the rapid growth of carbon emissions from the transportation industry resulted in the proportion of its share of the global total rising faster, accelerating the growth pole, weakening the polarization effect of the United States, and accelerating the balance of the spatial distribution of carbon emissions from the global transportation industry. The Gini coefficient value again showed a slow decline, from 0.8122 in 2010 to 0.8071 in 2018, which in spatial distribution again showed slow decentralization characteristics. After the 2008 financial crisis, the development of various countries and regions was constrained, affecting their transportation industry development.

4.3. Evolution of Spatial Correlations

4.3.1. Global Autocorrelation

GeoDA (v1.14.0.0.) software was used to calculate the global Moran’s I index for six sections to measure the degree of spatial correlation of carbon emissions from the global transportation industry and to test its significance in

Table 1. Global Transportation Carbon Emissions Global Moran’s I Index, 1971–2018.

Year/Indicator	1971	1981	1991	2000	2009	2018
Moran’s I	0.1139	0.1768	0.1275	0.1283	0.1411	0.1130
Zscore	6.7446	8.5012	4.7593	4.8441	3.5440	2.2300
E(I)	−0.0079	−0.0079	−0.0079	−0.0079	−0.0079	−0.0079
Threshold (α = 0.05)	1.96	1.96	1.96	1.96	1.96	1.96

.

Between 1971 and 2018, the global Moran’s I index for carbon emissions from the global transportation industry was greater than zero. The Z value of the average statistic was significant (i.e., p < 0.05) at the level of α = 0.05 (with a critical value of 1.96), indicating a significant clustering trend in carbon emissions from the transportation industry across various countries or regions globally. This suggests that countries or regions with high carbon emissions from the transportation industry are surrounded by regions with similarly high emissions.

From 1971 to 1981, the value of the global Moran’s I index showed a sharp upward trend from 0.1139 to 0.1768, indicating that the degree of spatial correlation of global carbon emissions from the transportation industry tended to strengthen. Countries or regions with similar carbon emissions tended to be more spatially concentrated. From 1981 to 1991, the value of the global Moran’s I index showed a decreasing trend from 0.1768 to 0.1275, indicating that the degree of spatial correlation of global carbon emissions from transportation tended to weaken. Countries or regions with similar carbon emissions tended to be more spatially dispersed. From 1991 to 2009, the global Moran’s I index showed an upward trend from 0.1275 to 0.1411, indicating that the degree of spatial correlation of global carbon emissions from the transportation industry is once again strengthened, and countries or regions with similar carbon emissions tend to be spatially concentrated again. From 2009 to 2018, the value of the global Moran’s I index decreased from 0.1411 to 0.1130, returning to the level consistent with the value of the global Moran’s I index in 1971, indicating that the spatial correlation of global carbon emissions from the transportation industry has repeatedly weakened. Countries and regions with similar carbon emissions again tended to be spatially dispersed.

According to the dynamic change pattern of the global Moran’s I index, the degree of spatial correlation of carbon emissions from the global transportation industry recurred during the study period, coinciding with the change pattern of the Gini coefficient in the previous section.

4.3.2. Local Autocorrelation

Local spatial autocorrelation can be used to measure high- and low-value agglomeration occurring in different spatial locations, that is, the refined distribution of the degree of spatial elemental agglomeration. It measures spatial heterogeneity to a certain extent. To explore the local aggregation characteristics of global transportation carbon emissions more intuitively, this study analyzed the local autocorrelation characteristics of global transportation carbon emissions based on the GeoDA platform, obtained the LISA aggregation-type map, and applied the LISA clustering method to reveal the local similarities and differences in the spatial correlation of transportation carbon emissions among countries or regions at national scales (Figure 5). Global transportation carbon emissions for 1971–2008 are shown in Figure 5. In 2008, the number of countries or regions with significant local carbon emissions from the transportation industry showed an apparent upward trend, with increasing spatial dependence on local geography. Affected by the 2008 financial crisis, the number of significant countries or regions declined from 2009 to 2018 but increased overall from 1971 to 2018.

Specifically:

(1) “High-High” zone (High-High). There was a significant positive spatial correlation between countries or regions belonging to this type of region, with minor local differences in global carbon emissions from the transportation industry and relatively strong local homogeneity; that is, countries or regions with high carbon emissions also had high carbon emissions in the surrounding countries or regions. This type of region was characterized by its apparent “large concentration,” mainly concentrated in some developed countries, especially in North America, with the United States, Canada, and Mexico consistently in this zone during the study period. France and the Netherlands were in this zone from 1971 to 1981. From 2009 to 2018, India entered this zone because its abundant labor resources attracted substantial foreign investment and businesses, leading to rapid economic development and, consequently, high carbon emissions in the transportation sector.

(2) “Low-Low” zone (Low-Low). Countries or regions in this zone also had a significant positive correlation in spatial distribution. However, countries or regions in this spatial location and their neighboring countries or regions had smaller values of carbon emissions from the transportation industry than those of High-High, and spatial local differences were minor. This zone showed a relatively stable cluster spatial distribution, mainly in Africa, where economic development was relatively backward, such as in Zambia, Congo, Tanzania, and other countries or regions on the African continent that were politically and economically backward and geographically harsh, and the complex environment had insufficient infrastructure. However, the development of the transportation industry is complex.

(3) “High-Low” zone (High-Low). Countries or regions in this zone exhibited a significant negative spatial correlation in carbon emissions with the transportation industry, with substantial local differences and strong heterogeneity in emission values. Countries or regions in such spatial locations demonstrated high carbon emissions, and those surrounding them exhibited lower emissions than those aforementioned, forming localized heterogeneous “ hotspot areas.” This zone emerged after 1991 and has remained primarily stable in South Africa. As the second-largest economy in the African region, South Africa was leading in the production of commodities, such as gold and diamonds, contributing to relatively high living standards for its citizens.

(4) “Low-high “ zone (Low-High). Countries or regions in this zone also exhibited a significant negative spatial correlation with relatively large local spatial differences and strong local heterogeneity in emission values. This zone had lower carbon emissions than High-Low, and surrounding countries or regions exhibited relatively higher emissions, forming localized heterogeneous “cold spot areas.” This zone is primarily concentrated around “strong countries” and “growth poles,” forming a distinct accompanying trend. Countries or regions such as Norway and Finland in Europe, influenced by domestic climate and geographical conditions, form localized heterogeneous “cold spot areas” compared with countries such as the United Kingdom and France. In Southeast Asia, this zone primarily surrounds major carbon emission countries such as India, China, and Russia, reflecting to some extent the suction effect of major carbon-emitting countries in the transportation industry.

4.4. Empirical Study of Factors Influencing Carbon Emissions in the Global Transportation Sector

4.4.1. Modeling

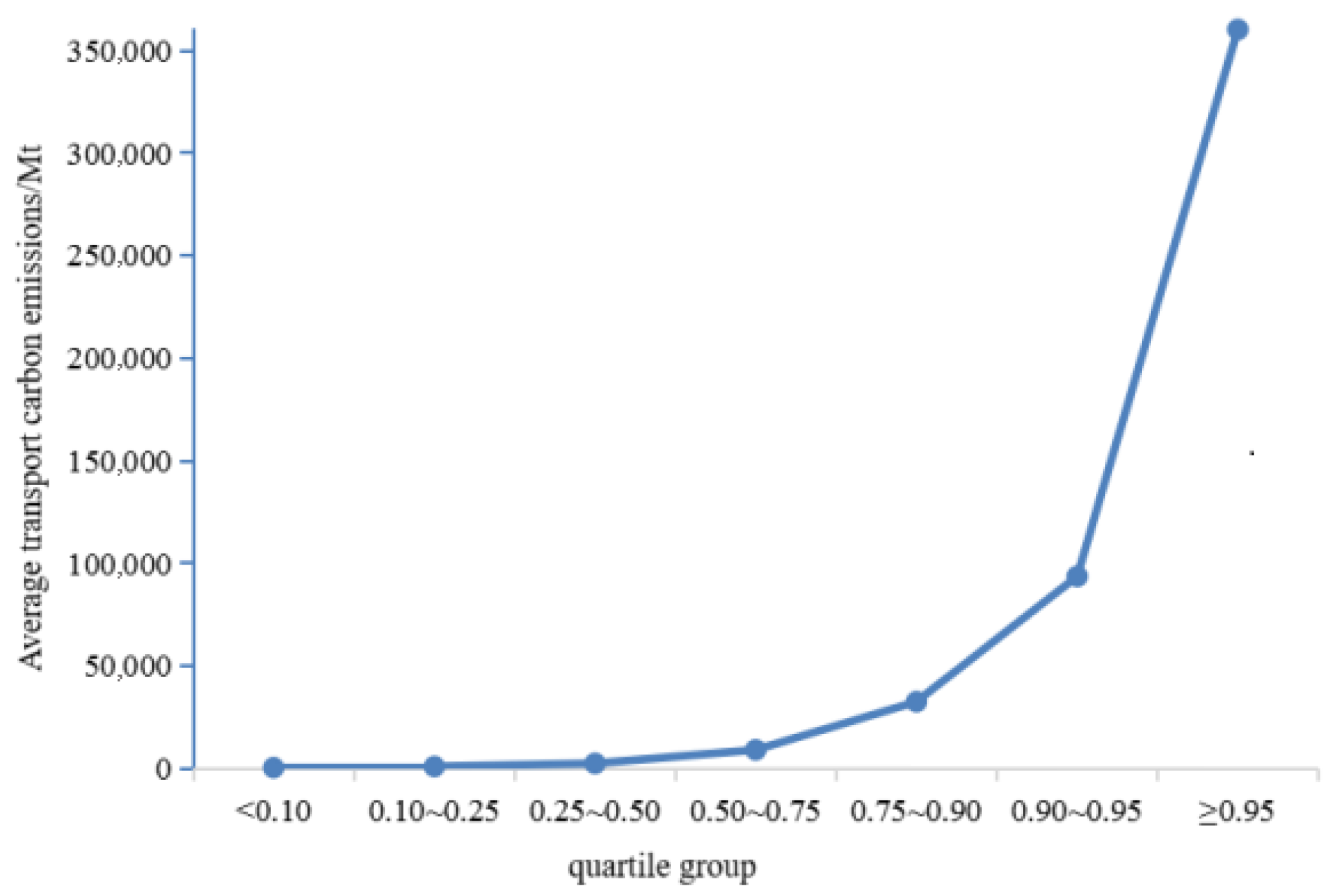
The τ value took six values, 0.1, 0.25, 0.5, 0.75, 0.9, and 0.95, and 140 countries or regions were divided into seven groups according to the quartile division in

Table 2. Grouping of countries or regions in the sample based on average CO₂ emissions from the transportation sector.

Quantile Groups	Country or Region
<0.10	Haiti, Equatorial Guinea, Niger, Tajikistan, and 14 other countries
0.10~<0.25	Cambodia, Estonia, Nepal, Brunei, Iceland, and 21 other countries
0.25~<0.50	Bolivia, Luxembourg, Bangladesh, Kenya, Cuba, and 36 other countries
0.50~<0.75	Colombia, Austria, Vietnam, Greece, Portugal, and 35 other countries
0.75~<0.90	Iran, Saudi Arabia, Indonesia, South Africa, and 23 other countries
0.90~<0.95	France, United Kingdom, India, Mexico, Italy, Spain, and Australia
≥0.95	USA, China, Japan, Germany, Canada, Russia, and Brazil

Note: This division is based on the average value of CO₂ emissions from the transportation sector over the study period.

. As shown in Figure 6, there are certain differences in the quartiles of transportation carbon emissions among different countries or regions. The quartile model adopted in this paper can be well adapted.

4.4.2. Statistics and Testing of Data

This paper has discussed the basic framework of the STIRPAT model and the mechanisms of various effects on carbon emissions from the global transportation industry in detail and has established an extended model (Equation (9)) to analyze the factors affecting carbon emissions; the specific variable descriptions are shown in

Table 3. Description of variables and descriptive statistics of sample data.

Variable	Explanation	Mean	Std	Min	Max
lnTCT(I)	Total carbon emissions from transportation/(Mt)	8.911	1.729	3.761	14.408
lnP(P)	Total population at the end of the year/(millions)	2.483	1.557	−1.204	7.229
lnGDP(A)	GDP/(million dollars)	4.193	1.837	0.693	9.811
lnTV(A)	Total value of the transportation sector/($ million)	11.907	3.760	0.231	19.112
lnFTR(A)	Share of tertiary sector/(%)	13.758	8.787	22.836	66.275
lnPGIN(A)	Per capita income level (US$/person)	8.283	1.783	3.859	11.556
lnCERC(T)	Share of carbon emissions from fossil fuels/(%)	0.793	0.222	0.122	1.001
lnCGDP(T)	The carbon emission intensity of the entire society(Mt/million dollars)	−0.917	0.768	−2.303	1.482
lnIEV(GVC)	Total foreign trade/(millions of dollars)	4.122	1.046	−1.787	6.081
lnTICR(GVC)	Share of exports of high-tech products and services/(%)	3.14	3.695	−10.622	48.869

. These variables cover the demographic, economic, technological, global value chain, and other dimensions that affect carbon emissions from the global transportation industry and provide a more comprehensive analysis of the factors affecting carbon emissions.

In this paper, the variance inflation factor (VIF value) was calculated using STATA software (StataMP 17) to determine whether there was multicollinearity among the variables (see

Table 4. Results of testing model variables.

Variant	VIF Value	1/VIF Value	Hadri	Smoothness	PP-Fisher	Smoothness
lntact			89.487 (***)	smoothly	6.859	uneven
lnPOP	4.870	0.205	102.908 (***)	smoothly	2.157	uneven
lnGDP	9.260	0.108	100.122 (***)	smoothly	6.707	uneven
lnTV	2.090	0.478	56.554 (***)	smoothly	−0.728	uneven
lnFTR	2.540	0.393	86.384 (***)	smoothly	0.091	uneven
lnPOPGIN	3.820	0.262	70.594 (***)	smoothly	4.757	uneven
lnCERC	1.300	0.771	71.899 (***)	smoothly	−4.894 (***)	smoothly
lnCGDP	1.190	0.839	56.002 (***)	smoothly	−2.455 (**)	smoothly
lnIEV	1.250	0.802	56.727 (***)	smoothly	−1.456 (*)	smoothly
lnTICR	1.120	0.896	35.976 (***)	smoothly	−6.732 (***)	smoothly

Note: The unit root test for each variable includes a constant term and a trend term; ***, **, and * indicate significance at the 1%, 5%, and 10% levels, respectively.

). The results show that among all the variables included in the model, the variance inflation factor is less than 10, and there is no multicollinearity problem. The model can be established.

Generally speaking, most economic variables are non-stationary, and using non-stationary sequences for analysis will lead to false regression. Therefore, before using software for regression estimation, it is necessary to test the stationarity of the variables. To ensure the robustness of the test results, this paper selects two methods, Hadri test and Fisher-PP test, for combined testing. As can be seen from Table 4, all variables are stationary under the Hadri test, but most variables are not stationary in the PP test. Considering the actual situation, there are significant heterogeneity among countries or regions in the world in many aspects related to the economy and society. Therefore, the results of the PP test are relatively more in line with the objective facts. Therefore, it is necessary to further study whether there is a cointegration relationship among the variables. KAO test is Kao Test; ADF is augmented Dickey–Fuller Test. The test results show that ADF = −3.8259 (p = 0.0001) passing the test of significance at the 1% level and indicating a cointegration relationship between carbon emissions from the transportation industry and the influencing factors, which can be analyzed by regression.

Descriptive statistics of the sample data are presented in Table 3. Stata software (StataMP 17) was used to calculate the variance inflation factor (VIF) to determine whether multicollinearity existed among the variables in Table 4. Among all the variables included in the model, the VIF was less than 10. There were no problems with multicollinearity, and the model could be established.

To ensure the robustness of the test results, we used a combination of the Hadri and Fisher-PP tests. As shown in Table 4, all variables were smooth under the Hadri test, and most were not smooth under the P.P. test. Considering the actual situation, there was significant heterogeneity among countries or regions globally in many aspects of the economy and society, showing that the results of the P.P. test were more consistent with the objective facts. Therefore, whether a cointegration relationship exists between the variables requires further research. The result of the KAO test was ADF = −3.8259 (p = 0.0001), passing the test of significance at the 1% level and indicating a cointegration relationship between carbon emissions from the transportation industry and the influencing factors, which can be analyzed by regression.

4.4.3. Empirical Results and Analysis

To compare the differences in the results between regressions of different quartiles and regressions of means, a general fixed-effects regression was conducted; the empirical results are shown in

Table 5. Mean and quantile regression results.

Variant/Model	(1) Average Value	(2) 0.10	(3) 0.25	(4) 0.50	(5) 0.75	(6) 0.90	(7) 0.95
POP	0.111 ***	0.199 ***	0.154 ***	0.133 ***	0.119 ***	0.055 ***	0.022
	(9.723)	(9.466)	(10.036)	(11.496)	(8.041)	(4.066)	(1.118)
GDP	0.847 ***	0.756 ***	0.787 ***	0.829 ***	0.856 ***	0.922 ***	0.913 ***
	(63.587)	(30.842)	(44.027)	(61.314)	(49.619)	(58.383)	(40.084)
TV	0.011 ***	0.004	0.014 ***	0.019 ***	0.014 ***	0.006	0.007
	(3.593)	(0.714)	(3.361)	(6.139)	(3.497)	(1.573)	(1.248)
FTR	−0.008 ***	0.002	−0.000	−0.016 ***	−0.015 ***	−0.019 ***	−0.012 **
	(−2.759)	(0.313)	(−0.123)	(−5.218)	(−4.018)	(−5.254)	(−2.292)
PGIN	0.024 ***	0.174 ***	0.046 ***	0.007	−0.005	−0.023 **	−0.007
	(2.763)	(10.754)	(3.849)	(0.744)	(−0.397)	(−2.189)	(−0.481)
CERC	−0.203 ***	−0.426 ***	−0.127 **	−0.107 **	−0.142 ***	−0.357 ***	−0.284 ***
	(−4.937)	(−5.621)	(−2.300)	(−2.570)	(−2.667)	(−7.318)	(−4.036)
CGDP	0.482 ***	0.472 ***	0.443 ***	0.443 ***	0.494 ***	0.608 ***	0.575 ***
	(42.201)	(22.453)	(28.891)	(38.213)	(33.400)	(44.902)	(29.456)
IEV	−0.001	−0.063 ***	−0.017	0.010	0.033 ***	0.043 ***	0.034 **
	(−0.073)	(−4.001)	(−1.496)	(1.184)	(2.941)	(4.199)	(2.288)
TICR	−0.003	−0.018 ***	0.008 ***	0.004	0.000	−0.003	−0.007 *
	(−1.256)	(−4.257)	(2.673)	(1.548)	(0.071)	(−1.269)	(−1.859)
_cons	6.009 ***	3.979 ***	5.022 ***	6.689 ***	6.910 ***	7.657 ***	7.117 ***
	(22.173)	(7.980)	(13.806)	(24.310)	(19.690)	(23.832)	(15.357)
N	2240	2240	2240	2240	2240	2240	2240

Note: ***, **, and * indicate significance at the 1%, 5%, and 10% levels, respectively. The above (1)–(7) refer to the serial numbers of the model. For the mean reversion coefficients within different variables, the values in parentheses are displayed as T-statistics or Z-statistics, which are used to test whether the coefficients are significantly non-zero and to assist in evaluating their statistical reliability.

and

Table 6. The fitting error of the mean and quantile regression results of the variable.

The Fitting Errors of the Variable/Model	(1) Average Value	(2) 0.10	(3) 0.25	(4) 0.50	(5) 0.75	(6) 0.90	(7) 0.95
POP	0.111 ***	0.000044	0.000043	0.00016	0.00028	0.00038	0.00041
GDP	0.847 ***	0.00029	0.00024	0.00015	0.000047	0.0000098	0.000017
TV	0.011 ***	0.000043	0.000105	0.00021	0.00033	0.00039	0.00042
FTR	−0.008 ***	0.000043	0.00011	0.00022	0.00033	0.000393	0.00042
PGIN	0.024 ***	0.000033	0.000091	0.00022	0.00033	0.00039	0.00042
CERC	−0.203 ***	0.000145	0.000054	0.000175	0.000271	0.00024	0.00029
CGDP	0.482 ***	0.000166	0.000086	0.000025	0.000114	0.00013	0.00016
IEV	−0.001	0.000016	0.000104	0.00021	0.00032	0.00038	0.00041
TICR	−0.003	0.000037	0.00010	0.00022	0.00033	0.00040	0.00042
_cons	6.009 ***	0.00173	0.00202	0.00276	0.00275	0.00302	0.00275
N	2240	2240	2240	2240	2240	2240	2240

Note: *** indicate significance at the 1%, levels.

.

To compare the differences in results between regression of different quantiles and mean regression, a common fixed-effect regression was conducted. The empirical results are shown in Table 5. First, pay attention to the impact of population size (P) on carbon emissions in the global transportation industry. Analysis of the coefficients of all regression results reveals that, except for the regression coefficient at the quantile with a τ value equal to 0.95 which is not significant, the mean regression and the regression coefficients of the other five different quantiles all show a significant promoting effect at the 1% confidence level, that is, the direction of population size is consistent with the change in carbon emissions from the transportation industry. The expansion of population size will lead to an increase in carbon emissions from the transportation industry. By comparing the mean reversion coefficient and the quantile reversion coefficient, it can be seen that the mean reversion coefficient is 0.111, which is greater than the regression coefficient when the τ value is greater than 0.90, indicating that mean reversion exaggerates the positive effect of population size on carbon emissions in the transportation industry of high-ranking countries or regions. By analyzing the fractional regression coefficients, it can be seen that the regression coefficients at different quantiles show a significant downward trend. This indicates that there are differences in the impact of population size at different quantiles of carbon emissions in the transportation industry on carbon emissions. As the scale of carbon emissions in the transportation industry increases, the promoting effect of population on it gradually decreases, which is in line with the changing law of the environmental Kuznets curve. Hypothesis 1 was verified the impact of population on carbon emissions in the transportation industry is manifested in two aspects. First, the increase in the total population will inevitably lead to a rise in total social demand, energy demand, and transportation service demand. The characteristics of the transportation industry result in a relatively large demand for energy. Considering the current economic activity situation, Energy, especially non-renewable and non-clean energy, remains the fundamental guarantee for human life and production activities. Overall, there is still a significant positive correlation between population size and carbon dioxide emissions from the transportation industry. On the other hand, the increase in the total population has led to a rise in population density in some countries or regions, promoting the sharing of public infrastructure and services within the country or region, and facilitating the formation of an agglomeration economy, thereby enhancing the overall productivity of society and reducing energy consumption. In countries or regions with high scores, the industry scale of the transportation sector has already demonstrated scale effects and agglomeration effects, forming a certain technological spillover effect and, thus, has begun to curb the positive driving effect of population size on carbon dioxide emissions from transportation. Its technical effect was further verified in the variable coefficients symbolizing technology.

Analyze the impact of affluence on carbon emissions in the transportation industry. The positive effect of the total social and economic scale (GDP) was significant at a confidence interval of 1% in all seven models. By comparing the coefficients of the regression at different quantiles, it can be seen that the regression coefficient of GDP showed a significant upward trend at different quantiles, which reveals that for countries or regions with high carbon emissions in the transportation industry, the total scale of the social economy has a stronger promoting effect on carbon emissions in the transportation industry, verifying Hypothesis 1A. The increase in the total social and economic volume will inevitably bring a large amount of resources and production factors to the development of the transportation industry, thereby promoting the growth of its carbon emissions. For the industrial structure (FTR), by comparing the results of mean reversion and quantile regression, it can be seen that, relatively speaking, mean reversion underestimates the extent to which the structural effect of the industrial structure affects carbon emissions in the transportation industry. By comparing the regression coefficients of different quantiles, it can be seen that the structural effect is significant at the medium and high quantiles, with the regression coefficients showing negative values. Moreover, there is no obvious consistent trend of change when fluctuating around the value when τ = 0.50. This confirms Hypothesis 2 of the structural effect, that is, the higher the proportion of the tertiary industry, the more optimized the industrial structure, and the lower the carbon dioxide emissions of the transportation industry. For the per capita income level (PGIN), by comparing the results of mean reversion and quantile reversion, it can be seen that mean reversion overestimates the significance and role level of per capita income for countries or regions with medium to high carbon emissions in the transportation industry. By comparing the regression results of different quantiles, it can be seen that the regression coefficient of PGIN shows a relatively obvious inverted “U” curve pattern. This verifies Hypothesis 3, that is, when the per capita income level is low, economic agents will prioritize meeting their own basic material living needs and ignore environmental protection, thereby positively affecting the carbon emissions of the transportation industry. However, when the income level reaches a certain value, economic agents will take into account a green and environmentally friendly lifestyle, thereby reducing carbon emissions in the transportation industry. Looking at the three variables (GDP, PGIN, and TV) that comprehensively represent the degree of wealth, compared with countries or regions in the lower percentile, the sensitivity of countries or regions in the higher percentile to changes in the degree of wealth is decreasing. This is consistent with Kuznetz’s theory that when the scale expands to a certain extent, Environmental pollution, that is, the carbon dioxide emissions from the transportation industry, will show a certain inverted “U” curve relationship with the economic scale.

Analyze the impact of technological progress on carbon emissions in the transportation industry. Overall, the model results confirm Hypothesis 4 of the technological effect, that is, technological progress restrains the growth of carbon emissions in the transportation industry. By comparing the results of mean reversion and quantile regression, it can be seen that the proportion of clean energy (CERC) is significant within the 0.05 confidence interval in both mean reversion and different quantiles, and the regression coefficient value is negative. That is, the structural effect of energy is manifested as a significant inhibitory effect on carbon emissions in the transportation industry. The higher the proportion of clean energy, the lower the carbon dioxide emissions in the transportation industry. By comparing the regression results under different τ values, it can be seen that the regression coefficients change significantly, presenting a clear “U”-shaped curve form. Carbon emissions from the transportation industry are jointly influenced by multiple factors. In countries or regions with low carbon emissions from the transportation industry, based on the analysis of population size and wealth level, it can be known that the influence degrees of scale effect, structure effect and income effect are relatively higher. The investment in clean energy and changes in scale, structure, etc., consistently form an effect of “1 + 1 > 2”. Therefore, it makes its elasticity coefficient relative to carbon emissions larger. For countries or regions with high scores in the transportation industry, fossil energy still accounts for a large share in social and economic development. The transportation industry involves multiple sectors such as railways, aviation, and shipping, and the energy consumption involved is more extensive than that of other industries in the economy and society. Therefore, technological innovation based on its own characteristics and increasing the development and utilization of clean energy, such as in the field of aviation fuel, play a significant role in reducing the carbon emissions of the entire industry. By comparing the results of mean reversion and quantile regression, it can be seen that energy intensity (CGDP) is significant at the 1% level in all models, and the coefficient of mean reversion is less than the regression coefficient when τ ≥ 0.75, underestimating the elasticity of high-score countries or regions to changes in energy intensity. By comparing the regression results under different τ values, it can be seen that as the τ value increases, the elastic coefficient shows a significant upward trend, which indicates that the inhibitory effect of social and technological progress on carbon emissions in the transportation industry is strengthening. The larger the τ value, the greater the base amount of carbon emissions in the transportation industry. The improvement of technological level will increase the utilization rate of industry resources, thereby expanding the change amount of carbon emissions in the transportation industry. That is to say, the base amount expands, the utilization rate increases, and the change amount increases.

Analyze the impact of the global value chain on carbon emissions in the transportation industry. By comparing the results of mean reversion and quantile regression, it can be seen that the total foreign trade volume (IEV) is significantly positive at the high percentile where τ ≥ 0.75, but not significant at the mean reversion and other percentiles. That is to say, the increase in the total foreign trade volume leads to an increase in carbon emissions in the transportation industry, confirming Hypothesis 5A, that is, the participation in the global value chain has a positive effect on carbon emissions in the transportation industry. According to the data and analysis of the country groups in Table 2, countries or regions with high carbon emissions in the transportation industry have relatively larger economic development scales and better economic and political situations. On the basis of a good economic momentum in their own countries, they are more suitable for strengthening their horizontal participation in the global value chain. In other words, on the basis of a stable supply and demand relationship in the domestic market, more extensive participation in the global international division of labor will lead to an increase in international trade volume, further promoting the development of the transportation industry and causing its carbon emissions to rise. The proportion of high-tech product and service exports (TICR) was significant when the τ value was 0.10 and 0.95, and the regression coefficient was negative. This indicates that the higher the proportion of high-tech product and service exports, the lower the carbon emission value of the transportation industry. This confirms Hypothesis 5B, that is, the international division of labor position in the global value chain will suppress the carbon emission of the transportation industry. Firstly, from the perspective of technological progress brought about by the evolution of the global value chain division of labor status, as the global value chain division of labor status further evolves, more and more countries or regions are increasingly attaching importance to increasing investment in technology, which leads to the development of production activities within the country or region towards cleanliness and greenness, and more and more clean energy is being put into use, and the energy utilization efficiency has been significantly enhanced. As the second largest energy-consuming industry after industry, the transportation sector is bound to benefit from this, leading to a reduction in its carbon dioxide emissions. According to Table 2, it can be known that countries or regions with a τ value of 0.10 generally have a backward economic development level, and the total carbon emissions also vary greatly compared with other countries or regions. This leads to the situation that when the division of labor status is enhanced, the reduction in carbon emissions in backward countries or regions accounts for a relatively large proportion compared with the already extremely low total. That is, the rate of change in carbon emissions brought about by the improvement of the division of labor status is relatively large. Countries or regions with a τ value of 0.95 are mostly in a stage of strong economic development. Firstly, similar to the explanation of technological progress, the total carbon emissions base of these countries or regions is large, and there is a magnitude difference compared to other countries or regions. This leads to a greater reduction in carbon emissions from the transportation industry in developed countries or regions when the division of labor status is enhanced. That is, when the elasticity coefficients of the improvement of the division of labor status are the same, the change in carbon emissions in developed countries or regions is relatively large. Secondly, developed countries or regions have a higher level of clean and green development. Most of the advanced and core technologies are mastered by these countries or regions. The improvement of their division of labor status has a stronger influence on the carbon emissions of their transportation industry. Secondly, by analyzing the current status of the division of labor in the global value chain and the factor endowments and advantageous industries of various countries or regions around the world, it is found that backward countries or regions are basically stable at the end of the global value chain, and have long been engaged in the production and export of resource-consuming products. This leads to the situation that, compared with other countries or regions at the medium and high ends, the global value chain division of labor status of less developed countries or regions has more room for improvement and is prone to a “bottoming out and rebound”. In contrast, developed countries or regions have always participated in the global value chain in a state of releasing high-carbon emission industries. Therefore, they have a first-mover advantage, and their high-tech and service industrial chains are more mature. The difficulty of enhancing its position in the global value chain is extremely low compared to other countries or regions. Overall, developed countries or regions as well as backward ones are more sensitive to the evolution of their division of labor in the global value chain.

4.4.4. Robustness Tests

This study categorized the sample countries or regions into three groups according to United Nations standards: developed countries or regions, developing countries or regions, and underdeveloped countries or regions. The regressions were conducted separately for robustness tests, and the results are presented in

Table 7. Robustness tests: results for sample subgroups of developed countries or regions.

Variant /Model	(1) Average Value	(2) 0.10	(3) 0.25	(4) 0.50	(5) 0.75	(6) 0.90	(7) 0.95
POP	0.127 ***	0.176 ***	0.246 ***	0.247 ***	0.170 ***	0.089	0.064 **
	(5.470)	(5.037)	(9.846)	(9.069)	(5.764)	(1.485)	(2.164)
GDP	0.882 ***	0.888 ***	0.733 ***	0.689 ***	0.813 ***	0.919 ***	1.003 ***
	(30.829)	(20.734)	(23.841)	(20.540)	(22.424)	(12.430)	(27.681)
TV	0.025 ***	0.026 ***	0.013 *	−0.001	0.011	0.015	0.079 ***
	(3.858)	(2.667)	(1.811)	(−0.069)	(1.276)	(0.900)	(9.437)
FTR	−0.024 **	−0.068 ***	−0.032 ***	0.020	0.004	0.030	0.011
	(−2.072)	(−3.984)	(−2.615)	(1.512)	(0.296)	(1.011)	(0.744)
PGIN	0.104 ***	0.223 ***	0.167 ***	0.140 ***	0.113 ***	0.052	0.061 **
	(5.253)	(7.549)	(7.887)	(6.070)	(4.502)	(1.018)	(2.454)
CERC	−0.474 ***	−0.587 ***	−0.250 ***	−0.297 ***	−0.117	−0.382 **	−0.673 ***
	(−6.662)	(−5.507)	(−3.268)	(−3.556)	(−1.303)	(−2.076)	(−7.466)
CGDP	0.544 ***	0.635 ***	0.479 ***	0.467 ***	0.502 ***	0.533 ***	0.496 ***
	(24.319)	(18.973)	(19.950)	(17.824)	(17.722)	(9.228)	(17.516)
IEV	−0.100 ***	−0.171 ***	−0.246 ***	−0.213 ***	−0.187 ***	0.010	0.066 *
	(−3.483)	(−3.972)	(−7.982)	(−6.331)	(−5.140)	(0.138)	(1.821)
TICR	−0.057 ***	−0.028	−0.005	−0.067 ***	−0.118 ***	−0.204 ***	−0.191 ***
	(−4.876)	(−1.576)	(−0.365)	(−4.881)	(−7.916)	(−6.710)	(−12.857)
_cons	6.975 ***	9.888 ***	8.028 ***	4.007 ***	5.382 ***	2.832	2.985 **
	(6.658)	(6.304)	(7.130)	(3.263)	(4.056)	(1.047)	(2.250)
N	720	720	720	720	720	720	720

Note: ***, **, and * indicate significance at the 1%, 5%, and 10% levels, respectively.

.

According to the estimation results, the significance of population size, affluence, technology level, and GVC was consistent with the results of the empirical analysis. Among them, the trajectory of the regression coefficients of population size and affluence was the same as that of empirical analysis, aligning with the changing law of the inverted “U”-curve of environmental Kuznets. The impact of GVC participation in developed countries or regions differed from that in the previous section, which generally showed significant inhibition at the 0.01 confidence interval. This difference was observed because developed countries or regions were more prosperous in capital and technological resources but more scarce in labor resources; therefore, in the process of participating in GVCs, developed countries or regions will export some resource- and labor-intensive industries to other countries or regions, especially processing trade with high carbon emissions, reducing carbon emissions from their countries or regions, which also fits the empirical analysis of the impact of the division of labor status in GVCs. This is also in line with the impact of the division of labor in the global value chain in the empirical analysis.

According to the estimation results, for developing countries or regions and underdeveloped countries or regions in

Table 8. Robustness tests: results for sample subgroups of developing countries.

Variant /Model	(1) Average Value	(2) 0.10	(3) 0.25	(4) 0.50	(5) 0.75	(6) 0.90	(7) 0.95
P	0.084 ***	0.073 **	0.088 ***	0.162 ***	0.173 ***	0.135 ***	0.133 ***
	(4.740)	(2.303)	(2.741)	(11.589)	(11.962)	(4.522)	(5.824)
GDP	0.892 ***	0.885 ***	0.862 ***	0.816 ***	0.834 ***	0.900 ***	0.921 ***
	(43.193)	(23.663)	(23.010)	(49.669)	(49.274)	(25.722)	(34.356)
TV	0.008 **	0.001	0.009	0.004	0.003	−0.001	−0.013 **
	(1.998)	(0.071)	(1.237)	(1.096)	(1.000)	(−0.196)	(−2.410)
FTR	−0.026 ***	−0.031 ***	−0.021 ***	−0.016 ***	−0.020 ***	−0.033 ***	−0.038 ***
	(−7.322)	(−4.886)	(−3.324)	(−5.584)	(−6.756)	(−5.489)	(−8.321)
PGIN	0.014	0.108 ***	0.022	0.023 **	0.022 **	−0.002	0.009
	(1.051)	(4.418)	(0.918)	(2.178)	(1.975)	(−0.087)	(0.504)
CERC	−0.065	−0.412 ***	−0.126	0.028	−0.037	0.004	0.170 ***
	(−1.396)	(−4.882)	(−1.497)	(0.761)	(−0.965)	(0.052)	(2.818)
CGDP	0.352 ***	0.281 ***	0.282 ***	0.293 ***	0.346 ***	0.367 ***	0.391 ***
	(23.349)	(10.311)	(10.338)	(24.459)	(28.000)	(14.388)	(20.016)
IEV	0.058 ***	0.063 ***	0.024	0.025 ***	0.031 ***	0.068 ***	0.081 ***
	(5.376)	(3.230)	(1.242)	(2.941)	(3.509)	(3.748)	(5.840)
TICR	0.004 *	0.010 **	0.006	0.003	0.002	−0.001	−0.003
	(1.703)	(2.312)	(1.530)	(1.441)	(1.070)	(−0.385)	(−0.976)
_cons	7.289 ***	6.745 ***	6.838 ***	6.569 ***	7.020 ***	8.370 ***	8.867 ***
	(23.049)	(11.775)	(11.923)	(26.123)	(27.071)	(15.622)	(21.598)
N	1200	1200	1200	1200	1200	1200	1200

Note: ***, **, and * indicate significance at the 1%, 5%, and 10% levels, respectively.

and

Table 9. Robustness tests: results for subgroups of samples from lagging countries or regions.

Variant /Model	(1) Average Value	(2) 0.10	(3) 0.25	(4) 0.50	(5) 0.75	(6) 0.90	(7) 0.95
POP	0.155 ***	0.335 ***	0.177 ***	0.184 ***	0.195 ***	0.071 ***	0.044
	(5.383)	(5.175)	(3.044)	(6.662)	(4.494)	(2.703)	(1.453)
GDP	0.886 ***	0.701 ***	0.834 ***	0.870 ***	0.818 ***	0.951 ***	0.982 ***
	(20.509)	(7.242)	(9.563)	(21.069)	(12.597)	(24.121)	(21.915)
TV	0.019 **	0.015	0.020	0.017 **	0.010	0.016 **	0.015 *
	(2.507)	(0.911)	(1.330)	(2.423)	(0.880)	(2.305)	(1.956)
FTR	0.020 ***	0.037 **	0.013	0.011	0.023 **	0.009	0.004
	(2.706)	(2.264)	(0.847)	(1.537)	(2.077)	(1.368)	(0.478)
PGIN	0.050 ***	0.245 ***	0.013	0.006	0.007	−0.012	−0.020
	(2.803)	(6.168)	(0.364)	(0.367)	(0.259)	(−0.714)	(−1.104)
CERC	−0.906 ***	−0.949 ***	−0.642 ***	−0.468 ***	−0.587 ***	−0.873 ***	−0.958 ***
	(−9.376)	(−4.386)	(−3.293)	(−5.068)	(−4.040)	(−9.907)	(−9.570)
CGDP	0.720 ***	0.669 ***	0.794 ***	0.753 ***	0.723 ***	0.692 ***	0.687 ***
	(28.888)	(11.987)	(15.795)	(31.668)	(19.320)	(30.469)	(26.596)
IEV	0.011	−0.030	0.016	0.056 ***	0.077 ***	0.094 ***	0.098 ***
	(0.669)	(−0.783)	(0.462)	(3.443)	(3.004)	(6.113)	(5.603)
TICR	−0.082 ***	−0.129 ***	−0.077 ***	−0.066 ***	−0.058 ***	−0.053 ***	−0.065 ***
	(−8.920)	(−6.260)	(−4.161)	(−7.523)	(−4.185)	(−6.280)	(−6.802)
_cons	3.444 ***	0.309	4.288 ***	4.370 ***	3.553 ***	4.911 ***	5.521 ***
	(5.048)	(0.202)	(3.113)	(6.706)	(3.465)	(7.893)	(7.806)
N	528	528	528	528	528	528	528

Note: ***, **, and * indicate significance at the 1%, 5%, and 10% levels, respectively.

, the significant results of population size, affluence, technology level, and the global value chain were also consistent with those in the empirical analyses, verifying the robustness of the empirical results.

5. Discussion and Conclusions

5.1. Discussion

This study aimed to overcome the limitation of literature focusing mainly on the analysis of carbon emissions from the transportation industry in individual countries or regions. To achieve this objective, this study analyzed the evolution of carbon emissions in 140 countries or regions and then analyzed the spatial distribution pattern, spatial dispersion pattern, and spatial correlation pattern of carbon emissions globally, providing insights into the study of global carbon emission mitigation from the transportation industry. On this basis, this study examined the differences in carbon emissions among countries and regions, divided them into quartiles, and introduced a quartile regression model to explore the influence of influencing factors on the countries or regions with carbon emissions. This is of practical significance for countries worldwide to formulate carbon dioxide emission reduction targets and low-carbon development policies for the transportation industry according to their local conditions. This study also comprehensively utilized various analytical methods to analyze global carbon emissions in multiple dimensions. The results are more comprehensive and in-depth than those in the literature, and the data were collected over an extended period; therefore, this study’s results are more representative and persuasive than those in the literature.

This study’s findings indicate a decrease in the polarization of the global distribution of carbon emissions over time. Thus, because of the global nature of carbon emissions, countries must collectively enhance international cooperation to address the challenges of climate change. Governments can promote international carbon emission reduction targets and jointly promote the reduction in global carbon emissions by strengthening international exchanges and cooperation and sharing technological experiences and best practices. For instance, strengthening exchange and cooperation between developed and developing countries in technology, financing, and policies. Additionally, it jointly promotes the low-carbon transformation of the global transportation industry. Joint research on carbon emission mitigation in the global transportation sector should be conducted, and low-carbon transport technologies and experiences should be shared.

The results of the influencing factors indicate that economic restructuring should be actively promoted to achieve carbon emissions reduction targets. Because of the positive correlation between economic affluence and carbon emissions from the transportation sector, governments can encourage the optimization and upgrading of the economic structure, increase the development of tertiary industries, accelerate the transformation of high carbon emission industries, and promote the transformation of the economy to low-carbon and green industries.

The quartile regression results revealed that countries or regions in different quartiles implemented distinct policy measures. Countries or regions in the low quartile of carbon emissions from the transportation industry can focus on the pressure on carbon emissions from population growth and strengthen their control of population growth and structural adjustment. Active participation in global value chain cooperation should be encouraged to enhance industrial competitiveness and low-carbon development capacity for countries or regions in the high quartile transportation industry, increase carbon emission reduction efforts, and formulate stricter carbon emission targets and policy measures. Also necessary are prioritizing the development of new and renewable energy sources, accelerating the pace of transportation electrification, vigorously developing green transport infrastructure, and improving public transportation systems.

Nevertheless, this study has limitations. The transportation industry can be divided into several subsectors according to different criteria, and this study only analyzed the transportation industry as a whole and did not conduct targeted research on the division within the industry. Therefore, further research could divide the transportation industry into land transportation, pipeline transportation, maritime transportation, and aviation according to the division of the World Input-Output Database (WIOD) or subdivide the transportation industry according to the means of transportation or the main body of the transportation (e.g., private automobile transportation, public transportation) to continuously enrich and improve the analysis of the carbon emission of the internal sectors of the transportation industry. Additionally, this study conducted an analysis of the factors influencing the transportation industry. Further research could conduct a comparative analysis of carbon emission factors in the transportation industry in different regions and stages of development, identify their differences and commonalities, and propose more detailed and conducive strategies for implementing targeted carbon emission reduction than those in this paper. Finally, for the calculation of carbon emissions from transportation, ensuring the quality of data at the micro scale for both global and local regional objects is of great significance, as it affects the validity of the final analysis results. The selection of models and the restrictive role of hypotheses will, to a certain extent, enhance the credibility of the research.

5.2. Conclusions

The main conclusions obtained in this paper are as follows:

(1) From the perspective of spatial pattern, the global carbon emissions from the transportation industry show an apparent fluctuation and rising trend and spatially show prominent polarization characteristics, presenting the distribution trend of “one strong multi-pole” to “two strong multi-pole” transformation, and its growth pole shows significant diffusion trend. The shift in the direction of “northwest-southeast” is more prominent.

(2) From the perspective of dispersion patterns, the Gini coefficient of carbon emissions from the global transportation industry shows a significant downward trend, and the spatial distribution is more balanced. According to the law of dynamic change, it is divided into four stages: the Gini coefficient value of global carbon emissions in the first and third stages shows a rapid decline, and the spatial distribution is characterized by rapid decentralization; the value of the Gini coefficient in the second and fourth stages shows a slow fluctuating decline, and the spatial distribution as a whole is characterized by slow decentralization.

(3) From the perspective of the correlation pattern, from 1971 to 2018, the global Moran’s I index of global carbon emissions is more significant than zero. The carbon emissions of all countries worldwide show a significant distribution of agglomeration; that is, the countries with high carbon emissions have high carbon emissions in the surrounding countries. The results of the local Moran’s I index show that the number of locally significant countries or regions of global carbon emissions from the transportation industry during 1971–2008 show a distinct upward trend, the number of significant types gradually increases, the spatial dependence on local geography strengthens. From 2009 to 2018, the number of locally significant countries or regions began to decline. However, in the overall view of 1971–2018, the global number of locally significant countries or regions for carbon emissions increases.

(4) Regarding influencing factors, population size significantly and positively affects CO₂ emissions; affluence is positively related to CO₂ emissions from the transportation sector through a combination of income, structural, and scale effects; the level of technology significantly suppresses CO₂ emissions, especially for countries or regions in the high carbon emission quartile; and the level of participation in global value chains significantly contributes to CO₂ emissions. The level of technology significantly suppresses carbon emissions, especially for countries or regions in the high carbon-emissions quartile, and participation in value chains significantly promotes carbon emissions.

6. Policy Recommendations

After conducting in-depth research on global transportation carbon emissions, the following policy suggestions can be put forward to better integrate theory with practice.

(1) Accelerate the construction of a multimodal transport system. For instance, expand railway logistics bases and dedicated railway lines for port collection and distribution, and promote the transfer of bulk goods from road to rail and water.

(2) Strengthen the promotion and support of new energy heavy-duty trucks. Incorporate the construction of battery swap stations into the national spatial planning, give priority to the layout of charging and battery swapping facilities in logistics hubs, and provide operational subsidies to battery banks.

(3) Implement the policy of giving priority to road rights and reducing expressway tolls for new energy heavy-duty trucks to enhance their economic advantages. Carry out low-carbon transformation of highways. Establish carbon emission accounting standards for highways, promote green infrastructure technologies such as photovoltaic pavement and permeable asphalt, and enhance carbon sink potential. Implement dynamic charging on congested sections, optimize traffic flow in combination with intelligent transportation systems, and reduce idle emissions.

(4) Deepen the integration of transportation and energy. Build wind power/photovoltaic facilities on a large scale in highway service areas and ports.