Research on the Main Influencing Factors and Variation Patterns of Basal Area Increment (BAI) of Pinus massoniana
Abstract
1. Introduction
2. Materials and Methods
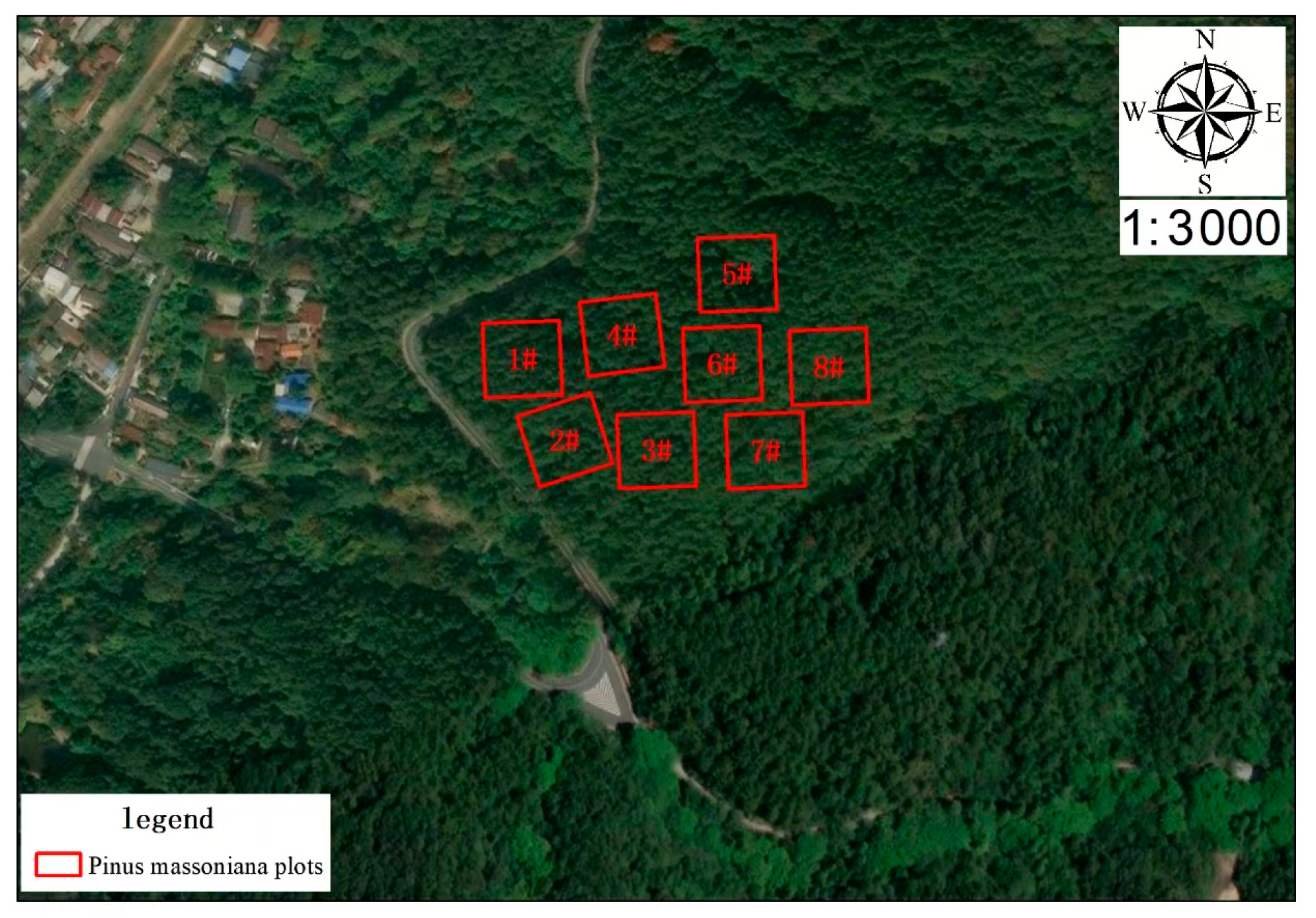
2.1. Study Area
2.2. Data Collection
2.2.1. Plot Information and Increment Core Collection
2.2.2. Competition Index
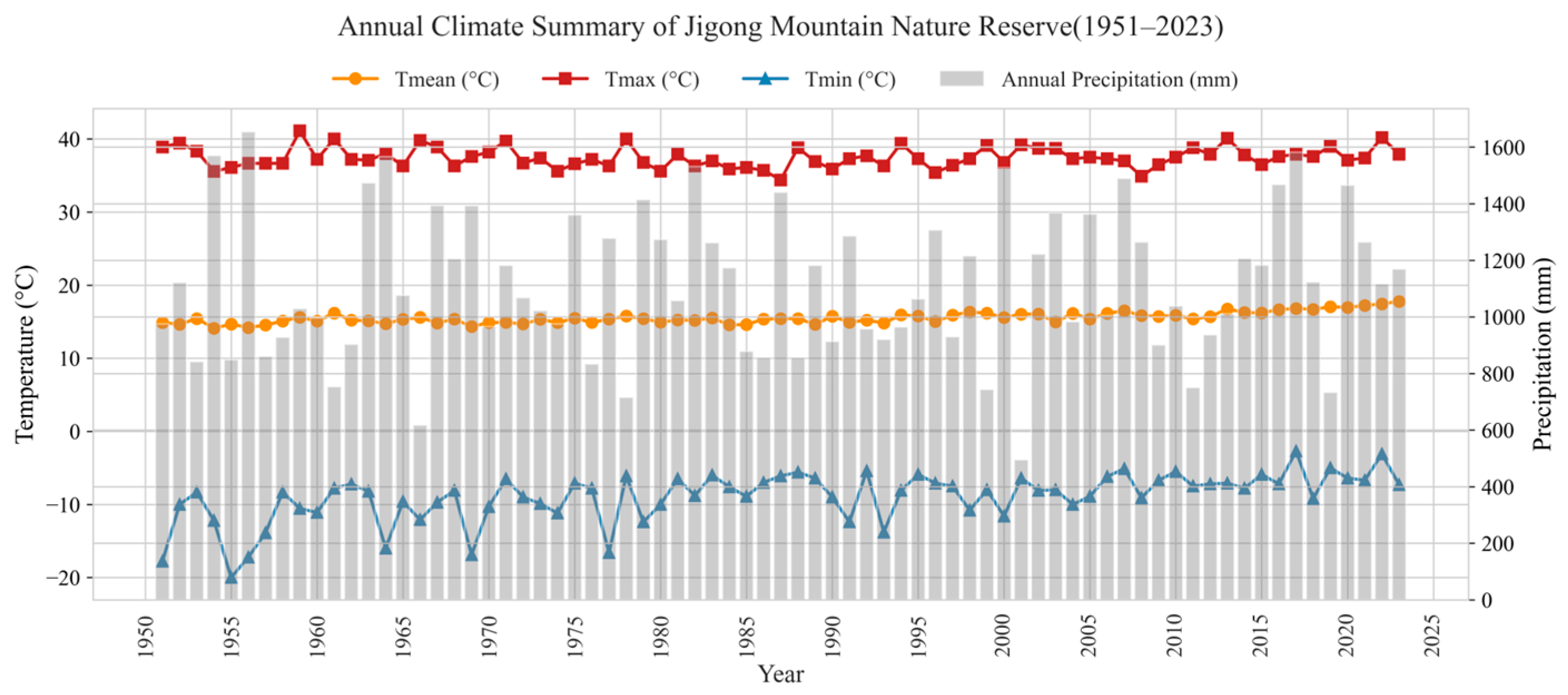
2.2.3. Climate Data
2.3. Methods for Evaluating the Importance of Variables
2.3.1. Principal Component Analysis (PCA)
2.3.2. Redundancy Analysis (RDA)
2.3.3. Random Forest (RF)
2.3.4. Boosted Regression Tree (BRT)
2.3.5. Extreme Gradient Boosting (XGBoost)
2.4. Generalized Additive Model (GAM)
3. Results
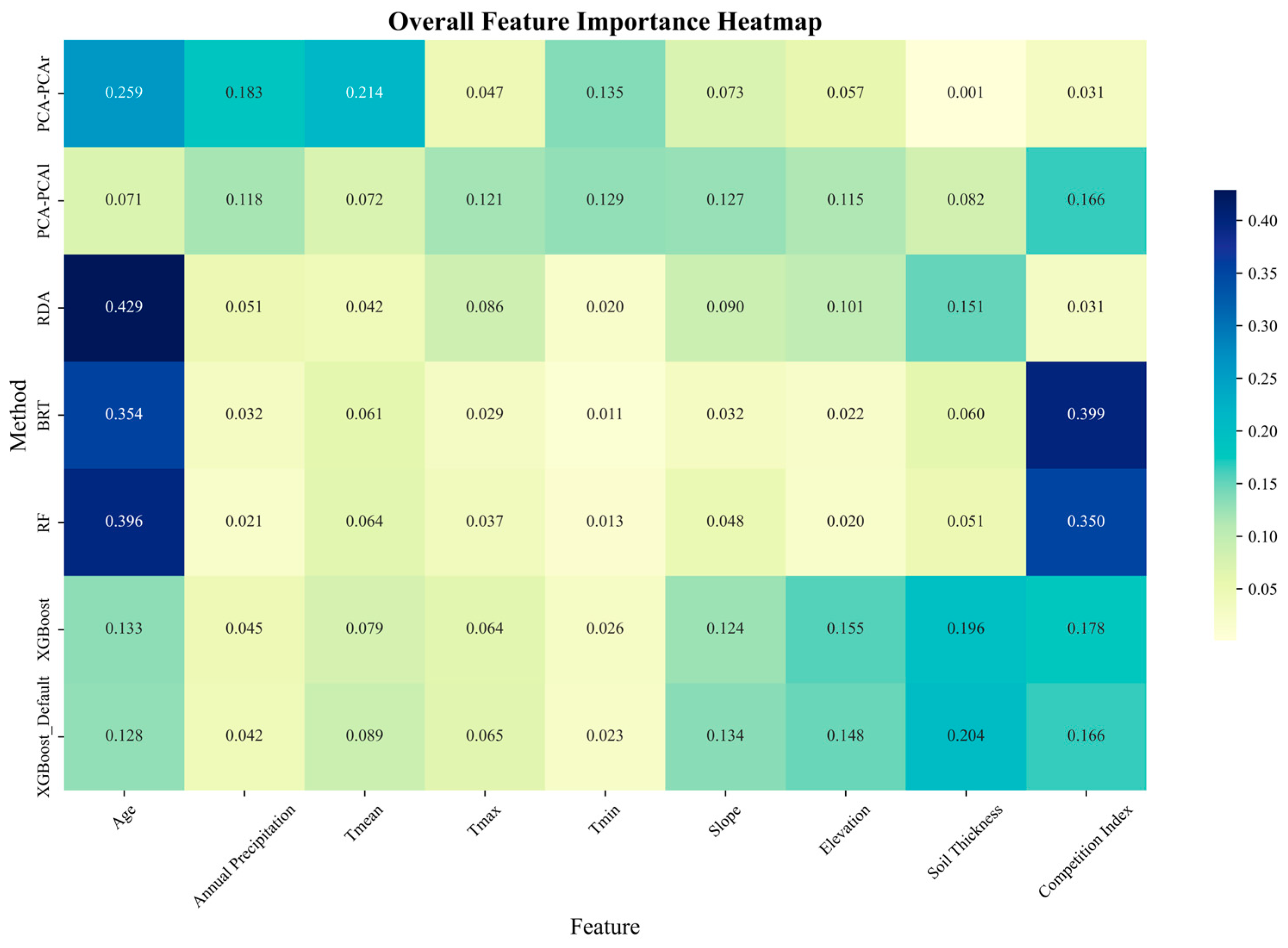
3.1. Results of the Importance of Different Variables
3.2. The Modeling Process of GAMs
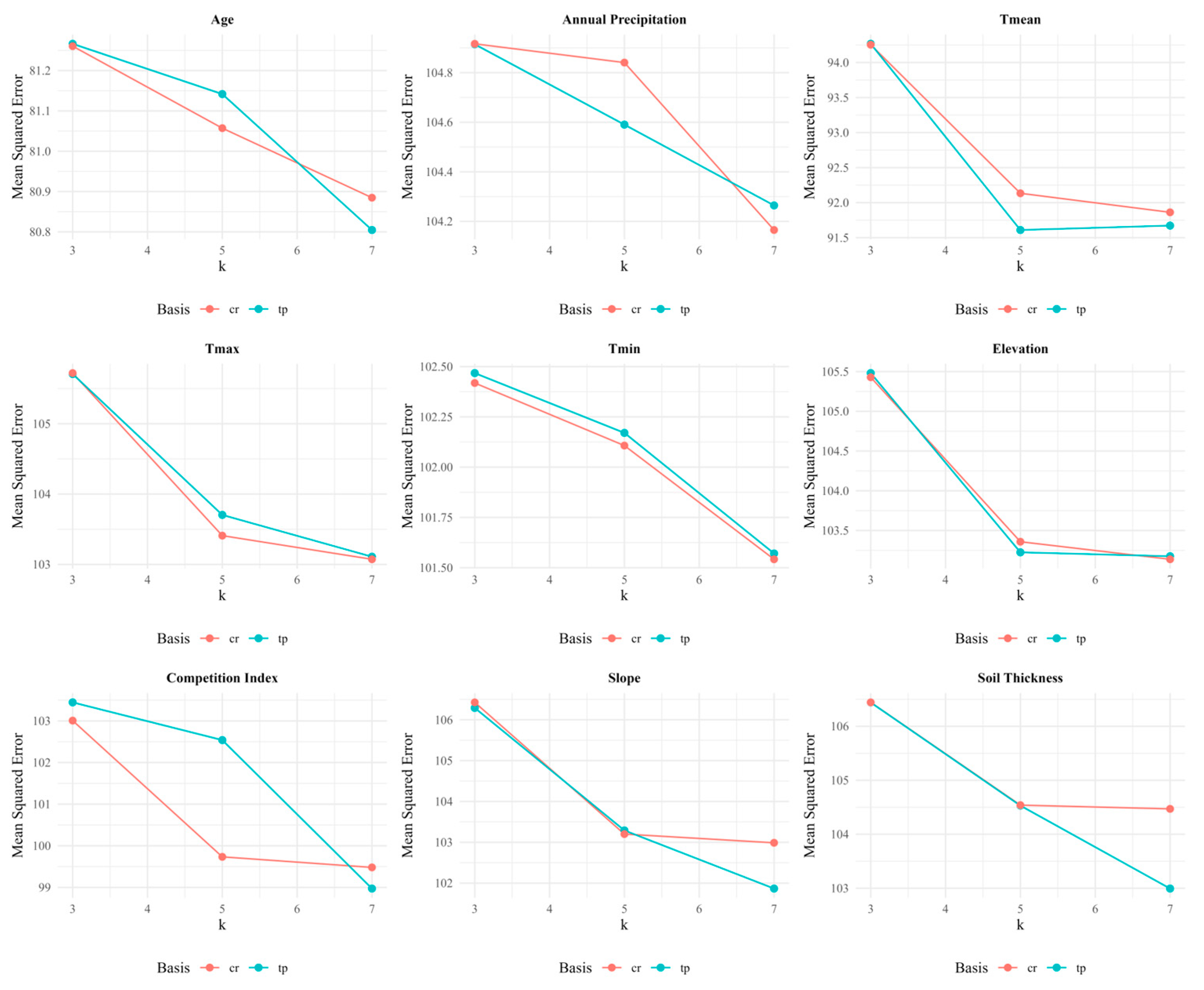
3.2.1. Parameter Selection of GAMs
3.2.2. Fitting Results of GAMs
4. Discussion
4.1. Comparisons Among Different Importance Evaluation Methods
4.2. Influencing Variables of BAI in P. massoniana
4.3. Limitations and Future Directions
5. Conclusions
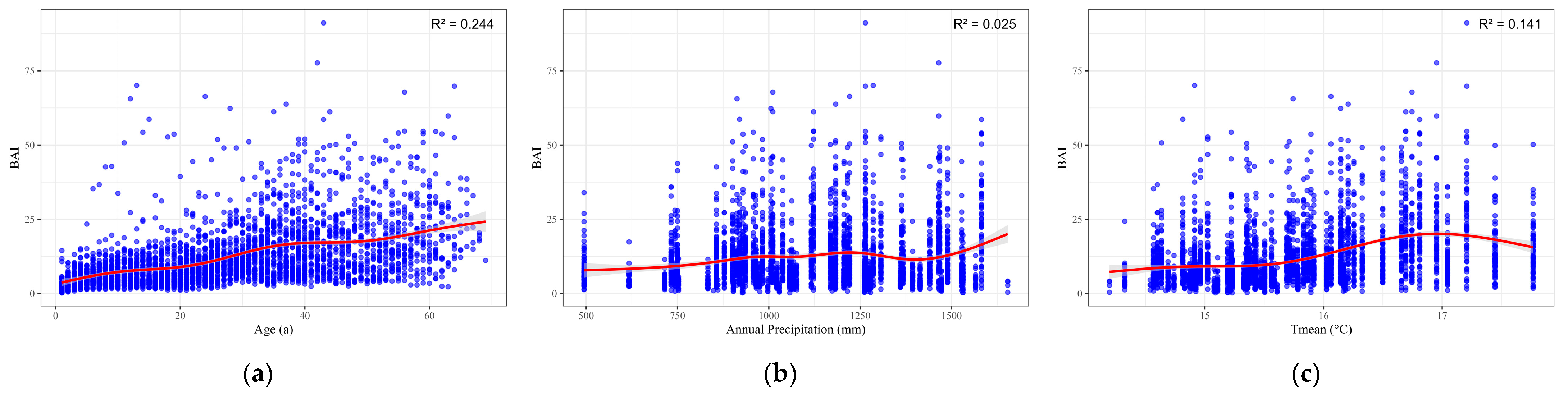
- Among all the candidate variables, Age, Competition Index, and Tmean exhibited the most significant influence on the BAI in P. massoniana.
- When the tree age was less than 70 years, the BAI of P. massoniana increased with the increase in Age.
- From the overall trend, the BAI of P. massoniana decreased with the increase in Competition Index.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boukhris, I.; Marano, G.; Dalmonech, D.; Valentini, R.; Collalti, A. Modeling Forest Growth Under Current and Future Climate. Curr. For. Rep. 2025, 11, 17. [Google Scholar] [CrossRef]
- Wei, Y.; Ye, Q.; Lu, G.; Feng, W.; Han, X.; Huang, Z.; Deng, W. Response of Radial Growth of Cunninghamia lanceolata to Climate Change in the Jinggangshan National Nature Reserve. Chin. J. Agrometeorol. 2025, 46, 179–188. (In Chinese) [Google Scholar]
- Wang, T.; Sun, Y.; Qiao, J. Response of tree-ring width of Pinus massoniana to climate change in the Jiangle Forest Farm. J. Beijing For. Univ. 2019, 41, 30–39. (In Chinese) [Google Scholar]
- Yang, L. Response of Pinus massoniana and Pinus tabuliformis Growth to Climatic Factors in Jigong Mountain. Master’s Thesis, Henan University, Kaifeng, China, 2020. (In Chinese). [Google Scholar]
- Pandey, U.; Nakatsuka, T.; Mehrotra, N.; Zhen, L.; Kato, Y.; Sano, M.; Shah, S.K. Tree-Rings Stable Isotope (δ18O and δ2H) Based 368 Years Long Term Precipitation Reconstruction of South Eastern Kashmir Himalaya. Sci. Total Environ. 2023, 892, 164640. [Google Scholar] [CrossRef] [PubMed]
- Ortega Rodriguez, D.R.; Sánchez-Salguero, R.; Hevia, A.; Granato-Souza, D.; Cintra, B.B.L.; Hornink, B.; Andreu-Hayles, L.; Assis-Pereira, G.; Roig, F.A.; Tomazello-Filho, M. Climate Variability of the Southern Amazon Inferred by a Multi-Proxy Tree-Ring Approach Using Cedrela fissilis Vell. Sci. Total Environ. 2023, 871, 162064. [Google Scholar] [CrossRef]
- Harvey, J.E.; Smiljanić, M.; Scharnweber, T.; Buras, A.; Cedro, A.; Cruz-García, R.; Drobyshev, I.; Janecka, K.; Jansons, Ā.; Kaczka, R.; et al. Tree Growth Influenced by Warming Winter Climate and Summer Moisture Availability in Northern Temperate Forests. Glob. Change Biol. 2020, 26, 2505–2518. [Google Scholar] [CrossRef]
- Kasper, J.; Leuschner, C.; Walentowski, H.; Petritan, A.M.; Weigel, R. Winners and Losers of Climate Warming: Declining Growth in Fagus and Tilia vs. Stable Growth in Three Quercus Species in the Natural Beech–Oak Forest Ecotone (Western Romania). For. Ecol. Manag. 2022, 506, 119892. [Google Scholar] [CrossRef]
- Yuan, D.; Zhu, L.; Cherubini, P.; Li, Z.; Zhang, Y.; Wang, X. Species-Specific Indication of 13 Tree Species Growth on Climate Warming in Temperate Forest Community of Northeast China. Ecol. Indic. 2021, 133, 108389. [Google Scholar] [CrossRef]
- Bose, A.K.; Scherrer, D.; Camarero, J.J.; Ziche, D.; Babst, F.; Bigler, C.; Bolte, A.; Dorado-Liñán, I.; Etzold, S.; Fonti, P.; et al. Climate Sensitivity and Drought Seasonality Determine Post-Drought Growth Recovery of Quercus petraea and Quercus robur in Europe. Sci. Total Environ. 2021, 784, 147222. [Google Scholar] [CrossRef]
- Su, J.; Gou, X.; HilleRisLambers, J.; Deng, Y.; Fan, H.; Zheng, W.; Zhang, R.; Manzanedo, R.D. Increasing Climate Sensitivity of Subtropical Conifers along an Aridity Gradient. For. Ecol. Manag. 2021, 482, 118841. [Google Scholar] [CrossRef]
- Huang, Y.; Deng, X.; Zhao, Z.; Xiang, W.; Yan, W.; Ouyang, S.; Lei, P. Monthly Radial Growth Model of Chinese Fir (Cunninghamia lanceolata (Lamb.) Hook.), and the Relationships between Radial Increment and Climate Factors. Forests 2019, 10, 757. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, Z.-P.; Zhang, D.-Y.; Li, X.-Y.; Luo, T.-R.; Wang, X.-R.; Li, L.-L.; Zhao, Y.-R. Responses of Radial Growth of Different Tree Species to Abrupt Temperature Change in the Northern Greater Khingan Mountains, China. Chin. J. Appl. Ecol. 2024, 35, 2933–2941. [Google Scholar] [CrossRef]
- Ma, J.; Guo, J.; Wang, Y.; Liu, Z.; Gao, D.; Hong, L.; Zhang, Z. Variations in Stem Radii of Larix principis-rupprechtii to Environmental Factors at Two Slope Locations in the Liupan Mountains, Northwest China. J. For. Res. 2021, 32, 513–527. [Google Scholar] [CrossRef]
- Carrer, M.; Urbinati, C. Age-Dependent Tree-Ring Growth Responses to Climate in Larix decidua and Pinus cembra. Ecology 2004, 85, 730–740. [Google Scholar] [CrossRef]
- Yun, Z.; Yin, C.; Tian, K.; Zhang, W.; He, R.; He, W.; Sun, J.; Liu, Z. Radial Growth Responses of Picea likiangensis to Climate Variabilities at Different Altitudes in Yulong Snow Mountain, Southwest China. Chin. J. Plant Ecol. 2018, 42, 629. [Google Scholar] [CrossRef]
- Shan, Q.; Wang, Z.; Ling, H.; Zhang, G.; Yan, J.; Han, F. Unreasonable Human Disturbance Shifts the Positive Effect of Climate Change on Tree-Ring Growth of Malus sieversii in the Origin Area of World Cultivated Apples. J. Clean. Prod. 2021, 287, 125008. [Google Scholar] [CrossRef]
- Zhang, J.; Gou, X.; Rademacher, T.; Wang, L.; Li, Y.; Sun, Q.; Wang, F.; Cao, Z. Interaction of Age and Elevation on Xylogenesis in Juniperus przewalskii in a Cold and Arid Region. Agric. For. Meteorol. 2023, 337, 109480. [Google Scholar] [CrossRef]
- Cuapio-Hernández, L.; Reyes-Ortiz, J.L.; Rosa, A.B.D.L.; Pavón, N.P.; López-Herrera, M.; Villanueva-Díaz, J.; Sánchez-González, A. Is There a Response Pattern between Radial Growth of Trees and Elevation Gradient? Tree-Ring Res. 2023, 79, 12–26. [Google Scholar] [CrossRef]
- Diao, Y.; Zhang, S.; Liu, Y.; Jin, G.; Tian, S.; Liu, Y. Effects of Topography on Radial Growth of Tree Species with Different Mycorrhizal Types. Forests 2023, 14, 546. [Google Scholar] [CrossRef]
- Li, J.; Peng, J.; Wei, X.; Peng, M.; Li, X.; Liu, Y.; Li, J. Stability Assessment of Tree Ring Growth of Pinus Armandii Franch in Response to Climate Change Based on Slope Directions at the Lubanling in the Funiu Mountains, China. J. For. Res. 2024, 35, 44. [Google Scholar] [CrossRef]
- Kobal, M.; Grčman, H.; Zupan, M.; Levanič, T.; Simončič, P.; Kadunc, A.; Hladnik, D. Influence of Soil Properties on Silver Fir (Abies alba Mill.) Growth in the Dinaric Mountains. For. Ecol. Manag. 2015, 337, 77–87. [Google Scholar] [CrossRef]
- Meyer, M.D.; North, M.P.; Gray, A.N.; Zald, H.S.J. Influence of Soil Thickness on Stand Characteristics in a Sierra Nevada Mixed-Conifer Forest. Plant Soil 2007, 294, 113–123. [Google Scholar] [CrossRef]
- Luo, T.; Wang, Z.; Zhang, D.; Li, X.; Wang, X. Response of Radial Growth of Dahurian Larch (Larix gmelinii) to Climate Factors at Different Altitudes in the Northern Part of the Greater Khingan Mountains. Front. For. Glob. Change 2024, 7, 1434773. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, Y.; Liu, J.; Yuan, S.; Cui, M.; Xiong, Q.; Waili, Y.; Kang, M.; Xu, H. Divergent Responses to Climatic Conditions in Radial Growth of Abies fargesii along Elevation at the Eastern Edge of the Tibetan Plateau. Trees-Struct. Funct. 2024, 38, 1035–1048. [Google Scholar] [CrossRef]
- Lu, K.; Chen, N.; Zhang, C.; Dong, X.; Zhao, C. Drought Enhances the Role of Competition in Mediating the Relationship between Tree Growth and Climate in Semi-Arid Areas of Northwest China. Forests 2019, 10, 804. [Google Scholar] [CrossRef]
- Ford, K.R.; Breckheimer, I.K.; Franklin, J.F.; Freund, J.A.; Kroiss, S.J.; Larson, A.J.; Theobald, E.J.; HilleRisLambers, J. Competition alters tree growth responses to climate at individual and stand scales. Can. J. For. Res. 2017, 47, 53–62. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, X.; Zhang, X.; Xiao, F.; Zheng, R.; Yang, B.; Xiang, W. Variations of Monthly Radial Growth of Chinese Fir [Cunninghamia lanceolata (Lamb.) Hook.] Considering Its Responses to Climatic Factors. Eur. J. For. For. Res. 2024, 143, 1525–1539. [Google Scholar] [CrossRef]
- Xie, S.; Yan, T.; Sun, X.; Chen, H.; Sun, M.; Zhang, Y. Radial Growth Response of Pinus yunnanensis to Climate in High Mountain Forests of Northwestern Yunnan, Southwestern China. Front. For. Glob. Change 2024, 7, 1343730. [Google Scholar] [CrossRef]
- Li, Q. Intra-Annual Radial Growth Dynamics of Common Tree Species and Its Influencing Factors in the Tianma National Nature Reserve, Anhui, China. Master’s Thesis, East China Normal University, Shanghai, China, 2024. (In Chinese). [Google Scholar]
- Liu, P.; Hu, S.; Wei, H.; He, W.; Zhou, Y.; Wang, Y. Response of Radial Growth of Pinus sylvestris Var. Mongolica of Different Stand Ages to Climate and Extreme Drought Events in the Semi-Arid Region of Western Liaoning, Northeast China. Front. For. Glob. Change 2023, 6, 1272477. [Google Scholar] [CrossRef]
- Liu, Z.; Li, J.; Shi, S.-L.; Yang, R.; Luo, W.-W.; Ma, Y.-L.; Bie, X.-J.; Wang, G.-Y. Response of Radial Growth of Different Timberline Species to Climate Change in Yading Nature Reserve, Sichuan, China. Chin. J. Appl. Ecol. 2024, 35, 1177–1186. [Google Scholar] [CrossRef]
- Scolforo, J.R.S.; Maestri, R.; Ferraz Filho, A.C.; de Mello, J.M.; de Oliveira, A.D.; de Assis, A.L. Dominant Height Model for Site Classification of Eucalyptus Grandis Incorporating Climatic Variables. Int. J. For. Res. 2013, 2013, 139236. [Google Scholar] [CrossRef]
- He, X.; Lei, X.; Xu, Q.; Lan, J.; Wu, B.; Guo, H.; Gao, W.; Liu, D. Combining Multiple Feature Selection Methods and Structural Equation Modelling for Exploring Factors Affecting Stand Biomass of Natural Coniferous-Broad Leaved Mixed Forests. Sci. Total Environ. 2024, 954, 176669. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.F.; Jalilvand, H.; Fallah, A.; Asadi, H.; Tafazoli, M. Machine Learning Methods for Basal Area Prediction of Fagus orientalis Lipsky Stands Based on National Forest Inventory. Trees-Struct. Funct. 2025, 39, 40. [Google Scholar] [CrossRef]
- He, X.; Lei, X.; Liu, D.; Lei, Y. Developing Machine Learning Models with Multiple Environmental Data to Predict Stand Biomass in Natural Coniferous-Broad Leaved Mixed Forests in Jilin Province of China. Comput. Electron. Agric. 2023, 212, 108162. [Google Scholar] [CrossRef]
- Bui, Q.-T.; Pham, Q.-T.; Pham, V.-M.; Tran, V.-T.; Nguyen, D.-H.; Nguyen, Q.-H.; Nguyen, H.-D.; Do, N.T.; Vu, V.-M. Hybrid Machine Learning Models for Aboveground Biomass Estimations. Ecol. Inf. 2024, 79, 102421. [Google Scholar] [CrossRef]
- Wei, X.-X.; Peng, J.-F.; Peng, M.; Li, X.; Cui, J.-Y.; Li, J.-K.; Wei, Y.-F. Response of Radial Growth of Pinus tabuliformis to Climatic Factors in the North-South Transition Zone of China—A Case Study of Jigong Mountain National Nature Reserve. Geogr. Sci. 2024, 44, 1643–1652. (In Chinese) [Google Scholar]
- Holmes, R.L. Computer-Assisted Quality Control in Tree-Ring Dating and Measurement. Tree-Ring Soc. 1983, 43, 69–78. [Google Scholar]
- He, X.; Lei, X.; Zhou, C.; Duan, G.; Zhou, M.; Shi, J. Application of R program package ForestStatTool in statistics of individual tree and stand factors in forestry. J. Beijing For. Univ. 2024, 46, 125–135. [Google Scholar] [CrossRef]
- Hegyi, F. A simulation model for managing jack-pine stands. In Growth Models for Tree and Stand Simulation; Fries, J., Ed.; Research Note No. 30; Royal College of Forestry: Stockholm, Sweden, 1974; pp. 74–90. [Google Scholar]
- Yoon, S.; Lee, W.-H. Methodological Analysis of Bioclimatic Variable Selection in Species Distribution Modeling with Application to Agricultural Pests (Metcalfa pruinosa and Spodoptera litura). Comput. Electron. Agric. 2021, 190, 106430. [Google Scholar] [CrossRef]
- Rao, C.R. The Use and Interpretation of Principal Component Analysis in Applied Research. Sankhyā Indian J. Stat. Ser. A (1961–2002) 1964, 26, 329–358. [Google Scholar]
- Soykan, C.U.; Eguchi, T.; Kohin, S.; Dewar, H. Prediction of Fishing Effort Distributions Using Boosted Regression Trees. Ecol. Appl. 2014, 24, 71–83. [Google Scholar] [CrossRef]
- Win, K.; Sato, T.; Hiroshima, T. Applicability of Remote Sensing and Machine Learning for Predicting Bulk Soil Electrical Conductivity under Different Forest Types in Central Japan. Soil Adv. 2025, 3, 100045. [Google Scholar] [CrossRef]
- Yao, J.; Lei, X.; Wang, X.; Fu, L.; Zheng, Y.; Guo, X.; Duan, G.; Song, X. Influence of moisture content on needle resistance measured by micro-drilling resistance device. J. Cent. South Univ. For. Technol. 2022, 42, 137–147. (In Chinese) [Google Scholar]
- Bolón-Canedo, V.; Alonso-Betanzos, A. Ensembles for Feature Selection: A Review and Future Trends. Inf. Fusion 2019, 52, 1–12. [Google Scholar] [CrossRef]
- Zhang, X.; Lei, Y.; Cao, Q.V.; Chen, X.; Liu, X. Improving Tree Survival Prediction with Forecast Combination and Disaggregation. Can. J. For. Res. 2011, 41, 1928–1935. [Google Scholar] [CrossRef]
- Ryan, M.G.; Binkley, D.; Fownes, J.H. Age-Related Decline in Forest Productivity: Pattern and Process. In Advances in Ecological Research; Begon, M., Fitter, A.H., Eds.; Academic Press: Cambridge, MA, USA, 1997; Volume 27, pp. 213–262. [Google Scholar]
- Mencuccini, M.; Martínez-Vilalta, J.; Vanderklein, D.; Hamid, H.A.; Korakaki, E.; Lee, S.; Michiels, B. Size-Mediated Ageing Reduces Vigour in Trees. Ecol. Lett. 2005, 8, 1183–1190. [Google Scholar] [CrossRef] [PubMed]
- Gower, S.T.; McMurtrie, R.E.; Murty, D. Aboveground Net Primary Production Decline with Stand Age: Potential Causes. Trends Ecol. Evol. 1996, 11, 378–382. [Google Scholar] [CrossRef]
- Rozendaal, D.M.A.; Phillips, O.L.; Lewis, S.L.; Affum-Baffoe, K.; Alvarez-Davila, E.; Andrade, A.; Aragão, L.E.O.C.; Araujo-Murakami, A.; Baker, T.R.; Bánki, O.; et al. Competition influences tree growth, but not mortality, across environmental gradients in Amazonia and tropical Africa. Ecology 2020, 101, e03052. [Google Scholar] [CrossRef]
- Looney, C.E.; Zhang, J. Site Quality and Intensive Early Stand Management Practices Affect Growth Dominance, Structural Complexity, and Tree Growth in Ponderosa pine Plantations. For. Ecol. Manag. 2022, 519, 120318. [Google Scholar] [CrossRef]
- Pretzsch, H.; Bravo-Oviedo, A.; Hilmers, T.; Ruiz-Peinado, R.; Coll, L.; Löf, M.; Ahmed, S.; Aldea, J.; Ammer, C.; Avdagić, A.; et al. With increasing site quality, asymmetric competition and mortality reduce Pinus sylvestris L. stand structuring across Europe. For. Ecol. Manag. 2022, 520, 120365. [Google Scholar] [CrossRef]
- Chen, S.Y.; Zhao, S.Y.; Jin, F.; Hu, S.B.; Fang, K.Y. Environmental information recorded by Pinus massoniana of different ages on Gushan Mountain, Fuzhou. J. Subtrop. Resour. Environ. 2019, 14, 19–27. (In Chinese) [Google Scholar]
- Schwab, N.; Kaczka, R.J.; Janecka, K.; Böhner, J.; Chaudhary, R.P.; Scholten, T.; Schickhoff, U. Climate Change-Induced Shift of Tree Growth Sensitivity at a Central Himalayan Treeline Ecotone. Forests 2018, 9, 267. [Google Scholar] [CrossRef]
- Nie, K.; Xu, M.; Yang, Y.L.; Zhang, J.; Wen, C.Y.; Zhang, J. Response of Pinus massoniana radial growth to climate change in central Guizhou. J. Southwest For. Univ. (Nat. Sci.) 2023, 43, 32–38. (In Chinese) [Google Scholar]
- Yan, J.; Liu, X.; Tang, X.; Yu, G.; Zhang, L.; Chen, Q.; Li, K. Substantial Amounts of Carbon Are Sequestered during Dry Periods in an Old-Growth Subtropical Forest in South China. J. Res. 2013, 18, 21–30. [Google Scholar] [CrossRef]
- Huang, X.; Dai, D.; Xiang, Y.; Yan, Z.; Teng, M.; Wang, P.; Zhou, Z.; Zeng, L.; Xiao, W. Radial Growth of Pinus massoniana Is Influenced by Temperature, Precipitation, and Site Conditions on the Regional Scale: A Meta-Analysis Based on Tree-Ring Width Index. Ecol. Indic. 2021, 126, 107659. [Google Scholar] [CrossRef]
- Hacket-Pain, A.J.; Cavin, L.; Friend, A.D.; Jump, A.S. Consistent Limitation of Growth by High Temperature and Low Precipitation from Range Core to Southern Edge of European Beech Indicates Widespread Vulnerability to Changing Climate. Eur. J. For. Res. 2016, 135, 897–909. [Google Scholar] [CrossRef]
- Li, J.Y.; Guo, M.G.; Sui, D.D.; Bai, C.M.; Zhao, W.D.; Jiang, W.J.; Huang, S.Q.; Guo, X.L. Intra-annual xylem formation dynamics of Pinus massoniana in southern Guangxi and its response to climate. Quat. Sci. 2024, 44, 996–1007. [Google Scholar] [CrossRef]
- Wu, Q.; Ding, J.; Yan, H.; Zhang, S.; Fang, T.; Ma, K. Effects of Simulated Precipitation and Nitrogen Addition on Seedling Growth and Biomass in Five Tree Species in Gutian Mountain, Zhejiang Province, China. Chin. J. Plant Ecol. 2011, 35, 256. [Google Scholar] [CrossRef]
- Xiao, S.G. Effect of site conditions on the growth of Cotinus coggygria in Yiling District of Yichang Municipality. J. Southwest For. Univ. 2009, 29, 31–34. [Google Scholar] [CrossRef]
- Gu, H.; Wang, J.; Ma, L.; Shang, Z.; Zhang, Q. Insights into the BRT (Boosted Regression Trees) Method in the Study of the Climate-Growth Relationship of Masson Pine in Subtropical China. Forests 2019, 10, 228. [Google Scholar] [CrossRef]
- Lan, T.; Xia, B.; He, S. Tree Ring Analysis on Relation of Pinus massoniana Growth to Climate Factors. Chin. J. Appl. Ecol. 1994, 5, 422. [Google Scholar]
- Xia, B.; Lan, T.; He, S. Nonlinear Response Function of Growth of Pinus massomiana to Climate. Chin. J. Plant Ecol. 1996, 20, 51–56. [Google Scholar]
- Jing, M.; Zhu, L.; Cherubini, P.; Yuan, D.; Li, Z.; Wang, X.; Liu, S. Responses of Radial Growth of Pinus massoniana and Castanopsis eyrei to Climate Change at Different Elevations in South China. Ecol. Indic. 2022, 145, 109602. [Google Scholar] [CrossRef]
- Li, D.; Fang, K.; Li, Y.; Chen, D.; Liu, X.; Dong, Z.; Zhou, F.; Guo, G.; Shi, F.; Xu, C.; et al. Climate, Intrinsic Water-Use Efficiency and Tree Growth over the Past 150 Years in Humid Subtropical China. PLoS ONE 2017, 12, e0172045. [Google Scholar] [CrossRef]
- Rossi, S.; Anfodillo, T.; Čufar, K.; Cuny, H.E.; Deslauriers, A.; Fonti, P.; Frank, D.; Gričar, J.; Gruber, A.; Huang, J.-G.; et al. Pattern of Xylem Phenology in Conifers of Cold Ecosystems at the Northern Hemisphere. Glob. Change Biol. 2016, 22, 3804–3813. [Google Scholar] [CrossRef]
- Zhai, L.; Bergeron, Y.; Huang, J.-G.; Berninger, F. Variation in Intra-Annual Wood Formation, and Foliage and Shoot Development of Three Major Canadian Boreal Tree Species. Am. J. Bot. 2012, 99, 827–837. [Google Scholar] [CrossRef]
| Variables | Mean | Standard Deviation | Max | Min |
|---|---|---|---|---|
| Age/a | 52.470 | 11.320 | 69.000 | 25.000 |
| Elevation/m | 217.900 | 12.032 | 240.000 | 203.000 |
| Slope/° | 29.300 | 7.439 | 40.000 | 20.000 |
| Soil Thickness/dm | 6.560 | 1.438 | 9.000 | 5.000 |
| Variables | Mean | Standard Deviation | Max | Min |
|---|---|---|---|---|
| Annual Mean Temperature (Tmean)/°C | 15.540 | 0.780 | 17.770 | 14.100 |
| Annual Max Temperature (Tmax)/°C | 37.480 | 1.380 | 41.110 | 34.400 |
| Annual Min Temperature (Tmin)/°C | −8.930 | 3.410 | −2.700 | −20.000 |
| Annual Precipitation/mm | 1116.220 | 259.290 | 1653.790 | 494.300 |
| Feature | PCA-PCAr | PCA-PCAl | RDA | BRT | RF | XGBoost | AvgImportance |
|---|---|---|---|---|---|---|---|
| Age | 0.259 | 0.071 | 0.429 | 0.354 | 0.396 | 0.133 | 0.274 |
| Annual Precipitation | 0.183 | 0.118 | 0.051 | 0.032 | 0.021 | 0.045 | 0.075 |
| Tmean | 0.214 | 0.072 | 0.042 | 0.061 | 0.064 | 0.079 | 0.088 |
| Tmax | 0.047 | 0.121 | 0.086 | 0.029 | 0.037 | 0.064 | 0.064 |
| Tmin | 0.135 | 0.129 | 0.020 | 0.011 | 0.013 | 0.026 | 0.056 |
| Slope | 0.073 | 0.127 | 0.090 | 0.032 | 0.048 | 0.124 | 0.082 |
| Elevation | 0.057 | 0.115 | 0.101 | 0.022 | 0.020 | 0.155 | 0.078 |
| Soil Thickness | 0.001 | 0.082 | 0.151 | 0.060 | 0.051 | 0.196 | 0.090 |
| Competition Index | 0.031 | 0.166 | 0.031 | 0.399 | 0.350 | 0.178 | 0.193 |
| Variable | BS | K | MSE |
|---|---|---|---|
| Age | TP | 7 | 80.805 |
| Annual Precipitation | CR | 7 | 104.165 |
| Tmean | TP | 5 | 91.610 |
| Tmax | CR | 7 | 103.073 |
| Tmin | CR | 7 | 101.542 |
| Elevation | CR | 7 | 103.138 |
| Competition Index | TP | 7 | 98.972 |
| Slope | TP | 7 | 101.867 |
| Soil Thickness | TP | 7 | 102.994 |
| Variable | EDF | Deviance Explained/% | |||
|---|---|---|---|---|---|
| Age | 5.278 | <0.001 | 170.452 | 0.244 | 24.53 |
| Annual Precipitation | 5.486 | <0.001 | 12.395 | 0.025 | 2.64 |
| Tmean | 3.894 | <0.001 | 124.755 | 0.141 | 14.26 |
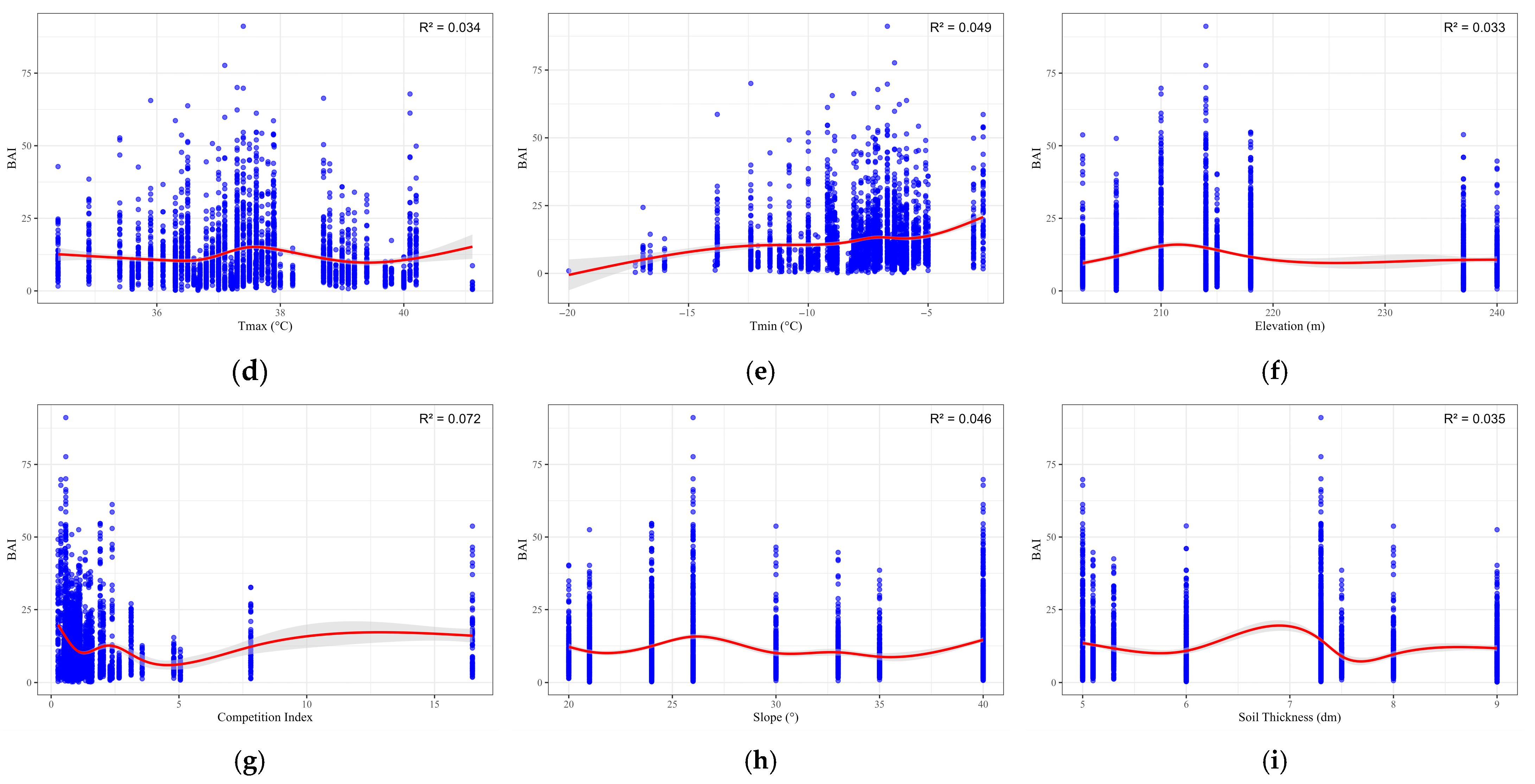
| Tmax | 5.567 | <0.001 | 18.522 | 0.034 | 3.53 |
| Tmin | 5.312 | <0.001 | 26.689 | 0.049 | 5.11 |
| Elevation | 5.12 | <0.001 | 18.97 | 0.033 | 3.51 |
| Competition Index | 5.863 | <0.001 | 40.341 | 0.072 | 7.33 |
| Slope | 5.766 | <0.001 | 25.353 | 0.046 | 4.76 |
| Soil Thickness | 5.849 | <0.001 | 18.665 | 0.035 | 3.68 |
| Variable | Optimum (X) | Max BAI | 95% CI for BAI |
|---|---|---|---|
| Age | 69 | 24.211 | 20.726–27.697 |
| Annual Precipitation | 1653.79 | 20.05 | 17.058–23.041 |
| Tmean | 16.96 | 20.102 | 19.233–20.971 |
| Tmax | 41.11 | 15.227 | 11.056–19.398 |
| Tmin | −2.7 | 20.797 | 18.845–22.750 |
| Elevation | 211.55 | 15.953 | 14.972–16.934 |
| Competition Index | 0.27 | 19.809 | 18.636–20.982 |
| Slope | 26.23 | 15.743 | 14.780–16.706 |
| Soil Thickness | 6.89 | 19.511 | 17.685–21.337 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhao, C.; Lu, J.; Yao, J.; Li, Y.; Zhou, M.; Ha, D. Research on the Main Influencing Factors and Variation Patterns of Basal Area Increment (BAI) of Pinus massoniana. Sustainability 2025, 17, 7137. https://doi.org/10.3390/su17157137
Li Z, Zhao C, Lu J, Yao J, Li Y, Zhou M, Ha D. Research on the Main Influencing Factors and Variation Patterns of Basal Area Increment (BAI) of Pinus massoniana. Sustainability. 2025; 17(15):7137. https://doi.org/10.3390/su17157137
Chicago/Turabian StyleLi, Zhuofan, Cancong Zhao, Jun Lu, Jianfeng Yao, Yanling Li, Mengli Zhou, and Denglong Ha. 2025. "Research on the Main Influencing Factors and Variation Patterns of Basal Area Increment (BAI) of Pinus massoniana" Sustainability 17, no. 15: 7137. https://doi.org/10.3390/su17157137
APA StyleLi, Z., Zhao, C., Lu, J., Yao, J., Li, Y., Zhou, M., & Ha, D. (2025). Research on the Main Influencing Factors and Variation Patterns of Basal Area Increment (BAI) of Pinus massoniana. Sustainability, 17(15), 7137. https://doi.org/10.3390/su17157137






