Optimal Governance for Post-Concession Logistics Infrastructure: A Comparative Study of Self-Operation vs. Delegation Under Information Asymmetry

Abstract

Public–private partnership (PPP) logistics infrastructure projects have become increasingly prevalent globally. Consequently, the effective management of these projects as their concession periods expire presents a crucial challenge for governments, vital for the sustainable management of PPP logistics infrastructure. This study addresses this challenge by focusing on the pivotal post-concession decision: whether the government should self-operate the mature logistics infrastructure or re-delegate its management to a private entity. Our theoretical model, built on a principal–agent framework, first establishes a social welfare baseline under government self-operation and then analyzes delegated operation under symmetric information, identifying efficiency frontiers. Under symmetric information, we find that government self-operation is more advantageous when its own operational efficiency is sufficiently high, irrespective of the private enterprise’s efficiency; conversely, delegating to an efficient private enterprise is optimal only when government operational efficiency is low. We also demonstrate that if the government can directly specify the demand quantity and service level and delegates operation via a fixed fee, the enterprise can be incentivized to align with the social optimum. However, under asymmetric information, potential welfare gains from delegation are inevitably offset by informational rent and output distortion. We further uncover non-monotonic impacts of parameters like the proportion of low-cost firms on social welfare loss and demonstrate how information asymmetry can indirectly compromise the long-term resilience of the infrastructure. Ultimately, our work asserts that delegation is only superior if its potential efficiency gains sufficiently offset the inherent losses stemming from information asymmetry.

1. Introduction

Currently, logistics infrastructures such as ports, airports, and highways serve as the economic backbone of nations. They are crucial for underpinning international trade, fostering regional development, and maintaining the resilience of global supply chains. The construction and maintenance of these large-scale infrastructure projects typically demand substantial long-term capital investment. Moreover, their operational efficiency and resilience directly influence national economic competitiveness and recovery capabilities in the face of uncertainty. Consequently, governments worldwide have extensively adopted public–private partnership (PPP) models, particularly forms like build–operate–transfer (BOT), to effectively leverage private capital and specialized operational expertise [1]. During these long-term concession periods, private enterprises are responsible for the infrastructure’s construction and management [2]. However, upon the expiry of the concession term, these assets, which embody significant public value and economic benefits, are contractually transferred back to government control for subsequent management and operation. With a growing number of early PPP projects reaching their concession expiry, the question of how governments can effectively take over and manage these critical assets while ensuring both their operational efficiency and long-term resilience has become an increasingly urgent and complex global public management issue.

At this critical juncture of post-concession transfer, governments confront a significant strategic decision: whether to self-operate these complex logistics infrastructure assets or to delegate their management to specialized private enterprises. The advantage of government self-operation lies in maintaining direct control over the infrastructure, ensuring its alignment with long-term public policy objectives, and potentially mitigating the private sector’s profit-driven, short-term behaviors. However, its primary trade-off involves inherent systemic challenges such as lower efficiency, bureaucratic inertia [3], a lack of specialized management expertise, and insufficient innovation incentives, which can impede both daily operational efficiency and the agility to respond to unforeseen events. In contrast, delegating management to specialized firms promises higher operational efficiency, greater market responsiveness, and technological innovation [4]. Nevertheless, this approach entails a loss of direct control and potentially introduces principal–agent problems. For private enterprises, their core objective is maximizing profit, necessitating a precise balance between operational costs and revenue while adhering to contractually stipulated service levels—a complex trade-off in itself.

However, what truly complicates this decision and introduces significant social welfare risks is the pervasive problem of information asymmetry [5]. In practice, specialized enterprises managing logistics infrastructure inherently possess private information [6,7], such as their operational efficiency, maintenance costs, and investment costs. This significant information gap creates immense challenges for governments in designing effective delegation contracts and effectively monitoring enterprise performance [7]. Governments struggle not only to precisely set “first-best” incentive schemes to guide enterprise behavior but may also be forced to accept informational rent (excess profits beyond the firm’s reservation utility) due to unobservable or unverifiable cost information. Concurrently, to mitigate such rent, governments often tolerate reductions in output and service levels, particularly from higher-cost enterprises. These distortions undermine daily operational efficiency and can subtly erode the infrastructure’s inherent resilience, making it more vulnerable to external shocks (e.g., natural disasters, pandemics, or supply chain disruptions), ultimately harming overall social welfare. These are not merely incidental inefficiencies but represent systematic, structural welfare losses under conditions of information asymmetry, thereby underscoring the critical need for a rigorous theoretical analysis of this crucial governmental decision-making mechanism.

Building upon the context and core challenges outlined above, this study aims to develop a sophisticated theoretical model to investigate how governments can make optimal operational management decisions for the post-PPP-concession logistics infrastructure and to quantify the impact of information asymmetry on social welfare. Specifically, this research seeks to answer the following core questions: (1) How should governments balance self-operation versus delegation for post-PPP logistics infrastructure to maximize social welfare under information asymmetry? (2) How do key parameters (e.g., market sensitivity, firm cost differences, and low-cost firm proportion) affect welfare, losses, and resilience in delegated logistics operations? (3) Given private firm information, how can governments design optimal incentive contracts to balance delegation gains against information losses and foster long-term resilience for logistics infrastructure?

To address these core research questions, this paper constructs a rigorous principal–agent theoretical model tailored to government operational management decisions for post-PPP logistics infrastructure. The study begins by analyzing government self-operation, establishing a social welfare baseline to measure the government’s inherent operational efficiency without delegation. Subsequently, the model transitions to analyze government-delegated operation under symmetric information. In this phase, we systematically explore the efficiency frontiers of delegated operation under various contract forms (e.g., revenue-sharing, fixed fees, government-specified service levels, and output), identifying optimal contract designs and conditions for maximizing social welfare in an ideal setting. Finally, and forming the core of this research, we extend the model to incorporate asymmetric information, deeply analyzing how the government, as the principal, designs incentive-compatible contracts when the private operator (agent) possesses private information regarding its operational costs (e.g., maintenance costs). Through analytical derivations and comparative static analyses, this paper quantifies the social welfare levels and efficiency losses across different decision scenarios, thereby providing a robust basis for government decision making. Our analysis reveals the following main findings.

First, our study reveals that, under symmetric information, delegating post-PPP logistics infrastructure operations to specialized private enterprises can significantly enhance social welfare, potentially achieving social optimality when the government can directly specify service levels and output. However, once information asymmetry is introduced, these potential welfare gains are inevitably offset by informational rent (additional profits paid to efficient firms to incentivize truthful revelation) and output distortion (the strategic reduction in service levels and output for less efficient firms to limit rent). This implies that achieving first-best social welfare is not feasible under information asymmetry.

Second, this research extensively demonstrates how various crucial operational and market parameters influence the welfare outcomes of delegated logistics infrastructure operations and the efficiency losses arising from information asymmetry. For instance, higher market sensitivity to service levels and larger cost differences between enterprise types generally lead to increased information asymmetry losses. More notably, we find a non-monotonic impact of the proportion of low-cost enterprises on total social welfare loss: there exists a critical threshold where the loss increases with this proportion up to the threshold and then decreases thereafter, offering a nuanced perspective for governments evaluating market heterogeneity.

Third, this study provides a clear decision criterion: whether the government should delegate logistics infrastructure operations critically depends on whether the potential efficiency gains from leveraging a specialized private enterprise can fully compensate for the inherent losses (including informational rent and output distortion) incurred due to information asymmetry. Furthermore, we highlight that output distortions caused by information asymmetry not only reduce daily efficiency but can also indirectly compromise the inherent resilience of the infrastructure, making it more vulnerable to unforeseen external shocks. Therefore, optimal contract design must balance efficiency and incentives while also considering its impact on the long-term resilience of the infrastructure, thereby maximizing social welfare in complex informational environments.

The contributions of this study are threefold. First, this study provides a pioneering decision-making framework for post-PPP logistics infrastructure management. To the best of our knowledge, we constructed a customized theoretical model that systematically analyzes how governments strategically choose between self-operation and delegating to specialized private enterprises after a concession period. This fills a significant gap in the literature and offers clear analytical tools and insights for policymakers. Second, this study quantitatively reveals the profound impact of information asymmetry on critical infrastructure operational efficiency and resilience. Our rigorous modeling quantifies the social welfare losses attributable to informational rent and output distortion. Crucially, we identify novel non-monotonic effects of parameters such as the proportion of low-cost firms on these losses while also elucidating how information asymmetry indirectly compromises the long-term resilience of infrastructure. Third, this study offers actionable, quantifiable decision-making guidance for governments to maximize social welfare in complex informational environments. It distills a clear decision criterion: delegation is only superior if its potential efficiency gains sufficiently offset the inherent losses stemming from information asymmetry. This provides direct and implementable strategic guidance for policymakers to effectively maximize social welfare.

The rest of this paper is organized as follows. In Section 2, we review the related literature. The model settings, game structure, and profit functions are illustrated in Section 3. In Section 4, we conduct a comparative analysis of government self-operation and government-delegated operation under symmetric information. Section 5 extends the delegated operation model to incorporate asymmetric information, investigating its impact on governmental decisions and social welfare. Section 6 presents the conclusions, managerial insights, and future research directions. The derivations and proofs are provided in Appendix Section.

2. Literature Review

Our work is intertwined with three fundamental research streams: (1) public service outsourcing and delegated governance, (2) contract design in logistics infrastructure PPPs, and (3) logistics infrastructure operations and management. In this section, we expound on the placement of our work within each research stream and delineate its unique contribution.

2.1. Public Service Outsourcing and Delegated Governance

Governments worldwide increasingly utilize outsourcing and delegated governance mechanisms to enhance the delivery of diverse public services. This strategic approach is often driven by motivations to improve efficiency, reduce costs, increase service capacity, and leverage specialized private sector expertise [8,9]. The scope of services subjected to such delegation is broad, encompassing critical areas like waste management (e.g., [10,11,12]), healthcare logistics and procurement (e.g., [9,13,14]), data management for utilities (e.g., [15]), natural resource governance (e.g., [16]), and even the internal delegation of regulatory authority within government agencies (e.g., [17]). However, the literature also highlights significant challenges and complexities inherent in these arrangements. Studies investigate optimal governance structures, balancing perceived risks with cost efficiency [9,14], determining the appropriate scale for outsourcing [10,12], and managing the discretion and information asymmetry when delegating authority, even within the public sector [17]. Researchers employ a variety of methodologies, including empirical analyses of efficiency, decision-support tools for risk evaluation, game-theoretic models, and comparative case studies, to provide insights into effective public service delivery through delegated governance [9,12,13,17]. The overarching goal is to optimize public service outcomes through judicious selection and management of external or decentralized service providers.

This study shares a fundamental interest with the “public service outsourcing and delegated governance” literature in exploring optimal public service delivery, acknowledging the strategic nature of governance choices, and considering factors such as efficiency, cost, and risk in decision making. Both fields analyze complex principal–agent relationships in the context of service provision. However, a key distinction lies in the specific lifecycle stage and asset context under scrutiny. While existing public service outsourcing literature often focuses on the initial decision to outsource a new service, the design of new outsourcing contracts, or the ongoing management of existing delegated services, our research addresses a unique strategic juncture: the post-concession expiry phase of a PPP logistics infrastructure project. This involves a fundamental re-evaluation of the governance mode for an already-established, high-value, and often complex asset rather than the initial delegation of a public service. The decision (self-operation versus re-delegation) is inherently influenced by the specific characteristics of this mature asset and the government’s evolved capabilities post transfer, factors less centrally explored in the general outsourcing literature. Thus, our work extends the conventional understanding of public service delegation by providing a comprehensive framework for strategic governance choices at a critical asset lifecycle transition point.

2.2. Contract Design in Logistics Infrastructure PPPs

The global landscape of logistics infrastructure development increasingly relies on PPP models, especially BOT schemes, driven by escalating travel demand and persistent government fiscal pressures [1,2]. These projects, characterized by substantial upfront investments and lengthy concession periods, necessitate meticulously crafted contracts to reconcile the often-divergent goals of the government (maximizing social welfare) and the private firm (aiming for profit maximization). The current body of research predominantly scrutinizes the pre-implementation phase of contract design for highway BOT projects. This includes determining optimal toll charges, project capacity, and concession periods through game-theoretic models to balance stakeholder interests [1,18,19]. Furthermore, existing studies delve into the vital role of government subsidies (e.g., construction, operating, and lump sum) and guarantees (like minimum traffic guarantees) in attracting private investment and mitigating inherent project risks [1,2,20,21,22]. A critical focus is also placed on managing information asymmetry and deep uncertainty—concerning future traffic demand and private firm costs—by exploring information disclosure strategies, signaling mechanisms, and robust decision-making frameworks that influence contract terms and outcomes [5,7,23,24,25]. Lastly, some research integrates service quality as a contractible variable and investigates optimal auction mechanisms for concession awards [6,26,27].

This research shares conceptual commonalities with the existing literature, particularly in leveraging optimization and game-theoretic approaches for PPP project contract design and understanding stakeholder incentives. Differently, this study uniquely addresses the strategic decision-making process post concession expiry, moving beyond the typical focus on initial contract formation or in-period management. We provide a novel framework for governments to choose between self-operation and re-delegation for mature assets, a critical yet underexplored lifecycle stage. Furthermore, our research rigorously quantifies the social welfare impacts of information asymmetry in post-concession re-contracting, identifying novel non-monotonic effects and explicitly linking information asymmetry to long-term infrastructure resilience.

2.3. Logistics Infrastructure Operations and Management

The field of logistics infrastructure operations and management has garnered considerable academic attention, with extensive foundational reviews available across various modalities (e.g., Meng and Lu [2] for roads; Stahlbock and Voß [28], Kim and Lee [29] for maritime; Feng et al. [30] for aviation). Most of the previous studies focus on pricing, capacity management, operational optimization, and inter-modal coordination. Within pricing, Alvarez-SanJaime et al. [31] examined how per-passenger infrastructure fees significantly influence cooperation and competition between high-speed rail and airlines, impacting social welfare. This work underscores the critical role of pricing policies as a mechanism for market shaping. Building on this, He et al. [32] delved into pricing and revenue allocation mechanisms for regional road networks utilizing cyber–physical internet (CPI) technology. Their models analyze optimal tolling and revenue sharing strategies among road operators to enhance operational efficiency and foster collaboration. Similarly, Feng et al. [33] proposed collaborative road pricing strategies for heterogeneous vehicles, integrating congestion and emission pricing to improve network service and sustainability. These studies demonstrate how sophisticated pricing models can optimize resource utilization and achieve broader system objectives. Regarding capacity management, Guo and Jiang [34] developed a multi-stage model for optimal capacity investment and exit decisions within port clusters under demand uncertainty. Their research highlights the strategic importance of balancing supply and demand to maximize social welfare in dynamic environments. Complementing this, Chen et al. [35] addressed the pressing issue of port overcapacity by proposing government-led integration models that optimize capacity adjustments and market share transactions to minimize social cost, fostering sustainable port development. In terms of operational optimization, Tiwari et al. [36] focused on the competitive hub location problem for airlines, presenting models and solution approaches for maximizing market share through efficient network design. This work provides tactical guidance for individual firm operations within existing infrastructure. Moreover, governments play a crucial role in these aforementioned areas. For instance, Hou et al. [37] strategically compared “group management” versus “localized management” for multi-airport systems (MASs), integrating air-rail intermodality. Their findings suggest that group management often maximizes social welfare, directly informing policymakers on optimal governance structures for large-scale transportation infrastructure. This exemplifies the direct influence of governmental strategic choices on the operational frameworks and outcomes of critical logistics assets.

This study fundamentally shifts the focus of logistics infrastructure management from the predominantly tactical or operational levels (e.g., pricing, capacity optimization, and specific operational mechanisms) to a strategic level. Specifically, it investigates the overarching governmental strategic choice regarding whether to self-operate or delegate the management of logistics infrastructure to external entities. Furthermore, while incorporating tactical-level decision problems concerning logistics infrastructure, such as pricing (demand) and service quality, this study distinguishes itself by providing actionable insights into designing optimal incentive contracts for this crucial strategic transition, ultimately contributing a holistic, life-cycle perspective to PPP governance and sustainable infrastructure management.

3. Model

For a PPP logistics infrastructure project approaching the conclusion of its concession period, the government confronts a pivotal strategic choice regarding its future operational model. This dilemma involves two primary alternatives: either the government assumes direct responsibility for the project’s operation, encompassing all aspects from maintenance to revenue collection, or it delegates operational management to a private enterprise via a contractual agreement, with the enterprise overseeing the project for a defined term in return for a share of revenues or other stipulated compensation.

To thoroughly investigate the government’s strategic decision regarding the delegation of operations to a private entity, we delineate two archetypal scenarios. Scenario $S$ represents direct government self-operation of the project, while Scenario $D$ depicts the delegation of the project to a private enterprise. For clarity and convenience, the associated notations and definitions are comprehensively summarized in

Table 1. Notations and definitions.

Notations	Definitions
$Q$	Market demand
$e$	Service level of logistics infrastructure
$P(Q,e)$	Inverse function of demand (i.e., service price)
$a$	Base market potential
$b$	Demand sensitivity to price
$\gamma$	Service level sensitivity of price
$C(e,k)$	The project’s maintenance cost
$k$	Cost coefficient of service level
${\pi }_G$	Profit of the government
${\pi }_E$	Profit of the enterprise
$CS$	Consumer surplus
$SW$	Social welfare
$\lambda$	The proportion of revenue sharing obtained by the enterprise in delegated operation
$F$	Fixed fee charged by the government to the enterprise in delegated operation
$k_i$	The types of enterprise service level cost coefficients ($i\in \{L,H\}$)
$p_i$	The prior probability that the enterprise is of type $k_i$ $(i\in \{L,H\}$)
$U_0$	The retained utility of an enterprise (the revenue when not involved)

. Subscripts $G$ and $E$ refer to equilibrium solutions specifically for the government and the enterprise, respectively.

The inverse demand function for logistics infrastructure services within a specified period is formulated as

$$P\left(Q,e\right)=a-bQ+\gamma e.$$

Here, $a (>0)$ signifies the base market potential, $b (>0)$ represents the demand sensitivity to price, $e (>0)$ denotes the service level of logistics infrastructure, and $\gamma (>0)$ indicates the service level sensitivity of price. This implies that an increase in service level ($e$) can either enhance consumers’ willingness to pay for the service (leading to a higher price) or augment the demand quantity at a given price. This type of demand function is widely used in the previous literature (e.g., [38,39,40]). The input variables for our demand function should be interpreted as aggregate market-level observations relevant to the entire logistics infrastructure system under consideration. A detailed clarification is provided in Appendix A.

The project’s maintenance cost function is defined as

$$C\left(e,k\right)={\displaystyle \frac{1}{2}}k{e}^2.$$

Here, the quadratic term ${\displaystyle \frac{1}{2}}k{e}^2$ captures the non-linear increase in maintenance costs as the service level ($e$) rises, with $k>0$ denoting the service level’s cost coefficient [41,42]. This functional form implies that higher service levels incur disproportionately greater maintenance expenses. Generally, the economics literature defines consumer surplus as the area under the demand curve above the given price. Consequently, the consumer surplus can be expressed as

$$CS\left(Q,e\right)={\int }_0^Q\left(P\left(x,e\right)-P\left(Q,e\right)\right)dx ={\displaystyle \frac{1}{2}}b{Q}^2.$$

It is imperative to note that the calculation of consumer surplus, given a specific service level ($e$), is solely dependent on the demand quantity ($Q$) and the demand sensitivity to price ($b$). Consequently, social welfare, being the sum of government profit, enterprise profit and consumer surplus, can be expressed as

$$SW={\pi }_G+{\pi }_E+CS.$$

Notably, when the government self-operates the project, the enterprise’s profit (${\pi }_E$) is zero.

3.1. Scenario $S$: Government Self-Operation

In this foundational model, the government directly operates the logistics infrastructure project. The government’s objective is to maximize social welfare by strategically choosing the optimal service level and market demand quantity/price. The government’s profit function is thus specified as

$${\pi }_G=P\left(Q,e\right)Q-C\left(e,k_G\right)=\left(a-bQ+\gamma e\right)Q-{\displaystyle \frac{1}{2}}{k}_G{e}^2.$$

where $k_G$ represents the service level cost coefficient when the government self-operates the project. Consequently, social welfare, defined as the sum of government profit and consumer surplus, can be expressed as

$$SW={\pi }_G+CS=aQ-{\displaystyle \frac{1}{2}}b{Q}^2+\gamma eQ-{\displaystyle \frac{1}{2}}{k}_G{e}^2.$$

The equilibrium solution for this scenario is derived through backward induction and detailed in Appendix B. We use the superscript $S$ to represent the equilibrium outcome in Scenario $S$. Next, we examine how the government’s service level cost coefficient ($k_G$) and the service level sensitivity of price ($\gamma$) influence the equilibrium outcomes. The analytical results are summarized in Proposition 1.

Proposition 1.

In Scenario $S$, the sensitivity analysis of equilibrium concerning $k_G$ and $\gamma$ yields the following:

(a) 

A higher government’s service level cost coefficient ($k_G$) leads to a lower optimal service level ($e_G^S$) and reduced market demand ($Q_G^S$), consequently resulting in a decrease in social welfare;

(b) 

An increased service level sensitivity of price ($\gamma$) results in a higher optimal service level ($e_G^S$), increased market demand ($Q_G^S$), and enhanced social welfare.

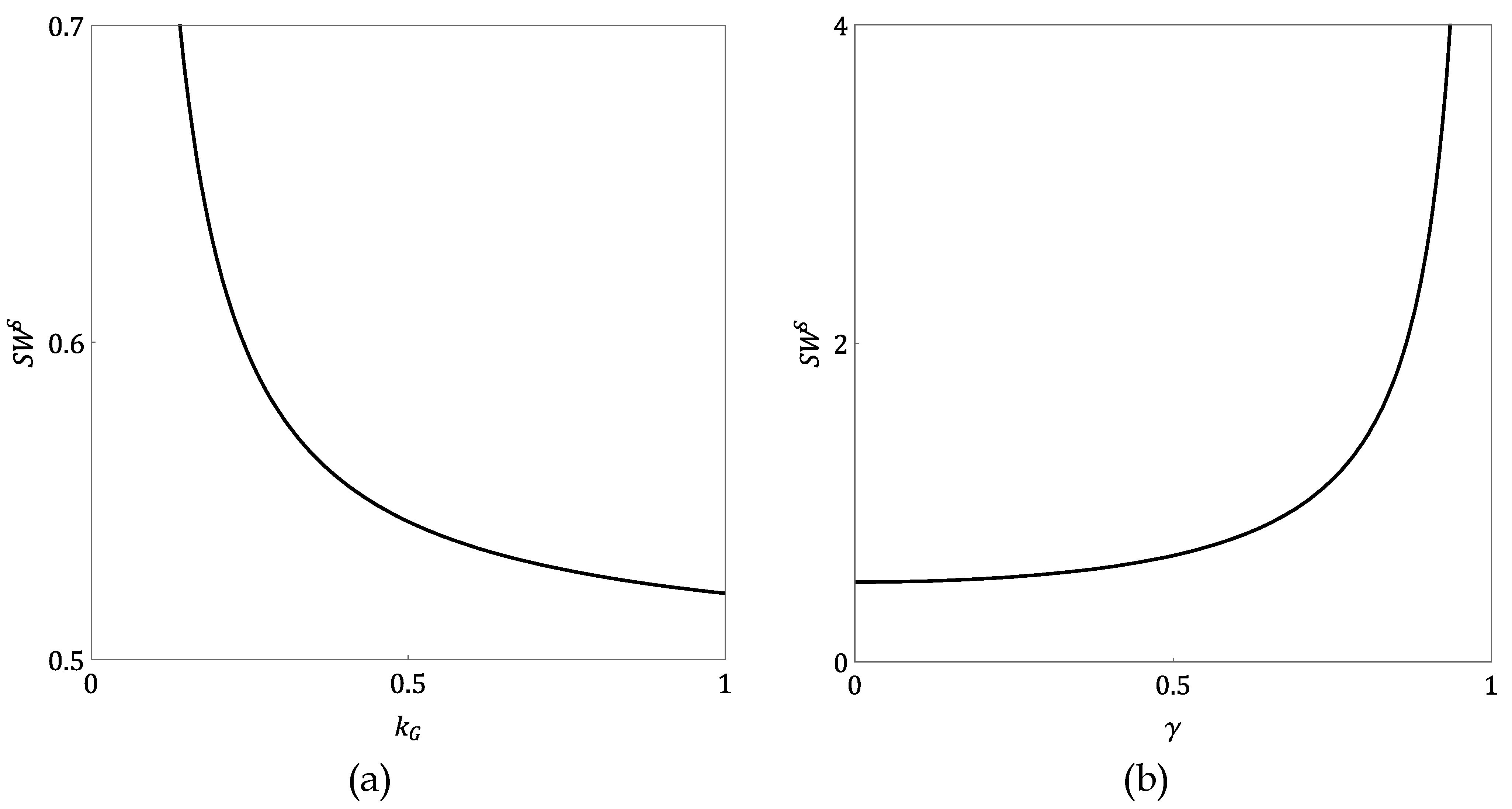
The core reason for $k_G$’s negative impact on social welfare (see Figure 1a) lies in the trade-off between service quality costs and benefits. As the government’s service level cost coefficient ($k_G$) increases, the marginal cost of providing service quality rises. To maximize overall social welfare, the government must rationally reduce the optimal service level ($e_G^S$) to align with these higher costs. This reduction in service quality, in turn, directly leads to a decrease in consumer willingness to pay and thus a reduction in market demand ($Q_G^S$) for the logistics infrastructure service. The combined effect of lower service levels and reduced market size ultimately translates into a decrease in total social welfare, as both market demand and service level are positive contributors to social welfare. This highlights a crucial insight: for public service provision, internal cost efficiency ($k_G$) is fundamental. If the government cannot control its own costs effectively, even direct operation will result in suboptimal outcomes, emphasizing that simply providing a service does not guarantee social benefit; it must be done efficiently.

Conversely, an increase in the service level sensitivity of price ($\gamma$) enhances social welfare (see Figure 1b) by making investments in service quality more valuable. A higher $\gamma$ signifies that consumers are more responsive to improvements in service quality, translating a small increase in service level ($e$) into a larger increase in the price consumers are willing to pay and thus higher total revenue. Recognizing this magnified benefit, the government, as a social welfare maximizer, will rationally opt to increase the optimal service level ($e_G^S$). This higher service level, perceived by consumers as greater value, drives a subsequent increase in market demand ($Q_G^S$). The synergistic rise in both service level and market demand directly contributes to a higher overall social welfare. This reveals a critical principle: investing in higher service quality is economically justifiable and socially beneficial when the public highly values quality and is willing to pay for it. It underscores the importance of value-driven service provision in areas where quality significantly enhances public utility.

3.2. Scenario $D$: Government-Delegated Operation

In Scenario $D$, the government, acting as a principal, delegates the operation of logistics infrastructure services to a private enterprise, which serves as the agent. This delegation structure is commonly observed in PPP logistics infrastructure projects, driven by the government’s motivation to leverage the private sector’s presumed superior efficiency and innovation. To achieve its objective of maximizing social welfare, the government designs a comprehensive contract mechanism. This contract aims to align the enterprise’s inherent profit-seeking behavior with the broader public objectives. It typically comprises two core elements: a revenue sharing ratio ($\lambda$) and a fixed fee ($F$). The revenue sharing ratio $\lambda$ dictates the proportion of total operating revenue the enterprise retains, with the government keeping ($1 - \lambda$), and $\lambda$ ranges from 0 to 1. The fixed fee $F$ is a lump-sum payment that can be either charged by the government to the enterprise or paid to the enterprise. This fee acts as a crucial transfer payment mechanism, allowing the government to adjust the enterprise’s profit and, critically, ensure its willingness to participate in the delegation.

Within this framework, the interaction unfolds as a Stackelberg game. The government, as the leader, first determines the optimal $\lambda$ and $F$. This initial decision is paramount, as it establishes the precise incentives for the enterprise. The government must carefully balance encouraging the enterprise to perform optimally with securing its own revenue from the project. The enterprise, acting as the follower, then maximizes its own profit by choosing the optimal market demand ($Q$) and service level ($e$) based on the government’s set $\lambda$ and $F$.

The enterprise’s profit function (${\pi }_E$) represents the net revenue it obtains from operations after accounting for costs and the fixed fee. It is specifically expressed as

$${\pi }_E=\lambda \left(a-bQ+\gamma e\right)Q-{\displaystyle \frac{1}{2}}{k}_E{e}^2-F$$

Here, $k_E$ is the enterprise’s service level cost coefficient, reflecting its operational efficiency in providing service quality. The government’s profit can be expressed as

$${\pi }_G=(1-\lambda )(a-bQ+\gamma e)Q+F$$

The social welfare function (SW) remains the overarching objective for the government, representing the aggregate societal benefit derived from the project. It is defined as

$$SW={\pi }_G+{\pi }_E+CS=aQ-{\displaystyle \frac{1}{2}}b{Q}^2+\gamma eQ-{\displaystyle \frac{1}{2}}{k}_E{e}^2.$$

Crucially, the fixed fee $F$, being an internal transfer payment between the principal and the agent, does not affect the total social welfare. Thus, the structure of the social welfare function mirrors that of the government self-operation model. However, in this delegated context, the specific values of $Q$ and $e$ that determine social welfare are the outcomes of the enterprise’s profit-maximizing decisions, which are, in turn, driven by the contractual incentives designed by the government. A key risk in this setup is that if the government’s incentives are insufficient or misaligned, the enterprise might strategically reduce service levels or volumes to cut its own costs, thereby compromising overall social welfare. The equilibrium solution for Scenario $D$ is derived through backward induction and detailed in Appendix C. We use the superscript $D$ to represent the equilibrium outcome in Scenario $D$.

4. Analysis

Next, we focus on assessing the comparative advantages between government self-operation and delegated operation by examining their respective equilibrium outcomes, particularly regarding social welfare. The comparative analysis results are presented in Proposition 2.

Proposition 2.

Under symmetric information, the comparison of social welfare between government self-operation ($S{W}^S$) and delegated operation ($S{W}^D$) is as follows:

(a) 

If the government’s service level cost coefficient ($k_G$) is sufficiently low, specifically when $k_G\le {\displaystyle \frac{2{\gamma }^2}{b}}$, then government self-operation always yields higher social welfare than delegated operation, i.e., $S{W}^S>S{W}^D$for all valid $k_E$;

(b) 

If the government’s service level cost coefficient ($k_G$) is relatively high, specifically when  $k_G>{\displaystyle \frac{2{\gamma }^2}{b}}$, there exists a unique threshold  $k_0$ for the enterprise’s service level cost coefficient ($k_E$) such that

(i) 

If $k_E\le k_0$, then $S{W}^S\le S{W}^D$.

(ii) 

If $k_E>k_0$, then $S{W}^S>S{W}^D$.

Proposition 2 offers crucial insights into the optimal choice between government self-operation and delegating public service delivery to a private enterprise under symmetric information. It systematically delineates the conditions under which each operational model yields higher social welfare, emphasizing the pivotal role of their respective service level cost coefficients: $k_G$ for the government and $k_E$ for the enterprise.

Proposition 2(a) establishes that when the government’s own service level cost coefficient ($k_G$) is sufficiently low (specifically $k_G\le {\displaystyle \frac{2{\gamma }^2}{b}}$, as shown in Figure 2a), government self-operation consistently outperforms delegated operation in terms of social welfare irrespective of the private enterprise’s efficiency ($k_E$). This condition signifies an exceptionally efficient public sector. In such scenarios, the government’s ability to provide service at a very low cost means that the inherent complexities and potential for residual inefficiencies in a delegated contract—even one designed for optimal social welfare (as discussed in Proposition 4)—outweigh any potential gains from involving the private sector. The transaction costs, design complexities, and potential for uncaptured value in delegation render it suboptimal when the government is already highly efficient. This may help explain why some logistics infrastructure projects built under BOT schemes, such as the Guangfo Expressway in China, have been transferred to the Chinese government after their concession periods expired and are now operated by a professional, large, state-owned enterprise, effectively acting as an arm of the Chinese government.

Conversely, Proposition 2(b) explores scenarios where the government’s service level cost coefficient ($k_G$) is relatively high (i.e., $k_G>{\displaystyle \frac{2{\gamma }^2}{b}}$, as shown in Figure 2b), indicating a less efficient public sector. In these situations, the door opens for delegated operation to potentially deliver superior social welfare. The proposition identifies a unique threshold, $k_0$, for the enterprise’s cost coefficient ($k_E$). If the private enterprise is sufficiently efficient, meaning its $k_E$ is at or below this threshold ($k_E\le k_0$), then delegating the operation leads to equal or higher social welfare. This represents the optimal scenario for outsourcing, where the private sector’s efficiency advantages are significant enough to offset the challenges of delegation. However, if the enterprise’s cost coefficient exceeds this threshold ($k_E>k_0$), even if it is a private entity, it is not efficient enough to compensate for the complexities of delegation, making government self-operation the superior choice. This may help explain why some logistics infrastructure projects built under BOT schemes continue to be operated by private companies after their concession periods expire. For instance, Hong Kong’s Cross-Harbour Tunnel was operated by The Cross-Harbour (Holdings) Limited and subsequently by Serco Group after its concession period expired in 1999. Both of these companies specialize in transportation management.

While Proposition 2 provides a comprehensive framework for deciding between government self-operation and delegation based on relative efficiencies, it is essential to understand the inherent performance characteristics of the delegated operation model itself when the enterprise retains autonomy over its decisions. Our subsequent analysis, therefore, specifically contrasts the equilibrium outcomes arising from the enterprise’s autonomous decision making within the government-delegated operation framework with the socially optimal outcomes, where a benevolent social planner directly determines market demand ($Q$) and service level ($e$) and maximizes overall social welfare ($SW$). This comparative analysis culminates in Proposition 3.

Proposition 3.

Under symmetric information, if the government delegates the project’s operation to an enterprise using a revenue-sharing ratio ($\lambda$) and a fixed fee ($F$), and the enterprise autonomously determines the market demand and service level, then both the market demand and the service level provided by the enterprise will typically be lower than their respective socially optimal levels that maximize social welfare. Consequently, the total social welfare achieved by such a delegated operation model will also be lower than the maximum possible social welfare, implying it cannot fully achieve social optimality.

Proposition 3 reveals that, within the government-delegated operation model, the equilibrium levels of market demand and service level, autonomously determined by the enterprise, consistently fall short of their respective socially optimal levels, thereby hindering the attainment of full social optimality. (A numerical tabular comparison is provided in

Table A2. Equilibrium social welfare across various scenarios.

No.	${\mathit{k}}_{\mathit{G}}$	${\mathit{k}}_{\mathit{E}}$	$\mathit{S}{\mathit{W}}^{\mathit{S}}$	$\mathit{S}{\mathit{W}}^{\mathit{D}}$	$\mathit{S}{\mathit{W}}^{\mathit{S}\mathit{O}}$
(1)	1.5	1.2	1.500	0.796	3.000
(2)	1.5	1.5	1.500	0.656	1.500
(3)	1.5	1.8	1.500	0.586	1.125
(4)	3	1.2	0.750	0.796	3.000
(5)	3	1.5	0.750	0.656	1.500
(6)	3	1.8	0.750	0.586	1.125

in Appendix F to facilitate intuitive comprehension.) This inherent suboptimality stems from the fundamental divergence in objectives: While the government aims to maximize total social surplus, the enterprise, in its profit maximization, does not internalize the marginal benefits accruing to consumers. Consequently, a contract mechanism relying solely on revenue sharing and fixed fees, which grants the enterprise autonomous operational decisions, is insufficient to achieve full social welfare maximization, consistently yielding inefficiently low outputs. To attain social optimality, the government would therefore need to implement more direct intervention, such as mandating specific demand volumes and service levels.

Building upon the analysis of efficiency losses stemming from the enterprise’s autonomous decisions regarding market demand and service level, we now investigate how external factors can influence the magnitude of this social welfare gap. This analysis leads to the following proposition.

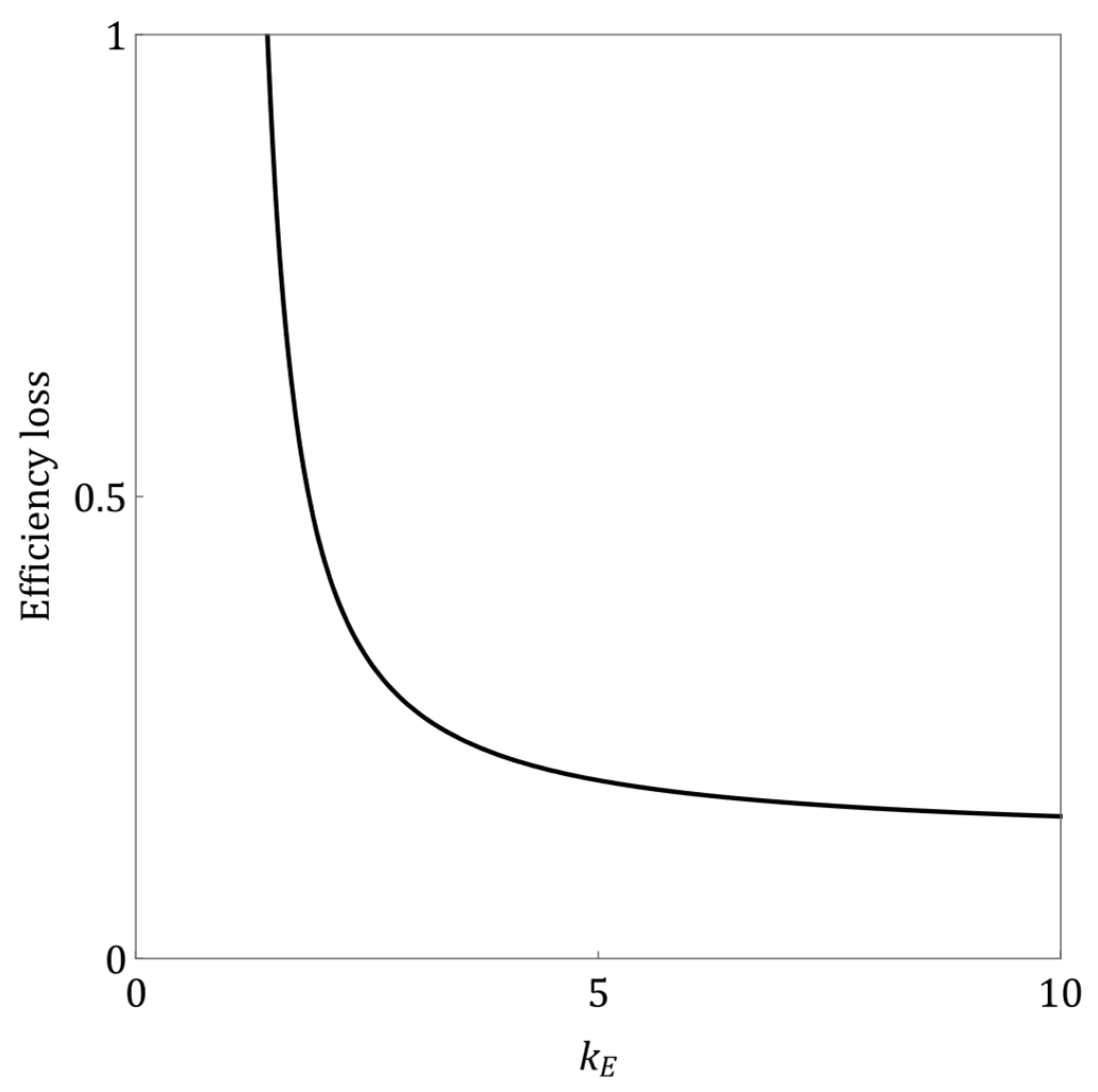
Proposition 4.

In the government-delegated operation model, the efficiency loss (defined as the difference between the socially optimal welfare and the welfare achieved under the enterprise’s autonomous decision making) decreases as the enterprise’s service level cost coefficient ($k_E$) increases.

Proposition 4 reveals a counter-intuitive but significant insight: higher costs associated with service levels can actually reduce the inefficiency inherent in the delegated operation model (see Figure 3 and the numerical analysis in Appendix F for visual representation). The welfare gap primarily stems from the enterprise’s under-provision of demand and service level relative to the socially optimal outcome, driven by its inability to fully internalize consumer surplus. However, as the service level cost coefficient ($k_E$) increases, providing high service levels becomes progressively more expensive for both society and the enterprise. Consequently, the maximum achievable social welfare (the first-best benchmark) significantly declines as higher service levels become economically prohibitive. When this optimal social welfare benchmark itself shrinks due to escalating costs, the absolute magnitude of the under-provision and, by extension, the resulting social welfare gap between the ideal and actual outcomes diminishes. In essence, the rising cost of service limits the overall “ambition” for service levels, thereby narrowing the absolute difference between what is theoretically possible and what is achieved under delegation.

While Proposition 3 and our subsequent analysis highlight the inherent limitations of indirect incentive mechanisms, where the enterprise’s autonomous decisions lead to suboptimal social welfare, a crucial question remains: can full social optimality be achieved under a different delegation framework? To address this, Proposition 5 explores an alternative scenario where the government exerts more direct control. Specifically, it examines a model where the government explicitly specifies the market demand quantity and service level, delegating project operation to the enterprise solely through a fixed fee ($F$).

Proposition 5.

Under symmetric information, if the government can directly specify the demand quantity and service level and delegates operation to an enterprise through a fixed fee ($F$), then the enterprise can be incentivized to provide a market demand quantity and service level aligned with the social optimum, thereby maximizing social welfare. In this scenario, the enterprise will earn its reservation utility.

Proposition 5 elucidates how delegated operation can achieve full social optimality under ideal conditions of complete information and robust governmental intervention capabilities. The core mechanism involves the government, as the principal, leveraging its complete insight into the enterprise’s (agent’s) operating costs and capabilities. This allows the government to precisely calculate and directly mandate the optimal market demand and service level that maximize social welfare. Simultaneously, to ensure the enterprise’s voluntary participation and prevent rent extraction, the government strategically sets a fixed fee such that the enterprise’s profit precisely equals its reservation utility. This contractual design ensures that all value generated by the enterprise’s efficient operation is fully captured as social welfare, thereby achieving the same efficiency level as direct provision by a benevolent social planner.

Proposition 5’s significance is that it provides a critical theoretical benchmark. It demonstrates how, in the absence of informational barriers, the government can fully leverage the private sector’s efficiency advantages to maximize public good. This is crucial for understanding ideal public service delegation models and underscores the central role of information transparency and precise regulation in contract design. In practice, Proposition 5 is more commonly used as a reference point against which to measure the effectiveness of complex, real-world delegation contracts. By comparing it to actual scenarios (which typically involve asymmetric information), we can quantify and identify efficiency losses arising from information imperfections, thereby guiding policymakers in balancing efficiency with informational challenges in public service outsourcing.

Proposition 5 provides a theoretical benchmark for achieving social optimality under ideal conditions, where the government directly mandates output. However, a critical question in operations management and public service delegation is whether delegating to the private sector can truly lead to superior outcomes when enterprises possess inherent efficiencies not available to the government. This brings us to Proposition 6, which directly addresses this efficiency advantage.

Proposition 6.

Under symmetric information, if the service level cost coefficient of the delegated enterprise ($k_E$) is lower than that of government self-operation ($k_G$) (i.e., the enterprise is more efficient), then the delegated operation where the government directly specifies market demand and service level yields higher social welfare. Conversely, if $k_E\ge k_G$, government self-operation yields higher social welfare.

Proposition 6 fundamentally emphasizes the decisive role of cost efficiency in a government’s decision to delegate operations. It states that, under ideal conditions of information transparency, the choice between government self-operation and delegated enterprise operation hinges entirely on which party can provide services at a lower cost. If a private enterprise possesses higher efficiency in delivering logistics infrastructure services (i.e., a lower cost coefficient $k_E$), then outsourcing the operation to that enterprise will lead to greater social welfare. Conversely, if the government itself holds a cost advantage, then self-operation is the superior choice.

This provides a clear guiding principle for public service outsourcing: the fundamental advantage of delegation is not merely the formal act of privatization but also its genuine capacity to deliver higher operational efficiency and lower costs. If an enterprise does not possess such an efficiency advantage, delegation will not only fail to increase social welfare but also may lead to a suboptimal allocation of resources. Therefore, when considering public service outsourcing, the key is to conduct a rigorous cost–benefit analysis and capability assessment rather than basing decisions solely on ideology or conventional wisdom.

5. Extended Model with Asymmetric Information

Our preceding analysis assumed symmetric information, where both the government and the enterprise had complete knowledge of the enterprise’s service level cost coefficient ($k_E$). However, this is often unrealistic in real-world public service delegation. Typically, the enterprise holds private information about its true operational efficiency that the government cannot fully observe. This introduces information asymmetry, a fundamental challenge in contract theory that profoundly alters optimal delegation contract design.

In this extended model, the enterprise’s service level cost coefficient ($k_E$) is precisely this private information. The government (principal) does not know the enterprise’s true efficiency type, while the enterprise (agent) does. We assume $k_E$ can take one of two types: a low-cost type ($k_L$) or a high-cost type ($k_H$), where $k_L<k_H$. The government knows the probability of the high-cost type is $p_H$, and thus, the probability of the low-cost type is

$$p_L=1-p_H.$$

This assumption of two discrete cost types (low and high) for private enterprises is a standard and widely accepted practice in the principal–agent literature, particularly in models dealing with information asymmetry. It is crucial for maintaining analytical tractability and enabling the derivation of closed-form solutions that provide clear, interpretable economic insights. While real-world operating costs may exhibit continuous characteristics, a two-type setting is sufficient to capture the fundamental challenge of distinguishing between different efficiency levels and the resulting phenomena of informational rent and output distortion. This approach provides robust qualitative insights into optimal governance choices and their impact on social welfare, which would be obscured by the analytical complexity of a continuous distribution.

5.1. Decision Variables and Sequence

The government, acting as the principal, designs a menu of contracts $\left\{\left(Q_i,e_i,F_i\right)\right\}$, where $i\in \left\{L,H\right\}$. The government’s objective is to maximize expected social welfare by strategically designing this menu to induce enterprises to reveal their true cost type. As demonstrated in Appendix C, the government optimally selects the largest feasible $\lambda$ to incentivize the enterprise. Consequently, in this context, we set $\lambda = 1$. The enterprise, acting as the agent, observes this contract menu. Based on its private information—its true maintenance cost coefficient (type, $k_i$)—it then chooses the contract from the menu that maximizes its own profit. The sequence of decisions is as follows:

(1)

Government announces a contract menu $\left\{\right(Q_L,e_L,F_L),(Q_H,e_H,F_H\left)\right\}$;

(2)

Enterprise chooses a contract: Based on its true type ($k_i$), the enterprise selects the contract from the announced menu that maximizes its expected profit;

(3)

Enterprise determines actual output: Under the chosen contract, the enterprise determines its actual market demand and service level to maximize its profit. As Proposition 5 states, under conditions of complete information, the government can achieve social optimality by directly specifying market demand, service levels, and the fixed fee. Then, we assume that the government specifies $Q_i$ and $e_i$, and the enterprise provides these outputs if it accepts the contract;

(4)

Revenues are realized.

For an enterprise of type $k_i$, its profit function is

$${\pi }_{E_i}(Q,e,F_j)=P(Q,e)Q-{\displaystyle \frac{1}{2}}{k}_i{e}^2-F_j.$$

Here, $j$ refers the type of contract chosen by the enterprise, which can be $L$ or $H$.

The government aims to maximize the expected social welfare, which can be expressed as

$$E\left[SW\right]=p_L·SW(Q_L,e_L,F_L)+p_H·SW(Q_H,e_H,F_H).$$

Note that $Q_L$, $e_L$, $Q_H$, and $e_H$ here represent the outputs induced by the government’s chosen contract. The equilibrium solution for the extended model with asymmetric information is derived and detailed in Appendix D.

5.2. Analysis with Asymmetric Information

Next, we analyze the efficiency distortions and information rent under asymmetric information, as demonstrated by Proposition 7.

Proposition 7.

When the enterprise’s service level cost coefficient is private information, the government cannot achieve full social welfare maximization, as it must incentivize enterprises to truthfully reveal their types. The market demand and service level provided by the low-cost enterprise reach the socially optimal level, but those provided by the high-cost enterprise are distorted downwards (below their socially optimal level).

Under asymmetric information, the equilibrium outcome represents a delicate balance between efficiency and incentive compatibility. The low-cost enterprise (L-type) will produce at socially optimal (first-best) levels ($Q_L = Q^{FB} \left(k_L\right)$ and $e_L = e^{FB} \left(k_L\right)$), but it will earn positive information rent, which is profit exceeding its reservation utility ($U_0$). This rent serves as the essential price the government pays to incentivize the efficient type to truthfully reveal its private information. In contrast, the high-cost enterprise (H-type) will earn exactly its reservation utility ($U_0$), meaning it receives no information rent. However, its production will be distorted downwards ($Q_H$ and $e_H$ will be below their socially optimal, first-best levels), leading to an inefficiency. This distortion is a deliberate choice by the government to limit the information rent captured by the low-cost type. Consequently, the overall expected social welfare will be suboptimal, falling below the level achievable under symmetric information. This shortfall directly represents the inherent cost of asymmetric information, reflecting the necessary trade-off between maximizing social welfare and ensuring truthful revelation.

Proposition 8.

Analysis of the impact of key parameters on delegation decisions under information asymmetry reveals the following:

(a) 

The higher the sensitivity of market demand to service level $\gamma$, the greater the total social welfare loss caused by information asymmetry;

(b) 

The greater the service level cost difference between the two enterprise types ($k_H-k_L$), the greater the total social welfare loss caused by information asymmetry.

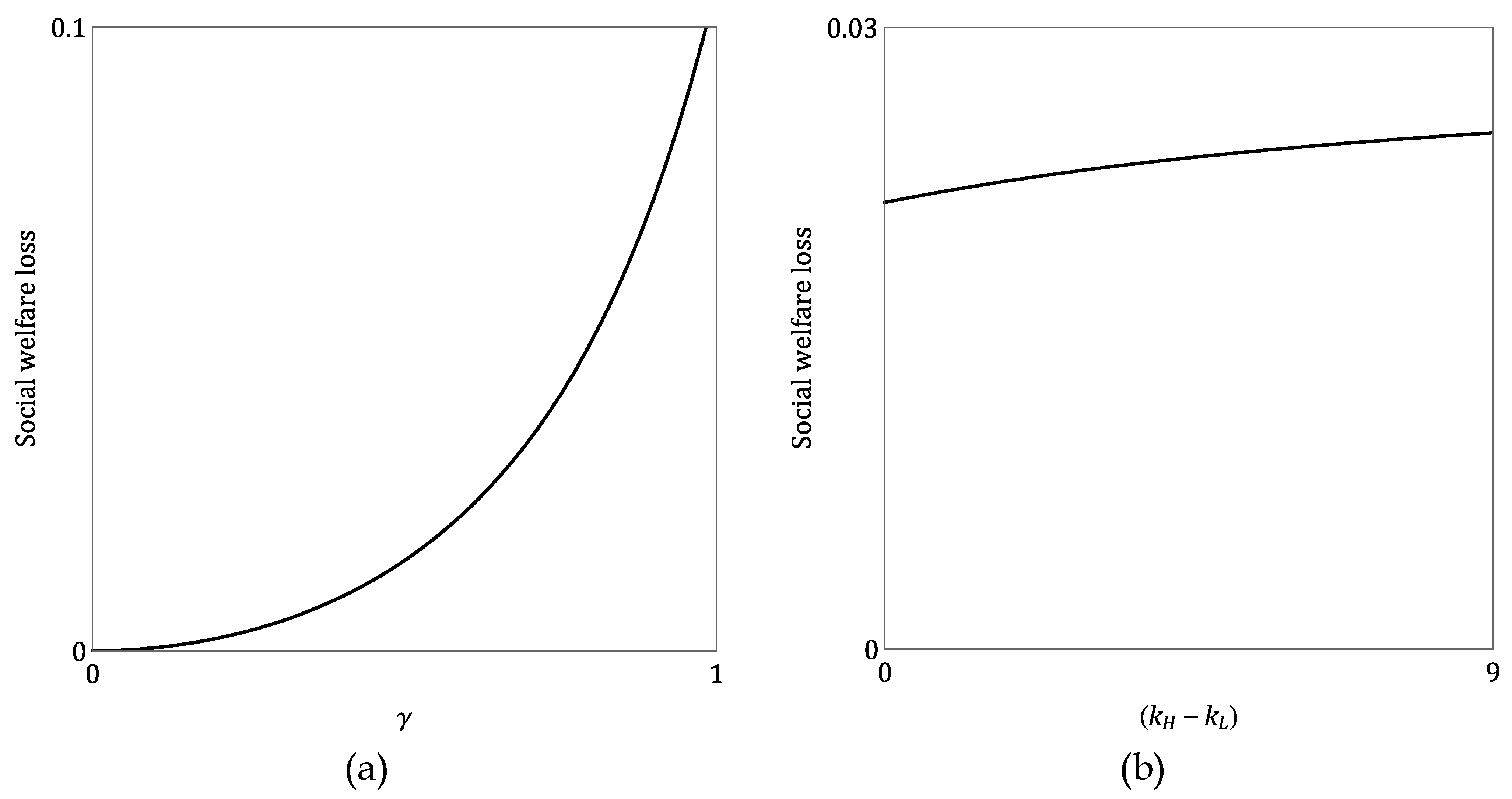
Proposition 8(a) indicates that a higher sensitivity of market demand to service level ($\gamma$) leads to a greater social welfare loss caused by information asymmetry (see Figure 4a). This outcome arises because the government, in its attempt to curb informational rents to the low-cost enterprise, is compelled to distort the service level offered to the high-cost enterprise. In scenarios where $\gamma$ is high, the social value derived from achieving optimal service levels is greatly amplified. Consequently, even a marginal reduction in the high-cost type’s service level results in a disproportionately substantial social welfare loss, as the cost of not being able to perfectly realize the socially optimal service level is significantly magnified. This underscores the need for exceptional caution when considering delegation for public services where quality is paramount and directly drives public benefit, such as in specialized healthcare or critical infrastructure. If significant information asymmetry persists in such critical areas, the implementation of robust monitoring mechanisms for service quality, along with accurate measurement of demand sensitivity ($\gamma$), becomes essential, or the exploration of alternative provision models may be warranted.

Proposition 8(b) states that an increasing service level cost difference between enterprise types consistently escalates the total social welfare loss caused by information asymmetry (see Figure 4b), primarily due to the heightened distortion of the high-cost enterprise’s contract. This proposition’s logic hinges on how an expanding cost difference impacts the two primary components of total social welfare loss under asymmetric information: as the cost difference ($k_H - k_L$) grows, the low-cost enterprise’s efficiency advantage becomes more pronounced, compelling the government to significantly distort the high-cost enterprise’s optimal service level downward to prevent mimicking. This increased distortion directly leads to a greater efficiency loss ($D_H$) for the high-cost segment, which, despite the complex and potentially non-monotonic behavior of informational rent, ultimately dominates the overall efficiency cost of achieving incentive compatibility. Consequently, to effectively manage delegated operations, policymakers must recognize that greater inherent efficiency differences between potential service providers inherently lead to higher overall social welfare losses. Governments should therefore prioritize policies that reduce significant cost disparities among potential contractors, either by fostering competition that encourages efficiency improvements across all types or by targeting delegation to markets with more homogenous provider capabilities, thereby mitigating the overall efficiency cost of asymmetric information.

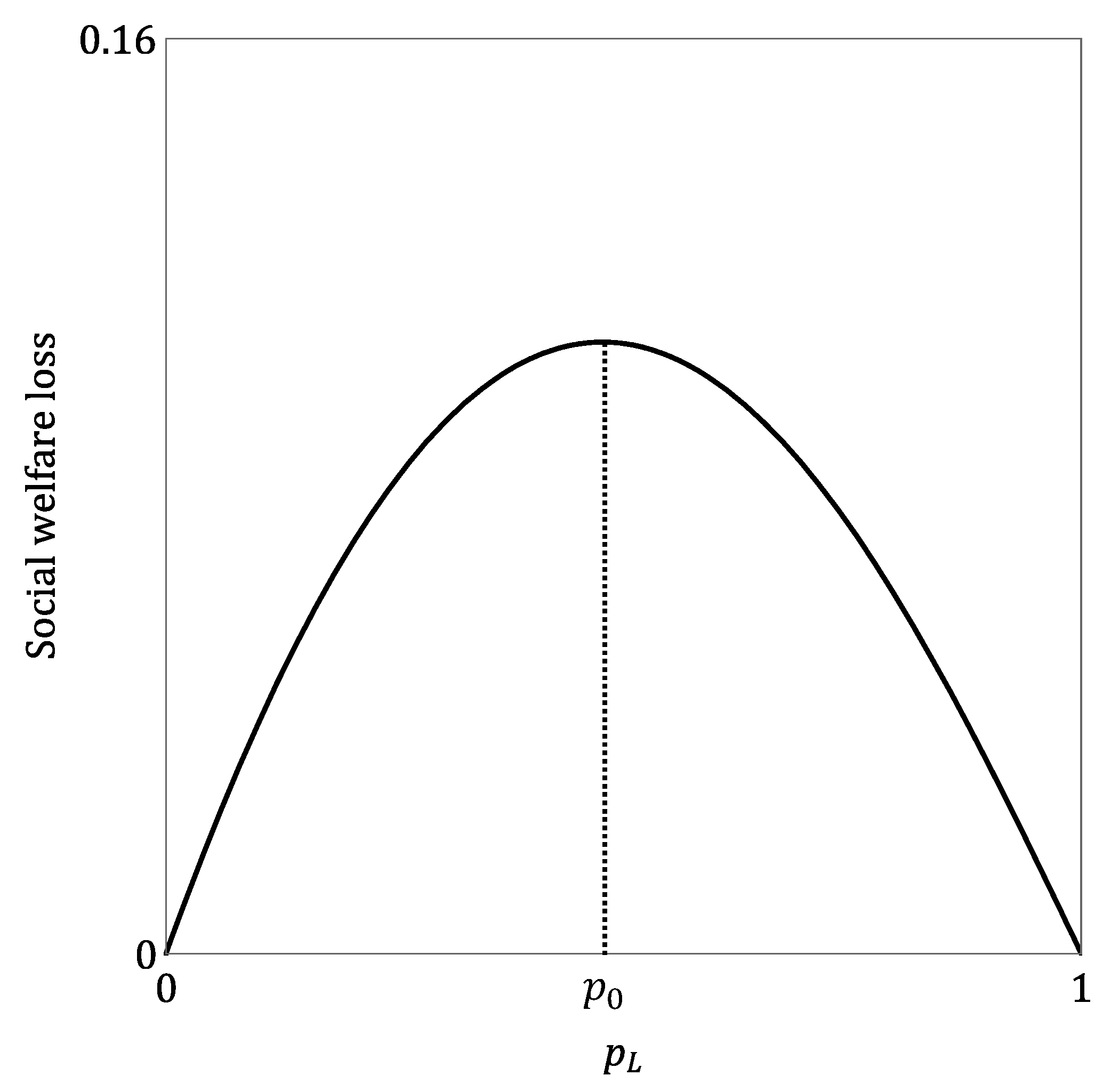
Proposition 9.

The proportion of low-cost enterprises ($p_L$) in the market has a non-monotonic impact on the average social welfare loss caused by information asymmetry: there exists a threshold $p_0\in \left(\mathrm{0,1}\right)$ such that the loss increases with $p_L$ when $p_L<p_0$, and it decreases with $p_L$ when $p_L>p_0$.

Proposition 9 indicates that the proportion of low-cost enterprises ($p_L$) in the market has a non-monotonic impact on the average social welfare loss caused by information asymmetry (see Figure 5). There exists a threshold $p_0\in \left(\mathrm{0,1}\right)$ such that when the proportion of low-cost enterprises is low ($p_L<p_0$), the average social welfare loss increases with $p_L$; conversely, when the proportion of low-cost enterprises is high ($p_L>p_0$), the average social welfare loss decreases with $p_L$. This implies that the attractiveness of delegated operation does not follow a simple pattern, and its optimal applicability may lie within specific ranges of $p_L$. This non-monotonic relationship stems from the shifting dominance of informational rent costs and efficiency distortion losses across different ranges of $p_L$.

When $p_L<p_0$ (low-cost enterprises are rare), in this range, the government’s cost of achieving incentive compatibility primarily involves two aspects: first, paying informational rents to the relatively rare low-cost enterprises; second, the distortion imposed on high-cost enterprises to differentiate the types. As $p_L$ increases, although low-cost enterprises remain relatively scarce, the expected informational rent paid by the government to ensure their truthful revelation begins to increase significantly. Concurrently, to maintain incentive compatibility, the degree of distortion in the high-cost contract also intensifies with increasing $p_L$. The combined effect of these factors leads to an initial increase in the total welfare loss due to information asymmetry as $p_L$ rises.

When $p_L>p_0$ (low-cost enterprises are prevalent), in this range, low-cost enterprises become much more common. While this means informational rents must be paid to a larger number of low-cost firms, as $p_L$ further increases (and thus $p_H = 1 - p_L$ decreases), the proportion of high-cost enterprises in the market becomes very small. In such a scenario, the government might tend to reduce the distortion applied to high-cost enterprises, as the cost of managing rare types (whether through distortion or rent) decreases in its overall welfare proportion. Crucially, the sheer abundance of efficient enterprises leads to a higher potential ceiling for the overall social welfare level, and the marginal loss effect of paying informational rents, relative to total gains, may diminish. The system reaches a balancing point at p0, after which a further increase in $p_L$ can more effectively enhance net social welfare, thereby reducing the average loss caused by information asymmetry.

To effectively manage delegated operations under information asymmetry, governments must assess the distribution of provider cost types ($p_L$) in the market, as its impact on social welfare loss is non-monotonic. This requires dynamically adjusting delegation strategies based on where the market’s $p_L$ stands relative to a critical threshold ($p_0$). For instance, if $p_L$ is low ($p_L<p_0$), the focus should be on cost control and rent reduction. However, if $p_L$ is high ($p_L>p_0$), delegation’s advantages should be actively leveraged, as overall losses decrease. Such insights are crucial for optimizing supplier development and market competition policies and making informed trade-offs between information asymmetry losses and potential benefits across varying market conditions.

Proposition 10.

In asymmetric information scenarios, whether delegating public service operations enhances social welfare depends on whether the efficiency gains provided by the delegated enterprise can offset the inherent losses from information asymmetry (e.g., informational rent and output distortion).

Proposition 10 highlights the core trade-off in public service delegation decisions. Under ideal symmetric information, the government could simply choose the most efficient operator. However, when enterprises possess private information about their operating costs, the situation fundamentally changes. While private firms may offer higher operational efficiency due to specialization or flexible structures, this advantage comes with a cost. To incentivize enterprises (especially low-cost types) to truthfully reveal their information and provide services, the government must pay informational rent. Simultaneously, to limit this rent, the government often has to accept downward distortions in the output and service levels of high-cost enterprises. These factors collectively constitute a loss in social welfare. Therefore, the government’s decision hinges on a sophisticated cost–benefit analysis, calculating the net efficiency advantage of delegation. Delegation is only the superior choice if the enterprise’s potential efficiency gains fully compensate for the rent and distortion caused by information asymmetry.

When considering public service delegation, decision makers must move beyond simple cost comparisons and conduct in-depth information economics analysis. Governments should focus on assessing whether potential delegated enterprises can deliver significant operational cost reductions through their technology or management models. These gains must effectively compensate for the additional costs arising from information asymmetry. If the enterprise’s efficiency advantage is not substantial, or if the losses from information asymmetry (e.g., a high probability of high-cost types or a large cost difference) are too great, then government self-operation might achieve higher social welfare. This underscores the critical importance of understanding the nature of information asymmetry and its welfare implications in public service outsourcing decisions.

6. Conclusions

This study deeply investigates how governments can make optimal decisions regarding the operation of logistics infrastructure after the expiry of PPP concessions, specifically aiming to maximize social welfare and ensure the long-term resilience of these assets when confronting the challenges of information asymmetry arising from private firm information. We developed a tailored principal–agent theoretical model, first establishing an efficiency benchmark by comparatively analyzing social welfare under government self-operation (Scenario $S$) and delegated operation with symmetric information (Scenario $D$). Subsequently, we extended the model to incorporate information asymmetry, systematically analyzing optimal contract designs, social welfare levels, and their influencing factors in this more complex scenario. The core findings of this research revealed following significant insights:

First, our study found that, under symmetric information, when government operation is sufficiently efficient, government self-operation is better, regardless of the private enterprise’s operational efficiency. Only when government operational efficiency is low is delegating to an efficient private enterprise the superior choice. We also found that under symmetric information, if the government can directly specify the demand quantity and service level and delegates operation through a fixed fee, the enterprise can be incentivized to provide a market demand quantity and service level aligned with the social optimum.

Second, our study unequivocally shows that while delegating logistics infrastructure operations to specialized private firms holds significant efficiency potential, information asymmetry inherently leads to unavoidable social welfare losses. These losses manifest as informational rent captured by efficient firms (paid to incentivize truthful type revelation) and strategic output distortion applied to less efficient firms (to limit rent extraction). This means that in real-world scenarios, achieving the theoretically “first-best” social welfare is impossible, and governments must accept this inherent efficiency trade-off.

Third, we further elucidated the intricate effects of key parameters, such as market sensitivity and inter-firm cost differences, on these losses. Crucially, for the first time, this research revealed the non-monotonic impact of the proportion of low-cost firms on total social welfare loss: there exists a critical threshold where the loss increases with this proportion up to that point and then decreases thereafter. Furthermore, we emphasize that information asymmetry-induced output distortion not only impacts daily efficiency but can also indirectly compromise the inherent resilience of the infrastructure, making it more vulnerable to external shocks.

Finally, this study provides a clear and quantifiable decision criterion: the government’s delegation choice is optimal for maximizing social welfare only if the potential efficiency gains from delegation are sufficient to compensate for the inherent costs and losses stemming from information asymmetry. This criterion underscores the necessity of a comprehensive cost–benefit analysis when weighing the pros and cons of delegation and implicitly encourages decision makers to embed considerations for the long-term resilience of infrastructure within contract design.

The practical implications of this research are substantial. For the growing number of logistics infrastructure assets globally transitioning post PPP concession, this study offers governments a systematic decision-making framework. It alerts policymakers that while pursuing efficiency advantages from the private sector, they must fully quantify and manage potential welfare losses due to information asymmetry. Governments, when designing delegation contract terms, should more meticulously consider incentive mechanisms, balancing rent payments with the degree of output distortion, to ensure social welfare maximization and safeguard the long-term sustainable operation and resilience of critical infrastructure.

Despite its significant advancements, this study acknowledges certain limitations. For instance, the model assumes only two types of firms; future research could explore a continuous distribution of firm types. Additionally, introducing asymmetric information from the government’s side or considering multi-level agency relationships (e.g., government–private firm–subcontractor) to analyze information problems also represents promising avenues for future research.