Multicriterial Heuristic Optimization of Cogeneration Supercritical Steam Cycles
Abstract
1. Introduction
2. Materials and Methods
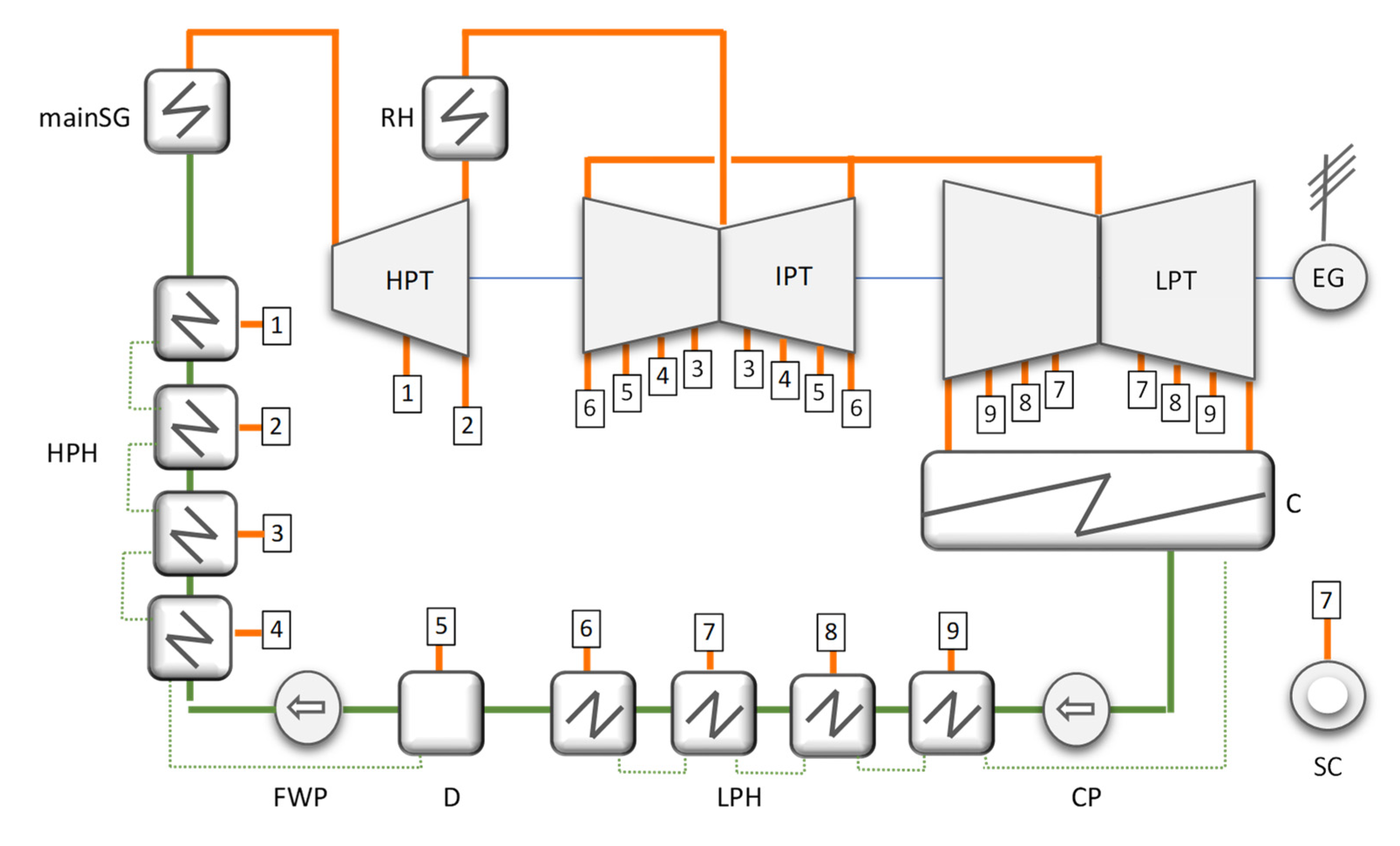
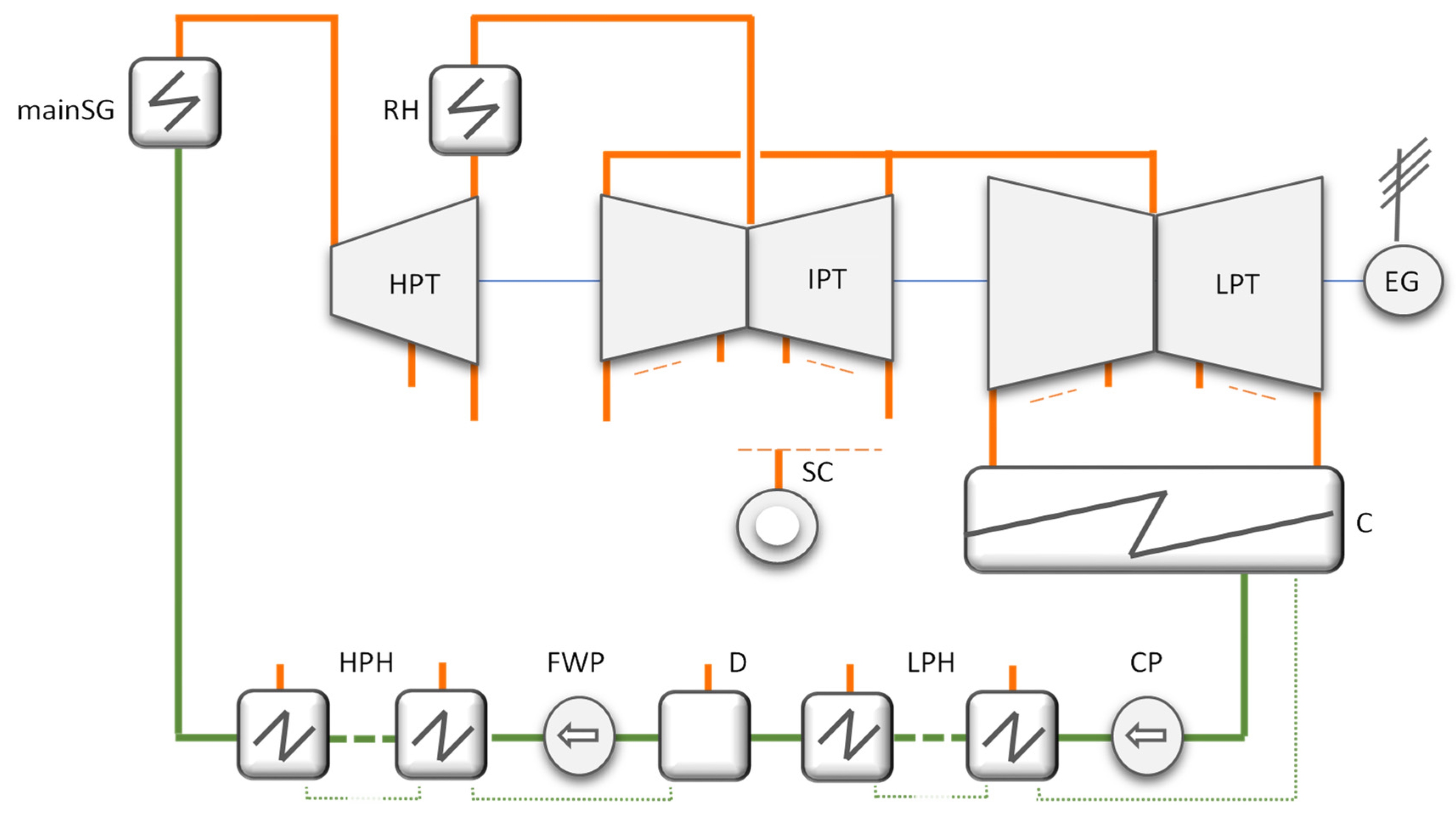
2.1. Supercritical Steam Cogeneration Power Plants
2.2. Thermodynamic Model
2.2.1. Assumptions and Restrictions
- Steam generator: imposed fuel heat flow rate into SG (QSG), known mass flow rate (FSG), and SG efficiency ();
- Preheating line design: minimum number of preheaters (z), fewer HPHs than LPHs (zHPH ≤ zLPH), a maximum acceptable deaerator pressure (pd-max), and preferably an equal temperature increase (∆tPH) on each preheater within a maximum limit (∆tPH-max); steam extraction that is closest to the SC is adjusted to its value;
- Steam consumer: known pressure (pSC) and heat flow rate (QSC), and the option to recover the SC condensate into the deaerator or replace it by adding supply water into the condenser;
- Turbine and pumps: the isentropic efficiency of the turbine depends on the volumetric steam flow rate through each turbine zone and on the isentropic expansion of its turbine section; at the exit of the LPT, a minimum steam quality (xoutLPT-min) is required; the isentropic efficiency of the pumps is imposed;
- Specific investment in equipment (IsEQ): costs depend mainly on fluid parameters and mass flow rates.
2.2.2. Input Data and Main Equations
- The heat flow rate into the steam generator: QSG, in kW;
- The pressure of the main steam: pms, in bar;
- The temperature of the main steam: tms, in °C;
- The reheat temperature of the main steam: trh, in °C;
- The ratio between the reheating pressure (prh) and the main steam pressure (pms), dimensionless, computed as:
- The steam pressure at the condenser: pc, in bar;
- The steam pressure for the SC: pSC, in bar.
- Steam turbine (T):
- Electrical generator (EG):
- Preheaters (HPH, D, LPH) and condenser (C):
- Electrical pumps (CP and FWP):
- Steam generator (SG):
- The overall global efficiency of the CHP plant (ηgl), in percentages [36]:
- The specific investment in equipment (IsEQ), in USD/kW:
2.3. Thermodynamic Cycle Multicriterial Optimization
- The choice of the SC parametric input values, specifically, the minimum and the maximum pSC values (pSC-min, pSC-max);
- The use of heuristic optimization for each SC parametric pSC input value (Figure 2).
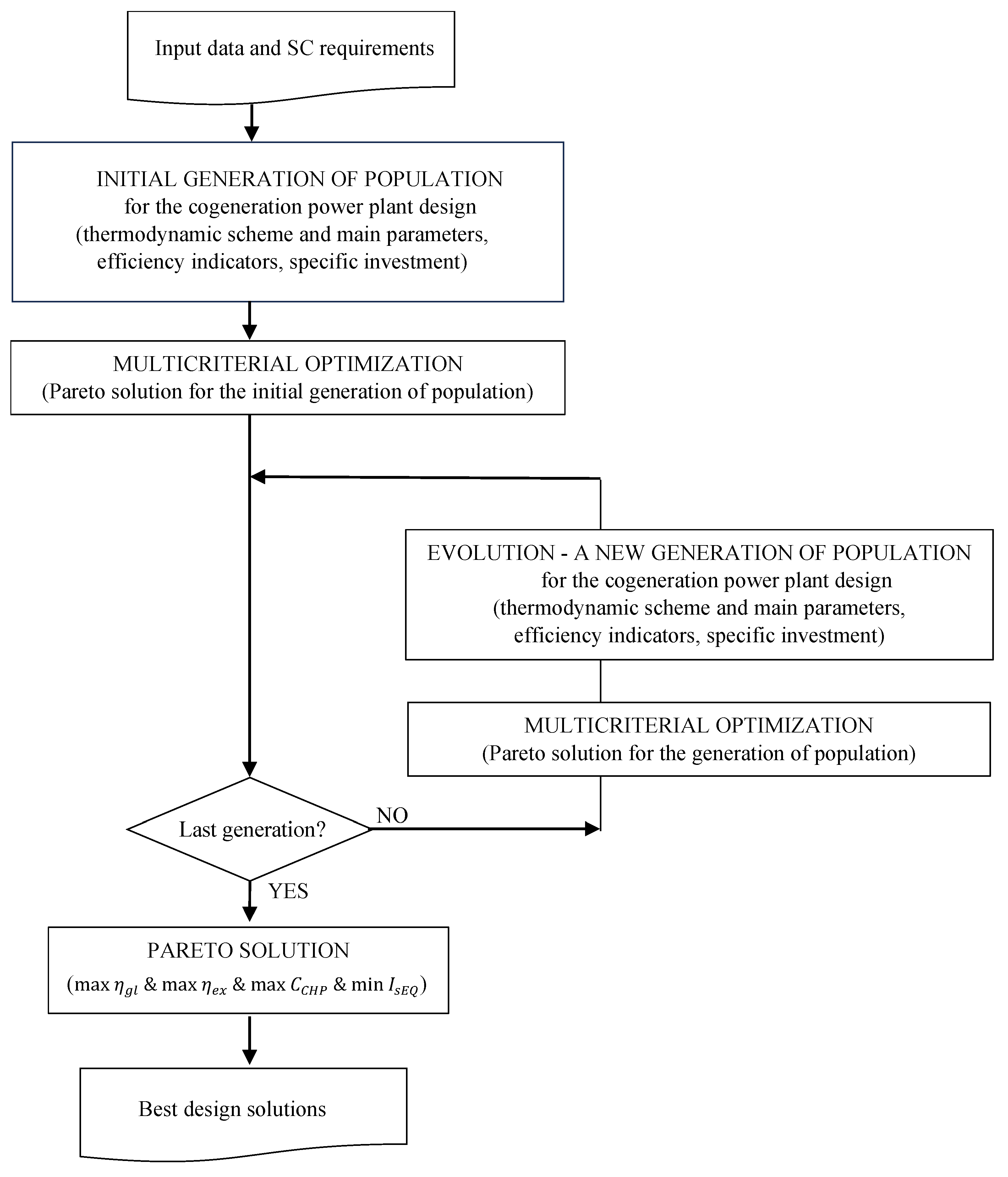
3. Results and Discussion
3.1. Inputs into the Optimization Model
- Main steam pressure: pms = 240–280 bar;
- Main steam temperature: tms = 550–600 °C;
- Reheat temperature: trh = 550–620 °C;
- Ratio between the reheat pressure (prh) and the main steam pressure (pms): rp = 0.08–0.22;
- Condensing pressure: pc = 0.04–0.05 bar.
3.2. Multi-Objective Optimization
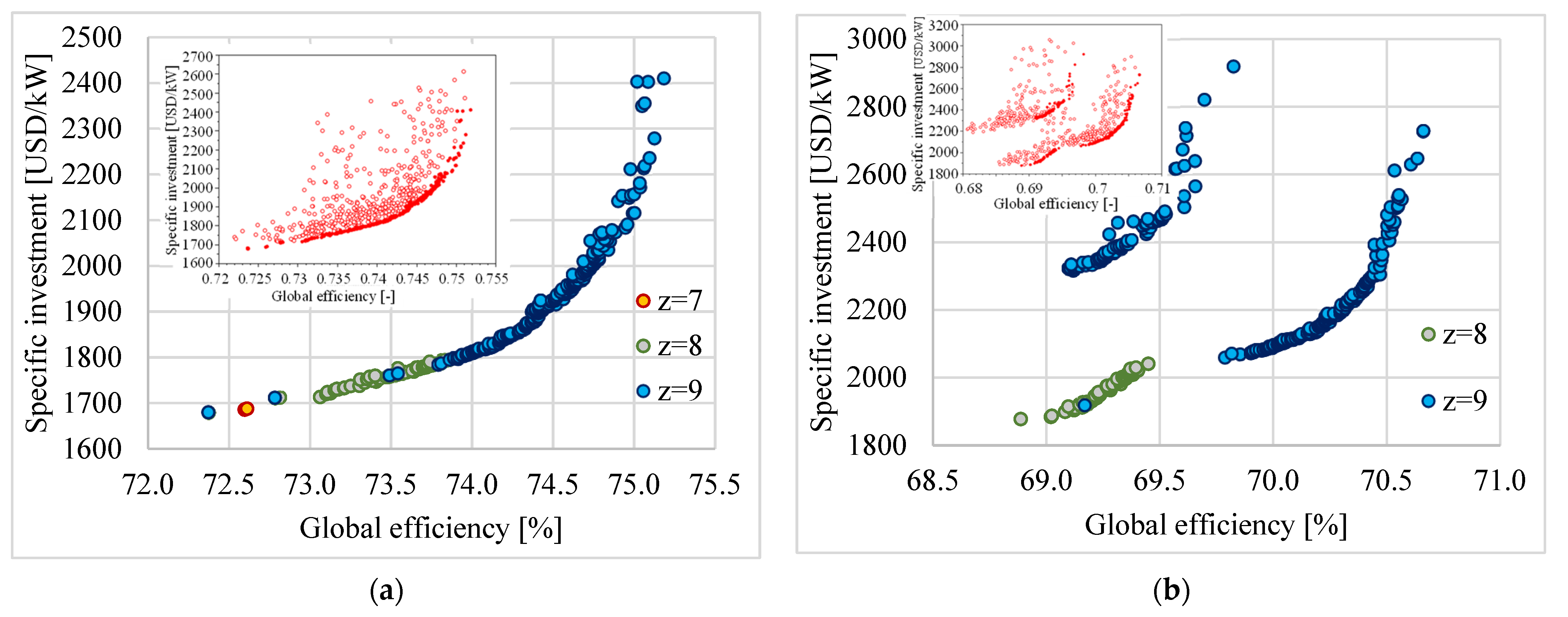
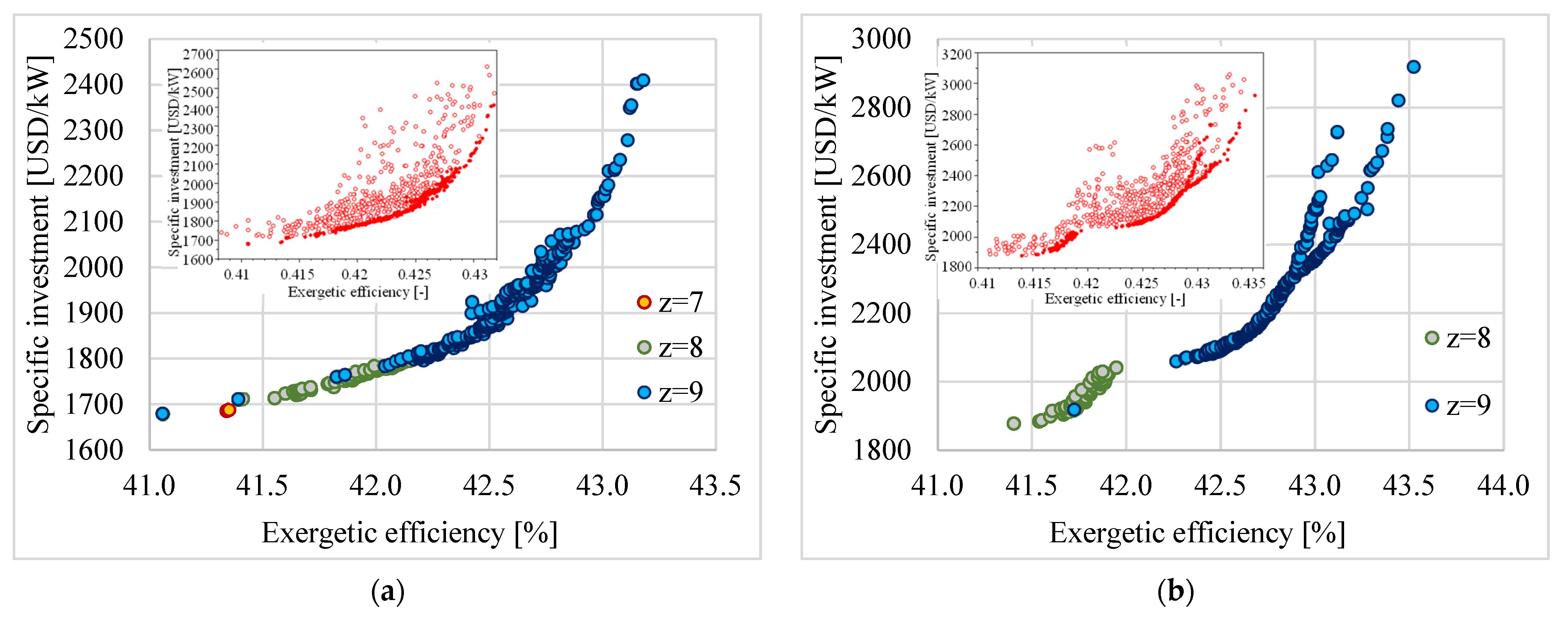

3.3. Optimization of Input Variables
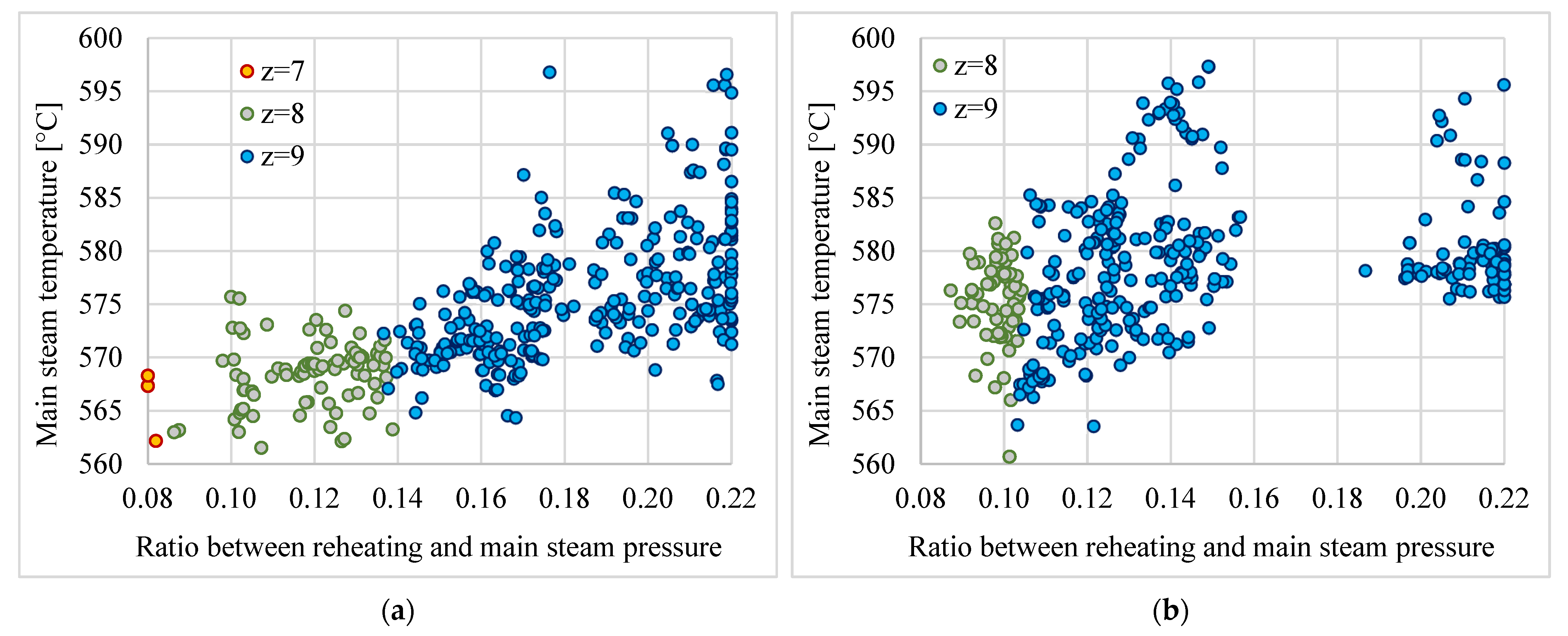
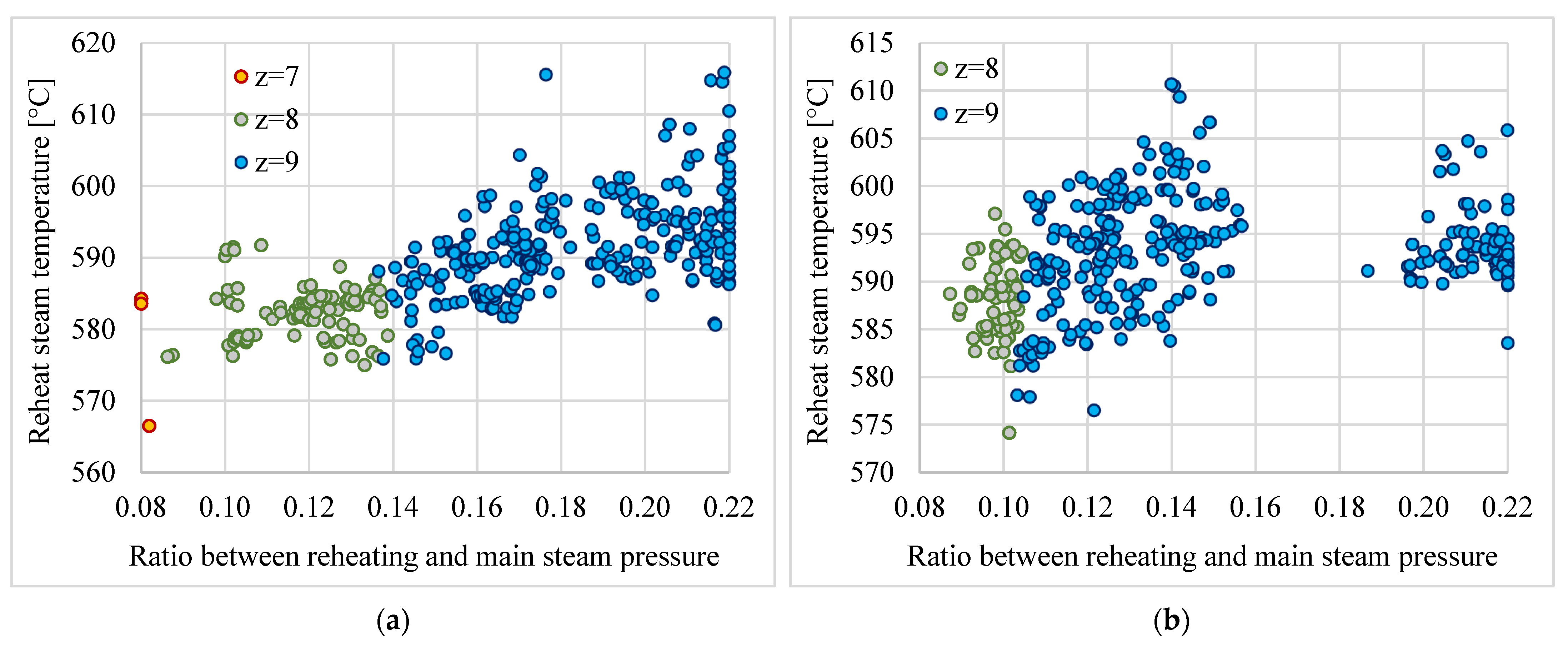
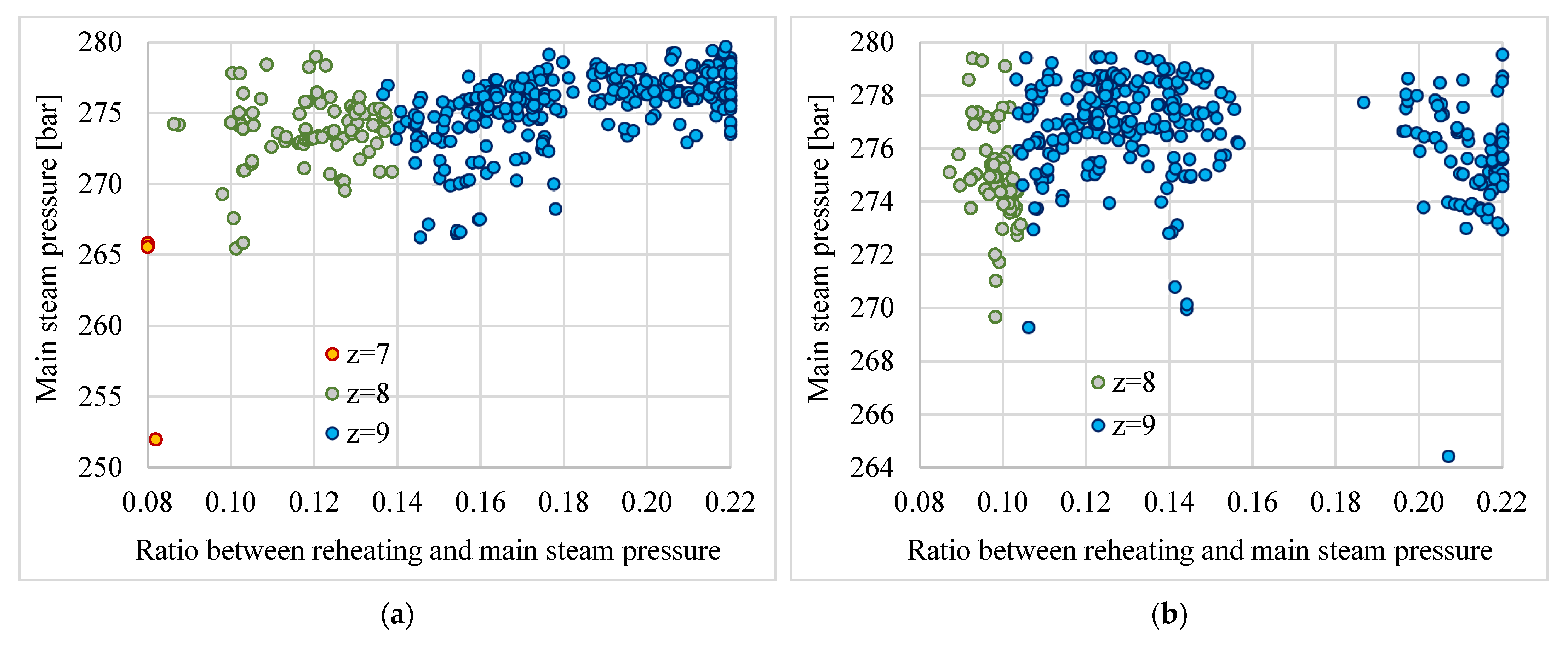
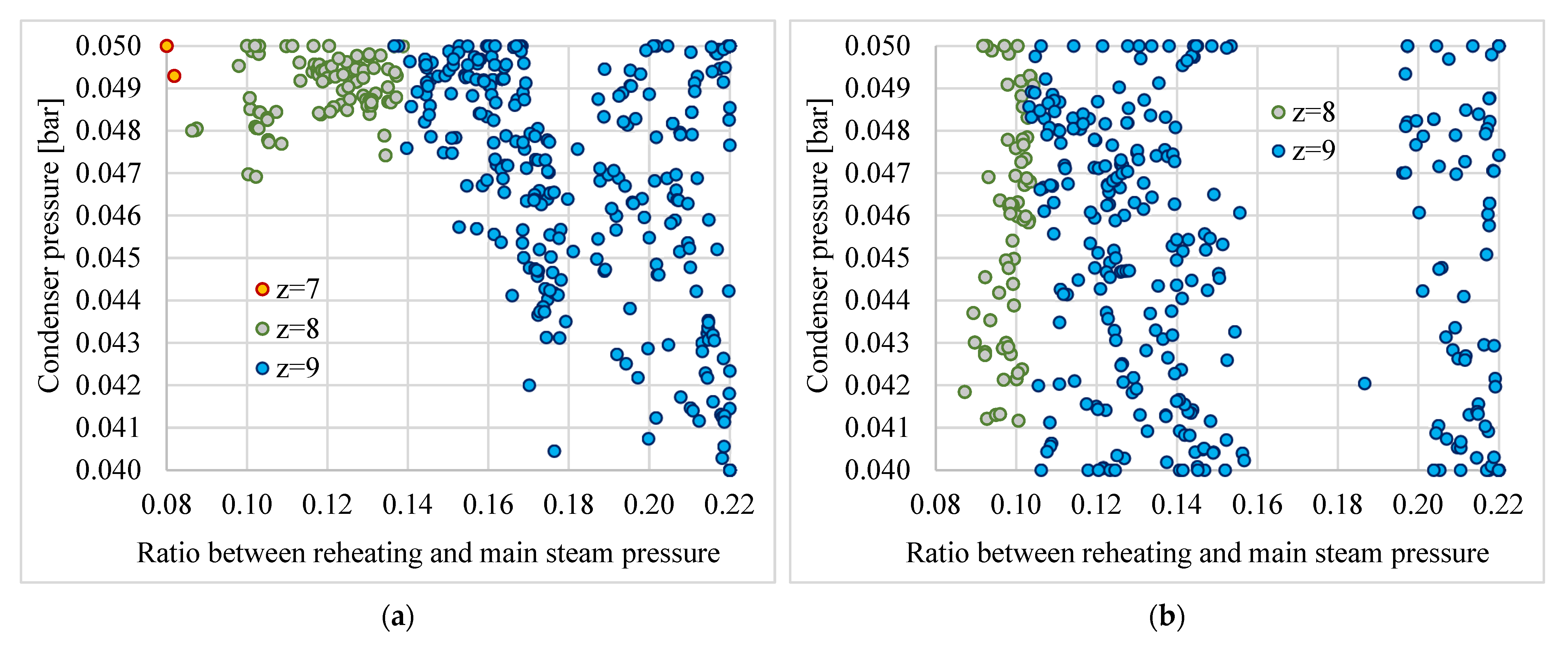
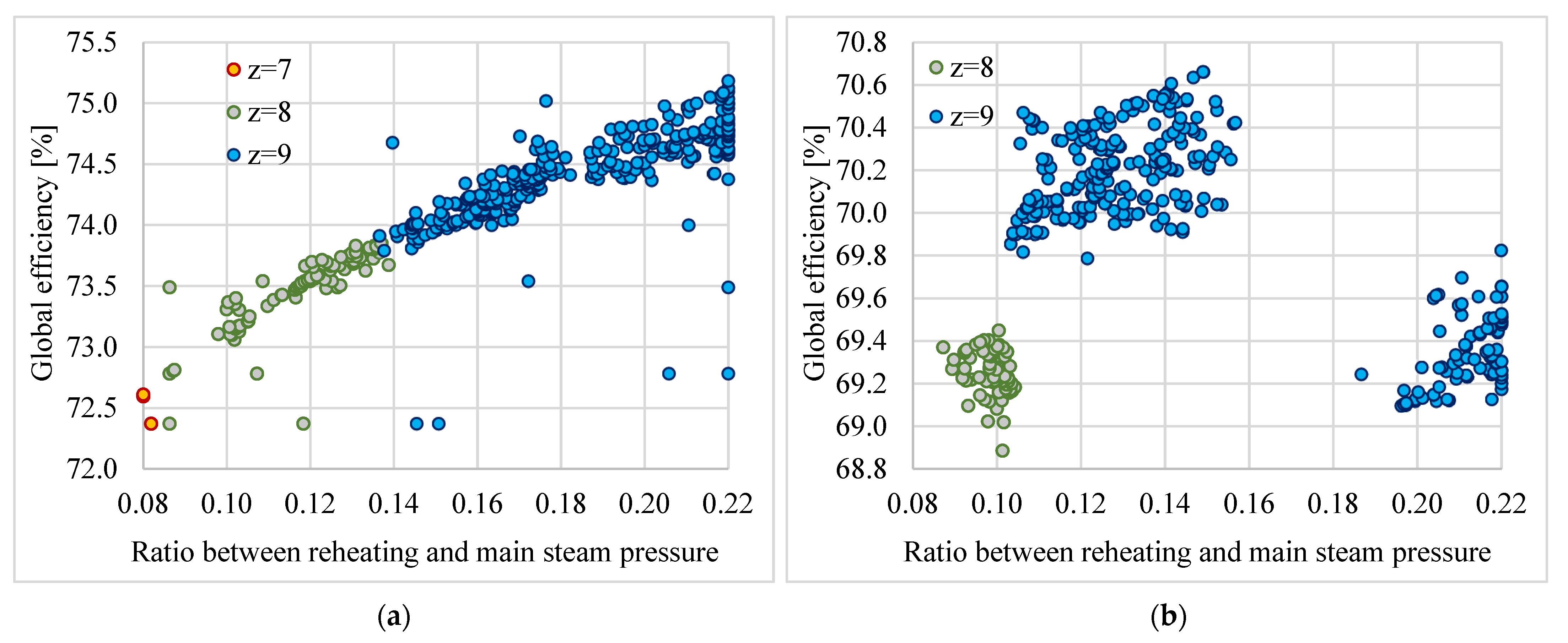
3.4. Optimization of the Ratio Between Reheating and Main Steam Pressure
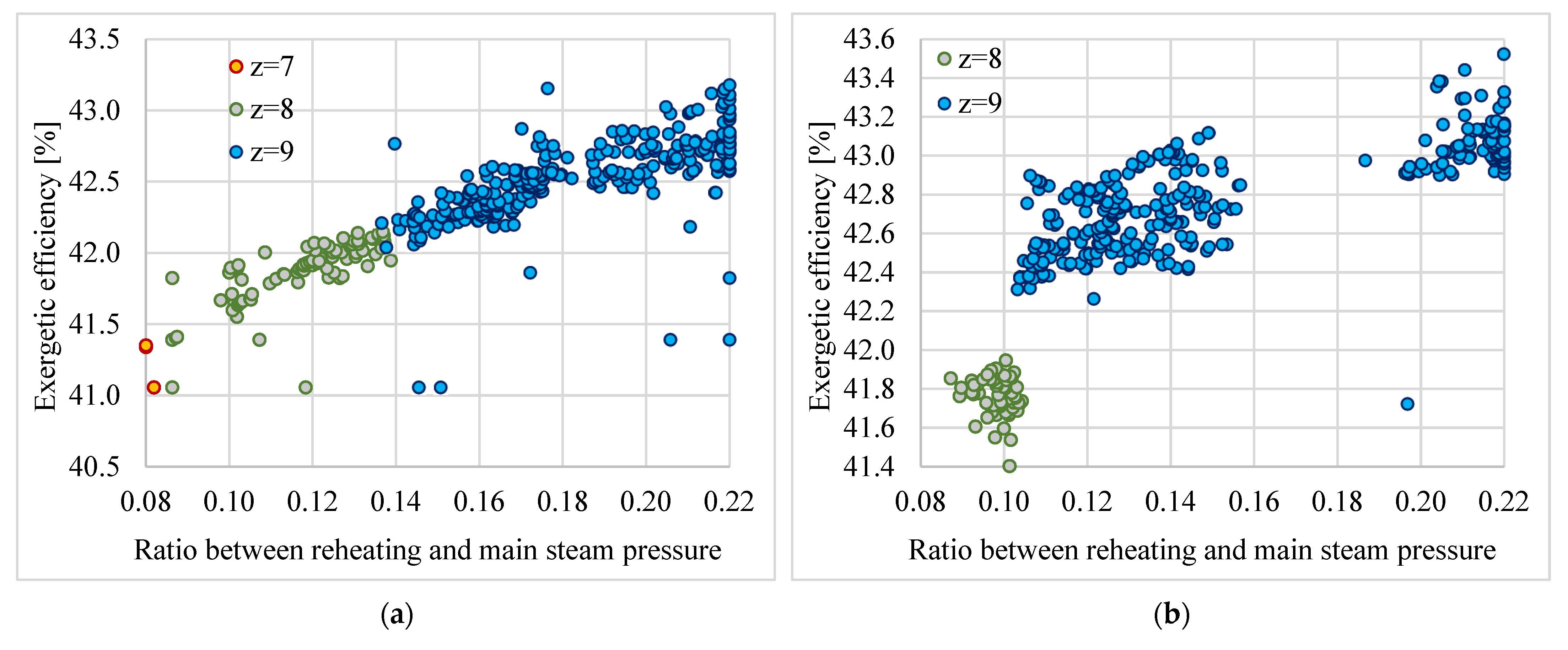
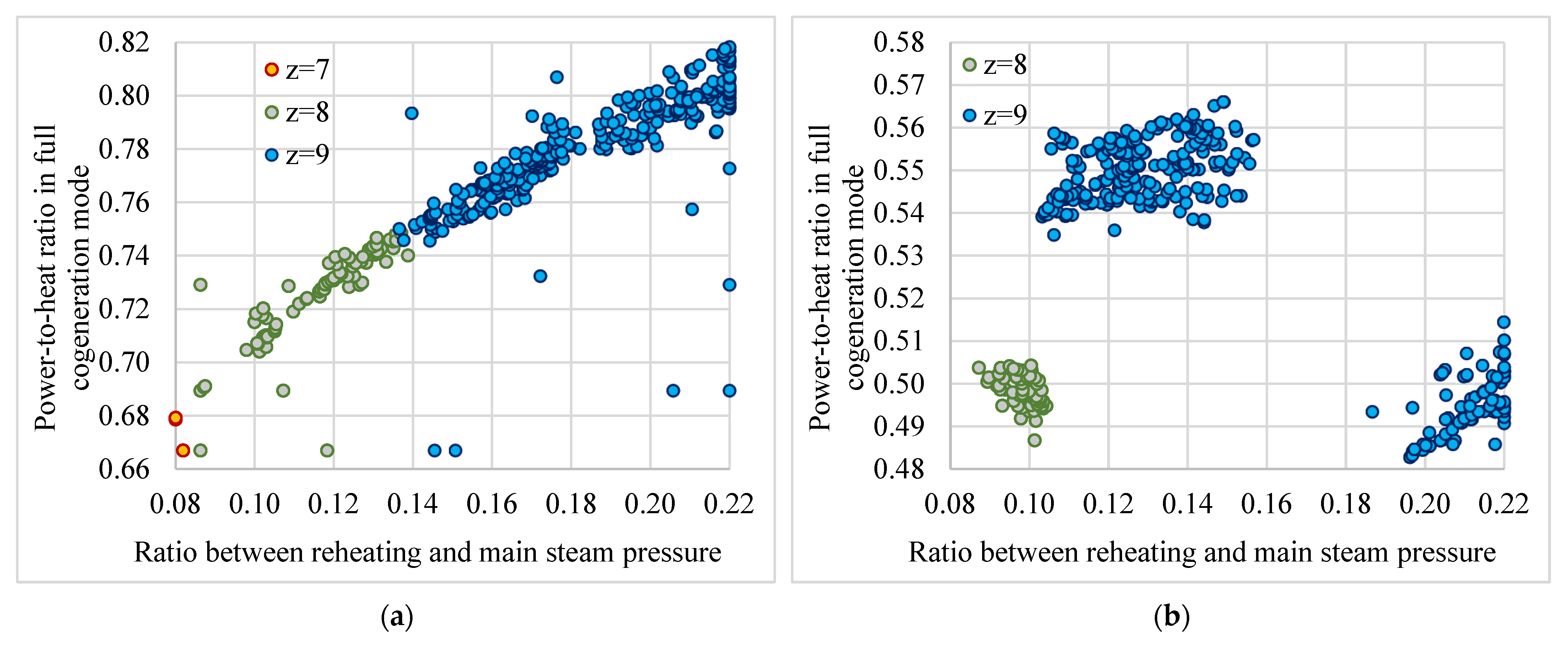
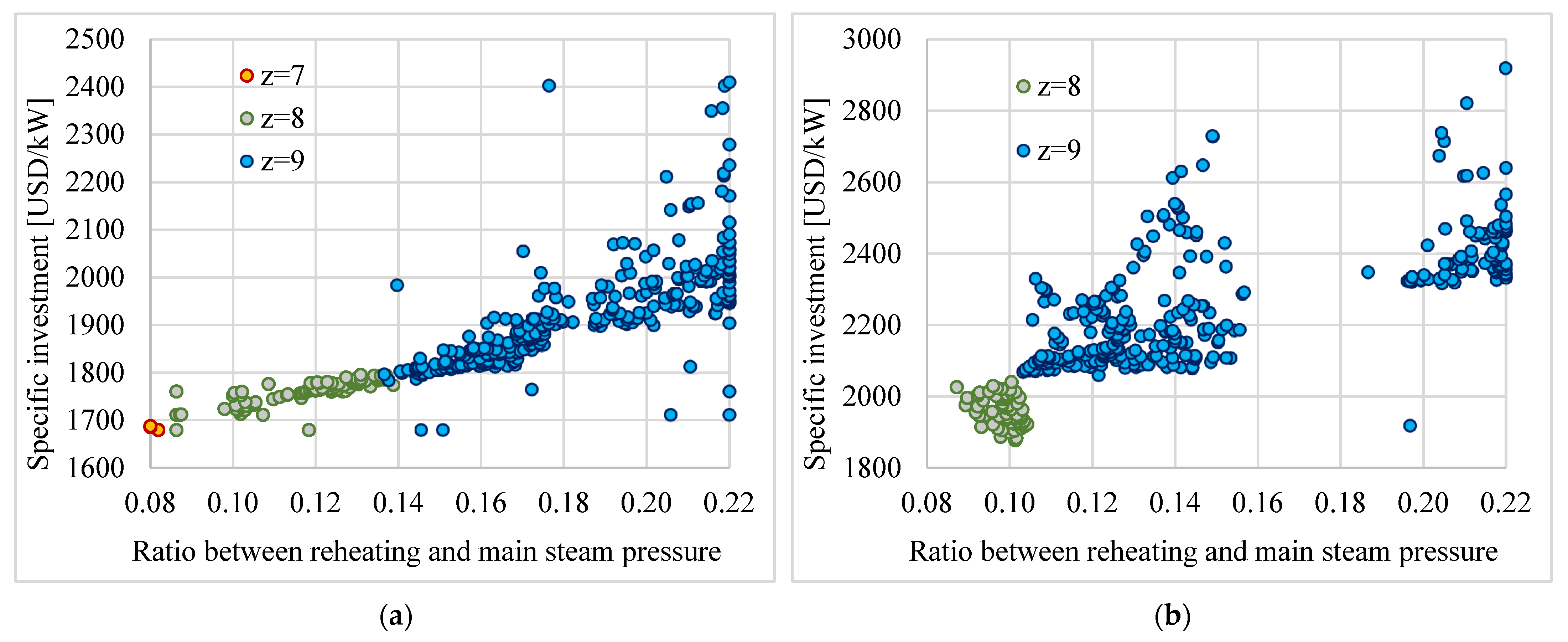
3.5. Model Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CHP | combined heat and power |
| T | turbine |
| HPT | high-pressure turbine |
| IPT | intermediate-pressure turbine |
| LPT | low-pressure turbine |
| SC | steam consumer |
| C | condenser |
| CP | condensate pumps |
| FWP | feedwater pumps |
| LPH | low-pressure heaters |
| HPH | high-pressure heaters |
| D | deaerator |
| SG | steam generator |
| mainSG | main part of the steam generator |
| RH | steam reheater |
| EG | electrical generator |
References
- Directive, E.E. Directive 2012/27/EU of the European Parliament and of the Council of 25 October 2012 on Energy Efficiency, Amending Directives 2009/125/EC and 2010/30/EU and Repealing Directives 2004/8/EC and 2006/32/EC. Off. J. Eur. Union 2012, 315, 1–56. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX:32012L0027 (accessed on 4 April 2023).
- Kurmayer, N.J. New EU Energy Efficiency Directive Sets 11.7% Reduction Target by 2030. Euractiv, 10 March 2023. Available online: https://www.euractiv.com/section/energy-environment/news/new-eu-energy-efficiency-directive-sets-11-7-reduction-target-by-2030/ (accessed on 4 April 2023).
- Zhi, L.-H.; Hu, P.; Chen, L.-X.; Zhao, G. Performance analysis and optimization of engine waste heat recovery with an improved transcritical-subcritical parallel organic Rankine cycle based on zeotropic mixtures. Appl. Therm. Eng. 2020, 181, 115991. [Google Scholar] [CrossRef]
- Dzierwa, P.; Taler, J.; Peret, P.; Taler, D.; Trojan, M. Transient CFD simulation of charging hot water tank. Energy 2022, 239, 122241. [Google Scholar] [CrossRef]
- Trojan, M.; Taler, D.; Dzierwa, P.; Taler, J.; Kaczmarski, K.; Wrona, J. The use of pressure hot water storage tanks to improve the energy flexibility of the steam power unit. Energy 2019, 173, 926–936. [Google Scholar] [CrossRef]
- Iodice, P.; Langella, G.; Amoresano, A.; Senatore, A. Comparative exergetic analysis of solar integration and regeneration in steam power plants. J. Energy Eng. 2017, 143, 04017042. [Google Scholar] [CrossRef]
- Lozano, M.A.; dos Santos, R.; Santos, J.J.; Serra, L.M. Optimal modes of operation and product cost allocation in sugarcane steam cogeneration plants. Therm. Sci. Eng. Prog 2024, 52, 102686. [Google Scholar] [CrossRef]
- da Silva, L.M.C.; Alcântara, M.T.; Higa, M. Cogeneration and thermal integration of multiple effect evaporator in sugarcane industry. Therm. Sci. Eng. Prog 2025, 63, 103715. [Google Scholar] [CrossRef]
- Norişor, M.; Darie, G.; Cenuşă, V.; Pătraşcu, R.; Minciuc, E. CCS economic integration issues in a steam power plant. UPB Sci. Bull. Ser. C 2014, 76, 259–268. [Google Scholar]
- Dzierwa, P.; Taler, D.; Taler, J.; Trojan, M. Optimum Heating of Thick Wall Pressure Components of Steam Boilers. In Proceedings of the ASME 2014 Power Conference, Baltimore, MD, USA, 28–31 July 2014. [Google Scholar] [CrossRef]
- Taler, D.; Dzierwa, P.; Kaczmarski, K.; Taler, J. Increase the flexibility of steam boilers by optimisation of critical pressure component heating. Energy 2022, 250, 123855. [Google Scholar] [CrossRef]
- Taler, J.; Dzierwa, P.; Taler, D. Optimum heating of pressure components of large steam boilers. Forsch. Im Ingenieurwesen 2009, 73, 183–192. [Google Scholar] [CrossRef][Green Version]
- Choi, S.; Kim, S.; Jung, M.; Lee, J.; Lim, J.; Kim, M. Comparative analysis of exergy-and enthalpy-based allocation methods for cogeneration businesses in the industrial complex of South Korea. Energy 2022, 240, 122837. [Google Scholar] [CrossRef]
- Ali, R.H.; Samee, A.A.A.; Attalla, M.; Maghrabie, H.M. Energy-exergy approach of a cogeneration system in pulp and paper industry with a chemical recovery of black liquor and soda. Case Stud. Therm. Eng. 2023, 42, 102712. [Google Scholar] [CrossRef]
- Pérez, Á.A.D.; Palacio, J.C.E.; Venturini, O.J.; Reyes, A.M.M.; Orozco, D.J.R.; Lora, E.E.S.; del Olmo, O.A.A. Thermodynamic and economic evaluation of reheat and regeneration alternatives in cogeneration systems of the Brazilian sugarcane and alcohol sector. Energy 2018, 152, 247–262. [Google Scholar] [CrossRef]
- Shen, F.; Zhao, L.; Du, W.; Zhong, W.; Qian, F. Large-scale industrial energy systems optimization under uncertainty: A data-driven robust optimization approach. Appl. Energy 2020, 259, 114199. [Google Scholar] [CrossRef]
- Manesh, M.K.; Navid, P.; Baghestani, M.; Abadi, S.K.; Rosen, M.; Blanco, A.; Amidpour, M. Exergoeconomic and exergoenvironmental evaluation of the coupling of a gas fired steam power plant with a total site utility system. Energy Convers. Manag. 2014, 77, 469–483. [Google Scholar] [CrossRef]
- Li, D.; Wang, J. Study of supercritical power plant integration with high temperature thermal energy storage for flexible operation. J. Energy Storage 2018, 20, 140–152. [Google Scholar] [CrossRef]
- Eslick, J.C.; Zamarripa, M.A.; Ma, J.; Wang, M.; Bhattacharya, I.; Rychener, B.; Pinkston, P.; Bhattacharyya, D.; Zitney, S.E.; Burgard, A.P.; et al. Predictive modeling of a subcritical pulverized-coal power plant for optimization: Parameter estimation, validation, and application. Appl. Energy 2022, 319, 119226. [Google Scholar] [CrossRef]
- Wu, Y.; Fu, L.; Zhang, S.; Tang, D. Study on a novel co-operated heat and power system for improving energy efficiency and flexibility of cogeneration plants. Appl. Therm. Eng. 2019, 163, 114429. [Google Scholar] [CrossRef]
- Tian, A.-Q.; Lv, H.-X.; Wang, X.-Y.; Pan, J.-S.; Snášel, V. Bioinspired Discrete Two-Stage Surrogate-Assisted Algorithm for Large-Scale Traveling Salesman Problem. J. Bionic Eng. 2025. [Google Scholar] [CrossRef]
- Sornek, K.; Jankowski, M.; Borsukiewicz, A.; Filipowicz, M. The Optimization of Steam Generation in a Biomass-Fired Micro-Cogeneration Prototype Operating on a Modified Rankine Cycle. Sustainability 2024, 16, 9. [Google Scholar] [CrossRef]
- Zeitoun, O.; Orfi, J.; Khan, S.U.-D.; Al-Ansary, H. Desalinated Water Costs from Steam, Combined, and Nuclear Cogeneration Plants Using Power and Heat Allocation Methods. Energies 2023, 16, 2752. [Google Scholar] [CrossRef]
- Javaherian, A.; Ghasemi, S.; Seyed Mahmoudi, S.M.; Rosen, M.A.; Sadeghi, M. Two-Objective Optimization of a Cogeneration System Based on a Gas Turbine Integrated with Solar-Assisted Rankine and Absorption Refrigeration Cycles. Sustainability 2023, 15, 15624. [Google Scholar] [CrossRef]
- Al bkoor Alrawashdeh, K.; Al-Samrraie, L.; Al Bsoul, A.; Khasawneh, A.; Ammary, B.; Gul, E. Parametric Optimization of Multi-Stage Flashing Desalination System Using Genetic Algorithm for Efficient Energy Utilization. ChemEngineering 2024, 8, 83. [Google Scholar] [CrossRef]
- Simtech. The Process Simulation, Environment IPSEpro. Available online: https://simtechnology.com/ipsepro/process-simulation-and-heat-balance-software (accessed on 25 April 2025).
- TRNSYS Transient System Simulation Tool. Available online: https://www.trnsys.com/ (accessed on 25 April 2025).
- EBSILON Professional. Available online: https://www.ebsilon.com/en/ (accessed on 25 April 2025).
- Panowski, M.; Zarzycki, R.; Kobyłecki, R. Conversion of steam power plant into cogeneration unit-Case study. Energy 2021, 231, 120872. [Google Scholar] [CrossRef]
- Saari, J.; Martinez, C.M.; Kaikko, J.; Sermyagina, E.; Mankonen, A.; Vakkilainen, E. Techno-economic optimization of a district heat condenser in a small cogeneration plant with a novel greedy cuckoo search. Energy 2022, 239, 122622. [Google Scholar] [CrossRef]
- Abdel-Dayem, A.; Hawsawi, Y.M. Feasibility study using TRANSYS modelling of integrating solar heated feed water to a cogeneration steam power plant. Case Stud. Therm. Eng. 2022, 39, 102396. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, Y.; Liu, H.; Li, C. Optimizing thermal–electric load distribution of large-scale combined heat and power plants based on characteristic day. Energy Convers. Manag. 2021, 248, 114792. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, C.; Duan, F.; Tian, Z. Thermodynamic Comparison of the Steam Ejectors Integrated at Different Locations in Cogeneration Systems. Energies 2024, 17, 2463. [Google Scholar] [CrossRef]
- Wang, X.; Duan, L. Comparative study of multiple-mode collaborative operation strategy and traditional heat and power decoupling technologies for cogeneration system based on GTCC. Case Stud. Therm. Eng. 2023, 49, 103213. [Google Scholar] [CrossRef]
- Jukić, P.; Guzović, Z.; Rašković, P.; Lončar, D. Efficiency enhancement of heat supply steam turbines. Appl. Therm. Eng. 2025, 279, 127524. [Google Scholar] [CrossRef]
- Cenușă, V.-E.; Opriș, I. Design optimization of cogeneration steam power plants with supercritical parameters. Sustain. Energy Technol. Assess. 2024, 64, 103727. [Google Scholar] [CrossRef]
- Scilab Enterprises. Scilab 6.0.1. Available online: https://www.scilab.org/ (accessed on 4 April 2023).
- Opriș, I.; Cenușă, V.-E. Parametric and heuristic optimization of multiple schemes with double-reheat ultra-supercritical steam power plants. Energy 2023, 266, 126454. [Google Scholar] [CrossRef]
- Kler, A.M.; Zharkov, P.V.; Epishkin, N.O. Parametric optimization of supercritical power plants using gradient methods. Energy 2019, 189, 116230. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Y.; Dong, C.; Morosuk, T.; Tsatsaronis, G. Parametric optimization of supercritical coal-fired power plants by MINLP and differential evolution. Energy Convers. Manag. 2014, 85, 828–838. [Google Scholar] [CrossRef]
- Cenușă, V.-E.; Opriș, I. Optimal Design Parameters for Supercritical Steam Power Plants. Thermo 2025, 5, 1. [Google Scholar] [CrossRef]
- Costinaş, S.; Georgescu, S.C.; Opriş, I. Smart solutions for the auxiliary power supplies schemes in hydropower plants. UPB Sci. Bull Ser. C 2014, 76, 245–253. [Google Scholar]
- Khaleel, O.J.; Ismail, F.B.; Ibrahim, T.K.; bin Abu Hassan, S.H. Energy and exergy analysis of the steam power plants: A comprehensive review on the Classification, Development, Improvements, and configurations. Ain Shams Eng. J. 2022, 13, 101640. [Google Scholar] [CrossRef]
- Shokri, Y.; Ghazi, M.; Nikiyan, M.; Maleki, A.; Rosen, M.A. Optimal equipment arrangement of a total site for cogeneration of thermal and electrical energy by using exergoeconomic approach. Energy Rep. 2021, 7, 5330–5343. [Google Scholar] [CrossRef]
- Frangopoulos, C.A. A method to determine the power to heat ratio, the cogenerated electricity and the primary energy savings of cogeneration systems after the European Directive. Energy 2012, 45, 52–61. [Google Scholar] [CrossRef]
- Vellini, M.; Gambini, M.; Stilo, T. High-efficiency cogeneration systems for the food industry. J. Clean. Prod. 2020, 260, 121133. [Google Scholar] [CrossRef]
- Urošević, D.; Gvozdenac, D.; Grković, V. Calculation of the power loss coefficient of steam turbine as a part of the cogeneration plant. Energy 2013, 59, 642–651. [Google Scholar] [CrossRef]
- Gvozdenac, D.; Urošević, B.G.; Menke, C.; Urošević, D.; Bangviwat, A. High efficiency cogeneration: CHP and non-CHP energy. Energy 2017, 135, 269–278. [Google Scholar] [CrossRef]
- Bondarenko, O.; XSteam. Water and steam properties according to IAPWS IF-97. 2020. Available online: https://fileexchange.scilab.org/toolboxes/502000 (accessed on 4 April 2023).
- Daneh-Dezfuli, A.; Ghanad-Dezfuli, M.; Changizian, M. A novel 4E-based optimization framework for circular biomass multi-generation systems integrating NSGA-II and ANN to enhance resource efficiency and sustainability. Int. Commun. Heat Mass Transf. 2025, 164, 108849. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, P. NSGA-II algorithm based control parameters optimization strategy for megawatt novel nuclear power systems. Energy 2025, 316, 134444. [Google Scholar] [CrossRef]
- Nicolae, A.E.; Necula, H.; Carutasiu, B.M. Optimization of energy rehabilitation processes of existing buildings. UPB Sci. Bull Ser. C 2023, 85, 327–338. [Google Scholar]
- Hassanat, A.; Almohammadi, K.; Alkafaween, E.; Abunawas, E.; Hammouri, A.; Prasath, V.B.S. Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach. Information 2019, 10, 390. [Google Scholar] [CrossRef]
- Lai, F.; Wang, S.; Liu, M.; Yan, J. Operation optimization on the large-scale CHP station composed of multiple CHP units and a thermocline heat storage tank. Energy Convers. Manag. 2020, 211, 112767. [Google Scholar] [CrossRef]
- Liu, H.; Geng, Z.; Gu, Y.; Mo, Z.; Yu, Z.; He, X.; Lu, S. A regional integrated energy system with a coal-fired CHP plant, screw turbine and solar thermal utilization: Scenarios for China. Energy Convers. Manag. 2020, 212, 112812. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, M.; Zhao, Y.; Zhang, S.; Yan, H.; Yan, J. Thermo-economic optimization of the thermal energy storage system extracting heat from the reheat steam for coal-fired power plants. Appl. Therm. Eng. 2022, 215, 119008. [Google Scholar] [CrossRef]
- Xu, C.; Xu, G.; Zhao, S.; Zhou, L.; Yang, Y.; Zhang, D. An improved configuration of lignite pre-drying using a supplementary steam cycle in a lignite fired supercritical power plant. Appl. Energy 2015, 160, 882–891. [Google Scholar] [CrossRef]
- Xu, G.; Dong, W.; Xu, C.; Liu, Q.; Yang, Y. An integrated lignite pre-drying system using steam bleeds and exhaust flue gas in a 600 MW power plant. Appl. Therm. Eng. 2016, 107, 1145–1157. [Google Scholar] [CrossRef]
- Rocha, D.H.; Silva, R.J. Exergoenvironmental analysis of a ultra-supercritical coal-fired power plant. J. Clean. Prod. 2019, 231, 671–682. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Q.; Duan, X.; Zhang, Y.; Yang, Z.; Che, D. Thermodynamic analysis of a modified system for a 1000 MW single reheat ultra-supercritical thermal power plant. Energy 2018, 145, 25–37. [Google Scholar] [CrossRef]
- Wang, D.; Li, S.; Liu, F.; Gao, L.; Sui, J. Post combustion CO2 capture in power plant using low temperature steam upgraded by double absorption heat transformer. Appl. Energy 2018, 227, 603–612. [Google Scholar] [CrossRef]
- Xu, G.; Xu, C.; Yang, Y.; Fang, Y.; Zhou, L.; Zhang, K. Novel partial-subsidence tower-type boiler design in an ultra-supercritical power plant. Appl. Energy 2014, 134, 363–373. [Google Scholar] [CrossRef]
| pSC [bar] | Statistical Analysis | ηgl [%] | IsEQ [USD/kW] | CCHP [-] | ηex [%] |
|---|---|---|---|---|---|
| 3.6 | med ± σ | 74.2 ± 0.8 | 1985 ± 159 | 0.76 ± 0.03 | 42.6 ± 0.2 |
| min–max | 73.2–74.9 | 1794–2350 | 0.72–0.8 | 42.4–43.1 | |
| 40 | med ± σ | 69.8 ± 0.5 | 2208 ± 191 | 0.53 ± 0.03 | 42.6 ± 0.5 |
| min–max | 68.9–70.7 | 1878–2919 | 0.48–0.57 | 41.4–43.5 |
| pSC [bar] | Statistical Analysis | pms [bar] | tms [°C] | trh [°C] | pc [bar] |
|---|---|---|---|---|---|
| 3.6 | med ± σ | 275.1 ± 2.8 | 573.9 ± 6.4 | 589.3 ± 7.6 | 0.047 ± 0.003 |
| min–max | 252–279.7 | 561.5–596.8 | 566.5–615.9 | 0.04–0.05 | |
| 40 | med ± σ | 276.3 ± 2 | 578.4 ± 6.3 | 592.6 ± 5.7 | 0.045 ± 0.003 |
| min–max | 264.4–279.5 | 560.7–597.3 | 574.2–610.7 | 0.04–0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cenușă, V.-E.; Opriș, I. Multicriterial Heuristic Optimization of Cogeneration Supercritical Steam Cycles. Sustainability 2025, 17, 6927. https://doi.org/10.3390/su17156927
Cenușă V-E, Opriș I. Multicriterial Heuristic Optimization of Cogeneration Supercritical Steam Cycles. Sustainability. 2025; 17(15):6927. https://doi.org/10.3390/su17156927
Chicago/Turabian StyleCenușă, Victor-Eduard, and Ioana Opriș. 2025. "Multicriterial Heuristic Optimization of Cogeneration Supercritical Steam Cycles" Sustainability 17, no. 15: 6927. https://doi.org/10.3390/su17156927
APA StyleCenușă, V.-E., & Opriș, I. (2025). Multicriterial Heuristic Optimization of Cogeneration Supercritical Steam Cycles. Sustainability, 17(15), 6927. https://doi.org/10.3390/su17156927







