Optimization of Mining Sequence for Ion-Adsorbed Rare Earth Mining Districts Incorporating Environmental Costs
Abstract
1. Introduction
2. Construction of the Mining Sequence Optimization Model
2.1. Principles and Assumptions of Model Construction
2.2. Objective Functions
2.2.1. Economic Benefit Objective
- CIt is the cash inflow in year t;
- COt is the cash outflow in year t;
- n is the project life (or calculation period);
- i0 is the benchmark discount rate.
- (1)
- The average annual profit and mining time of each mine.
- Pe is the sales price of rare earth ore products from the e-th mine (in 104 CNY/ton);
- Ce is the unit production cost (in 104 CNY/ton);
- te is the mining life (year);
- Qe is the annual production of the e-th mine (ton).
- ηe is the comprehensive mining and beneficiation recovery rate of the e-th mine (%);
- Qzi is the total resource reserve (TR2O3) of the mine (ton);
- Ge is the leaching rate (%);
- Qe is the annual production of the e-th mine (ton).
- Qe represents the output of ionic rare earth (unit: ton);
- Q∗ denotes the resource reserves of ionic rare earth (unit: ton).
- (2)
- The commencement and termination times of mining in each mine.
- tu(n) is the mining time of the mine when the mining sequence is n.
- (3)
- The NPV of the i-th mine in the mining sequence, denoted as NPVu,i (in 104 CNY).
- ➀
- If the commencement and termination times of mining are in the same calendar year, i.e., the integer parts of Tu1,i (T*u1,i) and Tu2,i (T*u1,i) are equal, the NPV is calculated as follows:
- Ru(i) is the average annual profit of the i-th mine in the mining sequence;
- d is the annual discount rate (%).
- ➁
- If the commencement and termination times of mining do not fall within the same calendar year, the NPV is calculated as follows:
- (4)
- The objective function of the optimization model for ion-adsorption rare earth mining district based on maximizing economic benefits is formulated as follows:
- NPV is the total net present value of the mining district (in 104 CNY);
- N is the number of mines in the mining district.
2.2.2. Environmental Cost Target
- (1)
- Environmental pollution factors.
- (2)
- Objective function.
- CWu is the cost of water pollution control (in 104 CNY/year);
- PW is the unit cost of wastewater treatment (in CNY/m3);
- QW is the volume of wastewater (in 104 m3/year);
- U and U* are the actual and maximum allowable concentrations of the main pollutant (in mg/L), respectively.
- CLu is the land reclamation cost (in 104 CNY);
- PLY is the unit area cost of land reclamation for in situ leaching sites (in CNY/m2);
- SLY is the total area of land reclamation for in situ leaching sites (in m2);
- PLB is the unit area cost of land reclamation for temporary waste dumps and topsoil stockpiles (in CNY/m2);
- SLB is the total area of land reclamation for temporary waste dumps and topsoil stockpiles (in m2);
- PLM is the unit area cost of land reclamation for pregnant solution and tailwater treatment plants (in CNY/m2);
- SLM is the total area of land reclamation for mother liquid and tailwater treatment plants (in m2).
- CVu is the vegetation maintenance cost (in 104 CNY);
- PV is the maintenance cost per unit area (in CNY/m2·year);
- QV is the maintenance area (in m2);
- T* is the maintenance period (in years).
- Cu(i) is the environmental cost of the i-th mine in the mining sequence (in 104 CNY);
- CWu(i) is the average annual cost of water pollution control for the i-th mine in the mining sequence (in 104 CNY);
- CLu(i) is the average annual cost of land reclamation for the i-th mine in the mining sequence (in 104 CNY);
- CVu(i) is the average annual cost of vegetation maintenance for the i-th mine in the mining sequence (in 104 CNY);
- d is the annual discount rate (%).
- CE is the total environmental cost of the mining district (in 104 CNY);
- N is the number of mines in the mining district.
2.3. Constraints
2.3.1. Constraints on Mining Scale
2.3.2. Constraints on Production Conditions
2.3.3. Constraints on Mining Sequence
2.4. Optimization Model
3. Model Application
3.1. Project Overview
3.2. Algorithm Analysis
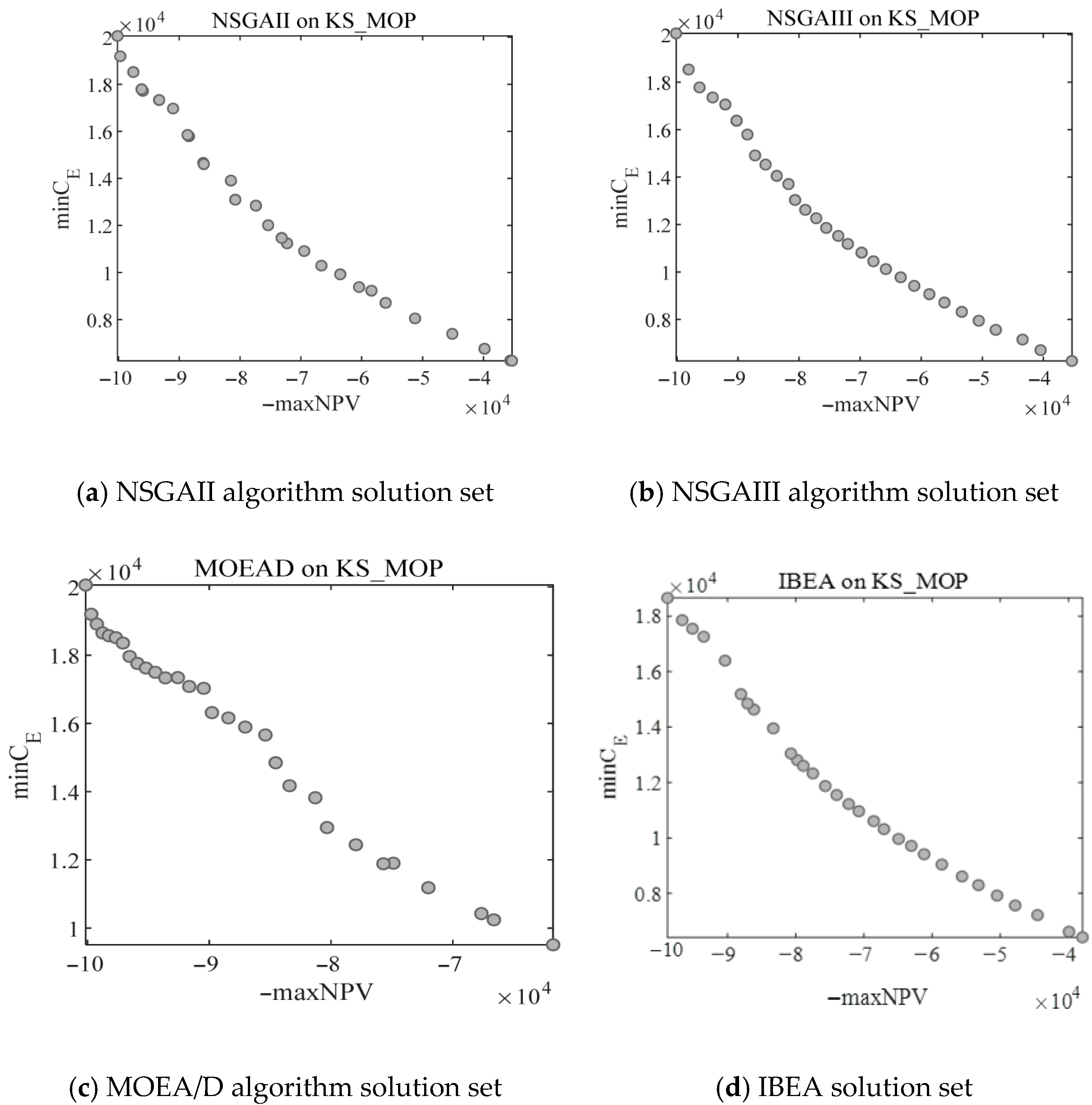
- (1)
- Distribution of the Solution Set.
- (2)
- Running time.
- (3)
- HV value.
3.3. Results Analysis
4. Further Discussion
4.1. Transformation of Multi-Objective Problems into Single-Objective Problems
4.2. Comparison of Single-Objective Optimization Solutions
4.3. Emission-Reduction Measures for Mine-Site Planning
- (1)
- Siting Wastewater Treatment Plants in Low-Topography Areas.
- (2)
- Concurrent Mining and Restoration.
- (3)
- Science-Based Vegetation Maintenance Plan.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NPV | Net Present Value |
| CE | Net Present Value of Environmental Costs |
| REs | Rare Earths |
| HV | Hypervolume |
| GA | Genetic Algorithm |
| REO | Rare Earth Oxide |
| NSGAII | Non-dominated Sorting Genetic Algorithm II |
| NSGAIII | Non-dominated Sorting Genetic Algorithm III |
| IBEA | Indicator-Based Evolutionary Algorithm |
| MOEA/D | Multi-Objective Evolutionary Algorithm based on Decomposition |
References
- Li, X.; Ge, J.; Chen, W.; Wang, P. Scenarios of rare earth elements demand driven by automotive electrification in China: 2018–2030. Resour. Conserv. Recycl. 2019, 145, 322–331. [Google Scholar] [CrossRef]
- Barteková, E.; Kemp, R. National strategies for securing a stable supply of rare earths in different world regions. Resour. Policy 2016, 49, 153–164. [Google Scholar] [CrossRef]
- Wang, X.; Ge, J.; Li, J.; Han, A. Market impacts of environmental regulations on the production of rare earths: A computable general equilibrium analysis for China. Clean. Prod. 2017, 154, 614–620. [Google Scholar] [CrossRef]
- Chanda, E.; Dagdelen, K. Optimal blending of mine production using goal programming and interactive graphics systems. Surf. Min. Reclam. 1995, 9, 203–208. [Google Scholar] [CrossRef]
- Li, S.J.; Xu, Z.H. Application of Linear Programming Approach in Mining Schedule Planning. Met. Mine 2009, 44, 20–21, 25. [Google Scholar]
- Liu, L.; Chen, J.H.; Zheng, H.L. Application of fuzzy grey predictability linear programming in capacity allocation of mine. J. Cent. South Univ. (Sci. Technol.) 2012, 57, 611–619. [Google Scholar]
- Pourrahimian, Y.; Askari-Nasab, H. An application of mathematical programming to determine the best height of draw in block-cave sequence optimization. Min. Technol. 2014, 123, 162–172. [Google Scholar] [CrossRef]
- Wang, L.G.; Ren, Z.L.; Pan, C.P. Optimization analysis of stope mining sequence based on mixed integer programming. Chin. J. Nonferrous Met. 2016, 26, 173–179. [Google Scholar]
- Liu, X.; Xu, Z.; Chen, X.; Zhong, D. Underground mine extraction planning based on mixed-integer programming. J. Northeast. Univ. (Nat. Sci.) 2017, 38, 880–885. [Google Scholar]
- Liu, D.; Wang, L.; Chen, X.; Zhong, D.; Xu, Z. Study on Multi Objective Optimization and Application of Medium and Long Term Plan for Underground Mine. Gold Sci. Technol. 2018, 26, 228–233. [Google Scholar]
- Xu, T.J.; Yang, P. Optimization of mine ore blending based on the fuzzy multi-objective optimum algorithm. Chin. J. Eng. 2009, 31, 1363–1367. [Google Scholar]
- Bai, Y.; Wu, Z.Y. Mine construction schedule controlled by multi scheme network plan. Coal Sci. Technol. 2006, 34, 64–66. [Google Scholar]
- Chen, D.G.; Hu, N.L.; Li, G.Q. Compilation and Research of Underground Mine Construction Plan Based on CCPM. Met. Mine 2009, 44, 96–99. [Google Scholar]
- Li, L.; Yang, L.; Zheng, M.; Dai, Y.; Jiao, Y.; Liao, C. Research progress on rare earth extraction and separation technology and extractants. J. Chin. Soc. Rare Earths 2022, 40, 920–935. [Google Scholar]
- Mancheri, N.A.; Sprecher, B.; Bailey, G.; Ge, J.; Tukker, A. Effect of Chinese policies on rare earth supply chain resilience. J. Resources. Conserv. Recycl. 2019, 42, 101–112. [Google Scholar] [CrossRef]
- GB/T 35067-2018; Technical Specifications for in-situ Leaching Mining of Ionic Rare Earth Ore. Chinese Standard: Beijing, China, 2018.
- Meng, Q.J. Review of the Current Status of Ionic Rare Earth Resource Mining Technology and Ecological Environment Impact Issues. Rare Earth Inf. 2020, 37, 24–25. [Google Scholar]
- Luo, X.P.; Hang, Y.B.Z. Review on the Development and Utilization of Ionic Rare Earth Ore. Minerals 2022, 12, 554. [Google Scholar] [CrossRef]
- Guan, H.; Mu, Y.; Song, R.; Lan, Y.; Du, X.; Li, J.; Chi, W.; Sang, W. Soil Microbial Communities in Desert Grassland around Rare Earth Mine: Diversity, Variation, and Response Patterns. Sustainability 2022, 14, 15629. [Google Scholar] [CrossRef]
- Xu, F.; Li, H.G.; Wang, X.L. Progress in Environmental Problems and Cost Assessment of Ion-adsorption Rare Earth Mining. Chin. Rare Earths 2020, 41, 119–127. [Google Scholar]
- Wei, J.P.; Wang, H.N.; Yan, J.B. Environmental damages and control measures in exploiting ion-absorbed rare earth of South China. Nonferrous Met. Sci. Eng. 2016, 7, 125–132. [Google Scholar]
- Zheng, X.K.; Feng, X.J.; Chen, Z.; Zhang, Y. Research progress on environmental problems of ionic rare earth mining and restoration of abandoned land. Appl. Chem. Ind. 2019, 48, 681–684. [Google Scholar]
- Liang, X.; Ye, M.; Yang, L.; Fu, W.; Li, Z. Evaluation and Policy Research on the Sustainable Development of China’s Rare Earth Resources. J. Sustain. 2018, 10, 3792. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Protić, M.; Petrović, N. Multi-objective optimization of energy performance for a detached residential building with a sunspace using the NSGA-II genetic algorithm. Sol. Energy 2021, 224, 1426–1444. [Google Scholar] [CrossRef]
- Bi, X.; Wang, C. An improved NSGA-III algorithm based on objective space decomposition for many-objective optimization. Soft Comput. 2017, 21, 4269–4296. [Google Scholar] [CrossRef]
- Wang, X.; Wei, J.; Zhou, X.; Gu, X. A multi-objective evolutionary algorithm based on hypervolume indicator. J. East China Univ. Sci. Technol. (Nat. Sci. Ed.) 2020, 46, 780–791. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D:A multi-objective evolutionary algorithm based on decomposition. Trans. Evol. Comput. 2008, 11, 712–731. [Google Scholar] [CrossRef]
- Lingling, L.; Weiming, S. An improved NSGA-II with local search for multi-objective integrated production and inventory scheduling problem. J. Manuf. Syst. 2023, 68, 99–116. [Google Scholar]
- Gadhvi, B.; Savsani, V.; Patel, V. Multi-Objective Optimization of Vehicle Passive Suspension System Using NSGA-II, SPEA2 and PESA-II. Procedia Technol. 2016, 23, 361–368. [Google Scholar] [CrossRef]
- Gao, W.F.; Liu, L.L.; Wang, Z.K.; Gong, M.G. Survey on Multi-objective Optimization Evolutionary Algorithm Based on Decomposition. J. Softw. 2023, 34, 4743–4771. [Google Scholar]
- Samir, M.; Brahim, N. Improved Memetic NSGA-II Using a Deep Neighborhood Search. Int. J. Appl. Metaheuristic Comput. (IJAMC) 2021, 12, 138–154. [Google Scholar]
- Dhiman, G.; Soni, M.; Pandey, H.M.; Slowik, A.; Kaur, H. A novel hybrid hypervolume indicator and reference vector adaptation strategies based evolutionary algorithm for many-objective optimization. Eng. Comput. 2020, 37, 3017–3035. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multi objective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach. Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Feng, S.M.; Wang, X.K.; Sun, X.L. Multi-objective Shortest Path Algorithm Based on Road Section Assignment Method. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2018, 37, 87–92. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]

| Mine ID | Pe | Ce | te | Q0 | Qzi | Qe | β | Ge | d | CWu | CLu | CVu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 26 | 12.50 | 10.76 | 1401.94 | 9943 | 500 | 0.07 | 0.6636 | 0.11 | 1429.03 | 12.49 | 117.8 |
| A2 | 26 | 11.80 | 16.20 | 1853.64 | 16,241 | 600 | 0.09 | 0.7343 | 0.11 | 2137.93 | 7.26 | 123.55 |
| A3 | 26 | 11.30 | 5.61 | 420.28 | 2881 | 300 | 0.07 | 0.7162 | 0.11 | 1201.34 | 6.23 | 37.78 |
| A4 | 26 | 12.20 | 20.69 | 2234.67 | 20,692.8 | 600 | 0.09 | 0.7359 | 0.11 | 2855.61 | 6.36 | 131.27 |
| A5 | 26 | 12.40 | 13.58 | 1641.83 | 13,912 | 600 | 0.08 | 0.7188 | 0.11 | 2133.82 | 4.25 | 47.86 |
| A6 | 26 | 10.90 | 7.52 | 369.28 | 3507 | 300 | 0.09 | 0.7896 | 0.11 | 914.82 | 4.58 | 31.41 |
| A7 | 26 | 11.70 | 1.49 | 109.59 | 785 | 300 | 0.07 | 0.7004 | 0.11 | 831.44 | 8.68 | 11.58 |
| A8 | 26 | 11.60 | 6.50 | 685.49 | 5651 | 500 | 0.08 | 0.7056 | 0.11 | 1428.82 | 10.00 | 59.71 |
| A9 | 26 | 12.10 | 10.71 | 1063.08 | 9317 | 500 | 0.09 | 0.7049 | 0.11 | 1747.87 | 7.26 | 61.81 |
| A10 | 26 | 13.00 | 5.87 | 395.87 | 3130 | 300 | 0.08 | 0.6897 | 0.11 | 1163.83 | 6.75 | 37.71 |
| A11 | 26 | 11.80 | 5.80 | 89.40 | 1322 | 150 | 0.07 | 0.8065 | 0.11 | 548.54 | 2.71 | 11.37 |
| Algorithm | NSGAII | NSGAIII | IBEA | MOEA/D |
|---|---|---|---|---|
| Average run time (seconds) | 2.3426 | 2.3184 | 1.9299 | 7.6950 |
| Max run time (seconds) | 2.7829 | 2.8466 | 2.1393 | 8.2502 |
| Minimum run time (seconds) | 1.9639 | 1.7940 | 1.8012 | 6.0301 |
| Algorithm | NSGAII | NSGAIII | IBEA | MOEA/D |
|---|---|---|---|---|
| Mean value | 0.5763 | 0.6112 | 0.6163 | 0.5636 |
| Maximum value | 0.5815 | 0.6116 | 0.6181 | 0.5602 |
| Minimum value | 0.5752 | 0.6107 | 0.6137 | 0.5684 |
| Algorithm | NSGAII | NSGAIII | MOEA/D |
|---|---|---|---|
| t | 140.9142 | 18.1870 | 185.4677 |
| +/−/= | 0/1/0 | 0/1/0 | 0/1/0 |
| Frequency | Mining Sequence | NPV (Ten Thousand CNY) | CE (Ten Thousand CNY) |
|---|---|---|---|
| 1 | [2, 8, 6, 11, 7, 1, 10, 3, 9, 5, 4] | 72,837.10 | 17,904.32 |
| 2 | [2, 8, 1, 6, 7, 11, 3, 5, 10, 4, 9] | 74,218.36 | 18,205.73 |
| 3 | [7, 6, 8, 11, 1, 3, 10, 2, 5, 4, 9] | 45,351.29 | 9401.39 |
| 4 | [2, 7, 6, 8, 11, 3, 1, 10, 9, 5, 4] | 71,382.48 | 17,623.26 |
| 5 | [2, 4, 5, 8, 9, 1, 7, 6, 3, 10, 11] | 76,969.05 | 20,537.86 |
| 6 | [8, 7, 2, 1, 6, 5, 11, 3, 10, 9, 4] | 67,177.58 | 14,942.93 |
| 7 | [2, 8, 5, 1, 6, 11, 7, 10, 3, 9, 4] | 75,589.89 | 18,739.96 |
| 8 | [8, 1, 7, 6, 2, 11, 10, 3, 9, 5, 4] | 61,810.01 | 12,898.58 |
| 9 | [6, 11, 8, 1, 2, 7, 5, 10, 3, 9, 4] | 42,743.39 | 9088.22 |
| 10 | [8, 1, 7, 6, 11, 2, 5, 10, 3, 9, 4] | 60,558.91 | 12,585.33 |
| 11 | [8, 1, 2, 6, 5, 11, 7, 3, 10, 9, 4] | 65,250.29 | 13,938.52 |
| 12 | [8, 6, 1, 7, 11, 5, 3, 10, 2, 9, 4] | 56,558.60 | 11,663.78 |
| 13 | [7, 6, 8, 1, 11, 2, 5, 10, 3, 9, 4] | 48,805.60 | 10,093.20 |
| 14 | [8, 1, 2, 4, 5, 9, 6, 7, 3, 10, 11] | 65,947.79 | 14,329.89 |
| 15 | [8, 7, 6, 11, 10, 1, 3, 2, 9, 5, 4] | 51,862.29 | 10,772.25 |
| 16 | [8, 7, 6, 1, 11, 3, 10, 9, 5, 2, 4] | 55,226.73 | 11,329.15 |
| 17 | [8, 7, 6, 1, 2, 5, 9, 3, 11, 10, 4] | 57,908.97 | 11,976.25 |
| 18 | [8, 7, 1, 2, 11, 6, 10, 3, 9, 5, 4] | 62,829.57 | 13,299.63 |
| 19 | [8, 2, 7, 6, 11, 1, 4, 5, 10, 9, 3] | 68,249.21 | 15,412.39 |
| 20 | [7, 6, 11, 8, 1, 10, 3, 2, 5, 9, 4] | 41,303.32 | 8693.17 |
| 21 | [8, 7, 1, 6, 11, 2, 10, 3, 9, 5, 4] | 59,303.26 | 12,276.03 |
| 22 | [11, 6, 8, 7, 1, 3, 10, 9, 2, 4, 5] | 35,915.25 | 7916.81 |
| 23 | [7, 11, 6, 8, 1, 2, 5, 4, 9, 3, 10] | 37,654.17 | 8202.56 |
| 24 | [8, 1, 7, 2, 6, 11, 10, 3, 9, 5, 4] | 64,086.60 | 13,597.17 |
| 25 | [7, 8, 6, 1, 11, 10, 2, 3, 4, 9, 5] | 53,727.84 | 11,042.56 |
| 26 | [11, 7, 6, 10, 3, 8, 1, 9, 5, 2, 4] | 31,986.55 | 7493.33 |
| 27 | [8, 2, 1, 6, 7, 9, 11, 3, 5, 10, 4] | 69,594.78 | 15,673.73 |
| 28 | [6, 8, 11, 7, 1, 2, 10, 3, 9, 5, 4] | 46,865.97 | 9763.18 |
| 29 | [6, 8, 1, 11, 7, 2, 5, 10, 3, 9, 4] | 50,252.58 | 10,435.11 |
| 30 | [8, 2, 5, 7, 1, 6, 11, 10, 3, 4, 9] | 70,735.18 | 16,157.01 |
| Mining Sequence | Optimization Plan 1 | Optimization Plan 2 | ||||
|---|---|---|---|---|---|---|
| Mine ID | NPV (Ten Thousand CNY) | CE (Ten Thousand CNY) | Mine ID | NPV (Ten Thousand CNY) | CE (Ten Thousand CNY) | |
| 1 | A2 | 63,159.51 | 15,905.97 | A2 | 63,159.51 | 15,905.97 |
| 2 | A4 | 12,289.44 | 4247.36 | A5 | 10,372.12 | 2717.50 |
| 3 | A5 | 1196.48 | 313.54 | A8 | 1442.18 | 288.57 |
| 4 | A8 | 170.96 | 34.22 | A4 | 1512.09 | 522.55 |
| 5 | A9 | 111.27 | 28.11 | A1 | 108.35 | 23.14 |
| 6 | A1 | 35.48 | 7.58 | A9 | 6.24 | 9.15 |
| 7 | A6 | 6.25 | 1.27 | A6 | 6.25 | 1.27 |
| 8 | A3 | 2.25 | 0.62 | A7 | 0.71 | 0.14 |
| 9 | A7 | 0.40 | 0.08 | A3 | 1.93 | 0.53 |
| 10 | A10 | 0.98 | 0.29 | A10 | 0.98 | 0.29 |
| 11 | A11 | 0.29 | 0.07 | A11 | 0.29 | 0.07 |
| Sum | 76,973.31 | 20,539.11 | 76,640.65 | 19,469.18 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, L.; Zeng, Y.; Zheng, M. Optimization of Mining Sequence for Ion-Adsorbed Rare Earth Mining Districts Incorporating Environmental Costs. Sustainability 2025, 17, 6871. https://doi.org/10.3390/su17156871
Yi L, Zeng Y, Zheng M. Optimization of Mining Sequence for Ion-Adsorbed Rare Earth Mining Districts Incorporating Environmental Costs. Sustainability. 2025; 17(15):6871. https://doi.org/10.3390/su17156871
Chicago/Turabian StyleYi, Lu, Yi Zeng, and Minggui Zheng. 2025. "Optimization of Mining Sequence for Ion-Adsorbed Rare Earth Mining Districts Incorporating Environmental Costs" Sustainability 17, no. 15: 6871. https://doi.org/10.3390/su17156871
APA StyleYi, L., Zeng, Y., & Zheng, M. (2025). Optimization of Mining Sequence for Ion-Adsorbed Rare Earth Mining Districts Incorporating Environmental Costs. Sustainability, 17(15), 6871. https://doi.org/10.3390/su17156871






