Assessing the Hazard of Flooding from Breaching of the Alacranes Dam in Villa Clara, Cuba
Abstract
1. Introduction
2. Materials and Methods
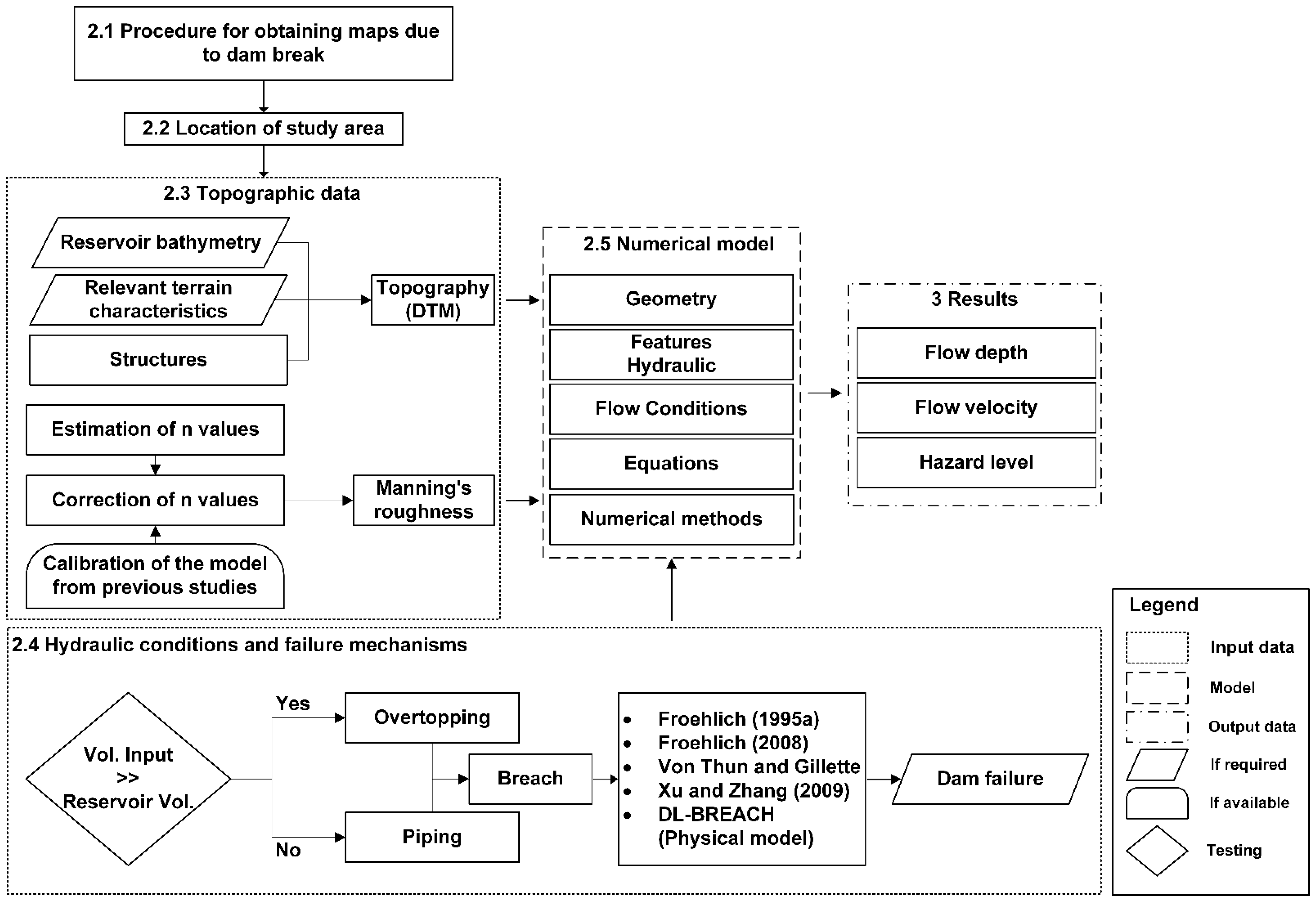
2.1. Procedure for Obtaining Maps for Reservoir Failure
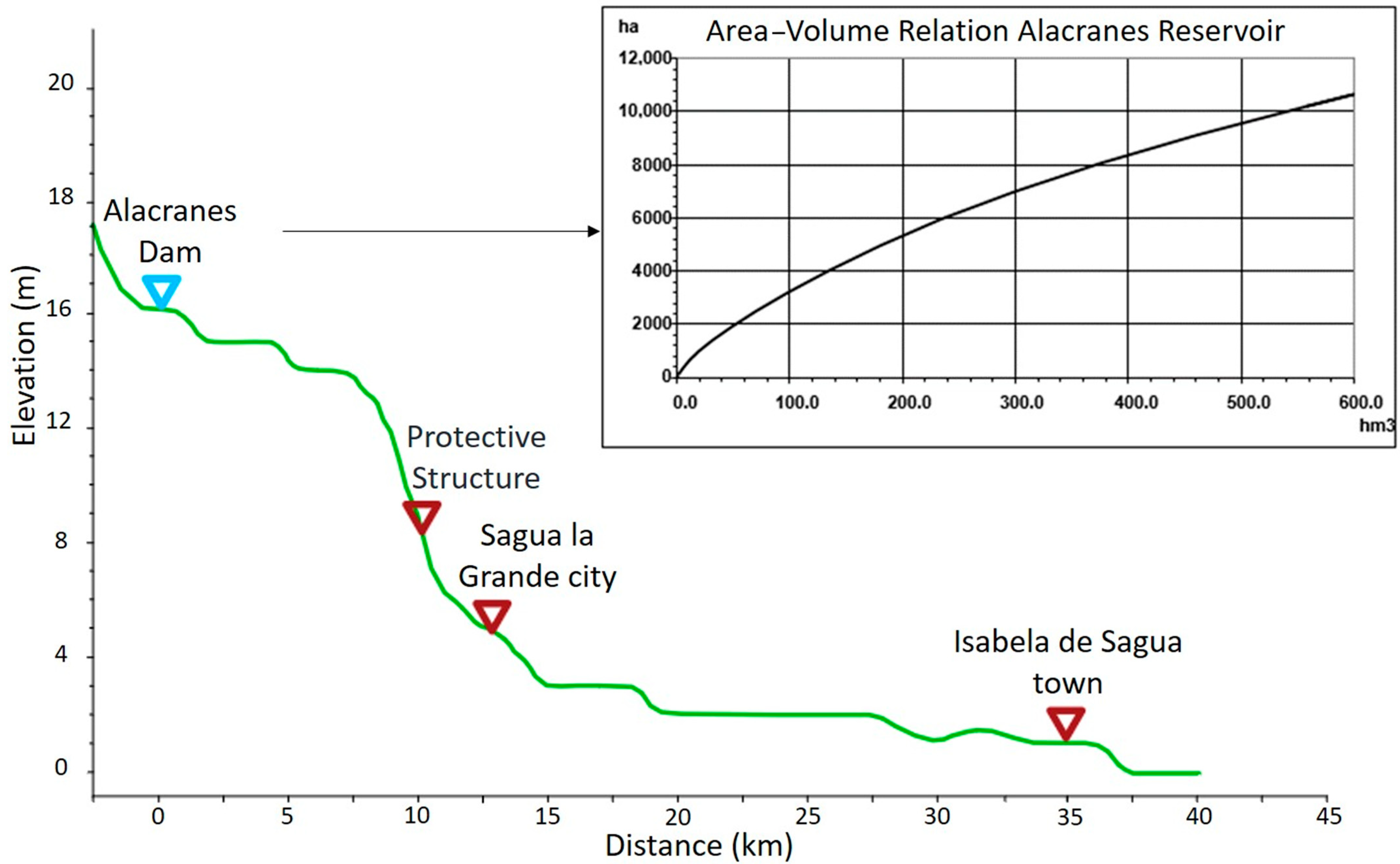
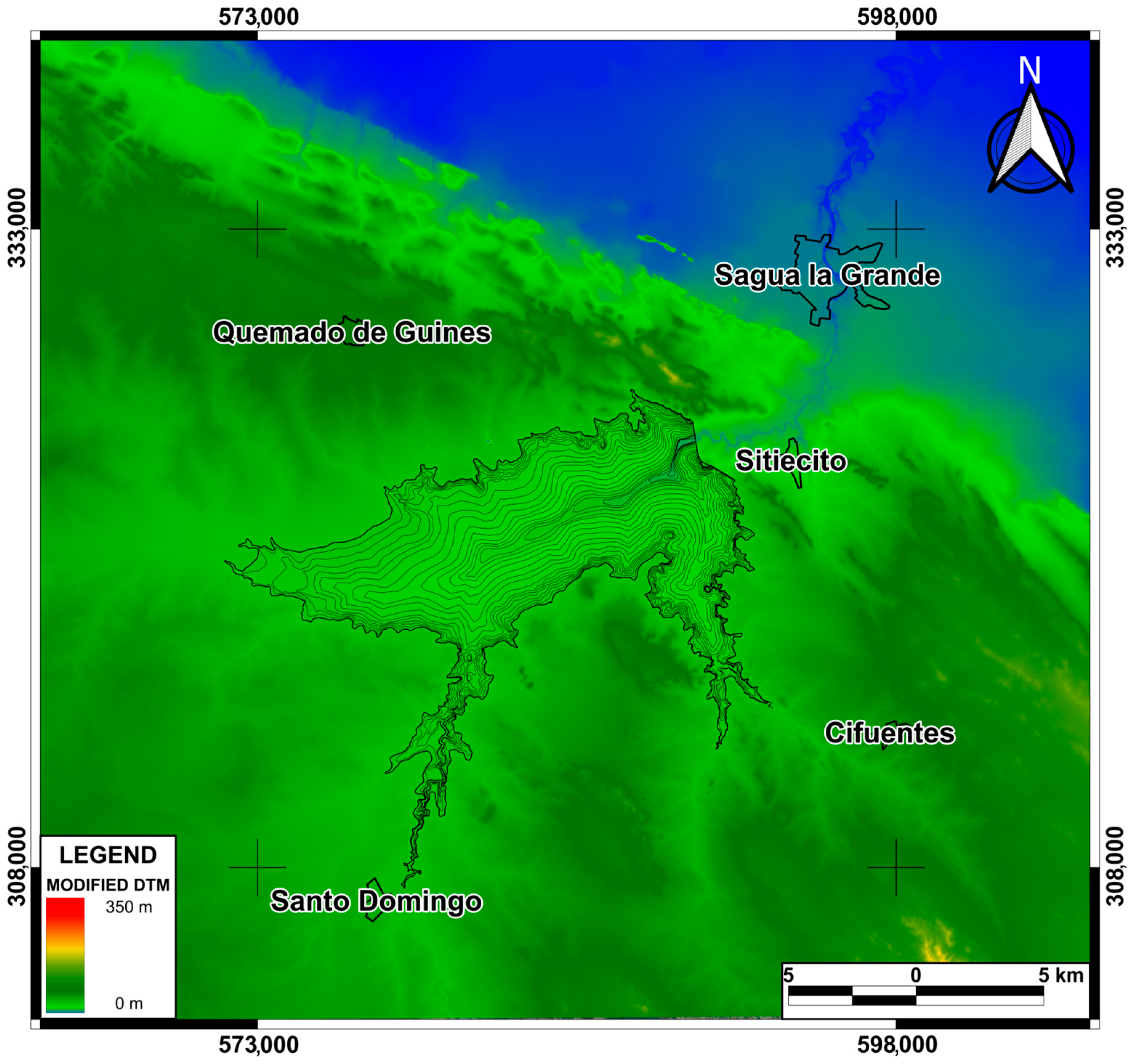
2.2. Location of Study Area
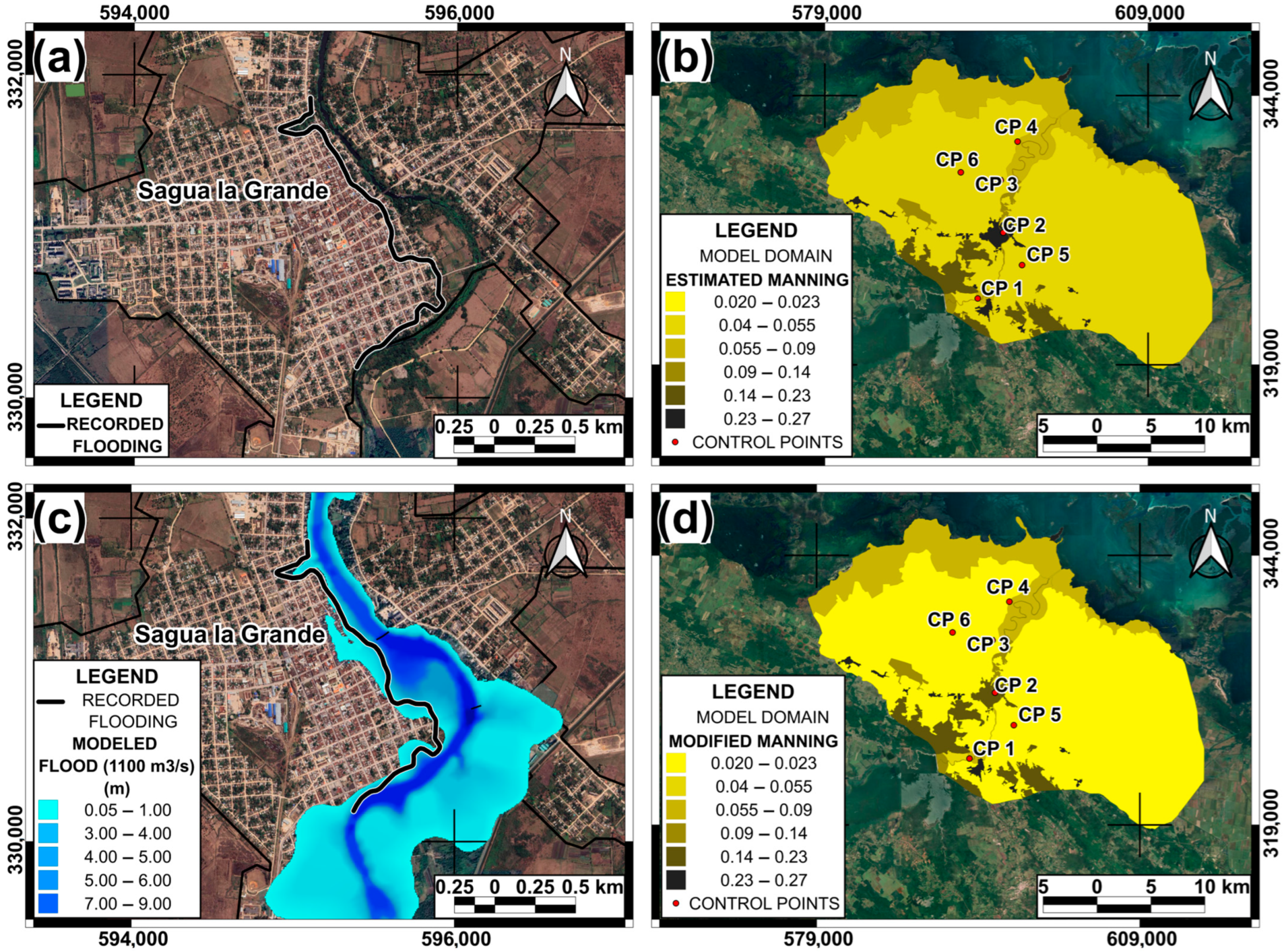
2.3. Topographic Data
2.4. Hydraulic Conditions and Failure Mechanisms
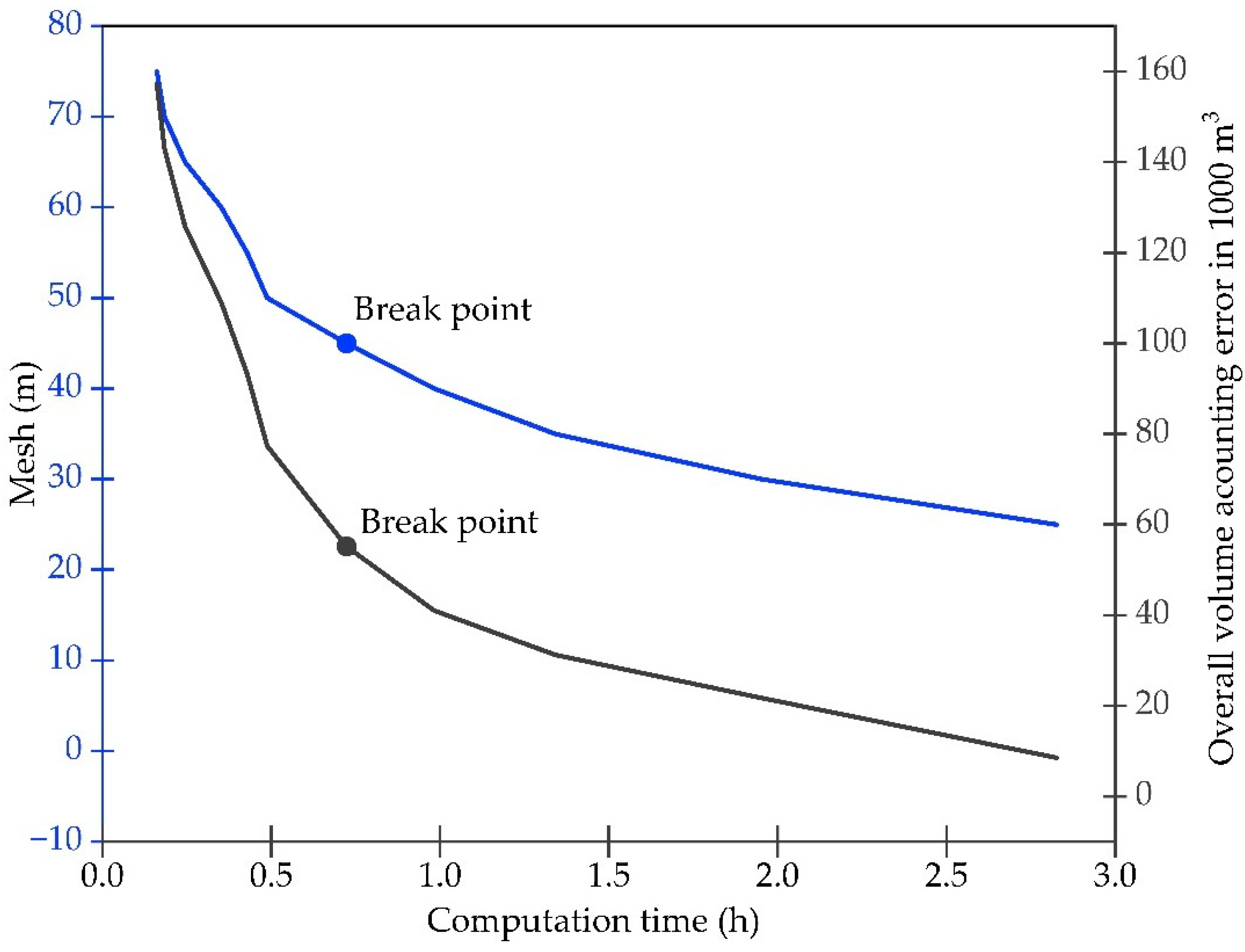
2.5. Numerical Model
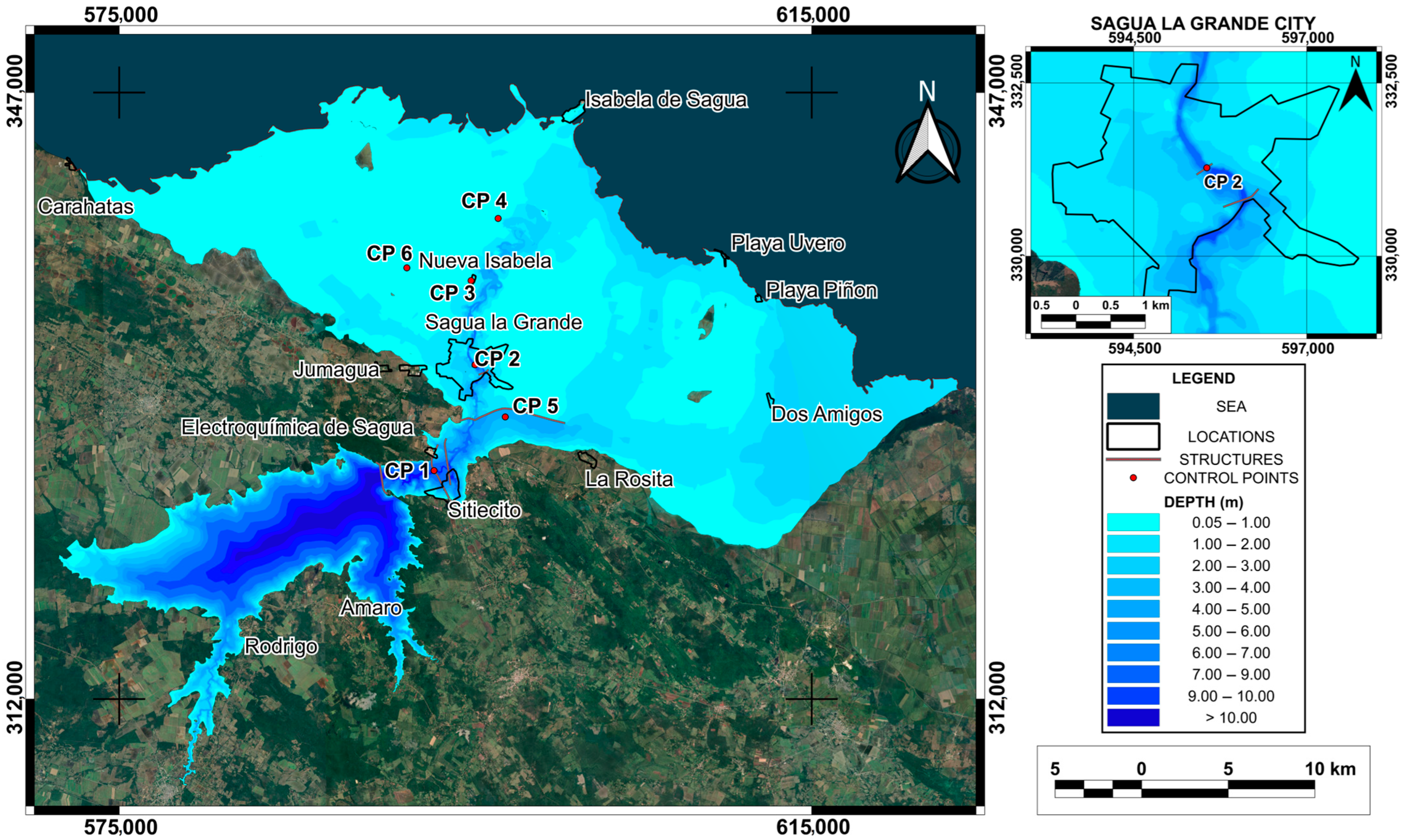
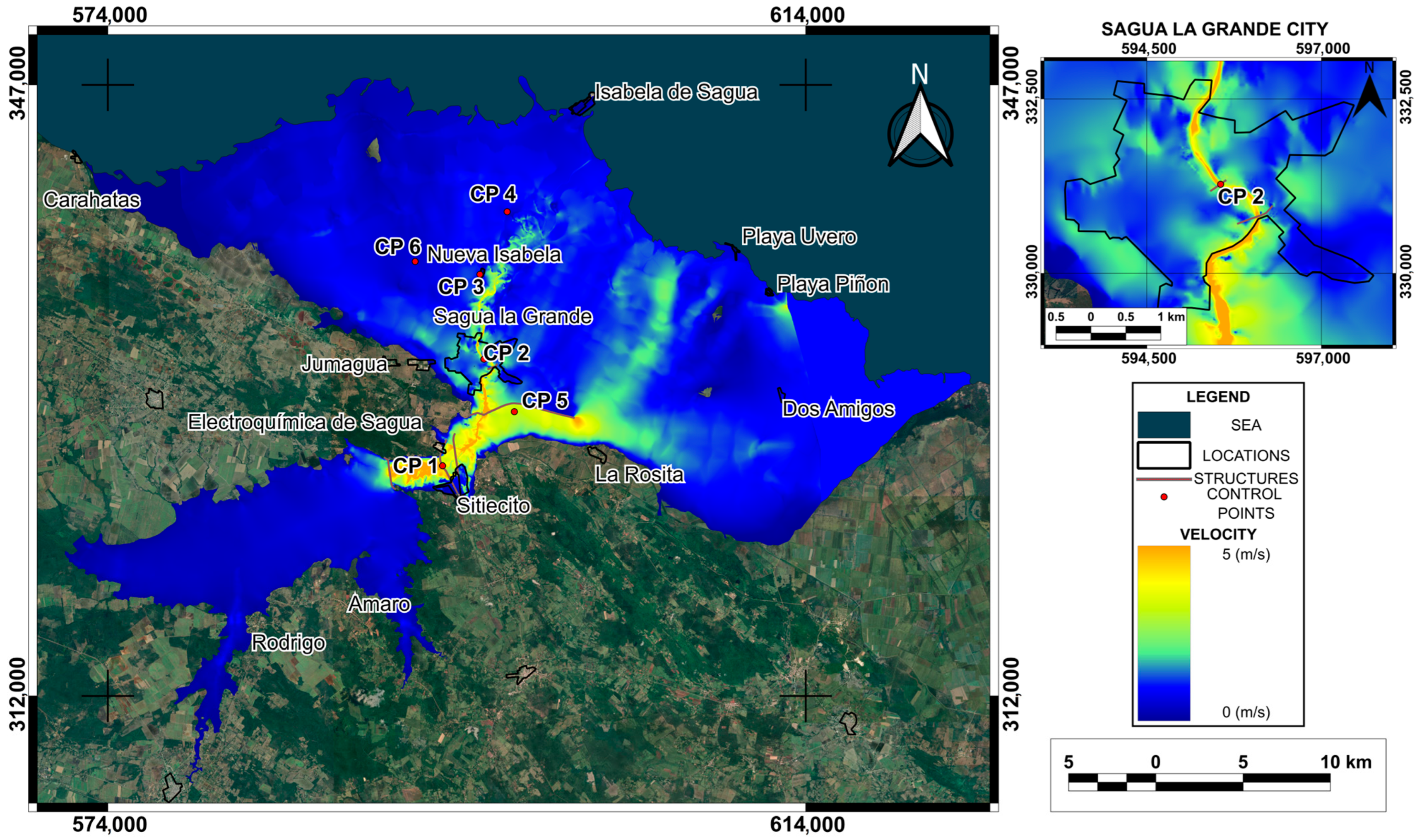
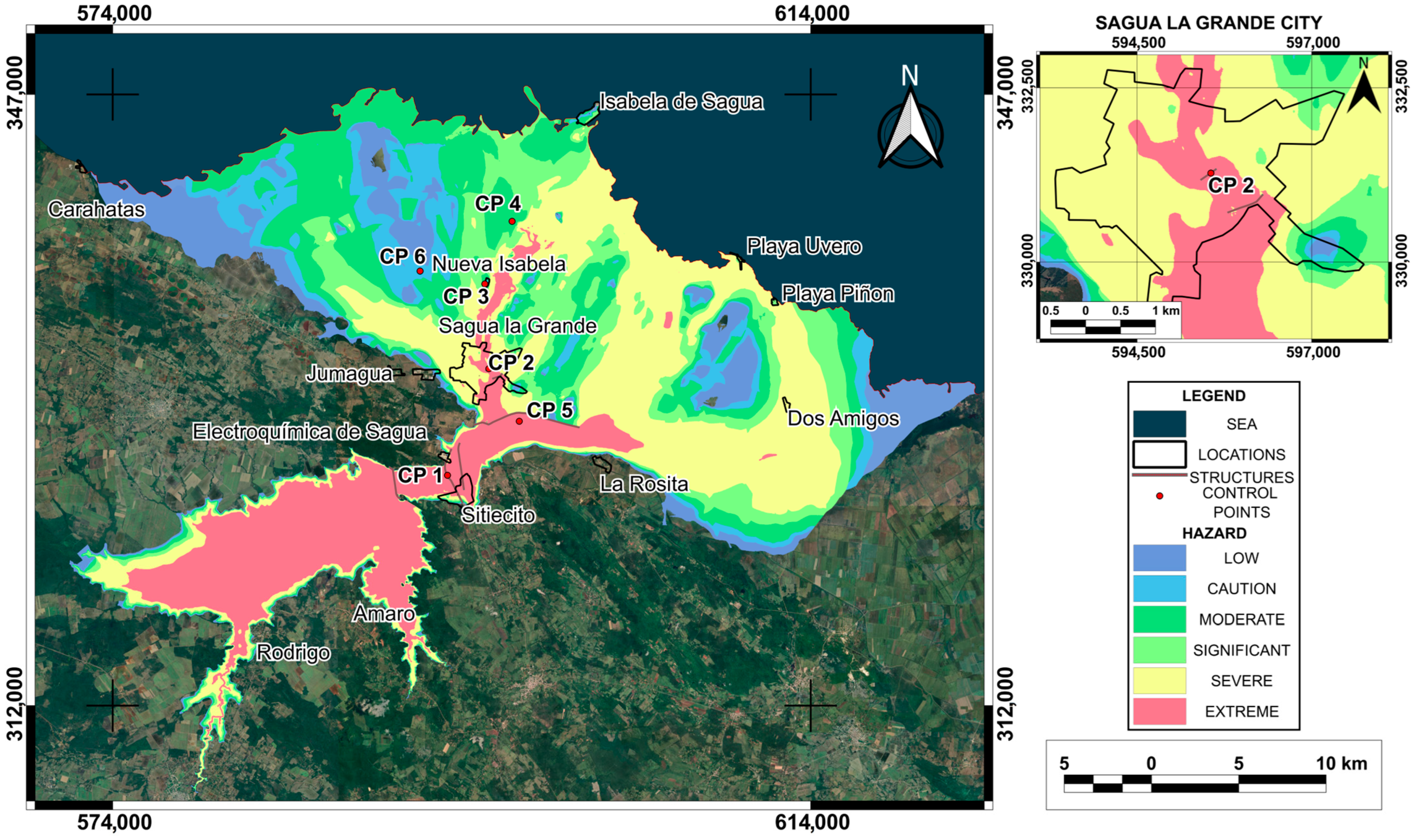
3. Results
4. Discussion
5. Conclusions
- Dam safety management: The hazard maps produced offer a valuable tool to assess the vulnerability of critical infrastructure and downstream communities. They can guide maintenance and reinforcement decisions for the Alacranes dam, thereby minimizing failure hazard. These results underscore the need to incorporate modeling studies into local hazard management policies, particularly in regions where hydraulic infrastructure dates back several decades and population exposure has grown significantly over time.
- Early warning system planning: The flood-wave arrival times identified in this study (some as short as less than two hours) are critical for designing realistic evacuation drills and improving coordination among institutions responsible for civil defense. These findings can inform the development of effective early warning protocols, ensuring communities receive timely alerts and have sufficient lead time to respond in the event of a dam failure.
- Regional risk mitigation: The findings pinpoint high-hazard zones in the city of Sagua La Grande, helping to prioritize investments in mitigation measures such as upgrades to drainage infrastructure and coastal defenses. By pinpointing the most hazardous zones (such as the urban area of Sagua La Grande) this analysis enables authorities to concentrate efforts on communities situated near aging, outdated earth dams where the risk is most imminent. For the first time, depth, velocity, and hazard maps have been produced for the areas downstream of the Alacranes dam in Cuba. However, the value of this study extends well beyond the local scale. By adapting robust methodologies to a data-limited context (e.g., in the absence of detailed bathymetry and high-resolution datasets), this work offers a replicable methodological framework. In practice, it demonstrates to authorities in other regions with similar constraints that it is feasible to develop precise, actionable risk-assessment tools. Consequently, rather than serving merely as a case study, this research provides a blueprint for strengthening emergency planning and resilience in vulnerable communities worldwide.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fattorelli, S.; Fernández, P.C. Diseño Hidrológico, 2nd ed.; WASA-GN: Madrid, Spain, 2011; p. 379. [Google Scholar]
- Costa, J.E. Floods from Dam Failures; 85-560; US. Geological Survey: Denver, CO, USA, 1985; pp. 9–11.
- USACE. HEC-RAS Hydraulic Reference Manual, 6.3; US Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2022.
- Chaudhry, M.H.; Mays, L. Computer Modeling of Free-Surface and Pressurized Flows; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Mourad, Y. Searchers Look for More Than 10,000 Missing in Flooded Libyan City Where Death Toll Eclipsed 11,000. Available online: https://apnews.com/article/libya-floods-derna-storm-daniel-mass-graves-72307547f3e0ff4fbf715a7f64c69383 (accessed on 24 June 2024).
- Aureli, F.; Maranzoni, A.; Petaccia, G. Review of Historical Dam-Break Events and Laboratory Tests on Real Topography for the Validation of Numerical Models. Water 2021, 13, 1968. [Google Scholar] [CrossRef]
- USACE. HEC-RAS 2D User’s Manual, 6.3; US Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2022.
- Bellos, V.; Tsakiris, V.K.; Kopsiaftis, G.; Tsakiris, G. Propagating Dam Breach Parametric Uncertainty in a River Reach Using the HEC-RAS Software. Hydrology 2020, 7, 72. [Google Scholar] [CrossRef]
- Froehlich David, C. Peak Outflow from Breached Embankment Dam. J. Water Resour. Plan. Manag. 1995, 121, 90–97. [Google Scholar] [CrossRef]
- Froehlich David, C. Embankment Dam Breach Parameters Revisited. In Proceedings of the First International Conference, Water Resource Engineering, Environmental and Water Resources Institute ASCE, Water Resources Engineering Proceedings, San Antonio, TX, USA, 14–18 August 1995. [Google Scholar]
- Froehlich David, C. Embankment Dam Breach Parameters and Their Uncertainties. J. Hydraul. Eng. 2008, 134, 1708–1721. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.M. Breaching Parameters for Earth and Rockfill Dams. J. Geotech. Geoenviron. Eng. 2009, 135, 1957–1970. [Google Scholar] [CrossRef]
- USACE. HEC-RAS User’s Manual, 6.3; US Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2022.
- Peramuna, P.D.P.O.; Neluwala, N.G.P.B.; Wijesundara, K.K.; DeSilva, S.; Venkatesan, S.; Dissanayake, P.B.R. Review on model development techniques for dam break flood wave propagation. WIREs Water 2024, 11, e1688. [Google Scholar] [CrossRef]
- Socas, R.A.; González, M.A.; Marín, Y.R.; Castillo-García, C.L.; Jiménez, J.; da Silva, L.D.; González-Rodríguez, L. Simulating the Flood Limits of Urban Rivers Embedded in the Populated City of Santa Clara, Cuba. Water 2023, 15, 1805. [Google Scholar] [CrossRef]
- Albu, L.-M.; Enea, A.; Iosub, M.; Breabăn, I.-G. Dam Breach Size Comparison for Flood Simulations. A HEC-RAS Based, GIS Approach for Drăcșani Lake, Sitna River, Romania. Water 2020, 12, 1090. [Google Scholar] [CrossRef]
- Marangoz, H.O.; Anilan, T. Two-dimensional modeling of flood wave propagation in residential areas after a dam break with application of diffusive and dynamic wave approaches. Nat. Hazards 2022, 110, 429–449. [Google Scholar] [CrossRef]
- Ongdas, N.; Akiyanova, F.; Karakulov, Y.; Muratbayeva, A.; Zinabdin, N. Application of HEC-RAS (2D) for Flood Hazard Maps Generation for Yesil (Ishim) River in Kazakhstan. Water 2020, 12, 2672. [Google Scholar] [CrossRef]
- Pilotti, M.; Milanesi, L.; Bacchi, V.; Tomirotti, M.; Maranzoni, A. Dam-Break Wave Propagation in Alpine Valley with HEC-RAS 2D: Experimental Cancano Test Case. J. Hydraul. Eng. 2020, 146, 05020003. [Google Scholar] [CrossRef]
- El Bilali, A.; Taleb, I.; Nafii, A.; Taleb, A. A practical probabilistic approach for simulating life loss in an urban area associated with a dam-break flood. Int. J. Disaster Risk Reduct. 2022, 76, 103011. [Google Scholar] [CrossRef]
- Mao, J.; Wang, S.; Ni, J.; Xi, C.; Wang, J. Management System for Dam-Break Hazard Mapping in a Complex Basin Environment. ISPRS Int. J. Geo-Inf. 2017, 6, 162. [Google Scholar] [CrossRef]
- Luke, A.; Mahajan, R.; Pilotti, M.; Ruebel, M.; Pasternack, G.; Faries, J.; Rosen, D.; Holmes, R.; Ahmad, M. Flood Hazard Maps Based on 2D Modeling. Available online: https://collaborate.asce.org/waterforum/discussion/flood-hazard-maps-based-on-2d-modeling-1 (accessed on 23 May 2017).
- Morejón, S.M.; Haramboure, Y.G.; Rodríguez, O.Á. Comportamiento de las fallas de presas de materiales sueltos en Cuba. In Proceedings of the 18 Convención Científica de Ingeniería y Arquitectura, Palacio de las Convenciones de La Habana, La Habana, Cuba, 7–11 November 2016. [Google Scholar]
- Flores Berenguer, I.; Castro Martínez, I.; García Tristá, J.; González Haramboure, Y. Influencia de la permeabilidad del suelo no saturado en los taludes de presas de tierra. Ing. Hidráulica Y Ambient. 2019, 40, 86–100. [Google Scholar]
- Flores Berenguer, I.; García Tristá, J.; Haramboure, Y.G. Estabilidad de taludes durante un desembalse rápido en presas de tierra con suelos parcialmente saturados. Ing. Y Desarro. 2020, 38, 13–31. [Google Scholar] [CrossRef]
- González Haramboure, Y.; Flores Berenguer, I.; García Tristá, J. Efecto de desembalse en la estabilidad de presas de tierra: Dos casos de estudio en Cuba. Ing. Hidráulica Y Ambiental. 2021, 42, 42–53. [Google Scholar]
- Urquiza-López, Y.M.; Galbán-Rodriguez, L.; Nápoles-Fajardo, N.; Chuy-Rodríguez, T.J. El impacto de fenómenos geoambientales en cortinas de presas de tierra en Cuba. Ciencia en su PC 2017, 1, 56–69. [Google Scholar]
- NC 1239-2018; Especificaciones Para el Diseño y Construcción de Alcantarillado Sanitario y Drenaje Pluvial Urbano. Oficina Nacional de Normalización (ONN): La Habana, Cuba, 2018.
- Stucchi, L.; Bignami, D.F.; Bocchiola, D.; Del Curto, D.; Garzulino, A.; Rosso, R. Assessment of Climate-Driven Flood Risk and Adaptation Supporting the Conservation Management Plan of a Heritage Site. The National Art Schools of Cuba. Climate 2021, 9, 23. [Google Scholar] [CrossRef]
- Ferrari, A.; Vacondio, R.; Mignosa, P. High-resolution 2D shallow water modelling of dam failure floods for emergency action plans. J. Hydrol. 2023, 618, 129192. [Google Scholar] [CrossRef]
- Wu, W. Simplified Physically Based Model of Earthen Embankment Breaching. J. Hydraul. Eng. 2013, 139, 837–851. [Google Scholar] [CrossRef]
- NSW; DPIE. Flood Risk Management Committee Handbook: A Guide for Committee Members; State of NSW and Department of Planning Industry and Environment: Parramatta, Australia, 2019. [Google Scholar]
- Mo, C.; Shen, Y.; Lei, X.; Ban, H.; Ruan, Y.; Lai, S.; Cen, W.; Xing, Z. Simulation of one-dimensional dam-break flood routing based on HEC-RAS. Front. Earth Sci. 2023, 10, 1027788. [Google Scholar] [CrossRef]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; No. 2339; USGPO: Washington, DC, USA, 1989.
- Te Chow, V.; Saldarriaga, J.G. Hidráulica de Canales Abiertos; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Kiwanuka, M.; Chelangat, C.; Mubialiwo, A.; Lay, F.J.; Mugisha, A.; Mbujje, W.J.; Mutanda, H.E. Dam breach analysis of Kibimba Dam in Uganda using HEC-RAS and HEC-GeoRAS. Environ. Syst. Res. 2023, 12, 31. [Google Scholar] [CrossRef]
- Mohamed, M.J.; Karim, I.R.; Fattah, M.Y.; Al-Ansari, N. Modelling Flood Wave Propagation as a Result of Dam Piping Failure Using 2D-HEC-RAS. Civ. Eng. J. 2023, 9, 2503–2515. [Google Scholar] [CrossRef]
- Paşa, Y.; Peker, İ.B.; Hacı, A.; Gülbaz, S. Dam failure analysis and flood disaster simulation under various scenarios. Water Sci. Technol. 2023, 87, 1214–1231. [Google Scholar] [CrossRef] [PubMed]
- NC 974-2013; Presas, Diques de Protección, Canales y Obras Asociadas. Categorías Para Nuevos Proyectos o Para el Rediseño de Estructuras Existentes en un Escenario de Cambio Climático Cambiante. Oficina Nacional de Normalización (ONN): La Habana, Cuba, 2013.
- WikiSysop. Localidades de Sagua la Grande, Quemado de Güines y Encrucijada. 2009. EcuRed. Sagua La Grande. Available online: https://www.ecured.cu/Sagua_la_Grande#Consejos_populares (accessed on 10 October 2024).
- Latrubesse, E.M.; Park, E.; Sieh, K.; Dang, T.; Lin, Y.N.; Yun, S.-H. Dam failure and a catastrophic flood in the Mekong basin (Bolaven Plateau), southern Laos, 2018. Geomorphology 2020, 362, 107221. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Hidrología Aplicada; Suárez, M.E., Ed.; McGraw-Hill Interamericana: Bogotá, Colombia, 1994. [Google Scholar]
- Gaagai, A.; Aouissi, H.A.; Krauklis, A.E.; Burlakovs, J.; Athamena, A.; Zekker, I.; Boudoukha, A.; Benaabidate, L.; Chenchouni, H. Modeling and Risk Analysis of Dam-Break Flooding in a Semi-Arid Montane Watershed: A Case Study of the Yabous Dam, Northeastern Algeria. Water 2022, 14, 767. [Google Scholar] [CrossRef]
- Al-Salahat, M.; Al-Weshah, R.; Al-Omari, S. Dam break risk analysis and flood inundation mapping: A case study of Wadi Al-Arab Dam. Sustain. Water Resour. Manag. 2024, 10, 74. [Google Scholar] [CrossRef]
- Al-Weshah, R.; Tarawneh, A.; Al-Salahat, M. Dam Breach Risk Analysis and Mapping: A Case Study of the Wala Dam, Jordan. Jordan J. Civ. Eng. 2025, 19, 115–127. [Google Scholar] [CrossRef]
- Eldeeb, H.; Mowafy, M.H.; Salem, M.N.; Ibrahim, A. Flood propagation modeling: Case study the Grand Ethiopian Renaissance dam failure. Alex. Eng. J. 2023, 71, 227–237. [Google Scholar] [CrossRef]
- DWR; SDSOD. California Dam Breach Inundation Maps. Available online: https://fmds.water.ca.gov/maps/damim/ (accessed on 6 March 2025).
| Point Name | Modified Manning’s Coefficient | 0 Variation Manning’s Roughness Coefficient | −20% Variation Manning’s Roughness Coefficient | +20% Variation Manning’s Roughness Coefficient | |||
|---|---|---|---|---|---|---|---|
| Depth (m) | Velocity (m/s) | Depth (m) | Velocity (m/s) | Depth (m) | Velocity (m/s) | ||
| CP1 | 0.074 | 8.41 | 1.35 | 7.95 | 1.57 | 8.82 | 1.21 |
| CP2 | 0.091 | 9.37 | 2.28 | 9.15 | 2.76 | 9.55 | 1.99 |
| CP3 | 0.029 | 0.20 | 0.21 | 0.17 | 0.22 | 0.23 | 0.2 |
| CP4 | 0.056 | 0.52 | 0.36 | 0.45 | 0.41 | 0.57 | 0.31 |
| CP5 | 0.029 | 0.69 | 1.04 | 0.51 | 1.05 | 0.85 | 1.00 |
| CP6 | 0.029 | 0.24 | 0.39 | 0.20 | 0.43 | 0.27 | 0.36 |
| Scenarios | Formulation | Type of Dam Failure |
|---|---|---|
| Scenario 1 | Froehlich David [9] | Overtopping |
| Scenario 2 | Froehlich David [11] | |
| Scenario 3 | Von Thun and Gillette (1990) A * | |
| Scenario 4 | Von Thun and Gillette (1990) B * | |
| Scenario 5 | Von Thun and Gillette (1990) C * | |
| Scenario 6 | Xu and Zhang [12] | |
| Scenario 7 | Froehlich David [9] | Piping |
| Scenario 8 | Froehlich David [11] | |
| Scenario 9 | Von Thun and Gillette (1990) A * | |
| Scenario 10 | Von Thun and Gillette (1990) B * | |
| Scenario 11 | Von Thun and Gillette (1990) C * | |
| Scenario 12 | Xu and Zhang [12] | |
| Scenario 13 | HEC RAS Physical model [30] | Overtopping |
| Scenarios | Type of Failures | Breach Bottom Width (m) | Breach Development Time (h) | Running Time | Overall Volume Accounting Error | Qmax (m3/s) | Courant Coefficient | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| h | min | s | 1000 m3 | % | Max | Min | |||||
| Scenario 1 | Overtopping | 345.0 | 11.88 | 32 | 26 | 2 | 21,303.00 | 2.352 | 19,505 | 1 | 0.45 |
| Scenario 2 | 311.0 | 10.34 | 19 | 3 | 8 | 94.44 | 0.011 | 19,893 | |||
| Scenario 3 | 100.4 | 0.50 | 26 | 32 | 12 | 71.60 | 0.008 | 13,480 | |||
| Scenario 4 | 100.4 | 1.00 | 27 | 13 | 14 | 76.85 | 0.009 | 12,983 | |||
| Scenario 5 | 95.0 | 0.65 | 13 | 14 | 9 | 34.07 | 0.004 | 15,184 | |||
| Scenario 6 | 207.0 | 11.71 | 31 | 51 | 59 | 89.96 | 0.010 | 15,553 | |||
| Scenario 7 | Piping | 171.0 | 6.69 | 23 | 50 | 14 | 93.14 | 0.020 | 12,423 | ||
| Scenario 8 | 166.0 | 6.02 | 15 | 17 | 37 | 85.00 | 0.018 | 11,291 | |||
| Scenario 9 | 90.0 | 0.40 | 19 | 55 | 27 | 55.38 | 0.012 | 6860 | |||
| Scenario 10 | 90.0 | 1.20 | 20 | 15 | 7 | 50.58 | 0.011 | 7064 | |||
| Scenario 11 | 85.0 | 0.57 | 18 | 58 | 40 | 59.86 | 0.013 | 8122 | |||
| Scenario 12 | 109.0 | 9.70 | 26 | 46 | 36 | 66.49 | 0.014 | 8297 | |||
| Scenario 13 | Overtopping | 350.0 | 0.67 | 31 | 29 | 40 | 22,928.00 | 2.531 | 35,726 | ||
| Scenarios | Type of Failures | TFA (km2) | MWD (CP1) (m) | MWV (CP1) (m/s) | FAT (CP2) (h) | RET (h) | TTF (h) | AWV (CP2) (m/s) |
|---|---|---|---|---|---|---|---|---|
| Scenario 1 | Overtopping | 595.7 | 10.76 | 3.46 | 1.67 | 40.00 | 26.66 | 2.57 |
| Scenario 2 | 594.1 | 10.80 | 3.42 | 1.67 | 34.00 | 29.00 | 2.50 | |
| Scenario 3 | 562.1 | 9.73 | 3.60 | 1.58 | 49.50 | 64.75 | 2.63 | |
| Scenario 4 | 561.5 | 9.68 | 3.38 | 1.67 | 49.50 | 64.00 | 2.94 | |
| Scenario 5 | 567.9 | 9.79 | 3.60 | 1.33 | 52.00 | 38.00 | 3.07 | |
| Scenario 6 | 585.1 | 10.16 | 3.32 | 1.83 | 46.00 | 29.34 | 2.60 | |
| Scenario 7 | Piping | 556.6 | 9.57 | 3.22 | 3.00 | 36.00 | 23.67 | 2.29 |
| Scenario 8 | 548.8 | 9.35 | 3.22 | 3.00 | 34.00 | 25.00 | 2.32 | |
| Scenario 9 | 501.7 | 8.48 | 3.31 | 2.67 | 49.50 | 34.66 | 2.74 | |
| Scenario 10 | 510.8 | 8.58 | 3.35 | 2.21 | 45.25 | 32.37 | 2.65 | |
| Scenario 11 | 519.9 | 8.69 | 3.40 | 1.75 | 41.00 | 30.08 | 2.56 | |
| Scenario 12 | 530.7 | 8.81 | 3.19 | 3.33 | 45.00 | 30.34 | 2.53 | |
| Scenario 13 | Overtopping | 604.6 | 12.47 | 5.55 | 1.33 | 43.67 | 23.34 | 3.21 |
| Flood Hazard Ratings | ||||||
|---|---|---|---|---|---|---|
| City or Locality | Low | Caution | Moderate | Significant | Severe | Extreme |
| Sagua La Grande | 1 | 1 | 3 | 5 | 61 | 30 |
| Sitiecito | 3 | 2 | 6 | 9 | 16 | 63 |
| Isabela de Sagua | 11 | 16 | 49 | 24 | 0 | 0 |
| La Rosita 1 | 0 | 0 | 0 | 0 | 50 | 50 |
| Nueva Isabela | 26 | 32 | 40 | 2 | 0 | 0 |
| Dos Amigos | 0 | 0 | 0 | 0 | 100 | 0 |
| Playa Uvero | 0 | 0 | 0 | 64 | 36 | 0 |
| Playa Piñon | 0 | 0 | 0 | 81 | 19 | 0 |
| Caharatas 2 | 100 | 0 | 0 | 0 | 0 | 0 |
| Total affected area | 9 | 10 | 27 | 18 | 30 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|
| Alacranes | Cuba | 21 | 350 | O | 350 | 604.6 | 10.8 | 3.5 | 35,726 | This study |
| Ain Kouachia | Marruecos | 22 | 11 | O | 88 | 3.2 | 20.3 | 8.0 | 9238 | [20] |
| Yabous | Argelia | 43 | 8 | O | 26 | 23.9 | 14.1 | 38.6 | 8767 | [43] |
| Kibimba | Uganda | 4.5 | 15 | O | 43 | N/A | 6.0 | 10.0 | 1935 | [36] |
| Xe Namnoy | Laos | 34 | 1050 | O | N/A | 46.0 | 9.5 | 12.0 | 8500 | [41] |
| Chengbi River | China | 70 | 1121 | O | 125 | N/A | N/A | N/A | 335,693 | [33] |
| Wadi Al-Arab | Jordania | 84 | 20 | O | 102 | N/A | 37.6 | 8.9 | 10,800 | [44] |
| Wala | Jordania | 54 | 25 | O | 133 | N/A | 43.0 | 17.1 | 12 | [45] |
| Grand Ethiopian Renaissance (GERD) | Etiopía | 145 | 74,000 | O | 200 | N/A | 50.0 | 7.0 | 325,928 | [46] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvajal González, V.M.; Castillo García, C.L.; González-Rodriguez, L.; Silva, L.; Jiménez, J. Assessing the Hazard of Flooding from Breaching of the Alacranes Dam in Villa Clara, Cuba. Sustainability 2025, 17, 6864. https://doi.org/10.3390/su17156864
Carvajal González VM, Castillo García CL, González-Rodriguez L, Silva L, Jiménez J. Assessing the Hazard of Flooding from Breaching of the Alacranes Dam in Villa Clara, Cuba. Sustainability. 2025; 17(15):6864. https://doi.org/10.3390/su17156864
Chicago/Turabian StyleCarvajal González, Victor Manuel, Carlos Lázaro Castillo García, Lisdelys González-Rodriguez, Luciana Silva, and Jorge Jiménez. 2025. "Assessing the Hazard of Flooding from Breaching of the Alacranes Dam in Villa Clara, Cuba" Sustainability 17, no. 15: 6864. https://doi.org/10.3390/su17156864
APA StyleCarvajal González, V. M., Castillo García, C. L., González-Rodriguez, L., Silva, L., & Jiménez, J. (2025). Assessing the Hazard of Flooding from Breaching of the Alacranes Dam in Villa Clara, Cuba. Sustainability, 17(15), 6864. https://doi.org/10.3390/su17156864








